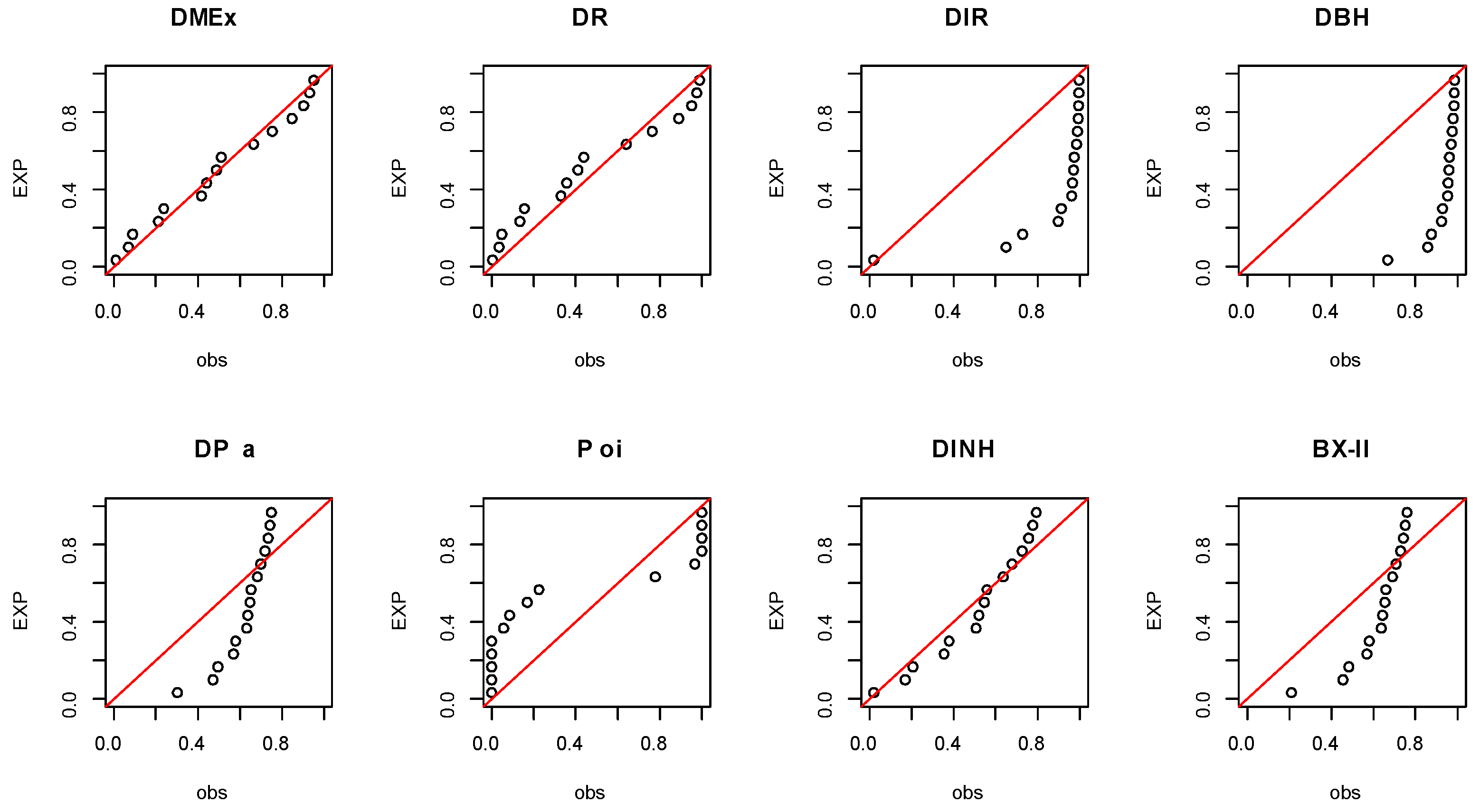Author Contributions
Conceptualization, M.S.E.; data curation, M.E.-M. and H.S.S.; formal analysis, M.S.E. and B.A.; investigation, M.E.-M. and H.S.S.; methodology, M.E.-M. and M.S.E.; resources, H.S.S. and B.A.; software, M.E.-M., H.S.S. and M.S.E.; validation, M.S.E. and B.A.; writing— review and editing, M.S.E. All authors have read and agreed to the published version of the manuscript.
Figure 1.
PMF visualization plots for the DMEx model.
Figure 1.
PMF visualization plots for the DMEx model.
Figure 2.
HRF and RHRF visualization plots for the DMEx model.
Figure 2.
HRF and RHRF visualization plots for the DMEx model.
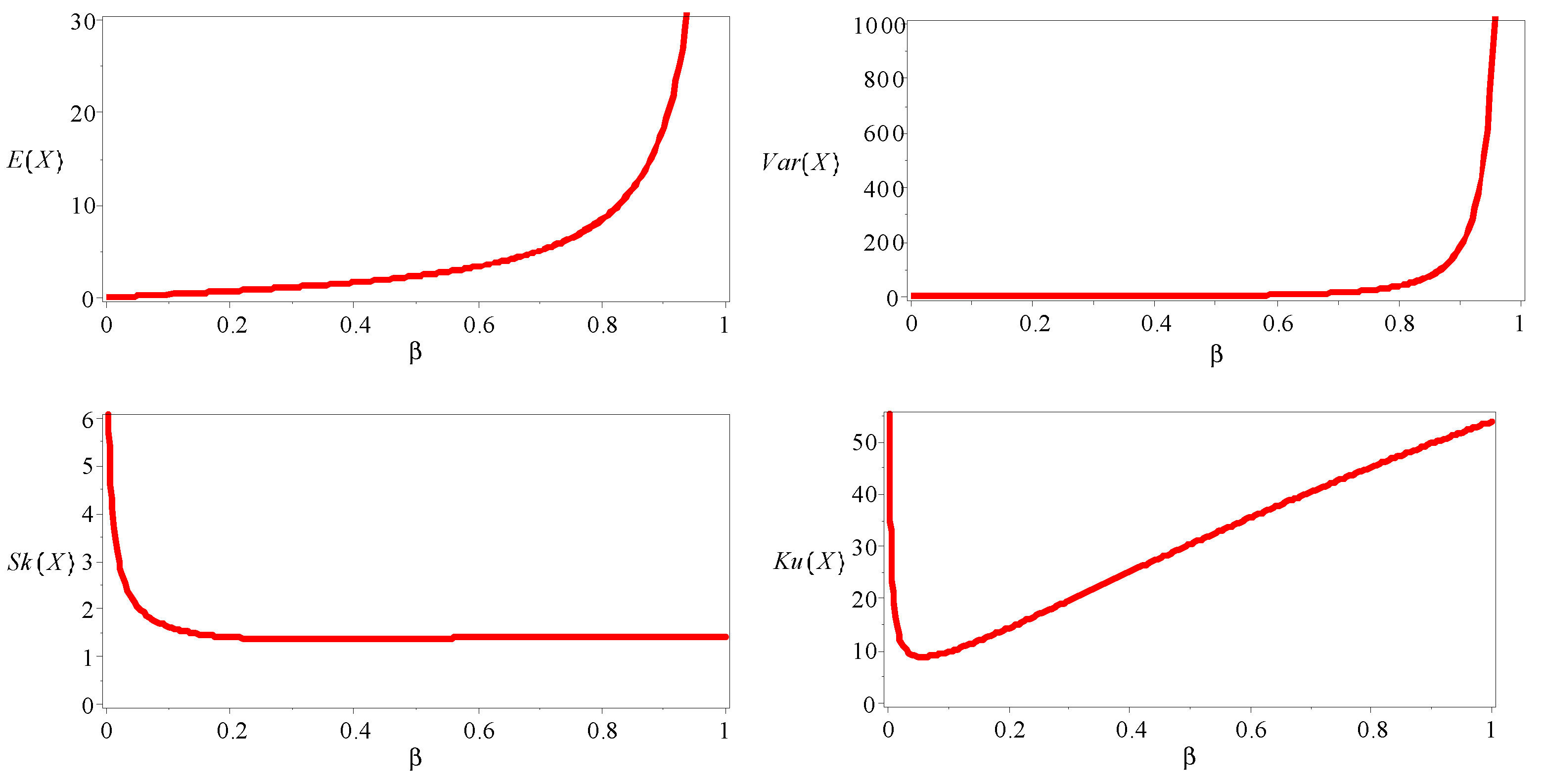
Figure 3.
The plots of descriptive measures of the DMEx distribution.
Figure 3.
The plots of descriptive measures of the DMEx distribution.
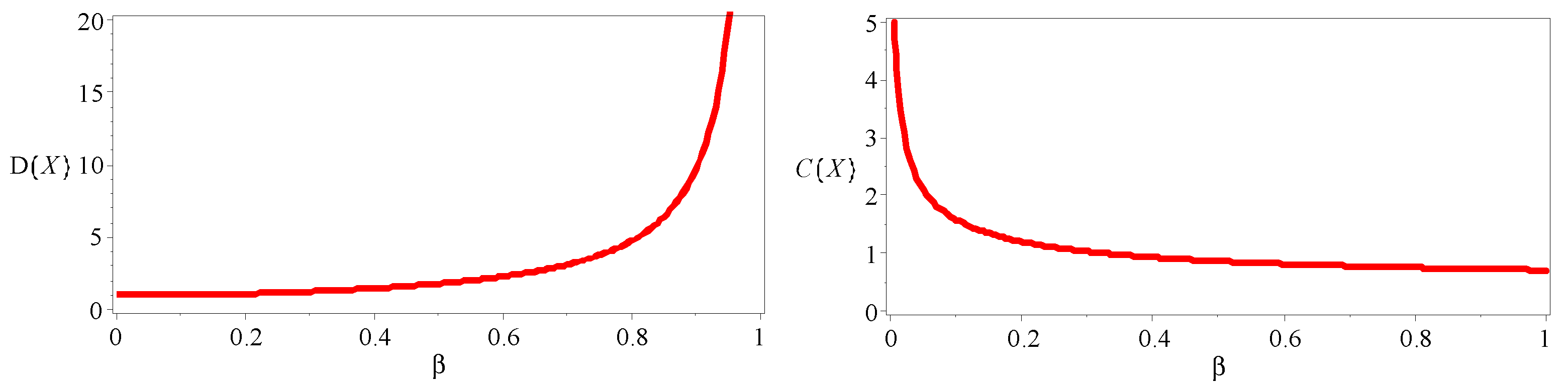
Figure 4.
Plots of the and statistics of the DMEx distribution.
Figure 4.
Plots of the and statistics of the DMEx distribution.
Figure 5.
Simulation for .
Figure 5.
Simulation for .
Figure 6.
Simulation for .
Figure 6.
Simulation for .
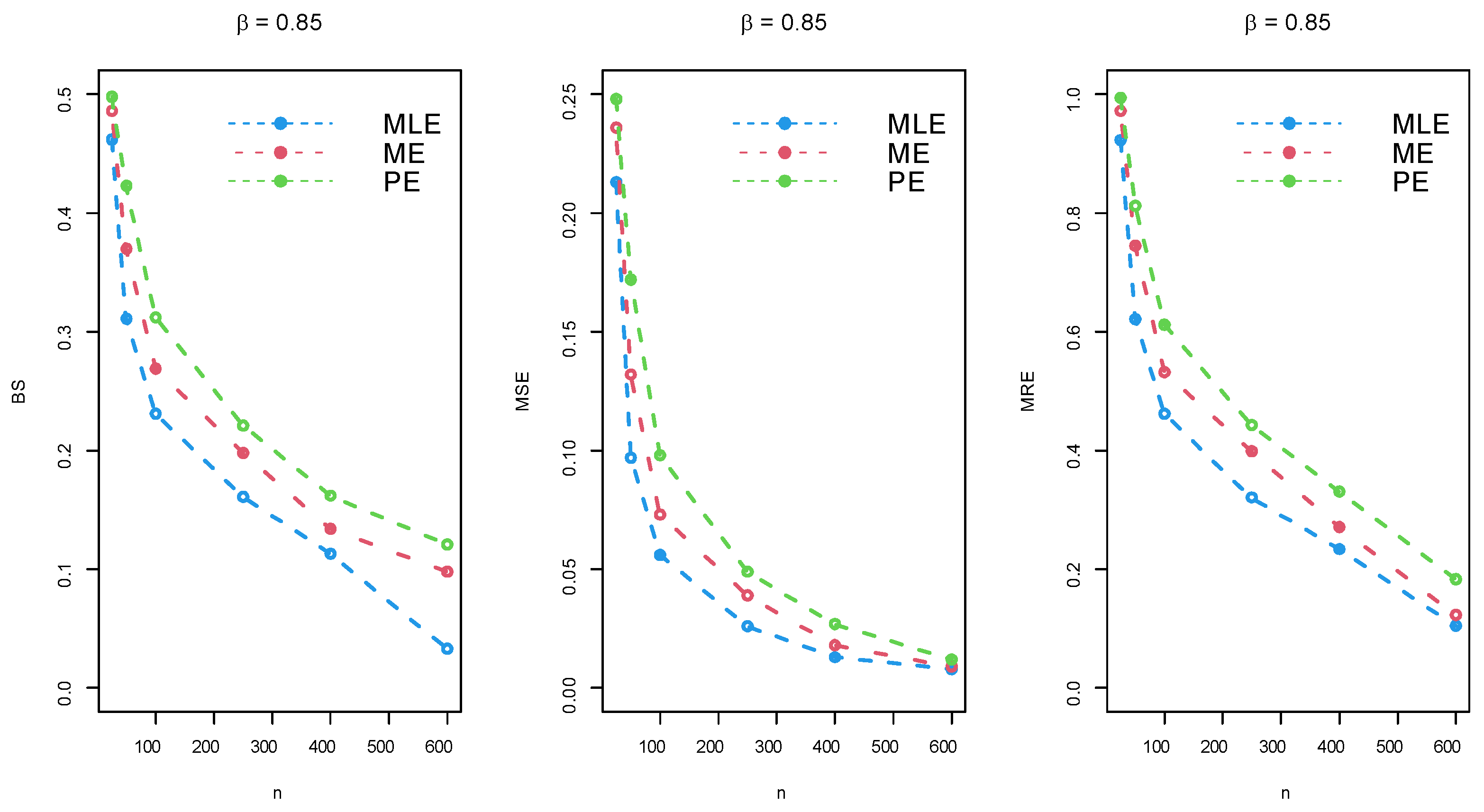
Figure 7.
Simulation .
Figure 7.
Simulation .
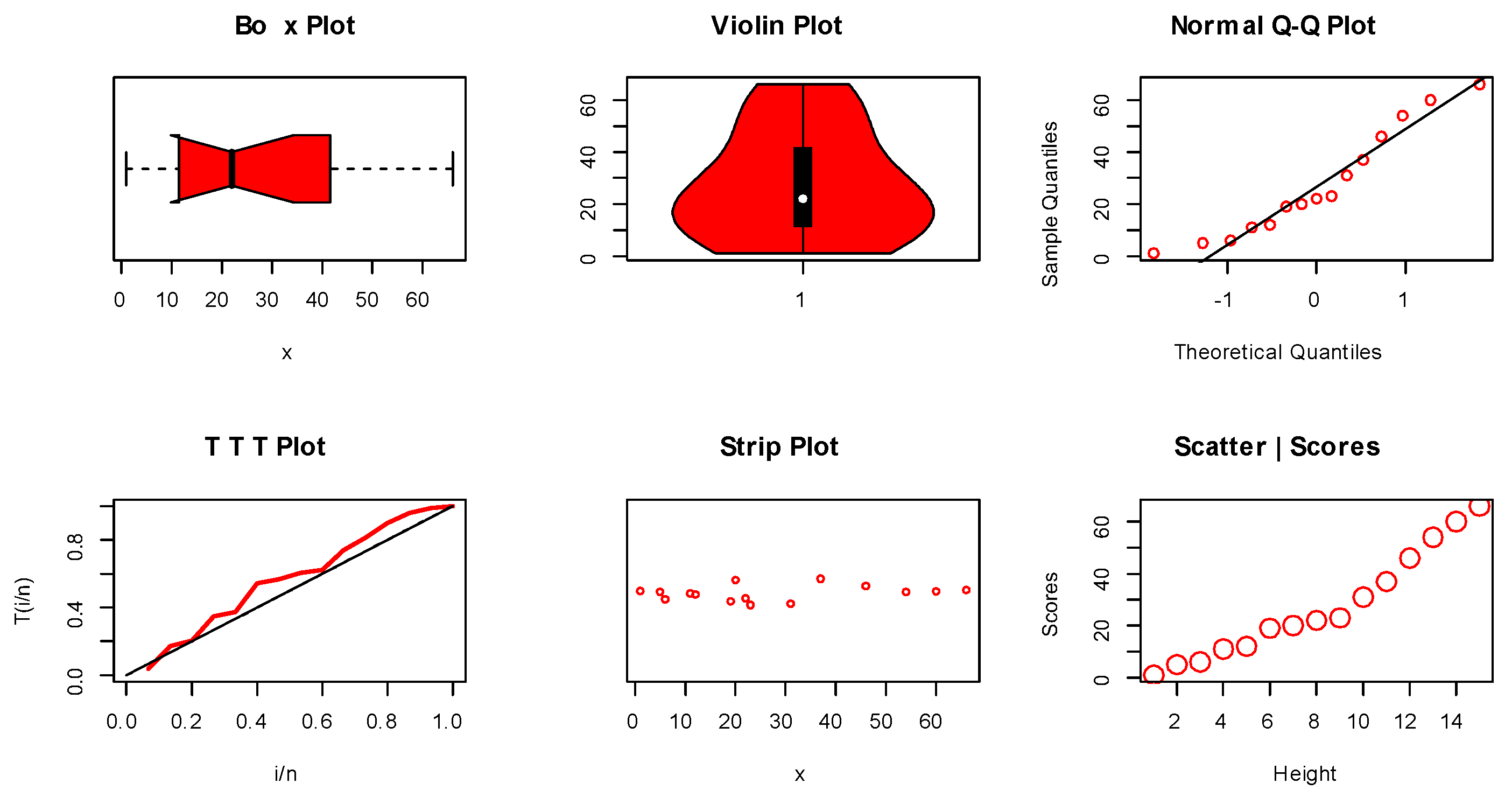
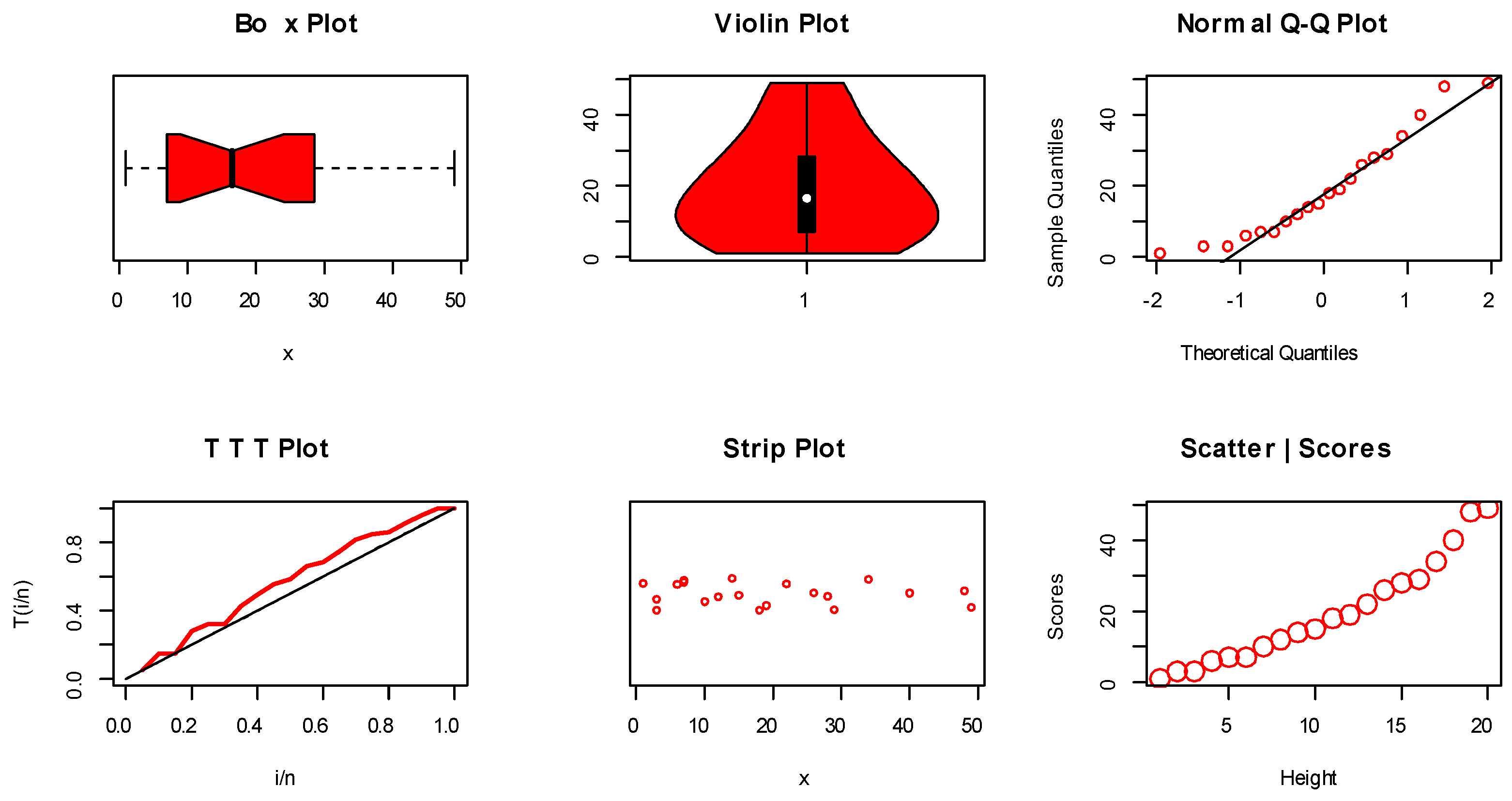
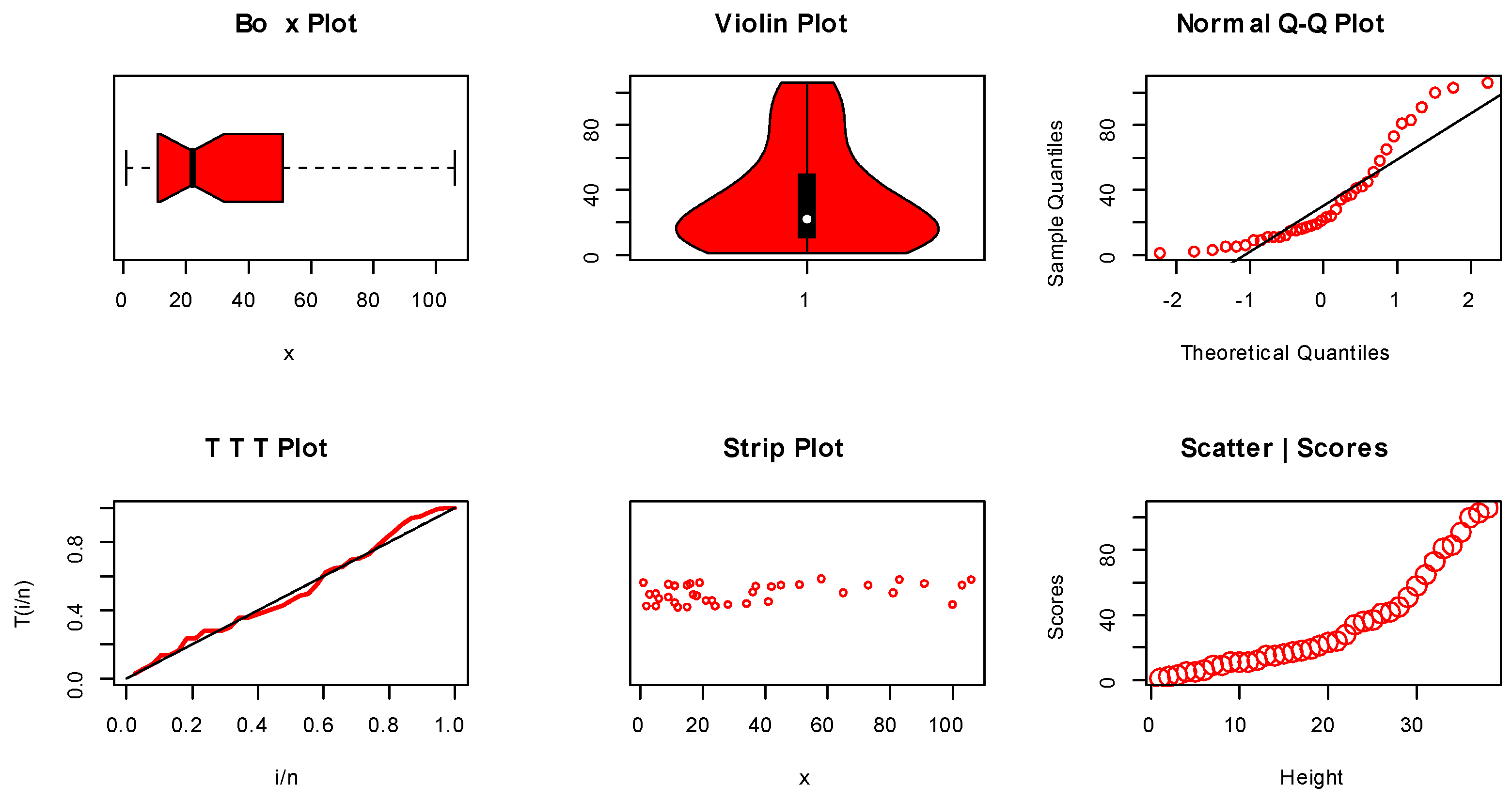
Figure 8.
Non-parametric visualization plots for EC data.
Figure 8.
Non-parametric visualization plots for EC data.
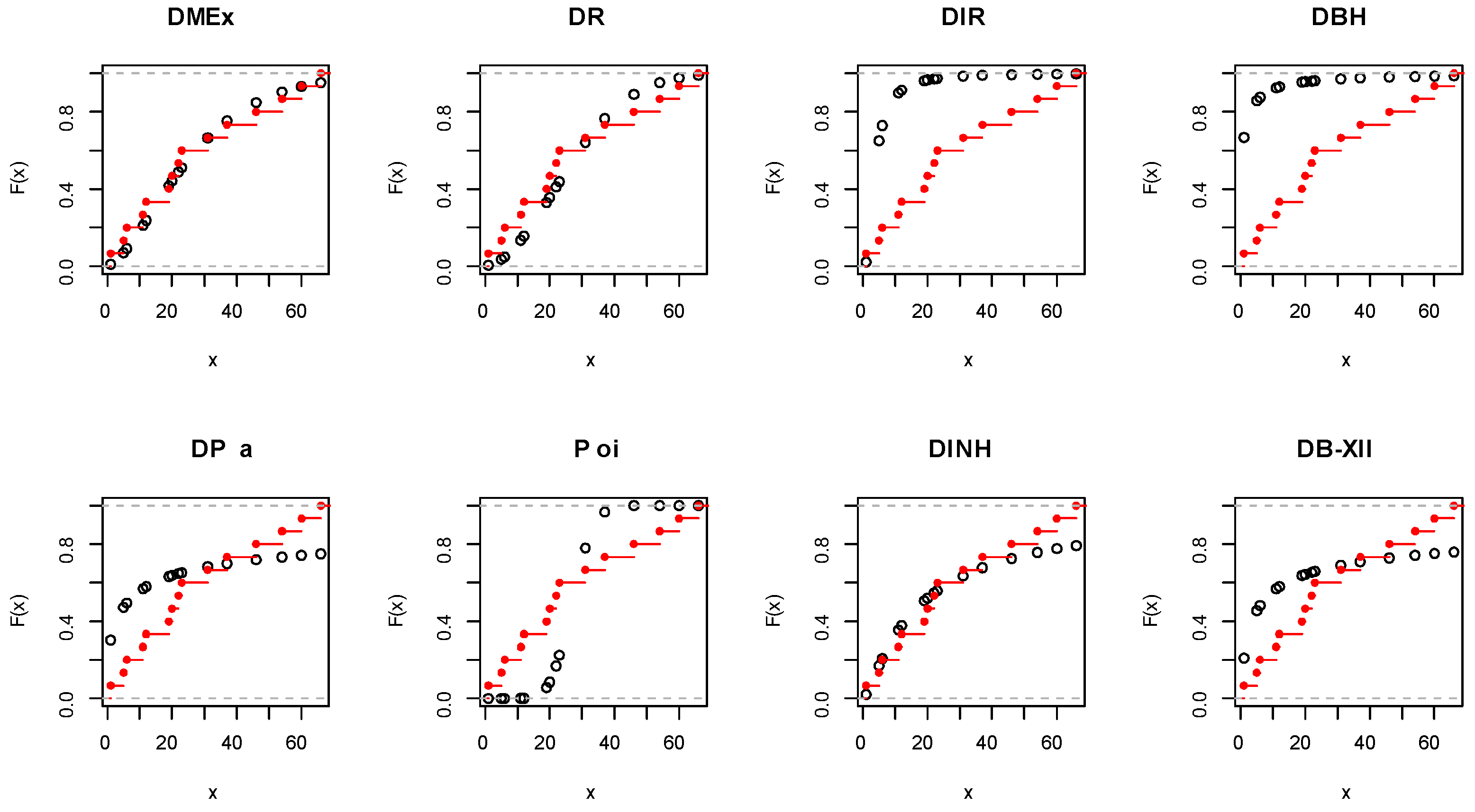
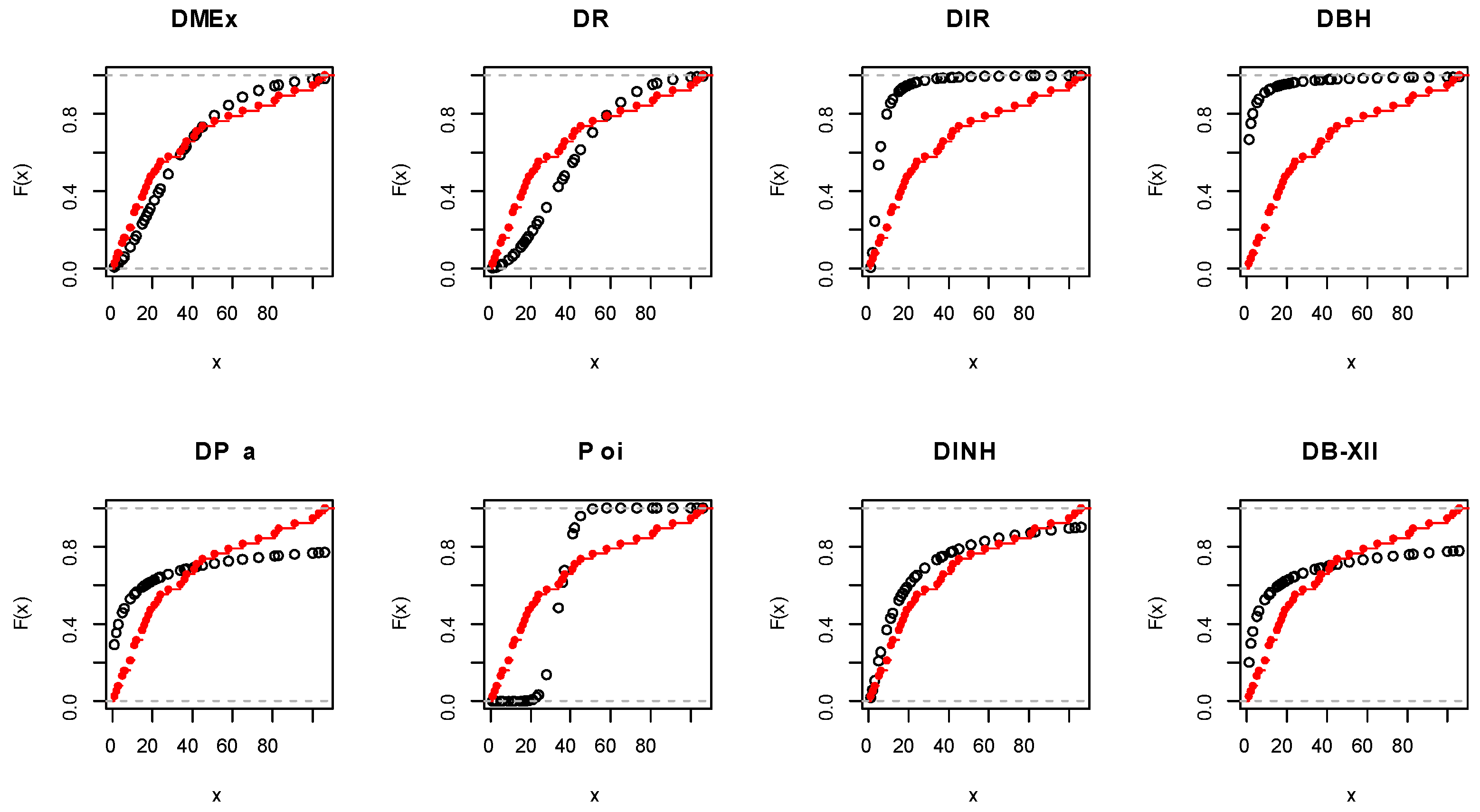
Figure 9.
Empirical CDF visualization plots for EC data.
Figure 9.
Empirical CDF visualization plots for EC data.
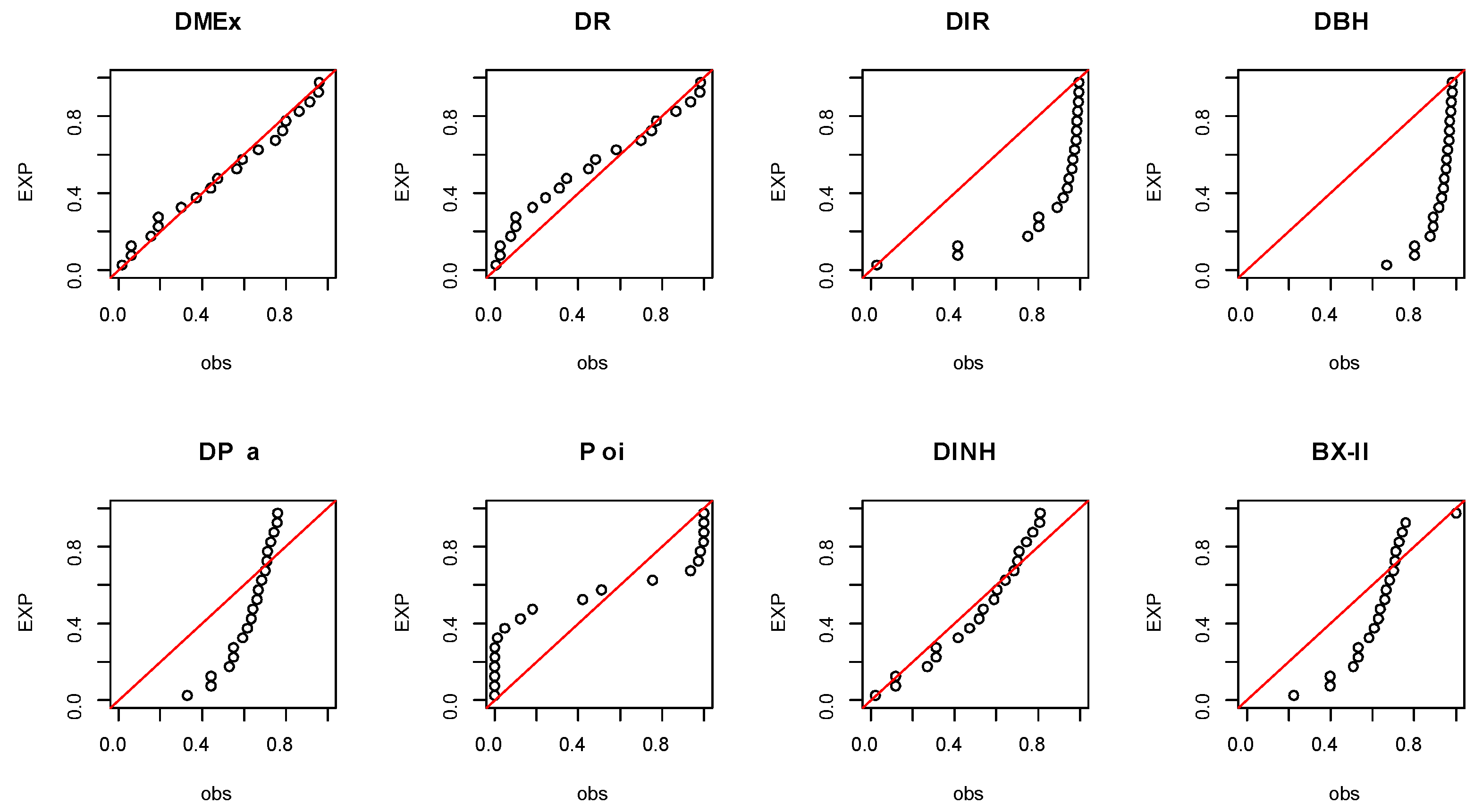
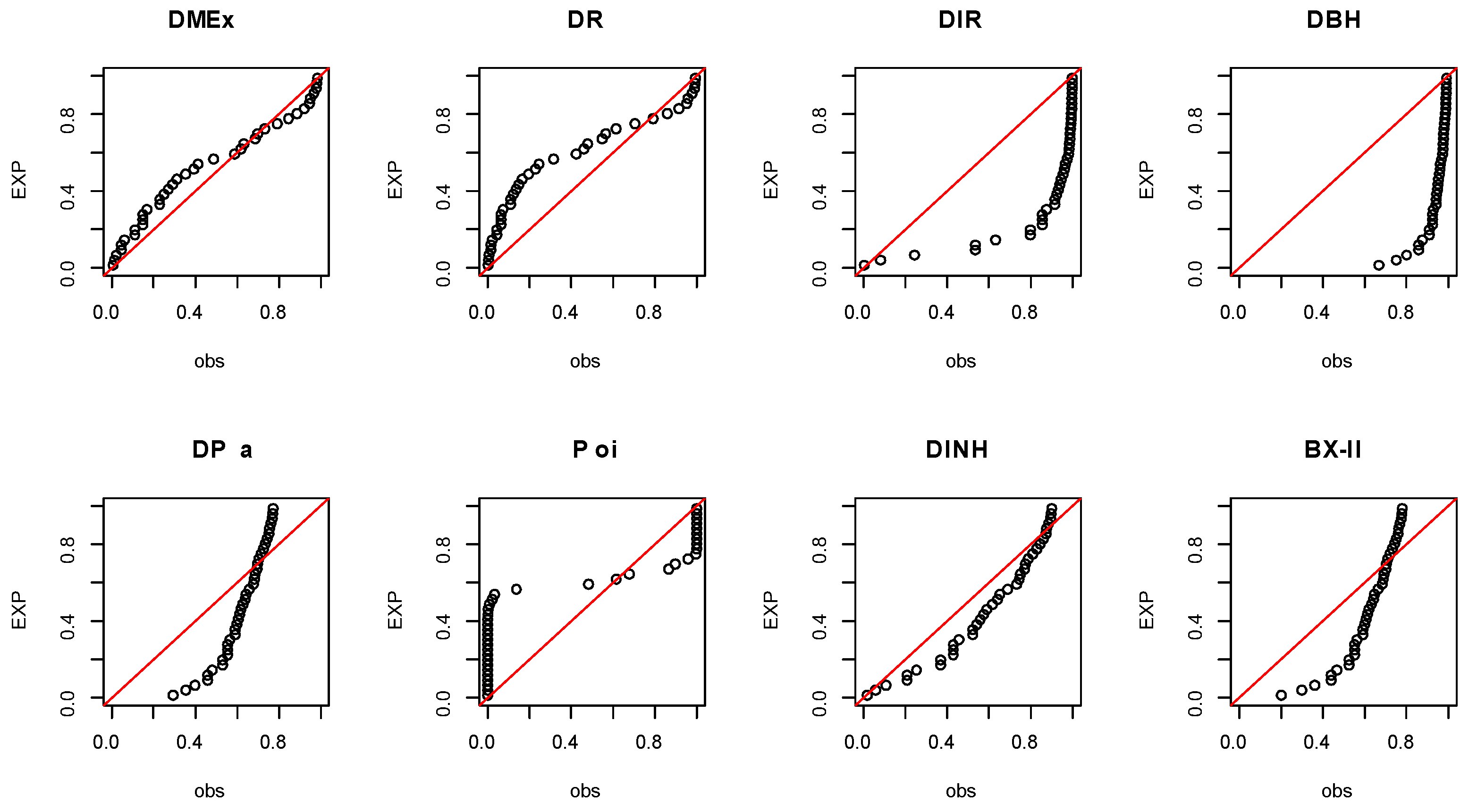
Figure 10.
P-P visualization plots for EC data.
Figure 10.
P-P visualization plots for EC data.
Figure 11.
Non-parametric visualization plots for LR data.
Figure 11.
Non-parametric visualization plots for LR data.
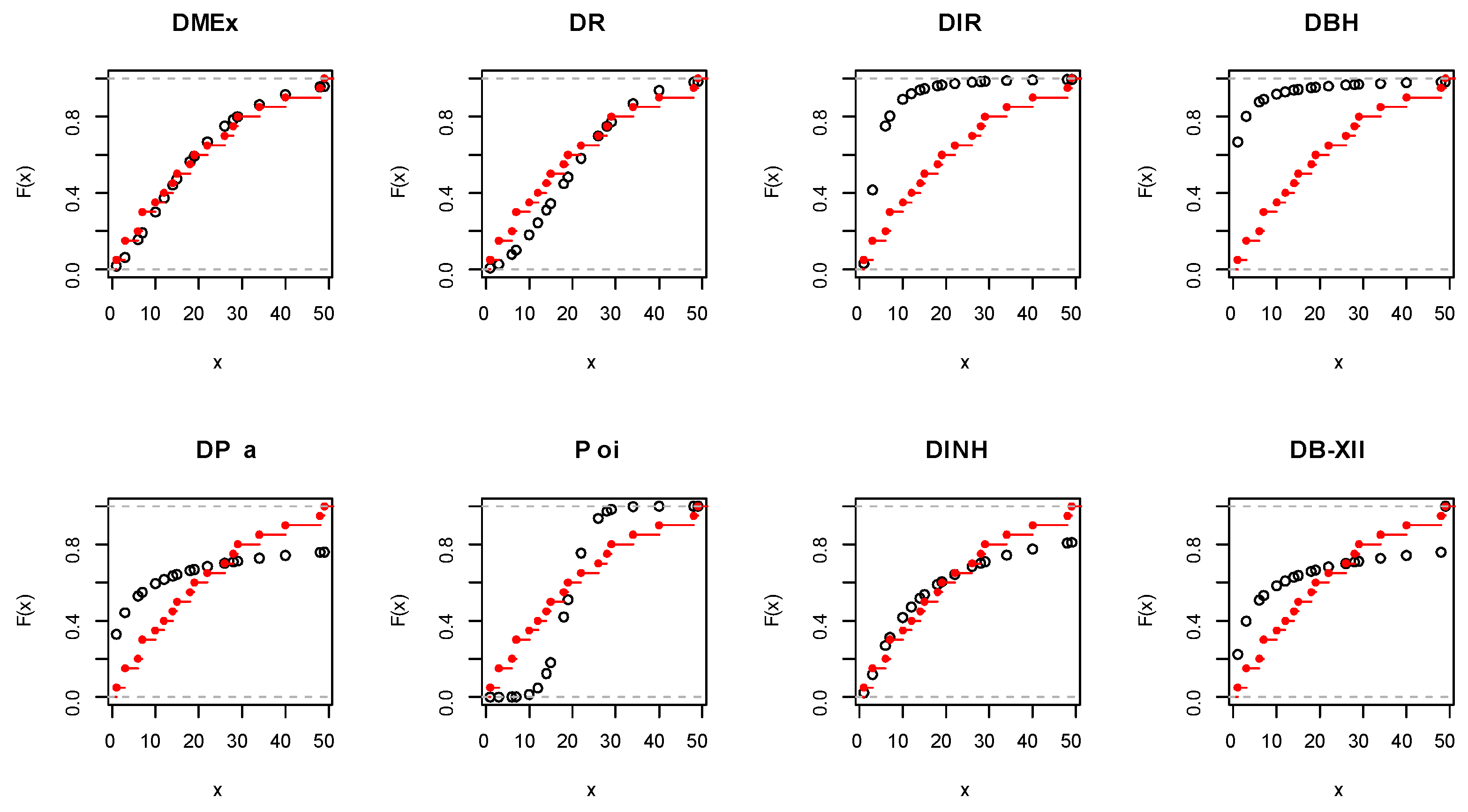
Figure 12.
Empirical CDF visualization plots for LR data.
Figure 12.
Empirical CDF visualization plots for LR data.
Figure 13.
P-P visualization plots for LR data.
Figure 13.
P-P visualization plots for LR data.
Figure 14.
Non-parametric visualization plots for COV-P data.
Figure 14.
Non-parametric visualization plots for COV-P data.
Figure 15.
Empirical CDF visualization plots for COV-P data.
Figure 15.
Empirical CDF visualization plots for COV-P data.
Figure 16.
P-P visualization plots for COV-P data.
Figure 16.
P-P visualization plots for COV-P data.
Figure 17.
The profiles plots of L for data sets.
Figure 17.
The profiles plots of L for data sets.
Figure 18.
Empirical CDF visualization plots for different estimation methods.
Figure 18.
Empirical CDF visualization plots for different estimation methods.
Table 1.
Some CS of the DMEx distribution.
Table 1.
Some CS of the DMEx distribution.
| | | | | | | | | |
|---|
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
| | | | | | | | | |
Table 2.
The and statistics of the DMEx distribution.
Table 2.
The and statistics of the DMEx distribution.
| | | | | | | | | |
|---|
| | | | | | | | | |
| | | | | | | | | |
Table 3.
Simulation results for = 0.15.
Table 3.
Simulation results for = 0.15.
| n | Criteria | MLE | ME | PE |
|---|
| 25 | | | | |
| | MSE | | | |
| | MRE | | | |
| 50 | | | | |
| | MSE | | | |
| | MRE | | | |
| 100 | | | | |
| | MSE | | | |
| | MRE | | | |
| 250 | | | | |
| | MSE | | | |
| | MRE | | | |
| 400 | | | | |
| | MSE | | | |
| | MRE | | | |
| 600 | | | | |
| | MSE | | | |
| | MRE | | | |
Table 4.
Simulation results for = 0.35.
Table 4.
Simulation results for = 0.35.
| n | Criteria | MLE | ME | PE |
|---|
| 25 | | | | |
| | MSE | | | |
| | MRE | | | |
| 50 | | | | |
| | MSE | | | |
| | MRE | | | |
| 100 | | | | |
| | MSE | | | |
| | MRE | | | |
| 250 | | | | |
| | MSE | | | |
| | MRE | | | |
| 400 | | | | |
| | MSE | | | |
| | MRE | | | |
| 600 | | | | |
| | MSE | | | |
| | MRE | | | |
Table 5.
Simulation results for = 0.85.
Table 5.
Simulation results for = 0.85.
| n | Criteria | MLE | ME | PE |
|---|
| 25 | | | | |
| | MSE | | | |
| | MRE | | | |
| 50 | | | | |
| | MSE | | | |
| | MRE | | | |
| 100 | | | | |
| | MSE | | | |
| | MRE | | | |
| 250 | | | | |
| | MSE | | | |
| | MRE | | | |
| 400 | | | | |
| | MSE | | | |
| | MRE | | | |
| 600 | | | | |
| | MSE | | | |
| | MRE | | | |
Table 6.
The MLE, SE, and CI for EC data.
Table 6.
The MLE, SE, and CI for EC data.
| Model | | |
|---|
| MLE | SE | CI | MLE | SE | CI |
|---|
| DMEx | | | | − | − | − |
| DR | | | | − | − | − |
| DIR | | | | − | − | − |
| DBH | | | | − | − | − |
| DPa | | | | − | − | − |
| Poi | | | | − | − | − |
| DINH | | | | | | |
| DB-XII | | | | | | |
Table 7.
The GOF test for EC data.
Table 7.
The GOF test for EC data.
| Statistic | DMEx | DR | DIR | DBH | DPa | Poi | DINH | DB-XII |
|---|
| | | | | | | | |
| AIC | | | | | | | | |
| CAIC | | | | | | | | |
| BIC | | | | | | | | |
| HQIC | | | | | | | | |
| KS | | | | | | | | |
| p-value | | | < | < | | | | |
Table 8.
Different estimators for EC data.
Table 8.
Different estimators for EC data.
| Technique | | KS | p-Value |
|---|
| ME | | | |
| PE | | | |
Table 9.
The EDS for EC data.
Table 9.
The EDS for EC data.
| Approach | | | | | |
|---|
| MLE | | | | | |
| PE | | | | | |
| ME | | | | | |
Table 10.
The MLE, SE, and CI for LR data.
Table 10.
The MLE, SE, and CI for LR data.
| Model | | |
|---|
| MLE | SE | CI | MLE | SE | CI |
|---|
| DMEx | | | | − | − | − |
| DR | | | | − | − | − |
| DIR | | − | − | − | − | − |
| DBH | | | | − | − | − |
| DPa | | | | − | − | − |
| Poi | | | | − | − | − |
| DINH | | | | | | |
| DB-XII | | | | | | |
Table 11.
The GOF test for LR data.
Table 11.
The GOF test for LR data.
| Statistic | DMEx | DR | DIR | DBH | DPa | Poi | DINH | DB-XII |
|---|
| | | | | | | | |
| AIC | | | | | | | | |
| CAIC | | | | | | | | |
| BIC | | | | | | | | |
| HQIC | | | | | | | | |
| KS | | | − | | | | | |
| p-value | | | − | <0.001 | | | | |
Table 12.
Different estimators for LR data.
Table 12.
Different estimators for LR data.
| Technique | | KS | p-Value |
|---|
| ME | | | |
| PE | | | |
Table 13.
The EDS for LR data.
Table 13.
The EDS for LR data.
| Approach | | | | | |
|---|
| MLE | | | | | |
| PE | | | | | |
| ME | | | | | |
Table 14.
The MLE, SE, and CI for COV-P data.
Table 14.
The MLE, SE, and CI for COV-P data.
| Model | | |
|---|
| MLE | SE | CI | MLE | SE | CI |
|---|
| DMEx | | | | − | − | − |
| DR | | | | − | − | − |
| DIR | | − | − | − | − | − |
| DBH | | | | − | − | − |
| DPa | | | | − | − | − |
| Poi | | | | − | − | − |
| DINH | | | | | | |
| DB-XII | | | | | | |
Table 15.
The GOF test for COV-P data.
Table 15.
The GOF test for COV-P data.
| Statistic | DMEx | DR | DIR | DBH | DPa | Poi | DINH | DB-XII |
|---|
| | | | | | | | |
| AIC | | | | | | | | |
| CAIC | | | | | | | | |
| BIC | | | | | | | | |
| HQIC | | | | | | | | |
| KS | | | | | | | | |
| p-value | | | <0.001 | <0.001 | <0.001 | <0.001 | 0.245 | <0.001 |
Table 16.
Different estimators for COV-P data.
Table 16.
Different estimators for COV-P data.
| Technique | | KS | p-Value |
|---|
| ME | | | |
| PE | | | |
Table 17.
The EDS for COV-P data.
Table 17.
The EDS for COV-P data.
| Approach | | | | | |
|---|
| MLE | | | | | |
| PE | | | | | |
| ME | | | | | |