Optimization of the Heap Leaching Process through Changes in Modes of Operation and Discrete Event Simulation
Abstract
1. Introducion:
1.1. Overview
1.2. Heap Leaching
2. Materials and Methods
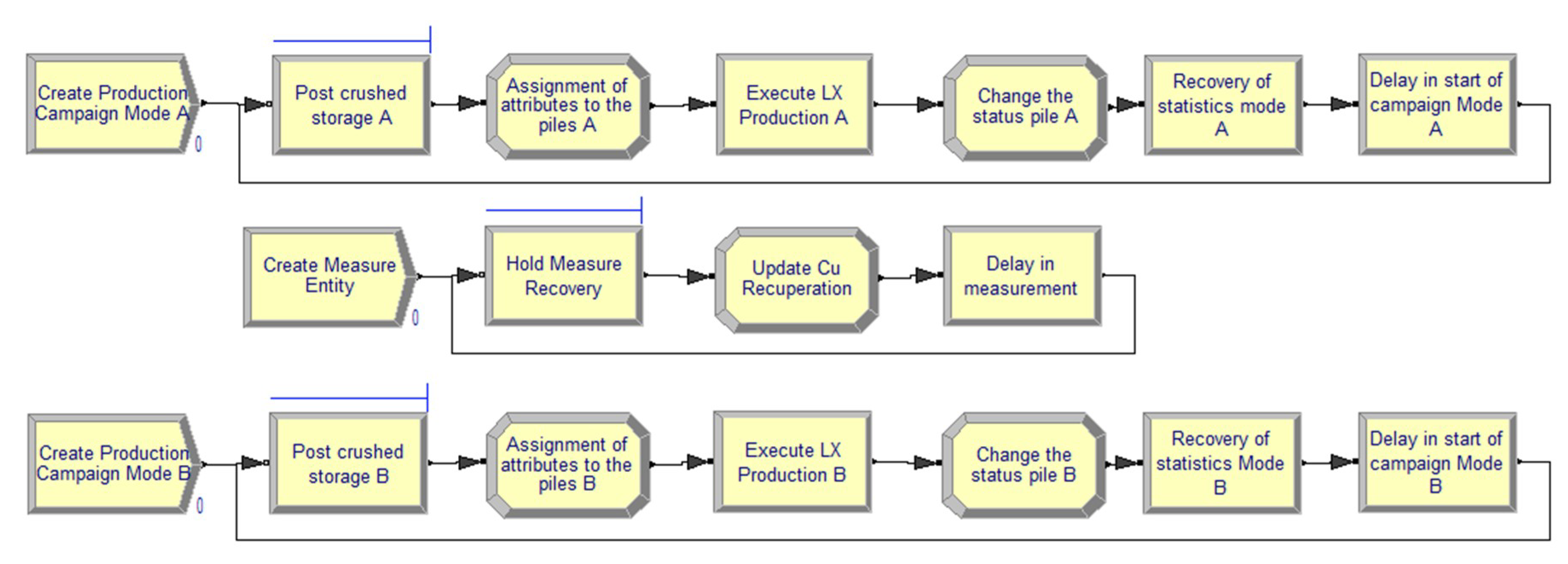
2.1. Discrete Event Simulation
2.2. Mathematical Modeling of Heap Leaching
2.3. Adjustment of the Analytical Model for the Recovery of Copper from Copper Oxides
2.4. Adjustment of Analytical Model for Copper Recovery from Secondary Copper Sulfides
2.5. Adjustment of Analytical Models for Copper Recovery from Secondary Copper Sulfide Ores Adding Chlorides
2.6. Modeling and Simulation of Heap Leaching Using a DES Framework
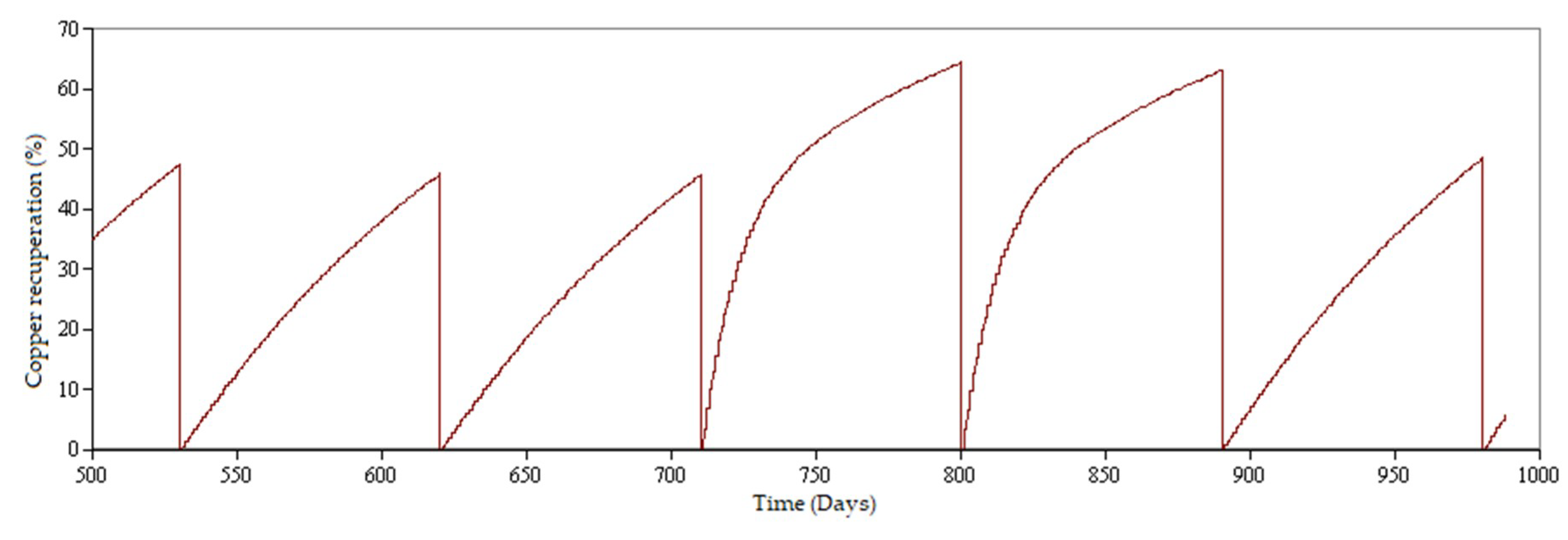
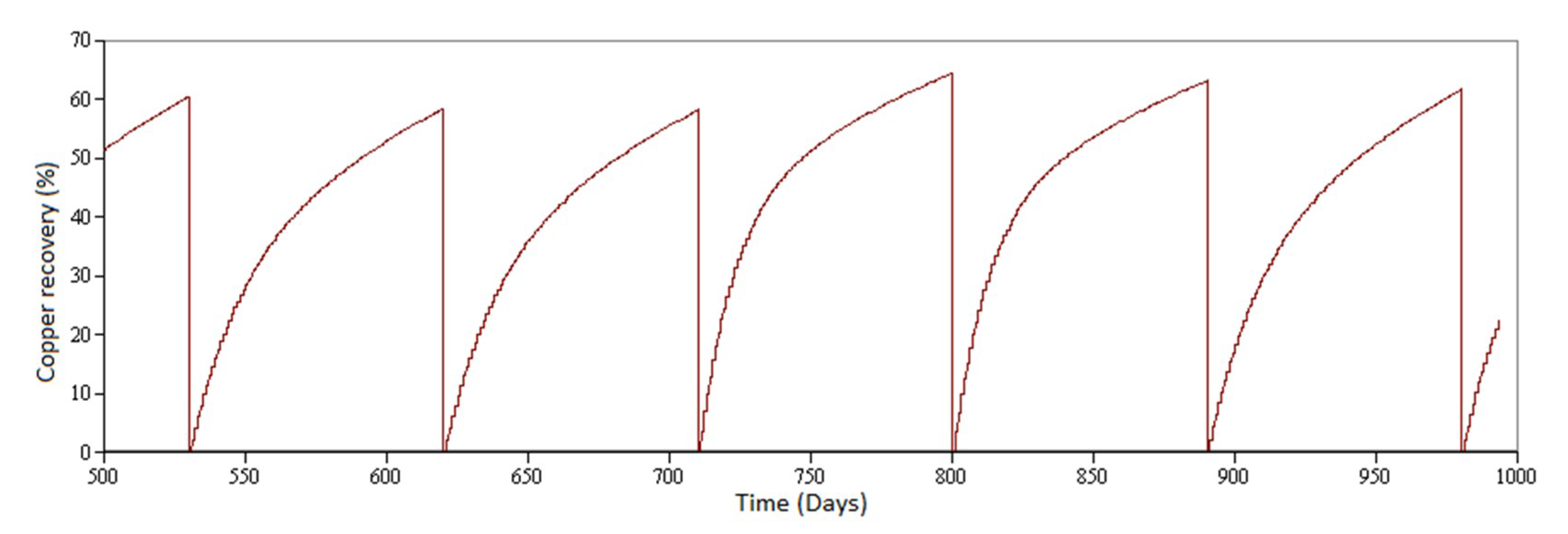
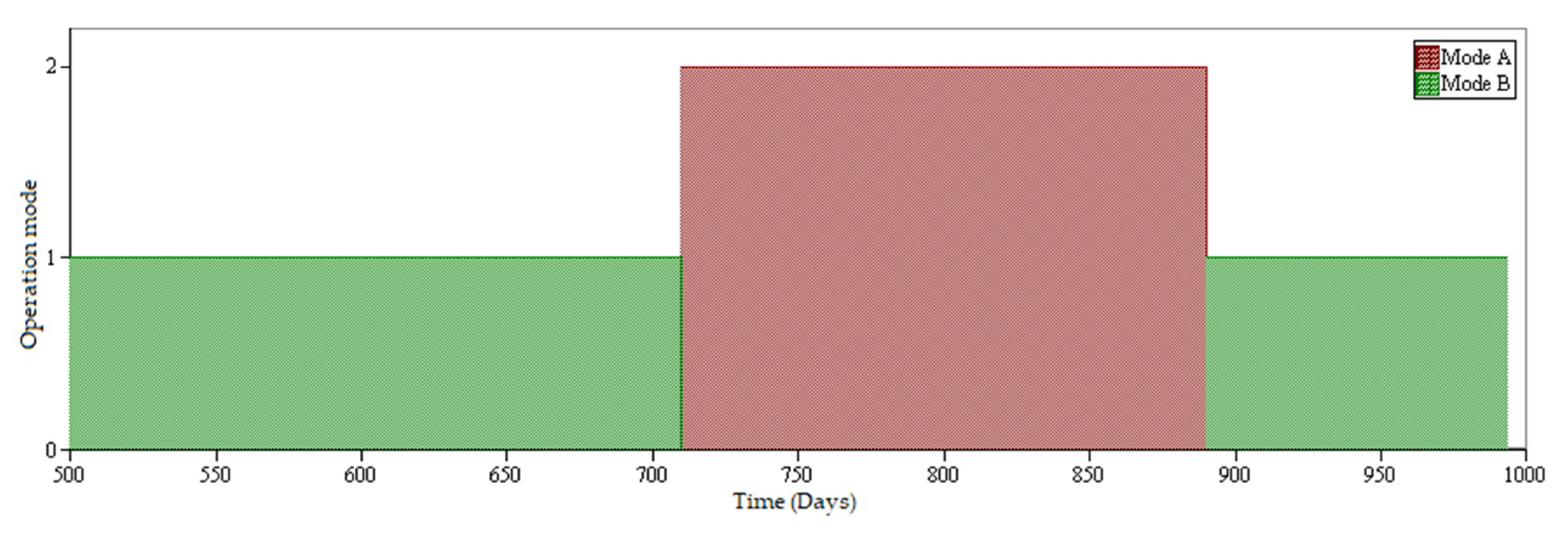
- Mode A: Leaching of copper oxides.
- Mode B: Leaching of copper sulfide minerals (secondary sulfides).
3. Discussion of Results
3.1. Simulated Scenarios
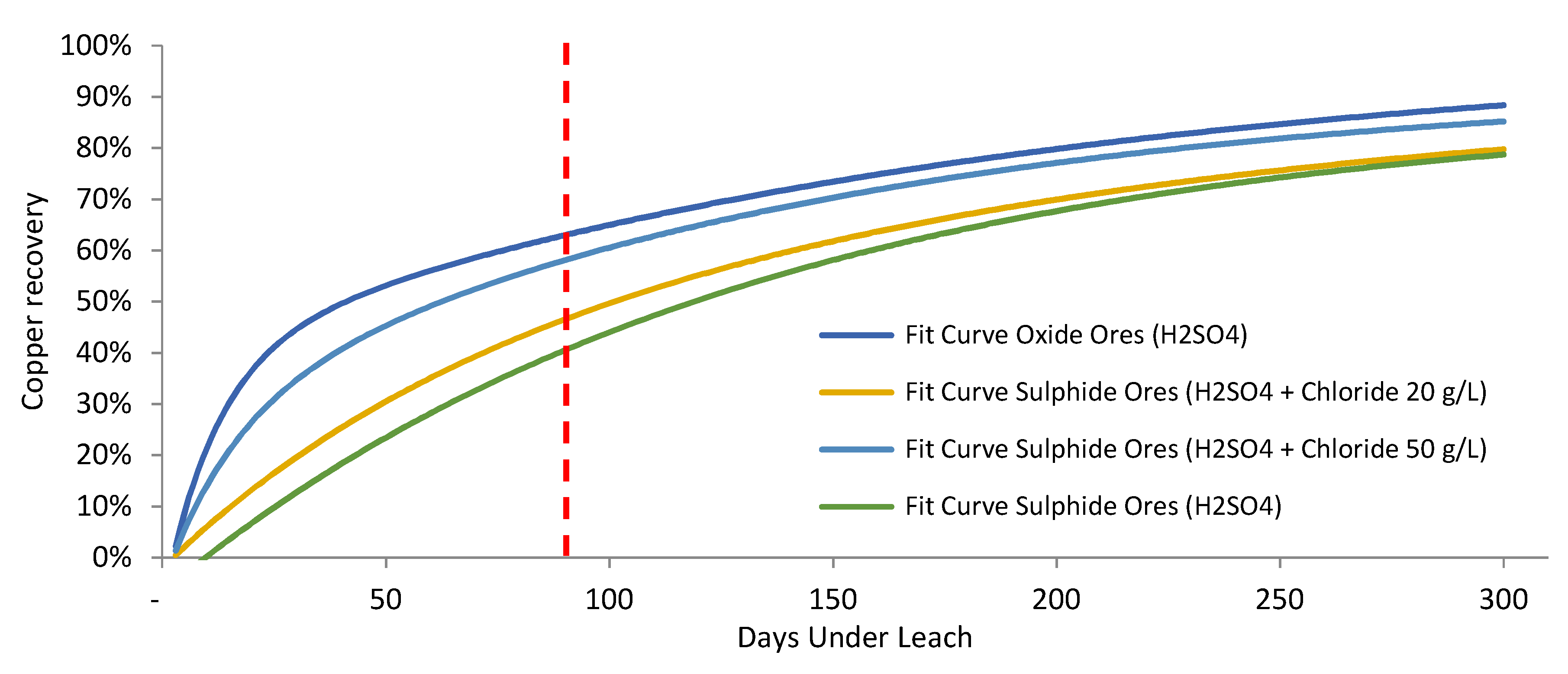
- Scenario 1 (standard operation): Leaching of copper oxides and secondary copper sulfides adding sulfuric acid only. The leaching of secondary sulfides with sulfuric acid slows down the process of extracting ore from the rock, increasing the time required until the marginal extraction of ore is negligible [12,34].
3.2. Comparison of Samples
4. Conclusions
4.1. Conclusions
4.2. Future Work
- Include other modes of operation and analytical models that incorporate more operational variables to the process, together with parameters that have a significant impact on recovery.
- Study the impact on an industrial scale of operating the leaching process with alternating modes of operation, including the analysis operating and capital costs.
Author Contributions
Funding
Conflicts of Interest
References
- Navarra, A.; Alvarez, M.; Rojas, K.; Menzies, A.; Pax, R.; Waters, K. Concentrator operational modes in response to geological variation. Miner. Eng. 2019, 134, 356–364. [Google Scholar] [CrossRef]
- Hustrulid, W.; Kuchta, M.; Martin, R. Open Pit Mine Planning and Design; CRC Press: Boca Raton, FL, USA, 2013; ISBN 9781466575127. [Google Scholar]
- Dimitrakopoulos, R. Strategic mine planning under uncertainty. J. Min. Sci. 2011, 47, 138–150. [Google Scholar] [CrossRef]
- Rahmanpour, M.; Osanloo, M. Determination of value at risk for long-term production planning in open pit mines in the presence of price uncertainty. J. S. Afr. Inst. Min. Metall. 2016, 116, 8–11. [Google Scholar] [CrossRef]
- Upadhyay, S.P.; Askari-Nasab, H. Simulation and optimization approach for uncertainty-based short-term planning in open pit mines. Int. J. Min. Sci. Technol. 2018, 28, 153–166. [Google Scholar] [CrossRef]
- Drebenstedt, C.; Singhal, R. Mine Planning and Equipment Selection; Brookfield: Rotterdam, The Netherlands, 2014; ISBN 978-3-319-02677-0. [Google Scholar]
- Harris, G.B.; White, C.W.; Demopoulos, G.P.; Ballantyne, B. Recovery of copper fromamassive polymetallic sulphide by high concentration chloride leaching. Can. Metall. Q. 2008, 47, 347–356. [Google Scholar] [CrossRef]
- Robertson, S.W.; Van Staden, P.J.; Seyedbagheri, A. Advances in high-temperature heap leaching of refractory copper sulphide ores. J. S. Afr. Inst. Min. Metall. 2012, 112, 1045–1050. [Google Scholar]
- Petersen, J. Heap leaching as a key technology for recovery of values from low-grade ores—A brief overview. Hydrometallurgy 2016, 165, 206–212. [Google Scholar] [CrossRef]
- COCHILCO. Caracterización de los Costos de la Gran Minería del Cobre; COCHILCO: Santiago, Chile, 2015. [Google Scholar]
- Lu, J.; Dreisinger, D.; West-Sells, P. Acid curing and agglomeration for heap leaching. Hydrometallurgy 2017, 167, 30–35. [Google Scholar] [CrossRef]
- Schlesinger, M.; King, M.; Sole, K.; Davenport, W. Extractive Metallurgy of Copper, 5th ed.; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 9780080967899. [Google Scholar]
- Liu, H.; Xia, J.; Nie, Z.; Ma, C.; Zheng, L.; Hong, C.; Zhao, Y.; Wen, W. Bioleaching of chalcopyrite by Acidianus manzaensis under different constant pH. Miner. Eng. 2016, 98, 80–89. [Google Scholar] [CrossRef]
- Ruan, R.; Zou, G.; Zhong, S.; Wu, Z.; Chan, B.; Wang, D. Why Zijinshan copper bioheapleaching plant works efficiently at low microbial activity-Study on leaching kinetics of copper sulfides and its implications. Miner. Eng. 2013, 48, 36–43. [Google Scholar] [CrossRef]
- Lee, J.; Acar, S.; Doerr, D.L.; Brierley, J.A. Comparative bioleaching and mineralogy of composited sulfide ores containing enargite, covellite and chalcocite by mesophilic and thermophilic microorganisms. Hydrometallurgy 2011, 105, 213–221. [Google Scholar] [CrossRef]
- Zhang, R.; Sun, C.; Kou, J.; Zhao, H.; Wei, D.; Xing, Y. Enhancing the leaching of chalcopyrite using acidithiobacillus ferrooxidans under the induction of surfactant Triton X-100. Minerals 2018, 9, 11. [Google Scholar] [CrossRef]
- Ma, L.; Wang, X.; Liu, X.; Wang, S.; Wang, H. Intensified bioleaching of chalcopyrite by communities with enriched ferrous or sulfur oxidizers. Bioresour. Technol. 2018, 268, 415–423. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Wu, J.; Liu, X.; Tan, L.; Wang, X. The detoxification potential of ferric ions for bioleaching of the chalcopyrite associated with fluoride-bearing gangue mineral. Appl. Microbiol. Biotechnol. 2019, 103, 2403–2412. [Google Scholar] [CrossRef] [PubMed]
- CESCO. La Minería Como Plataforma Para el Desarrollo: Hacia Una Relación Integral y Sustentable de la Industria Minera en Chile; CESCO: Santiago, Chile, 2013. [Google Scholar]
- Beiza, L. Lixiviación de Mineral y Concentrado de Calcopirita en Medios Clorurados; Universidad Católica del Norte: Antofagasta, Chile, 2012. [Google Scholar]
- Devore, J. Probability & Statistics for Engineering and the Sciences, 8th ed.; Cengage Learning: Boston, MA, USA, 2010; ISBN 0-538-73352-7. [Google Scholar]
- Neeraj, R.R.; Nithin, R.P.; Niranjhan, P.; Sumesh, A.; Thenarasu, M. Modelling and simulation of discrete manufacturing industry. Mater. Today Proc. 2018, 5, 24971–24983. [Google Scholar] [CrossRef]
- Kelton, W.D. Simulation with Arena; McGraw-Hill Education: New York, NY, USA, 2015; ISBN 978-0-07-340131-7. [Google Scholar]
- Van Staden, P.J.; Kolesnikov, A.V.; Petersen, J. Comparative assessment of heap leach production data—1. A procedure for deriving the batch leach curve. Miner. Eng. 2017, 101, 47–57. [Google Scholar] [CrossRef]
- Ordóñez, J.; Condori, A.; Moreno, L.; Cisternas, L. Heap leaching of caliche ore. modeling of a multicomponent system with particle size distribution. Minerals 2017, 7, 180. [Google Scholar]
- Morrison, R.D.; Shi, F.; Whyte, R. Modelling of incremental rock breakage by impact—For use in DEM models. Miner. Eng. 2007, 20, 303–309. [Google Scholar] [CrossRef]
- Leiva, C.; Flores, V.; Salgado, F.; Poblete, D.; Acuña, C. Applying softcomputing for copper recovery in leaching process. Sci. Prog. 2017, 2017, 6. [Google Scholar] [CrossRef]
- Miki, H.; Nicol, M.; Velásquez-Yévenes, L. The kinetics of dissolution of synthetic covellite, chalcocite and digenite in dilute chloride solutions at ambient temperatures. Hydrometallurgy 2011, 105, 321–327. [Google Scholar] [CrossRef]
- Mellado, M.E.; Cisternas, L.A.; Gálvez, E.D. An analytical model approach to heap leaching. Hydrometallurgy 2009, 95, 33–38. [Google Scholar] [CrossRef]
- Mellado, M.E.; Gálvez, E.D.; Cisternas, L.A. Stochastic analysis of heap leaching process via analytical models. Miner. Eng. 2012, 33, 93–98. [Google Scholar] [CrossRef]
- Mellado, M.; Cisternas, L.; Lucay, F.; Gálvez, E.; Sepúlveda, F. A posteriori analysis of analytical models for heap leaching using uncertainty and global sensitivity analyses. Minerals 2018, 8, 44. [Google Scholar] [CrossRef]
- Dixon, D.G.; Hendrix, J.L. A mathematical model for heap leaching of one or more solid reactants from porous ore pellets. Metall. Trans. B 1993, 24, 1087–1102. [Google Scholar] [CrossRef]
- Dixon, D.G.; Hendrix, J.L. A general model for leaching of one or more solid reactants from porous ore particles. Metall. Trans. B 1993, 24, 157–169. [Google Scholar] [CrossRef]
- Helle, S.; Jerez, O.; Kelm, U.; Pincheira, M.; Varela, B. The influence of rock characteristics on acid leach extraction and re-extraction of Cu-oxide and sulfide minerals. Miner. Eng. 2010, 23, 45–50. [Google Scholar] [CrossRef]
- Jones, D.A.; Paul, A.J.P. Acid leaching behavior of sulfide and oxide minerals determined by electrochemical polarization measurements. Miner. Eng. 1995, 8, 511–521. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Lawson, F. The kinetics of leaching chalcocite in acidic oxygenated sulphate-chloride solutions. Hydrometallurgy 1991, 27, 249–268. [Google Scholar] [CrossRef]
- Ruiz, M.C.; Honores, S.; Padilla, R. Leaching kinetics of digenite concentrate in oxygenated chloride media at ambient pressure. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 1998, 29, 961–969. [Google Scholar] [CrossRef]
- Douglas, C. Montgomery: Design and Analysis of Experiments, 8th ed.; John Wiley & Sons: New York, NY, USA, 2012; ISBN 978-1-118-14692-7. [Google Scholar]
- Mathews, P.G. Design of Experiments with MINITAB; William, A., Ed.; ASQ Quality Press: Milwaukee, WI, USA, 2005; ISBN 0873896378. [Google Scholar]
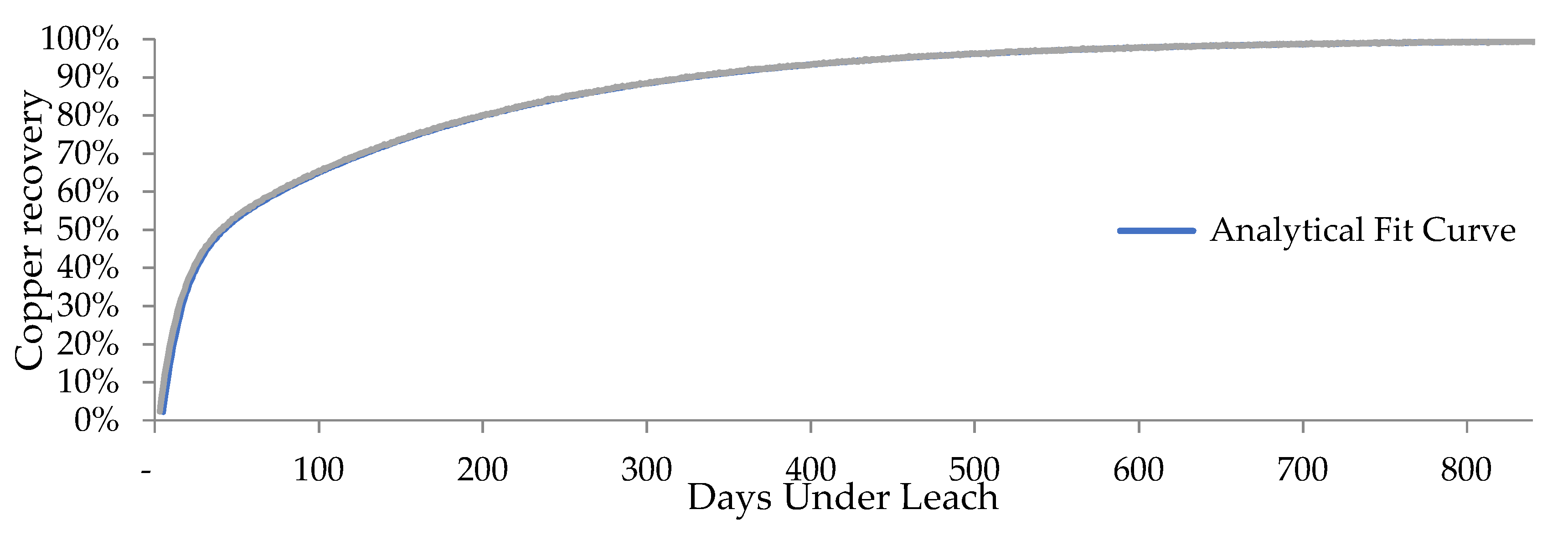
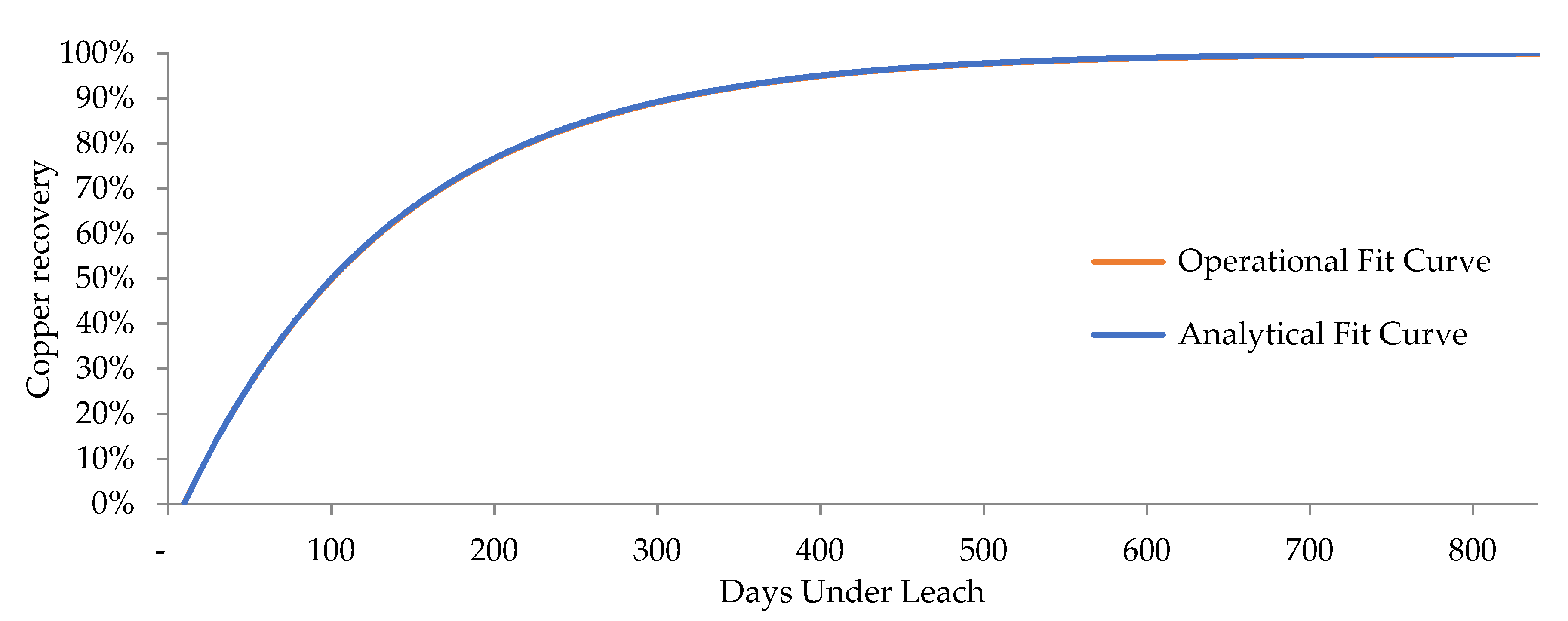




| Curve/Statistic | MAD | MSE | MAPE |
|---|---|---|---|
| R(t) (Oxides) | 1.008 × 10−2 | 1.222 × 10−4 | 1.28 × 10−2 |
| Curve/Statistic | MAD | MSE | MAPE |
|---|---|---|---|
| R(t) (Oxides) | 6.63 × 10−4 | 5.068 × 10−7 | 8.93 × 10−4 |
| Curve/Statistic | MAD | MSE | MAPE |
|---|---|---|---|
| R(t) (Chloride 20 g/L) | 1.68 × 10−4 | 4.59 × 10−7 | 5.40 × 10−4 |
| R(t) (Chloride 50 g/L) | 9.17 × 10−5 | 5.23 × 10−7 | 5.89 × 10−4 |
| Configuration | Recovery (%) |
|---|---|
| Leaching of secondary copper sulfides with sulfuric acid | 40.5 |
| Leaching of secondary copper sulfides adding chlorides (20 g/L) | 46.5 |
| Leaching of secondary copper sulfides adding chlorides (50 g/L) | 58.1 |
| Leaching of copper oxides with sulfuric acid | 64.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saldaña, M.; Toro, N.; Castillo, J.; Hernández, P.; Navarra, A. Optimization of the Heap Leaching Process through Changes in Modes of Operation and Discrete Event Simulation. Minerals 2019, 9, 421. https://doi.org/10.3390/min9070421
Saldaña M, Toro N, Castillo J, Hernández P, Navarra A. Optimization of the Heap Leaching Process through Changes in Modes of Operation and Discrete Event Simulation. Minerals. 2019; 9(7):421. https://doi.org/10.3390/min9070421
Chicago/Turabian StyleSaldaña, Manuel, Norman Toro, Jonathan Castillo, Pía Hernández, and Alessandro Navarra. 2019. "Optimization of the Heap Leaching Process through Changes in Modes of Operation and Discrete Event Simulation" Minerals 9, no. 7: 421. https://doi.org/10.3390/min9070421
APA StyleSaldaña, M., Toro, N., Castillo, J., Hernández, P., & Navarra, A. (2019). Optimization of the Heap Leaching Process through Changes in Modes of Operation and Discrete Event Simulation. Minerals, 9(7), 421. https://doi.org/10.3390/min9070421









