Characterization of Mine Waste and Acid Mine Drainage Prediction by Simple Testing Methods in Terms of the Effects of Sulfate-Sulfur and Carbonate Minerals
Abstract
:1. Introduction
2. Experimental Methods
2.1. Geochemical Characteristics
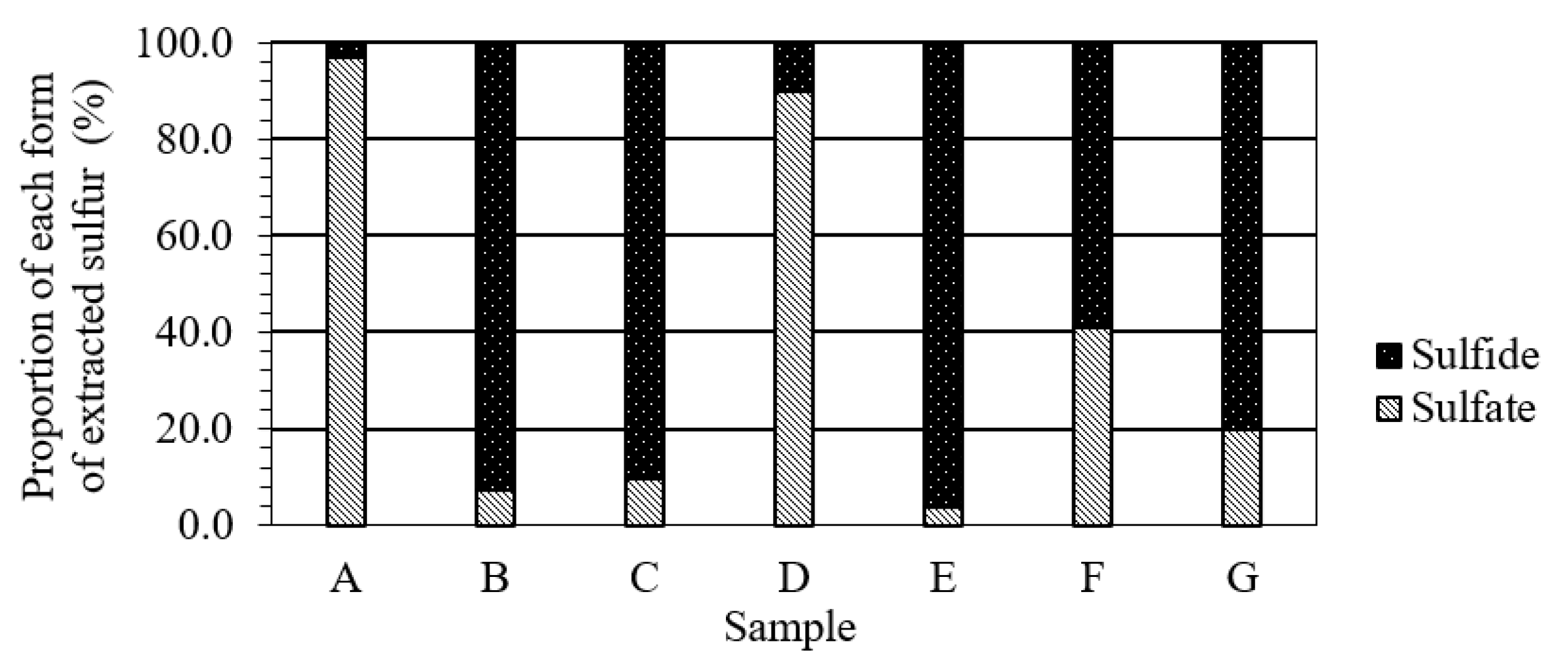
2.2. Sequential Acid Extraction
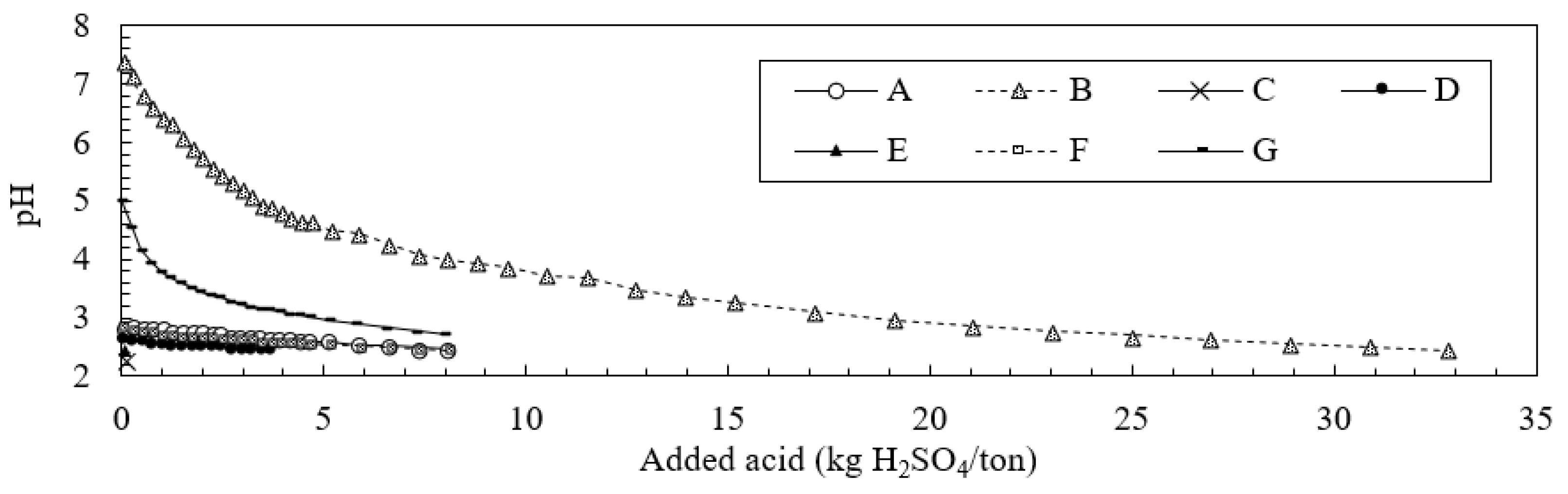
2.3. ABCC Test
2.4. Sequential NAG Test
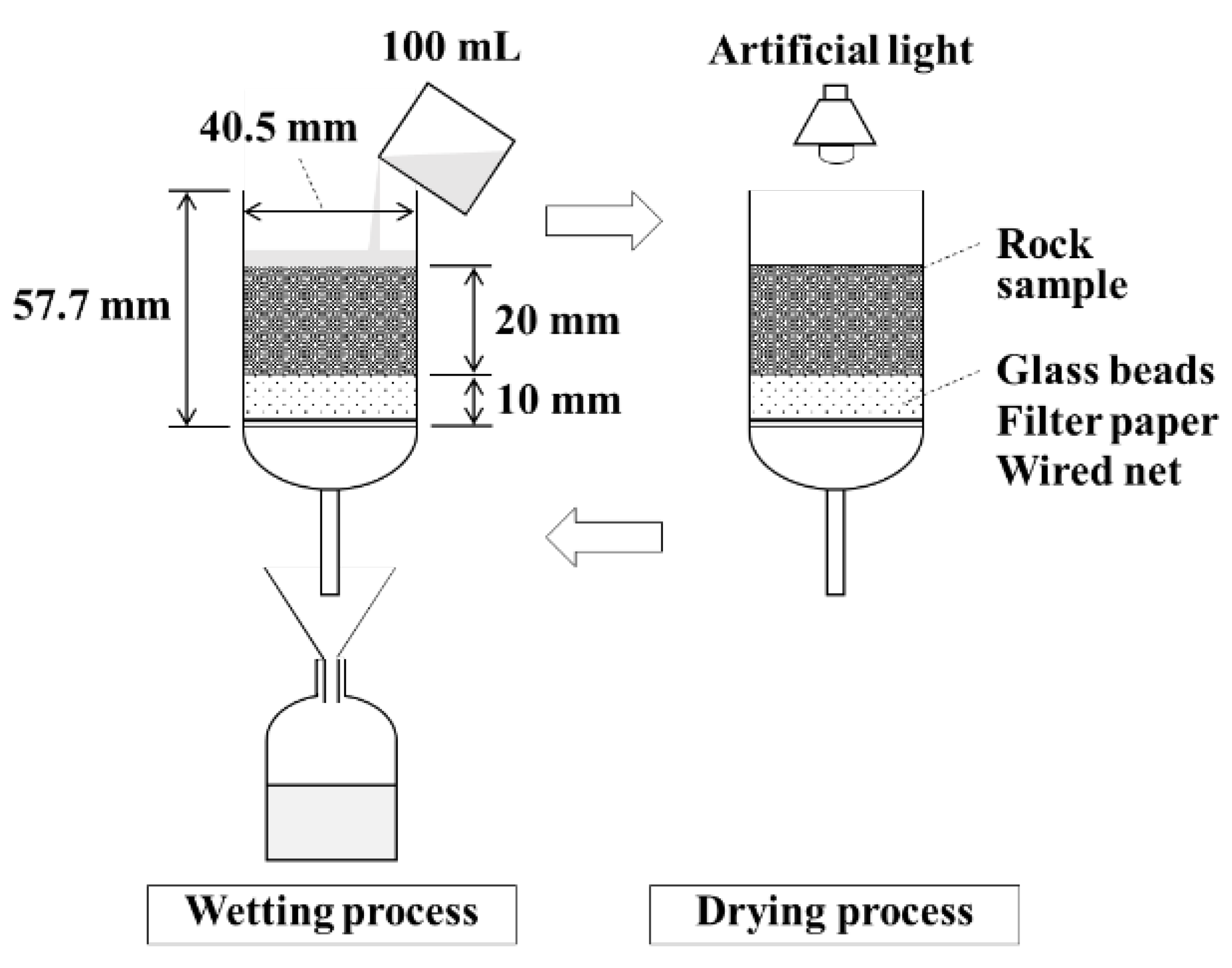
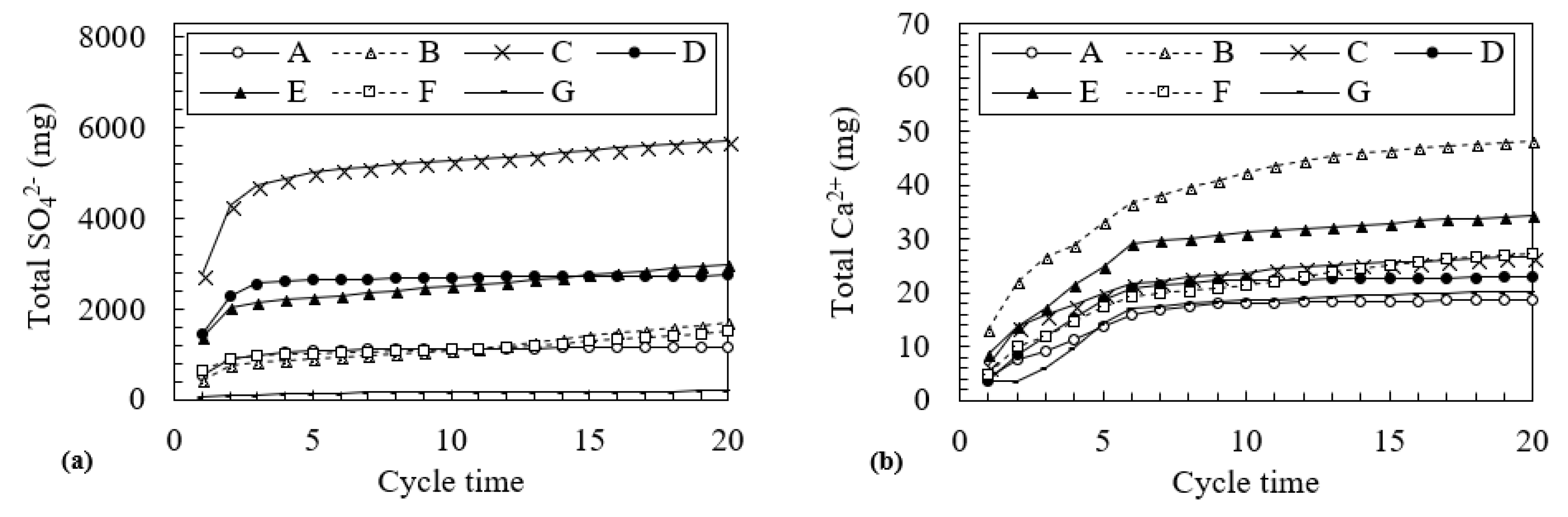
2.5. Column Leaching Test
3. Results and Discussion
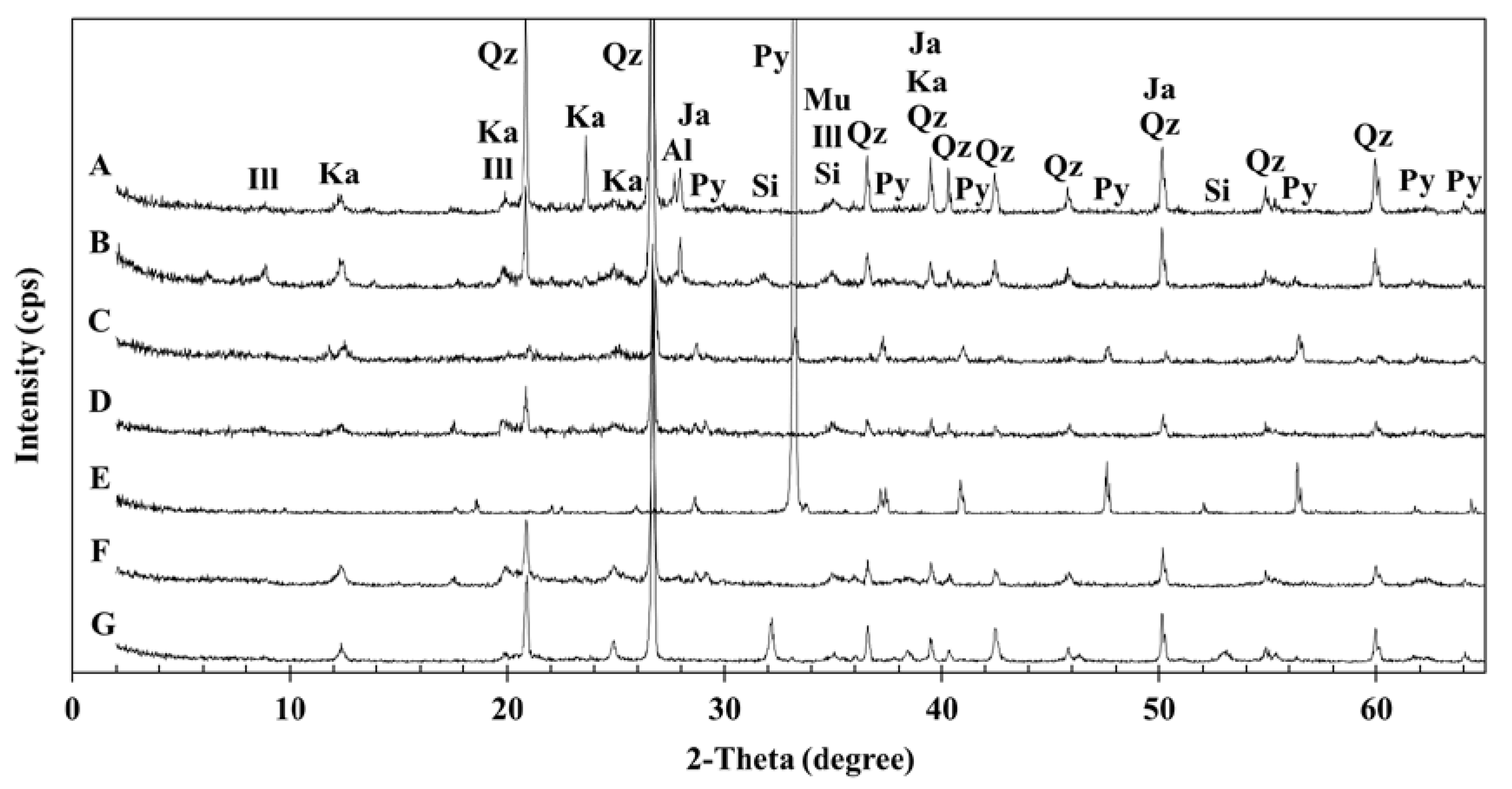
3.1. Geochemical Characteristics
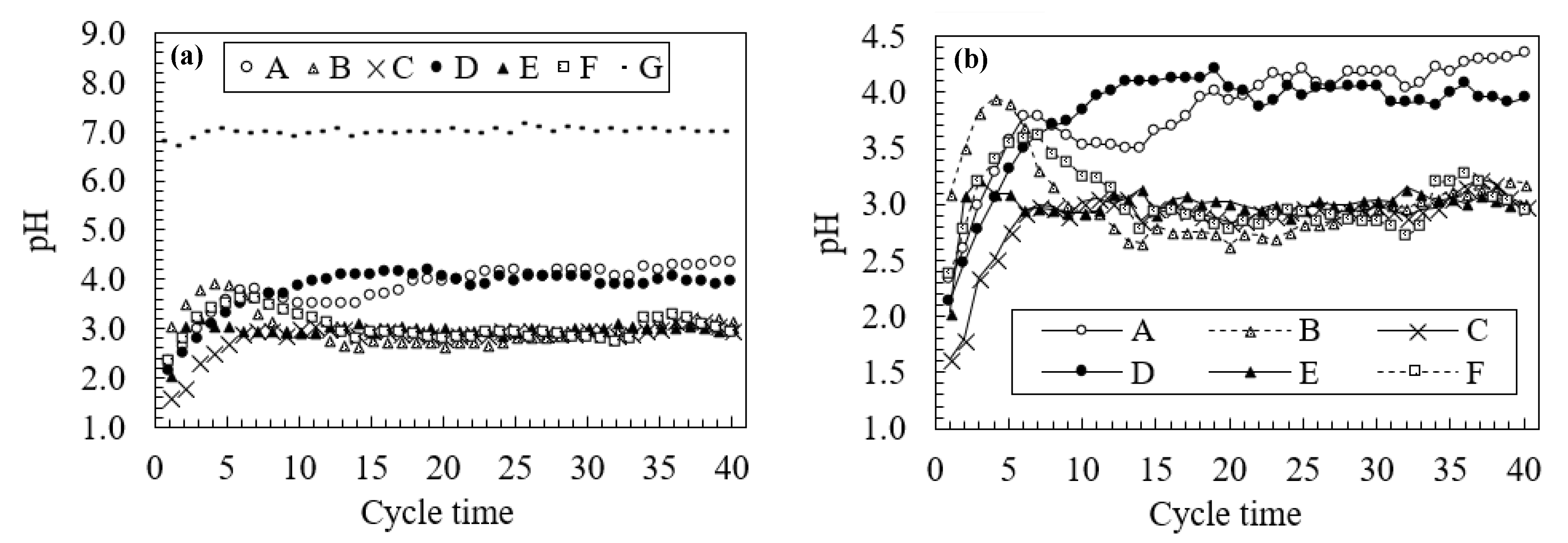
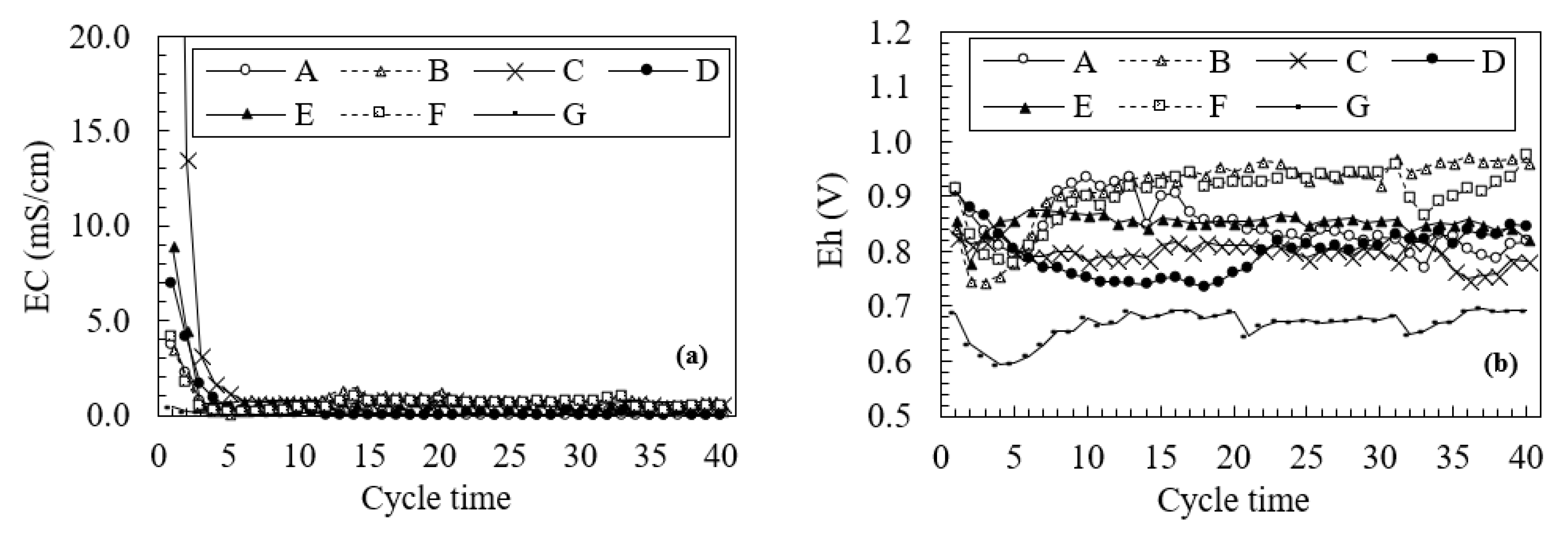
3.2. Changes in Water Quality During the Leaching Test
3.3. Neutralization Effects
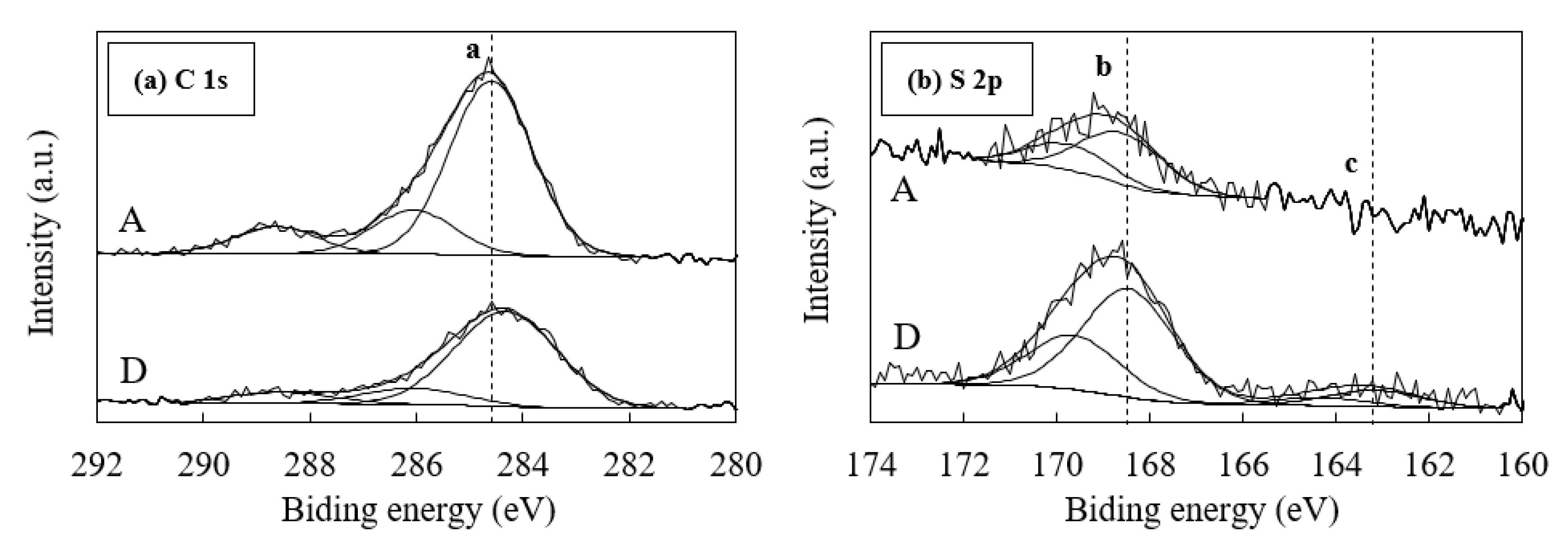
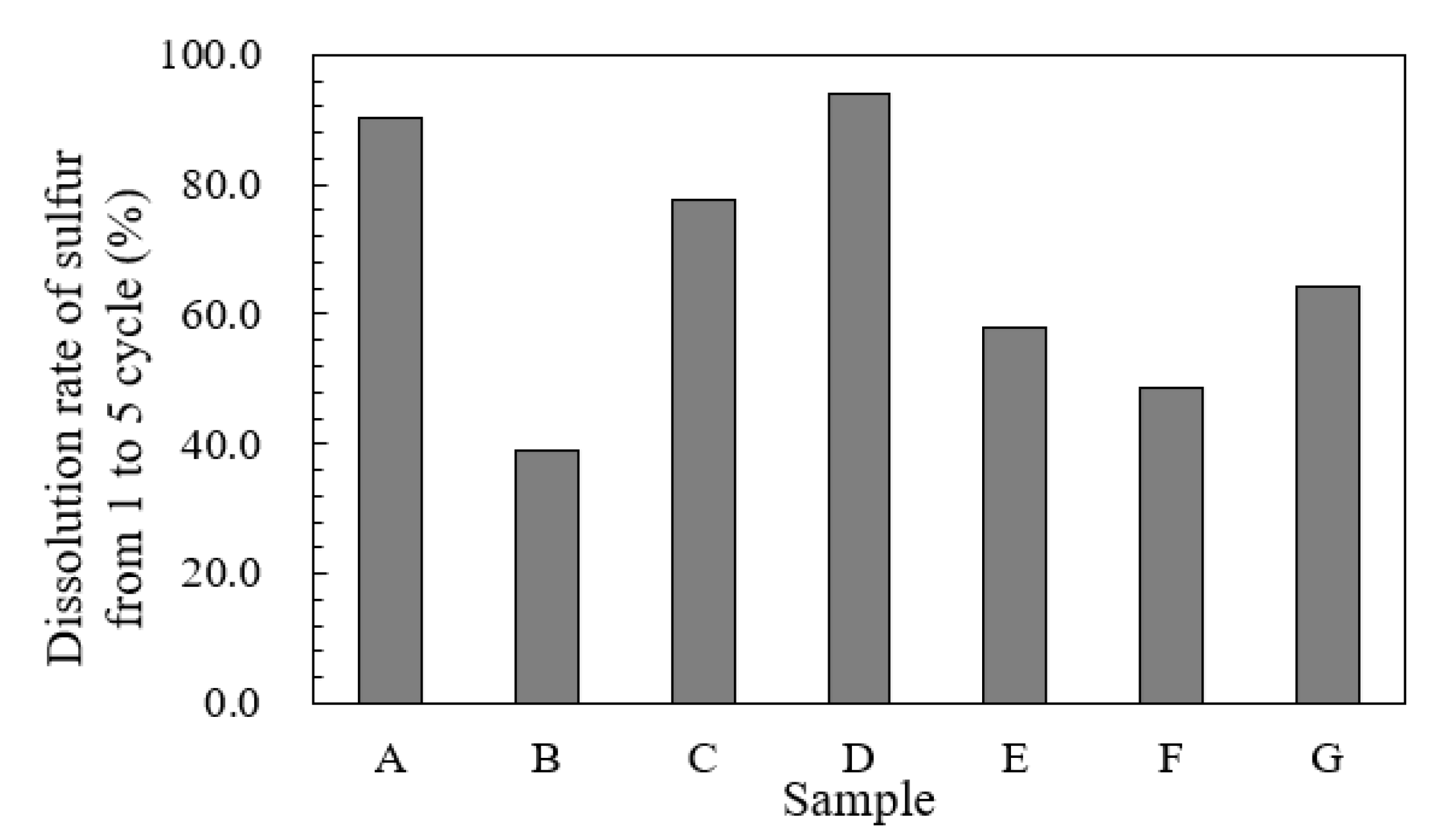
3.4. Effects of the Form of Sulfur
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Matsumoto, S.; Shimada, H.; Sasaoka, T. The key factor of acid mine drainage (AMD) in the history of the contribution of mining industry to the prosperity of the United States and South Africa: A review. Nat. Resour. 2016, 7, 445–460. [Google Scholar] [CrossRef]
- Qureshi, A.; Maurice, C.; Öhlander, B. Potential of coal mine waste rock for generating acid mine drainage. J. Geochem. Explor. 2016, 160, 44–54. [Google Scholar] [CrossRef]
- Maree, J.P.; Mujuru, M.; Bologo, V.; Daniels, N.; Mpholoane, D. Neutralisation treatment of AMD at affordable cost. Water SA 2013, 39, 245–250. [Google Scholar] [CrossRef]
- Trumm, D. Selection of active and passive treatment systems for AMD–flow charts for New Zealand conditions. N. Z. J. Geol. Geophys. 2010, 53, 195–210. [Google Scholar] [CrossRef]
- Sheoran, A.S. Management of acidic mine waste water by constructed wetland treatment systems: A bench scale study. Eur. J. Sustain. Dev. 2017, 6, 245–255. [Google Scholar] [CrossRef]
- Fernández-Rubio, R.; Fernández-Lorca, S.; Esteban Arlegui, J. Preventive techniques for controlling acid water in underground mines by flooding. Int. J. Mine Water 1987, 6, 39–52. [Google Scholar] [CrossRef]
- Benzaazoua, M.; Bussiere, B.; Kongolo, M.; McLaughlin, J.; Marion, P. Environmental desulphurization of four Canadian mine tailings using froth flotation. Int. J. Miner. Process. 2000, 60, 57–74. [Google Scholar] [CrossRef]
- Skousen, J.G.; Sexstone, A.; Ziemkiewicz, P.F. Acid mine drainage control and treatment. In Reclamation of Drastically Disturbed Lands Agronomy. No. 41; Barnhisel, R.I., Darmody, R.G., Daniels, W.L., Eds.; American Society of Agronomy and American Society for Surface Mining and Reclamation: Madison, WI, USA, 2000; pp. 131–168. [Google Scholar]
- Pozo-Antonio, S.; Puente-Luna, I.; Lagüela-López, S.; Veiga-Ríos, M. Techniques to correct and prevent acid mine drainage: A review. Dyna 2014, 81, 73–80. [Google Scholar] [CrossRef]
- Matsumoto, S.; Shimada, H.; Sasaoka, T.; Kusuma, G.J.; Gautama, R.S. Construction of dry cover system for prevention of acid mine drainage at mine waste dump in open cast coal mines, Indonesia. J. Environ. Prot. 2016, 7, 160–169. [Google Scholar] [CrossRef]
- Margarete, K.; William, N.W.; Sören, B. Acid rock drainage or not-oxidative vs. reductive biofilms—A microbial question. Minerals 2018, 8, 199. [Google Scholar] [CrossRef]
- Mine Environment Neutral Drainage Program (MEND), Construction and Instrumentation of a Multi-layer Cover Les Terrains Aurifères. MEND Report 2.22.4a. 1999. Available online: http://mend-nedem.org/wp-content/uploads/2013/01/2.22.4a-E.pdf (accessed on 26 June 2018).
- Pope, J.; Weber, P.; Olds, W. Control of acid mine drainage by managing oxygen ingress into waste rock dumps at bituminous coal mines in New Zealand. In Proceedings of the IMWA2016 Annual Conference, Freiberg, Germany, 11–15 July 2016; pp. 368–376. [Google Scholar]
- AMIRA International. ARD Test Handbook: Prediction & Kinetic Control of Acid Mine Drainage, AMIRA P387A; Ian Wark Research Institute and Environmental Geochemistry International Ltd.: Melbourne, Australia, 2002. [Google Scholar]
- Matsumoto, S.; Ishimatsu, H.; Shimada, H.; Sasaoka, T.; Matsui, K.; Kusuma, G.J. Prevention of acid mine drainage (AMD) by using sulfur-bearing rocks for a cover layer in a dry cover system in view of the form of sulfur. J. Pol. Miner. Eng. Soc. 2015, 36, 29–35. [Google Scholar]
- Vithana, C.L.; Sullivan, L.A.; Bush, R.T.; Burton, E.D. Acidity fractions in acid sulfate soils and sediments: Contributions of schwertmannite and jarosite. Soil Res. 2013, 51, 203–214. [Google Scholar] [CrossRef]
- Stewart, W.A.; Miller, S.D.; Smart, R. Advances in Acid Rock Drainage (ARD) Characterisation of Mine Wastes. In Proceedings of the 7th International Conference on Acid Rock Drainage (ICARD), St. Louis, MO, USA, 26–30 March 2006; pp. 2098–2119. [Google Scholar]
- Dold, B. Acid rock drainage prediction: A critical review. J. Geochem. Explor. 2017, 172, 120–132. [Google Scholar] [CrossRef]
- Pope, J.; Weber, P.; Mackenzie, A.; Newman, N.; Rait, R. Correlation of acid base accounting characteristics with the geology of commonly mined coal measures, West Coast and Southland, New Zealand. N. Z. J. Geol. Geophys. 2010, 53, 153–166. [Google Scholar] [CrossRef]
- Skousen, J.G.; Renton, J.; Brown, H.; Evans, P.; Leavitt, B.; Brady, K.; Cohen, L.; Ziemkiewicz, P. Neutralization potential of overburden samples containing siderite. J. Environ. Qual. 1997, 26, 673–681. [Google Scholar] [CrossRef]
- Gottlieb, P.; Wilkie, G.J.; Sutherland, D.N.; Ho-Tun, E.; Suthers, S.; Perera, K.; Jenkins, B.; Spencer, S.; Butcher, A.; Rayner, J. Using quantitative electron microscopy for process mineralogy applications. JOM 2000, 52, 24–25. [Google Scholar] [CrossRef]
- Charles, J.C.; Barnes, A.; Declerq, J.; Warrender, R.; Brough, C.; Bowell, R.J. Difficulties of interpretation of NAG test results on net neutralizing mine wastes: Initial observations of elevated pH conditions and theory of CO2 disequilibrium. In Proceedings of the IMWA2015 Annual Conference, Santiago, Chile, 21–24 April 2015; pp. 1–10. [Google Scholar]
- Schumann, R.; Stewart, W.; Miller, S.; Kawashima, N.; Li, J.; Smart, R. Acid-base accounting assessment of mine wastes using the chromium reducible sulfur method. Sci. Total Environ. 2012, 424, 289–296. [Google Scholar] [CrossRef] [PubMed]
- Qian, G.; Schumann, R.C.; Li, J.; Short, M.D.; Fan, R.; Li, Y.; Kawashima, N.; Zhou, Y.; Smart, R.S.C.; Gerson, A.R. Strategies for reduced acid and metalliferous drainage by pyrite surface passivation. Minerals 2017, 7, 42. [Google Scholar] [CrossRef]
- Dold, B.; Fontboté, L. Element cycling and secondary mineralogy in porphyry copper tailings as a function of climate, primary mineralogy, and mineral processing. J. Geochem. Explor. 2001, 74, 3–55. [Google Scholar] [CrossRef]
- White, W.W., III; Lapakko, K.A.; Cox, R.L. Static-test methods most commonly used to predict acid mine drainage: Practical guidelines for use and interpretation. In The Environmental Geochemistry of Ore Deposits. Part A: Processes, Techniques, and Health Issues; Reviews in Economic Geology; Plumlee, G.S., Logsdon, M.J., Eds.; Society of Economic Geologists: Littleton, CO, USA, 1999; pp. 325–338. [Google Scholar]
- Sasaki, K.; Haga, T.; Hirajima, T.; Kurosawa, K.; Tsunekawa, M. Distribution and transition of heavy metals in mine tailing dumps. Mater. Trans. 2002, 43, 2778–2783. [Google Scholar] [CrossRef]
- Milliman, J.D.; Muller, G.; Forstner, F. Recent Sedimentary Carbonates: Part 1 Marine Carbonates; Springer-Verlag GmbH & Co., KG: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Muller, G.; Gatsner, M. Chemical analysis. Neues Jahrbuch für Mineralogie Monatshefte 1971, 10, 466–469. [Google Scholar]
- Dold, B. Speciation of the most soluble phases in a sequential extraction procedure adapted for geochemical studies of copper sulfide mine waste. J. Geochem. Explor. 2003, 80, 55–68. [Google Scholar] [CrossRef]
- Dold, B.; Weibel, L. Biogeometallurgical pre-mining characterization of ore deposits: An approach to increase sustainability in the mining process. Environ. Sci. Pollut. Res. 2013, 20, 7777–7786. [Google Scholar] [CrossRef] [PubMed]
- DDK-TOA Corporation 2001–2018. Available online: https://www.toadkk.co.jp/english/product/useful/useful10.html (accessed on 30 August 2018).
- Shirley, D.A. High resolution X-ray photoelectron spectrum of the valence bands of gold. Phys. Rev. B 1972, 5, 4709–4714. [Google Scholar] [CrossRef]
- Matsumoto, S.; Shimada, H.; Sasaoka, T. Interaction between physical and chemical weathering of argillaceous rocks and the effects on the occurrence of acid mine drainage (AMD). Geosci. J. 2017, 21, 1–10. [Google Scholar] [CrossRef]
- Lawrence, R.W.; Poling, G.W.; Ritcey, G.M.; Marchant, P.B. Assessment of Predictive Methods for the Determination of AMD Potential in Mine Tailings and Waste Rock, Tailings and Effluent Management; Pergamon Press: Elmsford, NY, USA, 1989; pp. 317–331. [Google Scholar]
- Climate-Data. ORG Climate: Pasar Tanjung Enim. Available online: http://en.climate-data.org/location/570291/ (accessed on 26 June 2018).
- Miller, S.; Robertson, A.; Donahue, T. Advances in acid drainage prediction using the net acid generation (NAG) test. In Proceedings of the 4th International Conference on Acid Rock Drainage, Vancouver, BC, Canada, 31 May–6 June 1997; pp. 533–549. [Google Scholar]
- Lamas, F.; Irigaray, C.; Oteo, C.; Chacon, J. Selection of the most appropriate method to determine the carbonate content for engineering purposes with particular regard to marls. Eng. Geol. 2005, 81, 32–41. [Google Scholar] [CrossRef]
- Liu, Y.; Che, D.; Xu, T. X-ray photoelectron spectroscopy determination of the forms of sulfur in coal and its chars. J. Xian Jiaotong Univ. 2004, 38, 101–104. [Google Scholar]
- Frost, D.C.; Leeder, W.R.; Tapping, R.L. X-ray photoelectron spectroscopic investigation of coal. Fuel 1974, 53, 206–211. [Google Scholar] [CrossRef]
- Kelemen, S.R.; George, G.N.; Gorbaty, M.L. Direct determination and quantification of sulfur forms in heavy petroleum and coals. part I: The X-ray photoelectron spectroscopy (XPS) approach. Fuel Chem. Div. Am. Chem. Soc. 1989, 34, 729–737. [Google Scholar]
| Sample | Sulfur (%) | AP (kg H2SO4/ton) | ANC (kg H2SO4/ton) | NAPP (kg H2SO4/ton) | Paste pH | NAG pH | Carbonate (%) |
|---|---|---|---|---|---|---|---|
| A | 0.89 | 27.4 | 0.0 | 27.4 | 3.10 | 2.80 | 0.50 |
| B | 0.77 | 23.5 | 20.3 | 3.2 | 2.82 | 2.28 | 1.58 |
| C | 12.55 | 383.9 | 0.0 | 383.9 | 1.21 | 1.04 | 0.23 |
| D | 4.99 | 152.8 | 0.0 | 152.8 | 1.74 | 1.47 | 0.30 |
| E | 25.46 | 779.1 | 2.5 | 776.6 | 1.24 | 1.08 | 0.38 |
| F | 5.67 | 173.5 | 3.7 | 169.8 | 4.80 | 2.90 | 0.24 |
| G | 0.93 | 28.7 | 9.2 | 19.6 | 6.16 | 4.37 | 0.29 |
| Sample/Stage | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| A | 2.65 | 3.49 | 4.20 | 4.35 | 4.65 | - | - |
| B | 2.28 | 2.81 | 3.34 | 3.81 | 4.12 | 4.22 | 4.31 |
| C | 2.01 | 2.64 | 2.94 | 3.38 | 3.71 | 4.00 | 4.07 |
| D | 2.14 | 2.77 | 2.79 | 2.88 | 3.28 | 3.77 | 3.95 |
| E | 1.66 | 1.87 | 1.81 | 2.01 | 2.30 | 2.83 | 3.21 |
| F | 2.41 | 2.84 | 3.05 | 3.66 | 4.02 | 4.22 | 4.12 |
| G | 2.81 | 3.39 | 3.86 | 4.21 | 4.53 | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsumoto, S.; Ishimatsu, H.; Shimada, H.; Sasaoka, T.; Kusuma, G.J. Characterization of Mine Waste and Acid Mine Drainage Prediction by Simple Testing Methods in Terms of the Effects of Sulfate-Sulfur and Carbonate Minerals. Minerals 2018, 8, 403. https://doi.org/10.3390/min8090403
Matsumoto S, Ishimatsu H, Shimada H, Sasaoka T, Kusuma GJ. Characterization of Mine Waste and Acid Mine Drainage Prediction by Simple Testing Methods in Terms of the Effects of Sulfate-Sulfur and Carbonate Minerals. Minerals. 2018; 8(9):403. https://doi.org/10.3390/min8090403
Chicago/Turabian StyleMatsumoto, Shinji, Hirotaka Ishimatsu, Hideki Shimada, Takashi Sasaoka, and Ginting Jalu Kusuma. 2018. "Characterization of Mine Waste and Acid Mine Drainage Prediction by Simple Testing Methods in Terms of the Effects of Sulfate-Sulfur and Carbonate Minerals" Minerals 8, no. 9: 403. https://doi.org/10.3390/min8090403
APA StyleMatsumoto, S., Ishimatsu, H., Shimada, H., Sasaoka, T., & Kusuma, G. J. (2018). Characterization of Mine Waste and Acid Mine Drainage Prediction by Simple Testing Methods in Terms of the Effects of Sulfate-Sulfur and Carbonate Minerals. Minerals, 8(9), 403. https://doi.org/10.3390/min8090403





