Next Article in Journal
Effects of Xanthate on Flotation Kinetics of Chalcopyrite and Talc
Next Article in Special Issue
Evaluation of Magnetic Separation Efficiency on a Cassiterite-Bearing Skarn Ore by Means of Integrative SEM-Based Image and XRF–XRD Data Analysis
Previous Article in Journal
Cr Release from Cr-Substituted Goethite during Aqueous Fe(II)-Induced Recrystallization
Previous Article in Special Issue
Determination of Dissolution Rates of Ag Contained in Metallurgical and Mining Residues in the S2O32−-O2-Cu2+ System: Kinetic Analysis
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Minerals
Volume 8
Issue 9
10.3390/min8090368
minerals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

New Insights into the Configurations of Lead(II)-Benzohydroxamic Acid Coordination Compounds in Aqueous Solution: A Combined Experimental and Computational Study

by
Jianyong He
1,†,
Haisheng Han
1,†,
Chenyang Zhang
1,2,*,
Yuehua Hu
1,
Dandan Yuan
3,
Mengjie Tian
1,
Daixiong Chen
2,* and
Wei Sun
1,*
1
Key Laboratory of Hunan Province for Clean and Efficient Utilization of Strategic Calcium-Containing Mineral Resources, School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, Hunan, China
2
Key Laboratory of Hunan Province for Comprehensive Utilization of Complex Copper-Lead Zinc Associated Metal Resources, Hunan Research Institute for Nonferrous Metals, Changsha 410100, Hunan, China
3
Institute of Theoretical and Computational Chemistry, Nanjing University, Nanjing 210023, Jiangsu, China
*
Authors to whom correspondence should be addressed.
†
These authors have equally contributed to this work.
Minerals 2018, 8(9), 368; https://doi.org/10.3390/min8090368
Submission received: 22 July 2018 / Revised: 15 August 2018 / Accepted: 19 August 2018 / Published: 25 August 2018
(This article belongs to the Special Issue Modeling, Design and Optimization of Multiphase Systems in Minerals Processing)
Browse Figures
Versions Notes

Abstract

:
Novel collector lead(II)-benzohydroxamic acid (Pb(II)–BHA) complexes in aqueous solution were characterized by using experimental approaches, including Ultraviolet-visible (UV-Vis) spectroscopy and electrospray ionization-mass spectrometry (ESI-MS), as well as first-principle density functional theory (DFT) calculations with consideration for solvation effects. The Job plot delineated that a single coordinated Pb(BHA)+ should be formed first, and that the higher coordination number complexes can be formed subsequently. Moreover, the Pb(II)–BHA species can aggregate with each other to form complicated structures, such as Pb(BHA)2 or highly complicated complexes. ESI-MS results validated the existence of Pb-(BHA)n=1,2 under different solution pH values. Further, the first-principles calculations suggested that Pb(BHA)+ should be the most stable structure, and the Pb atom in Pb(BHA)+ will act as an active site to attack nucleophiles. These findings are meaningful to further illustrate the adsorption mechanism of Pb(II)–BHA complexes, and are helpful for developing new reagents in mineral processing.

1. Introduction

Metal–organic coordination complexes have been widely used in the materials, chemistry. Recently, their promising applications in mining have attracted research attention [1,2,3,4,5,6,7,8]. For instance, lead(II)-benzohydroxamic acid (Pb(II)–BHA) complexes are effective collectors in the beneficiation of oxide minerals, including tungsten minerals, cassiterite, and rutile [9,10]. Given the excellent selectivity and good collecting ability of Pb(II)–BHA, the scheelite flotation process could be simplified remarkably without the addition of sodium silicate, overcoming the shortage of heating in the routine flotation of scheelite [9,10,11]. The beneficiation of scheelite is currently one of the most challenging problems worldwide in the field of mineral processing. Conventionally, separating scheelite from calcium bearing minerals, such as fluorite and calcite, by using anionic collectors (especially for fatty acid) is difficult due to their highly similar properties in calcium-bearing surfaces [12,13]. Fortunately, our group first introduced the Pb complexes of benzohydroxamic acid (Pb(II)–BHA complexes) to effectively separate scheelite from calcium-bearing gangues by properly regulating the Pb/BHA ratio and pH [9,11]. Furthermore, as displayed in Figure 1a, the novel flotation scheme (Scheme i in Figure 1b), with Pb(II)–BHA complexes used as the collector, has shown better performance than the traditional activation flotation scheme (Scheme ii in Figure 1b), which first added Pb(II) as the activator and subsequently added BHA as the collector [10,14,15,16,17,18,19,20,21,22,23]. The effective microstructures of Pb(II)–BHA complexes in the solution, however, as well as their interaction mechanisms with oxide minerals remain unclear. Considering the using of Pb(II) ions may result in environmental/public health issues, a further understanding of this activating mechanism can be helpful for exploring the alternative reagents.
The hydroxamic acid group (–CO–NH–OH) is the functional group of the BHA [25,26,27]. The functional group has different properties that remain poorly characterized; in fact, a reliable assignment of the correct structure is challenging because the several possible conformations strongly depend on concentration, temperature, and the nature of the solvent [28]. The hydroxamate collectors, such as benzohydroxamic acid (BHA), naphthenic hydroxamate, and amide hydroxamate, have been useful as highly selective flotation collectors in recent years. The role to function as collectors in mineral flotation has been documented by Lynch et al. [29]. The chelate between hydroxamic acids and the metal ion, however, has remained poorly investigated. Currently, first-principle calculations based on density functional theory (DFT) and some advanced experimental technologies are used to obtain more information on the molecular structure of BHA [30]. Wander et al.’s benchmarking calculations indicate that the DFT calculation can achieve near chemical accuracy of hydrolysis constants for metal ions in most cases [31]. Nuclear magnetic resonance and DFT calculations performed by Garcia et al. show that the adopted BHA conformation of BHA aqueous solution is a closed Z (cis) configuration in aqueous solution [32]. Both Z (cis) and E (trans) conformations in Scheme 1 regularly co-exist in solvent. The concentration and environmental factors determine the ratio of Z type to E type conformations to some extent, and potential barriers are present among different conformations [33,34].
BHA can chelate with metal ions, such as copper(II) cadmium(II), cobalt(II), nickel(II), manganese(II), lead(II), zinc(II), aluminum(III), iron(III), and bismuth(III), thus taking on diverse chelate structures [26,35]. Very few heavy metal ion complexes of BHA chelates have been extensively investigated for their special uses, such as the bismuth(III) complex that has activity against Helicobacter pylori; however, reports about the novel Pb(II)–BHA complexes are also few. Understanding the microstructures of Pb(II)–BHA complexes is essential to improve the technique working in flotation practice and fundamental field of lead chemistry [36,37,38,39].
This current study aims to investigate configurations of Pb(II)–BHA coordination complexes in aqueous solution. Accordingly, UV-Vis spectroscopy and electrospray ionization mass spectrometry (ESI-MS) were performed to characterize the configuration of Pb(II)–BHA complexes. Furthermore, first-principle DFT calculations were performed to understand the constituents and properties of Pb(II)–BHA complexes at the molecular level. The frontier molecular orbital [40] and natural atomic orbitals (NAOs) [41] were used to describe the reactivity of the studied Pb(II)–BHA complex. This work has shed new light on effective microstructures of Pb(II)–BHA coordination complexes for mineral flotation.

2. Methodology

2.1. Experimental Details

2.1.1. Materials

Analytical grade BHA (>98%) was purchased from Tokyo Chemical Industry Co., Ltd. in Japan. Analytical grade lead nitrate (>99%) was used. pH regulators were prepared with the stock solution of sodium hydroxide (>96%) and hydrochloric acid (36~38%). All purity is in mass percent. The 18.2 MΩ pure water produced by Arium Mini Plus (Sartorius Weighing Technology, Goettingen, Germany) was used in this work.

2.1.2. UV-Vis Tests

The UV-Vis spectrum of the Pb(II)-hydroxide system has been investigated elsewhere [42]. Here we will not assign the characteristic peaks of the Pb(II)–BHA complex. The Job plot [43], proposed by Job, provides qualitative and quantitative insight into the stoichiometry with the underlying association of ligand- and solvent-dependent reaction rates. The Job plot was used to track the full reaction path. Moreover, we changed the guest and host solution to comprehensively understand the stoichiometry of the product. In this work, the concentration of the Pb(II)–BHA complex, as determined by integration of the intensity of specific wavenumber, was plotted against the mole fraction XA (the guest solution is BHA solution) and XB (the guest solution is Pb(II) ion solution). A Shimadzu UV2600/2700 Ultraviolet spectrophotometer was used to obtain the UV-Vis spectra at a fixed concentration of Pb(II) ion at 0.1 mM using the equimolar continuous change method and molar ratio method.

2.1.3. ESI-MS Tests

ESI-MS patterns were collected in positive ion mode with a Bruker Q-TOF Qualification Standard Kit, using solutions of the 0.1 mM/L mixture of lead nitrate and BHA. ESI-MS patterns were used to obtain the proof of coordinated compounds of Pb(II)–BHA complexes at the molar ratio of 1:1 (v:v, at the natural pH 4.4) and 1:2 (v:v, at pH 13.0). The natural pH was selected for exclusion of guest species so that we can get a relatively simple Pb–BHA structure in aqueous solution. A high pH of 13.0 was selected in according to a report that high pH can result in more complicated solution species [10]. The two case studies, regarded as representatives of both acid and alkaline solutions, are supposed to provide evidence of Pb–BHA complexes.

2.2. Computational Methods

All calculations were performed with the Gaussian 09 (version D.01) quantum chemistry package, based on the B3LYP method: A three-parameter hybrid functional by replacing a certain amount of the PW91 generalized gradient approximation (GGA) correlation functional with the LYP GGA correlation functional [44,45,46]. The implicit solvation effects were considered using the polarized continuum models (PCM) in the calculation [47]. On the other hand, the water molecules in the first hydration of Pb(II)–BHA complex were also considered with the explicit solvation model. The aug-cc-pVDZ basis set was employed as all-electron basis set in all types of calculation on the light atoms H, C, N, and O, except for the Pb atom in Pb(II)–BHA complex systems. The aug-cc-pVDZ-PP basis set with a relativistic pseudopotential was used for the Pb atom. The basis set, obtained from EMSL Basis Set Exchange web site, has already been verified as producing acceptable thermodynamic information of hydrated Pb(II) ions [30,48,49]. The Los Alamos effective core potential double-ξ (LanL2Dz) was used for the primary geometry optimization of modeled benzohydroxamic acid and its Pb(II) complex in ionic form. LanL2Dz replaced 78 core electrons with relativistic effective core potential (RECP) [50]; therefore, only two valence electrons of Pb(II) ions were described [51]. To refine the structure and calculate the molecular orbitals, we further used the larger aug-cc-pVDZ basis set for the light atoms, such as hydrogen, oxygen, nitrogen, and carbon, and we used the aug-cc-pVDZ–PP with RECP of the inner 60 electrons for Pb(II) ions to calculate the frequency [52]. The default convergence parameters (with maximum force within 4.5 × 10−4, force RMS within 1.8 × 10−3) in the Gaussian 09 software were retained to optimize the structure. All calculations were successfully converged, without virtual frequencies in the vibration analysis.
There are three protonation sites in the BHA molecule. The carbonyl oxygen site is found to be the preferred site for protonation by Arora et al. [53] in aqueous solution. In the building of BHA anion models [54], the proton at the carbonyl oxygen was removed according to the preferred deprotonation site reported by Begoña et al. [32]. The Pb(II) ion was set as the metal center ion which would be the coordination center of the bidentate BHA anions. The envisaged conformations were ligated by two, three and four BHA anions. Thermodynamic values for Gibbs free energy [55] were obtained using the PCM with the context:
Δ G r = ∑ G p r o d − ∑ G r e a c t
where G p r o d and G r e a c t are the free energy or the products and the reactants included in the reaction, respectively.
The Gauss View was used as a visualization tool in this paper. In addition, all calculations including the mapped molecular orbitals in this work were performed at the theory level of PCM-B3LYP/aug-cc-pVDZ on light atoms (C, H, O, and N) and PCM -B3LYP/aug-cc-pVDZ-PP on Pb atoms [56]. Molecular orbital contours for the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the cluster model were computed at the same theoretical level. The contributions of the Pb atom to the frontier molecular orbitals were calculated with a multifunctional wave function analyzer Multiwfn [57] based on the NAO method.

3. Results and Discussion

3.1. Experimental

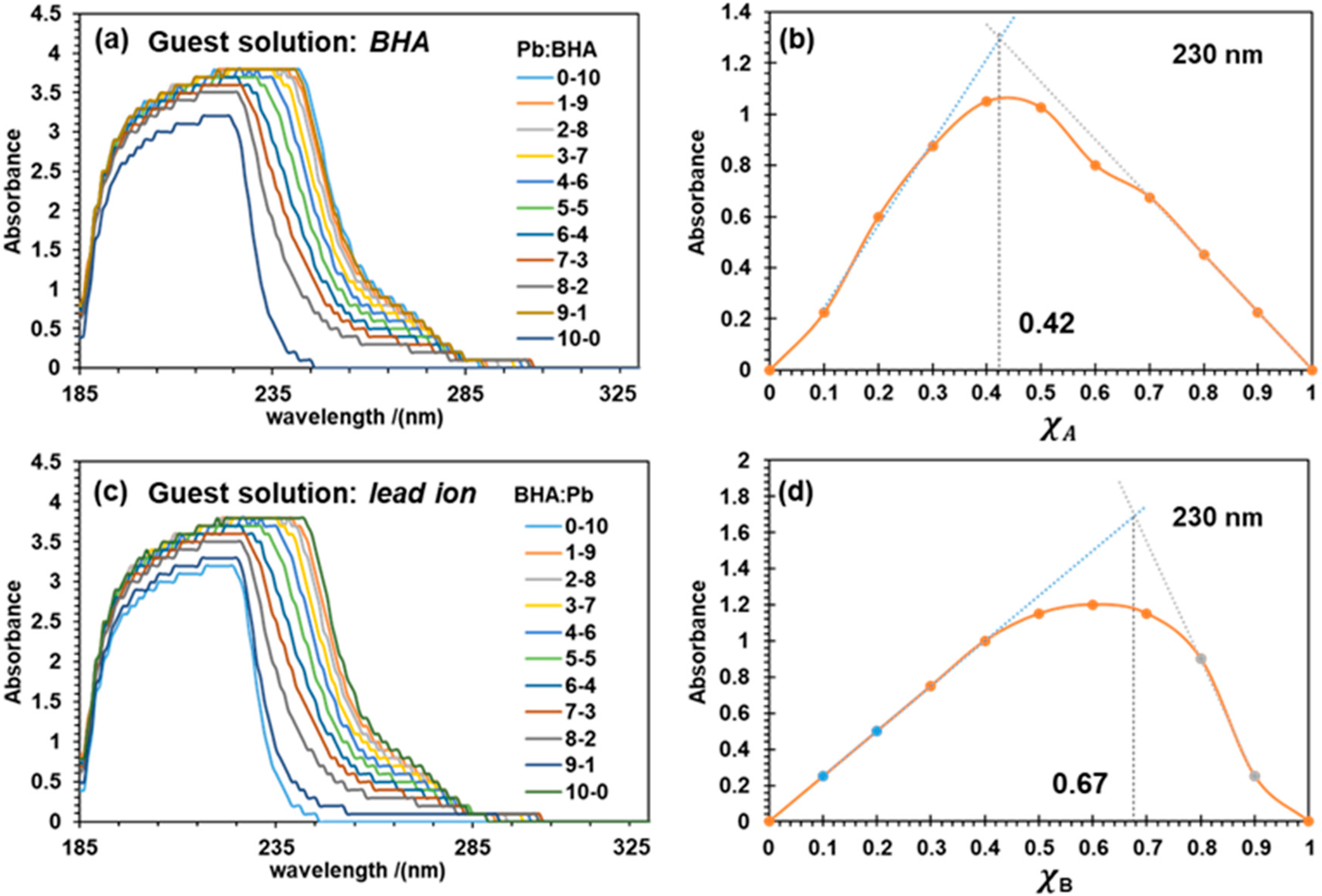
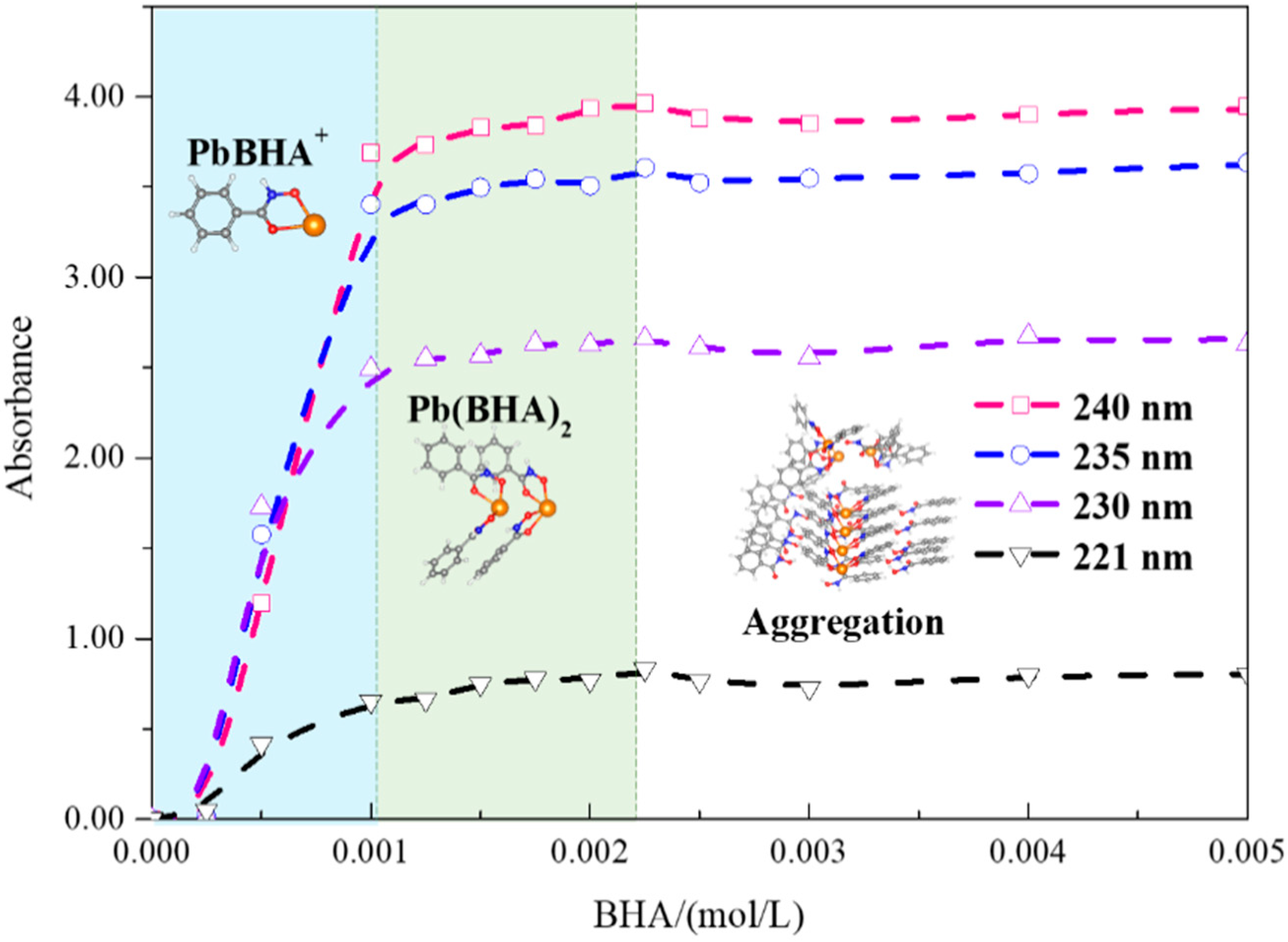
3.1.1. UV-Vis Results

Because of the superposition of UV-Vis absorbance peaks of the products and the reactants, carefully processing the collected UV-Vis data is essential. Initially, the first and the last points were fixed at zero absorbance because the complexity of the product might be different when one component is in excess, and the further fitting procedures would exclude the two points [58]. The starting second point and the last second point were connected to form a background. After deducing the background absorbance, the Job plots were plotted, as shown in Figure 2b,d. Here, Job plots were fitted using the method of initial tangents using experimental data close to the beginning points (the first and last points were not included due to the formation of hydrated Pb complexes and the solvation of BHA) [59]. As illustrated in Figure 2, XA and XB were the mole fractions of Pb(II) ions and BHA according to dosing method 1 and 2, respectively. The wavelength at 230 nm represents the significant changes in the solution components. The same trends can also be obtained by using other wavelengths between 230 nm and 240 nm (Figure 3).
Figure 2a,c shows that the increasing dosage of Pb(II) ions and BHA has strengthened and extended the absorbance peaks. Job plots have been obtained from the newly mixed Pb(II)–BHA mixture, with the collected characteristic absorbance peaks of UV-Vis spectra in aqueous solution having both dosing methods. The absorbance peak at 230 nm has been plotted with respect to the range of the molar ratios of Pb(II):BHA from 1:9 to 9:1. The obtained Job plots show that the stoichiometry of the complexes for the first one with BHA as a guest solution is XA = 0.42 (Figure 2b), which supports a stoichiometry of Pb(II):BHA between 1:1 to 1:2. Meanwhile, the reversing dosing method with the Pb(II) ion solution as the guest solution obtained XB = 0.67 (Figure 2d), clearly indicating that a stoichiometry of 1:2 corresponds to the structure of Pb(BHA)2. These results support the formation of Pb(BHA)2 complex when excessive BHA solution is added.
At the natural pH value of 4.4, the main components of Pb2+ solution are the Pb2+ cations [42]; as for the BHA solution, the mean components are BHA− anions [60]. Hence, both Pb2+ and BHA− should be the main reactants involved in the coordination reaction. In addition, the stability constants obtained in our previous work [10] for the Pb–BHA complexes are 9.14 ± 0.05 ((Pb)(BHA)+) and 12.63 ± 0.01 ((Pb)(BHA)2). Apparently, these experimental results support the existence of Pb(BHA)+ and Pb(BHA)2. Considering the order that we prepared the mixture for the UV-Vis tests can influence the reaction paths, the accepted potential reaction mechanism are described as follows:
BHA − + Pb 2 + → Pb ( BHA ) + → BHA − Pb ( BHA ) 2
2 BHA − + Pb 2 + → Pb ( BHA ) 2
where Equation (2) can be explained as the stepwise formation of the single coordinated Pb(BHA)+ complex, when a small quantity of BHA− solution is used as a guest specie, and Equation (3) is ideal for interpreting the formation of Pb(BHA)2, when Pb(II) solution is used as a guest specie. The water molecules and other ions are excluded to better identify the highest coordination number of BHA with Pb(II) as central metal ion.
Figure 3 shows the continued UV-Vis test results at the characteristic peaks of 221, 230, 235, and 240 nm that can explain the mechanism of forming high coordination complexes. These drawn curves show a consistent trend. For a clear illustration, we have divided these curves into three stages. At the beginning stage, the absorbance increases rapidly. At the end of the rising stage at 1 mM/L of BHA, a 1:1 (v:v) Pb(II)–BHA complex is formed, which is consistent with both the obtained result of the Pb(BHA)+ complex in the Job plots and the computational section. Afterward, the curves show a slow rising stage region with a small slope from 1 mM/L to 2.5 mM/L. The fluctuation of these collected data suggests that the component in the solution should be intricate. Interestingly, these trends end with the same proportion of Pb:BHA = 1:2.5, at which the Pb(BHA)2 complex can exist as indicated by the Job plots. When increasing the BHA concentration, these curves adopt a horizontal line-like region of the similar absorbance intensity to pure BHA solution.
The three stages in the curve can be seen as the stepwise formation of high coordination complexes, as interpreted by Equation (2). Note that the higher coordination components with more than 2 BHA as ligands are not sufficiently supported by the Job plots. Better experimental evidence has been collected from the electrospray ionization-mass spectrometry (ESI-MS) pattern.

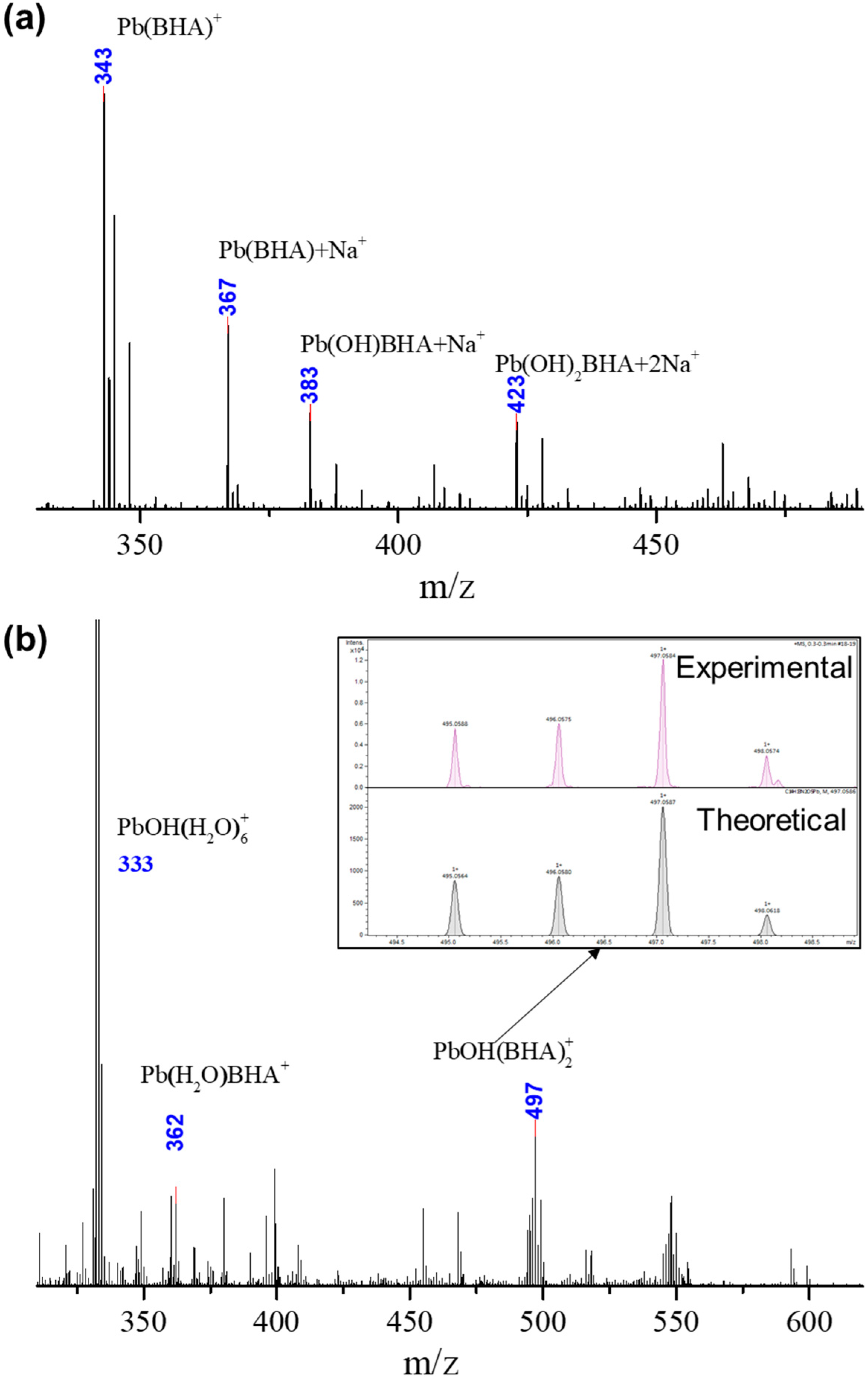
3.1.2. ESI-MS Results

To find out possible Pb(II)–BHA complexes formed in the solution, the collected ESI-MS data of reaction mixtures of lead nitrate and BHA with water as the solvent at the positive mode are shown in Figure 4. Figure 4a shows that when the solution pH is approximately 13.0 in the mixture, the main product is the single coordination complex Pb(BHA)+ with m/z values of 343. Figure 4b shows that Pb(II)–BHA complex at the molar ratio of 1:2 can produce m/z values of 362 and 497 responding to the (Pb(H2O)BHA)+ and (Pb(OH)BHA2)+ in aqueous solution, respectively. The later (Pb(OH)BHA2)+ configuration is quite abnormal, in which lead ion possesses a positive tetravalence. The reason for this is still unclear. However, this does not affect the following discussions and conclusions. The inset in Figure 4b shows the predicated spectra of (Pb(OH)BHA2)+ is in good agreement with the experimental one, further suggesting the existence of the double coordinated complexes. Proof of the single coordinated Pb(II) complex and double coordinated complex with BHA as ligands is provided, indicating that the Pb(BHA)+, Pb(BHA)2, and the possible high coordination complexes are closely related to the pH value. This finding is consistent with the result obtained from the continuous concentration change method. Meanwhile, these findings of the hydrated Pb(II) of (PbOH(H2O)6)+ and the Pb(II)–BHA complex, as shown in Figure 4b, suggested that the hydration shell of Pb(II) may be destroyed due to its coordination reaction with BHA.
The ESI-MS results have validated the existence of the Pb(II) complex with one and two BHA as ligands. The experimental approaches are not sufficient, however, to provide exact structures or properties at the microscopic scale; thus, the structures of Pb(II)–BHA complexes, have been further explored by using first-principle DFT calculations at high accuracy, including the solvation effects.

3.2. Theoretical Prediction

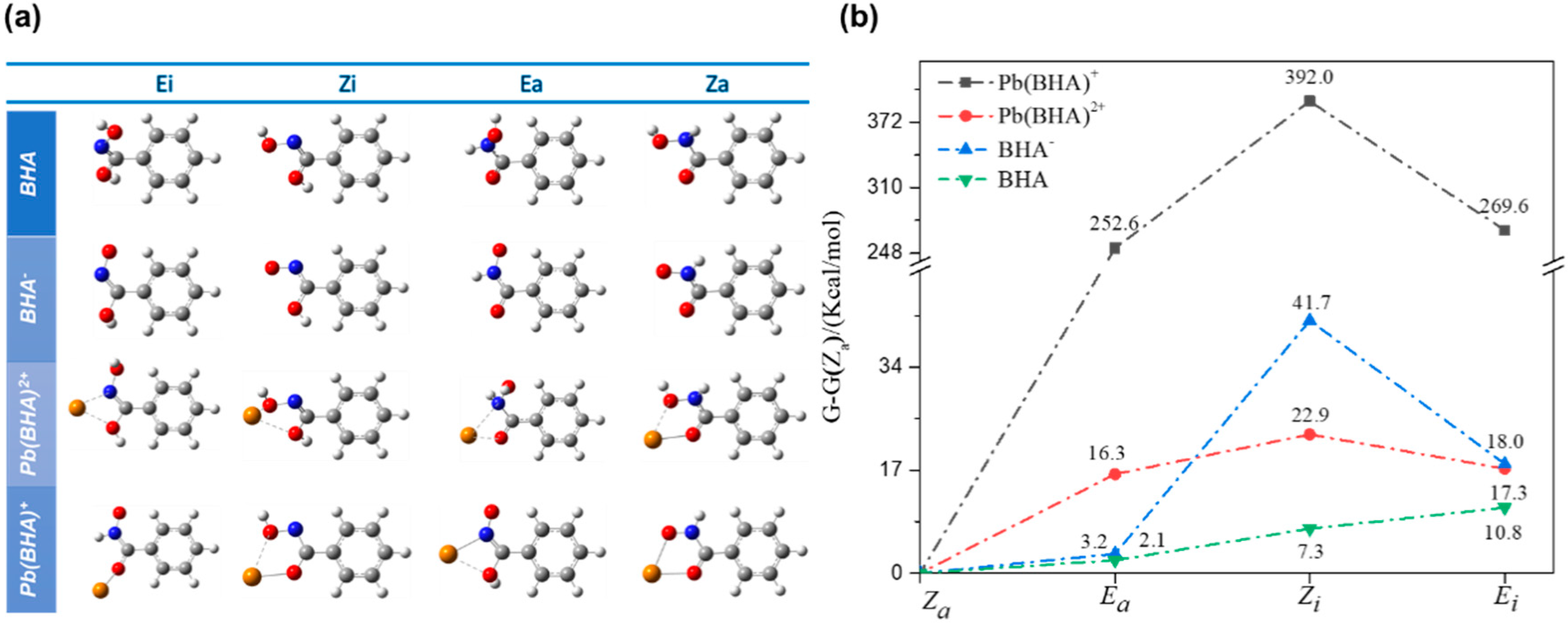
3.2.1. Prediction of Stable BHA Isomers and Pb(II)–BHA Complexes

All optimized BHA and BHA− (the anion of the BHA molecule with the dissociation of the proton) structures and their complexes with the Pb(II) ion are shown in the first two rows in Figure 5a at a B3LYP/aug-cc-pVDZ theoretical level. These optimized structures are divided into four categories called Ei, Zi, Ea, and Za. From the calculation results as shown in Figure 5b, it is clear that the corresponding Za type is most stable configuration for BHA, BHA−, Pb(BHA)2+, and Pb(BHA)+. The interesting finding is that BHA prefers to coordinate with Pb(II) to form a “Pb–O–C–N–O” five-membered ring, not a “Pb–O–C–N” four-membered ring, which is consistent with the previous report [26].
Because Za-type BHA is the most stable structure, it has been adopted in the following calculations and discussions. To better understand the interaction of Pb–BHA with water molecules, the influence of water molecules on the studied system has been further investigated using the explicit water molecules.

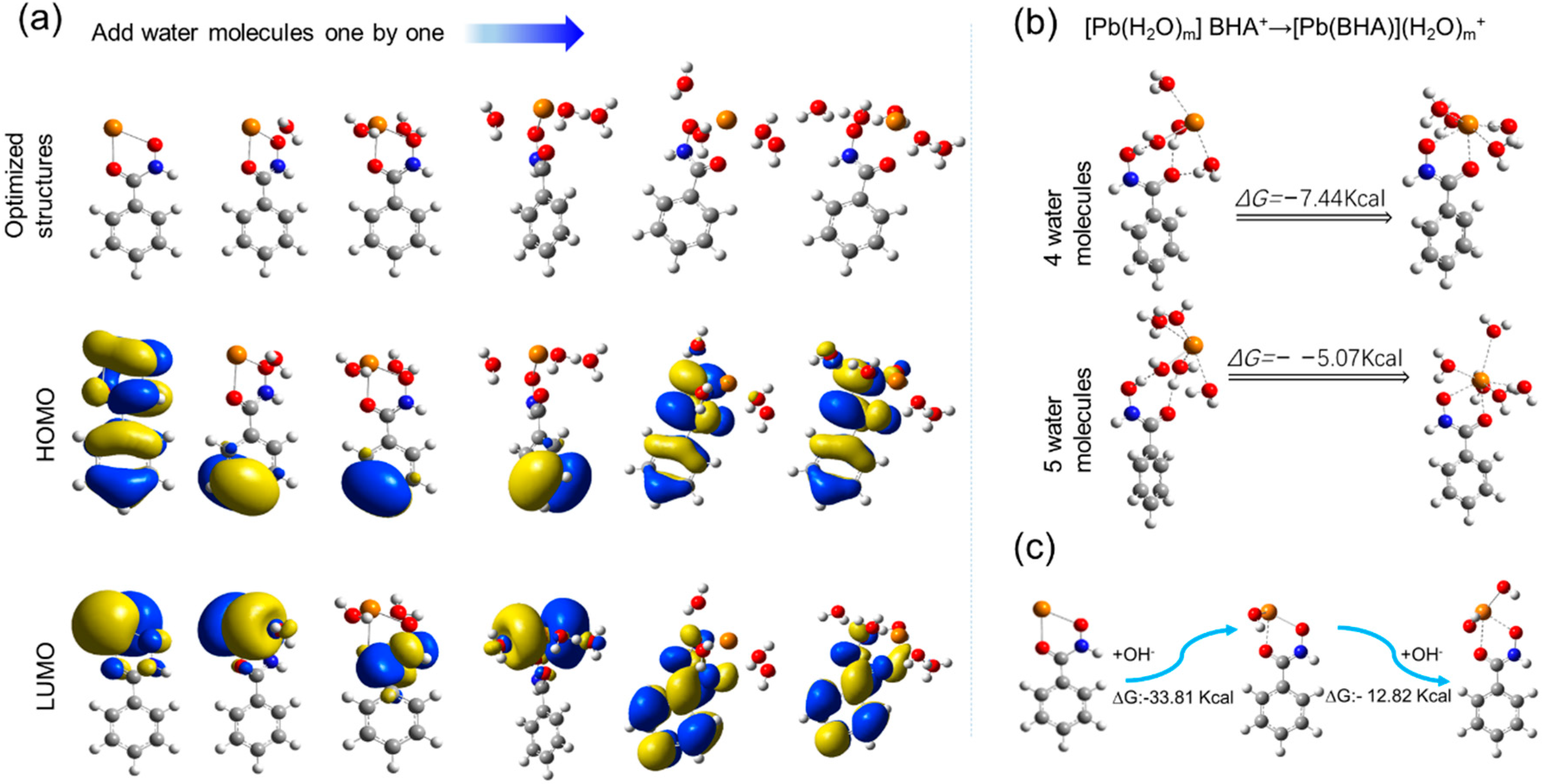
3.2.2. Single Pb–BHA in Aqueous Solution

The hydration of lead-BHA complex with different coordination water molecules has been investigated to consider the real aqueous environment. Figure 6a shows that water molecules were added one by one to coordinate with the Pb(BHA)+ complex. This procedure can be described by Equations (4) and (5) below:
Pb ( H 2 O )   m 2 + + BHA − ↔ Pb ( H 2 O ) m ( BHA ) +
Pb ( BHA ) + ( H 2 O ) m + H 2 O ↔ Pb ( BHA ) + H 2 O ( m + 1 )
where m(0→4). Here, the hydrated lead(II) cation is a six folded complex in the first hydration shell, according to the previous report [51].
As shown in Figure 6a, the electronical density distribution of LUMO (bottom (a)) shifted from the lead ion to the BHA molecule, indicating the active site of the lead-BHA complex can be influenced by the coordinated water molecules. The increasing number of water molecules from 0 to 3 results in small differences in the electronical density distribution of LUMO and HOMO, which suggests the active site of Pb(BHA)+ is stable. A fairly dispersed distribution of LUMO and HOMO on the whole complex has been observed, after adding more than 3 water molecules, which should be due to the influence of the surrounding water molecules.
Figure 6b shows the optimized structures of a BHA reacted with a hydrated lead(II) ion (left of Figure 6b, denoted as (Pb(H2O)m)BHA)+ and the hydration structure of Pb(BHA)+ (right of Figure 6b, denoted as (Pb–BHA)(H2O)m)+ with four (m = 4) and five (m = 5) water molecules, respectively. The Gibbs free energy differences between ((Pb(H2O)m)BHA)+ and ((Pb–BHA)(H2O)m)+ are −7.44 kcal/mol and −5.07 kcal/mol with respect to four (m = 4) and five (m = 5) water molecules, respectively. These calculated results show that ((Pb–BHA)(H2O)m)+ is more favorable in thermodynamics.
As is tabulated in Table 1, all the Gibbs free energy differences of the coordination reactions of (Pb–BHA)+(H2O)m (m > 0) with another water molecule shown are positive, although all the Gibbs free energy changes of the coordination reactions of Pb2+ with water molecule are negative. This indicates that Pb2+ prefers to coordinate with more than five water molecules, but (Pb–BHA)− will not like to coordinate with more than two water molecules (ΔG > 10 kcal/mol for the third water molecule), and in the hydration configurations of ((Pb–BHA)(H2O)m)+, (Pb–BHA)− and (Pb–BHA)−H2O should be the dominate species. These findings are consistent with the ESI-MS results.
On the other hand, with the addition of the coordinated water molecules, the average bond length of Pb–O in both hydration systems of (Pb–BHA)+(H2O)m and Pb(H2O)m2+ increased. The bond length of Pb–O in (Pb–BHA)+H2O is 2.53 Å, which is similar to the mean bond length of Pb–O in Pb(H2O)5 (2.55 Å). In structure chemistry, the basic idea is that the longer bond length, the less stable the corresponding complex. Thus, the changes of mean bond length of Pb–O in (Pb–BHA)+(H2O)m and Pb(H2O)m2+ also confirmed that (Pb–BHA)+(H2O)m are less stable than (Pb–BHA)+ and Pb(H2O)m2+.
In addition, the scheelite flotation [16] are usually performed at the alkaline pH, hydroxyl ion (OH−) are a key component in the pulp. Thus, the coordination reactions of Pb(BHA)+ with OH− were also investigated in this work. Herein, the coordination of the Pb(BHA)+ with OH− has been simulated in a stepwise order, as shown in Figure 6c. The reaction site has been chosen according to the LUMO of Pb(BHA)+. The optimized structures of Pb(BHA)(OH) and (Pb(BHA)(OH)2)− and the reaction Gibbs free energies changes (ΔG) are also given in Figure 6c. The hydroxyl binding with Pb(BHA)+ and PbOH(BHA) respond with binding energies of −33.81 Kcal/mol and −12.82 Kcal/mol, respectively. These results suggest that the coordination reaction of hydroxyl with the Pb(BHA)+ are thermodynamically favorable. At a natural pH of 4.4, both Pb2+ and BHA− should be the major reactants involved in the coordination reaction. At a real flotation plant, however, a higher pH value close to 9 is used. At such pH or a higher pH, both Pb(BHA)(OH) and (Pb(BHA)(OH)2)− could exist in the flotation solution. These results are in good accordance with experimental m/z value of 383 and 423 in ESI-MS patterns, which refer to (Pb(BHA)(OH)+Na)+ and the (Pb(BHA)(OH)2 + 2Na)+ species in Figure 4, respectively.
Consistently positive ΔG of the coordination reactions between (Pb–BHA)+(H2O)m (m > 1) and another water molecule should be ascribed to the result of the stronger coordination of BHA− with Pb2+ (ΔG is −356.55 kcal/mol as listed in Table 1). The coordination involving charge transfer from the ligand BHA− to the metal ion Pb2+ makes the properties and electronic structure of Pb–BHA less active than the independent lead(II) ion. The results agree well with the transformation in Figure 6b, where the bonded BHA is strong enough to protect the Pb2+ from the influence of surrounding water molecules.
Based on these results and discussions (the BHA− can coordinate with the Pb(II) smoothly), the following work has been conducted under the implicit model rather than explicit water molecules.

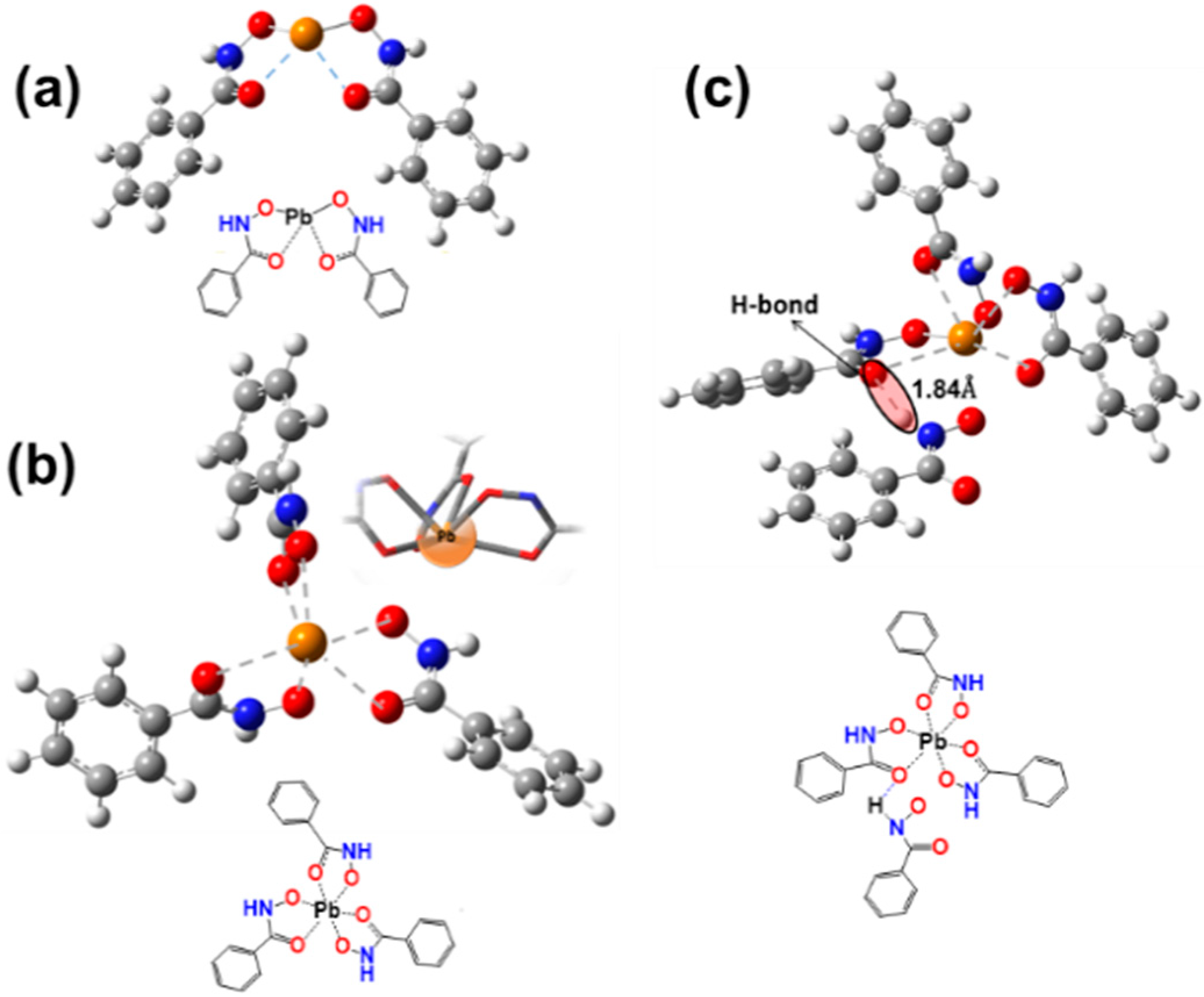
3.2.3. High Coordination Complexes

In thermodynamics, the isomer with the lowest Gibbs free energy (G) could be the most stable and most efficient isomer; Za type structures should be the optimal configurations and the dominant components according to the Gibbs free energies shown in Figure 5b, which is consistent with the results obtained by Begoña et al. [32]. The Za type structure as the ligand has been used for the subsequent calculations. The initial Pb(II)–BHA coordination complexes are modeled with the Pb(II) ion as the central metal ion, based on the stepwise mechanism in Equation (2). To obtain the possible high coordination compounds, we increased the coordination number of BHA ligand to 4.
As shown in Figure 7, all Pb(II)–BHA coordination complexes possess hemidirected geometry (in such configuration, BHA ligands occupy merely half of the space surrounding the Pb(II) atom) [7,51,61]. As shown in Table 2, the reaction between the BHA with the Pb(II) (Figure 7a) corresponds to a total reaction free energy change of −356.55 Kcal/mol, indicating the Pb–BHA− is a fairly favorable specie in thermodynamics. For the second BHA− ligand (Figure 7b), the total reaction free energy change is −27.20 Kcal/mol, excluding the reaction free energy of Pb(BHA)+. The reaction energy (−356.55 Kcal/mol) of BHA− with Pb2+ is much higher than that of water molecules with Pb (−50.48 Kcal/mol), indicating the coordination reaction of BHA− with Pb2+ will be more efficient than that of H2O with Pb2+. Thereafter, the coordination reaction of the third BHA− produces a positive change in Gibbs free energy of 0.03 Kcal/mol, implying that the binding of the third water molecule with the former Pb(BHA)2 is not favorable in thermodynamics. Moreover, as is shown in Figure 7c, when CN reaches 4, the intramolecular aggregation occurred due to a hydrogen bonding interaction (The highlighted N–H...O bond in Figure 7c) between the added BHA− and another adjoining BHA−, with the hydrogen bond (N–H...O) length of 1.84 Ǻ [26,62] and the N–H...O angle of 153.9°. A higher CN than 3 should not be stable, but a Pb(II)–BHA complex with three or more BHA ligands can appear due to the intermolecular interactions, including the Van der Waals’ force, H-bonding interaction.

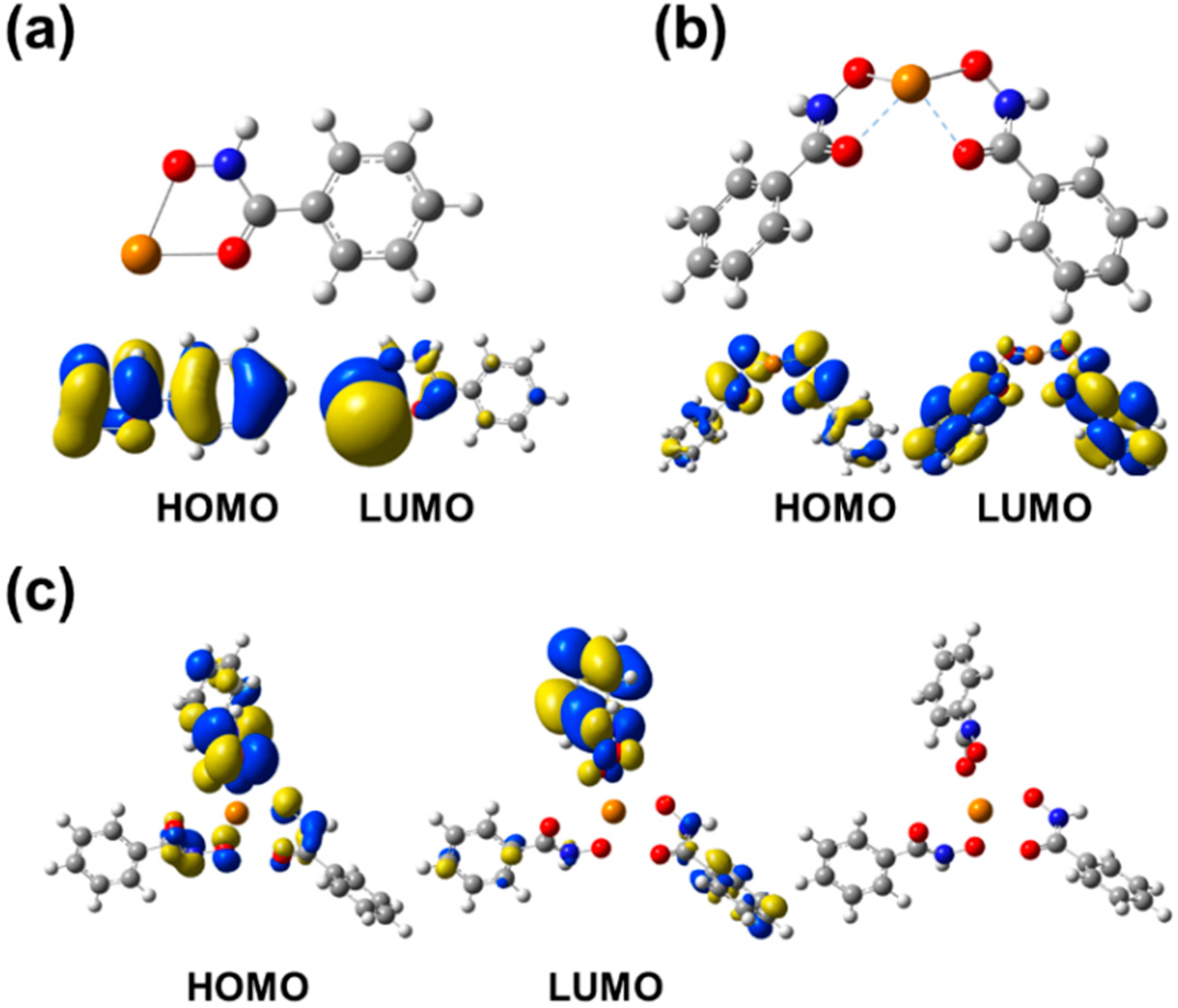
3.2.4. Frontier Molecular Orbital Analysis

In Figure 8 the ligands of Pb(BHA)2 (b) and (Pb(BHA)3)− (c) occupied just half of the space surrounding the Pb(II) ions. Pb(BHA)2 and (Pb(BHA)3)− adopted the hemidirected Pb(II)–BHA structures due to the lone pair electron contributed by BHA ligands [51,63]. Additionally, the structure of BHA can form some dimer structures and even interact with themselves. The adjoining BHA may result in aggregation due to intermolecular interaction [32].
As illustrated in Figure 8a, the LUMO of Pb(BHA)+ is mainly located at the Pb atom indicating that the Pb site of the Pb(BHA)+ should be active in electrophilic reaction. The LUMO of Pb(BHA)2 in Figure 7b and the (Pb(BHA)3)− in Figure 8c, however, spreads over the whole molecule, suggesting that the molecule is not active in electrophilic reaction. Because the Pb(II)–BHA is used as selective collector of oxide mineral, where the hydrated oxide mineral surface is an electron rich system, the Pb(BHA)+ can be more actively absorb onto the surface than other species in the Pb(II)–BHA solution. Additionally, as is shown in Table 3, the Pb atom contributes 91.93% to the LUMO, a rate much higher than that in other Pb(II)–BHA complexes, based on the NAO [64] method. These results have further verified that the Pb atom in Pb(BHA)+ can be the active site to adsorb onto the oxide minerals surface. This is consistent with the reported results [9,10,24,65].

4. Conclusions

In the present study, experimentally, Job plots considering two dosing strategies indicate that the Pb coordination compounds in solution may adopt the stoichiometry of Pb(BHA)+ and Pb(BHA)2. UV-Vis results obtained by the equimolar continuous change method show that the Pb(BHA)+ and the high coordination number compounds should be formed stepwise in aqueous solution. Thereafter, the electrospray ionization-mass spectrometry (ESI-MS) results provide strong proofs that the Pb(BHA)+ and (PbOH(BHA)2)+ should be the stable species at the alkaline pH in solution; and the Pb(BHA)+ should be the major component in aqueous solution at the natural pH. Furthermore, first-principles density functional theory (DFT) calculations show that: the Za type BHA should be the major structure; the Pb(BHA)+ can be stable in aqueous solution; and the formation of higher coordination number complexes are not favorable. Finally, the frontier molecular orbitals analyses show that the Pb atom of Pb(BHA)+ is the largest contributor to the LUMO. This suggests that the Pb atom in the structure should be the active site for accepting nucleophile and can also be the active site to adsorb onto the surface of oxide minerals. Both experimental results and theoretical results are in good accordance. These findings are meaningful to further illustrate the adsorption mechanism of Pb(II)–BHA complexes in mineral processing.

Author Contributions

C.Z. and W.S. conceived and designed the calculations; D.C. designed the experiments; C.Z. and J.H. performed the DFT calculations and analyzed computational results; H.H. and J.H. performed the experiments and analyzed experimental results; Y.H. analyzed the experimental data and modified the paper; J.H. and H.H. investigated literatures; D.Y. and M.T. constructed the computational model and drew the figures; C.Z. and J.H. wrote the paper.

Funding

The work was supported by Natural Science Foundation of China (No. 51704330); the Found of State Key Laboratory of Mineral Processing (No. BGRIMM-KJSKL-2017-13); Natural Science Foundation of China (No. 51374247); the Startup Fund of Central South University for Young Teachers (502044001); The Innovation Program for Postgraduate Students of Central South University (No. 2018zzts802); the National 111 Project (No. B14034); Collaborative Innovation Center for Clean and Efficient Utilization of Strategic Metal Mineral Resources; Innovation Driven Plan of Central South University (No. 2015CX005); Key Laboratory of Hunan Province for Clean and Efficient Utilization of Strategic Calcium-containing Mineral Resources (No. 2018TP1002); and the National Science and Technology Support Project of China.

Acknowledgments

This work was carried out in part using hardware and/or software provided by a Tianhe II supercomputer at the National Supercomputing Center in Guangzhou, and the High-Performance Computing Centers of Central South University and Nanjing University. ESI-MS measurements were conducted at the Modern Analysis and Testing Center of CSU.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hou, G.L.; Chen, B.; Transue, W.J.; Yang, Z.; Grutzmacher, H.; Driess, M.; Cummins, C.C.; Borden, W.T.; Wang, X.B. Spectroscopic characterization, computational investigation, and comparisons of ecx- (e = as, p, and n; x = s and o) anions. J. Am. Chem. Soc. 2017, 139, 8922–8930. [Google Scholar] [CrossRef] [PubMed]
  2. Kuta, J.; Clark, A.E. Trends in aqueous hydration across the 4f period assessed by reliable computational methods. Inorg. Chem. 2010, 49, 7808–7817. [Google Scholar] [CrossRef] [PubMed]
  3. Aguilo, E.; Moro, A.J.; Gavara, R.; Alfonso, I.; Perez, Y.; Zaccaria, F.; Guerra, C.F.; Malfois, M.; Baucells, C.; Ferrer, M.; et al. Reversible self-assembly of water-soluble gold(i) complexes. Inorg. Chem. 2017, 57, 1017–1028. [Google Scholar] [CrossRef] [PubMed]
  4. Akturk, E.S.; Scappaticci, S.J.; Seals, R.N.; Marshak, M.P. Bulky beta-diketones enabling new lewis acidic ligand platforms. Inorg. Chem. 2017, 56, 11466–11469. [Google Scholar] [CrossRef] [PubMed]
  5. Bhatta, S.R.; Mondal, B.; Vijaykumar, G.; Thakur, A. Ict-isomerization-induced turn-on fluorescence probe with a large emission shift for mercury ion: Application in combinational molecular logic. Inorg. Chem. 2017, 56, 11577–11590. [Google Scholar] [CrossRef] [PubMed]
  6. Choi, K.M.; Kim, D.; Rungtaweevoranit, B.; Trickett, C.A.; Barmanbek, J.T.D.; Alshammari, A.S.; Yang, P.; Yaghi, O.M. Plasmon-enhanced photocatalytic CO2 conversion within metal–organic frameworks under visible light. J. Am. Chem. Soc. 2017, 139, 356–362. [Google Scholar] [CrossRef] [PubMed]
  7. Jalilehvand, F.; Sisombath, N.S.; Schell, A.C.; Facey, G.A. Lead(II) complex formation with l-Cysteine in aqueous solution. Inorg. Chem. 2015, 54, 2160–2170. [Google Scholar] [CrossRef] [PubMed]
  8. Li, J.; Yu, X.; Xu, M.; Liu, W.; Sandraz, E.; Lan, H.; Wang, J.; Cohen, S.M. Metal–organic frameworks as micromotors with tunable engines and brakes. J. Am. Chem. Soc. 2017, 139, 611–614. [Google Scholar] [CrossRef] [PubMed]
  9. Han, H.; Hu, Y.; Sun, W.; Li, X.; Chen, K.; Zhu, Y.; Nguyen, A.V.; Tian, M.; Wang, L.; Yue, T.; et al. Novel catalysis mechanisms of benzohydroxamic acid adsorption by lead ions and changes in the surface of scheelite particles. Miner. Eng. 2018, 119, 11–22. [Google Scholar] [CrossRef]
  10. Tian, M.; Hu, Y.; Sun, W.; Liu, R. Study on the mechanism and application of a novel collector-complexes in cassiterite flotation. Colloid Surf. A Physicochem. Eng. Aspects 2017, 522, 635–641. [Google Scholar] [CrossRef]
  11. Han, H.; Hu, Y.; Sun, W.; Li, X.; Cao, C.; Liu, R.; Yue, T.; Meng, X.; Guo, Y.; Wang, J.; et al. Fatty acid flotation versus bha flotation of tungsten minerals and their performance in flotation practice. Int. J. Miner. Process. 2017, 159, 22–29. [Google Scholar] [CrossRef]
  12. Gao, Z.; Li, C.; Sun, W.; Hu, Y. Anisotropic surface properties of calcite: A consideration of surface broken bonds. Colloid Surf. A: Physicochem. Eng. Aspects 2017, 520, 53–61. [Google Scholar] [CrossRef]
  13. Li, C.; Gao, Z. Effect of grinding media on the surface property and flotation behavior of scheelite particles. Powder Technol. 2017, 322, 386–392. [Google Scholar] [CrossRef]
  14. Sun, L.; Hu, Y.; Sun, W. Effect and mechanism of octanol in cassiterite flotation using benzohydroxamic acid as collector. Trans. Nonferrous Met. Soc. China 2016, 26, 3253–3257. [Google Scholar] [CrossRef]
  15. Gao, Z.Y.; Sun, W.; Hu, Y.H. New insights into the dodecylamine adsorption on scheelite and calcite: An adsorption model. Miner. Eng. 2015, 79, 54–61. [Google Scholar] [CrossRef]
  16. Han, H.-S.; Liu, W.-L.; Hu, Y.-H.; Sun, W.; Li, X.-D. A novel flotation scheme: Selective flotation of tungsten minerals from calcium minerals using Pb–BHA complexes in shizhuyuan. Rare Met. 2017, 36, 533–540. [Google Scholar] [CrossRef]
  17. Hu, Y.; Qiu, G.; Miller, J.D. Hydrodynamic interactions between particles in aggregation and flotation. Int. J. Miner. Process. 2003, 70, 157–170. [Google Scholar] [CrossRef]
  18. Zhao, G.; Wang, S.; Zhong, H. Study on the activation of scheelite and wolframite by lead nitrate. Minerals 2015, 5, 247–258. [Google Scholar] [CrossRef]
  19. Filippova, I.V.; Filippov, L.O.; Duverger, A.; Severov, V.V. Synergetic effect of a mixture of anionic and nonionic reagents: Ca mineral contrast separation by flotation at neutral ph. Miner. Eng. 2014, 66, 135–144. [Google Scholar] [CrossRef]
  20. Deng, L.; Zhao, G.; Zhong, H.; Wang, S.; Liu, G. Investigation on the selectivity of N-((hydroxyamino)-alkyl) alkylamide surfactants for scheelite/calcite flotation separation. J. Ind. Eng. Chem. 2016, 33, 131–141. [Google Scholar] [CrossRef]
  21. Chen, Z.; Ren, Z.; Gao, H.; Lu, J.; Jin, J.; Min, F. The effects of calcium ions on the flotation of sillimanite using dodecylammonium chloride. Minerals 2017, 7, 28. [Google Scholar] [CrossRef]
  22. Materna, K.L.; Crabtree, R.H.; Brudvig, G.W. Anchoring groups for photocatalytic water oxidation on metal oxide surfaces. Chem. Soc. Rev. 2017, 46, 6099–6110. [Google Scholar] [CrossRef] [PubMed]
  23. Gao, Y.; Gao, Z.; Sun, W.; Yin, Z.; Wang, J.; Hu, Y. Adsorption of a novel reagent scheme on scheelite and calcite causing an effective flotation separation. J. Colloid Interf. Sci. 2018, 512, 39–46. [Google Scholar] [CrossRef] [PubMed]
  24. Tian, M.; Gao, Z.; Han, H.; Sun, W.; Hu, Y. Improved flotation separation of cassiterite from calcite using a mixture of lead(II) ion/benzohydroxamic acid as collector and carboxymethyl cellulose as depressant. Miner. Eng. 2017, 113, 68–70. [Google Scholar] [CrossRef]
  25. Schraml, J. Derivatives of hydroxamic acids. Appl. Organomet. Chem. 2000, 14, 604–610. [Google Scholar] [CrossRef]
  26. Codd, R. Traversing the coordination chemistry and chemical biology of hydroxamic acids. Coord. Chem. Rev. 2008, 252, 1387–1408. [Google Scholar] [CrossRef]
  27. Flipo, M.; Charton, J.; Hocine, A.; Dassonneville, S.; Deprez, B.; Deprez-Poulain, R. Hydroxamates: Relationships between structure and plasma stability. J. Med. Chem. 2009, 52, 6790–6802. [Google Scholar] [CrossRef] [PubMed]
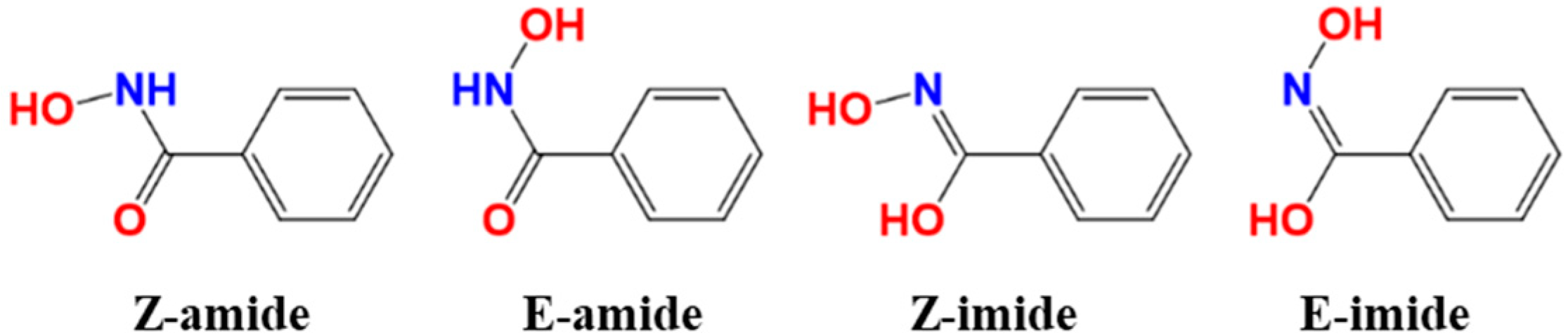
  28. Al-Saadi, A.A. Conformational analysis and vibrational assignments of benzohydroxamic acid and benzohydrazide. J. Mol. Struct. 2012, 1023, 115–122. [Google Scholar] [CrossRef]
  29. Lynch, A.J.; Watt, J.S.; Fich, J.A.; Harbort, G.J. History of flotation technology. In Forth Flotation: A Century of Innovation; SME: Littleton, CO, USA, 2007; pp. 65–91. [Google Scholar]
  30. Lei, X.L.; Pan, B.C. The geometries and proton transfer of hydrated divalent lead ion clusters [Pb(H2O)n]2+(n = 1–17). J. Theor. Comput. Chem. 2012, 11, 1149–1164. [Google Scholar] [CrossRef]
  31. Wander, M.C.F.; Rustad, J.R.; Casey, W.H. Influence of explicit hydration waters in calculating the hydrolysis constants for geochemically relevant metals. J. Phys. Chem. A 2010, 114, 1917–1925. [Google Scholar] [CrossRef] [PubMed]
  32. García, B.; Ibeas, S.; Leal, J.M.; Secco, F.; Venturini, M.; Senent, M.L.; Niño, A.; Muñoz, C. Conformations, protonation sites, and metal complexation of benzohydroxamic acid. A theoretical and experimental study. Inorg. Chem. 2005, 44, 2908–2919. [Google Scholar] [CrossRef] [PubMed]
  33. Adiguzel, E.; Yilmaz, F.; Emirik, M.; Ozil, M. Synthesis and characterization of two new hydroxamic acids derivatives and their metal complexes. An investigation on the keto/enol, E/Z and hydroxamate/hydroximate forms. J. Mol. Struct. 2017, 1127, 403–412. [Google Scholar] [CrossRef]
  34. Caudle, M.T.; Crumbliss, A.L. Dissociation kinetics of (N-methylacetohydroxamato) iron(III) complexes: A model for probing electronic and structural effects in the dissociation of siderophore complexes. Inorg. Chem. 1994, 33, 4077–4085. [Google Scholar] [CrossRef]
  35. O’Brien, E.C.; Farkas, E.; Gil, M.J.; Fitzgerald, D.; Castineras, A.; Nolan, K.B. Metal complexes of salicylhydroxamic acid (H2Sha), anthranilic hydroxamic acid and benzohydroxamic acid. Crystal and molecular structure of [Cu(phen)2(Cl)]Cl × H2Sha, a model for a peroxidase-inhibitor complex. J. Inorg. Biochem. 2000, 79, 47–51. [Google Scholar] [CrossRef]
  36. Bodwin, J.J.; Cutland, A.D.; Malkani, R.G.; Pecoraro, V.L. Cheminform abstract: The development of chiral metallacrowns into anion recognition agents and porous materials. Coord. Chem. Rev. 2001, 216, 489–512. [Google Scholar] [CrossRef]
  37. Pereira, C.F.; Howarth, A.J.; Vermeulen, N.A.; Almeida Paz, F.A.; Tomé, J.P.C.; Hupp, J.T.; Farha, O.K. Towards hydroxamic acid linked zirconium metal–organic frameworks. Mater. Chem. Front. 2017, 1, 1194–1199. [Google Scholar] [CrossRef]
  38. He, J.; Han, H.; Zhang, C.; Xu, Z.; Yuan, D.; Chen, P.; Sun, W.; Hu, Y. Novel insights into the surface microstructures of lead(ii) benzohydroxamic on oxide mineral. Appl. Surf. Sci. 2018, 458, 405–412. [Google Scholar] [CrossRef]
  39. Feng, Q.; Zhao, W.; Wen, S.; Cao, Q. Activation mechanism of lead ions in cassiterite flotation with salicylhydroxamic acid as collector. Sep. Purif. Technol. 2017, 178, 193–199. [Google Scholar] [CrossRef]
  40. Fukui, K.; Yonezawa, T.; Nagata, C. Theory of substitution in conjugated molecules. Bull. Chem. Soc. Jpn. 1954, 27, 423–427. [Google Scholar] [CrossRef]
  41. Glendening, E.D.; Landis, C.R.; Weinhold, F. Natural bond orbital methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 1–42. [Google Scholar] [CrossRef]
  42. Perera, W.N.; Hefter, G.A.; Sipos, P.M. An investigation of the lead(II)−hydroxide system. Inorg. Chem. 2001, 40, 3974–3978. [Google Scholar] [CrossRef] [PubMed]
  43. Renny, J.S.; Tomasevich, L.L.; Tallmadge, E.H.; Collum, D.B. Method of continuous variations: Applications of job plots to the study of molecular associations in organometallic chemistry. Angew. Chem. Int. Ed. 2013, 52, 11998–12013. [Google Scholar] [CrossRef] [PubMed]
  44. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; et al. Gaussian 09, Revision A. 02; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  45. Becke, A.D. Becke’s three parameter hybrid method using the lyp correlation functional. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  46. Yu, H.S.; Li, S.L.; Truhlar, D.G. Perspective: Kohn-sham density functional theory descending a staircase. J. Chem. Phys. 2016, 145, 130901. [Google Scholar] [CrossRef] [PubMed]
  47. Ho, J.; Ertem, M.Z. Calculating free energy changes in continuum solvation models. J. Phys. Chem. B 2016, 120, 1319–1329. [Google Scholar] [CrossRef] [PubMed]
  48. Feller, D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
  49. Malekghassemi, M. An Exploration of Molecular Mechanics and Quantum Chemical Methods. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.567.4830&rep=rep1&type=pdf (accessed on 18 August 2018).
  50. Lee, Y.S.; Ermler, W.C.; Pitzer, K.S. Ab initio effective core potentials including relativistic effects. V. SCF calculations with ω–ω coupling including results for Au2+, Tlh, Pbs, and PbSe. J. Chem. Phys. 1993, 73, 159–165. [Google Scholar] [CrossRef]
  51. Wander, M.C.F.; Clark, A.E. Hydration properties of aqueous Pb(II) ion. Inorg. Chem. 2008, 47, 8233–8241. [Google Scholar] [CrossRef] [PubMed]
  52. Ochterski, J.W. Vibrational Analysis in Gaussian. Available online: https://www.lindsayengineering.com/img/resources/vib.pdf (accessed on 18 August 2018).
  53. Arora, R.; Issar, U.; Kakkar, R. Theoretical study of the molecular structure and intramolecular proton transfer in benzohydroxamic acid. Comput. Theor. Chem. 2017, 1105, 18–26. [Google Scholar] [CrossRef]
  54. Steinberg, G.M.; Swidler, R. The benzohydroxamate anion. J. Org. Chem. 1965, 30, 2362–2365. [Google Scholar] [CrossRef]
  55. Ochterski, J.W. Thermochemistry in Gaussian. Available online: http://www.lct.jussieu.fr/manuels/Gaussian03/g_whitepap/thermo/thermo.pdf (accessed on 18 August 2018).
  56. Dennington, R.; Keith, T.; Millam, J. Gaussview, Version 5. Available online: https://gaussview.soft112.com (accessed on 18 August 2018).
  57. Lu, T.; Chen, F. Multiwfn: A multifunctional wave function analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
  58. Rekharsky, M.; Inoue, Y.; Tobey, S.; Metzger, A.; Anslyn, E. Ion-pairing molecular recognition in water:  Aggregation at low concentrations that is entropy-driven. J. Am. Chem. Soc. 2002, 124, 14959–14967. [Google Scholar] [CrossRef] [PubMed]
  59. Bruneau, E.; Lavabre, D.; Levy, G.; Micheau, J.C. Quantitative analysis of continuous-variation plots with a comparison of several methods: Spectrophotometric study of organic and inorganic 1:1 stoichiometry complexes. J. Chem. Educ. 1992, 69, 833. [Google Scholar] [CrossRef]
  60. Wise, W.M.; Brandt, W.W. Spectrophotometric determination of vandium(v) with benzohydroxamic acid and 1-hexanol. Anal. Chem. 1955, 27, 1392–1395. [Google Scholar] [CrossRef]
  61. Leon-Pimentel, C.I.; Amaro-Estrada, J.I.; Saint-Martin, H.; Ramirez-Solis, A. Born-Oppenheimer molecular dynamics studies of Pb(II) micro hydrated gas phase clusters. J. Chem. Phys. 2017, 146, 084307. [Google Scholar] [CrossRef] [PubMed]
  62. Azizi, A.; Ebrahimi, A. The X−···benzohydrazide complexes: The interplay between anion-π and H-bond interactions. Struct. Chem. 2017, 28, 687–695. [Google Scholar] [CrossRef]
  63. Moncomble, A.; Cornard, J.P.; Meyer, M. A quantum chemistry evaluation of the stereochemical activity of the lone pair in PbII complexes with sequestering ligands. J. Mol. Model. 2017, 23, 24. [Google Scholar] [CrossRef] [PubMed]
  64. Lu, T.; Chen, F. Calculation of molecular orbital composition. Acta Chim. Sin. 2011, 69, 2393–2406. [Google Scholar]
  65. Wei, Z.; Hu, Y.; Han, H.; Sun, W.; Wang, R.; Wang, J. Selective flotation of scheelite from calcite using Al-Na2SiO3 polymer as depressant and Pb–BHA complexes as collector. Miner. Eng. 2018, 120, 29–34. [Google Scholar] [CrossRef]
Minerals 08 00368 g001 550
Figure 1. (a) The flotation recovery of scheelite (S) [9] and cassiterite (C) [24] as a function of dosage of Pb(II) ion (1/2 in (a) represents the flotation scheme in i and ii in (b)); (b) two flotation schemes.
Figure 1. (a) The flotation recovery of scheelite (S) [9] and cassiterite (C) [24] as a function of dosage of Pb(II) ion (1/2 in (a) represents the flotation scheme in i and ii in (b)); (b) two flotation schemes.
Minerals 08 00368 g001
Minerals 08 00368 sch001 550
Scheme 1. BHA conformers.
Scheme 1. BHA conformers.
Minerals 08 00368 sch001
Minerals 08 00368 g002 550
Figure 2. (a,c) are the UV-Vis absorbance spectra spanning the wavelength from 185 nm to 325 nm for the different dosing strategies; (b,d) are the corresponding Job plots at 230 nm of (a,c), respectively. XA and XB are the mole fractions of Pb(II) ions and BHA according to dosing strategies 1 and 2, respectively. All stock solutions are prepared at 1 mM/L concentration.
Figure 2. (a,c) are the UV-Vis absorbance spectra spanning the wavelength from 185 nm to 325 nm for the different dosing strategies; (b,d) are the corresponding Job plots at 230 nm of (a,c), respectively. XA and XB are the mole fractions of Pb(II) ions and BHA according to dosing strategies 1 and 2, respectively. All stock solutions are prepared at 1 mM/L concentration.
Minerals 08 00368 g002
Minerals 08 00368 g003 550
Figure 3. UV-Vis absorbance changes of 1 mM/L Pb(II) ion solution with respect to the continuous addition of BHA (at wavelengths of 221, 230, 235, and 240 nm), based on the continuous concentration change method. Spheres for atoms Pb, C, H, O, and N in the inset are colored in orange, grey, white, red, and blue, respectively.
Figure 3. UV-Vis absorbance changes of 1 mM/L Pb(II) ion solution with respect to the continuous addition of BHA (at wavelengths of 221, 230, 235, and 240 nm), based on the continuous concentration change method. Spheres for atoms Pb, C, H, O, and N in the inset are colored in orange, grey, white, red, and blue, respectively.
Minerals 08 00368 g003
Minerals 08 00368 g004 550
Figure 4. ESI-MS results of the mixture of (a) Pb:BHA molar ratio of 1:1 at a pH value of 13.0 and (b) Pb:BHA molar ratio of 1:2 at the natural pH of 4.4. The inset in (b) is the comparative results of the theoretical spectra and the experimental spectra. (Solution concentrations are 1 mM/L).
Figure 4. ESI-MS results of the mixture of (a) Pb:BHA molar ratio of 1:1 at a pH value of 13.0 and (b) Pb:BHA molar ratio of 1:2 at the natural pH of 4.4. The inset in (b) is the comparative results of the theoretical spectra and the experimental spectra. (Solution concentrations are 1 mM/L).
Minerals 08 00368 g004
Minerals 08 00368 g005 550
Figure 5. (a) Optimized structures of BHA, BHA−, Pb(BHA)2+, and Pb(BHA)+. (b) Comparison of Gibbs free energy of BHA, BHA−, Pb(BHA)2+, and Pb(BHA)+ isomers with the Gibbs free energy of Za type as zero point. Spheres for Pb, C, H, O, and N atoms are colored in orange, gray, white, red, and blue, respectively.
Figure 5. (a) Optimized structures of BHA, BHA−, Pb(BHA)2+, and Pb(BHA)+. (b) Comparison of Gibbs free energy of BHA, BHA−, Pb(BHA)2+, and Pb(BHA)+ isomers with the Gibbs free energy of Za type as zero point. Spheres for Pb, C, H, O, and N atoms are colored in orange, gray, white, red, and blue, respectively.
Minerals 08 00368 g005
Minerals 08 00368 g006 550
Figure 6. The optimized structure (top (a)) of hydrated Pb(BHA)+ with the addition of water molecules one by one and the corresponding highest occupied molecular orbital (HOMO) (middle (a)) and lowest unoccupied molecular orbital (LUMO) (bottom (a)). (b) Gibbs free energy difference between the hydrated Pb(BHA)+ and hydrated Pb2+ +BHA complex with four and five water molecules. (c) The hydroxylation of Pb(BHA)+. The contours have been computed at the PCM-B3LYP level of theory with a threshold of 0.001 au, and spheres for Pb, C, H, O, and N atoms are colored in orange, gray, white, red, and blue, respectively.
Figure 6. The optimized structure (top (a)) of hydrated Pb(BHA)+ with the addition of water molecules one by one and the corresponding highest occupied molecular orbital (HOMO) (middle (a)) and lowest unoccupied molecular orbital (LUMO) (bottom (a)). (b) Gibbs free energy difference between the hydrated Pb(BHA)+ and hydrated Pb2+ +BHA complex with four and five water molecules. (c) The hydroxylation of Pb(BHA)+. The contours have been computed at the PCM-B3LYP level of theory with a threshold of 0.001 au, and spheres for Pb, C, H, O, and N atoms are colored in orange, gray, white, red, and blue, respectively.
Minerals 08 00368 g006
Minerals 08 00368 g007 550
Figure 7. (a–c) Optimized structures of Pb(II)–BHA with coordination numbers (CN) of Figure 2a, Figure 3b and Figure 4c. Spheres for Pb, C, H, O, and N atoms are colored in orange, gray, white, red, and blue, respectively.
Figure 7. (a–c) Optimized structures of Pb(II)–BHA with coordination numbers (CN) of Figure 2a, Figure 3b and Figure 4c. Spheres for Pb, C, H, O, and N atoms are colored in orange, gray, white, red, and blue, respectively.
Minerals 08 00368 g007
Minerals 08 00368 g008 550
Figure 8. (a–c) The frontier molecular orbitals (HOMO and LUMO) of Pb(II)–BHA complexes with 1 a, 2b, and 3c BHA ligands. The orbitals are generated at the B3LYP/aug-cc-pVDZ theory level with a threshold of 0.001 au, and the solvation effect is included with PCM model. Spheres for Pb, C, H, O, and N atoms are colored in orange, gray, white, red, and blue, respectively.
Figure 8. (a–c) The frontier molecular orbitals (HOMO and LUMO) of Pb(II)–BHA complexes with 1 a, 2b, and 3c BHA ligands. The orbitals are generated at the B3LYP/aug-cc-pVDZ theory level with a threshold of 0.001 au, and the solvation effect is included with PCM model. Spheres for Pb, C, H, O, and N atoms are colored in orange, gray, white, red, and blue, respectively.
Minerals 08 00368 g008
Table
Table 1. The changes in the reaction Gibbs free energy (ΔG) and the difference of Pb–O mean distance in the hydration system with coordination number (CN) m of water molecules varied from 1 to 5.
Table 1. The changes in the reaction Gibbs free energy (ΔG) and the difference of Pb–O mean distance in the hydration system with coordination number (CN) m of water molecules varied from 1 to 5.
CN of Water Molecules (m)ΔG/(Kcal/mol)Pb–O Mean Distance (Å)
(Pb–BHA)+(H2O)mPb(H2O)m2+(Pb–BHA)+(H2O)mPb(H2O)m2+
11.41−50.482.532.34
21.38−36.752.642.38
37.40−27.342.692.42
44.64−17.652.772.49
58.35−14.562.832.55
Table
Table 2. The changes in Gibbs free energy (ΔG) and Pb–O mean distance in Pb(II)–BHA complexes with CN of BHA ligands ranging from 1 to 3.
Table 2. The changes in Gibbs free energy (ΔG) and Pb–O mean distance in Pb(II)–BHA complexes with CN of BHA ligands ranging from 1 to 3.
CNReactionΔG(Kcal/mol)Pb–O (Å)εgap (eV)
1Pb2+ + BHA-−356.552.264.17
2Pb(BHA)+ + BHA-−27.202.404.50
3Pb(BHA)2 + BHA-+0.032.584.17
Table
Table 3. The contribution of the Pb atom to frontier molecular orbitals (HOMO+1, HOMO, LUMO, and LUMO−1) based on the NAO [64] method.
Table 3. The contribution of the Pb atom to frontier molecular orbitals (HOMO+1, HOMO, LUMO, and LUMO−1) based on the NAO [64] method.
Pb–BHAOrbital Composition Assigned to Pb atom/%
HOMO−1HOMOLUMOLUMO+1
Pb(BHA)+0.033.5591.9377.54
Pb(BHA)21.141.281.140.02
Pb(BHA) 3 − 1.010.750.130.00

Share and Cite

MDPI and ACS Style

He, J.; Han, H.; Zhang, C.; Hu, Y.; Yuan, D.; Tian, M.; Chen, D.; Sun, W. New Insights into the Configurations of Lead(II)-Benzohydroxamic Acid Coordination Compounds in Aqueous Solution: A Combined Experimental and Computational Study. Minerals 2018, 8, 368. https://doi.org/10.3390/min8090368

AMA Style

He J, Han H, Zhang C, Hu Y, Yuan D, Tian M, Chen D, Sun W. New Insights into the Configurations of Lead(II)-Benzohydroxamic Acid Coordination Compounds in Aqueous Solution: A Combined Experimental and Computational Study. Minerals. 2018; 8(9):368. https://doi.org/10.3390/min8090368

Chicago/Turabian Style

He, Jianyong, Haisheng Han, Chenyang Zhang, Yuehua Hu, Dandan Yuan, Mengjie Tian, Daixiong Chen, and Wei Sun. 2018. "New Insights into the Configurations of Lead(II)-Benzohydroxamic Acid Coordination Compounds in Aqueous Solution: A Combined Experimental and Computational Study" Minerals 8, no. 9: 368. https://doi.org/10.3390/min8090368

APA Style

He, J., Han, H., Zhang, C., Hu, Y., Yuan, D., Tian, M., Chen, D., & Sun, W. (2018). New Insights into the Configurations of Lead(II)-Benzohydroxamic Acid Coordination Compounds in Aqueous Solution: A Combined Experimental and Computational Study. Minerals, 8(9), 368. https://doi.org/10.3390/min8090368

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop