Multiple Kinetic Parameterization in a Reactive Transport Model Using the Exchange Monte Carlo Method
Abstract
1. Introduction
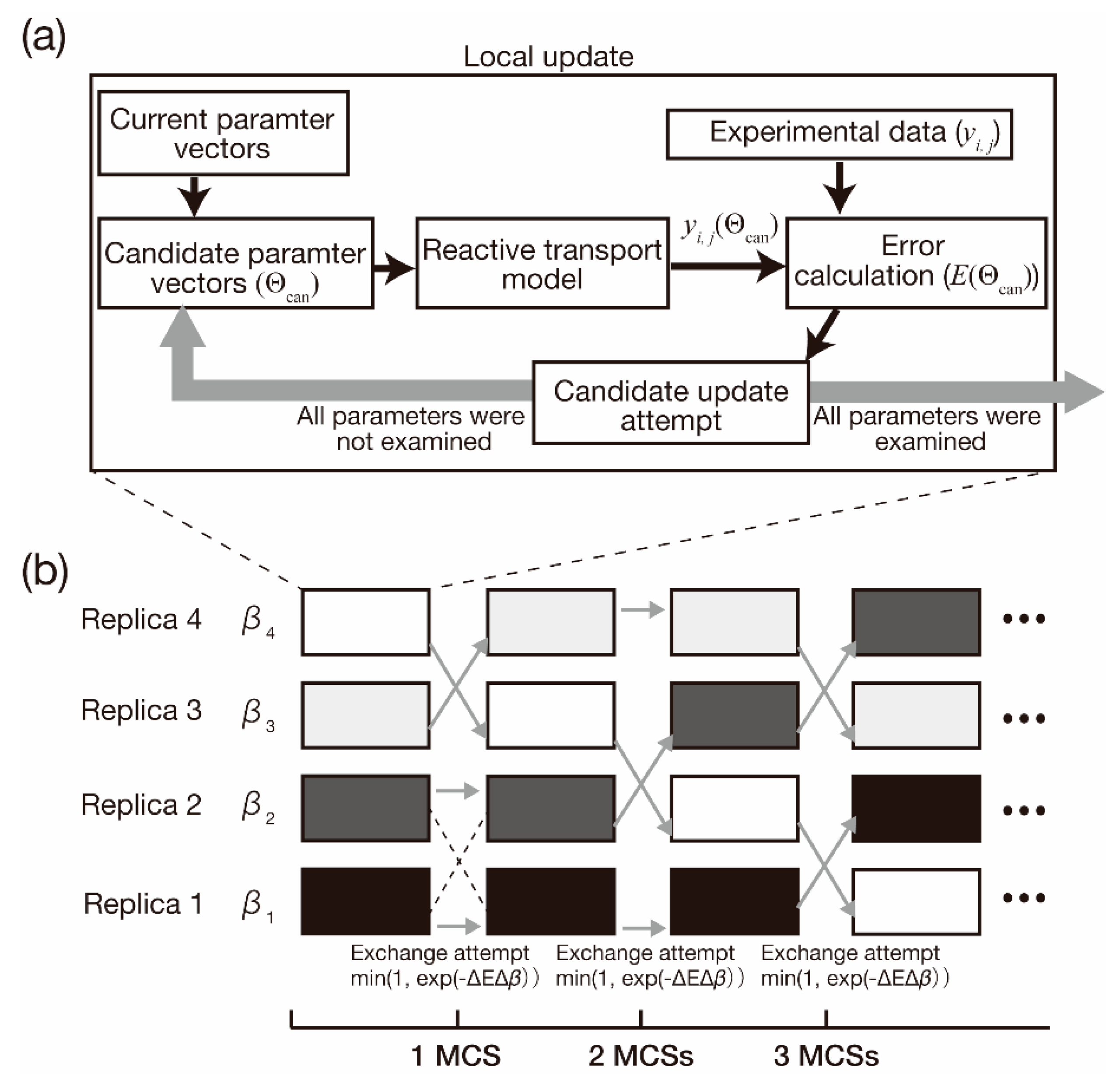
2. Methodology
2.1. General Framework
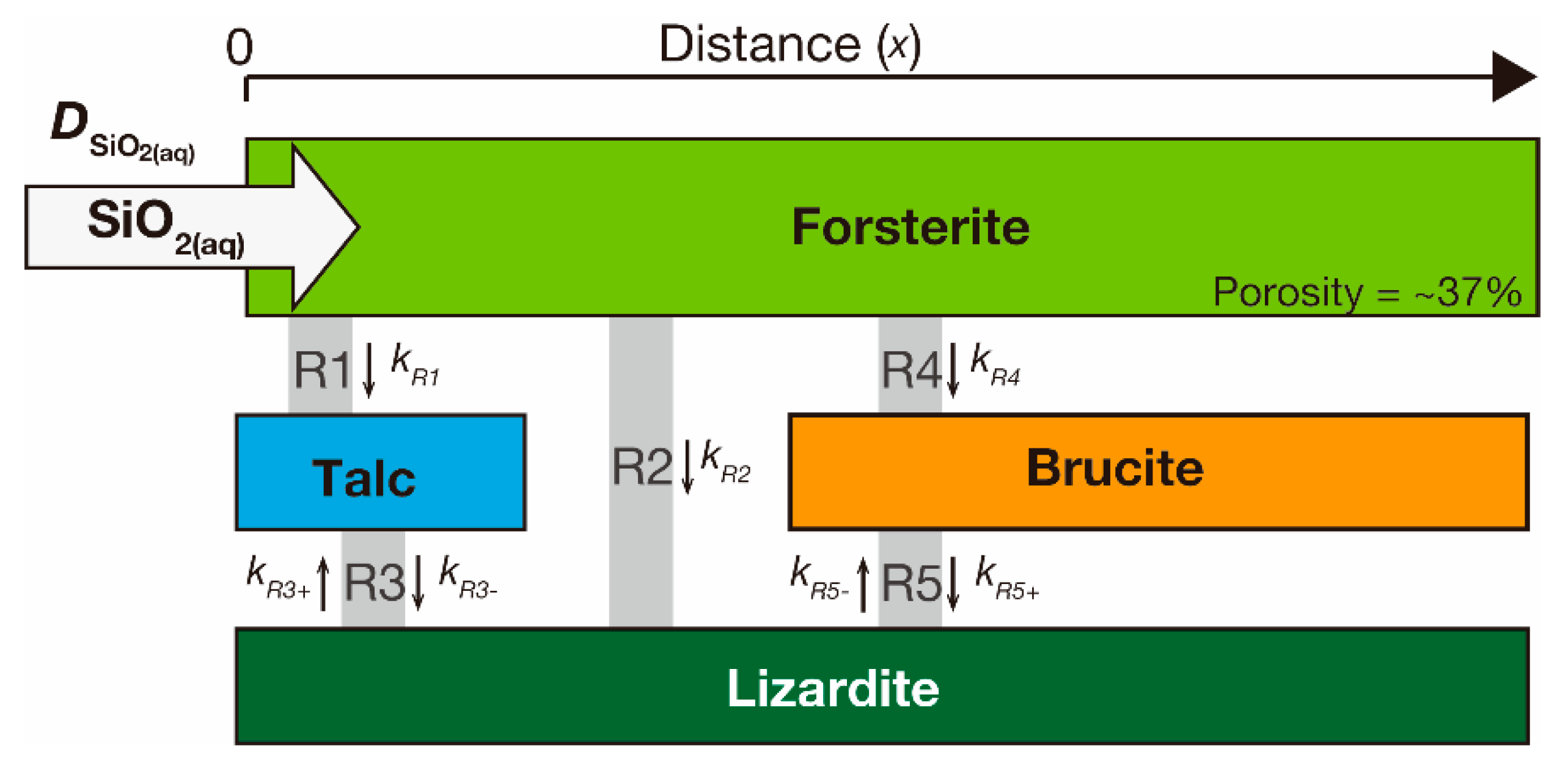
3. Synthetic Data: Silica Metasomatism in an Olivine–Quartz–H2O System
3.1. Model System
3.2. Kinetic Forward Model
3.3. Synthetic Datasets
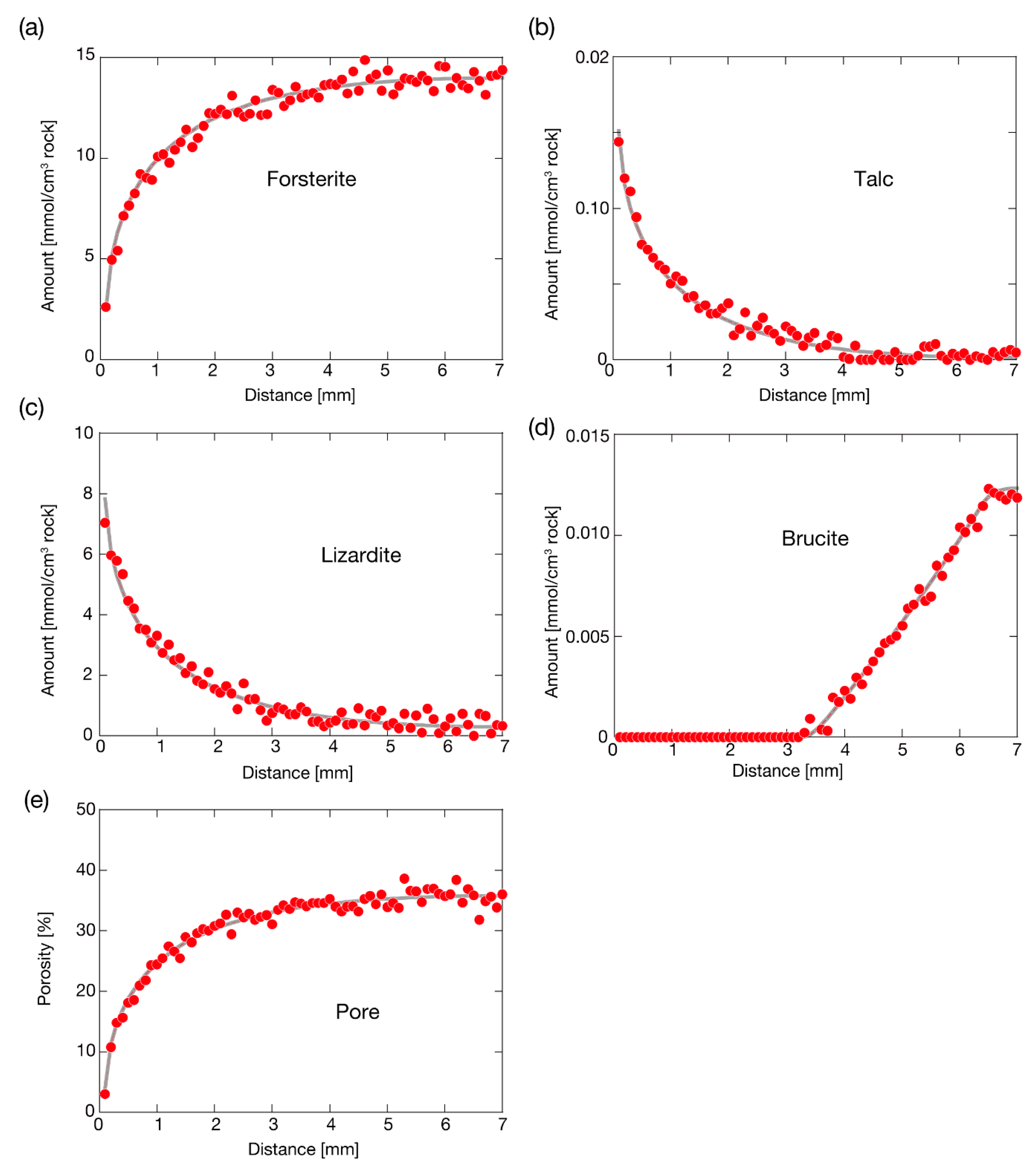
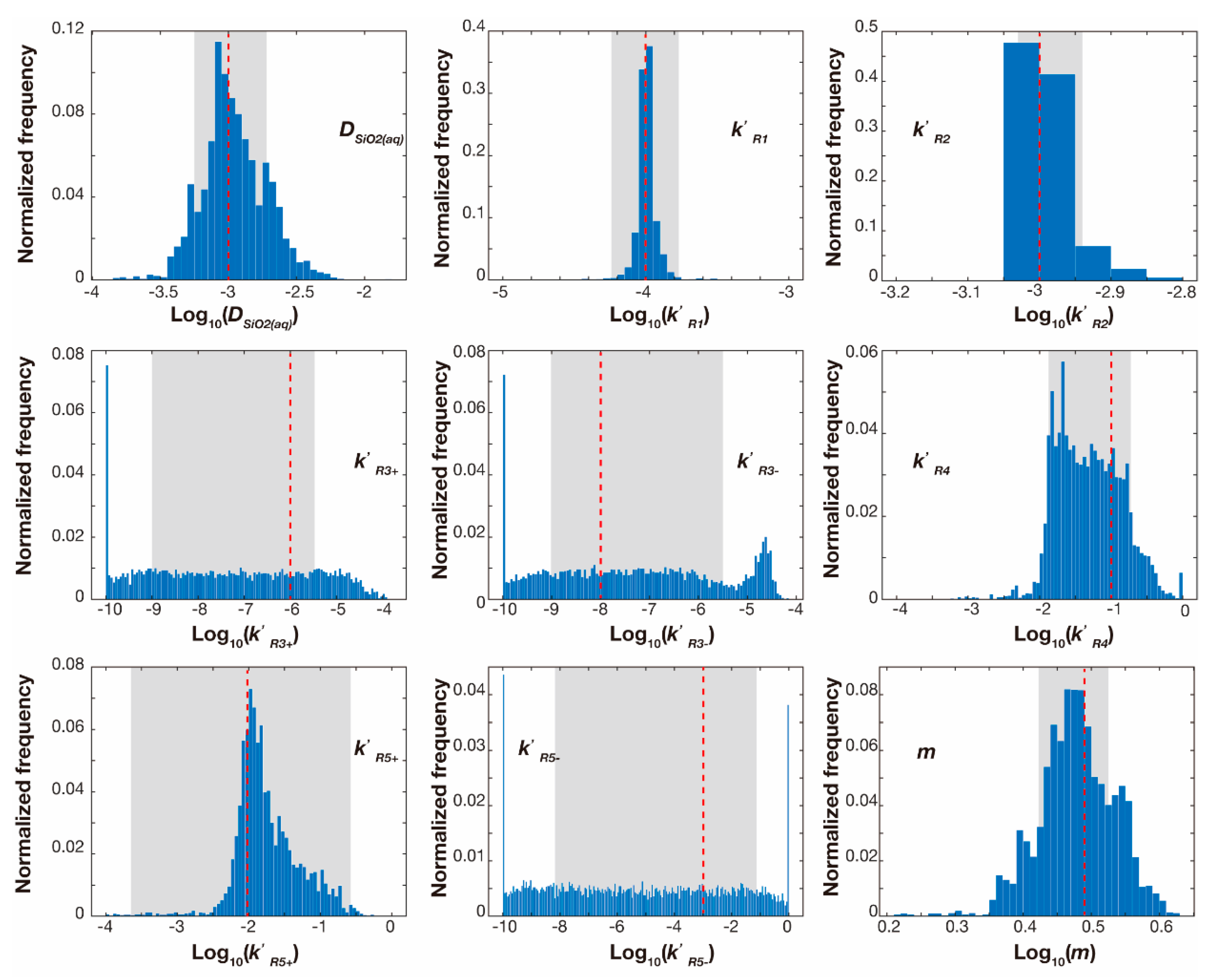
4. Results and Discussion
4.1. Extraction of Reaction Kinetic Parameters from Noisy Datasets with the Reactive Transport Model
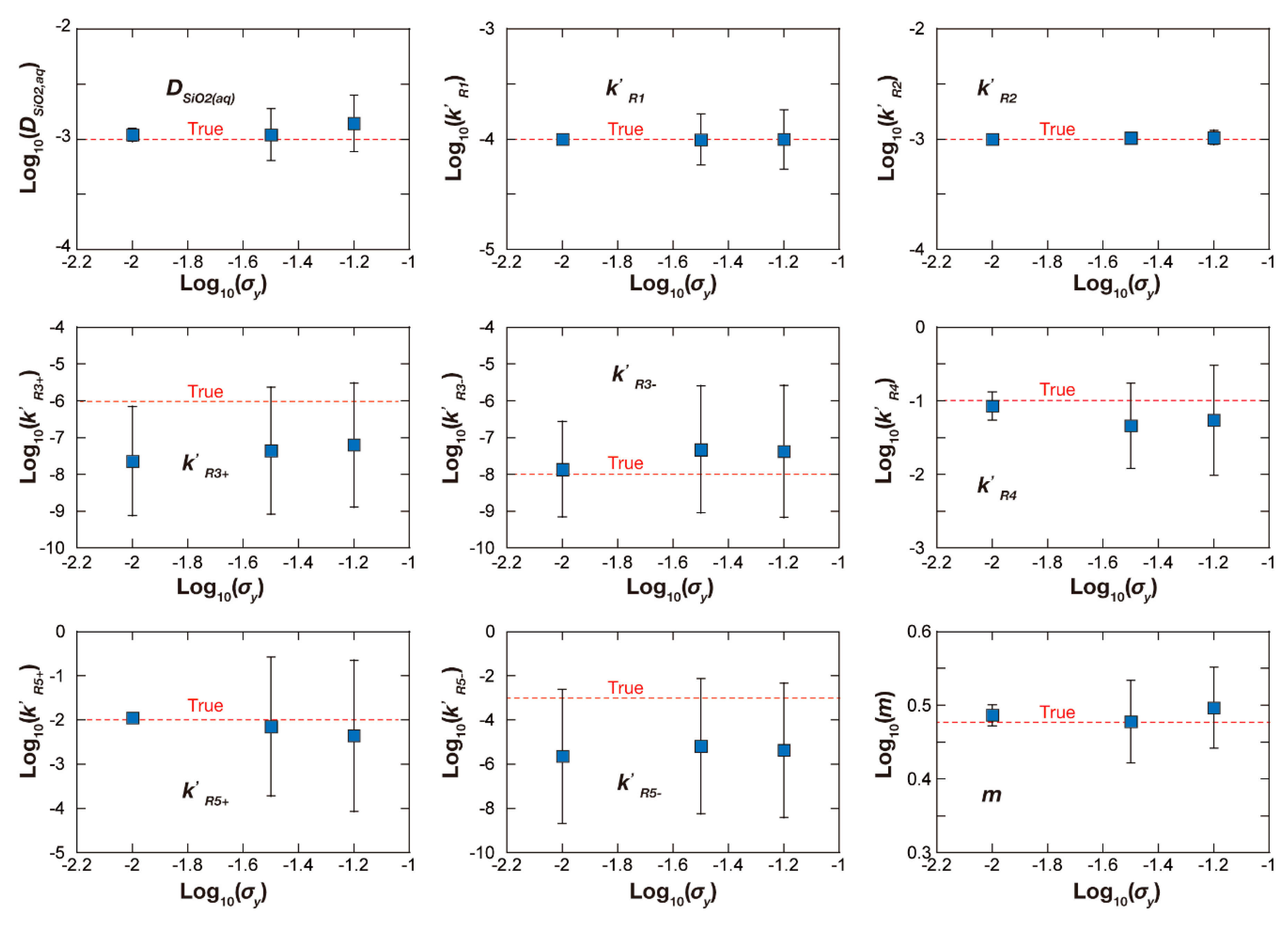
4.2. Dependence of Estimation Accuracy on Observation Noise
5. Summary and Outlook
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- John, T.; Gussone, N.; Podladchikov, Y.Y.; Bebout, G.E.; Dohmen, R.; Halama, R.; Klemd, R.; Magna, T.; Seitz, H.M. Volcanic arcs fed by rapid pulsed fluid flow through subducting slabs. Nat. Geosci. 2012, 5, 489–492. [Google Scholar] [CrossRef]
- Ague, J.J. Fluid infiltration and transport of major, minor, and trace elements during regional metamorphism of carbonate rocks, Wepawaug Schist, Connecticut, USA. Am. J. Sci. 2003, 303, 753–816. [Google Scholar] [CrossRef]
- Iyer, K.; Rüpke, L.H.; Morgan, J.P. Feedbacks between mantle hydration and hydrothermal convection at ocean spreading centers. Earth Planet. Sci. Lett. 2010, 296, 34–44. [Google Scholar] [CrossRef]
- Scott, S.; Driesner, T.; Weis, P. Geologic controls on supercritical geothermal resources above magmatic intrusions. Nat. Commun. 2015, 6, 1–6. [Google Scholar] [CrossRef] [PubMed]
- DePaolo, D.J.; Cole, D.R. Geochemistry of Geologic Carbon Sequestration: An Overview. Rev. Mineral. Geochem. 2013, 77, 1–14. [Google Scholar] [CrossRef]
- Hammond, G.E.; Lichtner, P.C. Field-scale model for the natural attenuation of uranium at the Hanford 300 Area using high-performance computing. Water Resour. Res. 2010, 46, 1–31. [Google Scholar] [CrossRef]
- Xu, T.; Apps, J.A.; Pruess, K.; Yamamoto, H. Numerical modeling of injection and mineral trapping of CO2 with H2S and SO2 in a sandstone formation. Chem. Geol. 2007, 242, 319–346. [Google Scholar] [CrossRef]
- Rimstidt, J.D.; Brantley, S.L.; Olsen, A.A. Systematic review of forsterite dissolution rate data. Geochim. Cosmochim. Acta 2012, 99, 159–178. [Google Scholar] [CrossRef]
- Zhu, C.; Lu, P.; Zheng, Z.; Ganor, J. Coupled alkali feldspar dissolution and secondary mineral precipitation in batch systems: 4. Numerical modeling of kinetic reaction paths. Geochim. Cosmochim. Acta 2010, 74, 3963–3983. [Google Scholar] [CrossRef]
- Maher, K.; Steefel, C.I.; DePaolo, D.J.; Viani, B.E. The mineral dissolution rate conundrum: Insights from reactive transport modeling of U isotopes and pore fluid chemistry in marine sediments. Geochim. Cosmochim. Acta 2006, 70, 337–363. [Google Scholar] [CrossRef]
- Lamadrid, H.M.; Rimstidt, J.D.; Schwarzenbach, E.M.; Klein, F.; Ulrich, S.; Dolocan, A.; Bodnar, R.J. Effect of water activity on rates of serpentinization of olivine. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Hellmann, R. The albite-water system: Part I. The kinetics of dissolution as a function of pH at 100, 200 and 300 °C. Geochim. Cosmochim. Acta 1994, 58, 595–611. [Google Scholar] [CrossRef]
- Rimstidt, J.D.; Barnes, H.L. The kinetics of silica-water reactions. Geochim Cosmochim Acta 1980, 44, 1683–1699. [Google Scholar] [CrossRef]
- Malvoisin, B.; Brunet, F.; Carlut, J.; Rouméjon, S.; Cannat, M. Serpentinization of oceanic peridotites: 2. Kinetics and processes of San Carlos olivine hydrothermal alteration. J. Geophys. Res. Solid Earth 2012, 117, 1–13. [Google Scholar] [CrossRef]
- Oyanagi, R.; Okamoto, A.; Harigane, Y.; Tsuchiya, N. Al-Zoning of Serpentine Aggregates in Mesh Texture Induced by Metasomatic Replacement Reactions. J. Petrol. 2018, 59, 613–634. [Google Scholar] [CrossRef]
- Watson, E.B.; Wark, D.A. Diffusion of dissolved SiO2 in H2O at 1 GPa, with implications for mass transport in the crust and upper mantle. Contrib. Mineral. Petrol. 1997, 130, 66–80. [Google Scholar] [CrossRef]
- Beig, M.S.; Lüttge, A. Albite dissolution kinetics as a function of distance from equilibrium: Implications for natural feldspar weathering. Geochim. Cosmochim. Acta 2006, 70, 1402–1420. [Google Scholar] [CrossRef]
- Wolery, T.J.; Jové Colón, C.F. Chemical thermodynamic data. 1. The concept of links to the chemical elements and the historical development of key thermodynamic data. Geochim. Cosmochim. Acta 2017, 213, 635–676. [Google Scholar] [CrossRef]
- Oelkers, E.H.; Benezeth, P.; Pokrovski, G.S. Thermodynamic Databases for Water-Rock Interaction. Rev. Mineral. Geochem. 2009, 70, 1–46. [Google Scholar] [CrossRef]
- McCollom, T.M.; Klein, F.; Robbins, M.; Moskowitz, B.; Berquó, T.S.; Jöns, N.; Bach, W.; Templeton, A. Temperature trends for reaction rates, hydrogen generation, and partitioning of iron during experimental serpentinization of olivine. Geochim. Cosmochim. Acta 2016, 181, 175–200. [Google Scholar] [CrossRef]
- Lafay, R.; Montes-Hernandez, G.; Janots, E.; Chiriac, R.; Findling, N.; Toche, F. Mineral replacement rate of olivine by chrysotile and brucite under high alkaline conditions. J. Cryst. Growth 2012, 347, 62–72. [Google Scholar] [CrossRef]
- Wegner, W.W.; Ernst, W.G. Experimentally determined hydration and dehydration reaction rates in the system MgO‒SiO2‒H2O. Am. J. Sci. 1983, 283 A, 151–180. [Google Scholar]
- Martin, B.; Fyfe, W. Some experimental and theoretical observations on the kinetics of hydration reactions with particular reference to serpentinization. Chem. Geol. 1970, 6, 185–202. [Google Scholar] [CrossRef]
- Bandstra, J.Z.; Brantley, S.L. Data Fitting Techniques with Applications to Mineral Dissolution Kinetics. In Kinetics of Water-Rock Interaction; Springer-New York: New York, NY, USA, 2008; pp. 211–257. ISBN 9780387735627. [Google Scholar]
- Aggarwal, M.; Carrayrou, J. Parameter estimation for reactive transport by a Monte-Carlo approach. AIChE J. 2006, 52, 2281–2289. [Google Scholar] [CrossRef]
- Hukushima, K.; Nemoto, K. Exchange Monte Carlo Method and Application to Spin Glass Simulations. J. Phys. Soc. Jpn. 1996, 65, 1604–1608. [Google Scholar] [CrossRef]
- Iba, Y. Extended Ensemble Monte Carlo. Int. J. Mod. Phys. C 2001, 12, 623–656. [Google Scholar] [CrossRef]
- Nagata, K.; Watanabe, S. Asymptotic behavior of exchange ratio in exchange Monte Carlo method. Neural Netw. 2008, 21, 980–988. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Kano, M.; Nagao, H.; Ishikawa, D.; Ito, S.I.; Sakai, S.; Nakagawa, S.; Hori, M.; Hirata, N. Seismic wavefield imaging based on the replica exchange Monte Carlo method. Geophys. J. Int. 2017, 208, 529–545. [Google Scholar] [CrossRef]
- Gupta, S.; Hainsworth, L.; Hogg, J.; Lee, R.; Faeder, J. Evaluation of Parallel Tempering to Accelerate Bayesian Parameter Estimation in Systems Biology. In Proceedings of the 2018 26th Euromicro International Conference on Parallel, Distributed and Network-based Processing (PDP), Cambridge, UK, 21–23 March 2018; pp. 690–697. [Google Scholar]
- Takahashi, T.; Obana, K.; Yamamoto, Y.; Nakanishi, A.; Kodaira, S.; Kaneda, Y. S wave attenuation structure on the western side of the Nankai subduction zone: Implications for fluid distribution and dynamics. J. Geophys. Res. Solid Earth 2014, 119, 7805–7822. [Google Scholar] [CrossRef]
- Nakakoji, T.; Hiraga, T.; Nagao, H.; Ito, S.; Kano, M. Diffusion creep and grain growth in forsterite + 20 vol% enstatite aggregates: 1. High-resolution experiments and their data analyses. J. Geophys. Res. Solid Earth 2018. [Google Scholar] [CrossRef]
- Lasaga, A.C. Kinetic Theory in the Earth Sciences; Princeton University Press: Princeton, NJ, USA, 1998; ISBN 0-691-03748-5. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT press: Cambridge, MA, USA, 2016. [Google Scholar]
- Okamoto, A.; Kuwatani, T.; Omori, T.; Hukushima, K. Free-energy landscape and nucleation pathway of polymorphic minerals from solution in a Potts lattice-gas model. Phys. Rev. E - Stat. Nonlinear, Soft Matter Phys. 2015, 92, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Earl, D.J.; Deem, M.W. Parallel tempering: Theory, applications, and new perspectives. Phys. Chem. Chem. Phys. 2005, 7, 3910. [Google Scholar] [CrossRef] [PubMed]
- Hukushima, K. Domain-wall free energy of spin-glass models: Numerical method and boundary conditions. Phys. Rev. E 1999, 60, 3606–3613. [Google Scholar] [CrossRef]
- Sanbonmatsu, K.Y.; García, A.E. Structure of Met-enkephalin in explicit aqueous solution using replica exchange molecular dynamics. Proteins Struct. Funct. Bioinforma. 2002, 46, 225–234. [Google Scholar] [CrossRef] [PubMed]
- Habeck, M.; Nilges, M.; Rieping, W. Replica-Exchange Monte Carlo Scheme for Bayesian Data Analysis. Phys. Rev. Lett. 2005, 94, 018105. [Google Scholar] [CrossRef] [PubMed]
- Lichtner, P.C.; Oelkers, E.H.; Helgeson, H.C. Interdiffusion with multiple precipitation/dissolution reactions: Transient model and the steady-state limit. Geochim. Cosmochim. Acta 1986, 50, 1951–1966. [Google Scholar] [CrossRef]
- Frantz, J.D.; Mao, H.K. Bimetasomatism resulting from intergranular diffusion; I, A theoretical model for monomineralic reaction zone sequences. Am. J. Sci. 1976, 276, 817–840. [Google Scholar] [CrossRef]
- Oyanagi, R.; Okamoto, A.; Hirano, N.; Tsuchiya, N. Competitive hydration and dehydration at olivine-quartz boundary revealed by hydrothermal experiments: Implications for silica metasomatism at the crust-mantle boundary. Earth Planet. Sci. Lett. 2015, 425. [Google Scholar] [CrossRef]
- Kimura, J.I.; Nakajima, J. Behaviour of subducted water and its role in magma genesis in the NE Japan arc: A combined geophysical and geochemical approach. Geochim. Cosmochim. Acta 2014, 143, 165–188. [Google Scholar] [CrossRef]
- Plümper, O.; John, T.; Podladchikov, Y.Y.; Vrijmoed, J.C.; Scambelluri, M. Fluid escape from subduction zones controlled by channel-forming reactive porosity. Nat. Geosci. 2017, 10, 150–156. [Google Scholar] [CrossRef]
- Fritz, B.; Clément, A.; Montes-Hernandez, G.; Noguera, C. Theoretical analysis of the kinetics of precipitation of lizardite and magnesite from olivine alteration. Chem. Geol. 2018, 497, 18–26. [Google Scholar] [CrossRef]
- Ogasawara, Y.; Okamoto, A.; Hirano, N.; Tsuchiya, N. Coupled reactions and silica diffusion during serpentinization. Geochim. Cosmochim. Acta 2013, 119, 212–230. [Google Scholar] [CrossRef]
- Steefel, C.I. Geochemical Kinetics and Transport. In Kinetics of Water-Rock Interaction; Springer-New York: New York, NY, USA, 2008; pp. 545–589. [Google Scholar]
- Zimmer, K.; Zhang, Y.; Lu, P.; Chen, Y.; Zhang, G.; Dalkilic, M.; Zhu, C. SUPCRTBL: A revised and extended thermodynamic dataset and software package of SUPCRT92. Comput. Geosci. 2016, 90, 97–111. [Google Scholar] [CrossRef]
- Walther, J.V.; Helgeson, H.C. Calculation of the thermodynamic properties of aqueous silica and the solubility of quartz and its polymorphs at high pressures and temperatures. Am. J. Sci. 1977, 277, 1315–1351. [Google Scholar] [CrossRef]
- Holland, T.J.B.; Powell, R. An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids. J. Metamorph. Geol. 2011, 29, 333–383. [Google Scholar] [CrossRef]
- Oelkers, E.H. Physical and chemical properties of rocks and fluids for chemical mass transport calculations. Rev. Mineral. 1997, 34, 131–192. [Google Scholar]
- Archie, G.E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics. Trans. AIME 1942, 146, 54–62. [Google Scholar] [CrossRef]
- Ildefonse, J.-P.; Gabis, V. Experimental study of silica diffusion during metasomatic reactions in the presence of water at 550 °C and 1000 bars. Geochim. Cosmochim. Acta 1976, 40, 297–303. [Google Scholar] [CrossRef]
- Yokoyama, T. Diffusivity of dissolved silica in rock pore water at 25 °C as characterized by through-diffusion experiments. Water Resour. Res. 2013, 49, 8299–8309. [Google Scholar] [CrossRef]
- Yokoyama, T.; Sakuma, H. The effects of charge, polymerization, and cluster size on the diffusivity of dissolved Si species in pore water. Geochim. Cosmochim. Acta 2018, 224, 301–312. [Google Scholar] [CrossRef]
- Omori, T.; Kuwatani, T.; Okamoto, A.; Hukushima, K. Bayesian inversion analysis of nonlinear dynamics in surface heterogeneous reactions. Phys. Rev. E 2016, 94, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kuwatani, T.; Nagao, H.; Ito, S.; Okamoto, A.; Yoshida, K.; Okudaira, T. Recovering the past history of natural recording media by Bayesian inversion. Phys. Rev. E 2018, 98, 043311. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Fischer, C.; Arvidson, R.S.; Lüttge, A. How predictable are dissolution rates of crystalline material? Geochim. Cosmochim. Acta 2012, 98, 177–185. [Google Scholar] [CrossRef]
- Fischer, C.; Luttge, A. Beyond the conventional understanding of water–rock reactivity. Earth Planet. Sci. Lett. 2017, 457, 100–105. [Google Scholar] [CrossRef]
- Lüttge, A.; Arvidson, R.S.; Fischer, C. A stochastic treatment of crystal dissolution kinetics. Elements 2013, 9, 183–188. [Google Scholar] [CrossRef]
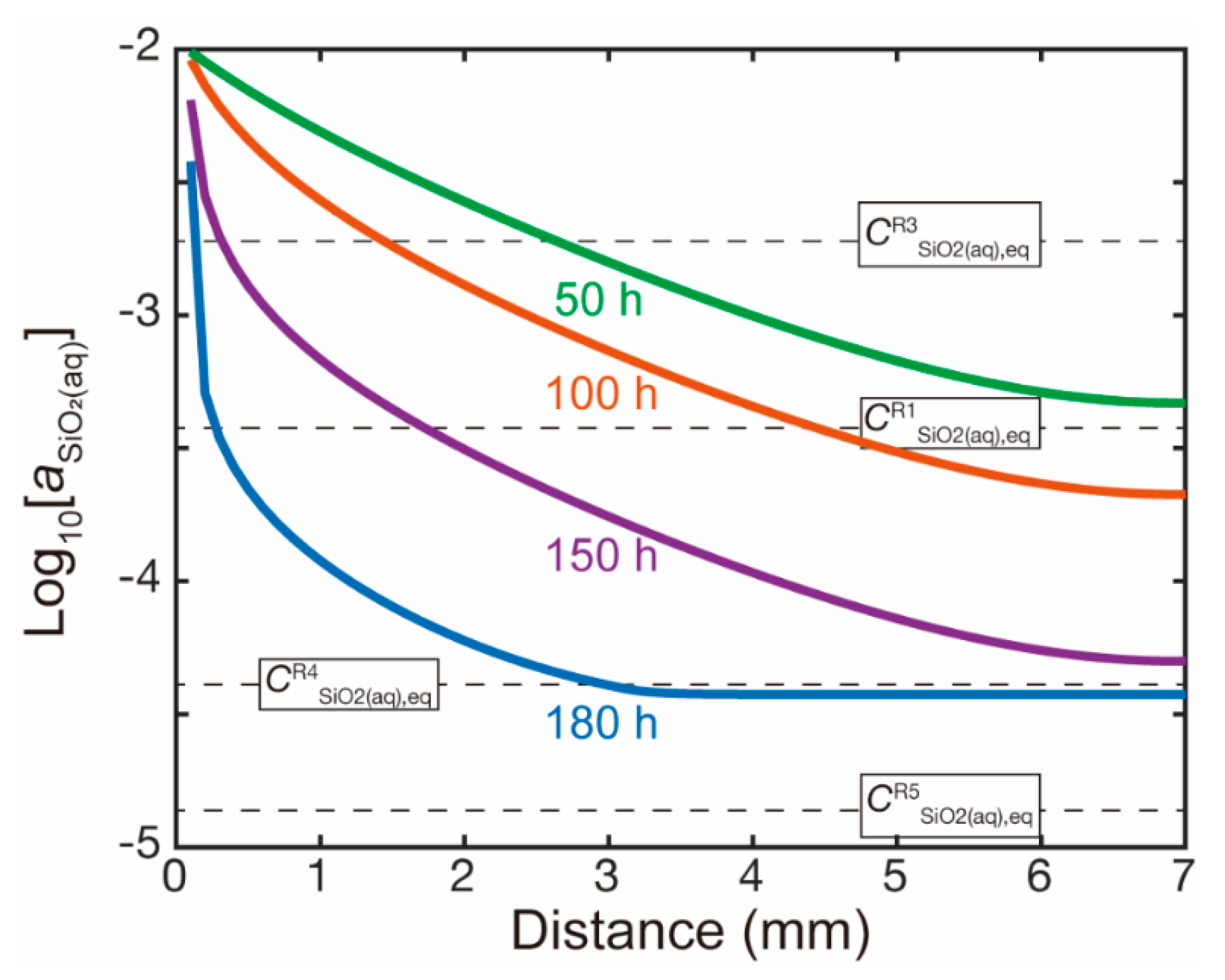
| Reaction Number | Log K § | CnSiO2(aq),eq ξ (mol/cm3 Solution) |
|---|---|---|
| R1 | 17.148 | 2.649 × 10–7 |
| R2 | 6.263 | 3.887 × 10–10 |
| R3 | 5.442 | 1.354 × 10–6 |
| R4 | –4.395 | 2.868 × 10–8 |
| R5 | 9.724 | 9.789 × 10–9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oyanagi, R.; Okamoto, A.; Tsuchiya, N. Multiple Kinetic Parameterization in a Reactive Transport Model Using the Exchange Monte Carlo Method. Minerals 2018, 8, 579. https://doi.org/10.3390/min8120579
Oyanagi R, Okamoto A, Tsuchiya N. Multiple Kinetic Parameterization in a Reactive Transport Model Using the Exchange Monte Carlo Method. Minerals. 2018; 8(12):579. https://doi.org/10.3390/min8120579
Chicago/Turabian StyleOyanagi, Ryosuke, Atsushi Okamoto, and Noriyoshi Tsuchiya. 2018. "Multiple Kinetic Parameterization in a Reactive Transport Model Using the Exchange Monte Carlo Method" Minerals 8, no. 12: 579. https://doi.org/10.3390/min8120579
APA StyleOyanagi, R., Okamoto, A., & Tsuchiya, N. (2018). Multiple Kinetic Parameterization in a Reactive Transport Model Using the Exchange Monte Carlo Method. Minerals, 8(12), 579. https://doi.org/10.3390/min8120579





