Abstract
An effective algorithm for the quasi-harmonic calculation of thermo-elastic stiffness constants of materials is discussed and implemented into the Crystal program for quantum-mechanical simulations of extended systems. Two different approaches of increasing complexity and accuracy are presented. The first one is a quasi-static approximation where the thermal dependence of elastic constants is assumed to be due only to the thermal expansion of the system. The second one is fully quasi-harmonic, takes into account thermal expansion, and explicitly computes Helmholtz free energy derivatives with respect to strain. The conversion of isothermal into adiabatic thermo-elastic constants is also addressed. The algorithm is formally presented and applied to the description of the thermo-elastic response of the forsterite mineral.
1. Introduction
In the last several decades, computational modeling has rapidly gained in popularity as a powerful complementary tool to the experimental characterization of materials. Taking a step forward, computational materials design is an emerging field of research where simulations guide the process of discovering new materials or engineering specific materials’ properties [1]. In this respect, the density functional theory (DFT) arguably represents the method-of-choice because of an ideal balance between its high accuracy (due to its rigorous quantum-mechanical derivation) and modest computational cost, particularly so if compared to other quantum-mechanical methodologies of comparable accuracy [2].
The state-of-the-art of computational materials design has recently been reviewed, the progresses made in the last decade illustrated and future challenges outlined [3]. Among others, recent progresses in the field of computational materials design include: (i) the ability of some software programs for quantum-mechanical simulations to efficiently exploit the parallel computing capabilities of high-performance computing (HPC) centers, thus allowing for the study of larger (more realistic) structural models [4,5,6,7,8,9,10]; (ii) the possibility of effectively including weak, dispersive interactions into the DFT formalism, thus allowing for the reliable simulation of properties of weakly-bound systems (such as molecular crystals) [11,12,13,14,15,16].
Many of the challenges current research on computational materials design is facing are related to getting a more accurate description of the electronic structure of the system (spin–orbit coupling, electron–phonon coupling, electronic transport properties, etc.) and of the conditions on which materials function (anharmonic thermal effects, phonon–phonon coupling, interaction with electric and magnetic fields, etc.) [1,2,3]. In particular, the effective inclusion of thermal effects (fully neglected by static DFT calculations) is much needed in order to widen the application domain and enhance the predictiveness of the computational approach.
In this context, let us briefly review some of the progresses made in the last few years in the development of the Crystal program for quantum-mechanical simulations of the condensed matter [17,18]. A massively-parallel version of the code has been developed, which was recently shown to efficiently scale up to 32,000 cores and which has been used to study several large systems (the largest one containing about 14,000 atoms/cell) [19]. London-type dispersive interactions are included with Grimme’s a posteriori correction (namely, DFT-D3) [20,21]. A fully-automated algorithm has been implemented to compute several quasi-harmonic thermal properties of materials (including thermal expansion, thermal dependence of the bulk modulus, and constant-pressure thermodynamic properties) [22,23,24,25].
Within the quasi-harmonic approximation, the thermal dependence of the bulk modulus can be determined at a relatively low computational cost by computing the lattice dynamics of the system at expanded and compressed space group symmetry-preserving configurations. However, the bulk modulus is just an average mechanical feature of the system. A more complete description of the anisotropic mechanical response of a material requires the fourth-rank elastic tensor to be determined. The evaluation of thermo-elastic constants (i.e., the thermal dependence of the elements of the elastic tensor) is a much more complicated task from a computational point of view as it requires phonons to be computed at several space group symmetry-breaking strained configurations. Nevertheless, the quasi-harmonic approximation [26,27] provides a formal framework for the calculation of thermo-elastic constants [28,29,30,31].
In this paper, we present and discuss an algorithm for the quasi-harmonic calculation of thermo-elastic constants of materials, which we have implemented in the Crystal program. Thermo-elastic constants are computed in two steps: (i) the equilibrium structure of the system at a given temperature T is determined from the quasi-harmonic description of thermal expansion; (ii) second derivatives of the Helmholtz free energy with respect to strain are computed numerically. Besides a fully quasi-harmonic scheme, a simplified quasi-static approach is also implemented and discussed, where the thermal dependence of elastic constants is assumed to be due entirely to the thermal expansion of the lattice. The quasi-static approach is characterized by a much lower computational cost than the fully quasi-harmonic one but only takes into account a fraction of the thermal effects on the mechanical response. The conversion of isothermal thermo-elastic constants into adiabatic ones is also discussed within the framework of the quasi-harmonic approximation.
We apply our quasi-harmonic algorithm to the description of the thermo-elastic response of forsterite, -Mg2SiO4: an end-member of the olivine solid solution series that is one of the most abundant silicates in the upper mantle of the Earth. The single-crystal thermo-elasticity of forsterite has been accurately determined experimentally at several temperatures from 300 K to 1700 K so that it represents an ideal system to validate and discuss our methodology [32].
2. Theoretical Aspects
2.1. The Athermal Elastic Tensor
We treat the crystal as a homogeneous anisotropic medium and we consider it in a reference state in which the three fundamental direct lattice vectors are , and so that the corresponding cell volume is . In standard density functional theory (DFT) calculations, the reference state is the fully-optimized structure that minimizes the static internal energy of the system E at the absolute zero with no zero-point motion corrections.
The elasticity of the system is given by the stress–strain relation. Both stress and pure strain (i.e., without rotational components) are described by symmetric second-rank tensors. The symmetric pure strain tensor is dimensionless and defines a strained lattice configuration where the deformed lattice vectors are expressed in terms of the undeformed reference ones (with = ) as follows:
where = are Cartesian indices, are Cartesian components of lattice vector , and is the Kronecker delta. The elements of the stress tensor are defined as energy density derivatives with respect to strain components and, through inversion of Equation (1), can be expressed in terms of energy gradients with respect to Cartesian components of lattice parameters:
where are Cartesian indices. The stress tensor can thus be evaluated from energy gradients with respect to the cell parameters [33]. The stress–strain relation for an anisotropic crystal is given by the generalized Hooke’s law:
which relates the second-rank stress tensor to the second-rank pure strain tensor through the elastic stiffness constants that define the fourth-rank elastic tensor . Therefore, the elastic constants are defined in terms of derivatives of stress components with respect to strain components:
By casting the first equality of Equation (2) into Equation (4), we get the following expression for the second-order elastic constants in terms of second energy density derivatives with respect to pairs of strain components:
As the pure strain tensor is symmetric, there are just six independent components to be considered. It is convenient to adopt Voigt’s notation, which maps the two Cartesian index notation or into a one index notation , where , , , , , and [34]. The elastic stiffness tensor can thus be expressed as a 6 × 6 matrix:
where are Voigt indices. From Equation (6), the equivalence is evident, which makes the 6 × 6 elastic stiffness matrix symmetric and reduces the number of its independent components from 36 to 21. Most quantum-mechanical solid-state programs can not compute the second energy derivatives in Equation (6) analytically, which thus need to be evaluated numerically either as first derivatives of analytical forces or as second derivatives of the energy. Let us briefly discuss these two approaches below.
2.1.1. Calculation from Analytical Forces
If first energy derivatives with respect to strain, , can be computed analytically, all the elastic stiffness constants can be determined by applying to the lattice only the six independent strain components as described below. The lattice is deformed according to the u-th independent component, , of the strain and the analytical energy gradients computed at the strained lattice configurations (for ) so that the u-th column of the elastic tensor is evaluated from numerical finite differences (via a double-sided formula):
where represents the amplitude of the applied strain. In the Crystal program, the energy gradients with respect to strain are computed analytically [35,36] and the strain amplitude has been optimized to the default value of 1% [37,38]. The nuclear-relaxation contribution to the elastic tensor can be evaluated by either relaxing atomic positions at strained configurations or computing the internal-strain Hessian tensor [39,40]. Thus, if analytical energy gradients can be exploited, only the fundamental independent strain components need to be applied to the lattice. The symmetry of the lattice further reduces the number of components to be applied [34].
2.1.2. Calculation from the Energy
If the elastic constants in Equation (6) are to be evaluated only from the energy of different lattice configurations (i.e., from numerical second derivatives), one can not compute all of them by only deforming the lattice according to the six independent components of the strain . More general strains are required that can be expressed as combinations of the fundamental ones. Let us introduce the following Voigt’s vector notation for the independent strain components:
These vectors clearly constitute a complete orthonormal basis. In order to ensure a unitary norm for all the independent components, their 3 × 3 Cartesian representations are:
Any general strain can thus be defined as a linear combination of the fundamental strains above:
where are the coefficients of the linear combination defining the strain shape. The amplitude of the strain is defined by an additional parameter . Let us introduce an example to make this notation clear. We consider a strain . The corresponding 3 × 3 tensor is:
Once a given strain shape is defined, the lattice is deformed accordingly for different values of the strain amplitude and the energy of the system computed at each distorted lattice configuration: . The energy is thus a function of and parametrically depends on the strain shape . The energy computed for different values of can then be fitted to a polynomial function (of second-order or higher) and the corresponding fitting parameters determined:
The second energy density derivative with respect to the strain amplitude of the expression above, at the equilibrium configuration, is obtained in terms of the fitting parameter and corresponds to a linear combination of elastic stiffness constants as follows:
As an example, for the particular strain shape in Equation (9), it gives:
In order to determine the value of all the elastic stiffness constants , different strain shapes have to be applied, each providing the value of a linear combination of them, until a linear system of equations can be solved to get all the individual values. Let us note that each diagonal elastic stiffness constant can be obtained as such by applying the corresponding fundamental strain . Let us further note that the symmetry of the lattice can significantly reduce the number of strain shapes to be actually applied. For instance, for a cubic lattice, only three strain shapes are necessary: that gives , that gives , and that gives to determine the three independent elastic stiffness constants , and .
2.2. The Elastic Tensor at a Finite Temperature
The inclusion of thermal effects on computed properties of materials requires the description of the lattice dynamics. The commonly adopted harmonic approximation (HA) for the description of lattice vibrations—as combined with the laws of statistical thermodynamics through the definition of a canonical partition function—is rather effective in the evaluation of constant-volume thermal properties of solids. However, the HA is unable to describe volume-dependent thermal properties so that thermal expansion would be null, constant-pressure thermodynamic functions would coincide with constant-volume ones, and the elastic response of the system would be independent of temperature [41,42]. In order to go beyond the above-mentioned limitations of the HA, the so-called quasi-harmonic approximation (QHA) can be invoked, which, due to its formal simplicity and relatively low computational cost, represents an effective method of choice for describing many volume-dependent thermal features of solids [22,23,26,27,42,43].
In order to compute isothermal elastic stiffness constants at a finite temperature T, Equation (6) needs to be generalized as follows:
where the reference lattice configuration is now the equilibrium one at temperature T, whose lattice parameters are , with , and whose corresponding volume is , and where the second derivatives with respect to strain are now expressed in terms of the Helmholtz free energy F of the system and no longer in terms of the static internal energy E. The evaluation of Equation (11) can thus be performed in two steps:
- The determination of the equilibrium structure of the system at temperature T;
- The calculation of the second free-energy derivatives with respect to strain.
We discuss these two steps in Section 2.2.1 and Section 2.2.2, respectively. Finally, we stress that the superscript T in Equation (11) is needed to distinguish isothermal from adiabatic elastic constants (see Section 2.2.3 below for more details on this).
2.2.1. The Equilibrium Structure at a Finite Temperature
The QHA introduces the explicit volume dependence of phonon frequencies by retaining the simple harmonic expression for the Helmholtz free energy of the system [26,27]:
where is Boltzmann’s constant, is the zero-temperature internal energy of the crystal, which includes the zero-point energy , and where the sum runs over phonons, whose vibration frequencies are . The Helmholtz free energy in Equation (12) can thus be evaluated from harmonic phonon frequencies computed at several volumes. The equilibrium volume of the system at a given temperature T is then obtained by minimizing the isothermal Helmholtz free energy of Equation (12) with respect to volume by keeping T as a fixed parameter. From the volume–temperature relation , the volumetric thermal expansion coefficient can be defined as:
where the derivative is taken at constant pressure. The isothermal bulk modulus of the system, , can also be obtained as an isothermal second derivative of Equation (12) with respect to the volume:
A fully-automated algorithm for computing the thermal expansion of the system (and derived properties) within the QHA has recently been implemented in the Crystal program [18,22,23], which relies on computing and fitting harmonic vibration frequencies at different compressed and expanded volumes (four volumes, including the equilibrium one, being enough for most systems) after having performed volume-constrained structural relaxations. This implementation of the QHA has been successfully applied to study several thermal properties (structural, thermodynamic, electronic) of various systems with different chemical features in the last couple of years: fully-covalent diamond [22], ionic MgO and CaO [23], LiF [44], mixed ionic/covalent corundum -Al2O3 [24], forsterite -Mg2SiO4 [25], calcium stannate CaSnO3 [45], and the molecular crystals of urea, purine and carbamazepine [43,46,47].
2.2.2. Free Energy Derivatives with Respect to Strain
From the methodology outlined in Section 2.2.1, the equilibrium structure of the system at temperature T is determined, whose volume is . In order to evaluate the isothermal elastic constants in Equation (11), the second derivatives of the Helmholtz free energy given in Equation (12) with respect to strain have to be computed. Such derivatives can not be computed analytically but rather need to be evaluated numerically from the free energy of strained lattice configurations. A scheme similar to that described in Section 2.1.2 can be adopted, where a strain shape is selected and the lattice distorted accordingly for different values of the strain amplitude . At each strained configuration, the harmonic vibration frequencies have to be computed in order to get the corresponding free energy: . The free energy is thus a function of and parametrically depends on the strain shape and on the temperature T. The free energy computed for different values of can be fitted to a polynomial function and the corresponding fitting parameters determined:
The second free energy density derivative with respect to the strain amplitude of the expression above, at the equilibrium configuration at temperature T, is given by and corresponds to a linear combination of isothermal elastic stiffness constants as follows:
As discussed in Section 2.1.2, in order to get the full set of elastic constants, several strain shapes have to be applied, each providing a linear combination of them. In the present implementation, the evaluation of the derivatives in Equation (16) with respect to the strain amplitude is fully-automated and requires a single run of the program per each temperature T and per each strain shape .
2.2.3. Adiabatic versus Isothermal Elastic Moduli
From an experimental point of view, elastic constants at finite temperature are generally measured in adiabatic rather than isothermal conditions, for instance through Brillouin scattering experiments. Adiabatic elastic moduli are always larger in value than their isothermal counterparts. In this section, we are going to illustrate how the isothermal bulk modulus and elastic constants can be transformed into adiabatic ones by means of quasi-harmonic calculations. At any temperature T, the adiabatic bulk modulus is given in terms of the isothermal bulk modulus as follows:
where is the isothermal bulk modulus defined in Equation (14), is the volumetric thermal expansion coefficient introduced in Equation (13), is the molar constant-volume specific heat of the system, and is the molar volume of the system. All the quantities entering Equation (17) can be computed with the HA and QHA. Adiabatic elastic stiffness constants are related to isothermal ones through the following relation [28]:
where the are defined as the isothermal derivatives of the entropy S with respect to strain or, equivalently, as the derivative of the stress with respect to temperature at constant strain, and, by exploiting the chain rule of differentiation:
where is the thermal expansion tensor [48]. For cubic, hexagonal, trigonal, tetragonal and orthorhombic crystals (i.e., those lattices where angles among fundamental lattice vectors are fixed by symmetry), we have:
More complicated expressions for the elements of the thermal expansion tensor are obtained for lower-symmetry systems. In particular, the expression for the most general triclinic case can be found elsewhere [49,50].
2.2.4. The Quasi-Static Approximation to Thermo-Elastic Moduli
As we have discussed above, the explicit quasi-harmonic calculation of thermo-elastic constants, as in Equation (11) requires the evaluation of two quantities: (i) the thermal expansion of the system ; and (ii) the second free energy derivatives with respect to strain. From a computational point of view, the latter is much more expensive than the former as it involves several phonon calculations at strained lattice configurations. A simplified way to obtain thermo-elastic constants has been suggested, which is based on the assumption that the thermal dependence of the elastic moduli is mostly due to thermal expansion [51,52,53]. Within this methodology, referred to as “quasi-static approximation” (QSA), the thermo-elastic constants are computed as follows:
where the thermal expansion of the system still has to be determined from the quasi-harmonic approximation, but the energy derivatives with respect to strain are computed in terms of static internal energy E. This approximation drastically reduces the computational cost of thermo-elastic calculations and often allows to take into account a significant fraction of thermal effects on the elastic response of the system.
3. The Implemented Algorithm
In this section, we sketch the algorithm that we have devised to compute quasi-harmonic thermo-elastic constants of materials. In particular, we explicitly illustrate the sequence of calculations that are required by stressing what steps can be performed automatically. The algorithm that we propose is the following:
- A full structural relaxation of the system is performed (both atomic positions and lattice parameters are optimized). The static equilibrium structure, with volume , is obtained.
- A space group symmetry-preserving QHA calculation is performed, which provides the thermal expansion of the system. A fully-automated algorithm is implemented in the Crystal program to perform this task [22,23], where four different volumes are explored (compressed and expanded with respect to ). For each volume, a volume-constrained, lattice symmetry-preserving structural relaxation is performed and phonon frequencies computed. By minimizing at several temperatures, the relation is determined. As a result, lattice parameters as a function of temperature are obtained.
- A value of temperature T is selected. Starting from the values of the lattice parameters at this temperature obtained at the end of the previous step, a volume-constrained, lattice symmetry-preserving structural relaxation is performed to get the equilibrium structure (also in terms of atomic positions) at the desired temperature.
- A given strain shape is chosen, which will provide a linear combination of elastic stiffness constants according to Equation (16).
- The second free energy derivatives with respect to the strain are computed as discussed in Section 2.2.2. A fully-automated algorithm has been implemented in the Crystal program for this task. The starting point is represented by the optimized structure obtained at the end of step 3 above (i.e., the equilibrium structure at temperature T). The structure is deformed, in terms of the strain shape , into four strained configurations (two with positive and two with negative strain amplitude ). At each strained configuration, atomic positions are relaxed and phonon frequencies computed. The computed quasi-harmonic free energy as a function of strain amplitude is fitted to a second-order polynomial and the corresponding second-derivative determined.
4. Computational Parameters
All the calculations reported in this study have been performed with algorithms implemented in a developmental version of the Crystal17 program [18]. An all-electron atom-centered Gaussian-type-function (GTF) basis set is used for all atoms; silicon, oxygen and magnesium atoms are described by (8s) (6311) (1d), (8s) (411) (1d) and (8s) (511) (1d) contractions of primitive GTFs, respectively. The exponents (in bohr−2 units) of the most diffuse shells are 0.32 and 0.13 (Si), 0.59 and 0.25 (O), and 0.68 and 0.22 (Mg); the exponents of the d shells are 0.6 (Si), 0.5 (O), and 0.5 (Mg). The same basis set has already been successfully utilized in a couple of recent studies of vibrational and spectroscopic properties of forsterite [25,54].
Thresholds controlling the accuracy of Coulomb and exchange series are set to default values. Reciprocal space is sampled using a Monkhorst–Pack mesh with a shrinking factor of 6 for the primitive cell of forsterite, corresponding to 64 independent k-points in the irreducible portion of the Brillouin zone. A pruned grid with 1454 radial and 99 angular points is used to calculate the DFT exchange-correlation contribution through numerical integration of the electron density over the unit cell volume. The self-consistent-field (SCF) convergence on energy was set to a value of 10−10 hartree for all geometry optimizations and phonon frequency calculations. In the calculation of phonon frequencies, the Hessian matrix is computed numerically from finite differences of analytical forces computed at a set of displaced nuclear configurations: a step of 0.003 Å is used.
Harmonic thermodynamic properties, such as the constant-volume specific heat used in Equation (17), are computed by sampling phonon dispersion over 27 k-points (corresponding to a supercell containing 756 atoms). All quasi-harmonic properties are computed by working in terms of the primitive cell of the system (containing 4 formula units or equivalently 28 atoms), which already ensures convergence.
5. Results and Discussion
We apply the quasi-harmonic methodology outlined in Section 2 to compute the thermo-elastic response of the orthorhombic forsterite mineral, -Mg2SiO4, that is characterized by nine independent elastic constants: , , , , , , , , . The first step of our algorithm, as sketched in Section 3, consists of a full structural relaxation of the system (i.e., both atomic positions and lattice parameters are optimized by minimizing the static internal energy E of the system). The second step of the algorithm is a lattice symmetry-preserving quasi-harmonic calculation, where harmonic phonon frequencies are evaluated at four volumes (one compressed, one equilibrium and two expanded) according to the fully-automated scheme previously suggested and implemented in the Crystal program by some of the authors [22,23]. From the calculation of phonon harmonic frequencies at different volumes, the Helmholtz free energy of the system as a function of temperature and volume can be evaluated as in Equation (12). By minimizing this function with respect to volume at each temperature, the relation is obtained that provides the thermal expansion of the system.
The first two steps of the algorithm, which we have just briefly described, have been performed by using four different functionals of the DFT, which belong to three different classes: the local-density approximation (LDA), two generalized-gradient approximation (GGA) functionals (PBE and PBEsol) and one hybrid functional (PBE0). The results in terms of the thermal expansion are presented in Figure 1, where the volume of forsterite is reported as a function of temperature up to 2000 K. Three independent sets of experimental data are reported from Bouhifd et al. [55] (filled circles), Ye et al. [56] (empty circles) and Hazen [57] (empty squares). The following considerations can be made: (i) as expected, different functionals provide different absolute values for the volume of forsterite, with the PBEsol and PBE0 functionals providing almost identical results in this case and the closest to the experimental values; (ii) all functionals provide a very satisfactory description of the thermal expansion of the system up to 2000 K. In particular, we want to stress that, despite predicting different absolute values for the equilibrium volume, different functionals provide an extremely consistent description of the thermal expansion of the system. This aspect has very interesting computational implications and is not specific of forsterite but is rather a common feature of all quasi-harmonic properties [22,23,24,45]. The computational implication is the following: while a more accurate (and costly) functional (like a hybrid one) is often needed to get a better description of the static absolute value of the equilibrium volume, one can safely work in terms of a less costly functional (like a GGA one) to get the thermal dependence of the volume.
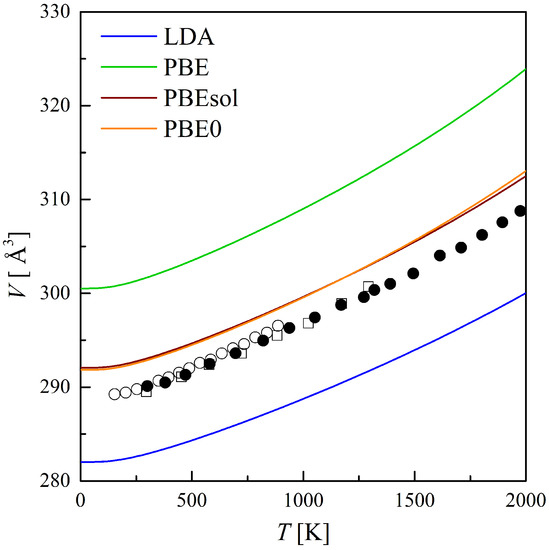
Figure 1.
Volumetric thermal expansion of forsterite up to 2000 K. Experimental data are from Bouhifd et al. [55] (filled circles), Ye et al. [56] (empty circles) and Hazen [57] (empty squares). Lines correspond to quasi-harmonic computed values with different functionals of the DFT: LDA (blue), PBE (green), PBEsol (red), and PBE0 (yellow).
From the second step of our algorithm, we can also compute the thermal dependence of the bulk modulus of the system by evaluating the second derivatives with respect to volume of the Helmholtz free energy, as in Equation (14). The bulk modulus evaluated in this way is the isothermal one, while the adiabatic one can be obtained from the correction as in Equation (17). The isothermal and adiabatic bulk modulus of forsterite are reported as a function of temperature up to 2000 K in the left and right panels of Figure 2, respectively. Experimental data are from Anderson et al. [58] (filled and empty black circles for isothermal and adiabatic moduli). The same considerations made above on the volume hold here on the bulk modulus: (i) different functionals provide different absolute values, with PBEsol and PBE0 resulting in very similar descriptions, almost matching the experimental values; (ii) the computed quasi-harmonic thermal dependence of the bulk modulus is basically insensitive to the particular functional of the DFT used. Let us stress that the adiabatic correction to the isothermal bulk modulus in Equation (17) requires a good description of both quasi-harmonic (such as , , and ) and harmonic (such as ) thermodynamic properties. We have computed quasi-harmonic properties by working in terms of the primitive cell (28 atoms/cell), which already ensures convergence, while we have used a supercell containing 756 atoms to converge harmonic thermodynamic properties, which show a much slower convergence with sampling of phonon dispersion. The results reported in the right panel of Figure 2 show the good description of all quasi-harmonic and harmonic thermodynamic properties.
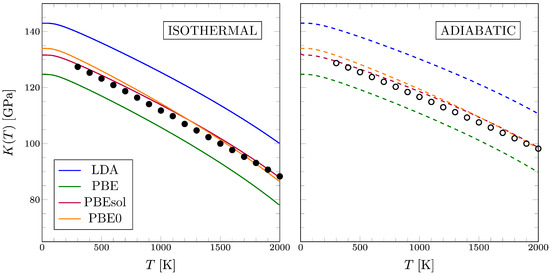
Figure 2.
Thermal dependence of the isothermal (left panel) and adiabatic (right panel) bulk modulus of forsterite up to 2000 K. Experimental data (filled and empty black circles) are from Anderson et al. [58]. Lines correspond to quasi-harmonic computed values with different functionals of the DFT: LDA (blue), PBE (green), PBEsol (red), and PBE0 (yellow).
We compute the thermal dependence of the elastic constants of forsterite by using the steps 3 to 5 of our quasi-harmonic algorithm, as described in Section 3. Eight different temperatures are considered from 50 K to 1450 K. In order to compute the nine independent elastic constants of forsterite, nine different shapes of deformations are considered. According to the formalism introduced in Section 2.1.2, from the deformation we get the constant, from we get , from we get , from we get , from we get , from we get , from we get the linear combination , from we get the linear combination , and from we get the linear combination . At each temperature T, and for each of the nine deformation shapes above, the second free energy derivatives in Equation (16) with respect to the deformation amplitude have to be evaluated numerically: five strained configurations corresponding to five different strain amplitudes are explored (including the equilibrium configuration), where harmonic phonon frequencies are computed. Therefore, a total of harmonic frequency calculations have been performed to characterize the thermo-elastic response of the orthorhombic crystal of forsterite. It is clear that this methodology is rather computationally expensive. Later on, we are going to discuss how the computational cost of the evaluation of thermo-elasticity can be drastically reduced by adopting a quasi-static approximation rather than a fully quasi-harmonic one.
The computed isothermal elastic constants are then transformed into adiabatic ones by means of Equation (18) in order to be compared to experimental values from Isaak et al. [32]. Figure S1 of the Supplementary Materials shows a comparison between isothermal and adiabatic computed values. Given that the fully quasi-harmonic description of the thermo-elasticity of forsterite is a rather computationally expensive task, and given that different functionals provide consistent trends for the thermal dependence of structural and mechanical properties of solids, we have decided to use the PBEsol functional for this task. This is because, from the analysis of the results shown in Figure 2, it provides a good description of the absolute value of the bulk modulus of the system, and, being a GGA functional, it has a lower cost than the hybrid PBE0 one.
The computed quasi-harmonic adiabatic elastic stiffness constants of forsterite are reported in Figure 3 (with lines) as a function of temperature, up to 1500 K, where they are compared with experimental data (circles). Very regular trends are obtained for all the nine independent elastic constants as a function of temperature. Given that each elastic constant required eight separate calculations at different volumes (corresponding to eight different temperatures), this is not trivial and shows the high numerical robustness of the implemented algorithm. The absolute values of all constants at low temperature is in good agreement with the experiments: for the at about 340 GPa, for at about 240 GPa, for at about 210 GPa, and for the bunch of other constants at about 70–80 GPa (see Figure S2 of the Supplementary Materials for a zoomed-in plot of these latter constants). This confirms the good description provided by the PBEsol functional already inferred from the analysis of both volume and bulk modulus in Figure 1 and Figure 2. The most important aspect of our thermo-elastic description is clearly the thermal dependence of the computed constants, which turns out to be in excellent agreement with the experimental data. Figure 3 confirms that a full quasi-harmonic approach provides an excellent description of the thermo-elasticity of crystalline materials.
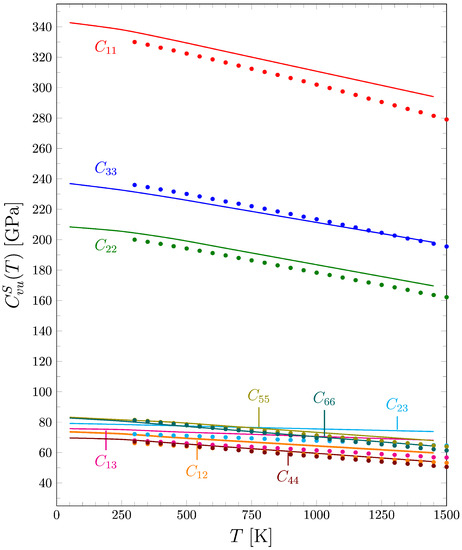
Figure 3.
Adiabatic single-crystal elastic stiffness constants of forsterite as a function of temperature. Circles are experimental data by Isaak et al. [32] while lines correspond to fully quasi-harmonic computed values.
The characterization of the thermal dependence of single-crystal elastic constants is clearly crucial if one wants to discuss the evolution with temperature of the mechanical anisotropy of a material. This is relevant to minerals of geophysical interest as well as to other classes of materials such as metal-organic frameworks, whose mechanical instability at room temperature often represents a limiting factor to their effective use [59]. Once all elastic constants are known, the spatial dependence of the Young modulus of a material can be computed [60]. In Figure 4, we report the spatial dependence of the Young modulus of forsterite as a function of temperature. The experimental evolution of the mechanical anisotropy is reported as well as the computed one. Forsterite has a very anisotropic mechanical response. In particular, the system has a larger rigidity along the x-axis than along y and z, which results in strong mechanical anisotropies in the and planes, while the mechanical anisotropy is way less pronounced in the plane. From the analysis of the experimental data in Figure 4, we see that, as temperature increases, the mechanical response of the system changes in two respects: (i) the Young modulus shrinks, which corresponds to an overall softening of the system with temperature; and (ii) the mechanical anisotropy becomes more pronounced (clearly seen in the 2D projections of the Young modulus in the right panels). Both these effects are nicely reproduced by the full quasi-harmonic description of the thermo-elasticity, apart from a slight underestimation of the mechanical anisotropy in the plane.
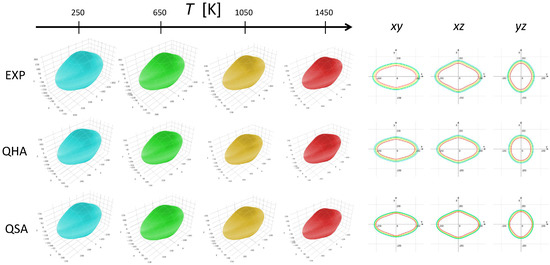
Figure 4.
Effect of temperature on the Young modulus of forsterite. Left: 3D representation of the spatial dependence of the Young modulus as a function of temperature from experimental elastic constants, quasi-harmonic computed constants, and quasi-static computed constants. Right: 2D projections of the Young modulus in three different planes (, and ) as a function of temperature (blue for 250 K, green for 650 K, yellow for 1050 K and red for 1450 K).
As we have discussed above, the full quasi-harmonic description of the thermo-elastic response of forsterite is rather computationally expensive as it required about 360 harmonic frequency calculations at different strained lattice configurations. In Section 2.2.4, we have introduced a simplified approach, called quasi-static approximation (QSA), to the calculation of thermo-elastic constants where the thermal dependence of the mechanical response is only due to the thermal expansion of the system. Within the QSA, isothermal elastic constants are computed according to Equation (20) by starting from the equilibrium structure at temperature T and by computing the second energy derivatives in terms of internal static energy E rather than of Helmholtz free energy F. This results in a dramatic reduction of the complexity of the algorithm as very few (just four, in our algorithm) phonon frequency calculations are needed to determine the relation and none for the second energy derivatives. At the same time, the QSA is a further approximation with respect to the full QHA one that typically results in the underestimation of thermal effects. We have computed the nine thermo-elastic constants of forsterite as a function of temperature with the QSA (they are reported in Figure S3 of the Supplementary Materials). The bottom panels of Figure 4 show the thermal dependence of the Young modulus of forsterite as obtained from the QSA computed constants, as compared with experimental and fully quasi-harmonic values. It can be seen that the two main effects of temperature on the mechanical response of forsterite are both correctly described by the QSA from a qualitative point of view: the shrinking of the Young modulus and the increased anisotropy. From a quantitative point of view, the shrinking of the Young modulus with temperature (i.e., the thermal softening of the mechanical response) is underestimated, as can be clearly seen from the small separation of the different lines in the 2D projections, compared to the experimental ones.
6. Conclusions
Two computational approaches for the first-principles calculation of thermo-elastic stiffness constants of crystalline materials have been formally illustrated and implemented into the public Crystal program for quantum-mechanical simulations of the condensed matter. Both schemes are based on the quasi-harmonic description of the thermal expansion of the system. The first approach, referred to as the quasi-static approximation, assumes that the whole thermal dependence of the mechanical properties of a solid is due to its thermal expansion and therefore involves second energy derivatives with respect to the strain in terms of the purely static internal energy E. The second scheme is a full quasi-harmonic one where thermal expansion is taken into account and second energy derivatives with respect to strain are computed in terms of the Helmholtz free energy F. The latter approach is much more computationally expensive than the former but also ensures a better description of thermal effects on the mechanical response of the system. Both approaches have been applied to the description of the thermo-elasticity of the forsterite mineral.
Supplementary Materials
The following are available online at http://www.mdpi.com/2075-163X/9/1/16/s1, Figure S1: Isothermal versus adiabatic elastic constants of forsterite as a function of temperature; Figure S2: Low-valued adiabatic elastic stiffness constants of forsterite as a function of temperature; Figure S3: Thermo-elastic constants of forsterite as computed with the quasi-static approximation.
Author Contributions
A.E. conceived this contribution and supervised the activities of M.D., C.R. and A.C.; A.E., C.R. and M.D. devised the algorithm; A.E. and M.D. implemented the algorithm; A.E., M.D., C.R. and A.C. analyzed the data; A.E. wrote the paper, with contributions from M.D.
Funding
This research was funded by Compagnia di San Paolo and University of Torino through grant number CSTO169372.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kuehmann, C.J.; Olson, G.B. Computational materials design and engineering. Mater. Sci. Technol. 2009, 25, 472–478. [Google Scholar] [CrossRef]
- Hafner, J.; Wolverton, C.; Ceder, G. Toward Computational Materials Design: The Impact of Density Functional Theory on Materials Research. MRS Bull. 2006, 31, 659–668. [Google Scholar] [CrossRef]
- Curtarolo, S.; Hart, G.; Nardelli, M.; Mingo, N.; Sanvito, S.; Levy, O. The high-throughput highway to computational materials design. Nat. Mater. 2013, 12, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Varini, N.; Ceresoli, D.; Martin-Samos, L.; Girotto, I.; Cavazzoni, C. Enhancement of DFT-calculations at petascale: Nuclear Magnetic Resonance, Hybrid Density Functional Theory and Car-Parrinello calculations. Comput. Phys. Commun. 2013, 184, 1827–1833. [Google Scholar] [CrossRef]
- Corsetti, F. Performance Analysis of Electronic Structure Codes on HPC Systems: A Case Study of SIESTA. PLoS ONE 2014, 9, e95390. [Google Scholar] [CrossRef] [PubMed]
- Hutter, J.; Iannuzzi, M.; Schiffmann, F.; VandeVondele, J. CP2K: Atomistic simulations of condensed matter systems. WIREs Comput. Mol. Sci. 2014, 4, 15–25. [Google Scholar] [CrossRef]
- Maniopoulou, A.; Davidson, E.R.; Grau-Crespo, R.; Walsh, A.; Bush, I.J.; Catlow, C.R.A.; Woodley, S.M. Introducing k-point parallelism into VASP. Comput. Phys. Commun. 2012, 183, 1696–1701. [Google Scholar] [CrossRef]
- Kendall, R.A.; Aprá, E.; Bernholdt, D.E.; Bylaska, E.J.; Dupuis, M.; Fann, G.I.; Harrison, R.J.; Ju, J.; Nichols, J.A.; Nieplocha, J.; et al. High performance computational chemistry: An overview of NWChem a distributed parallel application. Comput. Phys. Commun. 2000, 128, 260–283. [Google Scholar] [CrossRef]
- Orlando, R.; Delle Piane, M.; Bush, I.J.; Ugliengo, P.; Ferrabone, M.; Dovesi, R. A new massively parallel version of CRYSTAL for large systems on high performance computing architectures. J. Comput. Chem. 2012, 33, 2276–2284. [Google Scholar] [CrossRef]
- Bush, I.J.; Tomic, S.; Searle, B.G.; Mallia, G.; Bailey, C.L.; Montanari, B.; Bernasconi, L.; Carr, J.M.; Harrison, N.M. Parallel implementation of the ab initio CRYSTAL program: Electronic structure calculations for periodic systems. Proc. R. Soc. A Math. Phys. Eng. Sci. 2011, 467, 2112. [Google Scholar] [CrossRef]
- Wen, S.; Nanda, K.; Huang, Y.; Beran, G.J.O. Practical quantum mechanics-based fragment methods for predicting molecular crystal properties. Phys. Chem. Chem. Phys. 2012, 14, 7578–7590. [Google Scholar] [CrossRef] [PubMed]
- Moellmann, J.; Grimme, S. DFT-D3 Study of Some Molecular Crystals. J. Phys. Chem. C 2014, 118, 7615–7621. [Google Scholar] [CrossRef]
- Bucko, T.; Hafner, J.; Lebegue, S.; Angyan, J.G. Improved Description of the Structure of Molecular and Layered Crystals: Ab Initio DFT Calculations with van der Waals Corrections. J. Phys. Chem. A 2010, 114, 11814–11824. [Google Scholar] [CrossRef] [PubMed]
- Tkatchenko, A.; DiStasio, R.A.; Car, R.; Scheffler, M. Accurate and Efficient Method for Many-Body van der Waals Interactions. Phys. Rev. Lett. 2012, 108, 236402. [Google Scholar] [CrossRef] [PubMed]
- Civalleri, B.; Zicovich-Wilson, C.; Valenzano, L.; Ugliengo, P. B3LYP augmented with an empirical dispersion term (B3LYP-D*) as applied to molecular crystals. CrystEngComm 2008, 10, 405. [Google Scholar] [CrossRef]
- Neumann, M.A.; Perrin, M.A. Energy Ranking of Molecular Crystals Using Density Functional Theory Calculations and an Empirical van der Waals Correction. J. Phys. Chem. B 2005, 109, 15531–15541. [Google Scholar] [CrossRef] [PubMed]
- Dovesi, R.; Orlando, R.; Erba, A.; Zicovich-Wilson, C.M.; Civalleri, B.; Casassa, S.; Maschio, L.; Ferrabone, M.; De La Pierre, M.; D’Arco, P.H.; et al. CRYSTAL14: A Program for the Ab initio Investigation of Crystalline Solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. [Google Scholar] [CrossRef]
- Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-Mechanical Condensed Matter Simulations with CRYSTAL. WIREs Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
- Erba, A.; Baima, J.; Bush, I.; Orlando, R.; Dovesi, R. Large Scale Condensed Matter DFT Simulations: Performance and Capabilities of the Crystal Code. J. Chem. Theory Comput. 2017, 13, 5019–5027. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Brandenburg, J.; Grimme, S. Dispersion Corrected Hartree-Fock and Density Functional Theory for Organic Crystal Structure Prediction. In Prediction and Calculation of Crystal Structures; Atahan-Evrenk, S., Aspuru-Guzik, A., Eds.; Topics in Current Chemistry; Springer: Berlin/Heidelberg, Germany, 2014; Volume 345, pp. 1–23. [Google Scholar]
- Erba, A. On combining temperature and pressure effects on structural properties of crystals with standard ab initio techniques. J. Chem. Phys. 2014, 141, 124115. [Google Scholar] [CrossRef] [PubMed]
- Erba, A.; Shahrokhi, M.; Moradian, R.; Dovesi, R. On How Differently the Quasi-harmonic Approximation Works for Two Isostructural Crystals: Thermal Properties of MgO and CaO. J. Chem. Phys. 2015, 142, 044114. [Google Scholar] [CrossRef] [PubMed]
- Erba, A.; Maul, J.; Demichelis, R.; Dovesi, R. Assessing Thermochemical Properties of Materials through Ab initio Quantum-mechanical Methods: The Case of α-Al2O3. Phys. Chem. Chem. Phys. 2015, 17, 11670–11677. [Google Scholar] [CrossRef] [PubMed]
- Erba, A.; Maul, J.; De La Pierre, M.; Dovesi, R. Structural and Elastic Anisotropy of Crystals at High Pressure and Temperature from Quantum-mechanical Methods: The Case of Mg2SiO4 Forsterite. J. Chem. Phys. 2015, 142, 204502. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.E.; De Wette, F.W. Calculation of Dynamical Surface Properties of Noble-Gas Crystals. I. The Quasiharmonic Approximation. Phys. Rev. 1969, 179, 873–886. [Google Scholar] [CrossRef]
- Boyer, L.L. Calculation of Thermal Expansion, Compressiblity, an Melting in Alkali Halides: NaCl and KCl. Phys. Rev. Lett. 1979, 42, 584. [Google Scholar] [CrossRef]
- Davies, G. Effective elastic moduli under hydrostatic stress. Quasi-harmonic theory. J. Phys. Chem. Solids 1974, 35, 1513–1520. [Google Scholar] [CrossRef]
- Karki, B.B.; Wentzcovitch, R.M.; de Gironcoli, S.; Baroni, S. High-pressure lattice dynamics and thermoelasticity of MgO. Phys. Rev. B 2000, 61, 8793–8800. [Google Scholar] [CrossRef]
- Wu, Z.; Wentzcovitch, R.M. Quasiharmonic thermal elasticity of crystals: An analytical approach. Phys. Rev. B 2011, 83, 184115. [Google Scholar] [CrossRef]
- Karki, B.B.; Wentzcovitch, R.M.; de Gironcoli, S.; Baroni, S. First-Principles Determination of Elastic Anisotropy and Wave Velocities of MgO at Lower Mantle Conditions. Science 1999, 286, 1705–1707. [Google Scholar] [CrossRef]
- Isaak, D.G.; Anderson, O.L.; Goto, T.; Suzuki, I. Elasticity of single-crystal forsterite measured to 1700 K. J. Geophys. Res. Solid Earth 1989, 94, 5895–5906. [Google Scholar] [CrossRef]
- Doll, K. Analytical stress tensor and pressure calculations with the CRYSTAL code. Mol. Phys. 2010, 108, 223–227. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals; Oxford University Press: Oxford, UK, 1957. [Google Scholar]
- Doll, K.; Dovesi, R.; Orlando, R. Analytical Hartree-Fock gradients with respect to the cell parameter for systems periodic in three dimensions. Theor. Chem. Acc. 2004, 112, 394–402. [Google Scholar] [CrossRef]
- Doll, K.; Dovesi, R.; Orlando, R. Analytical Hartree-Fock gradients with respect to the cell parameter: Systems periodic in one and two dimensions. Theor. Chem. Acc. 2006, 115, 354–360. [Google Scholar] [CrossRef]
- Perger, W.F.; Criswell, J.; Civalleri, B.; Dovesi, R. Ab-initio calculation of elastic constants of crystalline systems with the CRYSTAL code. Comput. Phys. Commun. 2009, 180, 1753–1759. [Google Scholar] [CrossRef]
- Erba, A.; Mahmoud, A.; Orlando, R.; Dovesi, R. Elastic Properties of Six Silicate Garnet End-members from Accurate Ab initio Simulations. Phys. Chem. Miner. 2014, 41, 151–160. [Google Scholar] [CrossRef]
- Erba, A. The Internal-Strain Tensor of Crystals for Nuclear-relaxed Elastic and Piezoelectric Constants: On the Full Exploitation of its Symmetry Features. Phys. Chem. Chem. Phys. 2016, 18, 13984–13992. [Google Scholar] [CrossRef]
- Erba, A.; Caglioti, D.; Zicovich-Wilson, C.M.; Dovesi, R. Nuclear-relaxed Elastic and Piezoelectric Constants of Materials: Computational Aspects of Two Quantum-mechanical Approaches. J. Comput. Chem. 2017, 38, 257–264. [Google Scholar] [CrossRef]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College: Philadelphia, PA, USA, 1976. [Google Scholar]
- Baroni, S.; Giannozzi, P.; Isaev, E. Density-Functional Perturbation Theory for Quasi-Harmonic Calculations. Rev. Miner. Geochem. 2010, 71, 39–57. [Google Scholar] [CrossRef]
- Erba, A.; Maul, J.; Civalleri, B. Thermal Properties of Molecular Crystals through Dispersion-corrected Quasi-harmonic Ab initio Calculations: The Case of Urea. Chem. Commun. 2016, 52, 1820–1823. [Google Scholar] [CrossRef]
- Erba, A.; Maul, J.; Itou, M.; Dovesi, R.; Sakurai, Y. Anharmonic Thermal Oscillations of the Electron Momentum Distribution in Lithium Fluoride. Phys. Rev. Lett. 2015, 115, 117402. [Google Scholar] [CrossRef] [PubMed]
- Maul, J.; Santos, I.M.G.; Sambrano, J.R.; Erba, A. Thermal properties of the orthorhombic CaSnO3 perovskite under pressure from ab initio quasi-harmonic calculations. Theor. Chem. Acc. 2016, 135, 1–9. [Google Scholar] [CrossRef]
- Ruggiero, M.T.; Zeitler, J.; Erba, A. Intermolecular Anharmonicity in Molecular Crystals: Interplay between Experimental Low-Frequency Dynamics and Quantum Quasi-Harmonic Simulations of Solid Purine. Chem. Commun. 2017, 53, 3781–3784. [Google Scholar] [CrossRef] [PubMed]
- Brandenburg, J.G.; Potticary, J.; Sparkes, H.A.; Price, S.L.; Hall, S.R. Thermal Expansion of Carbamazepine: Systematic Crystallographic Measurements Challenge Quantum Chemical Calculations. J. Phys. Chem. Lett. 2017, 8, 4319–4324. [Google Scholar] [CrossRef] [PubMed]
- Belousov, R.I.; Filatov, S.K. Algorithm for calculating the thermal expansion tensor and constructing the thermal expansion diagram for crystals. Glass Phys. Chem. 2007, 33, 271–275. [Google Scholar] [CrossRef]
- Paufler, P.; Weber, T. On the determination of linear expansion coefficients of triclinic crystals using X-ray diffraction. Eur. J. Mineral. 1999, 11, 721. [Google Scholar] [CrossRef]
- Fortes, A.D.; Wood, I.G.; Knight, K.S. The crystal structure and thermal expansion tensor of MgSO4–11D2O(meridianiite) determined by neutron powder diffraction. Phys. Chem. Miner. 2008, 35, 207–221. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, J.J.; Zhang, H.; Manga, V.R.; Shang, S.L.; Chen, L.Q.; Liu, Z.K. A first-principles approach to finite temperature elastic constants. J. Phys. Condens. Matter 2010, 22, 225404. [Google Scholar] [CrossRef] [PubMed]
- Kádas, K.; Vitos, L.; Ahuja, R.; Johansson, B.; Kollár, J. Temperature-dependent elastic properties of α-beryllium from first principles. Phys. Rev. B 2007, 76, 235109. [Google Scholar] [CrossRef]
- Shang, S.L.; Zhang, H.; Wang, Y.; Liu, Z.K. Temperature-dependent elastic stiffness constants of α- and θ-Al2O3 from first-principles calculations. J. Phys. Condens. Matter 2010, 22, 375403. [Google Scholar] [CrossRef]
- De La Pierre, M.; Orlando, R.; Maschio, L.; Doll, K.; Ugliengo, P.; Dovesi, R. Performance of six functionals (LDA, PBE, PBESOL, B3LYP, PBE0 and WC1LYP) in the simulation of vibrational and dielectric properties of crystalline compounds. The case of forsterite Mg2SiO4. J. Comp. Chem. 2011, 32, 1775–1784. [Google Scholar] [CrossRef] [PubMed]
- Bouhifd, M.A.; Andrault, D.; Fiquet, G.; Richet, P. Thermal expansion of forsterite up to the melting point. Geophys. Res. Lett. 1996, 23, 1143–1146. [Google Scholar] [CrossRef]
- Ye, Y.; Schwering, R.A.; Smyth, J.R. Effects of hydration on thermal expansion of forsterite, wadsleyite, and ringwoodite at ambient pressure. Am. Mineral. 2009, 94, 899–904. [Google Scholar] [CrossRef]
- Hazen, R.M. Effects of temperature and pressure on the crystal structure of forsterite. Am. Mineral. 1976, 61, 1280–1293. [Google Scholar]
- Anderson, O.L.; Isaak, D.; Oda, H. High-temperature elastic constant data on minerals relevant to geophysics. Rev. Geophys. 1992, 30, 57–90. [Google Scholar] [CrossRef]
- Howarth, A.; Liu, Y.; Li, P.; Li, Z.; Wang, T.; Hupp, J.; Farha, O. Chemical, thermal and mechanical stabilities of metal-organic frameworks. Nat. Rev. Mater. 2016, 1, 15018. [Google Scholar] [CrossRef]
- Marmier, A.; Lethbridge, Z.A.; Walton, R.I.; Smith, C.W.; Parker, S.C.; Evans, K.E. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Comput. Phys. Commun. 2010, 181, 2102–2115. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).