Next Article in Journal
Fibrous Minerals and Naturally Occurring Asbestos (NOA) in the Metacarbonate Hosted Fe Oxide-Cu-Au-Co Mineralized Rocks from the Guelb Moghrein Mine, Akjoujt, Mauritania: Implications for In Situ Hazard Assessment and Mitigation Protocols
Previous Article in Journal
Geochemical Features and Mobility of Trace Elements in Technosols from Historical Mining and Metallurgical Sites, Tatra Mountains, Poland
Previous Article in Special Issue
Origin and Tectonic Implication of Cenozoic Alkali-Rich Porphyry in the Beiya Au-Polymetallic Deposit, Western Yunnan, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Minerals
Volume 15
Issue 9
10.3390/min15090989
minerals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Kinetics of Sulfide Dissolution Controlled by Sulfur Radical Diffusion: Implications for Sulfur Transport and Triggering of Volcanic Eruptions

by
Anastassia Borisova
Géosciences Environnement Toulouse, GET-UMR 5563-OMP-CNRS, 14 Avenue E. Belin, 31400 Toulouse, France
Minerals 2025, 15(9), 989; https://doi.org/10.3390/min15090989
Submission received: 25 August 2025 / Revised: 10 September 2025 / Accepted: 14 September 2025 / Published: 17 September 2025
(This article belongs to the Special Issue Advances in Mantle–Crust Interactions for Petrogenesis and Ore-Forming Processes)
Browse Figures
Versions Notes

Abstract

Chemical mixing of different types of magma, such as basaltic magma and silica-rich, hydrous magma, often triggers volcanic eruptions. However, the kinetics, mechanisms, and rates of sulfide dissolution reactions in hydrous melts are currently unknown, despite the fact that these reactions can influence the sulfur budget in the crust and mantle. I experimentally model dissolution of pyrrhotite minerals in hydrous rhyolite melt at conditions corresponding to the sulfate–sulfide transition field at 1 GPa pressure. The reaction results in the production of FeO, SO42−, H2, H2S and di- and tri-sulfur radical ions, (S2− or S3−) in fluid/melt. The calculated sulfur diffusion coefficient implies extremely fast sulfur diffusion in the hydrous hybrid melt. The production of S-rich magma is controlled by the fastest-ever-recorded chemical diffusion of sulfur in the form of S2− or S3− in hybrid magma under sulfate-sulfide transition conditions. I demonstrate that such dissolution reactions can be responsible for triggering explosive volcanic eruptions (e.g., the 1991 Mount Pinatubo eruption) in volcanic arc settings. The sulfide dissolution reaction can also promote the production of chalcophile metal (sulfur-loving Au, Cu and Pt) ore deposits associated with the formation of volcanic arcs.

Graphical Abstract

1. Introduction

Chemical mixing or physical mingling of contrasting types of magmas are principal factors triggering volcanic eruptions [1]. The strongest volcanic eruptions with a VEI (Volcanic Explosivity Index) higher than four, as those produced by Mount Pinatubo in 1991 were (VEI = 5), are triggered by either mixing of hydrous felsic magma with intruding mantle-derived basaltic magma or basaltic underplating, where the basaltic magmas regularly contain Fe-rich sulfide minerals or globules [2,3,4,5]. For example, the 1991 Mount Pinatubo eruption liberated 15–19 Mt of sulfur in the form of SO2 in the terrestrial stratosphere [6] and was associated with triggering by basaltic intrusion [4,7,8]. The release of SO2-H2O-fluid, which may have caused oxidation of the dacitic magma, preceded the 1991 eruption of Mount Pinatubo [4,9]. The liberated sulfur was related to the mixing of basaltic magmas with the overlaying hydrous felsic magma in a shallow reservoir [4,8]. In addition, numerous deep-level mixing events preceding the 1991 eruption were also recorded [10], suggesting deep basaltic underplating or mixing events, possibly at the crust–mantle transition zone. In this study, I experimentally model the interaction of FeS pyrrhotite as an important sulfur source hosted by mantle-derived basaltic magmas or by deep cumulates at the mantle–crust transition zone, or deep or lower crust with a hydrated silica-rich melt. Thermodynamic modeling of the fluid phase composition and the implication of the sulfur behavior are performed for the plumbing system preceding the 1991 Mount Pinatubo volcanic eruption.

2. Materials and Methods

2.1. Experimental Method

The experiments were performed at 0.5 to 1.0 GPa and 900 and 1000 °C using the “Max Voggenreiter” (Germany) end-loaded Boyd-England piston-cylinder apparatus at the Bavarian Research Institute of Experimental Geochemistry and Geophysics (BGI), Bayreuth, Germany, with conditions and apparatus similar to those used [11,12] (Table S1). The experimental design of the runs included a doubly polished cylinder of pure pyrrhotite mineral (BA-1881-59) [13] in the lower part, and the aluminosilicate powder in the upper part of the Au80Pd20 capsule. The doubly polished pyrrhotite Fe(1−x)S (x = 0) cylinder was placed together with the powder of the glass or volcanic ash (Table S1). The distilled waterMQ was directly introduced into the powder of Macusanite rhyolite glass (sulfur-free) which was previously characterized [14], or into the volcanic ash by micro-syringe. Redox conditions were controlled by sulfate–sulfide transition (Table S1) approaching the NNO mineral buffer (nickel–nickel oxide mineral buffer) at the run temperatures and limited by the intrinsic oxygen fugacity (see below) to allow me to establish redox conditions close to and above the NNO mineral buffer. Talc cells of 3/4 inch diameter with Pyrex sleeves were used. A tapered graphite furnace was inserted into each cell. Alumina (Al2O3) spacers were used as the pressure-transmitting medium. The pressure was calibrated using several metamorphic reactions (quartz to coesite transformation and albite = jadeite + quartz [15]. The Au80Pd20 capsule loaded with starting materials was placed in the central part of the assembly. A 20% pressure correction was applied for the friction between the talc cell and pressure vessel [11]. A molybdenum disulfide (MoS2) lubricant was introduced to minimize friction. The applied 3/4 inch assembly allowed me to obtain a ±0.05 GPa uncertainty. The temperature in the upper part of the capsules was controlled by a EUROTHERM (2404) controller and either W3Re97/W25Re75 (type D) or Pt6Rh94/Pt30Rh70 (type B) thermocouples accurate to ±0.5 °C. The samples were compressed to 0.5 (or 1.0) GPa for 20 min and then heated up to the run temperature at a rate of 100 °C/min. The samples were maintained at the run conditions for the desired durations. The successful samples were maintained at run conditions (900 and 1000 °C and 1.0 GPa, Table S1) for 30 min. All capsules were quenched by switching off the electrical power. The samples were decompressed after the quenching, over periods ranging from 20 min to 3 h. The quench rate to room temperature was ~300 °C/min.
The intrinsic oxygen fugacity (fO2) during piston-cylinder runs generally varied between −0.5 and +3 log units, relative to the synthetic fayalite–magnetite–quartz oxygen buffer (i.e., QFM−0.5 to QFM+3) for a piston-cylinder apparatus up to 3 GPa and ~1000 °C [16]. The water-rich runs in this work were performed using a similar experimental technique and capsule material at 1.0 GPa and 1000 °C runs at NNO to NNO+2, based on XANES measurement of Fe2+/Fe3+ in the quenched glasses [11]. These redox conditions are favorable for the production of sulfur radical species, as S2− and S3− are known to be stable at high temperatures [17,18]. All numerical data are given in Tables S1–S5.

2.2. Micro-Raman and ATR-FTIR Spectroscopy

The background-normalized integrated intensities of SO42− contents in the glasses at contact with the reacting pyrrhotite have been obtained with profiles of the experimental reaction zone by Raman spectroscopy (Figure 1A, Table S2). The Raman spectra were recorded with a HORIBA Jobin Yvon LabRAM HR800 Vis Raman spectrometer (Taiwan) (grating 1800 lines/mm, focal length 800 mm, confocal pinhole 1000 µm, slit aperture 100 µm), equipped with a Synapse back-illuminated CCD detector (2048 × 512 pixels) and an Olympus BXFM microscope with a motorized XYZ sample stage in CEMES laboratory, Toulouse. The unpolarized spectra were acquired with backscattering geometry, using an Olympus SLMPlan N 20× objective (Japan) with a working distance of 25 mm [18] and a COBOLT Blues™ DPSS laser (Sweden) (wavelength 473 nm, power stability).
The Attenuated Total Reflectance (ATR) micro-FTIR technique by Thermo (Nicolet iN10) (Waltham, MA, USA) requires only a singly polished sample for quantitative results. The maximal absorbance on the peak of 3500 cm−1 peak was used for the H2O quantification [19]. The H2O contents were calibrated based on the background-subtracted absorbance on peaks of 3500 cm−1 using three reference glasses of rhyolitic composition (Macusanite) [13] with different water content (0.1 to 6 wt% H2O). Because the same rhyolitic glasses were applied in the runs, no density correction was applied for the calibration. The calibration was extrapolated to ~9 wt% H2O, assuming the same trend of the water absorbance intensity versus the glass water contents. In addition, the high H2O contents below the water fluid saturation obtained by micro-FTIR are in good agreement with the bulk water contents and the approximate estimations, based on the electron probe analysis (Tables S1 and S3).

2.3. Electron Probe Microanalysis

Microanalyses of major and minor element contents in the experimental minerals and glasses and the experimental sample imaging were performed at the Géosciences Environnement Toulouse (GET, Toulouse, France) laboratory (Table S3). The main experimental phases in the samples have been identified by using a scanning electron microscope (SEM) JEOL JSM-6360 LV microprobe technique (Japan) at GET (Toulouse, France) [11]. Major and minor element compositions of the crystals and glasses were analyzed using a CAMECA SX-Five microprobe (France) at the Centre de Microcaractérisation Raimond Castaing (Toulouse, France). An electron beam of 15 kV accelerating voltage and of 20 nA current was defocused on the glass sample to give an analytical lateral resolution of 5 μm2. The following synthetic and natural standards were used for calibration: albite (Na), corundum (Al), wollastonite (Si, Ca), sanidine (K), pyrophanite (Mn, Ti), hematite (Fe), periclase (Mg), tugtupite (Cl), and celestine-MAC10617 (S). Element and background counting times for most analyzed elements were 10 and 5 s, respectively, and 60 s for S and 30 s for the background. The detection limits for S and Cl in the felsic glasses were of about 200 ppm. The silicate reference materials such as NIST SRM-610 and other reference glasses [20,21], were analyzed as unknown samples to additionally monitor the analysis accuracy. The silicate reference material analysis allowed me to control precision for the major and minor (e.g., S, Cl in glasses) element analyses to be within the limit of the analytical uncertainty (related to the count statistics). The accuracy estimated for the reference glasses ranges from 0.5% to 3% (1σ RSD = relative standard deviation), depending on the element contents in the reference glasses.

2.4. Thermodynamic Modeling

To assess the sulfur content in the aqueous fluid produced by pyrrhotite dissolution, and thus, to estimate its potential role in the transport and fractionation of the elements in experimental systems, the thermodynamic equilibrium calculations in the FeS-to-FeO melt-fluid system (Equation (4)) were applied. The calculations were conducted at a temperature of up to 1000 °C, redox conditions of NNO and above NNO and pressure up to 1.0 GPa. Table S5 summarizes the predicted dissolved sulfur concentrations in the aqueous fluid phase, depending on the pH in the fluid and FeO in the melt. The calculations were performed using the current version 4.6 of HCh software package and the associated Unitherm database, allowing chemical equilibrium predictions in multicomponent fluid-mineral systems. This approach is based on the minimization of the Gibbs free energy of the system [22], while accounting for non-ideality of the species in aqueous solution by using the extended Debye-Hückel equation [23]. The thermodynamic properties of the end members of FeS and FeO phases were adopted from [24] (HP11 database) and the thermodynamic models [22,24] were used. In the absence of an appropriate thermodynamic model, using solid FeO instead of FeO in the melts (αFeO < 1) is currently the only way to calculate our large range of elements and temperature-pressure-composition conditions in the presence of an aqueous fluid. The uncertainties of such predictions are dependent on FeO content in the hybrid melt and the pH in the fluid (Table S5). Nevertheless, these uncertainties are much lower compared to the extremely large range of the predicted solubility for sulfur. Therefore, I am confident that my calculations provide a robust first-order estimate of concentrations and relative abundances in the aqueous fluids formed during FeS dissolution under the applied experimental conditions.

3. Results

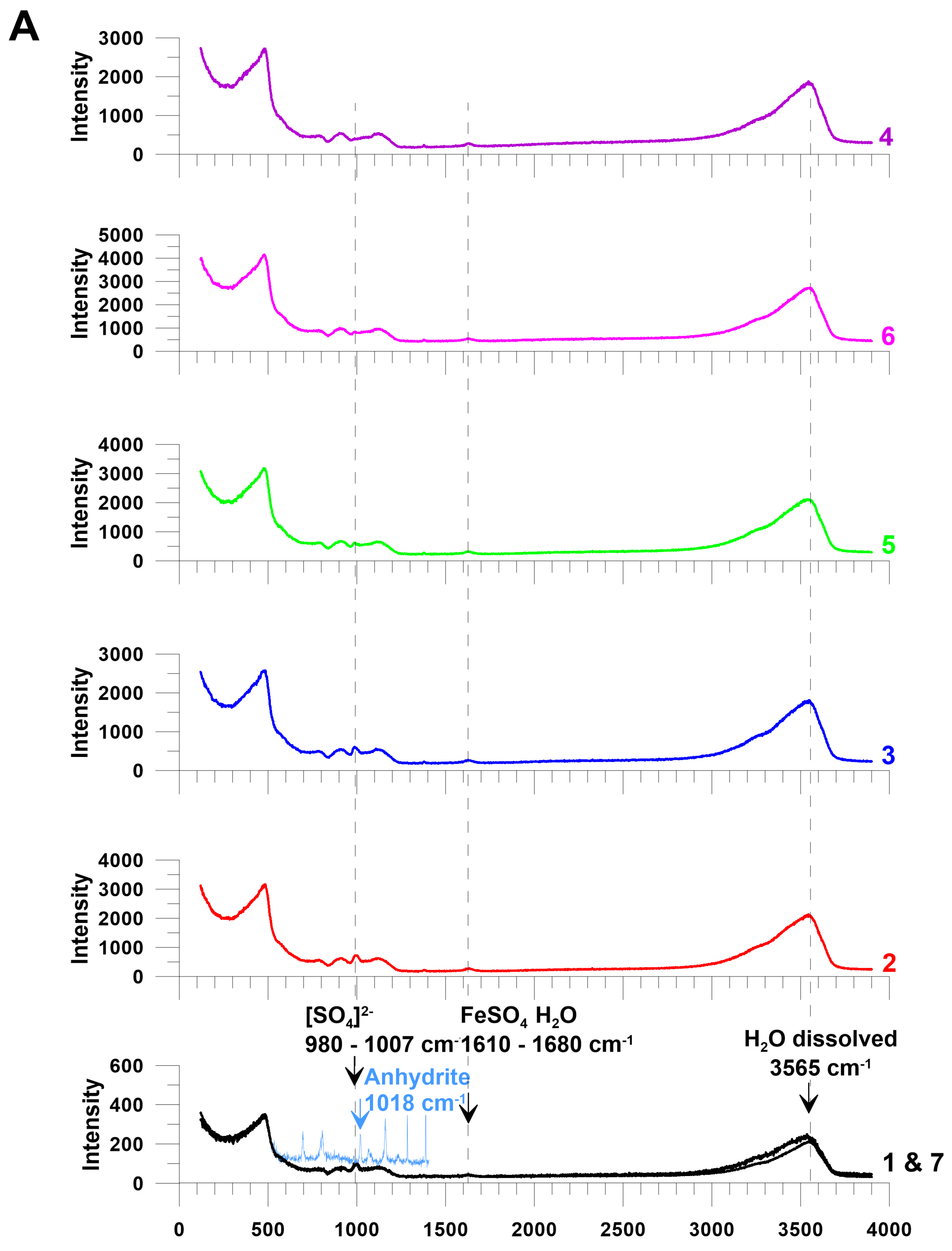
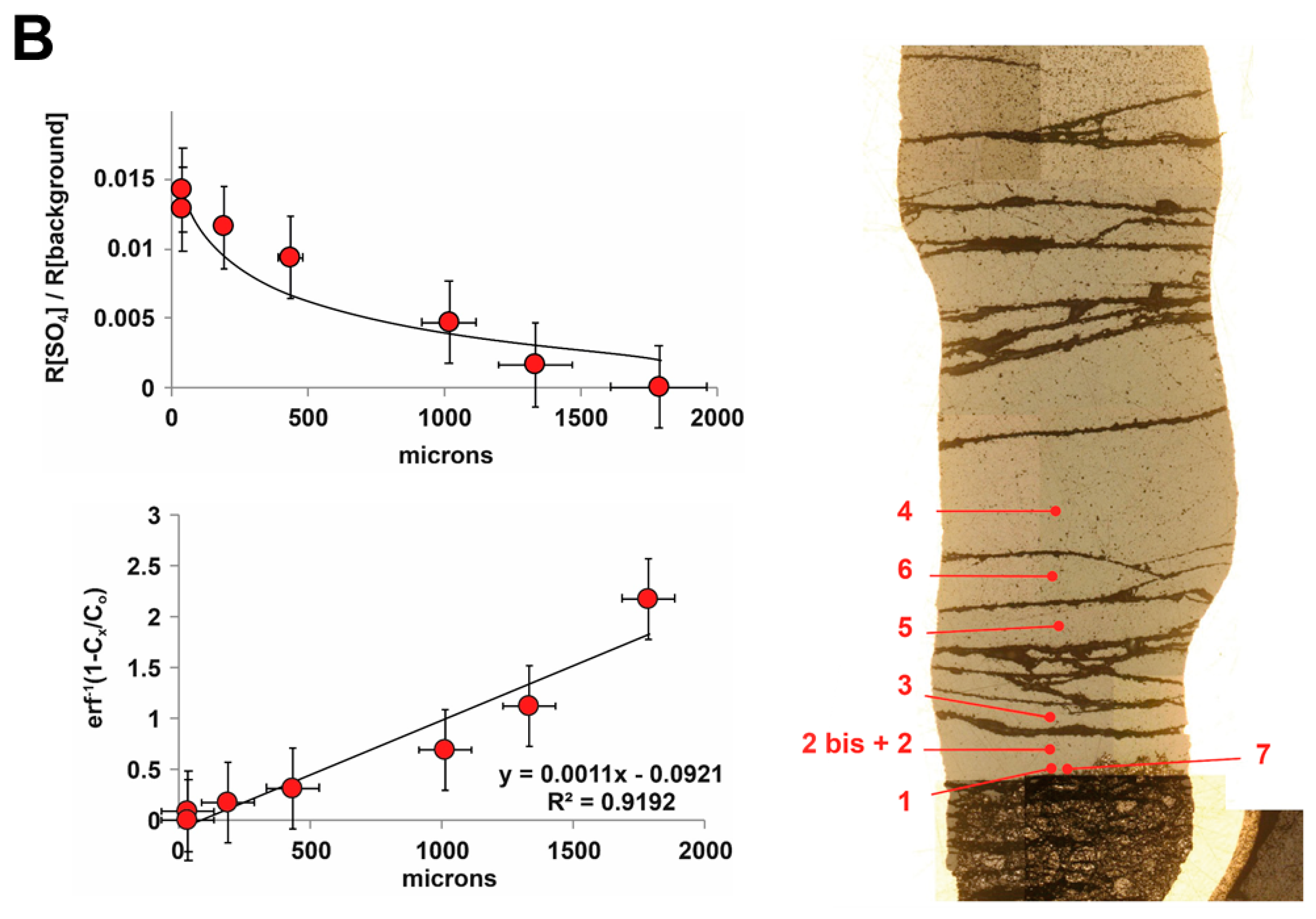
Sulfide Dissolution Reactions and the Reaction Products

The performed experimental runs modeled the reaction of a pure pyrrhotite mineral with a hydrous melt and production of S-rich magma (Table S1). The first two preliminary runs at 0.5 GPa were initiated at run temperatures but were promptly terminated and quenched, due to the presence of a strong hydrogen sulfide (H2S) odor in the liberated fluid. This was likely caused by leakage of the capsule and cooling of the sulfur-bearing fluid, which escaped from the capsule due to an excess of the fluid phase.
S2− + 1.5 H2 = HS− + H2S
or
S3− + 2.5 H2 = HS− + 2 H2S
These two preliminary runs at 0.5 GPa record the H2S liberation upon the reaction. Subsequently, I increased the pressure and performed the successful runs with the same starting materials at 1.0 GPa for 30 min (Table S1). The successful runs at 1.0 GPa (PS3, PS4) (Table S1) demonstrate the presence of pyrrhotite, quenched hydrous glass, and anhydrite crystals at the interface between the two in the PS4 run sample, whereas the PS3 sample contains only the glass and the pyrrhotite. The micro-size anhydrite crystals were identified by the scanning electron microscope (SEM) (JEOL, Japan) uniquely at the interface between the glass and the reacted pyrrhotite in the PS4 sample.
In the quenched hydrous glasses of these runs, I observed the Raman peaks of 980 to 1007 cm−1 corresponding to species of SO42− (Figure 1A,B, Tables S1 and S2). The important point is that the large Raman SO42− peaks in the rhyolitic glasses of the PS3 sample are different from the characteristic peak of anhydrite of 1018 cm−1, suggesting that there was no contamination of the quenched glass with the anhydrite crystals. All analyzed hydrous glasses recorded the peaks (from 1610 to 1680 cm−1) similar to the peak of 1648 cm−1 for the solid phase of FeSO4 × 7H2O [25], which is interpreted as a solid species of [FeSO4 H2O] as possible nanoscale Fe-S-(Au-Pd)-nuggets, related to the quenching effect. All spectra demonstrate the broad peak of the dissolved H2O (around 3565 cm−1), similar to the natural glasses hosted by quartz [8].

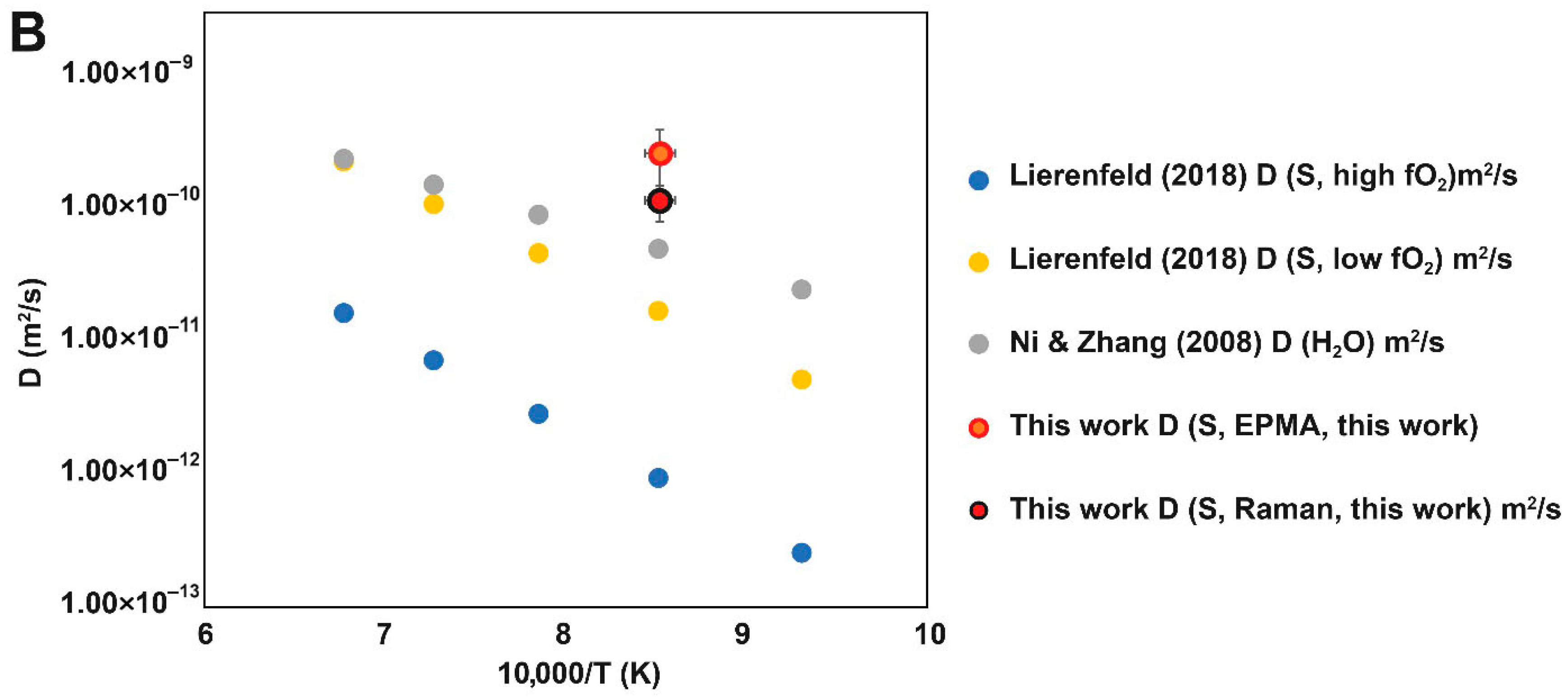
4. Discussion

Sulfur Diffusion and Speciation in Hybrid System

To calculate the sulfur diffusion coefficients at 900 °C and 1.0 GPa and 8.9 wt% H2Omelt, I have applied the diffusion extraction method based on the sulfur concentration profiles in the glasses, perpendicular to the interface between the pyrrhotite mineral and quenched glass [26,27]. Figure 1B and Figure 2A demonstrate that the calculated diffusion rate of the sulfur species at 1.0 GPa and 900 °C based on the Raman intensities of the SO42− species (1.1 × 10−10 m2/s) is similar to the SO3 diffusion coefficient (2.6 × 10−10 m2/s) extracted from the SO3 wt% analysis by electron probe microanalysis (EPMA). This suggests extremely fast sulfur diffusion, as S-bearing species dissolved in the hydrous rhyolite melt. Importantly, high-pressure and high-temperature species of S2− and S3− were recorded in situ at the conditions of sulfate-to-sulfide transition during the high-temperature pressure experiment by diamond anvil cells [17,18] and specific oxygen fugacity of NNO and above the nickel-nickel oxide buffer, which is the case for this study of pyrrhotite dissolution experiments. The S2- and S3- species existing at high temperature were transformed to H2S upon cooling, explaining the strong odor of H2S in the two initial runs of the common configuration. In the performed experimental runs (Table S1), the recorded H2S in the liberated fluid of the first runs (Equations (1) and (2)), as well as SO42− identified here by micro-Raman spectroscopy in the hydrous glasses, suggest the following reactions:
2 FeS(po) + 2 H2O = 2 FeO(melt) + S2− + H+ + 1.5 H2
and
3 FeS(po) + 3 H2O = 3 FeO(melt) + S3− + H+ + 2.5 H2
and
S3− + 0.75 O2 + 2.5 H2O = SO42− + 2 H2S + H+
or
8 S3− + 20 H2O = 19 H2S + 5 SO42− + 2H+
and
8 S2− + 2 H+ + 12 H2O = 13 H2S + 3 SO42−,
at 900–1000 °C and 1.0 GPa pressure, where FeS(po) is pyrrhotite, FeO(melt)—FeO and SO42− and H2S, and H2 and S2−, S3− components of the hydrous felsic melt or fluid. H2O is H2O dissolved in the hydrous melt and can be the fluid phase at conditions of fluid saturation. These reactions are also confirmed by the similar behaviors of SO3 (or SO42−) and FeO contents in the interface glass measured by electron probe microanalysis, EPMA (Figure 2A).
The micro-Raman and EPMA data used to quantify the diffusion coefficients are given in Tables S2–S4. According to the slope of 0.004 on the plot of FeO profiles in the rhyolitic glasses at the interface with pyrrhotite and the erf−1 error function versus the distance from the interface (in µm) (Table S3), the FeO diffusion is 8.01 × 10−10 m2/s, which is slightly faster than the SO42− and SO3 diffusion coefficients (1.06 × 10−10 and 2.62 × 10−10 m2/s, respectively, Tables S1 and S4). Nevertheless, Figure 2B, plotted based on these diffusion data, demonstrates that the SO42− and SO3 diffusion coefficients obtained in this work are higher for oxidized and reduced sulfur species [28] and for water [29] in comparison to those of recent data. The sulfur diffusion coefficients for the hydrous melts obtained in this work are much higher than those for water, as well as for reduced and oxidized sulfur species, at 900 °C (equivalent to 10,000/T = 8.5). These coefficients correspond to the redox conditions of NNO and above NNO at 1 GPa and 900 °C. This indicates the production of sulfur species that have not been investigated before.
Previous S diffusion studies [28] demonstrated that a direct comparison of S and H2O diffusion reveals that S diffusion is slower than that of H2O (H2O ≤ 7 wt%), whereas my new data imply that the oxidized sulfur species can diffuse in highly hydrated melt (9 wt% H2O) faster than water. This fast S diffusion is controlled by the presence of highly volatile S3− and S2− radical species. My experiments demonstrate that Fe diffusion is decoupled from the S species diffusion, even in the Fe-rich sulfide dissolution system, suggesting that sulfur speciation is independent from that of Fe. The previous Fe-free experiment-based conclusion [30] states that alkalis are only available for sulfate complexation when they are present in excess, compared to the required amount to charge balance for the Si4+ to Al3+ substitution in the melt structure. In contrast, [31] hypothesized the presence of (Fe,Ca)SO4 nH2O or (Na,K)2SO4 nH2O at similar physical-chemical conditions and a similar hydrous system. In the experimental system studied here, the sulfur transport in the hydrous melt is decoupled from water, iron, and alkalis and is related to the sulfur radical species, which have very poor solubility and chemical bonding to the aluminosilicate melt [18], explaining the extremely rapid diffusion of these sulfur species in the hydrous melts.

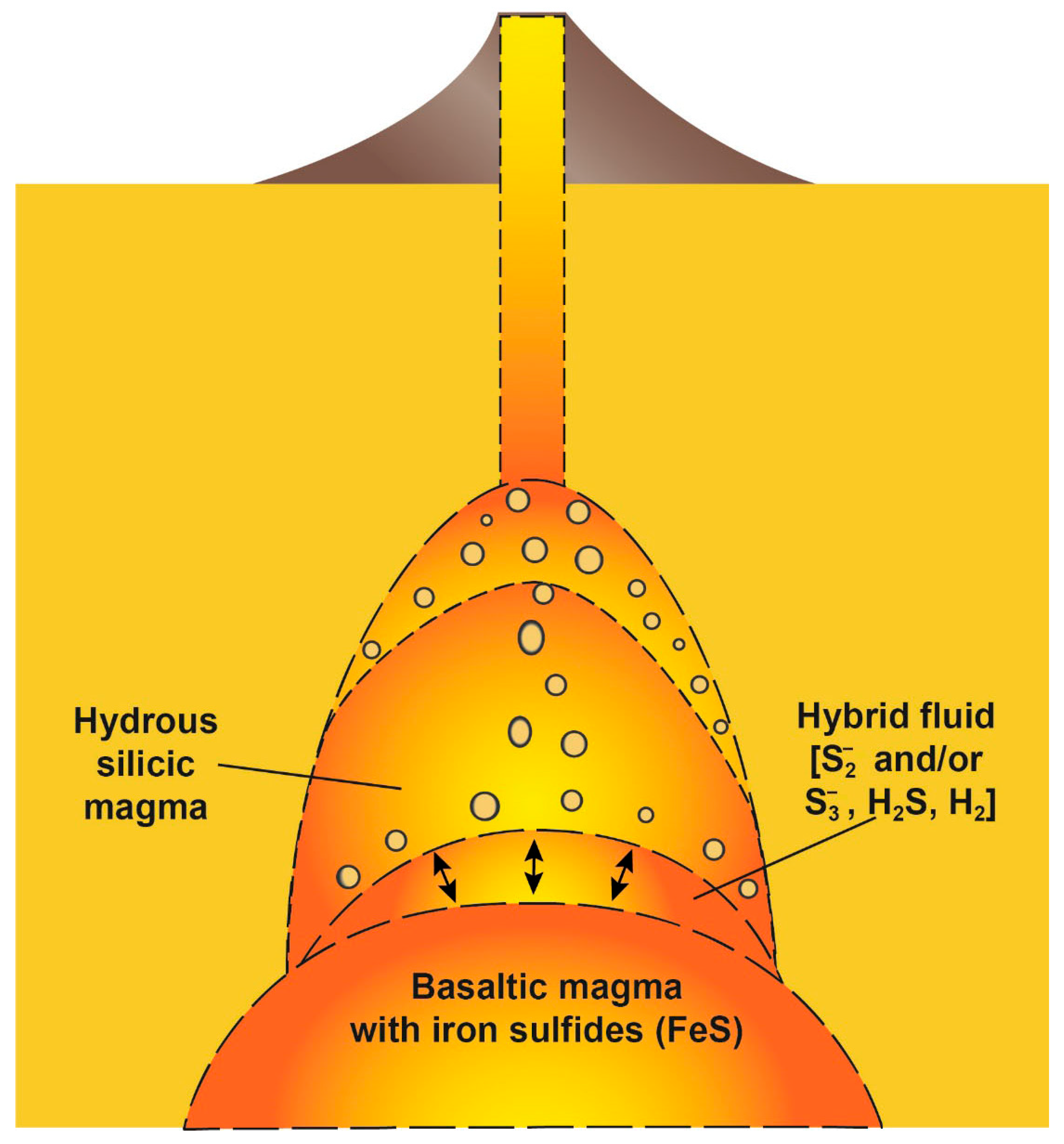
5. Implications

5.1. Hybrid S-Rich Magma and Its Role in Explosive Eruptions

Hybrid mafic fragments from the 1991 Mount Pinatubo eruption contain Fe-rich sulfide globules [2,3,5]. However, the previously reported high oxidation state of the basaltic magma [32] suggests relatively high oxidation states (NNO+1.4 – NNO+2) of the 1991 Mount Pinatubo magmas. These conditions where sulfide was present and likely dissolved are similar to the experimental out of equilibrium conditions of the pyrrhotite dissolution runs performed here. Based on my experimental runs at 9 wt% H2Omelt, the equilibrium S concentrations in the hybrid melt measured at the interface between pyrrhotite and hydrous felsic melt is of 2000 ppm S at 900 °C (Table 1). Similar high concentrations of 1300–2900 ppm S were recorded in the natural dacitic to rhyolitic melt inclusions in the 1991 Mount Pinatubo enclaves of basaltic composition [32], the hybrid andesite [33], and the groundmass glass near the partially dissolved sulfides [34], reflecting hybrid S-rich magma formation in direct relation to the sulfide dissolution and saturation with sulfur.
Equation (4) suggests that the equilibrium S content in the hybrid fluid produced by sulfide dissolution in the hydrous aluminosilicate melt is a strong function of the FeO contents in the hybrid melt and pH of the fluid (Table S5). For example, 3 to 5 wt% FeO in the hybrid melt will result in 7 to 20 wt% S in the aqueous fluid (Table 1 and Table S5), similar to 3 wt% SO2 in the 1991 Mount Pinatubo pre-eruptive fluid. Thermodynamic calculations (Table S5) of modeled fluid composition give the fluid sulfur concentrations of 70,000 ppm S, which is similar to the reported in experiments on sulfate–sulfide transition [18] and highly hydrated systems [31]. The maximal sulfur concentrations in the fluid of 300,000 ppm S for the S2− and S3−—bearing systems are estimated here based on high fluid-melt partitioning (KD) of 50 to 150, which is typical for the sulfate–sulfide transition [18,38]. Indeed, the modeled mass of S in the pre-eruptive fluid is similar to the measured masses of the liberated S in form of SO2 of the Mount Pinatubo pre-eruptive fluid (Table 1). If the pre-eruptive sulfur is uniquely derived from the dissolution of the Fe-rich sulfides [34], the 1991 Mount Pinatubo eruption related to the magma mixing events [8] could be triggered by such S-rich fluid (Equation (4)). The bulk mass of sulfur in the S-bearing fluid phase produced due to sulfide decomposition may be considerable, provided that all sulfur is derived from the basaltic source (e.g., sulfides). The required percentage of Fe-rich sulfides in the parental basaltic magma is 0.2–0.6 wt% (Table 1). Such sulfide concentrations are in agreement with typical S contents of 900 to 2500 ppm recorded in the primitive arc basalts [38].
In fact, two main stages of the mixing event could happen in the 1991 Mount Pinatubo plumbing system. (1) Previous studies of the 1991 Mount Pinatubo hybrid andesitic and basaltic quartz-hosted fluid inclusions suggest that the following reaction occurred at shallow levels, corresponding to the pressure of 0.3 GPa:
4SO2 + 4H2O = 3HSO4− + H2S + 3H+,
where the reaction yields sulfate, sulfide, and an increase in fluid acidity. The reaction shifts to the right with decreasing temperature. The fact that SO42− ion is systematically present in the (pseudo-)secondary H2O–CO2–S fluid inclusions [8] is consistent with the transformation of the supercritical S-rich fluid upon cooling, rather than with post-entrapment modifications within the fluid inclusions.
(2) In addition, an important source of deep sulfur-fluxing periods [10,32] due to dissolution of deep-settled sulfides (e.g., Fe-rich sulfides) could happen as described by reactions (Equations (3)–(7)). Indeed, hybrid S-rich magma was recorded by high S contents (up to 2900 ppm, respectively) into the felsic melt inclusions entrapped in amphiboles of the 1991 Mount Pinatubo basalt [32]. This magma could be formed due to sulfide decomposition during deep mixing events, which could occur at depths of up to 45 km (1.5 GPa), based on the Al2O3 content recorded in the quenched melts and those of the host amphiboles [39]. This scenario of deep sulfide dissolution is compatible with the presence of sulfide accumulation layers formed in the lower crust and the mantle–crust transition zone [40,41].
This scenario implies that these S-rich magma-forming reactions, in addition to the previously assumed Equation (8) for the shallow levels, could be related to multiple mixing events with hydrous felsic magmas. The percolating hydrous felsic magma could react to the deep sulfide layers upon its transport through the lower crustal cumulates and the mantle–crust transition zone. Thus, if the sulfide-enriched layer reacted with the felsic magma percolating from the subducting slab [39], hybrid S-rich magma would form. These facts and estimations indicate that if the reactions (Equations (3)–(7)) triggered by dissolution of the pyrrhotite or other Fe-rich sulfides proceeded upon the magma mixing, the fastest sulfur diffusion mechanism ever observed for sulfur species in hydrous hybrid magma would occur.
The results of experiments and thermodynamic modeling summarized in Table 1 and Table S5 show that the interaction of hydrous felsic magmas with the Fe-rich sulfides through magma transport to shallower magma reservoirs is a viable mechanism for the effective transport of S. The reactions established here (Equations (3)–(7)) imply that such dissolution of sulfides in hydrous magmas can happen in the arc geodynamic settings at different levels and can result in the extremely efficient enrichment of sulfur. The dissolution reactions, if controlled by NNO to NNO+2 redox conditions, imply that sulfides can react with hydrous felsic magma, as shown in Figure 3. This reaction of sulfide dissolution is extremely rapid at shallow and deep levels and can promote the production of S-rich magma. It can also increase the pressure of the pre-eruptive hybrid fluid associated with the release and diffusion of S-radical species at shallow and deep levels. Thus, the accumulation of the hybrid S-rich fluid can trigger explosive eruptions of hybrid magmas. Future numerical modeling of hybrid, fluid-saturated systems can benefit from the sulfur radical diffusion data obtained here. These data can be used to create numerical models of explosive eruptions, paying particular attention to the role of sulfide dissolution reactions.

5.2. Sulfur-Loving (Chalcophile) Metal-Rich Magma Formation

The observed sulfide dissolution reaction mechanism, generating magma that is rich in sulfur, has to be enriched with the associated chalcophile metals of Au, Cu, and Pt [4,31,42,43,44], derived from the dissolving sulfide components. Such a hybrid, S-rich magma can promote the production of an S-rich fluid that is highly enriched in chalcophile metals, resulting in porphyry ore deposit formation [38,45,46,47]. Thus, magma mixing and sulfide dissolution can be the main physical-chemical mechanism of chalcophile metal transport from the mantle to the crust. This conclusion is also consistent with the recently described behavior of S and Cu in the mantle–crust transition zone, which is a zone of sulfide segregation and sulfide-controlled metal storage [48], and it is in agreement with the Au-Cu-rich nature of adakite magmas [41,45]. The described sulfide dissolution mechanism can thus be considered to be the main physicochemical process, explaining how sulfur behaves during magma-fluid-crustal interaction. This mechanism can be considered to be one of the physical-chemical mechanisms that controls crustal metallogeny.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/min15090989/s1, Table S1: Experimental conditions, starting material, resulting phases and diffusion coefficients; Table S2: Micro-Raman data; Table S3: EPMA data; Table S4: Numerical data on diffusion coefficients; Table S5: Thermodynamic modeling.

Funding

This research was supported by Institut National des Sciences de l’Univers—Centre National d’Études Spatiales (INSU-CNES, France; 2022–2023) PLAGIOGRAN grant to A.Y.B. This article is funded by the European Union (ERC, PLANETAFELSIC, project 101141259) to AYB. Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.

Data Availability Statement

All data needed to evaluate conclusions in the paper are supported by the paper and the Supplementary Materials (Tables S1–S5). Additional data related to this paper may be requested from the author, Anastassia Y. Borisova.

Acknowledgments

Three anonymous reviewers and L. Dubrovinsky are thanked. The author thanks N. Zagrtdenov, A. Colin, G. Pokrovski, M. Portnyagin for help in the experiment preparation and important suggestions and comments on the initial versions of this manuscript.

Conflicts of Interest

The author declares no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
EPMAElectron Probe Microanalysis
FTIRFourier Transform Infrared Spectroscopy
XANESX-ray absorption near edge structure

References

  1. Sparks, S.R.J.; Sigurdsson, H.; Wilson, L. Magma mixing: A mechanism for triggering acid explosive eruptions. Nature 1977, 267, 315–318. [Google Scholar] [CrossRef]
  2. Matthews, S.J.; Jones, A.P.; Bristow, C.S. A simple magma-mixing model for sulphur behaviour in calc-alkaline volcanic rocks: Mineralogical evidence from Mount Pinatubo 1991 eruption. J. Geol. Soc. 1992, 149, 863–866. [Google Scholar]
  3. Hattori, K. High-sulfur magma, a product of fluid discharge from underlying mafic magma: Evidence from Mount Pinatubo, Philippines. Geology 1993, 21, 1083–1086. [Google Scholar] [CrossRef]
  4. Kress, V. Magma mixing as a source for Pinatubo sulfur. Nature 1997, 389, 591–593. [Google Scholar] [CrossRef]
  5. Hattori, K.; Sato, H. Magma evolution recorded in plagioclase zoning in 1991 Pinatubo eruption products. Am. Mineral. 1996, 81, 982–994. [Google Scholar] [CrossRef]
  6. Bluth, G.J.S.; Doiron, S.D.; Schnetzler, C.C.; Krueger, A.J.; Walter, L.S. Global tracking of the SO2 clouds from the June 1991 Mount Pinatubo eruption. Geophys. Res. Lett. 1992, 19, 151–154. [Google Scholar] [CrossRef]
  7. Pallister, J.S.; Hoblitt, R.P.; Reyes, A.G. A basalt trigger for the 1991 eruptions of Pinatubo volcano? Nature 1992, 356, 426–428. [Google Scholar] [CrossRef]
  8. Borisova, A.Y.; Toutain, J.-P.; Dubessy, J.; Pallister, J.; Zwick, A.; Salvi, S. H2O–CO2–S fluid triggering the 1991 Mount Pinatubo climactic eruption (Philippines). Bull. Volcanol. 2014, 76, 800. [Google Scholar] [CrossRef]
  9. Johnson, M.C.; Anderson, A.T., Jr.; Rutherford, M.J. Pre-eruptive volatile contents of magmas. In Reviews in Mineralogy, Volatiles in Magmas; Carroll, M.R., Holloway, J.R., Eds.; De Gruyte: Berlin, Germany, 1994; pp. 281–323. [Google Scholar]
  10. Van Hoose, A.E.; Streck, M.J.; Pallister, J.S.; Wälle, M. Sulfur evolution of the 1991 Pinatubo magmas based on apatite. J. Volcanol. Geotherm. Res. 2013, 257, 72–89. [Google Scholar] [CrossRef]
  11. Borisova, A.Y.; Zagrtdenov, N.R.; Toplis, M.J.; Ceuleneer, G.; Safonov, O.G.; Pokrovski, G.S.; Bychkov, A.Y. Hydrated peridotite–basaltic melt interaction Part II: Fast assimilation of serpentinized mantle by basaltic magma. Front. Earth Sci. 2020, 8, 84. [Google Scholar] [CrossRef]
  12. Borisova, A.Y.; Zagrtdenov, N.R.; Toplis, M.J.; Bohrson, W.A.; Nédélec, A.; Safonov, O.G.; Pokrovski, G.S.; Ceuleneer, G.; Bindeman, I.N.; Melnik, O.E.; et al. Hydrated Peridotite–Basaltic Melt Interaction Part I: Planetary Felsic Crust Formation at Shallow Depth. Front. Earth Sci. 2021, 9, 640464. [Google Scholar] [CrossRef]
  13. Vikentyev, I.; Vikent’eva, O.; Tyukova, E.; Nikolsky, M.; Ivanova, J.; Sidorova, N.; Palyanova, G. Noble metal speciations in hydrothermal sulphides. Minerals 2021, 11, 488. [Google Scholar] [CrossRef]
  14. Borisova, A.Y.; Pokrovski, G.S.; Pichavant, M.; Freydier, R.; Candaudap, F. Amorphous Materials: Properties, Structure, and Durability. Arsenic enrichment in hydrous peraluminous melts: Insights from femtosecond laser ablation-inductively coupled plasma-quadrupole mass spectrometry, and in situ X-ray absorption fine structure spectroscopy. Am. Mineral. 2010, 95, 1095–1104. [Google Scholar]
  15. Bromiley, G.; Hilaret, N.; McCammon, C. Solubility of hydrogen and ferric iron in rutile and TiO2 (II): Implications for phase assemblages during ultrahigh-pressure metamorphism and for the stability of silica polymorphs in the lower mantle. Geophys. Res. Lett. 2004, 31, 310. [Google Scholar] [CrossRef]
  16. Matjuschkin, V.; Woodland, A.B.; Yaxley, G.M. Methane-bearing fluids in the upper mantle: An experimental approach. Contrib. Mineral Petrol. 2019, 174, 1. [Google Scholar] [CrossRef]
  17. Pokrovski, G.S.; Dubrovinsky, L.S. The S3–ion is stable in geological fluids at elevated temperatures and pressures. Science 2011, 331, 1052–1054. [Google Scholar] [CrossRef] [PubMed]
  18. Colin, A.; Schmidt, C.; Pokrovski, G.S.; Wilke, M.; Borisova, A.Y.; Toplis, M.J. In situ determination of sulfur speciation and partitioning in aqueous fluid-silicate melt systems. Geochem. Persp. Let. 2020, 14, 31–35. [Google Scholar] [CrossRef]
  19. King, P.L.; Ramsey, M.S.; McMillan, P.F.; Swayze, G. Laboratory Fourier transform infrared spectroscopy methods for geologic samples. Infrared Spectrosc. Geochem. Explor. Remote Sens. 2004, 33, 57–91. [Google Scholar]
  20. Jarosewich, E.; Nelen, J.A.; Norberg, J.A. Reference samples for electron microprobe analysis. Geostand. Newsl. 1980, 4, 43–47. [Google Scholar] [CrossRef]
  21. Jochum, K.P.; Weis, U.; Stoll, B.; Kuzmin, D.; Yang, Q.; Raczek, I.; Enzweiler, J. Determination of reference values for NIST SRM 610–617 glasses following ISO guidelines. Geostand. Geoanalytical Res. 2011, 35, 397–429. [Google Scholar] [CrossRef]
  22. Shvarov, Y.V. A suite of programs, OptimA, OptimB, OptimC, and OptimS compatible with the Unitherm database, for deriving the thermodynamic properties of aqueous species from solubility, potentiometry and spectroscopy measurements. Appl. Geochem. 2015, 55, 17–27. [Google Scholar]
  23. Helgeson, H.C.; Kirkham, D.H.; Flowers, G.C. Theoretical prediction of thermodynamic behavior of aqueous electrolytes at high temperatures and pressures. IV. Calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 5 kb and 600 °C. Am. J. Sci. 1981, 281, 1249–1516. [Google Scholar]
  24. Holland, T.J.B.; Powell, R. An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids. J. Metamorph. Geol. 2011, 29, 333–383. [Google Scholar] [CrossRef]
  25. Chio, C.H.; Sharma, S.K.; Muenow, D.W. The hydrates and deuterates of ferrous sulfate (FeSO4): A Raman spectroscopic study. J. Raman Spectrosc. 2007, 38, 87–99. [Google Scholar]
  26. Harrison, T.M.; Watson, E.B. Kinetics of zircon dissolution and zirconium diffusion in granitic melts of variable water content. Contrib. Mineral. Petrol. 1983, 84, 66–72. [Google Scholar]
  27. Borisova, A.Y.; Bindeman, I.N.; Toplis, M.J.; Zagrtdenov, N.R.; Guignard, J.; Safonov, O.G.; Bychkov, A.Y.; Shcheka, S.; Melnik, O.E.; Marchelli, M.; et al. Zircon survival in shallow asthenosphere and deep lithosphere. Am. Mineral. 2020, 105, 1662–1671. [Google Scholar]
  28. Lierenfeld, M.B.; Zajacz, Z.; Bachmann, O.; Ulmer, P. Sulfur diffusion in dacitic melt at various oxidation states: Implications for volcanic degassing. Geochim. Cosmochim. Acta 2018, 226, 50–68. [Google Scholar]
  29. Ni, H.; Zhang, Y. H2O diffusion models in rhyolitic melt with new high pressure data. Chem. Geol. 2008, 250, 68–78. [Google Scholar] [CrossRef]
  30. Zajacz, Z. The effect of melt composition on the partitioning of oxidized sulfur between silicate melts and magmatic volatiles. Geochim. Cosmochim. Acta 2015, 158, 223–244. [Google Scholar] [CrossRef]
  31. Xu, T.; Liu, X.; Xiong, X.; Wang, J. Sulfur dissolution capacity of highly hydrated and fluid-saturated dacitic magmas at the lower crust and implications for porphyry deposit formation. Geochim. Cosmochim. Acta 2022, 333, 107–123. [Google Scholar] [CrossRef]
  32. De Hoog, J.C.M.; Hattori, K.H.; Hoblitt, R.P. Oxidized sulfur-rich mafic magma at Mount Pinatubo, Philippines. Contrib. Mineral. Petrol. 2004, 146, 750–761. [Google Scholar] [CrossRef]
  33. Pallister, J.S.; Hoblitt, R.P.; Meeker, G.P.; Knight, R.J.; Siems, D.F. Magma mixing at Mount Pinatubo: Petrographic and chemical evidence from the 1991 deposits. In FIRE and MUD Eruptions and Lahars of Mount Pinatubo, Philippines; U.S.Geological Survey: Reston, VA, USA, 1996; pp. 687–731. Available online: https://pubs.usgs.gov/pinatubo/index.html (accessed on 12 September 2025).
  34. Di Muro, A.; Pallister, J.; Villemant, B.; Newhall, C.; Semet, M.; Martinez, M.; Mariet, C. Pre-1991 sulfur transfer between mafic injections and dacite magma in the Mt. Pinatubo reservoir. J. Volcanol. Geotherm. Res. 2008, 175, 517–540. [Google Scholar] [CrossRef]
  35. Jégo, S.; Dasgupta, R. The fate of sulfur during fluid-present melting of subducting basaltic crust at variable oxygen fugacity. J. Petrol. 2014, 55, 1019–1050. [Google Scholar]
  36. Hervo, M.; Quennehen, B.; Kristiansen, N.I.; Boulon, J.; Stohl, A.; Fréville, P.; Pichon, J.-M.; Picard, D.; Labazuy, P.; Gouhier, M.; et al. Physical and optical properties of 2010 Eyjafjallajökull volcanic eruption aerosol: Ground-based, Lidar and airborne measurements in France. Atmos. Chem. Phys. 2012, 12, 1721–1736. [Google Scholar] [CrossRef]
  37. Gerlach, T.M.; Westrich, H.R.; Symonds, R.B. Fire and mud: Eruptions and lahars of Mount Pinatubo. Philippines 1996, 415, 33. [Google Scholar]
  38. Li, L.; Liu, X.; Xu, T.; Xiong, X.; Wang, J.; Li, L. Sulfur partitioning between aqueous fluids and felsic melts at high pressures: Implications for sulfur migration in subduction zones. Sci. Rep. 2025, 15, 4273. [Google Scholar] [CrossRef]
  39. Prouteau, G.; Scaillet, B.; Pichavant, M.; Maury, R. Evidence for mantle metasomatism by hydrous silicic melts derived from subducted oceanic crust. Nature 2001, 410, 197–200. [Google Scholar] [CrossRef]
  40. Jenner, F.E. Cumulate causes for the low contents of sulfide-loving elements in the continental crust. Nat. Geosci. 2017, 10, 524–529. [Google Scholar] [CrossRef]
  41. Liu, S.A.; Rudnick, R.L.; Liu, W.R.; Teng, F.Z.; Wu, T.H.; Wang, Z.Z. Copper isotope evidence for sulfide fractionation and lower crustal foundering in making continental crust. Sci. Adv. 2023, 9, eadg6995. [Google Scholar] [CrossRef]
  42. Pokrovski, G.S.; Kokh, M.A.; Guillaume, D.; Borisova, A.Y.; Gisquet, P.; Hazemann, J.L.; Dubessy, J. Sulfur radical species form gold deposits on Earth. Proc. Natl. Acad. Sci. USA 2015, 112, 13484–13489. [Google Scholar] [CrossRef] [PubMed]
  43. Pokrovski, G.S.; Kokh, M.A.; Desmaele, E.; Laskar, C.; Bazarkina, E.F.; Borisova, A.Y.; Saitta, A.M. The trisulfur radical ion S3−controls platinum transport by hydrothermal fluids. Proc. Natl. Acad. Sci. USA 2021, 118, e2109768118. [Google Scholar] [CrossRef]
  44. Chiaradia, M.; Caricchi, L. Supergiant porphyry copper deposits are failed large eruptions. Commun. Earth Environ. 2022, 3, 107. [Google Scholar] [CrossRef]
  45. Borisova, A.Y.; Pichavant, M.; Polvé, M.; Wiedenbeck, M.; Freydier, R.; Candaudap, F. Trace element geochemistry of the 1991 Mt. Pinatubo silicic melts, Philippines: Implications for ore-forming potential of adakitic magmatism. Geochim. Cosmochim. Acta 2006, 70, 3702–3716. [Google Scholar] [CrossRef]
  46. Borisova, A.Y.; Martel, C.; Gouy, S.; Pratomo, I.; Sumarti, S.; Toutain, J.P.; Bindeman, I.N.; de Parseval, P.; Métaxian, J.P. Highly explosive 2010 Merapi eruption: Evidence for shallow-level crustal assimilation and hybrid fluid. J. Volcanol. Geotherm. Res. 2013, 261, 193–208. [Google Scholar] [CrossRef]
  47. He, D.Y.; Qiu, K.F.; Simon, A.C.; Pokrovski, G.S.; Yu, H.C.; Connolly, J.A.; Deng, J. Mantle oxidation by sulfur drives the formation of giant gold deposits in subduction zones. Proc. Natl. Acad. Sci. USA 2024, 121, e2404731121. [Google Scholar] [CrossRef] [PubMed]
  48. Pieterek, B.; Tribuzio, R.; Matusiak-Małek, M.; Ciążela, J.; Horn, I.; Weyer, S.; Strauss, H.; Kuhn, T.; Muszyński, A. Underplated melts control sulfide segregation at the continental crust-mantle transition. Commun. Earth Environ. 2024, 5, 45. [Google Scholar] [CrossRef]
Minerals 15 00989 g001aMinerals 15 00989 g001b
Figure 1. (A) Raman spectra with visible peaks of 980 to 1007 cm−1, 1610 to 1680 cm−1 and 3565 cm−1 correspond to the dissolved [SO42−] and [FeSO4 H2O] as well as dissolved H2O in hydrous rhyolitic glass of the PS3 sample. Micro-Raman peak of anhydrite-bearing inclusion is afterwards [8]. (B) Background-normalized integrated Raman peak intensity of SO42− and erf−1(1 − Cx/CO), where Cx is micro-Raman intensity and Co is the intensity at the interface with pyrrhotite in the experimental sample, imaged using optical microscope. This allows extraction of diffusion coefficient of the bulk S species identified in hydrous rhyolitic glasses by micro-Raman spectroscopy. The diffusion coefficient extracted from the profile corresponds to 1.06 × 10−10 m2/s at 900 °C, 1 GPa, and ~9 wt% H2O in the rhyolitic melt. The data are summarized in the Tables S1–S3.
Figure 1. (A) Raman spectra with visible peaks of 980 to 1007 cm−1, 1610 to 1680 cm−1 and 3565 cm−1 correspond to the dissolved [SO42−] and [FeSO4 H2O] as well as dissolved H2O in hydrous rhyolitic glass of the PS3 sample. Micro-Raman peak of anhydrite-bearing inclusion is afterwards [8]. (B) Background-normalized integrated Raman peak intensity of SO42− and erf−1(1 − Cx/CO), where Cx is micro-Raman intensity and Co is the intensity at the interface with pyrrhotite in the experimental sample, imaged using optical microscope. This allows extraction of diffusion coefficient of the bulk S species identified in hydrous rhyolitic glasses by micro-Raman spectroscopy. The diffusion coefficient extracted from the profile corresponds to 1.06 × 10−10 m2/s at 900 °C, 1 GPa, and ~9 wt% H2O in the rhyolitic melt. The data are summarized in the Tables S1–S3.
Minerals 15 00989 g001aMinerals 15 00989 g001b
Minerals 15 00989 g002aMinerals 15 00989 g002b
Figure 2. (A) Modeling of the bulk S and Fe diffusion in hydrous rhyolitic melt based on SO3 and FeO (wt%) contents in the glasses measured by EPMA at the interface with pyrrhotite. SO3 and FeO wt% contents and erf−1 function versus the distance from the interface (in µm) are plotted. The bulk sulfur diffusion coefficient extracted from the EPMA profile corresponds to 2.62 × 10−10 m2/s at 900 °C, 1 GPa and 8.9 wt% H2O in the rhyolitic melt. (B) Diffusion coefficients of sulfur and water (in m2/s) versus 104/T (in K−1), according to the available data on the coefficients at different temperature conditions and new data obtained in this work at 900 °C. The available diffusion data are from [28] (4.5 wt% H2O) [29] (up to 7.0 wt% H2O). All numerical data are summarized in Table S4.
Figure 2. (A) Modeling of the bulk S and Fe diffusion in hydrous rhyolitic melt based on SO3 and FeO (wt%) contents in the glasses measured by EPMA at the interface with pyrrhotite. SO3 and FeO wt% contents and erf−1 function versus the distance from the interface (in µm) are plotted. The bulk sulfur diffusion coefficient extracted from the EPMA profile corresponds to 2.62 × 10−10 m2/s at 900 °C, 1 GPa and 8.9 wt% H2O in the rhyolitic melt. (B) Diffusion coefficients of sulfur and water (in m2/s) versus 104/T (in K−1), according to the available data on the coefficients at different temperature conditions and new data obtained in this work at 900 °C. The available diffusion data are from [28] (4.5 wt% H2O) [29] (up to 7.0 wt% H2O). All numerical data are summarized in Table S4.
Minerals 15 00989 g002aMinerals 15 00989 g002b
Minerals 15 00989 g003
Figure 3. The principal schema of magma mixing triggering explosive eruptions. The following reactions are suggested to control liberation of the hybrid fluid triggering explosive eruptions: (1) 2 FeS(po) + 2 H2O = 2 FeO(melt) + S2− + H+ + 1.5 H2 and (2) 3 FeS(po) + 3 H2O = 3 FeO(melt) + S3− + H+ + 2.5 H2 and (3) S3− + 0.75 O2 + 2.5 H2O = SO42−(fluid/melt) + 2 H2S + H+ or (4) 8 S3− + 20 H2O = 19 H2S + 5 SO42−(fluid/melt) + 2H+ and (5) 8 S2− + 2 H+ + 12 H2O = 13 H2S + 3 SO42−(fluid/melt). The arrows indicate a zone of S-rich magma and fluid production, and the circles indicate the fluid phase degassing.
Figure 3. The principal schema of magma mixing triggering explosive eruptions. The following reactions are suggested to control liberation of the hybrid fluid triggering explosive eruptions: (1) 2 FeS(po) + 2 H2O = 2 FeO(melt) + S2− + H+ + 1.5 H2 and (2) 3 FeS(po) + 3 H2O = 3 FeO(melt) + S3− + H+ + 2.5 H2 and (3) S3− + 0.75 O2 + 2.5 H2O = SO42−(fluid/melt) + 2 H2S + H+ or (4) 8 S3− + 20 H2O = 19 H2S + 5 SO42−(fluid/melt) + 2H+ and (5) 8 S2− + 2 H+ + 12 H2O = 13 H2S + 3 SO42−(fluid/melt). The arrows indicate a zone of S-rich magma and fluid production, and the circles indicate the fluid phase degassing.
Minerals 15 00989 g003
Table 1. Parameters of sulfide dissolution reaction applied to the 1991 Mount Pinatubo eruption.
Table 1. Parameters of sulfide dissolution reaction applied to the 1991 Mount Pinatubo eruption.
ParametersDissolution Experiment
and Thermodynamic Modeling Data		Parameters for the Explosive Eruption1991 Mount Pinatubo Eruption
S in FeS37.7 wt%377,000 ppm SMass of ash (literature) ****13,000Mt
SO3 melt at the interface 0.5 wt%2000 ppm SMass of aqueous fluid
(literature) ****		95Mt
Fluid Sthermodynamics7.0–
20 wt%		70,000–300,000 ppm S
Fluid SO3 *25 wt%-Mass of erupted S10–13Mt
Fluid S *** experiment10 wt%100,126 ppm S
KD (fluid/sulfide)
Estimate **		0.2–0.5Mass of liberated SO2
(literature) ****		19–27Mt
KD (fluid/melt) ***50–150
Model calculations $
1991 Mount Pinatubo eruption
Mass of FeS in basalt25–32Mt
FeS in the hybrid magma0.2–0.6wt%
* Thermodynamically constrained S concentrations in the water fluid (Table S5). ** Kd (fluid/sulfide) estimate is performed based on the fluid/melt partitioning and the thermodynamic modeling (Table S5) constraints. *** Kd (fluid/melt) typical [18,35] for the conditions of the experiments (and the corresponding thermodynamic modeling). **** Literature data [7,36,37,38]. The maximal KD (fluid/melt) of 150 is according to the sulfur solubility at NNO, 1 GPa and 950 °C [38]. $ Mass balance calculations performed, suggesting that the total mass of the liberated sulfur-bearing fluid is derived from Fe-rich sulfides.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Borisova, A. Kinetics of Sulfide Dissolution Controlled by Sulfur Radical Diffusion: Implications for Sulfur Transport and Triggering of Volcanic Eruptions. Minerals 2025, 15, 989. https://doi.org/10.3390/min15090989

AMA Style

Borisova A. Kinetics of Sulfide Dissolution Controlled by Sulfur Radical Diffusion: Implications for Sulfur Transport and Triggering of Volcanic Eruptions. Minerals. 2025; 15(9):989. https://doi.org/10.3390/min15090989

Chicago/Turabian Style

Borisova, Anastassia. 2025. "Kinetics of Sulfide Dissolution Controlled by Sulfur Radical Diffusion: Implications for Sulfur Transport and Triggering of Volcanic Eruptions" Minerals 15, no. 9: 989. https://doi.org/10.3390/min15090989

APA Style

Borisova, A. (2025). Kinetics of Sulfide Dissolution Controlled by Sulfur Radical Diffusion: Implications for Sulfur Transport and Triggering of Volcanic Eruptions. Minerals, 15(9), 989. https://doi.org/10.3390/min15090989

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop