Classification of Thin-Section Rock Images Using a Combined CNN and SVM Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset of Rock Thin Sections
2.2. EfficientNetv2 Model
2.3. VGG16 Model
2.4. The Proposed Hybrid Model
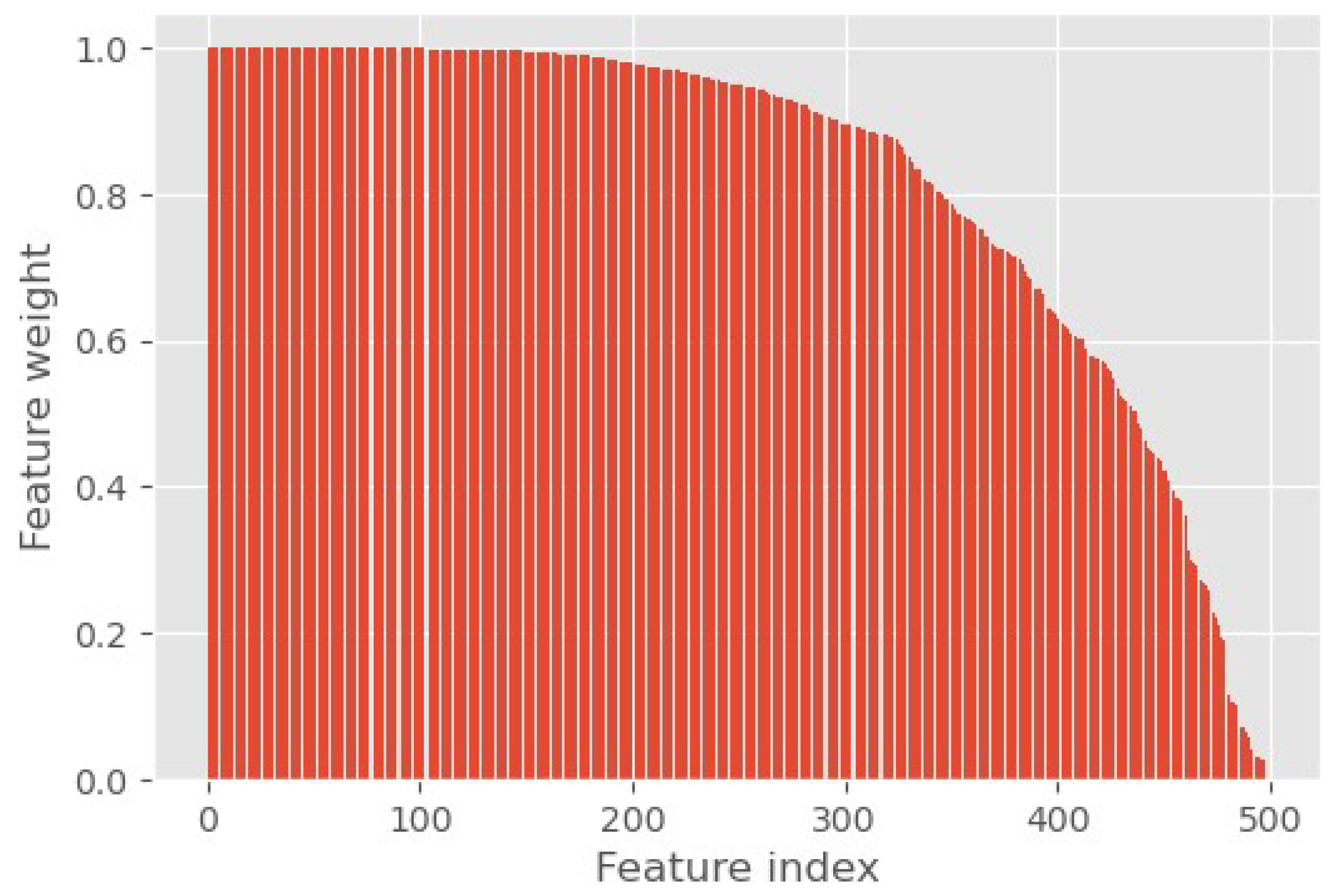
2.5. FSHNet
| Algorithm 1 Relief Feature Selection Algorithm |
| Require: Dataset X with m instances and n features, class labels Y |
| Ensure: Feature weights W representing feature importance 1: Initialize all feature weights W[j] = 0 for j = 1,2,…,n 2: for i = 1 to m do 3: Find nearest neighbors: 4: Nhit = nearest instance to i with the same class label 5: Nmisst = nearest instance to i with different class label 6: for j = 1 to n do 7: W[j] = W[j] − ∣xi,j − xNhit,j∣/m + ∣xi,j − xN miss,j∣/m 8: end for 9: end for 10: Normalize weights W to range [0, 1] 11: Rank features based on weights W 12: return W |
3. Evaluation Metrics
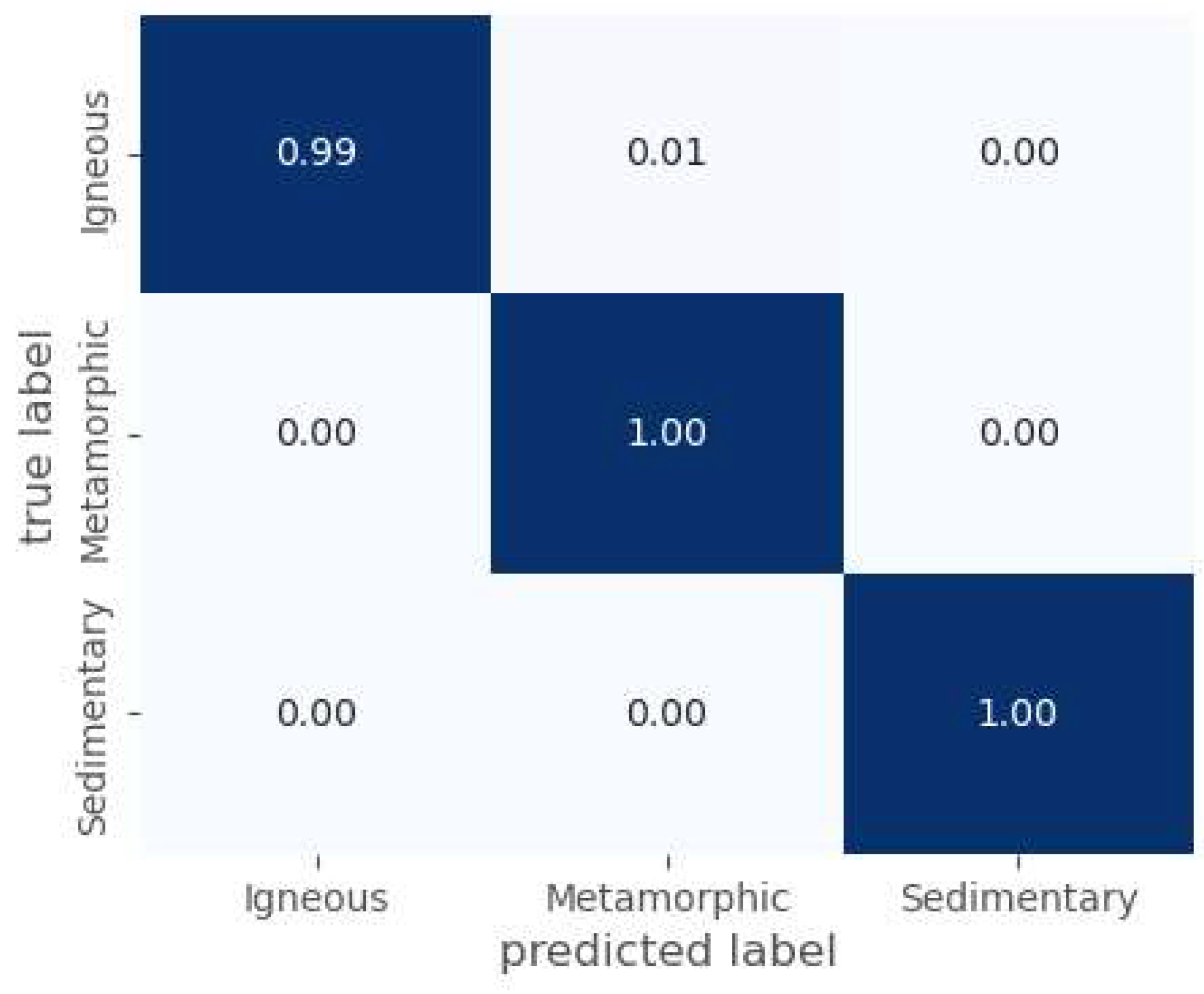
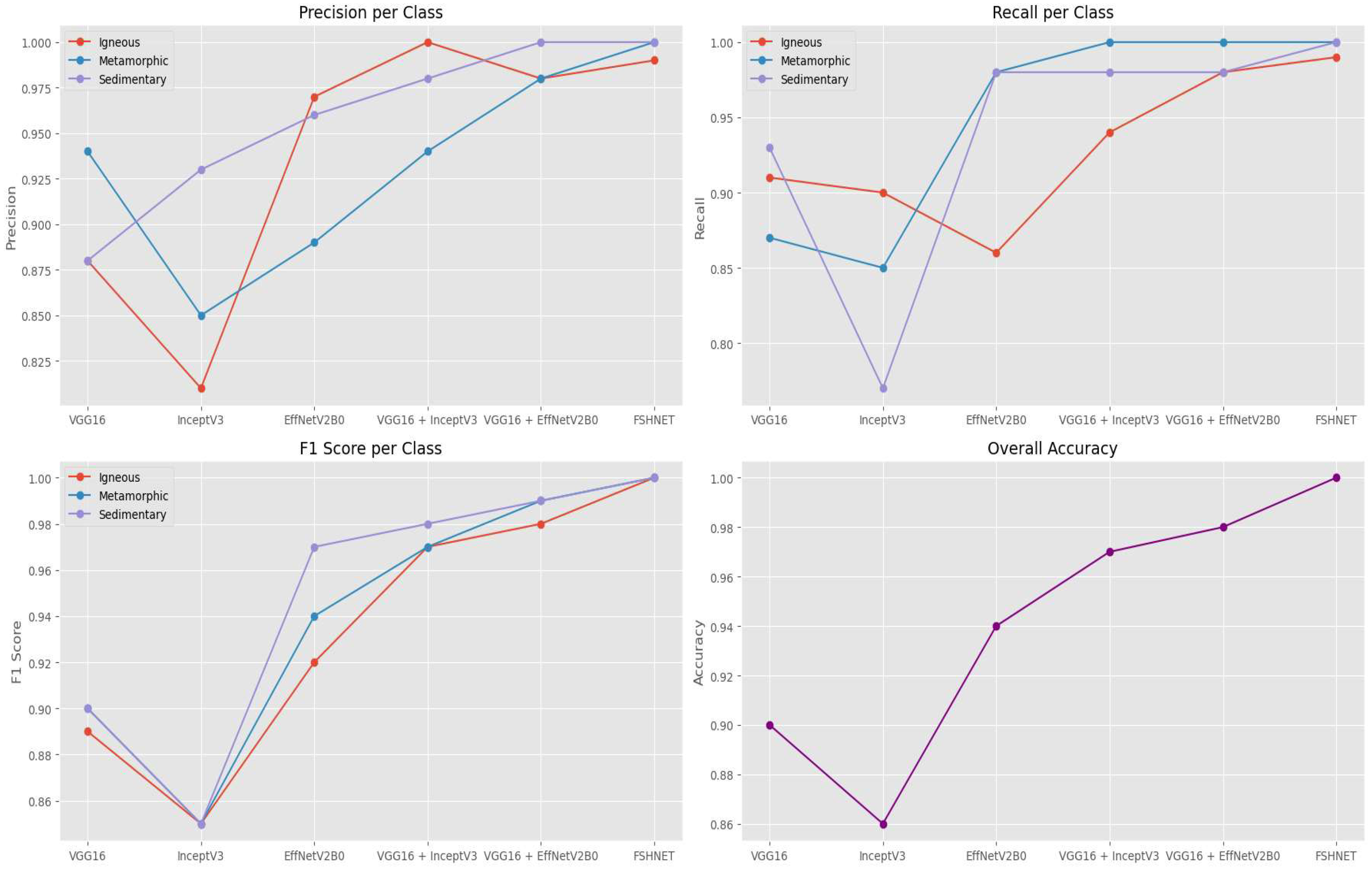
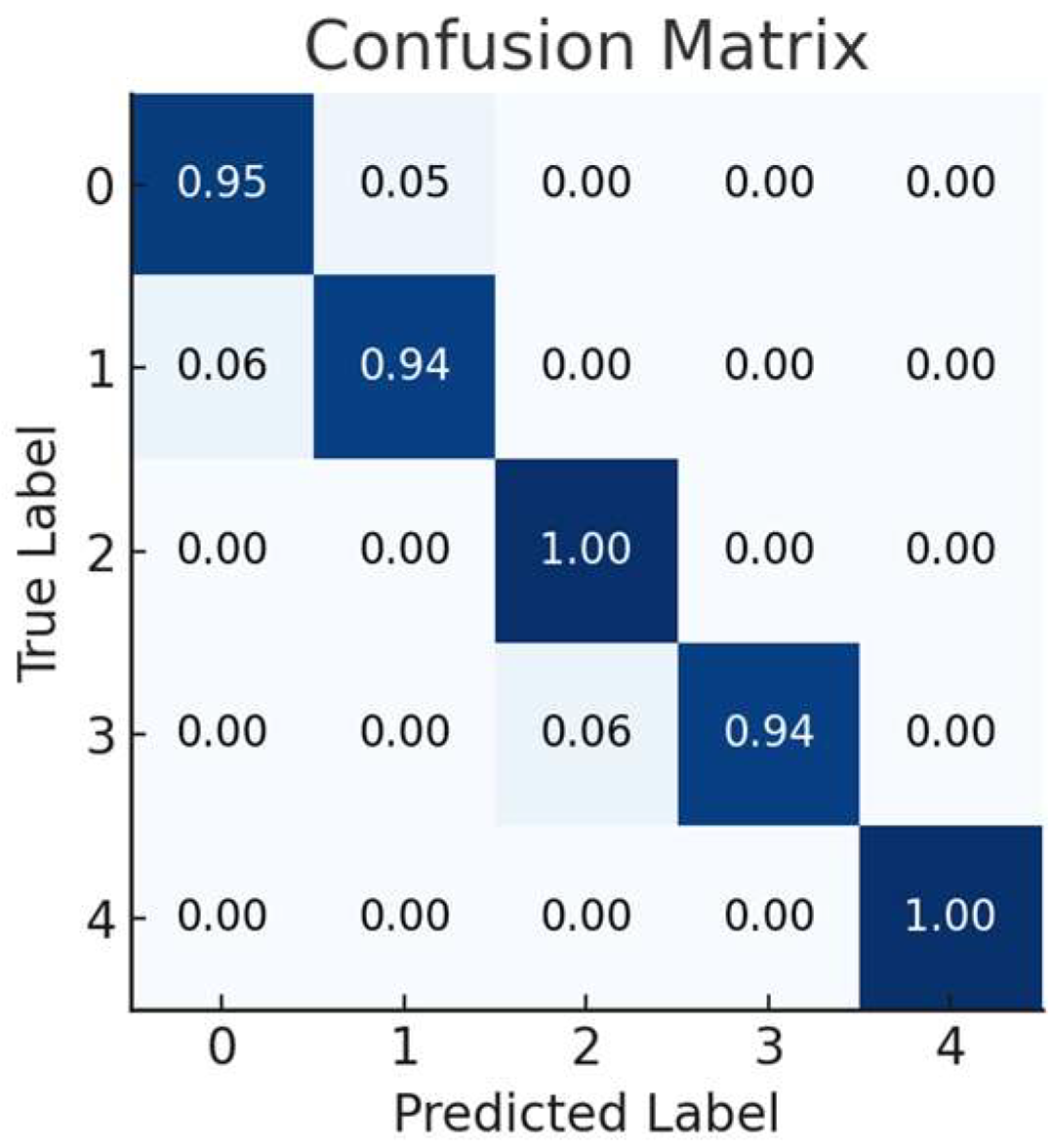
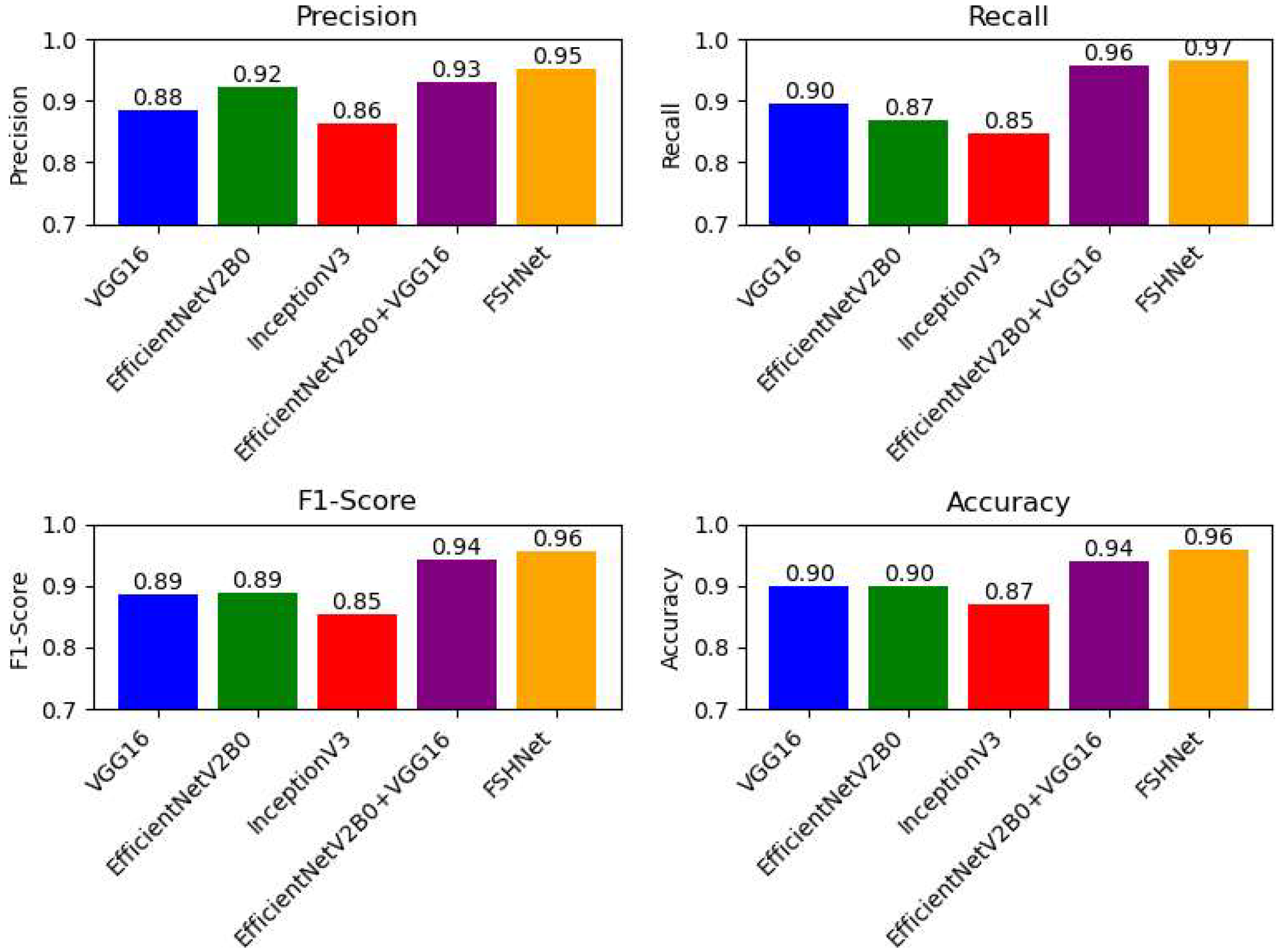
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, N.; Hao, H.; Gu, Q.; Wang, D.; Hu, X. A transfer learning method for automatic identification of sandstone microscopy images. Comput. Geosci. 2017, 103, 111–121. [Google Scholar] [CrossRef]
- Li, H.; He, S.; Radwan, A.E.; Xie, J.; Qin, Q. Quantitative analysis of pore complexity in lacustrine organic-rich shale and comparison to marine shale: Insights from experimental tests and fractal theory. Energy Fuels 2024, 38, 16171–16188. [Google Scholar] [CrossRef]
- Yu, J.; Wellmann, F.; Virgo, S.; Von Domarus, M.; Jiang, M.; Schmatz, J.; Leibe, B. Superpixel segmentations for thin sections: Evaluation of methods to enable the generation of machine learning training datasets. Comput. Geosci. 2023, 170, 105232. [Google Scholar] [CrossRef]
- de Lima, R.P.; Duarte, D.; Nicholson, C.; Slatt, R.; Marfurt, K.J. Petrographic microfacies classification with deep convolutional neural networks. Comput. Geosci. 2020, 142, 104481. [Google Scholar] [CrossRef]
- Aydın, İ.; Kılıç, A.D.; Şener, T.K. Improving Rock Type Identification Through Advanced Deep Learning-Based Segmentation Models: A Comparative Study. Appl. Sci. 2025, 15, 1630. [Google Scholar] [CrossRef]
- Ma, H.; Han, G.; Peng, L.; Zhu, L.; Shu, J. Rock thin sections identification based on improved squeeze-and-Excitation Networks model. Comput. Geosci. 2021, 152, 104780. [Google Scholar] [CrossRef]
- Zheng, D.; Zhong, H.; Camps-Valls, G.; Cao, Z.; Ma, X.; Mills, B.; Ma, C. Explainable deep learning for automatic rock classification. Comput. Geosci. 2024, 184, 105511. [Google Scholar] [CrossRef]
- Li, D.; Zhao, J.; Ma, J. Experimental studies on rock thin-section image classification by deep learning-based approaches. Mathematics 2022, 10, 2317. [Google Scholar] [CrossRef]
- Wang, B.; Han, G.; Ma, H.; Zhu, L.; Liang, X.; Lu, X. Rock thin sections identification under harsh conditions across regions based on online transfer method. Comput. Geosci. 2022, 26, 1425–1438. [Google Scholar] [CrossRef]
- Tatar, A.; Haghighi, M.; Zeinijahromi, A. Experiments on image data augmentation techniques for geological rock type classification with convolutional neural networks. J. Rock Mech. Geotech. Eng. 2024, 17, 106–125. [Google Scholar] [CrossRef]
- Seo, W.; Kim, Y.; Sim, H.; Song, Y.; Yun, T.S. Classification of igneous rocks from petrographic thin section images using convolutional neural network. Earth Sci. Inform. 2022, 15, 1297–1307. [Google Scholar] [CrossRef]
- Ishikawa, S.T.; Gulick, V.C. An automated mineral classifier using Raman spectra. Comput. Geosci. 2013, 54, 259–268. [Google Scholar] [CrossRef]
- Das, R.; Mondal, A.; Chakraborty, T.; Ghosh, K. Deep neural networks for automatic grain-matrix segmentation in plane and cross-polarized sandstone photomicrographs. Appl. Intell. 2022, 52, 2332–2345. [Google Scholar] [CrossRef]
- Yesiloglu-Gultekin, N.; Keceli, A.S.; Sezer, E.A.; Can, A.B.; Gokceoglu, C.; Bayhan, H. A computer program (TSecSoft) to determine mineral percentages using photographs obtained from thin sections. Comput. Geosci. 2012, 46, 310–316. [Google Scholar] [CrossRef]
- Baykan, N.; Yilmaz, N. Mineral identification using color spaces and artificial neural networks. Comput. Geosci. 2010, 36, 91–97. [Google Scholar] [CrossRef]
- Singh, N.; Singh, T.N.; Tiwary, A. Textural identification of basaltic rock mass using image processing and neural network. Comput. Geosci. 2010, 14, 301–310. [Google Scholar] [CrossRef]
- Shang, C.; Barnes, D. Support vector machine-based classification of rock texture images aided by efficient feature selection. In Proceedings of the 2012 International Joint Conference on Neural Networks (IJCNN 2012), Brisbane, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- Alexandre, P. Editorial for Special Issue “Novel Methods and Applications for Mineral Exploration”. Minerals 2020, 10, 246. [Google Scholar] [CrossRef]
- Cheng, G.-J.; Ma, W.; Wei, X.-S.; Rong, C.-L.; Nan, J.-X. Research of Rock Texture Identification based on Image Processing and Neural Networks. J. Xi’an Shiyou Univ. 2013, 27, 105–109. [Google Scholar]
- Lan, X.; Zou, C.; Kang, Z.; Wu, X. Log Facies Identification in Carbonate Reservoirs Using Multiclass Semi-Supervised Learning Strategy. Fuel 2021, 302, 121–145. [Google Scholar] [CrossRef]
- Pathare, A.R.; Joshi, A.S. Dimensionality Reduction of Multivariate Images Using the Linear & Nonlinear Approach. In Proceedings of the 2023 International Conference on Device Intelligence, Computing and Communication Technologies, (DICCT), Dehradun, India, 17–18 March 2023; pp. 234–237. [Google Scholar]
- Tariq, A.; Jiango, Y.; Li, Q.; Gao, J.; Lu, L.; Soufan, W.; Almutairi, K.F.; Habib-ur-Rahman, M. Modelling, Mapping and Monitoring of Forest Cover Changes, Using Support Vector Machine, Kernel Logistic Regression and Naive Bayes Tree Models With Optical Remote Sensing Data. Heliyon 2023, 9, e13212. [Google Scholar] [CrossRef]
- Dabek, P.; Chudy, K.; Nowak, I.; Zimroz, R. Superpixel-Based Grain Segmentation in Sandstone Thin-Section. Minerals 2023, 13, 219. [Google Scholar] [CrossRef]
- Li, P. Lithological Discrimination Using Aster Image and Geostatistical Texture. J. Mineral. Petrol. 2004, 24, 116–120. [Google Scholar]
- Fu, P.; Wang, J. Lithology identification based on improved Faster R-CNN. Minerals 2024, 14, 954. [Google Scholar] [CrossRef]
- Koeshidayatullah, A.; Morsilli, M.; Lehrmann, D.J.; Al-Ramadan, K.; Payne, J.L. Fully Automated Carbonate Petrography Using Deep Convolutional Neural Networks. Mar. Petrol. Geol. 2020, 122, 104–687. [Google Scholar]
- Wei, W.; Jiang, J.; Qiu, J.; Yu, J.; Hu, X. A photomicrograph dataset of rocks for petrology teaching at Nanjing University. China Sci. Data 2020, 5, 21–33. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556 2014. [Google Scholar] [CrossRef]
- Christianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods 2003; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Kononenko, I.; Simec, E.; Robnik-Sikonja, M. Overcoming the myopia of inductive learning algorithms with RELI44 EFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- Robnik-Sikonja, M.; Kononenko, I. Theoretical and empirical analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Su, C.; Xu, S.J.; Zhu, K.Y.; Zhang, X.C. Rock classification in petrographic thin section images based on concatenated convolutional neural networks. Earth Sci. Inform. 2020, 13, 1477–1484. [Google Scholar] [CrossRef]
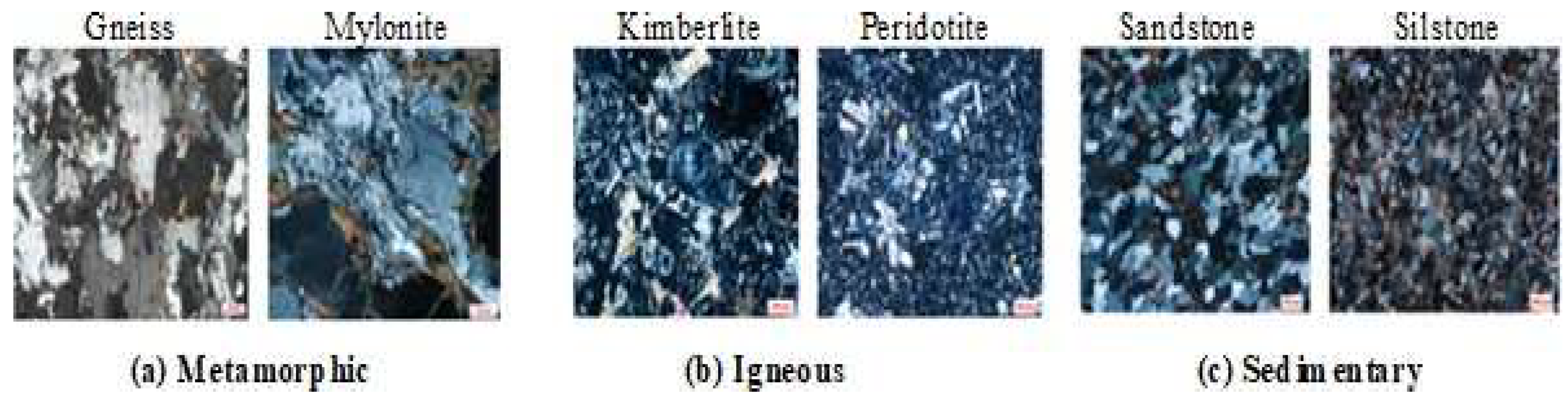
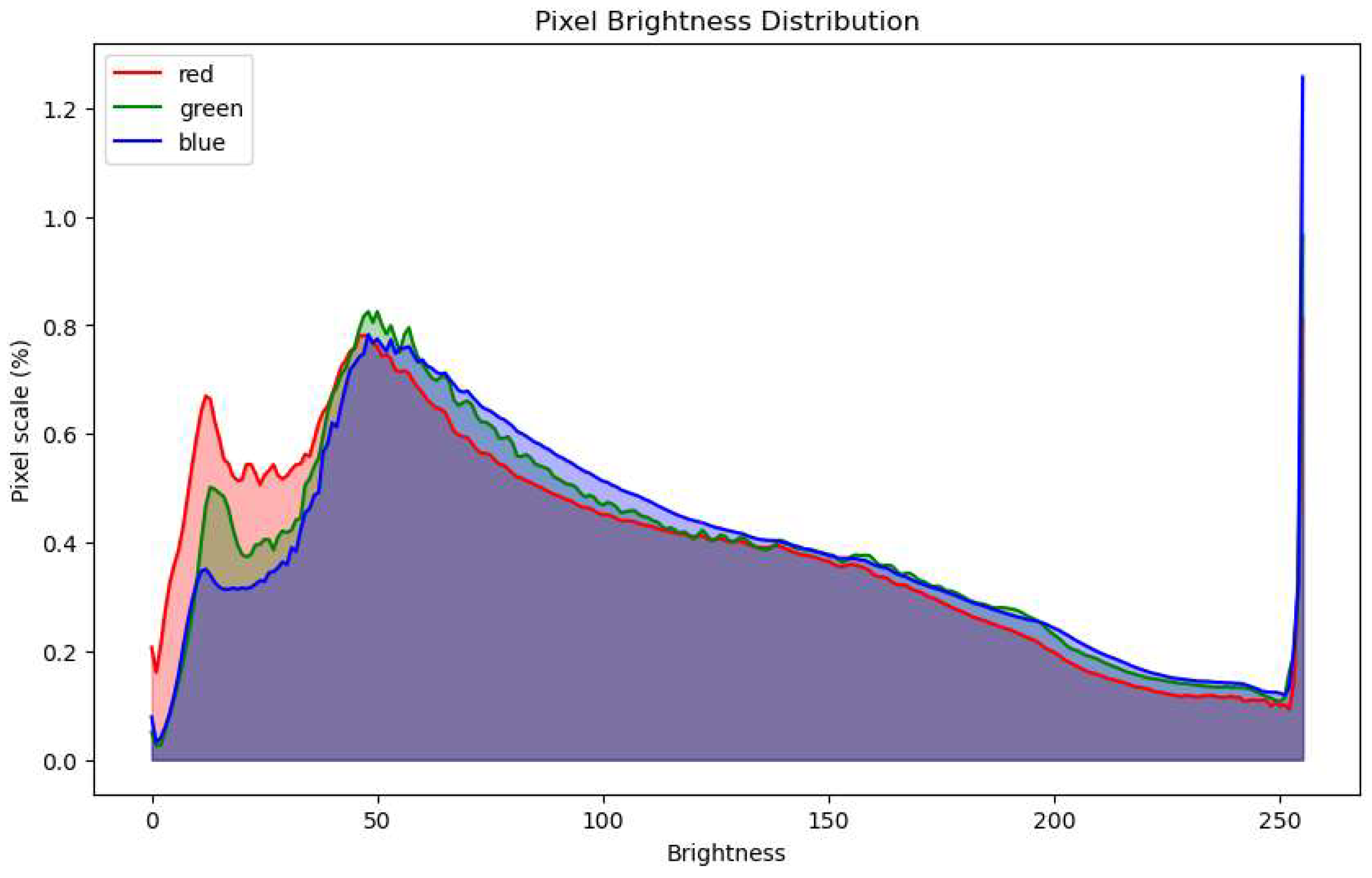

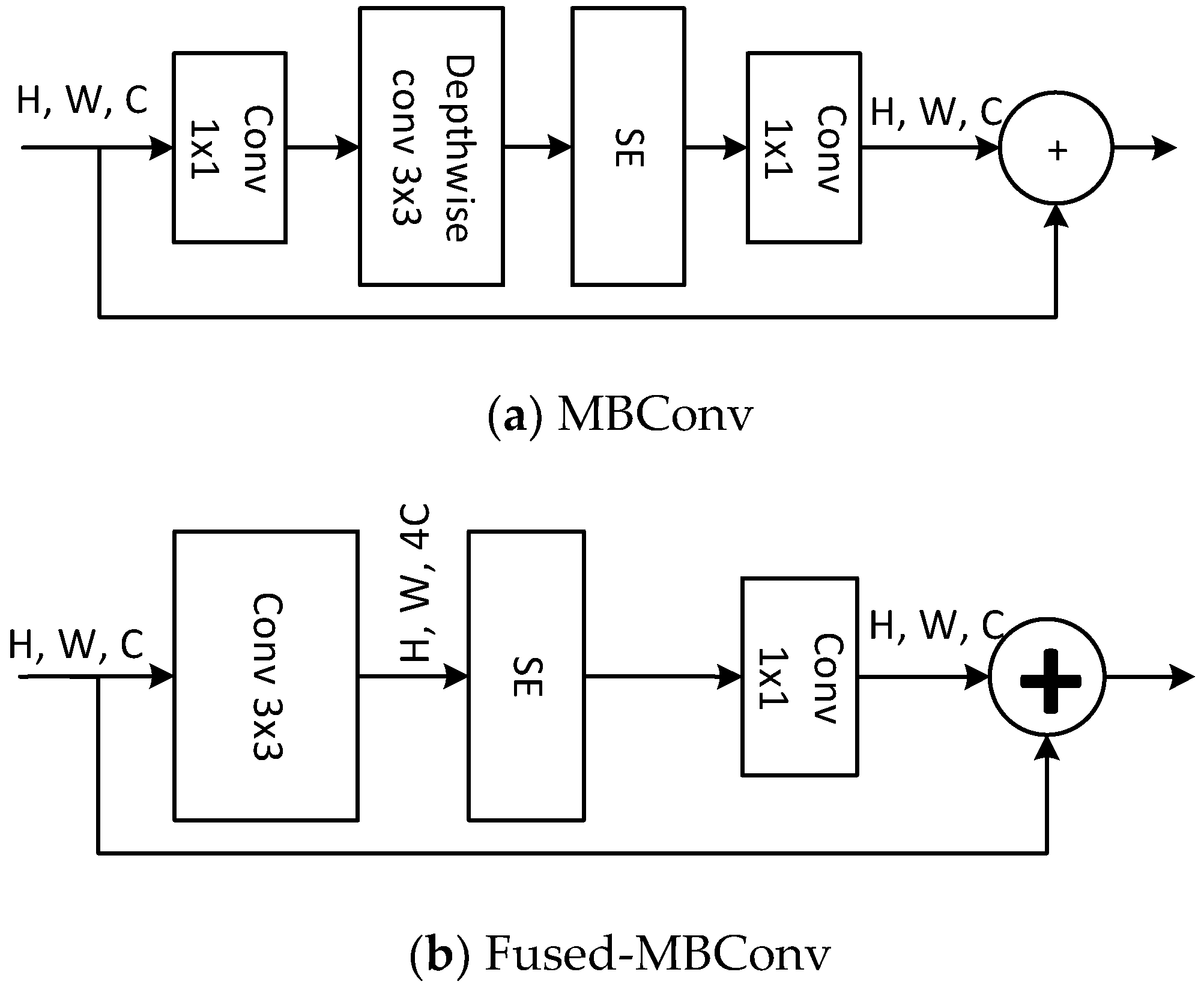



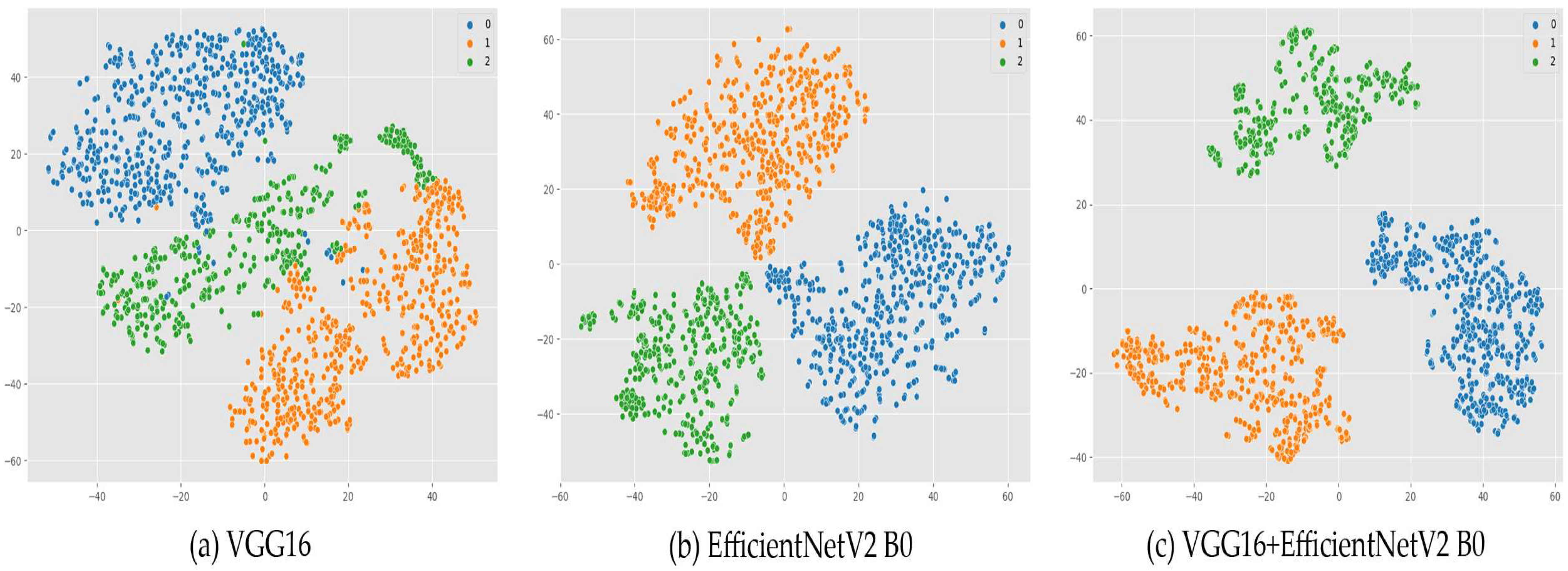
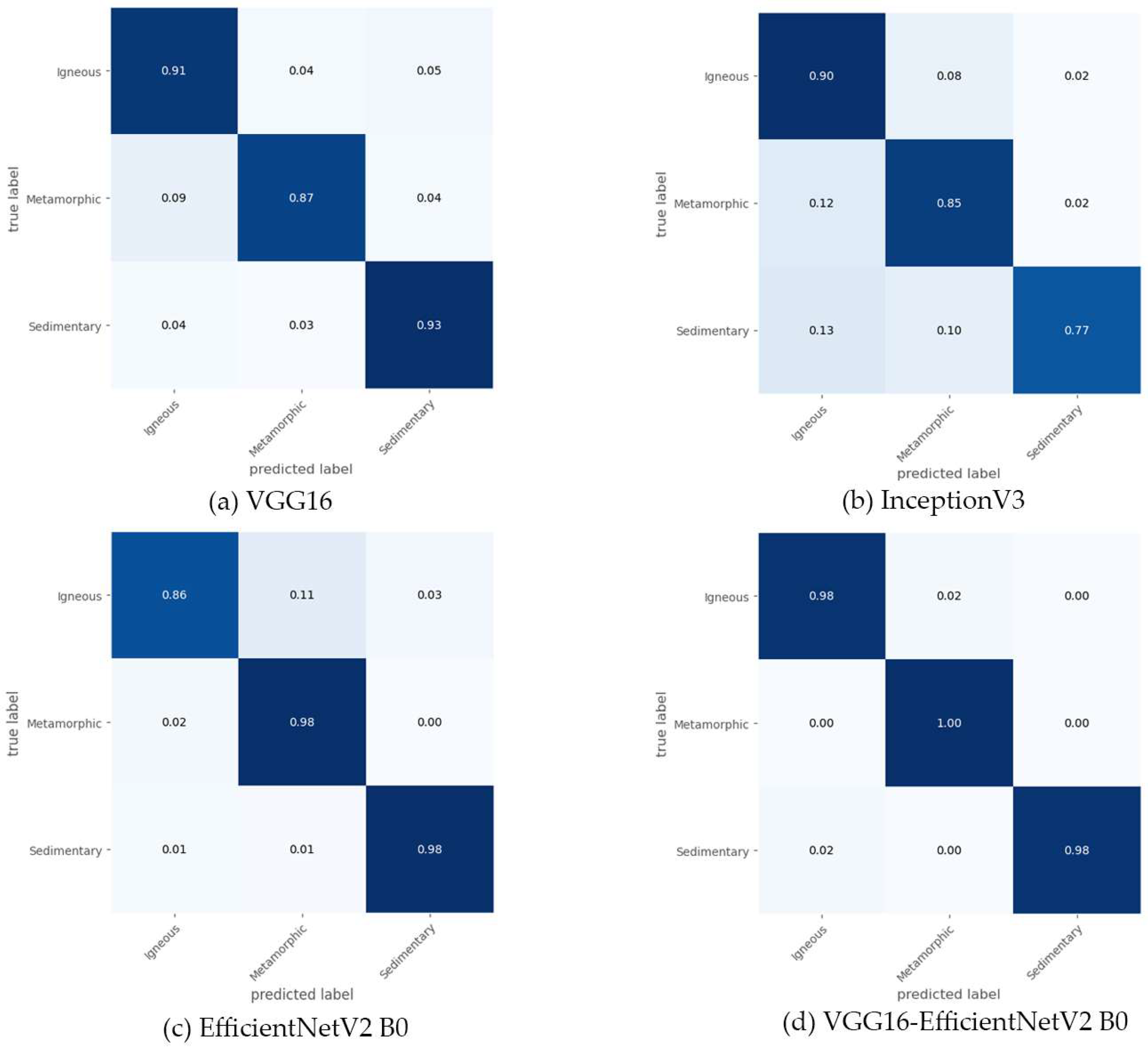
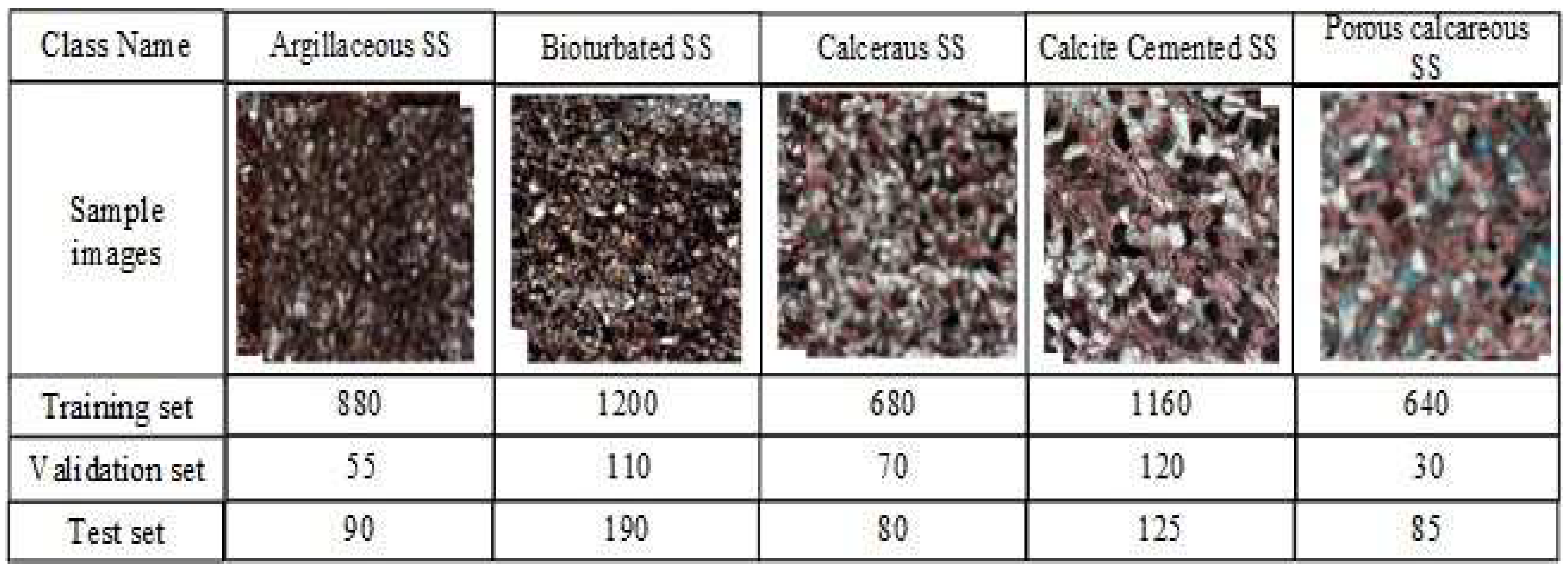
| Rock Type | Number of Images |
|---|---|
| Igneous | 963 |
| Metamorphic | 972 |
| Sedimentary | 699 |
| Feature | Value |
|---|---|
| Epoch | 20 |
| Batch size | 32 |
| Optimizer | Adam |
| Learning rate | 4 × 10−5 |
| Loss function | Categorical cross entropy |
| Classification function | Softmax |
| Model | Total Training Time (Second) | Test Time per Image (Millisecond) |
|---|---|---|
| VGG16 | 326.73 | 6.54 |
| InceptionV3 | 200.86 | 15.09 |
| EfficientNetV2B0 | 202.34 | 13.64 |
| VGG16+InceptionV3 | 1294.96 | 9.90 |
| VGG16+EfficientNetV2B0 | 1065.74 | 7.21 |
| FSHNet | - | 3.32 |
| Reference | Method | Dataset | Classes | Accuracy (%) |
|---|---|---|---|---|
| [2] | DenseNet121 | Magmatic thin-section rocks | 6 | 98.44 |
| [4] | Resnet50 | Pethrographic thin-section rocks | 6 | 96.00 |
| [6] | MSAResnet | Rock thin-section images | 3 | 90.89 |
| [7] | Resnet based XAI | Sedimentary rock thin-section images | 6 | 94.00 |
| [8] | ShuffleNetV2 | Rock thin-section images | 3 | 96.00 |
| [9] | Resnet50 | Rock thin-section images | 3 | 94.40 |
| [11] | VGG19 | Igneous rock type thin-section images | 6 | 97.10 |
| [33] | Concatenated CNN | Pethrographic thin-section rocks | 13 | 89.97 |
| This study | VGG16+EfficientNetV2B0 | Rock thin-section images | 3 | 98.00 |
| This study | FSHNET | Rock thin-section images | 3 | 99.66 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aydın, İ.; Şener, T.K.; Kılıç, A.D.; Derviş, H. Classification of Thin-Section Rock Images Using a Combined CNN and SVM Approach. Minerals 2025, 15, 976. https://doi.org/10.3390/min15090976
Aydın İ, Şener TK, Kılıç AD, Derviş H. Classification of Thin-Section Rock Images Using a Combined CNN and SVM Approach. Minerals. 2025; 15(9):976. https://doi.org/10.3390/min15090976
Chicago/Turabian StyleAydın, İlhan, Taha Kubilay Şener, Ayşe Didem Kılıç, and Hüseyin Derviş. 2025. "Classification of Thin-Section Rock Images Using a Combined CNN and SVM Approach" Minerals 15, no. 9: 976. https://doi.org/10.3390/min15090976
APA StyleAydın, İ., Şener, T. K., Kılıç, A. D., & Derviş, H. (2025). Classification of Thin-Section Rock Images Using a Combined CNN and SVM Approach. Minerals, 15(9), 976. https://doi.org/10.3390/min15090976








