Abstract
Mineral resource classification plays a critical role in communicating confidence levels, yet supporting methodologies such as drill-hole spacing analysis and geostatistical simulations are not consistently applied in routine updates of deterministic resource models. As a result, both local and global uncertainty quantification remain underutilized, and drilling requirements are often defined without a clear link to uncertainty reduction. This paper introduces a mineral resource uncertainty and drilling policy framework developed and applied at Compañía Minera Doña Inés de Collahuasi (CMDIC). The framework quantifies the uncertainty of each mineral resource model update when new data are available and provides an initial approach to determining drilling requirements based on CMDIC’s risk acceptance policies for different project stages. The proposed approach is a stochastic workflow that uses the current deterministic mineral resource model and database to generate geostatistical simulations. These simulations account for data quality, quantity, geological variability, and copper-grade variability. They form the basis for mineral resource classification with an explicit uncertainty quantification and provide an optimized drilling campaign to achieve desired risk levels subject to budget constraints. Because stochastic modeling updates faster than deterministic modeling, it provides timely insights from new drilling campaigns and delivers valuable insights for subsequent deterministic geological and grade modeling updates. The implementation of this workflow demonstrates its feasibility as a standard step following deterministic modeling, leading to cost-effective mineral resource development and management by aligning technical practices with the organization’s strategic objectives and risk preferences.
1. Introduction
The estimation of in situ and recoverable resources in a mineral deposit is subject to uncertainty due to the variability of ore-body characteristics (rock types, ore types, grades, etc.) and limited sampling data, impacting project development, production targets, costs, and financial returns. Traditional methods for mineral resource estimation, relying on deterministic geological and grade models and expert judgment, often fail to capture the full range of possible outcomes and their downside or upside effects across the mineral value chain. To manage this uncertainty, the industry employs a two-part framework: the stage-gate system for project development, and the internationally recognized mineral resource/mineral reserve classification system defined in the international reporting codes.
The stage-gate system [1,2] ensures that each phase is rigorously validated before advancing, reducing risks, optimizing project success, and improving resource allocation. Meanwhile, the classification system provides a standardized framework for public disclosure of mineral resources and mineral reserves, supporting investment decisions throughout all mining project stages [3,4,5].
While the current approach is fundamental to the mining industry, evidence suggests persistent challenges related to mineral resource and reserve modeling and classification [6,7]. Recently, Booth et al. [8] analyzed 381 projects listed between 2015 and 2021 and found that 60% exhibited at least two of four key indicators of potential resource or category inflation based on a risk-ranking methodology. Additionally, Randolph [9] identified the misinterpretation of ore-body characteristics, ground conditions, and metallurgical recoveries as a primary driver of lower-than-expected investment returns, emphasizing that errors in these predictions can lead to increased costs and financial losses.
In response to these challenges, Compañía Minera Doña Inés de Collahuasi (CMDIC), a tier-one global copper producer, is collaborating with GeoInnova and the University of Chile to develop and implement an internal framework for mineral resource uncertainty management. As an initial step, CMDIC has conducted a comprehensive review of industry practices, followed by the development of a systematic uncertainty quantification process. This process integrates geostatistical simulations that reflect geological and grade uncertainties into deterministic model updates to enhance communication of mineral resource uncertainty within the organization. Additionally, it aims to support technical decision making in areas such as mineral resource classification; geotechnical, geometallurgical, and hydro-geological modeling; drilling campaign design; mineral reserve modeling and scenario analysis; and financial risk assessment.
By regularly applying stochastic models, CMDIC aims to improve resource characterization, streamline risk communication, and optimize decisions across disciplines. As part of this process, this paper presents the following:
- 1.
- 2.
- The initial conceptual framework for CMDIC’s uncertainty management approach (Section 4).
- 3.
- 4.
- An illustration of drill-hole placement optimization, considering both geological and financial aspects (Section 6).
- 5.
- An illustration of the mineral resource classification scheme and uncertainty communication tools using geostatistical simulations (Section 7).
- 6.
- A discussion on mineral resource uncertainty management (Section 9).
2. Current Mineral Resource Uncertainty Management Practices
This section outlines a simplified presentation of the key components of the current framework, shown in Figure 1, including industry methods for mineral resource classification and the corresponding drilling requirements.
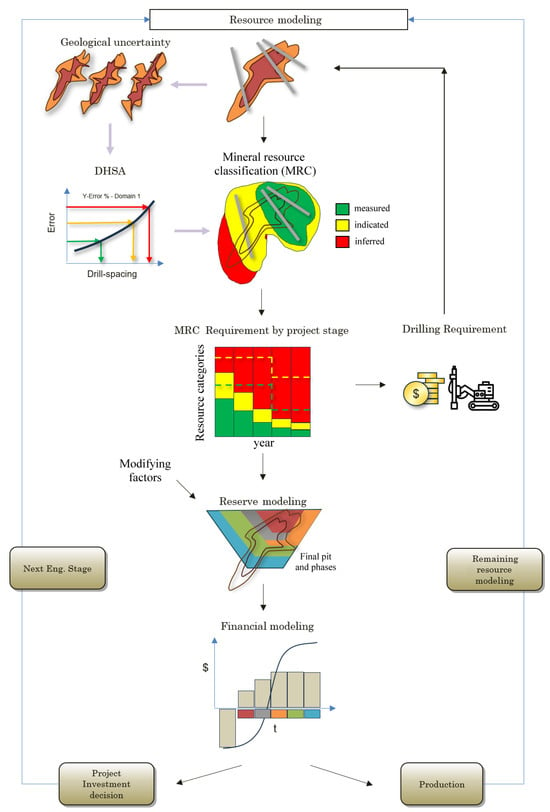
Figure 1.
Illustration of the key components of the current framework for managing mineral resource uncertainty, including mineral resource estimation and classification, category requirements by project stage, mineral reserve modeling, and financial modeling. Although DHSA studies often rely on stochastic models, mineral resource uncertainty is primarily used for defining mineral resource categories geometrically and does not fully extend into subsequent stages such as mine planning and financial assessment.
The starting point is mineral resource estimation based on expert geological knowledge and on information from drilling data, which leads to a mineral resource model; that is, a 3D array of blocks discretizing the mineral deposit, where each block is assigned categorical attributes such as its rock type, ore type, or alteration type, and quantitative attributes such as its ore grades, rock density, and geotechnical and geometallurgical variables.
Following mineral resource estimation, mineral resource classification (MRC) takes place. In this respect, the Committee for Mineral Reserves International Reporting Standards (CRIRSCO) distinguishes three categories of mineral resources—measured, indicated, and inferred—that depend on the confidence of the block estimations [3]. The category assigned to a block is established by a qualified or competent person (QCp); it is quite often based on geometric criteria involving the distances from the block to the drilling data [10,11,12]. In this way, resource confidence progresses in accordance with the proportion of each resource category required at each project stage, which in turn defines the drilling needs to advance to the next engineering phase or to the subsequent production cycle.
Once mineral resources are classified, mineral reserves are modeled, setting periods for financial assessments and decision making.
In more structured cases, classification criteria are supported by drill-hole spacing analyses (DHSAs) [13,14,15,16,17], sometimes using stochastic models to link drilling design with expected estimation errors. However, mineral resource uncertainty often remains confined to the DHSA–MRC sub-cycle, with limited transfer in mine planning or stochastic financial evaluations. Consequently, economic assessments of reserves still rely on deterministic technical variables alone, without fully incorporating mineral resource uncertainty into broader risk-informed decisions.
Ultimately, this cycle is iterative, taking place both in the context of investment decisions to move on to the next engineering stage and within a production cycle, where the framework is reapplied to the remaining resources from the previous stage.
3. Current Mineral Resource Classification Practices
Many public mineral resource reports classify resources primarily based on drill-hole spacing or spatial data density, rather than through formal uncertainty quantification. Although industry best practice increasingly recommends incorporating mineral resource uncertainty into classification decisions, several authors [10,11,12] underscore its ongoing absence in real-world applications. This omission has two major consequences: it complicates the interpretation of mineral resource categories and, just as importantly, prevents a robust evaluation of the financial impact of mineral resource uncertainty—thereby limiting both the ability to demonstrate the value of mitigation efforts and the rationale for investing in them.
3.1. Mineral Resource Classification and Project Stages
Requirements on proportions of mineral resource categories by project stage remain an underexplored aspect of industry practice. A survey in [18] among mineral resource managers found that half of the companies lacked internal guidelines defining the required balance of measured and indicated resources to support engineering studies. Likewise, Booth et al. [8] point out that resource inflation persists in publicly listed mining companies and warn that each stage of project maturity should show a reasonable progression in the mineral resource quantity and classification categories, consistent with exploration results and investments.
As an example of a mineral resource category split balance, Figure 2 presents Codelco’s requirements for different project stages [19], in place since 2003–2004. The required proportion of measured or indicated resources is high at the early project stages and decreases for medium- and long-term stages. However, the approach does not specify relative accuracy levels for each category or the total mineral resources by period, focusing on resource quantity (estimated tonnages, grades, and metal contents for each resource category) rather than on resource quality (reliability of these estimates). This issue is widespread—according to [18], half of the surveyed companies lack quantitative guidelines for assessing uncertainty when defining measured or indicated resources. As a remarkable case of mineral resource uncertainty quantification, Minera Escondida, operated by BHP, has used geostatistical simulations for resource classification since 2007, as declared in the technical report by [20]. This approach highlights the benefits of classifying mineral resources based on uncertainty quantification, increasing the transparency in the uncertainty communication to the stakeholders by providing an accuracy and confidence level for each category within a production volume, as shown in Table 1, following the definition in [21].
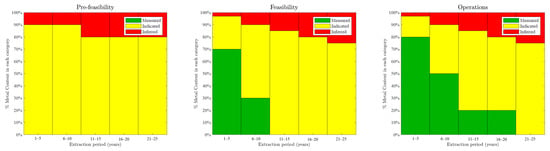
Figure 2.
Resource sustainability matrix by project stage of Codelco (Chilean stated-owned copper company), used since early 2000. The matrix sets the required proportion of each confidence category for each project stage, and reflects the scale of Codelco’s projects, which typically have a life-of-mine of over fifty years.

Table 1.
Mineral resource category definition based on geostatistical simulation in Minera Escondida since 2007. Modified from [20].
In summary, without quantifying the uncertainty by mineral resource category, a mining company assumes that the proportion of resources in each category is enough to meet the expectations of the business owners or their representatives, regardless of its quality. The proportion split between mineral resources categories is a pointless exercise without defining the quality of each category and the expected combined uncertainty by production periods.
3.2. Accuracy Level by Project Stage
Although some guidelines, such as [5,22,23], propose accuracy levels for capital and operating costs, there is still no clear consensus on these levels—or on other aspects—within mining projects. Moreover, existing frameworks overlook the accuracy of mineral resource and mineral reserve estimates, despite their direct financial impact as the primary revenue source. For instance, in [24] the authors illustrate, for a hypothetical financial model, how different levels of technical uncertainty can substantially affect the net present value (NPV) of a gold project. One common method is to define that most mineral resources should be measured or indicated over the payback period of the project, with a safety margin period [18]. While this aims to ensure investment recovery, it is unclear that the measured or indicated resources truly guarantee the projected cash flows, or even the payback period itself.
In the absence of clear definitions regarding the expectations and risk levels that business owners are willing to accept or disclose to the market, it becomes difficult to determine both the quantity and quality of mineral resources or mineral reserves required to meet those expectations. Consequently, the same applies to the drilling needed for each classification goal by project stage—leaving open the question of how much certainty (and drilling) is truly necessary to support the anticipated project economics.
3.3. Drilling Policy Practices
In drilling design, it is common practice to manually plan drill holes with the primary goal of upgrading mineral resources from lower to higher confidence categories based on an established classification criterion [25]. Consequently, the focus remains on mineral resource quantity in each category. This approach is typically applied by project stages or rolling production periods, following proportion requirements. However, drilling policies and designs that focus solely on resource quantity requirements often fail to quantify mineral resource uncertainty reduction, missing a key opportunity to demonstrate how decreasing uncertainty plays a paramount role in mitigating technical and financial risks.
3.4. Drill-Hole Spacing Studies and Risk Preferences
Drill-hole spacing analysis (DHSA) aims to determine the required drill spacing to achieve a relative accuracy level in mineral resource assessment. It typically models the relationship between the information level and the expected estimation error in production volumes, using kriging variances or geostatistical simulations [14]. A common practice is to consider 15% accuracy at a 90% confidence level, with quarterly or monthly targets for measured resources and yearly targets for indicated resources [21,26,27,28] used as a guide to define the drilling requirement and classification. DHSA is a useful tool that provides a reference expected error given an information level, but it does not accurately reflect the uncertainty in mineral resource categories or the project context. First, it is usually computed by geological domains on representative production volumes; therefore, it does not reflect the local variation of uncertainty over space and primarily focuses on grade uncertainty, often neglecting geological uncertainty, i.e., uncertainty in the spatial layout of geological domains (rock type, mineral, alteration, or structural domains) that impacts the tonnages and metal contents. Second, it is used as a support for geometrical resource classification schemes, which do not provide an accurate uncertainty quantification.
Finally, there is no in-depth, project-by-project justification for the “90%–15% rule” commonly used to define the indicated resources. This rule is often rationalized by practical, experience-based heuristics, such as those presented in [27,28]: (i) it is enough to ensure the visual continuity of grades and geology in plan views and sections, (ii) the idea that a 15% deviation in tonnage or grade can be absorbed in annual cash flows without jeopardizing project viability, (iii) the assumption that such shortfalls can be mitigated by rescheduling production, and (iv) its alignment with the ±15% accuracy used in capital and operating cost estimates for feasibility studies. However, these arguments remain disconnected from rigorous financial modeling: they fail to consider the full propagation of mineral resource uncertainty into multi-year cash-flow forecasts, and do not account for project-specific factors such as commodity type, life-of-mine plan, cost structure, or project stage. Critically, they overlook how the risk preferences and expectations of shareholders or investors—often reflected in the discount rate [29]—should be considered. Consequently, the “rule” may create a false sense of precision or comparability between projects that are structurally different in terms of risk and value exposure.
Consequently, the industry’s current classification and drilling practices often prioritize reaching a target proportion of high-confidence categories over explicit, quantifiable measures of mineral resource uncertainty. This “quantity over quality” focus obscures a project’s true risk profile, leading to misunderstandings or unmet expectations [7]. As a result, classification and drilling programs may become misaligned with the actual mineral resource uncertainty, jeopardizing a project’s operational and financial success.
4. Proposed Conceptual Framework
The conceptual framework proposed in this work is based on the fundamental industry best practices and principles, complemented by clear expectations for mineral resource quantity and quality, and a classification system based on mineral resource uncertainty quantification. Figure 3 illustrates how these elements come together to support effective mineral resource uncertainty management.
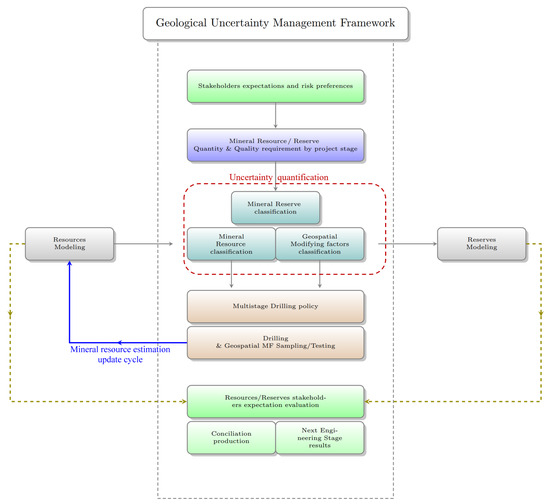
Figure 3.
Geological uncertainty management framework. This conceptual framework outlines the iterative process for managing mineral resource and mineral reserve uncertainty across the project life cycle. It begins with stakeholders’ expectations and risk preferences, which define quality and quantity requirements by project stage. These requirements drive the uncertainty quantification of mineral resources, reserves, and spatial modifying factors (MFs), leading to a multistage drilling strategy. The resulting data from drilling and MF testing update the resource model, refine classification, and feed into reserve modeling. A feedback loop connects stakeholder expectation evaluation with production reconciliation and engineering outcomes, enabling continuous alignment between technical decisions and economic goals.
- 1.
- Stakeholder engagement: Involves bringing business owner or the executive team into the discussion to clarify strategic objectives, expectations, and risk preferences. This alignment ensures that each project stage remains consistent with broader corporate goals.
- 2.
- Quantity–quality requirements: Defines structured targets covering both the proportion of mineral resource/mineral reserve categories (quantity) and the desired accuracy level (quality) or combined accuracy level. These targets reflect the company’s accepted risk levels, guiding data acquisition efforts at each project phase.
- 3.
- Classification implementation: Adopt a simple and articulate implementation for classifying mineral resources with geospatial modifying factors and mineral reserves to meet the above requirements, in compliance with the international public reporting codes.
- 4.
- Multi-stage drilling policy: Develop a multistage drilling and geometallurgical sampling policy, triggered by the mineral resource/mineral reserve classification system.
- 5.
- Reality checks and iteration: Conduct “reality checks” through resource reconciliation and reviews at each subsequent engineering stage. This feedback loop helps to validate assumptions, refine the framework, and re-engage the organization.
Within this framework, quantifying mineral resource uncertainty has three primary functions:
- 1.
- Supporting or defining mineral resource classification;
- 2.
- Demonstrating to the company how geological and grade uncertainties translate into financial implications for a given information level;
- 3.
- Informing drilling strategies and demonstrating the economic value of mitigating risk through targeted data acquisition.
This framework does not prescribe a single method for quantifying mineral resource uncertainty or defining the quantity–quality requirements. Rather, it aims to retain flexibility for adapting to geostatistical tools and to the unique risk profile of each business in the mining cycle, given the geological variability of the deposit. Ultimately, it is intended as a practical, data-driven guide to address uncertainty rooted in data quality, data quantity, and geological or geometallurgical variability—empowering the QCp to apply structured professional judgment when classifying mineral resources, while providing robust evidence to justify and communicate their decisions under recognized reporting standards.
5. Stochastic Workflow for Mineral Resource Uncertainty Management
5.1. Overview
CMDIC’s operation and expansion project focused on three main deposits: Rosario, Rosario Oeste and Ujina. Ujina and Rosario are copper–molybdenum porphyry systems, while Rosario Oeste is a high-sulfidation deposit with strong structural controls. Figure 4 shows the stochastic workflow for quantifying mineral resource uncertainty, designed for routine use across all three deposits—from long-term to short-term model updates.
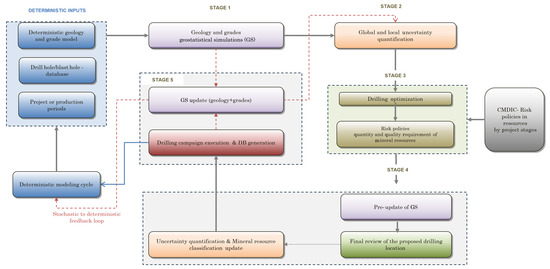
Figure 4.
Stochastic workflow for mineral resource uncertainty management at CMDIC, illustrating how geostatistical simulations (GSs), uncertainty quantification, and drilling optimization are integrated to support resource classification and decision making. GSs are used to compute uncertainty metrics that guide drill design based on corporate risk policies. Newly acquired data are incorporated to update the GS models, refine uncertainty estimates, and inform the deterministic modeling cycle. This iterative process ensures continuous alignment between technical modeling and project requirements.
- In stage 1, the deterministic geological models of the deposit serve as inputs to generate a set of geostatistical simulations for geological layers (e.g., lithology, alteration, veins, mineral zone). Then, the grades are simulated within geological domains defined from the geological layers in the same way as for the deterministic grade model, except that these layers are now simulated instead of being interpreted deterministically.
- In stage 2, a set of post-processing tools are employed to analyze global and local uncertainties. These include metrics such as uncertainty by production periods at different cut-off grades and localized moving uncertainty metrics in grade, tonnage, and metal content, providing insights into the variability and confidence levels of the mineral resources.
- Stage 3 is the intersection between the company’s policies and technical decisions. At this stage, the framework integrates the quantity and quality requirements of mineral resource categories for each project stage. It also involves an optimization process to determine the location and number of additional drill holes needed to meet the required operational and budgetary constraints while aligning with the company’s expectation for a given project stage. An illustrative drilling optimization algorithm is provided in the following section.
- In stage 4, the proposed drilling design undergoes a final manual review and refinement. Once the design is adjusted, the following actions take place:
- 1.
- A preliminary update of the geostatistical simulations (GSs) of geological layers and grades is performed by treating a specific simulation outside the original set of simulations as if it were “real” and sampled in the final drilling design.
- 2.
- Using this hypothetical “database”, a first potential evaluation is conducted to assess the impact of the new drilling campaign on mineral resource classification and uncertainty quantification. We emphasize the term “potential” because this analysis occurs prior to having actual drilling data (grade assays and geological logs).
- In stage 5, after the drilling campaign is completed, with data logged, assayed, reviewed, and incorporated into the database (DB), the framework provides a shortcut within the stochastic workflow before returning to the deterministic modeling cycle. The newly acquired data are used to update the set of geostatistical simulations, offering preliminary insights into how the new drill-hole information may affect expected values and uncertainty metrics, even before generating the final deterministic geological and grade models with the new information. This interim GS model can serve as a valuable reference for the deterministic workflow, for instance, to identify areas of high uncertainty, using probability of ore, and zones with low prediction levels that require additional focus during the deterministic modeling stage, especially geological modeling.
The following subsection details the workflow’s implementation and highlights some of its key components.
5.2. Quantifying Mineral Resource (Geological and Grade) Uncertainty
Mineral resource uncertainty is assessed by means of geostatistical simulation, which aims at constructing equally probable representations (scenarios) of the mineral deposit. It is based on a hierarchical plurigaussian simulation of geological domains [30], followed by a grade simulation conditioned to the simulated geological domains, as described in [31] and summarized below.
- Geological-domain simulation
- 1.
- Generate a set of plurigaussian simulations of the geological layers (rock types, mineral zones, alteration types, etc.) relevant to the modeling of grades [30,32].
- 2.
- Integrate all the simulated geological layers into the simulated geological domains.
- Grade simulation
- 1.
- For each simulation of the geological domains, generate a grade simulation within each geological domain, based on the well-known multigaussian model.
The hierarchical plurigaussian model used for the geological-domain simulation is highly versatile and can describe a large variety of geological settings [30,31,32,33,34]. The hierarchy mirrors that of deterministic geological modeling, based on observed contact relationships between domains and the relative timing of geological events. The simulation algorithm can also be accommodated to the modeling of folded geometries when the geological continuity follows curvilinear paths rather than straight lines [35,36].
The process assumes an initial information level and subsequently incorporates a new set of information (e.g., from drilling campaigns). The updating of the simulations—so that they account for new drilling data—can be achieved efficiently by use of Gibbs sampling for the geological-domain simulations [37] and of the kriging update equations for the grade simulations [38,39].
Each geological or grade simulation is generated at a point support, consistent with the sampling and modeling methodology, and is then upscaled to block supports as required by the deposit characteristics and resource model objectives.
6. Illustration of Drill-Hole Optimization Considering Geological and Financial Aspects
This section outlines an illustrative procedure for determining target drilling locations linked to a corporate goal, for instance, a financial risk metric. As a simplifying assumption to provide a tractable and easy-to-follow approach, we consider a mining project in an early stage, supported by a deterministic strategic mine plan with annual granularity and a specified cut-off grade policy, with no stockpile or blending requirements to feed the plant, and using a deterministic financial model. We assume that all the run-of-mine material may be sourced from different production zones but exhibits sufficiently similar geometallurgical characteristics, making a blending model unnecessary at this stage of the project.
6.1. Linking Mineral Resource and Financial Uncertainties: Quantifying NPV Uncertainty
To demonstrate the value of an ensemble of geostatistical simulations of the mineral deposit in shaping a drilling policy, consider a project stage where the primary goal of drilling is to reduce mineral resource uncertainty and to mitigate financial risk metrics—for instance, the variance of net present value (NPV). Consider an existing mining sequence of T periods, a set of simulations of the geological domains and ore grades, and deterministic financial and cost parameters, excluding taxes and debt. The stochastic NPV associated with the simulated geological domains and grades is the following:
where is the net present value associated with the optimized mine plan for an ensemble of s geostatistical simulations, is the cash flow in period t, and r is the discount rate. Based on the stochastic NPV, its variance can be expressed as
Interestingly, the uncertainty in the NPV is controlled not only by the uncertainty of each period, but also by the cash-flow correlations between different periods. Additionally, the discount rate not only discounts the value, but also discounts the uncertainty. The temporal correlations between cash flows depend on the spatial correlations between geological and geometallurgical variables and on the spatial and temporal extraction areas of the mine plan.
To simplify further, consider the income from the metal content as the primary driver of cash flows for each period in the life of the mine. Using the simulated geological domains and grades, an ensemble of metal content simulations can be derived. Each cash flow can then be expanded as the sum of the income contributions from individual blocks, , within a fine grid, where b represents the index of all blocks belonging to period t. This allows the variance of the NPV to be expressed as follows:
Now it is clear that the uncertainty in the NPV is sourced from the extraction sequence given by the mine plan and from the spatial uncertainty and dependence relationships between the geological and geometallurgical variables.
While cash-flow uncertainty encompasses commodity prices, costs, processing, and other commercial factors, the geological–technical spatial component of uncertainty can be actively mitigated by geoscience teams through additional data acquisition and geological understanding. As such, targeted drilling and robust deposit characterization directly reduce the volatility in NPV and support the project’s financial outlook.
6.2. Reducing NPV Uncertainty Related to Geological Variables
A key motivation behind drilling campaigns is to gather additional geological information that refines the mineral resource model, thereby reducing geological risk. Let us assume that the company’s main goal at this stage is to enhance confidence in future cash flows and therefore to reduce NPV uncertainty. Hence, the central question arises: Where should drilling take place to maximize the reduction in NPV uncertainty?
By using an ensemble of geological-domain and grade simulations—and treating the remaining economic variables as deterministic—it is possible to compute a probability distribution of cash flows and consequently a distribution of the NPV. An approximate uncertainty reduction factor can then be derived. This approach involves analyzing a set of possible NPVs, the corresponding geostatistical simulations, and the discount factors by period—all of which reflect both the time value of money and the company’s perception of risk and opportunity cost.
Imagine drilling each possible location in a disjoint and individual manner (e.g., with vertical drill holes). The conditional variance of the NPV, given that a set of locations d will be drilled, can be expressed as follows (details in Appendix A):
where C denotes the covariance matrices derived from the ensemble of geostatistical simulations. The superscripts −1 and T refer to the inverse and transpose operators, respectively. The last term in the above equation is the NPV reduction factor (RF), which accounts for the impact of sampling the group of locations d in the NPV uncertainty reduction.
Consequently, the problem is to identify the set of locations d that most effectively reduces NPV uncertainty. These locations may not be those with the highest geological or grade uncertainty; instead, they are the ones most correlated with the deposit zones or features that critically influence the NPV.
It is important to note that using the NPV variance as an objective here serves as an illustrative example, highlighting the importance of incorporating geological–technical uncertainty into financial assessments. This approach improves communication, underscores the relevance of geoscientific data acquisition, and demonstrates how drilling policies can synchronize geological risk mitigation with key financial metrics.
The proposed drilling algorithm to minimize NPV uncertainty by mitigating geological risk is as follows:
- 1.
- Initialization
- (a)
- Generate or use a previous set of geostatistical simulations (geology + grade) conditioned on existing drilling data.
- (b)
- Set key parameters such as discount rate, maximum number of additional drill holes, and economic metrics.
- 2.
- Identify candidate drilling locations
- (a)
- Calculate the reduction factor (RF) for each potential drill-hole location.
- (b)
- Compute the effect of drilling at each candidate location on overall NPV uncertainty.
- (c)
- Identify the location with the highest RF, as it offers the greatest uncertainty reduction.
- 3.
- Simulation update
- (a)
- Given the candidate drilling samples, update the geostatistical simulations.
- 4.
- Recompute NPV and uncertainty
- (a)
- Recalculate the NPV distribution to reflect the updated (reduced) mineral resource uncertainty.
- (b)
- Track improvements in economic metrics and overall uncertainty reductions.
- 5.
- Iterate
- (a)
- Repeat the process of identifying, sampling, and updating simulations for each candidate drill hole and recomputing the reduction factor.
- (b)
- Stop once the budget constraints are reached, the maximum number of drill holes is reached, or the uncertainty is sufficiently reduced.
The previous approach is intentionally simplified for illustration. In a real-world mining context, the problem grows far more complex when integrating additional financial components—such as advanced risk metrics, multiple income stream, taxes, debt, and hedging options. From an operational perspective, aspects like geological variability, mining and operational dilution, blast-hole movement, mine plan compliance, as well as stockpile management, become critical. Moreover, one could incorporate different processing and beneficiation models, including specific blending–response functions, if those are available. In more intricate scenarios such as these, it is no longer possible to derive a simple expression as presented earlier. However, the core principle endures: The deposit’s intrinsic geological and geometallurgical characteristics ultimately drive value. Hence, the problem remains valid and solvable through numerical simulations or metaheuristic optimization techniques.
7. Case Study: Ujina Collahuasi
Although Collahuasi is a tier-one mega-deposit, Ujina was selected to illustrate key components of the framework in a setting representative of a broader range of base metal projects worldwide. The Ujina deposit presents a classic porphyry-style system, featuring a substantial secondary enrichment zone and economically significant hypogene mineralization. Ujina produced from the enrichment zone until 2012 and is scheduled to re-enter production in 2032 as part of CMDIC’s expansion initiatives.
Figure 5 shows the interpreted geological domains and the deterministic copper-grade model. Ujina faces significant geological and grade uncertainties, especially near the enrichment–hypogene boundary, where barren intrusions disrupt mineralization, and due to internal grade variability within the hypogene zone.
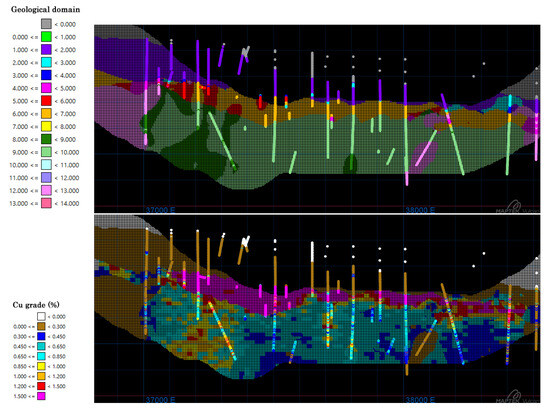
Figure 5.
Cross-section showing the main geological domains (top) and estimated copper grades (bottom). Estimation was made below the 2020 topographic surface.
7.1. Illustration of Mineral Resource Classification and Drilling Policy to Achieve Expectations
To illustrate the previous concepts and to protect CMDIC’s strategic information, this section is based on CMDIC’s deterministic data and models to generate a set of geological-domain and grade simulations that show the trends and correct spatial structure, but with no drill holes. These simulations serve to construct a baseline case, allowing for the evaluation of its evolution through drilling policies, uncertainty reduction strategies (e.g., using reduction factors), and the alignment with resource classification methodologies.
7.2. Drilling to Reduce NPV Uncertainty
The examples provided here are set in the context of project development, using representative parameters for an illustrative base-metal project, considering a 20-year mine life and an 8% discount rate [40,41].
One of the main components of the proposal is the use of reduction factors, which identify areas where drilling is relevant for reducing NPV uncertainty. This is illustrated in Figure 6 for the Ujina deposit, assuming vertical drilling at each grid node of the block model. Red areas highlight locations that are most relevant for reducing NPV uncertainty.
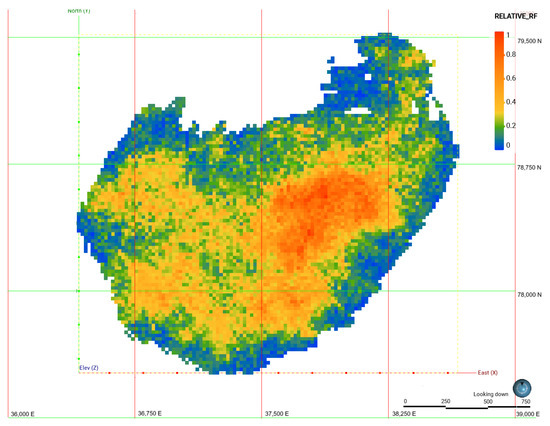
Figure 6.
Plan view of NPV variance reduction factor assuming vertical drilling located at the center of each block at Ujina. Reduction factor scaled by minimum and maximum. Red colors highlight relevant areas to drill to reduce the NPV uncertainty.
Using the risk factor, the drilling algorithm was applied to the base case simulation. A range of drill-hole grid spacings, including four regular and embedded grids, was used, varying from 640 m × 640 m to 120 m × 120 m. Figure 7 shows the evolution of NPV uncertainty reduction relative to the meters drilled under the proposed scheme and under a classical scheme based on a regular drill-hole spacing.
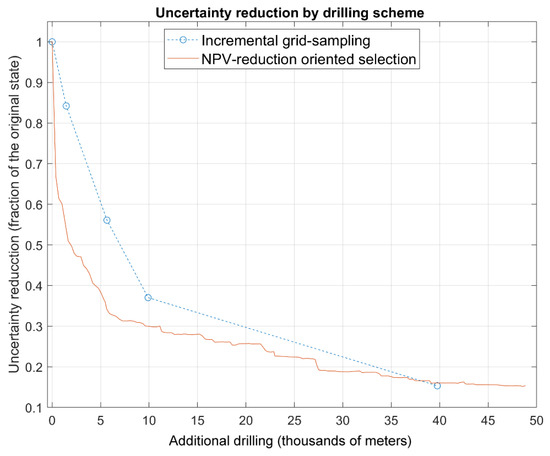
Figure 7.
Uncertainty reduction for each drilling scheme by additional drilling. Uncertainty reduction is computed as the ratio between the NPV variance after virtual drilling and the original NPV variance computed from the geostatistical simulations. The red line shows the proposed drilling approach, while the blue dotted line corresponds to a regular incremental grid spacing scheme.
The proposed approach achieves greater NPV uncertainty reduction at lower drilling cost during early stages, compared to regular incremental grid spacing. As the project advances, the criteria embedded in the drilling policies should adapt—focusing, for example, on reducing uncertainty annually or minimizing classification mismatches in production scenarios. Beyond the performance, the key shift in mindset is to re-frame drilling design and optimization not just as a means of cost reduction, but as a strategy to enhance project value by effective geological risk mitigation.
This also illustrates how drilling decisions can be linked to broader technical and financial aspects, such as mineral reserve definitions (production rate, life-of-mine) and discount rate—highlighting the need for integrated decision making across geology and mine planning, and project valuation depending on the project context and business goals.
7.3. Quality Criterion for Mineral Resource Classification
A key element of the proposed approach is clearly defining the quantity requirement of each mineral resource category and an uncertainty metric that aligns with the company’s objectives by project stage. As shown in Figure 8, the proposed sustainability matrix (SM) not only specifies the required proportion of each resource category but also sets a maximum annual metal content uncertainty. The proportions may be expressed in terms of metal or tonnage, and the use of uncertainty, accuracy, or precision metrics depends on whether the focus is on deterministic predictive modeling or stochastic modeling. In either case, the reconciliation of accuracy for deterministic models and the accuracy and precision of stochastic models with new information is mandatory.
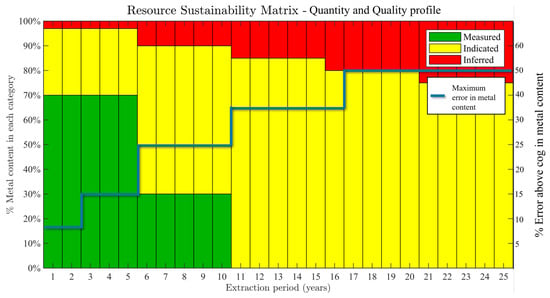
Figure 8.
Proposed sustainability matrix format that defines, for a given project stage, the required proportion of each confidence category and the target maximum annual uncertainty in metal content. Although individual category levels can also be defined, showing the total uncertainty composition by year turns the matrix into a tool that embeds uncertainty reduction as an explicit project-development goal. Values are to illustrate the elements of the SM.
In this context, mineral resource classification schemes underpinned by, or integrated with, stochastic modeling are better positioned to meet explicit uncertainty requirements. Regardless of the chosen classification method, it proves valuable to communicate the annual uncertainty levels so that interested actors can clearly see the associated risk. Moreover, a drilling strategy that stems from both quantity and quality requirements ensures alignment with broader corporate objectives. Rather than simply increasing the proportion of high-confidence resource categories, the emphasis shifts to explicitly reducing mineral resource uncertainty, with drilling guided by the mineral resource classification. Naturally, close collaboration among geoscience, mining, processing, and finance teams is essential to define or refine the accepted uncertainty criteria, ensuring that inherent geological variability aligns with the organization’s overall risk expectations and strategic goals.
7.4. Mineral Resource Classification Based on Geostatistical Simulations
This section presents a straightforward approach for classifying mineral resources using geostatistical simulations (GSs) as part of the proposed workflow. It also introduces the sustainability matrix, which incorporates an uncertainty metric to support classification decisions. The method builds upon the principles of resource classification based on GSs, as outlined in [28,42,43], and proposes using local uncertainty metrics to define resource categories. A simple approach is calculating uncertainty metrics above a given cut-off grade, such as the , defined as
where stands for the expected value of the simulated distribution, and for the value associated with the x-percentile of the target variable, such as metal content, tonnage, or mean grade above a cut-off grade. A worked example is presented in Appendix B.
This metric can be calculated block by block or over a moving panel with a relevant volume, centered at each block, as shown in Figure 9, using a monthly support, or over any volume part of a defined mine plan. An advantage of this approach is that thresholding this variable provides a clear and intuitive way to communicate the uncertainty at specific locations and a way to define a mineral resource classification. This enables better-informed decisions and facilitates organizational understanding of spatial uncertainty across the deposit.
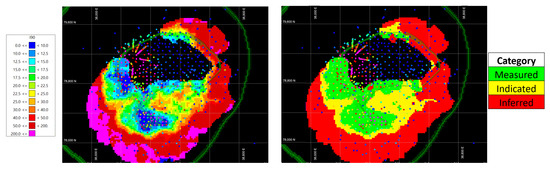
Figure 9.
Moving metal-content () index at monthly production volume. Cooler colors indicate lower metal-content uncertainty, while warmer colors reflect higher uncertainty (left), used as an input for defining mineral resource classification (right). Directly thresholding an uncertainty metric provides transparency about the meaning of each resource category.
7.5. Communicating Current Uncertainty in the Sustainability Matrix
The sustainability matrix, along with the same metric calculated annually, can be derived from the geostatistical simulations generated during the process (Figure 10), giving an uncertainty metric at an annual support but categorized on a local scale. This approach provides transparency across the organization and establishes a clear understanding of the mineral resource uncertainty levels associated with the intrinsic variability of the deposit’s geology and grades, with the current state of information, and with a given mine plan.
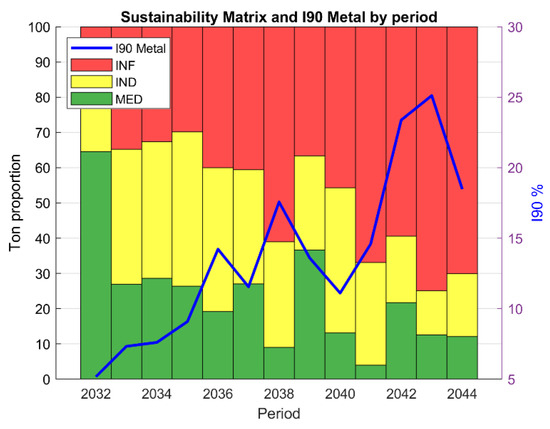
Figure 10.
Proposed sustainability matrix showing the proportion of each mineral resource category in the current mine plan (Y-left)—determined by applying a local uncertainty metric threshold—as well as the annual uncertainty derived from the geostatistical simulations and composition of the uncertainties of different resource categories (Y-right). Both metrics are computed for a single, common cut-off grade.
Explicit uncertainty metrics, such as I90, provide a tangible and standardized measure of risk, improving communication and enabling consistent comparisons between projects or phases. Their use allows for tracking uncertainty reduction over time and supports more informed decisions on data acquisition and mine planning.
7.6. Communicating Uncertainty by Period
While the sustainability matrix is an excellent tool to communicate the quantity and quality of mineral resource categories, a more detailed way to communicate the uncertainty by period is to compute a table with a structure similar to Table 2.

Table 2.
Illustration of annual resources estimated from a stochastic model for a pre-feasibility copper project, using a 0.5% Cu cut-off grade. Columns and show the 5th and 95th percentiles of the tonne, metal, and grade distributions above the cut-off grade. is the expected value of those distributions. denotes the deterministic estimate (E-type, computed block-by-block from the geostatistical simulations). is the associated uncertainty metric in percent.
This format lets the organization see, at a glance, the spread of possible outcomes: the 5th–95th-percentile bounds for tonnes, grades, and contained metal; the expected values; and the metric. The deterministic estimate is still presented as a reference, but showing it alongside the outputs of stochastic resource modeling exposes its limitations and helps stakeholders appreciate the additional insight that a risk-informed resource evaluation brings to the organization.
8. Stochastic Workflow Implementation at CMDIC
8.1. Overview
This section presents some implementation aspects of the stochastic workflow developed at CMDIC.
Stage 1: Geostatistical simulation of geological domains and grades. Simulations are carried out on a 5 m × 5 m × 5 m regular grid, capturing geological and grade variability at a resolution consistent with the deposit’s structural complexity. The interpreted geological model serves as an input to define local proportions in the plurigaussian simulation process [32], which preserves the hierarchical modeling scheme and contact relationships among the simulated domains compared to deterministic modeling, producing geologically feasible and realistic outcomes. Copper grades are then simulated sequentially for each domain based on the deterministic model’s estimation parameters and decisions. In total, 100 simulations are produced and validated by verifying the reproduction of geological-domain proportions, as well as copper-grade statistics, distribution, and variogram per domain, ensuring consistency with the deterministic mineral resource model.
Stage 2: Uncertainty quantification. The uncertainty is quantified at both global and local scales (Figure 11). Local uncertainty maps are used to illustrate confidence levels and variability within the mineral resource model. These outputs provide actionable insights for mineral resource classification and operational planning, by highlighting areas of high geological or grade uncertainty that require additional drilling or mid-term mine-planning management.
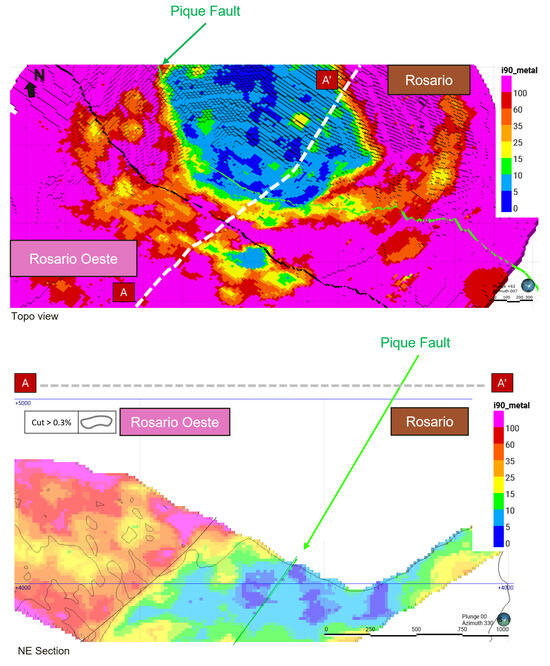
Figure 11.
Plan view and NE section of local uncertainty metric over a moving monthly production volume for a given cut-off grade, showing the different uncertainty levels between Rosario and Rosario Oeste. This type of visualization makes the uncertainty more tangible for the organization and provides greater detail than the three mineral resource categories.
Stage 3: Drilling optimization. The workflow includes a drilling optimization step that aligns uncertainty metrics with project-specific criteria—such as quantity and/or quality requirements for mineral resource categories, or other stage-based objectives—and practical constraints such as budget limits, cost structures, feasible drilling areas and permissible hole lengths and surveys (Figure 12).
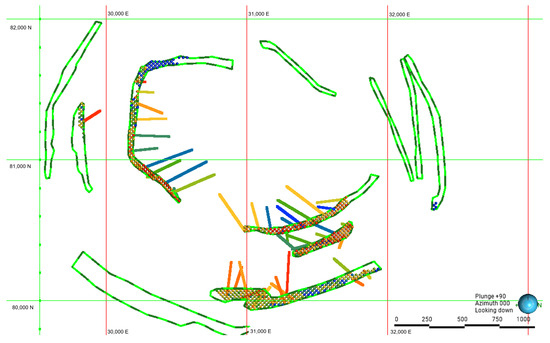
Figure 12.
Plan view of a 15,000 m campaign resulting from the optimization process in Rosario. Polygons are the available areas to drill in a period of time and the circles inside represent potential drilling platform locations.
Stage 4: Geostatistical simulation updating. To maintain a dynamic and up-to-date mineral resource model, the stochastic framework uses the kriging update equations [38,39] to efficiently assimilate new data into a set of existing geostatistical simulations. Rather than re-running the entire workflow from scratch, the algorithm updates the model locally wherever new drill-hole information is available. This iterative process offers timely insights into the evolving geological scenario, facilitating proactive planning and continuous improvement in mineral resource evaluation (Figure 13).
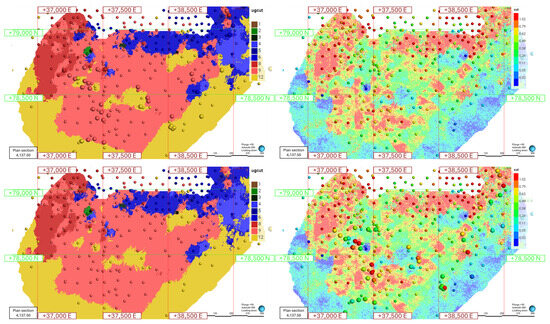
Figure 13.
Example of geostatistical simulations and their updates using the optimized drilling campaign. The top row illustrates a simulation of geological domains and grades based on the original drill-hole database, while the bottom row presents a simulation incorporating the new drill holes from the optimized campaign.
In CMDIC, the main routines are written in C++ with GPU and CPU parallelization. A full simulation run for the three deposits—of a total 45 million blocks, two to three geological layers per deposit to define the geological domains, and two grades with 6–10 domains, with over a million drilled meters—takes 12–18 h on an Amazon EC2 instance.
8.2. Status of the Implementation
The implementation of the stochastic framework involves far more than computational execution. It requires targeted discussion sessions to align interpretations, executives’ engagement meetings, communication of uncertainty findings in formats accessible to both technical and non-technical relevant actors, and geostatistical simulation workshops that engage geology, mine planning, and financial teams alike. Together, these efforts ensure all teams understand geological variability and uncertainty, creating a shared basis for informed decisions. The current implementation status is presented in Table 3.

Table 3.
Status of implementation of the stochastic framework at CMDIC. GS: geostatistical simulation, D: done, W: work in progress.
As shown in the table, CMDIC is moving towards stochastically modeling the spatial modifying factors to help convert mineral resources into mineral reserves, while also incorporating these stochastic models into the mine-planning process. Additionally, CMDIC, given this new approach and findings, is evaluating its risk policies by project stage, including the high-confidence category estimates and their accuracy.
9. Discussion, Part 1: Toward a Holistic Approach to Mineral Resource Uncertainty Management
Effective mineral resource classification, drilling strategies, geometallurgical sampling, mineral reserve modeling, and financial assessment are inherently interconnected. However, industry practice often isolates these components, leading to inefficiencies in decision making, resource allocation, and ultimately, project sustainability.
A holistic approach to uncertainty management requires moving beyond categorical classification and embracing stochastic-driven decision frameworks [44,45,46,47]. This study demonstrates how a structured stochastic workflow provides a more transparent and adaptive framework for mineral resource uncertainty quantification, mineral resource classification, and drilling policy formulation.
9.1. Bridging the Gap Between Uncertainty and Mineral Resource Classification
In many projects, the main objective is simply to boost the percentage of measured and indicated resources while relying on distance- or spacing-based categories—a “quantity over quality” mindset [25,48]. While this approach can satisfy certain project milestones or listing-rule requirements, it often understates local geological and grade variability and fails to convey the potential economic consequences of unquantified mineral resource uncertainty. Using geostatistical simulations or similar methods links mineral resource classification to explicit uncertainty metrics, enabling the QCp to justify their decisions with greater transparency and enhance public disclosures, reducing the subjectivity [11,49,50] reflected in the diversity of methods in public reports.
9.2. Optimizing Drilling Strategies Through a Risk-Based Approach
Within this integrated perspective, drilling programs no longer need to just increase the proportion of high-confidence mineral resource categories. Instead, targeted drilling can be used to reduce uncertainty in key geological–technical variables, with the consequent operational and financial risk mitigation [51,52,53,54]. This re-frames drilling from a nominal compliance-driven exercise into a value-enhancing investment: each new data sample/test reduces the likelihood of costly surprises in production or unmet expectations in project development. In the authors’ view, the data acquisition or drilling policy and its design are as relevant as mineral reserve modeling, since both are key levers for managing mineral resource and reserve uncertainty in the mining industry.
9.3. Future Industry Market Needs
As the demand for critical minerals surges and more projects seek funding, international reporting codes must evolve. Regulators and stock exchanges face a flood of new proposals, creating a need for clearer standards to identify deposits worthy of capital and ultimately to convert a far larger proportion of early-stage prospects into producing operations. Public disclosures that include explicit geological-risk measures will enable investors to better assess each project and therefore increase the success ratio from prospect to production.
Modern computing solutions—ranging from high-performance cloud infrastructure to low-code geostatistical platforms—now make near-real-time modeling feasible. This shift allows iterative geostatistical simulations and rapid mineral resource updates, once limited to a few major companies, to be integrated into day-to-day decisions across the industry [55]. A key barrier to adoption across the mining industry—regardless of company size—remains the transition toward stochastic thinking, which requires not only accessible technical tools but also a workforce capable of integrating geology, mining, and metallurgy with advanced concepts in uncertainty and risk analysis.
9.4. Ongoing Research and Development of the Proposed Framework
The CMDIC team is now advancing the framework on three complementary fronts. First, integrating spatial modifying factors, such as rougher recovery and throughput uncertainties, directly into the resource-to-reserve conversion process and developing clear ways to communicate their impact across the organization.
Second, a sub-framework is under construction for quantifying the financial value of geoscientific information, from exploration through production, that treats data acquisition as a capital-allocation decision rather than a fixed geological cost, thereby aligning data collection strategies with shareholder value.
The drilling optimization step is being refined to incorporate multiple collar locations at once—following the approaches of [56,57] while tailoring the objective function to each project stage. This includes valuing alternative data types such as additional drilling, geometallurgical variability tests, geophysical surveys, or other proxies.
An interesting research avenue is the full stochastic modeling of financial aspects, including commodity price simulations over time and capital and operating cost scenarios. This approach could be used not only to support technical decisions such as drilling or mine planning, but also to evaluate financial risk mitigation strategies—such as hedging—or to define term structures relevant to long-term project valuation, following the approaches of [58,59].
10. Discussion, Part 2: Re-Framing Mineral Resource Classification
International reporting codes aim to ensure that mineral resource and reserve estimates are reported in a manner that is transparent, consistent, and technically credible—enabling stakeholders to make informed decisions based on reliable information [3,4]. These frameworks were originally designed to serve as representations of technical confidence, primarily for public reporting purposes, rather than as tools for economic decision making.
However, treating mineral resource and reserve classification schemes as agnostic to business risk preferences may lead to a persistent disconnection between technical assessments and financial outcomes. This point was raised early by Wober and Morgan [60], who proposed a reserve classification scheme that explicitly incorporated economic expectations, metal grades, and their uncertainty. Although Wober’s original proposal was not adopted, elements such as production volume and confidence levels can be traced in subsequent classification-related discussions [21,27,61]. Nonetheless, the explicit inclusion of risk preferences—Wober’s main contribution—remains absent in current reporting codes. Later, Tulcanaza and Ferguson [62] made a further contribution by proposing a link between the proportion of high-confidence resource categories and project development stages, laying the basis for what is now referred to as the sustainability matrix. This need to link technical confidence with financial and development-stage considerations is also reflected in the framework proposed by Noppé [63], which presents a matrix for benchmarking resource projects by jointly considering the confidence in geological estimates, the development stage of the project, and the level of technical–economic assessment. Noppé et al. [18] state that there is a lack of characterization of the quality and quantity of mineral resource categories, as well as a need to establish a link between mineral resource classification and the levels of techno-economic studies and relative precision. Taken together, these contributions underscore a growing recognition that mineral resource classification should not be treated as an isolated geological–technical act, but as an integral part of a broader risk-informed project development and valuation process.
This separation—often justified on the grounds of preserving the independence of the QCp—can obscure the implications of uncertainty on investment decisions, especially when project owners or investors assume levels of reliability or economic performance that are not actually supported by the mineral resource model. As evidenced by recurrent cost overruns, category inflation [8], and performance gaps in both feasibility-stage projects and operations [7,9], such misalignments are not isolated events, but systemic indicators of a framework that fails to reconcile technical confidence with economic expectations. Ironically, the persistence of the current framework is sustained not by its predictive validity, but by the very geological variability and uncertainty it claims to inform—an uncertainty so intrinsic to mining that it effectively subsidizes the framework’s under-performance by masking its limitations.
Although most discussions of mineral resource classification have traditionally focused on development-stage decisions, the implications of technical confidence extend well into the operating phase of a mining project. In production, the consequences of misaligned confidence in geological modifying factors are no longer abstract—they manifest as deviations between planned and actual outputs, missed delivery targets, or even breaches of financial covenants, as illustrated in Table 4 for different mining companies.

Table 4.
Illustrative cases of major mining companies that recently reported production reduction or deviation due to mineral resources or modifying factors.
From the authors’ perspective, rather than subordinating one to the other, a more robust approach is to establish mechanisms for alignment between technical decisions—such as mineral resource and reserve classification—and stakeholder risk preferences. This involves not only defining the required quantity of each mineral resource category by project stage but also incorporating explicit uncertainty metrics and linking them to decision-relevant financial parameters. In this way, mineral resource and reserve classification becomes a shared language between geoscientists, mine planners, operators, and business decision-makers—rather than an isolated technical assurance process. The proposed framework reflects this philosophy through the tools provided in this work and by embedding mineral resource uncertainty at the core of key project decisions.
Ultimately, the question is not whether business stakeholders should dictate technical parameters, but whether the technical criteria used to classify mineral resources and reserves meaningfully inform the risk-adjusted decisions those stakeholders or potential investors must make. In this context, the role of QCp is not merely to assign categories to deterministic mineral resource models, but to quantify and transparently communicate uncertainty—in terms that are relevant to financial and operational decision-makers—so that risk-informed choices can be made throughout the project life cycle [72,73]. As mining projects operate under increasing geological complexity and environmental, social, and governance requirements, decoupling technical confidence from business preferences risks is not only inefficient, but also suggests a loss of credibility in the very mineral resource classification systems intended to underpin investment-level decisions across the mining sector.
A shift is therefore needed—from treating classification as a static compliance requirement, to embracing it as a dynamic interface between technical confidence and strategic decision making. Future frameworks must explicitly integrate uncertainty metrics into financial planning and operational governance, enabling more resilient, transparent, and economically grounded decisions throughout the mine life cycle.
11. Conclusions
This study proposes a streamlined, iterative approach that integrates mineral resource (geological domains and grades) uncertainty quantification and expectation into mineral resource classification and drilling decisions. By mapping local and global uncertainty metrics onto operational targets, drilling policies become strategic investments in risk reduction rather than mere geometrical exercises. Moreover, geostatistical simulations can be rapidly updated, ensuring that new drilling data promptly refine both the mineral resource model and economic projections. This adaptability unifies geologists, engineers, and finance stakeholders under realistic assumptions about deposit variability, potentially avoiding unforeseen cost overruns, production shortfalls, or resource downgrades. As reporting standards evolve to demand explicit accounting of geological risk, this framework offers a practical way to communicate confidence levels and justify targeted drilling. By emphasizing a sustainability matrix with uncertainty metrics, the approach clarifies not merely how much mineral resource is labeled as measured or indicated, but also how certain those categories are considered.
Currently, the framework at Compañía Minera Doña Inés de Collahuasi remains under active implementation, illustrating that true organizational transformation arises from ongoing workshops and open dialogue among geoscientists, engineers, and financial managers. The next phase involves adapting the approach to actively incorporate spatial modifying factors into the conversion of mineral resources into mineral reserves. This marks a significant advance toward an integrated and transparent method for managing mineral resource uncertainty—enabling mining companies to navigate complex mineral deposits more effectively and to align investments with rigorously quantified, realistic risk profiles.
Author Contributions
Investigation: A.C. and X.E.; conceptualization: A.C., F.I. and J.P.; data curation: S.S.; methodology: A.C., S.S. and G.F.; software: A.C. and S.S.; validation: F.I., G.F. and A.P.; writing—original draft: A.C. and X.E.; writing—review and editing: A.C. and X.E.; project administration: J.P.; supervision, A.P. and R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded and supported by Codelco (Piensa Minería grant) and by the National Agency for Research and Development of Chile (grants ANID PIA AFB230001, ANID Fondecyt 1250008, and postgraduate study scholarship ANID-Subdirección de Capital Humano/Doctorado Nacional/2022-21220171).
Data Availability Statement
The data used is this paper is unavailable for privacy restrictions.
Acknowledgments
The authors are grateful to Compañía Minera Doña Inés de Collahuasi and to GeoInnova for supporting this initiative. Thanks to Mineral Reserves Technology SpA for providing the GEOGNOSIM software for hierarchical plurigaussian simulation. We also acknowledge the CMDIC Geoscience team—R. Orbezo, A. Sanhueza, and J. Quiroga, the Geometalurgical Team C. Burgoa, R. Schmidt, the Geotechnical Team. M. Riveros, A. Quispe —and the GeoInnova team—J. Ortíz, N. Molina, A. Cancino, M. Nahuelpán, and S. Reyes—for their support and collaboration. Finally, we thank the many colleagues who, over the years, have contributed valuable discussions on this topic.
Conflicts of Interest
Alejandro Cáceres, Rodrigo Riquelme, and Sebastián Seguel are employees of GeoInnova Consultores. Felipe Ibarra, Jorge Perez, Gonzalo Fuster, and Andres Pérez are employees of Compañıa Minera Dona Inés de Collahuasi. The research was conducted independently, and no funding was received from the aforementioned companies. The manuscript does not represent the views of these affiliated organizations. The authors declare no commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CMDIC | Compañía Minera Doña Inés de Collahuasi |
| DB | Database |
| DHSA | Drill-hole spacing analysis |
| GS | Geostatistical simulation |
| MRC | Mineral resource classification |
| MF | Modifying factors |
| NPV | Net present value |
| QCp | Qualified or competent person |
| RF | Uncertainty reduction factor |
| SM | Sustainability matrix |
Appendix A. Derivation of the Risk Factor
Let us define the net present value (NPV) for a given mine plan and the ensemble of geostatistical simulations s as
where
- r is the discount rate;
- denotes a block extracted during period t;
- is the expected economic value of block b derived from its simulated metal content in the ensemble.
The variance of the NPV is therefore
The NPV variance depends on the spatial correlation between blocks and the mine scheduling strategy. This variance could be considered as the variance conditional on the current state of information. The effect of current data is embedded within the correlations between simulated block values.
Appendix A.1. NPV Variance Conditional to a Single Known Block
Let us introduce as the discount factor of block b that is extracted in period t. The NPV (Equation (A2)) can be written as
Now assume that one block, say , is perfectly known (e.g., it has been sampled or estimated with high precision). The variance of the NPV conditional to this piece of information is
This result follows from standard regression theory. Importantly, it does not require to be directly observed—only that information is gained about through its correlation with known variables (e.g., new drilling data in nearby blocks).
Appendix A.2. Generalization to a Set of Sampled Locations
Now let d represent a subset of locations (e.g., drill holes):
- : vector of known, sampled, or drilled block values;
- : vector of uncertain blocks;
- , : corresponding discount factor weights.
The NPV can be decomposed into two parts:
Since is known, only contributes to the variance conditioned to the new information:
Assuming that the block values approximately follow a joint Gaussian distribution, the covariance between uncertain blocks, conditional on the set of known blocks, is
where represents the covariance matrices between the uncertain blocks (), between the known or drilled locations (), and between the uncertain blocks and drilled locations (, ). Hence, the conditional NPV variance can be computed as
Notably, this framework does not require that the known variables correspond to the exact block values in the mine plan. It is sufficient that they are correlated with the block values that drive the NPV value and uncertainty, including information such as drilling, geometallurgical sampling, or geophysical information. This allows for flexibility in how data are acquired, its relevance in the total uncertainty, and its use in supporting data acquisition decisions.
Therefore, the NPV reduction factor (RF) quantifies the additional uncertainty reduction attributable to data acquisition, over and above the existing information. The effect of the current data is embedded within the correlations between simulated block values and therefore within the correlations between periods and the simulations of NPV.
Appendix B. I90 Uncertainty Metric Example
The metric expresses the relative width of the central 90% interval (from to ) as a percentage of the expected value, and is defined as
where
- and are the 5th and 95th percentiles of the simulated distribution;
- is the expected value (mean) across all simulated scenarios.
Suppose 100 geostatistical simulations of copper grades are constructed, and for each simulation the average grade above a 0.4% copper cut-off is computed. The results yield a distribution with the statistics indicated in Table A1.

Table A1.
Uncertainty summary from 100 copper-grade simulations.
Table A1.
Uncertainty summary from 100 copper-grade simulations.
| Variable | Expected () | ||
|---|---|---|---|
| Cu grade (%) | 0.51 | 0.44 | 0.56 |
Using the formula,
This indicates that in 90% of the simulated scenarios, the average grade above the cut-off is within ±12% of the expected value of 0.51% Cu. The provides a summary of simulation-based uncertainty and can be used as a local uncertainty metric or computed inside a production volume, push-back, or pit. It is applicable to any variable, such as grade, tonnage, metal content, income, etc.
References
- Buchanan, D.L. Metals and Energy Finance: Advanced Textbook on the Evaluation of Mineral and Energy Projects; Imperial College Press: London, UK, 2015. [Google Scholar]
- Bustillo Revuelta, M. Mineral Resources; Springer Textbooks in Earth Sciences, Geography and Environment; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- CRIRSCO. International Reporting Template for the Public Reporting of Exploration Targets, Exploration Results, Mineral Resources and Mineral Reserves; International Council on Mining and Metals: London, UK, 2024. [Google Scholar]
- JORC. Australasian Code for Reporting of Exploration Results, Mineral Resources and Ore Reserves (the JORC Code, 2012 Edition): Report Prepared by the Joint Ore Reserve Committee of the Australasian Institute of Mining and Metallurgy, Australian Institute of Geoscientists and Minerals Council of Australia; Australasian Institute of Mining and Metallurgy: Carlton, Australia, 2012. [Google Scholar]
- CIM. CIM Definition Standards for Mineral Resources & Mineral Reserves; Canadian Institute of Mining, Metallurgy and Petroleum: Montreal, QC, Canada, 2014. [Google Scholar]
- Bertinshaw, R.; Lipton, I. Estimating mining factors (dilution and Ore loss) in open pit mines. In Proceedings of the Sixth Large Open Pit Mining Conference, Perth, Australia, 10–11 September 2007; The Australasian Institute of Mining and Metallurgy: Melbourne, Australia, 2007; pp. 13–17. [Google Scholar]
- McCarthy, P.L. Managing Risk in Feasibility Studies. In Mineral Resource and Ore Reserve Estimation: The AusIMM Guide to Good Practice; Edwards, A.C., Ed.; Number 30 in Monograph; Australian Institute of Mining and Metallurgy: Carlton, Australia, 2014; p. 6. [Google Scholar]
- Booth, G.; Hargreaves, R.; Bond, M. Resource and Reserve category inflation—Known rewards, hidden risks. In Proceedings of the Mineral Resource Estimation Conference, Perth, Australia, 24–25 May 2023; Australasian Institute of Mining and Metallurgy: Carlton, Australia, 2023. [Google Scholar]
- Randolph, M. Current Trends in Mining. In SME Mining Engineering Handbook, 3rd ed.; Darling, P., Ed.; SME-Soc. for Mining, Metallurgy, and Exploration: Englewood, CO, USA, 2011. [Google Scholar]
- Silva, D.S.F.; Boisvert, J.B. Mineral resource classification: A comparison of new and existing techniques. J. S. Afr. Inst. Min. Metall. 2014, 114, 265–273. [Google Scholar]
- Owusu, S.K.A.; Dagdelen, K. Critical review of mineral resource classification techniques in the gold mining industry. In Mining Goes Digital; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- McManus, S.; Rahman, A.; Coombes, J.; Horta, A. Uncertainty assessment of spatial domain models in early stage mining projects—A review. Ore Geol. Rev. 2021, 133, 104098. [Google Scholar] [CrossRef]
- Rojas, O.; Caceres, A. The use of Conditional Simulation for Drill Hole Spacing Evaluation and Decision-Making in Telégrafo Project, Northern Chile. In Proceedings of the Eighth International Mining Geology Conference, Queenstown, New Zealand, 22–24 August 2011; p. 9. [Google Scholar]
- Cornah, A.; Vann, J.; Driver, I. Comparison of three geostatistical approaches to quantify the impact of drill spacing on resource confidence for a coal seam (with a case example from Moranbah North, Queensland, Australia). Int. J. Coal Geol. 2013, 112, 114–124. [Google Scholar] [CrossRef]
- Afonseca, B.; Miguel-Silva, V. Defining optimal drill-hole spacing: A novel integrated analysis from exploration to ore control. J. S. Afr. Inst. Min. Metall. 2022, 122, 305–315. [Google Scholar] [CrossRef]
- Glacken, I.; Rondon, O.; Levett, J. Drill hole spacing analysis for classification and cost optimisation—A critical review of techniques. In Proceedings of the Mineral Resource Estimation Conference 2023, Perth, Australia, 24–25 May 2023. [Google Scholar]
- Jewbali, A.; Allen, L. An evolution of drill hole spacing studies at Newmont Corporation. In Proceedings of the Mineral Resource Estimation Conference 2023, Perth, Australia, 24–25 May 2023; pp. 111–123. [Google Scholar]
- Noppé, M.; Reid, D.; McKibben, J. Linking Mineral Resource and Ore Reserve classification with techno-economic study levels and forecast relative accuracy. In Proceedings of the International Mining Geology Conference 2022, Online, 22–23 March 2022; pp. 515–524. [Google Scholar]
- Zuniga, P.; Mansilla, M.; Henríquez, J.; Jara, E. Categorización de Recursos y Reservas. Norma Corporativa NCC 31 Rev 05 Technical Report; Codelco Chile: Santiago, Chile, 2018. [Google Scholar]
- Maureira, R.; Barrera, F.; Salazar, A.; Delgado, C. Technical Report Summary—Minera Escondida Limitada SEC S-K 229.1300 Technical Report Summary Stage of Property: Production/Pre-Feasibility Study. Technical Report; BHP Group Limited: Melbourne, Australia, 2022. Available online: https://www.sec.gov/Archives/edgar/data/811809/000119312523228105/d430164dex961.pdf (accessed on 5 August 2025).
- Parker, H.M.; Dohm, C. Evolution of mineral resource classification from 1980 to 2014: Current Best Practice. Presented at Finex 2014 Julius Wernher Lecture. 2014. Available online: https://crirsco.com/wp-content/uploads/2024/04/H_Parker_Finex.pdf (accessed on 5 August 2025).
- White, M.E.; Harrington, I. Feasibility Studies? Scope and Accuracy. In Mineral Resource and Ore Reserve Estimation: The AusIMM Guide to Good Practice; Edwards, A.C., Ed.; Number 30 in Monograph; Australasian Institute of Mining and Metallurgy: Carlton, Australia, 2014; p. 12. [Google Scholar]
- SEC. Modernization of Property Disclosures for Mining Registrants; Technical Report; U.S. Securities and Exchange Commission: Washington, DC, USA, 2018. [Google Scholar]
- Morley, C.; Snowden, V.; Day, D. Financial impact of resource/reserve uncertainty. J. S. Afr. Inst. Min. Metall. 1999, 99, 293–301. [Google Scholar]
- Silva, D.S.; Jewbali, A.; Boisvert, J.B.; Deutsch, C.V. Drillhole placement subject to constraints for improved resource classification. CIM J. 2018, 9, 21–32. [Google Scholar] [CrossRef]
- Yeates, G.; Hodson, D. Resource Classification—Keeping the End in Sight. In Proceedings of the International Mining Geology Conference, Darwin, Australia, 21–23 August 2006; p. 8. [Google Scholar]
- Verly, G.; Postolski, T.; Parker, H.M. Assessing Uncertainty with Drill Hole Spacing Studies—Applications to Mineral Resources. In Proceedings of the Orebody Modelling And Strategic Mine Planning Symposium 2014, Perth, Australia, 24–26 November 2014; Australasian Institute of Mining and Metallurgy: Carlton, Australia, 2014; p. 10. [Google Scholar]
- Verly, G.; Parker, H.M. Conditional Simulation for Mineral Resource Classification and Mining Dilution Assessment from the Early 1990s to Now. Math. Geosci. 2021, 53, 279–300. [Google Scholar] [CrossRef]
- Lilford, E. Natural resources: Cost of capital and discounting – Risk and uncertainty. Resour. Policy 2023, 80, 103242. [Google Scholar] [CrossRef]
- Maleki, M.; Emery, X.; Cáceres, A.; Ribeiro, D.; Cunha, E. Quantifying the uncertainty in the spatial layout of rock type domains in an iron ore deposit. Comput. Geosci. 2016, 20, 1013–1028. [Google Scholar] [CrossRef]
- Mery, N.; Emery, X.; Cáceres, A.; Ribeiro, D.; Cunha, E. Geostatistical modeling of the geological uncertainty in an iron ore deposit. Ore Geol. Rev. 2017, 88, 336–351. [Google Scholar] [CrossRef]
- Madani, N.; Emery, X. Simulation of geo-domains accounting for chronology and contact relationships: Application to the Río Blanco copper deposit. Stoch. Environ. Res. Risk Assess. 2015, 29, 2173–2191. [Google Scholar] [CrossRef]
- Ekolle Essoh, F.; Emery, X.; Meying, A. Assessing the uncertainty in lithology, grades and recoverable resources in an iron deposit in Southern Cameroon. Nat. Resour. Res. 2023, 32, 2515–2540. [Google Scholar] [CrossRef]
- Veliz, V.; Maleki, M.; Madani, N.; Soltani-Mohammadi, S.; Mery, N.; Emery, X. Plurigaussian modeling of non-stationary geological domains to assess geological uncertainty in a porphyry copper deposit. Ore Geol. Rev. 2023, 162, 105707. [Google Scholar] [CrossRef]
- Boisvert, J.B.; Deutsch, C.V. Programs for kriging and sequential Gaussian simulation with locally varying anisotropy using non-Euclidean distances. Comput. Geosci. 2011, 37, 495–510. [Google Scholar] [CrossRef]
- Koltsidopoulou, M.; Pavlides, A.; Varouchakis, E.A. Enhancing Geostatistical Analysis of Natural Resources Data with Complex Spatial Formations through Non-Euclidean Distances. In Proceedings of the GeoEnv 2024, Crete, Greece, 19–21 June 2024; pp. 69–70. [Google Scholar]
- Armstrong, M.; Galli, A.; Beucher, H.; Loc’h, G.; Renard, D.; Doligez, B.; Eschard, R.; Geffroy, F. Plurigaussian Simulations in Geosciences; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Chevalier, C.; Ginsbourger, D.; Emery, X. Corrected Kriging Update Formulae for Batch-Sequential Data Assimilation. In Mathematics of Planet Earth, Proceedings of the 15th Annual Conference of the International Association for Mathematical Geosciences, Madrid, Spain, 2–6 September 2013; Pardo-Igúzquiza, E., Guardiola-Albert, C., Heredia, J., Moreno-Merino, L., Durán, J.J., Vargas-Guzmán, J.A., Eds.; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2014; pp. 119–122. [Google Scholar] [CrossRef]
- Chevalier, C.; Emery, X.; Ginsbourger, D. Fast update of conditional simulation ensembles. Math. Geosci. 2015, 47, 771–789. [Google Scholar] [CrossRef]
- Smith, L.D. Discount rates and risk assessment in mineral project evaluations. Trans. Inst. Min. Metall. Sect. A Min. Ind. 1994, 103, 137–147. [Google Scholar]
- Rudenno, V.; Safari, a.O.M.C. The Mining Valuation Handbook: Mining and Energy Valuation for Investors and Management, 4th ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Sadeghi, B.; Madani, N.; Carranza, E.J.M. Combination of geostatistical simulation and fractal modeling for mineral resource classification. J. Geochem. Explor. 2015, 149, 59–73. [Google Scholar] [CrossRef]
- Mery, N.; Maleki, M.; País, G.; Molina, A.; Cáceres, A.; Emery, X. Fuzzy classification of mineral resources: Moving toward overlapping categories to account for geological, economic, metallurgical, environmental, and operational criteria. Nat. Resour. Res. 2025, 34, 1271–1299. [Google Scholar] [CrossRef]
- Dowd, P. Risk assessment in reserve estimation and open-pit planning. Trans. Inst. Min. Metall. Sect. A Min. Technol. 1994, 103, 148–154. [Google Scholar]
- Rendu, J.M. Geostatistical Simulations for Risk Assessment and Decision Making: The Mining Industry Perspective. Int. J. Surf. Mining, Reclam. Environ. 2002, 16, 122–133. [Google Scholar] [CrossRef]
- Jackson, S.; Vann, J.E.; Coward, S.; Moayer, S. Scenario-based Project Evaluation—Full Mineral Value Chain Stochastic Simulation to Evaluate Development and Operational Alternatives. In Proceedings of the Mining Geology Conference 2014, Perth, Australia, 10–11 June 2014; The Australasian Institute of Mining and Metallurgy: Carlton, Australia, 2014; pp. 21–31. [Google Scholar]
- Botín, J.A. Gestión de riesgo en decisiones de inversión minera: Un enfoque global. Boletín Geol. Min. 2019, 130, 67–80. [Google Scholar] [CrossRef]
- Maleki, M.; Baeza, D.; Soltani Mohammadi, S.; Madani, N.; Díaz, E.; Anguita, F. Optimising the placement of additional drill holes to enhanced mineral resource classification: A case study on a porphyry copper deposit. Int. J. Min. Reclam. Environ. 2024, 39, 134–151. [Google Scholar] [CrossRef]
- Emery, X.; Ortiz, J.M.; Rodriguez, J.J. Quantifying uncertainty in mineral resources by use of classification schemes and conditional simulations. Math. Geol. 2006, 38, 445–464. [Google Scholar] [CrossRef]
- Cevik, I.S.; Leuangthong, O.; Caté, A.; Ortiz, J.M. On the Use of Machine Learning for Mineral Resource Classification. Min. Metall. Explor. 2021, 38, 2055–2073. [Google Scholar] [CrossRef]
- Yang, D.; Deutsch, C.V. Managing Risk in Well Placement Optimization within an Expected Utility Framework. SPE Reserv. Eval. Eng. 2023, 26, 448–459. [Google Scholar] [CrossRef]
- Maturana, F.J. Quantitative Optimisation of Drilling for Brownfields Mineral Exploration. Ph.D. Thesis, Curtin University, Perth, Australia, 2022. [Google Scholar]
- Wang, Z.; Yin, Z.; Caers, J.; Zuo, R. A Monte Carlo-based framework for risk-return analysis in mineral prospectivity mapping. Geosci. Front. 2020, 11, 2297–2308. [Google Scholar] [CrossRef]
- Jeuken, R.; Forbes, M. The Value of Drilling—A Chance-Constrained Optimization Approach. Min. Metall. Explor. 2024, 41, 2279–2289. [Google Scholar] [CrossRef]
- Minniakhmetov, I.; Clarke, D. SBRE framework—Application to Olympic Dam deposit. In Proceedings of the Mineral Resource Estimation Conference 2023, Perth, Australia, 24–25 May 2023; pp. 266–276. [Google Scholar]
- Soltani-Mohammadi, S.; Safa, M.; Sohrabian, B. Reducing uncertainty in mineralization boundary by optimally locating additional drill holes through particle swarm optimization. Nat. Resour. Res. 2021, 30, 2067–2083. [Google Scholar] [CrossRef]
- Fatehi, M.; Asadi Haroni, H.; Hossein Morshedy, A. Designing infill directional drilling in mineral exploration by using particle swarm optimization algorithm. Arab. J. Geosci. 2017, 10, 487. [Google Scholar] [CrossRef]
- Spleit, M. Production Schedule Optimisation—Meeting Targets by Hedging Against Geological Risk While Addressing Environmental and Equipment Concerns. In Advances in Applied Strategic Mine Planning; Dimitrakopoulos, R., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 627–642. [Google Scholar] [CrossRef]
- Said, M.; El-Midany, A.A. Financial risk analysis with uncertainties of phosphate ore beneficiation. Min. Technol. 2022, 131, 115–127. [Google Scholar] [CrossRef]
- Wober, H.H.; Morgan, P.J. Classification of ore reserves based on geostatistical and economic parameters. CIM Bull. 1993, 86, 73–76. [Google Scholar]
- Dohm, C. Quantifiable Mineral Resource Classification: A Logical Approach. In Geostatistics Banff 2004; Leuangthong, O., Deutsch, C.V., Eds.; Quantitative Geology and Geostatistics; Springer: Dordrecht, The Netherlands, 2005; pp. 333–342. [Google Scholar] [CrossRef]
- Tulcanaza, E.; Ferguson, G.A. The value of information: A guide to the strategic development of projects founded on mineral resource categorization. Appl. Earth Sci. 2001, 110, 126–135. [Google Scholar] [CrossRef]
- Noppé, M.A. A Framework for Presenting and Benchmarking Resource Projects. In Proceedings of the Project Evaluation Conference, Adelaide, Australia, 8–9 March 2016; The Australasian Institute of Mining and Metallurgy: Carlton, Australia, 2016; pp. 260–274. [Google Scholar]
- Anglo American plc. Production Report for the Fourth Quarter Ended 31 December 2023; Technical Report; Anglo American plc: London, UK, 2024; Available online: https://www.angloamerican.com/~/media/Files/A/Anglo-American-Group-v5/PLC/media/press-release/releases/2024pr/q4-2023-production-report.pdf (accessed on 5 August 2025).
- BHP Group Limited. BHP Operational Review for the Nine Months Ended 31 March 2023; Technical Report; BHP Group Limited: Melbourne, Australia, 2023; Available online: https://www.bhp.com/-/media/documents/media/reports-and-presentations/2023/230421_bhpoperationalreviewfortheninemonthsended31march2023.pdf (accessed on 5 August 2025).
- Corporación Nacional del Cobre de Chile. Operational and Financial Report as of December 31, 2023; Technical Report; Codelco: Santiago, Chile, 2024; Available online: https://www.codelco.com/sites/site/docs/20230502/20230502200138/operational_and_financial_report_december_31_fv.pdf (accessed on 5 August 2025).
- Corporación Nacional del Cobre de Chile. Operational and Financial Report as of December 31, 2024; Technical Report; Codelco: Santiago, Chile, 2025; Available online: https://www.codelco.com/sites/site/docs/20240426/20240426181050/operational_and_financial_report_december_31_2024.pdf (accessed on 5 August 2025).
- Teck Resources Limited. 2023 Annual Report; Technical Report; Teck Resources Limited: Vancouver, BC, Canada, 2024; Available online: https://www.teck.com/media/2023-Annual-Report.pdf (accessed on 5 August 2025).
- Teck Resources Limited. 2022 Annual Report; Technical Report; Teck Resources Limited: Vancouver, BC, Canada, 2023; Available online: https://www.teck.com/media/2022-Annual-Report.pdf (accessed on 5 August 2025).
- Newmont Corporation. Newmont Reports Fourth Quarter and Full Year 2023 Results; Technical Report; Newmont Corporation: Denver, CO, USA, 2024; Available online: https://s24.q4cdn.com/382246808/files/doc_earnings/2023/q4/earnings-result/Newmont-Q4-2023-Earnings-Release_Final.pdf (accessed on 5 August 2025).
- Freeport-McMoRan Inc. Freeport-McMoRan Reports Fourth-Quarter and Year Ended 2023 Results; Technical Report; Freeport-McMoRan Inc.: Phoenix, AZ, USA, 2024. Available online: https://www.sec.gov/Archives/edgar/data/831259/000083125924000002/a4q2023exhibit991.htm (accessed on 5 August 2025).
- Noppé, M.A. Communicating confidence in Mineral Resources and Mineral Reserves. J. S. Afr. Inst. Min. Metall. 2014, 114, 10. [Google Scholar]
- Lindi, O.T.; Aladejare, A.E.; Ozoji, T.M.; Ranta, J.P. Uncertainty Quantification in Mineral Resource Estimation. Nat. Resour. Res. 2024, 33, 2503–2526. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).