Application of Attainable Region Technique to Optimize Copper Slag’s Desired Size Class
Abstract
1. Introduction
1.1. Flotation
1.2. Leaching
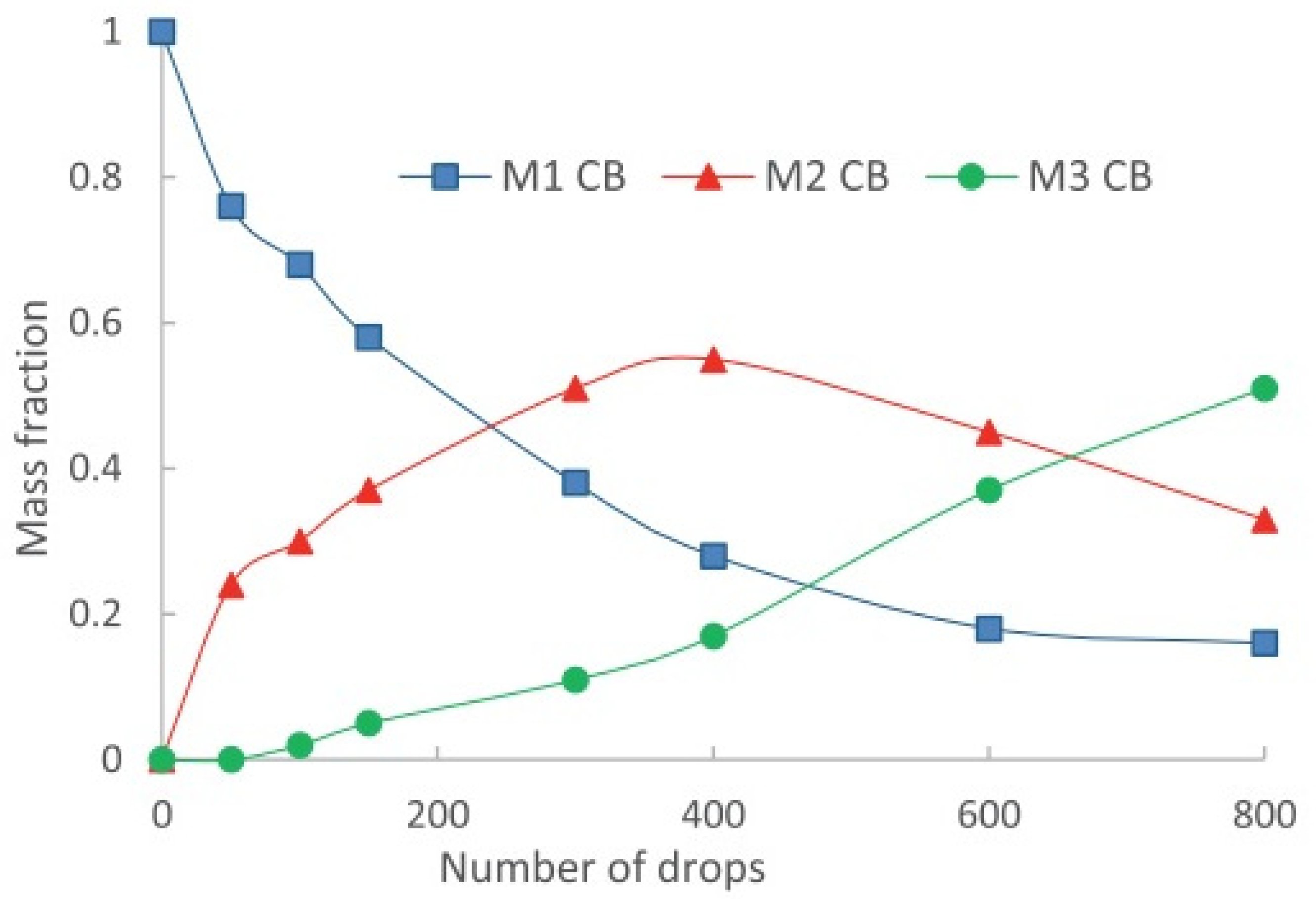
1.3. Attainable Region (A.R.) Method
- (a)
- T1 is the feed size which is collected as the coarse size class
- (b)
- T2 is the middle size class, which is created by intermediate breakage
- (c)
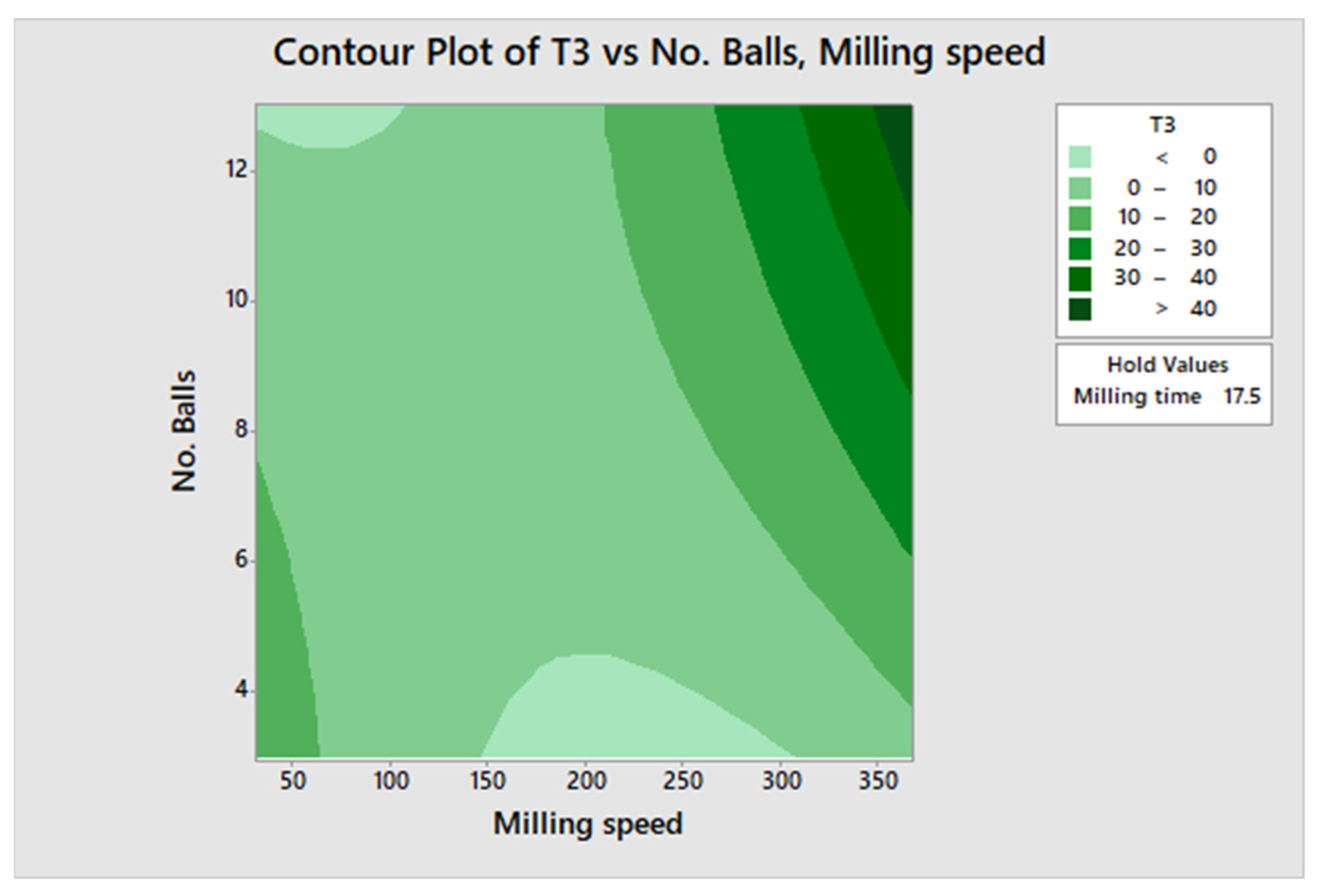
- T3 is the undersize or fines class, which is created by relatively intensive breakage
2. Materials and Methods
2.1. Material
Sample Preparation
2.2. Methods
2.2.1. Sieve Analysis
2.2.2. A.R. Technique
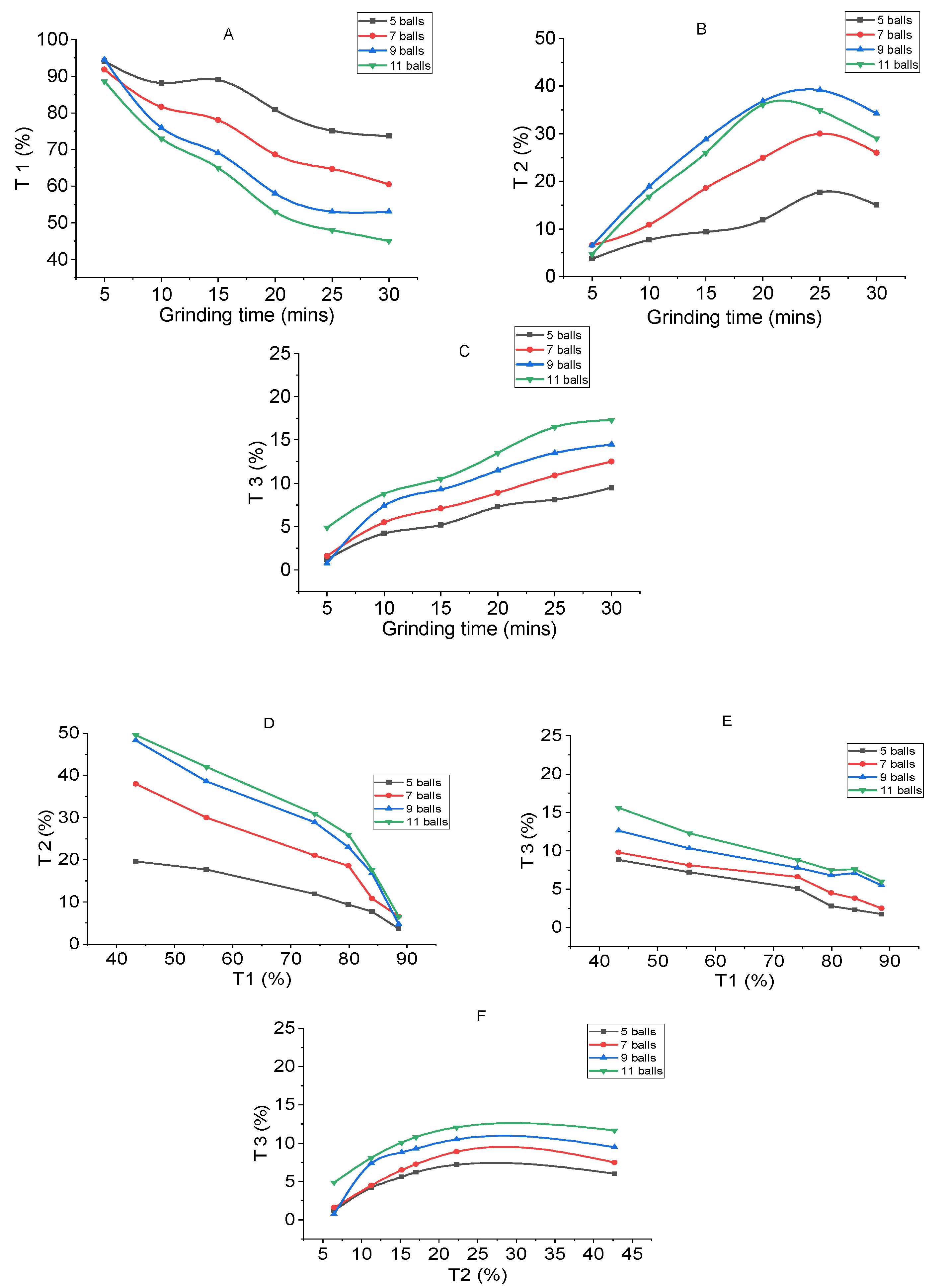
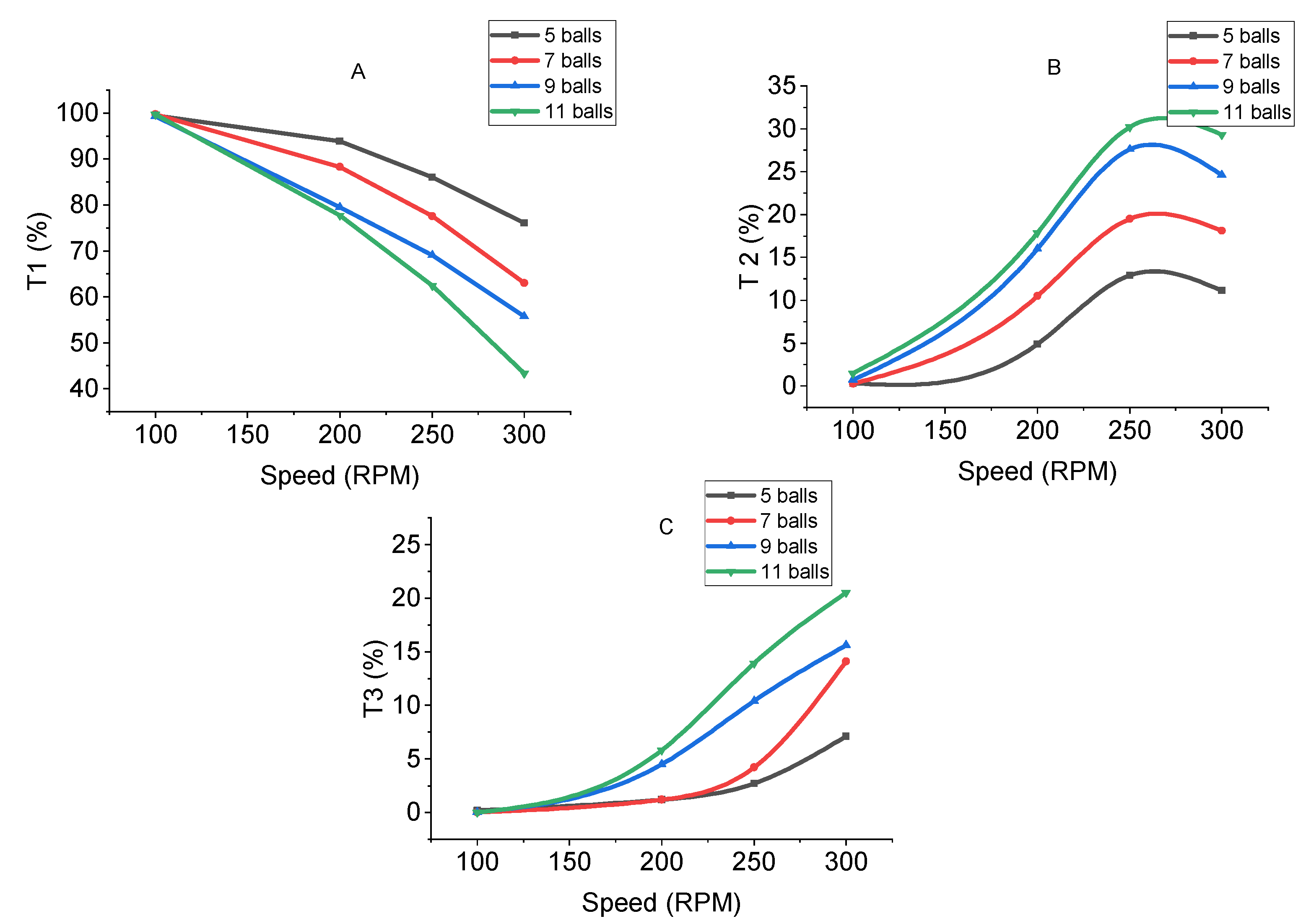
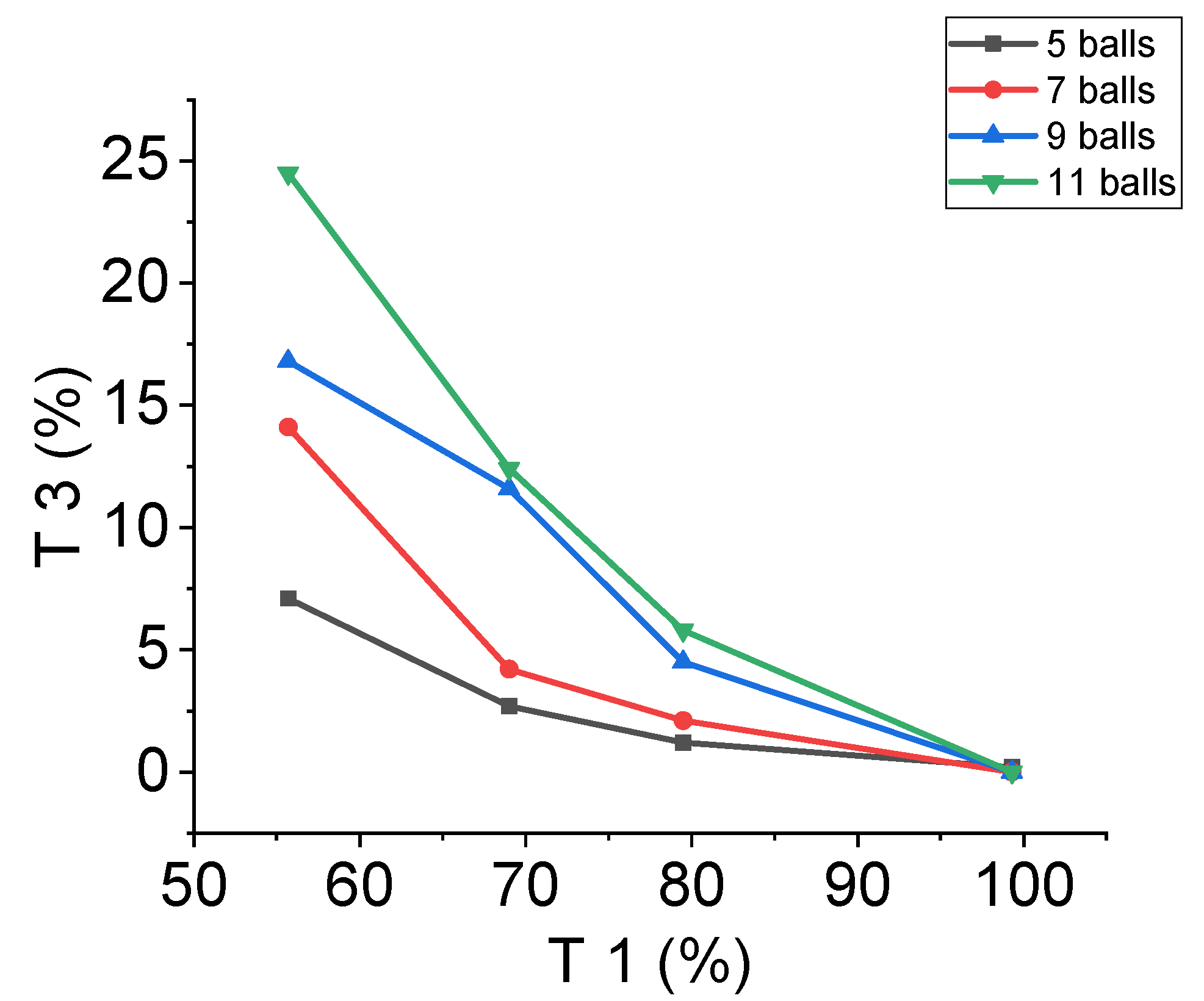
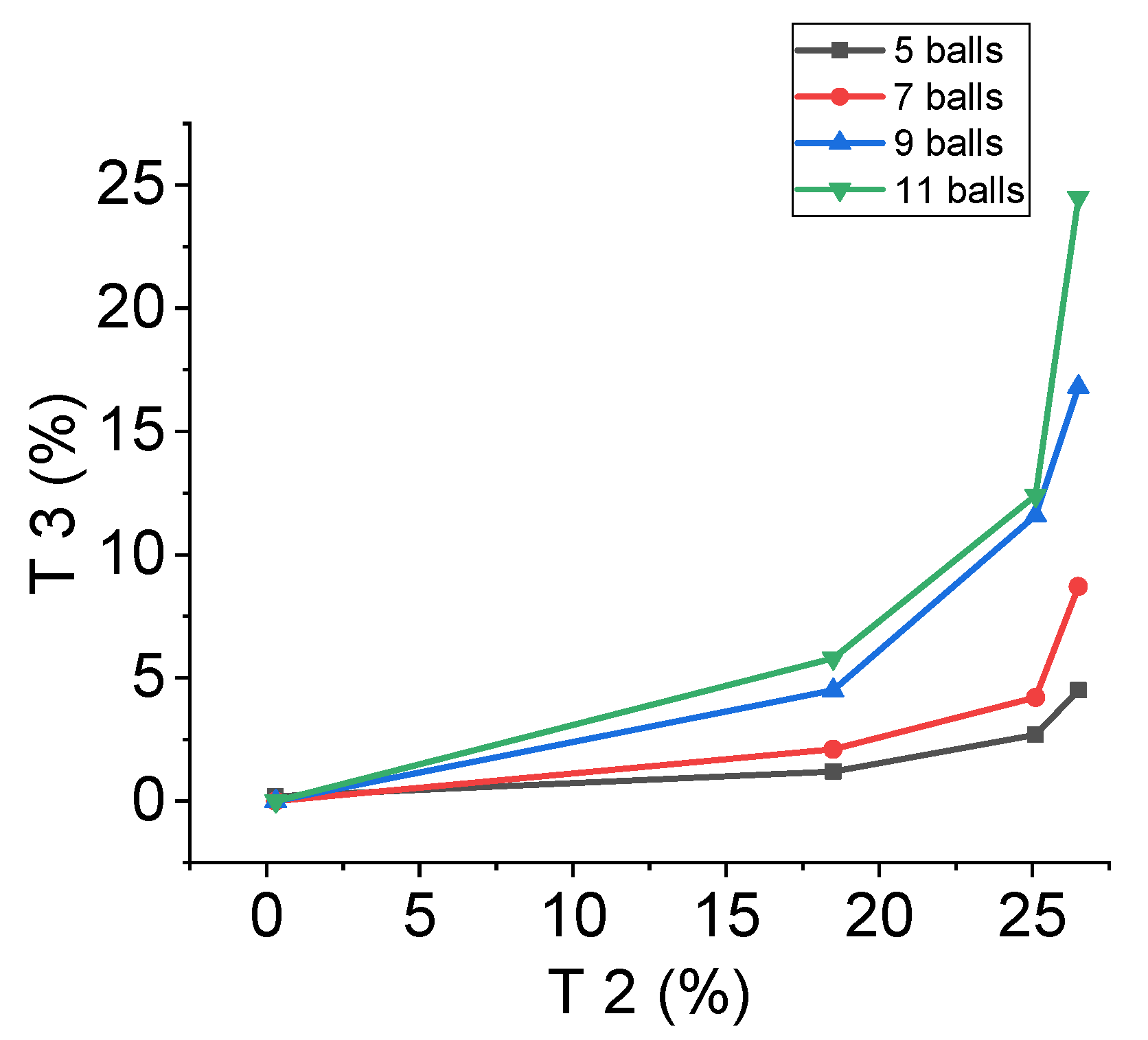
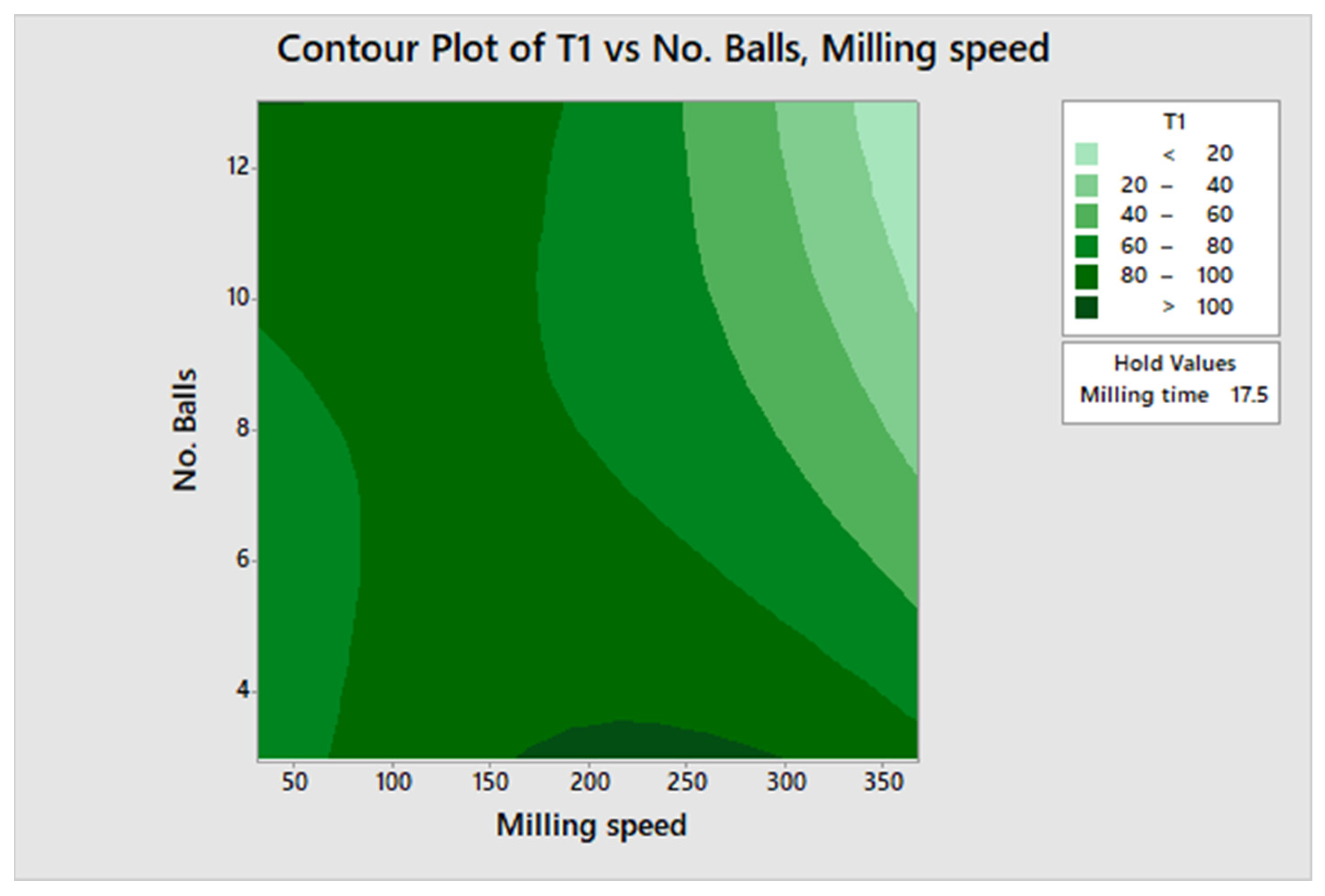
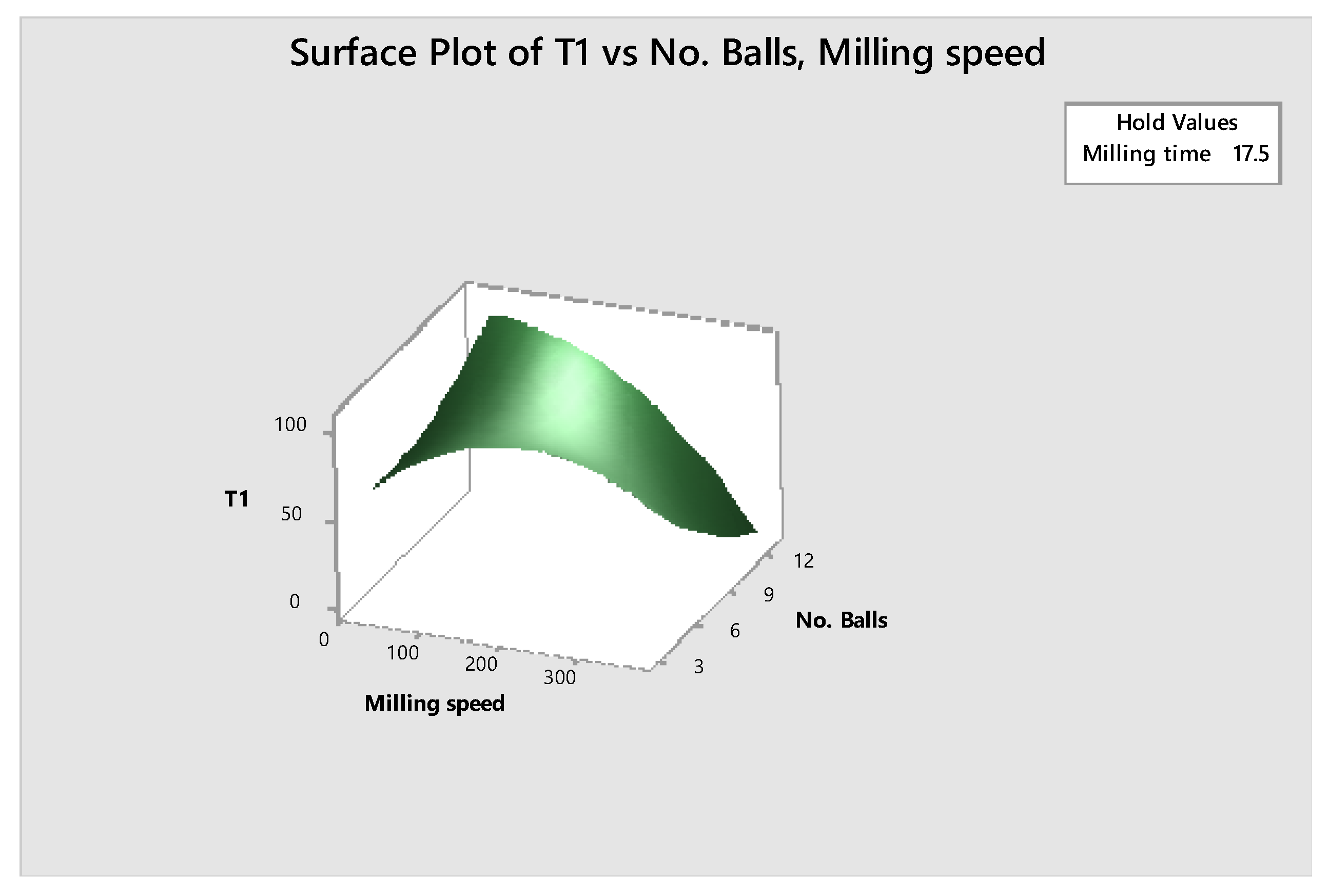
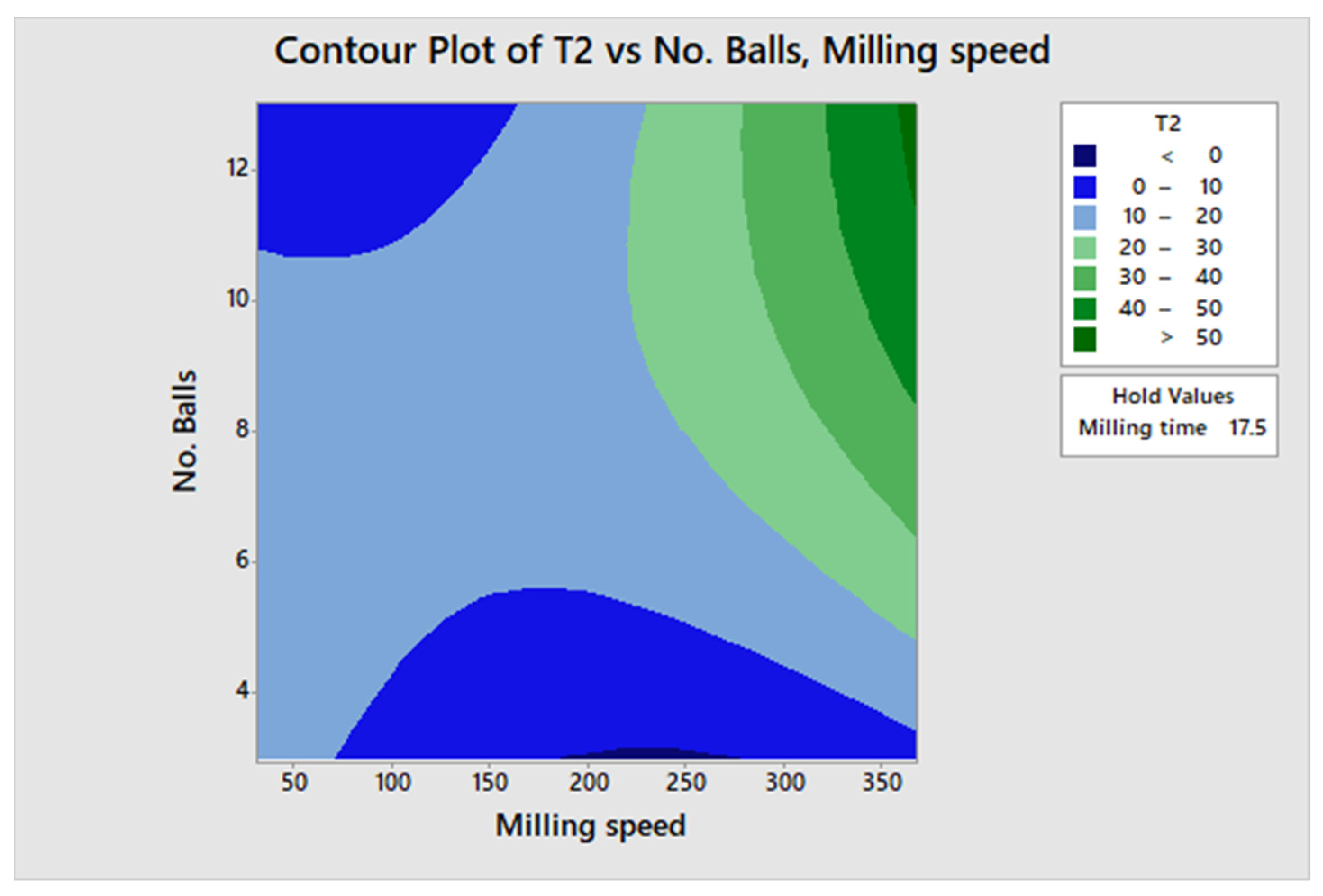
3. Results and Discussions
Attainable Region (A.R.) Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Carranza, F.; Iglesias, N.; Mazuelos, A.; Romero, R.; Forcat, O. Ferric leaching of copper slag flotation tailings Ferric leaching of copper slag flotation tailings. Miner. Eng. 2009, 22, 107–110. [Google Scholar] [CrossRef]
- Celep, O.; Deveci, H. New trends in Mining. In Proceedings of the 25 International Mining Congress and Exhibition of Turkey (IMCET 2017), Antalya, Turkey, 11–14 April 2017. [Google Scholar]
- Danha, D.; Hildebrandt, D.; Glasser, D.; Bhondayi, C. A laboratory scale application of the attainable region technique on a platinum ore. Powder Technol. 2015, 274, 14–19. [Google Scholar] [CrossRef]
- Emmanuel, E.; Anggraini, V.; Asadi, A. An investigation on the breakage behavior of olivine sand particles: An attainable region technique. Adv. Powder Technol. 2022, 33, 103422. [Google Scholar] [CrossRef]
- Gabasiane, T.S.; Danha, G.; Mamvura, T.A.; Mashifana, T.; Dzinomwa, G. Characterization of copper slag for beneficiation of iron and copper. Heliyon 2021, 7, e06757. [Google Scholar] [CrossRef]
- Taylor, P. Mineral Processing and Extractive Metallurgy Review: Particle size and shape Characteristics of Kemerburgaz quartz sands obtained by sieving, laser diffraction, and digital image processing methods. Miner. Process. Extr. Metall. Rev. 2009, 30, 37–41. [Google Scholar]
- Urosevic, D.M.; Dimitrijevic, M.D.; Jankovic, Z.D.; Antic, D.V. Recovery of Copper from Copper Slag and Copper Slag Flotation Tailings. Physicochem. Probl. Miner. Process. 2015, 51, 73–82. [Google Scholar]
- Sibanda, V.; Sipunga, E.; Danha, G.; Mamvura, T.A. Enhancing the flotation recovery of copper minerals in smelter slags from Namibia prior to disposal. Heliyon 2020, 6, e03135. [Google Scholar] [CrossRef]
- Wang, C.; Harbottle, D.; Liu, Q.; Xu, Z. Current state of mineral tailings treatment: A critical review on theory and practice. Miner. Eng. 2014, 58, 113–131. [Google Scholar] [CrossRef]
- Wang, X.; Geysen, D.; Padilla Tinoco, S.V.; D’Hoker, N.V.G.T.; Van Gerven, T.; Blanpain, B. Characterization of copper slag in view of metal recovery. Trans. Institutions Min. Metall. Sect. C Miner. Process. Extr. Metall. 2015, 124, 83–87. [Google Scholar] [CrossRef]
- Wills, B.A.; Napier-Munn, T. Mineral Processing Technology: An Introduction to the Practical Aspects of Ore Treatment and Mineral Recovery; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- You, J.; Solongo, S.K.; Gomez-Flores, A.; Choi, S.; Zhao, H.; Urik, M.; Ilyas, S.; Kim, H. Intensified bioleaching of chalcopyrite concentrate using adapted mesophilic culture in continuous stirred tank reactors. Bioresour. Technol. 2020, 307, 123181. [Google Scholar] [CrossRef]
- Guo, W.; Han, Y.; Gao, P.; Li, Y.; Tang, Z. A study of the grinding of magnetite/limestone mixture in a stirred mill by the attainable region method. Powder Technol. 2021, 389, 40–47. [Google Scholar] [CrossRef]
- Hlabangana, H.; Danha, D.; Mguni, N.G.; Madiba, M.S.; Bhondayi, C. Determining an optimal interstitial filling condition: An attainable Region approach. Powder Technol. 2018, 327, 9–16. [Google Scholar] [CrossRef]
- Hlabangana, N.; Danha, D.; Hildebrandt, D.; Glasser, D. Use of the attainable region approach to determine major trends and optimize particle breakage in a laboratory mill. Powder Technol. 2016, 291, 414–419. [Google Scholar] [CrossRef]
- Sibanda, V.; Khan, R.; Danha, G. The effect of chemical reagent on flotation performance of a Pentlandite ore: An attainable region approach. Powder Technol. 2019, 252, 464–469. [Google Scholar] [CrossRef]
- Hlabangana, N.; Danha, G.; Bwalya, M.M.; Hildebrandt, D.; Glasser, D. Application of attainable region method to determine optimal conditions for milling and leaching. Powder Technol. 2017, 317, 400–407. [Google Scholar] [CrossRef]
- Hlabangana, N.; Danha, G.; Muzenda, E. Effect of ball and feed particle size distribution on the milling efficiency of a ball mill: An attainable region approach. S. Afr. J. Chem. Eng. 2018, 25, 79–84. [Google Scholar] [CrossRef]
- Hlabangana, N.; Nhira, E.; Masayile, N.; Tembo, P.M.; Danha, G. A fundamental investigation on the breakage of a bed of PGM ore particles: An attainable region approach, part 2. Powder Technol. 2019, 346, 326–331. [Google Scholar] [CrossRef]
- Keith, J. Mineral Accounting, National Wealth and Adjusted Net Savings Calculations in Botswana. 2015. Econsult Botswana. Available online: https://www.wavespartnership.org/sites/waves/files/images/Botswana%20Mineral%20Accounts%20presentation.pdf (accessed on 1 December 2022).
- Khanzadi, M.; Behnood, A. Mechanical properties of high-strength concrete incorporating copper slag as coarse aggregate. Constr. Build. Mater. 2019, 23, 2183–2188. [Google Scholar] [CrossRef]
- Khumalo, N.; Glasser, D.; Hildebrandt, D.; Hausberger, B.; Kauchali, S. The application of attainable region analysis to comminution. Chem. Eng. Sci. 2006, 61, 5969–5980. [Google Scholar] [CrossRef]
- Khumalo, S.; Hlabangana, N.; Danha, G.; Muzenda, E. Effect of media shape on particle breakage in a batch ball mill: Lessons learnt from population balance model and attainable region technique. Procedia Manuf. 2019, 35, 75–79. [Google Scholar] [CrossRef]
- Lim, T.T.; Chu, J. Assessment of the use of spent copper slag for land reclamation. Waste Manag. Res. 2006, 24, 67–73. [Google Scholar] [CrossRef] [PubMed]
- Metzger, M.J.; Glasser, D.; Hausberger, D.; Glasser, B.J. Use of attainable region analysis to optimize particle breakage in a ball mill. Chem. Eng. Sci. 2009, 64, 3766–3777. [Google Scholar] [CrossRef]
- Ming, D.; David, G.; Diane, H.; Benjamin, G.; Matthew, M. Attainable Region Theory: An Introduction to Choosing an Optimal Reactor; John Wiley and Sons: New York, NY, USA, 2016; Volume 1. [Google Scholar]
- Muhlare, T.A.; Groot, D.R. Recovery of Copper from Reverberatory Copper Slag and Production of a Leach Residue used as a Portland Cement Additive. In Proceedings of the Copper Cobalt Africa, Incorporating the 8th Southern African Base Metals Conference, Livingstone, Zambia, 6–8 July 2015. [Google Scholar]
- Mulenga, F.K. An attainable region perspective on the role of residence time distribution in the ball milling. S. Afr. J. Chem. Eng. 2022, 33, 125–132. [Google Scholar] [CrossRef]
- Mulenga, F.K.; Chimwani, N. Introduction to the use of the attainable region method in determing the optimal residence time of the ball mill. Int. J. Miner. Process. 2013, 125, 39–50. [Google Scholar] [CrossRef]





| Type | Details |
|---|---|
| Minerals | Diamonds |
| Base metals | |
| Coal | |
| Gold | |
| Soda ash | |
| Land | Pasture |
| Arable farming | |
| Protected areas (national parks) | |
| Water | Rivers, dams, aquifers |
| Animals | Domestic animals |
| Wildfire |
| The Process Used by A.R. | References |
|---|---|
| Comminution | [18,21,22] |
| Improve material breakage inside a ball mill | [23,24,25] |
| Identify various ways of improving the milling efficiency | [23,26,27] |
| Ball loading and ball mix | [20,28] |
| Slurry density | [28,29] |
| Mill speed | [17,23,28] |
| Method | Wet or Dry | Fractionated Sample | Approx. Useful Size Range (Micro) |
|---|---|---|---|
| Test sieving | Both | Yes | 5–1,000,000 |
| Laser diffraction | Both | No | 0.1–2000 |
| Optical microscopy | Dry | No | 0.2–50 |
| Electron microscopy | Dry | No | 0.005–100 |
| Elutriation (cyclosizer) | Wet | Yes | 5–45 |
| Sedimentation (gravity) | Wet | Yes | 1–40 |
| Sedimentation (centrifuge) | Wet | Yes | 0.05–5 |
| Mill Parameter | Specification | Experimental Parameter | Specification |
|---|---|---|---|
| Diameter of steel balls | 20 mm | Number of steel balls | 5, 7, 9 and 11 |
| Weight of each ball | 9.73 g | - | - |
| Ball loading (J) | 20% | Grinding time (mins) | 5, 10, 15, 20, 25, 30 |
| Feed size | <850 µm | Speed (RPM) | 100, 200, 250, 300, 350 |
| % Intestinal filling (U) | 100 | Sampled bed mass (g) | Constant 250 g |
| Grinding bowl volume | 500 mL | - | - |
| Mill Speed | 50–400 RPM | - | - |
| Size Class | Upper Limit (µm) | Lower Limit (µm) | Classification |
|---|---|---|---|
| T1 | −850 | +106 | Coarse (Feed) |
| T2 | −106 | +45 | Desired size class (Intermediate) |
| T3 | −45 | To pan | Fines |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabasiane, T.S.; Danha, G.; Mamvura, T.; Mashifana, T.; Sibanda, V. Application of Attainable Region Technique to Optimize Copper Slag’s Desired Size Class. Minerals 2023, 13, 19. https://doi.org/10.3390/min13010019
Gabasiane TS, Danha G, Mamvura T, Mashifana T, Sibanda V. Application of Attainable Region Technique to Optimize Copper Slag’s Desired Size Class. Minerals. 2023; 13(1):19. https://doi.org/10.3390/min13010019
Chicago/Turabian StyleGabasiane, Tlotlo Solomon, Gwiranai Danha, Tirivaviri Mamvura, Tebogo Mashifana, and Vusumuzi Sibanda. 2023. "Application of Attainable Region Technique to Optimize Copper Slag’s Desired Size Class" Minerals 13, no. 1: 19. https://doi.org/10.3390/min13010019
APA StyleGabasiane, T. S., Danha, G., Mamvura, T., Mashifana, T., & Sibanda, V. (2023). Application of Attainable Region Technique to Optimize Copper Slag’s Desired Size Class. Minerals, 13(1), 19. https://doi.org/10.3390/min13010019






