A Dynamic Coupled Elastoplastic Damage Model for Rock-like Materials Considering Tension-Compression Damage and Pressure-Dependent Behavior
Abstract
:1. Introduction
2. Establishment of Constitutive Model
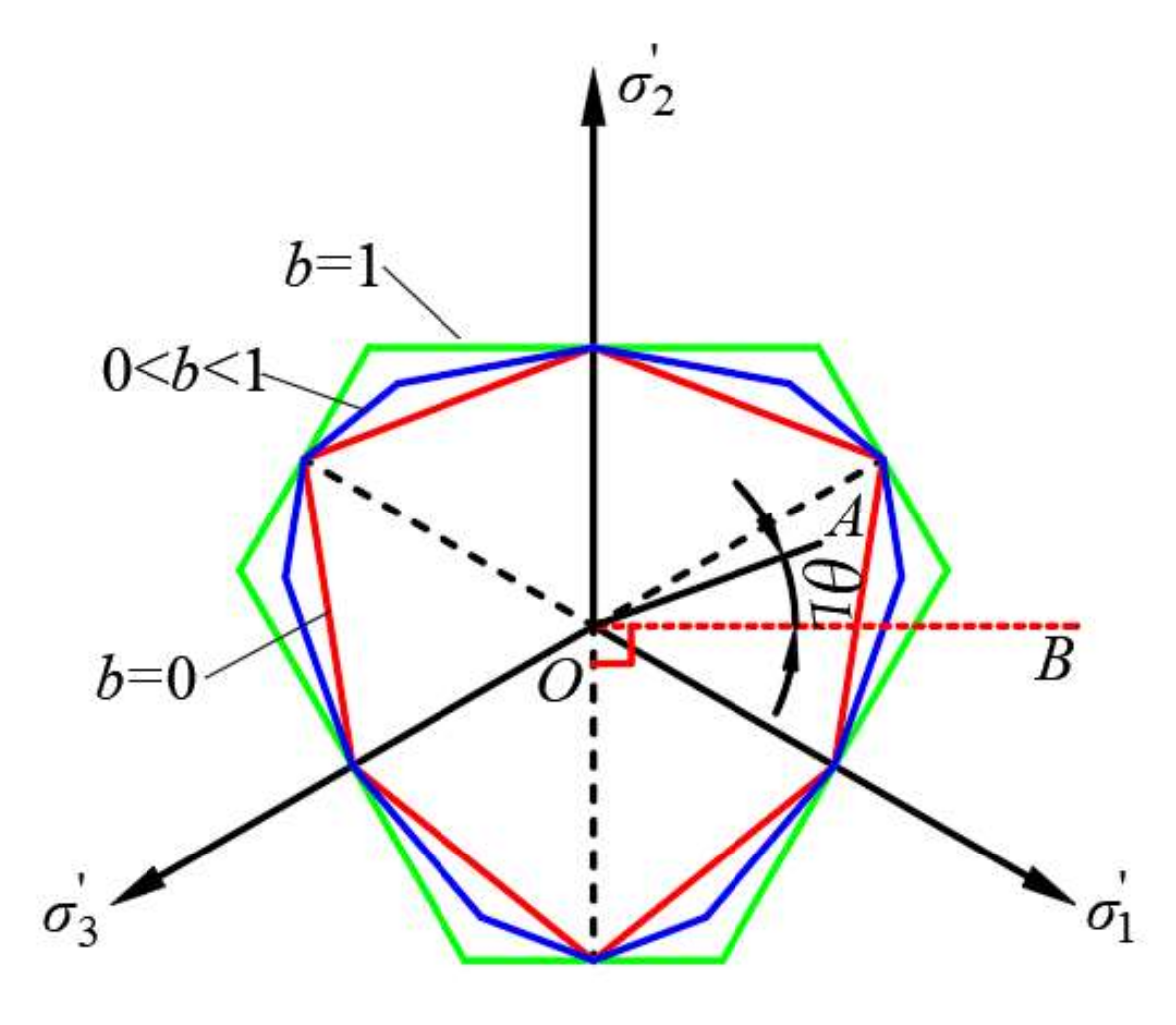
2.1. Yield Criterion
2.2. Strain Rate Effect
2.3. Plastic Flow
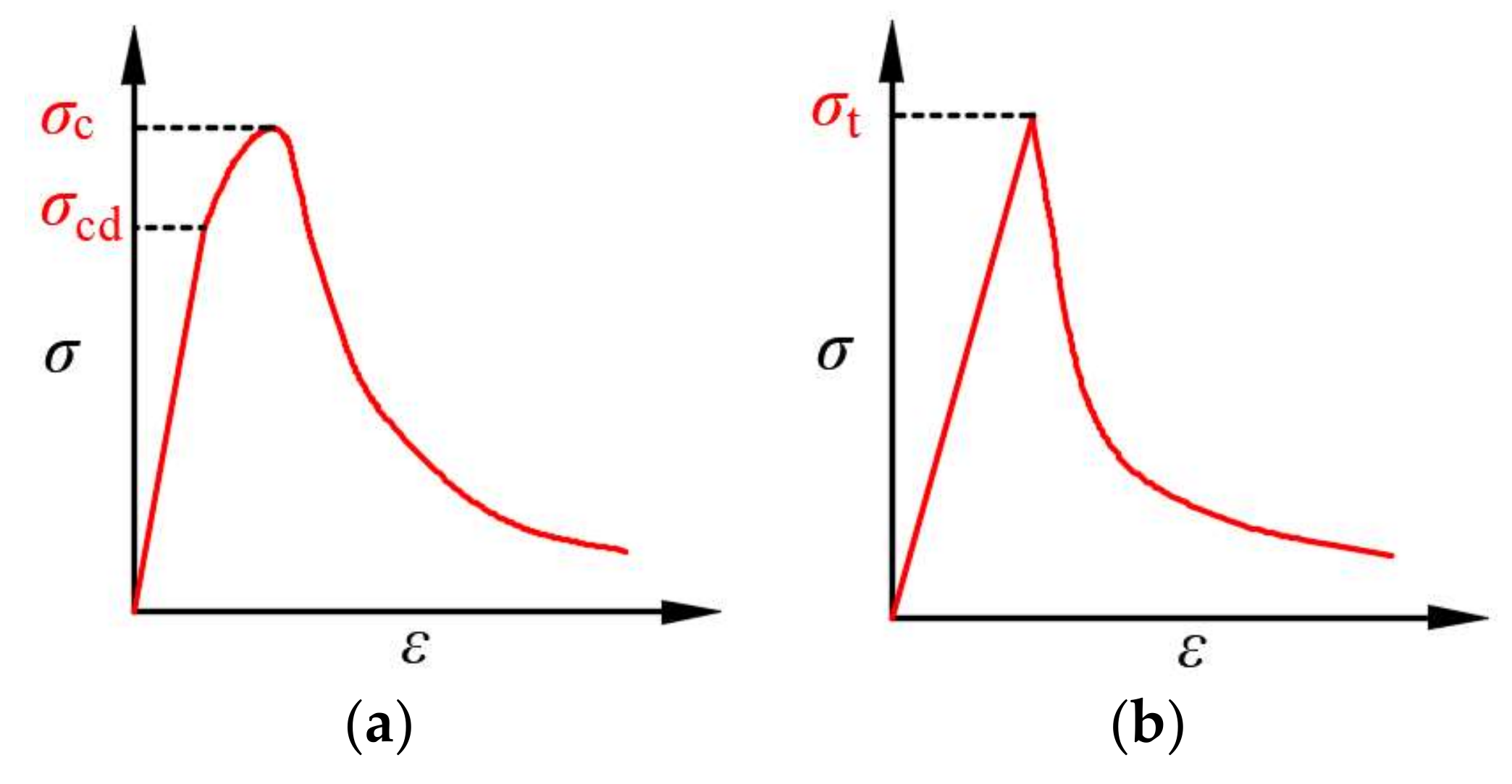
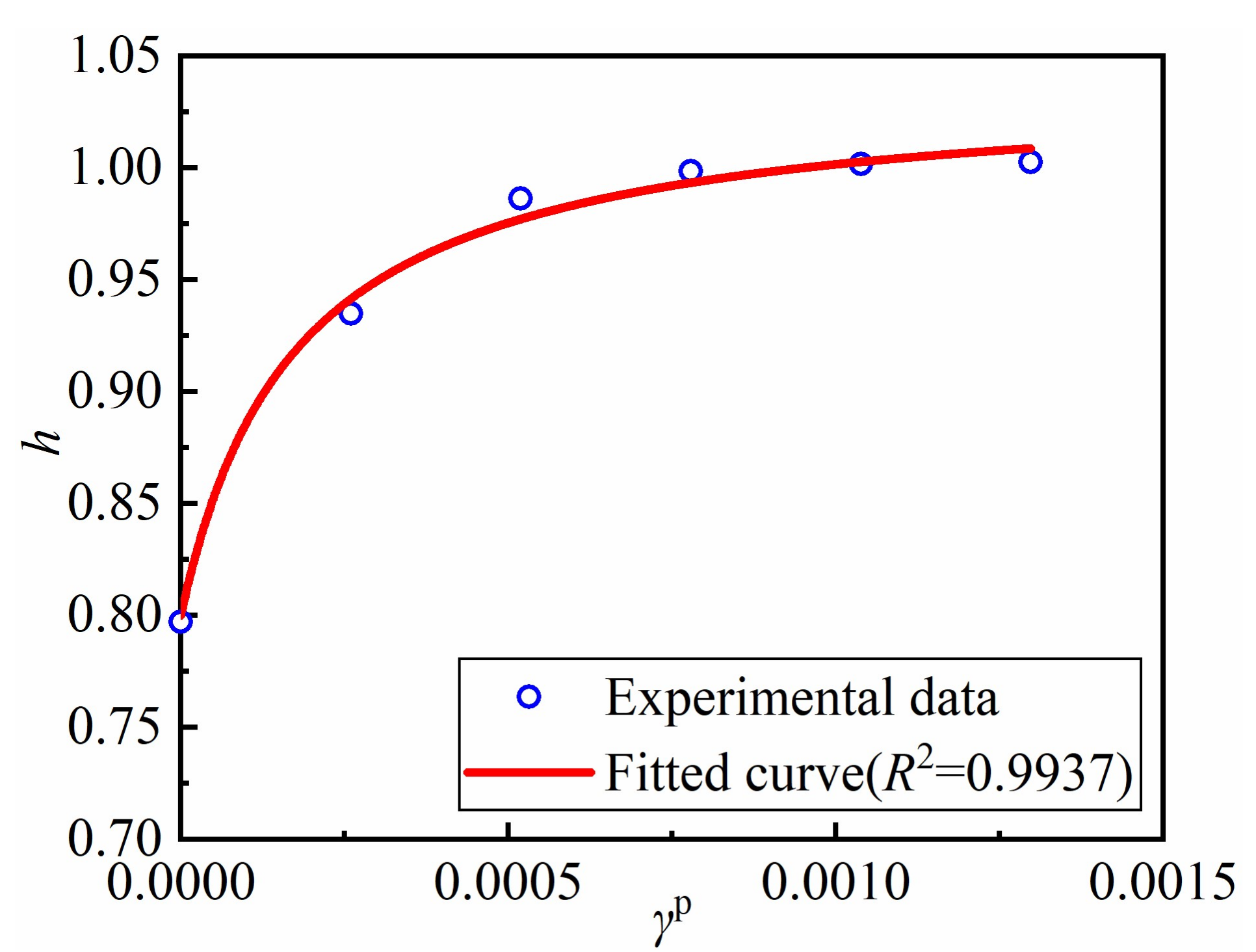
2.4. Damage Evolution
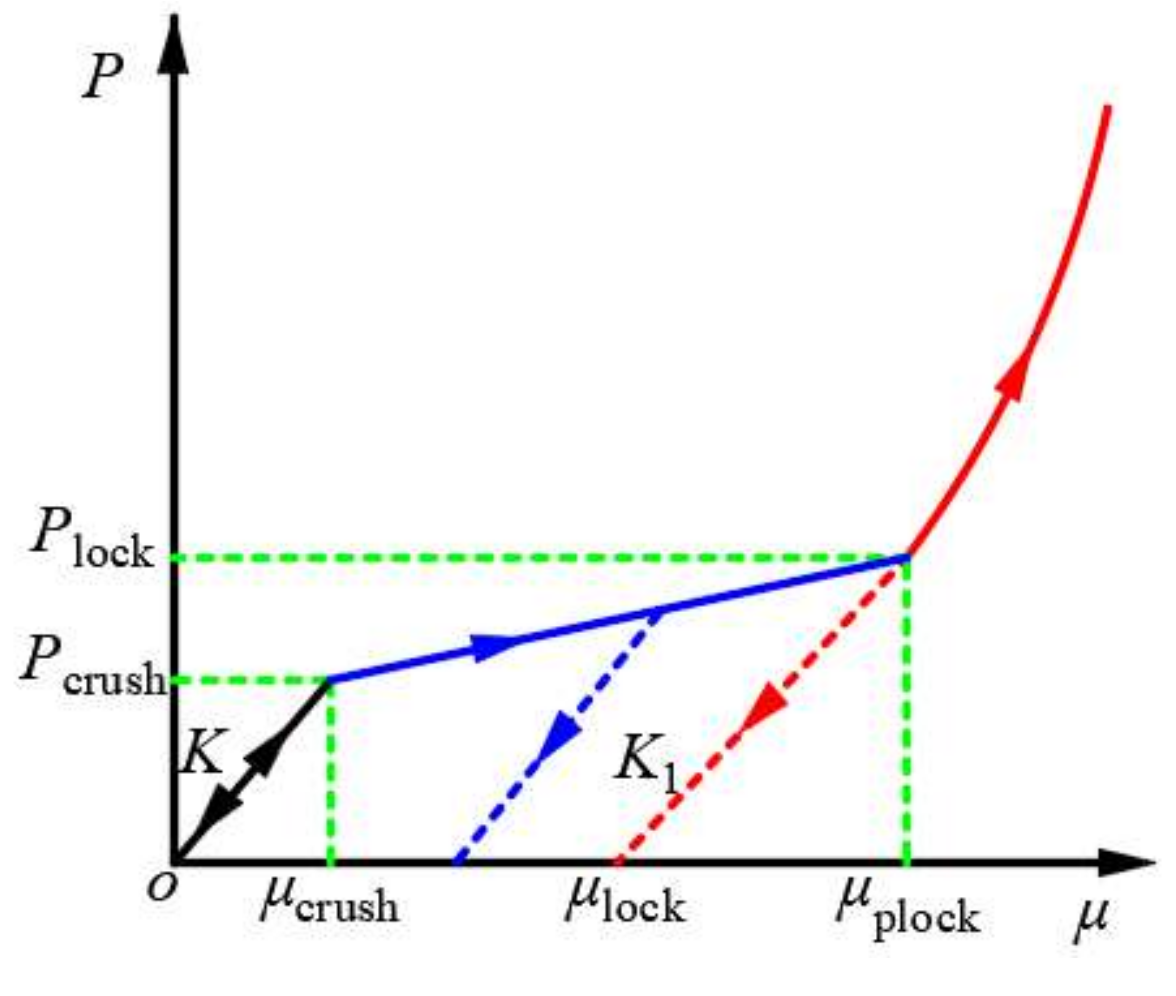
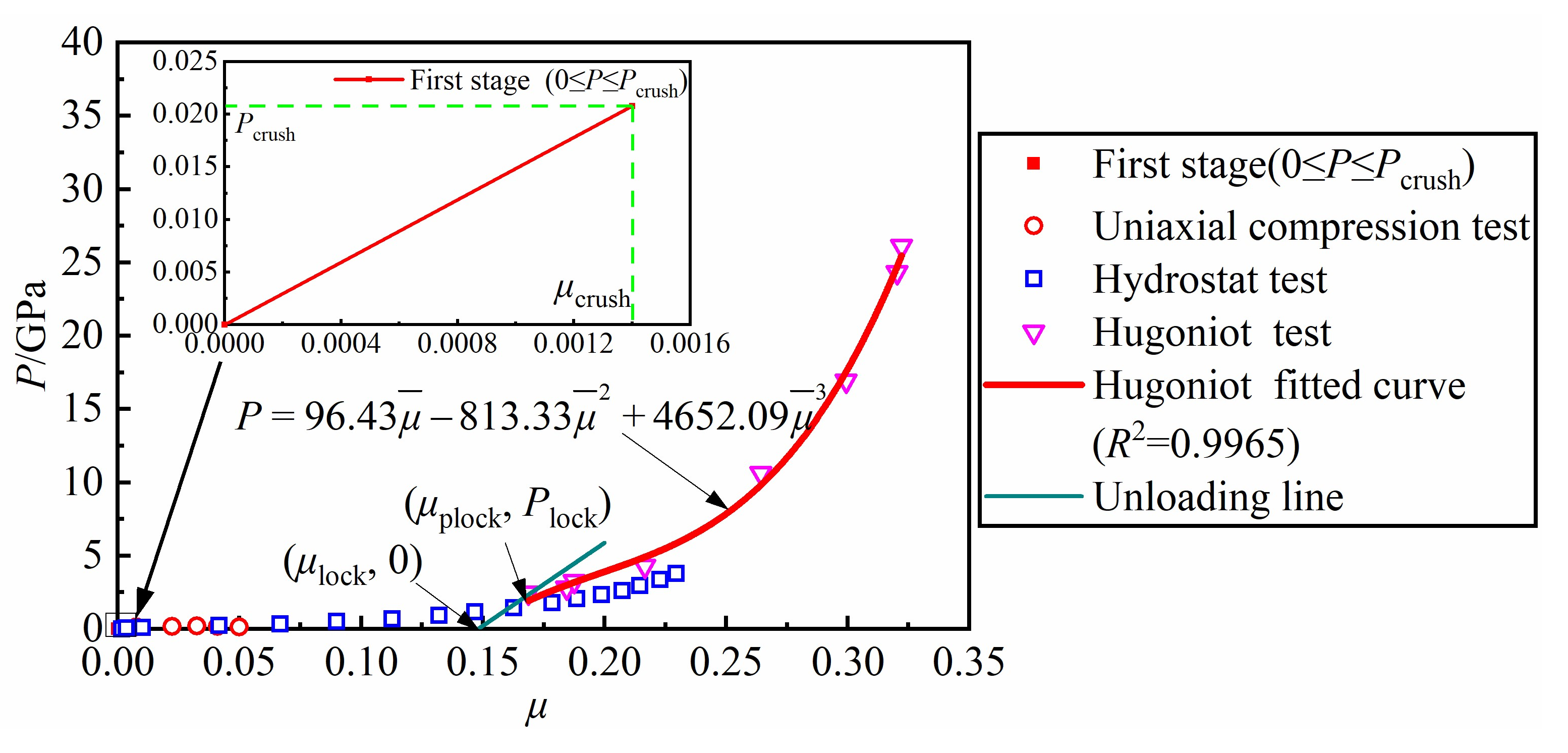
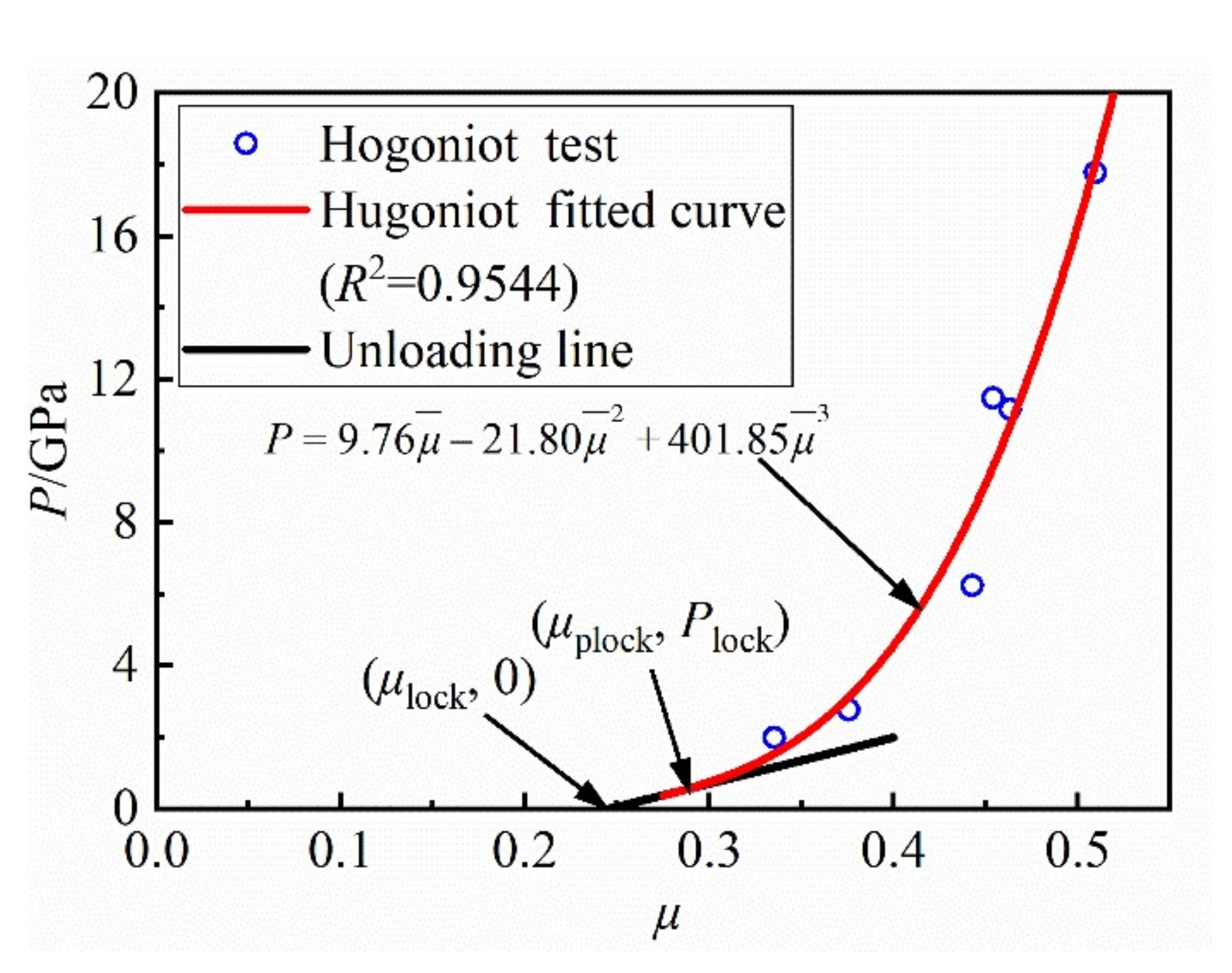
2.5. Equation of State
- (1)
- The linear elastic zone
- (2)
- The transition zone
- (3)
- The completely dense zone
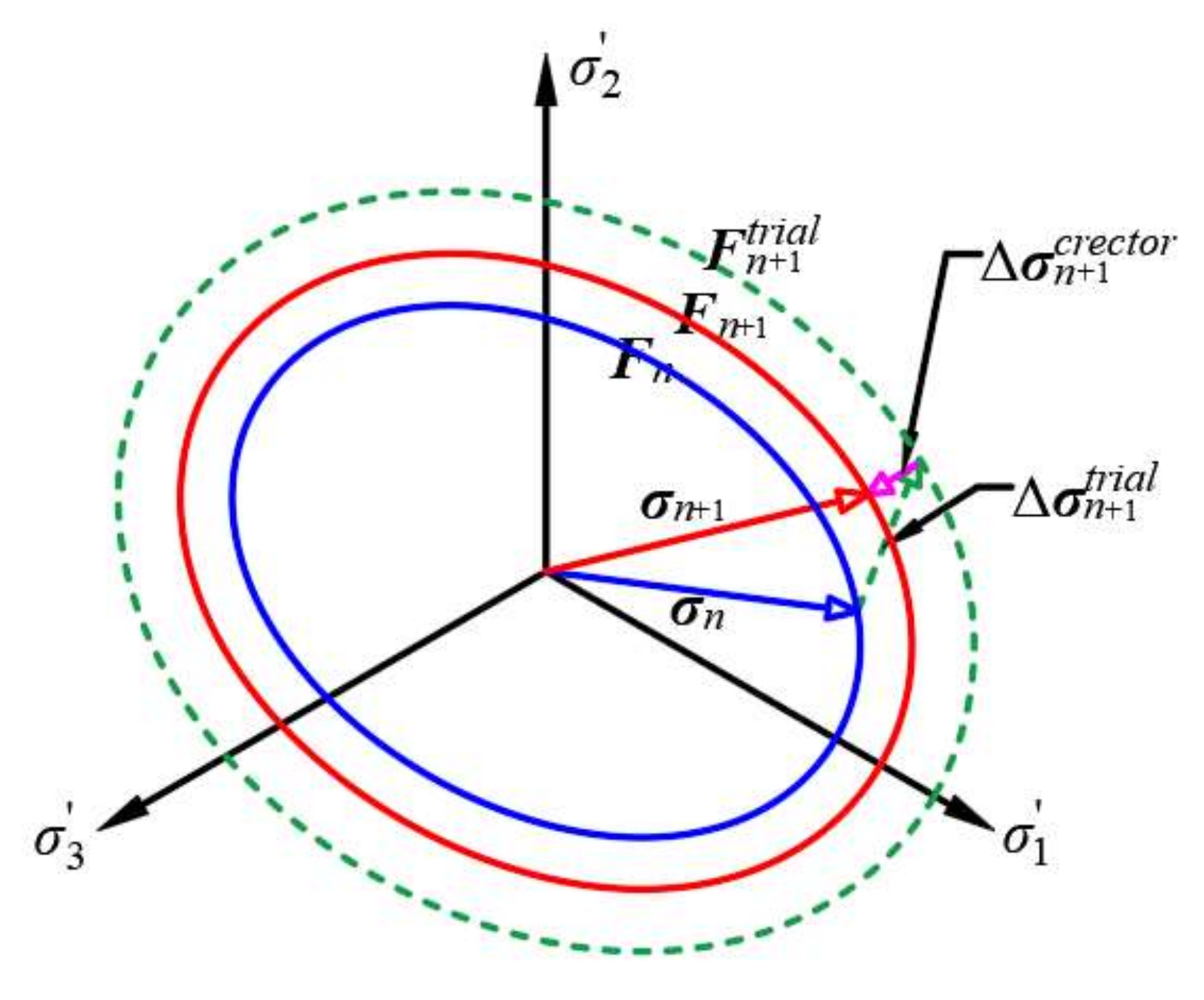
3. Numerical Implementation of Constitutive Model
4. Determination of Model Parameters
5. Validation of Model
5.1. Example 1: Rock Uniaxial Compression Test
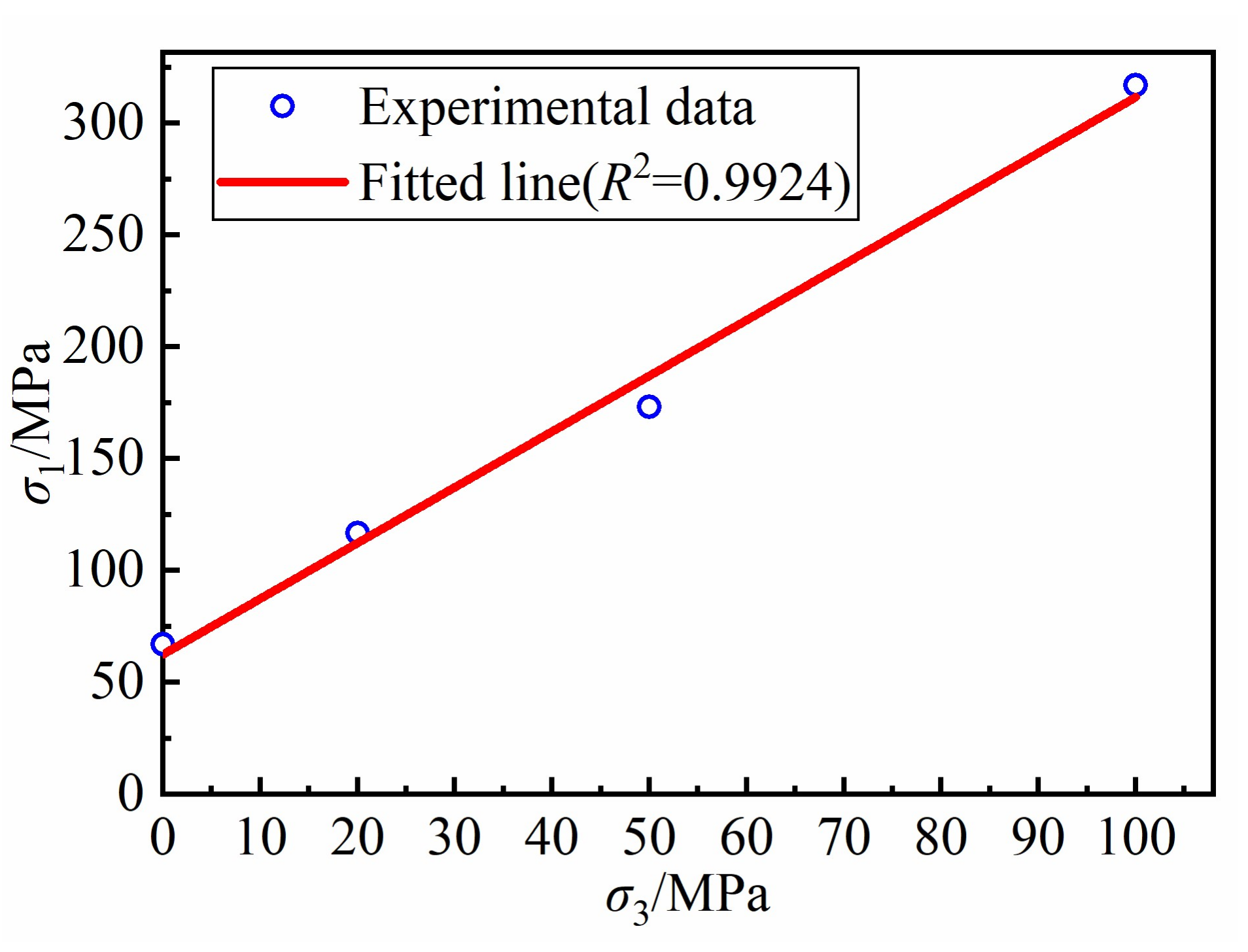
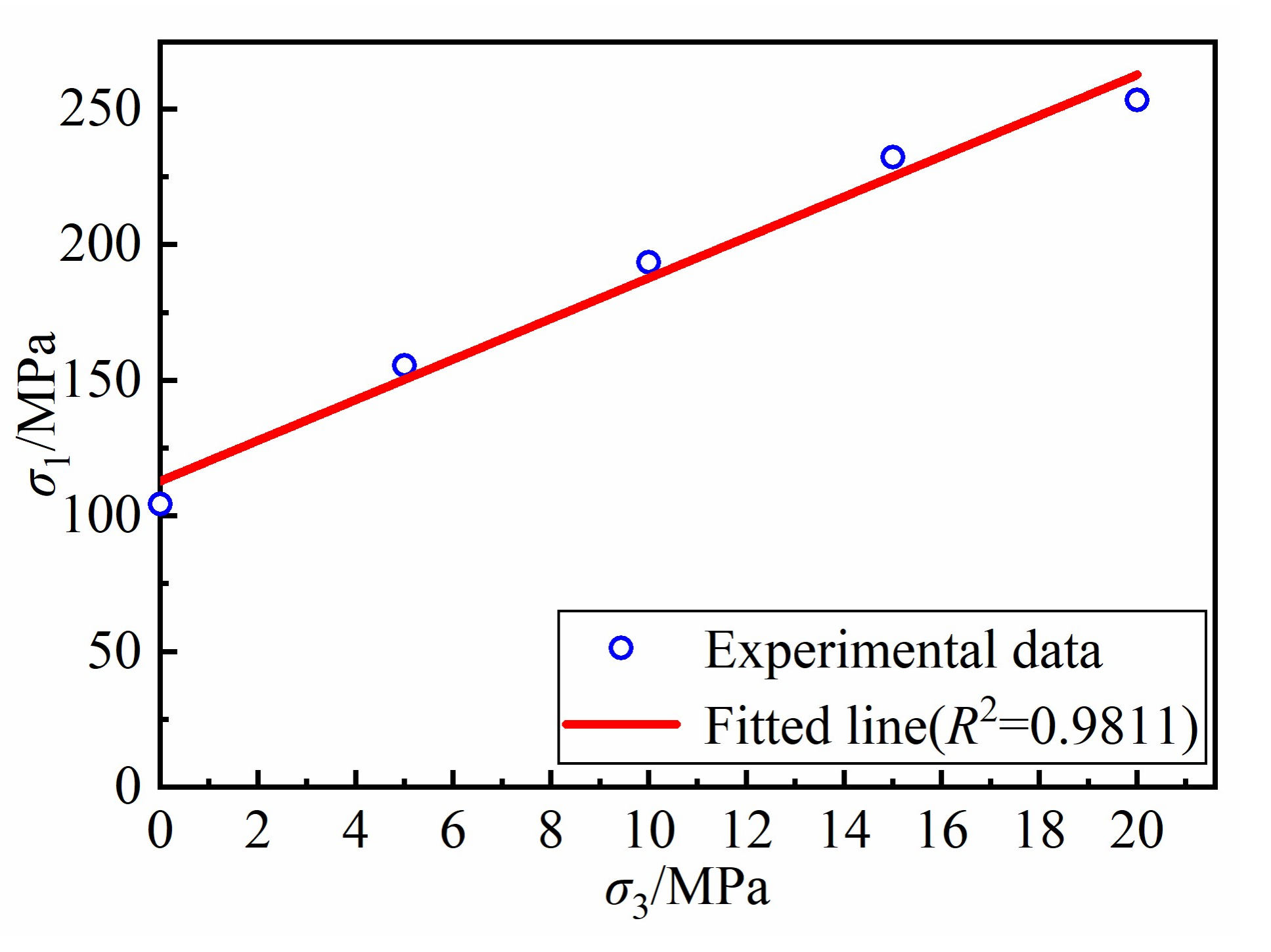
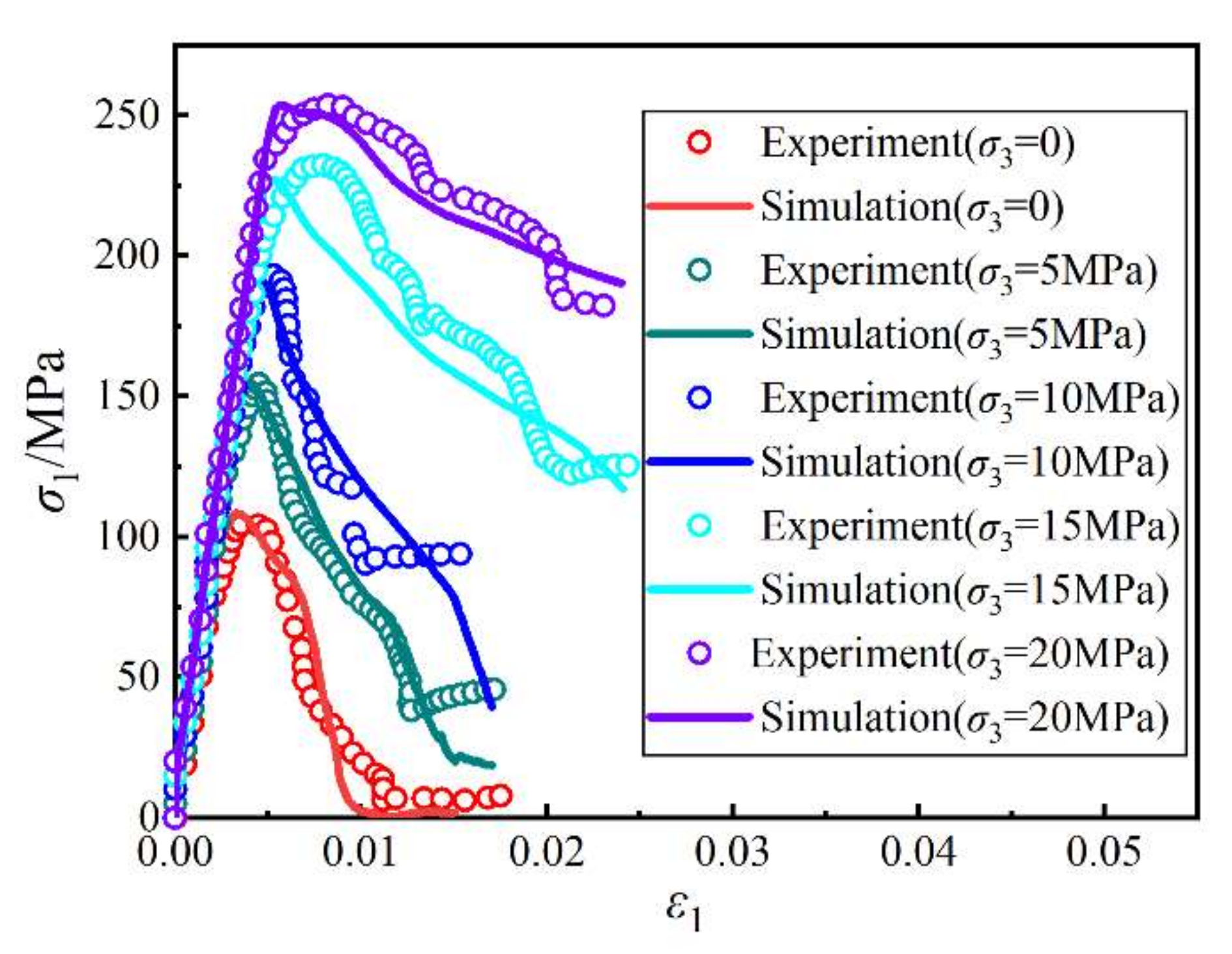
5.2. Example 2: Rock Triaxial Compression Test
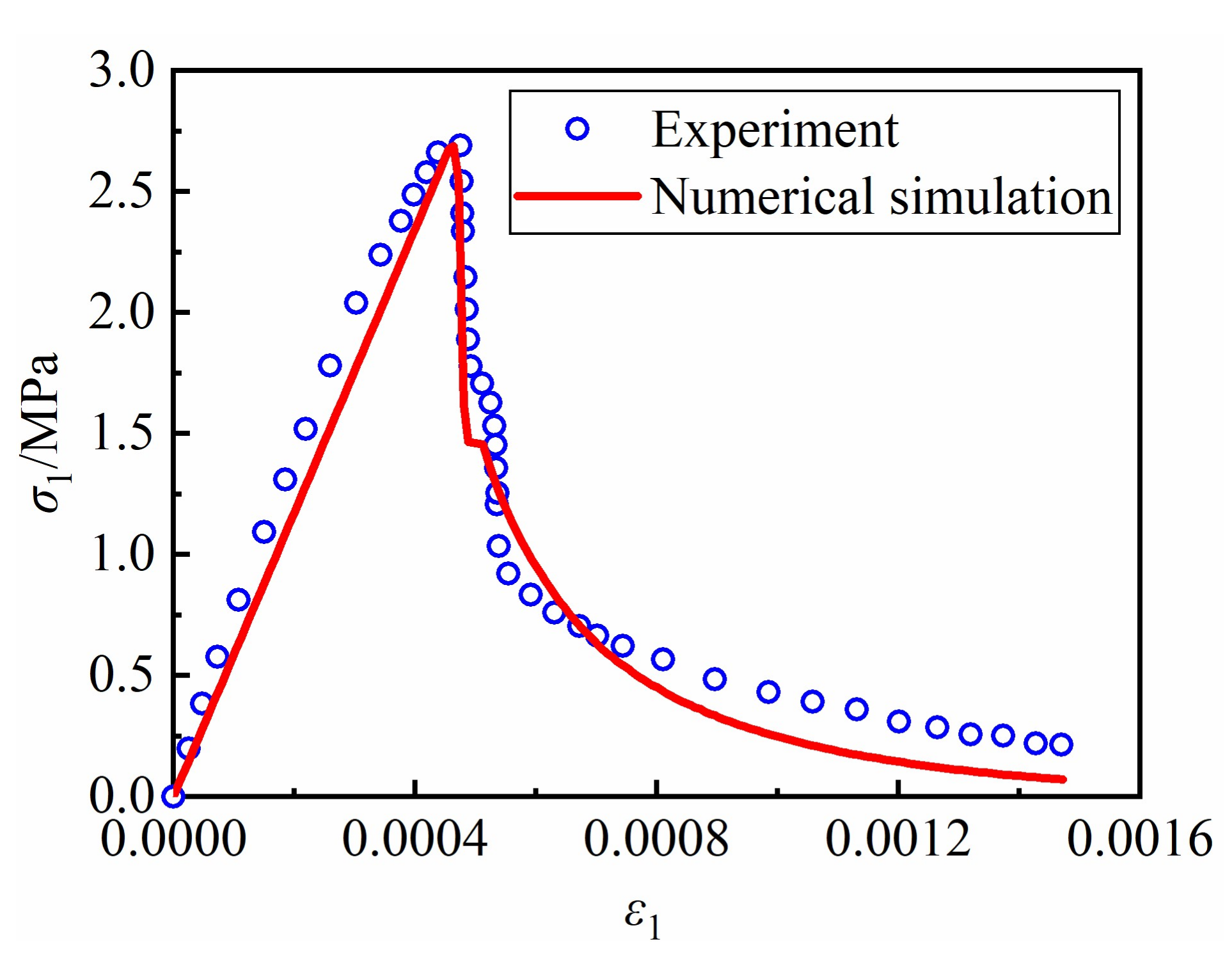
5.3. Example 3: Rock Uniaxial Tensile Test
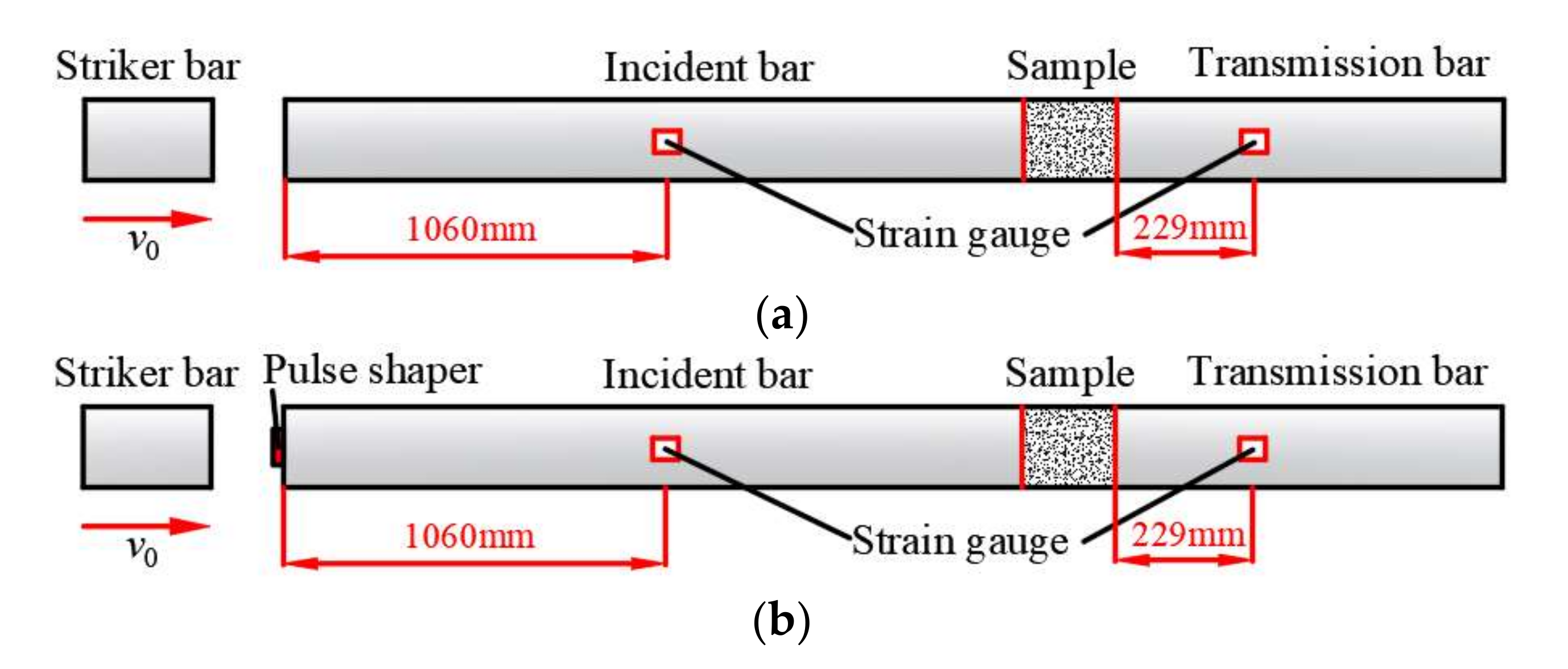
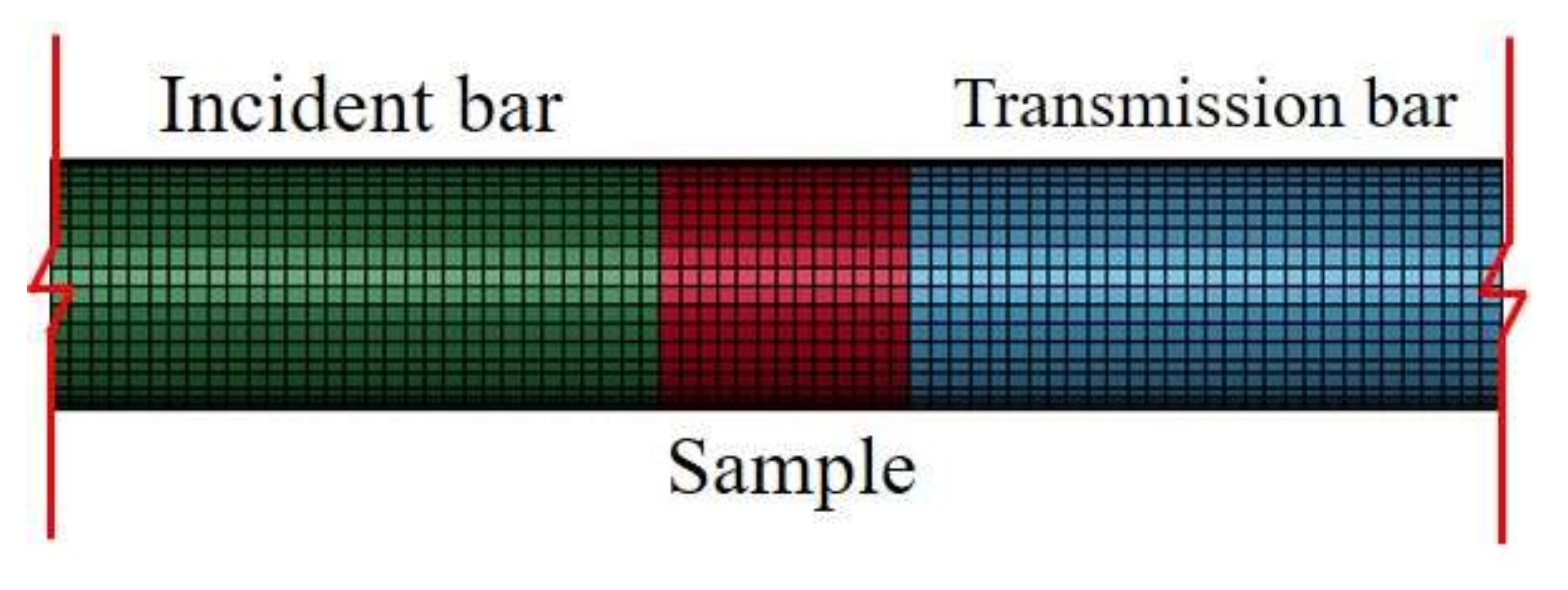
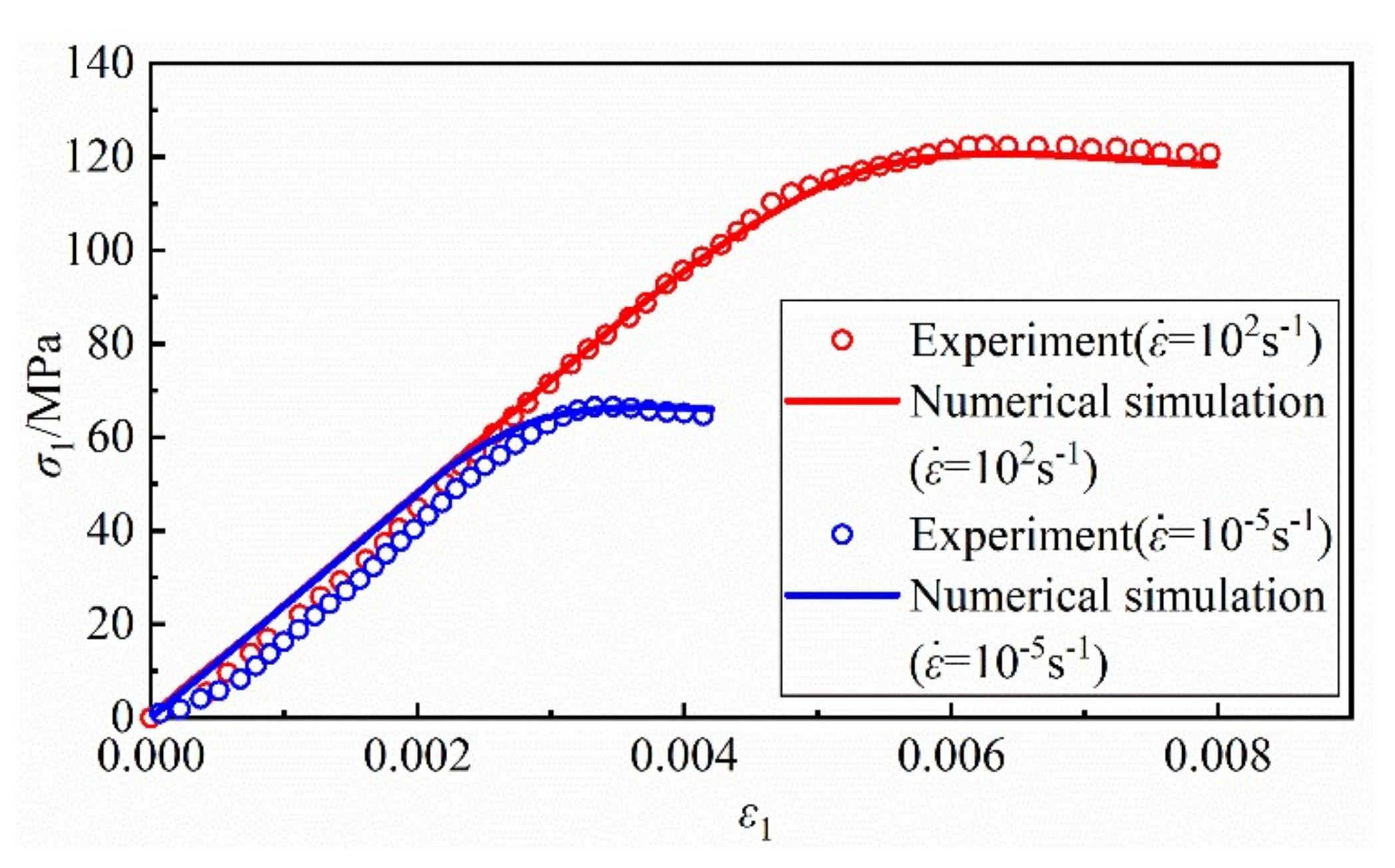
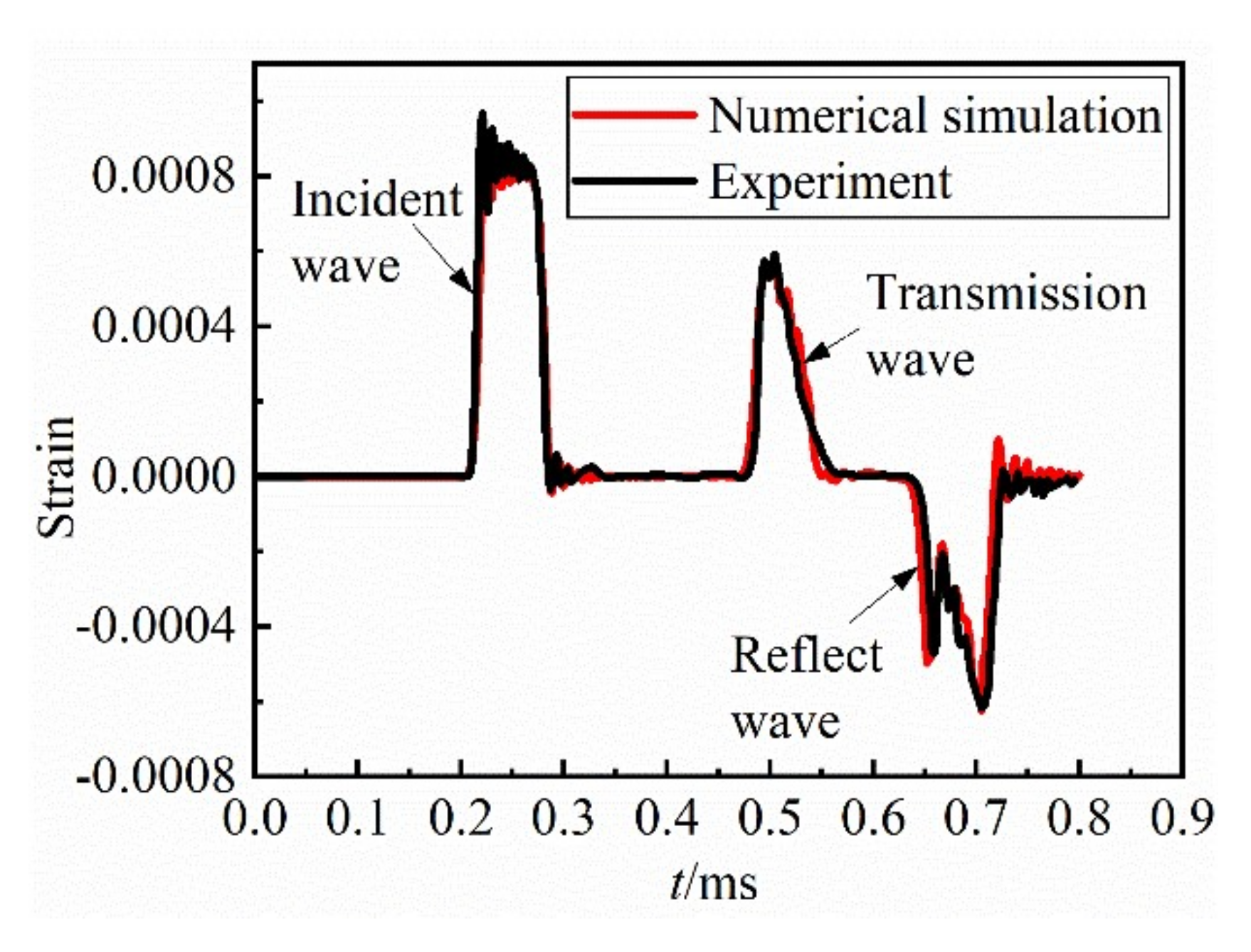
5.4. Example 4: Rock SHPB Test
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ning, Y.J.; Yang, J.; An, X.M.; Ma, G.W. Modelling rock fracturing and blast-induced rock mass failure via advanced discretisation within the discontinuous deformation analysis framework. Comput. Geotech. 2011, 38, 40–49. [Google Scholar] [CrossRef]
- Yi, C.P.; Sjöberg, J.; Johansson, D.; Petropoulos, N. A numerical study of the impact of short delays on rock fragmentation. Int. J. Rock Mech. Min. Sci. 2017, 100, 250–254. [Google Scholar] [CrossRef]
- Mukherjee, M.; Nguyen, G.D.; Mir, A.; Bui, H.H.; Shen, L.M.; El-Zein, A.; Maggi, F. Capturing pressure- and rate-dependent behaviour of rocks using a new damage-plasticity model. Int. J. Impact. Eng. 2017, 110, 208–218. [Google Scholar] [CrossRef]
- Xie, L.X.; Yang, S.Q.; Gu, J.C.; Zhang, Q.B.; Lu, W.B.; Jing, H.W.; Wang, Z.L. JHR constitutive model for rock under dynamic loads. Comput. Geotech. 2019, 108, 161–172. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Johnson, G.R.; Cook, W.H. A computational constitutive model for concrete subjected to large strains, high strain rates and high pressures. In Proceedings of the 14th International Symposium on Ballistics, Quebec City, QC, Canada, 26–29 September 1993. [Google Scholar]
- Murray, Y.D. Users Manual for LS-DYNA Concrete Material Model 159 (No. FHWA-HRT-05-062); Federal Highway Administration, Office of Research, Development, and Technology: Washington, DC, USA, 2007.
- Malvar, L.J.; Crawford, J.E.; Wesevich, J.W.; Simons, D. A plasticity concrete material model for DYNA3D. Int. J. Impact. Eng. 1997, 19, 847–873. [Google Scholar] [CrossRef]
- Riedel, W.; Thoma, K.; Hiermaier, S.; Schmolinske, E. Penetration of Reinforced Concrete by BETA-B-500 Numerical Analysis using a New Macroscopic Concrete Model for Hydrocodes. In Proceedings of the 9th International Symposium on Interaction of the Effects of Munitions with Structures, Berlin-Strausberg, Germany, 3–7 May 1999. [Google Scholar]
- Polanco-Loria, M.; Hopperstad, O.S.; Børvik, T.; Berstad, T. Numerical predictions of ballistic limits for concrete slabs using a modified version of the HJC concrete model. Int. J. Impact. Eng. 2008, 35, 290–303. [Google Scholar] [CrossRef]
- Liu, F.; Li, Q.M. Strain-rate effect on the compressive strength of brittle materials and its implementation into material strength model. Int. J. Impact. Eng. 2019, 130, 113–123. [Google Scholar] [CrossRef]
- Jiang, H.; Zhao, J.D. Calibration of the continuous surface cap model for concrete. Finite Elem. Anal. Des. 2015, 97, 1–19. [Google Scholar] [CrossRef]
- Kong, X.Z.; Fang, Q.; Li, Q.M.; Wu, H.; Crawford, J.E. Modified K&C model for cratering and scabbing of concrete slabs under projectile impact. Int. J. Impact. Eng. 2017, 108, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Tu, Z.G.; Lu, Y. Modifications of RHT material model for improved numerical simulation of dynamic response of concrete. Int. J. Impact. Eng. 2010, 37, 1072–1082. [Google Scholar] [CrossRef] [Green Version]
- Li, H.Y.; Shi, G.Y. A dynamic material model for rock materials under conditions of high confining pressures and high strain rates. Int. J. Impact. Eng. 2016, 89, 38–48. [Google Scholar] [CrossRef]
- Kong, X.Z.; Fang, Q.; Wu, H.; Peng, Y. Numerical predictions of cratering and scabbing in concrete slabs subjected to projectile impact using a modified version of HJC material model. Int. J. Impact. Eng. 2016, 95, 61–71. [Google Scholar] [CrossRef]
- Leppänen, J. Concrete subjected to projectile and fragment impacts: Modelling of crack softening and strain rate dependency in tension. Int. J. Impact. Eng. 2006, 32, 1828–1841. [Google Scholar] [CrossRef]
- Johnson, G.R.; Holmquist, T.J. An Improved Computational Constitutive Model for Brittle Materials. AIP. Conf. Proc. 1994, 309, 981–984. [Google Scholar]
- Furlong, J.; Alme, M.; Rajendran, A. Numerical modelling of ceramic penetration experiments. In Proceedings of the Fourth TACOM Armor Coordinating Conference for Light Combat Vehicles, Naval Postgraduate School, Monterey, CA, USA, 12 January 2022. [Google Scholar]
- Liu, L.; Katsabanis, P.D. Development of a continuum damage model for blasting analysis. Int. J. Rock Mech. Min. Sci. 1997, 34, 217–231. [Google Scholar] [CrossRef]
- Yu, M.H.; Zan, Y.W.; Zhao, J.; Yoshimine, M. A unified Strength criterion for rock material. Int. J. Rock Mech. Min. Sci. 2002, 39, 975–989. [Google Scholar] [CrossRef]
- Deng, L.S.; Fan, W.; Yu, M.H. Parametric study of a loess slope based on unified strength theory. Eng. Geol. 2018, 233, 98–110. [Google Scholar] [CrossRef]
- Chen, L.; Shao, J.F.; Huang, H.W. Coupled elasto-plastic damage modeling of anisotropic rocks. Comput. Geotech. 2010, 37, 187–194. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.P.; Liu, J.F.; Liu, J.; Wang, J.; Jia, F.; Shao, J. Damage and plastic deformation modeling of Beishan granite under compressive stress conditions. Rock Mech. Rock Eng. 2015, 48, 1623–1633. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. A review of dynamic experimental techniques and mechanical behavior of rock materials. Rock Mech. Rock Eng. 2014, 47, 1411–1478. [Google Scholar] [CrossRef] [Green Version]
- Gary, G.; Bailly, P. Behaviour of quasi-brittle material at high strain rate. Experiment and modelling. Eur. J. Mech-Solid. 1998, 17, 403–420. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.C.; Wang, G.S.; Du, X.L.; Wang, Y. A nonlinear dynamic uniaxial strength criterion that considers the ultimate dynamic strength of concrete. Int. J. Impact. Eng. 2017, 103, 124–137. [Google Scholar] [CrossRef]
- Grigoriev, A.S.; Shilko, E.V.; Skripnyak, V.A.; Psakhie, S.G. Kinetic approach to the development of computational dynamic models for brittle solids. Int. J. Impact. Eng. 2019, 123, 14–25. [Google Scholar] [CrossRef]
- Zhang, Q.B.; Zhao, J. Determination of mechanical properties and full-field strain measurements of rock material under dynamic loads. Int. J. Rock Mech. Min. Sci. 2013, 60, 423–439. [Google Scholar] [CrossRef]
- Kimberley, J.; Ramesh, K.T. The dynamic strength of an ordinary chondrite. Meteorit. Planet. Sci. 2011, 46, 1653–1669. [Google Scholar] [CrossRef]
- Wang, Y.N.; Tonon, F. Dynamic validation of a discrete element code in modeling rock fragmentation. Int. J. Rock Mech. Min. Sci. 2011, 48, 535–545. [Google Scholar] [CrossRef]
- Yuan, F.P.; Prakash, V.; Tullis, T. Origin of pulverized rocks during earthquake fault rupture. J. Geophys. Res-Sol. Earth 2011, 116, B06309. [Google Scholar] [CrossRef]
- Xia, K.; Nasseri, M.H.B.; Mohanty, B.; Lu, F.; Chen, R.; Luo, S.N. Effects of microstructures on dynamic compression of Barre granite. Int. J. Rock Mech. Min. Sci. 2008, 45, 879–887. [Google Scholar] [CrossRef]
- Li, X.B.; Lok, T.S.; Zhao, J. Dynamic Characteristics of Granite Subjected to Intermediate Loading Rate. Rock Mech. Rock Eng. 2005, 38, 21–39. [Google Scholar] [CrossRef]
- Doan, M.-L.; Billi, A. High strain rate damage of Carrara marble. Geophys. Res. Lett. 2011, 38, L19302. [Google Scholar] [CrossRef]
- Doan, M.-L.; D’hour, V. Effect of initial damage on rock pulverization along faults. J. Struct. Geol. 2012, 45, 113–124. [Google Scholar] [CrossRef]
- Doan, M.-L.; Gary, G. Rock pulverization at high strain rate near the San Andreas fault. Nat. Geosci. 2009, 2, 709–712. [Google Scholar] [CrossRef] [Green Version]
- Cai, M.; Kaiser, P.K.; Suorineni, F.; Su, K. A study on the dynamic behavior of the Meuse/Haute-Marne argillite. Phys. Chem. Earth 2007, 32, 907–916. [Google Scholar] [CrossRef]
- Klepaczko, J.R. Behavior of rock-like materials at high strain rates in compression. Int. J. Plast. 1990, 6, 415–432. [Google Scholar] [CrossRef]
- Liu, J.Z.; Xu, J.Y.; Lv, X.C.; Zhang, L.; Wang, Z.D. Experimental study on dynamic mechanical properties of amphibolites under impact compressive loading. Chin. J. Rock Mech. Eng. 2009, 28, 2113–2120. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J.Y.; Liu, J.; Lv, X.C. SHPB experimental study of sericite-quartz schist and sandstone. Chin. J. Rock Mech. Eng. 2011, 30, 1864–1871. [Google Scholar]
- Chakraborty, T.; Mishra, S.; Loukus, J.; Halonen, B.; Brady, B. Characterization of three Himalayan rocks using a split Hopkinson pressure bar. Int. J. Rock Mech. Min. Sci. 2016, 85, 112–118. [Google Scholar] [CrossRef]
- Mishra, S.; Khetwal, A.; Chakraborty, T. Dynamic Characterisation of Gneiss. Rock Eng. Rock Mech. 2019, 52, 61–81. [Google Scholar] [CrossRef]
- Meng, Q.S.; Fan, C.; Zeng, W.X.; Yu, K.F. Tests on dynamic properties of coral-reef limestone in South China Sea. Rock Soil. Mech. 2019, 40, 183–190. [Google Scholar] [CrossRef]
- Frew, D.J.; Forrestal, M.J.; Chen, W. A Split Hopkinson Pressure Bar Technique to Determine Compressive Stress-strain Data for Rock Materials. Exp. Mech. 2001, 46, 40–46. [Google Scholar] [CrossRef]
- Yu, M.H.; Yang, S.Y.; Fan, S.C.; Ma, G.W. Unified elasto-plastic associated and non-associated constitutive model and its engineering applications. Comput. Struct. 1999, 71, 627–636. [Google Scholar] [CrossRef]
- Kaiser, P.K.; Diederichs, M.S.; Eberhardt, E. Damage initiation and propagation in hard rock during tunnelling and the influence of near-face stress rotation. Int. J. Rock Mech. Min. Sci. 2004, 41, 785–812. [Google Scholar] [CrossRef]
- Zhu, Z.M.; Mohanty, B.; Xie, H.P. Numerical investigation of blasting-induced crack initiation and propagation in rocks. Int. J. Rock Mech. Min. Sci. 2007, 44, 412–424. [Google Scholar] [CrossRef]
- Ma, G.W.; An, X.M. Numerical simulation of blasting-induced rock fractures. Int. J. Rock Mech. Min. Sci. 2008, 45, 966–975. [Google Scholar] [CrossRef]
- Yao, C.; Shao, J.F.; Jiang, Q.H.; Zhou, C.B. Numerical study of excavation induced fractures using an extended rigid block spring method. Comput. Geotech. 2017, 85, 368–383. [Google Scholar] [CrossRef]
- Yang, L.; Lin, X.S.; Li, H.Y.; Gravina, R.J. A new constitutive model for steel fiber reinforced concrete subjected to dynamic loads. Compos. Struct. 2019, 221, 110849. [Google Scholar] [CrossRef]
- Zhang, H.M.; Lei, L.N.; Yang, G.S. Characteristic and representative model of rock under constant confining stress. J. China Univ. Mining. Technol. 2015, 44, 59–63. [Google Scholar]
- Zhang, J.C.; Xu, W.Y.; Wang, H.L.; Wang, R.B.; Meng, Q.X.; Du, S.W. A coupled elastoplastic damage model for brittle rocks and its application in modelling underground excavation. Int. J. Rock Mech. Min. Sci. 2016, 84, 130–141. [Google Scholar] [CrossRef]
- Le, L.A.; Nguyen, G.D.; Bui, H.H.; Sheikh, A.H.; Kotousov, A.; Khanna, A. Modelling jointed rock mass as a continuum with an embedded cohesive-frictional model. Eng. Geol. 2017, 228, 107–120. [Google Scholar] [CrossRef]
- Frew, D.J. Dynamic Response of Brittle Materials from Penetration and Split Hopkison Pressure Bar Experiments; Arizona State University: Phoenix, AZ, USA, 2000. [Google Scholar]
- Larson, D.B.; Anderson, G.D. Plane shock wave studies of porous geologic media. J. Geophys. Res. Solid Earth 1979, 84, 4592–4600. [Google Scholar] [CrossRef]
- Liao, Z.Y.; Zhu, J.B.; Xia, K.W. Determination of Dynamic Compressive and Tensile Behavior of Rocks from Numerical Tests of Split Hopkinson Pressure and Tension Bars. Rock Mech. Rock Eng. 2016, 49, 3917–3934. [Google Scholar] [CrossRef]
- Arthur, J.R.F.; Dunstan, T.; Al-ani, Q.A.J.L.; Assadi, A. Plastic deformation and failure in granular media. Geotechnique 1977, 27, 53–74. [Google Scholar] [CrossRef]
- Zhang, J.C. Experimental and Modelling Investigations of the Coupled Elastoplastic Damage of a Quasi-brittle Rock. Rock Mech. Rock Eng. 2018, 51, 465–478. [Google Scholar] [CrossRef]
- Okubo, S.; Fukui, K. Complete stress-strain curves for various rock types in uniaxial tension. Int. J. Rock Mech. Min. Sci. 1996, 33, 549–556. [Google Scholar] [CrossRef]









| E (GPa) | ρ0 (kg/m3) | ν | c (MPa) | φ | β0 | βm |
|---|---|---|---|---|---|---|
| 24 | 2300 | 0.23 | 21.1 | 25 | 0.8 | 1.037 |
| b1 | D1 | D2 | K1 (GPa) | K2 (GPa) | K3 (GP) | μcrush |
| 1.752 × 10−4 | 0.04 | 1.0 | 96.43 | −813.33 | 4652.09 | 1.197 × 10−3 |
| Pcrush (MPa) | μlock | Plock (GPa) | α | |||
| 17.73 | 0.148 | 2.14 | 50 |
| E (GPa) | ρ0 (kg/m3) | ν | c (MPa) | angle φ | β0 | βm |
|---|---|---|---|---|---|---|
| 45.51 | 2720 | 0.32 | 20.56 | 50 | 0.78 | 1.105 |
| b1 | μcrush | Pcrush (MPa) | D1 (GPa) | |||
| 2.64 × 10−3 | 0.633 × 10−3 | 26.67 | 0.05 |
| E (GPa) | ρ0 (kg/m3) | ν | σt (MPa) | σc (MPa) | β0 | βm |
|---|---|---|---|---|---|---|
| 58.7 | 1920 | 0.23 | 2.7 | 33 | 1.0 | 1.0 |
| b1 | D1 | D2 | K1 (GPa) | K2 (GPa) | K3 (GPa) | μcrush |
| 0.0 | 0.04 | 1.0 | 9.76 | −21.80 | 401.85 | 3.04 × 10−3 |
| Pcrush (MPa) | μlock | Plock (GPa) | α | |||
| 11.0 | 0.245 | 0.54 | 180 |
| Materials | E (GPa) | ν | Ρ0 (kg/m3) | κ (MPa) |
|---|---|---|---|---|
| VM350 steel | 200 | 0.23 | 8100 | 2500 |
| C11000 copper | 117 | 0.35 | 8930 | 750 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Zhang, M.; Xu, W.; Tu, M.; Yin, Z.; Zhang, X. A Dynamic Coupled Elastoplastic Damage Model for Rock-like Materials Considering Tension-Compression Damage and Pressure-Dependent Behavior. Minerals 2022, 12, 851. https://doi.org/10.3390/min12070851
Hu X, Zhang M, Xu W, Tu M, Yin Z, Zhang X. A Dynamic Coupled Elastoplastic Damage Model for Rock-like Materials Considering Tension-Compression Damage and Pressure-Dependent Behavior. Minerals. 2022; 12(7):851. https://doi.org/10.3390/min12070851
Chicago/Turabian StyleHu, Xuelong, Ming Zhang, Wenyao Xu, Min Tu, Zhiqiang Yin, and Xiangyang Zhang. 2022. "A Dynamic Coupled Elastoplastic Damage Model for Rock-like Materials Considering Tension-Compression Damage and Pressure-Dependent Behavior" Minerals 12, no. 7: 851. https://doi.org/10.3390/min12070851
APA StyleHu, X., Zhang, M., Xu, W., Tu, M., Yin, Z., & Zhang, X. (2022). A Dynamic Coupled Elastoplastic Damage Model for Rock-like Materials Considering Tension-Compression Damage and Pressure-Dependent Behavior. Minerals, 12(7), 851. https://doi.org/10.3390/min12070851






