Estimation of Mining-Induced Horizontal Strain Tensor of Land Surface Applying InSAR
Abstract
1. Introduction
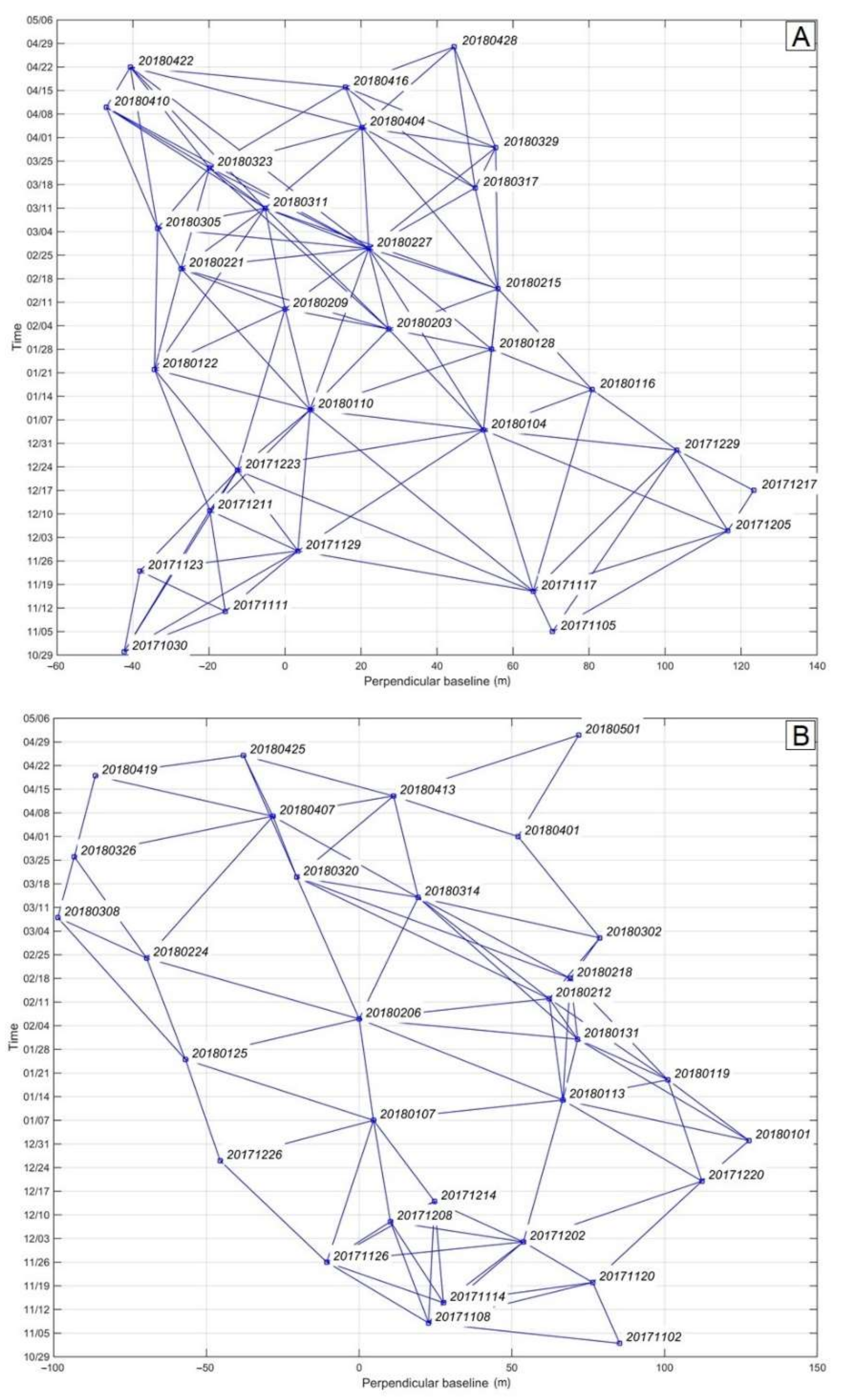
2. Study Area and Input Data
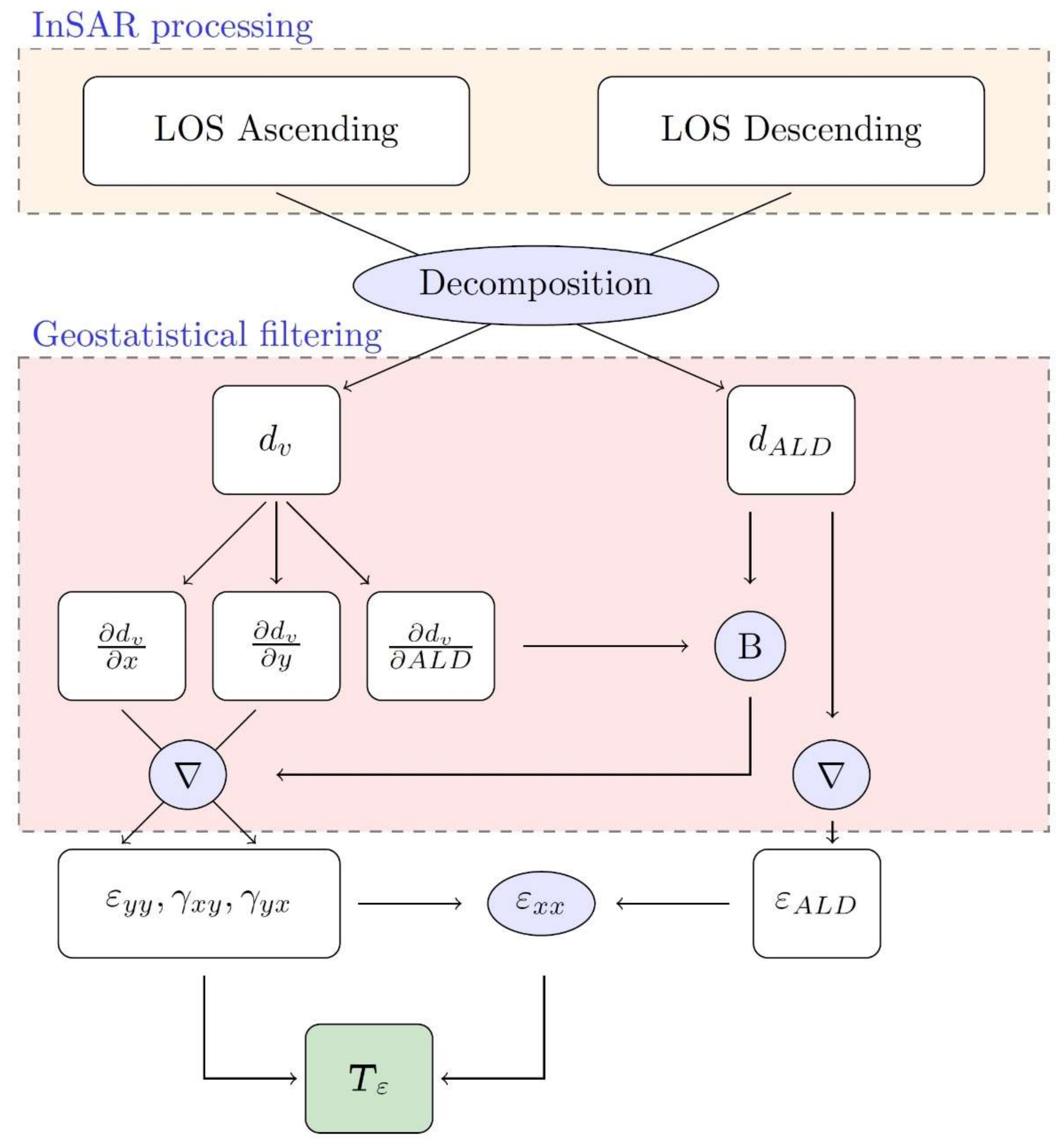
3. Research Methodology
4. Results and Discussion
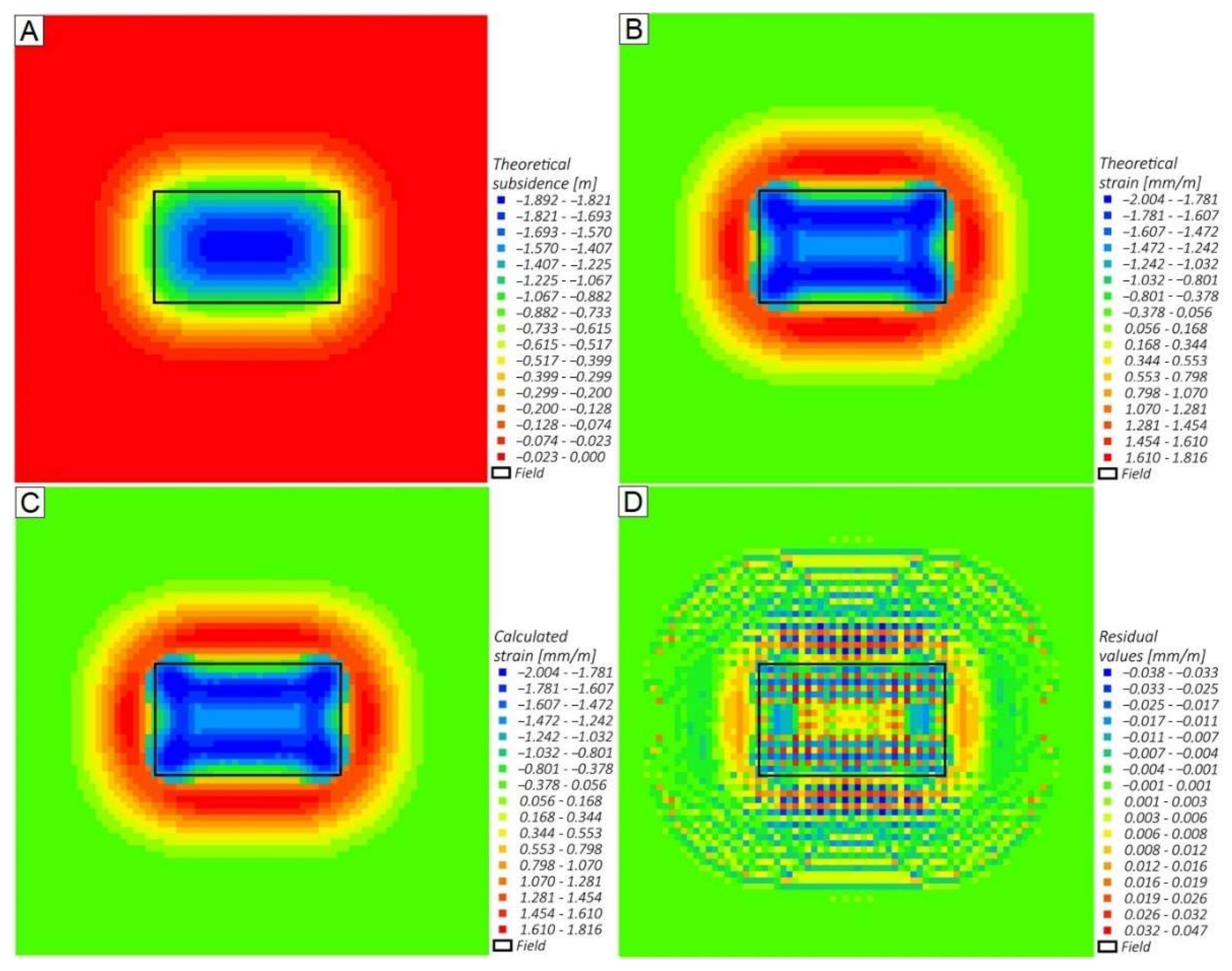
4.1. Experimental Data
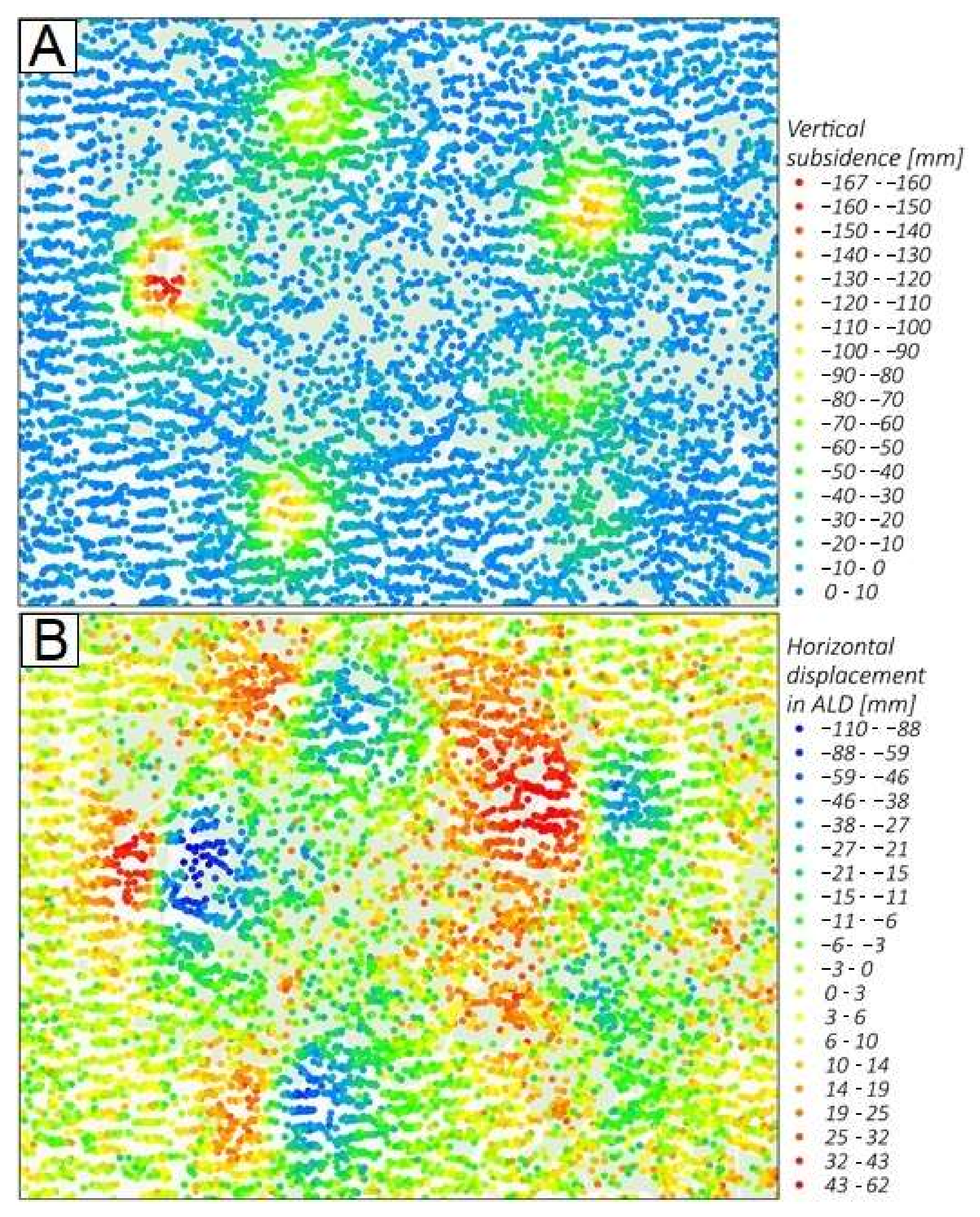
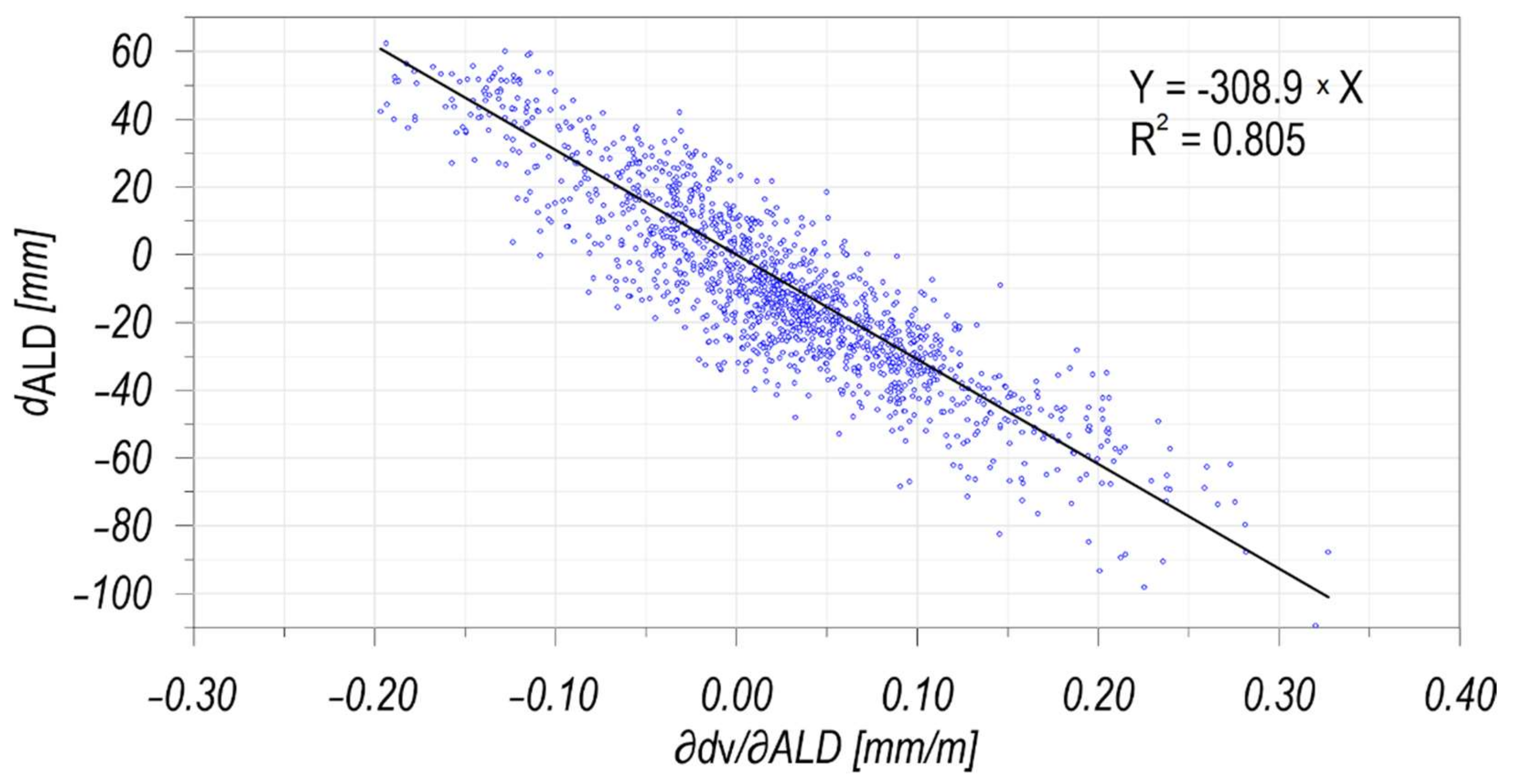
4.2. Real-World Case Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Daito, K.; Galloway, D.L. Preface: Prevention and Mitigation of Natural and Anthoropogenic Hazards Due to Land Subsidence. In Proceedings of the International Association of Hydrological Sciences; Copernicus GmbH: Göttingen, Germany, 2015; Volume 372, pp. 555–557. [Google Scholar] [CrossRef][Green Version]
- Shi, X.; Fang, R.; Wu, J.; Xu, H.; Sun, Y.Y.; Yu, J. Sustainable Development and Utilization of Groundwater Resources Considering Land Subsidence in Suzhou, China. Eng. Geol. 2012, 124, 77–89. [Google Scholar] [CrossRef]
- Rateb, A.; Abotalib, A.Z. Inferencing the Land Subsidence in the Nile Delta Using Sentinel-1 Satellites and GPS between 2015 and 2019. Sci. Total Environ. 2020, 729, 138868. [Google Scholar] [CrossRef]
- Oh, H.J.; Lee, S. Assessment of Ground Subsidence Using GIS and the Weights-of-Evidence Model. Eng. Geol. 2010. [Google Scholar] [CrossRef]
- Galloway, D.L. Subsidence Induced by Underground Extraction. In Encyclopedia of Earth Sciences Series; Springer: Dordrecht, The Netherlands, 2013; pp. 979–985. [Google Scholar] [CrossRef]
- Galloway, D.L.; Burbey, T.J. Review: Regional Land Subsidence Accompanying Groundwater Extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Guzy, A.; Ahmed, A.W.; Malinowska, A. Spatio-Temporal Distribution of Land Subsidence and Water Drop Caused by Underground Exploitation of Mineral Resources. In International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management; SGEM: Vienna, Austria, 2018. [Google Scholar] [CrossRef]
- International Association of Scientific Hydrology. Land Subsidence: Proceedings of the Tokyo Symposium September 1969. Affaissement Du Sol; Actes Du Colloque de Tokyo Septembre 1969; IASH/AIHS-Unesco: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Jones, C.E.; An, K.; Blom, R.G.; Kent, J.D.; Ivins, E.R.; Bekaert, D. Anthropogenic and Geologic Influences on Subsidence in the Vicinity of New Orleans, Louisiana. J. Geophys. Res. Solid Earth 2016. [Google Scholar] [CrossRef]
- Pacheco-Martínez, J.; Hernandez-Marín, M.; Burbey, T.J.; González-Cervantes, N.; Ortíz-Lozano, J.Á.; Zermeño-De-Leon, M.E.; Solís-Pinto, A. Land Subsidence and Ground Failure Associated to Groundwater Exploitation in the Aguascalientes Valley, México. Eng. Geol. 2013, 164, 172–186. [Google Scholar] [CrossRef]
- Feng, Q.Y.; Liu, G.J.; Lei, M.E.N.G.; Fu, E.J.; Zhang, H.R.; Zhang, K.F. Land Subsidence Induced by Groundwater Extraction and Building Damage Level Assessment—A Case Study of Datun, China. J. China Univ. Min. Technol. 2008, 18, 556–560. [Google Scholar] [CrossRef]
- Riesgo Fernández, P.; Rodríguez Granda, G.; Krzemień, A.; García Cortés, S.; Fidalgo Valverde, G. Subsidence versus Natural Landslides When Dealing with Property Damage Liabilities in Underground Coal Mines. Int. J. Rock Mech. Min. Sci. 2020, 126. [Google Scholar] [CrossRef]
- Whittaker, B.N.; Reddish, D.J. Subsidence: Occurrence, Prediction, and Control; Elsevier: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Kratzsch, H. Introduction; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar] [CrossRef]
- Hejmanowski, R.; Malinowska, A.A.; Kwinta, A.; Patykowski, G. Prediction of Land Subsidence and Deformations at Copper Ore Underground Mining Site: Experiences and Verification Based on KGHM Mines in Poland. In Proceedings of the 16th International Congress for Mine Surveying, Brisbane, Australia, 12–16 September 2016; pp. 183–186. [Google Scholar]
- Singh, R.P.; Yadav, R.N. Prediction of Subsidence Due to Coal Mining in Raniganj Coalfield, West Bengal, India. Eng. Geol. 1995. [Google Scholar] [CrossRef]
- Lee, S.; Park, I. Application of Decision Tree Model for the Ground Subsidence Hazard Mapping near Abandoned Underground Coal Mines. J. Environ. Manag. 2013, 127, 166–176. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Liu, F.; Li, S. Model for the Prediction of Subsurface Strata Movement Due to Underground Mining. J. Geophys. Eng. 2017, 14, 1608–1623. [Google Scholar] [CrossRef]
- Ambrožič, T.; Turk, G. Prediction of Subsidence Due to Underground Mining by Artificial Neural Networks. Comput. Geosci. 2003, 29, 627–637. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, H.; Yao, Z.; Wang, X. Application of the Improved Knothe Time Function Model in the Prediction of Ground Mining Subsidence: A Case Study from Heze City, Shandong Province, China. Appl. Sci. 2020, 10, 3147. [Google Scholar] [CrossRef]
- Hebblewhite, B. Fracturing, Caving Propagation and Influence of Mining on Groundwater above Longwall Panels—A Review of Predictive Models. Int. J. Min. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Truplett, T.; Yurchak, D. Determination of Intensity Functions for Predicting Subsidence from Coal Mining, Potash Mining, and Groundwater Withdrawal Using the Influence Function Technique. In Proceedings of the 6th International FIG Symposium on Deformation Measurements: Measurement, Modeling and Prediction, Hannover, Germany, 12–13 May 1996; pp. 761–773. [Google Scholar]
- Díaz-Fernández, M.E.; Álvarez-Fernández, M.I.; Álvarez-Vigil, A.E. Computation of Influence Functions for Automatic Mining Subsidence Prediction. Comput. Geosci. 2010. [Google Scholar] [CrossRef]
- Suh, J. An Overview of GIS-Based Assessment and Mapping of Mining-Induced Subsidence. Appl. Sci. 2020, 10, 7845. [Google Scholar] [CrossRef]
- Hejmanowski, R. Modeling of Time Dependent Subsidence for Coal and Ore Deposits. Int. J. Coal Sci. Technol. 2015. [Google Scholar] [CrossRef]
- Wang, B.; Xu, J.; Xuan, D. Time Function Model of Dynamic Surface Subsidence Assessment of Grout-Injected Overburden of a Coal Mine. Int. J. Rock Mech. Min. Sci. 2018, 104, 1–8. [Google Scholar] [CrossRef]
- Barbato, J.; Hebblewhite, B.; Mitra, R.; Mills, K. Prediction of Horizontal Movement and Strain at the Surface Due to Longwall Coal Mining. Int. J. Rock Mech. Min. Sci. 2016, 84, 105–118. [Google Scholar] [CrossRef]
- Fan, L.; Liu, S. Numerical Prediction of in Situ Horizontal Stress Evolution in Coalbed Methane Reservoirs by Considering Both Poroelastic and Sorption Induced Strain Effects. Int. J. Rock Mech. Min. Sci. 2018, 104, 156–164. [Google Scholar] [CrossRef]
- Ewy, R.T.; Hood, M. Surface Strain over Longwall Coal Mines: Its Relation to the Subsidence Trough Curvature and to Surface Topography. Int. J. Rock Mech. Min. Sci. 1984, 21, 155–160. [Google Scholar] [CrossRef]
- Sheorey, P.R.; Loui, J.P.; Singh, K.B.; Singh, S.K. Ground Subsidence Observations and a Modified Influence Function Method for Complete Subsidence Prediction. Int. J. Rock Mech. Min. Sci. 2000, 37, 801–818. [Google Scholar] [CrossRef]
- Marino, G.; Zamiran, S.; Talebi, M. Investigation of the Horizontal Displacement of Ground Surface Due to Longwall Mining. Geotech. Geol. Eng. 2020, 38, 5373–5387. [Google Scholar] [CrossRef]
- Dolinar, D.R. Variation of Horizontal Stresses and Strains in Mines in Bedded Deposits in the Eastern and Midwestern United States. In Proceedings of the 22nd International Conference on Ground Control in Mining, Morgantown, WV, USA, 5–7 August 2003; pp. 178–185. [Google Scholar]
- Sopata, P. Horizontal Strains over the Length of Single Section of Observation Line—Problem Analysis. Geoinformatica Pol. 2020, 19, 31–35. [Google Scholar] [CrossRef]
- Yavaşoğlu, H.H.; Kalkan, Y.; Tiryakioğlu, İ.; Yigit, C.O.; Özbey, V.; Alkan, M.N.; Bilgi, S.; Alkan, R.M. Monitoring the Deformation and Strain Analysis on the Ataturk Dam, Turkey. Geomat. Nat. Hazards Risk 2018, 9, 94–107. [Google Scholar] [CrossRef]
- Kłeczek, Z.; Niedojadło, Z.; Popiołek, E.; Skobliński, W.; Sopata, P.; Stoch, T.; Wójcik, A.; Zeljas, D. Mining Hazards Analysis with Simultaneous Mining Copper Ores and Salt Deposits in LGOM (Legnica-Głogów Copper Belt) Mines with Regard to Dynamic Influences. Arch. Min. Sci. 2016, 61, 553–570. [Google Scholar] [CrossRef][Green Version]
- Hejmanowski, R.; Malinowska, A.; Stoch, T.; Pluciński, P.; Warchała, M.; Kosior, R. New Interpretation of GPS Measurements Results. Gospod. Surowcami Miner. 2008, 24, 197–204. [Google Scholar]
- Minh, D.H.T.; Hanssen, R.; Rocca, F. Radar Interferometry: 20 Years of Development in Time Series Techniques and Future Perspectives. Remote Sens. 2020, 12, 1364. [Google Scholar] [CrossRef]
- Steinberg, A.; Sudhaus, H.; Heimann, S.; Krüger, F. Sensitivity of InSAR and Teleseismic Observations to Earthquake Rupture Segmentation. Geophys. J. Int. 2020, 223, 875–907. [Google Scholar] [CrossRef]
- Parker, A.L.; Biggs, J.; Lu, Z. Time-Scale and Mechanism of Subsidence at Lassen Volcanic Center, CA, from InSAR. J. Volcanol. Geotherm. Res. 2016, 320, 117–127. [Google Scholar] [CrossRef]
- Wasowski, J.; Pisano, L. Long-Term InSAR, Borehole Inclinometer, and Rainfall Records Provide Insight into the Mechanism and Activity Patterns of an Extremely Slow Urbanized Landslide. Landslides 2020, 17, 445–457. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, L.; Jiang, H.; Wang, H.; Ma, N.; Xu, H. Accelerated Glacier Mass Loss (2011–2016) over the Puruogangri Ice Field in the Inner Tibetan Plateau Revealed by Bistatic InSAR Measurements. Remote Sens. Environ. 2019, 231, 111241. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Wang, Y.; Wu, L. Use of SAR/InSAR in Mining Deformation Monitoring, Parameter Inversion, and Forward Predictions: A Review. IEEE Geosci. Remote Sens. Mag. 2020, 8, 71–90. [Google Scholar] [CrossRef]
- Strozzi, T.; Caduff, R.; Wegmüller, U.; Raetzo, H.; Hauser, M. Widespread Surface Subsidence Measured with Satellite SAR Interferometry in the Swiss Alpine Range Associated with the Construction of the Gotthard Base Tunnel. Remote Sens. Environ. 2017, 190, 1–12. [Google Scholar] [CrossRef]
- Thomas, A. Mapping of Surface Deformation and Displacement Associated with the 6.5 Magnitude Botswana Earthquake of 3 April 2017 Using Dinsar Analysis. Geomat. Environ. Eng. 2020, 14, 81–100. [Google Scholar] [CrossRef]
- Hanssen, R. Radar Interferometry—Data Interpretation and Error Analysis, 1st ed.; Remote Sensing and Digital Image Processing; Springer: Dordrecht, The Netherlands, 2001; Volume 2. [Google Scholar] [CrossRef]
- Wright, T.J.; Parsons, B.E.; Lu, Z. Toward Mapping Surface Deformation in Three Dimensions Using InSAR. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Preusse, A.; Hu, J.; Feng, G.; Wang, Y.; Papst, M. An InSAR-Based Temporal Probability Integral Method and Its Application for Predicting Mining-Induced Dynamic Deformations and Assessing Progressive Damage to Surface Buildings. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 472–484. [Google Scholar] [CrossRef]
- Hu, J.; Li, Z.W.; Ding, X.L.; Zhu, J.J.; Zhang, L.; Sun, Q. Resolving Three-Dimensional Surface Displacements from InSAR Measurements: A Review. Earth-Sci. Rev. 2014, 133, 1–17. [Google Scholar] [CrossRef]
- Fan, H.; Wang, L.; Wen, B.; Du, S. A New Model for Three-Dimensional Deformation Extraction with Single-Track InSAR Based on Mining Subsidence Characteristics. Int. J. Appl. Earth Obs. Geoinf. 2021, 94, 102223. [Google Scholar] [CrossRef]
- Ren, H.; Feng, X. Calculating Vertical Deformation Using a Single InSAR Pair Based on Singular Value Decomposition in Mining Areas. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102115. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Preusse, A.; Yi, H.; Hu, J.; Feng, G.; Papst, M. Retrieving 3-D Large Displacements of Mining Areas from a Single Amplitude Pair of SAR Using Offset Tracking. Remote Sens. 2017, 9, 338. [Google Scholar] [CrossRef]
- Liu, J.H.; Hu, J.; Li, Z.W.; Zhu, J.J.; Sun, Q.; Gan, J. A Method for Measuring 3-D Surface Deformations with InSAR Based on Strain Model and Variance Component Estimation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 239–250. [Google Scholar] [CrossRef]
- Kwinta, A. Prediction of Strain in a Shaft Caused by Underground Mining. Int. J. Rock Mech. Min. Sci. 2012, 55, 28–32. [Google Scholar] [CrossRef]
- Malinowska, A.; Hejmanowski, R. Building Damage Risk Assessment on Mining Terrains in Poland with GIS Application. Int. J. Rock Mech. Min. Sci. 2010, 47, 238–245. [Google Scholar] [CrossRef]
- Diao, X.; Bai, Z.; Wu, K.; Zhou, D.; Li, Z. Assessment of Mining-Induced Damage to Structures Using InSAR Time Series Analysis: A Case Study of Jiulong Mine, China. Environ. Earth Sci. 2018, 77, 166. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z.; Zhu, J.; Feng, G.; Wang, Q.; Hu, J.; Wang, C. Deriving Time-Series Three-Dimensional Displacements of Mining Areas from a Single-Geometry InSAR Dataset. J. Geod. 2018, 92, 529–544. [Google Scholar] [CrossRef]
- Samsonov, S.; Dille, A.; Dewitte, O.; Kervyn, F.; D’Oreye, N. Satellite Interferometry for Mapping Surface Deformation Time Series in One, Two and Three Dimensions: A New Method Illustrated on a Slow-Moving Landslide. Eng. Geol. 2020, 266, 105471. [Google Scholar] [CrossRef]
- Gourmelen, N.; Kim, S.W.; Shepherd, A.; Park, J.W.; Sundal, A.V.; Björnsson, H.; Pálsson, F. Ice Velocity Determined Using Conventional and Multiple-Aperture InSAR. Earth Planet. Sci. Lett. 2011, 307, 156–160. [Google Scholar] [CrossRef]
- Ligas, M.; Kulczycki, M. Kriging and Moving Window Kriging on a Sphere in Geometric (GNSS/Levelling) Geoid Modelling. Surv. Rev. 2018, 50, 155–162. [Google Scholar] [CrossRef]
- Kaczmarek, W.; Rożek, R. Budowa Geologiczna i Zagospodarowanie Złoża Głogów Głęboki-Przemysłowy (KGHM Polska Miedź S.A.). Gospod. Surowcami Miner. 2008, 24, 129–141. [Google Scholar]
- Burtan, Z. The Influence of Regional Geological Settings on the Seismic Hazard Level in Copper Mines in the Legnica-Głogów Copper Belt Area (Poland). In E3S Web of Conferences; EDP Sciences: Les Ulis, France, 2017; Volume 24, p. 01004. [Google Scholar] [CrossRef]
- Oszczepalski, S.; Speczik, S.; Zieliński, K.; Chmielewski, A. The Kupferschiefer Deposits and Prospects in SW Poland: Past, Present and Future. Minerals 2019, 9, 592. [Google Scholar] [CrossRef]
- Copper and Silver Resources in Poland—Polish Geological Institute-National Research Institute. Available online: https://www.pgi.gov.pl/en/psg-1/psg-2/informacja-i-szkolenia/wiadomosci-surowcowe/10934-copper-and-silver-resources-in-poland.html (accessed on 30 May 2021).
- Cieślik, J.; Burtan, Z.; Chlebowski, D.; Zorychta, A. Geomechanical Analysis of Location and Conditions for Mining-Induced Tremors in LGOM Copper Mines. J. Sustain. Min. 2017, 16, 94–103. [Google Scholar] [CrossRef]
- KGHM Corporate Website. Available online: https://kghm.com/en (accessed on 30 May 2021).
- Krawczyk, A.; Perski, Z. Application of Satellite Radar Interferometry on the Areas of Underground Exploitation of Copper Ore in LGOM—Poland. In Proceedings of the 11th International Congress of the International Society for Mine Surveying, Cracow, Poland, 5–10 September 2000; pp. 209–218. [Google Scholar]
- Zembaty, Z. Rockburst Induced Ground Motion-a Comparative Study. Soil Dyn. Earthq. Eng. 2004, 24, 11–23. [Google Scholar] [CrossRef]
- Kozłowska, M. Analysis of Spatial Distribution of Mining Tremors Occurring in Rudna Copper Mine (Poland). Acta Geophys. 2013, 61, 1156–1169. [Google Scholar] [CrossRef]
- Caputa, A.; Rudziński, Ł. Source Analysis of Post-Blasting Events Recorded in Deep Copper Mine, Poland. Pure Appl. Geophys. 2019, 176, 3451–3466. [Google Scholar] [CrossRef]
- Kozłowska, M.; Jamroz, M.; Olszewska, D. On the Aftershock Productivity in Mining-Induced Seismicity-Insight into Seismicity of Rudna Copper Ore Mine, Poland. Geophys. J. Int. 2021, 225, 1258–1270. [Google Scholar] [CrossRef]
- Kwiatek, G. A Search for Sequences of Mining-Induced Seismic Events at the Rudna Copper Mine in Poland. Acta Geophys. Pol. 2004, 52, 155–171. [Google Scholar]
- Owczarz, K.; Blachowski, J. Application of DInSAR and Spatial Statistics Methods in Analysis of Surface Displacements Caused by Induced Tremors. Appl. Sci. 2020, 10, 7660. [Google Scholar] [CrossRef]
- Milczarek, W. Investigation of Post Inducted Seismic Deformation of the 2016 Mw4.2 Tarnowek Poland Mining Tremor Based on DInSAR and SBAS Methods. Acta Geodyn. Geomater. 2019, 16, 183–193. [Google Scholar] [CrossRef]
- Tama, A.; Guzy, A.; Witkowski, W.; Hejmanowski, R.; Malinowska, A. Mapping Vertical Ground Movement Caused by Human-Induced Seismicity Applying Satellite Radar Interferometry and Geostatistics. In International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management; SGEM: Vienna, Austria, 2018; Volume 18, pp. 155–162. [Google Scholar] [CrossRef]
- Marcak, H.; Pilecki, Z. Assessment of the Subsidence Ratio Be Based on Seismic Noise Measurements in Mining Terrain. Arch. Min. Sci. 2019, 64, 197–212. [Google Scholar] [CrossRef]
- Ilieva, M.; Rudziński, Ł.; Pawłuszek-Filipiak, K.; Lizurek, G.; Kudłacik, I.; Tondaś, D.; Olszewska, D. Combined Study of a Significant Mine Collapse Based on Seismological and Geodetic Data-29 January 2019, Rudna Mine, Poland. Remote Sens. 2020, 12, 1570. [Google Scholar] [CrossRef]
- Owczarz, K.; Blachowski, J. Analysis of the Geometry of Surface Deformations Caused by Induced Tremors in the Area of Underground Copper Mining. In ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences; Copernicus GmbH: Göttingen, Germany, 2020; Volume 5, pp. 149–156. [Google Scholar] [CrossRef]
- Hejmanowski, R.; Malinowska, A.A.; Witkowski, W.T.; Guzy, A. An Analysis Applying InSAR of Subsidence Caused by Nearby Mining-Induced Earthquakes. Geosciences 2019, 9, 490. [Google Scholar] [CrossRef]
- Milczarek, W.; Kopeć, A.; Głąbicki, D.; Bugajska, N. Induced Seismic Events—Distribution of Ground Surface Displacements Based on InSAR Methods and Mogi and Yang Models. Remote Sens. 2021, 13, 1451. [Google Scholar] [CrossRef]
- Bugajska, N.J.; Milczarek, W.J. Remote Sensing Monitoring of Influence of Underground Mining in the Area of the S3 Express Road. IOP Conf. Ser. Earth Environ. Sci. 2021, 684, 012028. [Google Scholar] [CrossRef]
- Malinowska, A.A.; Witkowski, W.T.; Guzy, A.; Hejmanowski, R. Mapping Ground Movements Caused by Mining-Induced Earthquakes Applying Satellite Radar Interferometry. Eng. Geol. 2018, 246, 402–411. [Google Scholar] [CrossRef]
- Hejmanowski, R.; Witkowski, W.T.; Guzy, A.; Malinowska, A. Identification of the Ground Movements Caused by Mining-Induced Seismicity with the Satellite Interferometry. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 297–301. [Google Scholar] [CrossRef]
- Milczarek, W. Application of a Small Baseline Subset Time Series Method with Atmospheric Correction in Monitoring Results of Mining Activity on Ground Surface and in Detecting Induced Seismic Events. Remote Sens. 2019, 11, 1008. [Google Scholar] [CrossRef]
- Malinowska, A.; Hejmanowski, R.; Dai, H.Y. Ground Movements Modeling Applying Adjusted Influence Function. Int. J. Min. Sci. Technol. 2020, 30, 243–249. [Google Scholar] [CrossRef]
- Knothe, S. Equation of the Subsidence Profile. Arch. Min. Metall. 1953, 1, 22–38. [Google Scholar]
- Witkowski, W.T.; Hejmanowski, R. Software for Estimation of Stochastic Model Parameters for a Compacting Reservoir. Appl. Sci. 2020, 10, 3287. [Google Scholar] [CrossRef]
- European Space Agency. Open Access Hub. Available online: https://scihub.copernicus.eu/ (accessed on 16 July 2021).
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Pepe, A.; Calò, F. A Review of Interferometric Synthetic Aperture RADAR (InSAR) Multi-Track Approaches for the Retrieval of Earth’s Surface Displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef]
- Del Soldato, M.; Confuorto, P.; Bianchini, S.; Sbarra, P.; Casagli, N. Review of Works Combining GNSS and InSAR in Europe. Remote Sens. 2021, 13, 1684. [Google Scholar] [CrossRef]
- Hooper, A.J. A Multi-Temporal InSAR Method Incorporating Both Persistent Scatterer and Small Baseline Approaches. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Pawluszek-Filipiak, K.; Borkowski, A. Integration of DInSAR and SBAS Techniques to Determine Mining-Related Deformations Using Sentinel-1 Data: The Case Study of Rydułtowy Mine in Poland. Remote Sens. 2020, 12, 242. [Google Scholar] [CrossRef]
- Singh Virk, A.; Singh, A.; Mittal, S.K. Advanced MT-InSAR Landslide Monitoring: Methods and Trends. J. Remote Sens. GIS 2018, 7. [Google Scholar] [CrossRef]
- Mahmud, M.U.; Yakubu, T.A.; Oluwafemi, O.; Sousa, J.J.; Ruiz-Armenteros, A.M.; Arroyo-Parras, J.G.; Bakoň, M.; Lazecky, M.; Perissin, D. Application of Multi-Temporal Interferometric Synthetic Aperture Radar (MT-InSAR) Technique to Land Deformation Monitoring in Warri Metropolis, Delta State, Nigeria. In Procedia Computer Science; Elsevier B.V.: Amsterdam, The Netherlands, 2016; Volume 100, pp. 1220–1227. [Google Scholar] [CrossRef][Green Version]
- Devara, M.; Tiwari, A.; Dwivedi, R. Landslide Susceptibility Mapping Using MT-InSAR and AHP Enabled GIS-Based Multi-Criteria Decision Analysis. Geomat. Nat. Hazards Risk 2021, 12, 675–693. [Google Scholar] [CrossRef]
- Wu, S.; DIng, X.; Zhang, B. Continuous Monitoring the Ground Deformation by a Step-by-Step Estimator in MTInSAR. In International Geoscience and Remote Sensing Symposium (IGARSS); Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 1994–1997. [Google Scholar] [CrossRef]
- Gatsios, T.; Cigna, F.; Tapete, D.; Sakkas, V.; Pavlou, K.; Parcharidis, I. Copernicus Sentinel-1 MT-InSAR, GNSS and Seismic Monitoring of Deformation Patterns and Trends at the Methana Volcano, Greece. Appl. Sci. 2020, 10, 6445. [Google Scholar] [CrossRef]
- Luo, Q.; Zhou, G.; Perissin, D. Monitoring of Subsidence along Jingjin Inter-City Railway with High-Resolution TerraSAR-X MT-InSAR Analysis. Remote Sens. 2017, 9, 717. [Google Scholar] [CrossRef]
- Peng, M.M.; Zhao, C.Y.; Zhang, Q.; Zhang, J.; Liu, Y.Y. Ground Subsidence Monitoring with MT-InSAR and Mechanism Inversion over Xi’an, China. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives; International Society for Photogrammetry and Remote Sensing: Hannover, Germany, 2018; Volume 42, pp. 1375–1380. [Google Scholar] [CrossRef]
- Fatholahi, S.N.; He, H.; Wang, L.; Syed, A.; Li, J. Monitoring Surface Deformation over Oilfield Using MT-InSAR and Production Well Data. arXiv 2021, arXiv:2103.10985. [Google Scholar]
- Lanari, R.; Mora, O.; Manunta, M.; Mallorquí, J.J.; Berardino, P.; Sansosti, E. A Small-Baseline Approach for Investigating Deformations on Full-Resolution Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1377–1386. [Google Scholar] [CrossRef]
- Lanari, R.; Casu, F.; Manzo, M.; Zeni, G.; Berardino, P.; Manunta, M.; Pepe, A. An Overview of the Small BAseline Subset Algorithm: A DInSAR Technique for Surface Deformation Analysis. Pure Appl. Geophys. 2007, 164, 637–661. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witkowski, W.T.; Łukosz, M.; Guzy, A.; Hejmanowski, R. Estimation of Mining-Induced Horizontal Strain Tensor of Land Surface Applying InSAR. Minerals 2021, 11, 788. https://doi.org/10.3390/min11070788
Witkowski WT, Łukosz M, Guzy A, Hejmanowski R. Estimation of Mining-Induced Horizontal Strain Tensor of Land Surface Applying InSAR. Minerals. 2021; 11(7):788. https://doi.org/10.3390/min11070788
Chicago/Turabian StyleWitkowski, Wojciech T., Magdalena Łukosz, Artur Guzy, and Ryszard Hejmanowski. 2021. "Estimation of Mining-Induced Horizontal Strain Tensor of Land Surface Applying InSAR" Minerals 11, no. 7: 788. https://doi.org/10.3390/min11070788
APA StyleWitkowski, W. T., Łukosz, M., Guzy, A., & Hejmanowski, R. (2021). Estimation of Mining-Induced Horizontal Strain Tensor of Land Surface Applying InSAR. Minerals, 11(7), 788. https://doi.org/10.3390/min11070788








