Equation of State for Natural Almandine, Spessartine, Pyrope Garnet: Implications for Quartz-In-Garnet Elastic Geobarometry
Abstract
1. Introduction
2. Materials and Methods
Elastic Geobarometry
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Geller, S. Crystal chemistry of the garnets. In Zeitschrift fur Kristallographie—New Crystal Structures; De Gruyter: Berlin, Germany, 1967. [Google Scholar]
- Huang, S.; Chen, J. Equation of state of pyrope-almandine solid solution measured using a diamond anvil cell and in situ synchrotron X-ray diffraction. Phys. Earth Planet. Inter. 2014, 228, 88–91. [Google Scholar] [CrossRef]
- Wijbrans, C.H.; Rohrbach, A.; Klemme, S. An experimental investigation of the stability of majoritic garnet in the Earth’s mantle and an improved majorite geobarometer. Contrib. Mineral. Petrol. 2016, 50, 171. [Google Scholar] [CrossRef]
- Bosenick, A.; Dove, M.T.; Heine, V.; Geiger, C.A. Scaling of thermodynamic mixing properties in garnet solid solutions. Phys. Chem. Miner. 2001, 28, 177–187. [Google Scholar] [CrossRef]
- Ganguly, J.; Saxena, S.K. Mixing properties of aluminosilicate garnets: Constraints from natural and experimental data, and applications to geothermo- barometry: Clarifications. Am. Mineral. 1985, 70, 1320. [Google Scholar]
- Ganguly, J.; Cheng, W.; Tirone, M. Thermodynamics of aluminosilicate garnet solid solution: New experimental data, an optimized model, and thermometric applications. Contrib. Mineral. Petrol. 1996, 137–151, 126. [Google Scholar] [CrossRef]
- Bosenick, A.; Geiger, C.A.; Cemič, L. Heat capacity measurements of synthetic pyrope-grossular garnets between 320 and 1000 K by differential scanning calorimetry. Geochim. Cosmochim. Acta 1996, 17, 3215–3220. [Google Scholar] [CrossRef]
- Du, W.; Clark, S.M.; Walker, D. Excess mixing volume, microstrain, and stability of pyrope-grossular garnets. Am. Mineral. 2016, 60, 3215–3227. [Google Scholar] [CrossRef]
- Du, W.; Clark, S.M.; Walker, D. Thermo-compression of pyrope-grossular garnet solid solutions: Non-linear compositional dependence. Am. Mineral. 2015, 100, 215–222. [Google Scholar] [CrossRef]
- Milani, S.; Angel, R.J.; Scandolo, L.; Mazzucchelli, M.L.; Ballaran, T.B.; Klemme, S.; Domeneghetti, M.C.; Miletich, R.; Scheidl, K.S.; Derzsi, M.; et al. Thermo-elastic behavior of grossular garnet at high pressures and temperatures. Am. Mineral. 2017, 102, 851–859. [Google Scholar] [CrossRef]
- Zhang, L.; Ahsbahs, H.; Kutoglu, A.; Geiger, C.A. Single-crystal hydrostatic compression of synthetic pyrope, almandine, spessartine, grossular and andradite garnets at high pressures. Phys. Chem. Miner. 1999, 27, 52–58. [Google Scholar] [CrossRef]
- Zou, Y.; Gréaux, S.; Irifune, T.; Whitaker, M.L.; Shinmei, T.; Higo, Y. Thermal equation of state of Mg3Al2Si3O12 pyrope garnet up to 19 GPa and 1700 K. Phys. Chem. Miner. 2012, 39, 589–598. [Google Scholar] [CrossRef]
- Gréaux, S.; Yamada, A. P-V-T equation of state of Mn3Al2Si3O12 spessartine garnet. Phys. Chem. Miner. 2014, 41, 141–149. [Google Scholar] [CrossRef]
- Milani, S.; Nestola, F.; Alvaro, M.; Pasqual, D.; Mazzucchelli, M.L.; Domeneghetti, M.C.; Geiger, C.A. Diamond-garnet geobarometry: The role of garnet compressibility and expansivity. Lithos 2015, 227, 140–147. [Google Scholar] [CrossRef]
- Guiraud, M.; Powell, R. How well known are the thermodynamics of Fe-Mg-Ca garnet? Evidence from experimentally determined exchange equilibria. J. Metamorph. Geol. 1996, 14, 75–84. [Google Scholar] [CrossRef]
- Ungaretti, L.; Leona, M.; Merli, M.; Oberti, R. Non-ideal solid-solution in garnet: Crystal-structure evidence and modelling. Euro. J. Mineral. 1995, 7, 1299–1312. [Google Scholar] [CrossRef]
- Fan, D.W.; Zhou, W.G.; Liu, C.Q.; Liu, Y.G.; Wan, F.; Xing, Y.S.; Liu, J.; Bai, L.G.; Xie, H.S. The thermal equation of state of (Fe 0.86 Mg 0.07 Mn 0.07 ) 3 Al2Si3O12 almandine. Mineral. Mag. 2009, 73, 95–102. [Google Scholar] [CrossRef]
- Fan, D.; Xu, J.; Ma, M.; Liu, J.; Xie, H. P–V–T equation of state of spessartine–almandine solid solution measured using a diamond anvil cell and in situ synchrotron X-ray diffraction. Phys. Chem. Miner. 2015, 42, 63–72. [Google Scholar] [CrossRef]
- Sobolev, N.V.; Schertl, H.P.; Burchard, M.; Shatsky, V.S. An unusual pyrope-grossular garnet and its paragenesis from diamondiferous carbonate-silicate rocks of the Kokchetav massif, Kazakhstan. In Doklady Earth Sciences; Pleiades Publishing, Ltd.: New York, NY, USA, 2001. [Google Scholar]
- Geiger, C.A.; Feenstra, A. Molar volumes of mixing of almandine-pyrope and almandine-spessartine garnets and the crystal chemistry and thermodynamic-mixing properties of the aluminosilicate garnets. Am. Mineral. 1997, 82, 571–581. [Google Scholar] [CrossRef]
- Geiger, C.A.; Newton, R.C.; Kleppa, O.J. Enthalpy of mixing of synthetic almandine-grossular and almandine-pyrope garnets from high-temperature solution calorimetry. Geochim. Cosmochim. Acta 1987, 51, 1755–1763. [Google Scholar] [CrossRef]
- Geiger, C.A. Volumes of mixing in aluminosilicate garnets: Solid solution and strain behavior. Am. Mineral. 2000, 85, 893–897. [Google Scholar] [CrossRef]
- Thomas, J.B.; Spear, F.S. Experimental study of quartz inclusions in garnet at pressures up to 3.0 GPa: Evaluating validity of the quartz-in-garnet inclusion elastic thermobarometer. Contrib. Mineral. Petrol. 2018, 173, 1–14. [Google Scholar] [CrossRef]
- Angel, R.J.; Murri, M.; Mihailova, B.; Alvaro, M. Stress, strain and Raman shifts. In Zeitschrift fur Kristallographie—Crystalline Materials; De Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Angel, R.J.; Mazzucchelli, M.L.; Alvaro, M.; Nestola, F. EosFit-Pinc: A simple GUI for host-inclusion elastic thermobarometry. Am. Mineral. 2017, 102, 1957–1960. [Google Scholar] [CrossRef]
- Spear, F.S.; Thomas, J.B.; Hallett, B.W. Overstepping the garnet isograd: A comparison of QuiG barometry and thermodynamic modeling. Contrib. Mineral. Petrol. 2014, 168, 1059. [Google Scholar] [CrossRef]
- Kohn, M.J. “Thermoba-Raman-try”: Calibration of spectroscopic barometers and thermometers for mineral inclusions. Earth Planet. Sci. Lett. 2014, 388, 187–196. [Google Scholar] [CrossRef]
- Wolfe, O.M.; Spear, F.S. Determining the amount of overstepping required to nucleate garnet during Barrovian regional metamorphism, Connecticut Valley Synclinorium. J. Metamorph. Geol. 2018, 36, 79–94. [Google Scholar] [CrossRef]
- Zuza, A.V.; Levy, D.A.; Mulligan, S. Geologic field evidence for non-lithostatic overpressure recorded in the North American Cordillera hinterland, northeast Nevada. Geosci. Front. 2020. [Google Scholar] [CrossRef]
- Schmidt, C.; Ziemann, M.A. In-situ Raman spectroscopy of quartz: A pressure sensor for hydrothermal diamond-anvil cell experiments at elevated temperatures. Am. Mineral. 2000, 85, 1725–1734. [Google Scholar] [CrossRef]
- Bonazzi, M.; Tumiati, S.; Thomas, J.B.; Angel, R.J.; Alvaro, M. Assessment of the reliability of elastic geobarometry with quartz inclusions. Lithos 2019, 350–351, 105201. [Google Scholar] [CrossRef]
- Moulas, E.; Kostopoulos, D.; Podladchikov, Y.; Chatzitheodoridis, E.; Schenker, F.L.; Zingerman, K.M.; Pomonis, P.; Tajčmanová, L. Calculating pressure with elastic geobarometry: A comparison of different elastic solutions with application to a calc-silicate gneiss from the Rhodope Metamorphic Province. Lithos 2020, 378–379, 105803. [Google Scholar] [CrossRef]
- Kelly, E.D.; Hoisch, T.D.; Wells, M.L.; Vervoort, J.D.; Beyene, M.A. An Early Cretaceous garnet pressure–temperature path recording synconvergent burial and exhumation from the hinterland of the Sevier orogenic belt, Albion Mountains, Idaho. Contrib. Mineral. Petrol. 2015, 20, 170. [Google Scholar] [CrossRef]
- Kantor, I.; Prakapenka, V.; Kantor, A.; Dera, P.; Kurnosov, A.; Sinogeikin, S.; Dubrovinskaia, N.; Dubrovinsky, L. BX90: A new diamond anvil cell design for X-ray diffraction and optical measurements. Rev. Sci. Instrum. 2012, 83, 125102. [Google Scholar] [CrossRef]
- Klotz, S.; Chervin, J.C.; Munsch, P.; Le Marchand, G. Hydrostatic limits of 11 pressure transmitting media. J. Phys. D Appl. Phys. 2009, 42, 075413. [Google Scholar] [CrossRef]
- Syassen, K. Ruby under pressure. High Press. Res. 2008, 28, 75–126. [Google Scholar] [CrossRef]
- Matsui, M. High temperature and high pressure equation of state of gold. J. Phys. 2010, 215, 012197. [Google Scholar] [CrossRef]
- Prakapenka, V.B.; Kubo, A.; Kuznetsov, A.; Laskin, A.; Shkurikhin, O.; Dera, P.; Rivers, M.L.; Sutton, S.R. Advanced flat top laser heating system for high pressure research at GSECARS: Application to the melting behavior of germanium. High Press. Res. 2008, 28, 225–235. [Google Scholar] [CrossRef]
- Agilent. CrysAlisPro Data Collection and Processing Software for Agilent X-ray Diffractometers; Technologies UK Ltd.: Oxford, UK, 2014. [Google Scholar]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300∘K. J. Geophys. Res. 1978, 83, 1257–1268. [Google Scholar] [CrossRef]
- Angel, R.J.; Gonzalez-Platas, J.; Alvaro, M. EosFit7c and a Fortran module (library) for equation of state calculations. Z. Krist. 2014, 229, 405–419. [Google Scholar] [CrossRef]
- Isaak, D.G.; Anderson, O.L.; Oda, H. High-temperature thermal expansion and elasticity of calcium-rich garnets. Phys. Chem. Miner. 1992, 19, 106–120. [Google Scholar] [CrossRef]
- Wojdyr, M. Fityk: A general-purpose peak fitting program. J. Appl. Crystallogr. 2010, 43, 1120–1128. [Google Scholar] [CrossRef]
- Mazzucchelli, M.L.; Angel, R.J.; Alvaro, M. EntraPT: An online platform for elastic geothermobarometry. Am. Mineral. 2020, 106, 830–837. [Google Scholar] [CrossRef]
- Johnson, T.A.; Cottle, J.M.; Larson, K.P. Delineation of multiple metamorphic events in the Himalayan Kathmandu Complex, central Nepal. J. Metamorph. Geol. 2020, 39, 443–472. [Google Scholar] [CrossRef]
- Angel, R.J.; Alvaro, M.; Miletich, R.; Nestola, F. A simple and generalised P–T–V EoS for continuous phase transitions, implemented in EosFit and applied to quartz. Contrib. Mineral. Petrol. 2017, 29, 172. [Google Scholar] [CrossRef]
- Holland, T.; Powell, R. An enlarged and updated internally consistent thermodynamic dataset with uncertainties and correlations: The system K2O-Na2O-CaO-MgO-MnO-FeO-Fe2O3-Al2O3-TiO2-SiO2-C-H2-O2. J. Metamorph. Geol. 1990, 8, 89–124. [Google Scholar] [CrossRef]
- Hodges, K.V.; Spear, F.S. Geothermometry, geobarometry and the Al2SiO5 triple point at Mt. Moosilauke, New Hampshire. Am. Mineral. 1982, 67, 1118–1134. [Google Scholar]
- Hoisch, T.D. Equilibria within the mineral assemblage quartz + muscovite + biotite + garnet + plagioclase, and implications for the mixing properties of octahedrally-coordinated cations in muscovite and biotite. Contrib. Mineral. Petrol. 1991, 108, 43–54. [Google Scholar] [CrossRef]
- Holdaway, M.J. Application of new experimental and garnet Margules data to the garnet-biotite geothermometer. Am. Mineral. 2000, 85, 881–892. [Google Scholar] [CrossRef]
- Shen, G.; Wang, Y.; Dewaele, A.; Wu, C.; Fratanduono, D.E.; Eggert, J.; Klotz, S.; Dziubek, K.F.; Loubeyre, P.; Fat’yanov, O.V.; et al. Toward an international practical pressure scale: A proposal for an IPPS ruby gauge (IPPS-Ruby2020). High Press. Res. 2020, 40, 299–314. [Google Scholar] [CrossRef]
- Enami, M. Influence of garnet hosts on the raman spectra of quartz inclusions. J. Mineral. Petrol. Sci. 2012, 107, 173–180. [Google Scholar] [CrossRef]
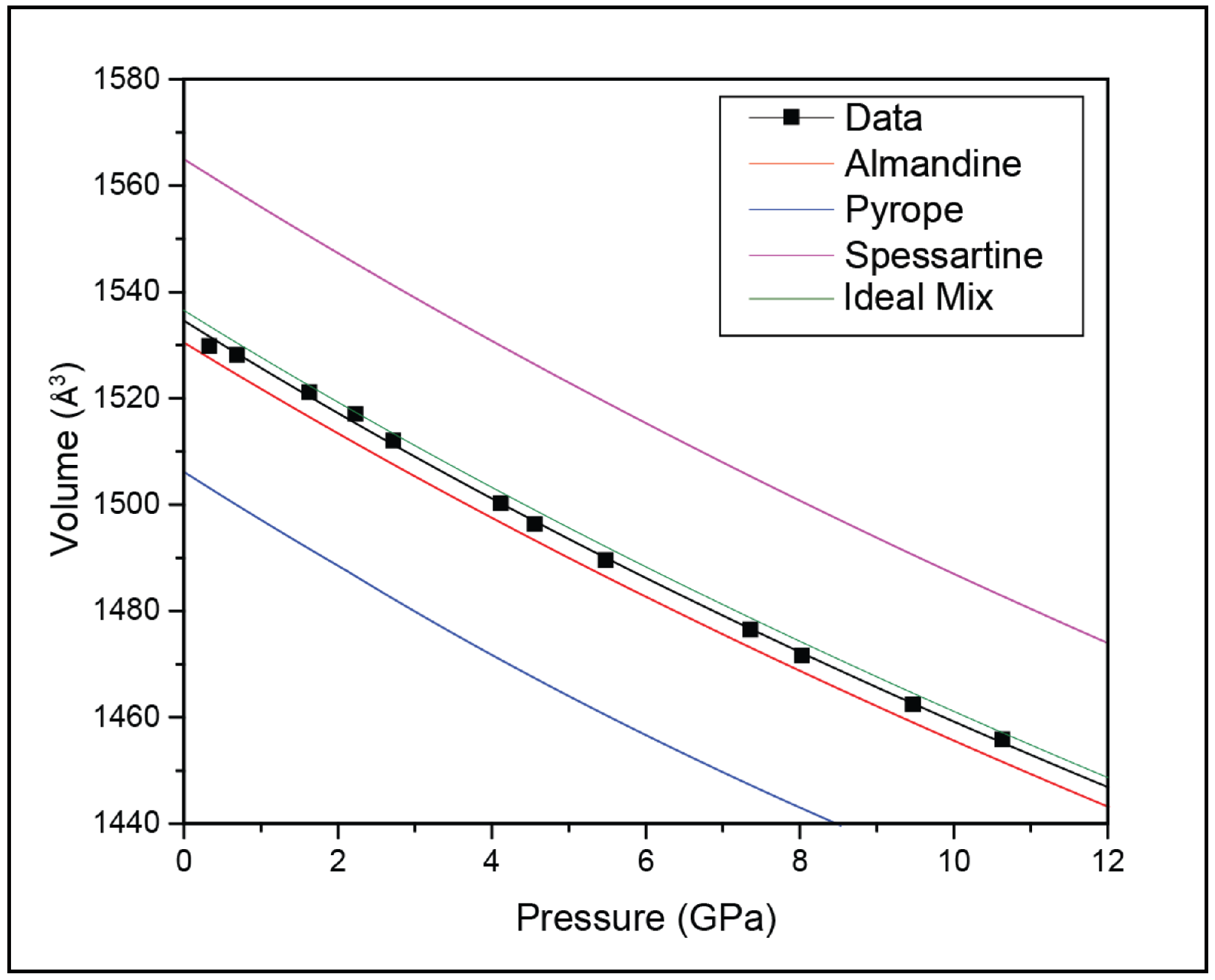
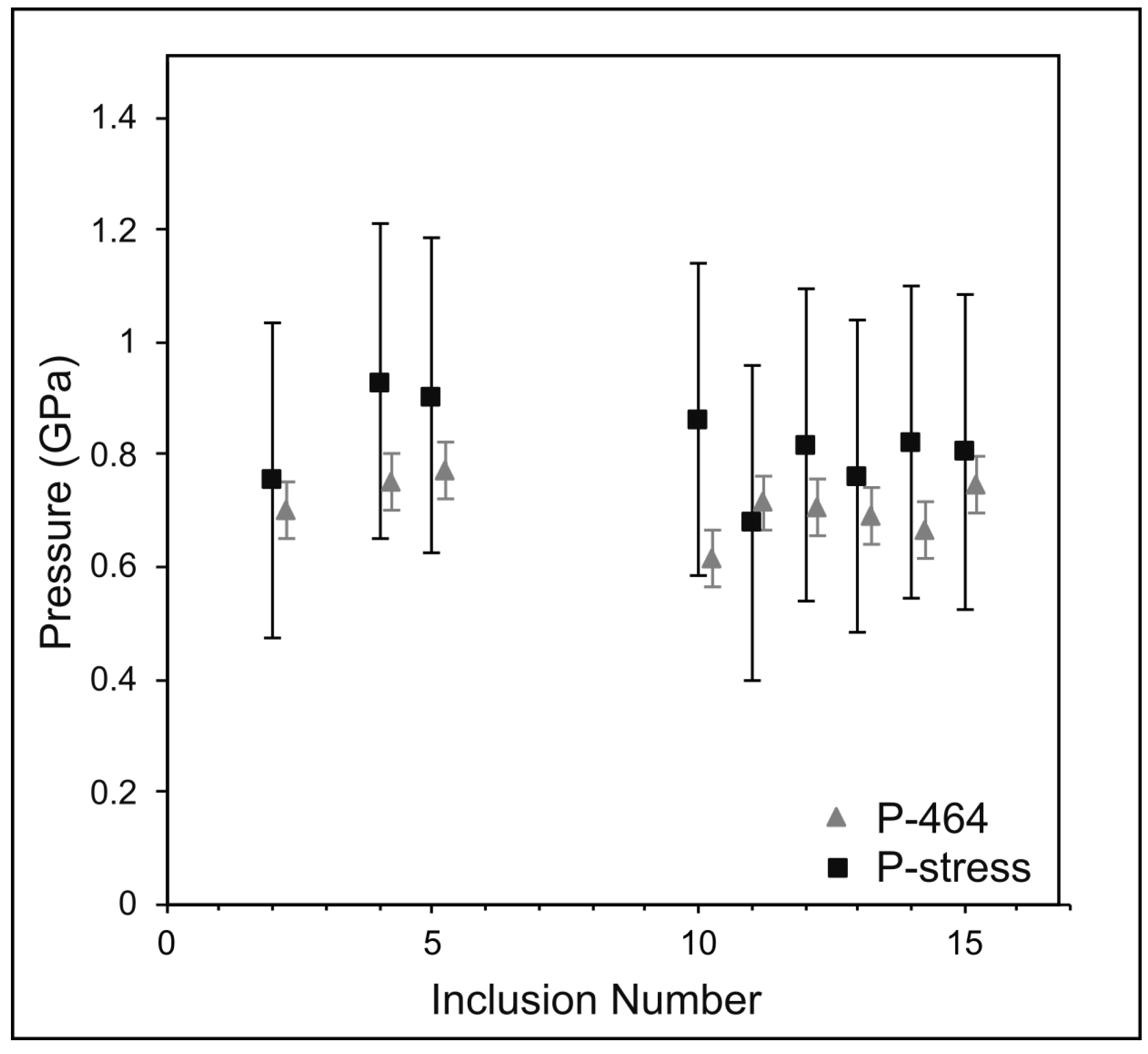
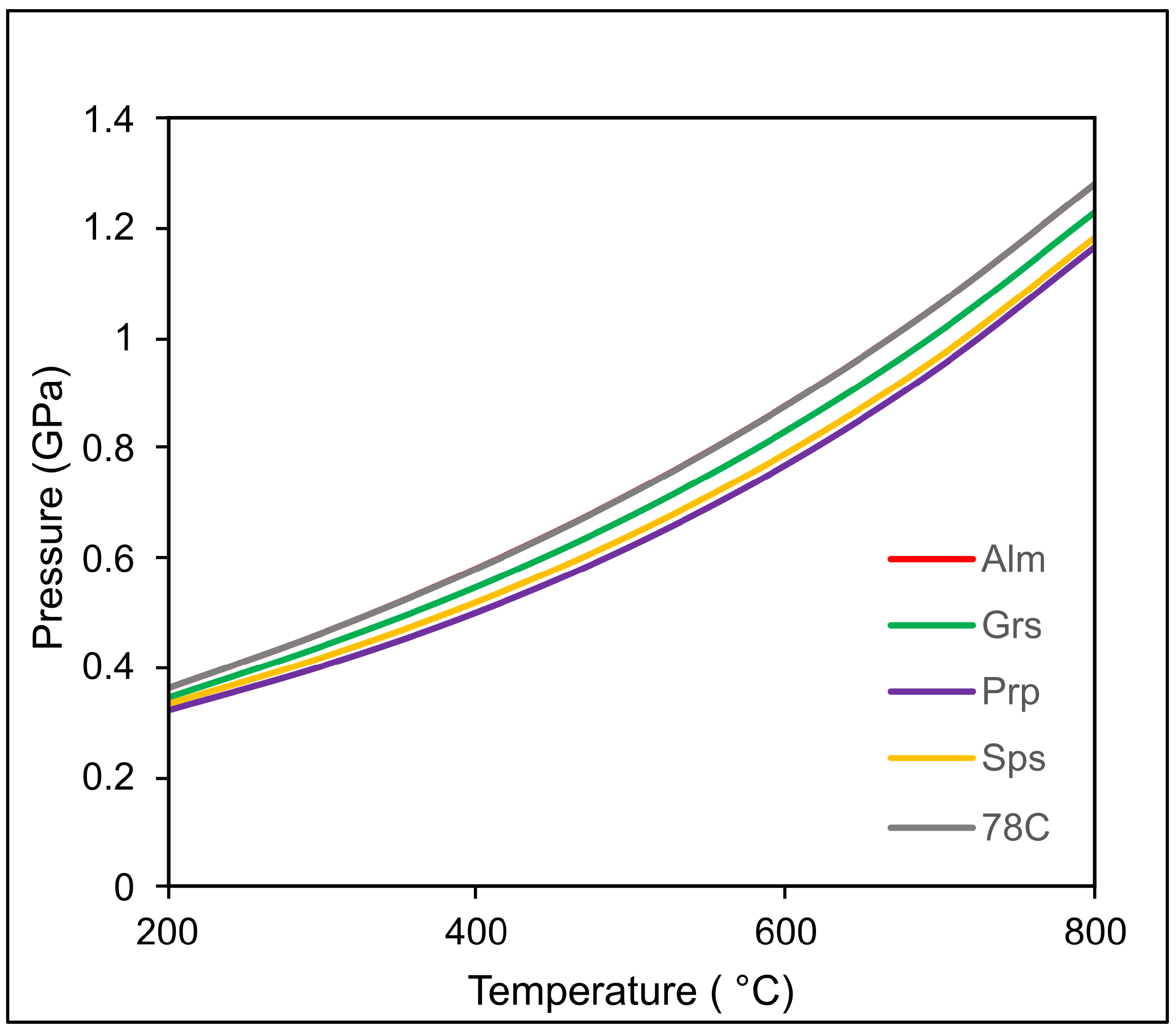
| P (GPa) | a(Å) | V(Å3) |
|---|---|---|
| 0.33 | 11.5225 (5) | 1529.82 (12) |
| 0.69 | 11.5182 (5) | 1528.12 (13) |
| 1.63 | 11.5007 (5) | 1521.13 (11) |
| 2.23 | 11.4903 (5) | 1517.03 (12) |
| 2.72 | 11.4777 (4) | 1512.03 (10) |
| 4.12 | 11.4478 (4) | 1500.26 (9) |
| 4.56 | 11.4378 (5) | 1496.34 (12) |
| 5.48 | 11.4206 (3) | 1489.58 (8) |
| 7.36 | 11.3870 (5) | 1476.49 (11) |
| 8.03 | 11.3744 (3) | 1471.58 (7) |
| 9.47 | 11.3508 (3) | 1462.46 (6) |
| 10.63 | 11.3337 (3) | 1455.84 (7) |
| Garnet | (GPa) | (Å3) | |
|---|---|---|---|
| Alm 1 [14] | 172.6 (1.5) | 5.8 (5) | 1530.48 (10) |
| Sps 1 [13] | 171 (4) | 5.3 (8) | 1564.70 (11) |
| Prp 1 [14] | 163.7 (1.7) | 6.4 (4) | 1506.15 (16) |
| Grs 1 [10] | 166.6 (2) | 4.96 (7) | 1664.46 (5) |
| Alm 2 [11] | 185 (3) | 4.2 (3) | 1528.63 (8) |
| Sps 2 [11] | 189 (1) | 4.2 | 1563.64 (8) |
| Prp 2 [11] | 171 (2) | 4.4 (2) | - |
| Grs 2 [11] | 175 (1) | 4.4 | 1660.22 (8) |
| This Study | 172.0 (57) | 6.2 (16) | 1534.59 (8) |
| V-ideal | 171.3 (14) | 5.8 (5) | 1536.52 (11) |
| Incl. | P-Alm | P-Grs | P-Prp | P-Sps | P-Mix | P-Tot | P-464 |
|---|---|---|---|---|---|---|---|
| G3-10 | 0.862 | 0.818 | 0.761 | 0.778 | 0.840 | 0.863 | 0.614 |
| G3-05 | 0.904 | 0.859 | 0.802 | 0.820 | 0.882 | 0.905 | 0.772 |
| G3-02 | 0.755 | 0.714 | 0.658 | 0.677 | 0.734 | 0.755 | 0.700 |
| G3-13 | 0.762 | 0.721 | 0.665 | 0.683 | 0.741 | 0.762 | 0.693 |
| G3-12 | 0.818 | 0.776 | 0.718 | 0.736 | 0.796 | 0.818 | 0.705 |
| G3-11 | 0.679 | 0.644 | 0.584 | 0.604 | 0.659 | 0.679 | 0.714 |
| G3-14 | 0.822 | 0.780 | 0.723 | 0.740 | 0.800 | 0.822 | 0.664 |
| G3-04 | 0.930 | 0.883 | 0.828 | 0.846 | 0.907 | 0.930 | 0.753 |
| G3-15 | 0.806 | 0.764 | 0.707 | 0.726 | 0.784 | 0.806 | 0.745 |
| Incl. | 207 (cm−1) | 464 (cm−1) | d207 (cm−1) | d464 (cm−1) | e1 | e1 + e2 | e3 | P207 (GPa) | P464 (GPa) | Pstress (GPa) |
|---|---|---|---|---|---|---|---|---|---|---|
| G3-10 | 209.14 | 465.03 | 2.47 | −0.10 | 0.0065 | −0.0129 | 0.00668 | 0.081 | −0.011 | 0.164 |
| G3-05 | 210.33 | 466.05 | 3.65 | 0.92 | 0.0045 | −0.0090 | 0.00285 | 0.122 | 0.102 | 0.192 |
| G3-02 | 208.43 | 465.61 | 1.76 | 0.48 | 0.0020 | −0.0040 | 0.00114 | 0.057 | 0.053 | 0.091 |
| G3-13 | 208.51 | 465.57 | 1.84 | 0.44 | 0.0024 | −0.0047 | 0.00160 | 0.060 | 0.049 | 0.096 |
| G3-12 | 209.12 | 465.64 | 2.45 | 0.51 | 0.0035 | −0.0070 | 0.00259 | 0.080 | 0.057 | 0.134 |
| G3-11 | 210.09 | 465.69 | 3.41 | 0.56 | 0.0057 | −0.0113 | 0.00467 | 0.114 | 0.062 | 0.038 |
| G3-14 | 208.98 | 465.37 | 2.31 | 0.24 | 0.0045 | −0.0089 | 0.00405 | 0.076 | 0.027 | 0.137 |
| G3-04 | 210.23 | 466.23 | 3.55 | 0.81 | 0.0066 | −0.0132 | 0.00588 | 0.118 | 0.090 | 0.209 |
| G3-15 | 209.22 | 465.88 | 2.55 | 0.76 | 0.0026 | −0.0051 | 0.00122 | 0.084 | 0.084 | 0.126 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mulligan, S.R.; Stavrou, E.; Chariton, S.; Tschauner, O.; Salamat, A.; Wells, M.L.; Smith, A.G.; Hoisch, T.D.; Prakapenka, V. Equation of State for Natural Almandine, Spessartine, Pyrope Garnet: Implications for Quartz-In-Garnet Elastic Geobarometry. Minerals 2021, 11, 458. https://doi.org/10.3390/min11050458
Mulligan SR, Stavrou E, Chariton S, Tschauner O, Salamat A, Wells ML, Smith AG, Hoisch TD, Prakapenka V. Equation of State for Natural Almandine, Spessartine, Pyrope Garnet: Implications for Quartz-In-Garnet Elastic Geobarometry. Minerals. 2021; 11(5):458. https://doi.org/10.3390/min11050458
Chicago/Turabian StyleMulligan, Suzanne R., Elissaios Stavrou, Stella Chariton, Oliver Tschauner, Ashkan Salamat, Michael L. Wells, Alexander G. Smith, Thomas D. Hoisch, and Vitali Prakapenka. 2021. "Equation of State for Natural Almandine, Spessartine, Pyrope Garnet: Implications for Quartz-In-Garnet Elastic Geobarometry" Minerals 11, no. 5: 458. https://doi.org/10.3390/min11050458
APA StyleMulligan, S. R., Stavrou, E., Chariton, S., Tschauner, O., Salamat, A., Wells, M. L., Smith, A. G., Hoisch, T. D., & Prakapenka, V. (2021). Equation of State for Natural Almandine, Spessartine, Pyrope Garnet: Implications for Quartz-In-Garnet Elastic Geobarometry. Minerals, 11(5), 458. https://doi.org/10.3390/min11050458







