Improving the Flocculation Performance of Clay-Based Tailings in Seawater: A Population Balance Modelling Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Seawater Treatment
2.3. Flocculation Tests
2.4. PBM Modelling
- The first and second terms describe the aggregate formation of size from smaller aggregates.
- The third and fourth terms describe the aggregation death of size to higher aggregates.
- The fifth term represents the breakage formation of size from the rupture of a higher aggregate.
- The sixth term represents the breakage death of size by creating smaller aggregates.
- The superscript max1 is the maximum number of intervals used to represent the complete aggregate size spectrum; max2 corresponds to the largest interval from which the aggregates in the current range are produced.
2.4.1. Aggregation Kernel
2.4.2. Breakage Kernel
2.4.3. Model Expressions
2.4.4. Model Optimisation
3. Results
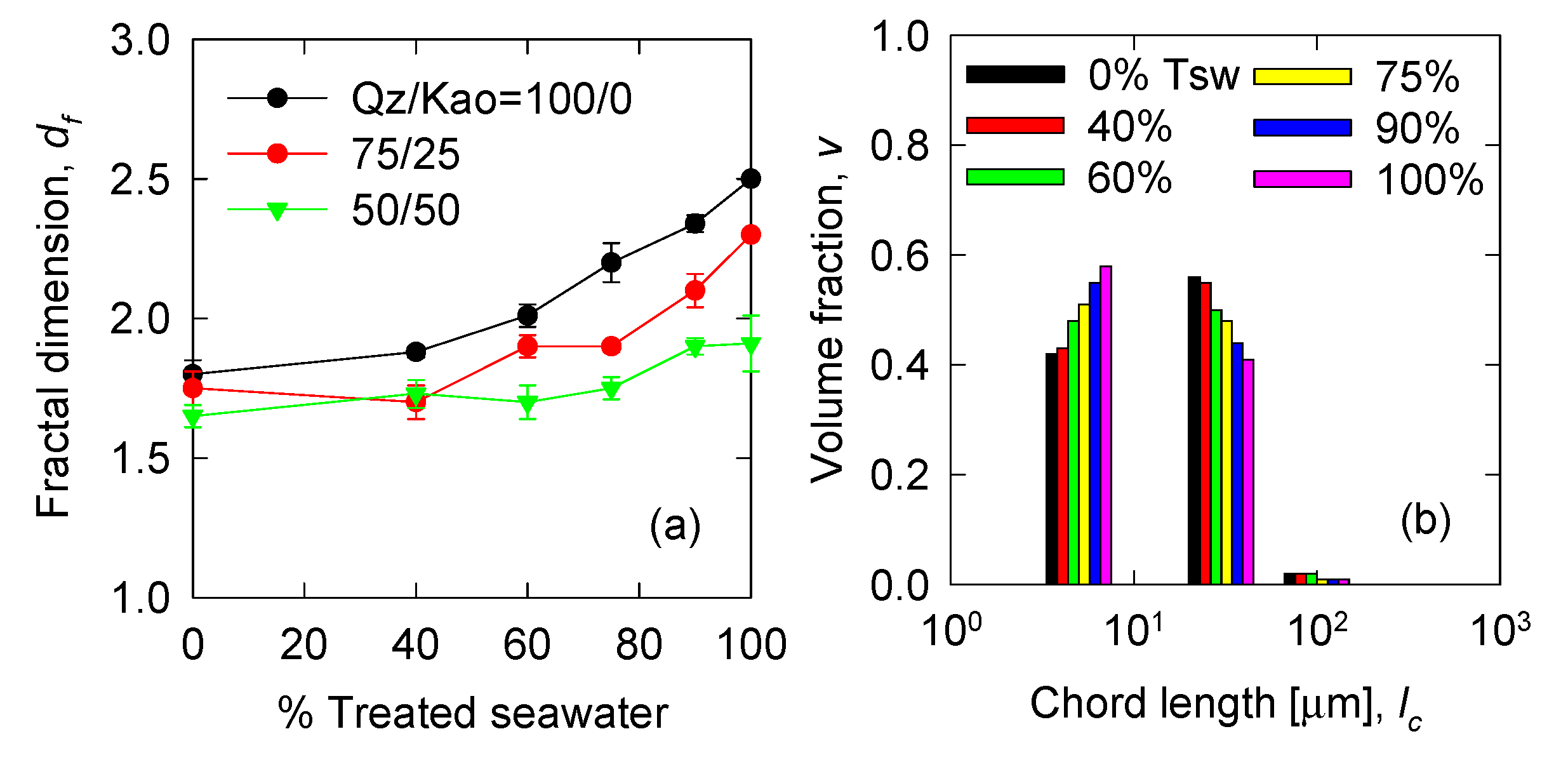
3.1. Fractal Dimension and Initial Volume Distribution
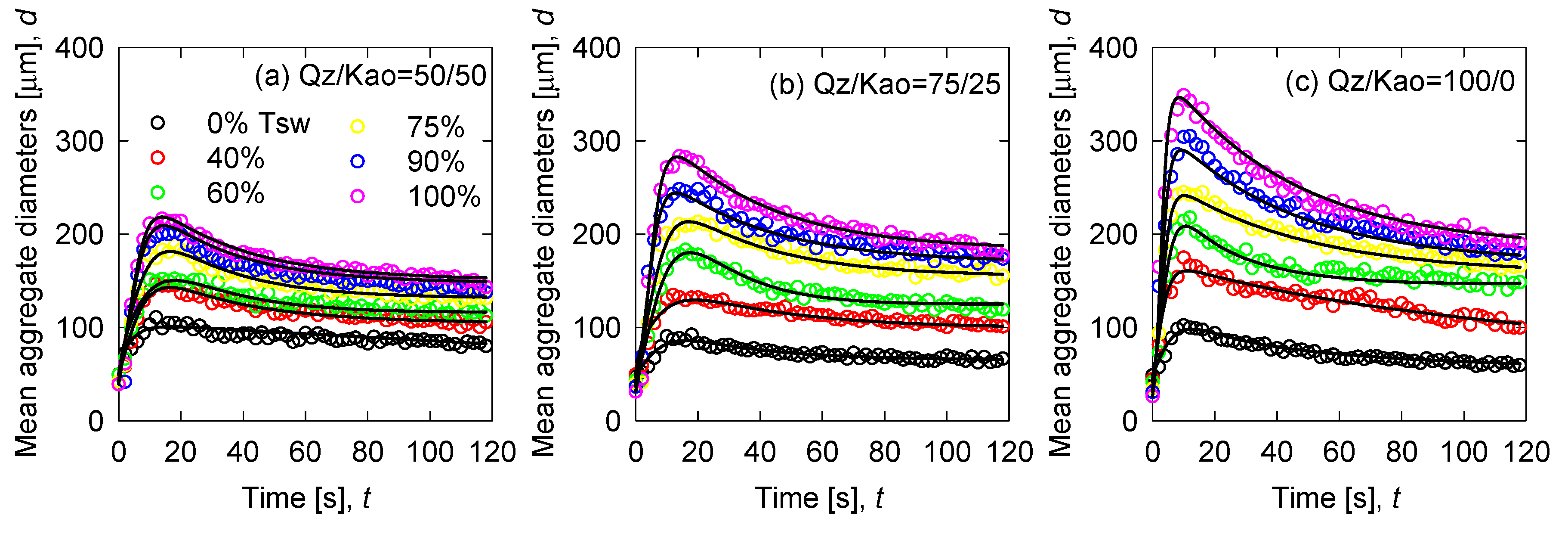
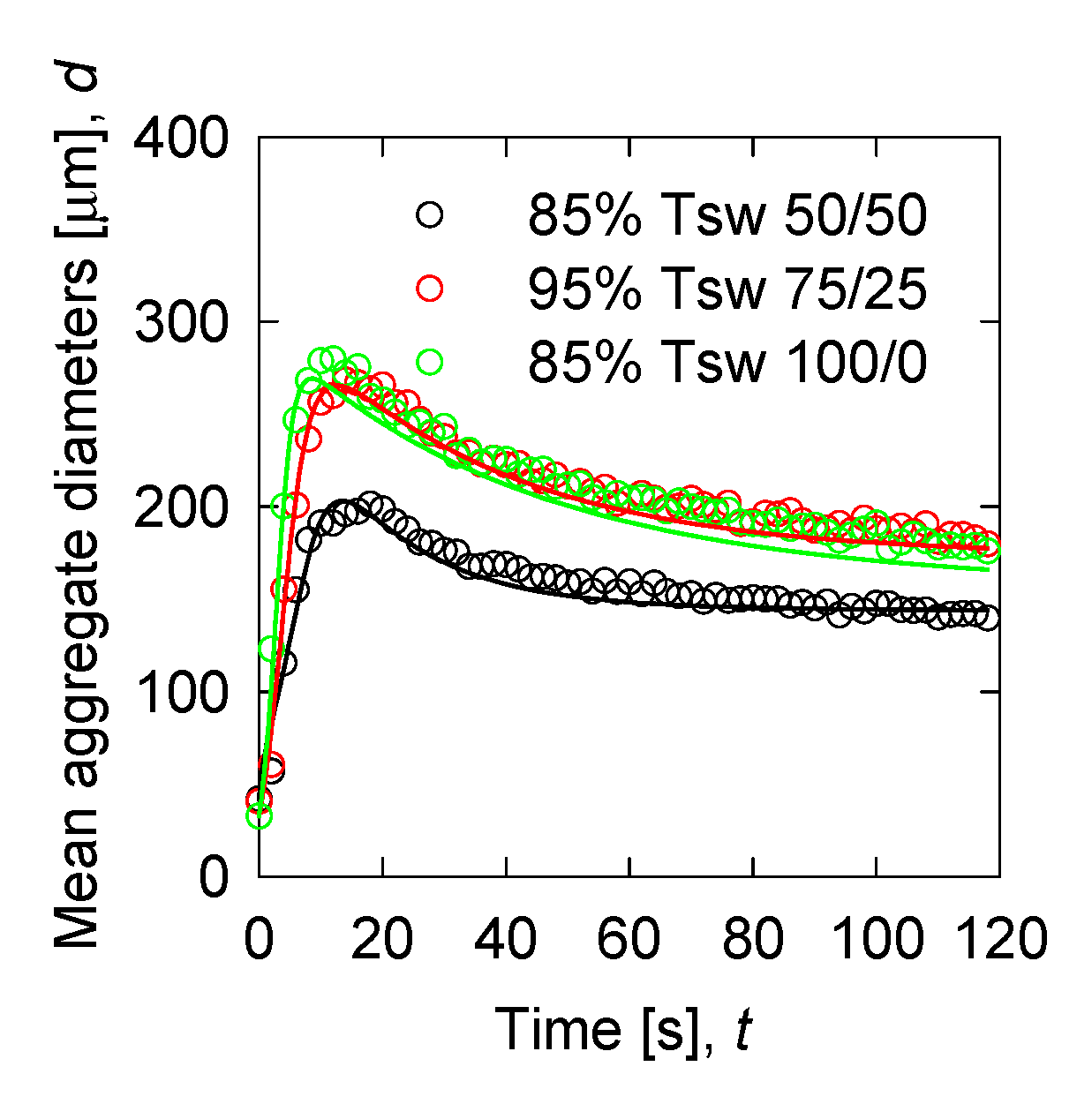
3.2. Flocculation Kinetics
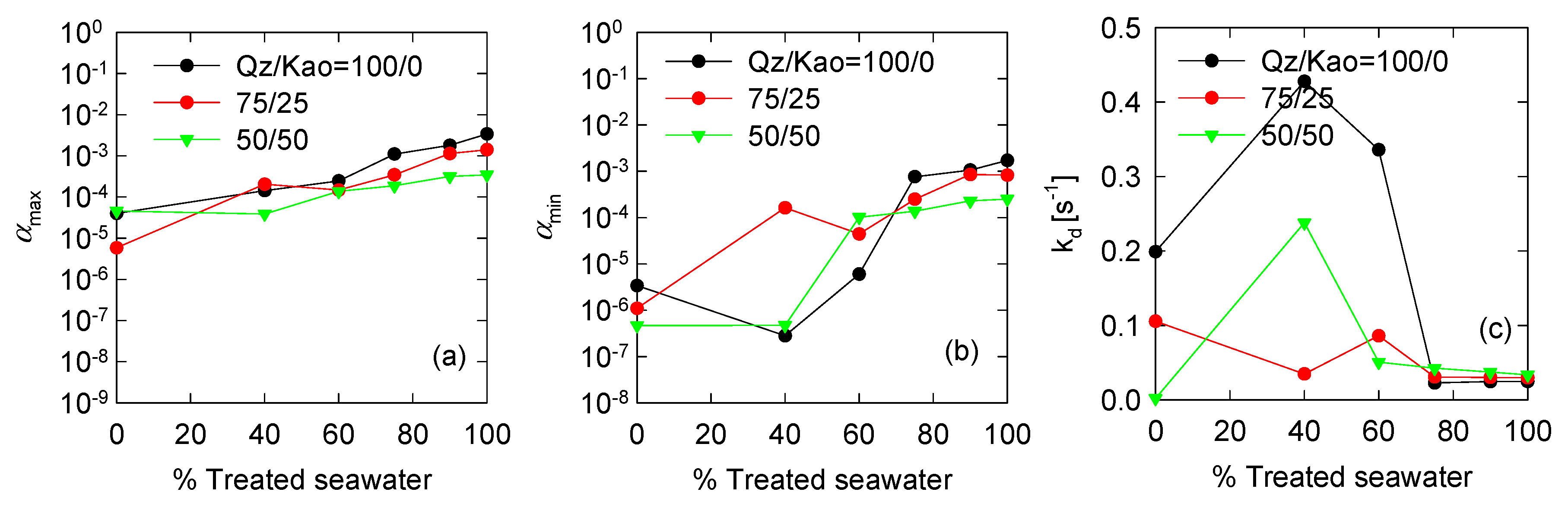
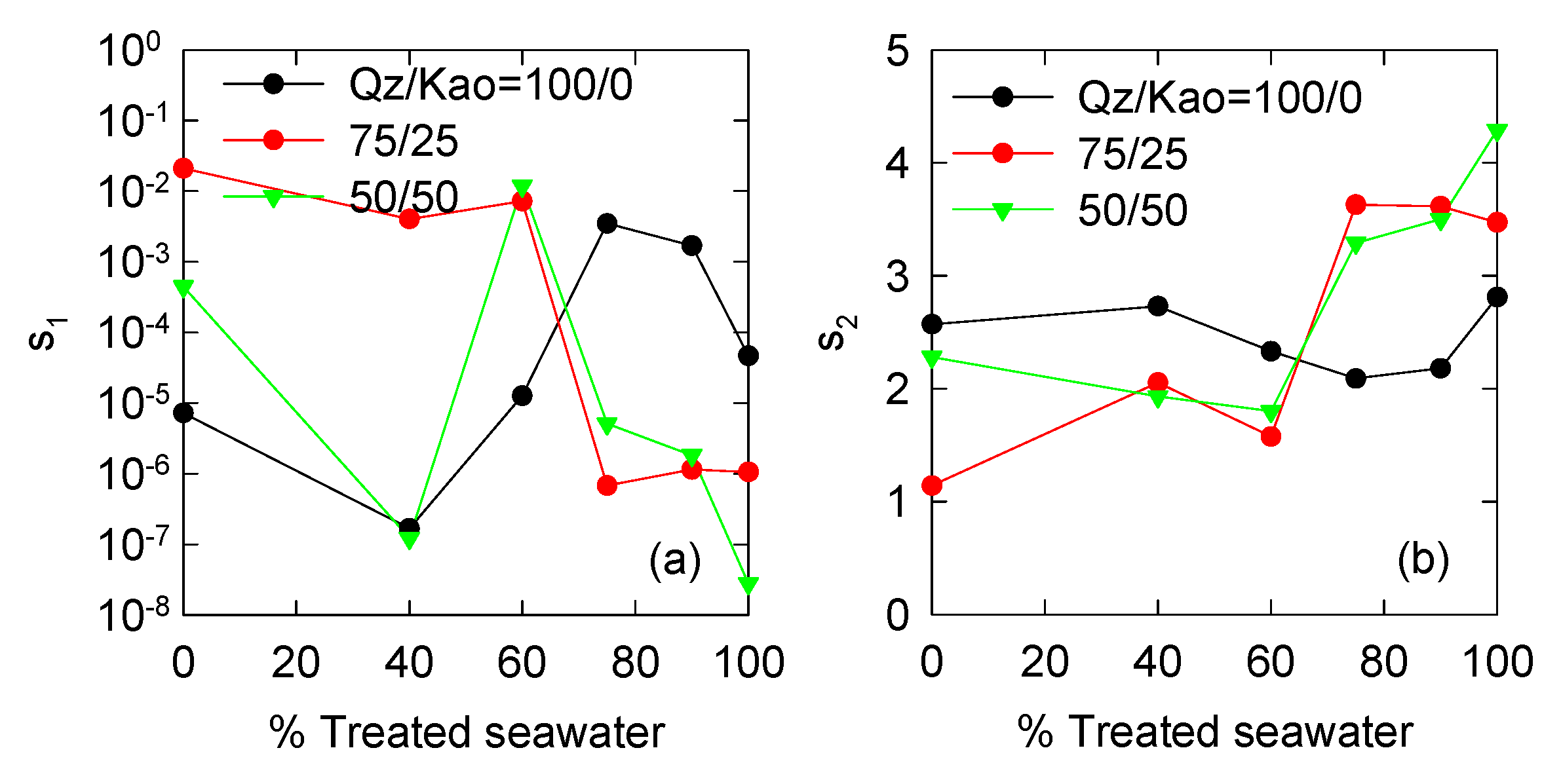
3.3. Optimized PBM Model Parameters
3.4. Physical Parameters Calculations
3.5. Modelling Validation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Northey, S.A.; Mudd, G.M.; Saarivuori, E.; Wessman-Jääskeläinen, H.; Haque, N. Water footprinting and mining: Where are the limitations and opportunities? J. Clean. Prod. 2016, 135, 1098–1116. [Google Scholar] [CrossRef]
- Wang, C.; Harbottle, D.; Liu, Q.; Xu, Z. Current state of fine mineral tailings treatment: A critical review on theory and practice. Miner. Eng. 2014, 58, 113–131. [Google Scholar] [CrossRef]
- de Kretser, R.; Scales, P.J.; Boger, D.V. Improving clay-based tailings disposal: Case study on coal tailings. AIChE J. 1997, 43, 1894–1903. [Google Scholar] [CrossRef]
- Cisternas, L.A.; Gálvez, E.D. The use of seawater in mining. Miner. Process. Extr. Metall. Rev. 2018, 39, 18–33. [Google Scholar] [CrossRef]
- Belessiotis, V.; Kalogirou, S.; Delyannis, E.; Belessiotis, V.; Kalogirou, S.; Delyannis, E. Water, the raw material for desalination. Therm. Sol. Desalin. 2016, 21–102. [Google Scholar] [CrossRef]
- Sadhwani, J.J.; Veza, J.M.; Santana, C. Case studies on environmental impact of seawater desalination. Desalination 2005, 185, 1–8. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Forbes, L.; Cisternas, L.A. Effect of seawater on sulfide ore flotation: A review. Miner. Process. Extr. Metall. Rev. 2016, 37, 369–384. [Google Scholar] [CrossRef]
- Hernández, P.; Taboada, M.; Herreros, O.; Graber, T.; Ghorbani, Y. Leaching of chalcopyrite in acidified nitrate using seawater-based media. Minerals 2018, 8, 238. [Google Scholar] [CrossRef]
- Cornejo, P.K.; Santana, M.V.E.; Hokanson, D.R.; Mihelcic, J.R.; Zhang, Q. Carbon footprint of water reuse and desalination: A review of greenhouse gas emissions and estimation tools. J. Water Reuse Desalin. 2014, 4, 238–252. [Google Scholar] [CrossRef]
- Cambridge, M.L.; Zavala-Perez, A.; Cawthray, G.R.; Statton, J.; Mondon, J.; Kendrick, G.A. Effects of desalination brine and seawater with the same elevated salinity on growth, physiology and seedling development of the seagrass posidonia australis. Mar. Pollut. Bull. 2019, 140, 462–471. [Google Scholar] [CrossRef]
- Israelachvili, J. Intermolecular and Surface Forces, 3rd ed.; Elsevier: Santa Barbara, CA, USA, 2011; ISBN 9780123919274. [Google Scholar]
- Qiu, Z.; Liu, G.; Liu, Q.; Zhong, H. Understanding the roles of high salinity in inhibiting the molybdenite flotation. Colloids Surf. A Physicochem. Eng. Asp. 2016, 509, 123–129. [Google Scholar] [CrossRef]
- Li, W.; Li, Y.; Wei, Z.; Xiao, Q.; Song, S. Fundamental studies of shmp in reducing negative effects of divalent ions on molybdenite flotation. Minerals 2018, 8, 404. [Google Scholar] [CrossRef]
- Ramos, J.; Leiva, W.H.; Castillo, C.; Ihle, C.F.; Fawell, P.D.; Jeldres, R.I. Seawater flocculation of clay-based mining tailings: Impact of calcium and magnesium precipitation. Miner. Eng. 2020, 154, 106417. [Google Scholar] [CrossRef]
- Jeldres, M.; Piceros, E.C.; Toro, N.; Robles, P.; Nieto, S.; Quezada, G.R.; Jeldres, R.I. Enhancing the sedimentation of clay-based tailings in seawater by magnesium removal treatment. Sep. Purif. Technol. 2020, 116762. [Google Scholar] [CrossRef]
- Castellón, C.I.; Piceros, E.C.; Toro, N.; Robles, P.; López-Valdivieso, A.; Jeldres, R.I. Depression of pyrite in seawater flotation by guar gum. Metals 2020, 10, 239. [Google Scholar] [CrossRef]
- Arias, D.; Villca, G.; Pánico, A.; Cisternas, L.A.; Jeldres, R.I.; González-Benito, G.; Rivas, M. Partial desalination of seawater for mining processes through a fluidized bed bioreactor filled with immobilized cells of bacillus subtilis LN8B. Desalination 2020, 482, 114388. [Google Scholar] [CrossRef]
- Biggs, C.A.; Lant, P.A. Activated sludge flocculation: On-line determination of floc size and the effect of shear. Water Res. 2000, 34, 2542–2550. [Google Scholar] [CrossRef]
- Heath, A.R.; Fawell, P.D.; Bahri, P.A.; Swift, J.D. Estimating average particle size by focused beam reflectance measurement (FBRM). Part. Part. Syst. Charact. 2002, 19, 84. [Google Scholar] [CrossRef]
- Heath, A.R.; Bahri, P.A.; Fawell, P.D.; Farrow, J.B. Polymer flocculation of calcite: Experimental results from turbulent pipe flow. AIChE J. 2006, 52, 1284–1293. [Google Scholar] [CrossRef]
- Owen, A.T.; Fawell, P.D.; Swift, J.D.; Labbett, D.M.; Benn, F.A.; Farrow, J.B. Using turbulent pipe flow to study the factors affecting polymer-bridging flocculation of mineral systems. Int. J. Miner. Process. 2008, 87, 90–99. [Google Scholar] [CrossRef]
- Nguyen, T.; Farrow, J.; Smith, J.; Fawell, P. Design and development of a novel thickener feedwell using computational fluid dynamics. J. South. Afr. Inst. Min. Metall. 2012, 112, 105–119. [Google Scholar]
- Ebrahimzadeh Gheshlaghi, M.; Soltani Goharrizi, A.; Aghajani Shahrivar, A. Simulation of a semi-industrial pilot plant thickener using CFD approach. Int. J. Min. Sci. Technol. 2013, 23, 63–68. [Google Scholar] [CrossRef]
- Von Smoluchowski, M. Versuch einer mathematischen theorie der koagulationskinetik kolloider Lösungen. Z. Phys. Chem. 1917. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Fawell, P.D.; Florio, B.J. Population balance modelling to describe the particle aggregation process: A review. Powder Technol. 2018, 326, 190–207. [Google Scholar] [CrossRef]
- Thomas, D.N.; Judd, S.J.; Fawcett, N. Flocculation modelling: A review. Water Res. 1999, 33, 1579–1592. [Google Scholar] [CrossRef]
- Selomulya, C.; Bushell, G.; Amal, R.; Waite, T.D. Understanding the role of restructuring in flocculation: The application of a population balance model. Chem. Eng. Sci. 2003, 58, 327–338. [Google Scholar] [CrossRef]
- Antunes, E.; Garcia, F.A.P.; Ferreira, P.; Blanco, A.; Negro, C.; Rasteiro, M.G. Modelling PCC flocculation by bridging mechanism using population balances: Effect of polymer characteristics on flocculation. Chem. Eng. Sci. 2010, 65, 3798–3807. [Google Scholar] [CrossRef]
- Heath, A.R.; Bahri, P.A.; Fawell, P.D.; Farrow, J.B. Polymer flocculation of calcite: Population balance model. AIChE J. 2006, 52, 1641–1653. [Google Scholar] [CrossRef]
- Vajihinejad, V.; Soares, J.B.P. Monitoring polymer flocculation in oil sands tailings: A population balance model approach. Chem. Eng. J. 2018, 346, 447–457. [Google Scholar] [CrossRef]
- Quezada, G.R.; Ayala, L.; Leiva, W.H.; Toro, N.; Toledo, P.G.; Robles, P.; Jeldres, R.I. Describing mining tailing flocculation in seawater by population balance models: Effect of mixing intensity. Metals 2020, 10, 240. [Google Scholar] [CrossRef]
- Fawell, P.D.; Nguyen, T.V.; Solnordal, C.B.; Stephens, D.W. Enhancing gravity thickener feedwell design and operation for optimal flocculation through the application of computational fluid dynamics. Miner. Process. Extr. Metall. Rev. 2019, 1–15. [Google Scholar] [CrossRef]
- Quezada, G.R.; Ramos, J.; Jeldres, R.I.; Robles, P.; Toledo, P.G. Analysis of the flocculation process of fine tailings particles in saltwater through a population balance model. Sep. Purif. Technol. 2020, 237, 116319. [Google Scholar] [CrossRef]
- Quezada, G.R.; Jeldres, M.; Toro, N.; Robles, P.; Jeldres, R.I. Reducing the magnesium content from seawater to improve tailing flocculation: Description by population balance models. Metals 2020, 10, 329. [Google Scholar] [CrossRef]
- Li, X.-Y.; Logan, B.E. Permeability of fractal aggregates. Water Res. 2001, 35, 3373–3380. [Google Scholar] [CrossRef]
- Pandya, J.D.; Spielman, L.A. Floc breakage in agitated suspensions: Effect of agitation rate. Chem. Eng. Sci. 1983. [Google Scholar] [CrossRef]
- Pretorius, C.; Wicklein, E.; Rauch-Williams, T.; Samstag, R.; Sigmon, C. How oversized mixers became an industry standard. Proc. Water Environ. Fed. 2015, 11, 4379–4411. [Google Scholar] [CrossRef]
- Veerapaneni, S.; Wiesner, M.R. Hydrodynamics of fractal aggregates with radially varying permeability. J. Colloid Interface Sci. 1996, 177, 45–57. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Self-affine fractals and fractal dimension. Phys. Scr. 1985, 32, 257. [Google Scholar] [CrossRef]
- Vainshtein, P.; Shapiro, M.; Gutfinger, C. Mobility of permeable aggregates: Effects of shape and porosity. J. Aerosol Sci. 2004, 35, 383–404. [Google Scholar] [CrossRef]
- Herrington, T.M.; Clarke, A.Q.; Watts, J.C. The surface charge of kaolin. Colloids Surf. 1992, 68, 161–169. [Google Scholar] [CrossRef]
- Shaikh, S.M.R.; Nasser, M.S.; Magzoub, M.; Benamor, A.; Hussein, I.A.; El-Naas, M.H.; Qiblawey, H. Effect of electrolytes on electrokinetics and flocculation behavior of bentonite-polyacrylamide dispersions. Appl. Clay Sci. 2018, 158, 46–54. [Google Scholar] [CrossRef]
- Chaiwong, N.; Nuntiya, A. Influence of pH, electrolytes and polymers on flocculation of kaolin particle. Chiang Mai J. Sci. 2008, 35, 11–16. [Google Scholar]




| Variable | Expression | Input Parameters | Reference |
|---|---|---|---|
| Collision efficiency | Vajihinejad and Soares [30] | ||
| Collision frequency | Veerapaeni and Wiesner [38] | ||
| Breakage rate | Pandya and Spielman [36] | ||
| Distribution breakage | |||
| Dimensionless frequency function | This work | ||
| Initial number concentration | |||
| Particle diameter | Mandelbrot [39] | ||
| Particle volume | |||
| Shear rate | |||
| Suspension density | |||
| Porosity | Vainshtein et al. [40] | ||
| Permeability | Li and Logan [35] |
| Variable | Expression |
|---|---|
| Objective function | |
| Model diameter | |
| Coefficient of determination | |
| Goodness of fit | |
| Standard error |
| System | Treated Seawater, % | R2 | GoF, % |
|---|---|---|---|
| 50/50 | 0 | 0.760 | 94.9 |
| 40 | 0.949 | 96.5 | |
| 60 | 0.918 | 95.8 | |
| 75 | 0.954 | 96.3 | |
| 90 | 0.899 | 93.9 | |
| 100 | 0.976 | 97.5 | |
| 75/25 | 0 | 0.885 | 95.8 |
| 40 | 0.900 | 95.6 | |
| 60 | 0.964 | 96.3 | |
| 75 | 0.957 | 96.0 | |
| 90 | 0.963 | 96.4 | |
| 100 | 0.984 | 97.2 | |
| 100/0 | 0 | 0.946 | 95.8 |
| 40 | 0.939 | 95.6 | |
| 60 | 0.945 | 96.0 | |
| 75 | 0.984 | 97.7 | |
| 90 | 0.957 | 95.7 | |
| 100 | 0.966 | 95.7 |
| System Qz/Kao, Tsw/Rsw | GoF | R2 | |||||
|---|---|---|---|---|---|---|---|
| 85/25, 50/50 | 3.07 × 10−4 | 2.64 × 10−4 | 6.55 × 10−2 | 1.81 × 10−6 | 3.69 | 95.4% | 0.933 |
| 95/5, 75/25 | 8.07 × 10−4 | 5.23 × 10−4 | 3.01 × 10−2 | 1.37 × 10−6 | 3.49 | 96.9% | 0.978 |
| 85/5, 100/0 | 1.32 × 10−4 | 9.41 × 10−4 | 2.21 × 10−2 | 2.63 × 10−3 | 2.22 | 93.6% | 0.890 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quezada, G.R.; Jeldres, M.; Robles, P.; Toro, N.; Torres, D.; Jeldres, R.I. Improving the Flocculation Performance of Clay-Based Tailings in Seawater: A Population Balance Modelling Approach. Minerals 2020, 10, 782. https://doi.org/10.3390/min10090782
Quezada GR, Jeldres M, Robles P, Toro N, Torres D, Jeldres RI. Improving the Flocculation Performance of Clay-Based Tailings in Seawater: A Population Balance Modelling Approach. Minerals. 2020; 10(9):782. https://doi.org/10.3390/min10090782
Chicago/Turabian StyleQuezada, Gonzalo R., Matías Jeldres, Pedro Robles, Norman Toro, David Torres, and Ricardo I. Jeldres. 2020. "Improving the Flocculation Performance of Clay-Based Tailings in Seawater: A Population Balance Modelling Approach" Minerals 10, no. 9: 782. https://doi.org/10.3390/min10090782
APA StyleQuezada, G. R., Jeldres, M., Robles, P., Toro, N., Torres, D., & Jeldres, R. I. (2020). Improving the Flocculation Performance of Clay-Based Tailings in Seawater: A Population Balance Modelling Approach. Minerals, 10(9), 782. https://doi.org/10.3390/min10090782








