Effect of Mg(II) and Na(I) Doping on the Electronic Structure and Mechanical Properties of Kaolinite
Abstract
1. Introduction
2. Materials and Methods
3. Results
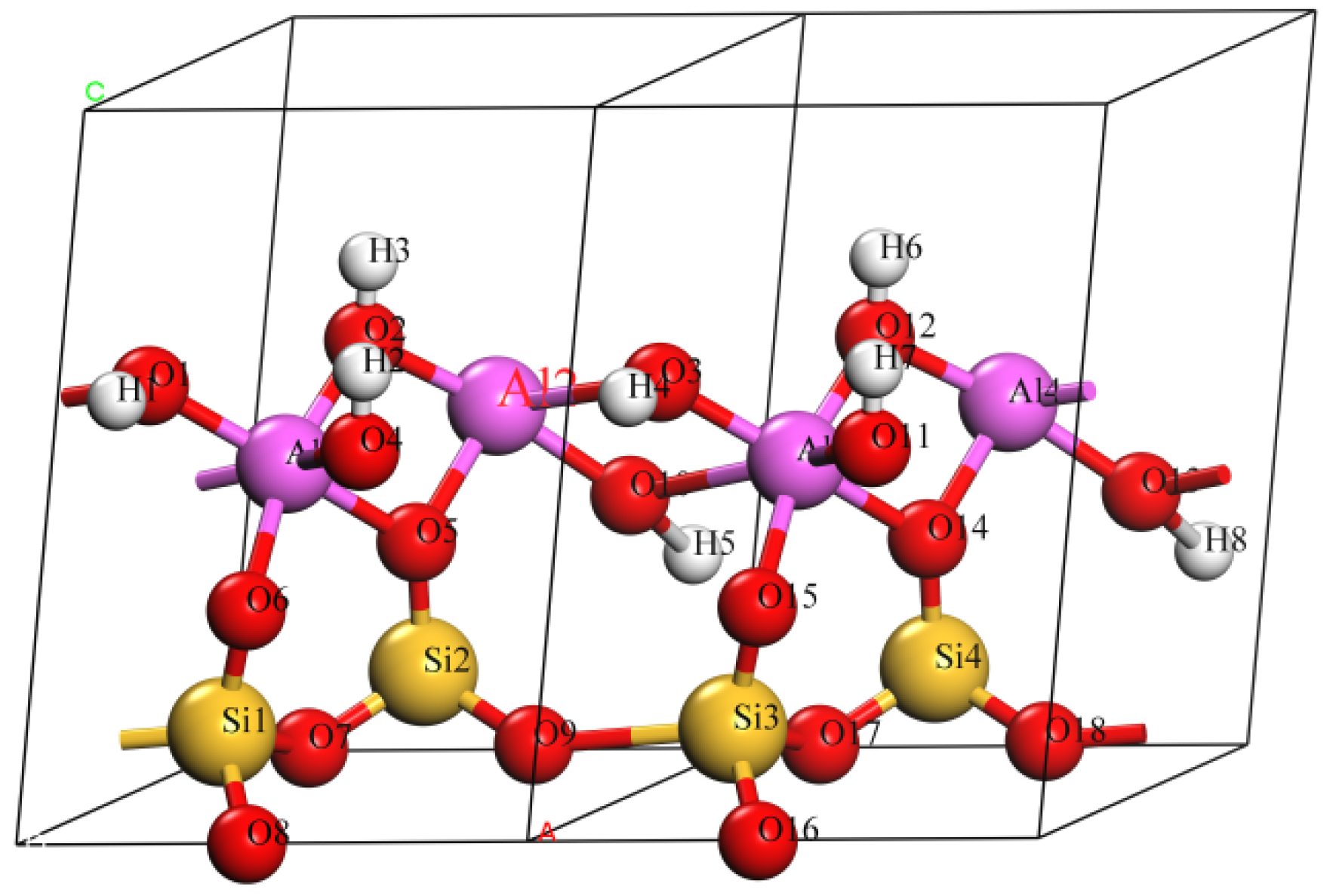
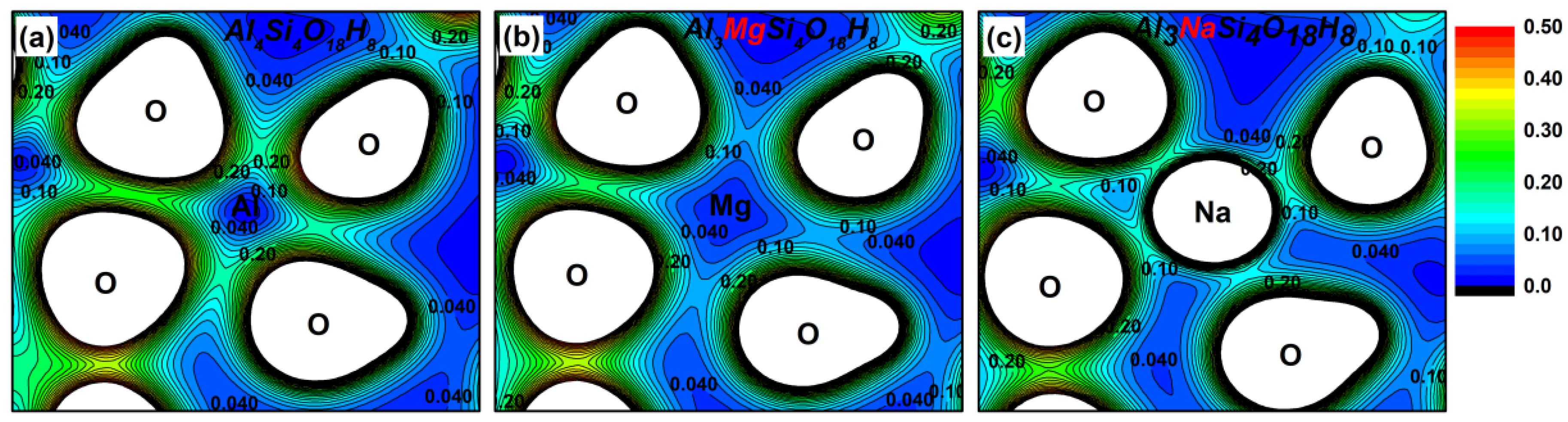
3.1. Effect on Crystal Structure of Kaolinite
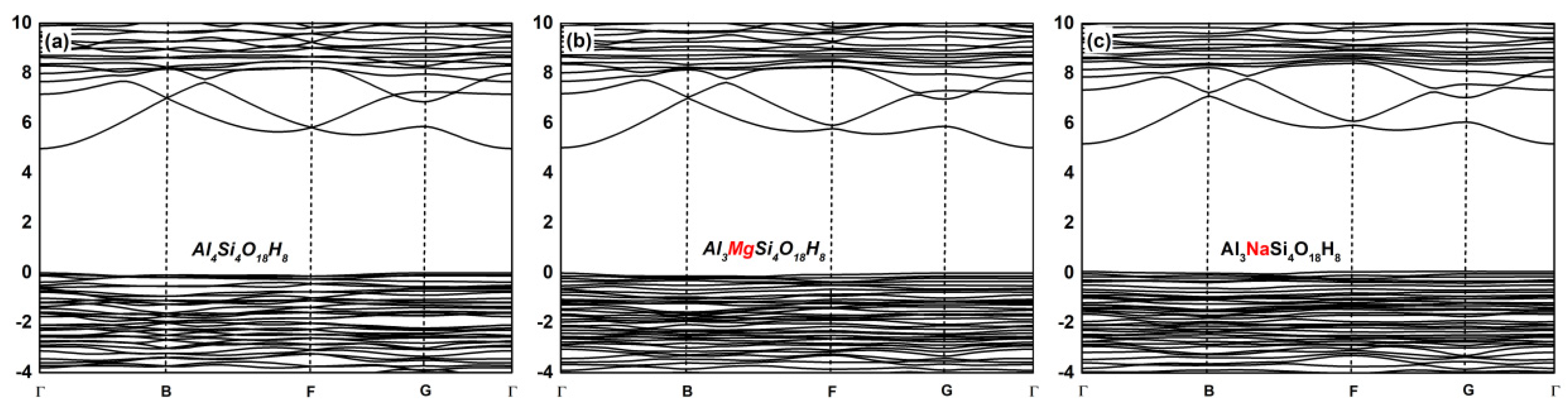
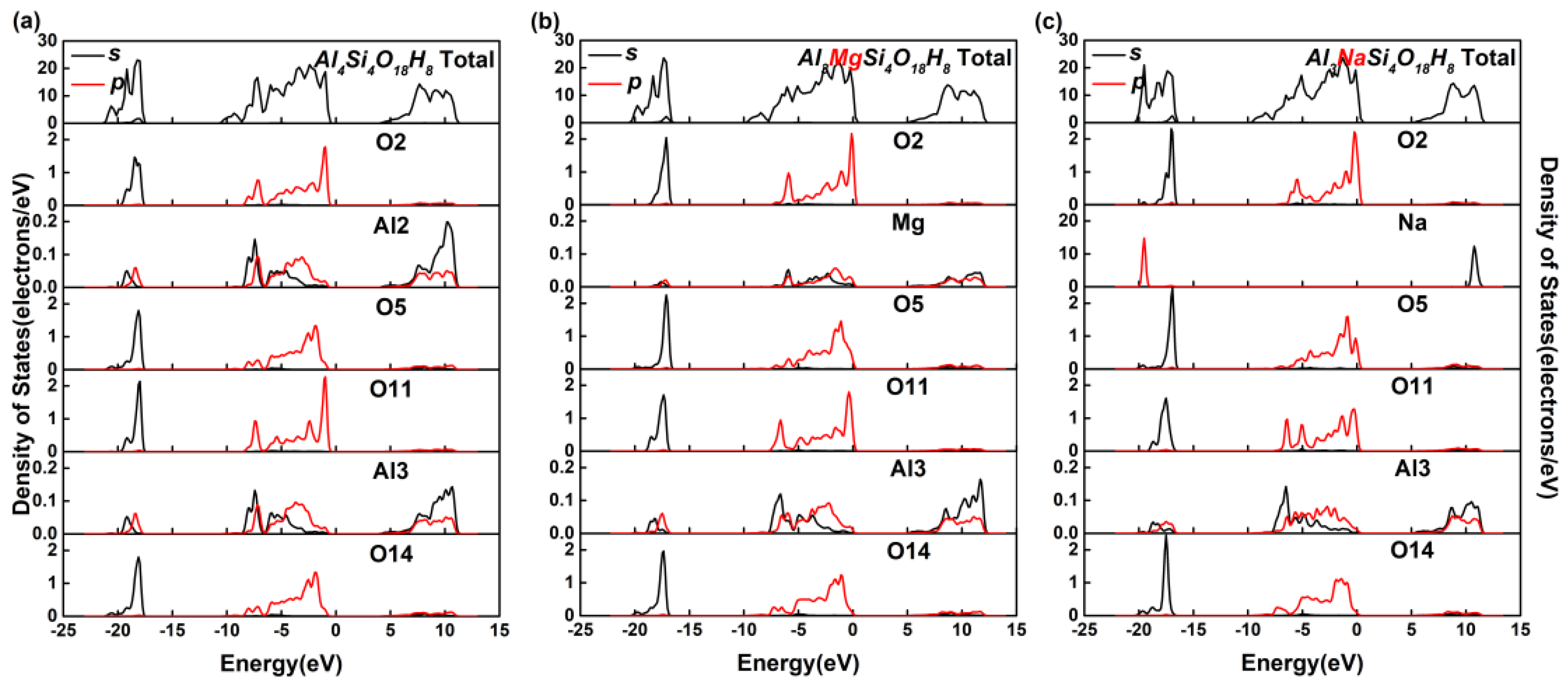
3.2. Effect on the Electronic Structure of Kaolinite
3.3. Effect on the Mechanical Properties of Kaolinite
4. Conclusions
- (1)
- The doping of Mg(II) and Na(I) changed the ionic bond and the atomic layer spacing in kaolinite crystals. The average bond length of the doped atom and the O atom was positively related to the atomic radius of the doped atom. The doping cations had a certain effect on the layer spacing of the Al–OH layer and Al–Oa layer, but had little effect on the layer spacing of the Si–Oa layer and Si–Ob layer, which were far away from doped atom.
- (2)
- By analyzing the electronic structure of the crystal, the band gap width of the Mg-doped and Na-doped kaolinite increased, which indicated that the doping of Mg(II) and Na(I) made it more difficult for the electrons to obtain enough energy to move from the valence to conduction band state. Compared with Al, Na and Mg had more electron transfer to the adjacent O; that is, the charge density around O decreased in the direction of the doped atom (Mg/Na), the covalent bond composition of Mg–O bond and Na–O bond became weaker than Al–O bond, and the ionic bond properties were stronger.
- (3)
- The influence of doping Mg(II) and Na(I) on C11 and C22 was greater than that on C33, indicating that doping had a greater influence on the stiffness in the direction of parallel crystal plane. In addition, the doping of Mg(II) and Na(I) reduced the elastic modulus of kaolinite crystal and weakened the rigidity of the material. As the Vickers hardness decreased, the hardening effect of the material weakened. The changes of Poisson’s ratio (μ), Pugh’s modulus ratio (G/B), and the Cauchy pressure (Pc) indicated that the directivity of atom bonding was weakened, and the plasticity and ductility of the material were improved.
Author Contributions
Funding
Conflicts of Interest
References
- He, M.C. Latest progress of soft rock mechanics and engineering in China. J. Rock Mech. Geotech. Eng. 2014, 6, 165–179. [Google Scholar] [CrossRef]
- Kanji, M.A. Critical issues in soft rocks. J. Rock Mech. Geotech. Eng. 2014, 6, 186–195. [Google Scholar] [CrossRef]
- Ighil Ameur, L.; Robin, G.; Hattab, M. Elastic properties in a clayey material under mechanical loading-an estimation through ultrasonic propagations. Eur. J. Environ. Civ. Eng. 2015, 20, 1127–1146. [Google Scholar] [CrossRef]
- Bourret, J.; Tessier-Doyen, N.; Guinebretiere, R.; Joussein, E.; Smith, D.S. Anisotropy of thermal conductivity and elastic properties of extruded clay-based materials: Evolution with thermal treatment. Apply Clay Sci. 2015, 116, 150–157. [Google Scholar] [CrossRef]
- LiBalan, E.; Pietrucci, F.; Gervais, C.; Blanchard, M.; Schott, J.; Gaillardet, J. First-principles study of boron speciation in kaolinite and aragonite. Geochim. Cosmochim. Acta 2016, 193, 119–131. [Google Scholar]
- Weck, P.F.; Kim, E.; Jové-Colón, C.F. Relationship between crystal structure and thermo-mechanical properties of kaolinite clay: Beyond standard density functional theory. Dalton Trans. 2015, 44, 12550–12560. [Google Scholar] [CrossRef]
- Fang, Z.J.; Zhai, X.S.; Li, Z.L.; Pan, R.J.; Mo, M. Pressure dependence of the electronic structure in kaolinite: A first-principles study. Mod. Phys. Lett. B 2017, 31, 1750194. [Google Scholar] [CrossRef]
- Prasad, M.; Kopycinska, M.; Rabe, U.; Arnold, W. Measurement of Young’s modulus of clay minerals using atomic force acoustic microscopy. Geophys. Res. Lett. 2002, 29, 13–16. [Google Scholar] [CrossRef]
- Vanorio, T.; Prasad, M.; Nur, A. Elastic properties of dry clay mineral aggregate, suspensions and sandstones. Geophys. J. Int. 2003, 155, 319–326. [Google Scholar] [CrossRef]
- He, M.C.; Zhao, J.; Fang, Z.J.; Zhang, P. First-principles study of isomorphic (dual-defect) substitution in kaolinite. Clays Clay Miner. 2011, 59, 501–506. [Google Scholar] [CrossRef]
- Hobbs, J.D.; Cygan, R.T.; Nagy, K.L.; Schultz, P.A.; Sears, M.P. All-atom ab initio energy minimization of the kaolinite crystal structure. Am. Mineral. 1997, 82, 657–662. [Google Scholar] [CrossRef]
- He, M.C.; Fang, Z.J.; Zhang, P. Theoretical studies on defects of kaolinite in clays. Chin. Phys. Lett. 2009, 26, 059101. [Google Scholar]
- He, M.C.; Zhao, J.; Fang, Z.J. First-principles study of atomic and electronic structures of kaolinite in soft rock. Chin. Phys. B 2012, 21, 039101. [Google Scholar] [CrossRef]
- He, M.C.; Zhao, J. Effects of Mg, Ca, and Fe(II) doping on the kaolinite (001) surface with H2O adsorption. Clays Clay Miner. 2012, 60, 330–337. [Google Scholar] [CrossRef]
- Zhao, J.; He, M.C. Theoretical study of heavy metal Cd, Cu, Hg, and Ni(II) adsorption on the kaolinite(001) surface. Appl. Surf. Sci. 2014, 317, 718–723. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B. 1996, 54, 11169–11173. [Google Scholar] [CrossRef]
- Zhao, F.; Chen, B.; Zhang, C.H. Effect of rare earth (Sc, Y, La, Sm and Gd) doping on mechanical and thermodynamic properties of Al12Mg17 intermetallic compounds. Mod. Phys. Lett. B 2019, 33, 1950442. [Google Scholar] [CrossRef]
- Zhang, T.; Yin, H.Q.; Zhang, C.; Yang, Z.; Deng, Z.H.; Yang, G.Q.; Zheng, Q.J.; Qu, X.H. First-principle calculations of mechanical properties and electronic structure of WCoB and Cr doped WCoB under high pressure. Mater. Res. Express 2019, 11, 116320. [Google Scholar] [CrossRef]
- Wang, N.; Liu, H.F. First-principles study of electronic structure and optical properties of Ca-Doped SnS2. Mater. Sci. 2018, 8, 1094–1101. [Google Scholar]
- Gao, X.; Wang, H.; Wang, C.; Chen, S.; Zhao, M.; Li, B. First-principles investigation of the effects of Re (La, Ce, Pr and Nd) doping on the diopside phase of glass–ceramics. J. Non-Cryst. Solids 2019, 526, 119701. [Google Scholar] [CrossRef]
- Islam, M.N.; Hadi, M.A.; Podder, J. Influence of Ni doping in a lead-halide and a lead-free halide perovskites for optoelectronic applications. AIP Adv. 2019, 9, 125321. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Y.; Duan, M.; Hou, H. Structure evolution, elastic and electronic properties of Pt-Doped Ti alloy under pressure. Phys. Status Solidi (b) 2019, 257, 1900360. [Google Scholar] [CrossRef]
- Sachse, W.; Ruoff, A.L. Elastic moduli of precompressed pyrophyllite used in ultrahigh, ressure research. J. Appl. Phys. 1975, 46, 3725–3730. [Google Scholar] [CrossRef]
- Pawley, A.; Clark, S.; Chinnery, N. Equation of state measurements of chlorite, pyrophyllite, and talc. Am. Mineral. 2002, 87, 1172–1182. [Google Scholar] [CrossRef]
- Adams, J.M. Hydrogen atom position kaolinite by neutron profile refinement. Clays Clay Miner. 1983, 31, 352–358. [Google Scholar] [CrossRef]
- Benco, L.; Tunega, D.; Hafner, J.; Lischka, H. Orientation of OH groups in kaolinite and dickite: Ab initio molecular dynamics study. Am. Mineral. 2001, 86, 1057–1065. [Google Scholar] [CrossRef]
- Bish, D.L. Rietveld refinement of the kaolinite structure at 1.5 K. Clays Clay Miner. 1993, 41, 738–744. [Google Scholar] [CrossRef]
- Hess, A.C.; Saunders, V.R. Periodic ab initio hartree-fock calculations of the low-symmetry mineral kaolinite. J. Phys. Chem. 1992, 96, 4367–4374. [Google Scholar] [CrossRef]
- Hu, X.L.; Angelos, M. Water on the hydroxylated (001) surface of kaolinite: From monomer adsorption to a flat 2D wetting layer. Surf. Sci. 2008, 602, 960–974. [Google Scholar] [CrossRef]
- Bailey, S.W. Summary of recommendations of AIPEA nomenclature committee. Clay Miner. 1980, 15, 85–93. [Google Scholar] [CrossRef]
- Schwieger, W.; Bergk, K.H.; Heidemann, D.; Lagaly, G.; Beneke, K. High-resolution Si-29 solid-state NMR-studies on A synthetic sodium-silicate hydrate (makatite) and its crystalline silicic-acid. Z. Fur Krist. 1991, 197, 1–12. [Google Scholar] [CrossRef]
- Giese, R.F., Jr. Interlayer bonding in kaolinite dickite and nacrite. Clays Clay Miner. 1973, 21, 145–149. [Google Scholar] [CrossRef]
- Hajjaji, W.; Andrejkovicova, S.; Pullar, R.C.; Tobaldi, D.M.; Lopez-Galindo, A.; Jammousi, F.; Rocha, F.; Labrincha, J.A. Effective removal of anionic and cationic dyes by kaolinite and TiO2/kaolinite composites. Clay Miner. 2016, 51, 19–27. [Google Scholar] [CrossRef]
- Neder, R.B.; Burghammer, M.; Grasl, T.H.; Schulz, H.; Bram, A.; Fiedler, S. Refinement of the kaolinite structure from single-crystal synchrotron data. Clays Clay Miner. 1999, 47, 487–494. [Google Scholar] [CrossRef]
- Wenk, H.R.; Voltolini, M.; Mazurek, M.; Van Loon, L.R.; Vinsot, A. Preferred orientations and anisotropy in shales: Callovo-Oxfordian shale (France) and opalinus clay. Clays Clay Miner. 2008, 56, 285–306. [Google Scholar] [CrossRef]
- Katahara, K.W. Clay mineral elastic properties. SEG Tech. Progr. Expand. Abstr. 1999, 15, 1691–1694. [Google Scholar]
- Wang, Z.; Wang, H.; Gates, M.E. Effective elastic properties of solid clays. Geophysics 2001, 66, 428–440. [Google Scholar] [CrossRef]
| Phase | a | b | c | α | β | γ | V |
|---|---|---|---|---|---|---|---|
| Calculated | 5.149 Å | 8.934 Å | 7.384 Å | 91.930° | 105.042° | 89.698° | 327.840 Å3 |
| Exp. [25] | 5.155 Å | 8.945 Å | 7.405 Å | 91.700° | 104.862° | 89.822° | 328.710 Å3 |
| Difference | 0.126% | 0.122% | 0.281% | 0.251% | 0.172% | 0.138% | 0.265% |
| Phase | OH–H | Al2–OH | Mg–OH | Na–OH | Al2–Oa | Mg–Oa | Na–Oa | Si2–Oa | Si2–Ob |
|---|---|---|---|---|---|---|---|---|---|
| Exp. [34] | 0.750 | 1.921 | - | - | 1.971 | - | - | 1.610 | 1.620 |
| Al4Si4O18H8 | 0.970 | 1.874 | - | - | 1.995 | - | - | 1.615 | 1.637 |
| Al3MgSi4O18H8 | 0.970 | - | 2.017 | - | - | 2.095 | - | 1.601 | 1.556 |
| Al3NaSi4O18H8 | 0.980 | - | - | 2.243 | - | - | 2.255 | 1.599 | 1.550 |
| Doped Kaolinite | Δd12(%) | Δd23(%) | Δd34(%) | Δd45(%) | Δd56(%) |
|---|---|---|---|---|---|
| Al3MgSi4O18H8 | −0.62 | 7.01 | 2.14 | −1.48 | −0.09 |
| Al3NaSi4O18H8 | −0.15 | 11.27 | 5.31 | −3.36 | −1.74 |
| Elastic Constants | Al4Si4O18H8 | Al3MgSi4O18H8 Calculated (GPa) | Al3NaSi4O18H8 Calculated (GPa) | ||
|---|---|---|---|---|---|
| Exp. [35] (GPa) | Exp. [36] (GPa) | Calculated (GPa) | |||
| C11 | 126.4 | 171.51 | 139.18 | 128.09 | 114.48 |
| C22 | - | - | 170.20 | 153.08 | 102.55 |
| C33 | 57.8 | 52.62 | 45.50 | 44.47 | 38.39 |
| C44 | 31.6 | 14.76 | 9.66 | 6.84 | 3.55 |
| C55 | - | - | 18.62 | 16.95 | 12.48 |
| C66 | 53.6 | 66.31 | 53.60 | 45.93 | 20.03 |
| C12 | - | - | 52.46 | 49.87 | 48.98 |
| C13 | 8.5 | 27.11 | 28.30 | 16.70 | 13.47 |
| C14 | - | - | −4.50 | 2.33 | −2.94 |
| C15 | - | - | −35.78 | −22.17 | −21.40 |
| C16 | - | - | −4.50 | 0.53 | −9.76 |
| C23 | - | - | 11.72 | 6.73 | 5.83 |
| C24 | - | - | −7.30 | −12.86 | 6.89 |
| C25 | - | - | −14.50 | −13.35 | −13.79 |
| C26 | - | - | −25.55 | −4.50 | 5.45 |
| C34 | - | - | −3.72 | 0.85 | −4.37 |
| C35 | - | - | −4.46 | 6.60 | −9.37 |
| C36 | - | - | 3.86 | 0.65 | −6.53 |
| C45 | - | - | −1.25 | 1.35 | 0.75 |
| C46 | - | - | −13.18 | −11.34 | 0.89 |
| C56 | - | - | 2.75 | 2.03 | 6.86 |
| Phase | Al4Si4O18H8 | Al3MgSi4O18H8 Calculated | Al3NaSi4O18H8 Calculated | |
|---|---|---|---|---|
| Exp. [37] | Calculated | |||
| Bulk modulus B (GPa) | 47.90 | 44.001 | 43.288 | 30.438 |
| Young’s modulus E (GPa) | 51.97 | 57.783 | 48.791 | 33.91 |
| Shear modulus G (GPa) | 19.70 | 22.552 | 18.592 | 12.900 |
| Poisson’s ratio μ | 0.319 | 0.281 | 0.312 | 0.315 |
| Vickers hardness Hv (GPa) | - | 2.643 | 1.103 | 0.264 |
| Pugh’s modulus G/B ratio | - | 0.513 | 0.429 | 0.424 |
| Cauchy pressure Pc (GPa) | - | 42.805 | 43.032 | 45.432 |
| Compression wave velocity υp (km/s) | 5.51 | 5.321 | 5.114 | 4.284 |
| Shear wave velocity υs (km/s) | 2.84 | 2.936 | 2.673 | 2.229 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Qin, X.; Wang, J.; He, M. Effect of Mg(II) and Na(I) Doping on the Electronic Structure and Mechanical Properties of Kaolinite. Minerals 2020, 10, 368. https://doi.org/10.3390/min10040368
Zhao J, Qin X, Wang J, He M. Effect of Mg(II) and Na(I) Doping on the Electronic Structure and Mechanical Properties of Kaolinite. Minerals. 2020; 10(4):368. https://doi.org/10.3390/min10040368
Chicago/Turabian StyleZhao, Jian, Xinzhan Qin, Jiamin Wang, and Manchao He. 2020. "Effect of Mg(II) and Na(I) Doping on the Electronic Structure and Mechanical Properties of Kaolinite" Minerals 10, no. 4: 368. https://doi.org/10.3390/min10040368
APA StyleZhao, J., Qin, X., Wang, J., & He, M. (2020). Effect of Mg(II) and Na(I) Doping on the Electronic Structure and Mechanical Properties of Kaolinite. Minerals, 10(4), 368. https://doi.org/10.3390/min10040368