Computer-Aided Panoramic Images Enriched by Shadow Construction on a Prism and Pyramid Polyhedral Surface
Abstract
:1. Introduction
2. General Aspects of Shadow Construction
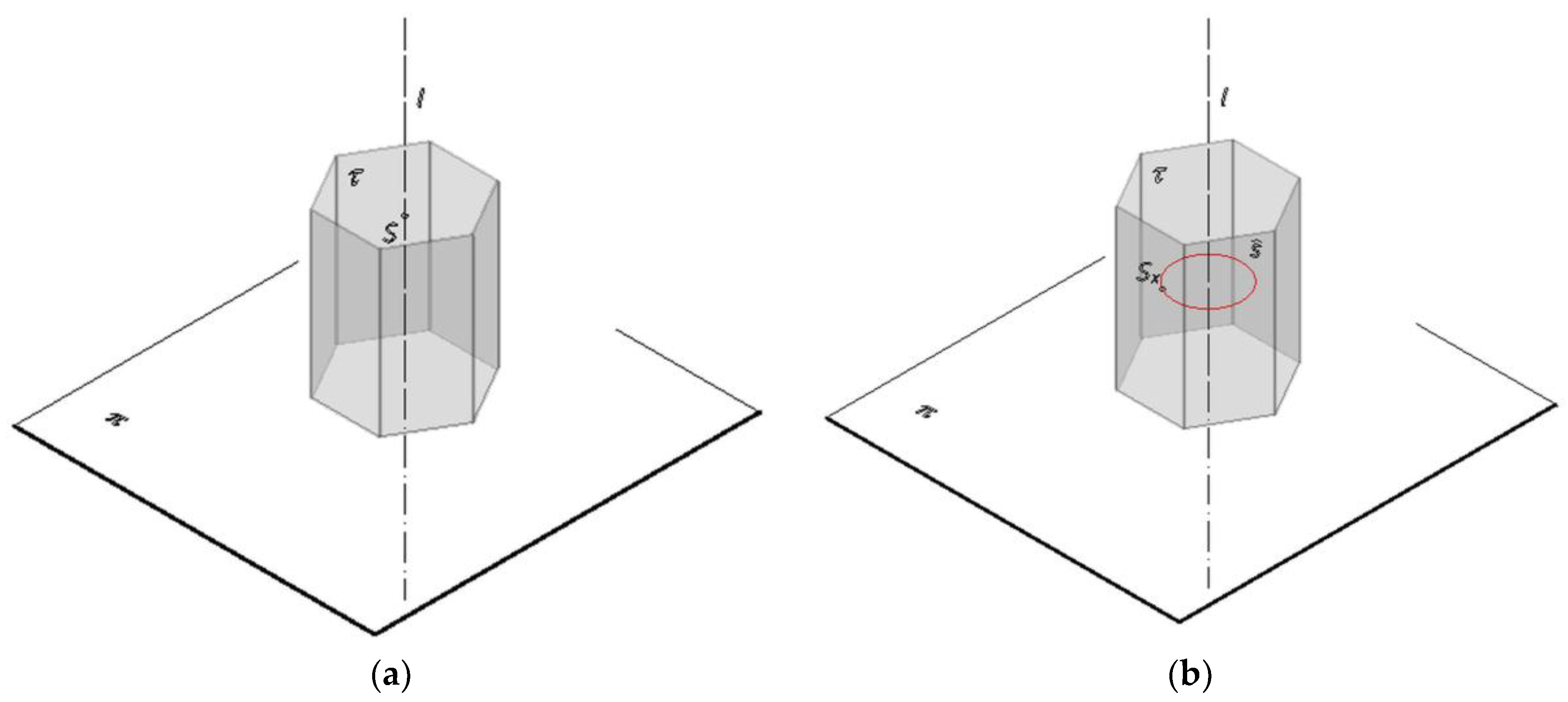
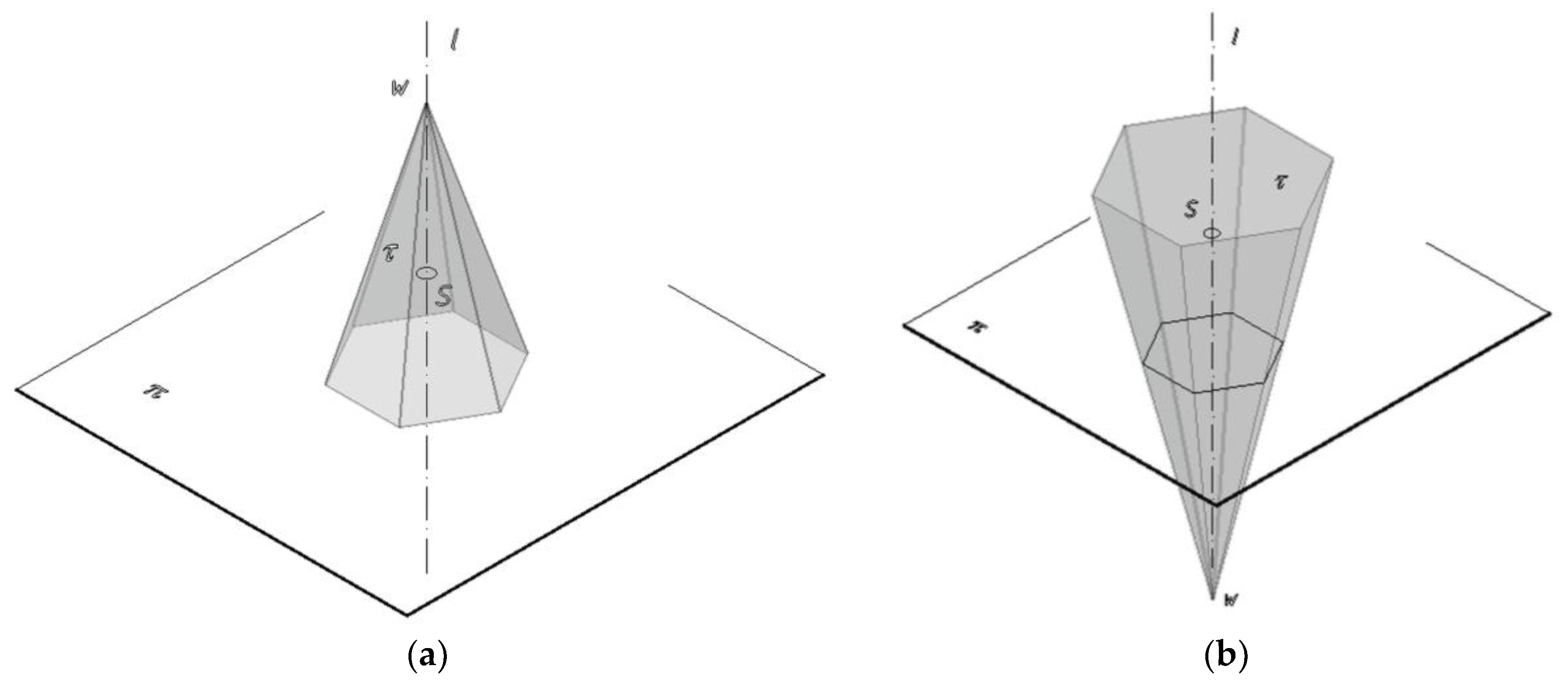
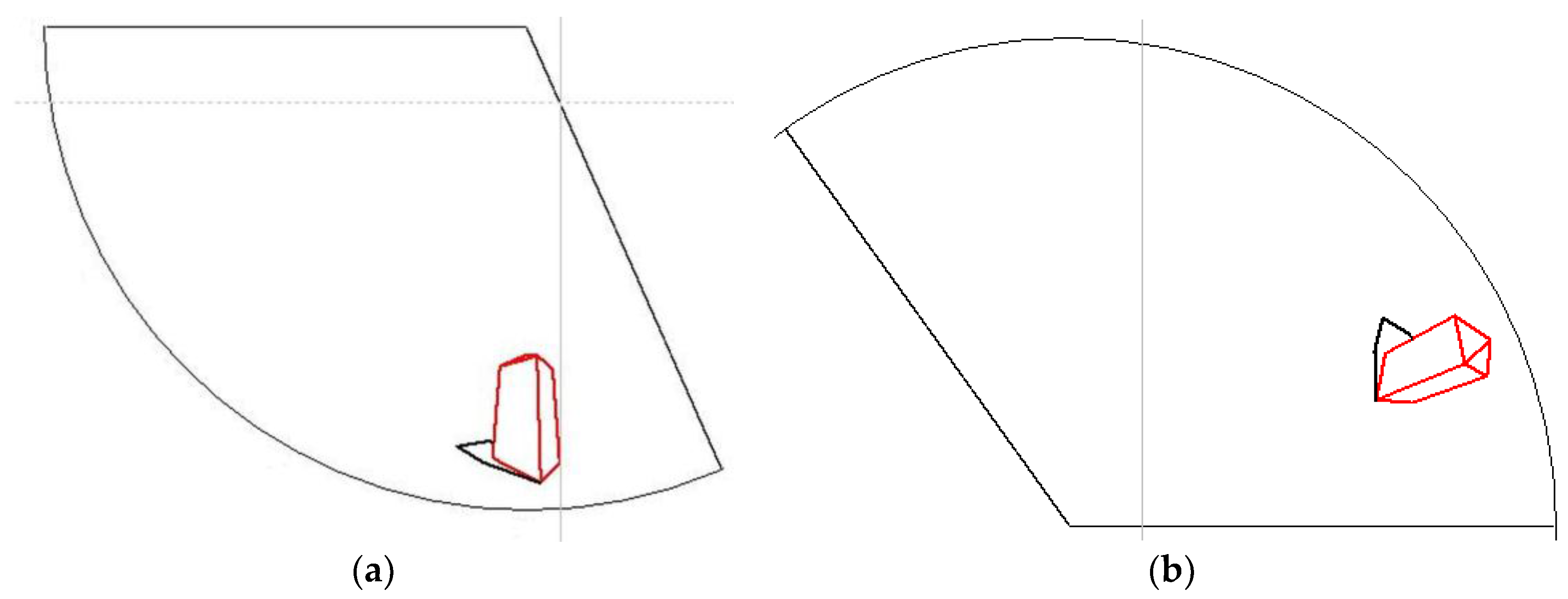
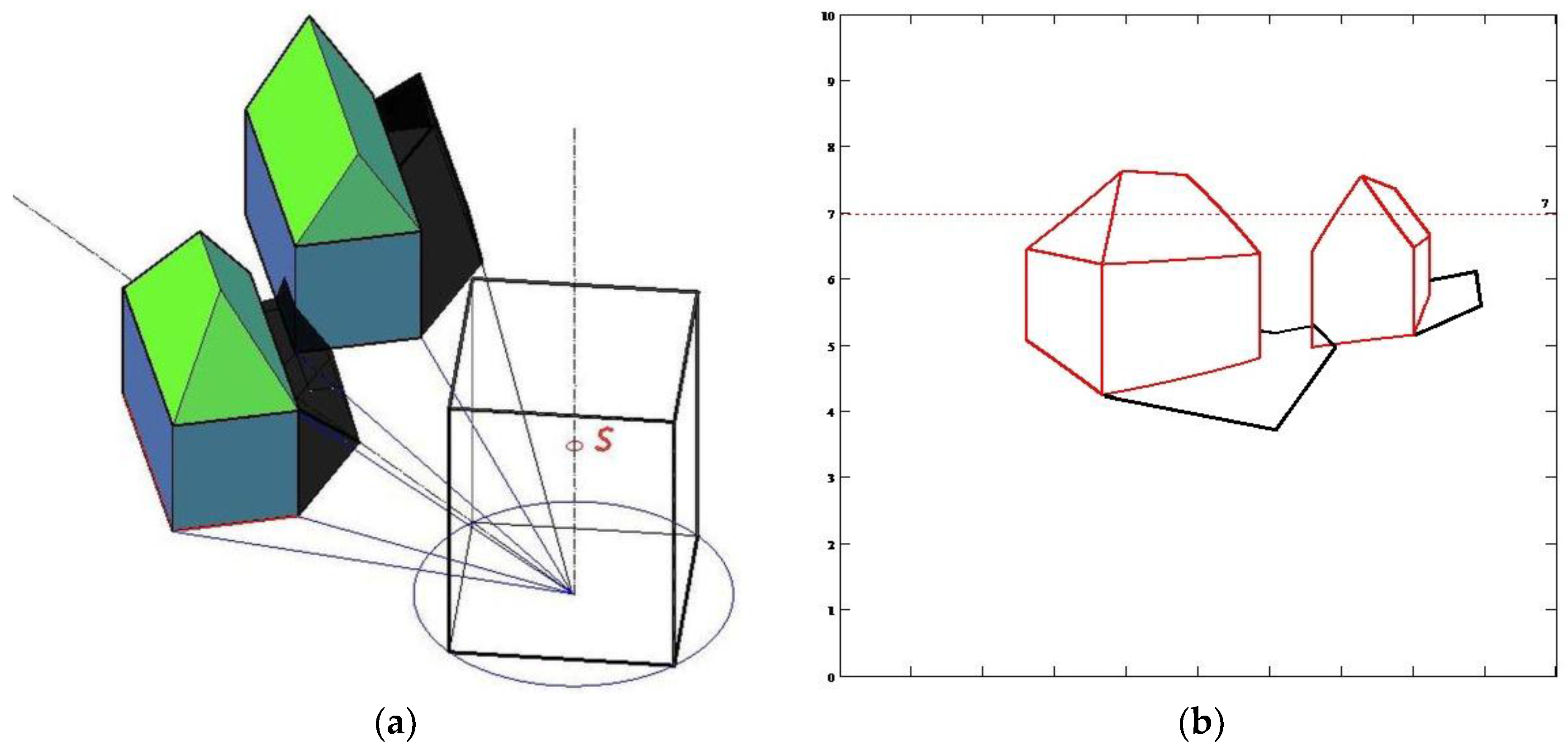
3. Geometrical Aspects of Panoramic Projection onto a Polyhedral Surface
4. Mapping Polyhedral Panorama Directly on an Unfolded Projection Surface
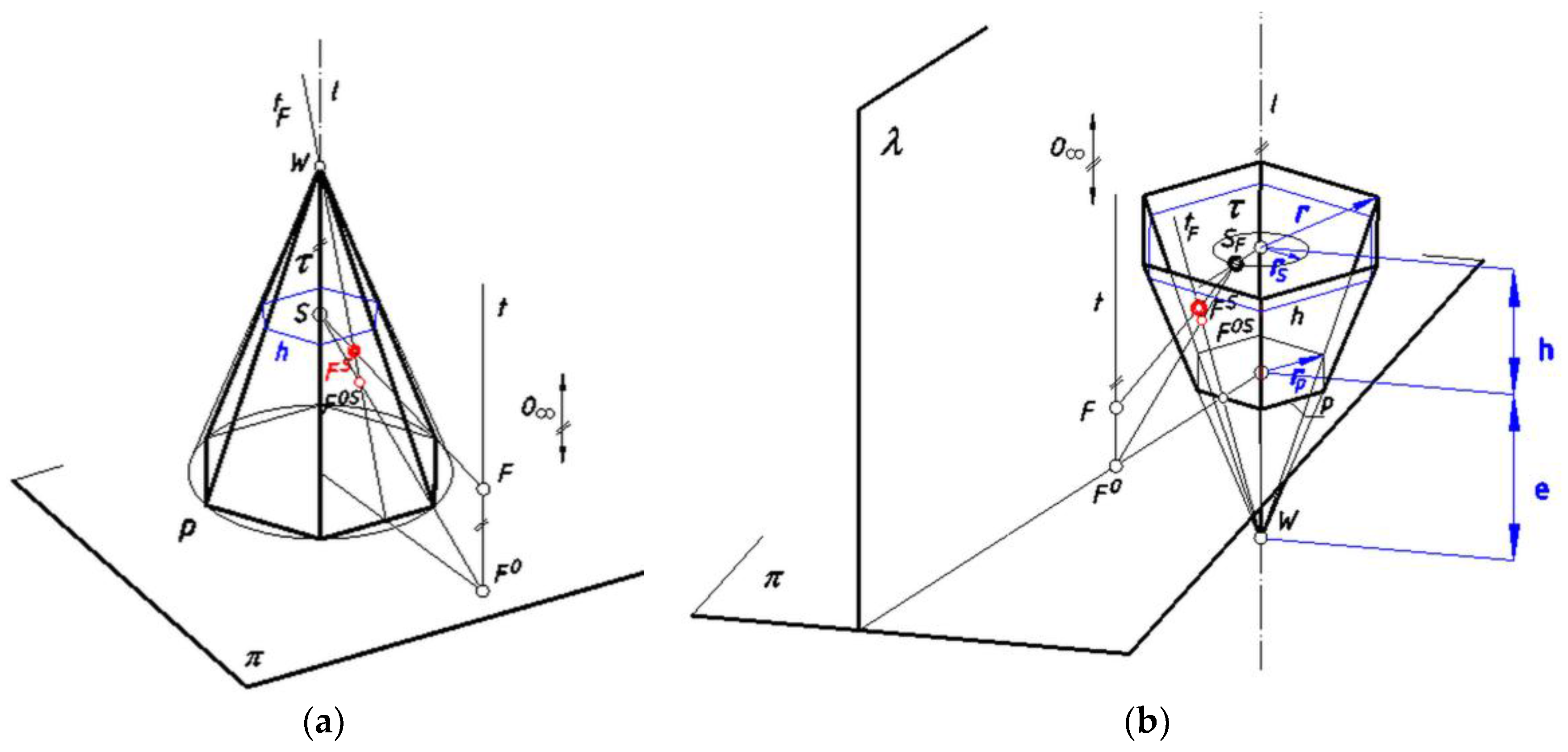
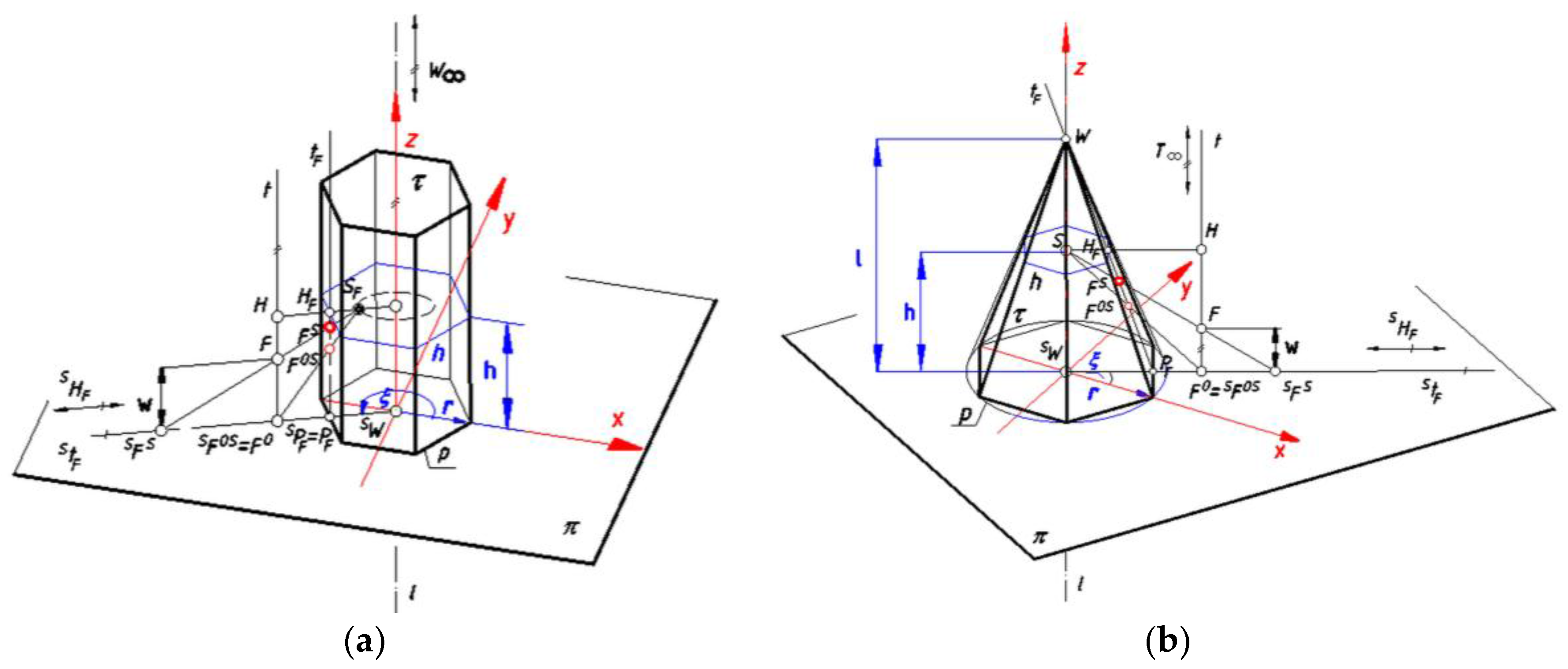
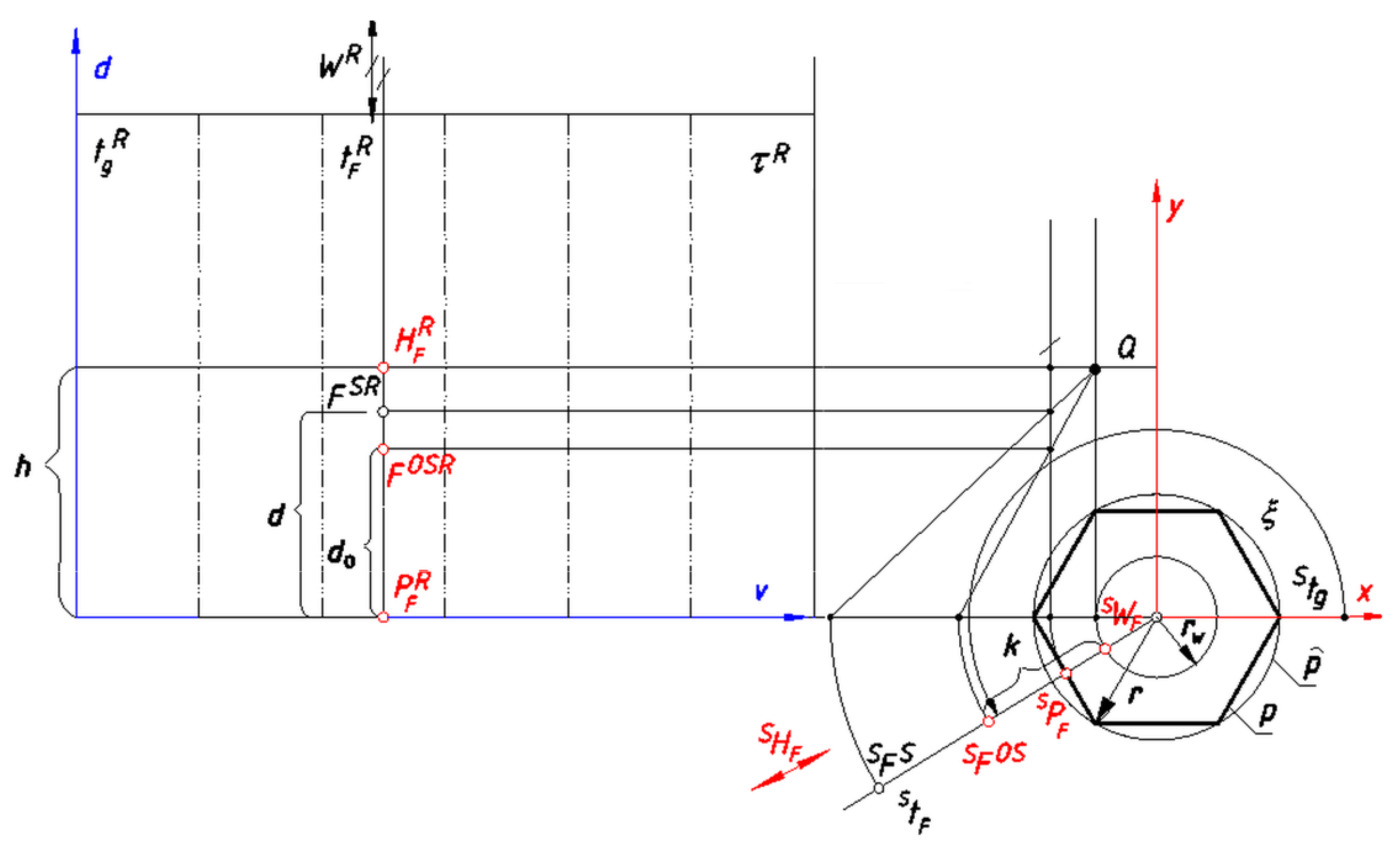
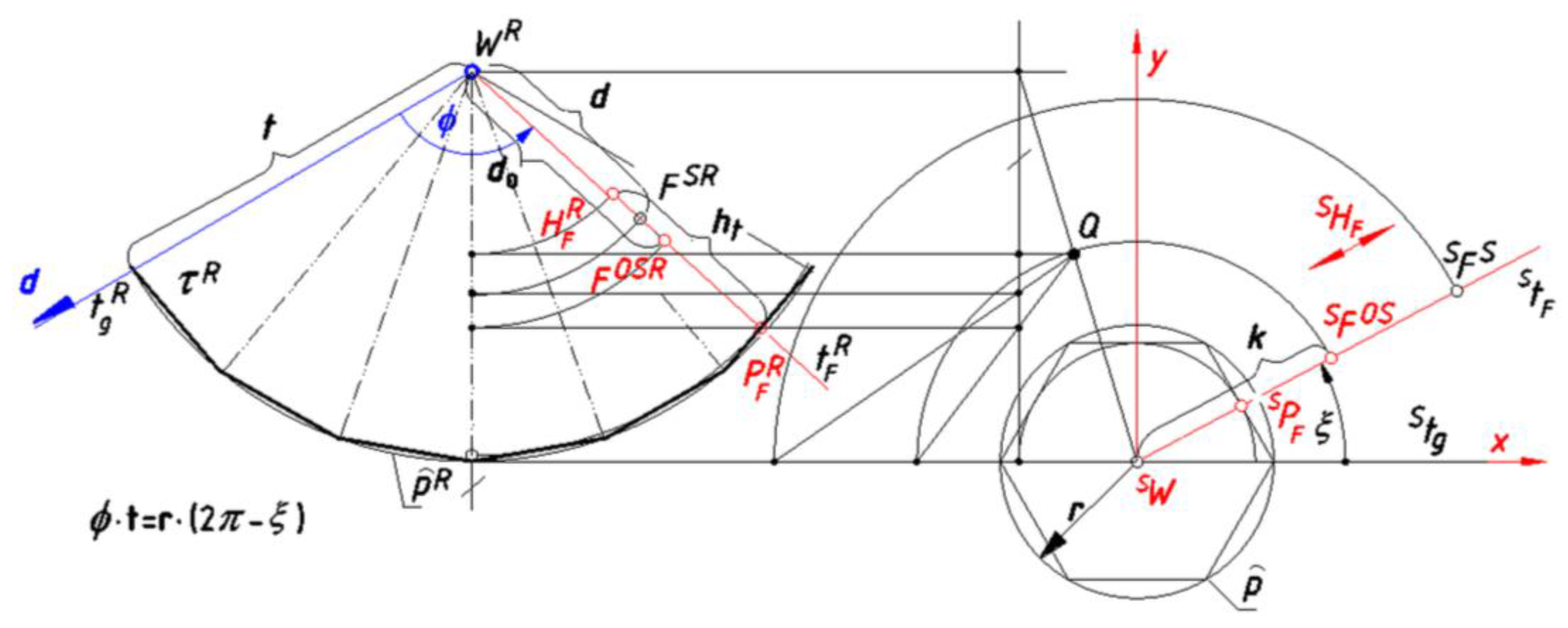
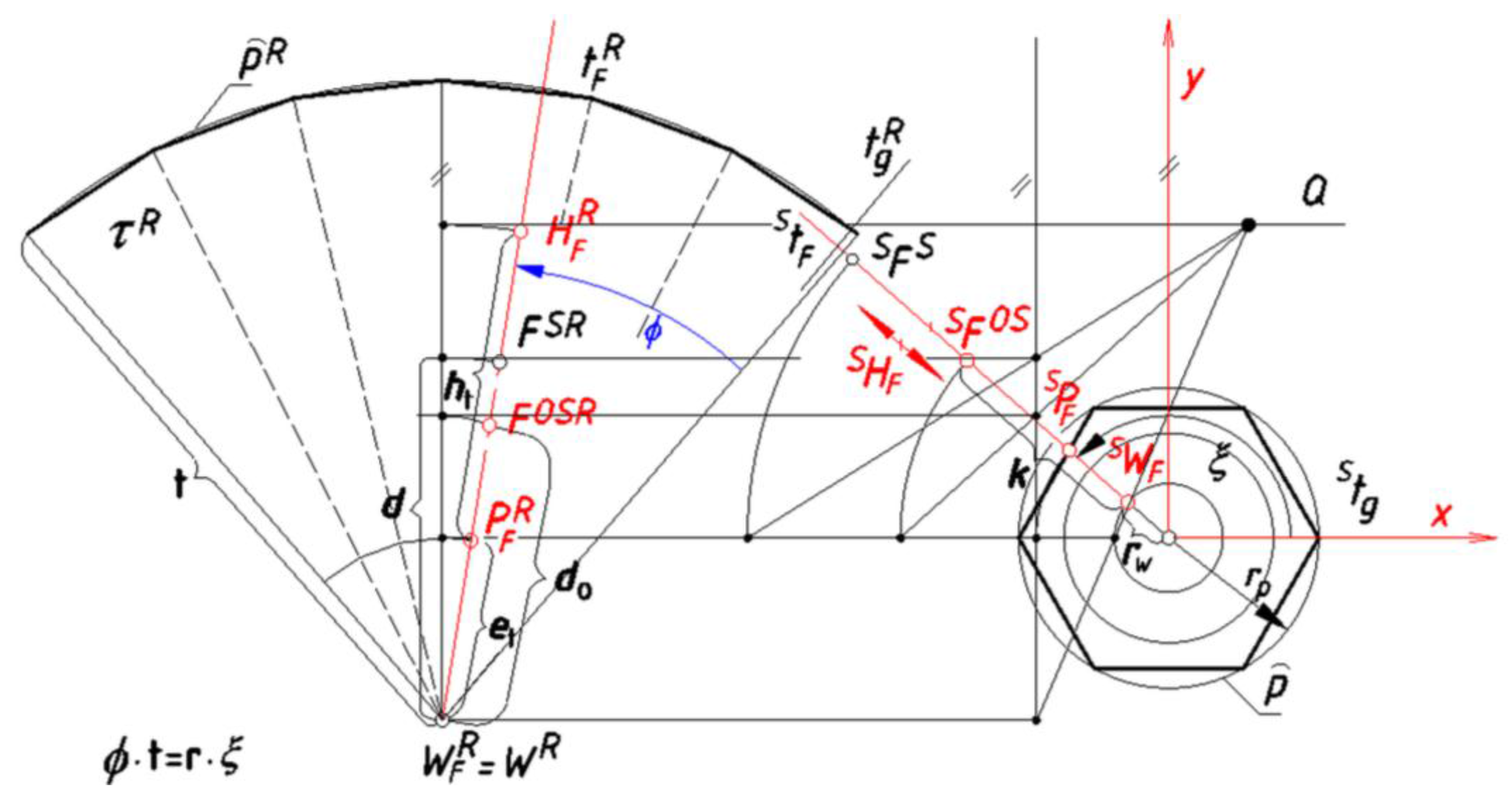
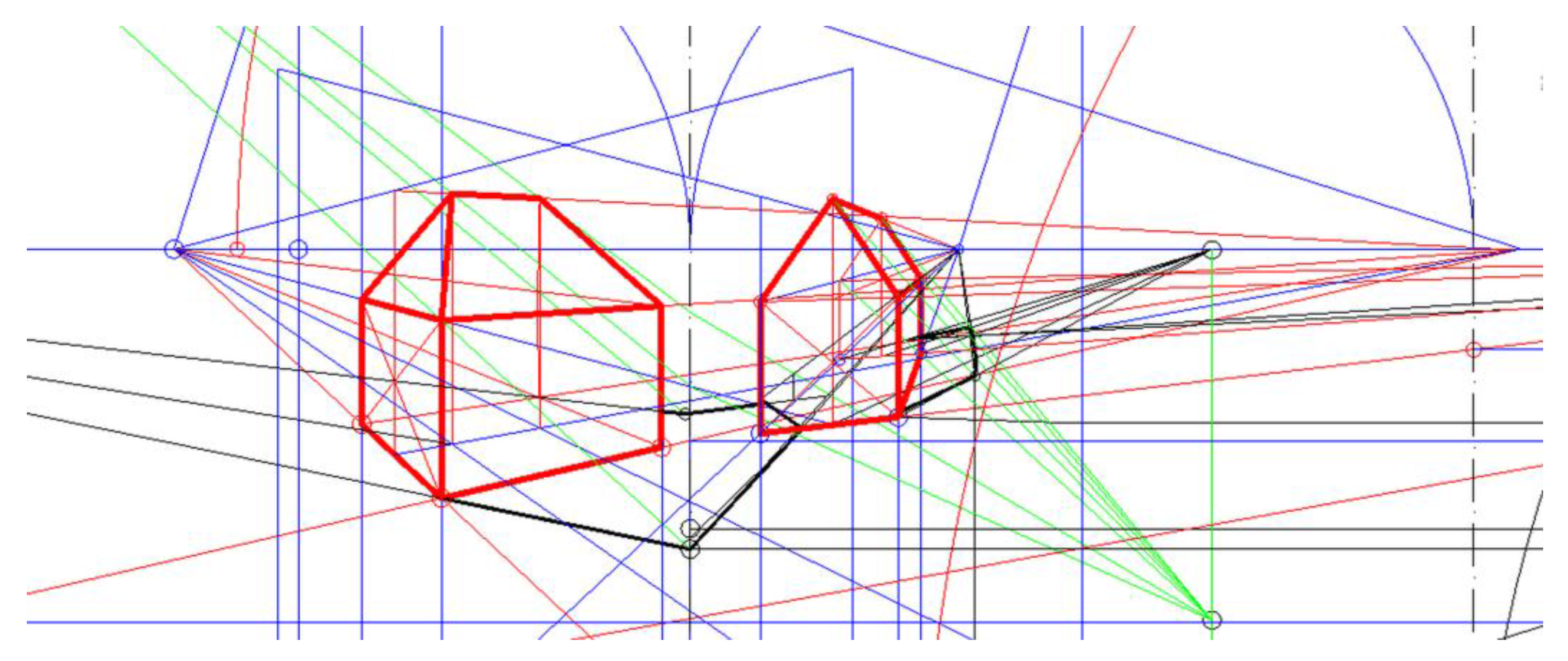
Establishing Equations Displaying Geometrical Relations Occurring during Projection
- the distance of the point SFO,S = FO from the point SW by k;
- the distance of the point FO,SR from the point PFR by do, if the case of the projection on a prism surface;
- the distance of the point FO,SR from the point WR by do, if the case of the projection on a pyramid surface;
- the distance of the point FSR from the point PFR by d, if the case of the projection on a prism surface;
- the distance of the point FSR from the point WR by d, if the case of the projection on a pyramid surface;
- the distance of the point HFR from the point PFR by ht;
- the distance of the point PFR from the point WR by t;
- the distance of the point PF from the point W by et;
- the distance of the point PF from the point SWF by rp, if the case of the projection on a pyramid surface of version B;
- the distance of the point SWF from the center of the base polygon p by rw.
5. Drawing Perspective with Computer Aid
5.1. Methods and Methodology
5.2. Results—Some Examples of the Application of the Algorithms
6. Discussion
Conflicts of Interest
References
- Small, J.P. Skenographia in Brief. In Performance in Greek and Roman Theatre, 1st ed.; Harrison, G.W.M., Liapēs, V., Liapis, V., Eds.; Brill: Leiden, The Netherlands, 2013; Volume 353, pp. 154–196. [Google Scholar]
- Biermann, V.; Borngasser Klein, B.; Evers, B.; Freigang, K.; Gronert, A.; Jobst, K.; Kremeier, J.; Lupfer, G.; Paul, J.; Ruhl, C.; et al. Architectural Theory from the Renaissance to the Present; Taschen Gmbh: Koln, Germany, 2003; pp. 8–126. [Google Scholar]
- Elkins, J. Piero della Francesca and the Renaissance Proof of Linear Perspective. Art Bull. 2014, 69, 220–230. [Google Scholar] [CrossRef]
- Argan, G.C.; Robb, N.A. The Architecture of Brunelleschi and the Origins of Perspective Theory in the Fifteenth Century. J. Warbg. Court. Inst. 1946, 9, 96–121. [Google Scholar] [CrossRef]
- Rapp, J.B. A Geometrical Analysis of Multiple Viewpoint Perspective in the Work of Giovani Battista Piranesi: An Application of Geometric Restitution of Perspective. J. Archit. 2008, 13, 701–736. [Google Scholar] [CrossRef]
- Cocchiarella, L.E. Perspective between Fiction: Pattern Mutations through Science and Art. J. Geom. Graph. 2015, 19, 237–256. [Google Scholar]
- Dusoiu, E.-C. Architectural Representation between Imagination and Revelation. J. Civ. Eng. Archit. 2017, 11, 199–211. [Google Scholar] [CrossRef]
- Hewitt, M. Representational Forms and Modes of Conception; An Approach to the History of Architectural Drawing. J. Archit. Educ. 2014, 39, 2–9. [Google Scholar]
- Unwin, S. Analyzing Architecture through Drawing. Build. Res. Inf. 2007, 35, 101–110. [Google Scholar] [CrossRef]
- Prokopska, A. Methodology of Architectural Design, Preliminary Phases of the Architectural Process; Publishing House of Rzeszow University of Technology: Rzeszow, Poland, 2015; pp. 39–121. (In Polish) [Google Scholar]
- Bruggeman, H.; Yonas, A.; Konczak, J. The Processing of Linear Perspective and Binocular Information for Action and Perception. Neuropsychologia 2007, 45, 1420–1426. [Google Scholar] [CrossRef] [PubMed]
- Elias, R. Projections. In Digital Media; Springer: Cham, Switzerland, 2014; pp. 319–386. [Google Scholar]
- Dzwierzynska, J. Reconstructing Architectural Environment from a Perspective Image. Procedia Eng. 2016, 161, 1445–1451. [Google Scholar] [CrossRef]
- Dzwierzynska, J. Single Image Based Modeling Architecture from a Historical Photograph. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, in press. [Google Scholar]
- Rojas-Sola, J.I.; Romero-Manchado, A. Use of Discrete Gradient Operators for the Automatic Determination of Vanishing Points: Comparative Analysis. Expert Syst. Appl. 2012, 39, 11183–11193. [Google Scholar] [CrossRef]
- Romero-Manchado, A.; Rojas-Sola, J.I. Application of Gradient-Based Edge Detectors to Determine Vanishing Points in Monoscopic Images: Comparative Study. Image Vis. Comput. 2015, 43, 1–15. [Google Scholar] [CrossRef]
- Andalo, F.A.; Taubin, G.; Goldenstein, S. Efficient Height Measurements in Single Images Based on the Detection of Vanishing Points. Comput. Vis. Image Underst. 2015, 138, 51–60. [Google Scholar] [CrossRef]
- Alashaikh, A.H.; Bilani, H.M.; Alsalman, A.S. Modified Perspective Cylindrical Map Projection. Arab. J. Geosci. 2014, 7, 1559–1565. [Google Scholar] [CrossRef]
- Dzwierzynska, J. Descriptive and Computer Aided Drawing Perspective on an Unfolded Polyhedral Projection Surface. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, in press. [Google Scholar]
- Dzwierzynska, J. Cylindrical Panorama-Two Approaches. J. Biul. Pol. Soc. Geom. Eng. Graph. 2009, 19, 9–14. [Google Scholar]
- Dzwierzynska, J. Direct Construction of an Inverse Panorama from a Moving View Point. Procedia Eng. 2016, 161, 1608–1614. [Google Scholar] [CrossRef]
- Pottman, H.; Asperl, A.; Hofer, M.; Kilian, A. Architectural Geometry, 1st ed.; Bentley Institute Press: Exton, PA, USA, 2007; pp. 35–194. [Google Scholar]
- Knill, D.C.; Mammasian, P.; Kersten, D. Geometry of Shadows. J. Opt. Soc. Am. 1997, 14, 3216–3232. [Google Scholar] [CrossRef]
- Mollicone, A. The Theory of Linear Shadows and Chiaro-Scuro. In Proceedings of the Conference: The Ways of Merchants _ X International Forum of Studies, Aversa, Italy, 31 May–1 June 2012. [Google Scholar]
- Pepper, S. Leonardo da Vinci and the Perspective of Light. Fidelino, J. Poetry Sci. Statecraft. 2001, 10, 33–53. [Google Scholar]
- Welsh, W.; Orosz, J. (Eds.) The Discovery of Ellipsoidal Variations in the Kepler Light Curve of Hat-P-7. Astrophys. J. Lett. 2012. [Google Scholar] [CrossRef]
- Trujillo, S.; Hernan, J. Calculation of the Shadow-Penumbra Relation and Its Application on Efficient Architectural Design. Sol. Energy 2014, 110, 139–150. [Google Scholar] [CrossRef]
- Segal, M.; Korobkin, C.; van Widenfelt, R.; Foran, J.; Haeberli, P. Fast Shadows and Lighting Effects Using Texture Mapping. In SIGGRAPH ‘92 Proceedings of the 19th Annual Conference on Computer Graphics and Interactive Techniques, Chicago, IL, USA, 26–31 July 1992; Volume 26, pp. 249–252. [Google Scholar] [CrossRef]
- Dzwierzynska, J. A Conical Perspective Image of an Architectural Object Close to Human Perception. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, in press. [Google Scholar]
- Haglund, L.; Fleet, D.J. Stable Estimation of Image Orientation. In Proceedings of the 1st International Conference on Image Processing, Austin, TX, USA, 13–16 November 1994; pp. 68–72. [Google Scholar]
- Salomon, D. Perspective Projection. In Transformations and Projections in Computer Graphics; Springer-Verlag: London, UK, 2006; pp. 71–144. ISBN 978-1-84628-620-9. [Google Scholar]



© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dzwierzynska, J. Computer-Aided Panoramic Images Enriched by Shadow Construction on a Prism and Pyramid Polyhedral Surface. Symmetry 2017, 9, 214. https://doi.org/10.3390/sym9100214
Dzwierzynska J. Computer-Aided Panoramic Images Enriched by Shadow Construction on a Prism and Pyramid Polyhedral Surface. Symmetry. 2017; 9(10):214. https://doi.org/10.3390/sym9100214
Chicago/Turabian StyleDzwierzynska, Jolanta. 2017. "Computer-Aided Panoramic Images Enriched by Shadow Construction on a Prism and Pyramid Polyhedral Surface" Symmetry 9, no. 10: 214. https://doi.org/10.3390/sym9100214
APA StyleDzwierzynska, J. (2017). Computer-Aided Panoramic Images Enriched by Shadow Construction on a Prism and Pyramid Polyhedral Surface. Symmetry, 9(10), 214. https://doi.org/10.3390/sym9100214




