Abstract
The classical matrix theory is deficient to express the vagueness of the real life. The fuzzy set theory has been successfully applied to bridge this gap. Much work has already been done on a two-person zero sum matrix game with fuzzy goals. In continuation, this paper is dedicated to define and study a multi-criteria two-person zero sum game with intuitionistic fuzzy goals. It is shown that solving such games is equivalent to solving two crisp multi object linear programming problems. Our work generalizes the previous study on a multi-criteria game with fuzzy goals by adopting the approach of linear programming with intuitionistic fuzzy sets. Finally, an illustrative numerical example is provided to elaborate the proposed approach.
1. Introduction
Classically solving the two-person zero sum matrix game is proved to be equivalent to solving two linear programming models. Much work has been done in this direction. Classical mathematics programming has certain deficiencies in modeling all the essences of real life. See the work of Chanas [], Werners [,] and Zimmerman [,,]. Even if some problem is modeled correctly, sometimes the solution does not match the real-life intuition (see Werners []).
In the traditional game theory, each player has predominantly a well-defined quantitative utility function over a set of the player decision space. Each person attempts to optimize the expected utility and each is assumed to know the extensive game in full []. In many of such complex situations, each player has a heuristic knowledge of the desires of the other players and a heuristic knowledge of the control choices that they will make in order to meet their ends. Therefore, the uncertainty should be considered in the game theory problems []. In the recent past, there have been attempts to extend the results of crisp game theory to those conflict resolution problems that are fuzzy in nature, e.g., Sharifan et al. [], Faizi et al. [], and Sun et al. []. These developments have lead to the emergence of a new area in the literature called fuzzy games. Chen et al. have presented a fuzzy differential game theory to solve the n-player nonlinear differential game problems, which are not easily tackled by the conventional methods []. Chekari et al. have worked on fuzzy Nash equilibrium to determine a graded representation of Nash equilibriums in crisp and fuzzy games [,,,,]. This interpretation shows the distribution of equilibriums in the matrix form of a game and handles uncertainties in payoffs [,,].
After the initiation of the fuzzy set theory by Zadeh [], a new era has begun, modeling more uncertainties and vagueness of real life, giving more appropriate solutions that are compatible with human intuition, closer to real life []. The decision theory on the basis of mathematical programming progressed very rapidly in the fuzzy environment. In the 1970s, Bellman and Zadeh [] defined the notions of fuzzy constraints, fuzzy decisions and fuzzy goals, which lead to the development of mathematical programs with fuzzy objective functions, with fuzzy constraints (see Tanaka et al. []). These fuzzy modeling tools are also successfully applied in making and solving a two-person zero sum matrix game in different perspectives. See Campos [], Sakawa and Nishizaki [,], Bector and Chandra []. Many researchers worked in different ways, making a payoff matrix with triangular fuzzy numbers (Vijay et al. [], Li [], interval value matrix games Li [], Nayak and Pal [] and multiple payoff matrices Aggarwal and Khan []).
In many decision problems, the decision makers know not only the degree of membership, but also the degree to which an object does not belong to a set. For this purpose, in 1986, Atanassov introduced the concept of Intuitionistic Fuzzy Set (IFS), which is the extension of a fuzzy set [,]. Despite the IFS’s criticism, it has been successful in modeling more complex real phenomena that cannot be modeled with fuzzy sets. Linear programming models and matrix games are also developed in an intuitionistic fuzzy environment (see Aggarwal et al. [], Angelov [], Chakrabortty et al. [], Dubey et al. []). In 1997, Angelov [] defined the optimization process by converting a decision-making problem in an IFS environment into a crisp linear programming model with a score function of IFS as an objective function. Later, in 2012, Aggarwal et al. [] used the idea of Angelov to develop linear programming with I-fuzzy (Intuitionistic fuzzy) goals and employed it into solving two-person zero sum games with I-fuzzy goals. Recently, Razmi et al. [] studied a multi-object optimization problem in the IFS framework and devolved a common solution of maximizing the degree of satisfaction and minimizing the degree of dissatisfaction.
Matrix games in the intuitionistic fuzzy domain are explored with various ideas. Often the problems in real life lead to multi-object scenarios, which result in multiple payoff matrix games. In literature, mostly single payoff matrix games are studied, and Aggarwal and Khan [] worked with multiple payoff matrices to achieve fuzzy goals, also said to be a multi-criteria two-person zero sum matrix game with fuzzy goals. In this paper, our aim is to generalize their ideal by discussing I-fuzzy goals with many payoff matrices. We generalize the notion of Pareto-Optimal Security Strategies (POSS) and security level to I-fuzzy POSS and I-fuzzy security level, respectively, in order to study I-fuzzy multi-criteria matrix games and prove that I-fuzzy POSS and I-fuzzy security level can be obtained by solving a pair of I-fuzzy multi-criteria linear programming problems. The I-fuzzy goals are taken in the same way as in [].
This paper is organized as follows: in Section 2, basic definitions and arithmetic operations of IFS are given. In Section 3, a detailed review about a (crisp) two-person zero sum multi-criteria matrix game and its generalization with fuzzy goals is given. In Section 4, we extend the work of [] from a two-person zero sum fuzzy multi-criteria matrix game to a two-person I-fuzzy multi-criteria matrix game. Furthermore, the concepts of I-fuzzy POSS and I-fuzzy security level for such games in terms of suitable membership and non-membership functions are presented. The main result of this paper is also presented in this section, which states that solving such an I-fuzzy game is equivalent to solving a pair of (crisp) multi-criteria linear programming problems. In Section 5, an illustrative numerical example is given and a thorough comparison with existing models is presented. Some concluding remarks are presented in the last section.
2. Preliminaries
This section provides some relevant basics of the IFS from [,], which will be used in the following sections.
Definition 1.
Let X be a universal set. An IFS A in a given universal set X is a triplet given by (1):
where the functions and define the degree of membership and the degree of non-membership of an element to the set A, respectively, such that 0 ≤ + ≤ 1. If + = 1; then, IFS A degenerates into a fuzzy set in X.
Definition 2.
Let A and B be two IFSs in the set X. Then, union and intersection of A and B are defined as follows:
Definition 3.
Let A and B be two IFSs in the set X. Then, we say iff and for all
Definition 4.
Let A and B be two IFSs in the set X. Then, iff and for all
Definition 5.
Let A be an IFS in the universal set X. Then, the score function of A is defined as Equation (3):
where
3. Multi-Criteria Zero Sum Game
In this section, a review of (crisp) multi-criteria zero sum game of two persons model (given by Fernandez et al. [], while its generalized model with fuzzy goals was proposed by Aggarwal and Khan in []) are presented.
Let denote the n-dimensional Euclidean space and be its non-negative orthant. Let be matrices with real entries of order , be a vector of ones whose dimension is specified as per the specific context. By a (crisp) multi-criteria zero sum game of two persons G, we mean:
where and are convex polytops. In the terminology of the matrix game theory, and are called strategy spaces for Player I and Player II, respectively, and the matrix is called the payoff matrix corresponding to the criterion. It should also be noted that Player I is taken as a maximizing player and Player II is taken as a minimizing player, as per convention. Furthermore, for , the expected payoff for Player I is defined as a vector = = where = = Since the game is a zero-sum game, the expected payoff for Player II is To define the solution of a game, the following terminologies are used in the literature.
Definition 6.
(Security level for Player I) The security level of Player I for a strategy corresponding to payoff matrix is defined as:
where denotes the column of the matrix Thus, the security level for Player I is a vector of tuples, defined by:
Definition 7.
(Security level for Player II) The security level of Player II for a strategy , corresponding to payoff matrix is defined as:
where denotes the row of the matrix . Thus, the security level for Player I is a vector of tuples, defined by:
Definition 8.
(POSS for Player I) Let be a strategy, then this strategy is called POSS for Player I if there is no such that:
and:
Definition 9.
(POSS for Player II) Let be a strategy, then this strategy is called POSS for Player II if there is no such that:
and:
If is a POSS for Player I, then his security level is given by and the pair is a solution for Player I. In the same way, if is a POSS for player II, then his security level is given by and the pair is the solution for Player II.
Fernandez et al. [] showed that solving the game is equivalent to finding the efficient solutions of a multi-object linear problem, as described in the theorems presented below.
Theorem 1.
The strategy and the vector are POSS and security level for Player I, respectively, iff the pair is an efficient solution to the below multi-criteria programming problem;
subject to,
Theorem 2.
The strategy and the vector are POSS and security level for Player II, respectively, iff the pair is an efficient solution to the below multi-criteria programming problem;
subject to,
Aggarwal and Khan [] proposed the generalized version of this game with fuzzy goals as,
where , and , are the inspiration levels, tolerance levels of Player I and Player II, respectively, and the inequalities ≳ and ≲ are fuzzy inequalities taken in the sense of Zimmermann []. They adopt the model of Bector et al. [] and showed that solving the game is equivalent to solving the crisp multi-object linear problems (see [] Theorem 3.5, Theorem 3.6).
4. The Proposed Multi-Criteria Matrix Game Model with I-Fuzzy Goals
The IFS theory deals with more vague situations. Much work [,,,,] has already been done to make and solve models of I-fuzzy linear programming and duality. Aggarwal et al. [] defined the I-fuzzy inequalities and in a pessimistic or optimistic approach of decision-making. Following their lines, a multi-criteria multi-objective two-person zero sum matrix game with I-fuzzy goals will be defined.
Let and be the strategies spaces of Player I and Player II, respectively, and be the payoff matrix of criteria as defined earlier. The Multi-Object Intuitionistic Fuzzy Game denoted as MOIFG is:
where and are the levels of inspiration for Player I and Player II, respectively. The I-fuzzy inequalities and are taken either in a pessimistic or optimistic approach. The problem for Player I with payoff matrix is to find out in such a way that:
that is equivalent to:
where denotes the column of Analogously, for Player II, the problem is to find out in such a way that:
which is equivalent to:
where denotes the row of
To define the membership and non membership functions of IFS related to I-fuzzy inequalities, certain tolerance levels are needed. Let , be the tolerance levels pre-specified by Player I for accepting or rejecting the inspiration level related to criteria and, similarly, , be the tolerance levels pre-specified by Player II for accepting or rejecting the inspiration level . Therefore,
The membership functions and non-membership functions are defined in a similar way to [] for both Player I and Player II for the I-fuzzy inequities. From here on, only a pessimistic approach is taken, and the case of optimistic approach is analogous. The membership and non-membership functions for Player I related to .
Similarly, for Player II, the membership and non-membership functions associated with .
To properly express the solution of this game, some definitions are needed.
Definition 10.
Let be a strategy, then the I-fuzzy security level of satisfaction for Player I corresponding to payoff matrix is defined by:
i.e.,
Thus, an I-fuzzy security level of satisfaction for Player I is a vector of tuples, defined by:
Definition 11.
Let be a strategy, and then the I-fuzzy security level of satisfaction for Player II corresponding to payoff matrix is defined by:
i.e.,
Thus, an I-fuzzy security level of satisfaction for Player II is a vector of tuples, defined by:
Definition 12.
Let be a strategy; then, this strategy is called an I-fuzzy POSS for Player I if there is no such that:
i.e.,
and:
Definition 13.
Let be a strategy; then, this strategy is called an I-fuzzy POSS for Player II if there is no such that:
i.e.,
and:
The level of security for Player I is given by if is an I-fuzzy POSS for Player I. Similarly, the level of security for Player II is given by If is an I-fuzzy POSS for Player II, the pair is then understood as a solution of the given two-person zero sum game for Player I. The pair is interpreted in the same way as a solution of the given game multi-criteria intuitionistic fuzzy matrix for Player II.
Our aim is to prove the equivalence between solving MOIFG (16) and solving the following two (crisp) multi-object linear programming problems named CMPI (Crisp Model Player I) and CMPII (Crisp Model Player II) for Player I and Player II, respectively.
Models: Let denote the minimal degree of acceptance and denote the maximal degree of rejection of the I-fuzzy constraint of Player I. Similarly, let denote the minimal degree of acceptance and denote the maximal degree of I-fuzzy constraints of Player II. Then, consider:
subject to,
subject to,
where and denote the column and the row of respectively.
Usually, in multi-criteria linear programming, the problems’ global solutions are rare, and, most of the time, we have Pareto-optimal solutions, also known as efficient solutions; for details, one can see Steuer [].
Theorem 3.
The strategy and the vector are I-fuzzy POSS and I-fuzzy security level of satisfaction for Player I, respectively, iff the pair is an efficient solution to the multi-criteria programming problem below
Proof.
Suppose that is an I-fuzzy POSS for Player I; then, by definition, there is no such that:
Thus, for all either or there is some index p, relative to x, such that
That is, for each , either = , or there is some index such that ≤ .
Therefore, by the definition of efficient solution, is an efficient solution of the multi-criteria I-fuzzy programming problem
Now, using the representations of the various membership functions and non-membership functions given in Equations (17) and (18), respectively, we get:
Conversely, assuming, on the contrary, that the efficient solution of CMFPI is not an I-fuzzy POSS for Player I, then, there is some , such that:
Theorem 4.
The strategy and the vector are I-fuzzy POSS and I-fuzzy security level of satisfaction for Player II, respectively, iff the pair is an efficient solution to the multi-criteria programming problem below:
Proof.
The proof can be easily done in the same fashion as the proof of Theorem . ☐
The next step is to determine the relationship between duality and , in I-fuzzy logic. For this, first turn the two problems in their scalar counter parts using a weighted sum approach with the same weight. In the same vein, consider the weights which are associated with the objective function of and , and obtain the scalar counter entirety as and , respectively, as follows:
and:
The following theorem will establish a weak duality between and in the I-fuzzy sense.
Theorem 5.
Let and be feasible for and , respectively. Then,
Proof.
The proof can be easily done in the same fashion as the proof of [] Theorem 1. ☐
Figure 1 presents a flowchart of the proposed approach, i.e., application of intuitionistic-fuzzy goals in multi-criteria matrix games. In the following steps, for each player, the following are determined: strategy space, inspiration levels, the tolerance levels, an intuitionistic fuzzy security level of satisfaction, intuitionistic fuzzy Pareto-optimal security strategy, the level of security, a minimal degree of acceptance and maximal degree of rejection. The final results are obtained by solving a multi-object linear programming problem for each player separately.
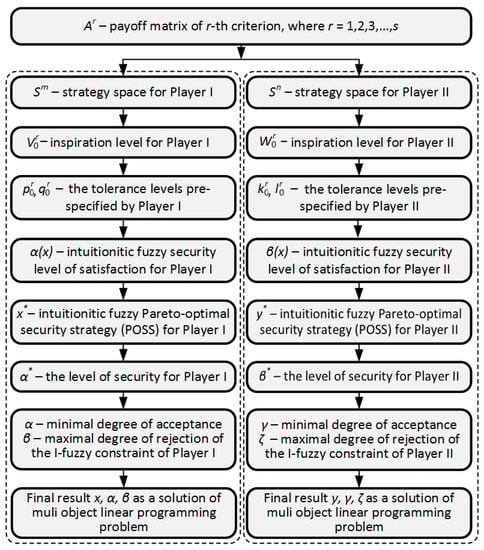
Figure 1.
The flowchart of the proposed approach.
The computational complexity of the proposed approach is equivalent to the computational complexity of multi-criteria linear programming problems. The worst case complexity of multi-objective optimization problems has been shown to be NP-hard (non-deterministic polynomial-time hard). However, linear programming shows the theoretical (but far from practical) polynomial solvability of multi-criteria linear programming, and the possibility of computing non-dominated extreme points in multi-criteria linear programming with polynomial delay [].
5. Illustrative Example
To illustrate our multi-criteria model and show its resourcefulness, the same example is solved as taken by Cook [], Nishizaki and Sakwaw [] and Aggarwal and Imran []. The choice of this example will lead us to making a comprehensive comparison with the existing models. The Matlab (R2012a, 7.14.0.739, MathWorks, Natick, Massachusetts, United States) is used to acquire the numerical results.
Example 1.


Consider the following payoff matrices
described as the cost matrix, the time matrix and the productivity matrix, respectively. For Player I, the parameters are chosen as follows: , , , , , , , and . Therefore, the multi-criteria problem for Player I is subject to:
Table 1 shows the acquired results that looks promising as in all of the solutions.

Table 1.
I-fuzzy Pareto-optimal security strategies (POSS) and securities for Player I.
For Player II, the following parameters are chosen: , , , , , , , and . Therefore, the multi-criteria problem for Player II is:
Solving the above model yields a good payoff for Player II as , shown in Table 2.

Table 2.
I-fuzzy POSS and securities levels for Player II.
5.1. Comparison with Existing Models
In [], Nishizaki and Sakwaw presented their model to solve a two-person zero sum game with fuzzy goals. Their approach was to aggregate membership functions related to payoff’s matrices by taking the minimum. Altogether, their solution achieved aggregated fuzzy goals and critical information about the individual fuzzy goal is missing. The results after applying their model to Example 1 are as follows.
The solution model of Aggarwal and Khan [] is much better, as it explicitly deals with the individual fuzzy goal related to the different criteria; in addition, their results are far better. Their solutions to Example 1 are presented in Table 3 and Table 4 for Player I and Player II respectively.

Table 3.
Aggarwal and Khan [] for Player I.

Table 4.
Aggarwal and Khan [] for Player II.
The proposed model takes the fuzzy goals as a sub case, the advantages of our model and its superiority over the exiting models are summarized as follows.
- From Table 5, the disadvantages of Nishizaki and Sakwaw’s model are apparent, and it does not give information about fuzzy goals and strategies regarding the individual criteria, whereas the inspection of Table 1, Table 2 will reveal the strategies optimized for all the three criteria: cost, time and productivity.
 Table 5. Nishizaki and Sakwaw [].
Table 5. Nishizaki and Sakwaw []. - In addition, there are some other lapses in the Nishizaki and Sakwaw’s model, like the slight error in the linear programming model for Player II explained in [,], and our model produces much better strategies with higher securities as and
- For Player I, whereas for all the strategies in Aggarwal and Khan’s model.
- For Player II, but in Aggarwal and Khan’s model for all the strategies.
6. Conclusions
In this paper, a new game with I-fuzzy goals named MOIFG has been constructed for solving multi-criteria programming problems, which is different from MOFG that was studied by Aggarwal and Khan []. For the solution of such games, certain definitions of I-fuzzy POSS and I-fuzzy security level are also defined. We have also extended the results (see [] Theorem 3.5, Theorem 3.6) by showing that solving MOIFG is equivalent to solving a pair of multi-criteria linear programming problems. Furthermore, a duality result is obtained that helps us to study a two-person zero sum multi-criteria game having I-fuzzy goals by taking motivation from Aggarwal et al. []. Although we have derived these results only for a pessimistic approach, for an optimistic approach, these are analogous. In addition, it is clear that the proposed models in this paper are a generalization of those developed by Aggarwal et al. []. It has been shown that the models of the multi-criteria two-person zero sum game with intuitionistic fuzzy goals can be used for the intuitionistic fuzzy matrix game. Finally, by illustrating a numerical example, it is shown that the solution with our approach is much better than those of Aggarwal and Khan []. It would be interesting to extend this approach for other types of games with different extensions of fuzzy parameters and goals using other concepts of solutions and other types of membership functions.
Acknowledgments
The work was supported by the National Science Centre, Decision No. DEC-2016/23/N/HS4/01931, and by the Faculty of Computer Science and Information Technology, West Pomeranian University of Technology, Szczecin statutory funds.
Author Contributions
Zia Bashir and Jarosław Wątróbski conceived and worked together to develop conceptions, assumptions, methods, and text. Jawad Ali and Jarosław Wątróbski conducted research. Zia Bashir and Wojciech Sałabun developed study results. Tabasam Rashid had research supervising.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chanas, S. The use of parametric programming in fuzzy linear programming. Fuzzy Sets Syst. 1983, 11, 229–241. [Google Scholar] [CrossRef]
- Werner, B. An interactive fuzzy programming systems. Fuzzy Sets Syst. 1987, 23, 131–147. [Google Scholar] [CrossRef]
- Werner, B. Interactive multiple object programming subject to flexible constraints. Eur. J. Oper. Res. 1987, 31, 342–349. [Google Scholar] [CrossRef]
- Zimmerman, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Zimmerman, H.J. Latent connectives in human decision making. Fuzzy Sets Syst. 1980, 4, 291–298. [Google Scholar] [CrossRef]
- Zimmerman, H.J. Application of fuzzy set theory to mathematical programming. Inf. Sci. 1985, 36, 29–58. [Google Scholar] [CrossRef]
- Bector, C.R.; Chandra, S. Fuzzy Mathematical Programming and Fuzzy Matrix Games; Springer: Berlin, Germany, 2005; Volume 169. [Google Scholar]
- Faizi, S.; Rashid, T.; Sałabun, W.; Zafar, S.; Wątróbski, J. Decision making with uncertainty using hesitant fuzzy sets. Int. J. Fuzzy Syst. 2017, 1–11. [Google Scholar] [CrossRef]
- Sharifian, S.; Chakeri, A.; Sheikholeslam, F. Linguisitc representation of Nash equilibriums in fuzzy games. In Proceedings of the 2010 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), Toronto, ON, Canada, 12–14 July 2010; pp. 1–6. [Google Scholar]
- Faizi, S.; Sałabun, W.; Rashid, T.; Wątróbski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Sun, L.; Liu, Y.; Zhang, B.; Shang, Y.; Yuan, H.; Ma, Z. An integrated decision-making model for transformer condition assessment using game theory and modified evidence combination extended by D numbers. Energies 2016, 9, 697. [Google Scholar] [CrossRef]
- Chen, B.S.; Tseng, C.S.; Uang, H.J. Fuzzy differential games for nonlinear stochastic systems: Suboptimal approach. IEEE Trans. Fuzzy Syst. 2002, 10, 222–233. [Google Scholar] [CrossRef]
- Chakeri, A.; Dariani, A.N.; Lucas, C. How can fuzzy logic determine game equilibriums better? In Proceedings of the 4th International IEEE Conference Intelligent Systems, Varna, Bulgaria, 6–8 September 2008; Volume 1, pp. 2–51. [Google Scholar]
- Chakeri, A.; Habibi, J.; Heshmat, Y. Fuzzy type-2 Nash equilibrium. In Proceedings of the Computational Intelligence for Modelling Control & Automation, Vienna, Austria, 10–12 December 2008; pp. 398–402. [Google Scholar]
- Chakeri, A.; Sadati, N.; Dumont, G.A. Nash equilibrium strategies in fuzzy games. In Game Theory Relaunched; InTech: Rijeka, Croatia, 2013. [Google Scholar]
- Chakeri, A.; Sadati, N.; Sharifian, S. Fuzzy Nash equilibrium in fuzzy games using ranking fuzzy numbers. In Proceedings of the 2010 IEEE International Conference on Fuzzy Systems (FUZZ), Barcelona, Spain, 18–23 July 2010; pp. 1–5. [Google Scholar]
- Chakeri, A.; Sheikholeslam, F. Fuzzy Nash equilibriums in crisp and fuzzy games. IEEE Trans. Fuzzy Syst. 2013, 21, 171–176. [Google Scholar] [CrossRef]
- Garagic, D.; Cruz, J.B. An approach to fuzzy noncooperative nash games. J. Optim. Theory Appl. 2003, 118, 475–491. [Google Scholar] [CrossRef]
- Qiu, D.; Xing, Y.; Chen, S. Solving multi-objective matrix games with fuzzy payoffs through the lower limit of the possibility degree. Symmetry 2017, 9, 130. [Google Scholar] [CrossRef]
- Tan, C.; Jiang, Z.Z.; Chen, X.; Ip, W.H. A Banzhaf function for a fuzzy game. IEEE Trans. Fuzzy Syst. 2014, 22, 1489–1502. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Sałabun, W.; Piegat, A. Comparative analysis of MCDM methods for the assessment of mortality in patients with acute coronary syndrome. Artif. Intell. Rev. 2016, 1–15. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision making in fuzzy environment. Manag. Sci. 1970, 17, B141–B146. [Google Scholar] [CrossRef]
- Tanaka, H.; Okuda, T.; Asai, K. On fuzzy mathematical programming. J. Cybern. 1974, 3, 37–46. [Google Scholar] [CrossRef]
- Campos, L. Fuzzy linear programming models to solve fuzzy matrix games. Fuzzy Sets Syst. 1989, 32, 275–289. [Google Scholar] [CrossRef]
- Nishizaki, I.; Sakwaw, M. Fuzzy and Multi-Criteria Games for Conflict Resolution; Physica-Verlag: Berlin, Germany, 2001. [Google Scholar]
- Sakawa, M.; Nishizaki, I. Max-min solutions for fuzzy multiobjective matrix games. Fuzzy Sets Syst. 1994, 61, 265–275. [Google Scholar] [CrossRef]
- Bector, C.R.; Chandra, S.; Vidyottama, V. Matrix gameswith fuzzy goals and fuzzy linear programming duality. Fuzzy Optim. Decis. Mak. 2004, 3, 255–269. [Google Scholar] [CrossRef]
- Vijay, V.; Chandra, S.; Bector, C.R. Matrix games with fuzzy goals and fuzzy payoffs. Omega 2005, 33, 425–429. [Google Scholar] [CrossRef]
- Li, D.F. Lexicographic method for matrix games with payoffs of triangular fuzzy numbers. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2008, 16, 371–389. [Google Scholar] [CrossRef]
- Li, D.F. Linear programming approach to solve interval-valued matrix games. Omega 2011, 39, 655–666. [Google Scholar] [CrossRef]
- Nayak, P.K.; Pal, M. Linear programming technique to solve two person matrix gams with interval pay-offs. Asia Pac. J. Oper. Res. 2009, 26, 285–305. [Google Scholar] [CrossRef]
- Aggarwal, A.; Khan, I. Solving multi-criteria fuzzy matrix games via multi-criteria linear programming approach. Kybernetika 2016, 52, 153–168. [Google Scholar]
- Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic Fuzzy Sets. Theory and Applications; Physica-Verlag: Heidelberg, Germany, 1999. [Google Scholar]
- Aggarwal, A.; Mehra, A.; Chandra, S. Application of linear programming with I-fuzzy sets to matrix games with I-fuzzy goals. Fuzzy Optim. Decis. Mak. 2012, 11, 465–480. [Google Scholar] [CrossRef]
- Angelov, P.P. Optimization in an intuitionistic fuzzy environment. Fuzzy Sets Syst. 1997, 86, 299–306. [Google Scholar] [CrossRef]
- Chakrabortty, S.; Pal, M.; Nayak, P.K. Intuitionistic fuzzy optimization technique for Pareto optimal solution of manufacturing inventory models with shortages. Eur. J. Oper. Res. 2013, 228, 381–387. [Google Scholar] [CrossRef]
- Dubey, D.; Chandra, S.; Mehra, A. Fuzzy linear programming under interval uncertainty based on IFS representation. Fuzzy Sets Syst. 2012, 188, 68–87. [Google Scholar] [CrossRef]
- Razim, J.; Jafarian, E.; Amin, S.H. An intuitionistic fuzzy goal programming approach for finding pareto-optimal solutions to multi-criteria programming problems. Exp. Syst. Appl. 2016, 65, 181–193. [Google Scholar] [CrossRef]
- Fernandez, F.R.; Puerto, J. Vector linear programming in zero sum multicriteria matrix games. J. Optim. Theory Appl. 1996, 89, 115–127. [Google Scholar] [CrossRef]
- Garg, H.; Rani, M.; Sharma, S.P.; Vishwakarma, Y. Intuitionistic fuzzy optimization technique for solving multi-criteria reliability optimization problems in interval environment. Exp. Syst. Appl. 2014, 41, 3157–3167. [Google Scholar] [CrossRef]
- Steuer, R.E. Multi Criteria Optimization: Theory, Computation and Application; John Wiley: New York, NY, USA, 1986. [Google Scholar]
- Bubeck, S. Convex optimization: Algorithms and complexity. Found. Trends Mach. Learn. 2015, 8, 231–357. [Google Scholar] [CrossRef]
- Cook, C.R. Zero-sum games with multiple goals. Nav. Res. Logist. Quart. 1976, 23, 615–622. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).