The Simultaneous Local Metric Dimension of Graph Families

Abstract

In a graph $G=(V,E)$, a vertex $v\in V$ is said to distinguish two vertices x and y if $d_G(v,x)\ne d_G(v,y)$. A set $S\subseteq V$ is said to be a local metric generator for G if any pair of adjacent vertices of G is distinguished by some element of S. A minimum local metric generator is called a local metric basis and its cardinality the local metric dimension of G. A set $S\subseteq V$ is said to be a simultaneous local metric generator for a graph family $\mathcal{G}=\{G_1,G_2,\dots ,G_k\}$, defined on a common vertex set, if it is a local metric generator for every graph of the family. A minimum simultaneous local metric generator is called a simultaneous local metric basis and its cardinality the simultaneous local metric dimension of $\mathcal{G}$. We study the properties of simultaneous local metric generators and bases, obtain closed formulae or tight bounds for the simultaneous local metric dimension of several graph families and analyze the complexity of computing this parameter.

1. Introduction

A generator of a metric space is a set S of points in the space with the property that every point of the space is uniquely determined by its distances from the elements of S. Given a simple and connected graph $G=(V,E)$, we consider the function $d_G:V\times V\to \mathbb{N}$, where $d_G(x,y)$ is the length of the shortest path between u and v and $\mathbb{N}$ is the set of non-negative integers. Clearly, $(V,d_G)$ is a metric space, i.e., $d_G$ satisfies $d_G(x,x)=0$ for all $x\in V$, $d_G(x,y)=d_G(y,x)$ for all $x,y\in V$ and $d_G(x,y)\le d_G(x,z)+d_G(z,y)$ for all $x,y,z\in V$. A vertex $v\in V$ is said to distinguish two vertices x and y if $d_G(v,x)\ne d_G(v,y)$. A set $S\subseteq V$ is said to be a metric generator for G if any pair of vertices of G is distinguished by some element of S.

Metric generators were introduced by Blumental [1] in the general context of metric spaces. They were later introduced in the context of graphs by Slater in [2], where metric generators were called locating sets, and, independently, by Harary and Melter in [3], where metric generators were called resolving sets. Applications of the metric dimension to the navigation of robots in networks are discussed in [4] and applications to chemistry in [5,6]. This invariant was studied further in a number of other papers including, for instance [7,8,9,10,11,12,13,14,15,16,17,18,19,20].

As pointed out by Okamoto et al. in [21], there exist applications where only neighboring vertices need to be distinguished. Such applications were the basis for the introduction of the local metric dimension. A set $S\subseteq V$ is said to be a local metric generator for G if any pair of adjacent vertices of G is distinguished by some element of S. A minimum local metric generator is called a local metric basis and its cardinality the local metric dimension of G, denoted by ${dim}_l\left(G\right)$. Additionally, Jannesari and Omoomi [16] introduced the concept of adjacency resolving sets as a result of considering the two-distance in $V\left(G\right)$, which is defined as $d_{G,2}(u,v)=min\{d_G(u,v),2\}$ for any two vertices $u,v\in V\left(G\right)$. A set of vertices $S^{\prime }$ such that any pair of vertices of $V\left(G\right)$ is distinguished by an element s in $S^{\prime }$ considering the two-distance in $V\left(G\right)$ is called an adjacency generator for G. If we only ask $S^{\prime }$ to distinguish the pairs of adjacent vertices, we call $S^{\prime }$ a local adjacency generator. A minimum local adjacency generator is called a local adjacency basis, and the cardinality of any such basis is the local adjacency dimension of G, denoted ${adim}_l\left(G\right)$.

The notion of simultaneous metric dimension was introduced in the framework of the navigation problem proposed in [4], where navigation was studied in a graph-structured framework in which the navigating agent (which was assumed to be a point robot) moves from node to node of a “graph space”. The robot can locate itself by the presence of distinctively-labeled “landmark” nodes in the graph space. On a graph, there is neither the concept of direction, nor that of visibility. Instead, it was assumed in [4] that a robot navigating on a graph can sense the distances to a set of landmarks. Evidently, if the robot knows its distances to a sufficiently large set of landmarks, its position on the graph is uniquely determined. This suggests the following problem: given a graph G, what are the fewest number of landmarks needed and where should they be located, so that the distances to the landmarks uniquely determine the robot’s position on G? Indeed, the problem consists of determining the metric dimension and a metric basis of G. Now, consider the following extension of this problem, introduced by Ramírez-Cruz, Oellermann and Rodríguez-Velázquez in [22]. Suppose that the topology of the navigation network may change within a range of possible graphs, say $G_1,G_2,\dots ,G_k$. This scenario may reflect several situations, for instance the simultaneous use of technologically-differentiated redundant sets of landmarks, the use of a dynamic network whose links change over time, etc. In this case, the above-mentioned problem becomes determining the minimum cardinality of a set S, which must be simultaneously a metric generator for each graph $G_i$, $i\in \{1,\dots ,k\}$. Therefore, if S is a solution for this problem, then each robot can be uniquely determined by the distance to the elements of S, regardless of the graph $G_i$ that models the network at each moment. Such sets we called simultaneous metric generators in [22], where, by analogy, a simultaneous metric basis was defined as a simultaneous metric generator of minimum cardinality, and this cardinality was called the simultaneous metric dimension of the graph family $\mathcal{G}$, denoted by $Sd\left(\mathcal{G}\right)$.

In this paper, we recover Okamoto et al.’s observation that in some applications, it is only necessary to distinguish neighboring vertices. In particular, we consider the problem of distinguishing neighboring vertices in a multiple topology scenario, so we deal with the problem of finding the minimum cardinality of a set S, which must simultaneously be a local metric generator for each graph $G_i$, $i\in \{1,\dots ,k\}$.

Given a family $\mathcal{G}=\{G_1,G_2,\dots ,G_k\}$ of connected graphs $G_i=(V,E_i)$ on a common vertex set V, we define a simultaneous local metric generator for $\mathcal{G}$ as a set $S\subseteq V$ such that S is simultaneously a local metric generator for each $G_i$. We say that a minimum simultaneous local metric generator for $\mathcal{G}$ is a simultaneous local metric basis of $\mathcal{G}$ and its cardinality the simultaneous local metric dimension of $\mathcal{G}$, denoted by ${Sd}_l\left(\mathcal{G}\right)$ or explicitly by ${Sd}_l(G_1,G_2,\dots ,G_k)$. 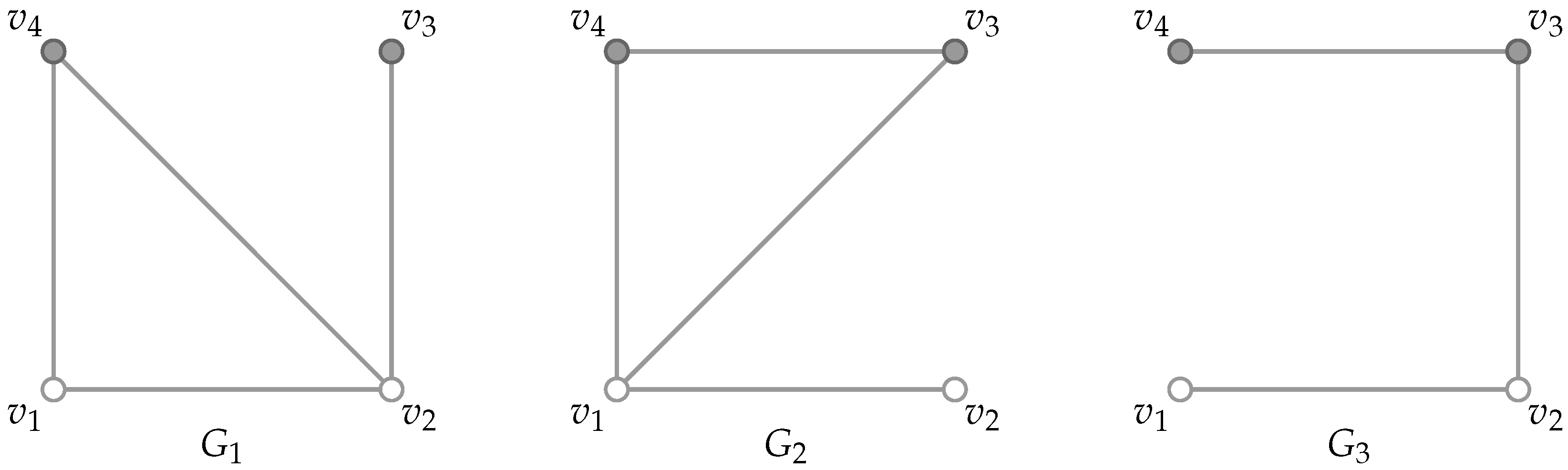An example is shown in Figure 1, where the set $\{v_3,v_4\}$ is a simultaneous local metric basis of $\{G_1,G_2,G_3\}$.

It will also be useful to define the simultaneous local adjacency dimension of a family $\mathcal{G}=\{G_1,G_2,\cdots ,G_k\}$ of connected graphs $G_i=(V,E_i)$ on a common vertex set V, as the cardinality of a minimum set $S\subseteq V$ such that S is simultaneously a local adjacency generator for each $G_i$. We denote this parameter as ${Sad}_l\mathcal{G}$.

In what follows, we will use the notation $K_n$, $K_{r,s}$, $C_n$, $N_n$ and $P_n$ for complete graphs, complete bipartite graphs, cycle graphs, empty graphs and path graphs of order n, respectively. Given a graph $G=(V,E)$ and a vertex $v\in V,$ the set $N_G\left(v\right)=\{u\in V:u\sim v\}$ is the open neighborhood of v, and the set $N_G\left[v\right]=N_G\left(v\right)\cup \left\{v\right\}$ is the closed neighborhood of v. Two vertices $x,y\in V\left(G\right)$ are true twins in G if $N_G\left[x\right]=N_G\left[y\right]$, and they are false twins if $N_G\left(x\right)=N_G\left(y\right)$. In general, two vertices are said to be twins if they are true twins or they are false twins. As usual, a set $A\subseteq V\left(G\right)$ is a vertex cover for G if for every $uv\in E\left(G\right)$, $u\in A$ or $v\in A$. The vertex cover number of G, denoted by $\beta \left(G\right)$, is the minimum cardinality of a vertex cover of G. The remaining definitions will be given the first time that the concept appears in the text.

The rest of the article is organized as follows. In Section 2, we obtain some general results on the simultaneous local metric dimension of graph families. Section 3 is devoted to the case of graph families obtained by small changes on a graph, while in Section 4 and Section 5, we study the particular cases of families of corona graphs and families of lexicographic product graphs, respectively. Finally, in Section 6, we show that the problem of computing the simultaneous local metric dimension of graph families is NP-hard, even when restricted to families of graphs that individually have a (small) fixed local metric dimension.

2. Basic Results

Remark 1.

Let $\mathcal{G}=\{G_1,\cdots ,G_k\}$ be a family of connected graphs defined on a common vertex set V, and let $G^{\prime }=(V,\cup E\left(G_i\right))$. The following results hold:

1.

${Sd}_l\left(\mathcal{G}\right)\ge {\displaystyle \underset{i\in \{1,\cdots ,k\}}{max}}\left\{{dim}_l\left(G_i\right)\right\}$.

2.

${Sd}_l\left(\mathcal{G}\right)\le Sd\left(\mathcal{G}\right)$.

3.

${Sd}_l\left(\mathcal{G}\right)\le min\left\{{\displaystyle \beta \left(G^{\prime }\right),\sum _{i=1}^k{dim}_l\left(G_i\right)}\right\}$.

Proof. 

(1) is deduced directly from the definition of simultaneous local metric dimension. Let B be a simultaneous metric basis of $\mathcal{G}$, and let $u,v\in V-B$ be two vertices not in B, such that $u{\sim }_{G_i}v$ in some $G_i$. Since in $G_i$ there exists $x\in B$ such that $d_{G_i}(u,x)\ne d_{G_i}(v,x)$, B is a simultaneous local metric generator for $\mathcal{G}$, so (2) holds. Finally, (3) is obtained from the following facts: (a) the union of local metric generators for all graphs in $\mathcal{G}$ is a simultaneous local metric generator for $\mathcal{G}$, which implies that ${Sd}_l\left(\mathcal{G}\right)\le {\sum }_{i=1}^k{dim}_l\left(G_i\right)$; (b) any vertex cover of $G^{\prime }$ is a local metric generator of $G_i$, for every $G_i\in \mathcal{G}$, which implies that ${Sd}_l\left(\mathcal{G}\right)\le \beta \left(G^{\prime }\right)$. ☐

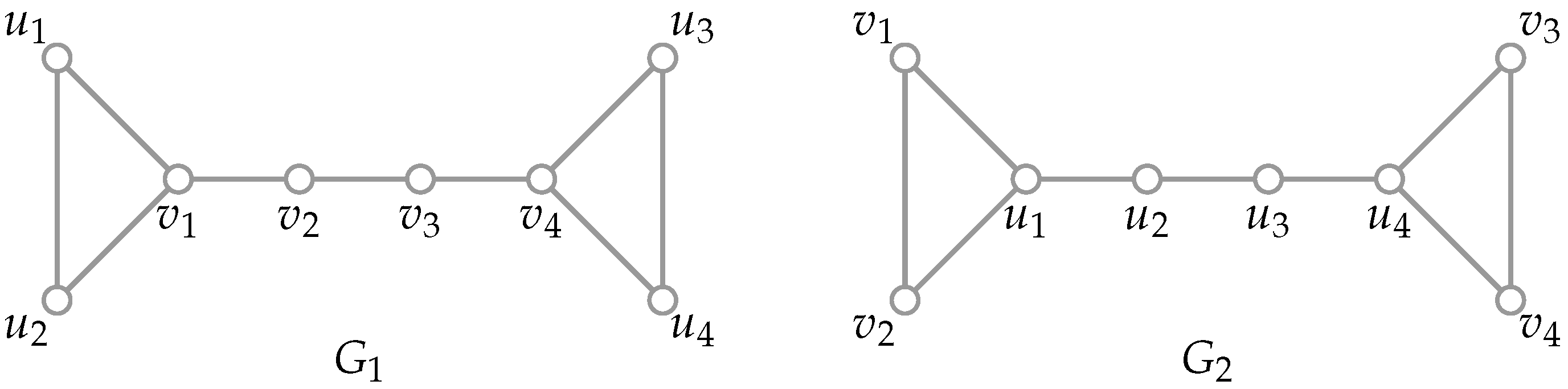
The inequalities above are tight. For example, the graph family $\mathcal{G}$ shown in Figure 1 satisfies ${Sd}_l\left(\mathcal{G}\right)=Sd\left(\mathcal{G}\right)$, whereas ${\displaystyle {Sd}_l\left(\mathcal{G}\right)=2={dim}_l\left(G_1\right)={dim}_l\left(G_2\right)=\underset{i\in \{1,2,3\}}{max}\left\{{dim}_l\left(G_i\right)\right\}}$. Moreover, the family $\mathcal{G}$ shown in Figure 2 satisfies ${\displaystyle {Sd}_l\left(\mathcal{G}\right)=3=\left|V\right|-1<\sum _{i=1}^6{dim}_l\left(G_i\right)=12}$, whereas the family $\mathcal{G}=\{G_1,G_2\}$ shown in Figure 3 satisfies ${Sd}_l\left(\mathcal{G}\right)=4={dim}_l\left(G_1\right)+{dim}_l\left(G_2\right)<\left|V\right|-1=7$.

We now analyze the extreme cases of the bounds given in Remark 1.

Corollary 1.

Let $\mathcal{G}$ be a family of connected graphs on a common vertex set. If $K_n\in \mathcal{G}$, then:

$${Sd}_l\left(\mathcal{G}\right)=n-1.$$

As shown in Figure 2, the converse of Corollary 1 does not hold. In general, the cases for which the upper bound ${Sd}_l\left(\mathcal{G}\right)\le \left|V\right|-1$ is reached are summarized in the next result.

Theorem 1.

Let $\mathcal{G}$ be a family of connected graphs on a common vertex set V. Then, ${Sd}_l\left(\mathcal{G}\right)=\left|V\right|-1$ if and only if for every $u,v\in V$, there exists a graph $G_{uv}\in \mathcal{G}$ such that u and v are true twins in $G_{uv}$.

Proof. 

We first note that for any connected graph $G=(V,E)$ and any vertex $v\in V$, it holds that $V-\left\{v\right\}$ is a local metric generator for G. Therefore, if ${Sd}_l\left(\mathcal{G}\right)=\left|V\right|-1$, then for any $v\in V$, the set $V-\left\{v\right\}$ is a simultaneous local metric basis of $\mathcal{G}$, and as a consequence, for every $u\in V-\left\{v\right\}$, there exists a graph $G_{uv}\in \mathcal{G}$, such that the set $V-\{u,v\}$ is not a local metric generator for $G_{uv}$, i.e., u and v are adjacent in $G_{uv}$ and $d_{G_{u,v}}(u,x)=d_{G_{u,v}}(v,x)$ for every $x\in V-\{u,v\}$. Therefore, u and v are true twins in $G_{u,v}$.

Conversely, if for every $u,v\in V$ there exists a graph $G_{uv}\in \mathcal{G}$ such that u and v are true twins in $G_{uv}$, then for any simultaneous local metric basis B of $\mathcal{G}$, it holds that $u\in B$ or $v\in B$. Hence, all but one element of V must belong to B. Therefore, $\left|B\right|\ge \left|V\right|-1$, which implies that ${Sd}_l\mathcal{G}=\left|V\right|-1$. ☐

Notice that Corollary 1 is obtained directly from the previous result. Now, the two following results concern the limit cases of Item (1) of Remark 1.

Theorem 2.

A family $\mathcal{G}$ of connected graphs on a common vertex set V satisfies ${Sd}_l\left(\mathcal{G}\right)=1$ if and only if every graph in $\mathcal{G}$ is bipartite.

Proof. 

If every graph in the family is bipartite, then for any $v\in V$, the set $\left\{v\right\}$ is a local metric basis of every $G_i\in \mathcal{G}$, so ${Sd}_l\left(\mathcal{G}\right)=1$.

Let us now consider a family $\mathcal{G}$ of connected graphs on a common vertex set V such that ${Sd}_l\left(\mathcal{G}\right)=1$ and assume that some $G\in \mathcal{G}$ is not bipartite. It is shown in [21] that ${dim}_l\left(G\right)\ge 2$, so Item (1) of Remark 1 leads to ${Sd}_l\left(\mathcal{G}\right)\ge 2$, which is a contradiction. Thus, every $G\in \mathcal{G}$ is bipartite. ☐

Paths, trees and even-order cycles are bipartite. The following result covers the case of families composed of odd-order cycles.

Theorem 3.

Every family $\mathcal{G}$ composed of cycle graphs on a common odd-sized vertex set V satisfies ${Sd}_l\left(\mathcal{G}\right)=2$, and any pair of vertices of V is a simultaneous local metric basis of $\mathcal{G}$.

Proof. 

For any cycle $C_i\in \mathcal{G}$, the set $\left\{v\right\}$, $v\in V$, is not a local metric generator, as the adjacent vertices $v_{j+⌊\frac{\left|V\right|}{2}⌋}$ and $v_{j-⌊\frac{\left|V\right|}{2}⌋}$ (subscripts taken modulo $\left|V\right|$) are not distinguished by v, so Item (1) of Remark 1 leads to ${Sd}_l\left(\mathcal{G}\right)\ge {\displaystyle \underset{G\in \mathcal{G}}{max}}\left\{{dim}_l\left(G\right)\right\}\ge 2$. Moreover, any set $\{v,v^{\prime }\}$ is a local metric generator for every $C_i\in \mathcal{G}$, as the single pair of adjacent vertices not distinguished by v is distinguished by $v^{\prime }$, so that ${Sd}_l\left(\mathcal{G}\right)\le 2$. ☐

The following result allows us to study the simultaneous local metric dimension of a family $\mathcal{G}$ from the family of graphs composed by all non-bipartite graphs belonging to $\mathcal{G}$.

Theorem 4.

Let $\mathcal{G}$ be a family of graphs on a common vertex set V, not all of them bipartite. If $\mathcal{H}$ is the subfamily of $\mathcal{G}$ composed of all non-bipartite graphs belonging to $\mathcal{G}$, then:

$${Sd}_l\left(\mathcal{G}\right)={Sd}_l\left(\mathcal{H}\right).$$

Proof. 

Since $\mathcal{H}$ is a non-empty subfamily of $\mathcal{G}$, we conclude that ${Sd}_l\left(\mathcal{G}\right)\ge {Sd}_l\left(\mathcal{H}\right).$ Since any vertex of a bipartite graph G is a local metric generator for G, if $B\subseteq V$ is a simultaneous local metric basis of $\mathcal{H}$, then B is a simultaneous local metric generator for $\mathcal{G}$ and, as a result, ${Sd}_l\left(\mathcal{G}\right)\le \left|B\right|={Sd}_l\left(\mathcal{H}\right).$ ☐

Some interesting situations may be observed regarding the simultaneous local metric dimension of some graph families versus its standard counterpart. In particular, the fact that false twin vertices need not be distinguished in the local variant leads to some cases where both parameters differ greatly. For instance, consider any family $\mathcal{G}$ composed of three or more star graphs having different centers. It was shown in [22] that any such family satisfies $Sd\left(\mathcal{G}\right)=\left|V\right|-1$, yet by Theorem 2, we have that ${Sd}_l\left(\mathcal{G}\right)=1$.

Given a family $\mathcal{G}=\{G_1,G_2,\cdots ,G_k\}$ of graphs $G_i=(V,E_i)$ on a common vertex set V, we define a simultaneous vertex cover of $\mathcal{G}$ as a set $S\subseteq V$, such that S is simultaneously a vertex cover of each $G_i$. The minimum cardinality among all simultaneous vertex covers of $\mathcal{G}$ is the simultaneous vertex cover number of $\mathcal{G}$, denoted by $\beta \left(\mathcal{G}\right)$.

Theorem 5.

For any family $\mathcal{G}$ of connected graphs with common vertex set V,

$${Sd}_l\left(\mathcal{G}\right)\le \beta \left(\mathcal{G}\right).$$

Furthermore, if for every $uv\in {\cup }_{G\in \mathcal{G}}E\left(G\right)$ there exists $G^{\prime }\in \mathcal{G}$ such that u and v are true twins in $G^{\prime }$, then ${Sd}_l\left(\mathcal{G}\right)=\beta \left(\mathcal{G}\right)$.

Proof. 

Let $B\subseteq V$ be a simultaneous vertex cover of $\mathcal{G}$. Since $V-B$ is a simultaneous independent set of $\mathcal{G}$, we conclude that ${Sd}_l\left(\mathcal{G}\right)\le \beta \left(\mathcal{G}\right)$.

We now assume that for every $uv\in {\cup }_{G\in \mathcal{G}}E\left(G\right)$, there exists $G^{\prime }\in \mathcal{G}$, such that u and v are true twins in $G^{\prime }$, and suppose, for the purpose of contradiction, that ${Sd}_l\left(\mathcal{G}\right)<\beta \left(\mathcal{G}\right)$. In such a case, there exists a simultaneous local metric basis $C\subseteq V$, which is not a simultaneous vertex cover of $\mathcal{G}$. Hence, there exist $u^{\prime },v^{\prime }\in V-C$ and $G\in \mathcal{G}$ such that $u^{\prime }{v}^{\prime }\in E\left(G\right)$, ergo $u^{\prime }{v}^{\prime }\in {\cup }_{G\in \mathcal{G}}E\left(G\right)$. As a consequence, $u^{\prime }$ and $v^{\prime }$ are true twins in some graph $G^{\prime }\in \mathcal{G}$, which contradicts the fact that C is a simultaneous local metric basis of $\mathcal{G}$. Therefore, the strict inequality does not hold, hence ${Sd}_l\left(\mathcal{G}\right)=\beta \left(\mathcal{G}\right)$. ☐

3. Families Obtained by Small Changes on a Graph

Consider a graph G whose local metric dimension is known. In this section, we address two related questions:

• If a series of small changes is repeatedly performed on $E\left(G\right)$, thus producing a family $\mathcal{G}$ of consecutive versions of G, what is the behavior of ${Sd}_l\left(\mathcal{G}\right)$ with respect to ${dim}_l\left(G\right)$?
• If several small changes are performed on $E\left(G\right)$ in parallel, thus producing a family $\mathcal{G}$ of alternative versions of G, what is the behavior of ${Sd}_l\left(\mathcal{G}\right)$ with respect to ${dim}_l\left(G\right)$?

Addressing this issue in the general case is hard, so we will analyze a number of particular cases. First, we will specify three operators that describe some types of changes that may be performed on a graph G:

• Edge addition: We say that a graph $G^{\prime }$ is obtained from a graph G by an edge addition if there is an edge $e\in E\left(\overline{G}\right)$ such that $G^{\prime }=(V\left(G\right),E\left(G\right)\cup \left\{e\right\})$. We will use the notation $G^{\prime }={add}_e\left(G\right)$.
• Edge removal: We say that a graph $G^{\prime }$ is obtained from a graph G by an edge removal if there is an edge $e\in E\left(G\right)$ such that $G^{\prime }=(V\left(G\right),E\left(G\right)-\left\{e\right\})$. We will use the notation $G^{\prime }={rmv}_e\left(G\right)$.
• Edge exchange: We say that a graph $G^{\prime }$ is obtained from a graph G by an edge exchange if there is an edge $e\in E\left(G\right)$ and an edge $f\in E\left(\overline{G}\right)$ such that $G^{\prime }=(V\left(G\right),(E\left(G\right)-\left\{e\right\})\cup \left\{f\right\})$. We will use the notation $G^{\prime }={xch}_{e,f}\left(G\right)$.

Now, consider a graph G and an ordered k-tuple of operations $O_k=({op}_1,{op}_2,\dots ,{op}_k)$, where ${op}_i\in \{{add}_{e_i},{rmv}_{e_i},{xch}_{e_i,f_i}\}$. We define the class ${\mathcal{C}}_{O_k}\left(G\right)$ containing all graph families of the form $\mathcal{G}=\{G,G_1^{\prime },G_2^{\prime },\dots ,G_k^{\prime }\}$, composed by connected graphs on the common vertex set $V\left(G\right)$, where $G_i^{\prime }={op}_i\left(G_{i-1}^{\prime }\right)$ for every $i\in \{1,\dots ,k\}$. Likewise, we define the class ${\mathcal{P}}_{O_k}\left(G\right)$ containing all graph families of the form $\mathcal{G}=\{G_1^{\prime },G_2^{\prime },\dots ,G_k^{\prime }\}$, composed by connected graphs on the common vertex set $V\left(G\right)$, where $G_i^{\prime }={op}_i\left(G\right)$ for every $i\in \{1,\dots ,k\}$. In particular, if ${op}_i={add}_{e_i}$ (${op}_i={rmv}_{e_i}$, ${op}_i={xch}_{e_i,f_i}$) for every $i\in \{1,\dots ,k\}$, we will write ${\mathcal{C}}_{A_k}\left(G\right)$ (${\mathcal{C}}_{R_k}\left(G\right)$, ${\mathcal{C}}_{X_k}\left(G\right)$) and ${\mathcal{P}}_{A_k}\left(G\right)$ (${\mathcal{P}}_{R_k}\left(G\right)$, ${\mathcal{P}}_{X_k}\left(G\right)$).

We have that performing an edge exchange on any tree T (path graphs included) either produces another tree or a disconnected graph. Thus, the following result is a direct consequence of this fact and Theorem 2.

Remark 2.

For any tree T, any $k\ge 1$ and any graph family $\mathcal{T}\in {\mathcal{C}}_{X_k}\left(T\right)\cup {\mathcal{P}}_{X_k}\left(T\right)$,

$${Sd}_l\left(\mathcal{T}\right)=1.$$

Our next result covers a large class of families composed by unicyclic graphs that can be obtained by adding edges, in parallel, to a path graph.

Remark 3.

For any path graph $P_n$, $n\ge 4$, any $k\ge 1$ and any graph family $\mathcal{G}\in {\mathcal{P}}_{A_k}\left(P_n\right)$,

$$1\le {Sd}_l\left(\mathcal{G}\right)\le 2.$$

Proof. 

Every graph $G\in \mathcal{G}$ is either a cycle or a unicyclic graph. If the cycle subgraphs of every graph in the family have even order, then ${Sd}_l\left(\mathcal{G}\right)=1$ by Theorem 2. If $\mathcal{G}$ contains at least one non-bipartite graph, then ${Sd}_l\left(\mathcal{G}\right)\ge 2$. We now proceed to show that in this case, ${Sd}_l\left(\mathcal{G}\right)\le 2$. To this end, we denote by $V=\{v_1,\cdots ,v_n\}$ the vertex set of $P_n$, where $v_i\sim v_{i+1}$ for every $i\in \{1,\cdots ,n-1\}$. We claim that $\{v_1,v_n\}$ is a simultaneous local metric generator for the subfamily ${\mathcal{G}}^{\prime }\subset \mathcal{G}$ composed by all non-bipartite graphs of $\mathcal{G}$. In order to prove this claim, consider an arbitrary graph $G\in {\mathcal{G}}^{\prime }$, and let $e=v_p{v}_q$, $1\le p<q\le n$ be the edge added to $E\left(P_n\right)$ to obtain G. We differentiate the following cases:

• $e=v_1{v}_n$. In this case, G is an odd-order cycle graph, so $\{v_1,v_n\}$ is a local metric generator.
• $1<p<q=n$. In this case, G is a unicyclic graph where $v_p$ has degree three, $v_1$ has degree one and the remaining vertices have degree two. Consider two adjacent vertices $u,v\in V-\{v_1,v_n\}$. If u or v belong to the path from $v_1$ to $v_p$, then $v_1$ distinguishes them. If both, u and v, belong to the cycle subgraph of G, then $d(u,v_1)=d(u,v_p)+d(v_p,v_1)$ and $d(v,v_1)=d(v,v_p)+d(v_p,v_1)$. Thus, if $v_p$ distinguishes u and v, so does $v_1$, otherwise $v_n$ does.
• $1=p<q<n$. This case is analogous to Case 2.
• $1<p<q<n$. In this case, G is a unicyclic graph where $v_p$ and $v_q$ have degree three, $v_1$ and $v_n$ have degree one and the remaining vertices have degree two. Consider two adjacent vertices $u,v\in V-\{v_1,v_n\}$. If u or v belong to the path from $v_1$ to $v_p$ (or to the path from $v_q$ to $v_n$), then $v_1$ (or $v_n$) distinguishes them. If both u and v belong to the cycle, then $d(u,v_1)=d(u,v_p)+d(v_p,v_1)$, $d(v,v_1)=d(v,v_p)+d(v_p,v_1)$, $d(u,v_n)=d(u,v_q)+d(v_q,v_n)$ and $d(v,v_n)=d(v,v_q)+d(v_q,v_n)$. Thus, if $v_p$ distinguishes u and v, so does $v_1$, otherwise $v_q$ distinguishes them, which means that $v_n$ also does.

According to the four cases above, we conclude that $\{v_1,v_n\}$ is a local metric generator for G, so it is a simultaneous local metric generator for ${\mathcal{G}}^{\prime }$. Thus, by Theorem 4, ${Sd}_l\left(\mathcal{G}\right)={Sd}_l\left({\mathcal{G}}^{\prime }\right)\le 2$. ☐

Remark 4.

Let $C_n$, $n\ge 4$, be a cycle graph, and let e be an edge of its complement. If n is odd, then

$${dim}_l\left({add}_e\left(C_n\right)\right)=2.$$

Otherwise,

$$1\le {dim}_l\left({add}_e\left(C_n\right)\right)\le 2.$$

Proof. 

Consider $e=v_i{v}_j$. We have that $C_n$ is bipartite for n even. If, additionally, $d_{C_n}(v_i,v_j)$ is odd, then the graph ${add}_e\left(C_n\right)$ is also bipartite, so ${dim}_l\left({add}_e\left(C_n\right)\right)=1$. For every other case, ${dim}_l\left({add}_e\left(C_n\right)\right)\ge 2$. From now on, we assume that $n\ge 5$ and proceed to show that ${dim}_l\left({add}_e\left(C_n\right)\right)\le 2$. Note that ${add}_e\left(C_n\right)$ is a bicyclic graph where $v_i$ and $v_j$ are vertices of degree three and the remaining vertices have degree two. We denote by $C_{n_1}$ and $C_{n-n_1+2}$ the two graphs obtained as induced subgraphs of ${add}_e\left(C_n\right)$, which are isomorphic to a cycle of order $n_1$ and a cycle of order $n-n_1+2$, respectively. Since $n\ge 5$, we have that $n_1>3$ or $n-n_1+2>3$. We assume, without loss of generality, that $n_1>3$. Let $a,b\in V\left(C_{n_1}\right)$ are two vertices such that:

• if $n_1$ is even, $ab\in E\left(C_{n_1}\right)$ and $d(v_i,a)=d(v_j,b)$,
• if $n_1$ is odd, $ax,xb\in E\left(C_{n_1}\right)$, where $x\in V\left(C_{n_1}\right)$ is the only vertex such that $d(x,v_i)=d(x,v_j)$.

We claim that $\{a,b\}$ is a local metric generator for ${add}_e\left(C_n\right)$. Consider two adjacent vertices $u,v\in V\left({add}_e\left(C_n\right)\right)-\{a,b\}$. We differentiate the following cases, where the distances are taken in ${add}_e\left(C_n\right)$:

• $u,v\in V\left(C_{n_1}\right)$. It is simple to verify that $\{a,b\}$ is a local metric generator for $C_{n_1}$, hence $d(u,a)\ne d(v,a)$ or $d(u,b)\ne d(v,b)$.
• $u\in V\left(C_{n_1}\right)$ and $v\in V\left(C_{n-n_1+2}\right)-\{v_i,v_j\}$. In this case, $u\in \{v_i,v_j\}$ and $d(u,a)<d(v,a)$ or $d(u,b)<d(v,b)$.
• $u,v\in V\left(C_{n-n_1+2}\right)-\{v_i,v_j\}$. In this case, if $d(u,a)=d(v,a)$, then $d(u,v_i)=d(v,v_i)$, so $d(u,v_j)\ne d(v,v_j)$ and, consequently, $d(u,b)\ne d(v,b)$.

According to the three cases above, $\{a,b\}$ is a local metric generator for ${add}_e\left(C_n\right)$, and as a result, the proof is complete. ☐

The next result is a direct consequence of Remarks 1 and 4.

Remark 5.

Let $C_n$, $n\ge 4$, be a cycle graph. If $e,e^{\prime }$ are two different edges of the complement of $C_n$, then:

$$1\le {Sd}_l({add}_e\left(C_n\right),{add}_{e^{\prime }}\left(C_n\right))={Sd}_l(C_n,{add}_e\left(C_n\right),{add}_{e^{\prime }}\left(C_n\right))\le 4.$$

4. Families of Corona Product Graphs

Let G and H be two graphs of order n and $n^{\prime }$, respectively. The corona product $G\odot H$ is defined as the graph obtained from G and H by taking one copy of G and n copies of H and joining by an edge each vertex from the i-th copy of H with the i-th vertex of G. Notice that the corona graph $K_1\odot H$ is isomorphic to the join graph $K_1+H$. Given a graph family $\mathcal{G}=\{G_1,\dots ,G_k\}$ on a common vertex set and a graph H, we define the graph family:

$$\mathcal{G}\odot H=\{G_1\odot H,\dots ,G_k\odot H\}.$$

Several results presented in [23,24] describe the behavior of the local metric dimension on corona product graphs. We now analyze how this behavior extends to the simultaneous local metric dimension of families composed by corona product graphs.

Theorem 6.

In references [23,25], Let G be a connected graph of order $n\ge 2$. For any non-empty graph H,

$${dim}_l(G\odot H)=n·{adim}_l\left(H\right).$$

As we can expect, if we review the proof of the result above, we check that if A is a local metric basis of $G\odot H$, then A does not contain elements in $V\left(G\right)$. Therefore, any local metric basis of $G\odot H$ is a simultaneous local metric basis of $\mathcal{G}\odot H$. This fact and the result above allow us to state the following theorem.

Theorem 7.

Let $\mathcal{G}$ be a family of connected non-trivial graphs on a common vertex set V. For any non-empty graph H,

$${Sd}_l(\mathcal{G}\odot H)=\left|V\right|·{adim}_l\left(H\right).$$

Given a graph family $\mathcal{G}$ on a common vertex set and a graph family $\mathcal{H}$ on a common vertex set, we define the graph family:

$$\mathcal{G}\odot \mathcal{H}=\{G\odot H:G\in \mathcal{G}\mathrm{and}H\in \mathcal{H}\}.$$

The following result generalizes Theorem 7. In what follows, we will use the notation $\langle v\rangle$ for the graph $G=(V,E)$ where $V=\left\{v\right\}$ and $E=\varnothing$.

Theorem 8.

For any family $\mathcal{G}$ of connected non-trivial graphs on a common vertex set V and any family $\mathcal{H}$ of non-empty graphs on a common vertex set,

$${Sd}_l(\mathcal{G}\odot \mathcal{H})=\left|V\right|·{Sad}_l\left(\mathcal{H}\right).$$

Proof. 

Let $n=\left|V\right|$, and let $V^{\prime }$ be the vertex set of the graphs in $\mathcal{H}$, $V_i^{\prime }$ the copy of $V^{\prime }$ corresponding to $v_i\in V$, ${\mathcal{H}}_i$ the i-th copy of $\mathcal{H}$ and $H_i\in {\mathcal{H}}_i$ the i-th copy of $H\in \mathcal{H}$.

We first need to prove that any $G\in \mathcal{G}$ satisfies ${Sd}_l(G\odot \mathcal{H})=n·{Sad}_l\left(\mathcal{H}\right)$. For any $i\in \{1,\dots ,n\}$, let $S_i$ be a simultaneous local adjacency basis of ${\mathcal{H}}_i$. In order to show that $X={\bigcup }_{i=1}^n{S}_i$ is a simultaneous local metric generator for $\mathcal{G}\odot \mathcal{H}$, we will show that X is a local metric generator for $G\odot H$, for any $G\in \mathcal{G}$ and $H\in \mathcal{H}$. To this end, we differentiate the following four cases for two adjacent vertices $x,y\in V(G\odot H)-X$.

• $x,y\in V_i^{\prime }$. Since $S_i$ is an adjacency generator of $H_i$, there exists a vertex $u\in S_i$ such that $|N_{H_i}\left(u\right)\cap \{x,y\}|=1$. Hence,

  $$d_{G\odot H}(x,u)=d_{\langle v_i\rangle +H_i}(x,u)\ne d_{\langle v_i\rangle +H_i}(y,u)=d_{G\odot H}(y,u).$$
• $x\in V_i^{\prime }$ and $y\in V$. If $y=v_i$, then for $u\in S_j$, $j\ne i$, we have:

  $$d_{G\odot H}(x,u)=d_{G\odot H}(x,y)+d_{G\odot H}(y,u)>d_{G\odot H}(y,u).$$

  Now, if $y=v_j$, $j\ne i$, then we also take $u\in S_j$, and we proceed as above.
• $x=v_i$ and $y=v_j$. For $u\in S_j$, we find that:

  $$d_{G\odot H}(x,u)=d_{G\odot H}(x,y)+d_{G\odot H}(y,u)>d_{G\odot H}(y,u).$$
• $x\in V_i^{\prime }$ and $y\in V_j^{\prime }$, $j\ne i$. In this case, for $u\in S_i$, we have:

  $$d_{G\odot H}(x,u)\le 2<3\le d_{G\odot H}(u,y).$$

Hence, X is a local metric generator for $G\odot H$, and since $G\in \mathcal{G}$ and $H\in \mathcal{H}$ are arbitrary graphs, X is a simultaneous local metric generator for $\mathcal{G}\odot \mathcal{H}$, which implies that:

$${Sd}_l(G\odot \mathcal{H})\le \sum _{i=1}^n\left|S_i\right|=n·{Sad}_l\left(\mathcal{H}\right).$$

It remains to prove that ${Sd}_l(\mathcal{G}\odot \mathcal{H})\ge n·{Sad}_l\left(\mathcal{H}\right).$ To do this, let W be a simultaneous local metric basis of $\mathcal{G}\odot \mathcal{H}$, and for any $i\in \{1,\dots ,n\}$, let $W_i=V_i^{\prime }\cap W$. Let us show that $W_i$ is a simultaneous adjacency generator for ${\mathcal{H}}_i$. To do this, consider two different vertices $x,y\in V_i^{\prime }-W_i$, which are adjacent in $G\odot H$, for some $H\in \mathcal{H}$. Since no vertex $a\in V(G\odot H)-V_i^{\prime }$ distinguishes the pair $x,y$, there exists some $u\in W_i$, such that $d_{G\odot H}(x,u)\ne d_{G\odot H}(y,u)$. Now, since $d_{G\odot H}(x,u)\in \{1,2\}$ and $d_{G\odot H}(y,u)\in \{1,2\}$, we conclude that $|N_{H_i}\left(u\right)\cap \{x,y\}|=1$, and consequently, $W_i$ must be an adjacency generator for $H_i$; and since $H\in \mathcal{H}$ is arbitrary, $W_i$ is a simultaneous local adjacency generator for ${\mathcal{H}}_i$. Hence, for any $i\in \{1,\dots ,n\}$, $|W_i|\ge {Sad}_l\left(H_i\right)$. Therefore,

$${Sd}_l(\mathcal{G}\odot \mathcal{H})=\left|W\right|\ge \sum _{i=1}^n\left|W_i\right|\ge \sum _{i=1}^n{Sad}_l\left({\mathcal{H}}_i\right)=n·{Sad}_l\left(\mathcal{H}\right).$$

This completes the proof. ☐

The following result is a direct consequence of Theorem 8.

Corollary 2.

For any family $\mathcal{G}$ of connected non-trivial graphs on a common vertex set V and any family $\mathcal{H}$ of non-empty graphs on a common vertex set,

$${Sd}_l(G\odot \mathcal{H})\ge \left|V\right|·{Sd}_l\left(\mathcal{H}\right).$$

Furthermore, if every graph in $\mathcal{H}$ has diameter two, then:

$${Sd}_l(G\odot \mathcal{H})=\left|V\right|·{Sd}_l\left(\mathcal{H}\right).$$

Now, we give another result, which is a direct consequence of Theorem 8 and shows the general bounds of ${Sd}_l(\mathcal{G}\odot \mathcal{H})$.

Corollary 3.

For any family $\mathcal{G}$ of connected graphs on a common vertex set V, $\left|V\right|\ge 2$ and any family $\mathcal{H}$ of non-empty graphs on a common vertex set $V^{\prime }$,

$$\left|V\right|\le {Sd}_l(G\odot \mathcal{H})\le \left|V\right|\left(\right|V^{\prime }|-1).$$

We now consider the case in which the graph H is empty.

Theorem 9.

In reference [24], Let G be a connected non-trivial graph. For any empty graph H,

$${dim}_l(G\odot H)={dim}_l\left(G\right).$$

The result above may be extended to the simultaneous scenario.

Theorem 10.

Let $\mathcal{G}$ be a family of connected non-trivial graphs on a common vertex set. For any empty graph H,

$${Sd}_l(\mathcal{G}\odot H)={Sd}_l\left(\mathcal{G}\right).$$

Proof. 

Let B be a simultaneous local metric basis of $\mathcal{G}=\{G_1,G_2,\dots ,G_k\}$. Since H is empty, any local metric generator $B^{\prime }\subseteq B$ of $G_i$ is a local metric generator for $G_i\odot H$, so B is a simultaneous local metric generator for $\mathcal{G}\odot H$. As a consequence, ${Sd}_l(\mathcal{G}\odot H)\le {Sd}_l\left(\mathcal{G}\right)$.

Suppose that A is a simultaneous local metric basis of $\mathcal{G}\odot H$ and $\left|A\right|<\left|B\right|$. If there exists $x\in A\cap V_{ij}$ for the j-th copy of H in any graph $G_i\odot H$, then the pairs of vertices of $G_i\odot H$ that are distinguished by x can also be distinguished by $v_i$. As a consequence, the set $A^{\prime }$ obtained from A by replacing by $v_i$ each vertex $x\in A\cap V_{ij},i\in \{1,\dots ,k\},j\in \{1,\dots ,n\}$ is a simultaneous local metric generator for $\mathcal{G}$ such that $\left|A^{\prime }\right|\le \left|A\right|<{Sd}_l\left(\mathcal{G}\right)$, which is a contradiction, so ${Sd}_l(\mathcal{G}\odot H)\ge {Sd}_l\left(\mathcal{G}\right)$. ☐

Theorem 11.

In reference [24], Let H be a non-empty graph. The following assertions hold.

1.

If the vertex of $K_1$ does not belong to any local metric basis of $K_1+H$, then for any connected graph G of order n,

$${dim}_l(G\odot H)=n·{dim}_l(K_1+H).$$

2.

If the vertex of $K_1$ belongs to a local metric basis of $K_1+H$, then for any connected graph G of order $n\ge 2$,

$${dim}_l(G\odot H)=n·\left({dim}_l(K_1+H)-1\right).$$

As for the previous case, the result above is extensible to the simultaneous setting.

Theorem 12.

Let $\mathcal{G}$ be a family of connected non-trivial graphs on a common vertex set V, and let $\mathcal{H}$ be a family of non-empty graphs on a common vertex set. The following assertions hold.

1.

If the vertex of $K_1$ does not belong to any simultaneous local metric basis of $K_1+\mathcal{H}$, then:

$${Sd}_l(\mathcal{G}\odot \mathcal{H})=\left|V\right|·{Sd}_l(K_1+\mathcal{H}).$$

2.

If the vertex of $K_1$ belongs to a simultaneous local metric basis of $K_1+\mathcal{H}$, then:

$${Sd}_l(\mathcal{G}\odot \mathcal{H})=\left|V\right|·\left({Sd}_l(K_1+\mathcal{H})-1\right).$$

Proof. 

As above, let $n=\left|V\right|$, and let $V^{\prime }$ be the vertex set of the graphs in $\mathcal{H}$, $V_i^{\prime }$ the copy of $V^{\prime }$ corresponding to $v_i\in V$, ${\mathcal{H}}_i$ the i-th copy of $\mathcal{H}$ and $H_i\in {\mathcal{H}}_i$ the i-th copy of $H\in \mathcal{H}$.

We will apply a reasoning analogous to the one used for the proof of Theorem 11 in [24]. If $n=1$, then $\mathcal{G}\odot \mathcal{H}\cong K_1+\mathcal{H}$, so the result holds. Assume that $n\ge 2$, Let $S_i$ be a simultaneous local metric basis of $\langle v_i\rangle +{\mathcal{H}}_i$, and let $S_i^{\prime }=S_i-\left\{v_i\right\}$. Note that $S_i^{\prime }\ne \varnothing$ because ${\mathcal{H}}_i$ is the family of non-empty graphs and $v_i$ does not distinguish any pair of adjacent vertices belonging to $V_i^{\prime }$. In order to show that $X={\cup }_{i=1}^n{S}_i^{\prime }$ is a simultaneous local metric generator for $\mathcal{G}\odot \mathcal{H}$, we differentiate the following cases for two vertices $x,y$, which are adjacent in an arbitrary graph $G\odot H$:

• $x,y\in V_i^{\prime }$. Since $v_i$ does not distinguish $x,y$, there exists $u\in S_i^{\prime }$ such that $d_{G\odot H}(x,u)=d_{\langle v_i\rangle +H_i}(x,u)\ne d_{\langle v_i\rangle +H_i}(y,u)=d_{G\odot H}(y,u)$.
• $x\in V_i^{\prime }$ and $y=v_i$. For $u\in S_j^{\prime }$, $j\ne i$, we have $d_{G\odot H}(x,u)=1+d_{G\odot H}(y,u)>d_{G\odot H}(y,u)$.
• $x=v_i$ and $y=v_j$. For $u\in S_j^{\prime }$, we have $d_{G\odot H}(x,u)=2=d_{G\odot H}(x,y)+1>1=d_{G\odot H}(y,u)$.

Hence, X is a local metric generator for $G\odot H$, and since $G\in \mathcal{G}$ and $H\in \mathcal{H}$ are arbitrary graphs, X is a simultaneous local metric generator for $\mathcal{G}\odot \mathcal{H}$.

Now, we shall prove (1). If the vertex of $K_1$ does not belong to any simultaneous local metric basis of $K_1+\mathcal{H}$, then $v_i\notin S_i$ for every $i\in \{1,\dots ,n\}$, and as a consequence,

$${Sd}_l(\mathcal{G}\odot \mathcal{H})\le \left|X\right|=\sum _{i=1}^n\left|S_i^{\prime }\right|=\sum _{i=1}^n{Sd}_l(\langle v_i\rangle +{\mathcal{H}}_i)=n·{Sd}_l(K_1+\mathcal{H}).$$

Now, we need to prove that ${Sd}_l(\mathcal{G}\odot \mathcal{H})\ge n·{Sd}_l(K_1+\mathcal{H}).$ In order to do this, let W be a simultaneous local metric basis of $\mathcal{G}\odot \mathcal{H}$, and let $W_i=V_i^{\prime }\cap W$. Consider two adjacent vertices $x,y\in V_i^{\prime }-W_i$ in $G\odot H$. Since no vertex $a\in W-W_i$ distinguishes the pair $x,y$, there exists $u\in W_i$ such that $d_{\langle v_i\rangle +H_i}(x,u)=d_{G\odot H}(x,u)\ne d_{G\odot H}(y,u)=d_{\langle v_i\rangle +H_i}(y,u)$. Therefore, we conclude that $W_i\cup \left\{v_i\right\}$ is a simultaneous local metric generator for $\langle v_i\rangle +{\mathcal{H}}_i$. Now, since $v_i$ does not belong to any simultaneous local metric basis of $\langle v_i\rangle +{\mathcal{H}}_i$, we have that $|W_i|+1=|W_i\cup \left\{v_i\right\}|>{Sd}_l(\langle v_i\rangle +{\mathcal{H}}_i)$ and, as a consequence, $|W_i|\ge {Sd}_l(\langle v_i\rangle +{\mathcal{H}}_i)$. Therefore,

$${Sd}_l(\mathcal{G}\odot \mathcal{H})=\left|W\right|\ge \sum _{i=1}^n\left|W_i\right|\ge \sum _{i=1}^n{Sd}_l(\langle v_i\rangle +{\mathcal{H}}_i)=n·{Sd}_l(K_1+\mathcal{H}),$$

and the proof of (1) is complete.

Finally, we shall prove (2). If the vertex of $K_1$ belongs to a simultaneous local metric basis of $K_1+\mathcal{H}$, then we assume that $v_i\in S_i$ for every $i\in \{1,\dots ,n\}$. Suppose that there exists B such that B is a simultaneous local metric basis of $\mathcal{G}\odot \mathcal{H}$ and $\left|B\right|<\left|X\right|$. In such a case, there exists $i\in \{1,\dots ,n\}$ such that the set $B_i=B\cap V_i^{\prime }$ satisfies $\left|B_i\right|<\left|S_i^{\prime }\right|$. Now, since no vertex of $B-B_i$ distinguishes the pairs of adjacent vertices belonging to $V_i^{\prime }$, the set $B_i\cup \left\{v_i\right\}$ must be a simultaneous local metric generator for $\langle v_i\rangle +{\mathcal{H}}_i$. Therefore, ${Sd}_l(\langle v_i\rangle +{\mathcal{H}}_i)\le |B_i|+1<|S_i^{\prime }|+1=|S_i|={Sd}_l(\langle v_i\rangle +{\mathcal{H}}_i)$, which is a contradiction. Hence, X is a simultaneous local metric basis of $\mathcal{G}\odot \mathcal{H}$, and as a consequence,

$${Sd}_l(\mathcal{G}\odot \mathcal{H})=\left|X\right|=\sum _{i=1}^n\left|S_i^{\prime }\right|=\sum _{i=1}^n({Sd}_l(\langle v_i\rangle +{\mathcal{H}}_i)-1)=n({Sd}_l(K_1+\mathcal{H})-1).$$

The proof of (2) is now complete. ☐

Corollary 4.

Let G be a connected graph of order $n\ge 2$, and let $\mathcal{H}=\{K_{r_1,n^{\prime }-r_1},K_{r_2,n^{\prime }-r_2},\dots ,K_{r_k,n^{\prime }-r_k}\}$, $1\le r_i\le n^{\prime }-1$, be a family composed by complete bipartite graphs on a common vertex set $V^{\prime }$. Then,

$${Sd}_l(G\odot \mathcal{H})=n.$$

Proof. 

For every $x\in V^{\prime }$, the set $\{v,x\}$ is a simultaneous local metric basis of $\langle v\rangle +\mathcal{H}$, so $Sd(G\odot \mathcal{H})=n·(Sd(K_1+\mathcal{H})-1)=n$. ☐

Lemma 1.

In reference [24], Let H be a graph of radius $r\left(H\right)$. If $r\left(H\right)\ge 4$, then the vertex of $K_1$ does not belong to any local metric basis of $K_1+H$.

Note that an analogous result holds for the simultaneous scenario.

Lemma 2.

Let $\mathcal{H}$ be a graph family on a common vertex set V, such that $r\left(H\right)\ge 4$ for every $H\in \mathcal{H}$. Then, the vertex of $K_1$ does not belong to any simultaneous local metric basis of $K_1+\mathcal{H}$.

Proof. 

Let B be a simultaneous local metric basis of $\{K_1+H_1,\dots ,K_1+H_k\}$. We suppose that the vertex v of $K_1$ belongs to B. Note that $v\in B$ if and only if there exists $u\in V-B$, such that $B\subseteq N_{K_1+H_i}\left(u\right)$ for some $H_i\in \mathcal{H}$. If $r\left(H_i\right)\ge 4$, proceeding in a manner analogous to that of the proof of Lemma 1 as given in [24], we take $u^{\prime }\in V$ such that $d_{H_i}(u,u^{\prime })=4$ and a shortest path $u{u}_1{u}_2{u}_3{u}^{\prime }$. In such a case, for every $b\in B-\left\{v\right\}$, we will have that $d_{K_1+H_i}(b,u_3)=d_{K_1+H_i}(b,u^{\prime })=2$, which is a contradiction. Hence, v does not belong to any simultaneous local metric basis of $\{K_1+H_1,K_1+H_2,\dots ,K_1+H_k\}$. ☐

As a direct consequence of item (1) of Theorem 12 and Lemma 2, we obtain the following result.

Proposition 1.

For any family $\mathcal{G}$ of connected graphs on a common vertex set V and any graph family $\mathcal{H}$ on a common vertex set $V^{\prime }$ such that $r\left(H\right)\ge 4$ for every $H\in \mathcal{H}$,

$${Sd}_l(\mathcal{G}\odot \mathcal{H})=\left|V\right|·{Sd}_l(K_1+\mathcal{H}).$$

5. Families of Lexicographic Product Graphs

Let $\mathcal{G}=\{G_1,\cdots ,G_r\}$ be a family of connected graphs with common vertex set $V=\{u_1,\cdots ,u_n\}$. For each $u_i\in V$, let ${\mathcal{H}}^i=\{H_{i1},\cdots H_{i{s}_i}\}$ be a family of graphs with common vertex set $V_i$. For each $i=1,\cdots ,n$, choose $H_{ij}\in {\mathcal{H}}^i$ and consider the family ${\mathcal{H}}_j=\{H_{1j},H_{2j},\cdots ,H_{nj}\}$. Notice that the families ${\mathcal{H}}^i$ can be represented in the following scheme where the columns correspond to the families ${\mathcal{H}}_j$.

$$\begin{array}{ccccccc}{\mathcal{H}}^1=& \{H_{11},& \cdots & H_{1j},& \cdots & H_{1s_1}\}& \mathrm{defined}\mathrm{on}{V}_1\\ ⋮& ⋮& & ⋮& & ⋮& \\ {\mathcal{H}}^i=& \{H_{i1},& \cdots & H_{ij},& \cdots & H_{i{s}_i}\}& \mathrm{defined}\mathrm{on}{V}_i\\ ⋮& ⋮& & ⋮& & ⋮& \\ {\mathcal{H}}^n=& \{H_{n1},& \cdots & H_{nj},& \cdots & H_{n{s}_n}\}& \mathrm{defined}\mathrm{on}{V}_n\end{array}$$

For a graph $G_k\in \mathcal{G}$ and the family ${\mathcal{H}}_j$, we define the lexicographic product of $G_k$ and ${\mathcal{H}}_j$ as the graph $G_k\circ {\mathcal{H}}_j$ such that $V(G_k\circ {\mathcal{H}}_j)={\bigcup }_{u_i\in V}(\left\{u_i\right\}\times V_i)$ and $(u_{i_1},v)(u_{i_2},w)\in E(G_k\circ {\mathcal{H}}_j)$ if and only if $u_{i_1}{u}_{i_2}\in E\left(G_k\right)$ or $i_1=i_2$ and $vw\in E\left(H_{i_{1}j}\right)$. Let $\mathcal{H}=\{{\mathcal{H}}_1,{\mathcal{H}}_2,\cdots {\mathcal{H}}_s\}$. We are interested in the simultaneous local metric dimension of the family:

$$\mathcal{G}\circ \mathcal{H}=\{G_k\circ {\mathcal{H}}_j:G_k\in \mathcal{G},{\mathcal{H}}_j\in \mathcal{H}\}.$$

The relation between distances in a lexicographic product graph and those in its factors is presented in the following remark.

Remark 6.

If $(u,v)$ and $(u^{\prime },v^{\prime })$ are vertices of $G\circ H$, then:

$$d_{G\circ \mathcal{H}}((u,v),(u^{\prime },v^{\prime }))=\left\{\begin{array}{cc}{d}_G(u,u^{\prime }),\hfill & ifu\ne u^{\prime },\hfill \\ min\{d_H(v,v^{\prime }),2\},\hfill & ifu=u^{\prime }.\hfill \end{array}\right.$$

We point out that the remark above was stated in [26,27] for the case where $H_{ij}\cong H$ for all $H_{ij}\in {\mathcal{H}}_j$. By Remark 6, we deduce that if $u\in V-\left\{u_i\right\}$, then two adjacent vertices $(u_i,w),(u_i,y)$ are not distinguished by $(u,v)\in V(\mathcal{G}\circ \mathcal{H})$. Therefore, we can state the following remark.

Remark 7.

If B is a simultaneous local metric generator for the family of lexicographic product graphs $\mathcal{G}\circ \mathcal{H}$, then $B_i=\{v:(u_i,v)\in B\}$ is a simultaneous local adjacency generator for ${\mathcal{H}}^i$.

In order to state our main result (Theorem 13), we need to introduce some additional notation. Let B be a simultaneous local adjacency generator for a family of non-trivial connected graphs ${\mathcal{H}}^i=\{H_{i1},\cdots ,H_{is}\}$ on a common vertex set $V_i$, and let $\mathcal{G}\circ \mathcal{H}$ be family of lexicographic product graphs defined as above.

• $D[{\mathcal{H}}^i,B]=\{v\in V_i:B\subseteq N_{H_{ij}}\left(v\right)\mathrm{for}\mathrm{some}{H}_{ij}\in {\mathcal{H}}^i\}$.
• If $D[{\mathcal{H}}^i,B]\ne \varnothing$, then we define the graph $\mathcal{D}[{\mathcal{H}}^i,B]$ in the following way. The vertex set of $\mathcal{D}[{\mathcal{H}}^i,B]$ is $D[{\mathcal{H}}^i,B]$, and two vertices $v,w$ are adjacent in $\mathcal{D}[{\mathcal{H}}^i,B]$ if and only if for for every $H_{ij}\in {\mathcal{H}}^i$, $vw\notin E\left(H_{ij}\right)$.
• If $D[{\mathcal{H}}^i,B]=\varnothing$, then define $\mathsf{\Psi }\left(B\right)=\left|B\right|$, otherwise $\mathsf{\Psi }\left(B\right)=\gamma \left(\mathcal{D}[{\mathcal{H}}^i,B]\right)+\left|B\right|$, where $\gamma \left(\mathcal{D}[{\mathcal{H}}^i,B]\right)$ represents the domination number of $\mathcal{D}[{\mathcal{H}}^i,B]$.
• $\mathsf{\Gamma }\left({\mathcal{H}}^i\right)=\{C\subseteq V_i:C\mathrm{is}\mathrm{a}\mathrm{simultaneous}\mathrm{local}\mathrm{adjacency}\mathrm{generator}\mathrm{for}{\mathcal{H}}^i\}$
• $\mathsf{\Psi }\left({\mathcal{H}}^i\right)=min\{\mathsf{\Psi }\left(B\right):B\in \mathsf{\Gamma }\left({\mathcal{H}}^i\right)\}.$
• ${\mathcal{S}}_0$ is a family composed by empty graphs.
• $\mathsf{\Phi }(V,\mathcal{H})=\{u_i\in V:{\mathcal{H}}^i\subseteq {\mathcal{S}}_0\}$
• $I(V,\mathcal{H})=\{u_i\in V:\mathsf{\Psi }\left({\mathcal{H}}^i\right)>{Sad}_l\left({\mathcal{H}}^i\right)\}.$ Notice that $\mathsf{\Phi }(V,\mathcal{H})\subseteq I(V,\mathcal{H})$.
• $\mathsf{{\rm Y}}(V,\mathcal{H})$ is the family of subsets of $I(V,\mathcal{H})$ as follows. We say that $A\in \mathsf{{\rm Y}}(V,\mathcal{H})$ if for every $u^{\prime },u^{″}\in I(V,\mathcal{H})-A$ such that $u^{\prime }{u}^{″}\in E\left(G_k\right)$, for some $G_k\in \mathcal{G}$, there exists $u\in (A\cup (V-\mathsf{\Phi }(V,\mathcal{H})))-\{u^{\prime },u^{″}\}$ such that $d_{G_k}(u,u^{\prime })\ne d_{G_k}(u,u^{″})$.
• $\mathbf{G}(\mathcal{G},I(V,\mathcal{H}\left)\right)$ is the graph with vertex set $I(V,\mathcal{H})$ and edge set $\mathbf{E}$ such that $u_i{u}_j\in \mathbf{E}$ if and only if there exists $G_k\in \mathcal{G}$ such that $u_i{u}_j\in E\left(G_k\right)$.

Remark 8.

$\mathsf{\Psi }\left({\mathcal{H}}^i\right)=1$ if and only if $H_{i,j}\cong N_{|V_i|}$ for every $H_{i,j}\in {\mathcal{H}}^i$.

Proof. 

If $H_{i,j}\cong N_{|V_i|}$ for every $H_{i,j}\in {\mathcal{H}}^i$, then $B=\varnothing$ is the only simultaneous local adjacency basis of ${\mathcal{H}}^i$, $\mathcal{D}[{\mathcal{H}}^i,\varnothing ]\cong K_{|V_i|}$, and then, $\mathsf{\Psi }\left({\mathcal{H}}^i\right)=\gamma \left(K_{|V_i|}\right)=1$. On the other hand, suppose that $H_{i,j}\cong N_{|V_i|}$ for some $H_{i,j}\in {\mathcal{H}}^i$. In this case, ${Sad}_l\left({\mathcal{H}}^i\right)\ge 1$. If ${Sad}_l\left({\mathcal{H}}^i\right)>1$, then we are done. Suppose that ${Sad}_l\left({\mathcal{H}}^i\right)=1$. For any simultaneous local adjacency basis $B=\left\{v_1\right\}$ of ${\mathcal{H}}^i$, there exists $v_2\in N_{H_{ij}}\left(v_1\right)$ for some $H_{ij}$, which implies that $D[{\mathcal{H}}^i,\left\{v_2\right\}]\ne \varnothing$ and so $\left|\gamma \right(\mathcal{D}[{\mathcal{H}}^i,\left\{v_2\right\}]\left)\right|\ge 1$. Therefore, $\mathsf{\Psi }\left({\mathcal{H}}^i\right)\ge 2$, and the result follows. ☐

As we will show in the next example, in order to get the value of $\mathsf{\Psi }\left({\mathcal{H}}^i\right)$, it is interesting to remark about the necessity of considering the family $\mathsf{\Gamma }\left({\mathcal{H}}^i\right)$ of all simultaneous local adjacency generators and not just the family of simultaneous local adjacency bases of ${\mathcal{H}}^i$.

Example 1.

Let $H_1\cong H_2\cong P_5$ be two copies of the path graph on five vertices such that $V\left(H_1\right)=V\left(H_2\right)=\{v_1,v_2,\cdots ,v_5\}$, whereas $E\left(H_1\right)=\{v_1{v}_2,v_2{v}_3,v_3{v}_4,v_4{v}_5\}$ and $E\left(H_2\right)=\{v_2{v}_1,v_1{v}_3,v_3{v}_5,v_5{v}_4\}$. Consider the family $\mathcal{H}=\{H_1,H_2\}$. We have that $B_1=\left\{v_3\right\}$ is a simultaneous local adjacency basis of $\mathcal{H}$ and $B_2=\{v_1,v_4\}$ is a simultaneous local adjacency generator for $\mathcal{H}$. Then, $D[\mathcal{H},B_1]=\{v_1,v_2,v_4,v_5\}$, $E\left(\mathcal{D}[\mathcal{H},B_1]\right)=\{v_1{v}_4,v_4{v}_2,v_2{v}_5,v_5{v}_1\}$, $\gamma \left(\mathcal{D}[\mathcal{G},B_1]\right)=2$, $\mathsf{\Psi }\left(B_1\right)=2+1=3$. However, $D[\mathcal{H},B_2]=\varnothing$ and $\mathsf{\Psi }\left(B_2\right)=2$.

We define the following graph families.

• ${\mathcal{S}}_1$ is the family of graphs having at least two non-trivial components.
• ${\mathcal{S}}_2$ is the family of graphs having at least one component of radius at least four.
• ${\mathcal{S}}_3$ is the family of graphs having at least one component of girth at least seven.
• ${\mathcal{S}}_4$ is the family of graphs having at least two non-singleton true twin equivalence classes $U_1,U_2$ such that $d(U_1,U_2)\ge 3$.

Lemma 3.

Let $\mathcal{H}\subseteq {\mathcal{S}}_0$ be a family of graphs on a common vertex set V. If ${\displaystyle \mathcal{H}\subseteq \bigcup _{i=0}^4{\mathcal{S}}_i}$, then:

$$\mathsf{\Psi }\left(\mathcal{H}\right)={Sad}_l\left(\mathcal{H}\right).$$

Proof. 

Let B be a simultaneous local adjacency generator for $\mathcal{H}$ and $v\in V$. We claim that $B\subseteq N_H\left(v\right)$. To see this, we differentiate the following cases for $H\in \mathcal{H}$.

• H has two non-trivial connected components $J_1,J_2$. In this case, $B\cap J_1\ne \varnothing$ and $B\cap J_2\ne \varnothing$, which implies that $B\subseteq N_H\left(v\right)$.
• H has one non-trivial component J such that $r\left(J\right)\ge 4$. If H has two non-trivial components, then we are in the first case. Therefore, we can assume that J is the only non-trivial component of H. Suppose that $B\subseteq N_H\left(v\right)$, and get $v^{\prime }\in V$ such that $d_H(v,v^{\prime })=4$. If $v{v}_1{v}_2{v}_3{v}^{\prime }$ is a shortest path from v to $v^{\prime }$, then $v_3$ and $v^{\prime }$ are adjacent, and they are not distinguished by the elements in B, which is a contradiction.
• H has one non-trivial component J of girth g$\left(J\right)\ge 7$. In this case, if H has two non-trivial components, then we are in the first case. Therefore, we can assume that H has just one non-trivial component of girth g$\left(J\right)\ge 7$. Suppose that $B\subseteq N_H\left(v\right)$. For each cycle $v_1{v}_2\cdots v_n{v}_1$, there exists $v_i{v}_{i+1}\in E\left(J\right)$ such that $d_H(v,v_i)\ge 3$ and $d_H(v,v_{i+1})\ge 3$; therefore, for each $b\in B$, we have $d_H(b,v_i)\ge 2$ and $d_H(b,v_{i+1})\ge 2$, which is a contradiction.
• H has two non-singleton true twin equivalence classes $U_1,U_2$ such that $d_H(U_1,U_2)\ge 3$. Since $B\cap U_1\ne \varnothing$ and $B\cap U_2\ne \varnothing$, we can conclude that $B\subseteq N_H\left(v\right)$.
• $H\cong N_{\left|V\right|}$. Notice that $B\ne \varnothing$, as $\mathcal{H}\subseteq {\mathcal{S}}_0$, so that $B\subseteq \varnothing =N_H\left(v\right)$.

According to the five cases above, ${\displaystyle \mathcal{H}\subseteq {\cup }_{i=0}^4{\mathcal{S}}_i}$ leads to $D[\mathcal{H},B]=\varnothing$, for any simultaneous local adjacency generator, which implies that $\mathsf{\Psi }\left(\mathcal{H}\right)={Sad}_l\left(\mathcal{H}\right)$. ☐

Remark 9.

If $A\in \mathsf{{\rm Y}}(V,\mathcal{H})$, then $A\cup (V-\mathsf{\Phi }(V,\mathcal{H}\left)\right)$ is a simultaneous local metric generator for $\mathcal{G}$. However, the converse is not true, as we can see in the following example.

Example 2.

Consider the family of connected graphs $\mathcal{G}=\{G_1,G_2,G_3\}$ on a common vertex set $V=\{u_1,\cdots ,u_8\}$ with $E\left(G_i\right)=\{u_1{u}_2,u_1{u}_{2i+1},u_2{u}_{2i+2},$$u_j{u}_{2i+1},u_j{u}_{2i+2},$ for $j\notin \{1,2,2i+1,2i+2\}\}$. Let ${\mathcal{H}}^i$ be the family consisting of only one graph $H_i$, as follows: $H_1\cong H_2\cong K_2$, $H_3\cong H_4\cong \cdots \cong H_8\cong N_2$. We have that $\mathcal{G}\circ \mathcal{H}=\{G_i\circ \{H_1,\cdots ,H_8\},i=1,2,3\}$ and $I(V,\mathcal{H})=V$. If we take $A=\varnothing$, then $A\cup (V-\mathsf{\Phi }(V,\mathcal{H}))=\{u_1,u_2\}\subseteq I(V,\mathcal{H})$ is a simultaneous local metric basis of $\mathcal{G}$. However, $\varnothing \notin \mathsf{{\rm Y}}(V,\mathcal{H})$ because $u_1$ is adjacent to $u_2$ in $G_i$, $i\in \{1,2,3\}$, and $(V-\mathsf{\Phi }(V,\mathcal{H}))-\{u_1,u_2\}=\varnothing$.

Lemma 4.

Let $\mathcal{G}\circ \mathcal{H}$ be a family of lexicographic product graphs. Let $B\subseteq V$ be a simultaneous local metric generator for $\mathcal{G}$. Then, $B\cap I(V,\mathcal{H})\in \mathsf{{\rm Y}}(V,\mathcal{H})$.

Proof. 

Let $A=B\cap I(V,\mathcal{H})$ and $u_i,u_j\in I(V,\mathcal{H})-A=I(V,\mathcal{H})-B$. Since $B\subseteq V$ is a simultaneous local metric generator for $\mathcal{G}$, for each $G_k\in \mathcal{G}$, there exists $b\in B$ such that $d_{G_k}(b,u_i)\ne d_{G_k}(b,u_j)$. If $b\notin I(V,\mathcal{H})$, then necessarily $b\in (V-I(V,\mathcal{H}))\subseteq ((V-\mathsf{\Phi }(V,\mathcal{H}))-\{u_i,u_j\})$, and if $b\in I(V,\mathcal{H})$, then $b\in A-\{u_i,u_j\}$; and we are done. ☐

Corollary 5.

If there exists a simultaneous local metric generator B for $\mathcal{G}$ such that $B\subseteq V-I(V,\mathcal{H})$ or the graph $\mathit{G}(\mathcal{G},I(V,\mathcal{H}\left)\right)$ is empty, then $\varnothing \in \mathsf{{\rm Y}}(V,\mathcal{H})$.

Remark 10.

If B is a vertex cover of $\mathit{G}(\mathcal{G},I(V,\mathcal{H})$, then $B\in \mathsf{{\rm Y}}(V,\mathcal{H})$.

Lemma 5.

Let $\mathcal{G}\circ \mathcal{H}$ be a family of lexicographic product graphs. For each $u_i\in V$, let $B_i\subseteq V_i$ be a simultaneous local adjacency generator for ${\mathcal{H}}^i$, and let $C_i\subseteq V_i$ be a dominating set of $\mathcal{D}[{\mathcal{H}}^i,B_i]$. Then, for any $A\in \mathsf{{\rm Y}}(V,\mathcal{H})$, the set $B=({\cup }_{u_i\in A}\left\{u_i\right\}\times (B_i\cup C_i))\bigcup ({\cup }_{u_i\notin A}\left\{u_i\right\}\times B_i)$ is a local metric generator for $\mathcal{G}\circ \mathcal{H}$.

Proof. 

In order to prove the lemma, let $G_k\in \mathcal{G}$, ${\mathcal{H}}_j\in \mathcal{H}$, and let $(u_{i_1},v_1),(u_{i_2},v_2)$ be a pair of adjacent vertices of $G_k\circ {\mathcal{H}}_j$. If $i_1=i_2$, then there exists $v\in B_{i_1}$ such that $(u_{i_1},v)$ distinguishes the pair. Otherwise, $i_1\ne i_2$, and we consider the following cases:

• $|\{u_{i_1},u_{i_2}\}\cap I(V,\mathcal{H})|\le 1$, say $u_{i_1}\notin I(V,\mathcal{H})$. In this case, there exists $v\in B_{i_1}$ such that $v{v}_1\notin E\left(H_{i_{1}j}\right)$, and then, $(u_{i_1},v)$ distinguishes the pair.
• $u_{i_1},u_{i_2}\in I(V,\mathcal{H})$ and $\{u_{i_1},u_{i_2}\}\cap A=\varnothing$. In this case, by definition of A, there exists $u_{i_3}\in (A\cup (V-\mathsf{\Phi }(V,\mathcal{H})))-\{u_{i_1},u_{i_2}\}$ such that $d_{G_k}(u_{i_3},u_{i_1})\ne d_{G_k}(u_{i_3},u_{i_2})$. For any $v\in B_{i_3}\cup C_{i_3}$,

  $$d_{G_k\circ {\mathcal{H}}_j}((u_{i_3},v),(u_{i_1},v_1))=d_{G_k}(u_{i_3},u_{i_1})\ne$$

  $$d_{G_k}(u_{i_3},u_{i_2})=d_{G_k\circ {\mathcal{H}}_j}((u_{i_3},v),(u_{i_2},v_2)).$$
• $u_{i_1},u_{i_2}\in I(V,\mathcal{H})$ and $\left|\right\{u_{i_1},u_{i_2}\}\cap A|\ge 1$, say $u_{i_1}\in A$. In this case, if there exists $v\in B_{i_1}$ such that $v{v}_1\notin E\left(H_{i_{1}j}\right)$, then $(u_{i_1},v)$ distinguishes the pair. Otherwise, $v_1$ is a vertex of $\mathcal{D}[{\mathcal{H}}^{i_1},B_{i_1}]$, and either $v_1\in C_{i_1}$ and $(u_{i_1},v_1)\in B$ distinguishes the pair or there exists $v\in C_{i_1}$, such that $v{v}_1\in E\left(\mathcal{D}[{\mathcal{H}}^{i_1},B_{i_1}]\right)$, which means $v{v}_1\notin E\left(H_{i_{1}j}\right)$; then, $(u_{i_1},v)$ distinguishes the pair.

 ☐

Corollary 6.

Let $\mathcal{G}\circ \mathcal{H}$ be a family of lexicographic product graphs. Then:

$${Sd}_l(\mathcal{G}\circ \mathcal{H})\le \underset{A\in \mathsf{{\rm Y}}(V,\mathcal{H})}{min}\left\{\sum _{u_i\in A}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+\sum _{u_i\notin A}{Sad}_l\left({\mathcal{H}}^i\right)\right\}.$$

Proof. 

Let $A\in \mathsf{{\rm Y}}(V,\mathcal{H})$. For each $u_i\notin A$, let $B_i\subseteq V_i$ be a simultaneous local adjacency basis of ${\mathcal{H}}^i$. For each $u_i\in A$, let $B_i$ be a local adjacency generator for ${\mathcal{H}}^i$ and $C_i\subseteq V_i$ a dominating set of $\mathcal{D}({\mathcal{H}}^i,B_i)$ such that $|B_i\cup C_i|=\mathsf{\Psi }\left({\mathcal{H}}^i\right)$. Let:

$$B=({\cup }_{u_j\in A}\left\{u_j\right\}\times (B_j\cup C_j))\bigcup ({\cup }_{u_i\notin A}\left\{u_i\right\}\times B_i)$$

then, by Lemma 5, B is a simultaneous local metric generator for $\mathcal{G}\circ \mathcal{H}$, and:

$${Sd}_l(\mathcal{G}\circ \mathcal{H})\le \left|B\right|=\sum _{u_i\in A}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+\sum _{u_i\notin A}{Sad}_l\left({\mathcal{H}}^i\right)$$

As $A\in \mathsf{{\rm Y}}(V,\mathcal{H})$ is arbitrary:

$${Sd}_l(\mathcal{G}\circ \mathcal{H})\le \underset{A\in \mathsf{{\rm Y}}(V,\mathcal{H})}{min}\left\{\sum _{u_i\in A}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+\sum _{u_i\notin A}{Sad}_l\left({\mathcal{H}}^i\right)\right\}$$

and the result follows. ☐

Lemma 6.

Let F be a simultaneous local metric basis of $\mathcal{G}\circ \mathcal{H}$. Let $F_i=\{v\in V_i:(u_i,v)\in F\}$ and $X_F=\{u_i\in I(V,\mathcal{H}):|F_i|\ge \mathsf{\Psi }\left({\mathcal{H}}^i\right)\}$. Then, $X_F\in \mathsf{{\rm Y}}(V,\mathcal{H})$.

Proof. 

Suppose, for the purpose of contradiction, that $X_F\notin \mathsf{{\rm Y}}(V,\mathcal{H})$. That means that there exist $u_{i_1},u_{i_2}\in I(V,\mathcal{H})-X_F$ and $G_k\in \mathcal{G}$ such that $u_{i_1}{u}_{i_2}\in E\left(G_k\right)$, and $d_{G_k}(u,u_{i_1})=d_{G_k}(u,u_{i_2})$ for every $u\in (X_F\cup (V-\mathsf{\Phi }(V,\mathcal{H})))-\{u_{i_1},u_{i_2}\}$. As $u_{i_1},u_{i_2}\in I(V,\mathcal{H})-X_F$, $|F_{i_1}|<\mathsf{\Psi }\left({\mathcal{H}}^{i_1}\right)$ and $|F_{i_2}|<\mathsf{\Psi }\left({\mathcal{H}}^{i_2}\right)$, so that there exist $H_{i_1{j}_1}\in {\mathcal{H}}^{i_1}$ and $H_{i_2{j}_2}\in {\mathcal{H}}^{i_2}$ such that for some $v_1\in V_{i_1}$, $v_2\in V_{i_2}$, $F_{i_1}\subseteq N_{H_{i_1{j}_1}}\left(v_1\right)$ and $F_{i_2}\subseteq N_{H_{i_2{j}_2}}\left(v_2\right)$. Let ${\mathcal{H}}_j$ be such that $H_{i_1{j}_1},H_{i_2{j}_2}\in {\mathcal{H}}_j$. Consider the pair of vertices $(u_{i_1},v_1),(u_{i_2},v_2)$ adjacent in $G_k\circ {\mathcal{H}}_j$. As F is a simultaneous local metric generator, there exists $(u_{i_3},v)\in F$ that resolves the pair, which implies that $F_{i_3}\ne \varnothing$. By hypothesis $u_{i_3}\in (\mathsf{\Phi }(V,\mathcal{H})-X_F)\cup \{u_{i_1},u_{i_2}\}$, and so, $u_{i_3}\in \{u_{i_1},u_{i_2}\}$. Without loss of generality, we assume that $u_{i_3}=u_{i_1}$ and, in this case,

$$\begin{array}{cc}\hfill d_{G_k\circ {\mathcal{H}}_j}((u_{i_3},v),(u_{i_1},v_1))& =d_{H_{i_1{j}_1},2}(v,v_1)\hfill \\ & =d_{G_k}(u_{i_3},u_{i_2})\hfill \\ & =d_{G_k\circ {\mathcal{H}}_j}((u_{i_3},v),(u_{i_2},v_2)),\hfill \end{array}$$

which is a contradiction. Therefore, $X_F\in \mathsf{{\rm Y}}(V,\mathcal{H})$. ☐

Theorem 13.

Let $\mathcal{G}\circ \mathcal{H}$ be a family of lexicographic product graphs.

$${Sd}_l(\mathcal{G}\circ \mathcal{H})=\underset{A\in \mathsf{{\rm Y}}(V,\mathcal{H})}{min}\left\{\sum _{u_i\in A}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+\sum _{u_i\notin A}{Sad}_l\left({\mathcal{H}}^i\right)\right\}$$

Proof. 

Let B be a simultaneous local metric basis of $\mathcal{G}\circ \mathcal{H}$. Let $B_i=\{v\in V_i:(u_i,v)\in B\}$ and $X_B=\{u_i\in I(V,\mathcal{H}):|B_i|\ge \mathsf{\Psi }\left({\mathcal{H}}^i\right)\}$. By Remark 7, $|B_i|\ge {Sad}_l\left({\mathcal{H}}^i\right)$ for every $u_i\in V$, so that Lemma 6 leads to:

$$\underset{A\in \mathsf{{\rm Y}}(V,\mathcal{H})}{min}\left\{\sum _{u_i\in A}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+\sum _{u_i\notin A}{Sad}_l\left({\mathcal{H}}^i\right)\right\}\le \sum _{u_i\in X_B}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+\sum _{u_i\notin X_B}{Sad}_l\left({\mathcal{H}}^i\right)\le \left|B\right|$$

and the result follows by Corollary 6. ☐

Now, we will show some cases where the calculation of ${Sd}_l(\mathcal{G}\circ \mathcal{H})$ is easy. At first glance, we have two main types of simplification: first, to simplify the calculation of $\mathsf{\Psi }\left({\mathcal{H}}^i\right)$ and, second, the calculation of the $A\in \mathsf{{\rm Y}}(V,\mathcal{H})$ that makes the sum achieves its minimum.

For the first type of simplification, we can apply Lemma 3 to deduce the following corollary.

Corollary 7.

If for each i, ${\mathcal{H}}^i\subseteq {\mathcal{S}}_0$ and ${\displaystyle {\mathcal{H}}^i\subseteq \bigcup _{j=0}^4{\mathcal{S}}_j}$, then:

$${Sd}_l(\mathcal{G}\circ \mathcal{H})=\sum {Sad}_l\left({\mathcal{H}}^i\right).$$

Given a family $\mathcal{G}$ of graphs on a common vertex set V and a graph H, we define the family of lexicographic product graphs:

$$\mathcal{G}\circ H=\{G\circ H:G\in \mathcal{G}\}.$$

By Theorem 13, we deduce the following result.

Corollary 8.

Let $\mathcal{G}$ be a family of graphs on a common vertex set V, and let H be a graph. If for every local adjacency basis B of H, $B\subseteq N_H\left(v\right)$ for every $v\in V\left(H\right)-B$, then:

$${Sd}_l(\mathcal{G}\circ H)=\left|V\right|{adim}_l\left(H\right).$$

By Corollary 5 and Theorem 13, we have the following result.

Proposition 2.

If $V-I(V,\mathcal{H})$ is a simultaneous local metric generator for $\mathcal{G}$ or the graph $\mathit{G}(\mathcal{G},I(V,\mathcal{H}\left)\right)$ is empty, then:

$${Sd}_l(\mathcal{G}\circ \mathcal{H})=\sum {Sad}_l\left({\mathcal{H}}^i\right)$$

For the second type of simplification, we have the following remark.

Remark 11.

As ${Sad}_l\left({\mathcal{H}}^i\right)\le \mathsf{\Psi }\left({\mathcal{H}}^i\right)$, if $A\subseteq B\subseteq V$, then:

$$\sum _{u_i\in A}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+\sum _{u_i\notin A}{Sad}_l\left({\mathcal{H}}^i\right)\le \sum _{u_i\in B}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+\sum _{u_i\notin B}{Sad}_l\left({\mathcal{H}}^i\right)$$

From Remark 11, we can get some consequences of Theorem 13.

Proposition 3.

Let $\mathcal{G}\circ \mathcal{H}$ be a family of lexicographic product graphs. For any vertex cover B of $\mathit{G}(\mathcal{G},I(V,\mathcal{H}\left)\right)$,

$${Sd}_l(\mathcal{G}\circ \mathcal{H})\le \sum _{u_i\in B}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+\sum _{u_i\notin B}{Sad}_l\left({\mathcal{H}}^i\right)$$

Proposition 4.

Let $\mathcal{G}$ be a family of connected graphs with common vertex set V, and let $\mathcal{G}\circ \mathcal{H}$ be a family of lexicographic product graphs. The following statements hold.

1.

If the subgraph of $G_j$ induced by $I(V,\mathcal{H})$ is empty for every $G_j\in \mathcal{G}$, then:

$${Sd}_l(\mathcal{G}\circ \mathcal{H})=\sum _{u_i\in V}{Sad}_l\left({\mathcal{H}}^i\right).$$

2.

Let $u_{i_0}\in I(V,\mathcal{H})$ be such that $\mathsf{\Psi }\left({\mathcal{H}}^{i_0}\right)=max\{\mathsf{\Psi }\left(u_i\right):u_i\in I(V,\mathcal{H})\}$. If ${Sd}_l\left(\mathcal{G}\right)=\left|V\right|-1$ and $\left|I\right(V,\mathcal{H}\left)\right|\ge 2$, then:

$${Sd}_l(\mathcal{G}\circ \mathcal{H})=\sum _{u_i\notin I(V,\mathcal{H})}{Sad}_l\left({\mathcal{H}}^i\right)+\sum _{u_i\in I(V,\mathcal{H})-\left\{u_{i_0}\right\}}\mathsf{\Psi }\left({\mathcal{H}}^i\right)+{Sad}_l\left({\mathcal{H}}^{i_0}\right)$$

Proof. 

It is clear that if the subgraph of $G_j$ induced by $I(V,\mathcal{H})$ is empty for every $G_j\in \mathcal{G}$, then $\varnothing \in \mathsf{{\rm Y}}(V,\mathcal{H})$, so that Theorem 13 leads to (1). On the other hand, let $\mathcal{G}$ be a family of connected graphs with common vertex set V such that ${Sd}_l\left(\mathcal{G}\right)=\left|V\right|-1$ and $\left|I\right(V,\mathcal{H}\left)\right|\ge 2$. By Lemma 1, for every $u_i,u_j\in I(V,\mathcal{H})$, there exists $G_{ij}\in \mathcal{G}$ such that $u_i,u_j$ are true twins in $G_{ij}$. Hence, no vertex $u\notin \{u_i,u_j\}$ resolves $u_i$ and $u_j$. Therefore, $A\in \mathsf{{\rm Y}}(V,\mathcal{H})$ implies $\left|A\right|=\left|I\right(V,\mathcal{H}\left)\right|-1$, and (2) follows from Theorem 13 and Remark 11. ☐

Proposition 5.

Let $\mathcal{G}$ be a family of non-trivial connected graphs with common vertex set V. For any family of lexicographic product graphs $\mathcal{G}\circ \mathcal{H}$,

$${Sd}_l(\mathcal{G}\circ \mathcal{H})\ge {Sd}_l\left(\mathcal{G}\right).$$

Furthermore, if $\mathcal{H}=\{N_{|V_1|},\cdots ,N_{|V_n|}\}$, then:

$${Sd}_l(\mathcal{G}\circ \mathcal{H})={Sd}_l\left(\mathcal{G}\right).$$

Proof. 

Let W be a simultaneous local metric basis of $\mathcal{G}\circ \mathcal{H}$ and $W_V=\{u\in V:(u,v)\in W\}$. We suppose that $W_V$ is not a simultaneous local metric generator for $\mathcal{G}$. Let $u_i,u_j\notin W_V$ and $G\in \mathcal{G}$ such that $u_i{u}_j\in E\left(G\right)$ and $d_G(u_i,u)=d_G(u_j,u)$ for every $u\in W_V$. Thus, for any $v\in V_i$, $v^{\prime }\in V_j$ and $(x,y)\in W$, we have:

$$d_{G\circ H_i}((x,y),(u_i,v))=d_G(x,u_i)=d_G(x,u_j)=d_{G\circ H_i}((x,y),(u_j,v^{\prime })),$$

which is a contradiction. Therefore, $W_V$ is a simultaneous local metric generator for $\mathcal{G}$ and, as a result, ${Sd}_l\left(\mathcal{G}\right)\le |W_V|\le |W|={Sd}_l(\mathcal{G}\circ \mathcal{H})$.

On the other hand, if $\mathcal{H}=\{N_{|V_1|},\cdots ,N_{|V_n|}\}$, then $V=I(V,\mathcal{H})=\mathsf{\Phi }(V,\mathcal{H})$. Let $B\subseteq V$ be a simultaneous local metric basis of $\mathcal{G}$. Now, for each $u_i\in B$, we choose $v_i\in V_i$, and by Remark 9, we claim that $B^{\prime }=\{(u_i,v_i):u_i\in B\}$ is a simultaneous local metric generator for $\mathcal{G}\circ \mathcal{H}$. Thus, ${Sd}_l(\mathcal{G}\circ \mathcal{H})\le |B^{\prime }|=|B|={Sd}_l\left(\mathcal{G}\right)$. ☐

Proposition 6.

Let $\mathcal{G}\ne \left\{K_2\right\}$ be a family of non-trivial connected bipartite graphs with common vertex set V and $\mathcal{H}\ne \{{\mathcal{H}}_1,\cdots ,{\mathcal{H}}_n\}$ such that ${\mathcal{H}}_j\subseteq {\mathcal{S}}_0$, for some j. If $V=I(V,\mathcal{H})$ and there exist $u_1,u_2\in V$ and $G_k\in \mathcal{G}$ such that $V-\mathsf{\Phi }(V,\mathcal{H})=\{u_1,u_2\}$ and $u_1{u}_2\in E\left(G_k\right)$, then:

$${Sd}_l(\mathcal{G}\circ \mathcal{H})=\sum {Sad}_l\left({\mathcal{H}}^i\right)+1,$$

otherwise,

$${Sd}_l(\mathcal{G}\circ \mathcal{H})=\sum {Sad}_l\left({\mathcal{H}}^i\right).$$

Proof. 

If $V=I(V,\mathcal{H})$ and there exist $u_1,u_2\in V$ and $G_k\in \mathcal{G}$ such that $V-\mathsf{\Phi }(V,\mathcal{H})=\{u_1,u_2\}$ and $u_1{u}_2\in E\left(G_k\right)$, then $\varnothing \notin \mathsf{{\rm Y}}(V,\mathcal{H})$ because no vertex in $(V-\mathsf{\Phi }(V,\mathcal{H}))-\{u_1,u_2\}=\varnothing$ distinguishes $u_1$ and $u_2$. Let $x,y\in I(V,\mathcal{H})$ such that $xy\in {\cup }_{G\in \mathcal{G}}E\left(G\right)$. Since any $u_i\in \mathsf{\Phi }(V,\mathcal{H})$ distinguishes x and y, we can conclude that $\left\{u_i\right\}\in \mathsf{{\rm Y}}(V,\mathcal{H})$, and by Remark 8, $\mathsf{\Psi }\left({\mathcal{H}}^i\right)=1$. Therefore, Theorem 13 leads to ${Sd}_l(\mathcal{G}\circ \mathcal{H})=\sum {Sad}_l\left({\mathcal{H}}^i\right)+1.$

Assume that there exists $u_i\in V-I(V,\mathcal{H})$, or $V-\mathsf{\Phi }(V,\mathcal{H})=\left\{u_i\right\}$, or $V-\mathsf{\Phi }(V,\mathcal{H})=\{u_i,u_j\}$ and, for every $G_k\in \mathcal{G}$, $u_i{u}_j\notin E\left(G_k\right)$ or $\{u_i,u_j,u_k\}\subseteq V-\mathsf{\Phi }(V,\mathcal{H})$. In any one of these cases $\left\{u_i\right\}$ is a simultaneous local metric basis of $\mathcal{G}$ and, for every pair $u_1,u_2$ of adjacent vertices in some $G_k\in \mathcal{G}$ such that $u_i\notin \{u_1,u_2\}$, $u_i$ distinguishes the pair. Since $u_i\in V-\mathsf{\Phi }(V,\mathcal{H})$, we can claim that $\varnothing \in \mathsf{{\rm Y}}(V,\mathcal{H})$, and by Theorem 13, ${Sd}_l(\mathcal{G}\circ \mathcal{H})=\sum {Sad}_l\left({\mathcal{H}}^i\right).$ ☐

5.1. Families of Join Graphs

For two graph families $\mathcal{G}=\{G_1,\dots ,G_{k_1}\}$ and $\mathcal{H}=\{H_1,\dots ,H_{k_2}\}$, defined on common vertex sets $V_1$ and $V_2$, respectively, such that $V_1\cap V_2=\varnothing$, we define the family:

$$\mathcal{G}+\mathcal{H}=\{G_i+H_j:1\le i\le k_1,1\le j\le k_2\}.$$

Notice that, since for any $G_i\in \mathcal{G}$ and $H_j\in \mathcal{H}$ the graph $G_i+H_j$ has diameter two,

$${Sd}_l(\mathcal{G}+\mathcal{H})={Sad}_l(\mathcal{G}+\mathcal{H}).$$

The following result is a direct consequence of Theorem 13.

Corollary 9.

For any pair of families $\mathcal{G}$ and $\mathcal{H}$ of non-trivial graphs on common vertex sets $V_1$ and $V_2$, respectively,

$${Sd}_l(\mathcal{G}+\mathcal{H})=min\{{Sd}_{A,l}\left(\mathcal{G}\right)+\mathsf{\Psi }\left(\mathcal{H}\right),{Sd}_{A,l}\left(\mathcal{H}\right)+\mathsf{\Psi }\left(\mathcal{G}\right)\}$$

Remark 12.

Let $\mathcal{G}$ be a family of graphs defined on a common vertex set $V_1$. If there exists B a simultaneous local adjacency basis of $\mathcal{G}$ such that $D[\mathcal{G},B]=\varnothing$, then for every $\mathcal{H}$ family of graphs defined on a common vertex set $V_2$, we have:

$${Sd}_l(\mathcal{G}+\mathcal{H})={Sad}_l\left(\mathcal{G}\right)+{Sad}_l\left(\mathcal{H}\right)$$

By Lemma 3 and Remark 12, we deduce the following result.

Proposition 7.

Let $\mathcal{G}$ and $\mathcal{H}$ be two families of non-trivial connected graphs on a common vertex set $V_1$ and $V_2$, respectively. If $\mathcal{G}\subseteq {\cup }_{i=1}^4{\mathcal{S}}_i$, then:

$${Sd}_l(\mathcal{G}+\mathcal{H})={Sad}_l\left(\mathcal{G}\right)+{Sad}_l\left(\mathcal{H}\right).$$

6. Computability of the Simultaneous Local Metric Dimension

In previous sections, we have seen that there is a large number of classes of graph families for which the simultaneous local metric dimension is well determined. This includes some cases of graph families whose simultaneous metric dimension is hard to compute, e.g., families composed by trees [22], yet the simultaneous local metric dimension is constant. However, as proven in [23], the problem of finding the local metric dimension of a graph is NP-hard in the general case, which trivially leads to the fact that finding the simultaneous local metric dimension of a graph family is also NP-hard in the general case.

Here, we will focus on a different aspect, namely that of showing that the requirement of simultaneity adds to the computational difficulty of the original problem. To that end, we will show that there exist families composed by graphs whose individual local metric dimensions are constant, yet it is hard to compute their simultaneous local metric dimension.

To begin with, we will formally define the decision problems associated with the computation of the local metric dimension of one graph and the simultaneous local metric dimension of a graph family.

• Local metric Dimension (LDIM)
  Instance: A graph $G=(V,E)$ and an integer p, $1\le p\le \left|V\right(G\left)\right|-1$.
  Question: Is ${dim}_l\left(G\right)\le p$?
• Simultaneous Local metric Dimension (SLD)
  Instance: A graph family $\mathcal{G}=\{G_1,G_2,\dots ,G_k\}$ on a common vertex set V and an integer p, $1\le p\le \left|V\right|-1$.
  Question: Is ${Sd}_l\left(\mathcal{G}\right)\le p$?

As we mentioned above, LDIM was proven to be NP-complete in [23]. Moreover, it is simple to see that determining whether a vertex set $S\subseteq V$, $\left|S\right|\le p$, is a simultaneous local metric generator can be done in polynomial time, so SLD is in NP. In fact, SLD can be easily shown to be NP-complete, since for any graph $G=(V,E)$ and any integer $1\le p\le \left|V\right(G\left)\right|-1$, the corresponding instance of LDIM can be trivially transformed into an instance of SLD by making $\mathcal{G}=\left\{G\right\}$.

For the remainder of this section, we will address the issue of the complexity added by the requirement of simultaneity. To this end, we will consider families composed by the so-called tadpole graphs [28]. An $(h,t)$-tadpole graph (or $(h,t)$-tadpole for short) is the graph obtained from a cycle graph $C_h$ and a path graph $P_t$ by joining with an edge a leaf of $P_t$ to an arbitrary vertex of $C_h$. We will use the notation $T_{h,t}$ for $(h,t)$-tadpoles. Since $(2q,t)$-tadpoles are bipartite, we have that ${dim}_l\left(T_{2q,t}\right)=1$. In the case of $(2q+1,t)$-tadpoles, we have that ${dim}_l\left(T_{2q+1,t}\right)=2$, as they are not bipartite (so, ${dim}_l\left(T_{2q+1,t}\right)\ge 2$), and any set composed by two vertices of the subgraph $C_{2q+1}$ is a local metric generator (so, ${dim}_l\left(T_{2q+1,t}\right)\le 2$). Additionally, consider the sole vertex v of degree three in $T_{2q+1,t}$ and a local metric generator for $T_{2q+1,t}$ of the form $\{v,x\}$, $x\in V\left(C_{2q+1}\right)-\left\{v\right\}$. It is simple to verify that for any vertex $y\in V\left(P_t\right)$, the set $\{y,x\}$ is also a local metric generator for $T_{2q+1,t}$.

Consider a family $\mathcal{T}=\{T_{h_1,t_1},T_{h_2,t_2},\dots ,T_{h_k,t_k}\}$ composed by tadpole graphs on a common vertex set V. By Theorem 4, we have that ${Sd}_l\left(\mathcal{T}\right)={Sd}_l\left({\mathcal{T}}^{\prime }\right)$, where ${\mathcal{T}}^{\prime }$ is composed by $(2q+1,t)$-tadpoles. As we discussed previously, ${dim}_l\left(T_{2q+1,t}\right)=2$. However, by Remark 1 and Theorem 1, we have that $2\le {Sd}_l\left({\mathcal{T}}^{\prime }\right)\le \left|V\right|-1$. In fact, both bounds are tight, since the lower bound is trivially satisfied by unitary families, whereas the upper bound is reached, for instance, by any family composed by all different labeled graphs isomorphic to an arbitrary $(3,t)$-tadpole, as it satisfies the premises of Theorem 1. Moreover, as we will show, the problem of computing ${Sd}_l\left({\mathcal{T}}^{\prime }\right)$ is NP-hard, as its associated decision problem is NP-complete. We will do so by showing a transformation from the hitting set problem, which was shown to be NP-complete by Karp [29]. The hitting set problem is defined as follows:

• Hitting Set Problem (HSP)
• Instance: A collection $\mathcal{C}=\{C_1,C_2,\dots ,C_k\}$ of non-empty subsets of a finite set S and a positive integer $p\le \left|S\right|$.
• Question: Is there a subset $S^{\prime }\subseteq S$ with $|S^{\prime }|\le p$ such that $S^{\prime }$ contains at least one element from each subset in $\mathcal{C}$?

Theorem 14.

The Simultaneous Local metric Dimension problem (SLD) is NP-complete for families of $(2q+1,t)$-tadpoles.

Proof. 

As we discussed previously, determining whether a vertex set $S\subseteq V$, $\left|S\right|\le p$, is a simultaneous local metric generator for a graph family $\mathcal{G}$ can be done in polynomial time, so SLD is in NP.

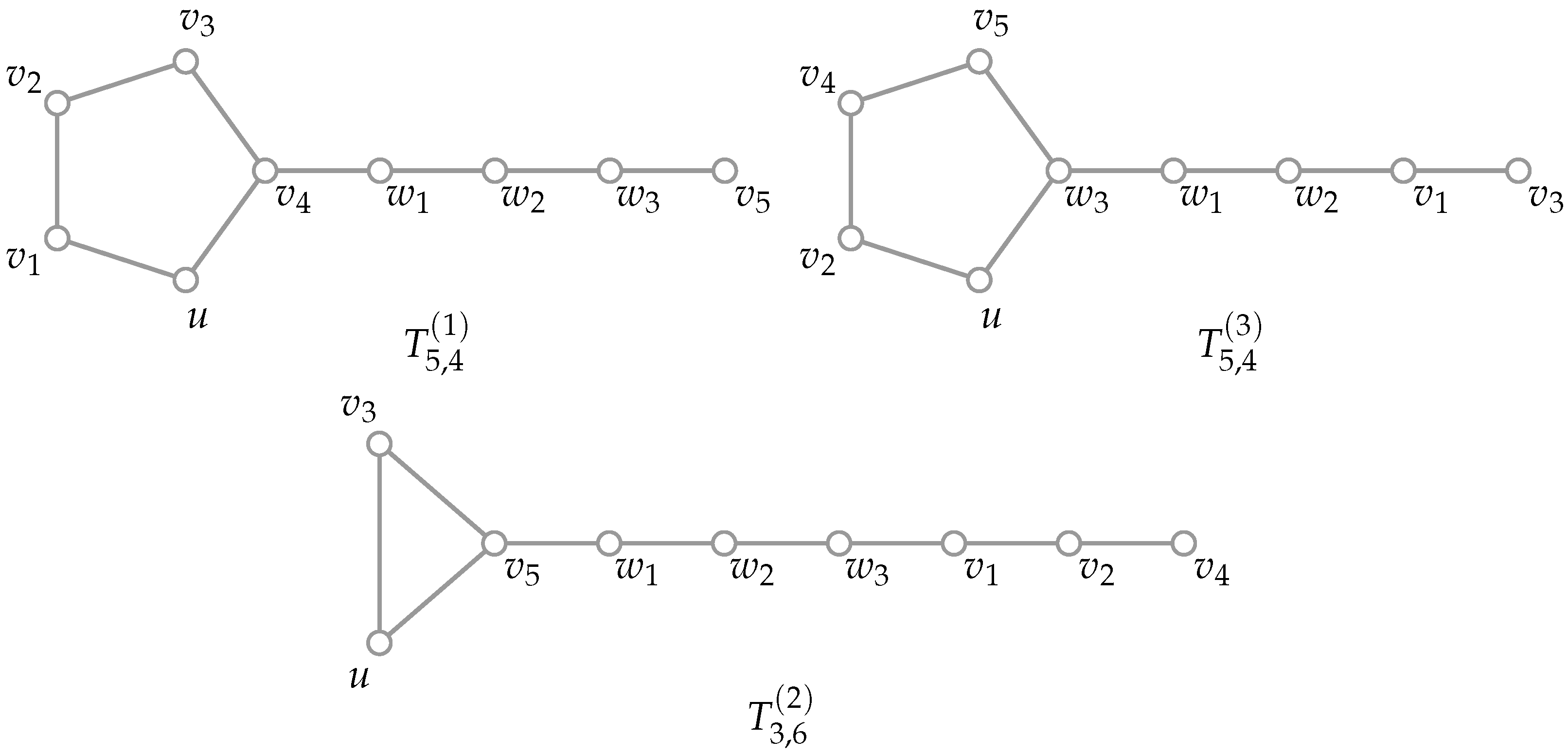
Now, we will show a polynomial time transformation of HSP into SLD. Let $S=\{v_1,v_2,\dots ,v_n\}$ be a finite set, and let $\mathcal{C}=\{C_1,C_2,\dots ,C_k\}$, where every $C_i\in \mathcal{C}$ satisfies $C_i\subseteq S$. Let p be a positive integer such that $p\le \left|S\right|$. Let $A=\{w_1,w_2,\dots ,w_k\}$ such that $A\cap S=\varnothing$. We construct the family $\mathcal{T}=\{T_{2q_1+1,t_1},T_{2q_2+1,t_2},\dots ,T_{2q_k+1,t_k}\}$ composed by $(2q+1,t)$-tadpoles on the common vertex set $V=S\cup A\cup \left\{u\right\}$, $u\notin S\cup A$, by performing one of the two following actions, as appropriate, for every $r\in \{1,\dots ,k\}$:

• If $|C_r|$ is even, let $C_{2q_r+1}$ be a cycle graph on the vertices of $C_r\cup \left\{u\right\}$; let $P_{t_r}$ be a path graph on the vertices of $(S-C_r)\cup A$; and let $T_{2q_r+1,t_r}$ be the tadpole graph obtained from $C_{2q_r+1}$ and $P_{t_r}$ by joining with an edge a leaf of $P_{t_r}$ to a vertex of $C_{2q_r+1}$ different from u.
• If $|C_r|$ is odd, let $C_{2q_r+1}$ be a cycle graph on the vertices of $C_r\cup \{u,w_r\}$; let $P_{t_r}$ be a path graph on the vertices of $(S-C_r)\cup (A-\left\{w_r\right\})$; and let $T_{2q_r+1,t_r}$ be the tadpole graph obtained from $C_{2q_r+1}$ and $P_{t_r}$ by joining with an edge the vertex $w_r$ to a leaf of $P_{t_r}$.

Figure 4 shows an example of this construction.

In order to prove the validity of this transformation, we claim that there exists a subset $S^{″}\subseteq S$ of cardinality $|S^{″}|\le p$ that contains at least one element from each $C_r\in \mathcal{C}$ if and only if ${Sd}_l\left(\mathcal{T}\right)\le p+1$.

To prove this claim, first assume that there exists a set $S^{″}\subseteq S$, which contains at least one element from each $C_r\in \mathcal{C}$ and satisfies $|S^{″}|\le p$. Recall that any set composed by two vertices of $C_{2q_r+1}$ is a local metric generator for $T_{2q_r+1,t_r}$, so $S^{″}\cup \left\{u\right\}$ is a simultaneous local metric generator for $\mathcal{T}$. Thus, ${Sd}_l\left(\mathcal{T}\right)\le p+1$.

Now, assume that ${Sd}_l\left(\mathcal{T}\right)\le p+1$, and let W be a simultaneous local metric generator for $\mathcal{T}$ such that $\left|W\right|=p+1$. For every $T_{2q_r+1,t_r}\in \mathcal{T}$, we have that $u\in V\left(C_{2q_r+1}\right)$ and ${\delta }_{T_{2q_r+1,t_r}}\left(u\right)=2$, so $|\left((W-\{x\left\}\right)\cup \left\{u\right\}\right)\cap V\left(C_{2q_r+1}\right)|\ge |W\cap V\left(C_{2q_r+1}\right)|$ for any $x\in W$. As a consequence, if $u\notin W$, any set $(W-\{x\left\}\right)\cup \left\{u\right\}$, $x\in W$, is also a simultaneous local metric generator for $\mathcal{T}$, so we can assume that $u\in W$. Moreover, applying an analogous reasoning for every set $C_r\in \mathcal{C}$ such that $W\cap C_r=\varnothing$, we have that, firstly, there is at least one vertex $v_{r_i}\in C_r$ such that $v_{r_i}\in V\left(C_{2q_r+1}\right)-\left\{u\right\}$ and ${\delta }_{T_{2q_r+1,t_r}}\left(v_{r_i}\right)=2$, and secondly, there is at least one vertex $x_r\in W\cap (\left\{w_r\right\}\cup V\left(P_{t_r}\right))$, which can be replaced by $v_{r_i}$. Then, the set:

$${\displaystyle W^{\prime }=\bigcup _{W\cap C_r=\varnothing }\left((W-\left\{x_r\right\})\cup \left\{v_{r_i}\right\}\right)}$$

is also a simultaneous local metric generator for $\mathcal{T}$ of cardinality $|W^{\prime }|=p+1$ such that $u\in W^{\prime }$ and $(W^{\prime }-\left\{u\right\})\cap C_r\ne \varnothing$ for every $C_r\in \mathcal{C}$. Thus, the set $S^{″}=W^{\prime }-\left\{u\right\}$ satisfies $|S^{″}|\le p$ and contains at least one element from each $C_r\in \mathcal{C}$.

To conclude our proof, it is simple to verify that the transformation of HSP into SLD described above can be done in polynomial time. ☐

7. Conclusions

In this paper we introduced the notion of simultaneous local dimension of graph families. We studied the properties of this new parameter in order to obtain its exact value, or sharp bounds, on several graph families. In particular, we focused on families obtained as the result of small changes in an initial graph and families composed by graphs obtained through well-known operations such as the corona and lexicographic products, as well as the join operation (viewed as a particular case of the lexicographic product). Finally, we analysed the computational complexity of the new problem, and showed that computing the simultaneous local metric dimension is computationally difficult even for families composed by graphs whose (individual) local metric dimensions are constant and well known.