Hierarchical Meta-Learning in Time Series Forecasting for Improved Interference-Less Machine Learning
Abstract
:1. Introduction
2. Background
2.1. Motivation for Noise Elimination in Time Series Data
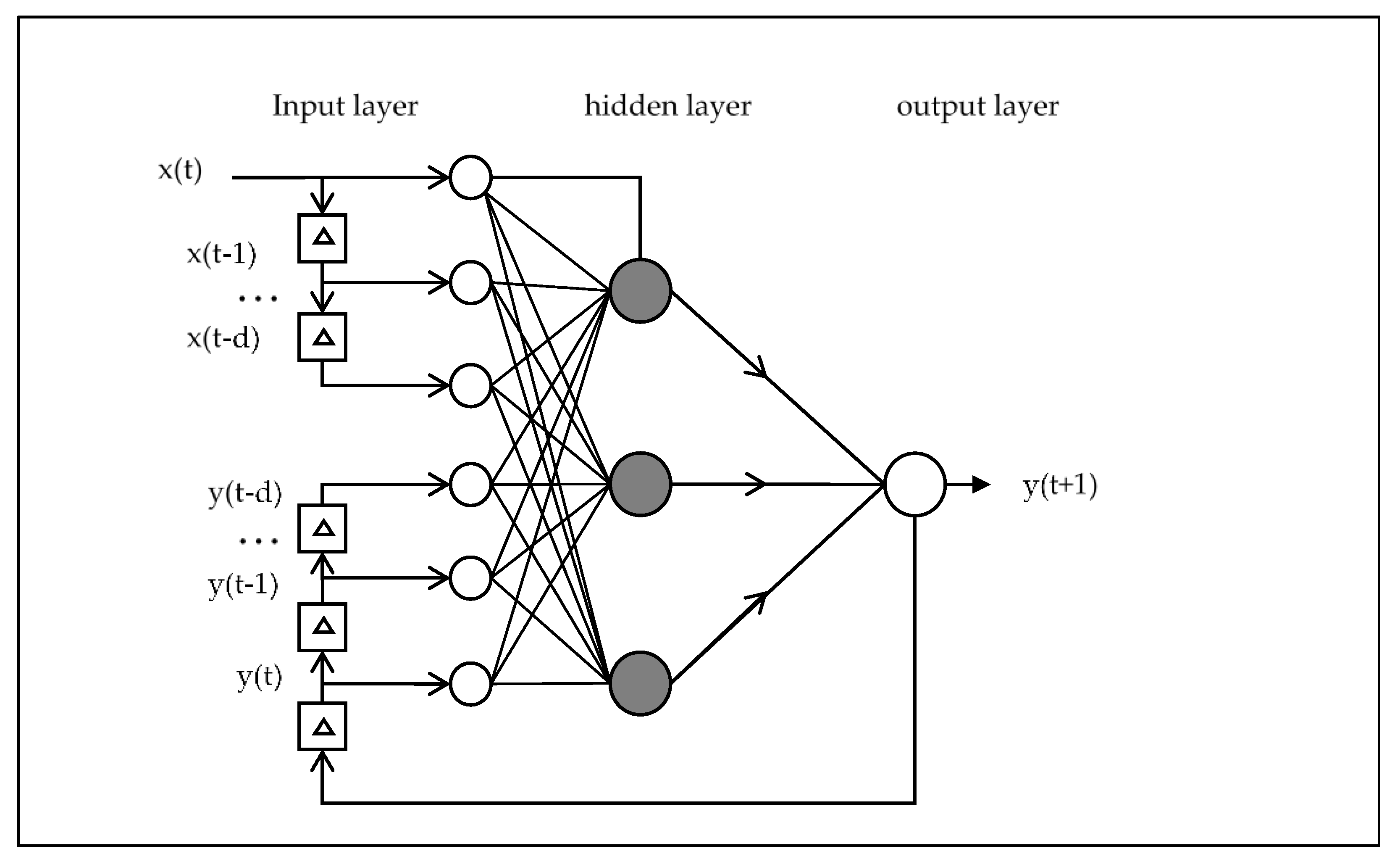
2.2. NAR and NARX
2.3. Moving Average
2.4. Empirical Mode Decomposition
- STEP 1:
- Let hi(t) = y(t), and i = 1.
- STEP 2:
- Find some local minima and maxima in hi(t).
- STEP 3:
- Connect all identified maxima and minima by a cubic spline as the upper envelope upi(t) and lower envelope lowi(t), and calculate local mean as mi(t) = [upi(t) + lowi(t)]/2.
- STEP 4:
- Update as hi(t) = hi(t) − mi(t).
- STEP 5:
- Ensure hi(t) fulfils the requirement of IMF. If not, then redo STEP 2 to STEP 5. If done, then IMFi(t) = hi(t), i = i + 1 and hi(t) = y(t) − IMFi−1(t).
- STEP 6:
- Check if hi(t) is a monotonic function or not. If it is not then redo STEP 2 to STEP 5 for the next IMF. If it is monotonic then hi(t) = rc(t) and end the EMD process.
3. Method
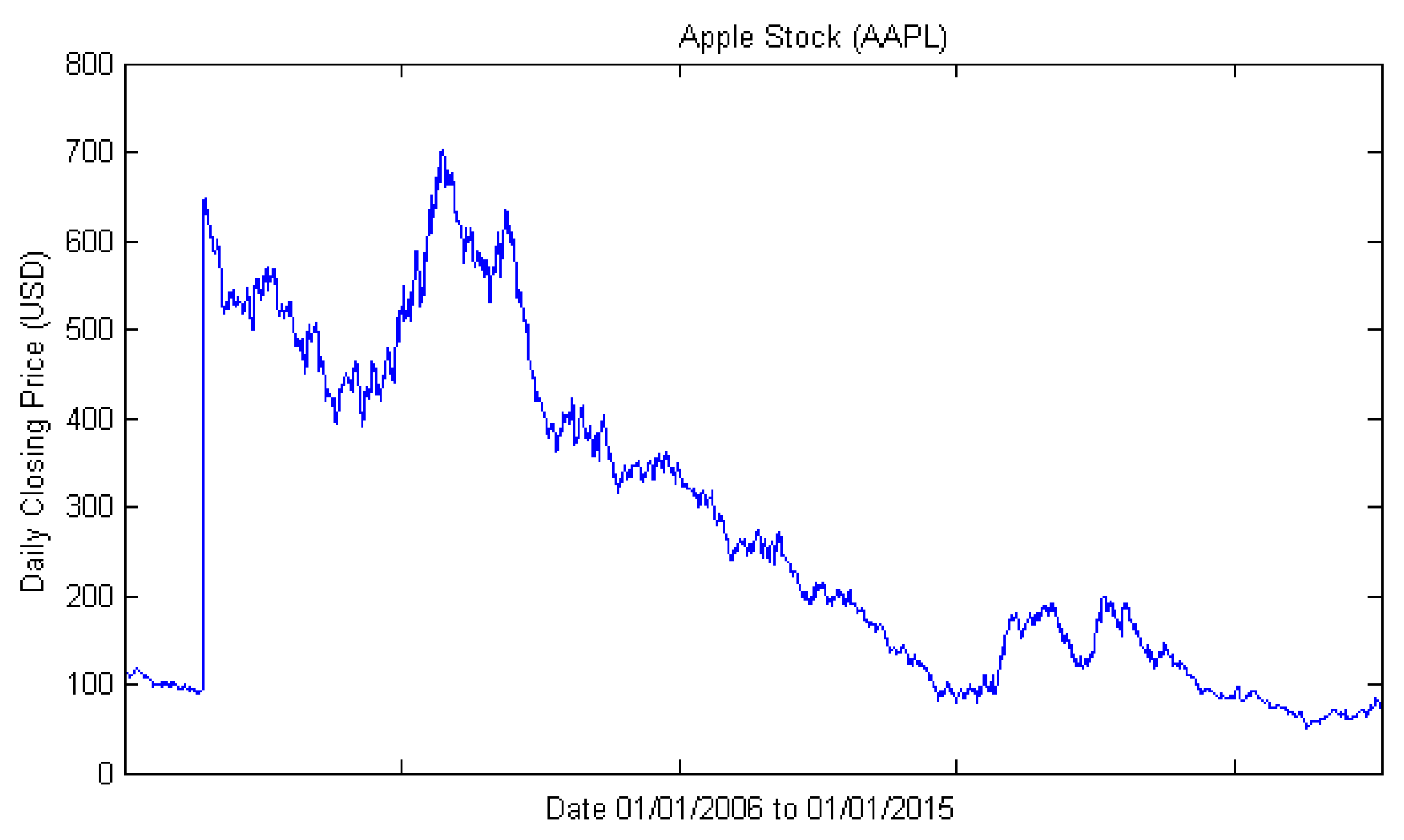
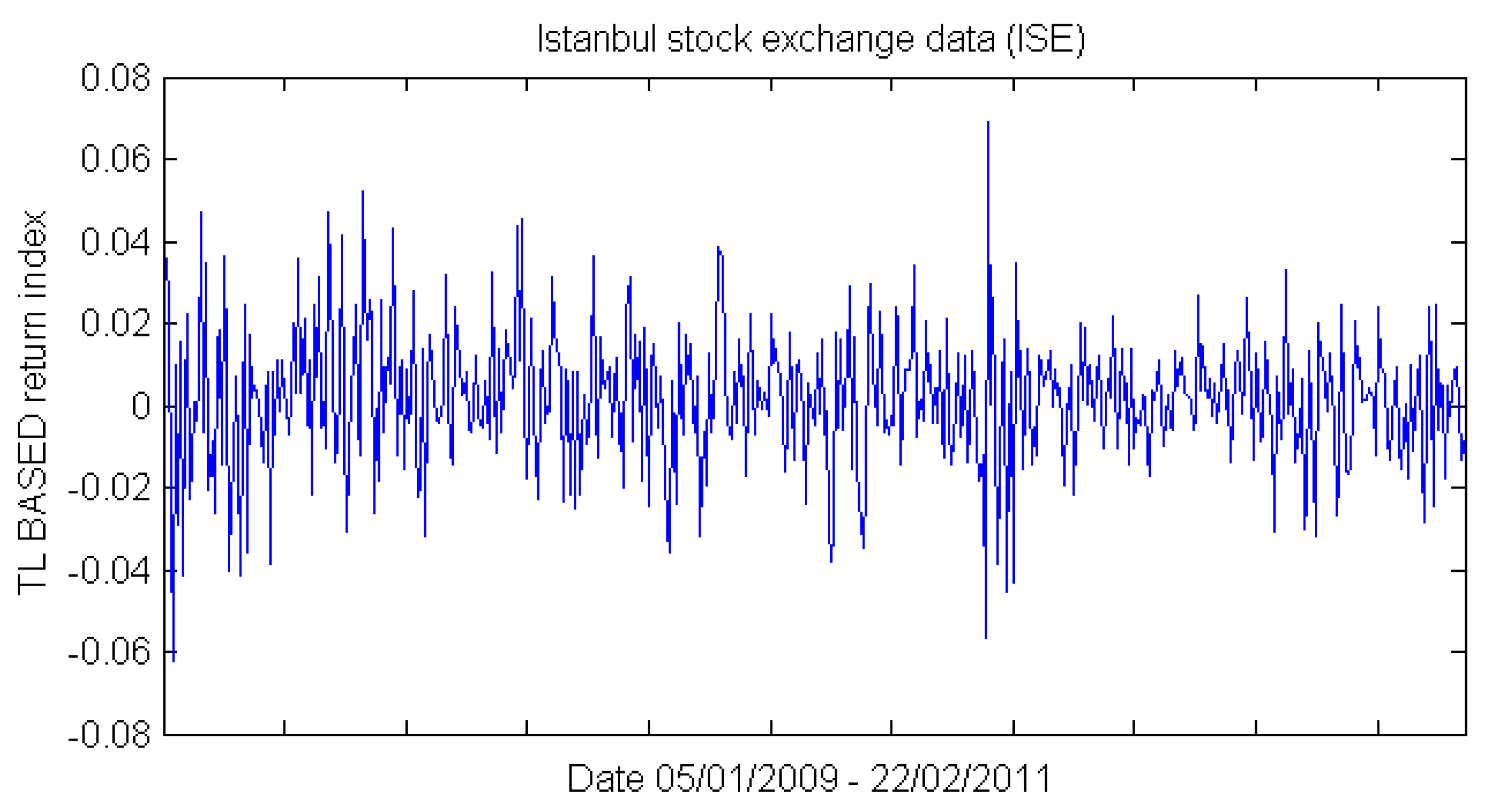
3.1. Dataset and Sample Selection
3.2. Algorithms and Learning process
- (1)
- The traditional approach, in which the time series is directly used by the NAR neural network for training. We denote this as NAR.
- (2)
- The NARX neural network is presented with the original time series as input, and an additional pre-processed meta-information from the moving average technique. Denoted as NARX-MA.
- (3)
- Finally, the NARX neural network inputs contain both the meta-information output of the EMD de-noising algorithm (see Section 3.4 for definition) and the original time series. Referred to as NARX-EMDv2 in this paper.
3.3. NARX-MA Algorithm (Moving Average)
3.4. NARX-EMDv2 Algorithm (EMD de-Noising Version 2)
- STEP 1:
- Run the EMD routine on the time series data using normal parameters in [13]. Let N be the total number of IMFs produced and set the number of neural network hidden neuron to 75% of N (rounded up). [The parameters used are: resolution (qResol) = 40 dB, residual energy (qResid) = 40 dB, and gradient step size (qAlfa) = 1. The tolerance level is determined by resolution (qResol) which terminates the IMF computation [13].]
- STEP 2:
- Based on use-case, set the input and feedback delays [i.e., number of past values presented to the artificial neural network model for prediction].
- STEP 3:
- Create N combinations of all IMF whilst progressively excluding higher frequency IMF in each combination.
- STEP 4:
- Create a modified input series x(t) from the remaining IMF in each combination which will either be summed [as a single input] or included directly [as multiple inputs] into the input [of the artificial neural network].
- STEP 5:
- Train the NARX model with each combination and test the performance to reveal a combination that contributes to noise reduction.
- STEP 6:
- If noise reduction requirement is not met, decrease N and repeat from STEP 3.
| Algorithm 1: EMDdenoiseV2 |
| Input: Time Series Data, x; Heuristic Data Division Value, d. |
| Output: Denoised meta_info; |
| 1 sequentially divide x into d approximately equal partitions |
| 2 for each partition p to dth |
| 3 | run EMD routine |
| 4 | initialize sub-NARX ANN and train by exempting one IMF at a time |
| 5 | identify IMF elimination that contributes to lowest MSE |
| 6 | sum valid IMF to create meta_info for pth partition |
| 7 end |
| 8 append meta_info from each partition sequentially to form series length equal to x. |
| 9 return meta_info |
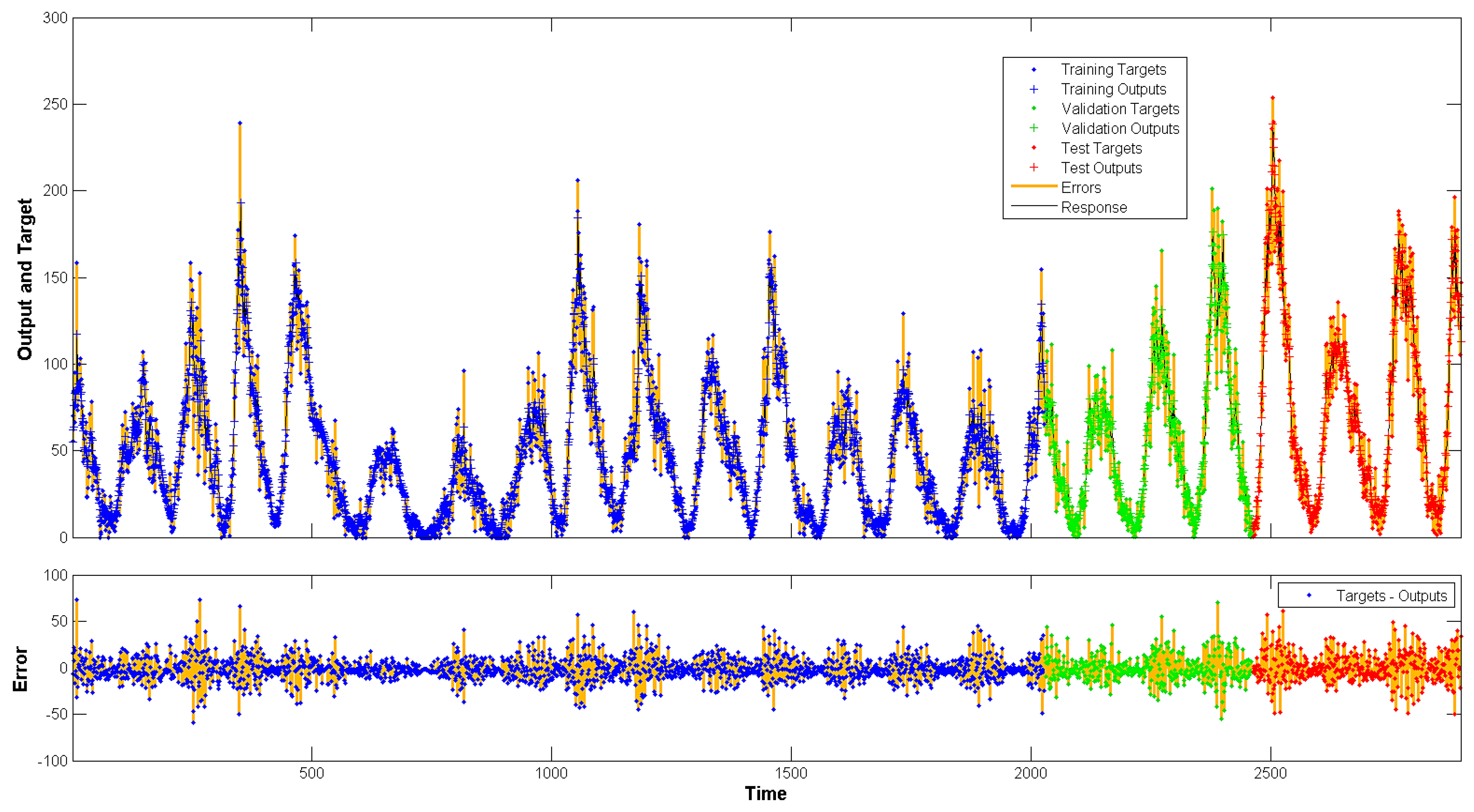
4. Results
5. Discussions
5.1. Performance on Non-Linear Autoregressive Neural Networks
5.2. Performance on Long Short-Term Memory Neural Network
5.3. Potential Application
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| Delay Window | lag: 5 | lag: 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | LSTM | LSTM-MA | LSTM-EMDv2 | LSTM | LSTM-MA | LSTM-EMDv2 | ||||||
| Division/ANN neurons | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 |
| Avg. Training Time (s) | 8.588 | 24.525 | 8.019 | 8.541 | 8.462 | 8.093 | 8.548 | 19.212 | 7.979 | 7.945 | 8.611 | 8.008 |
| Avg. Training Error | 0.1102562 | 0.0414285 | 0.1166426 | 0.0454050 | 0.1012255 | 0.1214790 | 0.0533478 | 0.0355548 | 0.0640460 | 0.0447802 | 0.0521724 | 0.0941153 |
| Avg. Test Error ± standard deviation | 0.1485295 ±0.0504588 | 0.0975778 ±0.0262894 | 0.1430151 ±0.0508515 | 0.0971847 ±0.0254819 | 0.1389314 ±0.0397565 | 0.2434674 ±0.0399610 | 0.0606585 ±0.0320497 | 0.0277204 ±0.0077224 | 0.0666034 ±0.0353700 | 0.0272315 ±0.0099083 | 0.0573101 ±0.0283412 | 0.0905659 ±0.0267799 |
| Minimum Test Error | 0.0456379 | 0.0314639 | 0.0302435 | 0.0458273 | 0.0450077 | 0.1499620 | 0.0029272 | 0.0112347 | 0.0017439 | 0.0054977 | 0.0038684 | 0.0398468 |
| p-value vs. best | 4.20 × 10−59 | 6.08 × 10−63 | 9.90 × 10−56 | 2.32 × 10−64 | 1.32 × 10−68 | 8.59 × 10−118 | 4.54 × 10−19 | 6.99 × 10−01 | 2.83 × 10−21 | best | 3.17 × 10−19 | 2.88 × 10−55 |
| Delay Window | lag: 5 | lag: 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | LSTM | LSTM-MA | LSTM-EMDv2 | LSTM | LSTM-MA | LSTM-EMDv2 | ||||||
| Division/ANN neurons | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 |
| Avg. Training Time (s) | 28.97 | 14.047 | 26.731 | 9.322 | 11.165 | 14.471 | 25.122 | 14.363 | 24.434 | 14.118 | 10.443 | 14.044 |
| Avg. Training Error | 0.1328087 | 0.1319767 | 0.1446349 | 0.1762698 | 0.1340337 | 0.1248077 | 0.1173348 | 0.1148004 | 0.1161796 | 0.1103128 | 0.0902734 | 0.0916366 |
| Avg. Test Error ± standard deviation | 0.2399828 ±0.0261120 | 0.2326393 ±0.0289071 | 0.2931989 ±0.0783809 | 0.3847042 ±0.1012203 | 0.2736516 ±0.0599508 | 0.2270046 ±0.0092213 | 0.1970842 ±0.0038476 | 0.1904281 ±0.0024817 | 0.1925080 ±0.0089283 | 0.1775317 ±0.0041043 | 0.1476351 ±0.0187093 | 0.2451787 ±0.0128595 |
| Minimum Test Error | 0.2170601 | 0.2168433 | 0.2207024 | 0.2125954 | 0.2065012 | 0.2056850 | 0.1874098 | 0.1834852 | 0.1709400 | 0.1698466 | 0.0876853 | 0.2181468 |
| p-value vs. best | 3.01 × 10−72 | 5.09 × 10−62 | 1.80 × 10−43 | 1.35 × 10−57 | 2.61 × 10−49 | 1.28 × 10−92 | 3.88 × 10−65 | 1.27 × 10−56 | 8.78 × 10−54 | 4.26 × 10−36 | best | 6.25 × 10−102 |
| Delay Window | lag: 5 | lag: 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | LSTM | LSTM-MA | LSTM-EMDv2 | LSTM | LSTM-MA | LSTM-EMDv2 | ||||||
| Division/ANN neurons | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 |
| Avg. Training Time (s) | 8.611 | 14.114 | 9.332 | 13.055 | 14.9695 | 11.737 | 9.95 | 14.079 | 9.667 | 11.7 | 8.717 | 14.801 |
| Avg. Training Error | 0.1801327 | 0.1110482 | 0.2093012 | 0.1134647 | 0.3633793 | 0.1815522 | 0.1286195 | 0.0688271 | 0.2099519 | 0.1354106 | 0.2999538 | 0.1037100 |
| Avg. Test Error ± standard deviation | 0.0559024 ±0.0109374 | 0.0320430 ±0.0024095 | 0.0852827 ±0.0300794 | 0.0439690 ±0.0263654 | 0.2403362 ±0.0383493 | 0.0501263 ±0.0092680 | 0.0461984 ±0.0277388 | 0.0215419 ±0.0157497 | 0.0846316 ±0.0376178 | 0.0512063 ±0.0184436 | 0.1679626 ±0.0297202 | 0.0413049 ±0.0068129 |
| Minimum Test Error | 0.0320886 | 0.0275861 | 0.0280625 | 0.0183325 | 0.1163166 | 0.0346829 | 0.0151599 | 0.0062204 | 0.0420030 | 0.0337207 | 0.0699817 | 0.0239597 |
| p-value vs. best | 4.82 × 10−43 | 4.65 × 10−10 | 1.47 × 10−45 | 8.34 × 10−12 | 3.52 × 10−118 | 3.37 × 10−36 | 6.70 × 10−13 | best | 1.12 × 10−35 | 8.37 × 10−26 | 6.01 × 10−103 | 1.19 × 10−23 |
| Delay Window | lag: 5 | lag: 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | LSTM | LSTM-MA | LSTM-EMDv2 | LSTM | LSTM-MA | LSTM-EMDv2 | ||||||
| Division/ANN neurons | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 |
| Avg. Training Time (s) | 10.196 | 9.938 | 14.837 | 9.787 | 10.333 | 11.108 | 9.47 | 9.876 | 9.626 | 9.654 | 9.733 | 10.293 |
| Avg. Training Error | 1.2221676 | 1.1722678 | 1.1575247 | 1.1340869 | 1.0323971 | 1.1280384 | 1.1382452 | 1.1299286 | 1.1250142 | 1.1185877 | 0.9930821 | 1.0977961 |
| Avg. Test Error ± standard deviation | 0.8087027 ±0.0319960 | 0.7857503 ±0.0253995 | 0.7791352 ±0.0138709 | 0.7713591 ±0.0026795 | 0.6444975 ±0.0672950 | 0.7715180 ±0.0032700 | 0.7830149 ±0.0070671 | 0.7808031 ±0.0080943 | 0.6521218 ±0.0564859 | 0.7650546 ±0.0046042 | 0.6521219 ±0.0564861 | 0.7560338 ±0.0085550 |
| Minimum Test Error | 0.7701950 | 0.7690272 | 0.7541847 | 0.7637071 | 0.4343486 | 0.7632934 | 0.7688600 | 0.7757211 | 0.4754810 | 0.7484215 | 0.4754810 | 0.7414659 |
| p-value vs. best | 7.19 × 10−55 | 4.45 × 10−48 | 5.92 × 10−48 | 9.55 × 10−46 | best | 8.55 × 10−46 | 1.81 × 10−50 | 1.95 × 10−49 | 3.89 × 10−01 | 6.62 × 10−43 | 3.89 × 10−01 | 1.27 × 10−38 |
References
- Bengio, Y.; Frasconi, P. Input-output HMMs for sequence processing. IEEE Trans. Neural Netw. 1996, 7, 1231–1249. [Google Scholar] [CrossRef] [PubMed]
- Gunn, S.R. Support Vector Machines for Classification and Regression. ISIS Tech. Rep. 1998, 14, 85–86. [Google Scholar]
- Štěpnička, M.; Pavliska, V.; Novák, V.; Perfilieva, I.; Vavříčková, L.; Tomanová, I. Time Series Analysis and Prediction Based on Fuzzy Rules and the Fuzzy Transform. In Proceedings of the Joint 2009 International Fuzzy Systems Association World Congress and 2009 European Society of Fuzzy Logic and Technology Conference, Lisbon, Portugal, 20–24 July 2009; pp. 483–488. [Google Scholar]
- Bemdt, D.J.; Clifford, J. Using Dynamic Time Warping to Find Patterns in Time Series. In Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 31 July–1 August 1994; pp. 359–370. [Google Scholar]
- Afolabi, D.O.; Guan, S.-U.; Man, K.L.; Wong, P.W.H. Meta-learning with Empirical Mode Decomposition for Noise Elimination in Time Series Forecasting. In Advanced Multimedia and Ubiquitous Engineering: FutureTech & MUE; Park, J.J.H., Jin, H., Jeong, Y.-S., Khan, M.K., Eds.; Springer Singapore: Singapore, 2016; pp. 405–413. ISBN 978-981-10-1536-6. [Google Scholar]
- Wong, W.; Miller, R.B. Repeated Time Series Analysis of ARIMA–Noise Models. J. Bus. Econ. Stat. 1990, 8, 243–250. [Google Scholar] [CrossRef]
- Pesentia, M.; Pirasa, M. A Modified Forward Search Approach Applied to Time Series Analysis. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Beijing, China, 2008; Volumn XXXVII, pp. 787–792. [Google Scholar]
- Yin, W.; Kann, K.; Yu, M.; Schütze, H. Comparative Study of CNN and RNN for Natural Language Processing. arXiv 2017, arXiv:1702.01923. [Google Scholar]
- Singh, S. Noise impact on time-series forecasting using an intelligent pattern matching technique. Pattern Recognit. 1999, 32, 1389–1398. [Google Scholar] [CrossRef]
- Lin, T.; Horne, B.G.; Tino, P.; Giles, C.L. Learning long-term dependencies in NARX recurrent neural networks. IEEE Trans. Neural Netw. 1996, 7, 1329–1338. [Google Scholar] [PubMed]
- Wei, W.W.-S. Time Series Analysis: Univariate and Multivariate Methods, 2nd ed.; Addison-Wesley Pearson Higher Ed: Boston, MA, USA, 2006; ISBN 978-0-321-32216-6. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, London, UK, 8 March 1998; Volumn 454, pp. 903–995. [Google Scholar]
- Rato, R.T.; Ortigueira, M.D.; Batista, A.G. On the HHT, its problems, and some solutions. Mech. Syst. Signal Process. 2008, 22, 1374–1394. [Google Scholar] [CrossRef]
- Kim, D.; Oh, H.-S. EMD: A package for empirical mode decomposition and hilbert spectrum. R J. 2009, 1, 40–46. [Google Scholar]
- Wei, Y.; Chaudhary, V. The Influence of Sample Reconstruction on Stock Trend Prediction via NARX Neural Network. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), IMiami, FL, USA, 9–11 December 2015; pp. 52–57. [Google Scholar]
- Hertz, P.; Feigelson, E.D. A sample of astronomical time series. In Applications of Time Series Analysis in Astronomy and Meteorology; Subba Rao, T., Priestley, M.B., Lessi, O., Eds.; Chapman & Hall: London, UK, 1997; pp. 340–356. [Google Scholar]
- Weigend, A.S. The Future of Time Series. In Proceedings of the International Conference On Neural Information Processing, Seoul, Korea, January 1994; Volumn 3, pp. 853–856. [Google Scholar]
- Akbilgic, O.; Bozdogan, H.; Balaban, M.E. A novel Hybrid RBF Neural Networks model as a forecaster. Stat. Comput. 2014, 24, 365–375. [Google Scholar] [CrossRef]
- Neural Network Time Series Prediction and Modeling—MATLAB & Simulink. Available online: http://www.mathworks.com/help/nnet/gs/neural-network-time-series-prediction-and-modeling.html (accessed on 15 February 2016).
- Chollet, F. Keras; GitHub: San Francisco, CA, USA, 2015. [Google Scholar]
- Zupan, B.; Bohanec, M.; Bratko, I.; Demsar, J. Machine learning by function decomposition. In Proceedings of the Fourteenth International Conference (ICML’97) on Machine Learning, Nashville, TN, USA, 8–12 July 1997; pp. 421–429. [Google Scholar]
- Wang, Y.-H.; Yeh, C.-H.; Young, H.-W.V.; Hu, K.; Lo, M.-T. On the computational complexity of the empirical mode decomposition algorithm. Phys. Stat. Mech. Its Appl. 2014, 400, 159–167. [Google Scholar] [CrossRef]
- Hua Ang, J.; Guan, S.-U.; Tan, K.C.; Mamun, A.A. Interference-less neural network training. Neurocomputing 2008, 71, 3509–3524. [Google Scholar] [CrossRef]


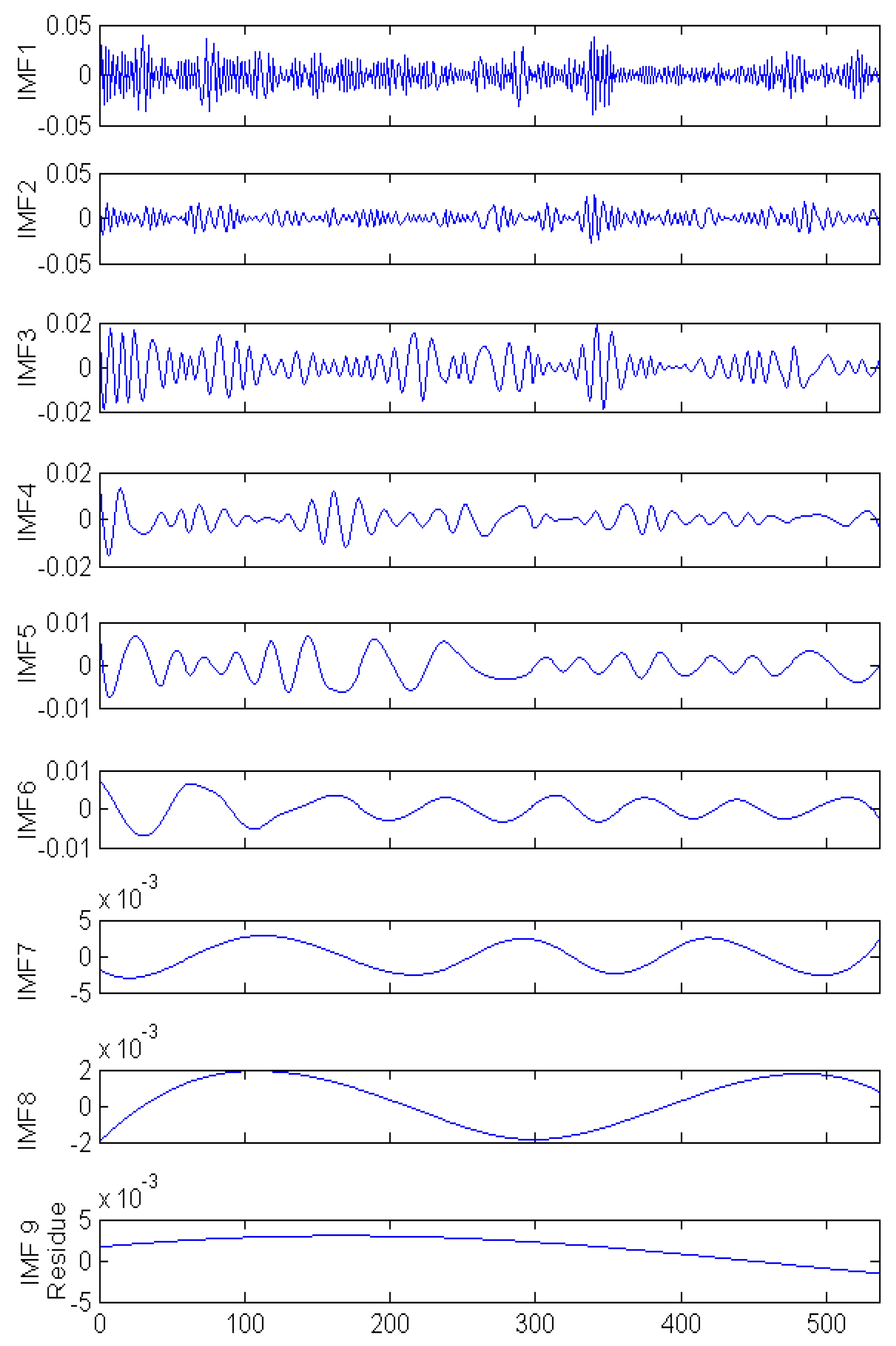

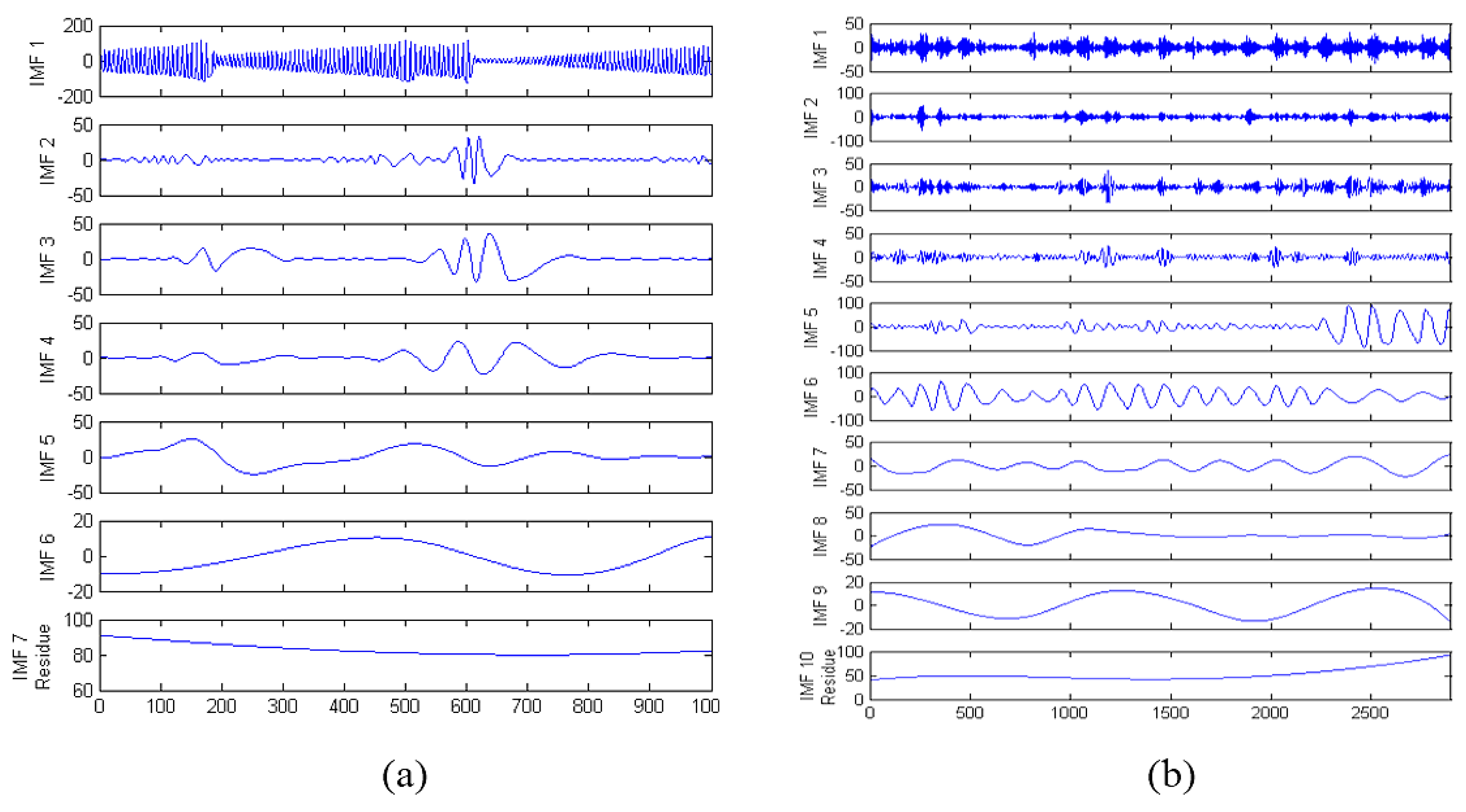
| Delay Window | lag: 5 | lag: 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | NAR | NARX-MA | NARX-EMDv2 | NAR | NARX-MA | NARX-EMDv2 | ||||||
| Division/ANN neurons | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 |
| Avg. Training Time (s) | 2.113 | 1.551 | 2.766 | 3.493 | 3.041 | 4.269 | 2.456 | 2.288 | 3.157 | 5.394 | 3.224 | 7.332 |
| Avg. Training Error | 0.0071252 | 0.0070175 | 0.0070970 | 0.0069618 | 0.0042749 | 0.0008638 | 0.0070956 | 0.0069004 | 0.0070665 | 0.0068903 | 0.0033542 | 0.0010875 |
| Avg. Test Error ± standard deviation | 0.0016678 ±0.0009144 | 0.0037132 ±0.0011296 | 0.0017700 ±0.0010237 | 0.0040955 ±0.0010815 | 0.0007602 ±0.0011614 | 0.0004631 ±0.0003893 | 0.0013870 ±0.0010336 | 0.0042773 ±0.0021347 | 0.0014124 ±0.0013610 | 0.0046522 ±0.0020343 | 0.0007500 ±0.0013131 | 0.0008448 ±0.0015741 |
| Minimum Test Error | 0.0003573 | 0.0009636 | 0.0004469 | 0.0022597 | 0.0000508 | 0.0000798 | 0.0003758 | 0.0015388 | 0.0004493 | 0.0019610 | 0.0000438 | 0.0000701 |
| p-value vs. best | 1.81 × 10−25 | 1.87 × 10−68 | 6.71 × 10−25 | 6.34 × 10−79 | 1.67 × 10−02 | best | 1.39 × 10−14 | 5.01 × 10−42 | 2.46 × 10−10 | 9.11 × 10−50 | 3.84 × 10−02 | 2.02 × 10−02 |
| Delay Window | lag: 5 | lag: 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | NAR | NARX-MA | NARX-EMDv2 | NAR | NARX-MA | NARX-EMDv2 | ||||||
| Division/ANN neurons | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 |
| Avg. Training Time (s) | 2.255 | 1.624 | 2.963 | 3.891 | 2.957 | 3.922 | 2.237 | 2.3 | 2.76 | 5.58 | 2.959 | 5.985 |
| Avg. Training Error | 0.1116833 | 0.1005595 | 0.1087313 | 0.0949837 | 0.0394043 | 0.0558120 | 0.1085390 | 0.0960426 | 0.1074148 | 0.0879532 | 0.0398371 | 0.0561283 |
| Avg. Test Error ± standard deviation | 0.3913484 ±0.7046393 | 0.8481608 ±0.4306742 | 0.3934549 ±1.1453019 | 0.8978903 ±1.1651971 | 0.0974777 ±0.0870907 | 0.6780297 ±0.5060787 | 0.2442256 ±0.0750881 | 0.6417264 ±0.4650035 | 0.2905302 ±0.1672015 | 0.6722254 ±0.6007605 | 0.0980438 ±0.0369733 | 0.6016824 ±0.4468190 |
| Minimum Test Error | 0.1883577 | 0.2696093 | 0.1931820 | 0.2058434 | 0.0553965 | 0.1643110 | 0.1886322 | 0.2116681 | 0.1804997 | 0.1979736 | 0.0609981 | 0.1521699 |
| p-value vs. best | 5.60 × 10−05 | 1.49 × 10−40 | 1.11 × 10−02 | 1.10 × 10−10 | best | 5.12 × 10−23 | 2.05 × 10−27 | 1.30 × 10−23 | 7.19 × 10−20 | 1.20 × 10−17 | 9.53 × 10−01 | 2.48 × 10−22 |
| Delay Window | lag: 5 | lag: 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | NAR | NARX-MA | NARX-EMDv2 | NAR | NARX-MA | NARX-EMDv2 | ||||||
| Division/ANN neurons | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 |
| Avg. Training Time (s) | 1.622 | 0.993 | 1.720 | 3.449 | 1.210 | 4.019 | 1.546 | 2.366 | 2.482 | 4.959 | 1.491 | 4.194 |
| Avg. Training Error | 0.0132433 | 0.0225547 | 0.0237647 | 0.0017928 | 0.0666883 | 0.0121078 | 0.0106071 | 0.0004086 | 0.0217637 | 0.0004789 | 0.0491124 | 0.0090752 |
| Avg. Test Error ± standard deviation | 0.0043834 ±0.0140755 | 0.0037581 ±0.0022762 | 0.0115036 ±0.0677390 | 0.0009243 ±0.0018475 | 0.0298414 ±0.0555601 | 0.0083077 ±0.0398612 | 0.0041026 ±0.0108263 | 0.0004567 ±0.0001875 | 0.0052185 ±0.0094118 | 0.0004919 ±0.0003914 | 0.0264680 ±0.0613395 | 0.0057052 ±0.0298941 |
| Minimum Test Error | 0.0007238 | 0.0017372 | 0.0004752 | 0.0003155 | 0.0020193 | 0.0008517 | 0.0003111 | 0.0002870 | 0.0002730 | 0.0002746 | 0.0006813 | 0.0003910 |
| p-value vs. best | 6.04 × 10−03 | 1.39 × 10−32 | 1.06 × 10−01 | 1.30 × 10−02 | 3.68 × 10−07 | 5.14 × 10−02 | 9.66 × 10−04 | best | 1.08 × 10−06 | 4.21 × 10−01 | 3.73 × 10−05 | 8.22 × 10−02 |
| Delay Window | lag: 5 | lag: 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm | NAR | NARX-MA | NARX-EMDv2 | NAR | NARX-MA | NARX-EMDv2 | ||||||
| Division/ANN neurons | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 | 10 | 50 |
| Avg. Training Time (s) | 0.616 | 0.451 | 0.637 | 0.797 | 0.682 | 0.748 | 0.591 | 0.667 | 0.640 | 1.077 | 0.591 | 1.032 |
| Avg. Training Error | 1.0466828 | 0.8795638 | 1.0366650 | 0.8866556 | 0.5577968 | 0.7428110 | 1.0480104 | 0.8458651 | 1.0099425 | 0.8149923 | 0.6001350 | 0.8643662 |
| Avg. Test Error ± standard deviation | 0.8579863 ±0.0516803 | 0.9902402 ±0.1252702 | 0.8677769 ±0.0810234 | 0.9540938 ±0.1115357 | 0.4721791 ±0.1063513 | 1.0481726 ±0.2227919 | 0.7809116 ±0.0359027 | 0.9983421 ±0.1287332 | 0.7878874 ±0.0559552 | 0.8587937 ±0.0783127 | 0.4165572 ±0.0513170 | 0.8576149 ±0.0742370 |
| Minimum Test Error | 0.7707221 | 0.8026880 | 0.7634348 | 0.8174138 | 0.3335602 | 0.7699630 | 0.7152155 | 0.7854705 | 0.6834771 | 0.7091668 | 0.3318121 | 0.7032872 |
| p-value vs. best | 2.20 × 10−129 | 7.32 × 10−101 | 4.92 × 10−109 | 2.15 × 10−103 | 5.16 × 10−06 | 1.64 × 10−69 | 4.78 × 10−126 | 3.92 × 10−100 | 4.19 × 10−112 | 2.41 × 10−109 | best | 4.79 × 10−112 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Afolabi, D.; Guan, S.-U.; Man, K.L.; Wong, P.W.H.; Zhao, X. Hierarchical Meta-Learning in Time Series Forecasting for Improved Interference-Less Machine Learning. Symmetry 2017, 9, 283. https://doi.org/10.3390/sym9110283
Afolabi D, Guan S-U, Man KL, Wong PWH, Zhao X. Hierarchical Meta-Learning in Time Series Forecasting for Improved Interference-Less Machine Learning. Symmetry. 2017; 9(11):283. https://doi.org/10.3390/sym9110283
Chicago/Turabian StyleAfolabi, David, Sheng-Uei Guan, Ka Lok Man, Prudence W. H. Wong, and Xuan Zhao. 2017. "Hierarchical Meta-Learning in Time Series Forecasting for Improved Interference-Less Machine Learning" Symmetry 9, no. 11: 283. https://doi.org/10.3390/sym9110283
APA StyleAfolabi, D., Guan, S.-U., Man, K. L., Wong, P. W. H., & Zhao, X. (2017). Hierarchical Meta-Learning in Time Series Forecasting for Improved Interference-Less Machine Learning. Symmetry, 9(11), 283. https://doi.org/10.3390/sym9110283







