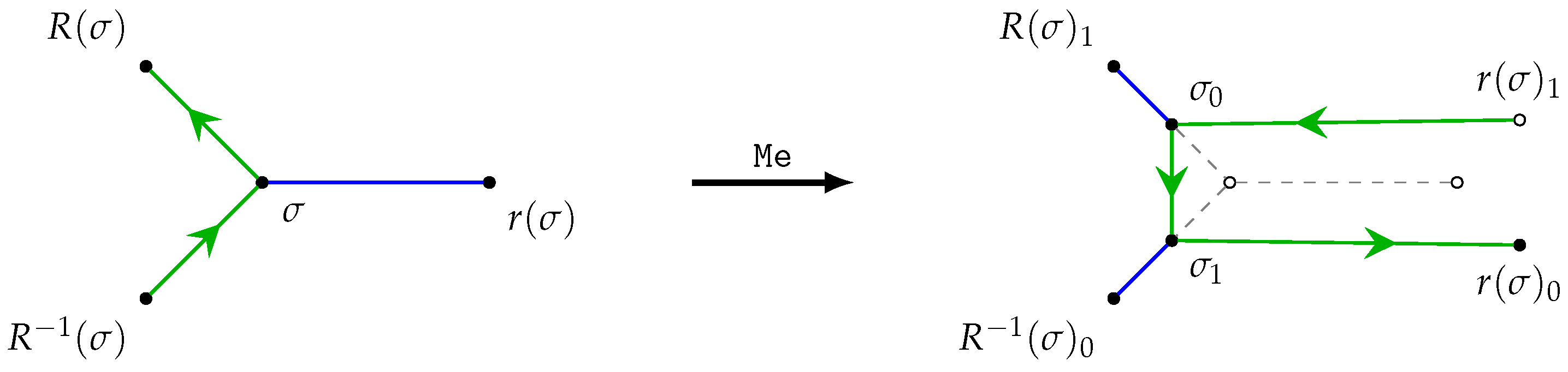1. Maps and Oriented Maps
A
map on a closed surface is a two-cell embedding of a finite connected graph
(see, e.g., [
1] or [
2]). Equivalently, every map can be viewed as a set of three fixed-point-free involutions
and
acting on a set of
flags with the property that
is also a fixed-point-free involution, in which case we denote the map as
; see, for instance, [
3] (p. 415). With this second point of view, each map can be described completely using a three-edge colored cubic graph, called the
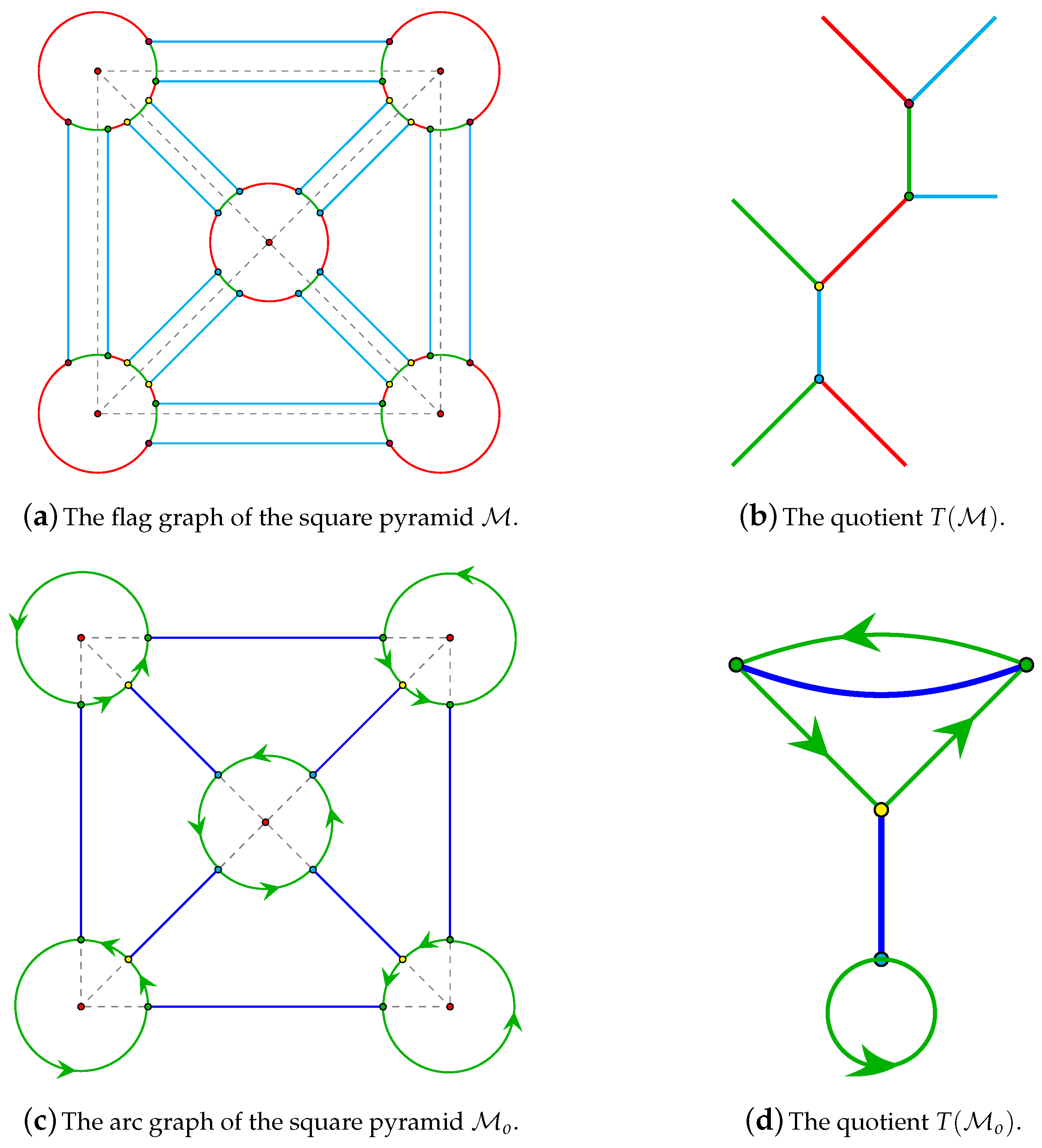
flag graph, whose vertices are elements of
, where
and
are connected by an edge colored
i in the flag graph if and only if
. Generally, only connected flag graphs are considered. The graph
G is called the
skeleton or the
underlying graph of a
map .
In some cases, one may relax the conditions and allow fixed points in some of the involutions and . Such a structure describes a map in a surface with a boundary and with its flag graph containing semi-edges. We call such a map and respective flag graph degenerate.
If the surface in which the map resides is orientable, then is said to be an orientable map. There is a well-known test involving flag graphs to determine whether a given map is orientable:
Proposition 1. A map is orientable if and only if its flag graph is bipartite.
In a bipartite flag graph, the flags (i.e., vertices) of the map come in two color classes; the vertices in a single color class of flags are called arcs. Restricting attention to one set of arcs corresponds to choosing an orientation of the orientable map, and we call the restricted graph an oriented map; each orientable map gives rise to two oppositely oriented oriented maps. We note that in a map there are four flags per edge of the skeleton, while in an oriented map there are two arcs per edge. That is, if denotes the set of flags of the flag graph, and denotes one of the sets of arcs of the oriented graph, then and , where E is the set of edges of the skeleton of the original map.
Considering only oriented maps, as we do in this paper, allows us to treat each of the two orientations of an orientable map separately. It also allows us to introduce the notion of an
oriented symmetry type graph, which captures the symmetry properties that are preserved under orientation-preserving automorphisms of an oriented map. Most researchers consider maps and oriented maps separately. A prominent exception is found in the lecture notes of Roman Nedela (see [
4]), where both maps and oriented maps are studied using the same tools. The main difference between our approach and Nedela’s is that Nedela puts the emphasis on groups, while we focus mainly on graphs (flag graphs and arc graphs).
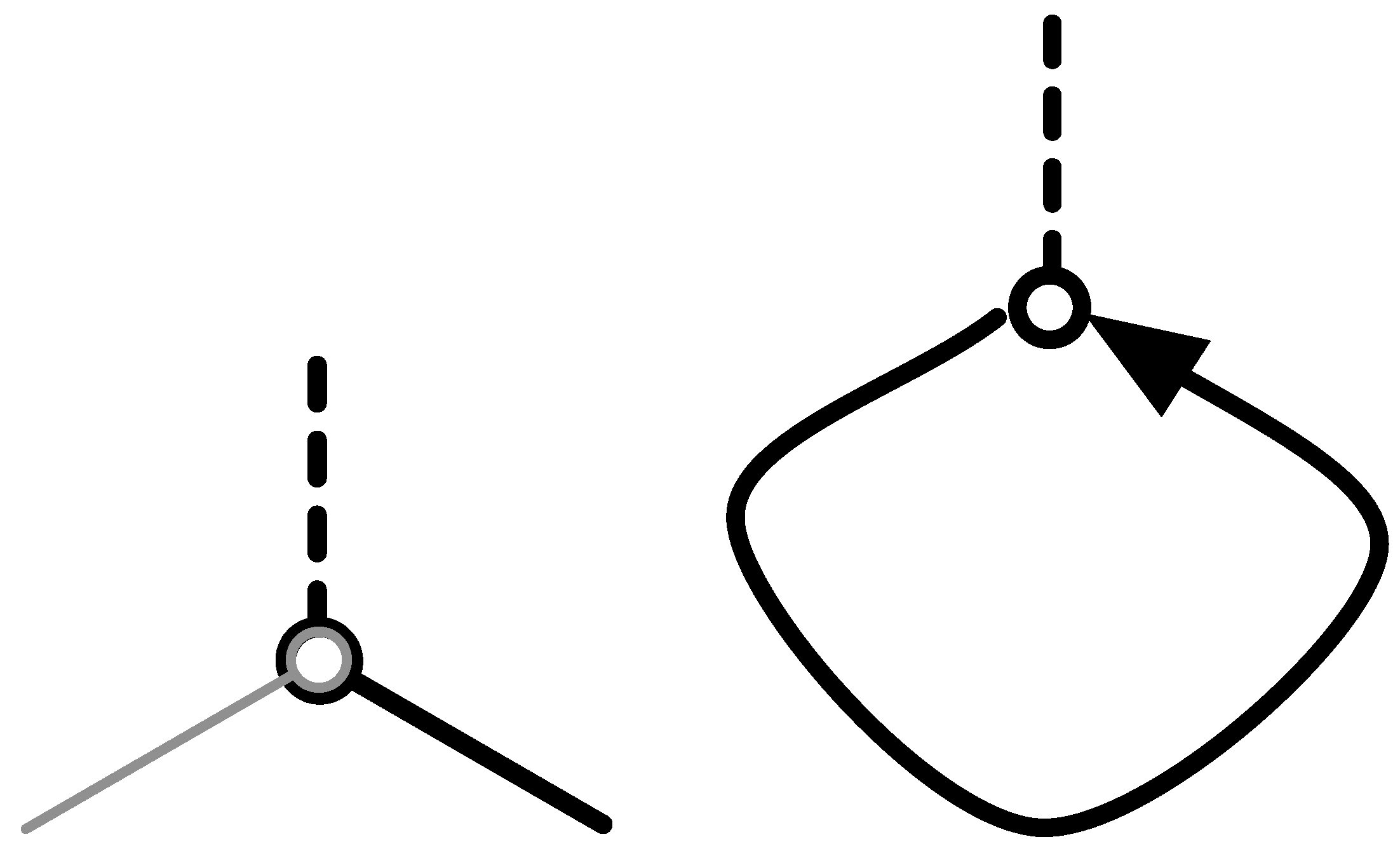
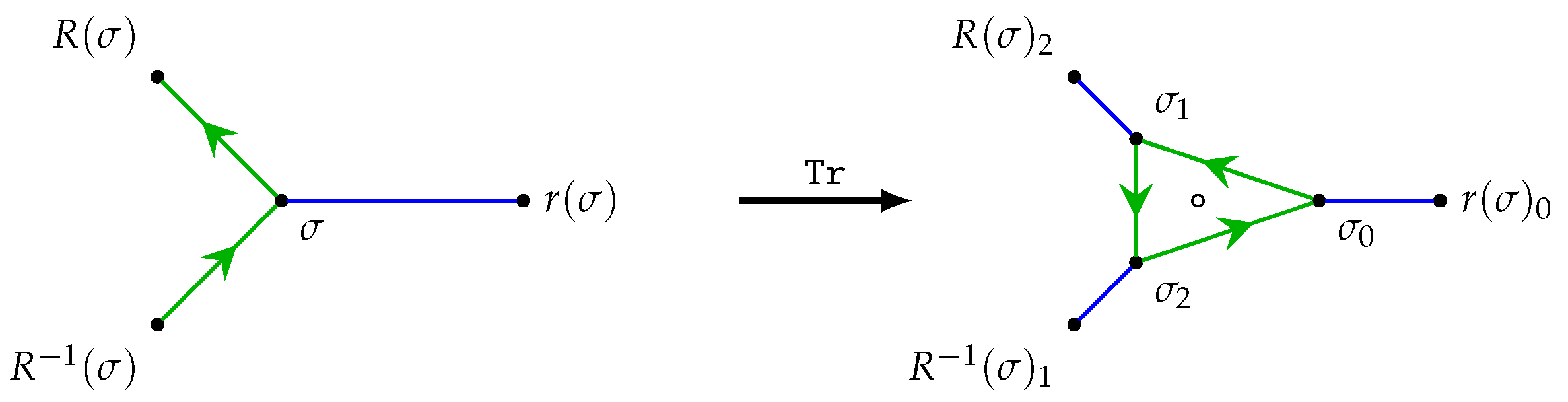
More technically, we define an oriented map to be a structure , where r is a fixed-point-free involution and R is any permutation acting on a set of objects , called arcs. We also view the oriented map as a partially directed graph, called an arc graph, whose vertices are elements of , having some edges directed and some undirected. The directed edges form a directed 2-factor, corresponding to the action of the permutation R on elements of . The undirected edges form an undirected 1-factor, corresponding to the action of the involution r on the elements of . Again, the only other constraint usually imposed on such a structure is the fact that the arc graph must be connected. If the involution r is not fixed-point-free, then we say that the corresponding arc graph is degenerate.
We note that each oriented map
gives rise to its
skeleton graph G in the following way: the vertices of
G are the orbits of
R on
and the edges of
G are the orbits of
r on
. A vertex is incident with an edge if and only if the corresponding orbits have a non-empty intersection. Using this description, we can generate an oriented map
from any orientable map
by first observing that, because
is orientable, the flag graph is bipartite, with bipartite sets
and
. We define
,
and
; we note that by the nature of the bipartition of the vertices of
, the elements of
are in one-to-one correspondence with the endpoints of the edges (i.e., the arcs) of the flag graph of
. (If we instead define
and
, then we get the “other” orientation of
.) A fragment of an oriented map
is shown in
Figure 1, with a portion of the underlying map
also shown.
Conversely, any oriented map
gives rise to the associated orientable map
in the following way: let
and
be two copies (colored using colors 0 and 1) of
, with elements
and
respectively, and define
It is straightforward to show that the skeleton of an oriented map is isomorphic as a graph to the skeleton of the underlying orientable map.
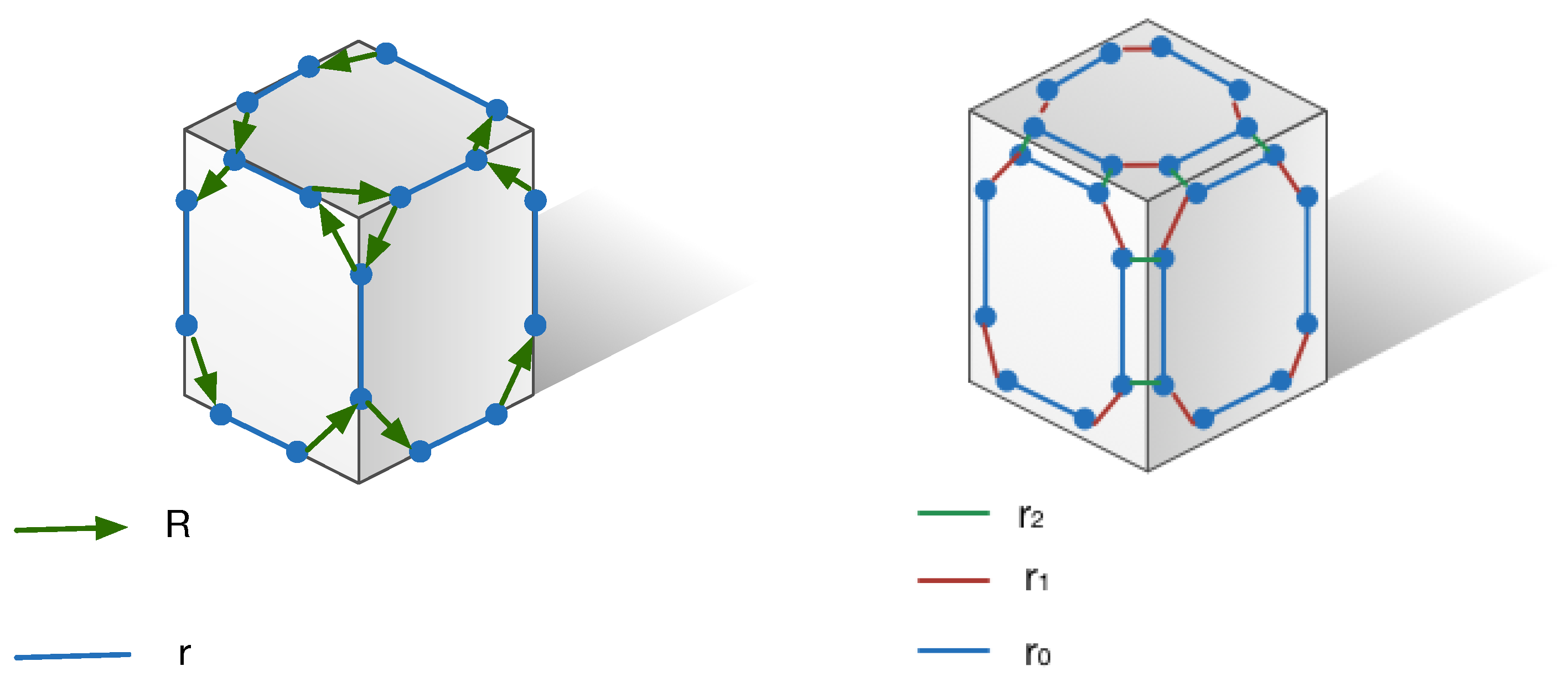
Example 1. The cube may be considered either as
an oriented map: , or
as an (orientable) map: .
These two representations are depicted in Figure 2. We recall that two maps and are isomorphic if there exists a bijection h between and such that for , and we call such a bijection a map isomorphism.
Similarly, we say that two oriented maps and are isomorphic if there exists a bijection h between and such that and . Such a bijection is called an oriented map isomorphism.
As usual, the isomorphisms of a structure to itself are called automorphisms and form a group. By we denote the group of map automorphisms, and similarly by we denote the group of oriented map isomorphisms.
Lemma 1 (Fundamental Lemma of Symmetries of Maps)
The action of the automorphism group of the map is semi-regular on the set of flags Ω.
Lemma 2 (Fundamental Lemma of Symmetries of Oriented Maps)
The action of the automorphism group of the oriented map is semi-regular on the set of arcs Σ.
The validity of both lemmas follows from the fact that for connected structures, any element (flag or arc) can be mapped to any other element in at most one way. Namely, if the image w of a given element v is chosen, then the images of all its neighbours are uniquely determined. By repeating the argument, either the full automorphism is constructed or a contradiction proves that no automorphism mapping v to w exists.
Definition 1. If the automorphism group of a map has k orbits, the map is called a k-orbit map.
Definition 2. If the automorphism group of an oriented map has k orbits, the oriented map is called a k-orbit oriented map.
The Fundamental Lemmas of Symmetries of Maps and Oriented Maps have several interesting consequences that follow by the application of basic permutation group theory:
Corollary 1. Let be a map.
The cardinality of each orbit of on Ω is equal to the order of .
is a divisor of .
The projection is a regular covering projection.
The quotient is a degenerate flag graph, called the symmetry type graph.
The order of is equal to , and is a k-orbit map.
For the definition of a regular covering projection, the reader is referred, for example, to [
1].
Symmetry type graphs have been used previously in the analysis of maps; see, for instance, [
5,
6,
7,
8,
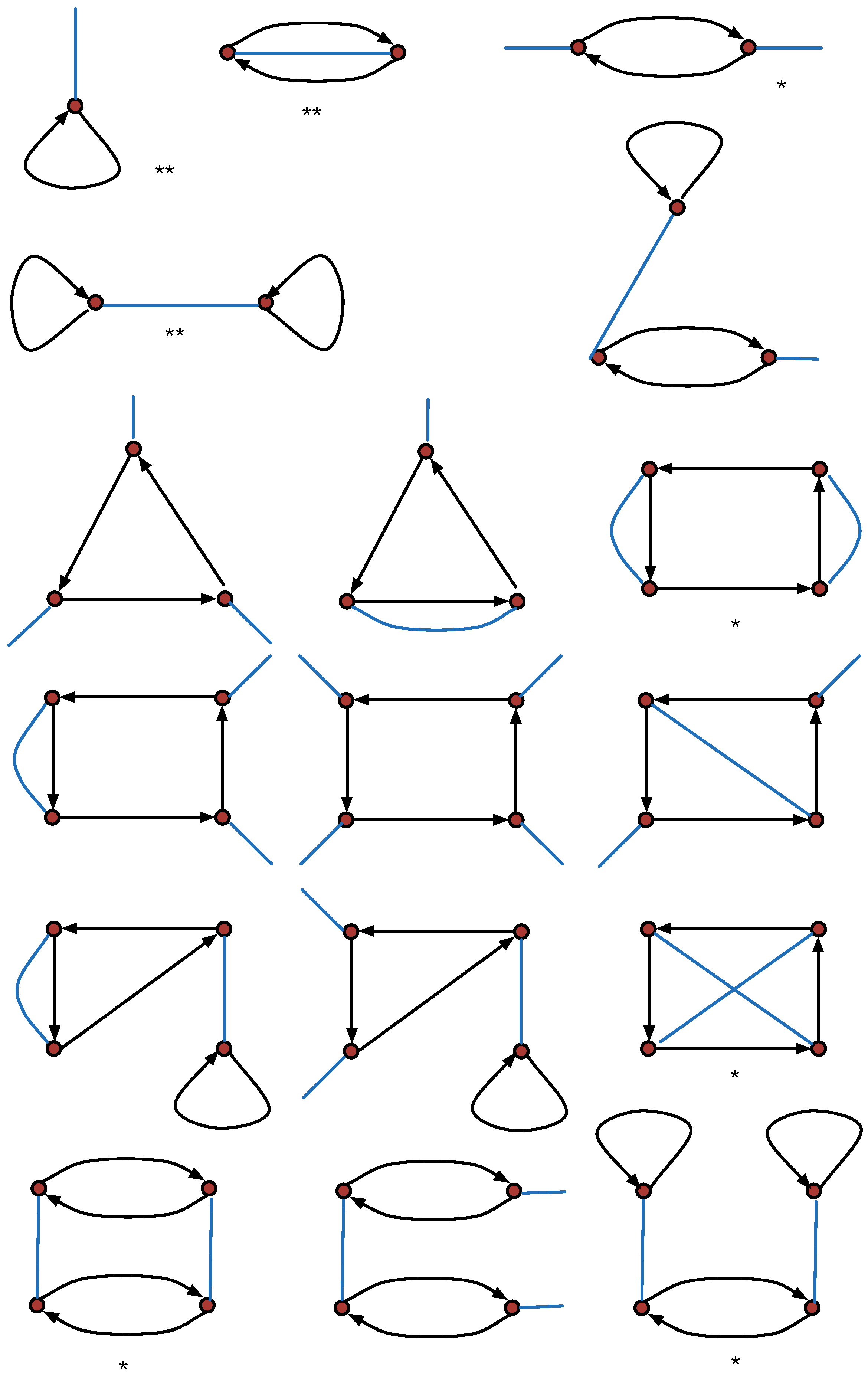
9] . We extend these results of maps to oriented maps in the obvious way by introducing a useful tool that we call an oriented symmetry type graph (see
Figure 3):
Corollary 2. Let be an oriented map.
The cardinality of each orbit of on Σ is equal to the order of .
is a divisor of .
The projection is a regular covering projection.
The quotient is a degenerate arc graph, called the oriented symmetry type graph.
The order of is equal to , and is a -orbit oriented map.
We now demonstrate an application of symmetry type graphs and oriented symmetry type graphs. A map is regular (in the strong sense, i.e., the order of its automorphism group is ) if and only if its symmetry type graph is a one-vertex graph (). Similarly, an oriented map is regular (i.e., the order if its orientation-preserving automorphism group is ) if and only if its symmetry type graph is a one-vertex graph (). We note that a regular oriented map may be either a regular or chiral (orientable) map.
In general, the underlying orientable map of a -orbit oriented map is either a - or -orbit map.
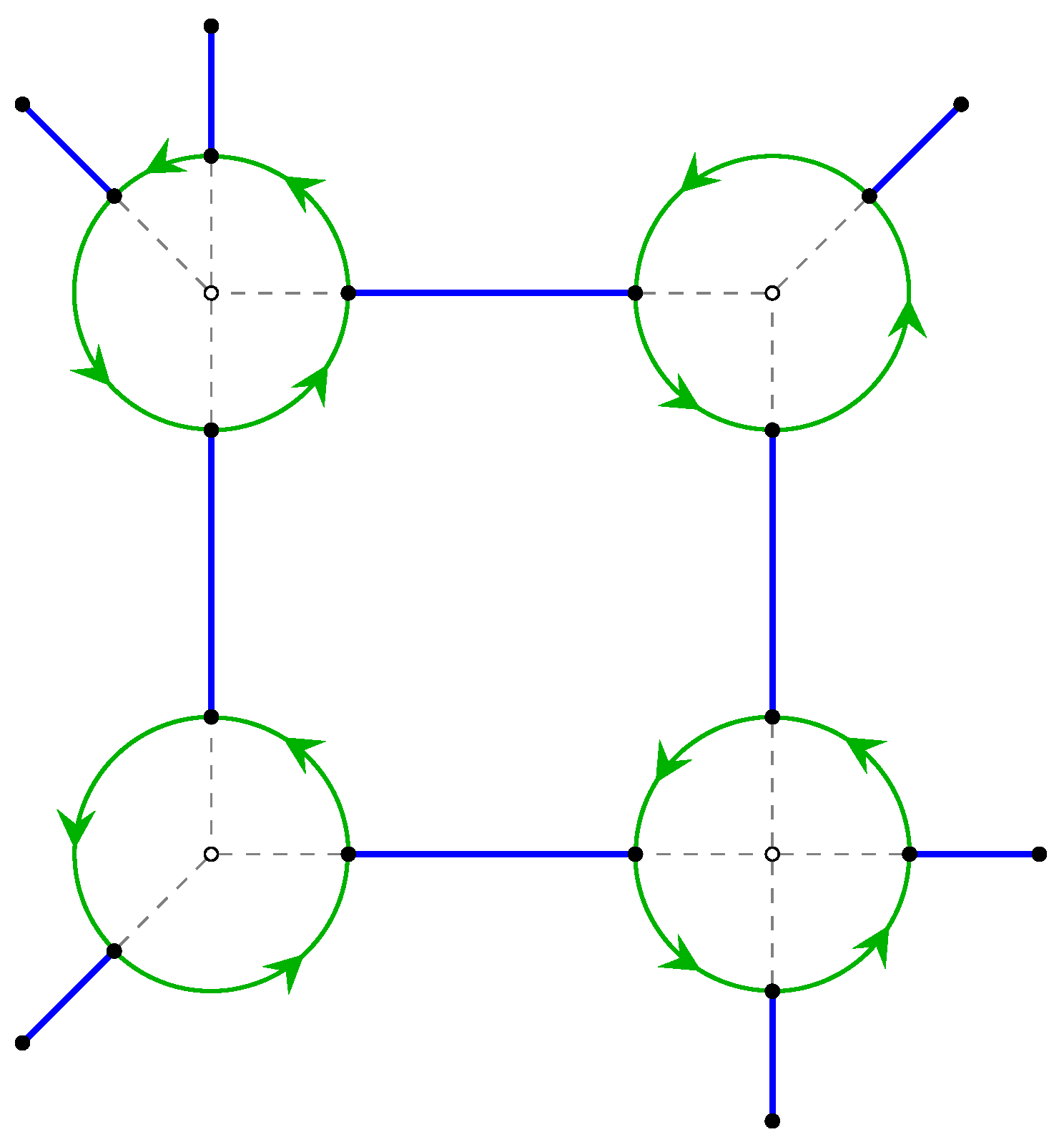
Example 2. The n-sided pyramids for all have the the same symmetry type graph and the same oriented symmetry type graph. The case is depicted in Figure 4 3. Some Properties of the Operations and k-Orbit Oriented Maps
There is an important paper by Orbanić, Pellicer and Weiss [
18] in which, among other things, the following theorem is proved.
Theorem 1. If is a k-orbit map, then its truncation is either a -, - or k-orbit map.
Motivated by [
18], we define the following:
Definition 3. Let be a map operation. If there exists a k-orbit map such that is a -orbit map, then λ is called a flag-orbit multiplier. By we denote the set of flag-orbit multipliers of .
For instance,
Problem 1. Investigate sets of flag-orbit multipliers for various operations on maps.
So far, flag-orbit multipliers have been investigated for truncation, medials and chamfering [
5,
8,
9,
18]. One could consider these operations on oriented maps, that is, as follows:
Definition 4. Let be an oriented-map operation. If there exists a k-orbit oriented map such that is a -orbit oriented map, then is called an arc-orbit multiplier. By we denote the set of arc-orbit multipliers of .
Problem 2. Investigate sets of arc-orbit multipliers for various operations on oriented maps.
In the case of maps, the main tools are symmetry type graphs. In the case of oriented maps, it seems natural that we should use oriented symmetry type graphs.
We note that the operations , such as and , have been studied for general maps, and in the context of oriented maps, they satisfy the following condition: . We call such operations amphicheiral—equivalent to their mirror image. On the other hand, this is not the case for the snub operation. We may define a different snub operation . Operations that are not amphicheiral are called chiral. Therefore, the snub is a chiral operation. The snub can only be defined for oriented maps. It certainly cannot be defined on a non-orientable map. If we try to define it for an orientable map, there is no way to distinguish between and ; hence we have to define them both simultaneously and name them arbitrarily.
We may carry this idea to oriented maps and to their oriented symmetry type graphs. We say that an oriented map or oriented symmetry type graph is
amphicheiral if
, or
. Otherwise, it is
chiral (in the sense of Conway). In practice, we may check whether a map is chiral by reversing the directions of arrows and checking whether the resulting map is orientably isomorphic to the original or not. All oriented symmetry type graphs up to four vertices are amphicheiral. The smallest chiral graph is depicted in
Figure 10.
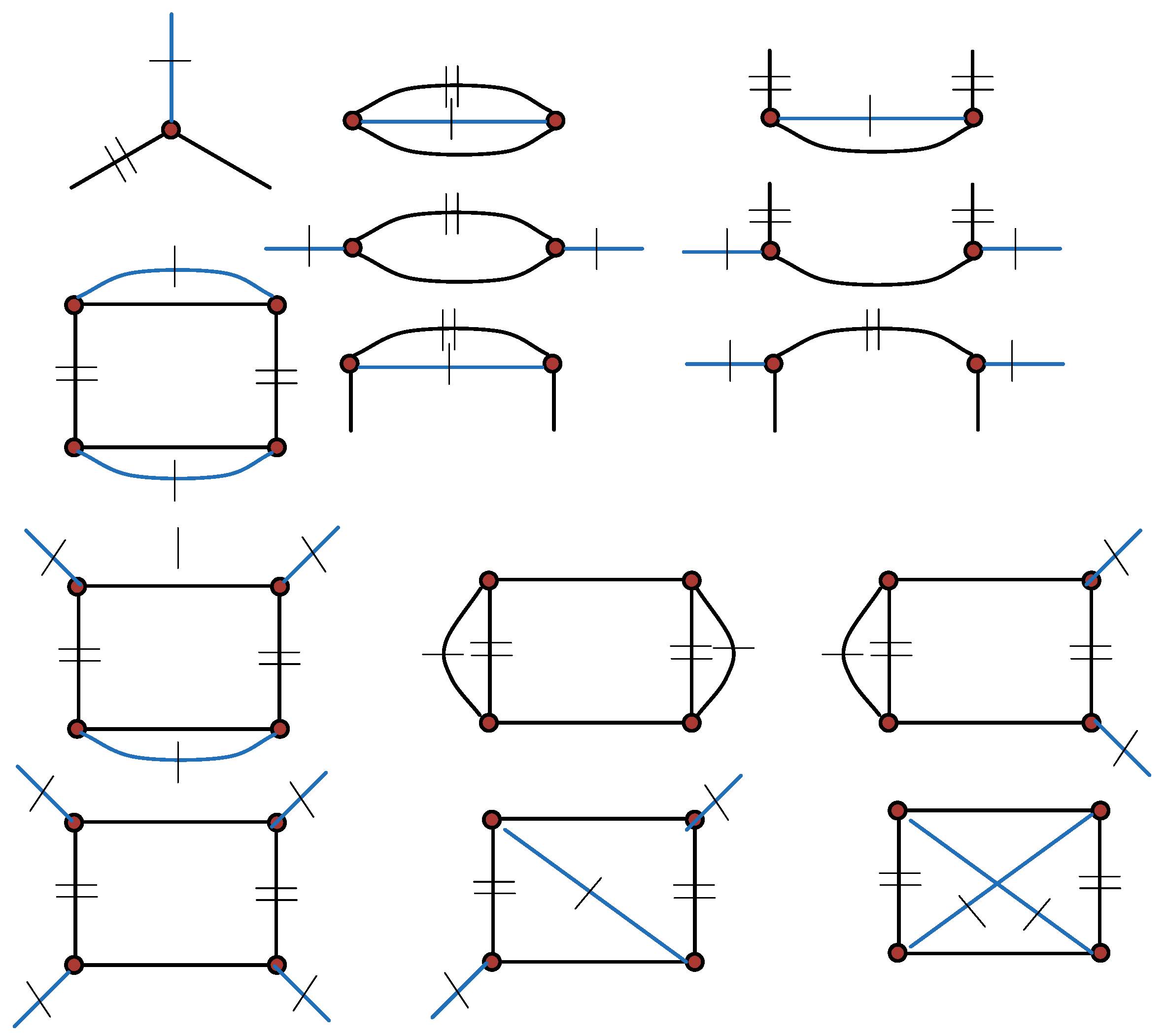
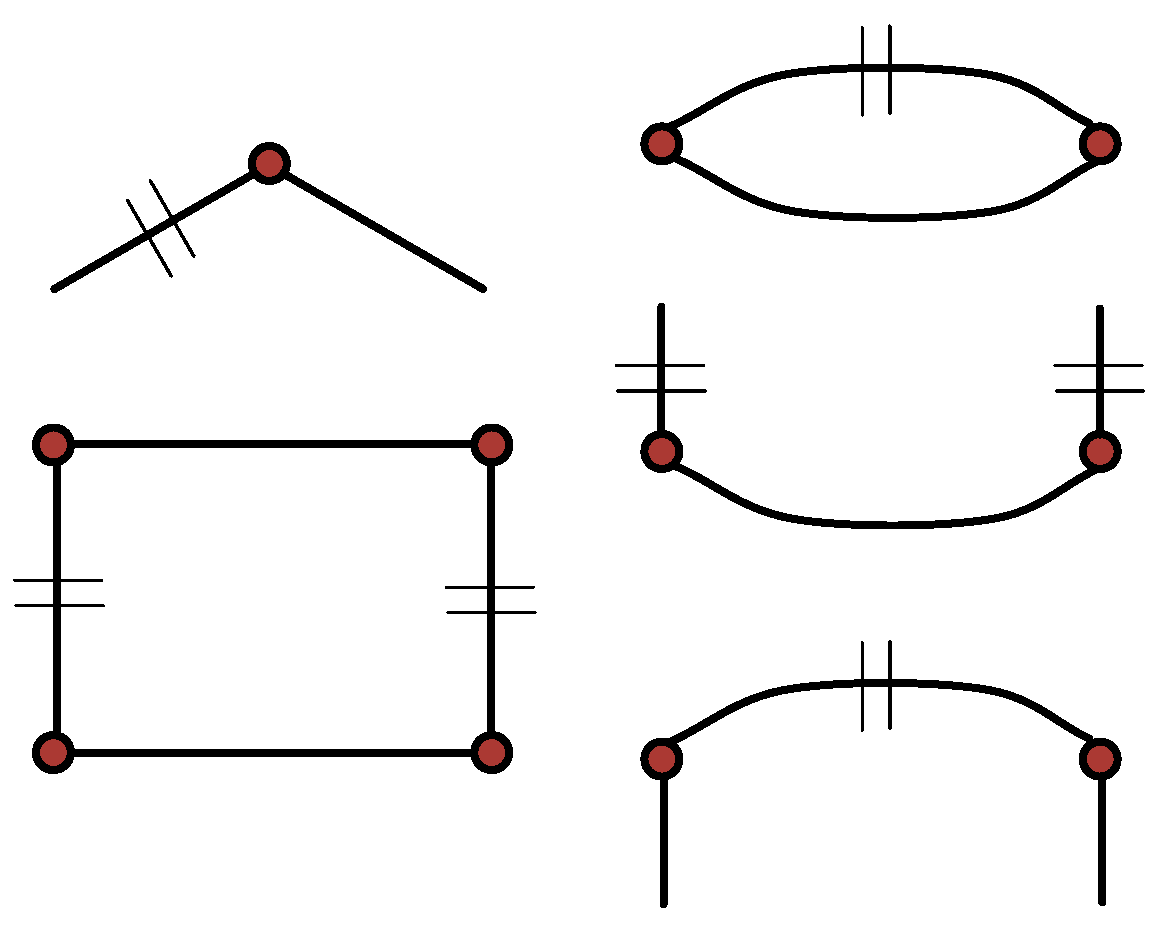
4. Edge-Transitive Oriented Maps
Recently it has been shown that symmetry type graphs are quite a powerful tool when studying certain types of maps. For instance, they provide combinatorial, group-free approaches to the question of classifying edge-transitive maps. In [
19], Graver and Watkins classified edge-transitive maps into 14 distinct types. In [
20], Širáň, Tucker and Watkins showed that each of the 14 types admits a realization by an oriented map. In [
6], Orbanić et al. showed that the 14 types can naturally be described by 14 symmetry type graphs, shown in
Figure 11.
The main idea of the proof is to use the fact that in the edge-transitive case, the spanning subgraph of the symmetry type graph determined by
must be connected. There are five possibilities, depicted in
Figure 12. By inserting the edges of
in all possible ways, one obtains exactly the 14 types.
Karabáš [
21] gives a list of low-genus orientable edge-transitive maps. Eight types of these maps are mentioned. Karabáš and Pisanski [
22] have shown that these eight classes correspond to eight different oriented symmetry type graphs.
We note that for an oriented map, the number of edge orbits according to the orientation-preserving automorphism group corresponds to the number of edges arising from in the respective oriented symmetry type graph. This limits the search to oriented symmetry type graphs on one or two vertices. We call such oriented maps edge-transitive in the strong sense.
On the other hand, an oriented map may not be edge-transitive in the strong sense, but it may have an edge-transitive underlying (orientable) map. Such a map is edge-transitive in the weak sense. One can classify such maps.
Theorem 2. ([22]) An oriented map is edge-transitive in the weak sense if and only if its oriented symmetry type graph has two edges corresponding to r and there exists an extended automorphism reversing the arrows of R that interchanges the two r-edges. This, in turn, implies that a weak edge-transitive oriented map has at most four arc symmetry classes, or equivalently, that its oriented symmetry type graph has at most four vertices.
Figure 13 depicts all 17 oriented symmetry type graphs on at most four vertices. In addition to three strong edge-transitive types, we obtain five weak edge-transitive types.
This rather simple combinatorial approach complements the much more sophisticated group-theoretic approach by Jones [
23].