Neutrosophic Duplet Semi-Group and Cancellable Neutrosophic Triplet Groups

Abstract

The notions of the neutrosophic triplet and neutrosophic duplet were introduced by Florentin Smarandache. From the existing research results, the neutrosophic triplets and neutrosophic duplets are completely different from the classical algebra structures. In this paper, we further study neutrosophic duplet sets, neutrosophic duplet semi-groups, and cancellable neutrosophic triplet groups. First, some new properties of neutrosophic duplet semi-groups are funded, and the following important result is proven: there is no finite neutrosophic duplet semi-group. Second, the new concepts of weak neutrosophic duplet, weak neutrosophic duplet set, and weak neutrosophic duplet semi-group are introduced, some examples are given by using the mathematical software MATLAB (MathWorks, Inc., Natick, MA, USA), and the characterizations of cancellable weak neutrosophic duplet semi-groups are established. Third, the cancellable neutrosophic triplet groups are investigated, and the following important result is proven: the concept of cancellable neutrosophic triplet group and group coincide. Finally, the neutrosophic triplets and weak neutrosophic duplets in BCI-algebras are discussed.

1. Introduction

Florentin Smarandache introduced the concept of a neutrosophic set from a philosophical point of view (see [1,2,3]). The neutrosophic set theory is applied to many scientific fields and also applied to algebraic structures (see [4,5,6,7,8,9,10]). Recently, Florentin Smarandache and Mumtaz Ali in [11], for the first time, introduced the notions of a neutrosophic triplet and neutrosophic triplet group. The neutrosophic triplet is agroup of three elements that satisfy certain properties with some binary operation; it is completely different from the classical group in the structural properties. In 2017, Florentin Smarandache wrote the monograph [12] that is present the latest developments in neutrodophic theories, including the neutrosophic triplet, neutrosophic triplet group, neutrosophic duplet, and neutrosophic duplet set.

In this paper, we focus on the neutrosophic duplet, neutrosophic duplet set, and neutrosophic duplet semi-group. We discuss some new properties of the neutrosophic duplet semi-group and investigate the idempotent element in the neutrosophic duplet semi-group. Moreover, we introduce some new concepts to generalize the notion of neutrosophic duplet sets and discuss weak neutrosophic duplets in BCI-algebras (for BCI-algebra and related generalized logical algebra systems, please see [13,14,15,16,17,18,19,20,21,22,23,24,25,26]).

2. Basic Concepts

2.1. Neutrosophic Triplet and Neutrosophic Duplet

Definition 1.

([11,12]) Let N be a set together with a binary operation *. Then, N is called a neutrosophic triplet set if for any a ∈ N, there exist a neutralof “a” called neut(a),different from the classical algebraic unitary element, and an opposite of “a” called anti(a), with neut(a) and anti(a) belonging to N, such that:

a * neut(a) = neut(a) * a = a;

a * anti(a) = anti(a) * a = neut(a).

The elements a, neut(a), and anti(a) are collectively called as a neutrosophic triplet, and we denote it by (a, neut(a), anti(a)). By neut(a), we mean neutral of a and, apparently, a is just the first coordinate of a neutrosophic triplet and nota neutrosophic triplet. For the same element “a” in N, there may be more neutrals to it neut(a) and more opposites of it anti(a).

Definition 2.

([11,12]) The element b in (N, *) is the second component, denoted as neut(·), of a neutrosophic triplet, if there exists other elements a and c in N such that a * b = b * a = a and a * c = c * a = b. The formed neutrosophic triplet is (a, b, c).

Definition 3.

([11,12]) The element c in (N, *) is the third component, denoted as anti(·), of a neutrosophic triplet, if there exists other elements a and b in N such that a * b = b * a = a and a * c = c * a = b. The formed neutrosophic triplet is (a, b, c).

Definition 4.

([11,12]) Let (N, *) be a neutrosophic triplet set. Then, N is called a neutrosophic triplet group, if the following conditions are satisfied:

(1) 

If (N, *) is well-defined, i.e., for any a, b ∈ N, onehas a * b ∈ N.

(2) 

If (N, *) is associative, i.e., (a * b) * c = a * (b * c) for all a, b, c ∈ N.

The neutrosophic triplet group, in general, is not a group in the classical algebraic way.

Definition 5.

([11,12]) Let (N, *) be a neutrosophic triplet group. Then, N is called a commutative neutrosophic triplet group if for all a, b ∈ N, we have a * b = b * a.

Definition 6.

([12]) Let U be a universe of discourse, and a set A ⊆ U, endowed with a well-defined law *.We say that ⟨a, neut(a)⟩, where a, neut(a) ∈ A, is a neutrosophic duplet in A if:

(1) 

neut(a) is different from the unit element of A with respect to the law * (if any);

(2) 

a * neut(a) = neut(a) * a = a;

(3) 

there is no anti(a) ∈ A such that a * anti(a) = anti(a) * a = neut(a).

Remark 1.

In the above definition, we have A ⊆ U. When A = U, “neutrosophic duplet in A” is simplified as “neutrosophic duplet”, without causing confusion.

Definition 7.

([12]) A neutrosophic duplet set, (D, *), is a set D, endowed with a well-defined binary law *, such that $\forall$a ∈ D, $\exists$a neutrosophic duplet⟨a, neut(a)⟩ such that neut(a) ∈ D. If associative law holds in neutrosophic duplet set (D, *), then call it neutrosophic duplet semi-group.

Remark 2.

The above definition is different from the original definition of a neutrosophic duplet set in [12]. In fact, the meaning of Theorem IX.2.1 in [12] is not consistent with the original definition of a neutrosophic duplet set. The original definition is modified to ensure that Theorem IX.2.1 in [12] is still correct.

Remark 3.

In order to include richer structure, the original concept of a neutrosophic triplet is generalized to neutrosophic extended triplet by Florentin Smarandache. For a neutrosophic extended triplet that is a neutrosophic triplet, the neutral of x (called “extended neutral”) is allowed to also be equal to the classical algebraic unitary element (if any). Therefore, the restriction “different from the classical algebraic unitary element, if any” is released. As a consequence, the “extended opposite” of x is also allowed to be equal to the classical inverse element from a classical group. Thus, a neutrosophic extended triplet is an object of the form (x, neut(x), anti(x)), for x ∈ N, where neut(x) ∈ N is the extended neutral of x, which can be equal or different from the classical algebraic unitary element, if any, such that: x * neut(x) = neut(x) * x = x, and anti(x) ∈ N is the extended opposite of x, such that: x * anti(x) = anti(x) * x = neut(x). In this paper, “neutrosophic triplet” means “neutrosophic extended triplet”, and “neutrosophic duplet” means “neutrosophic extended duplet”.

2.2. BCI-Algebras

Definition 8.

([15,22]) A BCI-algebra is an algebra (X; →, 1) of type (2,0) in which the following axioms are satisfied:

(i) 

(x → y) →((y → z) → (x → z)) = 1,

(ii) 

x → x = 1,

(iii) 

1 → x = x,

(iv) 

if x → y = y → x = 1, then x = y.

In any BCI-algebra (X; →, 1) one can define a relation ≤ by putting x ≤ y if and only if x → y = 1, then ≤ is a partial order on X.

Definition 9.

([16,20]) Let (X; →, 1) be a BCI-algebra. The set {x|x ≤ 1} is called the p-radical (or BCK-part) of X. A BCI-algebra X is called p-semisimple if its p-radical is equal to {1}.

Definition 10.

([16,20]) A BCI-algebra (X; →, 1) is called associative if

(x → y) → z = x→ (y → z), ∀x,y,z ∈ X.

Proposition 1.

([16]) Let (X; →, 1) be a BCI-algebra. Then the following are equivalent:

(i) 

X is associative;

(ii) 

x → 1 = x, ∀x ∈ X;

(iii) 

x → y = y → x, ∀x,y ∈ X.

Proposition 2.

([16,24]) Let (X; +, −, 1) be anAbel group. Define (X; ≤, →, 1), where

x → y = −x + y, x ≤ y if and only if –x + y = 1, ∀x,y ∈ X.

Then, (X; ≤, →, 1) is a BCI-algebra.

3. New Properties of Neutrosophic Duplet Semi-Group

For a neutrosophic duplet set (D, *), if a ∈ D, then neut(a) may not be unique. Thus, the symbolic neut(a) sometimes means one and sometimes more than one, which is ambiguous. To this end, this paper introduces the following notations to distinguish:

• neut(a): denote any certain one of neutral of a;
• {neut(a)}: denote the set of all neutral of a.

Remark 4.

In order not to cause confusion, we always assume that: for the same a, when multiple neut(a) are present in the same expression, they are always are consistent. Of course, if they are neutral of different elements, they refer to different objects (for example, in general, neut(a) is different from neut(b)).

Proposition 3.

Let (D, *) be a neutrosophic duplet semi-group with respect to * and a ∈ D. Then, for any x, y ∈ {neut(a)}, x * y ∈ {neut(a)}. That is,

{neut(a)} * {neut(a)} ⊆ {neut(a)}.

Proof. 

For any a ∈ D, by Definition 7, we have

a * neut(a) = a, neut(a) * a = a.

Assume x, y ∈ {neut(a)}, then

a * x = x * a = a; a * y = y * a = a.

From this, using associative law, we can get

a * (x * y) = (x * y) * a = a.

It follows that x * y is a neutral of a. That is, x * y ∈ {neut(a)}. This means that {neut(a)} * {neut(a)}⊆ {neut(a)}. ☐

Remark 5.

If neut(a) is unique, then

neut(a) * neut(a) = neut(a).

But, if neut(a) is not unique, for example, assume {neut(a)} = {s, t} ∈ D, then neut(a) denote any one of s, t. Thus neut(a) * neut(a)represents one of s * s, and t * t; and {neut(a)} * {neut(a)} = {s * s, s * t, t* s, t * t}. Proposition 3 means that s * s, s * t, t * s, t * t ∈ {neut(a)} = {s, t}, that is,

s * s = s, or s * s = t; s * t = s, or s * t = t.

t * s = s, or t * s = t; t * t = s, or t * t = t.

In this case, the equation neut(a) * neut(a) = neut(a) may not hold.

Proposition 4.

Let (D, *) be a neutrosophic duplet semi-group with respect to * and let a, b, c ∈ D. Then

(1) 

neut(a) * b = neut(a) * c ⇒ a * b = a * c.

(2) 

b * neut(a) = c * neut(a) ⇒ b *a = c * a.

Proof. 

(1) Assume neut(a) * b = neut(a) * c. Then

a * (neut(a) * b) = a * (neut(a) * c).

By associative law, we have

(a *neut(a)) * b = (a *neut(a)) * c.

Thus, a * b = a * c. That is, (1) holds.

Similarly, we can prove that (2) holds. ☐

Theorem 1.

Let (D, *) be a commutative neutrosophic duplet semi-group with respect to * and a, b ∈ D. Then

neut(a) * neut(b) ∈ {neut(a * b)}.

Proof. 

For any a, b ∈ D, we have

a * neut(a) * neut(b) * b = (a * neut(a)) * (neut(b) * b) = a * b.

From this and applying the commutativity and associativity of operation * we get

(neut(a) * neut(b)) * (a * b) = (a * b) * (neut(a) * neut(b)) = a * b.

This means thatneut(a) * neut(b) ∈ {neut(a * b)}. ☐

Theorem 2.

Let (D, *) be a neutrosophic duplet set with respect to *. Then there is no idempotent element in D, that is,

∀a ∈ D, a * a ≠ a.

Proof. 

Assume that there is a ∈ D such that a * a = a. Then a ∈ {neut(a)}, and a ∈ {anti(a)}, This is a contraction with Definition 6 (3). ☐

Since the classical algebraic unitary element is idempotent, we have

Corollary 1.

Let (D, *) be a neutrosophic duplet set with respect to *. Then there is no classical unitary element in D, that is, there is no e ∈ D such that $\forall$a ∈ D, a * e = e * a = a.

Theorem 3.

Let (D, *) be a neutrosophic duplet semi-group with respect to *. Then D is infinite. That is, there is no finite neutrosophic duplet semi-group.

Proof. 

Assume that D is a finite neutrosophic duplet semi-group with respect to *. Then, for any a ∈ D,

a, a * a = a², a * a * a = a³, …, aⁿ,… ∈ D.

Since D is finite, so there exists natural number m, k such that

a^m = a^m+k.

Case 1: if k = m, then a^m = a^2m, that is, a^m = a^m * a^m, a^m is an idempotent element in D, this is a contraction with Theorem 2.

Case 2: if k > m, then from a^m = a^m+k we can get

a^k = a^m * a^k−m = a^m+k * a^km = a^2k = a^k * a^k.

This means that a^k is an idempotent element in D, this is a contraction with Theorem 2.

Case 3: if k <m, then from a^m = a^m+k we can get

a^m = a^m+k = a^m * a^k = a^m+k * a^k = a^m+2k;

a^m = a^m+2k = a^m * a^2k = a^m+k * a^2k = a^m+3k;

……

a^m = a^m+mk.

Since m and k are natural numbers, then mk ≥ m. Therefore, from a^m = a^m+mk, applying Case 1 or Case 2, we know that there exists an idempotent element in D, this is a contraction with Theorem 2. ☐

Theorem 4.

Let (D, *) be a neutrosophic duplet semi-group with respect to *and a ∈ D. Then

neut(neut(a)) ∈ {neut(a)}.

Proof. 

For any a ∈ D, by the definition of neut(·), we have

neut(a) * neut(neu(a)) = neut(a);

neut(neut(a)) * neut(a) = neut(a).

Then

a * (neut(a) * neut(neut(a))) = a * neut(a);

(neut(neut(a)) * neut(a)) * a = neut(a) * a.

By associative law, we have

a * neut(neut(a)) = a; neut(neut(a)) * a = a.

From this, by the definition of neut(·), we get neut(neut(a)) ∈ {neut(a)}. ☐

Theorem 5.

Let (D, *) be a neutrosophic duplet semi-group with respect to *. Then

(1) 

$\forall$a ∈ D, ({neut(a)}, *) is a neutrosophic duplet semi-group with respect to *.

(2) 

$\forall$a ∈ D, {neut(a)} is infinite.

Proof. 

(1) For any x, y ∈ {neut(a)}, by Proposition 3, x * y ∈ {neut(a)}. Thus, ({neut(a)}, *) is a semi-group. Moreover, applying Theorem 4, neut(neut(a)) ∈ {neut(a)}, that is, for any x ∈ {neut(a)}, denote y = neut(neut(a)) ∈ {neut(a)},

x * y = y * x = x.

Since (D, *) is a neutrosophic duplet set, then, for any x ∈ {neut(a)}, there is no unit(x)∈ D such that

x * unit(x) = unit(x) * x = neut(x).

Thus, there is no unit(x) ∈ {neut(a)} such that

x * unit(x) = unit(x) * x = neut(x).

This means that there is no opposite of “x” for any x ∈ {neut(a)}. Hence, ({neut(a)}, *) is a neutrosophic duplet semi-group with respect to *.

(2) Applying (1) and Theorem 3 we know that {neut(a)} is infinite for any x ∈ D. ☐

Remark 6.

In the monograph [12] (p. 112), given an example of neutrosophic duplet semi-group. In fact, it was wrong, because the associative law does not hold:

(b * a) *c = a * c = c, but b * (a * c) = b * c = b.

4. Weak Neutrosophic Duplet Set (and Semi-Group)

From Theorems 3 and 5, we can see that the structure of the neutrosophic duplet semi-group is very scarce. What are the reasons for that? The key reason is that under the original definition of neutrosophic duplet, the idempotent element is not allowed (since it has a corresponding opposite element). In fact, for any idempotent element a, we have a ∈ {neut(a)} and a ∈ {anti(a)}, that is, (a, a, a) is a neutrosophic triplet. Therefore, in order for us to study it more widely, we slightly relaxed the condition that allowed such (a, a, a) to exist in a neutrosophic duplet set and introduced a new concept as follows.

Definition 11.

A weak neutrosophic duplet set, (D, *), is a set D, endowed with a well-defined binary law *, such that $\forall$a ∈ D, if a {neut(a)}, then $\exists$a neutrosophic duplet ⟨a, neut(a)⟩ such that neut(a) ∈ D. If the associative law holds in weak neutrosophic duplet set (D, *), then call it a weak neutrosophic duplet semi-group.

The situation is quite different from that of the neutrosophic duplet semi-group, as there are many finite weak neutrosophic duplet semi-groups. See the following examples.

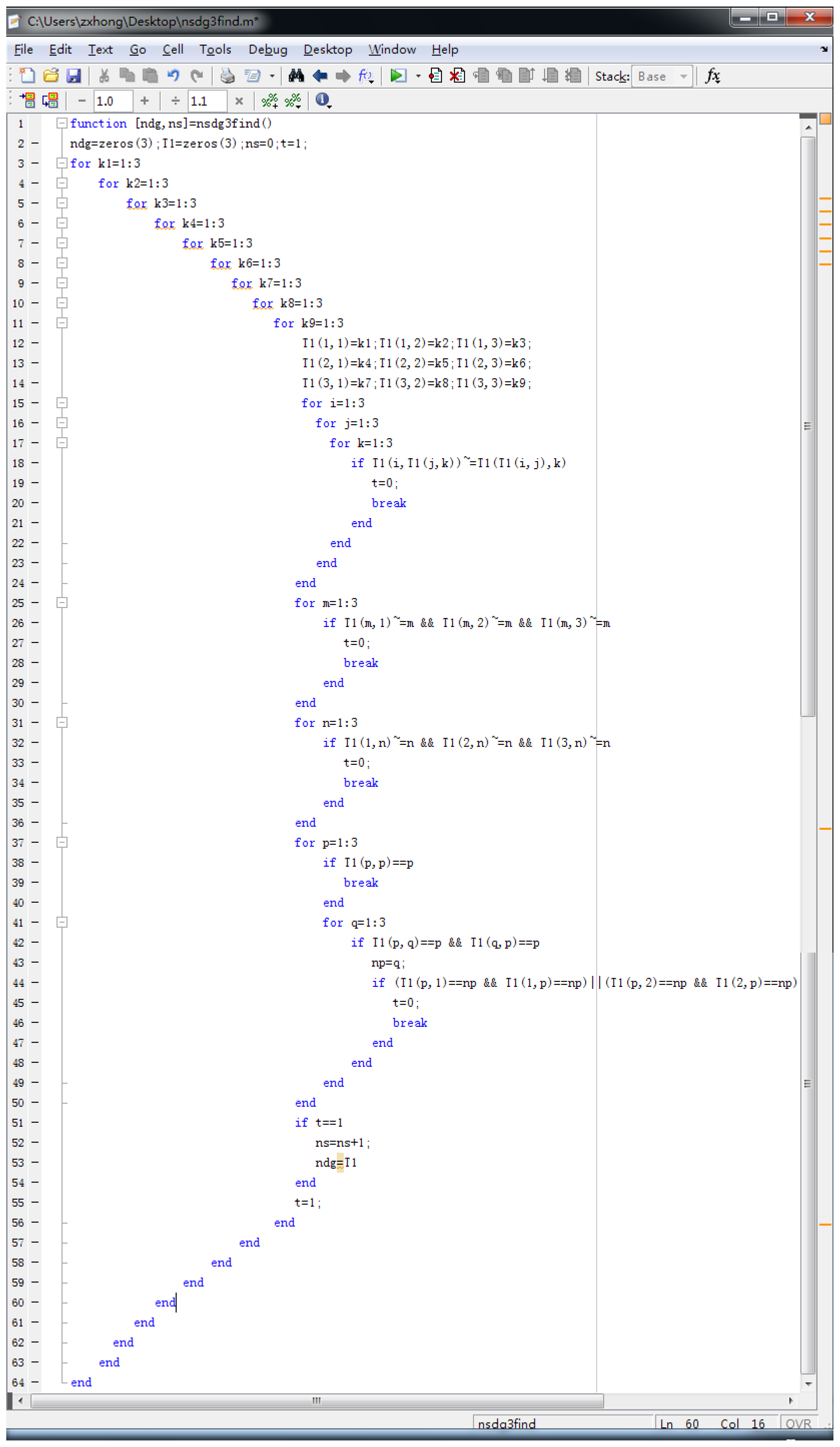
Example 1.

Let D = {1, 2, 3}. The operation * on D is defined as Table 1. Then, (D, *) is a commutative neutrosophic duplet semi-group.

Table 1. Weak neutrosophic duplet semi-group (1).

*	1	2	3
1	1	2	3
2	2	2	2
3	3	2	2

In fact, we can verify that (D, *) is a neutrosophic duplet semi-group by MATLAB programming, as shown in Figure 1.

Figure 1. Verity weak neutrosophic duplet semi-group by MATLAB.

In this example, “1” and “2” are idempotent elements in D, and neut(1) = 1, neut(2) = 2. Moreover, neut(3) = 1, but {anti(3)} = ∅.

Example 2.

Let D = {1, 2, 3}. The operation * on D is defined as Table 2. Then, (D, *) is a non-commutative neutrosophic duplet semi-group.

Table 2. Weak neutrosophic duplet semi-group (2).

*	1	2	3
1	1	1	1
2	1	2	3
3	3	3	3

In this example, “1”, “2”, and “3” are idempotent elements in D, and {neut(1)} = {1, 2},neut(2) = 2, {neut(3)} = {2, 3}.

Example 3.

Let D = {1, 2, 3, 4}. The operation * on D is defined as Table 3. Then, (D, *) is a commutative neutrosophic duplet semi-group.

Table 3. Weak neutrosophic duplet semi-group (3).

*	1	2	3	4
1	3	1	4	4
2	1	2	3	4
3	4	3	4	4
4	4	4	4	4

In this example, “2” and “4” are idempotent elements in D, and neut(2) = 2,{neut(4)} = {1, 2, 3, 4}. neut(1) = 2, {anti(1)} = ∅; neut(3) = 2, {anti(3)} = ∅.

Example 4.

Let D = {1, 2, 3, 4}. The operation * on D is defined as Table 4. Then, (D, *) is a non-commutative neutrosophic duplet semi-group.

Table 4. Weak neutrosophic duplet semi-group (4).

*	1	2	3	4
1	2	2	3	1
2	2	2	3	2
3	2	2	3	3
4	1	2	3	4

In this example, “2”, “3”, and “4” are idempotent elements in D, and neut(1) = 4,{anti(1)} = ∅.

Now, we explain all of the neutrosophic duplet semi-groups with three elements. In total, we can obtain 50 neutrosophic duplet semi-groups with three elements, some of which may be isomorphic. They are funded by MATLAB programming, as shown in Figure 2.

Figure 2. Find weak neutrosophic duplet semi-group by MATLAB.

Definition 12.

A weak neutrosophic duplet semi-group (D, *) is called to be cancellable, if it satisfies

∀a, b, c ∈ D, a *b = a * c ⇒ b = c;

∀a, b, c ∈ D, b * a = c * a ⇒ b = c.

The weak neutrosophic duplet semi-groups in Examples 1–4 are not cancellable. We give a cancellable example as follows.

Example 5.

Let D = {1, 2, 3, …}. The operation * on D is the multiplication of natural number. Then, (D, *) is a cancellable weak neutrosophic duplet semi-group.

In this example, for any element a in D, and neut(a) = 1.

Example 6.

Let D = {0, 1, 2, 3, …}. The operation * on D is the addition of natural number. Then, (D, *) is a cancellable weak neutrosophic duplet semi-group.

In this example, for any element a in D, and neut(a) = 0.

Theorem 6.

Let (D, *) be a cancellable weak neutrosophic duplet semi-group with respect to *. Then

(1) 

$\forall$a ∈ D, neut(a) is unique.

(2) 

$\forall$a ∈ D, neut(a) * neut(a) = neut(a).

(3) 

$\forall$a ∈ D, neut(a) * neut(a) = neut(a * a).

(4) 

$\forall$a, b ∈ D, neut(a) = neut(b).

Proof. 

(1) For any a ∈ D, we have

Case 1: if a ∈ {neut(a)}, then a * a = a. Thus

a * a = a = a * neut(a).

By Definition 12, we have a = neut(a). This means that {neut(a)} = {a}, that is, neut(a) is unique.

Case 2: if a {neut(a)}, assume x, y ∈ {neut(a)}, then

a * x = a = a * y.

By Definition 12, we havex = y. This means that |{neut(a)}| = 1, that is, neut(a) is unique.

(2) If a ∈ {neut(a)}, then a * a = a, by (1) we get a = neut(a), so neut(a) * neut(a) = neut(a).

If a {neut(a)}, by the same way with Proposition 3, we can prove that

{neut(a)} * {neut(a)} ⊆ {neut(a)}.

Using (1) we have neut(a) * neut(a) = neut(a).

(3) For any a ∈ D, since (by associative law)

(neut(a) * neut(a)) * (a * a) = a * a;

(a * a) * (neut(a) * neut(a)) = a * a.

This means that neut(a) * neut(a) ∈ {neut(a * a)}, but by (1) |{neut(a)}| = 1, thus

neut(a) * neut(a) = neut(a * a).

(4) For any a, b ∈ D, since (by associative law)

a * neut(a) * neut(b) *b = a * b.

From this, applying Definition 12,

neut(a) * neut(b) * b = b.

neut(a) * neut(b) * b = b = neut(b) * b.

Applying Definition 12 again,

neut(a) * neut(b) = neut(b).

Similarly, we can get

neut(a) * neut(b) = neut(a).

Hence, neut(a) = neut(b). ☐

Theorem 7.

Let (D,) be a cancellable weak neutrosophic duplet semi-group with respect to *. If D is a finite set, then D is a single point set, that is, |D| = 1.

Proof. 

By Theorem 6, we know that {neut(a) | a ∈ D} is a single point set. Denote neut(a) = e ($\forall$a ∈ D).

Assume that D is a finite set, if |D| ≠ 1, then there exists x ∈ D such that x ≠ e. Denote |D| = n, D = {a₁, a₂, …, a_n}. In the table of operation *, consider the line in which the x is located:

x * a₁, x * a₂, …, x * a_n

Since D is cancellable, then x * a₁, x * a₂, …, x * a_nare different from each other. Thus, $\exists$a_i such that x * a_i = e. It follows that ⟨x, neut(x) = e⟩ is not a neutrosophic duplet. Applying Definition 11, x ∈ {neut(x)} = {e}. That is, x ≠ e. This is a contraction with the hypothesis x ≠ e. Hence |D| = 1.

Applying Theorems 2 and 6, we can get the following theorem. ☐

Theorem 8.

Let (D, *) be a neutrosophic duplet semi-group with respect to *. Then D is not cancellable. That is, there is no cancellable neutrosophic duplet semi-group.

5. On Cancellable Neutrosophic Tripet Groups

Definition 13.

A neutrosophic triplet group (D, *) is called to be cancellable, if it satisfies

∀a, b, c ∈ D, a * b = a * c ⇒ b = c;

∀a, b, c ∈ D, b * a = c * a ⇒ b = c.

Example 7.

Let D = {1, 2, 3, 4}. The operation * on D is defined as Table 5. Then, (D, *) is a cancellable neutrosophic triplet group.

Table 5. Cancellable neutrosophic triplet group.

*	1	2	3	4
1	1	2	3	4
2	2	1	4	3
3	3	4	1	2
4	4	3	2	1

In this example, neut(1) = neut(2) = neut(3) = neut(4) = 1, and anti(1) = 1, anti(2) = 2, anti(3) = 3, anti(4) = 4.

Theorem 9.

Let (D, *) be a cancellable neutrosophic triplet group with respect to *. Then

(1) 

$\forall$a ∈ D, neut(a) is unique.

(2) 

$\forall$a ∈ D, anti(a) is unique.

(3) 

$\forall$a, b ∈ D, neut(a) = neut(b).

(4) 

(D, *) is a group, the unit is neut(a), $\forall$a ∈ D.

Proof. 

(1) For any a ∈ D, assume x, y ∈ {neut(a)}, then

A * x = a = a * y.

By Definition 13, we have x = y. This means that |{neut(a)}| = 1, that is, neut(a) is unique.

(2) For any a ∈ D, using (1), neut(a) is unique. Assume x, y ∈ {anti(a)}, then

a * x = neut(a) = a * y.

By Definition 13, we have x = y. This means that |{anti(a)}| = 1, that is, anti(a) is unique.

(3) For any a, b ∈ D, since (by associative law)

neut(a) * b = neut(a) * neut(b) * b.

From this, applying Definition 13,

neut(a) = neut(a) * neut(b).

On the other hand, since (by associative law)

a * neut(b) = a * (neut(a) * neut(b)).

From this, applying Definition 13 again,

neut(b) = neut(a) * neut(b).

Thus, neut(a) = neut(b).

(4) It follows from (1)~(3).  ☐

Since any group is a cancellable neutrosophic triplet group, by Theorem 9 (3), we have

Theorem 10.

The concepts of neutrosophic triplet group and group coincide.

The following example shows that there exists a non-cancellable neutrosophic triplet group, in which ($\forall$a ∈ D) neut(a) is unique and anti(a) is unique.

Example 8.

Let D = {1, 2, 3, 4}. The operation * on D is defined as Table 6. Then, (D, *) is a non-cancellable neutrosophic triplet group, but ($\forall$a ∈ D) neut(a) is unique and anti(a) is unique.

Table 6. Non-cancellable neutrosophic triplet group.

*	1	2	3	4
1	1	2	3	4
2	1	2	3	4
3	1	2	3	4
4	1	2	3	4

In this example, neut(1) = anti(1) = 1, neut(2) = anti(2) = 2, neut(3) = anti(3) = 3, neut(4) = anti(4) = 4.

Definition 14.

A neutrosophic triplet group (D, *) is called to be weak cancellable, if it satisfies

∀a, b, c ∈ D, (a * b = a * c and b * a = c * a) ⇒ b = c.

Obviously, acancellable neutrosophic triplet group is weak cancellable, but a weak cancellable neutrosophic triplet group may not be cancellable. In fact, the (D, *) in Example 8 is weak cancellable, but is not cancellable.

Theorem 11.

Let (D, *) be a weak cancellable neutrosophic triplet group with respect to *. Then

(1) 

$\forall$a ∈ D, neut(a) is unique.

(2) 

$\forall$a ∈ D, anti(a)is unique.

Proof. 

(1) For any a ∈ D, assume x, y ∈ {neut(a)}, then

a * x = a = a * y.

x* a = a = y * a.

By Definition 14, we have x = y. This means that |{neut(a)}| = 1, that is, neut(a) is unique.

(2) For any a ∈ D, using (1), neut(a) is unique. Assume x, y ∈ {anti(a)}, then

a * x = neut(a) = a * y.

x * a = neut(a) = y * a.

By Definition 14, we have x = y. This means that |{anti(a)}| = 1, that is, anti(a) is unique.

The following example shows that there exists a neutrosophic triplet group in which ($\forall$a ∈ D) neut(a) is unique and anti(a) is unique, but it is not weak cancellable. ☐

Example 9.

Let D = {1, 2, 3}. The operation * on D is defined as Table 7. Then, (D, *) is a neutrosophic triplet group, and ($\forall$a ∈ D) neut(a) is unique and anti(a) is unique. However, it is not weak cancellable, since

2 * 1 = 2 * 2, 1 * 2 = 2 * 2, 1 ≠ 2.

Table 7. Not weak cancellable neutrosophic triplet group.

*	1	2	3
1	1	2	3
2	2	2	3
3	3	3	2

In this example, we have

neut(1) = anti(1) = 1, neut(2) = anti(2) = 2, neut(3) = anti(3) = 2.

The following example shows that there exists a commutative neutrosophic triplet group which ($\exists$a ∈ D) anti(a) is not unique.

Example 10.

Consider (Z6, *), where * is classical multiplication. Then, (Z6, *) is a commutative neutrosophic triplet group, the binary operation * is defined in Table 8. For each a ∈ Z6, we have neut(a) in Z6. That is,

neut([0]) = [0], neut([1]) = [1], neut([2]) = [4],

neut([3]) = [3], neut([4]) = [4], neut([5]) = [1];

{anti([0])} = {[0], [1], [2], [3], [4], [5]},

{anti([1])} = {[1]},

{anti([2])} = {[2], [5]},

{anti([3])} = {[1], [3], [5]},

{anti([4])} = {[1], [4]},

{anti([5])} = {[5]}.

Table 8. Cayley table of (Z₆, *).

*	[0]	[1]	[2]	[3]	[4]	[5]
[0]	[0]	[0]	[0]	[0]	[0]	[0]
[1]	[0]	[1]	[2]	[3]	[4]	[5]
[2]	[0]	[2]	[4]	[0]	[2]	[4]
[3]	[0]	[3]	[0]	[3]	[0]	[3]
[4]	[0]	[4]	[2]	[0]	[4]	[2]
[5]	[0]	[5]	[4]	[3]	[2]	[1]

6. Neutrosophic Triplets and Weak Neutrosophic Duplets in BCI-Algebras

Now, we discuss BCI-algebra (X; →, 1).

Theorem 12.

Let (X; →, 1) be a BCI-algebra. Then

(1) 

$\forall$x ∈ X, if {neut (x)} ≠ ∅ and y ∈ {neut (x)}, then x → 1 = x, y → 1 = 1.

(2) 

$\forall$x ∈ X, if {neut (x)} ≠ ∅ and {anti (x)} ≠ ∅, then z → 1 = x for any z ∈ {anti (x)}.

Proof. 

(1) Assume y ∈ {neut(x)}, then

X → y = y → x = x.

Using the properties of BCI-algebras, we have

x → 1 = x → (y → y) = y →(x → y) = y → x = x.

y → 1 = y →(x → x) = x →(y → x) = x → x = 1.

(2) Assume z ∈ {anti(x)}, then

Z → x = x → z = neut(x).

Using (1) and the properties of BCI-algebras, we have

1 = neut(x) → 1 = (z → x) → 1 = (z → 1) → (x → 1) = (z → 1) → x.

1 = neut(x) → 1 = (x → z) → 1 = (x → 1) → (z → 1) = x→(z → 1).

Hence, z → 1 = x. ☐

Example 11.

Let D = {a, b, c, 1}. The operation → on D is defined as Table 9. Then, (D, →) is a BCI-algebra (it is a dual form of I_4-2-2 in [16]), and ⟨c, 1, c⟩ is a neutrosophic triplet in (D, →).

Table 9. Neutrosophic triplet in BCI-algebra.

→	a	b	c	1
a	1	c	c	1
b	c	1	1	c
c	b	a	1	c
1	a	b	c	1

Theorem 13.

Let (X; →, 1) be a BCI-algebra. Then (X, →) is a neutrosophic triplet group if and only if (X; →, 1) is an associative BCI-algebra.

Proof. 

Suppose that (X; →) is a neutrosophic triplet group. Then $\forall$x ∈ X, {neut(x)} ≠ ∅. By Theorem 12, x → 1 = x. Using Proposition 1, (X; →, 1) is an associative BCI-algebra.

Conversely, suppose that (X; →, 1) is an associative BCI-algebra. Then (X; →, 1) is a group. Hence, (X; →) is a neutrosophic triplet group. ☐

Example 12.

Let D = {a, b, c, 1}. The operation → on D is defined as Table 10. Then, (D; →, 1) is a BCI-algebra (it is a dual form of I_4-1-1 in [16]), and (D, →) is a neutrosophic triplet group.

Table 10. Neutrosophic triplet group and BCI-algebra.

→	a	b	c	1
a	1	c	c	1
b	c	1	1	c
c	b	a	1	c
1	a	b	c	1

Theorem 14.

Let (X; →, 1) be a BCI-algebra. Then (X, →) is not a neutrosophic duplet semi-group.

Proof. 

Proof. Since 1 = 1 → 1, so, applying Theorem 2, we get that (X, →) is not a neutrosophic duplet semi-group.  ☐

Theorem 15.

Let (X; →, 1) be a BCI-algebra. If (X, →) is a weak neutrosophic duplet semi-group, then X = {1}.

Proof. 

Assume that $\exists$x ∈ X − {1}. Since x → x = 1, so x {neut(x)}. Applying Definition 11, {neut(x)} ≠ ∅, from this and using Theorem 12 (1), x → 1 = x. Thus

x → 1 = 1 → x = x.

x → (x → 1) = (x → 1) → x = 1.

This means that 1 ∈ {neut(x)}, x → 1 ∈ {anti(x)}, this is a contraction with Definition 11. ☐

7. Conclusions

This paper is focused on the neutrosophic duplet semi-group. We proved some new properties of the neutrosophic duplet semi-group, and proved that there is no finite neutrosophic duplet semi-group. We introduced the new concept of weak neutrosophic duplet semi-groups and gave some examples by MATLAB. Moreover, we investigated cancellable neutrosophic triplet groups and proved that the concept of cancellable neutrosophic triplet group and group coincide. Finally, we discussed neutrosophic triplets and weak neutrosophic duplets in BCI-algebras.