Denoising and Feature Extraction Algorithms Using NPE Combined with VMD and Their Applications in Ship-Radiated Noise
Abstract
:1. Introduction
2. Theory Description
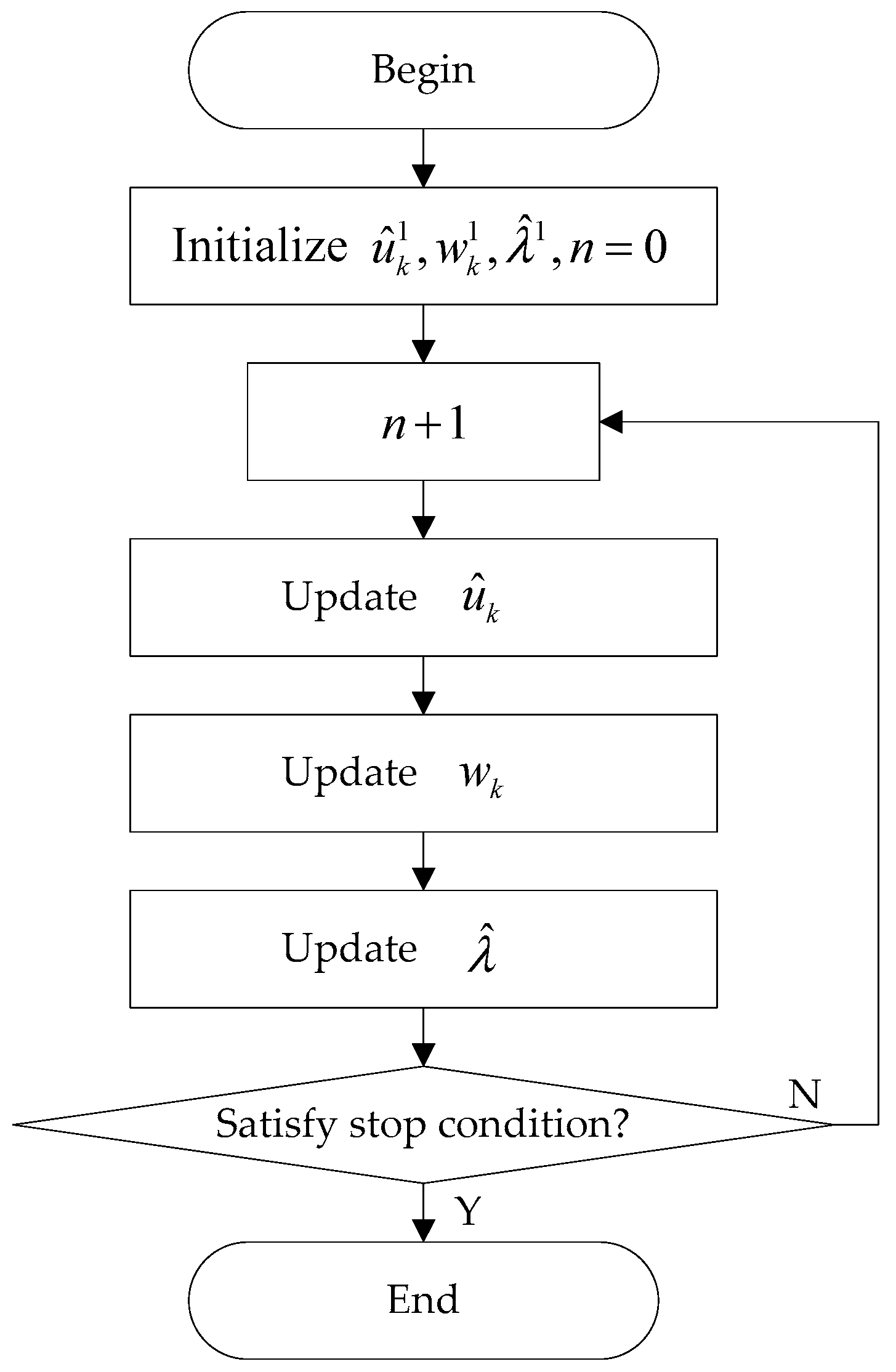
2.1. VMD Algorithm
2.2. PE and NPE
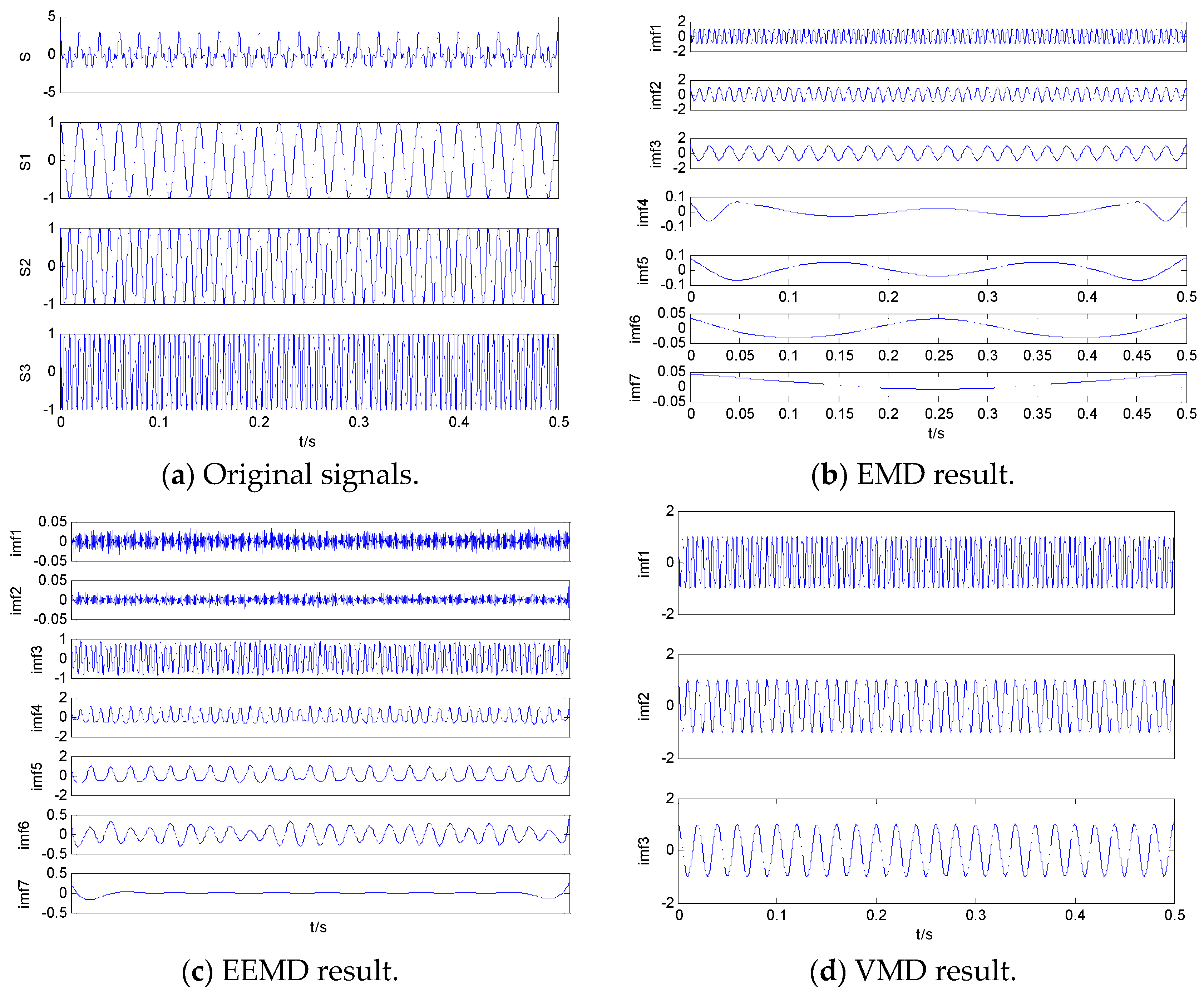
2.3. Analysis of the Simulation Signal Using VMD and NPE
3. Denoising and Feature Extraction Algorithms Using VMD and NPE
3.1. Denoising Algorithm
- Step 1
- Decompose signal by EMD.
- Step 2
- Select the decomposition level of VMD according to the decomposition level of EMD.
- Step 3
- Decompose signal by VMD, IMFs can be obtained.
- Step 4
- Calculate the NPE of each IMF.
- Step 5
- Screen out the noise IMFs according to the value of NPE. Normally when NPE of IMF is less than 0.1, it is regarded as the noise IMF.
- Step 6
- Reconstruct the useful IMFs with NPE greater than 0.1. After the reconstruction, the process of denoising is completed.
3.2. Feature Extraction Algorithm
- Step 1
- Decompose the reconstructed signal by EMD.
- Step 2
- Select the decomposition level of VMD according to the decomposition level of EMD.
- Step 3
- Decompose the reconstructed signal by VMD, IMFs can be obtained.
- Step 4
- Calculate the energy intensity of each IMF.
- Step 5
- Select the principal IMF, namely PIMF. Normally PIMF is the IMF with the maximum energy intensity.
- Step 6
- Calculate the NPEs of PIMFs.
- Step 7
- Put the NPEs of PIMFs into SVM, the classification results can reflect the effectiveness of the feature extraction algorithm.
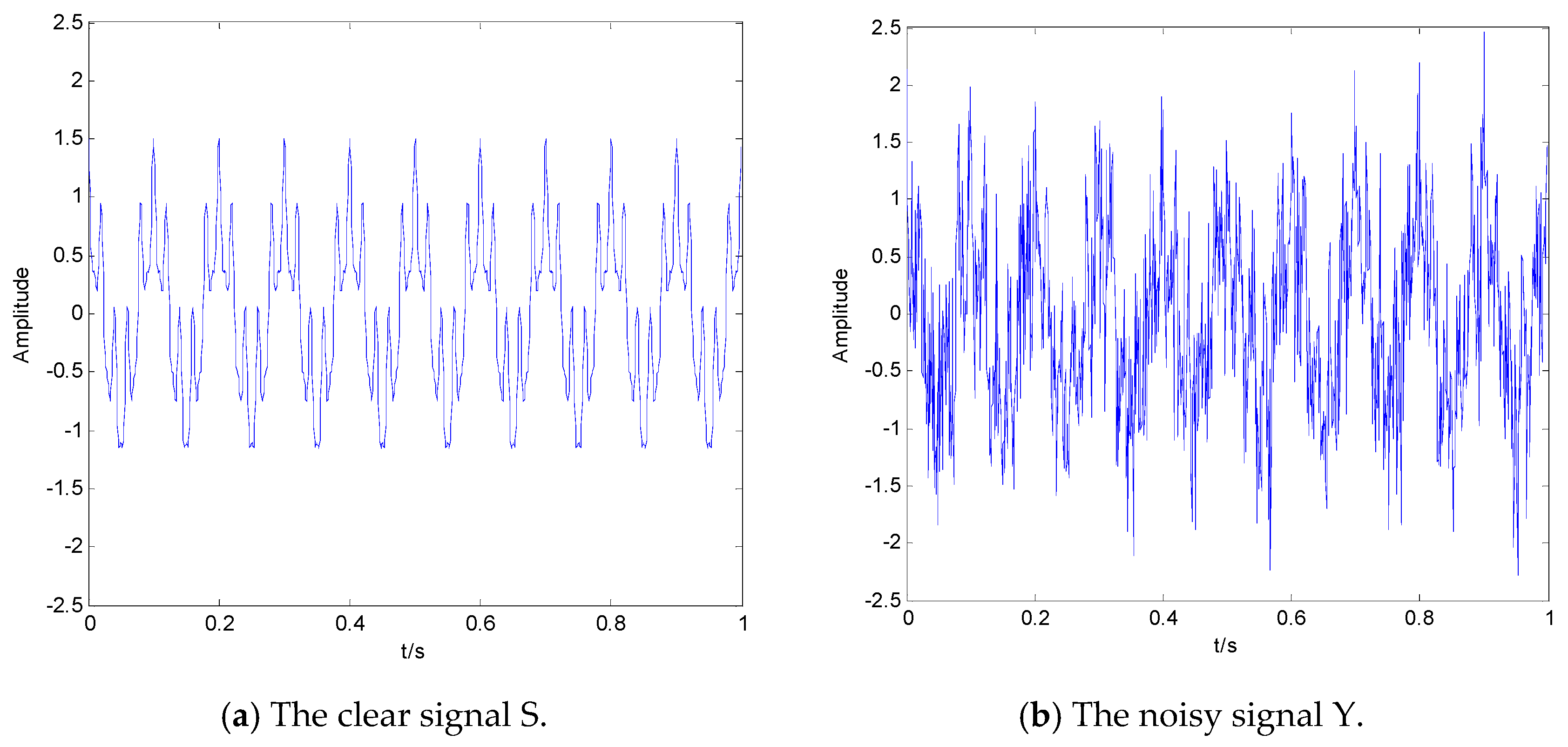
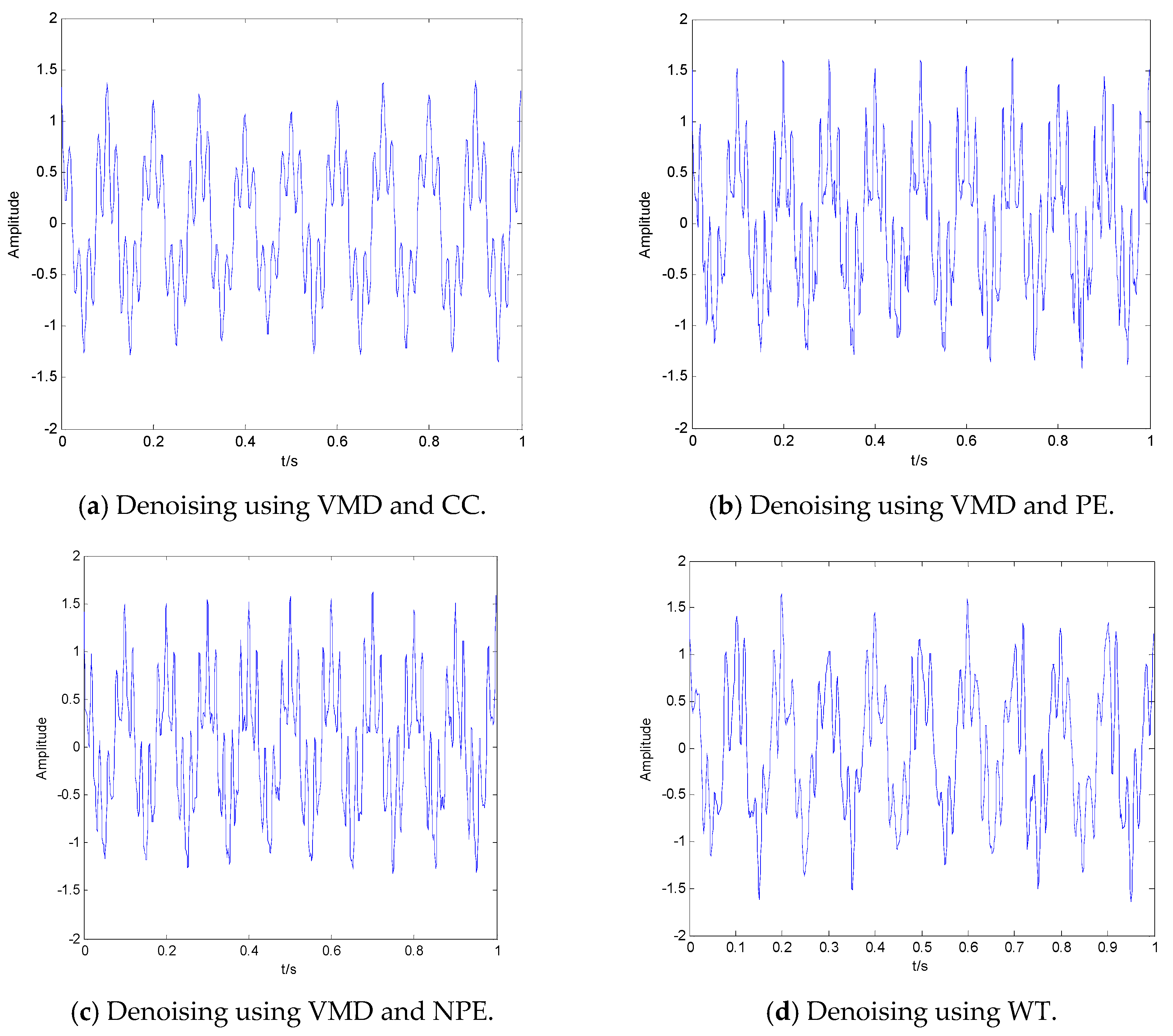
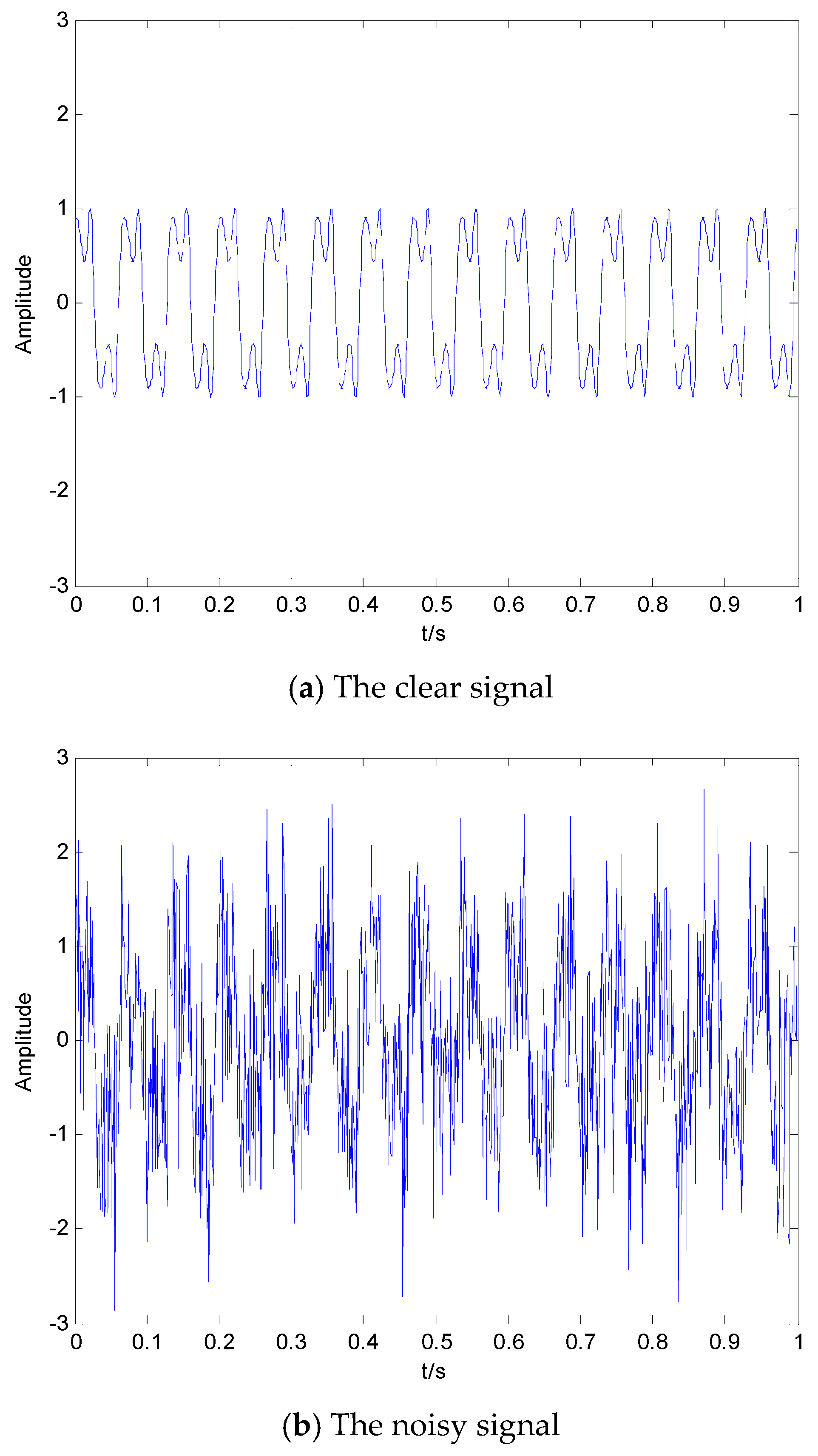
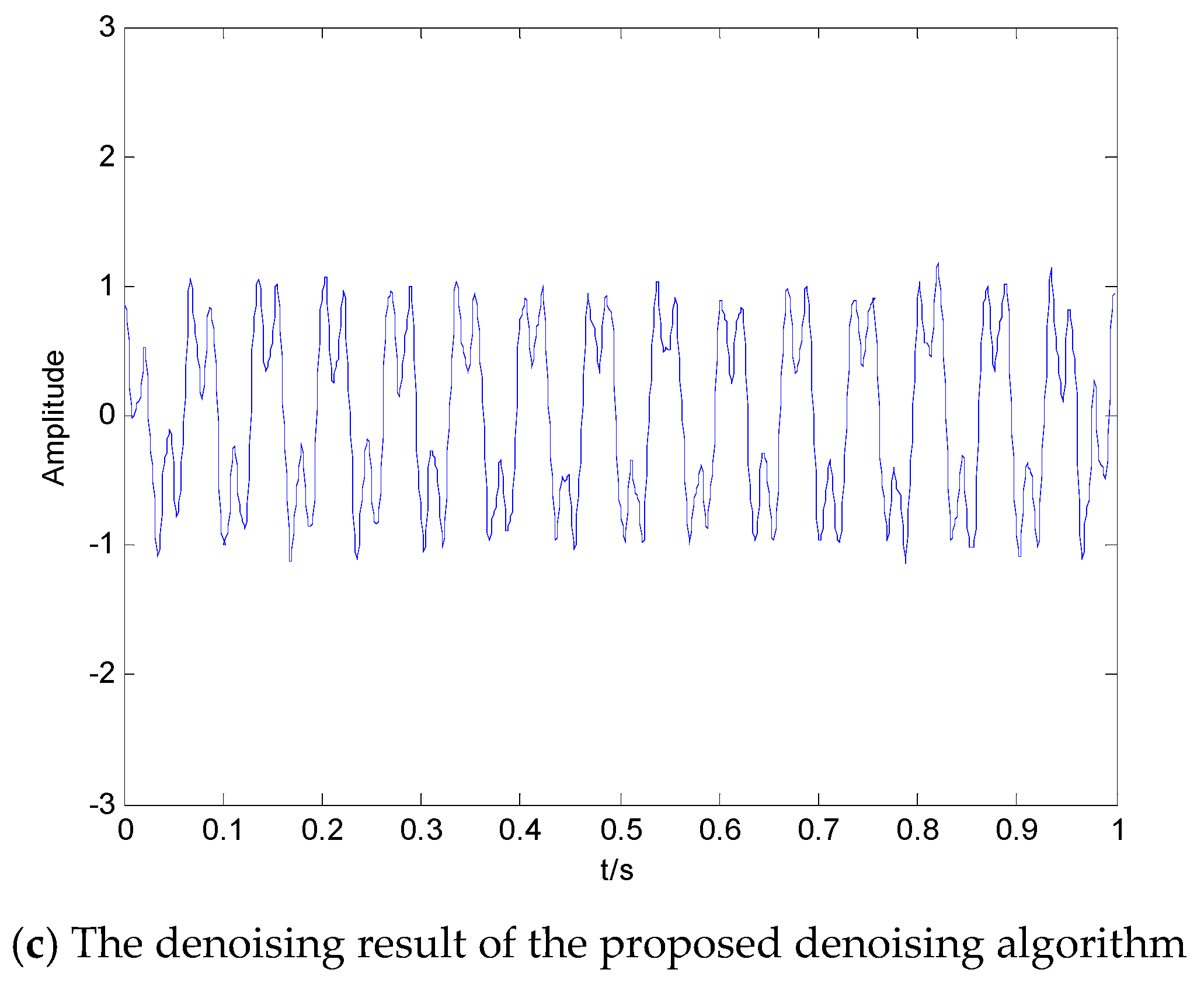
4. Denoising of Simulation Signal
4.1. Simulation Experiment 1
4.2. Simulation Experiment 2
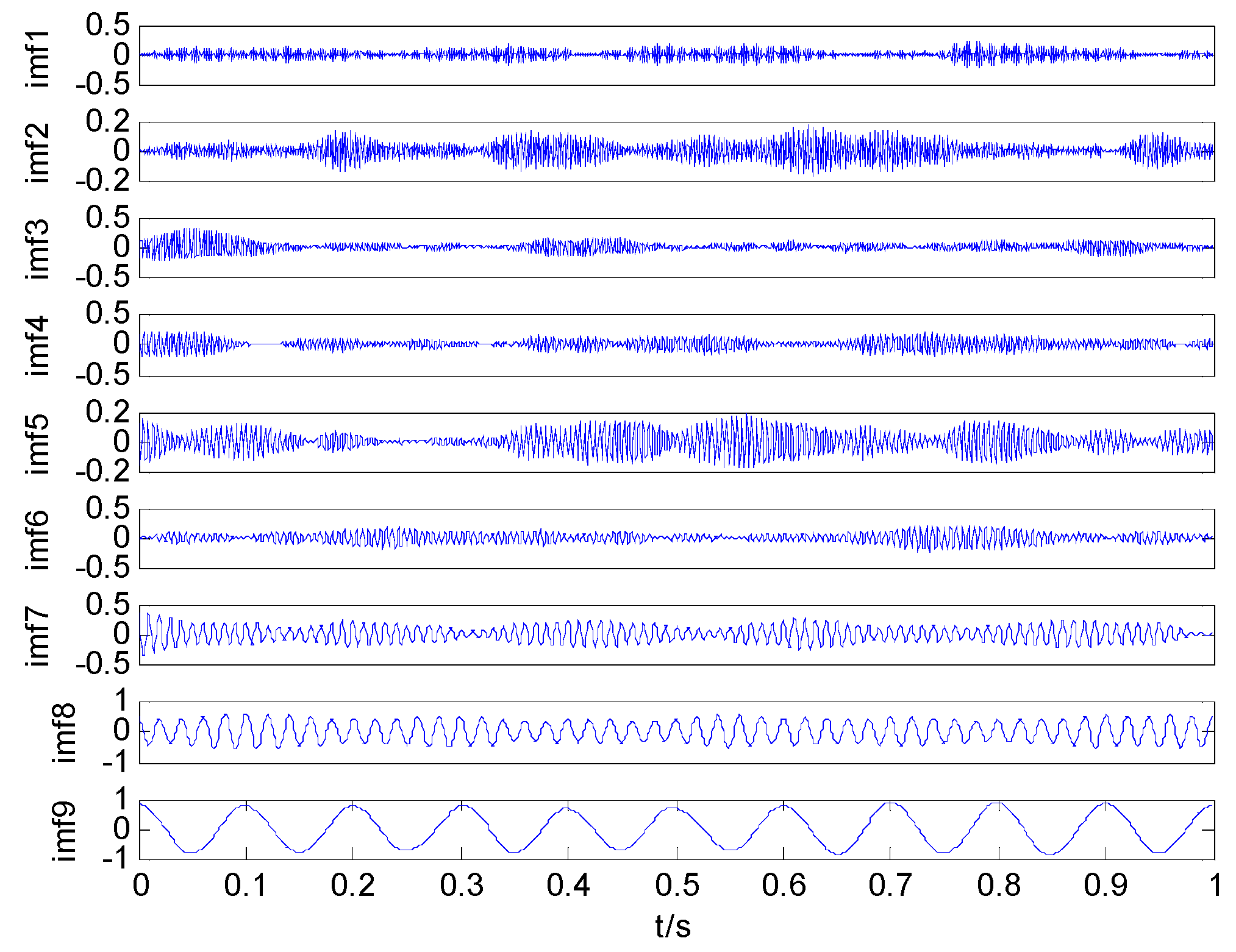
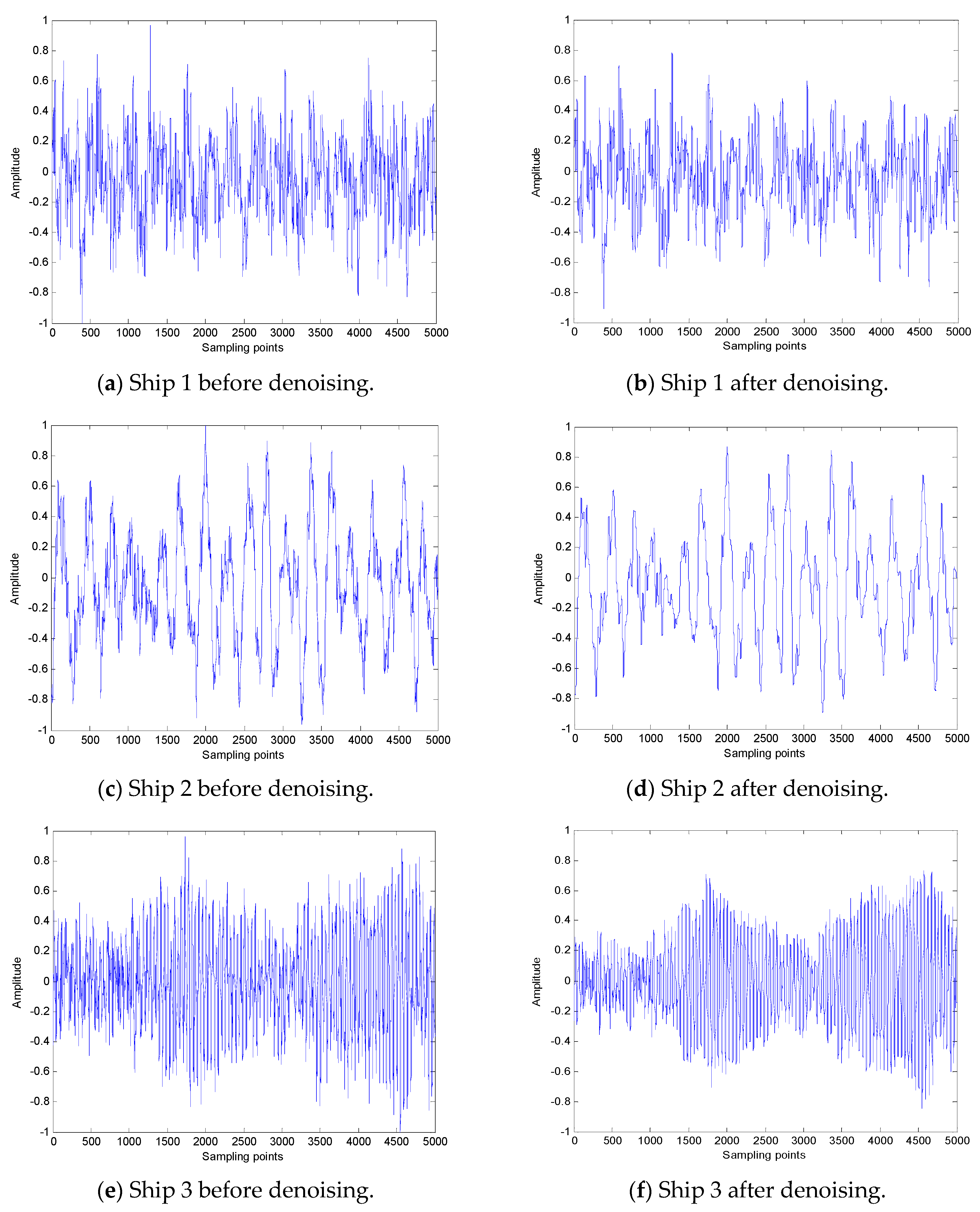
5. Feature Extraction of SN
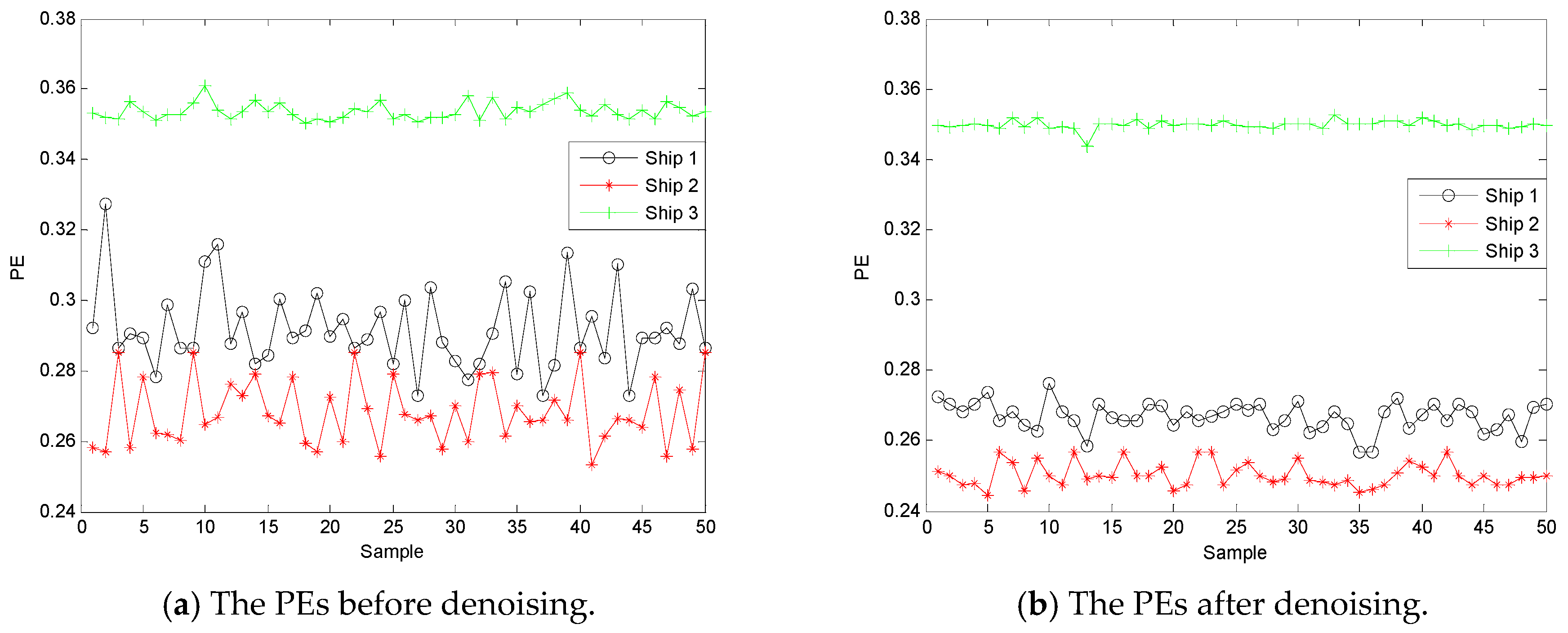
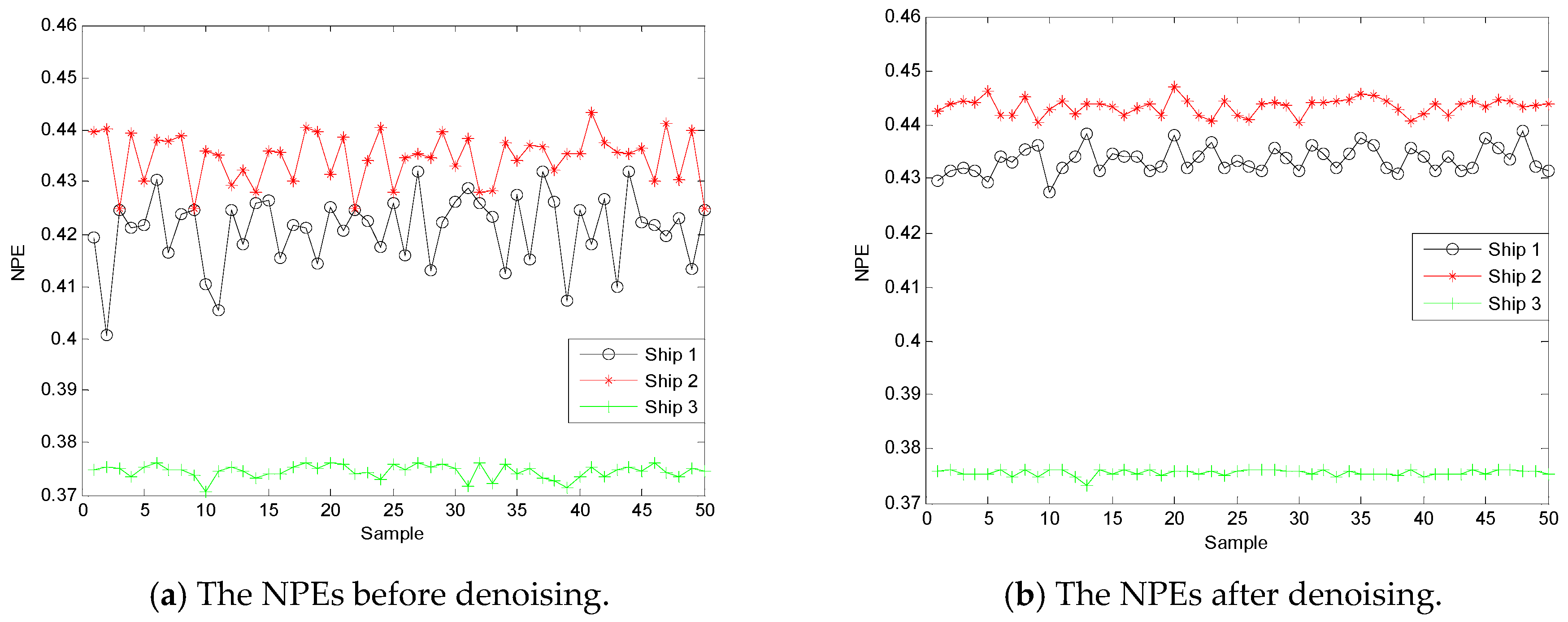
5.1. The Denoising of SN
5.2. The VMD of SN
5.3. Feature Extraction of SN
5.4. Classification of SN
6. Conclusions
- (1)
- NPE, a new kind of PE, is firstly applied to denoising and feature extraction of SN combined with VMD.
- (2)
- The simulation results show that the proposed denoising algorithm has better denoising performance than the existing algorithms and overcomes the problem of threshold selection.
- (3)
- The proposed denoising algorithm is used to denoise SN signal; it concluded that the features of PE and NPE after denoising are beneficial to classification and recognition for SN signal.
- (4)
- The proposed feature extraction algorithm is used to extract the feature of SN signal, the experimental results show that the feature of NPE has a higher recognition rate than that of PE in [11].
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Siddagangaiah, S.; Li, Y.; Guo, X.; Chen, X.; Zhang, Q.; Yang, K.; Yang, Y. A Complexity-Based Approach for the Detection of Weak Signals in Ocean Ambient Noise. Entropy 2016, 18, 101. [Google Scholar] [CrossRef]
- Wang, S.G.; Zeng, X.Y. Robust underwater noise targets classification using auditory inspired time-frequency analysis. Appl. Acoust. 2014, 78, 68–76. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.A.; Yen, N.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Wang, Y.; Marker, R. Filter bank property of variational mode decomposition and its applications. Signal Process. 2016, 120, 509–521. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Y.X.; Liu, F.Y.; Jiang, Z.S.; He, S.L.; Mo, Q.Y. Complex variational mode decomposition for signal processing applications. Mech. Syst. Signal Process. 2017, 86, 75–85. [Google Scholar] [CrossRef]
- Ping, X.; Yang, F.M.; Li, X.X.; Yong, Y.; Chen, X.L.; Zhang, L.T. Functional coupling analyses of electroencephalogram and electromyogram based on variational mode decomposition-transfer entropy. Acta Phys. Sin. 2016, 65, 118701. [Google Scholar]
- Tripathy, R.K.; Sharma, L.N.; Dandapat, S. Detection of shockable ventricular arrhythmia using variational mode decomposition. J. Med. Syst. 2016, 40, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.X.; Markert, R.; Xiang, J.W.; Zheng, W.G. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60–61, 243–251. [Google Scholar] [CrossRef]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. A Novel Feature Extraction Method for Ship-Radiated Noise Based on Variational Mode Decomposition and Multi-Scale Permutation Entropy. Entropy 2017, 19, 342. [Google Scholar]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M.; Zunino, L.; Rosso, O.A.; Papo, D. Permutation Entropy and Its Main Biomedical and Econophysics Applications: A Review. Entropy 2012, 14, 1553–1577. [Google Scholar] [CrossRef]
- Keller, K.; Mangold, T.; Stolz, I.; Werner, J. Permutation Entropy: New Ideas and Challenges. Entropy 2017, 19, 134. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Murguia, J.S.; Campos, C.E. Wavelet analysis of chaotic time series. Revista Mexicana De Fisica 2006, 52, 155–162. [Google Scholar]
- Liu, Y.X.; Yang, G.S.; Jia, Q. Adaptive Noise Reduction for Chaotic Signals Based on Dual-Lifting Wavelet Transform. Acta Electron. Sin. 2011, 39, 13–17. [Google Scholar]
- Zhang, L.; Bao, P.; Wu, X. Multiscale LMMSE-based image denoising with optimal wavelet selection. IEEE Trans. Circ. Syst. Video Technol. 2005, 15, 469–481. [Google Scholar] [CrossRef]
- Boudraa, A.O.; Cexus, J.C. EMD-Based Signal Filtering. IEEE Trans. Instrum. Meas. 2007, 56, 2196–2202. [Google Scholar] [CrossRef]
- Omitaomu, O.A.; Protopopescu, V.A.; Ganguly, A.R. Empirical Mode Decomposition Technique with Conditional Mutual Information for Denoising Operational Sensor Data. IEEE Sens. J. 2011, 11, 2565–2575. [Google Scholar] [CrossRef]
- Kopsinis, Y.; Mclaughlin, S. Development of EMD-Based Denoising Methods Inspired by Wavelet Thresholding. IEEE Trans. Signal Process. 2009, 57, 1351–1362. [Google Scholar] [CrossRef]
- Liu, J.; Lv, Y. Fault Diagnosis for Rolling Bearing Based on the Variational Mode Decomposition De-Noising. Mach. Des. Manuf. 2015, 10, 21–25. [Google Scholar]
- Li, X.; Li, C. Pretreatment and Wavelength Selection Method for Near-Infrared Spectra Signal Based on Improved CEEMDAN Energy Entropy and Permutation Entropy. Entropy 2017, 19, 380. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Yang, X.; Dong, C. A Fault Feature Extraction Method for Motor Bearing and Transmission Analysis. Symmetry 2017, 9, 60. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Ge, M.; Xiao, H.; Yu, X. Tensor Singular Spectrum Decomposition Algorithm Based on Permutation Entropy for Rolling Bearing Fault Diagnosis. Entropy 2017, 19, 139. [Google Scholar] [CrossRef]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale permutation entropy based on improved LMD and HMM for rolling bearing diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Li, Q.; Ji, X.; Liang, S.Y. Incipient Fault Feature Extraction for Rotating Machinery Based on Improved AR-Minimum Entropy Deconvolution Combined with Variational Mode Decomposition Approach. Entropy 2017, 19, 317. [Google Scholar] [CrossRef]
- Shang, H.; Lo, K.L.; Li, F. Partial Discharge Feature Extraction Based on Ensemble Empirical Mode Decomposition and Sample Entropy. Entropy 2017, 19, 439. [Google Scholar] [CrossRef]
- Li, Y.X.; Li, Y.A.; Chen, Z.; Chen, X. Feature extraction of ship-radiated noise based on permutation entropy of the intrinsic mode function with the highest energy. Entropy 2016, 18, 393. [Google Scholar] [CrossRef]
- Yang, H.; Li, Y.; Li, G. Energy analysis of ship-radiated noise based on ensemble empirical mode decomposition. J. Shock Vib. 2015, 34, 55–59. [Google Scholar]
- Li, Y.; Li, Y.; Chen, X. Ships’ radiated noise feature extraction based on EEMD. J. Shock Vib. 2017, 36, 114–119. [Google Scholar]
- Yi, C.; Lv, Y.; Dang, Z.; Xiao, H. A Novel Mechanical Fault Diagnosis Scheme Based on the Convex 1-D Second-Order Total Variation Denoising Algorithm. Appl. Sci. 2016, 6, 403. [Google Scholar] [CrossRef]

| Data Length | 100 Hz | 200 Hz | 500 Hz | 1000 Hz |
|---|---|---|---|---|
| 1000 | 0.445 | 0.4869 | 0.5937 | 0.7154 |
| 2000 | 0.4447 | 0.4866 | 0.5929 | 0.7139 |
| 3000 | 0.449 | 0.496 | 0.5834 | 0.6915 |
| Data Length | 100 Hz | 200 Hz | 500 Hz | 1000 Hz |
|---|---|---|---|---|
| 1000 | 0.3137 | 0.2948 | 0.2418 | 0.1678 |
| 2000 | 0.3137 | 0.2948 | 0.2419 | 0.1681 |
| 3000 | 0.3136 | 0.2945 | 0.2426 | 0.171 |
| Signal | PE | EMD | EEMD | VMD | |||
|---|---|---|---|---|---|---|---|
| S1 | 0.4213 | IMF3 | 0.4217 | IMF5 | 0.4291 | IMF3 | 0.4195 |
| S2 | 0.4483 | IMF2 | 0.449 | IMF4 | 0.4816 | IMF2 | 0.4469 |
| S3 | 0.4946 | IMF1 | 0.4962 | IMF3 | 0.4963 | IMF1 | 0.4936 |
| Signal | NPE | EMD | EEMD | VMD | |||
|---|---|---|---|---|---|---|---|
| S1 | 0.3235 | IMF3 | 0.3235 | IMF5 | 0.321 | IMF3 | 0.3235 |
| S2 | 0.3137 | IMF2 | 0.3137 | IMF4 | 0.3007 | IMF2 | 0.3137 |
| S3 | 0.2947 | IMF1 | 0.2944 | IMF3 | 0.2944 | IMF1 | 0.2946 |
| Parameter | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | IMF9 |
|---|---|---|---|---|---|---|---|---|---|
| CC | 0.1643 | 0.1425 | 0.1567 | 0.1633 | 0.147 | 0.1607 | 0.196 | 0.4075 | 0.6919 |
| Parameter | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | IMF9 |
|---|---|---|---|---|---|---|---|---|---|
| PE | 0.9296 | 0.9909 | 0.999 | 0.9764 | 0.9466 | 0.8782 | 0.7427 | 0.6054 | 0.4463 |
| Parameter | IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | IMF9 |
|---|---|---|---|---|---|---|---|---|---|
| NPE | 0.0458 | 0.0088 | 0.0017 | 0.0084 | 0.0383 | 0.0688 | 0.1642 | 0.2416 | 0.3146 |
| Parameter | Y | CC | PE | NPE | WT |
|---|---|---|---|---|---|
| SNR (db) | 2.7178 | 12.0307 | 14.7721 | 15.5929 | 8.3378 |
| RMSE | 0.56 | 0.1448 | 0.1453 | 0.1434 | 0.1671 |
| Denoising Algorithms | The Variance of Gaussian White Noise | ||
|---|---|---|---|
| 0.4 | 0.5 | 0.6 | |
| The Proposed Denoising Algorithm (db) | 12.58 | 11.69 | 11.25 |
| The Convex 1-D 2-Order Total Variation Algorithm (db) | 12.13 | 11.31 | 10.28 |
| The Convex 1-D 1-Order Total Variation Algorithm (db) | 4.69 | 3.31 | 2.17 |
| Wavelet Denoising Algorithm (db) | 10.28 | 9.20 | 8.31 |
| The noisy signal (db) | 0.9778 | –0.0494 | –0.8239 |
| Level | Ship 1 | Ship 2 | Ship 3 |
|---|---|---|---|
| The level of PIMF | 8 | 8 | 7 |
| Ship | Train | Test | Overall Correctness (%) | ||
|---|---|---|---|---|---|
| Number | Correctness (%) | Number | Correctness (%) | ||
| Ship 1 | 25 | 15 | 25 | 16 | 79.33 |
| Ship 2 | 25 | 0 | 25 | 0 | |
| Ship 3 | 25 | 0 | 25 | 0 | |
| Ship | Train | Test | Overall Correctness (%) | ||
|---|---|---|---|---|---|
| Number | Error | Number | Error | ||
| Ship 1 | 25 | 10 | 25 | 12 | 85.33 |
| Ship 2 | 25 | 0 | 25 | 0 | |
| Ship 3 | 25 | 0 | 25 | 0 | |
| Ship | Train | Test | Overall Correctness (%) | ||
|---|---|---|---|---|---|
| Number | Error | Number | Error | ||
| Ship 1 | 25 | 11 | 25 | 10 | 86 |
| Ship 2 | 25 | 0 | 25 | 0 | |
| Ship 3 | 25 | 0 | 25 | 0 | |
| Ship | Train | Test | Overall Correctness (%) | ||
|---|---|---|---|---|---|
| Number | Error | Number | Error | ||
| Ship 1 | 25 | 6 | 25 | 6 | 92 |
| Ship 2 | 25 | 0 | 25 | 0 | |
| Ship 3 | 25 | 0 | 25 | 0 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, Y.; Chen, X.; Yu, J. Denoising and Feature Extraction Algorithms Using NPE Combined with VMD and Their Applications in Ship-Radiated Noise. Symmetry 2017, 9, 256. https://doi.org/10.3390/sym9110256
Li Y, Li Y, Chen X, Yu J. Denoising and Feature Extraction Algorithms Using NPE Combined with VMD and Their Applications in Ship-Radiated Noise. Symmetry. 2017; 9(11):256. https://doi.org/10.3390/sym9110256
Chicago/Turabian StyleLi, Yuxing, Yaan Li, Xiao Chen, and Jing Yu. 2017. "Denoising and Feature Extraction Algorithms Using NPE Combined with VMD and Their Applications in Ship-Radiated Noise" Symmetry 9, no. 11: 256. https://doi.org/10.3390/sym9110256
APA StyleLi, Y., Li, Y., Chen, X., & Yu, J. (2017). Denoising and Feature Extraction Algorithms Using NPE Combined with VMD and Their Applications in Ship-Radiated Noise. Symmetry, 9(11), 256. https://doi.org/10.3390/sym9110256






