1. Introduction
In fuzzy logic, a fuzzy biconditional statement has the form of “
p if and only if
q”, where
p and
q are fuzzy statements. This is often abbreviated “
”. The corresponding biconditional logical connective denoted using a double-headed arrow (↔) is an operation of equivalence. As we know, join, meet, multiplication and implication are basic operations in several fuzzy logic systems, such as monoidal t-norm based logic (MTL) [
1], basic logic (BL) [
2] and their extensions product logic (
), Łukasiewicz logic (Ł) and Gödel logic (G). Then, the logical equivalence is a derived operation that is interpreted by the bi-implication
Based on this formula of equivalence, Georgescu [
3] investigated the similarity of fuzzy choice functions. Jin et al. [
4] and Dai et al. [
5] investigated the robustness of fuzzy inference methods, and Wang et al. [
6] and Duan et al. [
7] discussed fuzzy logic metric structures. In addition, Dyba and Novák [
8] developed a fuzzy equivalence based logic in which fuzzy equivalence is one of the basic connectives.
In the above-mentioned applications and logic systems, two fuzzy implications used in Formula (1) are consistent. However, there exist several fuzzy implications in one logic system. For example, Łukasiewicz implication and product implication are two of the basic connectives in Ł
[
9,
10], which is a complete fuzzy system joining
and Ł logic. Moreover, Gödel implication also is a derived operation in Ł
logic. This generates some special kinds of equivalence. For example, a fuzzy equivalence can be defined by setting the first operator in Formula (1) be Łukasiewicz implication and the latter one be product implication. In addition, this kind of equivalence-constructing method based on two or more different implications have been well studied in quantum logic (expressed as orthomodular lattice) [
11,
12,
13]. Enlightened by these, we can let the two implications in Formula (1) be different and then generalize a special class of equivalence. Since the new class of equivalence is asymmetrical, it is called asymmetric equivalence. Traditionally, equivalence corresponding to the biconditional logical connective is symmetric. Researchers naturally continue to study symmetric equivalence in the fuzzy logic systems. In our view, strategic use of the deliberate lack of symmetry is also a useful method to investigate and design fuzzy logic systems. In this paper, we show that the asymmetric equivalence has good expression of other operations (see
Section 3) and a straightforward application in constructions of quasi-metrics (see
Section 4).
The remainder of this paper is organized in the following way. In
Section 2, we review necessary concepts and two lemmas related to this paper. In
Section 3, we introduce the operations of asymmetric equivalence associated with two different fuzzy implications and give some of their properties. In
Section 4, we study the quasi-metrics induced by asymmetric equivalences. In
Section 5, we discuss the symmetrization of asymmetric equivalences. Conclusions are presented in
Section 6.
2. Preliminaries
In this section, we recall some basic concepts of t-norms and their residua. For more details, see [
2,
14,
15].
Definition 1. In reference [15], a function is called a t-norm if it is commutative, associative and nondecreasing in each place and for all . Definition 2. In reference [14], a function →: is called a fuzzy implication if it is non-increasing on the first component and non-decreasing on the second one, and , . A t-norm ∗ is said to be left-continuous if it is left-continuous in the first component. With any left-continuous t-norm ∗, the residual implication (R-implication)
induced by ∗ is the function defined as, for any
,
Obviously, the R-implication induced by the given left-continuous t-norm ∗ is a fuzzy implication.
We list several important left-continuous t-norms and their residua defined on [0, 1] as follows (see [
2]).
- (i)
Minimum t-norm and its residuum, Gödel implication
- (ii)
Łukasiewicz t-norm and its residuum, Łukasiewicz implication
- (iii)
Product t-norm and its residuum, product implication
For any two t-norms and , if holds for all , then we say that is weaker than or, equivalently, that is stronger than , denoted .
In [
15], it is shown that
Similarly, for any two implications and , if holds for all , then we say that is weaker than or, equivalently, that is stronger than , denoted .
In [
14], it is shown that
Definition 3. In reference [14], a function is called a fuzzy negation if it is decreasing and , . The negation operation ¬ associated with the given left-continuous t-norm ∗ is defined by
where
is an R-implication induced by ∗.
Lemma 1. In reference [2,15], let → be an R-implication induced by ∗, for any , the following properties hold - (i)
;
- (ii)
; furthermore, if ∗ is continuous, then ;
- (iii)
;
- (iv)
;
- (v)
.
Lemma 2. Let be real numbers,
- (i)
if and , then
- (ii)
if and , then
Proof. - (i)
Since and then
- (ii)
Since and then
☐
3. Asymmetric Equivalence Induced by R-Implication
Letting
be two fuzzy implications, we define an asymmetric equivalence operation as follows:
For an asymmetric equivalence
, its conjugate (or dual) asymmetric equivalence
is defined for all
by
Theorem 1. Let be two R-implications induced by two continuous t-norms. If asymmetric equivalence and its conjugate asymmetric equivalence are induced by and , then implications and negation operations can be expressed as follows:
- (i)
;
- (ii)
;
- (iii)
;
- (iv)
.
Proof. - (i)
Since t-norm
is continuous, from Lemma 1(ii),
, then using Lemma 1(i), we obtain
In addition, from Lemma 1(iii),
Hence,
- (ii)
can be proven similarly. Properties (iii) and (iv) are special cases of (i) and (ii), respectively, by setting .
☐
Theorem 1 shows the expression of the corresponding fuzzy implications and negations by asymmetric equivalence. Moreover, asymmetric equivalence has the following properties.
Theorem 2. For any , has the following properties
- (i)
Reflexivity: if and only if ;
- (ii)
Left monotonicity: ;
- (iii)
Right monotonicity: .
Proof. - (i)
follows immediately from Lemma 1 (iii) and (iv).
- (ii)
and (iii) follow immediately from the monotonicity of fuzzy implications.
☐
In classical and fuzzy logic [
1,
2,
10], (symmetric) equivalences also satisfy the above properties. In addition, left and right monotonicity properties are the same, as the equivalences are symmetric. What is important is that the asymmetric equivalence does not have to satisfy the symmetry property. The following examples are operations of the asymmetric equivalence induced by two different implication operators.
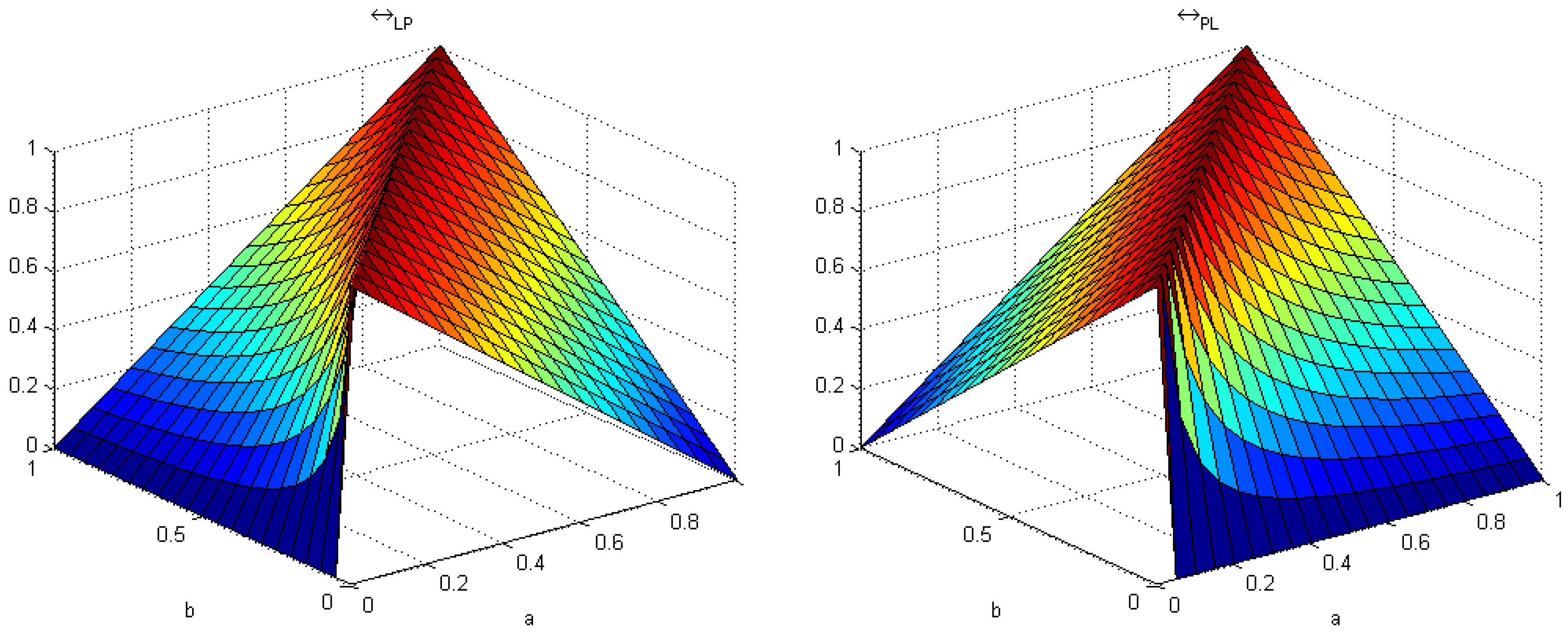
Example 1. If is Łukasiewicz implication, and is product implication, then is defined for all byand its conjugate asymmetric equivalence by As shown in Figure 1, , i.e., . For example, , but . However, from the concept of conjugate asymmetric equivalence, we have for any . Moreover, we havefor any . The above connectives and are Łukasiewicz negation and product negation, respectively. We also can obtain the expression of Gödel implication in the following way: , , (see Ł logic [9,10]). Example 2. If and are Łukasiewicz implication and Gödel implication, respectively, then is defined for all byand its conjugate asymmetric equivalence by Example 3. If and are Gödel implication and product implication, respectively, then is defined for all byand its conjugate asymmetric equivalence by 4. Quasi-Metrics Induced by Asymmetric Equivalences
Definition 4. In reference [16], a quasi-metric on a set U is a function having the following properties: for all - (i)
;
- (ii)
;
- (iii)
.
The axiom (iii) is the triangle inequality. The axiom (ii) is called the separation axiom. The pair
is called a quasi-metric space. If
d also satisfies the symmetry axiom,
, then
d is a metric and
is called a metric space. For more information about quasi-metric spaces, see [
16].
Theorem 3. Let be an asymmetric equivalence and be its conjugate asymmetric equivalence. If is a quasi-metric on , then also is a quasi-metric on , Proof. It is easy to prove that satisfies the axioms (i) and (ii). Now, we prove that satisfies the triangle inequality.
Since
d satisfies the triangle inequality, for any
,
From the concept of conjugate asymmetric equivalence in Formula (2), we obtain
Thus, . In consideration of the arbitrariness of , satisfies the triangle inequality. ☐
Theorem 4. Let be two continuous t-norms with with residuum and , respectively. If both and are stronger than Łukasiewicz t-norm , then is a quasi-metric on .
Proof. For any .
- (i)
Since , , then .
- (ii)
If , then we have , , from Lemma 1(iii), , thus . Similarly, we obtain .
- (iii)
Now, we prove that d satisfies the triangle inequality.
Since both
and
are stronger than Łukasiewicz t-norm
, hence
Then,
From Lemma 2(i), we obtain
i.e.,
Letting 2 minus both sides of the inequality, we then obtain immediately. ☐
The above theorem investigated the construction method of quasi-metrics based on asymmetric equivalences. A sufficient condition of
d to be a metric on
was proposed. In Ref. [
15],
. Consequently, the following corollary shows some examples of quasi-metrics induced by asymmetric equivalences.
Corollary 1. If , then is a quasi-metric on .
Proof. It can be proven from and Theorem 4. ☐
5. Symmetrization of Asymmetric Equivalences
In this section, we discuss the symmetrization of asymmetric equivalences.
Theorem 5. Let and be two R-implications induced by two left-continuous t-norms. If is a quasi-metric on , thenis a metric on . Proof. It is easy to prove that D satisfies the axioms (i) and (ii).
Since, for any
,
then
D satisfies the symmetry axiom.
Since
d satisfies the triangle inequality, for any
,
From Theorem 3,
also is a quasi-metric on
, for any
,
Since, for any
,
Moreover, we have and . Thus, Formula (33) is ☐
Theorem 6. Let and be two R-implications induced by two left-continuous t-norms. If is stronger than , thenwhere , . The above theorem investigated the method for symmetrization of asymmetric equivalences. Then, the following corollary shows some examples of symmetric equivalences using the symmetrisation methods above.
Proof. It can be proven from and Theorem 6. ☐
6. Conclusions
In this paper, we introduced the operation of asymmetric equivalence that is interpreted by two different fuzzy implications. We used this operation to express other connectives, such as implication and negation. The quasi-metric structures induced by asymmetric equivalence, , were investigated. We proposed a sufficient condition of d to be a quasi-metric on (see Theorem 4).
EQ-logic [
8] is an attempt to develop fuzzy logic by starting with equivalence (∼) instead of implication (→). Then, ∼ is one of the basic operations and → is a derived operation. Since ∼ has the symmetry, we can call it symmetric equivalence. Unlike symmetric equivalence, asymmetric equivalence can derive two different implication operations. As we know, Ł
logic starts with two different implication operations: Łukasiewicz implication and product implication. Thus, it is interesting to develop fuzzy logic by starting with asymmetric equivalence. Theorem 1 and Example 1 gave expressions of other operations by asymmetric equivalence. Indeed, simplification of formal systems is an important topic of fuzzy logic [
17,
18]. Can we give simplified formal systems for fuzzy logic that contain fewer axioms and rules by using asymmetric equivalence operation? It will be meaningful to discuss further.
In
Section 4, the constructions of quasi-metrics induced by asymmetric equivalences were investigated in detail. Quasi-metrics are common in control and theoretical computer science. Our results obtained in this section may be useful for some aspects of fuzzy theory and applications, such as upper and lower semicontinuity of fuzzy reasoning and stabilization of fuzzy control systems.
Acknowledgments
This project was supported by the Science and Technology Foundation of Guizhou Province, China (LKS (2013) 35 and the Guangxi University Science and Technology Research Project (Grant No. 2013YB193).
Author Contributions
Conceptualization, investigation and writing the original draft was done by Songsong Dai. Validation, formal analysis, review and editing was completed by Bo Hu, Lvqing Bi and Sizhao Li. Project administration and resources were provided by Bo Hu and Lvqing Bi. All authors have read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Esteva, F.; Godo, L. Monoidal t-norm based logic: Towards a logic for left-continuous t-norms. Fuzzy Sets Syst. 2001, 124, 271–288. [Google Scholar] [CrossRef]
- Hájek, P. Metamathematics of Fuzzy Logic; Kluwer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Georgescu, I. Similarity of fuzzy choice functions. Fuzzy Sets Syst. 2007, 158, 1314–1326. [Google Scholar] [CrossRef]
- Jin, J.; Li, Y.; Li, C. Robustness of fuzzy reasoning via logically equivalence measure. Inf. Sci. 2007, 177, 5103–5117. [Google Scholar] [CrossRef]
- Dai, S.; Pei, D.; Guo, D. Robustness analysis of full implication inference method. Int. J. Approx. Reason. 2013, 54, 653–666. [Google Scholar] [CrossRef]
- Wang, G.; Duan, J. Two types of fuzzy metric spaces suitable for fuzzy reasoning. Sci. China Inf. Sci. 2014, 44, 623–632. [Google Scholar]
- Duan, J.; Li, Y. Robustness analysis of logic metrics on F(X). Int. J. Approx. Reason. 2015, 61, 33–42. [Google Scholar] [CrossRef]
- Dyba, M.; Novák, V. EQ-logic: Non-commutative fuzzy logic based on fuzzy equality. Fuzzy Sets Syst. 2011, 172, 13–32. [Google Scholar] [CrossRef]
- Cintula, P. The LΠ and LΠ propositional and predicate logic. Fuzzy Sets Syst. 2001, 124, 289–302. [Google Scholar] [CrossRef]
- Esteva, F.; Godo, L.; Montagna, F. The LΠ and LΠ logic: Two complete fuzzy systems joining Łukasiewicz and product logic. Arch. Math. Logic 2001, 40, 39–67. [Google Scholar] [CrossRef]
- Megill, N.D.; Pavičićc, M. Equations, state, and lattices of infinite-dimensional hilbert spaces. Int. J. Theor. Phys. 2000, 39, 2337–2379. [Google Scholar] [CrossRef]
- Megill, N.D.; Pavičićc, M. Equivalences, identities, symmetric differences, and congruences in orthomodular lattices. Int. J. Theor. Phys. 2003, 42, 2797–2805. [Google Scholar] [CrossRef]
- Megill, N.D.; Pavičićc, M. Deduction, ordering, and operations in quantum logic. Found. Phys. 2002, 32, 357–378. [Google Scholar] [CrossRef]
- Baczyński, M.; Jayaram, B. Fuzzy Implications; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular Norms; Kluwer: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Fletcher, P.; Lindgren, W.F. Quasi-Uniform Spaces; Dekker: New York, NY, USA, 1982. [Google Scholar]
- Pei, D. Simplification and independence of axioms of fuzzy logic systems IMTL and NM. Fuzzy Sets Syst. 2005, 152, 303–320. [Google Scholar] [CrossRef]
- Wang, S.; Wu, J. Simplification of axiom systems of fuzzy logics NM and L∗. Fuzzy Syst. Math. 2006, 2, 18–22. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).