1. Introduction
The classical numerical system of real numbers is not efficient to express the vagueness, uncertainty and imprecision of real life. Fuzzy numbers and modal intervals are useful tools to get over those deficiencies.
The introduction of fuzzy sets by Zadeh [
1] was a novelty as they provide a graduation of the membership relation. When considering fuzzy numbers, the expression “to be an element of a set” makes no sense, whereas many expressions in which this membership relation is relativized do indeed make sense.
Fuzzy numbers can be considered from two different points of view: with their membership function or with their -cuts. The two ways of considering fuzzy numbers are equivalent, and, depending on the details we want to study, one can be better than the other. Among all types of fuzzy numbers, triangular and trapezoidal ones, whose names are derived from the shape obtained when their membership function is represented in the Cartesian plane, are the most commonly used. However, when we observe a fuzzy number from the point of view of its -cuts, what we are indeed getting is an intervalar point of view of the fuzzy number.
Fuzzy sets theory has evolved since its appearance in 1965. Nowadays, we can find applications of fuzzy sets in the most part of scientific disciplines, such as decision-making [
2,
3,
4], probability [
5], control theory [
6], medical sciences [
7], characterization of complex systems [
8], among others.
Modal intervals were introduced by Gardeñes [
9] and they implied a new treatment of interval analysis, providing new resources to solve problems and systematize their resolution, as well as to interpret correctly an intervalar calculus.
Fuzzy numbers and intervals are not far removed from each other. This is because a fuzzy number can be identified by its -cuts, which are intervals, and intervals can also be considered fuzzy numbers.
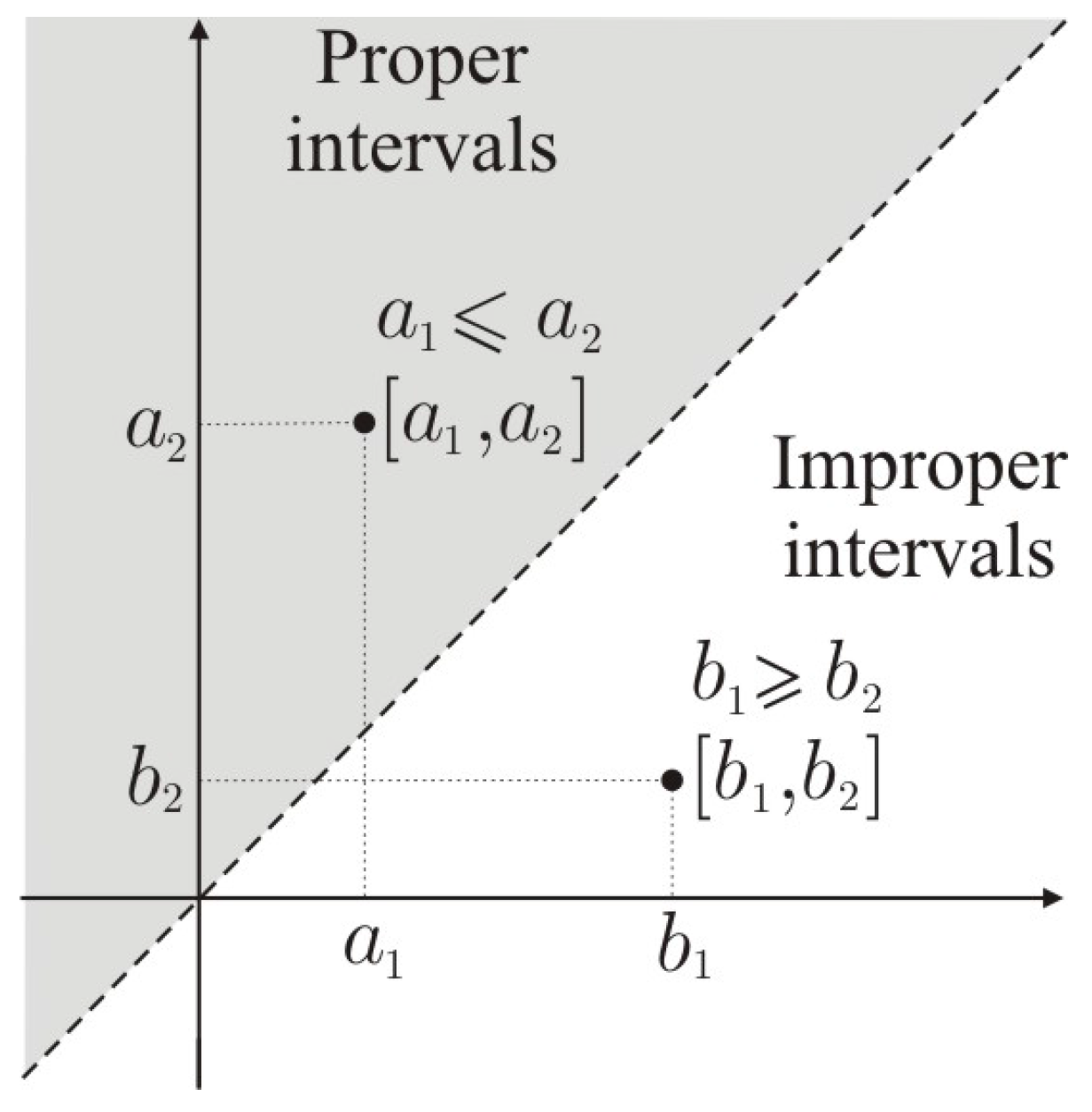
The set of intervals, in their classical point of view, has some deficiencies in the operative sense and also in the interpretation of the calculus. These deficiences remain in the set of fuzzy numbers. Modal intervals, which are an extension of classical intervals, solve some of the operative deficiencies (although the distributive property is neither satisfied), and they give, without ambiguity, the right semantical interpretations of the calculus. Moreover, modal intervals are a lattice with regard to the incluson relationship, while classical intervals are not.
The advantages that present modal intervals in front of classical intervals have motivated us to deepen the relationship between fuzzy sets theory and interval analysis theory using modal intervals. We are certain that, with this tool, we open new lines of research.
If the connection between intervals and fuzzy numbers is so obvious, why not use modal intervals when working with fuzzy numbers, especially if we take into account the fact that modal intervals are an efficient extension of classical intervals? This is what we want to do in this paper: we will focus on the modal interval point of view of the -cuts of trapezoidal fuzzy numbers.
Modal intervals have been used combined with fuzzy sets [
10,
11]. The study that we present is based on the set of trapezoidal fuzzy numbers, expanding this set using modal intervals. The new fuzzy numbers obtained by this extension are named
modal interval trapezoidal fuzzy numbers.
In this new set of modal interval trapezoidal fuzzy numbers (MITFNs), we study the inclusion relationship and we prove that this relationship provides a lattice structure. At the same time, in the set of MITFNs, we define the dual operator, inherited from the dual operator of modal intervals. The dual operator is an internal operator in the set of MITFNs, and it gives us the possibility to solve problems that, until now, had no solution in the set of traditional fuzzy numbers.
The rest of this paper is organized as follows. In
Section 2, some basic concepts related to modal intervals and to fuzzy numbers are given. In
Section 3, we provide the main definitions of this work and we also study the lattice structure of MITFNs with regard to the inclusion relation. In
Section 4, we define the modal extension of a real function, we study some properties of this extension and we present the semantic interpretability theorem.
Section 4 also includes an example to show some advantages when working on MITFNs instead of working with trapezoidal fuzzy numbers in their traditional sense. The conclusions and future research are described in
Section 5.
3. Modal Interval Trapezoidal Fuzzy Numbers
Definition 1. (Modal interval trapezoidal fuzzy number)
Given such that .
If, for any , we consider , then is an MITFN which we represent by
The modal interval that corresponds to is the support of A, and the modal interval that corresponds to is the core of Thus, .
We denote the set of MITFNs by extending the expression which denotes the set of modal intervals.
If
is an MITFN, we can define
as the trapezoidal fuzzy number (in its standard sense):
It is obvious that and
Definition 2. (Modality of an MITFN)
Given which is an MITFN, we define:
A is a proper-improper MITFN (MITFN) if is a proper interval and is an improper interval. We denote it by ;
A is an improper-proper MITFN (MITFN) if is an improper interval and is a proper interval. We denote it by ;
A is a proper-proper MITFN (MITFN) if both the support and core of A are proper intervals. We denote it by ;
A is an improper-improper MITFN (MITFN) if both the support and core of A are improper intervals. We denote it by .
In general, an MITFN
A will be:
where
is a trapezoidal fuzzy number in its traditional sense;
is the interval modality of the support of
that is, the modality of
; and
is the interval modality of the core of
that is, the modality of
.
If
A is an MITFN
, we will refer to
A as a proper trapezoidal fuzzy number; while if
A is an MITFN
, then we will refer to
A as an improper trapezoidal fuzzy number [
10]. Notice that if
A is an MITFN
, then
A is a trapezoidal fuzzy number in its classical sense.
Proposition 1. Given which is an MITFN or an MITFN, there exists a unique value such that the α-cut is a pointwise interval . Moreover, if then and if , then
Proof. If A is an MITFN
,
and
. As
.We must impose:
that is:
which has a unique solution as
Let
be the solution. If
, then
. If A is an MITFN
, then we have to prove that
is a proper interval. As
is a proper interval, then
. As
is an improper interval, then
as
and
but
is either
or
, so it follows that:
and then
so
which means that
is a proper interval.
If , then and the demonstration would be equivalent.
Similar reasoning holds for the case in which A is an MITFN. ☐
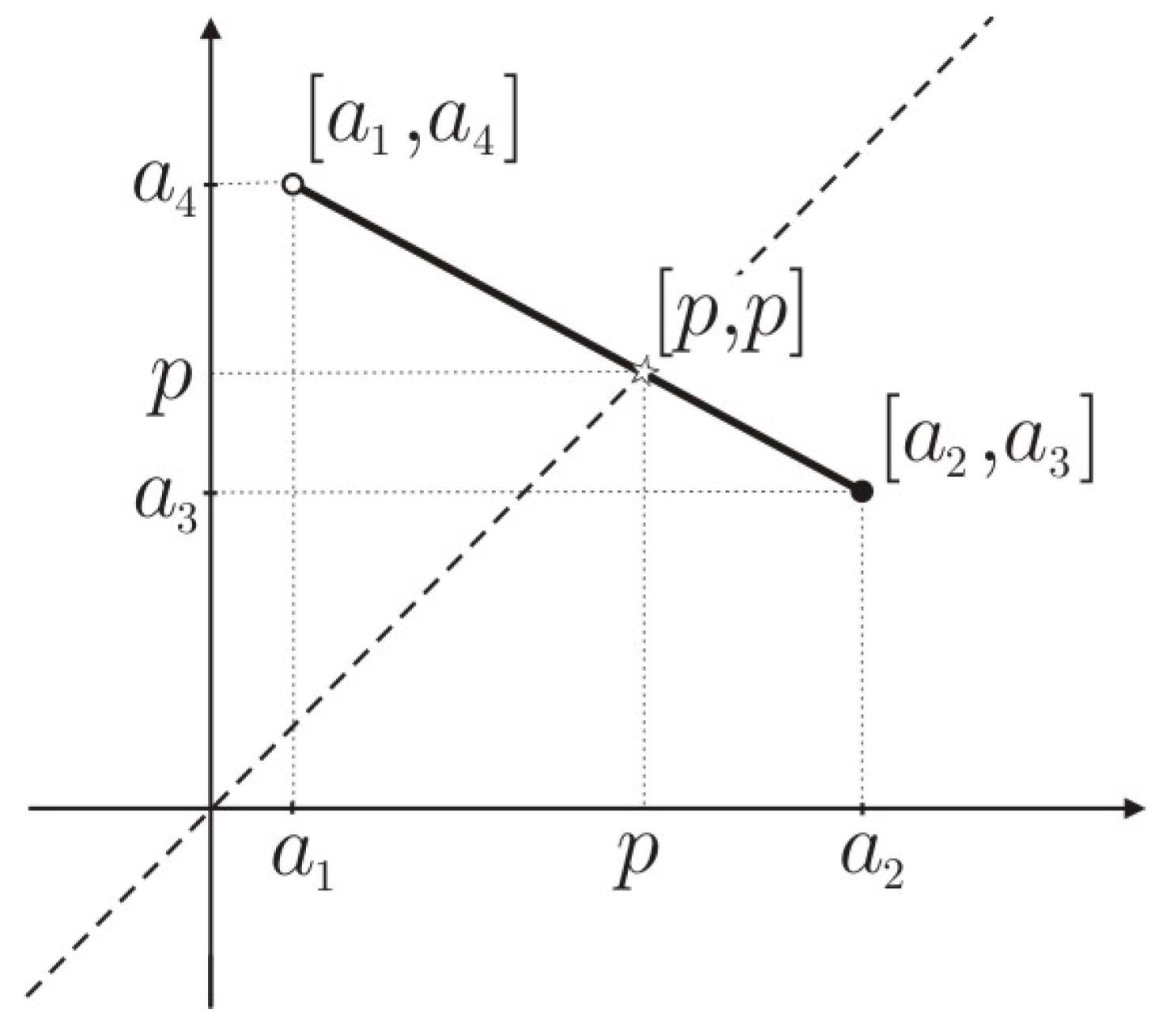
We will refer to
as the transition modality value of the MITFN,
A. The pointwise interval
is the transition
cut of
A, and its graphical representation is shown in Figure 4. If
is an MITFN
or an MITFN
and
is the transition
cut of
A, then
is a modal interval triangular non-normalized fuzzy number and its modality is the same as the interval modality of the support of
A, that is, if
A is an MITFN
, then
will be a proper triangular fuzzy number; while, if
A is an MITFN
, then
will be an improper triangular fuzzy number [
10].
Proposition 2. (Canonical characterization of an MITFN)
Let , then
A is an MITFN;
A is an MITFN;
A is an MITFN;
A is an MITFN.
Proof. If A is an MITFN, then is proper, that is, and is improper, that is,
As Definition 1 establishes , in this case, and which means , that is and
From , it follows that
If A is an MITFN, is an improper interval, that is, and is a proper interval, that is,
As it must be that and so it follows that , that is, and
From , it follows that
The proof of both case 3 and case 4 is trivial. ☐
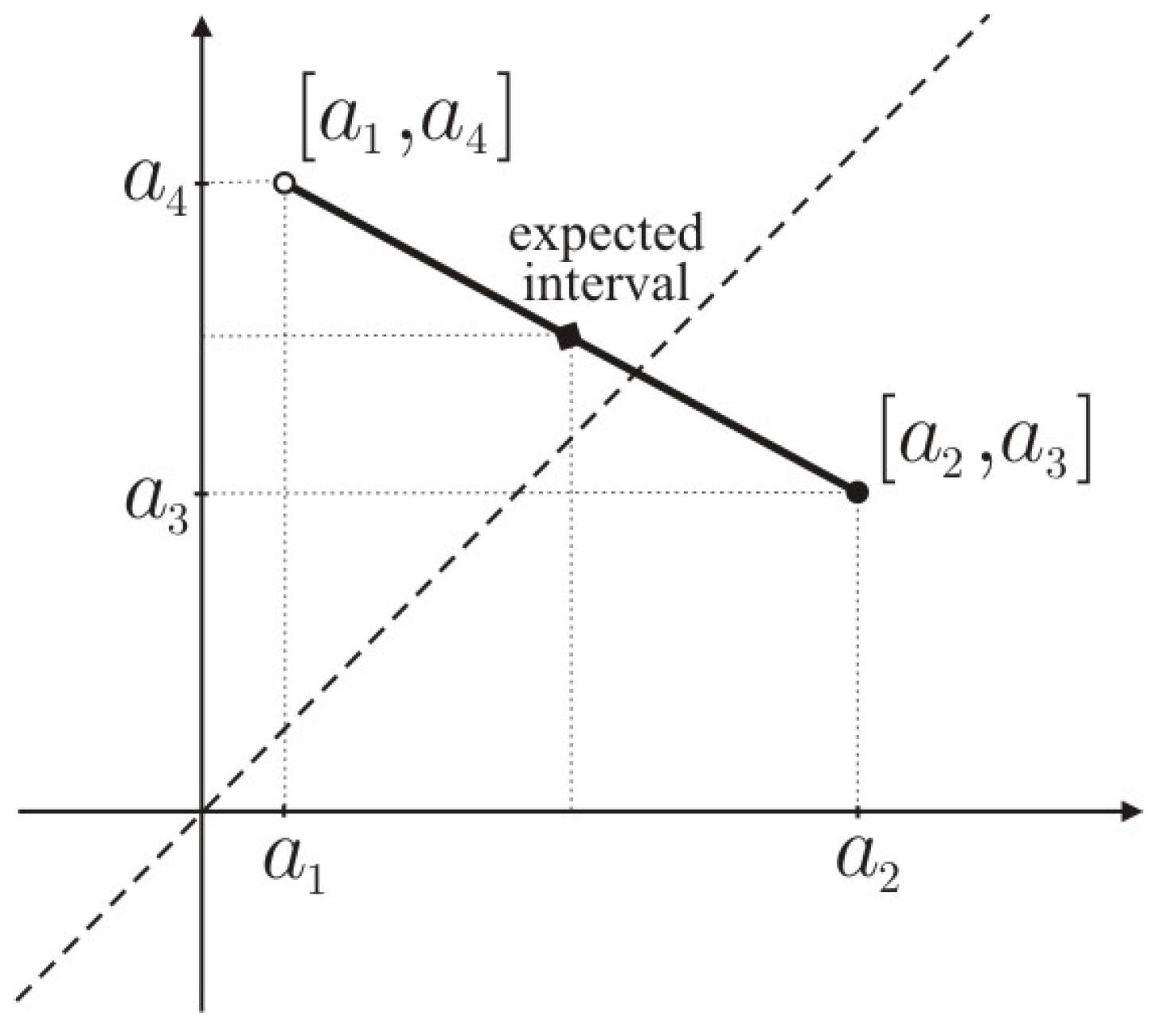
Proposition 3. (Interval modality of the expected interval)
If is an MITFN, then the interval modality of the expected interval is the same as the interval modality of the support of that is: Proof. The expected interval for a trapezoidal fuzzy number is
If both and are proper intervals, then and so and is a proper interval.
If both and are improper intervals, then and so and is an improper interval.
If is a proper interval and is an improper one, then and . As it holds that and Thus, is a proper interval.
If is an improper interval and is a proper interval, then and . As it holds that and Thus, is an improper interval.
☐
The graphical representation of the expected interval is shown in Figure 5.
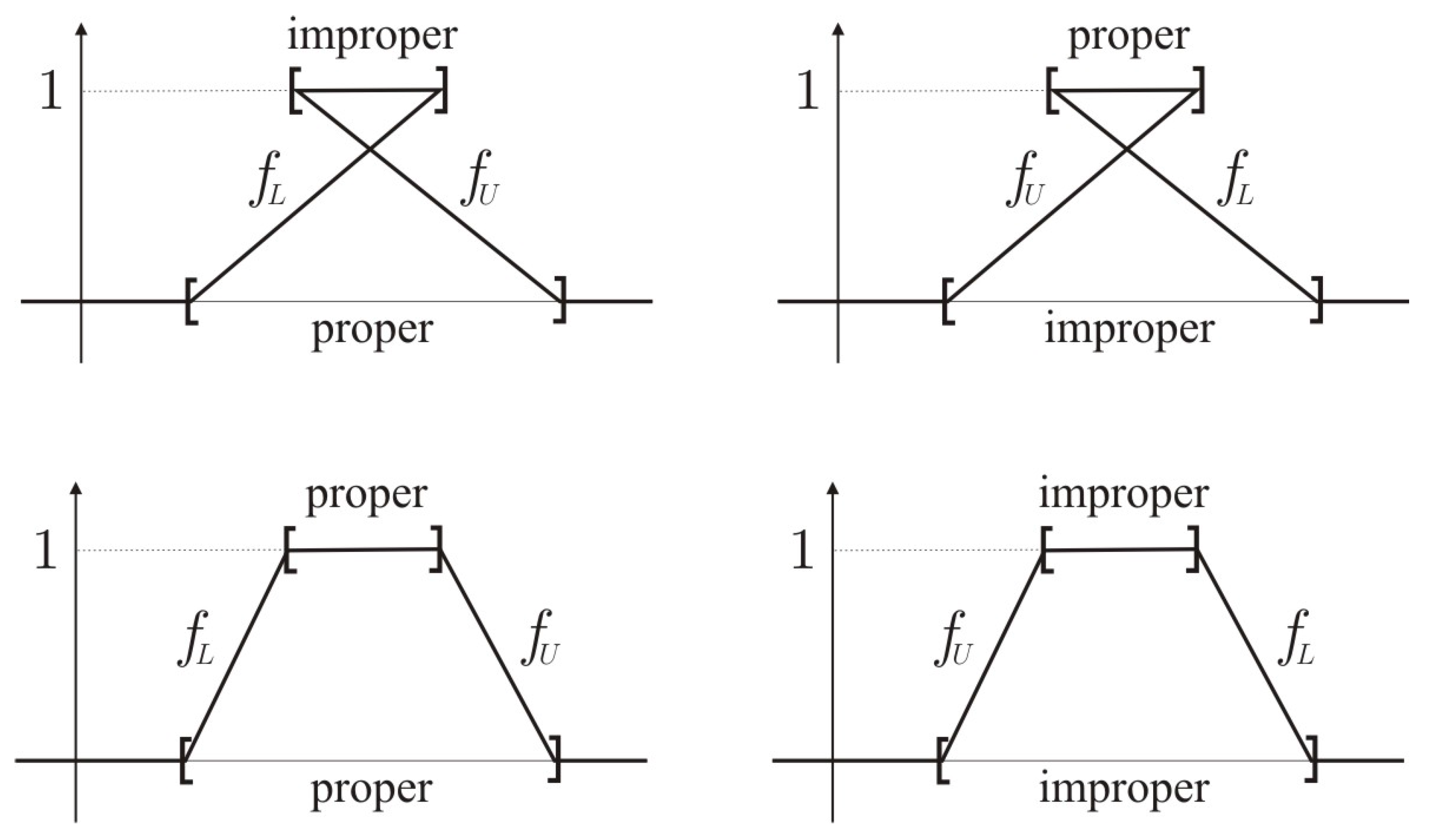
It is possible to consider the membership function of an MITFN, but it is difficult to represent improper intervals in the Cartesian plane. However, a graphical visualization of the functions
and
is provided in
Figure 2.
Next, we will define some operators on the set of MITFNs.
Dual operator. If
the dual operator on
A,
is defined as:
where
We will distinguish between the dual operator of an MITFN, which we will represent by and the dual operator of an interval, which we will represent by
If , then . Moreover, and, consequently, and , that is, if , then
It is obvious that if A is an MITFN, then is an MITFN; if A is an MITFN, then is an MITFN; if A is an MITFN, then is an MITFN; and if A is an MITFN, then is an MITFN.
Proper and improper operators. If
we define the proper operator on
as
and the improper operator on
A as
. Using the canonical notation, if
, then:
which coincides with
, and
Both
and
are quantified trapezoidal fuzzy numbers [
10].
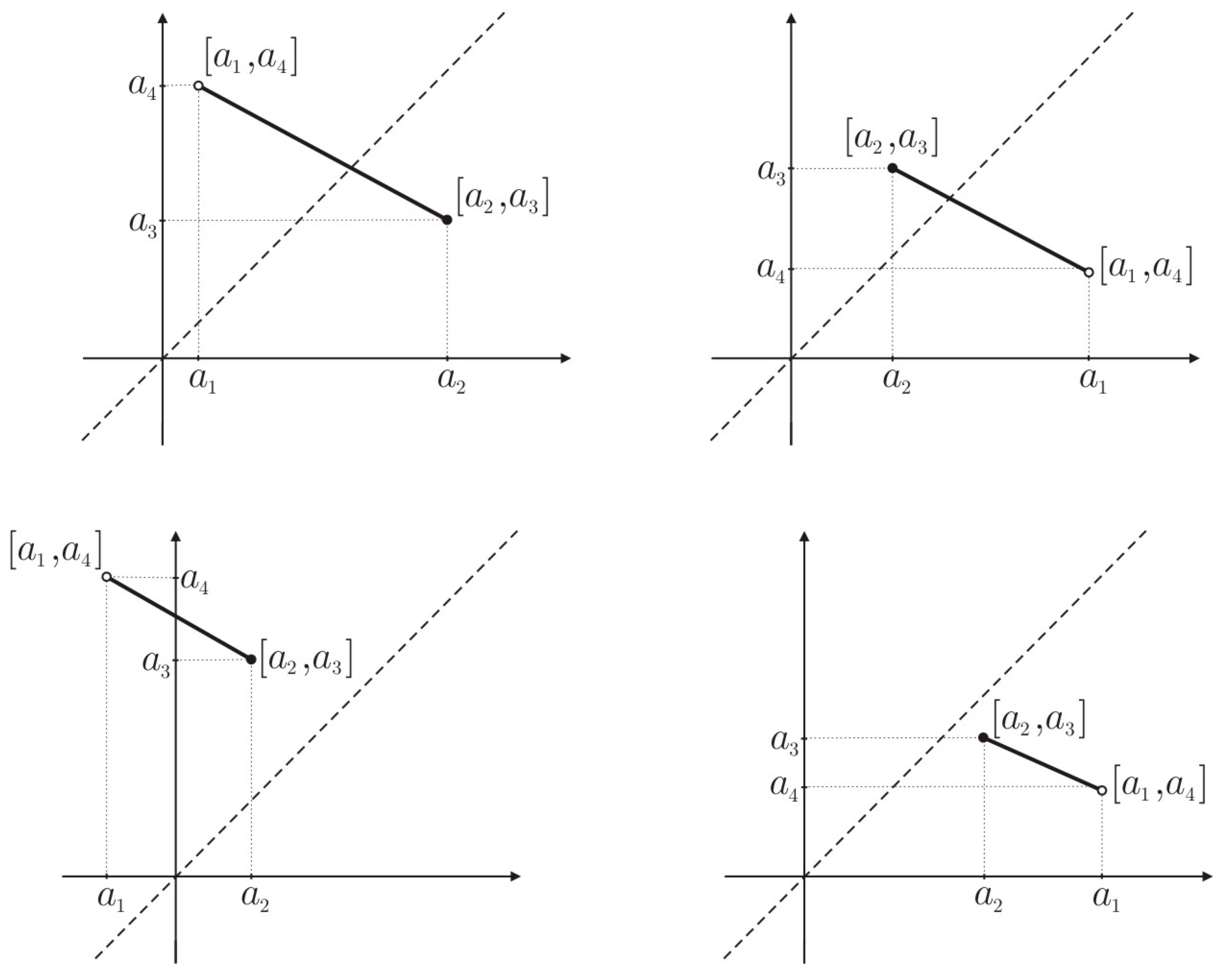
3.1. Graphical Representation of an MITFN in the Interval Plane
Trapezoidal fuzzy numbers, in their traditional sense, can be represented in Moore’s semiplane as decreasing segments in which the support is represented by ∘ and the core is represented by • [
30].
Moore’s semiplane is not detailed enough to represent an MITFN, and we must use the intervalar plane to represent them graphically. Using the same notation, that is, representing the support of an MITFN
A by ∘ and representing its core by •, the segment with ends ∘ and • represents the MITFN
A. The graphic representation of the four types of MITFNs, described in Definition 2, is shown in
Figure 3.
The following graphical representation
Figure 4 allows us to interpret the existence and uniqueness of the transition modality value easily, as well as the transition
-cut of an MITFN
or an MITFN
.
Figure 5 is the graphic representation of the expected interval of an MITFN.
3.2. The Lattice of MITFNs
We have defined the MITFN (Definition 1) using the
-cuts, and we will now define the inclusion relation between two MITFNs using the modal interval inclusion of the
-cuts, that is:
In the following proposition, we study the inclusion relation between two MITFNs A and B using the modalities of the support and the core of both A and B. There are 16 cases to be considered, but, using the properties of the modal interval duality, we can reduce those 16 cases to 10.
Lemma 1. Let , then: Proof. As , taking and , it follows that and .
and .
As and Moreover, as then
Thus, . ☐
Proposition 4. Given , where and it follows that:
If and , then
and ;
If and , then
;
If and , then
and ;
If and , then
;
If and , then
and ;
If and , then
and ;
If and , then
and ;
If and , then
and ;
If and , then
;
If and , then
and
Proof. As the inclusion of two modal intervals
conforms to the following (Gardeñes, [
9]):
By applying Lemma 1 to the -cuts and , which are modal intervals, we obtain the desired result. ☐
Notice that the following six cases:
, , ,
, , , are not treated in the above Proposition 4, as they are dual cases of some of those studied, and it is possible to apply the property
From the above Lemma 1, it is possible to express the inclusion relation of two MITFNs in terms of their coordinates. Thus, if
,
and
, then:
Definition 3. (Infimum and supremum)
Given ,
if and if there exists a such that and , then ;
if and if there exists a such that and , then
Proposition 5. Given , let us consider and , then Proof. We should consider the following four cases, depending on the modalities of and
and are proper intervals.
As and are proper intervals, then A and B are MITFNs. Thus, and so and as and are proper intervals, . If , then , and . Moreover, if conforms to and , then , and so and . That is, ; thus, Inf
is a proper interval and an improper interval.
As is a proper interval, is an improper interval and and it follows that We distinguish the following two cases according to the inclusion set of and :
- (a)
If , we can proceed as in the first case.
- (b)
If , then let us prove that corresponds to . Notice that, if , then ; thus, . It is obvious that . Moreover, and as . In a similar way, and . Therefore, and .
If conforms to and , then Notice that, as is an improper interval, will also be an improper interval and then .
We must prove that and, consequently, .
If is an improper interval, as , it follows that As , then .
If is a proper interval, as and , it follows that Using the inclusion , we obtain which contradicts the hypothesis .
is an improper interval and a proper one.
As is an improper interval, is a proper interval and , and it follows that ; thus, the demonstration follows as in the first case.
and are improper intervals.
- (a)
If , then . Let us prove that corresponds to . Notice that if , then and thus . It is obvious that . Moreover, and as . In a similar way, and . Therefore, and .
If conforms to and , then and . This implies that and are improper intervals.
Moreover, as , then due to the modality of and it will be the case that and as , it follows that . Thus,
- (b)
If , then . Let us prove that corresponds to . If , then , and . Moreover, if conforms to and , then , and so and . That is, ; thus, Inf
- (c)
If or , then let us prove that corresponds to . Notice that as and are improper intervals, thus and obviously and .
If conforms to and , then and . As and are both improper, and will also be improper intervals.
Moreover, as , then due to the modality of and , it will be the case that and as , it follows that and consequently . That is , thus .
☐
Proposition 6. Given , let us consider and , then: Proof. Applying modal interval properties relating duality and meet–join operators [
24], that is:
and
Let
be
. As
, then
In the same way, if , then
When we calculate Inf we should consider:
If
, then
and so:
If
, then
☐
4. Interpretability of the Calculations
Definition 4. (Modal extension of a real function)
Let be a real continuous function. We represent the modal interval trapezoidal fuzzy extension associated with f by and we define it over using the interval extension (see Sainz [
24,
31]
) over the cuts of the MITFNs As the
-cuts are modal intervals, we can express this modal interval trapezoidal fuzzy extension using the meet and join operators, and splitting the components of
into the proper ones:
and the improper ones:
which is equivalent to
Proposition 7. (Inclusivity of the modal extension)
If is the modal extension of a real continuous function , given such that , then: Proof. We can express the inclusion of MITFNs by using the inclusion of the
-cuts, that is
, as the interval extension
is inclusive ([
24] [Theorem 3.2.4]).
☐
Given a rational real continuous function
f, if
are the
-cuts of the classical trapezoidal fuzzy numbers
, then
, and the interval extension that we represent by
associated with
f can be interpreted as:
or also as:
because
f is a continuous function and the value
corresponds to:
In most of the cases,
the exact values
that define the fuzzy number
are difficult to calculate. This is the reason why we often replace every rational operator in the function
f by its corresponding intervalar operator. The result obtained with this replacement is not the same interval
, but an interval
which conforms to:
However, the only valid semantic application to this last calculus will be the interpretation given in Equation (
1)
and the semantic expressed in Equation (
2) will not be applicable to this last calculus
.
Theorem 1. (Interpretability theorem)
Let be the ∗-extension of a real continuous function , and let be a vector of MITFNs sorted by their modality, that is:where If conforms to and we consider and the transition modality values of the MITFNs and Z, respectively, then, given it holds that:
such that:where are the α-cuts of whose interval modality is proper, are the α-cuts of whose interval modality is improper, are the α-cuts of whose interval modality is proper and are the α-cuts of whose interval modality is improper, and if or if . Moreover,although the elements within these sets are not ordered in the same way. Proof. The interval semantic theorem (Sainz [
24]), states that if
is the ∗-semantic extension of a real function
f, and
X is a vector of modal intervals expressed as
where
are the proper components of
X and
are the improper components of
X, if
is such that
, then:
We will now apply this semantic theorem to the
-cuts of:
The modality of the -cuts is always proper and the modality of the -cuts is always improper.
Let
be the set
. Above this set
we define inductively
Then, given , there will exist such that For this value, we must consider the modality of the -cuts and , as some of these modalities have changed with regard to the modalities of the zero-cuts .
Thus, for this given , there will be in which the interval modality of their -cuts is proper, and there will be in which the interval modality of their -cuts is improper. At the same time, there will exist in which the interval modality of their -cuts is proper and in which the interval modality of their -cuts is improper. The interval modality of will be if and if . ☐
Corollary 1. Under the above conditions of Theorem 1, if , then:
such that Corollary 2. Under the above conditions of Theorem 1, if , then:
such that Definition 5. Let ⊙
be a binary real rational operator. Given : the extension of the operator ⊙
above the MITFNs A and B is represented by ⊗
and defined using the α-cuts of A and B as Definition 6. Let ⊙ be a binary real rational operator, and ⊗ its extension above the MITFNs. Given if C is an MITFN, C is said to be interpretability compatible with the exact value if .
Often, the result of calculating will not be an MITFN. There are some situations that clearly reflect this, such as the multiplication, the quotient and rounding results. This situation is well known when working with trapezoidal fuzzy numbers, in which not all the rational operators are internal operators. To preserve the inclusion expressed in the above Theorem 1, that is, , we will have to find such that .
The extension of a rational real operator ⊙ above two MITFNs A and B is always interpretability compatible with the calculation of as the intervalar extension above the -cuts and is always inclusive.
Sometimes, rounding results do not constitute a very important subject. However, if we center our study on the interpretability of the calculus, then when we evaluate we must find a modal trapezoidal fuzzy number C such that C is interpretability compatible with .
We have just mentioned Equation (
3) above, the difficulty of calculating the exact value
of a rational real function
f. The modal extension
of the real continuous function
f is even more difficult to evaluate. Thus, instead of calculating the modal extension
, we will evaluate a new function obtained by replacing every rational real operator in
f by its corresponding operator above MITFNs. Since, on many occasions, the result of calculating these rational operators will not be an MITFN, this result will be transformed into an MITFN that is interpretability compatible with the exact result.
What we have laid out leads us to evaluate an MITFN Z that contains the exact value. Of course, this is too general and we should impose some other conditions.
Many methods to convert a non-trapezoidal fuzzy number to a trapezoidal one have been studied. Many researches have studied how to find a fuzzy number that is the nearest to a non-trapezoidal fuzzy number, which is related to the approximation of fuzzy numbers under different points of view.
Abbasbandy and Asady [
32] used the metric distance between two fuzzy numbers to introduce a trapezoidal approximation. Other research such as Grzegorzewski and Mrówka [
33], and Grzegorzewski [
34] and Yeh [
35,
36] studied a nearest trapezoidal approximation preserving the expected interval.
Veerani et al. [
37] proposed a method to convert any fuzzy number to the nearest symmetric trapezoidal fuzzy number approximation also preserving the expected interval.
Preserving ambiguity, value and width, Ban, Coroianu and Khastan [
38] developed a general method to study the L-R approximations of fuzzy numbers. In addition, some methods for ranking fuzzy numbers using distances have been developed [
39,
40], but none of those trapezoidal approximations is useful to us because, although they preserve certain properties, they do not impose preservation of inclusivity and so they are not valid for semantic interpretations.
When possible, we will apply the optimal external inclusion introduced by Wagen [
41], although, in some special cases, it may be necessary to add some further conditions, referring to the inclusion of the core of the result.
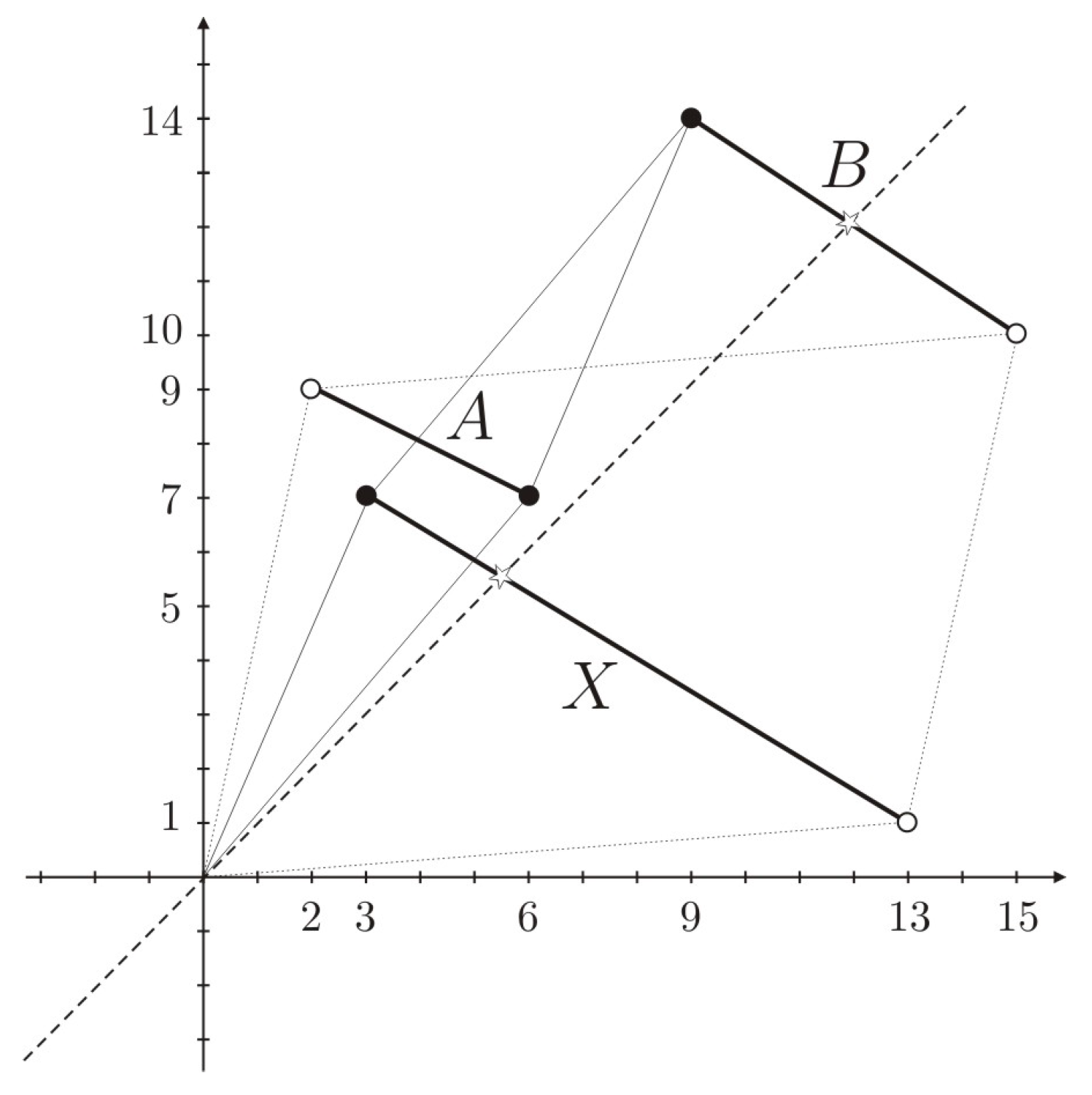
Example 1. The fuzzy trapezoidal equation whose solution is does not always have a solution in the classical sense. However, using MITFNs, many of these equations not only have a solution, but the solution can be semantically interpreted as well.
Let us take the MITFN
and
. Both
A and
B are proper trapezoidal fuzzy numbers, that is, trapezoidal fuzzy numbers in the classical sense. The solution of the equation
is
However, is an MITFN whose transition modality value is
Thus, the interpretation is:
Next, let us consider the fuzzy equation
, where
A is the MITFN
,
and
B is the MITFN
,
The solution for
X is:
which is an MITFN
(see
Figure 6). The transition modality value for
X is
and the transition modality value for
B is
; thus, the interpretation of the calculus
is:
5. Conclusions
In this paper, we have used the lattice structure of modal intervals to develop the lattice completion of trapezoidal fuzzy numbers, with regard to the inclusion relation. We have named the set obtained with this completion MITFNs. The elements of this new set have been defined allowing that their -cuts can be modal intervals and also allowing that the support modality and the core modality are not the same. This reticular completion has not simply been left in a theoretical study of the inclusion relationship between modal trapezoidal fuzzy numbers, but the calculation of the extensions of real continuous functions has also been addressed.
Moreover, we have not simply focused on the calculation of the real extensions on MITFNs, but we have also used the semantic theorem of modal interval analysis so as to interpret the calculus to the -cuts of the extensions. We are certain that knowing the meaning of a calculation is even more important than the calculation itself.
With the study presented in this paper, we have provided a new tool for fuzzy numbers. We have introduced an extension of traditional trapezoidal fuzzy numbers and we have solved a problem that had no solution in the set of traditional trapezoidal fuzzy numbers, while also providing the semantic interpretation of the result obtained.
Our future lines of research are twofold; on the one hand, further theoretical research will be conducted, and, on the other, some practical applications of our theoretical studies will be developed.
Regarding theoretical studies, we believe it is interesting to look for and implement algorithms that allow us to obtain a good inclusive approach to the semantic extension . Thus, we would reduce the typical enlargement of the interval results. This research should be supplemented with the study of optimality in the calculus of rational functions, understanding that optimality, in the sense of studying when a result obtained by replacing each of the rational operators in the real function f by the corresponding fuzzy operator, is the best possible result with regard to the inclusion relationship.
From an applied perspective, the application of MITFNs to the field of MultiCriteria Decision Making (MCDM) is also worth exploring, as there are many methods related to multicriteria analysis that use trapezoidal fuzzy numbers that could be extended to the MITFNs. Among these methods, we will pay special attention to the following: the CODAS method (Combinative Distance-based Assessment) [
42], QUALIFLEX method (QUALItative FLEXible) [
43], ELECTRE method (ELimination Et Choix Traduisant la REalité) [
44,
45], VIKOR method (VlseKriterijumska Optimizacija I Kompromisno Resenje) [
46,
47], MULTIMOORA method (Multiple Objective Optimization on the basis of Ratio Analysis) [
48], EAMRIT Method (Evaluation by an Area-based Method of Ranking Interval Type-2 Fuzzy sets) [
49], TOPSIS (Technique for Order of Preference by Similarity to Ideal Solution [
50], EDAS Method (Evaluation based on Distance from Average Solution) [
51], AFRAW Method (Assessment-based on Fuzzy Ranking and Aggregated Weights) [
52], TEDE Method (Total Effective Dose Equivalent) [
53], and WASPAS (Weighted Aggregated Sum Product ASsessment) [
54]. The extension of these methods to the field of MITFNs can provide new tools, from the point of view of both the calculations, as well as from the interpretative point of view.