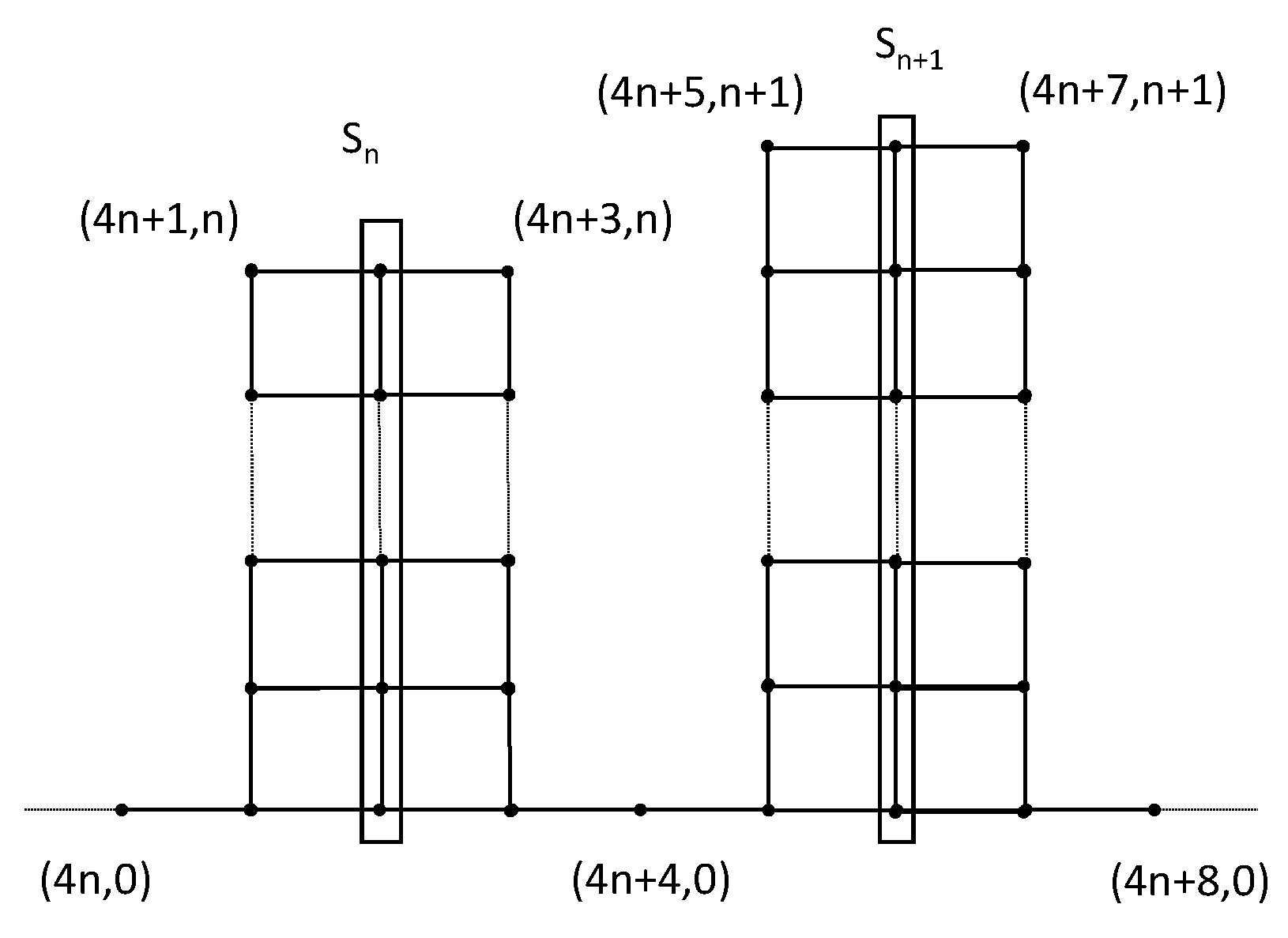1. Introduction
M. Gromov defined in [
1] his notion of hyperbolicity for the study of finitely-generated groups. Since then, Gromov hyperbolic spaces have been studied from a geometric point of view providing a wide variety of results and making them an important subclass of metric spaces [
2,
3,
4,
5,
6]. In particular, Gromov hyperbolicity is an important property to be studied in graphs [
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25]. Gromov hyperbolicity has found also interesting applications in phylogenetics [
26,
27], complex networks [
28,
29,
30,
31], virus propagation and secure transmission of information [
32,
33] and congestion in hyperbolic networks [
34].
Given a metric space and two points , a geodesic from x to y is an isometry, , from a closed interval of the real line to X such that and . We will make no distinction between the geodesic and its image. X is a geodesic metric space if for every pair of points , there is some geodesic joining x to y. Although geodesics need not be unique, for convenience, will denote any such geodesic.
Herein, we consider the graphs always endowed with the usual length metric where every edge has length one. Thus, for any pair of points in G, the distance between them will be the length of the shortest path in G joining them. Notice that we are considering also the interior points of the edges as points in G. Therefore, G with the length metric is a geodesic metric space. Let us also assume that the graphs are connected.
Gromov hyperbolicity, in the context of geodesic metric spaces, can be characterized by the Rips condition as follows. If
X is a geodesic metric space and
, the union of three geodesics
,
and
is called a geodesic triangle and will be denoted by
. If two vertices are identical then it is called a bigon. A triangle
T is
-thin if any side of
T is contained in the
-neighborhood of the union of the two other sides. A geodesic metric space
X is
-hyperbolic if every geodesic triangle is
-thin. By
, we denote the sharp hyperbolicity constant of
X, this is,
A metric space
X is hyperbolic if it is
-hyperbolic for some
. There exist other equivalent definitions of Gromov hyperbolicity. See [
4].
A graph
G is said to be chordal if every induced cycle has exactly three edges. Chordal graphs form an important subclass of perfect graphs, and as is pointed out in [
35] (see the further references therein), they have applications in scheduling, Gaussian elimination on sparse matrices and relational database systems. Furthermore, chordal graphs have applications in computer science; see [
36]. In [
37], it is proved that chordal graphs are hyperbolic. Wu and Zhang extended this result in [
38] proving that
k-chordal graphs are hyperbolic where a graph is
k-chordal if induced cycles have at most
k edges. In [
39], the authors defined some more natural generalizations of being chordal as being
-edge-chordal and
-path-chordal proving that
-edge-chordal graphs are hyperbolic and that hyperbolic graphs are
-path-chordal. In [
40], we continue this work and define being
-densely
-path-chordal and
-densely
k-path-chordal. In [
39,
40], edges were allowed to have any finite length, but in this work, we assume that all edges have length one. Therefore, the distinction between edge and path is unnecessary, and these properties are referred as
-chordal and
-densely
k-chordal. The main results in [
40] (with this simplified notation) state that:
and:
We also proved that the converse is false for all these implications, giving counterexamples, and that a graph is hyperbolic if and only if certain chordality property is satisfied on the triangles.
Herein, we continue this study analyzing some relations between these properties and vertex separators. There are some well-known relations between chordality and vertex separators. For example, Dirac proved in [
41] that a graph is chordal if and only if every minimal vertex separator is complete. Furthermore, the set of minimal vertex separators of a chordal graph allows one to decompose the graph into subgraphs that are again chordal, and the process can be continued until the subgraphs are cliques [
35]. Generalized versions of chordality are also related to minimal vertex separator [
42]. For further results about chordality and vertex separators, see also [
36] and the references therein. For an important application of minimal vertex separators in machine learning, see [
43]. Our main results are the following.
In
Section 2, we prove that being
-chordal implies that every minimal vertex separator has a uniformly-bounded diameter. We also obtain that, for uniform graphs, if every minimal vertex separator has a uniformly-bounded diameter, then the graph is
-densely
-chordal and therefore hyperbolic.
Section 3 studies the relation between generalized chordality and the bottleneck property, which is an important property on hyperbolic geodesic spaces. J. Manning defined it in [
44] and proved that a geodesic metric space satisfies bottleneck property, (BP), if and only if it is quasi-isometric to a tree. This characterization has proven to be very useful; see for example [
45]. For some other relations with (BP), see [
46,
47] and the references therein.
Here, we prove that a graph satisfies (BP) if and only if it is
-densely
-chordal, providing a characterization of being quasi-isometric to a tree in terms of chordality. Furthermore, the characterization of hyperbolicity from [
40] is re-written obtaining that a graph is hyperbolic if and only if it is
-densely
-chordal on the cycles that are geodesic triangles.
Furthermore, we prove that if G is a uniform graph and every minimal vertex separator has a uniformly-bounded diameter, then the graph satisfies (BP), and therefore, it is quasi-isometric to a tree. Finally, we prove directly that being -chordal implies (BP) .
In
Section 4, we generalize the concept of vertex separators defining vertex
r-separators. It is proven that if, in a uniform graph, all minimal vertex
r-separators have a uniformly-bounded diameter, then the graph is
-densely
-chordal and, therefore, quasi-isometric to a tree.
Section 5 introduces neighbor separators, generalizing also vertex separators. This concept allows one to characterize (BP) in terms of having a neighbor-separator vertex.
In
Section 6, we define neighbor obstructors. We use them to characterize the graphs where geodesics between vertices are stable and to prove that geodesics between vertices are stable if and only if the graph is
-densely
-chordal on the bigons defined by two vertices. We also prove that, in general, geodesics are stable if and only if the graph is
-densely
-chordal on the bigons.
2. Generalized Chordality and Minimal Vertex Separators
We are assuming that every path is finite and simple, that is, it has finite length and distinct vertices. By a cycle, we mean a simple closed curve, that is, a path where all the vertices are different except from the first one and the last one, which are the same.
Let be a path or a cycle. A shortcut in is a path joining two vertices in such that where denotes the length of the path and denotes the length metric on . A shortcut in is strict if . In this case, we say that p, q are shortcut vertices in associated with . A shortcut with length k is called a k-shortcut.
Remark 1. Suppose σ is a k-shortcut in a cycle C joining two vertices, . Then, σ contains a strict shortcut, and there are two shortcut vertices such that .
Definition 1. A metric graph G is k-chordal if for any cycle C in G with , there exists a shortcut σ of C.
Definition 2. A metric graph G is -chordal if for any cycle C in G with , there exists a shortcut σ of C such that . Notice that being chordal is equivalent to being -chordal.
Remark 2. Notice that in the definitions of k-chordal and -chordal, it makes no sense to consider nor m. Therefore, let us assume always that and m.
Definition 3. A subset is a separator if has at least two connected components. Two vertices a and b are separated by S if they are in different connected components of . If a and b are two vertices separated by S, then S is said to be an -separator.
Let us call a path joining the vertices an -path.
Definition 4. S is a minimal separator if no proper subset of S is a separator. Similarly, S is a minimal -separator if no proper subset of S separates a and b. Finally, S is a minimal vertex separator if it is a minimal separator for some pair of vertices.
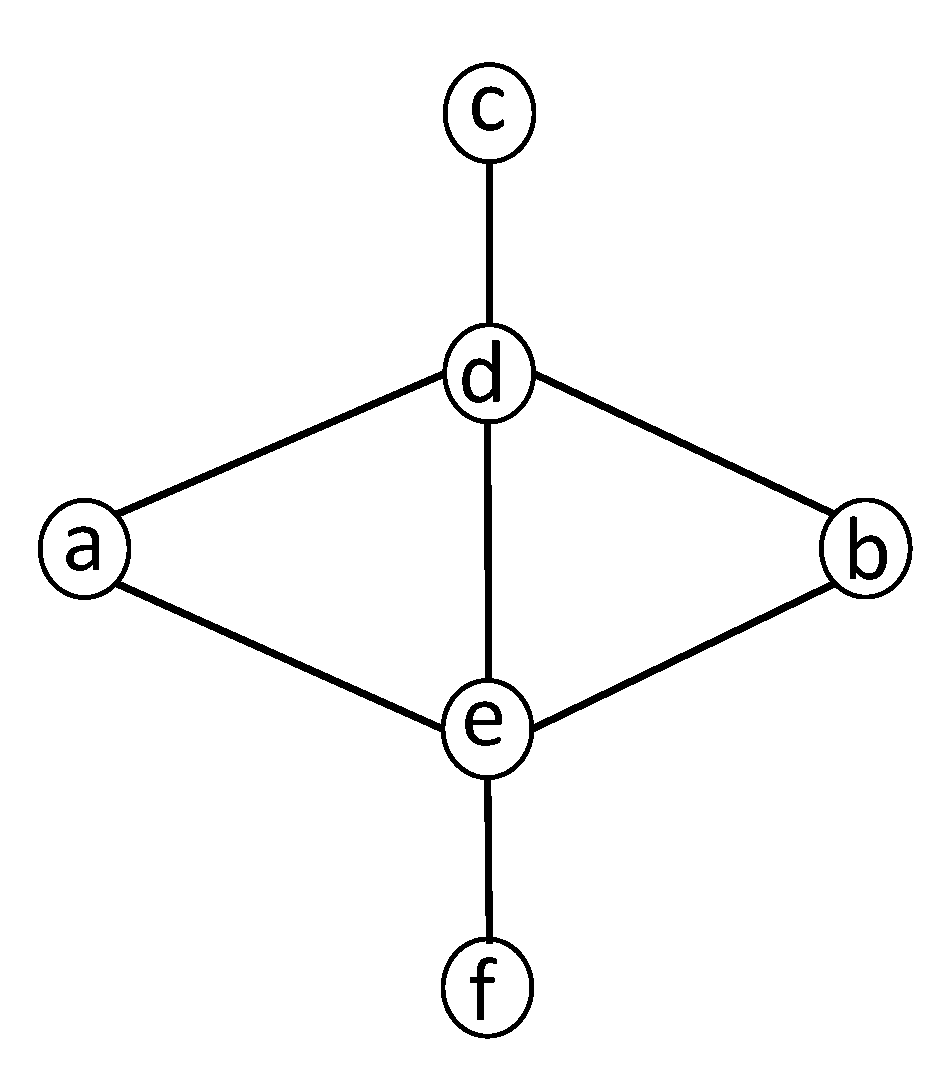
Note that being a minimal vertex separator does not imply being a minimal separator. See
Figure 1.
Remark 3. Let S be a minimal -separator, and let , be the connected components of containing a and b, respectively. Then, notice that every vertex v in S is adjacent to both and . Otherwise, is an -separator.
Proposition 1. If G is -chordal, then every minimal vertex separator has a diameter less than .
Proof. Let S be a minimal -separator, and suppose that . Let such that . Then, there are vertices in adjacent to x and y respectively, and since is connected, there is a path with . Similarly, there exist vertices in adjacent to y and x respectively and a path with . Moreover, let us assume that have minimal length. Then, defines a cycle in G, and since , . Then, since G is -chordal, there is a shortcut in C with . However, since S is an -separator, vertices in and cannot be adjacent, and since are supposed minimal, there is no possible one-shortcut on for . Thus, need to be adjacent, leading to a contradiction. ☐
The converse is not true.
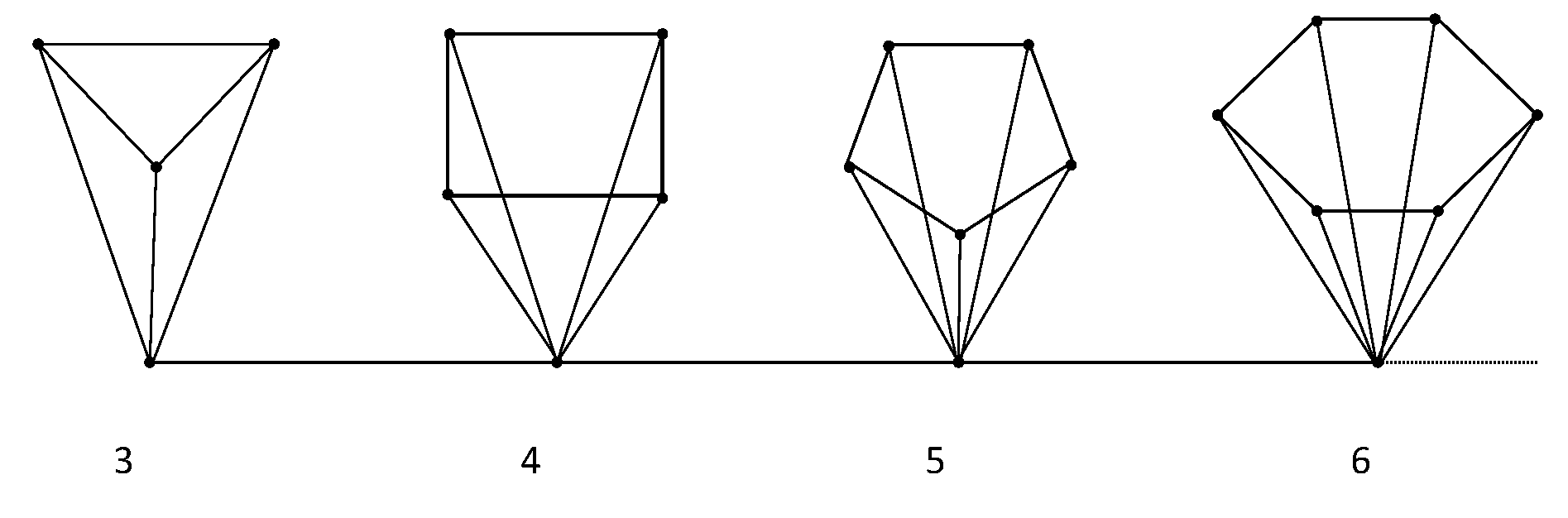
Example 1. Consider the graph whose vertices are and edges joining consecutive numbers. Now, let us define the graph G such that for every , there is cycle whose vertices are all adjacent to the vertex n in . See Figure 2. It is trivial to check that G is not -chordal for any since the cycles have no one-shortcut in G.
Let us see that every minimal vertex separator has diameter at most two. Consider any pair of non-adjacent vertices in G.
If for some n, then every vertex separator S must contain the vertex n and at least two vertices in . If S is minimal, then and .
If for any n, then the geodesic is contained in . Therefore, any -separator must contain some vertex and m separates a and b. Thus, if S is minimal, then S is just a vertex and .
Remark 4. Given two vertices , a path γ joining them and a vertex distinct from , there may not exist a minimal -separator containing . Consider, for example four vertices with edges for every and an edge . Then, there is no minimal -separator containing .
Given a graph G and a subgraph, , let us denote the vertices in A.
Definition 5. A graph Γ
is said to be μ-uniform if each vertex p of V has at most μ neighbors, i.e.,If a graph Γ
is μ-uniform for some constant μ, we say that Γ
is uniform. For any vertex
and any constant
, let us denote:
Lemma 1. Let G be a uniform graph. Given two vertices , a geodesic joining them and a vertex distinct from , then there is a minimal -separator containing .
Proof. Suppose any geodesic and with , and define . Since G is uniform, for every vertex , the set is finite for every . It is immediate to check that is an -separator and . Since is finite, then there is a minimal subset that is also an -separator. Finally, since , . ☐
Let us recall that a graph is countable if , i.e., if it has a countable number of vertices.
Remark 5. In the case of countable graphs and using the axiom of choice, Lemma 1 can be slightly improved. See Lemma 2 below.
Lemma 2. Let G be a uniform countable graph. Given two vertices , a path joining them and a vertex distinct from , then either there is a one-shortcut in or there is a minimal -separator containing .
Proof. If there is no -path in , it suffices to consider . If there is an -path in such that , then there is a one-shortcut in . Thus, let us suppose that every -path in contains a vertex, which is not in , and that there is at least one of these -paths.
Since is countable and G is uniform, there exist at most -paths of length k. Then, there exists at most a countable number (a countable union of countable sets) of -paths, in where if there exist exactly m such paths or if the number of those paths is not finite.
For every
, consider some vertex
in
, and let
. Now, let
, and for every
, define:
Notice that for every i, , and let .
Claim: S is a minimal -separator containing .
First, let us see that S is an -separator. Consider any -path, . Suppose , and assume for every . Then, it is trivial to check that there exist some vertex and, by construction, .
To check that S is minimal, first notice that, since for every , and is not an -separator. Now, suppose that there is some vertex with such that is also an -separator. Since , there is some such that and, in particular, , leading to a contradiction. Thus, S is a minimal -separator containing . ☐
Given a metric space and any , a subset is -dense if for every , there exists some such that .
Definition 6. A metric graph is ε-densely k-chordal if for every cycle C with length , there exist strict shortcuts such that their associated shortcut vertices define an ε-dense subset in .
Definition 7. A graph is ε-densely -chordal if for every cycle C with length , there exist strict shortcuts with and such that their associated shortcut vertices define an ε-dense subset in .
Theorem 1. Let G be a uniform graph. If every minimal vertex separator in G has diameter at most m, then G is -densely -chordal for any .
Proof. Let C be any cycle with . Let v be any vertex in C, and let be the two vertices in C such that . Let be the -path in C containing v. Then, by Lemma 1, either there is a shortcut in or there is a minimal -separator containing v.
If there is a shortcut in , then it has length at most . Therefore, it defines a shortcut in C with an associated shortcut vertex such that . Suppose, otherwise, that S is a minimal -separator containing v. By hypothesis, . Let be the -path in C not containing v. Since S is an -separator, there is some vertex and . Hence, there is an m-shortcut in C joining v to w and, by Remark 1, an associated shortcut vertex such that .
Thus, for every vertex v, there is a shortcut vertex such that , and therefore, shortcut vertices define a -dense subset in C for any . ☐
If the graph is countable, then we can improve quantitatively this result.
Theorem 2. Let G be a uniform countable graph. If every minimal vertex separator in G has diameter at most m, then G is -densely -chordal for any .
Proof. Let C be any cycle with . Let v be any vertex in C, and let be the two vertices in C such that . Let be the -path in C containing v. Then, by Lemma 2, either there is a one-shortcut in or there is a minimal -separator containing v.
If there is a one-shortcut in , then, in particular, there is an associated shortcut vertex such that . Suppose, otherwise, that S is a minimal -separator containing v. By hypothesis, . Let be the -path in C not containing v. Since S is an -separator, there is some vertex and . Hence, there is an m-shortcut in C joining v to w and, by Remark 1, an associated shortcut vertex such that .
Thus, for every vertex v, there is a shortcut vertex such that , and therefore, shortcut vertices define a -dense subset in C for any . ☐
Let us recall the following result:
Theorem 3. (Theorem 4 [40]). If G is ε-densely -chordal, then G is hyperbolic. Moreover, . Therefore, from Theorems 1–3, we obtain:
Corollary 1. Let G be a uniform graph. If every minimal vertex separator in G has diameter at most m, then G is hyperbolic. Moreover, .
Corollary 2. Let G be a uniform countable graph. If every minimal vertex separator in G has diameter at most m, then G is hyperbolic. Moreover, .
3. Bottleneck Property
Let us recall the following definition from [
44]:
Definition 8. A geodesic metric space satisfies the bottleneck property (BP) if there exists some constant so that given any two distinct points and a midpoint z such that , then every -path intersects .
Remark 6. This definition, although not being exactly the same, is equivalent to Manning’s. In the original definition, J. Manning asked only for the existence of such a midpoint for any pair of points . However, by Theorem 4 below, (BP) implies that the space is quasi-isometric to a tree and therefore δ-hyperbolic. Hence, it is an easy exercise in hyperbolic spaces to prove that if there is always a midpoint z such that every -path intersects , then this condition holds in general for any midpoint, possibly with a different constant depending only on Δ
and δ. See, for example, Chapter 2, Proposition 25 in [5]. Definition 9. A graph G satisfies (BP) on the vertices if there exists some constant so that given any two distinct vertices and a midpoint c such that , then every -path intersects .
Proposition 2. A graph G satisfies (BP) if and only if it satisfies (BP) on the vertices. Moreover, if G satisfies (BP) on the vertices with constant , it satisfies (BP) with .
Proof. The only if condition is trivial. Let us see that it suffices to check the property on the pairs of vertices.
Consider any pair of points , and let z be a midpoint of a geodesic . If , then (BP) is trivial with . Suppose . Then, the geodesic is a path with and . Let if x is a vertex and otherwise, and let if y is a vertex and otherwise. Then, there is a geodesic (possibly equal), and its midpoint, c, satisfies that .
Consider any -path , and let us define a -path as follows: First, if , let and if , let .
Then, if and , let and if and , let . By hypothesis, passes through . Since and , it is immediate to check that passes through . ☐
A map between metric spaces,
, is said to be a quasi-isometric embedding if there are constants
and
such that
,
If there is a constant such that , , then f is a quasi-isometry, and are quasi-isometric.
Theorem 4. (Theorem 4.6 [44]). A geodesic metric space is quasi-isometric to a tree if and only if it satisfies (BP). Theorem 5. A graph G satisfies (BP) if and only if it is ε-densely -chordal.
Proof. Suppose that G satisfies (BP) with parameter and consider any cycle C with . Consider any vertex and the two vertices such that . Thus, C defines two -paths, . Let us assume that . If is not geodesic, then there is a shortcut with length at most and a shortcut vertex in . Otherwise, since G satisfies (BP) with parameter , there is a vertex y in such that . Since and by Remark 1, there is a shortcut vertex z such that . Therefore, G is -densely -chordal for any .
Suppose that G is -densely -chordal and it does not satisfy (BP) with parameter . Then, there are two points, , a geodesic with midpoint c and a path such that . Then, it is immediate to check that there exist two points such that the restriction of , , and the restriction of , , joining to define a cycle C with . Since G is -densely -chordal, there is a strict shortcut with with an associated shortcut vertex w such that . Therefore, , and since is geodesic, the shortcut must join w to a vertex z in . Hence, and , leading to a contradiction. ☐
Corollary 3. A graph G is quasi-isometric to a tree if and only if it is ε-densely -chordal.
Definition 10. Given any family of cycles, a metric graph is ε-densely -chordal on if for every with length , there exist strict shortcuts with and such that their associated shortcut vertices define an ε-dense subset in .
Let us recall the following:
Lemma 3. (Lemma 2.1 [48]). Let X be a geodesic metric space. If every geodesic triangle in X which is a cycle is δ-thin, then X is δ-hyperbolic. Let
be the family of cycles that are geodesic triangles. It is immediate to check that, using Lemma 3, the proof of Theorem 13 in [
40] can be trivially re-written (we include it for completeness) to obtain the following:
Theorem 6. G is δ-hyperbolic if and only if G is ε-densely -chordal on .
Proof. Suppose that G is -densely -path-chordal on . Let us see that . Consider any cycle that is a geodesic triangle . If , it follows that every side of the triangle has length at most . Therefore, the hyperbolic constant is at most . Then, let , and let us prove that T is -thin. Consider any point , and let us assume that . If or , we are done. Otherwise, there is a shortcut vertex such that and a shortcut , with and . Since is a geodesic, does not connect two points in and . Then, by Lemma 3, .
Suppose that G is -hyperbolic, and consider any cycle that is a geodesic triangle with . Let , and let us assume, with no loss of generality, that . Since G is -hyperbolic, . If , then there is a path with joining p to . In particular, there is a shortcut with joining some shortcut vertex with to . Therefore, if , for every point , there is a shortcut vertex such that associated with a shortcut with length at most . Since , by triangle inequality, there is at most one side of the triangle with length at most . Then, for every point p in the triangle, there is a shortcut vertex such that associated with a shortcut with length at most . Thus, it suffices to consider , and . ☐
Remark 7. Notice that in Corollary 3, we obtain that a graph G is quasi-isometric to a tree if and only if all the cycles satisfy a certain property, and Theorem 6 states that the same property, restricted to the cycles that are geodesic triangles, characterizes being hyperbolic.
The following theorem can be also obtained as a corollary of Theorems 1 and 5. However, the direct proof provides a better bound for the parameter .
Theorem 7. Given a uniform graph G, if every minimal vertex separator has diameter at most m, then G satisfies (BP) (i.e., G is quasi-isometric to a tree). Moreover, it suffices to take .
Proof. If , it is trivial to see that G is a tree, and it satisfies (BP) with . Assume . By Proposition 2, it suffices to check the property for pairs of vertices. Thus, consider any pair of vertices , and let c be a midpoint of a geodesic .
If , then (BP) is trivial with . Suppose . Then, there is some vertex in the interior of with . By Lemma 1, since is a geodesic, there exists a minimal -separator S containing . Thus, every -path contains a vertex in S, and since , every -path passes through . Hence, (BP) is satisfied on the vertices with , and by Proposition 2, G satisfies (BP) with . ☐
The following example shows that the converse is not true.
Example 2. Let G be the graph whose vertices are all the pairs with either and or and for every , and such that is adjacent to if and only if either and or and . See Figure 3. Now, notice that defines a minimal -separator with diameter n for every . Therefore, G has minimal -separators arbitrarily big. However, to see that G satisfies (BP), consider the map such that for every and and the identity on the rest of the vertices. It is trivial to check that f extends to a -quasi-isometry on G where the image is a tree. Therefore, G is quasi-isometric to a tree and satisfies (BP) (and it is ε-densely -chordal).
Remark 8. In the case of uniform graphs, the following theorem can also be obtained as a corollary of Proposition 1 and Theorem 7. Furthermore, it follows from Theorem 3 in [40] and Theorem 5. However, the direct proof provides a better bound for the parameter. Theorem 8. If G is -chordal, then G satisfies (BP). Moreover, it suffices to take .
Proof. Consider any pair of vertices , any geodesic in G and the midpoint c in . If , then (BP) is trivially satisfied for . Suppose and that there is an -path not intersecting . Let and such that . Then, since does not intersect , there is a cycle C contained in such that and .
Claim: there is a one-shortcut in C joining a vertex in the interior of to a vertex in . Since G is -chordal, there is a one-shortcut, , in C. If joins a vertex in the interior of to a vertex in , we are done. Otherwise, we obtain a new cycle, , such that and, therefore, . Repeating the process, we finally obtain a one-shortcut joining a vertex in the interior of to a vertex in .
Therefore, and , leading to a contradiction.
Thus, G satisfies (BP) on the vertices with , and by Proposition 2, G satisfies (BP) with . ☐
Corollary 4. If G is -chordal, then G is quasi-isometric to a tree.
Remark 9. Corollary 4 follows also from Proposition 1 and Corollary 1 in the case of uniform graphs.
Remark 10. The converse to Theorem 8 or Corollary 4 is not true. It is immediate to check that the graph from Example 1 is quasi-isometric to a tree through the map sending every cycle to the vertex n.
Remark 11. Herein, the gap between being hyperbolic and being quasi-isometric to a tree is shown to depend on which cycles are ε-densely -chordal, only geodesic triangles or all of them. Furthermore, we have seen that (BP) characterizes geodesic spaces quasi-isometric to trees. There exist also properties that characterize when a hyperbolic space is quasi-isometric to a tree. Corollary 1.9 in [49] states that two visual hyperbolic geodesic spaces are quasi-isometric if and only if there is a PQ-symmetric homeomorphism f (where ’PQ’ stands for ’power quasi’) with respect to any visual metrics between their boundaries (The property of being visual has different names in the literature. For example, it is called “having a pole” in [50,51] or being “almost geodesically complete” in [52].). Furthermore, there is a one-to-one correspondence between rooted trees and bounded ultrametric spaces where every tree induces a bounded ultrametric space, and for every bounded ultrametric space X there is a tree whose boundary is X. See [53] or [54]. Thus, a visual hyperbolic space is quasi-isometric to a tree if and only if its boundary is PQ-symmetric homeomorphic to an ultrametric space.
Furthermore, Theorem 1 in [47] states that given a complete geodesic space X with uniformly generated, then X is quasi-isometric to a tree if and only if there is a function such that f is bornologous and metrically proper on the connected components. Since any hyperbolic space has uniformly generated , then it follows that for any hyperbolic graph G, G is quasi-isometric to a tree if and only if there is a function such that f is bornologous and metrically proper on the connected components.
4. Minimal Vertex r-Separators
Definition 11. Given , two vertices a and b are r-separated by a subset if considering the connected components of , and containing a and b respectively, for every pair of vertices and , . If a and b are two vertices r-separated by S, then S is said to be an -r-separator.
Remark 12. Notice that separated means one-separated.
Definition 12. S is a minimal -r-separator if no proper subset of Sr-separates a and b. Finally, S is a minimal vertex r-separator if it is a minimal r-separator for some pair of vertices.
Remark 13. Given any minimal -r-separator S, every vertex in S is either adjacent to or . Moreover, if , then there are two disjoint subsets and such that where the vertices in are adjacent to and the vertices in are adjacent to . Furthermore, for every vertex v in , .
Lemma 4. Let G be a uniform graph and . Given any geodesic with and two vertices distinct from with , then there is a minimal -r-separator containing .
Proof. Suppose is a geodesic with . Let us assume that , and define and . Since G is uniform, for every vertex the set is finite for every . Let . It is immediate to check that is an -r-separator and . Since is finite, then there is a minimal subset which is also an -r-separator. Finally, since , for . ☐
Theorem 9. Let G be a uniform graph and . If every minimal vertex r-separator has diameter at most m with , then G is -densely -chordal.
Proof. Let C be any cycle with , and let be any vertex in C. Then, consider two vertices in C such that , and . Let and be the two independent paths joining a and b defined by C, and assume . Consider with between and b such that (and ).
If is not a geodesic, then there is a shortcut with length at most r and a shortcut vertex v such that .
If is a geodesic, by Lemma 4, there exists a minimal -r-separator S containing . Then, there exist , with between a and , such that , and . Since , then . Since , there is a shortcut in C joining and with and with an associated shortcut vertex v such that .
Thus, for every vertex , there is a shortcut vertex v such that , and therefore, shortcut vertices define a -dense subset in C. ☐
Theorem 10. Let G be a uniform graph and . If for every minimal -r-separator S either or has diameter at most m, then G is ε-densely -chordal with and .
Proof. Let C be any cycle with and be any vertex in C. Then, consider two vertices in C such that , and if m is odd, and and if m is even. Let and be the two independent paths joining a and b defined by C, and assume . Consider with between and b such that (and therefore, ).
If is not a geodesic, then there is a shortcut with length at most and a shortcut vertex v such that .
If is a geodesic, consider S the minimal -r-separator containing built in the proof of Lemma 4, and let us assume, without loss of generality, that has diameter at most m. Then, by construction, there exists such that . Since , then . However, , and therefore, there is a shortcut in C joining and with . Moreover, there is a shortcut vertex v such that .
Thus, for every vertex , there is a shortcut vertex v with , and therefore, shortcut vertices define an -dense subset in C with . ☐
Then, from Theorems 5 and 10, we can obtain immediately the following:
Corollary 5. Let G be a uniform graph and . If for every minimal -r-separator S either or has diameter at most m, then G satisfies (BP), i.e.,, G is quasi-isometric to a tree.
Furthermore, from Theorems 3, 9 and 10, we obtain:
Corollary 6. Let G be a uniform graph and . If every minimal vertex r-separator has diameter at most m with , then G is δ-hyperbolic. Moreover, .
Corollary 7. Let G be a uniform graph and . If for every minimal -r-separator S either or has diameter at most m, then G is δ-hyperbolic. Moreover, .
5. Neighbor Separators
Given a set S in a graph G, let .
Definition 13. Given two vertices in a graph and some , a set is an --separator if a and b are in different components of . S is an -neighbor separator if it is an --separator for some r.
Notice that an -separator is just an --separator.
Theorem 11. G satisfies (BP) if and only if there is a constant such that for every pair of vertices with and any geodesic , there exists a vertex that is an --separator.
Proof. The only if part follows trivially from Proposition 2.
Suppose that for every pair of vertices with and any geodesic , there exists a point that is an --separator. Consider any pair of vertices in G, any geodesic and the midpoint z in .
If , then (BP) is trivially satisfied on for any .
If , by hypothesis, there is some vertex such that is an --separator. If , then it follows that every -path intersects and G satisfies (BP) on the vertices for . If , then we repeat the process with the part of the geodesic, or , containing z. Let us assume, without loss of generality, that . Since and , there is some point that is an --separator. Since there is a -path in , is also an --separator. If , we are done. Otherwise, we repeat the process until we obtain some point that is an --separator and such that . Therefore, G satisfies (BP) on the vertices for .
Thus, by Proposition 2, G satisfies (BP) with . ☐
Corollary 8. G is quasi-isometric to a tree if and only if there is a constant such that for every pair of vertices with and any geodesic , there exists a vertex that is an --separator.
Proposition 3. If G is -chordal, then for every pair of vertices , any geodesic with and every pair of vertices with and such that , is an --separator. In particular, for every pair of vertices in G with , there is a geodesic σ of length or such that σ is an --separator.
Proof. Consider any geodesic in G with and any pair of vertices with such that . Let be the vertex in adjacent to and be the vertex in adjacent to . Therefore, . Suppose that a and b are in the same connected component, A, of . Clearly, and are adjacent to A. Let be a path of minimal length joining and in the subgraph induced by . Therefore, defines a cycle, C, of length at least k. Since G is -chordal, then there is an edge joining two non-adjacent vertices in C. Since is geodesic and has minimal length, the edge must join a vertex, to a vertex in . Therefore, leading to a contradiction. ☐
Definition 14. A path γ in a graph G is chordal if it has no one-shortcuts in G.
Proposition 4. If G is -chordal, then for every chordal -path σ with and every pair of vertices with and such that , then the restriction of σ joining and , , is an --separator. In particular, for every pair of vertices in G joined by a chordal path with length at least k there is a chordal path of length such that is an --separator.
Proof. Consider any chordal path in G with endpoints and . Consider any pair of vertices with such that , and let . Let be the vertex in adjacent to closer in to a and be the vertex in adjacent to closer in to b. Therefore, if is the restriction of joining and , then . Suppose that a and b are in the same connected component, A, of . Clearly, and are adjacent to A. Let be a path of minimal length joining and in the subgraph induced by . Therefore, defines a cycle, C, of length at least k. Since G is -chordal, then there is an edge joining two non-adjacent vertices in C. Since is chordal and has minimal length, the edge must join a vertex to a vertex in . Therefore, , leading to a contradiction. ☐
Proposition 5. If a graph G satisfies that for some with , for every geodesic with and for every pair of vertices with and such that , is an --separator, then G is -densely -chordal.
Proof. Let C be any cycle with . Let v by any vertex in C and two vertices in C such that and , and therefore, . Let be the two -paths defined by the cycle, and let us assume that (and therefore, ). If there is a shortcut in , then there is a shortcut in C with length at most and with a shortcut vertex z such that . If there is no shortcut in , then is a geodesic with . Thus, let with and . Therefore, is an --separator. In particular, there is some vertex w in such that , defining a shortcut in C with length at most m and with a shortcut vertex z such that . ☐
Corollary 9. If a graph G satisfies that for some with , for every geodesic with and for every pair of vertices with and such that , is an --separator, then G is quasi-isometric to a tree.
6. Neighbor Obstructors
Definition 15. Given two vertices in a graph and some , a set is --obstructing if for every geodesic γ joining a and b, .
Given any metric space
and any pair of subsets
, let us recall that the Hausdorff metric,
, induced by
d is:
or equivalently,
Definition 16. In a geodesic metric space , we say that geodesics are stable if and only if there is a constant such that given two points and any geodesic , then every geodesic σ joining x to y satisfies that .
It is well known that if
X is a hyperbolic space, then quasi-geodesics are stable. See, for example, Theorem III.1.7 in [
2]. In particular, geodesics are stable in hyperbolic geodesic spaces.
Let be the family of cycles that are bigons.
Theorem 12. Given a graph G, geodesics are stable if and only if there exist constants and such that G is ε-densely -chordal on .
Proof. Suppose that G is -densely -chordal on . Consider any pair of points and any pair of geodesics, , joining them. Then, for any point , either or there is a cycle with . If , then . If , then either or there is an m-shortcut in C with a shortcut vertex v such that , and since is geodesic, . Thus, if , in any case. Hence, . The same argument proves that , and therefore, .
Suppose that geodesics are stable with constant R. Consider any pair of points with and two -geodesics such that defines a cycle C. Then, for any point (respectively with ) such that (resp. ), since , (resp. ), and there is a strict R-shortcut in C with a shortcut vertex v such that . Thus, shortcut vertices are -dense in C and G is -densely -chordal on . ☐
Definition 17. In a graph G, we say that geodesics between vertices are stable if and only if there is a constant such that given two vertices and any geodesic , then every geodesic σ joining a to b satisfies that .
Proposition 6. Given a graph G, geodesics between vertices are stable if and only if there is some constant so that for every pair of vertices with , every geodesic and every vertex such that , then v is an --obstructing vertex.
Proof. Suppose that geodesics between vertices are stable with constant R. Then, given any two vertices with and any geodesic , every geodesic joining a to b satisfies that . Thus, for every vertex there is some vertex such that . Suppose with . Hence, v is an --obstructing vertex.
Now, suppose that for every pair of vertices with , every geodesic and every vertex with , then v is an --obstructing vertex. Consider any pair of vertices and any pair of -geodesics . If , then it is trivial to check that . Suppose . Then, for every vertex such that , . Therefore, it follows immediately that . The same argument proves that , and therefore, . ☐
Let be the family of cycles that are bigons defined by two geodesics between vertices.
Proposition 7. If G is -densely -chordal on , then for every pair of vertices with , every geodesic and every vertex such that , is an --obstructing vertex. In particular, contains an --obstructing vertex.
Proof. Consider any pair of vertices with , any geodesic and any vertex with . Let be the vertex in with and be the vertex in with . Therefore, , and .
If there is no geodesic joining a to b disjoint from , we are done.
Suppose there is some geodesic joining a to b such that . Then, contains a cycle C (with possibly ) composed by two geodesics with and joining also to . Clearly, . Since G is -densely -chordal on , then there is a strict shortcut with joining two vertices in C with a shortcut vertex in . Furthermore, since and are geodesics, then joins to a vertex in . Therefore, (see Remark 2) and . ☐
Theorem 13. Given a graph G, geodesics between vertices are stable if and only if there exist constants and such that G is ε-densely -chordal on .
Proof. Suppose that G is -densely -chordal on . By Proposition 7, if , then for every pair of vertices with , every geodesic and every vertex such that , is an --obstructing vertex. Thus, by Proposition 6, geodesics are stable with constant .
Let us suppose that geodesics between vertices are stable with constant R. Let be two vertices with and C be a cycle that is a bigon defined by two -geodesics, . Therefore, . Consider any vertex (respectively, ) such that . Then, since geodesics between vertices are stable with parameter R, (respectively, ) and there is a strict R-shortcut in C with an associated shortcut vertex w such that , therefore shortcut vertices are -dense in C, and G is -densely -chordal on . ☐
The following example shows that having stable geodesics between vertices does not imply that geodesics are stable.
Example 3. Consider the family of odd cycles , and suppose we fix a vertex in each cycle; we define a connected graph G identifying the family as a single vertex v. Notice that in G geodesics between vertices are unique. If two vertices belong to the same cycle , then the geodesic is contained in the cycle, and it is clearly unique. Otherwise, the geodesic is the union of the two (unique) shortest paths joining the vertices to v. Thus, geodesics between vertices are stable with constant zero.
Let be the midpoint of an edge in such that . Then, is a bigon in G defined by two geodesics, joining to v and with k arbitrarily large.
Remark 14. Notice that the same property that characterizes being quasi-isometric to a tree (Corollary 3) also characterizes being hyperbolic, when restricted to triangles (Theorem 6), having stable geodesics, when restricted to bigons (Theorem 12), and having stable geodesics between vertices, when restricted to bigons between vertices (Theorem 13).
Remark 15. In the context of multi-path routing, (BP) implies that given any nominal path (with minimum cost) joining x and y, then any other path would remain close (at least at some point) to the nominal one. Furthermore, if we consider all paths with minimum cost, the stability of geodesics characterized above implies that every point of any minimal path is close to the nominal one.
The proof of Proposition 7 can be adapted to prove also the following:
Proposition 8. If G is -densely -chordal on with , then for every geodesic with and every pair of vertices with and such that , is an --obstructing set. In particular, for every pair of vertices in G with , there is a geodesic σ of length or such that σ is --obstructing.
Proof. Consider any geodesic with and any pair of vertices with and . Let be the vertex in with and be the vertex in with . Therefore, .
Suppose that there is some geodesic joining a and b such that . Then, contains a cycle C composed by two geodesics: with and . Clearly, . Consider the midpoint c in . Since G is -densely -chordal on , then there is a strict shortcut with joining two vertices in C with a shortcut vertex such that , and hence, . Furthermore, since and are geodesics, then joins to a vertex, , in . Therefore, and , leading to a contradiction. ☐