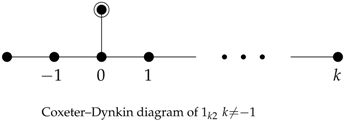
2.1. Smooth Rational Surfaces with
In this article, we consider smooth rational surfaces
S with the condition
. By the classification of surfaces [
1], each smooth rational surface has a minimal surface, a projective plane
, or a Hirzebruch surface
. In this article, we only consider the blow-ups of the projective plane
and the Hirzebruch surface
in general position. In fact, the studies of the blow-ups of the Hirzebruch surface
in general position have not done much so that there are no typical descriptions of the general positions of points in
. Below, we give a description of the blow-ups of the Hirzebruch surface
in general position matching our purpose.
First, we consider the smooth rational surface S with whose minimal surface is . We have a birational morphism decomposed by contractions of -curves (i.e., , where and . We remark that each can be obtained by a blow-up of a point on . The blow-ups at points allow infinitely near ones on . When the points on are in general position, we call S a del Pezzo surface with a degree whose anticanonical divisor is ample. We denote by the total transforms of -curves by , and . Then, the Picard group of S is generated by h and (i.e., ), where h is a pull-back of a line in by ρ. Note that the canonical divisor , and since .
Also, we deal with a smooth rational surface X with whose minimal surface is a Hirzebruch surface . As above we denote a birational morphism decomposed by contractions of -curves (i.e., , where and ; moreover, we have a map , which gives a fibration . We denote by f and a general fibre of and the special section of whose self-intersection number is a nonpositive integer , respectively. We use instead of unless there is no confusion. When we consider the contraction of as a (possibly infinitely near) blow-up of a point on , the point is located in the special section on or not. If is not a point in then . On the other hand, if is a point in then . Thus, we define that distinct points are located on in general position if each point , is not in a special section () and there are no two points for which are in a common general fibre of . As above, we denote by the total transforms of -curves by , and . Then the Picard group of X is generated by and (i.e. ). The canonical divisor is written as , and we have since .
Remark 1. We can consider an isometric isomorphism for defined byThen ψ preserves intersection pairings, root systems and the canonical divisor classes between and . Note the isometric isomorphism in the proof of Lemma 3.2 in [14]. Thus, we can naturally extend the correspondence between the special divisors of a del Pezzo surface and the subpolytopes of a Gosset polytope to one for . Because the correspondence was established for a del Pezzo surface in [10,12] at first, we use the argument of [10,12] in Section 3 and Section 4 to present the original idea, although we have the isometric isomorphism ψ. 2.2. -Polytopes
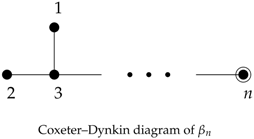
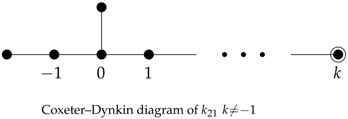
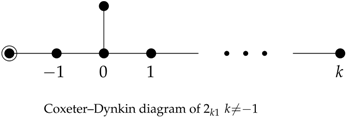
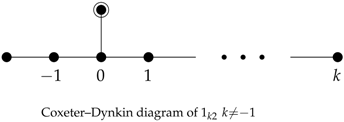
The polytopes under consideration in this article are characterized by the highly nontrivial symmetries given by
Coxeter groups. Moreover, the polytopes are determined by the corresponding Coxeter–Dynkin diagrams. In this subsection, we introduce the general theory of regular and semiregular polytopes according to their symmetry groups and the corresponding Coxeter–Dynkin diagrams. In particular, we consider a family of semiregular polytopes known as the Gosset polytopes, (
according to Coxeter),
and
. Here, we only present a brief introduction; for further detail, refer to [
10,
15].
2.2.1. Regular and Semiregular Polytopes
Let be a convex n-polytope in an n-dimensional Euclidean space. For each vertex of , when the set of midpoints of all the edges emanating from the vertex O in is contained in an affine hyperplane, the set consists of the vertices of an -polytope. This -polytope is called the vertex figure of at O. A regular polytope () is a polytope whose facets and the vertex figure at each vertex are regular. Thus, the facets of a regular are all congruent, and the vertex figures are the same. We also call a polytope a semiregular one if its facets are regular and the symmetry group of acts transitively on the vertices of . Here we consider two kinds of regular polytopes, a regular simplex and a crosspolytope. A regular simplex is an n-dimensional simplex with equilateral edges, and a crosspolytope is an n-dimensional polytope whose -vertices are the intersections between an n-dimensional Cartesian coordinate frame and a sphere centered at the origin. Below we also consider three kinds of families of semiregular polytopes given by Weyl action of .
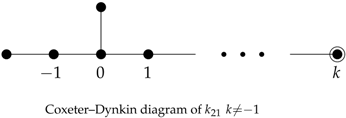
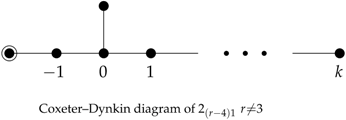
2.2.2. Coxeter–Dynkin Diagrams
Reflection groups generated by the reflections with respect to hyperplanes (called mirrors) are called Coxeter groups, and the relationships among generating reflections are presented in the Dynkin diagrams of Coxeter groups.
The Coxeter–Dynkin diagrams of Coxeter groups are graphs with labels where their nodes present indexed mirrors and the labels on edges present the order n, which is the dihedral angle between two mirrors. If , namely, two mirrors are perpendicular, we denote it as no edge joining two nodes presenting the corresponding mirrors. This also implies that the corresponding mirrors commute. For , since the dihedral angle appears very often, we denote it with an edge between two nodes without labels. We only label the edges when the corresponding order is . Each Coxeter–Dynkin diagram contains at least one ringed node which represents an active mirror; i.e., we choose a point off the mirrors corresponding to the ringed nodes, and on the mirrors corresponding to the nodes without rings. The construction of a polytope begins with reflecting the point by the active mirrors.
2.2.3. -Type Coxeter Groups and Isotropy Groups
We consider Coxeter groups of -type, and we call the polytopes given by Coxeter groups of -type -polytopes. In fact, the Coxeter–Dynkin diagrams of polytopes in this article have only one ringed node and no labeled edges. For these cases, the following simple procedure using the Coxeter–Dynkin diagrams describes possible subpolytopes and gives the total number of them. Each Coxeter–Dynkin diagram of subpolytopes is the connected subgraph Γ of the diagram containing the ringed node. The subgraph obtained by removing all the nodes joined with the subgraph Γ represents the isotropy group of . Furthermore, the index between the symmetry group of the ambient polytope and the isotropy group gives the total number of such subpolytopes. For example, by removing the ringed node, we obtain the subgraph corresponding to the isotropy group of a vertex where the isotropy group is the symmetry group of the vertex figure.
In fact, the complete list of -polytopes consists of various polytopes given by Weyl action. However, we consider only a few of them related to the studies in this article as below.
2.2.4. -Polytopes
(1) (A-polytope) A regular simplex is an n-dimensional simplex with equilateral edges. Inductively, is constructed as a pyramid based on an -dimensional simplex . The facets of a regular simplex are regular simplexes , and the vertex figure of is also . For a regular simplex , only regular simplexes , appear as subpolytopes.
(2) (D-polytope) A crosspolytope is an n-dimensional polytope whose -vertices are given as the intersections between an n-dimensional Cartesian coordinate frame and a sphere centered at the origin. is also inductively constructed as a bipyramid based on an ()-dimensional crosspolytope , and the n-vertices in form a simplex if any two vertices are not chosen from the same Cartesian coordinate line. The vertex figure of a crosspolytope is also a crosspolytope , and the facets of are simplexes . For a crosspolytope , only regular simplexes , appear as subpolytopes.
(3) (E-polytope) Gosset polytopes are -dimensional semiregular polytopes of the Coxeter groups discovered by Gosset. The vertex figure of is . For the facets of -polytopes are the regular simplexes and the crosspolytopes , but all the lower dimensional subpolytopes are regular simplexes. In fact, Coxeter called , and Gosset polytopes. We extend the list of Gosset polytopes along the extended list of . Note that a Gosset polytope , a triangular prism, especially has an isosceles triangle as the vertex figure different from an equilateral triangle.
(4) (E-polytope) are -dimensional semiregular polytopes of the Coxeter groups . Here the vertex figure of is a -demicube. For the facets of -polytopes are regular simplexes and semiregular polytopes .
(5) (E-polytope) are semiregular polytopes which are -dimensional polytopes whose symmetry groups are the Coxeter groups . Here the vertex figure of is a birectified -simplex. For , the facets of -polytopes are the semiregular polytopes and -demicubes, but all the lower dimensional subpolytopes are regular simplexes.
2.2.5. Subpolytopes in Gosset Polytopes
Below, it is useful to know the total numbers of subpolytopes in
for each
. The numbers of simplexes
in a Gosset polytope
are as follows in
Table 1 and
Table 2.
The numbers of crosspolytopes in for each are as follows.
2.3. Del Pezzo Surfaces and Gosset Polytopes
A del Pezzo surface is a smooth rational surface whose anticanonical divisor is ample. All del Pezzo surfaces are , a blow-up of at r points in general position, for and .
To define reflections on
in
, we consider a root system:
With a choice of simple roots
we have a Weyl group
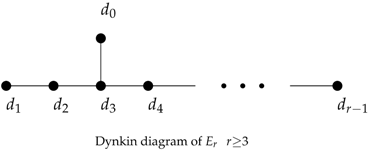
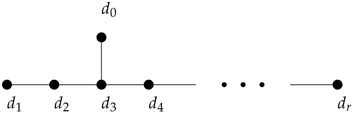
of
-type with the Dynkin diagram:
In [
10] we obtained correspondences between special divisors on del Pezzo surfaces
and the faces of Gosset polytopes
. For this purpose we define
affine hyperplane sections in
as
where
b is a real number.
After fixing a center
in
, for each divisor
we obtain
and
if
by Hodge index theorem and
. Therefore, we get a negative definite norm in
induced by the intersection product when we fix a center
in
.
Then, by applying reflections defined by the roots for the lines of del Pezzo surfaces
, we obtained the following theorem (in [
10]) about the vertices of Gosset polytopes
in
:
Theorem 2 (Theorem 4.2 in [
10]).
For each del Pezzo surface , the set of lines on is the set of vertices of a Gosset polytope in a hyperplane section . Remark 3. In fact, the convex hull of the set of lines in is the polytope .
We consider the set of
skew a-lines defined by
The following theorem gives a correspondence among the exceptional systems of , the -simplexes of , and the skew r-lines of .
After we observe the bijections between exceptional systems in del Pezzo surfaces and the top degree simplexes in
except for
, we deduced the following theorem (in [
10]).
Theorem 4 (Theorem 5.3 in [
10]).
When , each -simplex in corresponds to an exceptional system in the del Pezzo surfaces . Moreover, for , the Weyl group acts transitively on ; i.e.
, the set of exceptional systems in the del Pezzo surface . Finally is bijective to , the set of skew r-lines in . Remark 5. To explain the correspondence, we consider a transformation from to which satisfiesWhen , the set of exceptional systems consists of two orbits. One orbit, with 17280 elements, corresponds to the set of skew 8-lines in , and the other orbit, with 240 elements, corresponds to the set of -roots, because each -root d gives an exceptional system . To distinguish elements of two orbits, we check if is in or not. If so, there is a root satisfying , which otherwise corresponds to a skew 8-line via . Also, we had correspondences between rulings of
and
-crosspolytopes of
in [
10]:
Theorem 6 (Theorem 5.4 in [
10]).
For each ruling f in a del Pezzo surface ,, there is a pair of lines and with such that f is equivalent to the sum . Furthermore, the set of rulings in is bijective to the set of -crosspolytopes in and is acted transitively upon by the Weyl group . One can observe that there are two types of
-simplexes in
. In [
12], an
-simplex in
is called
of A-type if it is contained in an
-simplex in
, and of
B-type otherwise. In fact,
-simplexes in
form two Weyl orbits according to types and the total numbers of the simplexes of each orbit are as follows in
Table 3 and
Table 4.
For the set of quartic rational divisors consists of one orbit, . However, for the set consists of two orbits, . We say that a quartic rational divisor is of type I if it is in the orbit and of type II if it is in the orbit . The total number of such divisor classes in is finite and is given in the following table.
Then, we had correspondences between
-simplexes of
A-type in
and quartic rational divisors of type I in
as follows (in [
12]):
Theorem 7 (Theorem 1 in [
12]).
For disjoint lines on a del Pezzo surface , they produce a contraction to if there is a quartic rational divisor class q on satisfying . Moreover, the quartic rational divisor classes of type I are bijectively related to -simplexes of A-type in .