An Ultrasonic Lens Design Based on Prefractal Structures

Abstract

The improvement in focusing capabilities of a set of annular scatterers arranged in a fractal geometry is theoretically quantified in this work by means of the finite element method (FEM). Two different arrangements of rigid rings in water are used in the analysis. Thus, both a Fresnel ultrasonic lens and an arrangement of rigid rings based on Cantor prefractals are analyzed. Results show that the focusing capacity of the modified fractal lens is better than the Fresnel lens. This new lens is believed to have potential applications for ultrasonic imaging and medical ultrasound fields.

1. Introduction

It has been found that certain natural phenomena, such as snowflakes or the structure of leaves in certain plants, display self-similar patterns. These distinctive features can be associated with the fractal concept. Fractals are non-regular geometric shapes that have the same degree of non-regularity on all scales [1]. Fractal structures have attracted the interest of the scientific community due to their applications in several areas of science and technology [2].

Among the wave applications of fractal structures, several studies have been addressed in acoustics. Petri et al. [3] analyzed the vibrational properties of a hierarchical continuous system consisting of a Cantor-like sequence of piezoelectric and resin elements. Sapoval et al. [4] investigated numerically the acoustical properties of irregular cavities described by fractal shapes. They showed that the geometrical irregularity enhanced the low frequency modal density and localized many of the modes at the cavity boundaries, and that the damping characteristics of the cavity were modified. Lubniewski and Stepnowski [5] developed a simple method of sea bottom identification using elements of fractal analysis. Gibiat et al. [6] reported the homothetic acoustical features, forbidden bands, and wave trapping phenomena for an acoustic multiscattering one-dimensional system made of cylindrical tubes of different diameters, whose lengths follow a Cantor-like structure. Castiñeira-Ibañez et al. [7,8] presented an acoustic barrier for noise control formed by rigid cylinders arranged in fractal Sierpinski triangle geometry. Gomez-Lozano et al. [9] studied the acoustic transmission response of perforated plates with a fractal subwavelength holes array. The ultrasound transmission spectra showed that each iterative Sierpinski Carpet has the characteristic peaks and dips of the lattice constant of each array that formed the pattern. Targeting of ultrasonic beams of MHz order are essential for noninvasive tissue ablation.

Based on these studies, a new possibility of constructing lenses different from the most common cases that are constructed by refractive materials with curved surfaces is proposed. Thus, in this paper, a planar acoustic fractal lens is proposed, and the focusing properties are numerically analyzed using the finite element method (FEM). The results obtained with the proposed acoustic fractal lens are compared with those of a conventional planar acoustic Fresnel lens. For focusing acoustic waves in both air and water, acoustic Fresnel lenses have been investigated [10,11], and labyrinthine channels have recently been used in Fresnel lenses to increase their efficiency [12,13].

2. Modeling and Simulation

Analogously to optical lenses, it is common to construct acoustic lenses via refractive material with curved interfaces. As in optics, diffractive acoustic elements are essential if the focalization of the acoustic beam is made by means of flat transducers.

Fresnel zone plates (FZPs) focus waves through constructive interferences of diffracted fields [14]. Hence, FZPs is divided into ring segments that act alternatively as transparent (open-gaps) or opaque (rigid); the radii and width of these segments are so designed to produce constructive interference at the focus. Figure 1 shows a generation of a FZP. As a result, the zone radii, r_i, which defines the pattern for plane wave incidence and wavelength λ for a FZP is given by

$$r_i=\sqrt{i\lambda F+{\left(\frac{i\lambda }{2}\right)}^2}$$

(1)

where i = 1, 2, …, N, i is the total number of zones, and F is the focal distance.

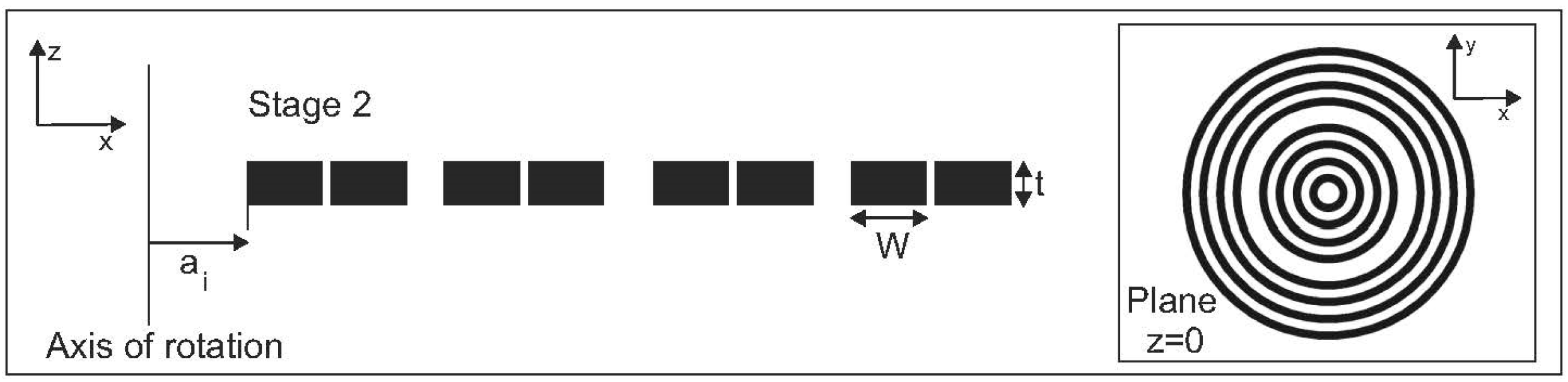
Due to the wave nature of light and sound, the physical phenomena developed in optics could be transferred to acoustics. With this in mind, a Cantor diffractal that is based on a polyadic Cantor set has been considered, with the construction procedure shown in Figure 2. Hence, for the Cantor rings, the zone radii is given by [15], and the parameter a has length dimensions and will be used to adjust the ring size to be compared with those obtained for the Fresnel zone plate:

$$a_i=a{\displaystyle \sum _{j=1}^s{\gamma }^{j-1}{b}_{c_j^i}}$$

(2)

where i = 0, 1, …, M − 1, and M is the total number of rings, which can be obtained by

$$M=\frac{1}{2}{4}^{s_{\max }}$$

(3)

where s is the stage of growth of the fractal structure, which, in this work, will be s = 0, 1, 2. For s_max = 2, the total number of rings will be M = 8; thus, the total number of zones are 2M + 1 = 19. The scaling ratio between successive stages of growth, γ, is given by

$$\gamma ={\left(n_{\text{gaps}}+1\right)}^{-1/D}$$

(4)

where n_gaps is the number of desired gaps, and D is the fractal dimension. In this work, n_gaps = 3 and D = 9/10. For the first stage (s = 0), the bar length is L, and this length varies with its stage through the expression $L_{\gamma }^s$. On the other hand, the coefficients $b_{c_j^i}$ in Equation (2) depends on γ and ε (the lacunarity) [16].

This parameter specifies the distribution of the N copies into the unit length segment. In fact, the lacunarity is essential to complete the characterization of the fractal because structures with different lacunarity can have the same fractal dimension. In this work, ε = 44/1000. It is noteworthy that this structure is not a regular Cantor fractal. The initial segment is divided into an odd number of segments, and the segment located in the even position is removed. This procedure is repeated through successive stages within the same rule.

Unlike the FZP, the wavelength does not appear in the expression of the Cantor rings’ radii. Therefore, in this work, the wavelength dependence has been considered through parameter a. Figure 1 and Figure 3 represent the corresponding zone plates with the FZP profile (Figure 1) and the FRZP profile (Figure 3) studied here.

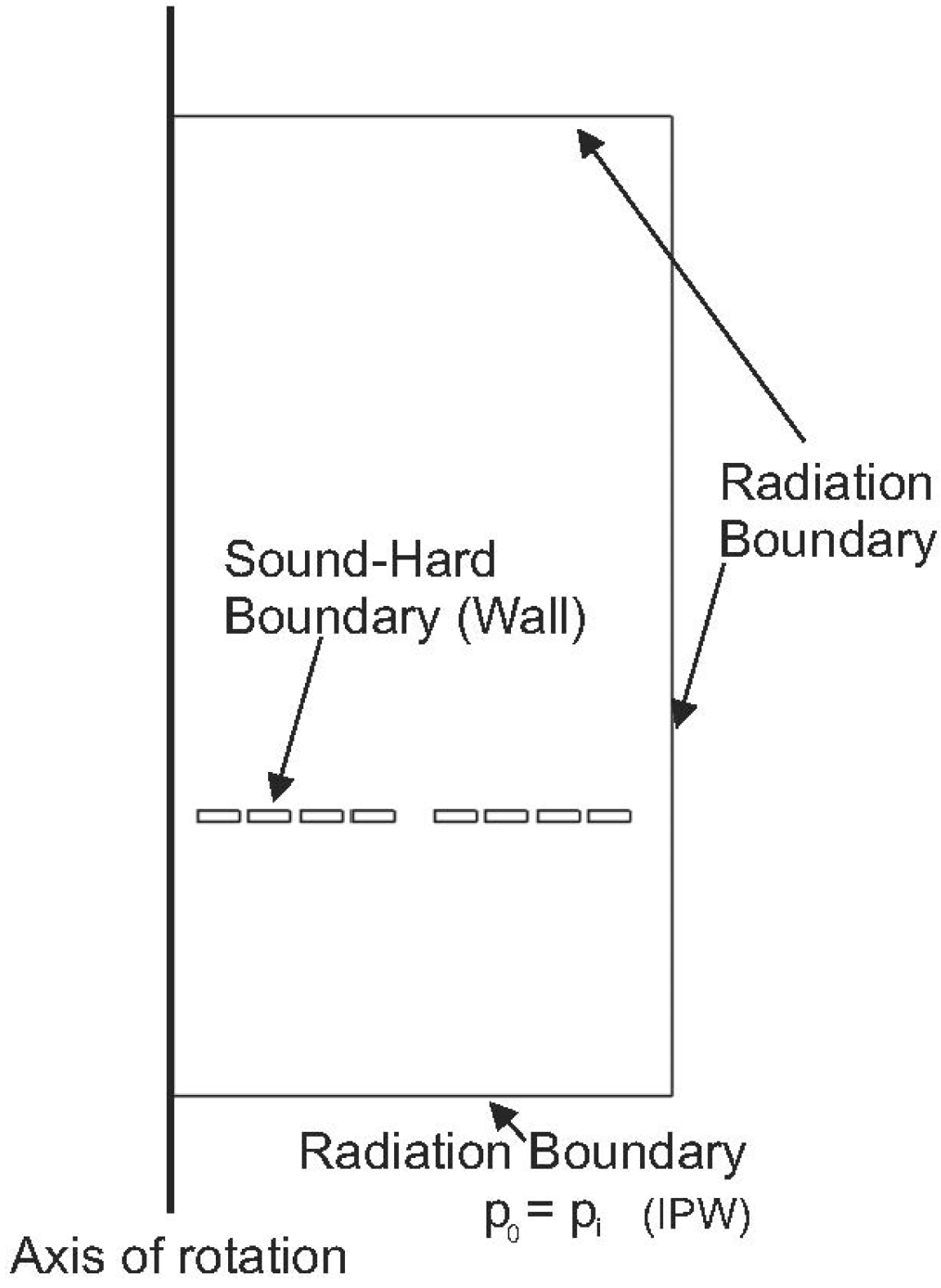
The interaction of ultrasound waves with ultrasonic lenses is a complex problem. The FEM seems to be an appropriate computational tool to determine the distribution of acoustic pressure and therefore the focal positions and the size of the focal spot. To decrease the computational cost of the simulations, the geometrical properties of the model that has been implemented must be taken into account. Both fractal and Fresnel lenses have axial symmetry since these structures arise as a result of the rotation of a plane around an axis. Furthermore, all the cutting half-planes along this axis have identical characteristics. Therefore, a half-plane, which corresponds to the longitudinal section of the semilens and makes the rotation around the axis, can be implemented. That is why the numerical calculation was made by means of the 2D axisymmetric method. The model included a piston source which consists of an axially oscillating disk of dimensions equal to the axysimetric lens. A plane wave with amplitude p_o (IPW) impinges on the axysimetric lenses upward along the y direction.

For this purpose, it is necessary to solve the Helmholtz equation given by

$$\nabla \left(-\frac{1}{\rho }\nabla p\right)=\frac{{\omega }^2}{\rho c^2}p$$

(5)

where ρ is the medium density, c is the ultrasound velocity, ω is the angular frequency, and p is the acoustic pressure. The assumptions made in the simulations are: (1) that the wavelength of the incident plane wave (IPW) is large compared to the thickness of the lens; (2) that the lens is considered to be acoustically rigid and, therefore, that the Newmann boundary condition (zero sound velocity) is applied; and (3) that the plane wave radiation condition is applied to the boundaries of the domain to simulate free space and emulate the Sommerfeld condition in the numerical solution of the wave problem, as shown in Figure 4.

To quantify the acoustic field, the sound pressure level is calculated as

$$SPL=20·{\text{log}}_{10}\left|\frac{p}{p_{\text{incident}}}\right|$$

(6)

where p is the sound pressure at a certain point, and p_incident is the lens incident pressure.

3. Results and Discussion

To implement the analytical model, lenses were designed based on Equations (1) and (2). Both FZP and FRZP lenses have an outermost radius of 0.12233 m and eight rings. The thickness of the blocking zone of both lenses was 0.003 m, and simulations were carried out at 200 kHz. The chosen medium was water with a density of 1000 kg/m³ and a sound velocity of 1500 m/s. The solved problem has 0.88 × 10⁶ elements.

To evaluate the focusing capability of both the FZP and FRZP lenses, both built within the parameters presented in the previous section, the focal gain was calculated using the expression

$$G_{\text{focus}}=20·{\text{log}}_{10}\left|\frac{p}{p_{\text{incident}}}\right|$$

(7)

where p is the pressure at the focal point, and p_incident is the pressure of the incident wave. For the FZP lens, the focal gain value was 19.4 dB, while for FRZP it was 13.1 dB. These results revealed that the focusing effect of FRZP lens do not improve the FZP lens. Therefore, the redistributing scattering centers (solid rings) of the fractal lens was modified by moving the distance W/2 of the dispersing element towards the rotation axis (see Figure 3), a_i being now the distance from the axis of rotation to the center of the ring segment i. This new structure was referred to as the “modified FRZP”. 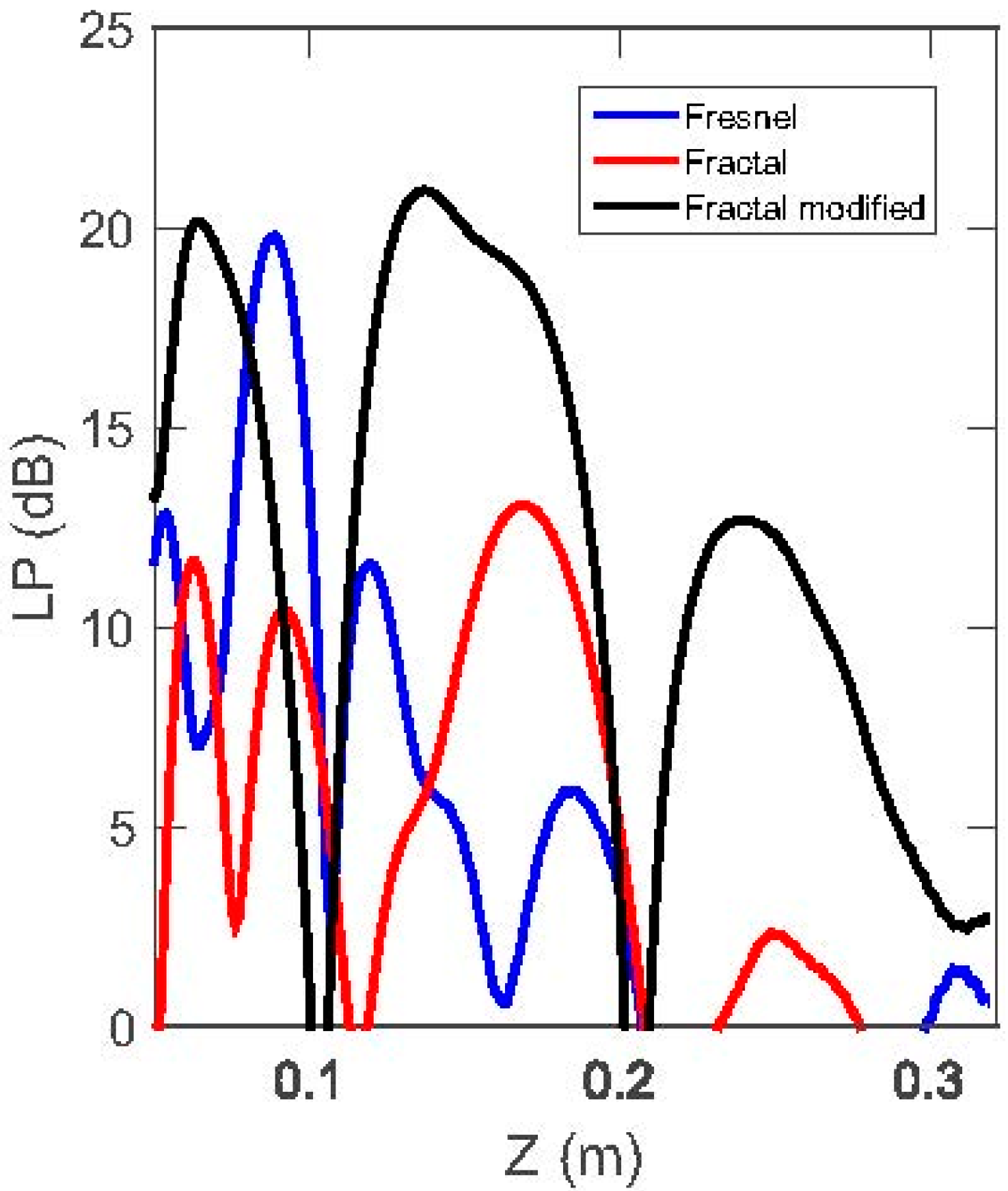Figure 5 shows a comparison of the transverse section of the sound pressure level along the y-axes of the three lens considered. It can be seen that only by redistributing the solid rings could the acoustic focalizing behavior improve considerably. For the modified FRZP, the focal gain was G_focus = 20.9 dB. Furthermore, a remarkable feature can be observed: Fractal structures produce multiple foci along the transversal axes with a high sound pressure level. This feature is characteristic of fractal diffractive lenses, which is a result of the phase sampling inherent to these type of lenses [17].

Figure 6 shows the spatial distribution of the sound pressure level of the modified FRZP and the FZP lens in the XY plane. Although in both lenses some focal zones can be considered, it is worth noticing that the modified FZRP presents separated multifoci, while in FZP the distance between foci is negligible. This fact can be explained as an interference phenomenon and is closely related to the phase shift along the rings. A normal plane wave incident upon a plate lens undergoes diffraction such that constructive interference occurs at a point. In a fractal lens, the phase is matched in a higher and separated area. On the other hand, the focal distance of FZP is 0.0875 m, while this parameter for FRZP is 0.137 m.

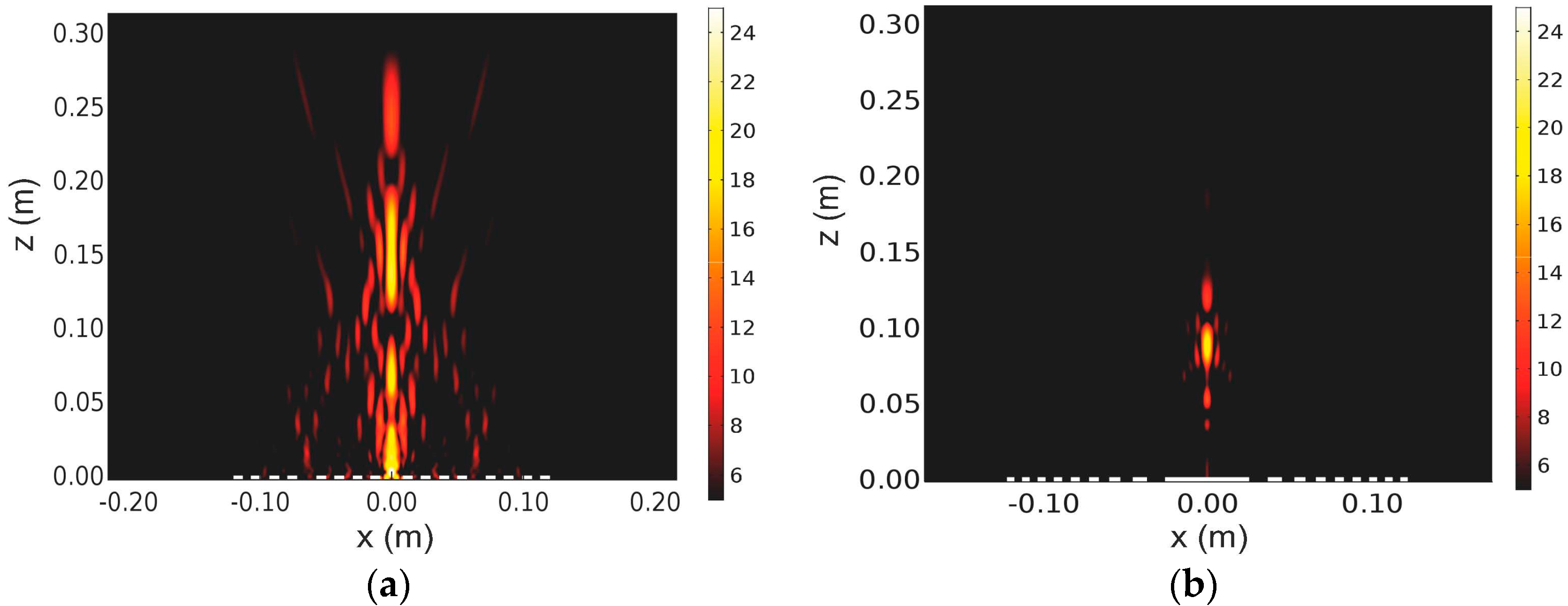
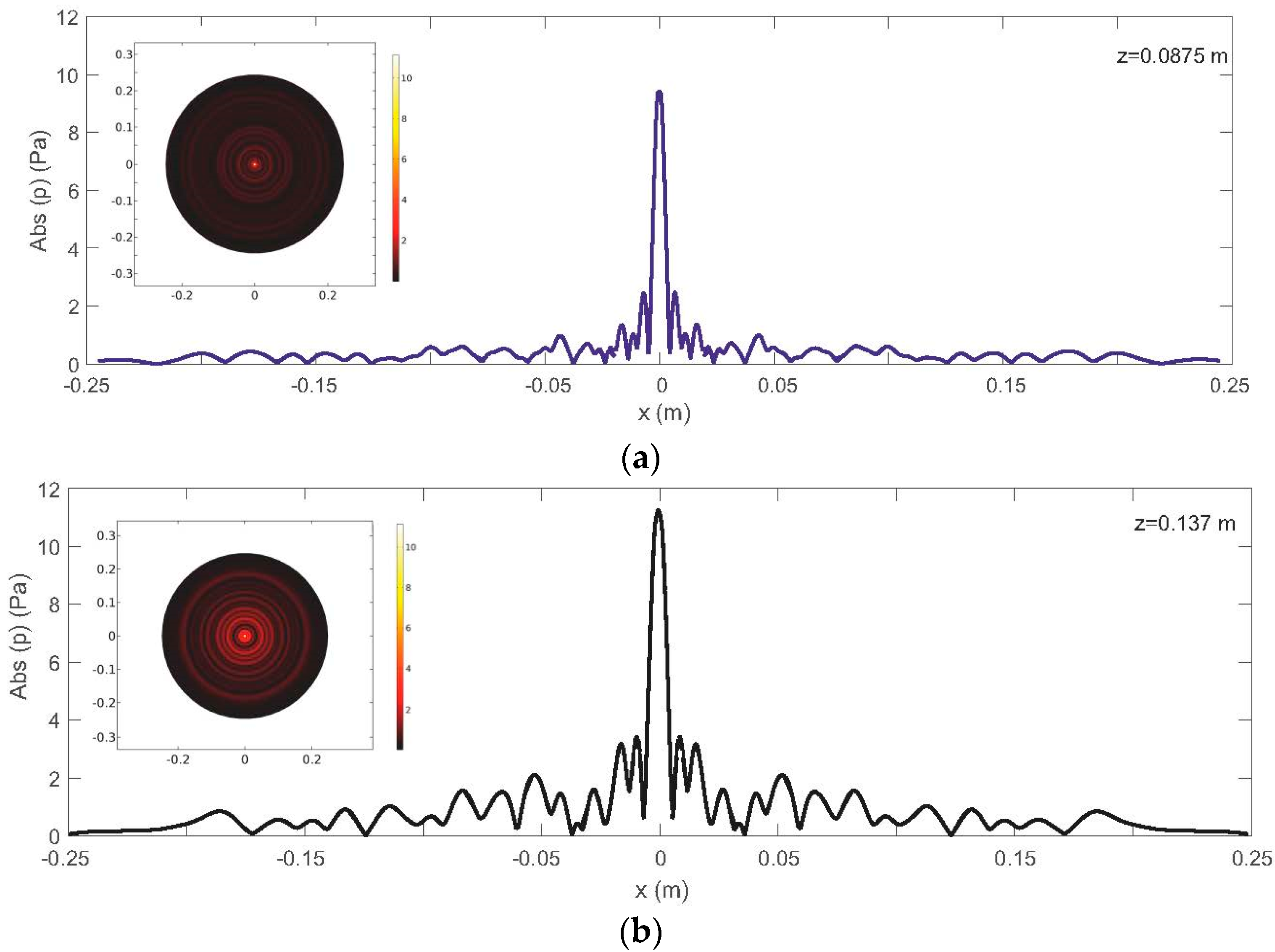
The cutline of the ultrasonic pressure field along the x-axis at the focus is shown in Figure 7a,b. Both lenses show similar behavior, but a difference in the side lobes was observed. In the FRZP lens, the side lobe has more intensity but is narrower than the FZP lens. On the other hand, it can be observed that the main lobe in the FRZP lens is wider, corresponding to the longer depth of the ultrasonic field, compared to the FZP lens. The radial pressure field at the focus in the insets also illustrates this fact. The width of the main lobe is important in both ultrasonic imaging and medical ultrasonics.

In this sense, another parameter that is used to evaluate the focusing capability of a lens is the full width at half maximum (FWHM) of the focus. The resolution of the focus is characterized by λ/2 < FWHM <λ for the analyzed frequency. Thus, the FWHM values obtained were 5.6 and 6.6 mm for FZP and FRZP, respectively.

4. Conclusions

In summary, the ultrasonic modified FRZP lens is here proposed as an alternative to the FZP ultrasonic lens. The focusing capability of the FZP and modified FRZP lenses has been evaluated by means of the focal gain and the FWHM of the focus. The focusing capacity of the modified FRZP lens is better than the FZP lens considering the gain increase of 1.5 dB. FRZP presents multifoci of considerable gain, while FZP has a single main focus. However, more research of different parameters of prefractal lens is needed to discover their influence on the focalization properties and therefore improve its behavior.

This new type of lens can have the same applications where conventional Fresnel lenses are currently applied, that is, in medical diagnosis and therapy, and acoustic imaging. Moreover, all improvements developed for Fresnel lenses could be applied for prefractal lenses.