Abstract
We review how nuclear forces emerge from low-energy quantum chromodynamics (QCD) via chiral effective field theory (EFT). During the past two decades, this approach has evolved into a powerful tool to derive nuclear two- and many-body forces in a systematic and model-independent way. We then focus on the nucleon-nucleon () interaction and show in detail how, governed by chiral symmetry, the long- and intermediate-range of the potential builds up order by order. We proceed up to sixth order in small momenta, where convergence is achieved. The final result allows for a full assessment of the validity of the chiral EFT approach to the interaction.
Keywords:
low-energy quantum chromodynamics (QCD); effective field theory; chiral perturbation theory; nucleon-nucleon scattering; nucleon-nucleon potentials PACS classifications:
13.75.Cs; 12.39.Fe; 21.30.-x; 21.45.Ff
1. Historical Perspective
After the discovery of the neutron by Chadwick in 1932 [1], it was clear that the atomic nucleus is made up from protons and neutrons. In such a system, electromagnetic forces cannot be the reason why the constituents of the nucleus are sticking together. Therefore, the concept of a new strong nuclear interaction was introduced. In 1935, the first theory for this new force was developed by the Japanese physicist Yukawa [2], who suggested that the nucleons would exchange particles between each other and this mechanism would create the force. Yukawa constructed his theory in analogy to the theory of the electromagnetic interaction where the exchange of a (massless) photon is the cause of the force. However, in the case of the nuclear force, Yukawa assumed that the “force-makers” carry a mass that was in-between the masses of the electron and the proton (which is why these particles were eventually called “mesons”). The mass of the mesons limits the effect of the force to a finite range, since the uncertainty principal allows massive virtual particles to travel only a finite distance. The meson predicted by Yukawa was finally found in 1947 in cosmic ray and in 1948 in the laboratory and called the pion. Yukawa was awarded the Nobel Prize in 1949. In the 1950s and 60s more mesons were found in accelerator experiments and the meson theory of nuclear forces was extended to include many mesons. These models became known as one-boson-exchange models, which is a reference to the fact that the different mesons are exchanged singly in this model. The one-boson-exchange model is very successful in explaining essentially all properties of the nucleon-nucleon interaction at low energies [3,4,5,6,7,8,9]. In the 1970s and 80s, also meson models were developed that went beyond the simple single-particle exchange mechanism. These models included, in particular, the explicit exchange of two pions with all its complications. Well-known representatives of the latter kind are the Paris [10] and the Bonn potentials [11].
Since these meson models were quantitatively very successful, it appeared that they were the solution of the nuclear force problem. However, with the discovery (in the 1970s) that the fundamental theory of strong interactions is quantum chromodynamics (QCD) and not meson theory, all “meson theories” had to be viewed as models, and the attempts to derive the nuclear force from first principals had to start all over again.
The problem with a derivation of nuclear forces from QCD is two-fold. First, each nucleon consists of three valence quarks, quark-antiquark pairs, and gluons such that the system of two nucleons is a complicated many-body problem. Second, the force between quarks, which is created by the exchange of gluons, has the feature of being very strong at the low energy-scale that is characteristic of nuclear physics. This extraordinary strength makes it difficult to find converging expansions. Therefore, during the first round of new attempts, QCD-inspired quark models became popular. The positive aspect of these models is that they try to explain nucleon structure (made up from three constituent quarks) and nucleon-nucleon interactions (six quarks) on an equal footing. Some of the gross features of the two-nucleon force, like the “hard core” are explained successfully in such models. However, from a critical point of view, it must be noted that these quark-based approaches are yet another set of models and not a theory. Alternatively, one may try to solve the six-quark problem with brute computing power, by putting the six-quark system on a four dimensional lattice of discrete points which represents the three dimensions of space and one dimension of time. This method has become known as lattice QCD and is making progress. However, such calculations are computationally very expensive and cannot be used as a standard nuclear physics tool.
Around 1990, a major breakthrough occurred when the nobel laureate Steven Weinberg applied the concept of an effective field theory (EFT) to low-energy QCD [12,13]. He simply wrote down the most general theory that is consistent with all the properties of low-energy QCD, since that would make this theory equivalent to low-energy QCD. A particularly important property is the so-called chiral symmetry, which is “spontaneously” broken. Massless spin- fermions posses chirality, which means that their spin and momentum are either parallel (“right-handed”) or anti-parallel (“left-handed”) and remain so forever. Since the quarks, which nucleons are made of (“up” and “down” quarks), are almost mass-less, approximate chiral symmetry is a given. Naively, this symmetry should have the consequence that one finds in nature mesons of the same mass, but with positive and negative parity. However, this is not the case and such failure is termed a “spontaneous” breaking of the symmetry. According to a theorem first proven by Goldstone, the spontaneous breaking of a symmetry creates a particle, here, the pion. Thus, the pion becomes the main player in the production of the nuclear force. The interaction of pions with nucleons is weak as compared to the interaction of gluons with quarks. Therefore, pion-nucleon processes can be calculated without problem. Moreover, this effective field theory can be expanded in powers of momentum over “scale”, where scale denotes the “chiral symmetry breaking scale” which is about 1 GeV. This scheme is also known as chiral perturbation theory (ChPT) and allows to calculate the various terms that make up the nuclear potential systematically power by power, or order by order. Another advantage of the chiral EFT approach is its ability to generate not only the force between two nucleons, but also many-nucleon forces, on the same footing [14]. In modern theoretical nuclear physics, the chiral EFT approach is becoming increasingly popular and is applied with great success [15,16].
This article is organized as follows. In Section 2, we will present a pedagogical introduction into the EFT approach to low-energy QCD, including the development of effective Lagrangians. Section 3 provides a broad overview of the hierarchy of nuclear forces as they emerge from EFT. Section 4, Section 5 and Section 6 then spell out in detail the development of the two-nucleon forces from long-range to short-range and the construction of quantitative potentials. Section 7 concludes the article.
2. Effective Field Theory for Low-Energy QC
QCD is the theory of strong interactions. It deals with quarks, gluons and their interactions and is part of the Standard Model of Particle Physics. QCD is a non-Abelian gauge field theory with color the underlying gauge group. The non-Abelian nature of the theory has dramatic consequences. While the interaction between colored objects is weak at short distances or high momentum transfer (“asymptotic freedom”); it is strong at long distances ( fm) or low energies, leading to the confinement of quarks into colorless objects, the hadrons. Consequently, QCD allows for a perturbative analysis at large energies, whereas it is highly non-perturbative in the low-energy regime. Nuclear physics resides at low energies and the force between nucleons is a residual color interaction similar to the van der Waals force between neutral molecules. Therefore, in terms of quarks and gluons, the nuclear force is a very complicated problem that, nevertheless, can be attacked with brute computing power on a discretized, Euclidean space-time lattice (known as lattice QCD). In a recent study [17], the neutron-proton scattering lengths in the singlet and triplet S-waves have been determined in fully dynamical lattice QCD, with a smallest pion mass of 354 MeV. This result is then extrapolated to the physical pion mass with the help of chiral perturbation theory. The pion mass of 354 MeV is still too large to allow for reliable extrapolations, but the feasibility has been demonstrated and more progress can be expected for the near future. In a lattice calculation of a very different kind, the nucleon-nucleon () potential was studied [18]. The central part of the potential shows a repulsive core plus attraction of intermediate range. This is a very promising result, but it must be noted that also in this investigation still rather large pion masses are being used. In any case, advanced lattice QCD calculations are under way and continuously improved. However, since these calculations are very time-consuming and expensive, they can only be used to check a few representative key-issues. For everyday nuclear structure physics, a more efficient approach is needed.
The efficient approach is an effective field theory. For the development of an EFT, it is crucial to identify a separation of scales. In the hadron spectrum, a large gap between the masses of the pions and the masses of the vector mesons, like and , can clearly be identified. Thus, it is natural to assume that the pion mass sets the soft scale, , and the rho mass the hard scale, , also known as the chiral-symmetry breaking scale. This is suggestive of considering an expansion in terms of the soft scale over the hard scale, . Concerning the relevant degrees of freedom, we noticed already that, for the ground state and the low-energy excitation spectrum of an atomic nucleus as well as for conventional nuclear reactions, quarks and gluons are ineffective degrees of freedom, while nucleons and pions are the appropriate ones. To make sure that this EFT is not just another phenomenology, it must have a firm link with QCD. The link is established by having the EFT observe all relevant symmetries of the underlying theory. This requirement is based upon a “folk theorem” by Weinberg [12]:
If one writes down the most general possible Lagrangian, including all terms consistent with assumed symmetry principles, and then calculates matrix elements with this Lagrangian to any given order of perturbation theory, the result will simply be the most general possible S-matrix consistent with analyticity, perturbative unitarity, cluster decomposition, and the assumed symmetry principles.
In summary, the EFT program consists of the following steps:
- Identify the soft and hard scales, and the degrees of freedom appropriate for (low-energy) nuclear physics.
- Identify the relevant symmetries of low-energy QCD and investigate if and how they are broken.
- Construct the most general Lagrangian consistent with those symmetries and symmetry breakings.
- Design an organizational scheme that can distinguish between more and less important contributions: a low-momentum expansion.
- Guided by the expansion, calculate Feynman diagrams for the process under consideration to the desired accuracy.
This program works well for π-π [19] and π-N [20], since in these cases the physical amplitudes can be calculated perturbatively. However, as it turns out, the scenario is more complicated. It involves a bound state (the deuteron) and large scattering lengths (in S-waves), which cannot be explained in terms of perturbation theory. Therefore, Weinberg suggested [13] to use the above (perturbative) scheme to derive the potential and to apply this potential then in a Schrodinger or Lippmann-Schwinger equation to obtain the amplitude. Notice that this procedure implies a nonperturbative resummation of the potential. Consequently, even when the potential is calculated at a well-defined order, the axact order of the amplitude is not clear due to the resummation. This will also obscure the error estimate of the predicted observables. An exception is scattering in peripheral partial waves, which can be calculated perturbatively. Therefore, later in this article, we will first consider peripheral scattering (Section 5) before we discuss potential construction with all its conceptual problems (Section 6, particularly, Section 6.3).
To proceed, we will now elaborate on the above-listed steps, one by one. Since we discussed the first step already, we will address now step two.
2.1. Symmetries of Low-Energy QCD
In this section, we will give a brief introduction into (low-energy) QCD, its symmetries and symmetry breakings. More detailed presentations of this topic are provided in Refs. [15,21].
2.1.1. Chiral Symmetry
The QCD Lagrangian reads
with the gauge-covariant derivative
and the gluon field strength tensor
(for group indices, we use Latin letters, , and, in general, do not distinguish between subscripts and superscripts.) In the above, q denotes the quark fields and the quark mass matrix. Further, g is the strong coupling constant and are the gluon fields. The are the Gell-Mann matrices and the the structure constants of the Lie algebra ; summation over repeated indices is always implied. The gluon-gluon term in the last equation arises from the non-Abelian nature of the gauge theory and is the reason for the peculiar features of the color force.
The masses of the up , down , and strange (s) quarks are [22]:
These masses are small as compared to a typical hadronic scale, i.e., a scale of low-mass hadrons which are not Goldstone bosons, e.g., .
It is therefore of interest to discuss the QCD Lagrangian in the limit of vanishing quark masses:
Defining right- and left-handed quark fields,
with
we can rewrite the Lagrangian as follows:
This equation revels that the right- and left-handed components of massless quarks do not mix in the QCD Lagrangian. For the two-flavor case, this is symmetry, also known as chiral symmetry. However, this symmetry is broken in two ways: explicitly and spontaneously.
2.1.2. Explicit Symmetry Breaking
The mass term in the QCD Lagrangian Equation (1) breaks chiral symmetry explicitly. To better see this, let’s rewrite for the two-flavor case,
The first term in the last equation in invariant under (isospin symmetry) and the second term vanishes for . Thus, isospin is an exact symmetry if . However, both terms in Equation (11) break chiral symmetry. Since the up and down quark masses (Equations (4) and (5)) are small as compared to the typical hadronic mass scale of GeV, the explicit chiral symmetry breaking due to non-vanishing quark masses is very small.
2.1.3. Spontaneous Symmetry Breaking
A (continuous) symmetry is said to be spontaneously broken if a symmetry of the Lagrangian is not realized in the ground state of the system. There is evidence that the (approximate) chiral symmetry of the QCD Lagrangian is spontaneously broken—for dynamical reasons of nonperturbative origin which are not fully understood at this time. The most plausible evidence comes from the hadron spectrum.
From chiral symmetry, one naively expects the existence of degenerate hadron multiplets of opposite parity, i.e., for any hadron of positive parity one would expect a degenerate hadron state of negative parity and vice versa. However, these “parity doublets” are not observed in nature. For example, take the ρ-meson which is a vector meson of negative parity () and mass 776 MeV. There does exist a meson, the , but it has a mass of 1230 MeV and, therefore, cannot be perceived as degenerate with the ρ. On the other hand, the ρ meson comes in three charge states (equivalent to three isospin states), the and the , with masses that differ by at most a few MeV. Thus, in the hadron spectrum, (isospin) symmetry is well observed, while axial symmetry is broken: is broken down to .
A spontaneously broken global symmetry implies the existence of (massless) Goldstone bosons. The Goldstone bosons are identified with the isospin triplet of the (pseudoscalar) pions, which explains why pions are so light. The pion masses are not exactly zero because the up and down quark masses are not exactly zero either (explicit symmetry breaking). Thus, pions are a truly remarkable species: they reflect spontaneous as well as explicit symmetry breaking. Goldstone bosons interact weakly at low energy. They are degenerate with the vacuum and, therefore, interactions between them must vanish at zero momentum and in the chiral limit ().
2.2. Chiral Effective Lagrangians
The next step in our EFT program is to build the most general Lagrangian consistent with the (broken) symmetries discussed above. An elegant formalism for the construction of such Lagrangians was developed by Callan, Coleman, Wess, and Zumino (CCWZ) [23,24] who worked out the group-theoretical foundations of non-linear realizations of chiral symmetry. (An accessible introduction into the rather involved CCWZ formalism can be found in Ref. [21].) It is characteristic for these non-linear realizations that, whenever functions of the Goldstone bosons appear in the Langrangian, they are always accompanied with at least one space-time derivative. The Lagrangians given below are built upon the CCWZ formalism.
As discussed, the relevant degrees of freedom are pions (Goldstone bosons) and nucleons. Since the interactions of Goldstone bosons must vanish at zero momentum transfer and in the chiral limit (), the low-energy expansion of the Lagrangian is arranged in powers of derivatives and pion masses. The hard scale is the chiral-symmetry breaking scale, GeV. Thus, the expansion is in terms of powers of where Q is a (small) momentum or pion mass. This is chiral perturbation theory (ChPT).
The effective Lagrangian can formally be written as,
where deals with the dynamics among pions, describes the interaction between pions and a nucleon, and contains two-nucleon contact interactions which consist of four nucleon-fields (four nucleon legs) and no meson fields. The ellipsis stands for terms that involve two nucleons plus pions and three or more nucleons with or without pions, relevant for nuclear many-body forces (an example for this in lowest order are the last two terms of Equation (18), below). The individual Lagrangians are organized order by order:
and
where the superscript refers to the number of derivatives or pion mass insertions (chiral dimension) and the ellipsis stands for terms of higher dimensions.
Above, we have organized the Lagrangians by the number of derivatives or pion-mass insertions. This is the standard way, appropriate particularly for considerations of π-π and π-N scattering. As it turns out (cf. Section 3.1), for interactions among nucleons, it is sometimes useful to also consider the so-called index of the interaction,
where d is the number of derivatives or pion-mass insertions and n the number of nucleon field operators (nucleon legs). We will now write down the Lagrangian in terms of increasing values of the parameter Δ and we will do so using the so-called heavy-baryon formalism which we indicate by a “hat” [25].
The leading-order Lagrangian reads,
and subleading Lagrangians are,
where we included terms relevant for a calculation of the two-nucleon force up to sixth order. The Lagrangians and can be found in Ref. [26] and contact Lagrangians are given below. The pion fields are denoted by π and the heavy baryon nucleon field by N (). Furthermore, , , , and are the axial-vector coupling constant, pion decay constant, pion mass, and nucleon mass, respectively. Numerical values for these quantities will be given later. The are low-energy constants (LECs) from the dimension two Lagrangian and α is a parameter that appears in the expansion of the pion fields, see Ref. [15] for more details. Results are independent of α.
The lowest order (or leading order) Lagrangian has no derivatives and reads [13]
where and are unknown constants which are determined by a fit to the data.
The second order Lagrangian can be stated as follows [27]
Similar to and of Equation (23), the of Equation (24) are unknown constants which are fixed in a fit to the data. Obviously, these contact Lagrangians blow up quite a bit with increasing order, which is why we do not give and explicitly here. The contact potentials that emerge from the Lagrangians are given in Section 6.1.
3. Nuclear Forces from EFT: Overview
In the beginning of Section 2, we listed the steps we have to take for carrying out the EFT program of a derivation of the nuclear potential. So far, we discussed steps one to three. What is left are steps four (low-momentum expansion) and five (Feynman diagrams). In this section, we will say more about the expansion we are using and give an overview of the Feynman diagrams that arise order by order.
3.1. Chiral Perturbation Theory and Power Counting
Effective Langrangians have infinitely many terms, and an unlimited number of Feynman graphs can be calculated from them. Therefore, we need a scheme that makes the theory manageable and calculable. This scheme which tells us how to distinguish between large (important) and small (unimportant) contributions is chiral perturbation theory (ChPT).
In ChPT, graphs are analyzed in terms of powers of small external momenta over the large scale: , where Q is generic for a momentum (nucleon three-momentum or pion four-momentum) or a pion mass and GeV is the chiral symmetry breaking scale (hadronic scale, hard scale). Determining the power ν has become known as power counting.
For the moment, we will consider only so-called irreducible graphs. By definition, an irreducible graph is a diagram that cannot be separated into two by cutting only nucleon lines. Following the Feynman rules of covariant perturbation theory, a nucleon propagator is , a pion propagator , each derivative in any interaction is Q, and each four-momentum integration . This is also known as naive dimensional analysis. Applying then some topological identities, one obtains for the power of an irreducible diagram involving A nucleons [15]
with
where C denotes the number of separately connected pieces and L the number of loops in the diagram; is the number of derivatives or pion-mass insertions and the number of nucleon fields (nucleon legs) involved in vertex i; the sum runs over all vertices i contained in the diagram under consideration. Note that for all interactions allowed by chiral symmetry. Purely pionic interactions have at least two derivatives (); interactions of pions with a nucleon have at least one derivative (); and nucleon-nucleon contact terms () have . This demonstrates how chiral symmetry guarantees a low-energy expansion.
An important observation from power counting is that the powers are bounded from below and, specifically, . This fact is crucial for the convergence of the low-momentum expansion.
Moreover, the power formula Equation (25) allows to predict the leading orders of connected multi-nucleon forces. Consider a m-nucleon irreducibly connected diagram (m-nucleon force) in an A-nucleon system (). The number of separately connected pieces is . Inserting this into Equation (25) together with and yields . Thus, two-nucleon forces () start at , three-nucleon forces () at (but they happen to cancel at that order), and four-nucleon forces at (they don’t cancel). More about this in the next sub-section.
For later purposes, we note that for an irreducible diagram (, ), the power formula collapses to the very simple expression
In summary, the chief point of the ChPT expansion is that, at a given order ν, there exists only a finite number of graphs. This is what makes the theory calculable. The expression provides a rough estimate of the relative size of the contributions left out and, thus, of the accuracy at order ν. In this sense, the theory can be calculated to any desired accuracy and has predictive power.
3.2. The Hierarchy of Nuclear Forces
Chiral perturbation theory and power counting imply that nuclear forces emerge as a hierarchy controlled by the power ν, Figure 1.
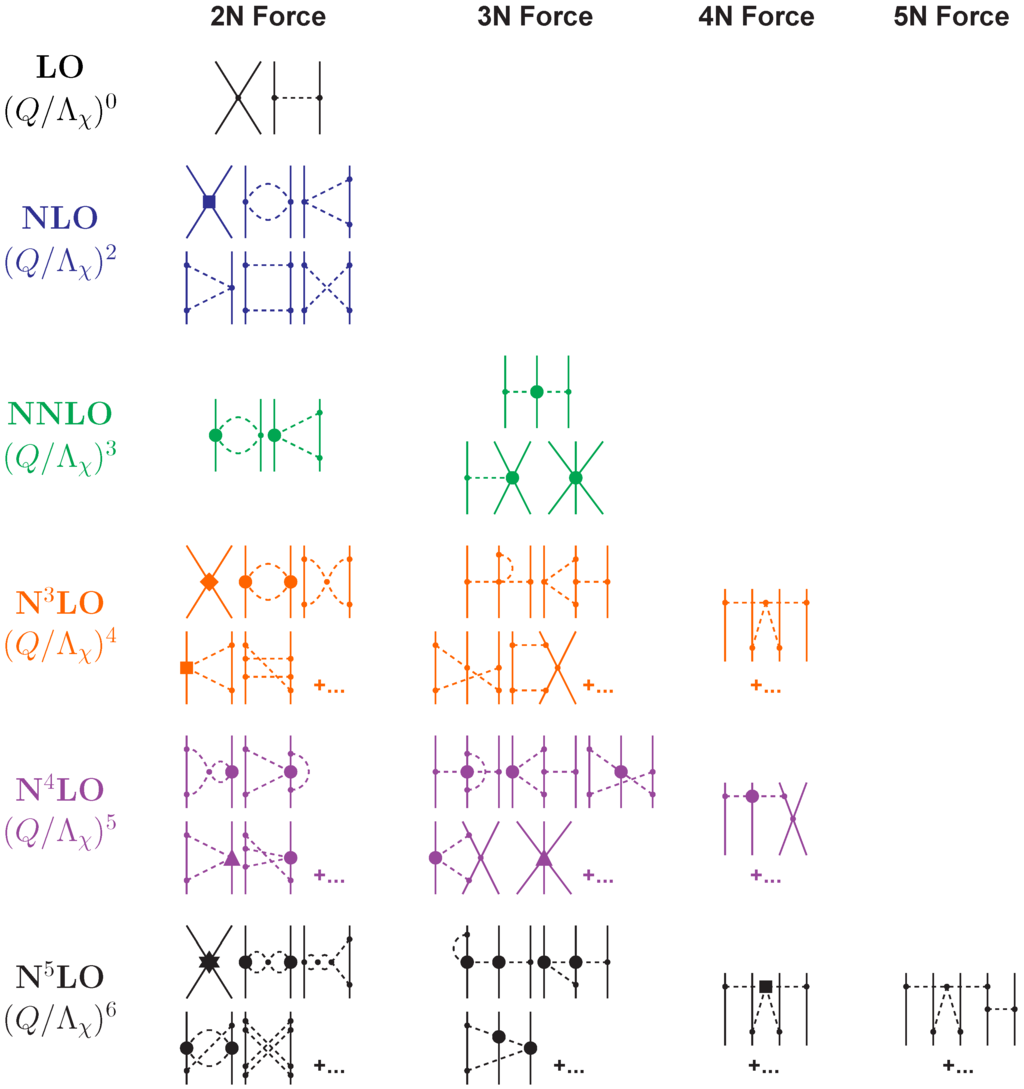
Figure 1.
Hierarchy of nuclear forces in chiral perturbation theory (ChPT). Solid lines represent nucleons and dashed lines pions. Small dots, large solid dots, solid squares, triangles, diamonds, and stars denote vertices of index 0, 1, 2, 3, 4, and 6, respectively. Further explanations are given in the text.
In lowest order, better known as leading order (LO, ), the amplitude is made up by two momentum-independent contact terms (), represented by the four-nucleon-leg graph with a small-dot vertex shown in the first row of Figure 1, and static one-pion exchange (1PE), second diagram in the first row of the figure. This is, of course, a rather rough approximation to the two-nucleon force (2NF), but accounts already for some important features. The 1PE provides the tensor force, necessary to describe the deuteron, and it explains scattering in peripheral partial waves of very high orbital angular momentum. At this order, the two contacts which contribute only in S-waves provide the short- and intermediate-range interaction which is somewhat crude.
In the next order, , all contributions vanish due to parity and time-reversal invariance.
Therefore, the next-to-leading order (NLO) is . Two-pion exchange (2PE) occurs for the first time (“leading 2PE”) and, thus, the creation of a more sophisticated description of the intermediate-range interaction is starting here. Since the loop involved in each pion-diagram implies already (cf. Equation (27)), the vertices must have . Therefore, at this order, only the lowest order and vertices are allowed which is why the leading 2PE is rather weak. Furthermore, there are seven contact terms of , shown by the four-nucleon-leg graph with a solid square, which contribute in S and P-waves. The operator structure of these contacts include a spin-orbit term besides central, spin-spin, and tensor terms. Thus, essentially all spin-isospin structures necessary to describe the two-nucleon force phenomenologically have been generated at this order. The main deficiency at this stage of development is an insufficient intermediate-range attraction.
This problem is finally fixed at order three (), next-to-next-to-leading order (NNLO). The 2PE involves now the two-derivative seagull vertices (proportional to the LECs) denoted by a large solid dot in Figure 1. These vertices represent correlated 2PE as well as intermediate -isobar contributions. It is well-known from the meson phenomenology of nuclear forces [10,11] that these two contributions are crucial for a realistic and quantitative 2PE model. Consequently, the 2PE now assumes a realistic size and describes the intermediate-range attraction of the nuclear force about right. There are no new contacts.
The reason why we talk of a hierarchy of nuclear forces is that two- and many-nucleon forces are created on an equal footing and emerge in increasing number as we go to higher and higher orders. At NNLO, the first set of nonvanishing three-nucleon forces (3NF) occur [28,29], cf. column “3N Force” of Figure 1. In fact, at the previous order, NLO, irreducible 3N graphs appear already, however, it has been shown by Weinberg [14] that these diagrams all cancel. Since nonvanishing 3NF contributions happen first at order , they are very weak as compared to the 2NF which starts at .
More 2PE is produced at , next-to-next-to-next-to-leading order (NLO), of which we show only a few symbolic diagrams in Figure 1. There is a large attractive one-loop 2PE contribution (the bubble diagram with two large solid dots ), which is slightly over-doing the intermediate-range attraction of the 2NF. Two-loop 2PE graphs show up for the first time and so does three-pion exchange (3PE) which necessarily involves two loops. 3PE was found to be negligible at this order [30,31]. Most importantly, 15 new contact terms arise and are represented by the four-nucleon-leg graph with a solid diamond. They include a quadratic spin-orbit term and contribute up to D-waves. Mainly due to the increased number of contact terms, a quantitative description of the two-nucleon interaction up to about 300 MeV lab. energy is possible, at NLO [15,32]. Besides further 3NF, four-nucleon forces (4NF) start at this order. Since the leading 4NF come into existence one order higher than the leading 3NF, 4NF are weaker than 3NF. Thus, ChPT provides a straightforward explanation for the empirically known fact that 2NF ≫ 3NF ≫ 4NF ….
Further, 2PE and 3PE occur at NLO (fifth order). The contribution to the 2NF at this order has been first calculated by Entem et al. [33]. It turns out to be moderately repulsive, thus, compensating for the attractive surplus generated at NLO by the bubble diagram with two solid dots. The long- and intermediate-range 3NF contributions at this order have been evaluated [26], but not applied yet in nuclear structure calculations. They are expected to be sizeable. Moreover, a new set of 3NF contact terms appear [34]. The NLO 4NF has not been derived yet. Due to the subleading seagull vertex (large solid dot ), this 4NF could be sizeable.
Finally turning to NLO (sixth order): The dominant 2PE and 3PE contributions to the 2NF have been derived by Entem et al. in Ref. [35], which represents the most sophisticated investigation ever conducted in chiral EFT for the system. The effects are small indicating the desired trend towards convergence of the chiral expansion for the 2NF. Moreover, a new set of 26 contact terms that contribute up to F-waves occurs (represented by the diagram with a star in Figure 1) bringing the total number of contacts to 50 [36]. The three-, four-, and five-nucleon forces of this order have not yet been derived.
This section has provided an overview. In the following sections, we will fill in all the details involved. We start by talking about the various pion-exchange contributions to the two-nucleon force.
4. Pion-Exchange Contributions to the Interaction
The various pion-exchange contributions to the potential may be analyzed according to the number of pions being exchanged between the two nucleons:
where the meaning of the subscripts is obvious and the ellipsis represents and higher pion exchanges. For each of the above terms, we have a low-momentum expansion:
where the superscript denotes the order ν of the expansion and the ellipses stand for contributions of seventh and higher orders. Due to parity and time-reversal, there are no first order contributions. Moreover, since n pions create loops, the leading order for n-pion exchange ocurrs at (cf. Equation (27)).
Order by order, the pion-exchange part of the potential builds up as follows:
where LO stands for leading order, NLO for next-to-leading order, etc.
The explicit expressions for the potentials will be stated in terms of contributions to the momentum-space amplitudes in the center-of-mass system (CMS), which arise from the following general decomposition:
where and denote the final and initial nucleon momenta in the CMS, respectively. Moreover, is the momentum transfer, the average momentum, and the total spin, with and the spin and isospin operators, of nucleon 1 and 2, respectively. For on-shell scattering, and () can be expressed as functions of and , only.
We will now discuss the contributions order by order.
4.1. Leading Order (LO)
At leading order, there is only the -exchange contribution, cf. Figure 1. The charge-independent -exchange is given by
Higher order corrections to the -exchange are taken care of by mass and coupling constant renormalizations which, in turn, are accounted for by working with the physical values. Note also that, on shell, there are no relativistic corrections. Thus, we apply -exchange in the form Equation (40) through all orders.
We use (instead of [37]) to account for the so-called Goldberger-Treiman discrepancy. Via the Goldberger-Treiman relation, , our value for together with MeV and MeV implies which is consistent with the empirical values obtained from and data analysis [38,39].
For results presented below, we will be specifically calculating neutron-proton () scattering and take the charge-dependence of the -exchange into account. Thus, the -exchange potential that we actually apply reads
where denotes the total isospin of the two-nucleon system and
We use MeV and MeV. Formally speaking, the charge-dependence of the 1PE exchange is of order NLO [15], but we include it already at leading order to make the comparison with the phase shifts more meaningful.
4.2. Next-to-Leading Order (NLO)
The 2PE contributions that occur at NLO (cf. Figure 1) are given by [40]:
where the (regularized) logarithmic loop function is given by:
with . denotes the cutoff of the spectral-function renormalization (SFR) [41]. Note that
is the logarithmic loop function of dimensional regularization.
4.3. Next-to-Next-to-Leading Order (NNLO)
The 2PE contributions to the 2NF at NNLO consist of a bubble diagram and a triangle diagram (cf. Figure 1). The bubble vanishes, because the loop integral involves an odd power of the time component the loop momentum. The triangle contribution is given by [40]:
The loop function that appears in the above expressions, regularized by spectral-function cut-off , is
and
yields the loop function used in dimensional regularization.
4.4. Next-to-Next-to-Next-to-Leading Order (NLO)
The 2PE contributions at NLO are shown in Figure 2. They consist of three parts, which we will discuss now one by one.
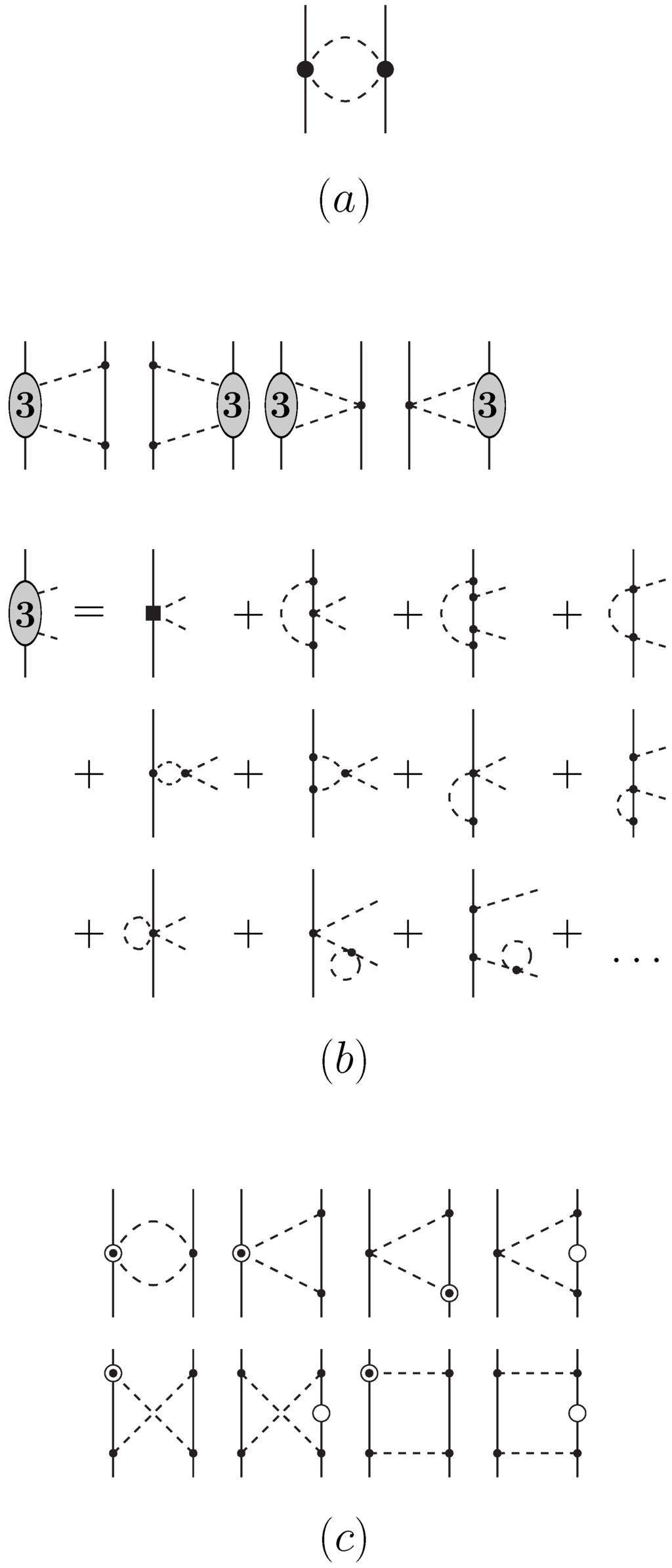
Figure 2.
Next-to-Next-to-Next-to-Leading Order (NLO) two-pion exchange contributions with (a) the NLO football diagram; (b) the leading 2PE two-loop contributions; and (c) the relativistic corrections of NLO diagrams. Notation as in Figure 1. Shaded ovals represent complete -scattering amplitudes with their order specified by the number in the oval. Open circles denote relativistic corrections.
4.4.1. Football diagram at NLO
4.4.2. Leading Two-Loop Contributions
The leading order -exchange two-loop diagrams are shown in Figure 2b. In terms of spectral functions, the results are [42]:
where .
The momentum space amplitudes and are obtained from the above expressions by means of subtracted dispersion integrals:
and similarly for . We use for the dispersion integrals that contribute at NLO and NLO, and at NLO. Moreover, is applied for two-pion exchange and for three-pion exchange. For the above dispersion integrals yield the results of dimensional regularization, while for finite we have what has become known as spectral-function regularization (SFR) [41]. The purpose of the finite scale is to constrain the imaginary parts to the low-momentum region where chiral effective field theory is applicable. In practice, we will keep GeV. Ideally, one may wish to take . However, it turns out that this leads to unrealistic results for reasons that are not fully understood at this time. This issue warrants further investigation.
4.4.3. Leading Relativistic Corrections
Counting , the relativistic corrections of the NLO diagrams, which are shown in Figure 2c, are of order NLO and are given by [15]:
4.4.4. Leading Three-Pion Exchange Contributions
The leading -exchange contributions that occur NLO are shown in Figure 3. They have been calculated in Refs. [30,31] and are found to be negligible. We, therefore, omit them.
Figure 3.
NLO three-pion exchange contributions. Notation as in Figure 1.
4.5. Next-to-Next-to-Next-to-Next-to-Leading Order (NLO)
4.5.1. Two-Pion Exchange Contributions at NLO
The -exchange contributions that occur at NLO are displayed graphically in Figure 4. We can distinguish between three groups of diagrams.
Figure 4.
NLO two-pion-exchange contributions. (a) The leading one-loop amplitude is folded with the chiral vertices proportional to ; (b) The one-loop amplitude proportional to is folded with the leading order chiral amplitude; (c) Relativistic corrections of next-to-next-to-leading order (NNLO) diagrams. Notation as in Figure 1 and Figure 2.
First, there are the NLO -exchange two-loop contributions of class (a), Figure 4a. For this class the spectral functions are obtained by integrating the product of the leading one-loop amplitude and the chiral vertex proportional to over the Lorentz-invariant -phase space.
Second, we have the NLO -exchange two-loop contributions of class (b), Figure 4b. Here, the product of the one-loop amplitude proportional to (see Ref. [26] for details) and the leading order chiral amplitude is integrated over the -phase space.
The analytic expressions for the spectral functions of class (a) and (b) are very involved, which is why we do not reprint them here. The interested reader is referred to Ref. [33].
Finally, there also some relativistic corrections. This group consists of diagrams with one vertex proportional to and one correction. A few representative graphs are shown in Figure 4c. Since in this investigation we count , these relativistic corrections are formally of order NLO. The result for this group of diagrams is [42]:
4.5.2. Three-Pion Exchange Contributions at NLO
The -exchange of order NLO is shown in Figure 5. The spectral functions for these diagrams have been calculated in Ref. [43]. We use here the classification scheme introduced in that reference and note that class XI vanishes. Moreover, we find that the class X and part of class XIV make only negligible contributions. Thus, we include in our calculations only class XII and XIII, and the contribution of class XIV. For the very involved expressions, we refer the interested reader to Ref. [33].
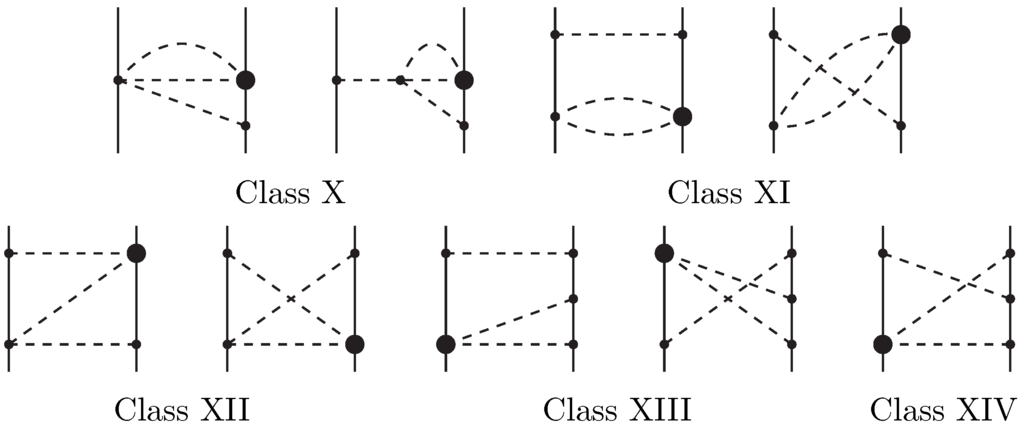
Figure 5.
NLO three-pion exchange contributions. Roman numerals refer to sub-classes following the scheme introduced in Refs. [33,43]. Notation as in Figure 1.
4.6. Next-to-Next-to-Next-to-Next-to-Next-to-Leading Order (NLO)
4.6.1. Two-Pion Exchange Contributions at NLO
The -exchange contributions that occur at NLO are displayed graphically in Figure 6. We will now discuss each class separately.
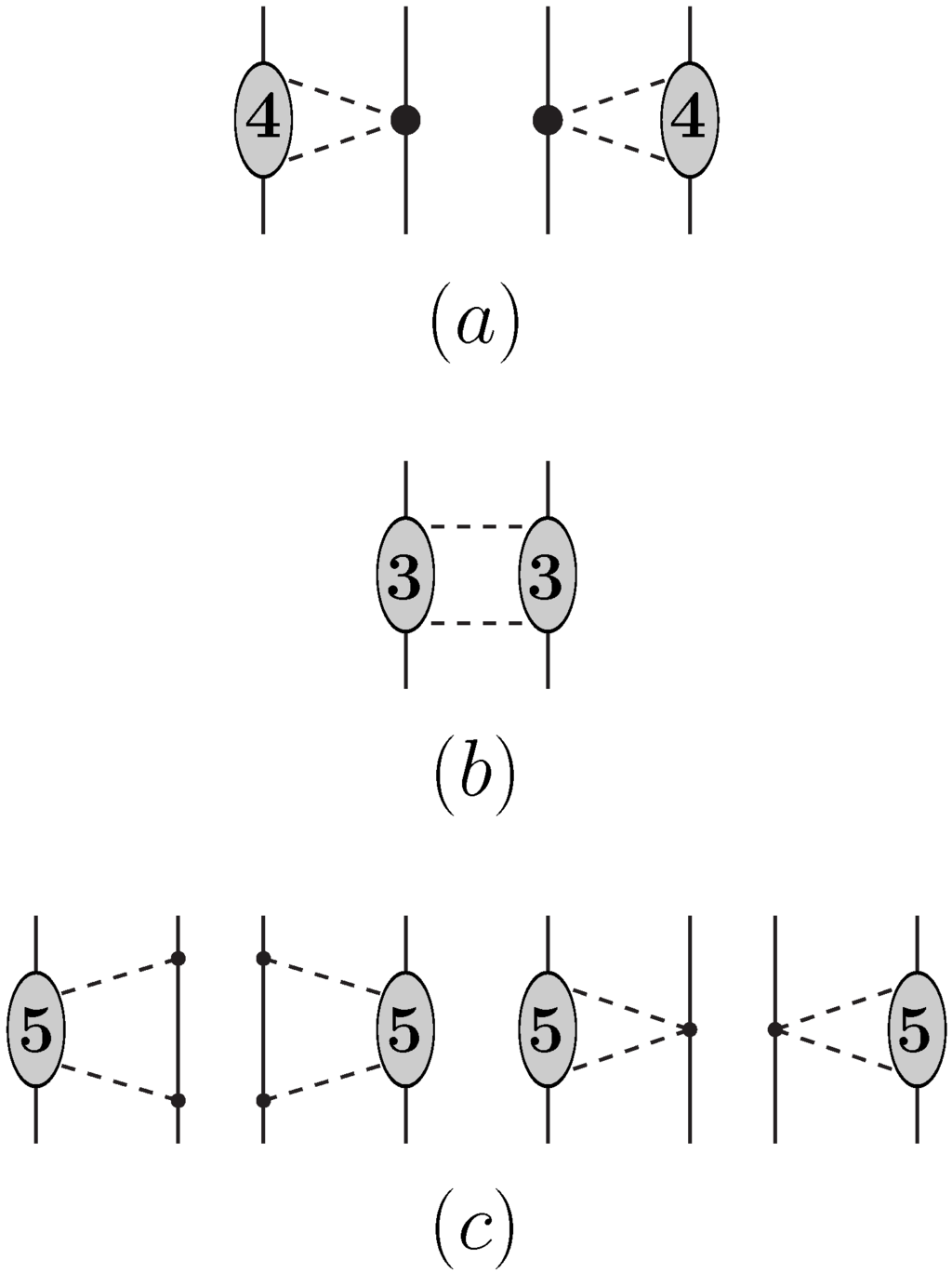
Figure 6.
NLO two-pion-exchange contributions. (a) The subleading one-loop -amplitude is folded with the chiral -vertices proportional to ; (b) The leading one-loop -amplitude is folded with itself; (c) The leading two-loop -amplitude is folded with the tree-level -amplitude. Notation as in Figure 1, Figure 2, and Figure 4.
The NLO -exchange two-loop contributions, denoted by class (a), are shown in Figure 6a. For this class the spectral functions are obtained by integrating the product of the subleading one-loop -amplitude (see Ref. [26] for details) and the chiral -vertex proportional to over the Lorentz-invariant -phase space [35].
A first set of -exchange contributions at three-loop order, denoted by class (b), is displayed in Figure 6b. Here, the leading one-loop -scattering amplitude is multiplied with itself and integrated over the -phase space [35].
Further -exchange three-loop contributions at NLO, denoted by class (c), are shown in Figure 6c. For these, the two-loop -scattering amplitude (which is of order five) would have to be folded with the tree-level -amplitude. To our knowledge, the two-loop elastic -scattering amplitude has never been evaluated in some decent analytical form. Note that the loops involved in the class (c) contributions include only leading order chiral -vertices. According to our experience such contributions are typically small. For these reasons, class (c) is neglected.
Besides the above, there are also some relativistic -corrections. This group consists of the -corrections to the chiral leading -exchange diagrams. Since we count , these relativistic corrections are formally of sixth order (NLO). The expressions for the corresponding -amplitudes can be found in Ref. [44]:
4.6.2. Three-Pion Exchange Contributions at NLO
The -exchange contributions of order NLO are shown in Figure 7. We can distinguish between two classes.
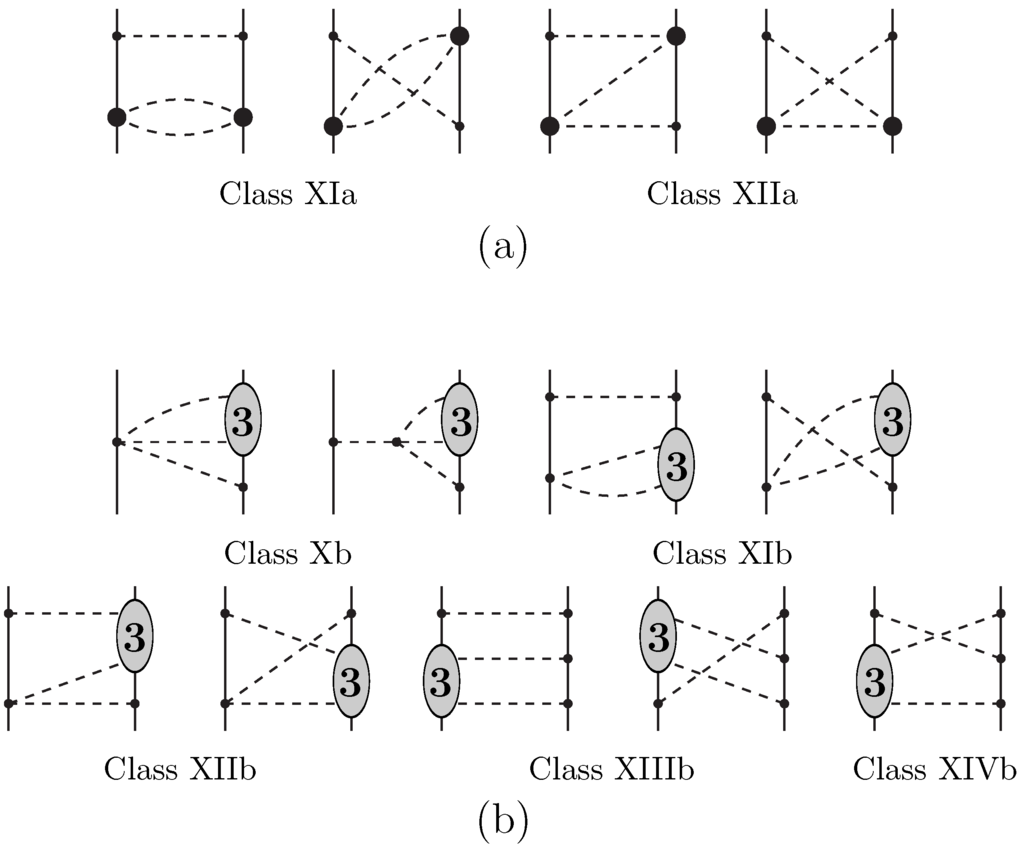
Class (a) consists of the diagrams displayed in Figure 7a. They are characterized by the presence of one subleading -vertex in each nucleon line. Using a notation introduced in Refs. [33,43], we distinguish between the various sub-classes of diagrams by roman numerals.
Class (b) is shown in Figure 7b. Each -exchange diagram of this class includes the one-loop -amplitude (completed by the low-energy constants ). Only those parts of the -scattering amplitude, which are either independent of the pion CMS-energy or depend on it linearly could be treated with the techniques available. The contributions are, in general, small. Results presented below include only the larger portions within this class. The omitted pieces are about one order of magnitude smaller. To facilitate a better understanding, we have subdivided this class into sub-classes labeled by roman numerals, following Refs. [33,43].
The very involved analytic expressions for the spectral function can be found in Ref. [35].
4.6.3. Four-Pion Exchange at NLO
The exchange of four pions between two nucleons occurs for the first time at NLO. The pertinent diagrams involve three loops and only leading order vertices, which explains the sixth power in small momenta. Three-pion exchange with just leading order vertices turned out to be negligibly small [30,31], and so we expect four-pion exchange with leading order vertices to be even smaller. Therefore, we can safely neglect this contribution.
5. Perturbative Scattering in Peripheral Partial Waves
Nucleon-nucleon scattering in peripheral partial waves is of special interest—for several reasons. First, these partial waves probe the long- and intermediate-range of the nuclear force. Due to the centrifugal barrier, there is only small sensitivity to short-range contributions; e.g., the contact terms at NLO make no contributions for orbital angular momenta . Thus, at NLO, for F and higher waves and energies below the pion-production threshold, we have a window in which the interaction is governed by chiral symmetry alone (chiral one- and multi-pion exchanges), and we can conduct a relatively clean test of how well the theory works. Using values for the LECs from analysis, the predictions are even parameter free. Moreover, the smallness of the phase shifts in peripheral partial waves suggests that the calculation can be done perturbatively. This avoids the complications and possible model-dependence (e.g., cutoff dependence) that the non-perturbative treatment of the Lippmann-Schwinger equation, necessary for low partial waves, is beset with.
The perturbative K-matrix for scattering is calculated as follows:
with as in Equation (41), and representing the once iterated one-pion exchange (1PE) given by
where denotes the principal value integral and . A calculation at LO includes only the first term on the right hand side of Equation (69), , while calculations at NLO or higher order also include the second term on the right hand side, . At NNLO, the twice iterated 1PE should be included, too; and at higher orders further iterations should be accounted for. However, we found that the difference between the once iterated 1PE and the infinitely iterated 1PE is so small that it could not be identified on the scale of our phase shift figures. For that reason, we omit iterations of 1PE beyond what is contained in . Furthermore, stands for terms where irreducible 2PE is iterated with 1PE.
Finally, the fourth term on the r.h.s. of Equation (69), , stands for the irreducible multi-pion exchange contributions that occur at the order at which the calculation is conducted. In multi-pion exchanges, we use the average pion mass MeV and, thus, neglect the charge-dependence due to pion-mass splitting in irreducible multi-pion diagrams.
Throughout this paper, we use
Based upon relativistic kinematics, the CMS on-shell momentum p is related to the kinetic energy of the incident neutron in the laboratory system (“Lab. Energy”), , by
with MeV and MeV the proton and neutron masses, respectively.
The K-matrix, Equation (69), is decomposed into partial waves following Ref. [45] and phase shifts are then calculated via
For more details concerning the evaluation of phase shifts, including the case of coupled partial waves, see Ref. [46] or the appendix of [9].
Chiral symmetry establishes a link between the dynamics in the -system and the -system (through common low-energy constants). In order to check the consistency, we use the LECs for subleading -couplings as determined in analyses of low-energy elastic -scattering. Appropriate analyses for our purposes are contained in Refs. [26], where -scattering has been calculated at fourth order using the same power-counting of relativistic -corrections as in the present work. Ref. [26] performed two fits, one to the GW [47] and one to the KH [48] partial wave analysis resulting in the two sets of LECs listed in Table 1.

Table 1.
Low-energy constants as determined in Ref. [26]. The sets “GW” and “KH” are based upon the partial wave analyses of Refs. [47,48], respectively. The appear in Equation (18) and are in units of GeV. The and belong to and (cf. Equations (19) and (20)) and are in units of GeV and GeV, respectively.
The contributions up to NLO and their impact on peripheral scattering have been discussed and demonstrated in detail in Ref. [15] and, therefore, we will not repeat it here. However, we will present the recent progress that has been made in the calculation of orders beyond NLO.
We first show how the individual NLO (fifth-order) contributions impact phase shifts in peripheral waves. For this purpose, we display in Figure 8 phase shifts for six important peripheral partial waves, namely, , , , , , and . In each frame, the following curves are shown:
- NLO.
- The previous curve plus the corrections (denoted by “c/M”), Figure 4c.
- The previous curve plus the NLO -exchange two-loop contributions of class (a), Figure 4a.
- The previous curve plus the NLO two-loop contributions of class (b), Figure 4b.
- The previous curve plus the NLO -exchange contributions, Figure 5.
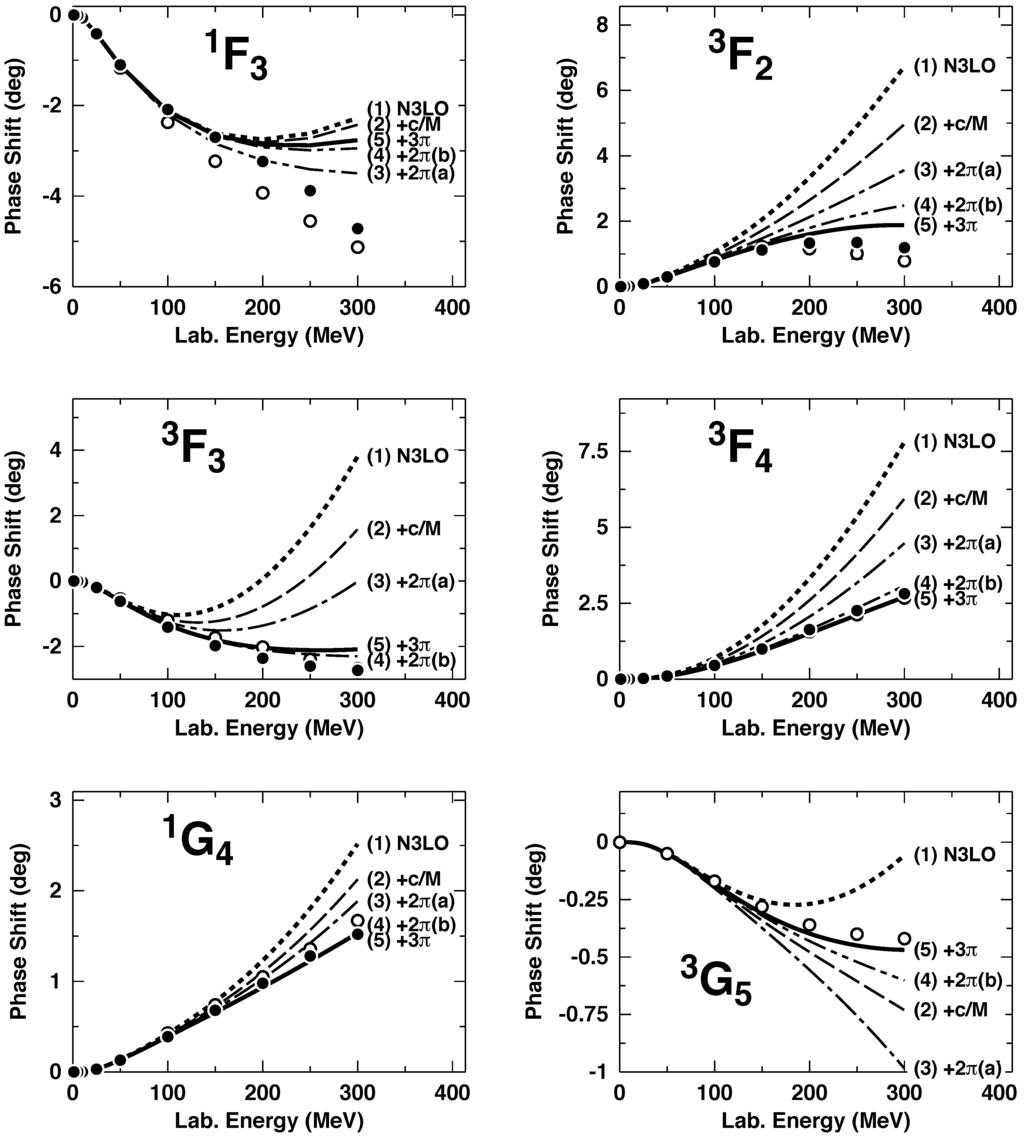
Figure 8.
Effect of individual NLO (fifth-order) contributions on the neutron-proton phase shifts of some selected peripheral partial waves. The individual contributions are added up successively in the order given in parenthesis next to each curve. Curve (1) is NLO and curve (5) is the complete NLO. The KH low-energy constants (LECs) are used and = 1.5 GeV. The filled and open circles represent the results from the Nijmegan multi-energy phase-shift analysis [50] and the VPI/GWU single-energy analysis SM99 [51], respectively.
In summary, the various curves add up successively the individual NLO contributions in the order indicated in the curve labels. The last curve in this series, curve (5), is the full NLO result. In these calculations, a SFR cutoff GeV is applied (cf. Equation (57)) and the KH LECs (cf. Table 1) are used.
From Figure 8, we make the following observations. In triplet F-waves, the corrections as well as the 2PE two-loops, class (a) and (b), are all repulsive and of about the same strength. As a consequence, the problem of the excessive attraction, that NLO is beset with, is overcome. A similar trend is seen in . An exception is , where the class (b) contribution is attractive leading to phase shifts above the data for energies higher than 150 MeV.
Now turning to the NLO 3PE contributions (curve (5) in Figure 8): they are substantially smaller than the 2PE two-loop ones, in all peripheral partial waves. This can be interpreted as an indication of convergence with regard to the number of pions being exchanged between two nucleons—a trend that is very welcome. Further, note that the total 3PE contribution is a very comprehensive one, cf. Figure 5. It is the sum of ten terms which, individually, can be fairly large. However, destructive interference between them leads to the small net result.
For all F- and G-waves (except ), the final NLO result is close to the empirical phase shifts. Notice that this includes also , which posed persistent problems at NLO [49].
It is also of interest to know how predictions change with variations of within a reasonable range. We have, therefore, varied between 0.7 and 1.5 GeV and show the predictions for all F and G-waves in Figure 9 and Figure 10, respectively, in terms of colored bands. It is seen that, at NLO, the variations of the predictions are very large and always too attractive while, at NLO, the variations are small and the predictions are close to the data or right on the data. Figure 9 and Figure 10 also include the lower orders (LO, NLO, and NNLO) such that a comparison of the relative size of the order-by-order contributions is possible. We observe that there is not much of a convergence, since obviously the magnitudes of the NNLO, NLO, and NLO contributions are about the same.
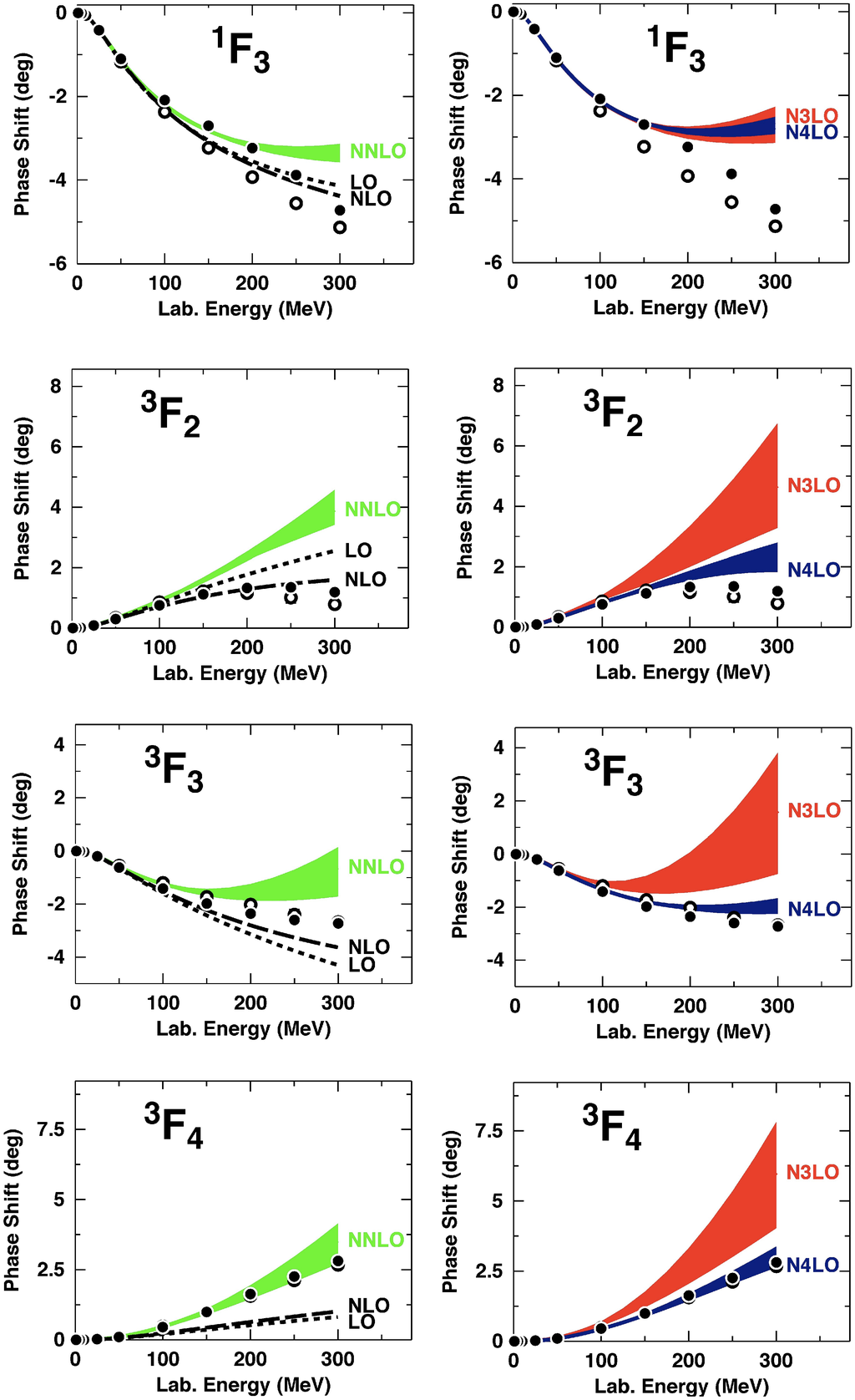
Figure 9.
Phase-shifts of neutron-proton scattering at various orders up to NLO. The colored bands show the variation of the predictions when the spectral-function renormalization (SFR) cutoff is changed over the range 0.7 to 1.5 GeV. The KH LECs are applied. Empirical phase shifts as in Figure 8.
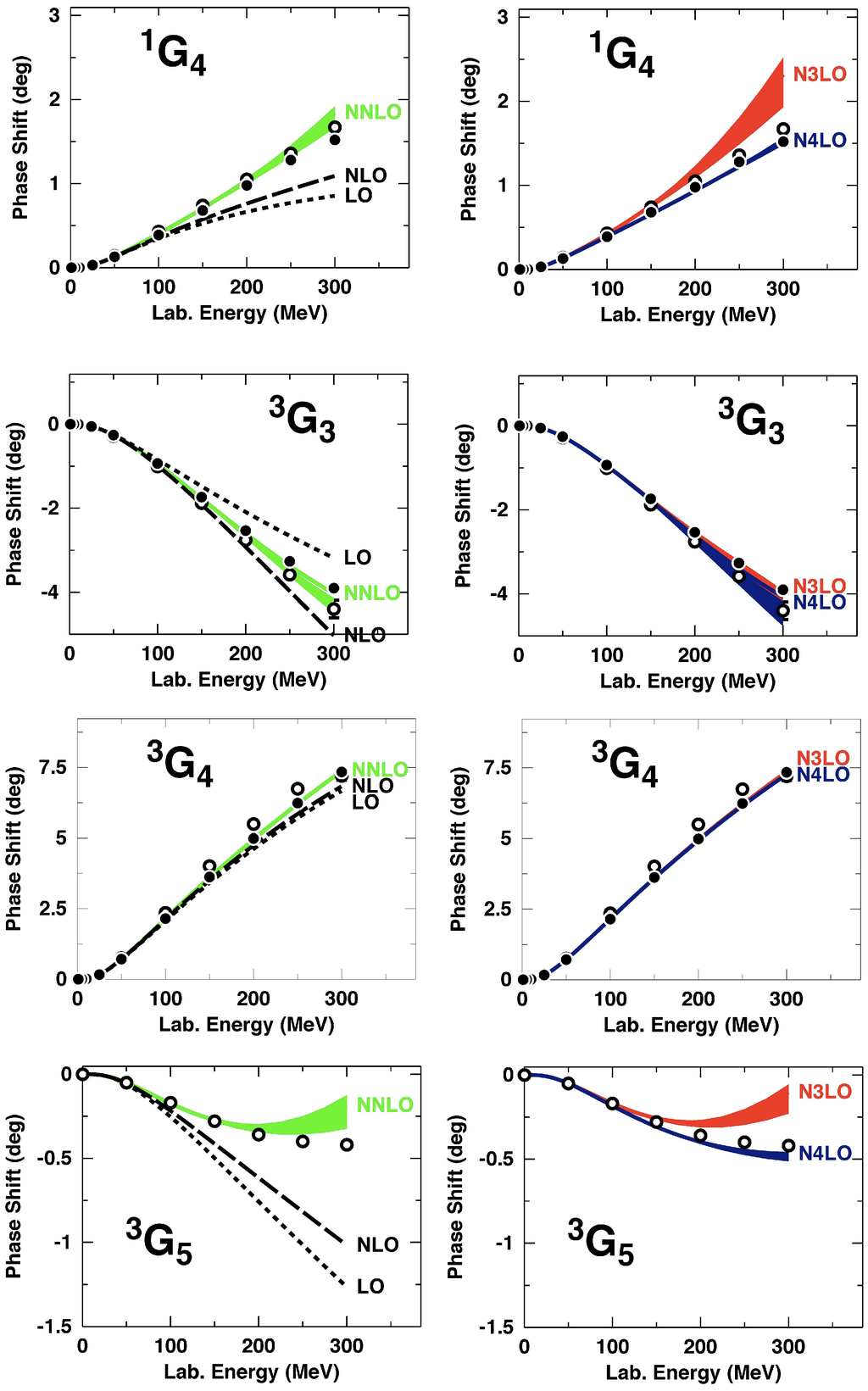
Figure 10.
Same as Figure 9, but for G-waves.
Therefore, next, we turn to the NLO contributon. As shown in Figure 6 and Figure 7, the sixth-order corrections consist of several contributions. As in the case of NLO, we will first show how the individual NLO contributions impact -phase-shifts in peripheral waves. In Figure 11, we display phase-shifts for two peripheral partial waves, namely, , and . The following curves are shown:
- NLO.
- The previous curve plus the NLO -exchange contributions of class (a), Figure 6a.
- The previous curve plus the NLO -exchange contributions of class (b), Figure 6b.
- The previous curve plus the NLO -exchange contributions of class (a), Figure 7a.
- The previous curve plus the NLO -exchange contributions of class (b), Figure 7b.
- The previous curve plus the -corrections (denoted by “1/M2”) [44].
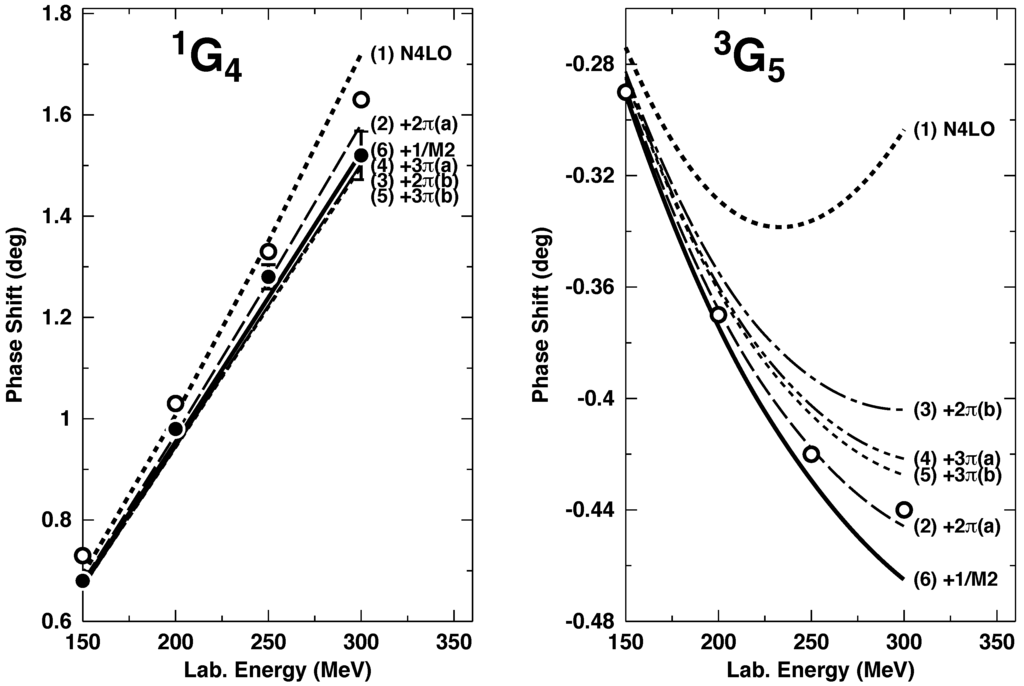
Figure 11.
Effect of individual NLO (sixth-order) contributions on the neutron-proton phase shifts of two G-waves. The individual contributions are added up successively in the order given in parentheses next to each curve. Curve (1) is NLO and curve (6) contains all NLO contributions calculated in Ref. [35]. A SFR cutoff MeV is applied and the GW LECs are used. The filled and open circles represent the results from the Nijmegen multi-energy phase-shift analysis [50] and the GWU -analysis SP07 [52], respectively.
The last curve in this series, curve (6), includes all NLO contributions calculated in Ref. [35]. For all curves of this figure, a SFR cutoff MeV (cf. Equation (57)) is employed and the GW (cf. Table 1) LECs are used.
From Figure 11, we see that the two-loop -exchange class (a), Figure 6a, generates a strong repulsive central force, while the spin-spin and tensor forces provided by this class are negligible. The fact that this class produces a relatively large contribution is not unexpected, since it is proportional to . The -exchange contribution class (b), Figure 6b, creates a moderately repulsive central force as seen by its effect on and a noticeable tensor force as the impact on demonstrates. The -exchange class (a), Figure 7a, is negligible in , but noticeable in and, therefore, it should not be neglected. This contribution is proportional to , which suggests a non-negligible size but it is typically smaller than the corresponding -exchange contribution class (a). The -exchange class (b) contribution, Figure 7b, turns out to be negligible (see the difference between curve (4) and (5) in Figure 11). This may not be unexpected since it is a three-loop contribution with only leading-order vertices. Finally the relativistic -corrections to the leading -exchange [44] have a small but non-negligible impact, particularly in .
The NLO predictions for all G and H-waves, are displayed in Figure 12 in terms of colored bands that are generated by varying the SFR cutoff (cf. Equation (57)) between 700 and 900 MeV. The figure clearly reveals again that, at NLO, the predictions are, in general, too attractive. As discussed, the NLO contribution, essentially, compensates this attractive surplus. NLO then adds additional repulsion bringing the final prediction right onto the data (i.e., empirical phase-shifts). Moreover, the NLO contribution is, in general, substantially smaller than the one at NLO, thus, showing a signature of convergence of the chiral expansion.
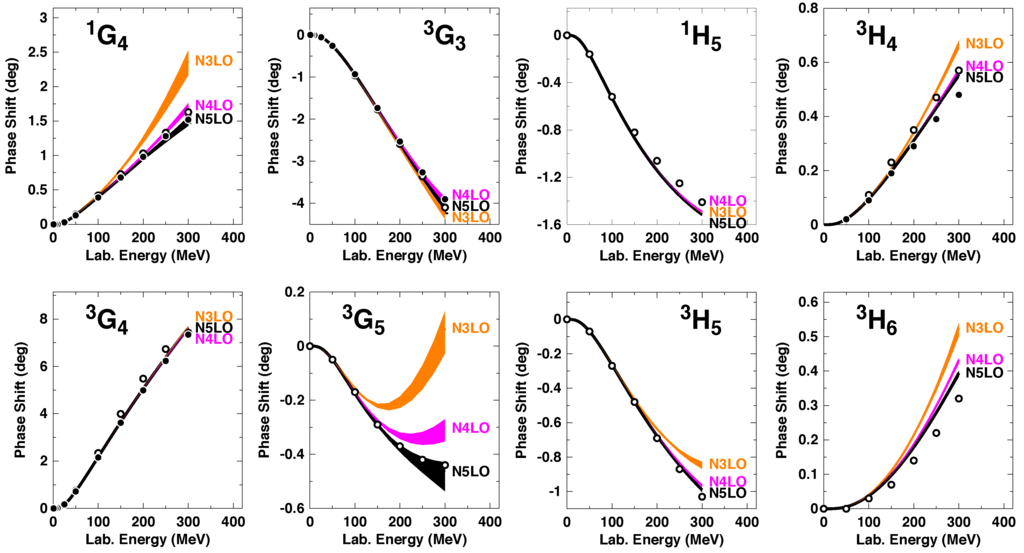
Figure 12.
Phase-shifts of neutron-proton scattering in G and H-waves at NLO, NLO, and NLO. The colored bands show the variations of the predictions when the SFR cutoff is changed over the range 700 to 900 MeV. The GW LECs are applied. Empirical phase shifts are as in Figure 11.
To summarize, we present in Figure 13 a comparison between all orders from LO to NLO. Note that the difference between the LO prediction (one-pion-exchange, dotted line) and the data (filled and open circles) is to be provided by two- and three-pion exchanges, i.e., the intermediate-range part of the nuclear force. How well that is accomplished is a crucial test for any theory of nuclear forces. NLO produces only a small contribution, but NLO creates substantial intermediate-range attraction (most clearly seen in , , and ). In fact, NLO is the largest contribution among all orders. This is due to the one-loop -exchange triangle diagram which involves one -contact vertex proportional to . This vertex represents correlated 2PE as well as intermediate -isobar excitation. It is well-known from the traditional meson theory of nuclear forces [10,11,53] that these two features are crucial for a realistic and quantitative 2PE model. Consequently, the one-loop -exchange at NLO is attractive and assumes a realistic size describing the intermediate-range attraction of the nuclear force about right. At NLO, more one-loop 2PE is added by the bubble diagram with two -vertices, a contribution that seemingly is overestimating the attraction. This attractive surplus is then compensated by the prevailingly repulsive two-loop - and -exchanges that occur at NLO and NLO.
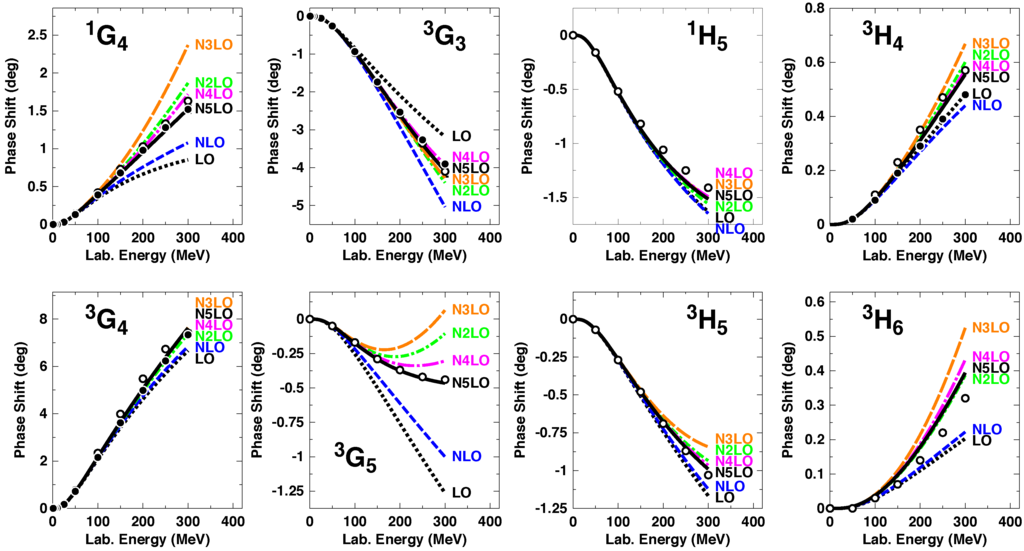
Figure 13.
Phase-shifts of neutron-proton scattering in G- and H-waves at all orders from LO to NLO. A SFR cutoff MeV is used and the GW LECs are applied. Empirical phase shifts are as in Figure 11.
In this context, it is worth to note that also in conventional meson theory [11] the one-loop models for the 2PE contribution always show some excess of attraction (cf. Figure 7, Figure 8 and Figure 9 of Ref. [49]). The same is true for the dispersion theoretic approach pursued by the Paris group [10,53]. In conventional meson theory, the surplus attraction is reduced by heavy-meson exchange (ρ- and ω-exchange) which, however, has no place in chiral effective field theory (as a finite-range contribution). Instead, in the latter approach, two-loop - and -exchanges provide the corrective action.
6. Constructing Chiral Potentials
In previous sections, we discussed the pion-exchange contributions to the interaction. They describe the long- and intermediate-range parts of the nuclear force, which are governed by chiral symmetry and rule the peripheral partial waves. However, for a “complete” nuclear force, we have to describe correctly all partial waves, including the lower ones. In fact, in calculations of observables at low energies (cross sections, analyzing powers, etc.), the partial waves with are the most important ones, generating the largest contributions. The same is true for microscopic nuclear structure calculations. The lower partial waves are dominated by the dynamics at short distances. Therefore, we need to look now into the short-range part of the potential.
6.1. Contact Terms
In conventional meson theory, the short-range nuclear force is described by the exchange of heavy mesons, notably the . Qualitatively, the short-distance behavior of the potential is obtained by Fourier transform of the propagator of a heavy meson,
ChPT is an expansion in small momenta Q, too small to resolve structures like a or meson, because . But the latter relation allows us to expand the propagator of a heavy meson into a power series,
where the ω is representative for any heavy meson of interest. The above expansion suggests that it should be possible to describe the short distance part of the nuclear force simply in terms of powers of , which fits in well with our over-all power expansion since . Since such terms act directly between nucleons, they are dubbed contact terms.
Contact terms play an important role in renormalization. Regularization of the loop integrals that occur in multi-pion exchange diagrams typically generates polynomial terms with coefficients that are, in part, infinite or scale dependent (cf. Appendix B of Ref. [15]). Contact terms absorb infinities and remove scale dependences, which is why they are also known as counter terms.
The partial-wave decomposition of a power has an interesting property. First note that Q can only be either the momentum transfer between the two interacting nucleons, q, or the average momentum k (see below Equation (39) for their definitions). In any case, for even ν,
where stands for a polynomial of degree m and θ is the CMS scattering angle. The partial-wave decomposition of for a state of orbital-angular momentum L involves the integral
where is a Legendre polynomial. Due to the orthogonality of the ,
Consequently, contact terms of order zero contribute only in S-waves, while order-two terms contribute up to P-waves, order-four terms up to D-waves, etc.
Due to parity, only even powers of Q are allowed. Thus, the expansion of the contact potential is formally given by
where the supersript denotes the power or order.
We will now present, one by one, the various orders of contact terms which result from the contact Lagrangians shown at the end of Section 2.2.
6.1.1. Zeroth Order (LO)
The contact Lagrangian , Equation (23), which is part of , Equation (17), leads to the following contact potential,
and, in terms of partial waves, we have
6.1.2. Second Order (NLO)
The contact Lagrangian , Equation (24), which is part of , Equation (19), generates the following contact potential
The coefficients used here in the contact potential are, of course, related to the coefficients that occur in the Lagrangian , Equation (24). The relation, which is unimportant for our purposes, can be found in Refs. [27,54].
There are many ways to perform the partial-wave decomposition of the above potential. We perceive the method presented by Erkelenz, Alzetta, and Holinde [45] as the most elegant one. Thus, one obtains
with
6.1.3. Fourth Order (NLO)
The contact potential of order four reads
The rather lengthy partial-wave expressions of this order are given in Appendix E of Ref. [15].
6.1.4. Sixth Order (NLO)
At sixth order, 26 new contact terms appear, bringing the total number to 50. These terms as well as their partial-wave decomposition have been worked out in Ref. [36]. So far, these terms have not been used in the construction of potentials.
6.2. Definition of Potential
We have now rounded up everything needed for a realistic nuclear force—long, intermediate, and short ranged components—and so we can finally proceed to the lower partial waves. However, here we encounter another problem. The two-nucleon system at low angular momentum, particularly in S-waves, is characterized by the presence of a shallow bound state (the deuteron) and large scattering lengths. Thus, perturbation theory does not apply. In contrast to π-π and π-N, the interaction between nucleons is not suppressed in the chiral limit (). Weinberg [13] showed that the strong enhancement of the scattering amplitude arises from purely nucleonic intermediate states (“infrared enhancement”). He therefore suggested to use perturbation theory to calculate the potential (i.e., the irreducible graphs) and to apply this potential in a scattering equation to obtain the amplitude. We will follow this prescription and discuss the problems with this approach in the next subsection.
The pion-exchange parts of the potential were spelled out in Equations (33)–(38). To obtain the complete potential, one just has to add to this the contact terms listed in Equation (79). Thus, one has to do the following extensions to some of the Equations (33)–(38):
and no changes to and .
The potential V as derived in previous sections is, in principal, an invariant amplitude and, thus, satisfies a relativistic scattering equation, for which we choose the BbS equation [15], which reads explicitly,
with . The advantage of using a relativistic scattering equation is that it automatically includes relativistic corrections to all orders. Thus, in the scattering equation, no propagator modifications are necessary when raising the order to which the calculation is conducted.
Defining
and
where the factor is added for convenience, the BbS equation collapses into the usual, nonrelativistic Lippmann-Schwinger (LS) equation,
Since satisfies Equation (93), it can be used like a nonrelativistic potential, and may be perceived as the conventional nonrelativistic T-matrix. In applications, it is more convenient to use the K-matrix instead of the T-matrix and to have the LS equation decomposed into partial waves: all these technical issues are explained in detail in Appendix A of Ref. [9] where also the formulas for the calculation of and (the latter with Coulomb) phase shifts are provided. The partial wave decomposition of the operators by which the potential is represented can be found in Section 4 of Ref. [45], and numerical methods for solving the LS equation are explained in Ref. [46].
6.3. Regularization and Non-Perturbative Renormalization
Iteration of in the LS equation, Equation (93), requires cutting off for high momenta to avoid infinities. This is consistent with the fact that ChPT is a low-momentum expansion which is valid only for momenta GeV. Therefore, the potential is multiplied with the regulator function ,
with
such that
Typical choices for the cutoff parameter Λ that appears in the regulator are GeV. At NLO and NLO, an appropriate choice for n is three.
Equation (96) provides an indication of the fact that the exponential cutoff does not necessarily affect the given order at which the calculation is conducted. For sufficiently large n, the regulator introduces contributions that are beyond the given order. Assuming a good rate of convergence of the chiral expansion, such orders are small as compared to the given order and, thus, do not affect the accuracy at the given order. In calculations, one uses, of course, the exponential form, Equation (95), and not the expansion Equation (96). On a similar note, we also do not expand the square-root factors in Equations (91)–(92) because they are kinematical factors which guarantee relativistic elastic unitarity.
It is pretty obvious that results for the T-matrix may depend sensitively on the regulator and its cutoff parameter. This is acceptable if one wishes to build models. For example, the meson models of the past [8,11] always depended sensitively on the choices for the cutoff parameters which, in fact, were important for the fit of the data. However, the EFT approach wishes to be fundamental in nature and not just another model.
In field theories, divergent integrals are not uncommon and methods have been developed for how to deal with them. One regulates the integrals and then removes the dependence on the regularization parameters (scales, cutoffs) by renormalization. In the end, the theory and its predictions do not depend on cutoffs or renormalization scales.
So-called renormalizable quantum field theories, like QED, have essentially one set of prescriptions that takes care of renormalization through all orders. In contrast, EFTs are renormalized order by order.
The renormalization of perturbative EFT calculations is not a problem. The problem is nonperturbative renormalization. This problem typically occurs in nuclear EFT because nuclear physics is characterized by bound states which are nonperturbative in nature. EFT power counting may be different for nonperturbative processes as compared to perturbative ones. Such difference may be caused by the infrared enhancement of the reducible diagrams generated in the LS equation.
Weinberg’s implicit assumption [13] was that the counterterms introduced to renormalize the perturbatively calculated potential, based upon naive dimensional analysis (“Weinberg counting”), are also sufficient to renormalize the nonperturbative resummation of the potential in the LS equation. In 1996, Kaplan, Savage, and Wise (KSW) [55,56,57] pointed out that there are problems with the Weinberg scheme if the LS equation is renormalized by minimally-subtracted dimensional regularization. This criticism resulted in a flurry of publications on the renormalization of the nonperturbative problem [58,59,60,61,62,63,64,65,66,67,68,69,70,71,72]. The literature is too comprehensive to discuss all contributions. Let us just mention some of the work that has particular relevance for our present discussion.
If the potential V consists of contact terms only (also known as pion-less theory), then the nonperturbative summation Equation (93) can be performed analytically and the power counting is explicit. However, when pion exchange is included, then Equation (93) can be solved only numerically and the power counting is less transparent. Perturbative ladder diagrams of arbitrarily high order, where the rungs of the ladder represent a potential made up from irreducible pion exchange, suggest that an infinite number of counterterms is needed to achieve cutoff independence for all the terms of increasing order generated by the iterations. For that reason, KSW [55,56,57] proposed to sum the leading-order contact interaction to all orders (analytically) and to add higher-order contacts and pion exchange perturbatively up to the given order. Unfortunately, it turned out that the order by order convergence of 1PE is poor in the - state [58,59]. The failure was triggered by the singularity of the 1PE tensor force when iterated to second order. Therefore, KSW counting is no longer taken into consideration (see, however, [60]). A balanced discussion of possible solutions is provided in [61].
Some researchers decided to take a second look at Weinberg’s original proposal. A systematic investigation of Weinberg counting in leading order has been conducted by Nogga, Timmermans, and van Kolck [62] in momentum space, and by Valderrama and Arriola at LO and higher orders in configuration space [63]. A comprehensive discussion of both approaches and their equivalence can be found in Ref. [64].
The LO potential is given in Equation (86) and consists of 1PE plus two nonderivative contact terms that contribute only in S-waves. Nogga et al. [62] find that the given counterterms renormalize the S-waves (i.e., stable results are obtained for ) and the naively expected infinite number of counterterms is not needed. This means that Weinberg power counting does actually work in S-waves at LO (ignoring the dependence of the contact interaction discussed in Refs. [55,61]). However, there are problems with a particular class of higher partial waves, namely those in which the tensor force from 1PE is attractive. The first few cases of this kind of low angular momentum are , , and , which need a counterterm for cutoff independence. The leading (nonderivative) counterterms do not contribute in P and higher waves, which is why Weinberg counting fails in these cases. But the second order contact potential provides counterterms for P-waves. Therefore, the promotion of, particularly, the and contacts from NLO to LO would fix the problem in P-waves. To take care of the problem, a NLO contact, i.e., a term from , needs to be promoted to LO. Partial waves with orbital angular momentum may be calculated in Born approximation with sufficient accuracy and, therefore, do not pose renormalization problems. In this way, one arrives at a scheme of “modified Weinberg counting” [62] for the leading order two-nucleon interaction.
6.3.1. Renormalization Beyond Leading Order
As shown below, for a quantitative chiral potential one needs to advance all the way to NLO. Thus, the renormalization issue needs to be discussed beyond LO. Naively, the most perfect renormalization procedure is the one where the cutoff parameter Λ is carried to infinity while stable results are maintained. This was done successfully at LO in the work by Nogga et al. [62] described above. At NNLO, the infinite-cutoff renormalization procedure has been examined in [68,69,70] for partial waves with total angular momentum and in [63] for all partial waves with . At NLO, an investigation of all partial waves up to has been conducted in Ref. [73]. From all of these works, it is evident that no counter term is effective in partial-waves with short-range repulsion and only a single counter term can effectively be used in partial-waves with short-range attraction. Thus, for the renormalization prescription, even at NLO, we have either one or no counter term per partial-wave state. This is inconsistent with any reasonable power-counting scheme and, therefore, defies the principals of an EFT.
A possible way out of this dilemma was proposed already in [62] and reiterated in a paper by Long and van Kolck [71]. In the latter reference, the authors examine the renormalization of an attractive potential perturbed by a correction. Generalizing their findings, they come to the conclusion that, for any attractive potential (with ), partial waves with low angular momentum L must be summed to all orders and one contact term is needed for each L to renormalize the LO contribution. However, there exists an angular momentum ( for the nuclear case, cf. Ref. [62]), above which the leading order can be calculated perturbatively. In short, naive dimensional analysis (NDA) does not apply at LO below . However, once this failure of NDA is corrected at LO, higher order corrections can be added in perturbation theory using counterterm that follow NDA [71].
Reference [71] used just a toy model. A full investigation using the chiral expansion has been performed by Valderrama [74,75]. The author renormalizes the LO interaction nonperturbatively and then uses the LO distorted wave to calculate the 2PE contributions at NLO and NNLO perturbatively. It turns out that perturbative renormalizability requires the introduction of 21 counterterms up to D-waves as compared to 9 counterterms in the Weinberg scheme, which reduces the predictive power. The distribution of the contact operators in Ref. [75] largely agrees with the related renormalization group analysis by Birse [65]. The perturbative treatment of the subleading pieces of the interaction requires rather soft cutoffs, which is worrysome.
However, even if one consideres the Valderrama project [74,75] as successful for scattering, there is doubt if the interaction generated in this approach is of any use for applications in nuclear few- and many-body problems. In applications, one would first have to solve the many-body problem with the renormalized LO interaction, and then add higher order corrections in perturbation theory. However, it was shown in Ref. [76] that the renormalized LO interaction is characterized by a very large tensor force from 1PE. This is no surprise since LO is renormalized with implying that the 1PE, particulary its tensor force, is totally uncut. As a consequence of this, the wound integral in nuclear matter, κ, comes out to be about 40%. The hole-line and coupled cluster expansions are know to converge with n the number of hole-lines or particles per cluster [77]. For conventional nuclear forces, the wound integral is typically between 5% and 10% and the inclusion of three-body clusters (or three hole-lines) are needed to obtain converged results in the many-body system [78]. Thus, if the wound integral is 40%, probably, up to six hole-lines need to be included for approximate convergence. Such calculations are not feasible even with the most powerful computers of today and will not be feasible any time soon. Therefore, even though the renormalization procedure pursued in [74,75] seems to work for scattering, the interaction produced will be highly impractical (to say the least) in applications in few- and many-body problems because of convergence problems with the many-body energy and wave functions.
6.3.2. Back to the Beginnings
The various problems with the renormalization procedures discussed above may have a simple common reason: An EFT that has validity only for momenta is applied such that momenta are heavily involved (because the regulator cutoff ). A paper by Epelbaum and Gegelia [79] illustrates the point: The authors construct an exactly solvable toy-model that simulates a pionful EFT and yields finite results for . However, as it turns out, these finite results are incompatible with the underlying EFT, while for cutoffs in the order of the hard scale consistency is maintained. In simple terms, the point to realize is this: If an EFT calculation produces (accidentally) a finite result for , then that does not automatically imply that this result is also meaningful.
This matter is further elucidated in the lectures by Lepage of 1997 [80]. Lepage points out that it makes little sense to take the momentum cutoff beyond the range of validity of the effective theory. By assumption, our data involves energies that are too low—wave lengths that are too long—to probe the true structure of the theory at very short distances. When one goes beyond the hard-scale of the theory, structures are seen that are almost certainly wrong. Thus, results cannot improve and, in fact, they may degrade or, in more extreme cases, the theory may become unstable or untunable. In fact, in the case, this is what is happening in several partial waves (as reported above). Therefore, Lepage suggests to take the following three steps when building an effective theory:
- Incorporate the correct long-range behavior: The long-range behavior of the underlying theory must be known, and it must be built into the effective theory. In the case of nuclear forces, the long-range theory is, of course, well known and given by one- and multi-pion exchanges.
- Introduce an ultraviolet cutoff to exclude high-momentum states, or, equivalent, to soften the short-distance behavior: The cutoff has two effects: First it excludes high-momentum states, which are sensitive to the unknown short-distance dynamics; only states that we understand are retained. Second it makes all interactions regular at , thereby avoiding the infinities that beset the naive approach.
- Add local correction terms (also known as contact or counter terms) to the effective Hamiltonian. These mimic the effects of the high-momentum states excluded by the cutoff introduced in the previous step. In the meson-exchange picture, the short-range nuclear force is described by heavy meson exchange, like the and . However, at low energy, such structures are not resolved. Since we must include contact terms anyhow, it is most efficient to use them to account for any heavy-meson exchange as well. The correction terms systematically remove dependence on the cutoff.
A systematic investigation of this kind has been conducted in Ref. [81]. In that work, the error of the predictions was quantified by calculating the /datum for the reproduction of the neutron-proton () elastic scattering data as a function of the cutoff parameter Λ of the regulator function Equation (95). Predictions by chiral potentials at order NLO and NNLO were investigated applying Weinberg counting for the counter terms ( contact terms). The results from this study for the energy range 35–125 MeV are shown in the upper frame of Figure 14 and for 125–183 MeV in the lower frame. It is seen that the reproduction of the data at these energies is generally poor at NLO, while at NNLO the /datum assumes acceptable values (a clear demonstration of order-by-order improvement). Moreover, at NNLO one observes “plateaus” of constant low for cutoff parameters ranging from about 450 to 850 MeV. This may be perceived as cutoff independence (and, thus, successful renormalization) for the relevant range of cutoff parameters.
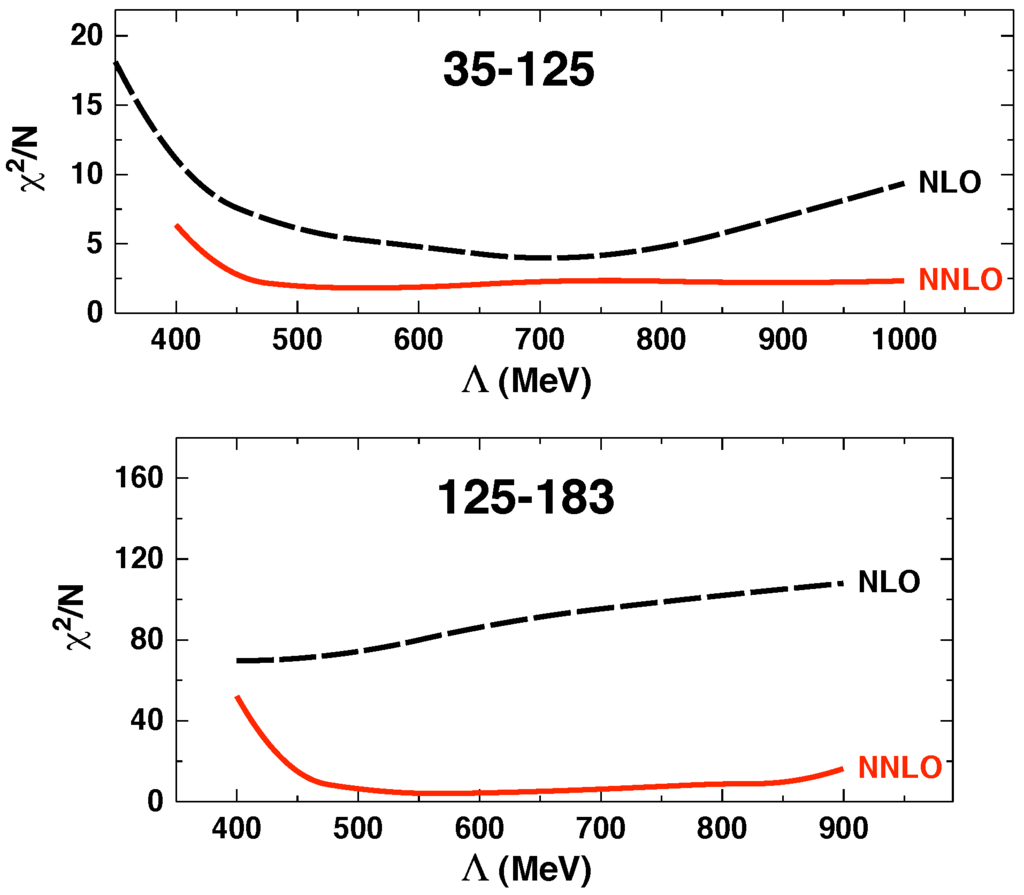
Figure 14.
/datum for the reproduction of the data in the energy range 35–125 MeV (upper frame) and 125–183 MeV (lower frame) as a function of the cutoff parameter Λ of the regulator function Equation (95). The (black) dashed curves show the /datum achieved with potentials constructed at order NLO and the (red) solid curves are for NNLO.
6.4. Potentials Order by Order
As discussed, potentials can be calculated at various orders, cf. Equations (33)–(38) and Equations (86)–(89), and the accuracy improves as the order increases. How well the chiral expansion converges in the important lower partial waves is demonstrated in Figure 15, where we show the phase parameters for potentials constructed through all orders from LO to NLO. These figures clearly reveal substantial improvements in the reproduction of the empirical phase shifts with increasing order.
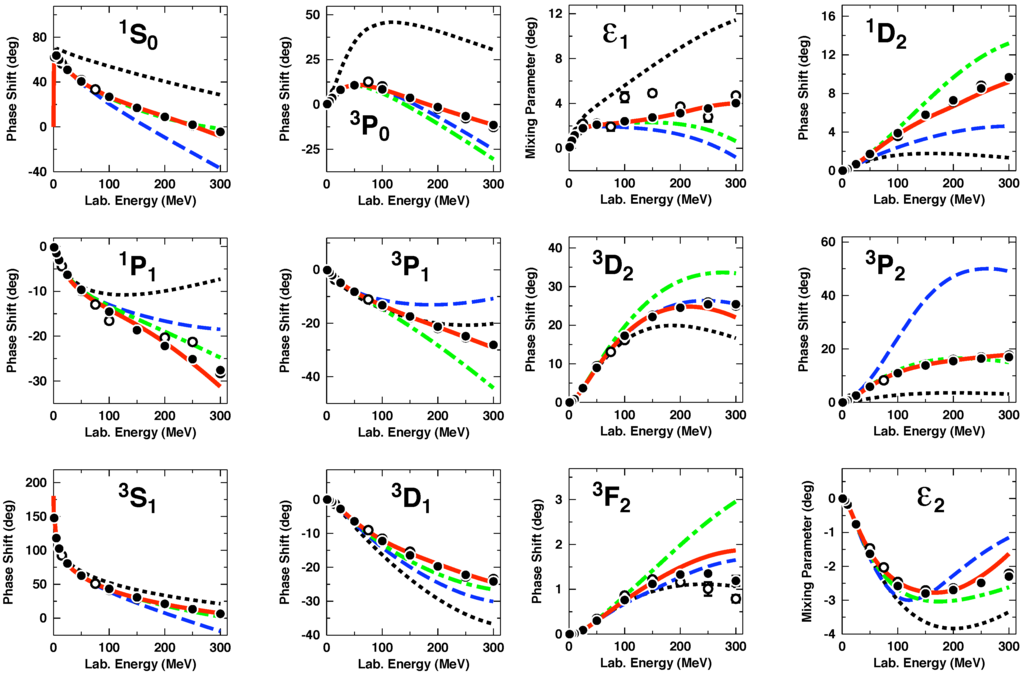
Figure 15.
Phase shifts of scattering as calculated from potentials at different orders of ChPT. The black dotted line is LO(500), the blue dashed is NLO(550/700) [41], the green dash-dotted NNLO(600/700) [41], and the red solid NLO(500) [32], where the numbers in parentheses denote the cutoffs in MeV. Phase parameters with total angular momentum are displayed. Empirical phase shifts (solid dots and open circles) as in Figure 8.
There is an even better way to confront theory with experiment. One calculates observables of scattering and compares this directly to the experimental data. It is customary to state the result of such a comparison in terms of the /datum where a value around unity would signify a perfect fit.
Let’s start with potentials developed to NLO and NNLO. In Table 2, we show the /datum for the fit of the world data below 290 MeV for families of potentials at NLO and NNLO constructed by the Bochum group [41]. The NLO potentials produce the very large /datum between 67 and 105, and the NNLO are between 12 and 27, consistent with the findings of Ref. [81] shown in Figure 14.

Table 2.
Columns three and four show the /datum for the reproduction of the 1999 database (defined in Ref. [9]) by families of potentials at NLO and NNLO constructed by the Bochum group [41]. The /datum is stated in terms of ranges which result from a variation of the cutoff parameters used in the regulator functions. The values of these cutoff parameters in units of MeV are given in parentheses. denotes the kinetic energy of the incident neutron in the laboratory system.
The rate of improvement from one order to the other is very encouraging, but the quality of the reproduction of the data at NLO and NNLO is obviously insufficient for reliable predictions. Based upon these facts, it has been pointed out in 2002 by Entem and Machleidt [49,82] that one has to proceed to NLO. Consequently, the first NLO potential was published in 2003 [32].
At NLO (), there are a total of 24 contact terms (24 parameters) which contribute to the partial waves with , while at NLO and NNLO there are only 9 contacts with (cf. Section 6.1 and Table 3). These LECs are essentially free constants which parametrize the short-ranged phenomenological part of the interaction. Table 3 shows how these terms are distributed over partial waves. One reason for the improved reproduction of the phase shifts (and observables) at NLO is the fact that, at that order, contacts appear for the first time in D-waves. D-waves are not truely peripheral and, therefore, 1PE plus 2PE alone do not describe them well. The D-wave contacts provide the necessary short-range corrections to predict the D-phases right. Furthermore, at NLO, another contact is added to each P-wave, which leads to substantial improvements, particularly, in and above 100 MeV (cf. Figure 15).

Table 3.
Number of parameters needed for fitting the data in the Nijmegen phase-shift analysis and by the high-precision CD-Bonn potential versus the total number of contact terms of EFT based potentials to different orders.
In Table 3, we also show the number of parameters used in the Nijmegen partial wave analysis (PWA93) [50] and in the high-precision CD-Bonn potential [9]. The table reveals that, for S and P-waves, the number of parameters used in high-precision phenomenology and in EFT at NLO () are about the same. Thus, the EFT approach provides retroactively a justification for the phenomenology used in the 1990s to obtain high-precision fits.
The 24 parameters of NLO are close to the 30+ used in PWA93 and high precision potentials. Consequently, at NLO, potentials can be constructed which are of about the same quality as the high-precision potentials of the 1990s [9,83,84]. This fact is clearly revealed in the datum for the fit of the and data below 290 MeV shown in Table 4 and Table 5, respectively. The Idaho NLO potential [32] with MeV produces a /datum = 1.1 for the world data below 290 MeV which compares well with the /datum = 1.04 by the Argonne potential. In 2005, also the Bochum group produced several NLO potentials [85], the best of which fits the data with a /datum = 1.7 and the worse with 7.9 (Table 4).

Table 4.
Columns three to five display the /datum for the reproduction of the 1999 database (defined in Ref. [9]) by various potentials. For the chiral potentials, the /datum is stated in terms of ranges which result from a variation of the cutoff parameters used in the regulator functions. The values of these cutoff parameters in units of MeV are given in parentheses. denotes the kinetic energy of the incident nucleon in the laboratory system.

Table 5.
Same as Table 4 but for .
As we turn now to , note first that the for data are typically larger than for because of the higher precision of data (Table 5). Thus, the Argonne produces a /datum = 1.4 for the world data below 290 MeV and the best Idaho NLO potential obtains 1.5. The fit by the best Bochum NLO potential results in a /datum = 2.9 and the worst produces 22.3. In view of these poor , the Bochum group has recently launched an attempt towards improving their chiral potentials [86,87]. However, as in their previous work [85], they have fitted their new potentials only to phase shifts and not the data. The for the reproduction of the data by the new Bochum potentials are not available and, thus, no reliable statement about the quality of the new potentials can be made. In the 1990s, the Nijmegen group has pointed out repeatedly that for high quality potentials it is insufficient to fit phase shifts only. A seemingly “good” fit of phase shifts can be misleading and can result in a poor for the reproduction of the data.
Turning now to NLO: Based upon the derivation of the 2PE and 3PE contributions to the interaction at NLO by Entem et al. [33] presented in Section 4.5 and applied in peripheral scattering in Section 5, potential at NLO have recently been developed [33,87]. Note that the lower partial waves, which are crucial for a quantitative reproduction of the data, are ruled by the contact terms. The number of contacts at NLO () is the same as at NLO (). Thus, the NLO potentials are not very different from the NLO ones. Note also that the high quality of some of the NLO potentials [15,32] leaves little room for improvements.
A further increase in accuracy (if needed) could be achieved at NLO (), where the number of contact terms advances to 50 (Table 3) [36]. As discussed in Section 4.6, the dominant 2PE and 3PE contributions at NLO have been derived [35]. Thus, all the mathematical material for the construction of NLO potentials is available. However, it is debatable if there is a need for them.
7. Conclusions
The past 15 years have seen great progress in our understanding of nuclear forces in terms of low-energy QCD. Key to this development was the realization that low-energy QCD is equivalent to an effective field theory (EFT) which allows for a perturbative expansion that has become known as chiral perturbation theory (ChPT). In this framework, two- and many-body forces emerge on an equal footing and the empirical fact that nuclear many-body forces are substantially weaker than the two-nucleon force is explained naturally.
In this review, we have focused on the two-nucleon force. We have presented the order-by-order contributions from LO () to NLO (). Using low-energy constants (LECs) determined from scattering, our predictions are parameter-free, except for the spectral function cutoff that regularizes the dispersion integrals which determine the amplitudes. This spectral-function regularization ensures that the calculated contributions are restricted to the long- and intermediate range, where chiral effective field theory is applicable. Specifically, we have calculated scattering in peripheral partial-waves, which is dominated by one-, two-, and three-pion exchanges ruled by chiral symmetry. The order-by-order covergence is slow, but is ultimately achieved at NLO, where predictions are in perfect agreement with empirical phase shifts.
This review has summarized the most comprehensive investigation of the implications of chiral symmtry for the system. The results provide the ultimate confirmation that chiral EFT is an adequate theory for the nucleon-nucleon interaction.
Acknowledgments
The reseach by the author is supported in part by the US Department of Energy under Grant No. DE-FG02-03ER41270.
Conflicts of Interest
The author declares no conflict of interest.
References and Notes
- Chadwick, J. The existence of a neutron. Proc. Roy. Soc. 1932, A136, 692–708. [Google Scholar] [CrossRef]
- Yukawa, H. On the interaction of elementary particles. I. Proc. Phys. Math. Soc. Jpn. 1935, 17, 48–57. [Google Scholar]
- Bryan, R.A.; Scott, B.L. Nucleon-nucleon scattering from one-boson-exchange potentials. Phys. Rev. 1964, 135, B434–B450. [Google Scholar] [CrossRef]
- Bryan, R.A.; Scott, B.L. Nucleon-nucleon scattering from one-boson-exchange potentials. III. S waves included. Phys. Rev. 1969, 177, 1435–1442. [Google Scholar]
- Erkelenz, K. Current status of the relativistic two-nucleon one boson exchange potential. Phys. Rep. 1974, 13, 191–258. [Google Scholar] [CrossRef]
- Holinde, K.; Machleidt, R. Momentum-space OBEP, two-nucleon and nuclear matter data. Nucl. Phys. 1975, A247, 495–520. [Google Scholar] [CrossRef]
- Holinde, K.; Machleidt, R. OBEP and eikonal form factor: (I). Results for two-nucleon data. Nucl. Phys. 1976, A256, 479–496. [Google Scholar] [CrossRef]
- Machleidt, R. The meson theory of nuclear forces and nuclear structure. Adv. Nucl. Phys. 1989, 19, 189–376. [Google Scholar]
- Machleidt, R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys. Rev. C 2001, 63, 024001. [Google Scholar] [CrossRef]
- Lacombe, M.; Loiseau, B.; Richard, J.M.; Vinh Mau, R.; Côté, J.; Pires, P.; de Tourreil, R. Parametrization of the Paris N-N potential. Phys. Rev. C 1980, 21, 861–873. [Google Scholar] [CrossRef]
- Machleidt, R.; Holinde, K.; Elster, C. The Bonn meson-exchange model for the nucleon-nucleon interaction. Phys. Rep. 1987, 149, 1–89. [Google Scholar] [CrossRef]
- Weinberg, S. Phenomenological Lagrangians. Physica 1979, 96A, 327–340. [Google Scholar] [CrossRef]
- Weinberg, S. Effective chiral Lagrangians for nucleon-pion interactions and nuclear forces. Nucl. Phys. 1991, B363, 3–18. [Google Scholar] [CrossRef]
- Weinberg, S. Three-body interactions among nucleons and pions. Phys. Lett. B 1992, 295, 114–121. [Google Scholar] [CrossRef]
- Machleidt, R.; Entem, D.R. Chiral effective field theory and nuclear forces. Phys. Rep. 2011, 503, 1–75. [Google Scholar] [CrossRef]
- Epelbaum, E.; Hammer, H.-W.; Meißner, U.-G. Modern theory of nuclear forces. Rev. Mod. Phys. 2009, 81, 1773. [Google Scholar] [CrossRef]
- Beane, S.R.; Bedaque, P.F.; Orginos, K.; Savage, M.J. Nucleon-nucleon scattering from fully dynamical lattice QCD. Phys. Rev. Lett. 2006, 97, 012001. [Google Scholar] [CrossRef] [PubMed]
- Ishii, N.; Aoki, S.; Hatsuda, T. Nuclear forces from lattice QCD. Phys. Rev. Lett. 2007, 99, 022001. [Google Scholar] [CrossRef] [PubMed]
- Gasser, G.; Leutwyler, H. Chiral perturbation theory to one loop. Ann. Phys. 1984, 158, 142–210. [Google Scholar] [CrossRef]
- Gasser, J.; Sanio, M.E.; Švarc, A. Nucleons with chiral loops. Nucl. Phys. 1988, B307, 779–853. [Google Scholar] [CrossRef]
- Scherer, S. Introduction to chiral perturbation theory. Adv. Nucl. Phys. 2003, 27, 277–538. [Google Scholar]
- Olive, K.A.; Particle Data Group. Review of Particle Physics. Chin. Phys. C 2014, 38, 090001. [Google Scholar] [CrossRef]
- Coleman, S.; Wess, J.; Zumino, B. Structure of phenomenological Lagrangians. I. Phys. Rev. 1969, 177, 2239. [Google Scholar] [CrossRef]
- Callan, C.G.; Coleman, S.; Wess, J.; Zumino, B. Structure of phenomenological Lagrangians. II. Phys. Rev. 1969, 177, 2247. [Google Scholar] [CrossRef]
- Fettes, N.; Meißner, U.-G.; Mojžiš, M.; Steininger, S. The chiral effective pion-nucleon Lagrangian of order p4. Ann. Phys. 2000, 283, 273–307. [Google Scholar] [CrossRef]
- Krebs, H.; Gasparyan, A.; Epelbaum, E. Chiral three-nucleon force at N4LO: Longest-range contribution. Phys. Rev. C 2012, 85, 054006. [Google Scholar] [CrossRef]
- Ordóñez, C.; Ray, L.; van Kolck, U. Two-nucleon potential from chiral Lagrangians. Phys. Rev. C 1996, 53, 2086–2105. [Google Scholar] [CrossRef]
- Van Kolck, U. Few-nucleon forces from chiral Lagrangians. Phys. Rev. C 1994, 49, 2932–2941. [Google Scholar] [CrossRef]
- Epelbaum, E.; Nogga, A.; Glöckle, W.; Kamada, H.; Meißner, U.-G.; Witala, H. Three-nucleon forces from chiral effective field theory. Phys. Rev. C 2002, 66, 064001. [Google Scholar] [CrossRef]
- Kaiser, N. Chiral 3π-exchange NN potentials: Results for representation-invariant classes of diagrams. Phys. Rev. C 2000, 61, 014003. [Google Scholar] [CrossRef]
- Kaiser, N. Chiral 3π-exchange NN potentials: Results for diagrams proportional to and . Phys. Rev. C 2000, 62, 024001. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys. Rev. C 2003, 68, 041001. [Google Scholar] [CrossRef]
- Entem, D.R.; Kaiser, N.; Machleidt, R.; Nosyk, Y. Peripheral nucleon-nucleon scattering at fifth order of chiral perturbation theory. Phys. Rev. C 2015, 91, 014002. [Google Scholar] [CrossRef]
- Girlanda, L.; Kievsky, A.; Viviani, M. Subleading contributions to the three-nucleon contact interaction. Phys. Rev. C 2011, 84, 014001. [Google Scholar] [CrossRef]
- Entem, D.R.; Kaiser, N.; Machleidt, R.; Nosyk, Y. Dominant contributions to the nucleon-nucleon interaction at sixth order of chiral perturbation theory. Phys. Rev. C 2015, 92, 064001. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R. Contact terms of EFT based NN potentials. Unpublished.
- Liu, J.; Mendenhall, M.P.; Holley, A.T.; Back, H.O.; Bowles, T.J.; Broussard, L.J.; Carr, R.; Clayton, S.; Currie, S.; Filippone, B.W.; et al. Determinaton of the axial-vector weak coupling constant with ultracold neutrons. Phys. Rev. Lett. 2010, 105, 181803. [Google Scholar] [CrossRef] [PubMed]
- Pavan, M.M.; Arndt, R.A.; Strakovsky, I.I.; Workman, R.L. Determination of the πNN coupling constant in the VPI/GWU πN → πN partial wave and dispersion relation analysis. Phys. Scr. 2000, T87, 65–70. [Google Scholar] [CrossRef]
- Arndt, R.A.; Strakovsky, I.I.; Workman, R.L.; Pavan, M.M. Sensitivity to the pion-nucleon coupling constant in partial wave analyses of πN → πN, NN → NN, γN → πN. Phys. Scr. 2000, T87, 62–64. [Google Scholar] [CrossRef]
- Kaiser, N.; Brockmann, R.; Weise, W. Peripheral nucleon-nucleon phase shifts and chiral symmetry. Nucl. Phys. 1997, A625, 758–788. [Google Scholar] [CrossRef]
- Epelbaum, E.; Glöckle, W.; Meißner, U.-G. Improving the convergence of the chiral expansion for nuclear forces - II: Low phases and the deuteron. Eur. Phys. J. 2004, A19, 401–412. [Google Scholar] [CrossRef]
- Kaiser, N. Chiral 2π-exchange NN potentials: Two-loop contributions. Phys. Rev. C 2001, 64, 057001. [Google Scholar] [CrossRef]
- Kaiser, N. Chiral 3π-exchange NN potentials: Results for dominat next-to-leading-order contributions. Phys. Rev. C 2001, 63, 044010. [Google Scholar] [CrossRef]
- Kaiser, N. Chiral 2π-exchange NN potentials: Relativistic 1/M2-corrections. Phys. Rev. C 2002, 65, 017001. [Google Scholar] [CrossRef]
- Erkelenz, K.; Alzetta, R.; Holinde, K. Momentum space calculations and helicity formalism in nuclear physics. Nucl. Phys. 1971, A176, 413–432. [Google Scholar] [CrossRef]
- Machleidt, R. One-boson-exchange potentials and nucleon-nucleon scattering. In Computational Nuclear Physics 2 – Nuclear Reactions; Langanke, K., Maruhn, J.A., Koonin, S.E., Eds.; Springer: New York, NY, USA, 1993; pp. 1–29. [Google Scholar]
- Arndt, R.A.; Briscoe, W.J.; Strakovsky, I.I.; Workman, R.L. Extended partial-wave analysis of πN scattering data. Phys. Rev. C 2006, 74, 045205. [Google Scholar] [CrossRef]
- Koch, R. A calculation of low-energy πN partial waves based on fixed-t analyticity. Nucl. Phys. 1986, A448, 707–731. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R. Chiral 2π exchange at fourth order and peripheral NN scattering. Phys. Rev. C 2002, 66, 014002. [Google Scholar] [CrossRef]
- Stoks, V.G.J.; Klomp, R.A.M.; Rentmeester, M.C.M.; de Swart, J.J. Partial-wave analysis of all nucleon-nucleon scattering data below 350 MeV. Phys. Rev. C 1993, 48, 792–815. [Google Scholar] [CrossRef]
- Arndt, R.A.; Strakovsky, I.I.; Workman, R.L. SAID, Scattering Analysis Interactive Dial-in Computer Facility; The George Washington University: Washington, DC, USA, 1999. [Google Scholar]
- Briscoe, W.J.; Strakovsky, I.I.; Workman, R.L. SAID Partial-Wave Analysis Facility, Data Analysis Center; The George Washington University: Washington, DC, USA, 2007. [Google Scholar]
- Mau, R.V. The Paris nucleon-nucleon potential. Mesons Nucl. 1979, 1, 151. [Google Scholar]
- Epelbaum, E.; Glöckle, W.; Meißner, U.-G. Nuclear forces from chiral Lagrangians using the method of unitary transformation (I): Formalism. Nucl. Phys. 1998, A637, 107–134. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Savage, M.J.; Wise, M.B. Nucleon-nucleon scattering from effective field theory. Nucl. Phys. 1996, B478, 629–659. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Savage, M.J.; Wise, M.B. A new expansion for nucleon-nucleon interactions. Phys. Lett. 1998, B424, 390–396. [Google Scholar] [CrossRef]
- Kaplan, D.B.; Savage, M.J.; Wise, M.B. Two-nucleon systems from effective field theory. Nucl. Phys. 1998, B534, 329–355. [Google Scholar] [CrossRef]
- Fleming, S.; Mehen, T.; Stewart, I.W. NNLO corrections to nucleon-nucleon scattering and perturbative pions. Nucl. Phys. 2000, A677, 313–366. [Google Scholar] [CrossRef]
- Fleming, S.; Mehen, T.; Stewart, I.W. NN scattering 3S1–3D1 mixing angle at next-to-next-to-leading order. Phys. Rev. C 2000, 61, 044005. [Google Scholar] [CrossRef]
- Beane, S.R.; Kaplan, D.B.; Vuorinen, A. Perturbative nuclear physics. Phys. Rev. C 2009, 80, 011001. [Google Scholar] [CrossRef]
- Beane, S.R.; Bedaque, P.F.; Savage, M.J.; van Kolck, U. Towards a perturbative theory of nuclear forces. Nucl. Phys. 2002, A700, 377–402. [Google Scholar] [CrossRef]
- Nogga, A.; Timmermans, R.G.E.; van Kolck, U. Renormalization of one-pion exchange and power counting. Phys. Rev. C 2005, 72, 054006. [Google Scholar] [CrossRef]
- Pavon Valderrama, M.; Ruiz Arriola, E. Renormalization of the NN interaction with a chiral two-pion exchange potential. II. Noncentral phases. Phys. Rev. C 2006, 74, 064004. [Google Scholar] [CrossRef]
- Entem, D.R.; Ruiz Arriola, E.; Pavón Valderrama, M.; Machleidt, R. Renormalization of chiral two-pion exchange NN interactions: Momentum space versus coordinate space. Phys. Rev. C 2008, 77, 044006. [Google Scholar] [CrossRef]
- Birse, M.C. Power counting with one-pion exchange. Phys. Rev. C 2006, 74, 014003. [Google Scholar] [CrossRef]
- Birse, M.C. Deconstructing triplet nucleon-nucleon scattering. Phys. Rev. C 2007, 76, 034002. [Google Scholar] [CrossRef]
- Birse, M.C. Functional renormalization group for two-body scattering. Phys. Rev. C 2008, 77, 047001. [Google Scholar] [CrossRef]
- Yang, C.-J.; Elster, C.; Phillips, D.R. Subtractive renormalization of the NN scattering amplitude at leading order in chiral effective theory. Phys. Rev. C 2008, 77, 014002. [Google Scholar] [CrossRef]
- Yang, C.-J.; Elster, C.; Phillips, D.R. Subtractive renormalization of the chiral potentials up to next-to-next-to-leading order in higher NN partial waves. Phys. Rev. C 2009, 80, 034002. [Google Scholar] [CrossRef]
- Yang, C.-J.; Elster, C.; Phillips, D.R. Subtractive renormalization of the NN interaction in chiral effective theory up to next-to-next-to-leading order: S waves. Phys. Rev. C 2009, 80, 044002. [Google Scholar] [CrossRef]
- Long, B.; van Kolck, U. Renormalization of singular potentials and power counting. Ann. Phys. 2008, 323, 1304–1323. [Google Scholar] [CrossRef]
- Machleidt, R.; Entem, D.R. Nuclear forces from chiral EFT: The unfinished business. J. Phys. G Nucl. Phys. 2010, 37, 064041. [Google Scholar] [CrossRef]
- Zeoli, C.; Machleidt, R.; Entem, D.R. Infinite-cutoff renormalization of the chiral nucleon-nucleon interaction up to N3LO. Few-Body Syst. 2013, 54, 2191–2205. [Google Scholar] [CrossRef]
- Valderrama, M.P. Perturbative Renormalizability of Chiral Two Pion Exchange in Nucleon-Nucleon Scattering. Phys. Rev. C 2011, 83, 024003. [Google Scholar] [CrossRef]
- Valderrama, M.P. Perturbative Renormalizability of Chiral Two Pion Exchange in Nucleon-Nucleon Scattering: P- and D-waves. Phys. Rev. C 2011, 84, 064002. [Google Scholar] [CrossRef]
- Machleidt, R.; Liu, P.; Entem, D.R.; Ruiz Arriola, E. Renormalization of the leading-order chiral nucleon-nucleon interaction and bulk properties of nuclear matter. Phys. Rev. C 2010, 81, 024001. [Google Scholar] [CrossRef]
- Bethe, H.A. Theory of nuclear matter. Ann. Rev. Nucl. Sci. 1971, 21, 93–244. [Google Scholar] [CrossRef]
- Day, B.D.; Wiringa, R.B. Brueckner-Bethe and variational calculations of nuclear matter. Phys. Rev. C 1985, 32, 1057–1062. [Google Scholar] [CrossRef]
- Epelbaum, E.; Gegelia, J. Regularization, renormalization and “peratization” in effective field theory for two nucleons. Eur. Phys. J. 2009, A41, 341–354. [Google Scholar] [CrossRef]
- Lepage, G.P. How to Renormalize the Schrödinger Equation. 1997; arXiv:nucl-th/9706029. [Google Scholar]
- Marji, E.; Canul, A.; MacPherson, Q.; Winzer, R.; Zeoli, C.; Entem, D.R.; Machleidt, R. Nonperturbative renormalization of the chiral nucleon-nucleon interaction up to next-to-next-to-leading order. Phys. Rev. C 2013, 88, 054002. [Google Scholar] [CrossRef]
- Entem, D.R.; Machleidt, R. Accurate Nucleon-Nucleon Potential Based upon Chiral Perturbation Theory. Phys. Lett. 2002, 524, 93–98. [Google Scholar] [CrossRef]
- Stoks, V.G.J.; Klomp, R.A.M.; Terheggen, C.P.F.; de Swart, J.J. Construction of high-quality NN potential models. Phys. Rev. C 1994, 49, 2950–2962. [Google Scholar] [CrossRef]
- Wiringa, R.B.; Stoks, V.G.J.; Schiavilla, R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys. Rev. C 1995, 51, 38–51. [Google Scholar] [CrossRef]
- Epelbaum, E.; Glöckle, W.; Meißner, U.-G. The two-nucleon system at next-to-next-to-next-to-leading order. Nucl. Phys. 2005, 747, 362–424. [Google Scholar] [CrossRef]
- Epelbaum, E.; Krebs, H.; Meißner, U.-G. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur. Phys. J. 2015, 51, 1–29. [Google Scholar] [CrossRef]
- Epelbaum, E.; Krebs, H.; Meißner, U.-G. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys. Rev. Lett. 2015, 115, 122301. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).