Abstract
After the observation of the strong near-threshold enhancement of proton-antiproton mass spectrum in decay, lots of theoretical investigations have been available such as new resonance, the final-state interaction (FSI), bound state (or baryonium), glueball, or other exotic (tetra-quark) states. Here, we provide a short review on the current status, especially on the pertinent discussions concerning its relation to interaction, for which the emphasis is put on the recently constructed chiral potential.
1. Introduction
With a large accumulation of data, a prominent -threshold enhancement is reported by BES collaboration [1].
Such a strong threshold enhancement can be both fitted with a Breit–Wigner (BW) form for S- and P-wave. The results are [1]
where M denotes the mass, Γ denotes the width and the errors are statistical only. Including the systematic error for S-wave, the best fitted result is , at 90% confidence level. The quantum number corresponding to the S-wave is (), while for P-wave, it is , neglecting the higher total angular momentum J. The charge symmetry in electromagnetic interaction has been used to obtain these quantum numbers, i.e., is conserved where L and S are the orbital angular momentum and total spin, respectively. These properties are not consistent with any existing particles and now have been named as the particle by Particle Data Group (PDG) [2]. Concerning its nature, it is still quite controversial so far. In the analysis of BES themselves, they used a new resonance (BW form) [1] to describe the peak observed around nucleon antinucleon () threshold, which is 1877 MeV [2]. Due to the proximity of the threshold, the common conjecture will be naturally whether it has something to do with interaction, or more interestingly, bound state (baryonium). The topic of baryonium dates back to Fermi and Yang’s idea in the 1950s [3]. There is still no definite answer on whether such a bound state really exists, and, in fact, none of them were observed and confirmed in the experiment. Besides the bound state nature, some other speculations are also available, e.g., glueball [4,5,6,7], the second radial excitation of [8], resonance [9], or just simple final-state-interaction (FSI) effects. FSI is an important ingredient that needs to be taken into account in the decay process, see e.g., the FSI in decay in order to better extract the Cabibbo-Kobayashi-Maskawa (CKM) matrix element [10,11,12]. For the scenario of interaction, the most up-to-date work is included in the Ref. [13], where one can find a large amount of literature, and here we refrain from listing all of these, but rather when it comes to the detailed discussion, we will mention them separately. The method used in Ref. [13] was also applied to and a nice reproduction of experimental data near threshold was obtained [14]. The concise results can be found in Ref. [15]. In this short review, we will discuss these issues, concentrating more on the aspects of the role played by .
2. and Interaction
Concerning the observation of from , many interpretations on its nature have been proposed, as also mentioned in the Introduction. Among them, one popular viewpoint is the bound state, or generally speaking, final state interaction (FSI). Note that we discriminate the terminology of FSI and a bound state. The fromer may be very strong in some cases (like the situation considered here), but not necessarily produce a bound state in the corresponding partial wave. Inversely, a bound state clearly indicates the importance of the two-body strong interaction. There is an interesting example: the enhancement of mass spectra in [16] can not be attributed to the near threshold bound state, see also the discussion in Ref. [14]. However, definitely in the channel , , FSI should play a non-neglegible role due to the conventional strong nuclear force problem. In what follows, we will discuss in detail the connection between and .
2.1. Historical Development: Working with Effective Range Expansion
The first explanation for the peak in , to our knowledge, would be the one from Datta and O’Donnell [17], where the difference in the binding energy of the deuteron (−2.225 MeV) and the one for this new state (−17.5 MeV) are explained by a color interaction between quark-quark () and quark-antiquark (). For in a baryon, the potential due to the color interaction involves an attraction factor of , where is the strong coupling constant, while, for in a meson, it would be , i.e., attract more by a factor of two [18]. In a deuteron, it should be rich in interaction due to its quark configurations, and assume this peak (which may be called X for simplicity from now on and the explanation by pure FSI will be also discussed below) is a bound state, where interaction abounds. The question is how this factor of two influences the phenomenological potential compared to (deuteron case) is not clear since both of these bound states are composed of six complicated quarks. However, one may still naively assume that there is a just simple factor of two between these two potentials, as a criterion to test the bound state, which is the idea taken in Ref. [17]. Then, they calculated the potential that is adapted to the binding energies for a deuteron and this X to examine whether it is indeed so or not. The simple square well potential was taken as an example there [17]. The corresponding location of the bound state is predicted by
where μ is the reduced mass, a and denotes the width and depth of the square potential, and is the binding energy. For the deuteron, and . From Equation (1), one gets . Similarly, taking the binding energy of −17.5 MeV for X, [17], which is a factor of 1.8 compared to the deuteron case, and very close to two. This constitutes their support for the conclusion of “deuteron-like singlet state” [17]. This should be viewed as a rather rough conjecture for the nature of the bound state due to its crude starting point. Furthermore, taking the current world average value of in PDG [2], the binding energy will be and the ratio becomes 2.6. Anyway, it provides a first bold exploration for the topic of the strongly enhanced peak.
Then, Zou and Chiang investigated the role of one-pion-exchange (OPE) potential played in the peak observed in [19], and pointed out that the FSI could be the reason. A relatively more detailed calculation along that line was performed in Ref. [20] by using Jost function [21]. In the zero-th order approximation, the Riccati–Bessel function and Riccati–Hankel function are simplified to the free-wave and sine function, and the Jost function is then calculated in a straightforward way in the coordinate space [20]. The enhancement factor for the cross section between the case with and without FSI was given by [22], where is the Jost function at on-shell momentum k (). Taking a pure phenomenological form for the production amplitude (can be considered as a parametrization for appearing in Ref. [19]), a good description of BES data was obtained [20], where C is fitted to data as a free parameter. BES also measured decay but did not observe the strong threshold enhancement [1]. In this channel, the occurs in isospin-1 , i.e., , the interaction considered in Ref. [19] is repulsive, which provides a qualitative argument for the non-observation of the peak. In addition, the enhancement factor shown in Ref. [20] supports this statement. However, in both of the Refs. [19,20], there will be difficulty for from current knowledge, where, for , it also involves isospin-0 , the same quantum number as , however, no threshold peak was found there [23,24]. Concerning the allowed quantum numbers (constrained from parity, charge conjugation and isospin symmetry) for various decay channels, one could refer to Ref. [13]. In fact, in both Refs. [19,20], only part of the OPE for was discussed, namely, the central Yukawa part [25]. The annihilation effect in is known to be an indispensable part, see e.g., Refs. [26,27]. Without considering annihilations, one can not get a realistic potenial, and then all their conclusions are rather qualitative.
Afterwards, many more sophisticated and realistic potential models are used to investigate FSI, see e.g., by the Paris potential [28,29], Jülich model [30], and the one constructed in consitute quark model [31]. For a review of the interaction, see Ref. [27]. At this stage, the popular and elegant treatment of the FSI is the one proposed by Waston and Migdal [32,33], which relates the total reaction amplitude to the scattering T-matrix simply by a constant, see e.g., the discussion in the Jülich work [30]. Note In Refs. [28,29,34,35], the scattering length approximation was used, and instead, not the direct T-matrix. Here, we will give a brief review of them and discuss different methods to treat FSI (an alternative one is based on dispersion theory, see e.g., Ref. [10] for inclusion of FSI). Adopting the convention in Ref. [21], T is expressed as with k denoting the on-shell momentum in CMS and δ the phase shift. Since , one has , where the ellipsis denotes the and higher order terms in effective range expansion (ERE). Note another convention for the sign of scattering length also appears in literature. Then the two-body transition amplitude from the channel i to f can be written as [28]
via a K-matrix approach which guarantees the unitarity condition. Here is the transition length, while denotes the corresponding scattering length of final state system. Similarly, for the transition itself, one has
These equations are slightly different from the original expressions in Ref. [28], however, the overall sign does not play a role in the observable. Combining Equations (2) and (3), one easily finds
and, in the case that the quantity has a very weak energy dependence, say, a constant, then one recovers
which is just the Watson–Migdal (WM) approximation [32,33]. The WM approach was developed in the study of the meson production process in collision [22], in which case, it involves large scattering lengths, e.g., for scattering, . However, for the case, the scattering length is an order of 1 fm, suggested by the experimental measurements of the level shifts and widths for antiprotonic hydrogen atoms [36]. In addition, due to the annihilation effects, the scattering length becomes a complex number, and it is not clear how WM approximation works in the sector. As pointed out in Ref. [28], such an approximation may work only up to the laboratory energy () for .
One indeed observes significant differences between the results from WM approximation and a sophisticated one that is called distorted-wave born approximation (DWBA). The discrepancy is clearly shown in Figure 1. Note that in Ref. [30], using the potential from A(OBE) model [37,38] the authors reproduce the near-threshold spectrum (the peak) rather well for decay based on the WM approximation. We then recalculate it, as a comparision, but now using the DWBA to take account of the FSI. It turns out that significant discrepancy appears, and in the new and advanced treatment, the peak disappears in the theory result. This finding is also supported by the calculation in Ref. [31]. In fact, one fails to describe the prominent peak around the threshold in this way. Moreover, there is no direct extension of WM approximation to the P-wave case. Next, we will introduce the chiral potential we constructed, where the four contact terms appearing up to next-to-next-to-leading order (NNLO) take care of both the scattering data and the in simultaneously. In addition, the DWBA will be elaborated in more detail.
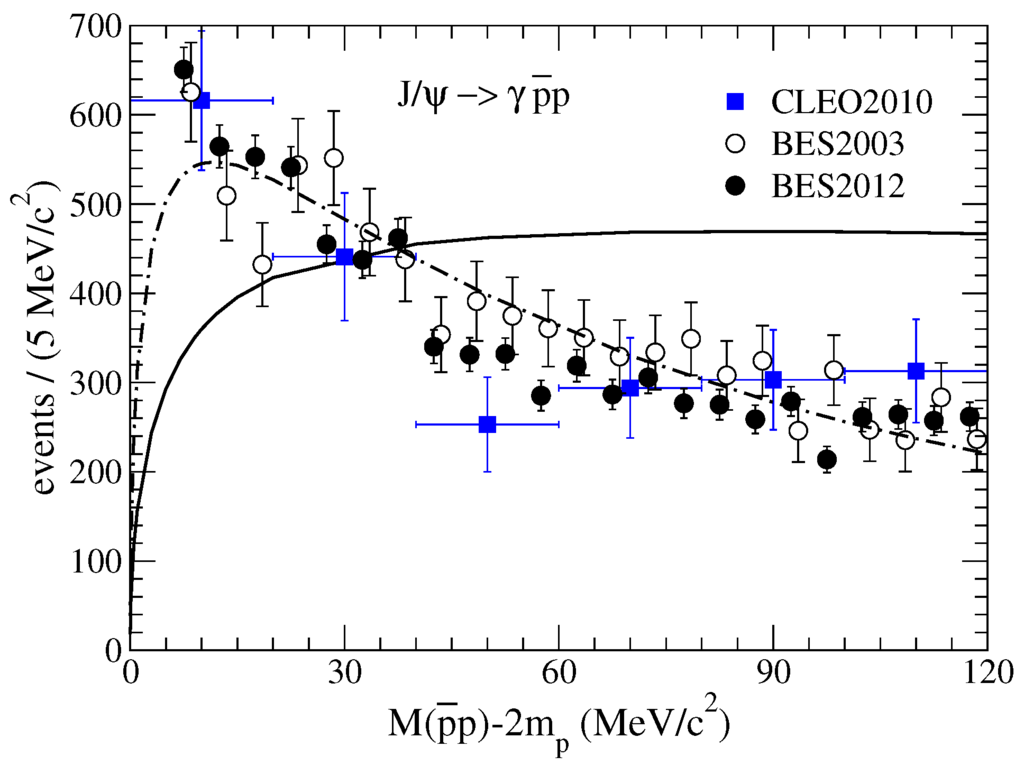
Figure 1.
Difference for the predicted spectrum in the decay resulting from the WM approximation (cf. Equation (5)) and the DWBA (cf. Equation (7) below). The potential in from the A(OBE) model was used as an input. The solid line denotes the result from DWBA while the dash-dotted curve corresponds to WM approximation. Data are taken from Refs. [1,39,40] and normalized to the one given by BES2012 [40]. Figure from Ref. [13].
2.2. Updates: More Refined Treatment of Interaction and FSI
Considering the above deficiencies, a most up-to date analysis of FSI was done in Ref. [13], where a systematically nice description of all the available experimental data for () and () was achieved. Moreover, the potential exploited in Ref. [13] is based on the consideration of the chiral symmetry. The elastic part, i.e., the pion-exchange potential is calculated from chiral effective field theory. It was also argued that in Ref. [13], there is no need to introduce a new scale to the annihilation and likewise is treated in chiral expansion. Since such effective field theory displays explicitly the chiral symmetry exhibited by Quantum Chromodynamics (QCD), it is believed to be a more fundemental theory than the pure phenomenological models. On the other hand, the systematic improvement can be achieved by considering the higher-order terms in the expansion.
The total reaction amplitude is written symbolically as
Here, the first term denotes the bare production amplitude ( is the on-shell amplitude) and the second one includes the FSI ( appears in the integral and the half-off-shell form is needed). in Equation (6) is the free Green’s function and T denotes the scattering T-matrix. At a short region of low energies, one can assume to take into account the near-threshold behavior. Explicitly, one has
Note this equation now can be applied to P-wave. The production amplitude actually involves a very complicated microscopic mechanism, and it is hard to write it in basic analytical expressions. In Refs. [28,29], it is approximated as , where is an overall constant, similar to Ref. [20], but as a range parameter was also obtained by fitting to the data. One should be cautious that the production amplitude itself should not produce the peak if one wants to demonstrate the strong FSI as the reason for the peak. Concerning the treatment for , the FSI factors for partial wave from the WM approximation were calculated, and it was found that it does not reproduce the data [28]. Then, the was argued to be dominant over and through some selected scenario for the production mechanism [28]. In fact, this also happens for the work based on Jülich model [30], i.e., fails to describe the experiment. However, in a more sophisticated treatment (DWBA), the FSI factor for partially agrees with the data rather well [13]. The Spain group has also been studied by using DWBA, but the data was not described [31]. However, their main purposes are still to demonstrate the WM approach reproduces the data well based on another potential constructed by them in the quark model, and to display the differences shown by WM and DWBA.
Recently, the interaction has also been investigated in the chiral effective field theory (EFT) up to NNLO [26,41,42,43], where the low-energy constants appearing are fitted to the amplitude from the partial-wave analysis [44]. As mentioned above, the chiral EFT is related to the underlying QCD through the chiral symmetry, and in view of the theory point, it is a more fundemental potential than the phenomenological models. Combining the most recent chiral potential and the above sophisticated way for inclusion of FSI, the decay channel is re-analyzed in Ref. [13]. The results are shown in Figure 2, where one can clearly find the pronounced peak is again reproduced in this way, but keep in mind that we are working with the more advanced tool. The three-body phase space behavior is also shown in the range we considered, as a backdrop for the huge enhancement. The red band in Figure 2 is made from the four cutoff combinations, where two of them are introduced to regularize the Lippmann–Schwinger equation, and the other two are used to cut off the spectral function for the two-pion exchange potential. The latter cutoff dependence is tiny compared to the former one. For more details, refer to the original publication [13].
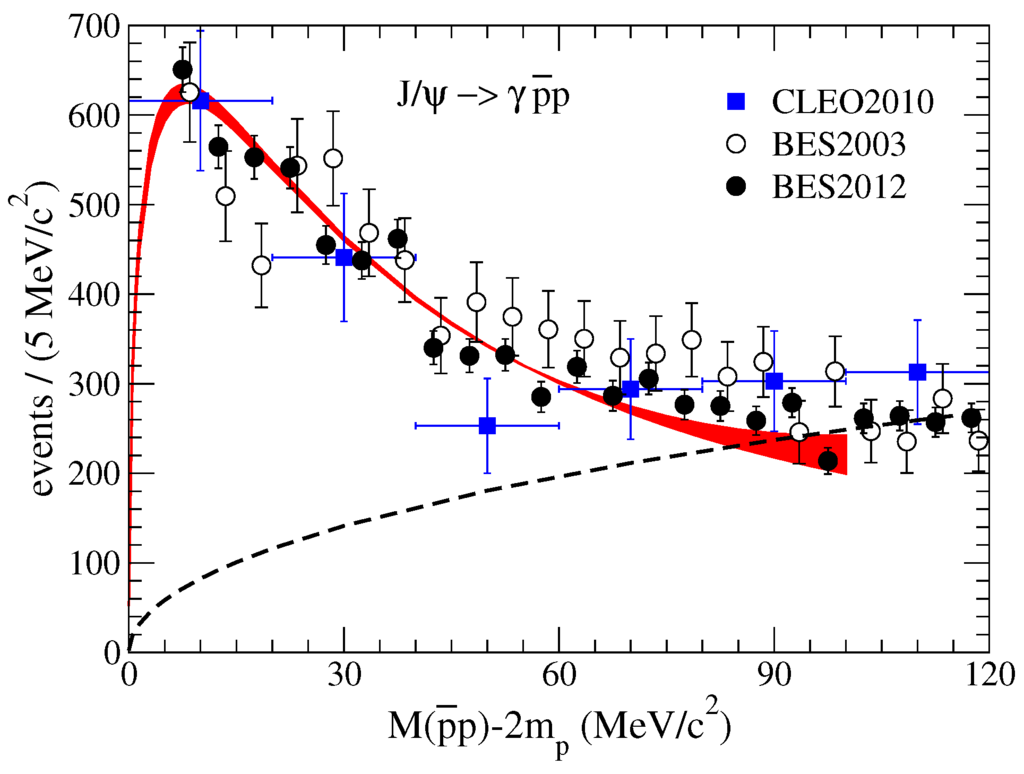
Figure 2.
spectrum for the decay . The red band represents our final results with (somewhat rough) error estimate. The dashed curve denotes the phase space behavior. For the notation of data and label, cf. Figure 1. Figure from Ref. [13].
The scattering length from the chiral potential was also predicted in Ref. [26]. Note that the scattering length in [13] is quite close to Ref. [26]. As a cross check of the quality of our chiral potential, we will compare the scattering length from different models below. On the other hand, more importantly, this lends itself to discussing more about the calculation utilizing effective range approximation. In Ref. [35], the data was also well reproduced up to by fitting the imaginary part of scattering length () to data. The S-wave scattering T-matrix is given by Equation (3), and the imaginary part reads
where , terms are not kept. From the dispersion theory, the real part reads
where denotes the principal value. Combining Equations (8) and (9), one obtains the expression for . The best fit for the event is based on . Here, Equations (8) and (9) are valid for both isospin, i.e., and in the terminology , (also surely including the isospin-average ). The isospin configuration used in Ref. [35] is not pointed out. In fact, the S-wave scattering length has been calculated comprehensively by theoretical calculation and also by the experimental information, i.e., measurement of the protonium level shifts [36]. For a comparison, the scattering length for partial wave is organized in Table 1 for the different interactions used for treatment of in this paper.

Table 1.
Scattering lengths (in fm) for the partial wave in the isospin and channels. The numbers given by Refs. [45] and [46] include the Coulomb correction while others do not. However, the Coulomb interaction only makes a difference of about 0.1 fm [47].
The one given from Grach et al. [45] and Pirner et al. [46] include the Coulomb correction but not for others. However, one should not take this as the reason for the quantum differences, since Coulomb correction induces a shift of only about 0.1 fm [47]. In other words, the differences here are really a reflection of the different models. The corresponding energy level shifts and widths for the antiprotonic hydrogen are calculated and compiled in Table 2. We observed that the chiral potential [26] predicts the value of energy level shifts at the lower side of the experimental number [51], and the larger value for the width Γ allowed by the experiment [50]. The enhancement factor used by Ref. [34] is more complicated and includes three ingredients: (i) both isospin-0 and isospin-1 are allowed in , and we infer from their formula that the isospin-average is used; (ii) the annihilation effect is taken into account; and (iii) Coulomb interaction between . It is shown in Figure 2 of Ref. [34] that the annihilation effect, ingredient (ii), is so large that it is non-negligible to get a quantitative calculation of the enhancement factor, as expected and also, as mentioned above, the ingredient (iii) only influences the enhancement factor by a few percent.

Table 2.
The calculated hadronic level shifts and widths in hyperfine states of antiprotonic hydrogen ( H) for partial wave. The ones corresponding to Grach et al. and Pirner et al. are deduced from the scattering lengths shown by them in Refs. [45,46]. The experimental information is taken from Refs. [50,51].
Finally, we give the connections between these different methods of treating FSI. Using the identity
and approximating the principal part as (c is a constant), one can get an approximation for Equation (7):
In Ref. [30], the authors point out that the case (c is generally a complex number) is very large such that the effect from other terms is invisible, Equation (11) is simplified then as the WM prescription. In fact, on the other hand, if is extremely small, say, , and very near the threshold region, k and are basically constant, and if they are much larger than 1, again it will be reduced to an overall constant multiplying T-matrix. From these arguments, one finds the WM approach is the special case of the general DWBA. Replacing the T-matrix by the effective low energy parameters, one could get the formalism used in Refs. [28,29,35], i.e., the method of effective range expansion.
Now, we discuss the resonance interpretation of X. It was explained by the threshold cusp effect and also includes many other examples in Ref. [35], which is very similar to the case in annihilate into multipion—the strong “dip” around threshold is explained due to the opening of the channel [52]. Threshold cusp effect and the resonance are discriminated, and it is pointed out in Ref. [35] that only under some special circumstances can it be recognized as a resonance. Ref. [35] provides two arguments against the interpretation of resonance: the small cross section for requires the almost identical isospin-0 and isospin-1 amplitudes to cancel out each other. If there is a narrow resonance, it should lie in both of these two isospins and degenerate in mass, width and coupling strength. This would be quite implausible since it is known that the meson exchange forces are very different for two isospins—for isospin-1, there is a factor of 1 and, for isospin-0, a factor of . On the other hand, the branching ratio for is measured to be [1] consistent with the measurement in 2011 [40], which is quite small compared to other typical rediative decay model with the same quantum numbers [35]. If it is a resonance (typically like ρ), one should also observe it in other decays, e.g., in , but the experiment does not support this [24]. From these arguments, it is implausible to interpret it as a resonance.
How about understanding it as a bound state? In Refs. [28,29], they do understand it as an isospin-0 bound state, located at , predicted from the updated Paris 2009 potential [49], where the real part means that it stays below the threshold, and the imaginary part indicates the width . We also favor the interpretation as a bound state [13], but the binding energy can not be well determined since, in the model, the isospin average amplitude is taken and, in principle, any isospin combination is allowed. This also introduces large uncertainty not as in the case of Ref. [28,29] where only the pure isospin-0 is considered. As for this point, the work of applying the same methodology of Ref. [13], i.e., a combined analysis of data and scattering data, to the pure isospin-0 would be thus also quite interesting [53]. More caution needs to be taken for the bound state predicted in Ref. [13], which is in isospin-1 , not isospin-0. The logic is that the isospin-0 is constrained from the data for [23,24] which does not show a peak at threshold, and thus the prominent peak in should come from isospin-1.
2.3. Potential Experimental Searches
Here, we comment that with the understanding of as baryonium state, its binding energy and width can not be well determined by only using the data above the threshold. For the illustration example, one refers to Ref. [54], where the tail of the Breit–Wigner shape for the resonance and can equally well describe the data. In order to explore more on the property of the bound state, one should exploit the information below threshold, e.g., measuring [34] (which can be done by CLAS collaboration at the Jefferson Lab [55]), or [56] that can be accessed by PANDA (antiProton ANnihilation at DArmstadt) experiment [57] at the Facility for Antiproton and Ion Research (FAIR), i.e., at least three-body final states containing pairs such that the phase space below threshold is accessible. These data are desired to pin down the bound state nature.
3. Mesonic Decay of
The peak is also observed in [58], and this is consistent with the previous findings in [1]. An updated analysis of is performed in 2010 [59]. In all of these analyses, the locations of the peaks (mass and width of ) are consistent with each other within error bars. In 2011, its quantum number was determined to be [40]. In other words, up to now, this peak has been observed not only in channel but also in with the decay width larger than the former [2]. Now the question is how to understand this peak in the mass spectrum, and, especially, whether it is the same stuff as observed from the case. In this section, we briefly review part of the progress in this direction.
Assuming as a baryonium state, it could be also observed in other mesonic decay channels. For the possible decay list of , one refers to Ref. [60], where the quantum number assignment for agrees with the experimental determination, that is . Two years later, the authors of Ref. [60] analyzed (qualitatively) the coupling of with and with . It was found that the former one is much larger than the latter by a factor of around 20, which indicates the large weight of component in the wave function of [61]. However, in Ref. [61] the branching ratio of was predicted to be larger than , and thus should be detected in the channel. In Ref. [62], some more quantitative calculations were performed, which rely on the constructed effective Lagragian, and the coupling constants therein are fixed by other experimental information from decay or the scattering observable. Its results show that:
Given the fact that [58], the corresponding theoretical result above is a factor of 10 smaller compared to the experiment, which seems somewhat disappointing, i.e., disfavoring the interpretation by baryonium. However, for us, this result suffers from large model dependence, especially for the determined coupling constant, which shows a large cutoff dependence, although the author chose as the cutoff region to do the numerical calculation (cf. Figure 2). Correspondingly, was used [62], and this value is consistent with the one in Ref. [60]. However, was not seen in the spectrum of the channel in the BES-II experiment [63], which became the obstacle to understand in the above way (i.e., couples to more strongly than ). In fact, up to now, there is still no definite conclusion for the existence of in and more reliable (confirmative) results need to be explored on the experimental side [64]. Nevertheless, one experimental fact is clear: is discovered in by BES-III collaboration [58,59]. This supports the theoretical calculations by Ding et al. [65] using the coherent state method. There, the is predicted to be suppressed by four orders comparing to although the former has much larger phase space available. See also Ref. [66] for a review on their own results combining understanding as baryonium from Skyrme model and the aforementioned result. A unifided discription for these two sides on and was also done in Ref. [67] by themselves, which was based on treating as baryonium with sizable gluon content. However, Ref. [29] also provides a unified description without mentioning the role of gluon, where they assume as the intermediate state to investigate the decay product , attributing this to the Paris potential constructed by them. The observed peak is then found to be due to the interference of the quasibound state with background amplitude.
Concerning the peak observed in the mass spectrum, other explanations in the scheme of the conventional meson () also exist, see e.g., Ref. [8] for indentifying it as second radial excitation of (principal number ). Inspired by this conjecture, some other X resonances are also explored in Ref. [68]. Along this line, doubt on the principal quantum number is put forward in the review by Klempt and Zaitsev [69]. There it is explained to be the first radial excitation, in which case, decays into and the singlet part of σ resonance, i.e., was believed to be a flavor singlet. Thus, it naturally explains the small fraction of due to the octet property of η meson. This interpretation is also consistent with the observation of in radiative but non-observation in ; see more discussion in Ref. [69]. In the following years, people began to reexamine its principal quantum number n. Then is supported in Ref. [70], where the strong decay of is investigated in the model considering the mixing with . The conclusion of is also made in Ref. [71] through the Regge trajectory and analysis of the Bethe–Saleter equation. In Ref. [9], is thought to be the dynamical generation of pseudoscalar resonances from the scattering. Last but not least, let us resort to the experimental measurement of Belle, which claims the existence of is only at the level of the marginal significance [72]. However, again, BES collaboration reports the discovery of from the recent measurement for [73]. The final definitive conclusion on whether the peak observed in is related to the enhancement from radiative decay still really needs a lot of effort from both theoretical colleagues and researchers on the experimental side.
4. Conclusions and Outlook
In this short review, we present the development of the topic exploiting interaction to explore the observed threshold enhancement in , and also discuss the relation to the channel . The main aim is to provide a historical development containing comprehensive references and summarize the status achieved so far, not to criticize and advocate part of this research. Considering the most advanced treatment of FSI available up to now, we favor the existence of a bound state, but, in the model, the binding energy and width (pole location in the complex energy plane) suffer from large uncertainty. More data on the invariant mass spectrum below the threshold, e.g., the aforementioned or , are needed to get more confirmative conclusions on the properties of . On the other hand, it is also found in the mesonic channels, and these aspects deserve further detailed study.
Acknowledgments
Xian-Wei Kang is thankful for the valuable discussions with Johann Haidenbauer and Ulf-G. Meißner, and also the careful reading of Ulf-G. Meißner. Because of the authors’ personal research interests, they apologize to those whose papers were not cited. This study is funded by the Importation and Development of High-Caliber Talents Project of Beijing Municipal Institutions (CIT&TCD20140311) and the Beijing Natural Science Fund (KZ201510016019).
Author Contributions
Yong-Feng Liu first suggested to write such a review to summarize the recent progress of interaction and the status of . Xian-Wei Kang considered the whole idea more deeply, polished the draft, and added more discussion. This work is financially supported by a grant to Yong-Feng Liu.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bai, J.Z.; Ban, Y.; Bian, J.G.; Cai, X.; Chang, J.F.; Chen, H.F.; Chen, H.S.; Chen, J.; Chen, J.; Chen, J.C.; et al. Observation of a near threshold enhancement in the mass spectrum from radiative J/ψ→γ decays. Phys. Rev. Lett. 2003, 91. [Google Scholar] [CrossRef] [PubMed]
- Olive, K.A.; Agashe, K.; Amsler, C.; Antonelli, M.; Arguin, J.-F.; Asner, D. M.; Baer, H.; Band, H.R.; Barnett, R.M.; Basaglia, T.; et al. Review of Particle Physics. Particle Data Group Collaboration. Chin. Phys. C 2014, 38. [Google Scholar] [CrossRef]
- Fermi, E.; Yang, C.N. Are mesons elementary particles? Phys. Rev. 1949, 76. [Google Scholar] [CrossRef]
- Li, B.A. A possible 0-+ glueball candidate X(1835). Phys. Rev. D 2006, 74. [Google Scholar] [CrossRef]
- Kochelev, N.; Min, D.P. X(1835) as the lowest mass pseudoscalar glueball and proton spin problem. Phys. Lett. B 2006, 633, 283–288. [Google Scholar] [CrossRef]
- Kochelev, N.; Min, D.P. Eta(c): Glueball mixing and resonance X(1835). Phys. Rev. D 2005, 72. [Google Scholar] [CrossRef]
- He, X.G.; Li, X.Q.; Liu, X.; Ma, J.P. Some properties of the newly observed X(1835) state at BES. Eur. Phys. J. C 2007, 49, 731–736. [Google Scholar] [CrossRef]
- Huang, T.; Zhu, S.L. X(1835): A Natural candidate of eta-prime’s second radial excitation. Phys. Rev. D 2006, 73. [Google Scholar] [CrossRef]
- Albaladejo, M.; Oller, J.A.; Roca, L. Dynamical generation of pseudoscalar resonances. Phys. Rev. D 2010, 82. [Google Scholar] [CrossRef]
- Kang, X.W.; Kubis, B.; Hanhart, C.; Meißner, U.G. Bl4 decays and the extraction of |Vub|. Phys. Rev. D 2014, 89. [Google Scholar] [CrossRef]
- Kang, X.W.; Kubis, B.; Hanhart, C.; Meißner, U.G. Bl4 decays and the extraction of |Vub|. In Proceedings of the 8th International Workshop on Chiral Dynamics, Pisa, Italy, 29 June–3 July 2015.
- Kang, X.W. Chiral Dynamics and Final State Interactions in Semileptonic B Meson Decay and Antinucleon-Nucleon Scattering, Ph.D. Thesis, Bonn University, Bonn, Germany, 2014. [Google Scholar]
- Kang, X.-W.; Haidenbauer, J.; Meißner, U.-G. Near-threshold invariant mass spectrum measured in J/ψ and ψ′ decays. Phys. Rev. D 2015, 91. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Kang, X.-W.; Meißner, U.-G. The electromagnetic form factors of the proton in the timelike region. Nucl. Phys. A 2014, 929, 102–104. [Google Scholar] [CrossRef]
- Kang, X.W. Antiproton-proton interaction and related hadron physics. In Proceedings of the 8th International Workshop on Chiral Dynamics, Pisa, Italy, 29 June–3 July 2015.
- Röder, M.; Borodina, E.; Clement, H.; Doroshkevich, E.; Dzhygadlo, R.; Ehrhardt, K.; Erhardt, A.; Eyrich, W.; Gast, W.; Gillitzer, A.; et al. Final-State Interactions in the Process →pK+Λ. Eur. Phys. J. A 2013, 49. [Google Scholar] [CrossRef]
- Datta, A.; O’Donnell, P.J. A New state of baryonium. Phys. Lett. B 2003, 567, 273–276. [Google Scholar] [CrossRef]
- De Rujula, A.; Georgi, H.; Glashow, S.L. Hadron masses in a gauge theory. Phys. Rev. D 1975, 12. [Google Scholar] [CrossRef]
- Zou, B.S.; Chiang, H.C. One pion exchange final state interaction and the near threshold enhancement in J/ψ→γ decays. Phys. Rev. D 2004, 69. [Google Scholar] [CrossRef]
- Zeng, Z.Q.; Guo, X.H.; Shen, P.N.; Ding, Y.B. final state interaction in J/ψ→γ. Chin. Phys. C 2012, 36. [Google Scholar] [CrossRef]
- Taylor, J.R. Scattering Theory: The Quantum Theory on Nonrelativistic Collisions; Johan Wiley and Sons, Inc.: New York, NY, USA, 1972; Chapter 11 and 12. [Google Scholar]
- Goldberger, M.L.; Watson, K.M. Collision Theory; Wiley: New York, NY, USA, 1964; Chapater 9.3. [Google Scholar]
- Ablikim, M.; Bai, J.Z.; Ban, Y.; Cai, X.; Chen, H.F.; Chen, H.S.; Chen, H.X.; Chen, J.C.; Chen, J.; Chen, Y.B.; et al. Study of J/ψ decaying into ω. Eur. Phys. J. C 2008, 53, 15–20. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Albayrak, O.; Ambrose, D.J.; An, F.F.; Bai, J.Z.; Ban, Y.; Becker, J.; Bian, J.M.; Boger, E.; et al. Study of J/ψ→ω at BESIII. Phys. Rev. D 2013, 87. [Google Scholar] [CrossRef]
- Ericson, T.E.O.; Weise, W. Pions and Nuclei; Clarendon Press: Oxford, UK, 1988; pp. 44–46. [Google Scholar]
- Kang, X.-W.; Haidenbauer, J.; Meißner, U.-G. Antinucleon-nucleon interaction in chiral effective field theory. JHEP 2014, 1402. [Google Scholar] [CrossRef]
- Klempt, E.; Batty, C.; Richard, J.M. The Antinucleon-nucleon interaction at low energy : Annihilation dynamics. Phys. Rept. 2005, 413, 197–317. [Google Scholar] [CrossRef]
- Loiseau, B.; Wycech, S. Antiproton-proton channels in J/ψ decays. Phys. Rev. C 2005, 72. [Google Scholar] [CrossRef]
- Dedonder, J.-P.; Loiseau, B.; El-Bennich, B.; Wycech, S. On the structure of the X(1835) baryonium. Phys. Rev. C 2009, 80. [Google Scholar] [CrossRef]
- Sibirtsev, A.; Haidenbauer, J.; Krewald, S.; Meißner, U.G.; Thomas, A.W. Near threshold enhancement of the mass spectrum in J/ψ decay. Phys. Rev. D 2005, 71. [Google Scholar] [CrossRef]
- Entem, D.R.; Fernandez, F. Final state interaction effects in near threshold enhancement of the mass spectrum in B and J/ψ decays. Phys. Rev. D 2007, 75. [Google Scholar] [CrossRef]
- Watson, K.M. The Effect of final state interactions on reaction cross-sections. Phys. Rev. 1952, 88, 1163–1171. [Google Scholar] [CrossRef]
- Migdal, A.B. The Theory of Nuclear Reactions with Production of Slow Particles. JETP 1955, 1, 2–6. [Google Scholar]
- Kerbikov, B.; Stavinsky, A.; Fedotov, V. Model independent view on the low mass proton anti-proton enhancement. Phys. Rev. C 2004, 69. [Google Scholar] [CrossRef]
- Bugg, D.V. Reinterpreting several narrow "resonances" as threshold cusps. Phys. Lett. B 2004, 598, 8–14. [Google Scholar] [CrossRef]
- Gotta, D. Precision spectroscopy of light exotic atoms. Prog. Part. Nucl. Phys. 2004, 52, 133–195. [Google Scholar] [CrossRef]
- Hippchen, T.; Holinde, K.; Plessas, W. The bonn meson exchange potential in the system. Phys. Rev. C 1989, 39, 761–765. [Google Scholar] [CrossRef]
- Hippchen, T.; Haidenbauer, J.; Holinde, K.; Mull, V. Meson - baryon dynamics in the nucleon - anti-nucleon system. 1. The Nucleon - anti-nucleon interaction. Phys. Rev. C 1991, 44, 1323–1336. [Google Scholar] [CrossRef]
- Alexander, J.P.; Cassel, D.G.; Das, S.; Ehrlich, R.; Fields, L.; Gibbons, L.; Gray, S.W.; Hartill, D.L.; Heltsley, B.K.; Kreinick, D.L.; et al. Study of ψ(2S) Decays to γ, π0 and η and search for threshold enhancements. Phys. Rev. D 2010, 82. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Alberto, D.; Ambrose, D.J.; An, F.F.; An, Q.; An, Z.H.; Bai, J.Z.; Baldini Ferroli, R.B.F.; Ban, Y.; et al. Spin-parity analysis of mass threshold structure in J/ψ and ψ′ radiative decays. Phys. Rev. Lett. 2012, 108. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.Y.; Ma, J.P. Scattering at NLO order in an effective theory. Phys. Rev. D 2011, 83. [Google Scholar] [CrossRef]
- Chen, G.Y.; Dong, H.R.; Ma, J.P. Rescattering effect and near threshold enhancement of system. Phys. Rev. D 2008, 78. [Google Scholar] [CrossRef]
- Chen, G.Y.; Dong, H.R.; Ma, J.P. Near threshold enhancement of system and elastic scattering. Phys. Lett. B 2010, 692, 136–142. [Google Scholar] [CrossRef]
- Zhou, D.; Timmermans, R.G.E. Energy-dependent partial-wave analysis of all antiproton-proton scattering data below 925 MeV/c. Phys. Rev. C 2012, 86. [Google Scholar] [CrossRef]
- Grach, I.L.; Kerbikov, B.O.; Simonov, Y.A. Effective range analysis of low-energy nucleon - anti-nucleon Interaction. Phys. Lett. B 1988, 208. [Google Scholar] [CrossRef]
- Pirner, H.J.; Kerbikov, B.; Mahalanabis, J. Updating the effective range expansion of low-energy scattering. Z. Phys. A 1991, 338, 111–112. [Google Scholar] [CrossRef]
- Carbonell, J.; Richard, J.M.; Wycech, S. On the relation between protonium level shifts and nucleon - anti-nucleon scattering amplitudes. Z. Phys. A 1992, 343, 325–329. [Google Scholar] [CrossRef]
- Mull, V.; Holinde, K. Combined description of scattering and annihilation with a hadronic model. Phys. Rev. C 1995, 51, 2360–2371. [Google Scholar] [CrossRef]
- El-Bennich, B.; Lacombe, M.; Loiseau, B.; Wycech, S. Paris potential constrained by recent antiprotonic-atom data and antineutron-proton total cross sections. Phys. Rev. C 2009, 79. [Google Scholar] [CrossRef]
- Ziegler, M.; Ahmad, S.; Amsler, C.; Armenteros, R.; Auld, E.G.; Axen, D.A.; Bailey, D.; Barlag, S.; Beer, G.A.; Bizot, J.C.; et al. Measurement of the Strong Interaction Shift and Broadening of the Ground State of the Atom. Phys. Lett. B 1988, 206. [Google Scholar] [CrossRef]
- Augsburger, M.; Anagnostopoulos, D.F.; Borchert, G.; Chatellard, D.; Egger, J.-P.; El-Khoury, P.; Gorke, H.; Gotta, D.; Hauser, P.; Indelicato, P.; et al. Measurement of the strong interaction parameters in anti-protonic hydrogen and probable evidence for an interference with inner bremsstrahlung. Nucl. Phys. A 1999, 658, 149–162. [Google Scholar] [CrossRef]
- Haidenbauer, J.; Hanhart, C.; Kang, X.W.; Meißner, U.G. Origin of the structures observed in e+e- annihilation into multipion states around the threshold. Phys. Rev. D 2015, 92. [Google Scholar] [CrossRef]
- Kang, X.-W. Bound state nature of X(1835). Unpublished work. 2016. [Google Scholar]
- Haidenbauer, J.; Meißner, U.G.; Sibirtsev, A. Near threshold enhancement in B and J/ψ decay. Phys. Rev. D 2006, 74. [Google Scholar] [CrossRef]
- Mecking, B.A.; Adams, G.; Ahmad, S.; Anciant, E.; Anghinolfi, M.; Asavapibhop, B.; Asryan, G.; Audit, G.; Auger, T.; Avakian, H.; et al. The CEBAF large acceptance spectrometer (CLAS). Nucl. Instrum. Meth. A 2003, 503, 513–553. [Google Scholar] [CrossRef]
- Haidenbauer, J. Near threshold enhancement in J/ψ decays. Available online: http://www.kitpc.ac.cn/files/activities/PF20120611/report/Johann%20Haidenbauer.pdf (accessed on 12 January 2016).
- Lutz, M.F.M.; Pire, B.; Scholten, O.; Timmermans, R.; Erni, W.; Keshelashvili, I.; Krusche, B.; Steinacher, M.; Heng, Y.; Liu, Z.; et al. Physics performance report for PANDA: Strong interaction studies with antiprotons. Available online: https://inspirehep.net/record/816045 (accessed on 12 January 2016).
- Ablikim, M.; Bai, J.Z.; Bian, J.G.; Cai, X.; Chen, H.F.; Chen, H.S.; Chen, H.X.; Chen, J.C.; Chen, J.; Chen, Y. B.; et al. Observation of a resonance X(1835) in J/ψ→π+π-η′. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [PubMed]
- Ablikim, M.; Achasov, M.N.; An, L.; An, Q.; An, Z.H.; Bai, J.Z.; Baldini, R.; Ban, Y.; Becker, J.; Berger, N.; et al. Confirmation of the X(1835) and observation of the resonances X(2120) and X(2370) in J/ψ→γπ+π-η′. Phys. Rev. Lett. 2011, 106. [Google Scholar] [CrossRef] [PubMed]
- Gao, C.S.; Zhu, S.L. Understanding the possible proton anti-proton bound state observed by BES collaboration. Available online: http://arxiv.org/pdf/hep-ph/0308205.pdf (accessed on 2 September 2015).
- Zhu, S.L.; Gao, C.S. X(1835): A possible baryonium? Commun. Theor. Phys. 2006, 46. [Google Scholar] [CrossRef]
- Ma, Y.L. Strong and electromagnetic decays of X(1835) as a baryonium state. J. Phys. G 2009, 36. [Google Scholar] [CrossRef]
- Bugg, D.V. Data on J/ψ→γ(K± π∓) and γ(ηπ+π-). Unpublished work. arXiv:0907.3015, 2009. [Google Scholar]
- Shan, J.; (Institute of High Energy Physics, Beijing, China). Personal communication, 2015.
- Ding, G.J.; Yan, M.L. Proton-antiproton annihilation in baryonium. Phys. Rev. C 2005, 72. [Google Scholar] [CrossRef]
- Yan, M.L. X(1835) as proton-antiproton bound state in Skyrme model. Unpublished work. 2006. [Google Scholar]
- Ding, G.J.; Yan, M.L. Productions of X(1835) as baryonium with sizable gluon content. Eur. Phys. J. A 2006, 28, 351–360. [Google Scholar] [CrossRef]
- Yu, J.S.; Sun, Z.F.; Liu, X.; Zhao, Q. Categorizing resonances X(1835), X(2120) and X(2370) in the pseudoscalar meson family. Phys. Rev. D 2011, 83. [Google Scholar] [CrossRef]
- Klempt, E.; Zaitsev, A. Glueballs, hybrids, multiquarks. Experimental facts versus QCD inspired concepts. Phys. Rept. 2007, 454, 1–202. [Google Scholar] [CrossRef]
- Li, D.M.; Ma, B. X(1835) and η(1760) observed by BES Collaboration. Phys. Rev. D 2008, 77. [Google Scholar] [CrossRef]
- Wang, Z.G. Analysis of the X(1835) and related baryonium states with Bethe-Salpeter equation. Eur. Phys. J. A 2011, 47. [Google Scholar] [CrossRef]
- Zhang, C.C.; Aihara, H.; Asner, D.M.; Aushev, T.; Bakich, A.M.; Ban, Y.; Belous, K.; Bischofberger, M.; Browder, T.E.; Chen, A.; et al. First study of ηc, η(1760) and X(1835) production via η′π+π- final states in two-photon collisions. Phys. Rev. D 2012, 86. [Google Scholar] [CrossRef]
- Ablikim, M.; Achasov, M.N.; Ai, X.C.; Albayrak, O.; Albrecht, M.; Ambrose, D.J.; Amoroso, A.; An, F.F.; An, Q.; Bai, J.Z.; et al. Observation and spin-parity determination of the X(1835) in J/ψ→γ η. Phys. Rev. Lett. 2015, 115. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).