Uncertainty Analysis of ²⁰⁸Pb Neutron Skin Predictions with Chiral Interactions

Abstract

We report predictions for the neutron skin in ²⁰⁸Pb using chiral two- and three-body interactions at increasing orders of chiral effective field theory and varying resolution scales. Closely related quantities, such as the slope of the symmetry energy, are also discussed. The sensitivity of the skin to just pure neutron matter pressure when going from order 2 to order 4 of chiral effective theory is singled out in a set of calculations that employ an empirical equation of state for symmetric nuclear matter.

1. Introduction

Microscopic predictions of the nuclear equation of state (EoS), together with empirical constraints from EoS-sensitive observables, are an ideal combination to learn about the in-medium behavior of the nuclear force. With this objective in mind, over the past several years we have taken a broad look at the EoS and explored diverse aspects of nuclear and neutron-rich matter [1].

From the experimental side, intense effort is going on to obtain reliable empirical information for the less known aspects of the EoS. Heavy-ion (HI) reactions are a popular way to seek constraints on the symmetry energy, through analyses of observables that are sensitive to the difference between the pressure in nuclear matter and the one in neutron matter. Isospin diffusion data in HI collisions, together with analyses based on isospin-dependent transport models, provide information on the slope of the symmetry energy. Naturally, different reaction conditions, in terms of energy per nucleon and/or impact parameter, will probe different density regions. For a recent review on available constraints from a broad spectrum of experiments, see [2].

Concerning the lower densities, isospin-sensitive observables can also be identified among the properties of normal nuclei. The neutron skin of neutron-rich nuclei is a powerful isovector observable, being sensitive to the slope of the symmetry energy, which determines to which extent neutrons are pushed outwards to form the skin. Parity-violating electron scattering experiments are now a realistic option to determine neutron distributions with unprecedented accuracy. These experiments at low momentum transfer are especially suitable to probe neutron densities, because the Z⁰ boson couples primarily to neutrons [3]. From the first electroweak observation of the neutron skin in a neutron-rich heavy nucleus, a value of ${0.33}_{-0.18}^{+0.16}$ for the neutron skin of ²⁰⁸Pb was determined [4], but the next PREX experiment aims to measure the skin within an uncertainty smaller by a factor of 3 (see [4] and references therein).

From the theoretical point of view, microscopic calculations with statistically meaningful uncertainties are essential to guide experiments. Although high-quality meson-theoretic interactions continue to be employed in nuclear structure and reaction calculations, since about the 1990s there exists a general trend to consider chiral effective field theory (EFT) [5] a more fundamental framework. First, chiral EFT has a firm connection with quantum chromodynamics through the symmetries of the effective Lagrangian. Second, it is a systematic approach that allows a reliable quantification of the theoretical error due to the contribution one leaves out (something unavoidable in any manageable calculation). In other words, at each order of chiral perturbation theory (χPT), the theoretical uncertainty associated with a particular prediction can be controlled and quantified. For these reasons, nuclear chiral effective theory is becoming increasingly popular. At this point, it is appropriate to make some additional observations with regard to the structure of the nucleon-nucleon (NN) potential in chiral EFT as compared to the traditional meson-exchange model. In the latter case, the pion, the intermediate-mass meson (typically, the fictitious σ), and the heavier bosons (the ρ and the ω), provide the long-, the intermediate-, and the short-range behavior, respectively, required by the phenomenology of the nuclear force. In chiral EFT, multi-pion exchange diagrams describe the longer and intermediate range part of the force, whereas “contact terms” encode the short-range components. Both philosophies have in common the outstanding role of the pion. Comprehensive reviews on effective field theories of nuclear forces and chiral dynamics in few- and many-body systems can be found in [6,7]. Following the spirit of [8], it is the purpose of this article to systematically examine and discuss predictions of the neutron skin in ²⁰⁸Pb at different orders of chiral EFT and changing resolution scale. Implementation of the full three-nucleon force (3NF) in nuclear matter at N³LO presents considerable challenges and has not yet been accomplished. Thus, at N³LO of the two-nucleon force (2NF), we include only the leading (N²LO) 3NF. Of course, both the 2NF and the 3NF should be complete at each order to explore definite order-by-order convergence, and we make no claim to have accomplished that. However, the result of the present approximation, which is widely used in the current literature, can provide valuable information and insight. Additional discussion of this procedure, particularly with regard to its application and validity in neutron matter, is included in the next section.

With reference to recent predictions of the neutron skin employing chiral interactions, it should be noted that these calculations differ from those of [9] both in philosophy and technical aspects. First, we address order-by-order pattern and estimate the uncertainty in a different way. Namely, at each order of the chiral expansion we change the resolution scale to explore both cutoff dependence and truncation error. (Other, smaller, sources of uncertainty are also considered as discussed in [8].) In contrast, the authors of [9] consider variations of the c_i low-energy constants (LECs) within the range allowed by πN scattering data and apply those variations in the three-nucleon force (3NF). We believe that changes in the πN LECs should be applied consistently in the two- and the three-body force, refitting accordingly both the NN phase shifts and the A=3 system. Our values for the c_i are the same in the 2NF and the 3NF.

Concerning few-nucleon forces, all 3NFs and 4NFs are included in the neutron matter (NM) calculations of [9]. In symmetric nuclear matter (SNM), however, such complete calculation, which requires refitting of the appropriate LECs to the properties of the three-nucleon system, is presently not available. Instead, in [9] an empirical parametrization is adopted for the EoS of SNM and, generally, for matter with a finite proton fraction. As explained above, in the present work the leading 3NF is retained in both NM and SNM, a standard scheme in contemporary ab initio nuclear structure calculations (see [8] for a more comprehensive discussion), and the corresponding microscopic EoS is used to make predictions for the neutron skin thickness and related properties.

Some comments are in place concerning such related properties. It is well established that the neutron skin thickness correlates with the derivative of the symmetry energy. The latter is often represented through the L parameter,

$$L=3{\mathrm{\rho }}_0{\left(\frac{\partial E_{sym}\left(\mathrm{\rho }\right)}{\partial \mathrm{\rho }}\right)}_{{\mathrm{\rho }}_0}\approx 3{\mathrm{\rho }}_0{\left(\frac{\partial e_{n.m.}\left(\mathrm{\rho }\right)}{\partial \mathrm{\rho }}\right)}_{{\mathrm{\rho }}_0}$$

(1)

which originates from an expansion of the symmetry energy around the saturation point, ρ₀. The second approximate equality is due to the vanishing of the first derivative of the energy per particle in SNM at ρ₀, leaving a term proportional to the pressure in neutron matter. Nevertheless, L depends sensitively on the saturation density, which can be quite different from model to model, particularly when considering different chiral orders and regulators. In other words, theoretical predictions of L carry larger EFT uncertainties than the ones of just neutron matter pressure at some fixed density. To explore this point further, we will also compare predictions and uncertainties with those obtained using a phenomenological EoS for SNM consistent with the empirical saturation point.

Conclusions are summarized in the last section.

2. Predictions of Symmetry Pressure and Neutron Skin

2.1. Predictions with Microscopic EoS for NM and SNM

We calculate proton and neutron density distributions with a method described in an earlier work [10]. The method is based on an energy functional derived from the semi-empirical mass formula, where the volume and symmetry terms are contained in the isospin-asymmetric equation of state. Thus, we write the energy of a (spherical) nucleus as

$$E(Z,A)=\int d^{3}re(\mathrm{\rho },\mathrm{\alpha })\mathrm{\rho }\left(r\right)+\int d^{3}r{f}_0({|\nabla \mathrm{\rho }|}^2+{\mathrm{\beta }|\nabla {\mathrm{\rho }}_I|}^2)+Coulombterm$$

(2)

In the above equation, ρ and ρ_I are the usual isoscalar and isovector densities, given by ρ_n + ρ_p and (ρ_n − ρ_p), respectively, α is the neutron asymmetry parameter, α = ρ_I/ρ, and e(ρ, α) is the energy per particle in isospin-asymmetric nuclear matter. The constant f₀ in Equation (2) is approximately 70 MeV fm⁵, whereas the magnitude of β is about 1/4 [11]. (Even with variations of β between −1 and +1, we found that the contribution from that term was negligibly small, so we disregarded its contribution.)

The symmetry energy, E_sym, is defined as the strength of the quadratic term in an expansion of the energy per particle in asymmetric matter with respect to the asymmetry parameter α:

$$e(\mathrm{\rho },\mathrm{\alpha })\approx e(\mathrm{\rho },\mathrm{\alpha }=0)+E_{\text{sym}}{\mathrm{\alpha }}^2+\mathcal{O}\left({\mathrm{\alpha }}^4\right)$$

(3)

The nearly linear behavior of e(ρ, α) with α² has been confirmed by many microscopic calculations (see for instance [12] and more recently [13,14]). It justifies the common approximation of neglecting powers beyond α² in the expansion above and thus defining the symmetry energy as the difference between the energy per particle in neutron matter and symmetric nuclear matter. Therefore,

$$e(\mathrm{\rho },\mathrm{\alpha })\approx e(\mathrm{\rho },\mathrm{\alpha }=0)+E_{\text{sym}}{\mathrm{\alpha }}^2$$

(4)

which we obtain in terms of the symmetric matter and neutron matter equations of state from [8].

The proton and neutron density functions are obtained by minimizing the value of the energy, Equation (2), with respect to the parameters of Thomas–Fermi distributions for proton and neutron densities. Although simple, this method has the advantage of allowing a very direct connection between the EoS and the properties of finite nuclei. Furthermore, microscopic structure calculations for A = 208 are presently not possible. In [10], our method was shown to yield realistic predictions for ⁴⁰Ca, ⁹⁰Zr, and ²⁰⁸Pb with some of the Bonn meson-exchange potentials [15].

The various equations of states employed in this work are described in details in [8]. Here we give a brief summary of the many-body method which we adopt. In our Brueckner–Hartree–Fock calculation, we retain the particle-particle (pp) ladder diagrams, which comprise the leading-order contributions within the traditional hole-line expansion. This choice was found to be adequate in [8] with respect to the overall uncertainty of our calculations. In particular, we estimated the impact of using a non-perturbative approach beyond pp correlations to be about ±1 MeV in nuclear matter around normal density and much smaller in neutron matter. To facilitate the inclusion of 3NFs in the particle-particle ladder approximation, we employ the density-dependent NN interaction derived in [16] from the N²LO chiral three-body force. This effective interaction is obtained by summing one particle line over the occupied states in the Fermi sea. Neglecting small contributions from terms depending on the center-of-mass momentum, the resulting NN interaction can be expressed in analytical form with operator structures identical to those of free-space NN interactions. For symmetric nuclear matter all three-body forces contribute, while for pure neutron matter only terms proportional to the low-energy constants c₁ and c₃ are nonvanishing [16].

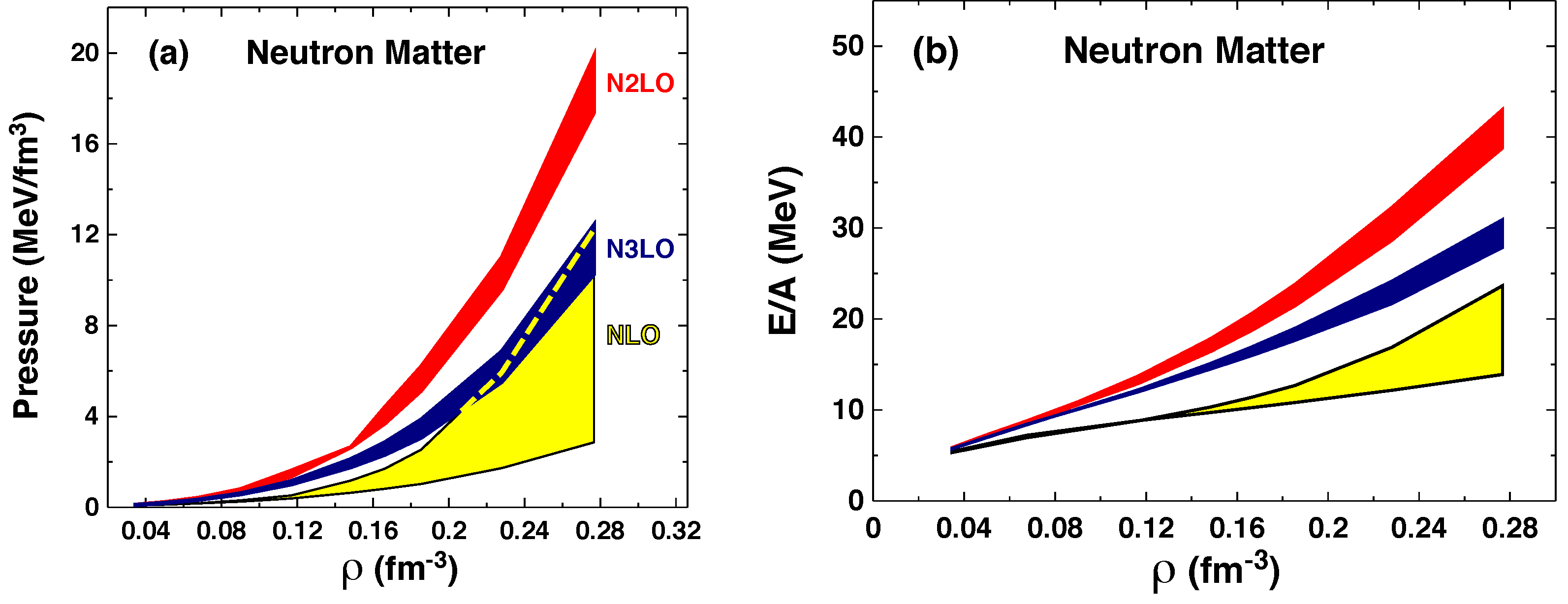
In the figures which follow, the size of each band is obtained from variations of the cutoff between 450 and 600 MeV in the regulator applied to the 2NF and the 3NF [8]. In Figure 1a, the pressure in neutron matter is shown. The yellow and red bands represent the uncertainties in the predictions due to cutoff variations as obtained in complete calculations at next-to-leading order (NLO) and next-to-next-to-leading order (N²LO), respectively. The blue band is the result of a calculation employing next-to-next-to-next-to-leading order (N³LO) NN potentials together with 3NFs at N²LO. The pressure is proportional to the slope of the various curves which make up the corresponding bands shown in Figure 1b. We observe moderate cutoff dependence except at NLO and a slow convergence tendency with increasing order.

Figure 1. (a) Pressure in pure neutron matter as a function of density, ρ. The yellow and red bands represent the uncertainties in the predictions due to cutoff variations as obtained in complete calculations at NLO and N²LO, respectively. The blue band is the result of a calculation employing N³LO NN potentials together with N²LO 3NFs. The dashed line shows the upper limit of the yellow band. (b) Energy per particle in pure neutron matter. The meaning of the bands is the same as in (a).

Figure 1. (a) Pressure in pure neutron matter as a function of density, ρ. The yellow and red bands represent the uncertainties in the predictions due to cutoff variations as obtained in complete calculations at NLO and N²LO, respectively. The blue band is the result of a calculation employing N³LO NN potentials together with N²LO 3NFs. The dashed line shows the upper limit of the yellow band. (b) Energy per particle in pure neutron matter. The meaning of the bands is the same as in (a).

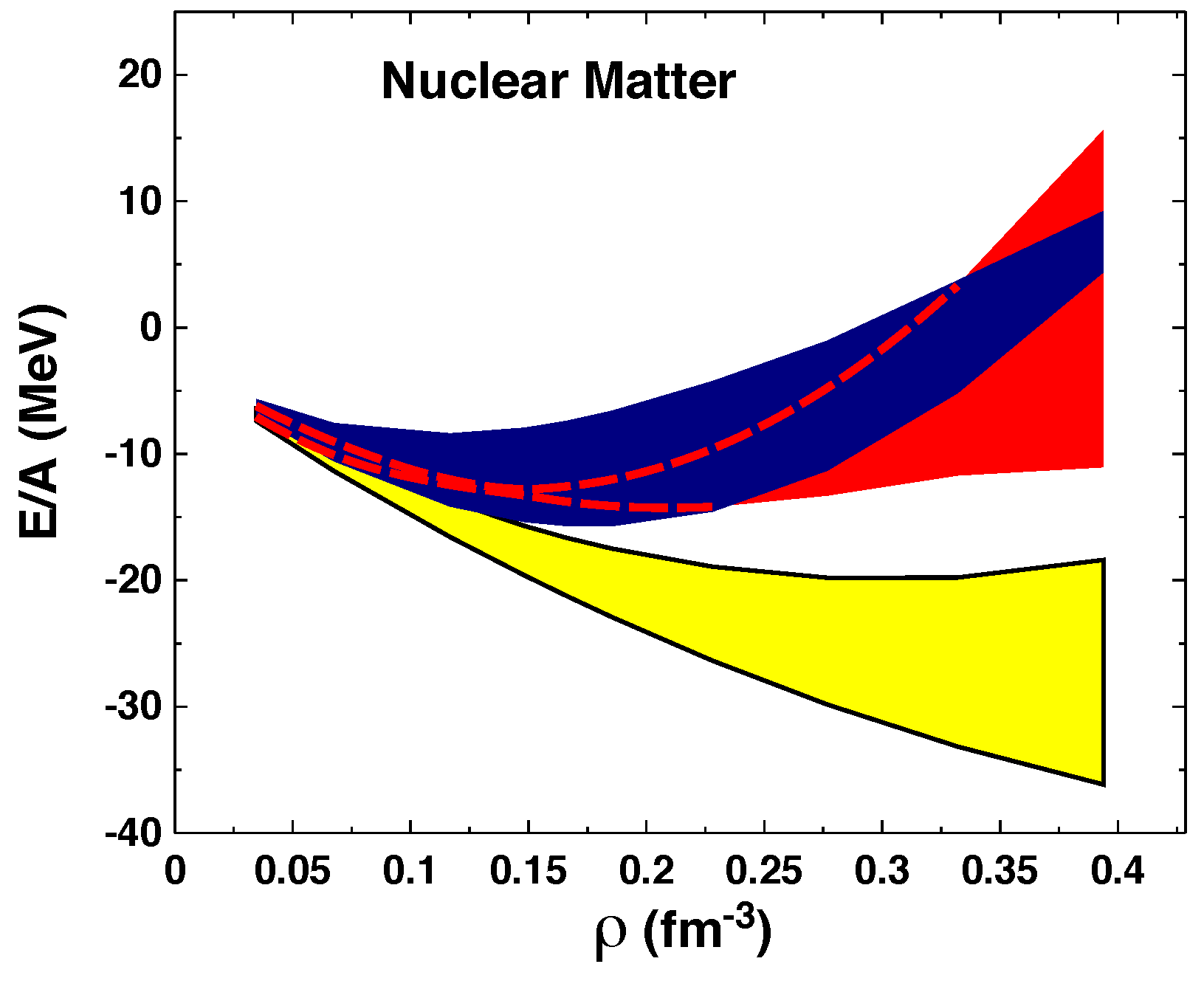
As already pointed out in the Introduction, the L parameter, defined as in Equation (1), is sensitive to the characteristics of the equation of state of symmetric matter through ρ₀. The latter changes dramatically from order to order as well as with changing cutoff, which can be clearly seen from Figure 2. In Figure 3, we show the L parameter as a function of density, i.e.,

$$L\left(\mathrm{\rho }\right)=3\mathrm{\rho }{\left(\frac{\partial E_{sym}\left({\mathrm{\rho }}^{\prime }\right)}{\partial {\mathrm{\rho }}^{\prime }}\right)}_{{\mathrm{\rho }}^{\prime }=\mathrm{\rho }}$$

(5)

which reflects the difference between the pressures in NM and in SNM at each density. The derivative of the EoS of SNM comes in through the symmetry energy and determines larger uncertainties than those seen in Figure 1a.

Figure 2. As in Figure 1b for symmetric nuclear matter.

Figure 2. As in Figure 1b for symmetric nuclear matter.

Figure 3. The L parameter as a function of density, as defined in Equation (5).

Figure 3. The L parameter as a function of density, as defined in Equation (5).

The predictions for the skin thickness of ²⁰⁸Pb are summarized in Table 1, along with the corresponding values of the L parameter at the appropriate saturation density, different in each case and also reported in Table 1. Note that we do not show predictions at NLO because, at this low order, only the EoS with the largest cutoff (of 600 MeV) displays some (late) saturating behavior, cf. Figure 2. The upper and lower errors are the distances of the largest and smallest values (when changing the cutoff) from the average.

Table 1. Neutron skin thickness, S, in ²⁰⁸Pb at the specified order of chiral EFT as explained in the text. The corresponding values of the L parameter and the saturation density are given in the last two columns.

Order	S(fm)	L(ρ0)(MeV)	ρ0(fm−3)
N2LO	${0.21}_{-0.02}^{+0.04}$	${77.4}_{-16.2}^{+31.2}$	${0.167}_{-0.022}^{+0.043}$
N3LO	${0.17}_{-0.01}^{+0.02}$	${39.9}_{-15.7}^{+17.2}$	${0.144}_{-0.032}^{+0.032}$

Table 1. Neutron skin thickness, S, in ²⁰⁸Pb at the specified order of chiral EFT as explained in the text. The corresponding values of the L parameter and the saturation density are given in the last two columns.

Order	S(fm)	L(ρ0)(MeV)	ρ0(fm−3)
N2LO	${0.21}_{-0.02}^{+0.04}$	${77.4}_{-16.2}^{+31.2}$	${0.167}_{-0.022}^{+0.043}$
N3LO	${0.17}_{-0.01}^{+0.02}$	${39.9}_{-15.7}^{+17.2}$	${0.144}_{-0.032}^{+0.032}$

The truncation error at order ν of chiral EFT is the difference between the predictions at orders ν + 1 and ν. Thus, from Table 1, we can estimate this error at N²LO to be about 0.04 fm. A similar estimate at N³LO would require knowledge of the prediction at N⁴LO, which is not available. Assuming a (pessimistic) truncation error at N³LO of similar size as the one at N²LO, we then summarize our predictions for the skin as 0.17 ± 0.04 fm, where the error is likely to be smaller assuming a reasonable convergence rate. In fact, if one takes the cutoff variation as a realistic estimate of the error (as it is approximately the case at N²LO, cf. Table 1), then our N³LO prediction carries an error of 0.02 fm.

2.2. Using a Phenomenological EoS for Symmetric Nuclear Matter

The nearly linear correlation between skins and neutron matter pressure typically observed in phenomenological investigations of skins [17,18] refers to a family of models with the same, or very similar, SNM properties that differ mostly in the slope of neutron matter. This scenario can be simulated, for instance, by combining an empirical SNM equation of state together with different (microscopic) NM EoS, thus separating out the role of neutron matter pressure and removing any model dependence originating from the details of the saturation point. At this time we recall that our calculations at N³LO include the leading 3NF. For pure neutron matter, we expect the contribution from the 3NF at N³LO to be very small, as it was shown in [19] for the potential of [20] (about −0.5 MeV at normal density). Thus, it is likely that the set of calculations we report below shows a realistic convergence pattern of the skin from NLO to N³LO as determined by the corresponding pattern in neutron matter. The impact of the 3NF at N³LO is larger (attractive and about 3 MeV at normal density) if the chiral NN potential of [21] is used instead. We note, though, that a different power counting scheme is used by the authors of those interactions, and thus a comparison, particularly within the context of examining order-by-order pattern, would be inconsistent. We also observe that, in [19], the 3NF at N²LO and at N³LO are applied at the Hartree–Fock level. The low-energy constants c_i are extracted from πN analyses at the respective orders, with uncertainties estimated by applying variations of those c_i in the 3NF but not in the corresponding 2NF. The resulting impact of the 3NF contribution at N³LO is an enhancement of about 3 MeV with the potential of [20]. We end these comments by stressing again the importance of complete calculations at each order beyond the Hartree–Fock approximation in order to reach definite conclusions on the convergence pattern of the neutron skin.

We repeated the calculations adopting, this time, the empirical EoS from [22] for SNM. The latter is obtained from a Skyrme-type energy density functional and has a realistic saturation point at ρ₀ = 0.16 fm⁻³ with energy per particle equal to −16.0 MeV. The corresponding findings are displayed in Table 2. For this test, we also show the results at NLO, since the saturation point can be defined for all cases. Although the midvalues are reasonably consistent with those in Table 1, the uncertainties are much smaller, particularly for the L parameter, as to be expected based on the previous observations. The much smaller uncertainty at N³LO reflects the negligible cutoff dependence of neutron matter pressure at that order, see Figure 1.

Table 2. As Table 1, but employing a phenomenological model for the EoS of SNM. See text for details.

Order	S(fm)	L(ρ0)(MeV)
NLO	${0.126}_{-0.003}^{+0.004}$	${20.4}_{-6.3}^{+8.8}$
N2LO	${0.20}_{-0.01}^{+0.01}$	${70.6}_{-8.0}^{+4.1}$
N3LO	${0.172}_{-0.005}^{+0.002}$	${44.9}_{-5.4}^{+3.8}$

Table 2. As Table 1, but employing a phenomenological model for the EoS of SNM. See text for details.

Order	S(fm)	L(ρ0)(MeV)
NLO	${0.126}_{-0.003}^{+0.004}$	${20.4}_{-6.3}^{+8.8}$
N2LO	${0.20}_{-0.01}^{+0.01}$	${70.6}_{-8.0}^{+4.1}$
N3LO	${0.172}_{-0.005}^{+0.002}$	${44.9}_{-5.4}^{+3.8}$

With similar considerations as above with respect to the truncation error, we define the uncertainty at N²LO as the difference between the prediction at this order and the one at the next order, which gives approximately 0.03. Assuming a similar uncertainty at N³LO, we estimate the skin thickness at N³LO, when adopting an empirical parametrization for the EoS of SNM, to be 0.17 ± 0.03. We note, again, that this reflects the uncertainty in pure neutron matter at the low densities probed by the skin. Such uncertainty is small, consistent with the low-density behavior seen in Figure 1a.

In closing, we observe that our final estimate is consistent with the value reported in [9], where the skin is obtained through correlations from [18], and including a study based on the liquid drop model. This strengthens our confidence in the method we adopt to obtain the skin.

3. Conclusions

The neutron skin is an important isospin-sensitive “observable”, essentially determined by the difference in pressure between symmetric and neutron matter. We calculated the neutron skin of ²⁰⁸Pb with two- and three-body chiral interactions. The neutron and proton density functions are obtained in a simple approach based on the semi-empirical mass formula. We observed that, in fully microscopic calculations, model dependence from the details of SNM at the saturation point does impact predictions of the symmetry pressure and, to a lesser extent, the neutron skin.

At the low densities typically probed by studies of the skin, the EFT theoretical uncertainties for the skin are small on a scale set by a realistic experimental uncertainty, particularly at the higher orders of chiral effective field theory.

Calculations at N⁴LO are needed for a better quantification of the truncation error at N³LO, and thus a reliable comparison of the EFT error with the target uncertainty set by future PREX experiments. Concerning the latter, from [4] we learn that the target uncertainty of PREX II is a factor of 3 smaller than the one from the first PREX experiment, thus approximately ±0.05. If accomplished, this small uncertainty, along with the measured central value, will allow to discriminate between theoretical predictions. For instance, the present EFT predictions would not be consistent with a measurement such as 0.33 (the current central value) ±0.05.