Continuous Learning Graphical Knowledge Unit for Cluster Identification in High Density Data Sets
Abstract
:1. Introduction
1.1 Related Work
2. Methodology
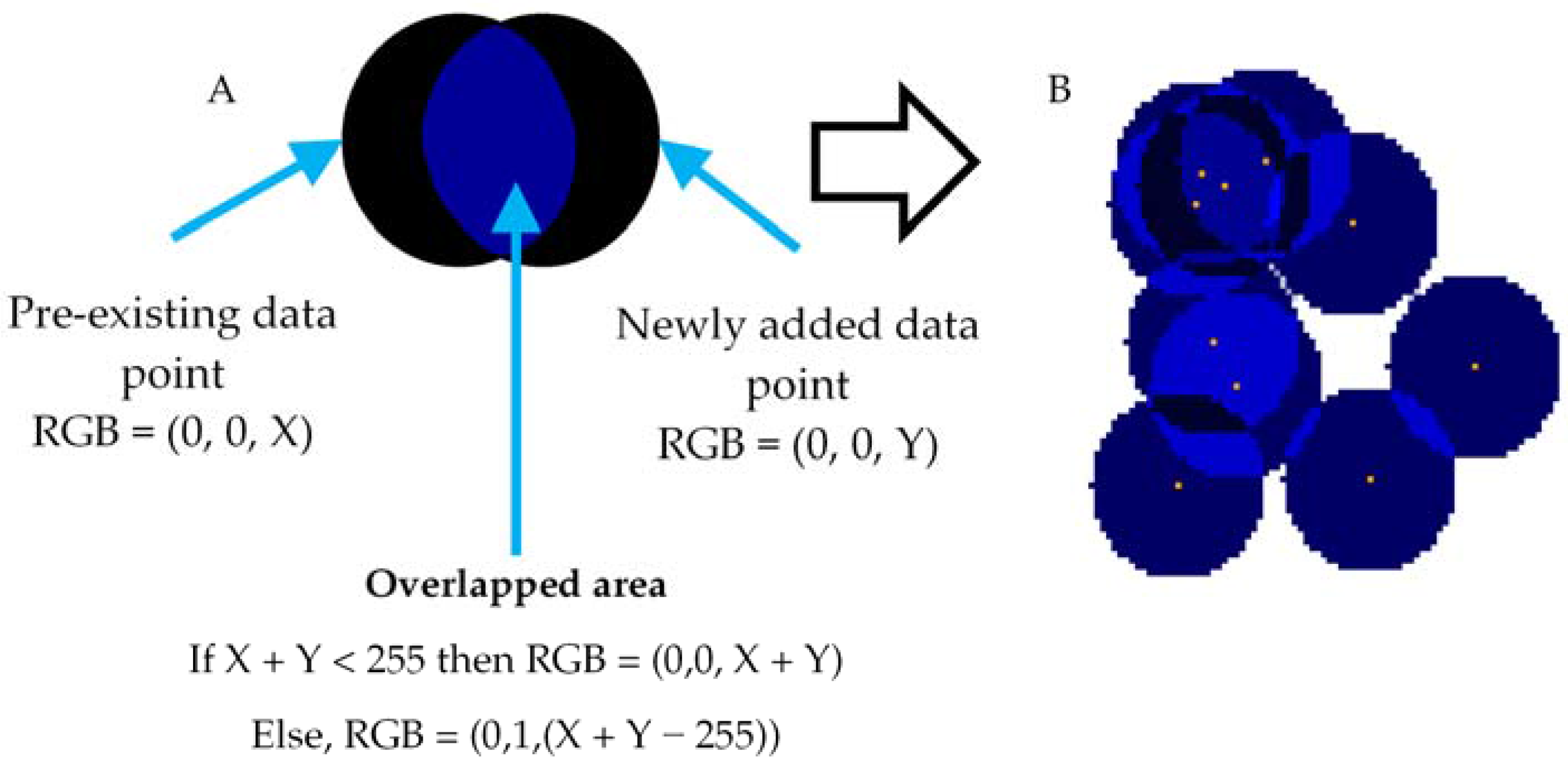
2.1. Colour Coding Method
2.2. Data Preparation
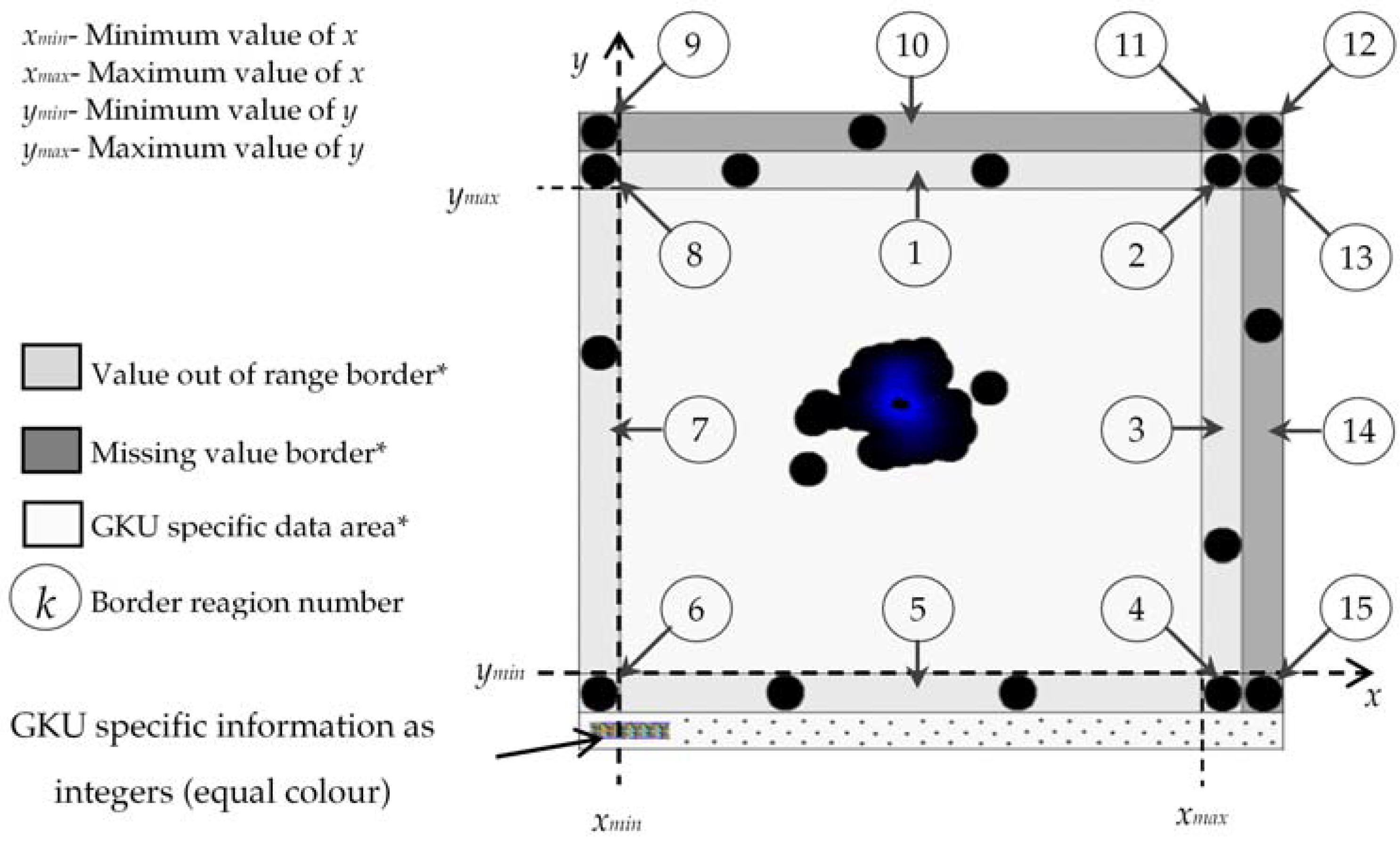
2.3. Visualization of Missing and Out of Range Values
2.4. Embed GKU Specific Information into Bitmap
2.5. GKU Evaluation Method
3. Results and Discussion
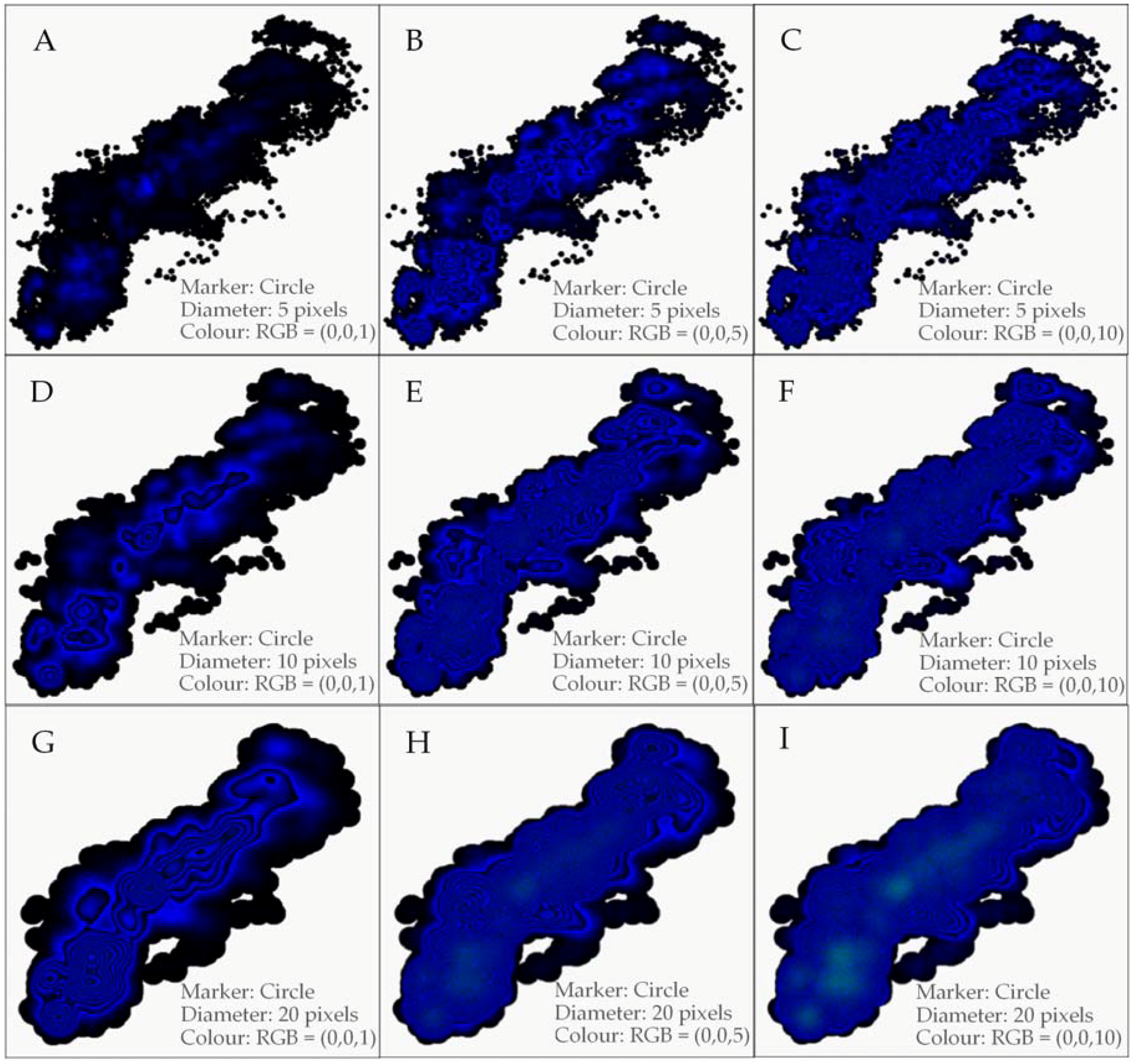
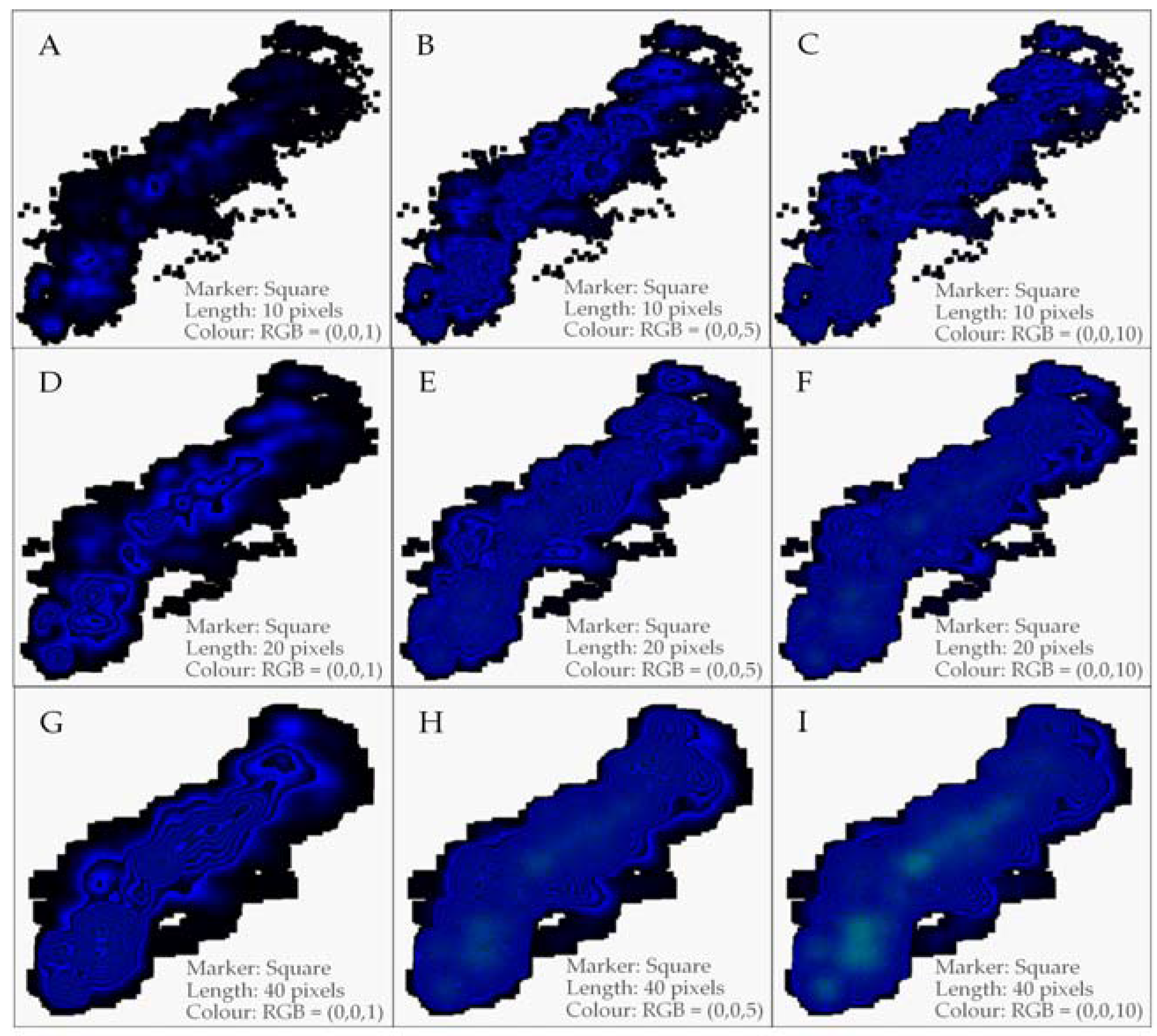
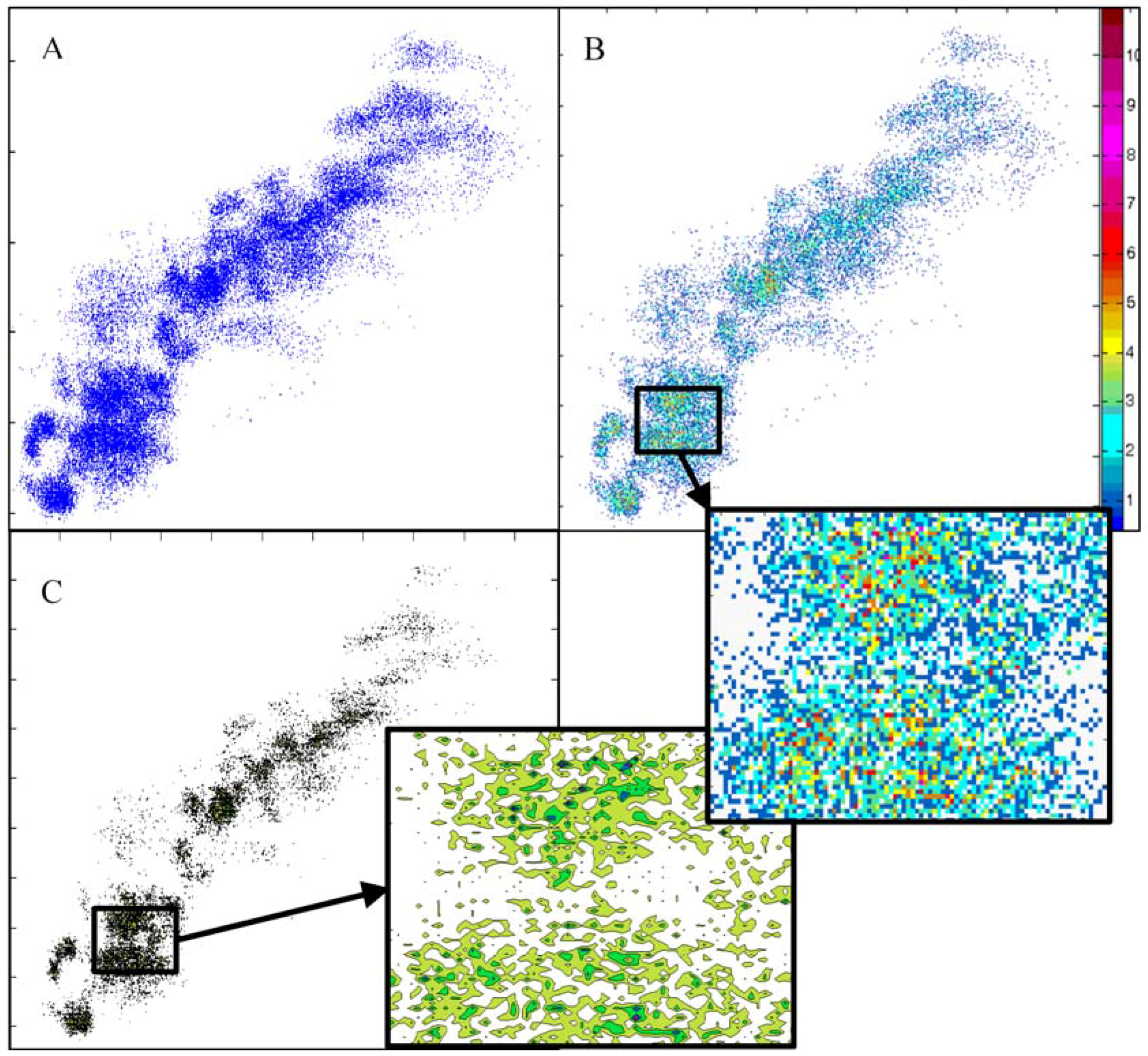
3.1. Reading GKUs
3.2. Anytime Cluster Formation
3.3. Representation of Missing and Out of Range Values and GKU Specific Data
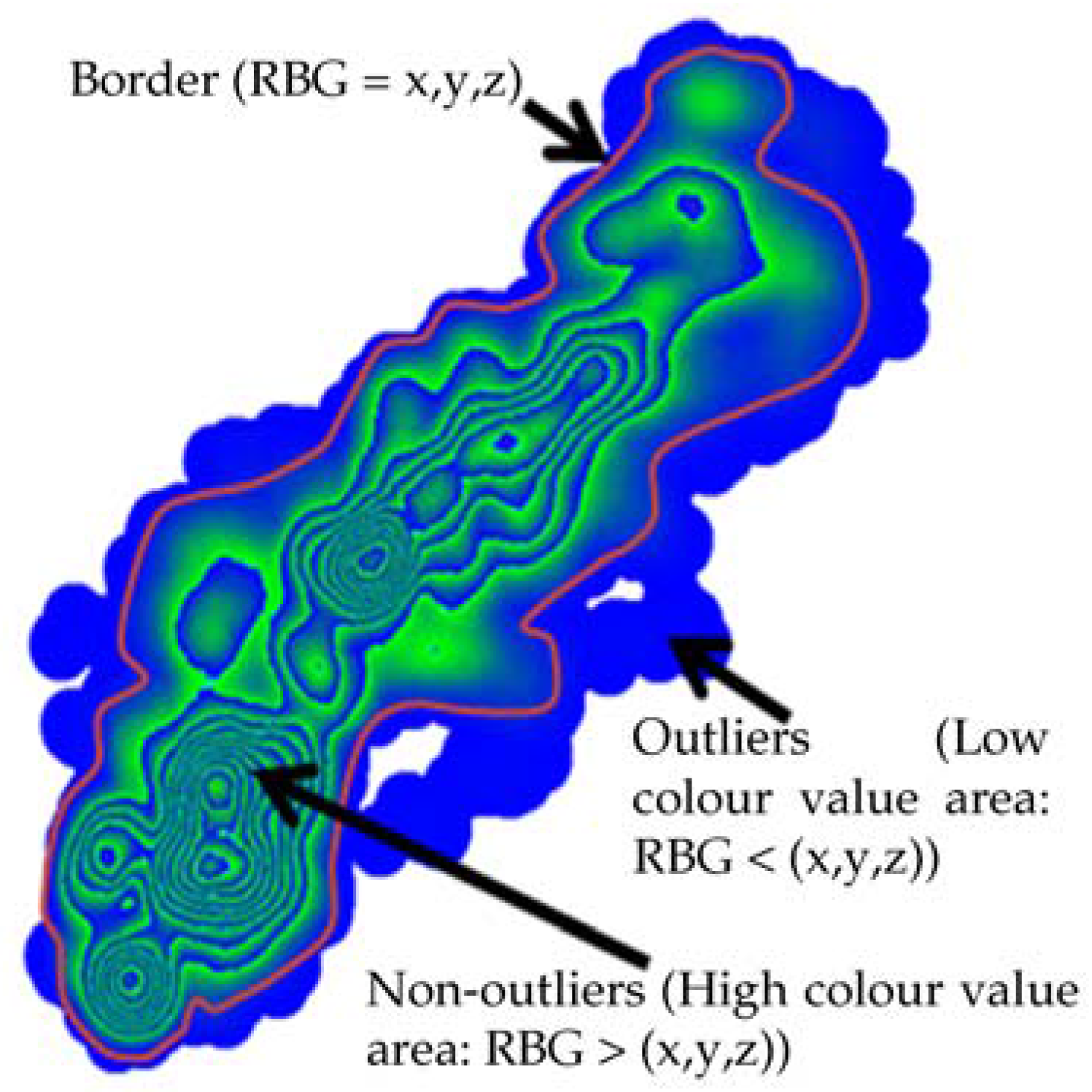
3.4. GKU as an Outlier Detection Method
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Stone, M.C.; Fishkin, K.; Bier, E.A. The Movable Filter as a User Interface Tool. In Proceedings of the ACM SIGCHI Conference on Human Factors in Computing Systems, Boston, MA, USA, 24–28 April 1994; pp. 306–312.
- Woodruff, A.; Landay, J.; Stonebraker, M. Constant density visualizations of non-uniform distributions of data. In Proceedings of the 11th Annual ACM Symposium on User Interface Software and Technology, San Francisco, CA, USA, 1–4 November 1998.
- Yang, J.; Ward, M.O.; Rundensteiner, E.A. Visual hierarchical dimension reduction for exploration of high dimensional datasets. In Proceedings of the Eurographics/IEEE TCVG Symposium on Visualization, Grenoble, France, 26–28 May 2003.
- Ellis, G.; Dix, A. A Taxonomy of Clutter Reduction for Information Visualisation. IEEE Trans. Vis. Comput. Graph. 2007, 13, 1216–1223. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chen, W.; Mei, H.; Liu, Z.; Zhou, K.; Chen, W.; Gu, W.; Ma, K.L. Visual Abstraction and Exploration of Multi-class Scatterplots. IEEE Trans. Vis. Comput. Graph. 2014, 20, 1683–1692. [Google Scholar] [CrossRef] [PubMed]
- Cleveland, W.S. Visualizing Data; Hobart Press: Hobart, Australia, 1993. [Google Scholar]
- Bachthaler, S.; Weiskopf, D. Efficient and Adaptive Rendering of 2-D Continuous Scatterplots. Comput. Graph. Forum 2009, 28, 743–750. [Google Scholar] [CrossRef]
- Mai, S.T.; He, X.; Feng, J.; Plant, C.; Böhm, C. Anytime density-based clustering of complex data. Knowl. Inform. Syst. 2015, 45, 319–355. [Google Scholar] [CrossRef]
- Hoffman, P.; Grinstein, G. Visualizations for High Dimensional Data Mining-Table Visualizations. 1997. Available online: http://web.simmons.edu/~benoit/infovis/MIV-datamining.pdf (accessed on 28 January 2014).
- Salomon, D. Raster Graphics. In The Computer Graphics Manual; Springer: Berlin/Heidelberg, Germany, 2011; pp. 29–131. [Google Scholar]
- Salomon, D. Graphics Standards. In The Computer Graphics Manual; Springer: Berlin/Heidelberg, Germany, 2011; pp. 947–972. [Google Scholar]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Index. In Cluster Analysis; John Wiley & Sons, Ltd.: New York, NY, USA, 2011; pp. 321–330. [Google Scholar]
- Lee, R.C.T. Clustering Analysis and Its Applications. Adv. Inform. Syst. Sci. 1981, 8, 169–292. [Google Scholar]
- Næs, T.; Brockhoff, P.B.; Tomic, O. Cluster Analysis: Unsupervised Classification. In Statistics for Sensory and Consumer Science; John Wiley & Sons, Ltd.: New York, NY, USA, 2010; pp. 249–261. [Google Scholar]
- Okun, O.; Priisalu, H. Unsupervised data reduction. Signal Process. 2007, 87, 2260–2267. [Google Scholar] [CrossRef]
- Anderberg, M.R. Cluster Analysis for Applications; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Chui, C.K.; Filbir, F.; Mhaskar, H.N. Representation of functions on big data: Graphs and trees. Appl. Comput. Harmon. Anal. 2015, 38, 489–509. [Google Scholar] [CrossRef]
- Avramenko, Y.; Ani, E.-C.; Kraslawski, A.; Agachi, P.S. Mining of graphics for information and knowledge retrieval. Comput. Chem. Eng. 2009, 33, 618–627. [Google Scholar] [CrossRef]
- Yu, H.; Yang, J.; Han, J.; Li, X. Making SVMs Scalable to Large Data Sets using Hierarchical Cluster Indexing. Data Min. Knowl. Discov. 2005, 11, 295–321. [Google Scholar] [CrossRef]
- De Vito, E.; Rosasco, L.; Toigo, A. Learning sets with separating kernels. Appl. Comput. Harmon. Anal. 2014, 37, 185–217. [Google Scholar] [CrossRef]
- Galluccio, L.; Michel, O.; Comon, P.; Hero, A.O., III. Graph based k-means clustering. Signal Process. 2012, 92, 1970–1984. [Google Scholar] [CrossRef]
- Sebzalli, Y.M.; Li, R.F.; Chen, F.Z.; Wang, X.Z. Knowledge discovery from process operational data for assessment and monitoring of operator’s performance. Comput. Chem. Eng. 2000, 24, 409–414. [Google Scholar] [CrossRef]
- Barbará, D.; Chen, P. Using Self-Similarity to Cluster Large Data Sets. Data Min. Knowl. Discov. 2003, 7, 123–152. [Google Scholar] [CrossRef]
- David, G.; Averbuch, A. Hierarchical data organization, clustering and denoising via localized diffusion folders. Appl. Comput. Harmon. Anal. 2012, 33, 1–23. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, C.; Song, Y.; Zhang, A.; Ramanathan, M. VizCluster and its Application on Classifying Gene Expression Data. Distrib. Parallel Databases 2003, 13, 73–97. [Google Scholar] [CrossRef]
- Johansson, J.; Ljung, P.; Jern, M.; Cooper, M. Revealing structure in visualizations of dense 2D and 3D parallel coordinates. Inform. Vis. 2006, 5, 125–136. [Google Scholar] [CrossRef]
- Wilkinson, L.; Friendly, M. The History of the Cluster Heat Map. Am. Stat. 2009, 63, 179–184. [Google Scholar] [CrossRef]
- Niida, A.; Tremmel, G.; Imoto, S.; Miyano, S. Multilayer Cluster Heat Map Visualizing Biological Tensor Data. In Proceedings of the 2013 8th Brazilian Symposium on Advances in Bioinformatics and Computational Biology, Recife, Brazil, 3–7 November 2013; Setubal, J., Almeida, N., Eds.; pp. 116–125.
- Weinstein, J.N. A Postgenomic Visual Icon. Science 2008, 319, 1772–1773. [Google Scholar] [CrossRef] [PubMed]
- Hao, M.C.; Dayal, U.; Sharma, R.K.; Keim, D.A.; Janetzko, H. Variable binned scatter plots. Inform. Vis. 2010, 9, 194–203. [Google Scholar] [CrossRef]
- Mayorga, A.; Gleicher, M. Splatterplots: Overcoming Overdraw in Scatter Plots. IEEE Trans. Vis. Comput. Graph. 2013, 19, 1526–1538. [Google Scholar] [CrossRef] [PubMed]
- Nievergelt, J.; Widmayer, P. Spatial data structures: Concepts and design choices. In Algorithmic Foundations of Geographic Information Systems; van Kreveld, M., Nievergelt, J., Roos, T., Widmayer, P., Eds.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 153–197. [Google Scholar]
- Yoo, J.; Bow, M. Mining spatial colocation patterns: A different framework. Data Min. Knowl. Discov. 2012, 24, 159–194. [Google Scholar] [CrossRef]
- Gross, M.; Pfister, H. Point-Based Graphics; Morgan Kaufmann Publishers Inc.: San Mateo, CA, USA, 2007; p. 248. [Google Scholar]
- Carr, D.B.; Littlefield, R.J.; Nicholson, W.L.; Littlefield, J.S. Scatterplot Matrix Techniques for Large N. J. Am. Stat. Assoc. 1987, 82, 424–436. [Google Scholar] [CrossRef]
- Imhof, E. Cartographic Relief Presentation; ESRI Press: Redlands, CA, USA, 2007; p. 111. [Google Scholar]
- Bowman, A.; Foster, P. Density based exploration of bivariate data. Stat. Comput. 1993, 3, 171–177. [Google Scholar] [CrossRef]
- Lampe, O.D.; Hauser, H. Interactive visualization of streaming data with Kernel Density Estimation. In Proceedings of the 2011 IEEE Pacific Visualization Symposium (PacificVis), Hong Kong, China, 1–4 March 2011.
- George, G.R. New Methods of Mathematical Modeling of Human Behavior in the Manual Tracking Task. Ph.D. Thesis, University of New York, Binghamton, NY, USA, 2008; p. 190. [Google Scholar]
- Krapf, L.C.; Heuwinkel, H.; Schmidhalter, U.; Gronauer, A. The potential for online monitoring of short-term process dynamics in anaerobic digestion using near-infrared spectroscopy. Biomass Bioenergy 2013, 48, 224–230. [Google Scholar] [CrossRef]
- Huang, Z. Extensions to the k-Means Algorithm for Clustering Large Data Sets with Categorical Values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Angiulli, F.; Fassetti, F. Exploiting domain knowledge to detect outliers. Data Min. Knowl. Discov. 2014, 28, 519–568. [Google Scholar] [CrossRef]
- Akoglu, L.; Tong, H.; Koutra, D. Graph based anomaly detection and description: A survey. Data Min. Knowl. Discov. 2015, 29. [Google Scholar] [CrossRef]
- Salomon, D. The Computer Graphics Manual; Springer: Berlin/Heidelberg, Germany, 2011; p. 967. [Google Scholar]
- Van Verth, J.M.; Bishop, L.M. Essential Mathematics for Games and Interactive Applications: A Programmer’s Guide, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; p. 264. [Google Scholar]

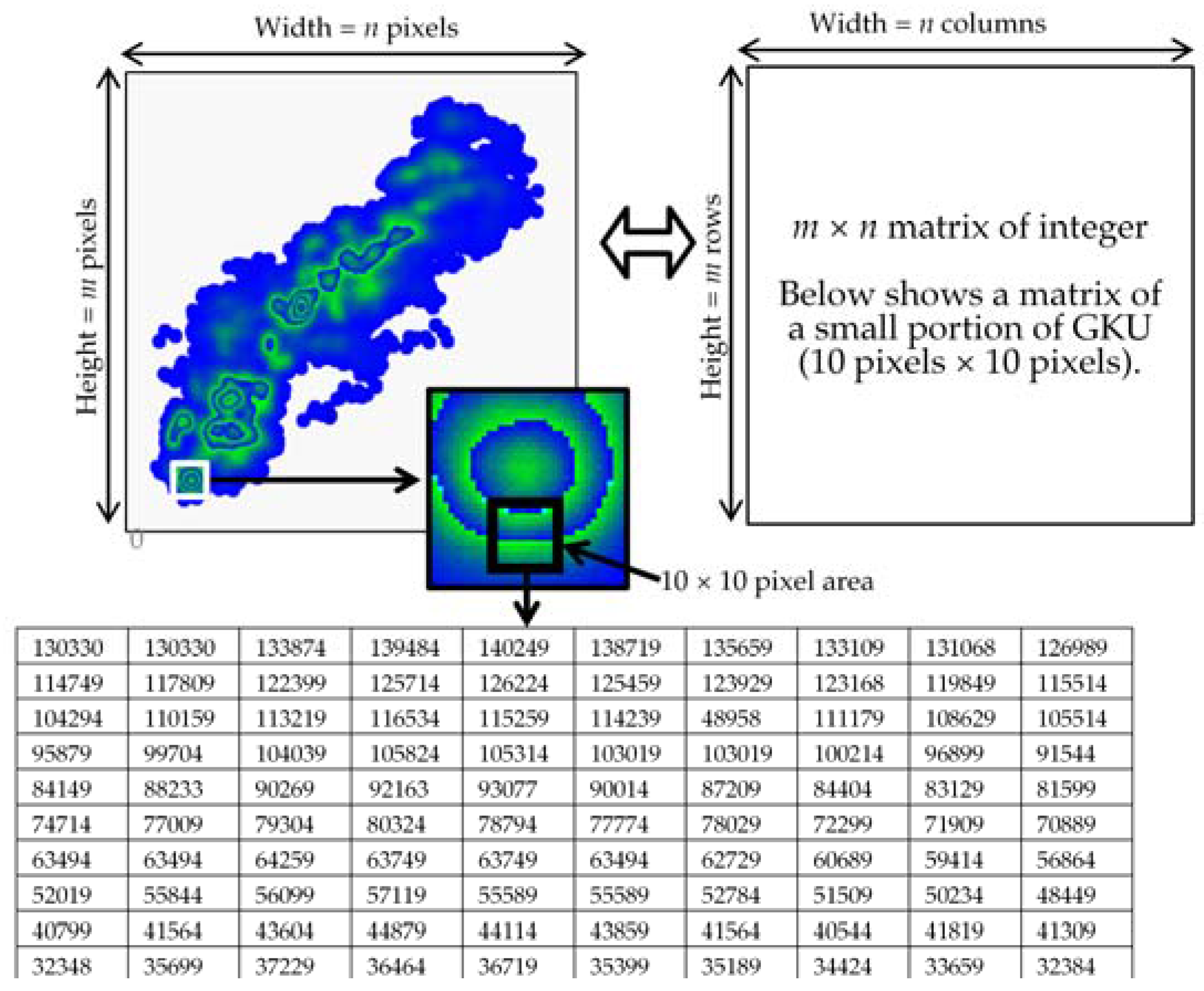
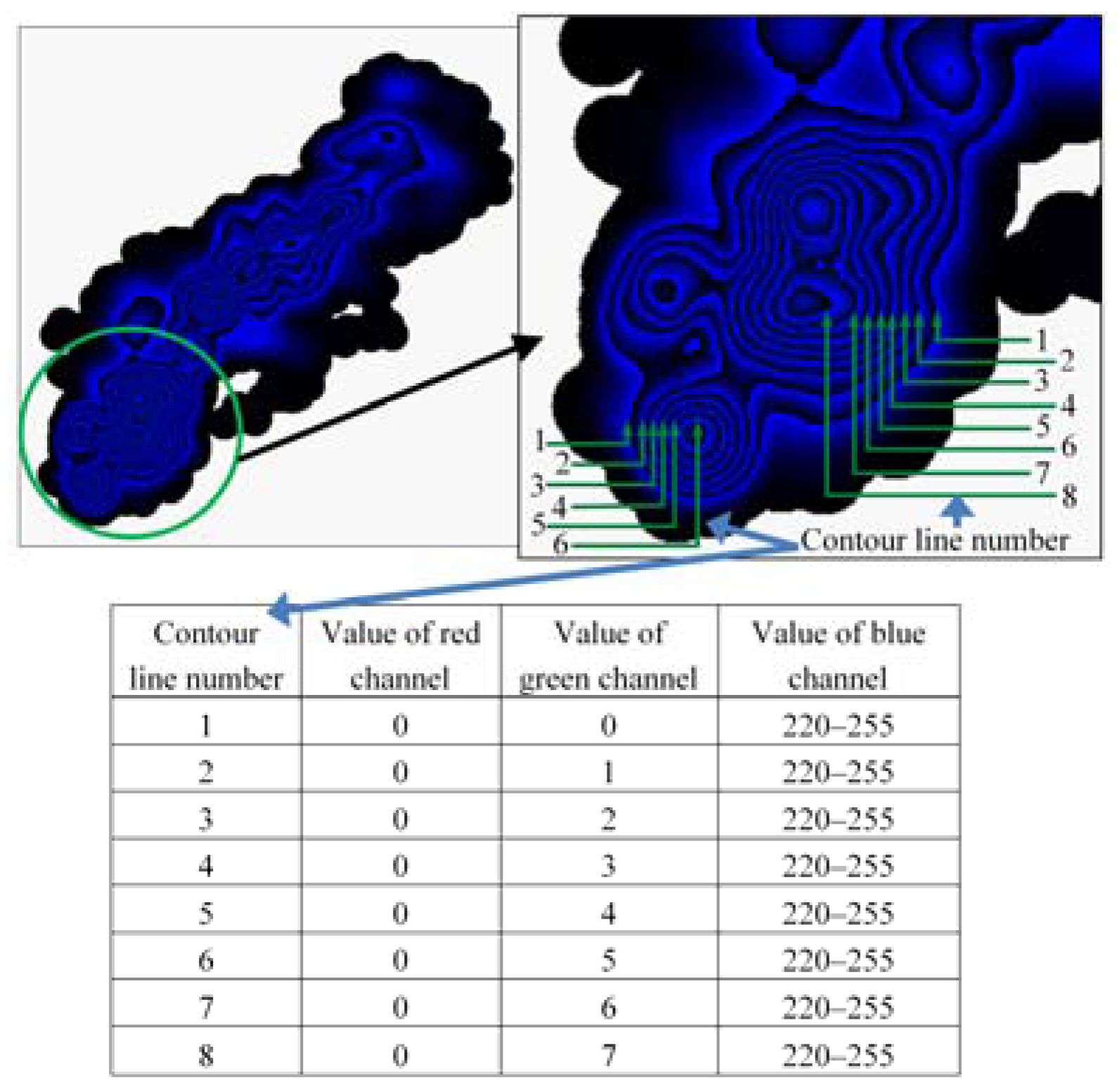
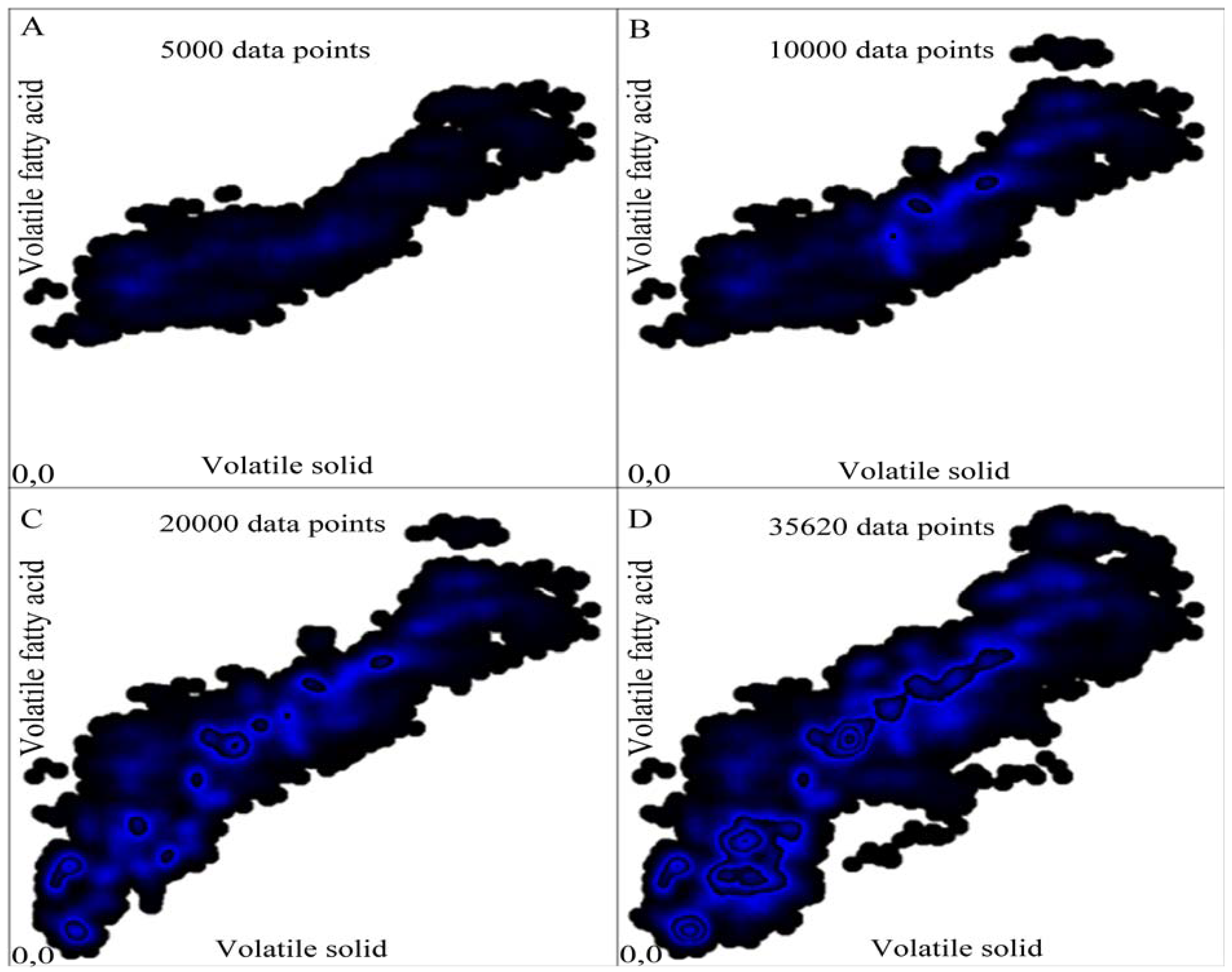
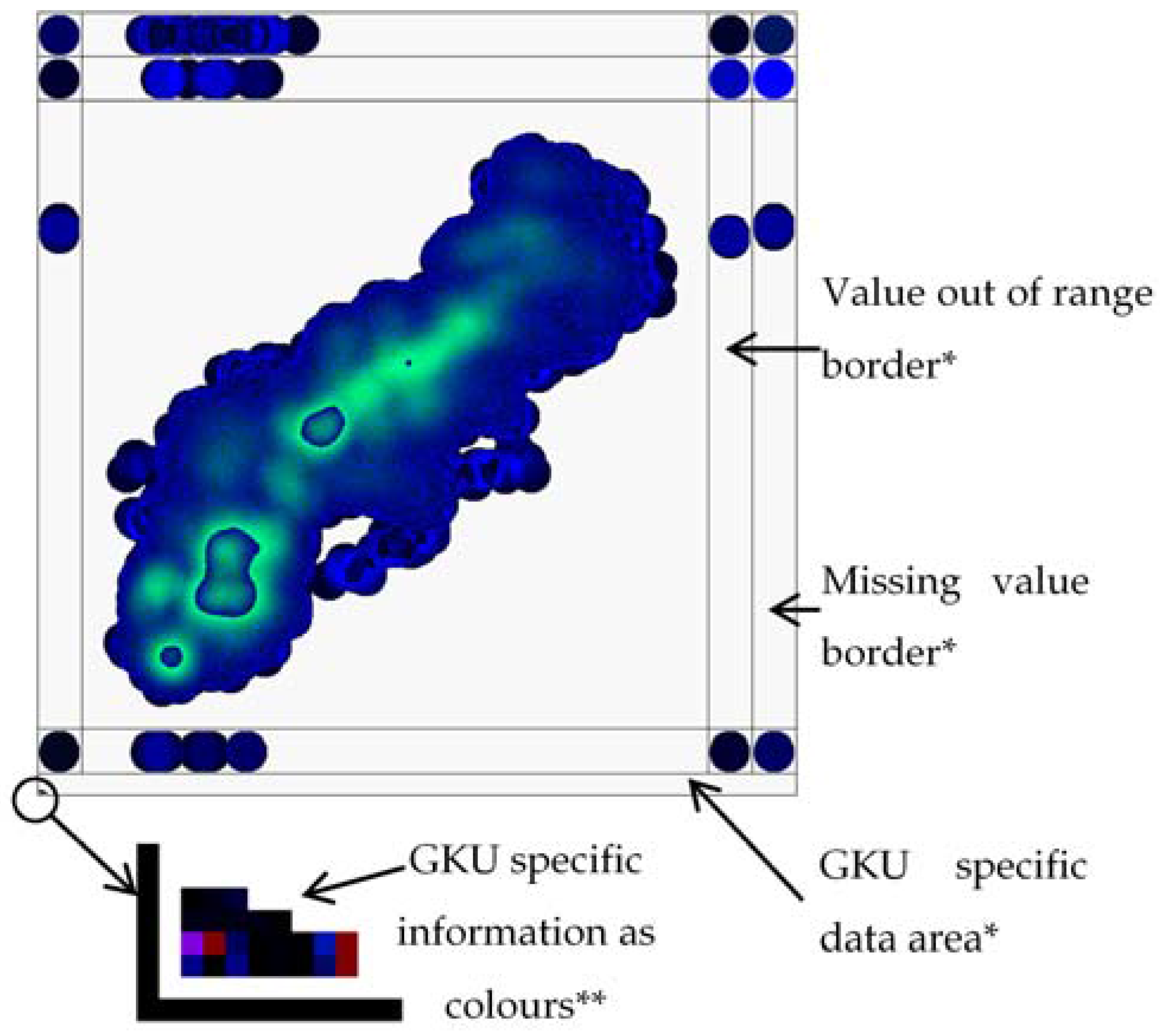
| Value Type | Transformation Technique |
|---|---|
| Negative integer values | Base line correction. This will convert all negative values to positive values while maintaining the same regression. |
| Very large values | Base line correction. This will convert large numbers to small numbers while maintaining the same regression. |
| Decimal values | Multiplication by 10d (d ϵ {1, 2, 3,…}). This will convert decimal values to integers (we named d as “decimal to integer factor”). |
| Small or large range | Scale up or down. This will change the range. |
| Header Section | Offset | Size/Bytes | Value | Description |
|---|---|---|---|---|
| Bitmap (BMP) Header (14 Bytes) | 0 | 2 | “BM” | Identification (ID) field |
| 2 | 4 | Size of BMP header, DIB header, and Image | Size of the BMP file | |
| 6 | 2 | Unused* | Application specific | |
| 8 | 2 | Unused | Application specific | |
| 10 | 4 | 54 Bytes (14 + 40) | Offset where the pixel array (bitmap data) can be found | |
| Device-independent bitmap (DIB) header | 12 | 40 Bytes | ||
| … | ||||
| 50 | ||||
| Bitmap data | 51 | m × n × 4 Bytes | ||
| … | ||||
| … |
| GKU Specific Data | Offset of Pixels | No. of Pixels | Content in the Pixels, According to the Order | Pixel Format Used to Store Information | Example |
|---|---|---|---|---|---|
| Properties of point marker | K | 3 | Data point = Circle (1 = circle, 2 = square, …), radius of the circle, colour of the circle. | unsigned 24-bit pixel format | 1, 10, 1 |
| Border widths | K + 1 | 5 | Out of range border, missing value border, GKU specific data border, border padding, offset. | unsigned 24-bit pixel format | 10, 10, 10, 1, 10 |
| X value information | K + 2 | 8 | Minimum value, maximum value, decimal to integer factor, scale up/down factor. | two signed 24-bit pixel format | (65, 0), (90, 0), (10, 0), (2, 0) |
| Y value information | K + 3 | 8 | Minimum value, maximum value, decimal to integer factor, scale up/down factor. | two signed 24-bit pixel format | (223, −2), (9055, −3), (10, 0), (3, 0) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adikaram, K.K.L.B.; Hussein, M.A.; Effenberger, M.; Becker, T. Continuous Learning Graphical Knowledge Unit for Cluster Identification in High Density Data Sets. Symmetry 2016, 8, 152. https://doi.org/10.3390/sym8120152
Adikaram KKLB, Hussein MA, Effenberger M, Becker T. Continuous Learning Graphical Knowledge Unit for Cluster Identification in High Density Data Sets. Symmetry. 2016; 8(12):152. https://doi.org/10.3390/sym8120152
Chicago/Turabian StyleAdikaram, K.K.L.B., Mohamed A. Hussein, Mathias Effenberger, and Thomas Becker. 2016. "Continuous Learning Graphical Knowledge Unit for Cluster Identification in High Density Data Sets" Symmetry 8, no. 12: 152. https://doi.org/10.3390/sym8120152
APA StyleAdikaram, K. K. L. B., Hussein, M. A., Effenberger, M., & Becker, T. (2016). Continuous Learning Graphical Knowledge Unit for Cluster Identification in High Density Data Sets. Symmetry, 8(12), 152. https://doi.org/10.3390/sym8120152






