Evaluation and Classification of Overseas Talents in China Based on the BWM for Intuitionistic Relations
Abstract
:1. Introduction
2. Discussion on Criteria Weight
- (1)
- .
- (2)
- It is obvious that, ; , if ; , if ; , if ; indicates which kind of preference relation of over is dominant, the preferred degree or the non-preferred degree.
- (3)
- Let and be two IMNs. If and , then .
3. A Non-Linear BWM for an Intuitionistic Relation
3.1. BWM for Intuitionistic Relations
3.2. Model Construction
3.3. Some Properties about the Non-Linear BWM for Intuitionistic Relations
4. The Illustrative Study
5. Conclusions and Further Research
- (a)
- The proposed method contains two parts: one is about calculating the weights of criteria and decision makers; the other one is about ranking the alternatives based on the obtained weights. We introduce the fuzz-based geometric index matrix to calculate the consistency degree of decision makers, whose weights can be obtained. Additionally, the criteria’s weights are given subsequently. The importance of decision makers’ weights is obvious, which can also be shown in Example 1. Based on the original BWM, we develop it into the intuitionistic preference relation’s environment and construct a non-linear BWM. Then, the decision process can be more effective than the other pairwise-based decision making method.
- (b)
- This paper studies the overseas talents’ evaluation and classification problem of China. After summarizing the published related references and analyzing the Chinese context, we construct a criteria table for evaluation. Then, we apply the proposed method to rank 20 overseas talents and classify them. According to the specificity of human resource evaluation, we add the comparison of non-preferred degree by introducing the intuitionistic preference relation. This extension is more suitable for human’s decision making psychology, leading to the decision making process being closer to reality. Additionally, it also can decrease the subjective influence on the decision results. Research studies on the overseas talents of China are rare, and the published papers do not consider the situation as extensively as this paper dose. Therefore, this paper is meaningful for the human resources practices system.
- (c)
- We transform the talents evaluation problem into a Multi-Criteria Group Decision Making (MCGDM) problem, and solve it through a combination MCGDM methodology. For this proposed methodology, we develop the related methods to make them more effective. Example 1 can show the importance of considering geometry consistency degree, rather than paying more attention to calculating the missing elements in the reference of [44]. The illustrative study demonstrates the applicable of the proposed model. We also give two properties to measure whether the decisions are within the reasonable range. That ensures the effectiveness and reasonableness of our methodology.
- (a)
- The proposed method is based on intuitionistic preference relations. However, in some more complicated conditions, this tool may still be insufficient to describe decision makers’ hesitation degree. Decision making of alternatives with incomplete information is not a focus in this paper. As the decision problem in reality becomes gradually more complicated, it is unavoidable to deal with the complex problems that decision making results may be incomplete.
- (b)
- The method is suitable for the overseas talent evaluation and classification problem, whose number of criteria and alternatives is moderate. Compared with the general pairwise comparison methods, we improve the practicability by introducing BWM. However, faced with large numbers of alternatives, our method may have heavy workloads and high cost.
- (c)
- During the step of calculating criteria and decision makers’ weights, we consider the geometry consistency degree. The consistency of BWM with intuitionistic preference relations has not been considered in this paper. This consistency degree may bring uncertain influence on the ranking results.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qu, L. The Chinese Dream of the Overseas Returned Talents–crack the returnees entrepreneurial puzzle. New Economy. 2000, 11, 6–14. [Google Scholar]
- Lai, Y.J. IMOST: Interactive multiple objective system technique. J. Oper. Res. Soc. 1995, 46, 958–976. [Google Scholar] [CrossRef]
- Iwamura, K.; Lin, B. Chance constrained integer programming models for capital budgeting environments. J. Oper. Res. Soc. 1998, 46, 854–860. [Google Scholar] [CrossRef]
- Labib, A.W.; Williams, G.B.; O’Connor, R.F. An intelligent maintenance model (system): An application of the analytic hierarchy process and a fuzzy rule-based controller. J. Oper. Res. Soc. 1998, 49, 745–757. [Google Scholar] [CrossRef]
- Chou, Y.; Sun, C.; Yen, H. Evaluating the criteria for human resource for science and technology (HRST) based on an integrated fuzzy AHP and fuzzy DEMATEL approach. Appl. Soft Comput. 2012, 12, 64–71. [Google Scholar] [CrossRef]
- Ahmad, Z.; Azamathulla, H.M.; Ghani, A.A. ANFIS-based approach for estimation transverse mixing coefficient. IWA Water Sci. Technol. 2011, 63, 1004–1009. [Google Scholar] [CrossRef] [PubMed]
- Golec, A.; Kahya, E. A fuzzy model for competency-based employee evaluation and selection. Comput. Ind. Eng. 2007, 52, 143–161. [Google Scholar] [CrossRef]
- Zhong, L. Fuzzy comprehensive evaluation on performance of high-level talents. J. WUT Inf. Manag. Eng. 2011, 33, 505–508. (In Chinese) [Google Scholar]
- Zhao, W.; Lin, F.; Peng, J.; Bao, X.; Qu, B.; Bai, C. Building of evaluation theory model of innovative scientific & technical talents. Sci. Technol. Manag. Res. 2012, 24, 131–135. (In Chinese) [Google Scholar]
- Chou, Y.; Hsu, Y.; Yen, H. Human resources for science and technology: Analyzing competitiveness using the analytic hierarchy process. Technol. Soc. 2008, 30, 141–153. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X. Research on evaluation mechanism of innovation-driven science and technology talents during the 13th five-year plan in China. Technol. Econ. 2015, 8, 76–80. (In Chinese) [Google Scholar]
- Shen, N.; Meng, F.; Jiang, B.; Li, W. A research on the establishment of S&T talents evaluation system from the perspective of innovation driven strategy. Sci. Res. Manag. 2016, 4, 602–606. (In Chinese) [Google Scholar]
- Liu, X.; Duan, Y.; Zhu, Z. Study on scholars’ evaluation method based on co-author network. J. Intell. 2014, 33, 77–82. (In Chinese) [Google Scholar]
- Liu, Y.; Wu, L. The application of biodata in assessment of the leaders in public sectors. Chin. Public Adm. 2016, 6, 76–80. (In Chinese) [Google Scholar]
- Peng, Z.; He, D.; Peng, J.; Zhao, W. Research on quality oriented evaluation and discovery mechanism of scientific and technical talents. Sci. Technol. Manag. Res. 2015, 9, 53–61. (In Chinese) [Google Scholar]
- Vahdani, B.; Mousavi, S.M.; Tavakkoli-Moghaddam, R. A new design of the elimination and choice translating reality method for multi-criteria group decision making in an intuitionistic fuzzy environment. Appl. Math. Model. 2013, 37, 1781–1799. [Google Scholar] [CrossRef]
- Shen, F.; Xu, J.P.; Xu, Z.S. An automatic ranking approach for multi-criteria group decision making under intuitionistic fuzzy environment. Fuzzy Optim. Decis. Mak. 2015, 14, 311–334. [Google Scholar] [CrossRef]
- Qin, J.D.; Liu, X.W. Multi-attribure group decision making using combined ranking value under interval type-2 fuzzy environment. Inf. Sci. 2015, 297, 293–315. [Google Scholar] [CrossRef]
- Baležentis, Y.; Zeng, S. Group multi-criteria decision making based upon interval-valued fuzzy numbers: An extension of the MULTIMOORA method. Expert Syst. Appl. 2013, 40, 543–550. [Google Scholar]
- Huang, C.L.; Yoon, K.P. Multiple Attributes Decision Making: Methods and Applications; Springer: New York, NY, USA, 1981. [Google Scholar]
- Bozoki, S.; Csato, L.; Temesi, J. An application of incomplete pairwise comparison matrices for ranking top tennis players. Eur. J. Oper. Res. 2016, 248, 211–218. [Google Scholar] [CrossRef]
- Papadopoulos, A.; Karagiannidis, A. Application of the multi-criteria analysis method ELECTRE III for the optimization of decentralized energy systems. Omega 2008, 36, 766–776. [Google Scholar] [CrossRef]
- Lazim, A.; Norsyahida, Z. Integration of fuzzy AHP and interval type-2 fuzzy DEMATEL: An application to human resource management. Expert Syst. Appl. 2015, 42, 4397–4409. [Google Scholar]
- Saaty, T.L. A scaling method for priorities in hierarchical strutures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Orlovsky, S.A. Decision-making with a fuzzy preference relation. Fuzzy Sets Syst. 1978, 1, 155–167. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Uncertainty and rank order in the analytic hierarchy process. Eur. J. Oper. Res. 1987, 32, 107–117. [Google Scholar] [CrossRef]
- Xu, Z.S. Goal programming models for obtaining the priority vector of incomplete fuzzy preference relation. Int. J. Approx. Reason. 2004, 26, 261–270. [Google Scholar] [CrossRef]
- Atanassov, K.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Systems 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Xia, M.M.; Chen, J. Preference relations based on intuitionistic multiplicative information. IEEE Trans. Fuzzy Syst. 2013, 22, 113–133. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. Using intuitionistic fuzzy sets in group decision making. Control Cybern. 2002, 31, 1037–1053. [Google Scholar]
- Deschrijver, G.; Kerre, E.E. On the composition of intuitionistic fuzzy relations. Fuzzy Sets Syst. 2003, 136, 333–361. [Google Scholar] [CrossRef]
- Zhang, H.M. A consistency model for group decision making problems with interval multiplicative preference relations. Appl. Soft Comput. 2015, 26, 60–71. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Z.; Xu, J. Interval-valued intuitionistic multiplicative set. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2014, 22, 385–406. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Z.S.; Yu, X.H. Compatibility measures and consensus models for group decision making with intuitionistic multipllicative preference relations. Appl. Soft Comput. 2013, 13, 2075–2086. [Google Scholar] [CrossRef]
- Liao, H.C.; Xu, Z.S.; Xia, M.M. Multiplicative consistency of hesitant fuzzy preference relation and its application in group decision making. Int. J. Inf. Technol. Decis. Mak. 2014, 13, 47–76. [Google Scholar] [CrossRef]
- Xu, Z.S. Priority weight intervals derived from intuitionistic multiplicative preference. IEEE Trans. Fuzzy Syst. 2013, 22, 624–654. [Google Scholar]
- Celik, M.; Kandakoglu, A.; Er, I.D. Structuring fuzzy integrated multi-stages evaluation model on academic personnel recruitment in MET institutions. Expert Syst. Appl. 2009, 36, 6918–6927. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Rezaei, J.; Wang, J.; Tavasszy, L. Linking supplier development to supplier segmentation using Best Worst Method. Expert Syst. Appl. 2015, 42, 9152–9164. [Google Scholar] [CrossRef]
- Rezaei, J. Best-worst multi-criteria decision-making method: Some properties and a linear model. Omega 2016, 64, 126–130. [Google Scholar] [CrossRef]
- Rezaei, J.; Nispeling, T.; Sarkis, J.; Tavasszy, L. A supplier selection life cycle approach integrating traditional and environmental criteria using the best worst method. J. Clean. Prod. 2016, 135, 577–588. [Google Scholar]
- Wang, T.C.; Chen, Y.H. Incomplete fuzzy linguistic preference relations under uncertain environments. Inf. Fusion 2010, 11, 201–207. [Google Scholar] [CrossRef]
- Liu, F.; Zhang, W.G.; Fu, J.H. A new method of obtaining the priority weights from an interval fuzzy preference relation. Inf. Sci. 2012, 185, 32–42. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Z.S.; Yu, X.H. Group decision making based on incomplete intuitionistic multiplicative preference relations. Inf. Sci. 2015, 295, 33–52. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S.; Liao, H.C. Preference relations based on intuitionistic multiplicative information. IEEE Trans. Fuzzy Syst. 2013, 21, 113–133. [Google Scholar]
- Alonso, S.; Herrera-Viedma, E.; Chiclana, F.; Herrera, F. A web based consensus support system for group decision making problems and incomplete preferences. Inf. Sci. 2008, 180, 4477–4495. [Google Scholar] [CrossRef]
- Lee, L.W. Group decision making with incomplete fuzzy preference relations based on the additive consistency and the order consistency. Expert Syst. Appl. 2012, 39, 11666–11676. [Google Scholar] [CrossRef]
- McClelland, D.C. Testing for competence rather than for intelligence. Am. Psychol. 1973, 28, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Spreitzer, G.; Mccall, M.; Mahoney, J. Early identification of international executive potential. J. Appl. Psychol. 1997, 82, 6–29. [Google Scholar] [CrossRef]
- Luo, H.T. Discussion on Talentism. Talent Dev. 2000, 7, 17–19. (In Chinese) [Google Scholar]
- Yan, T.; Chen, H. Study on the application of case analysis method. Sci. Manag. Res. 2004, 22, 116–120. (In Chinese) [Google Scholar]
- Xu, W.; Lan, L.; Zhang, H. Deconstructing the better-than-average effect. Sci. Technol. Process Policy 2014, 31, 125–128. (In Chinese) [Google Scholar]
- Wang, H. Contemporary Chinese Returnees; China Development Press: Beijing, China, 2007; pp. 12–32. [Google Scholar]
- Wright, R.W.; Ricks, D.A. Trends in international business research: Twenty-five years later. J. Int. Bus. Stud. 1994, 25, 687–701. [Google Scholar] [CrossRef]
- Tang, N.; Hong, Y. Preference relations based on intuitionistic multiplicative information. Cult. Intell. New Index Cross Cult. Adapt. 2005, 12, 11–14. [Google Scholar]
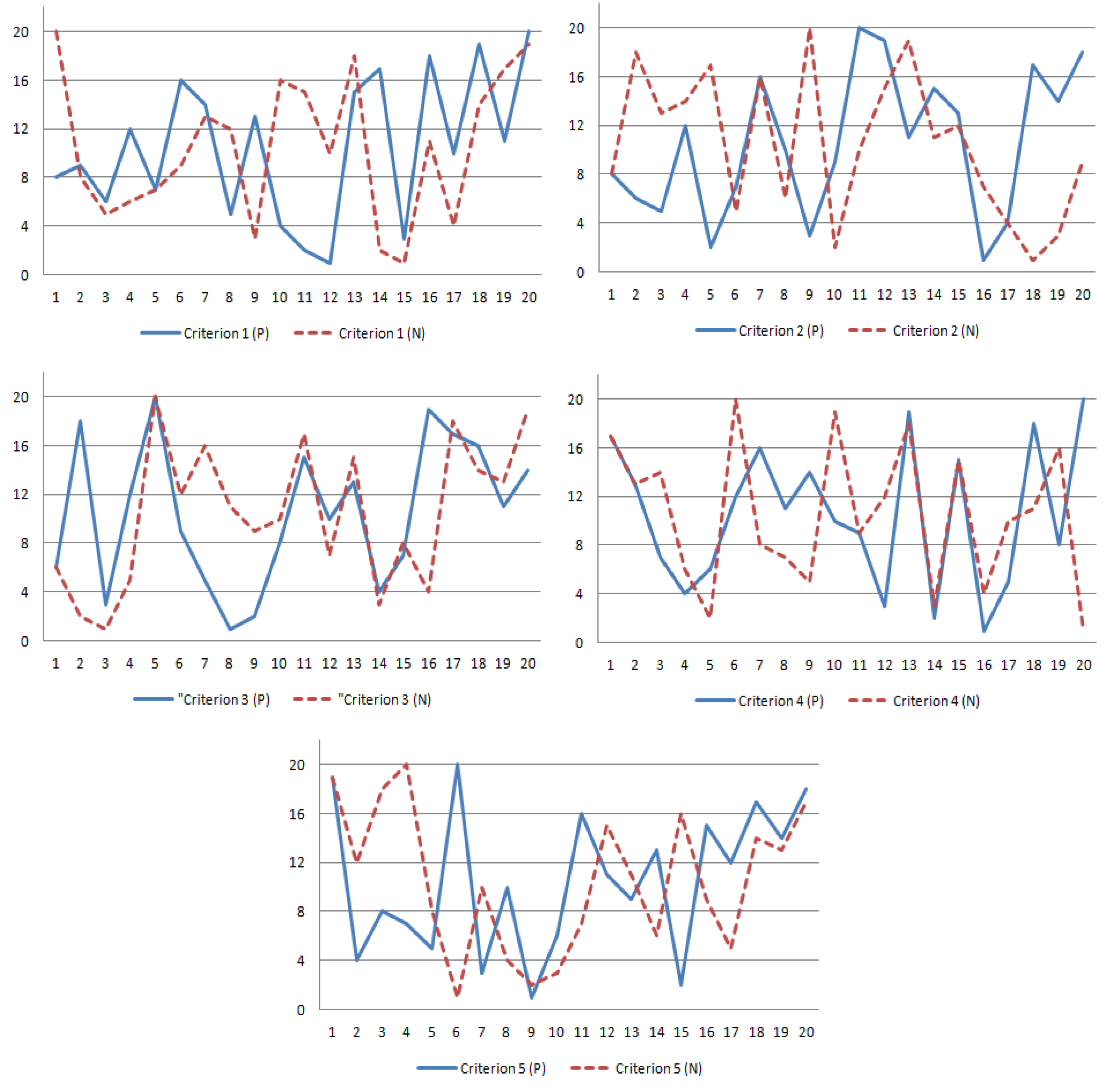
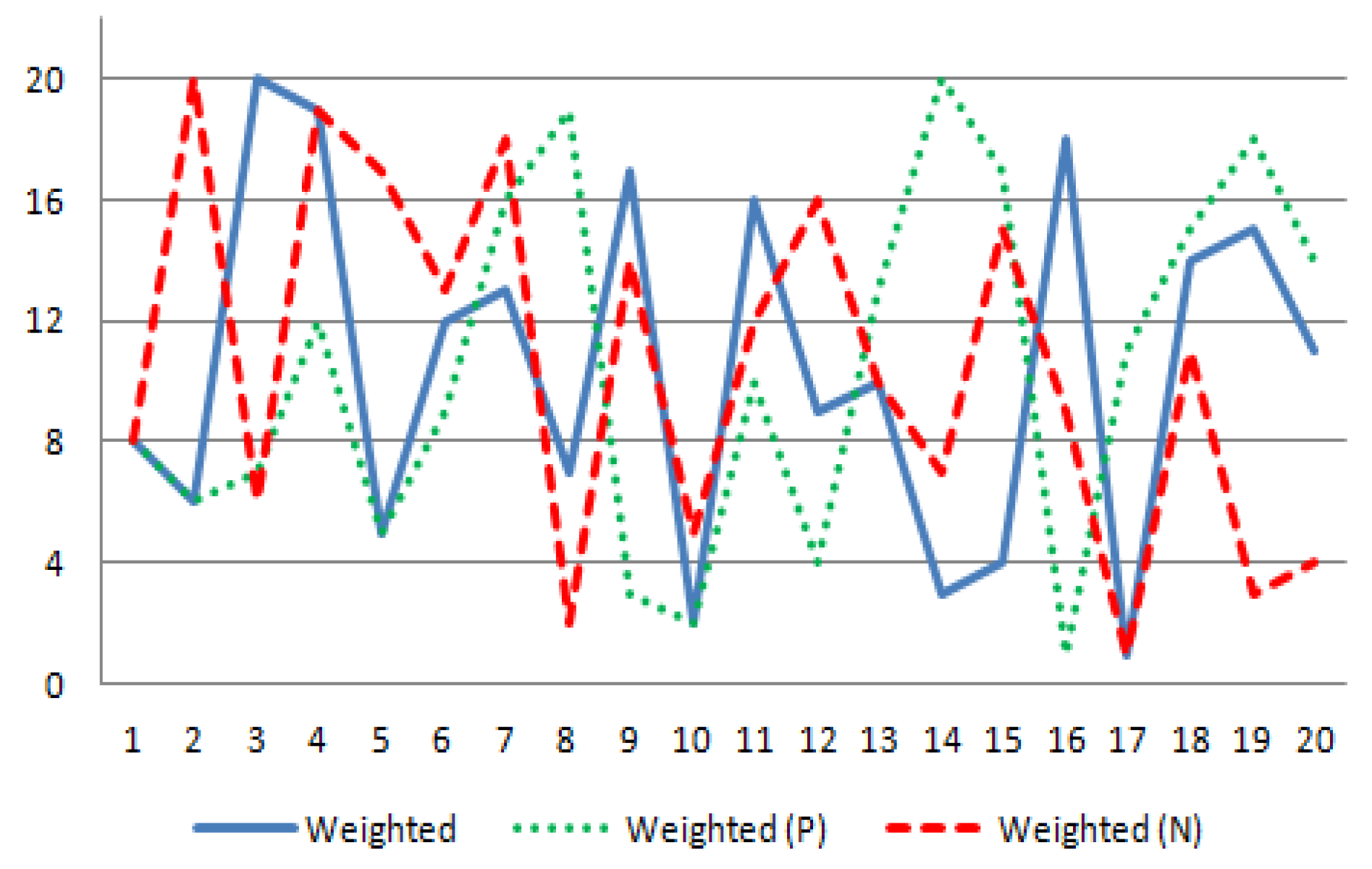
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|
| ξ | 0 | 0.4384 | 1.0000 | 1.6277 | 2.2984 | 3.0000 | 3.7251 | 4.4689 | 5.2280 |
| 1 | 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 | 1/8 | 1/9 | |
|---|---|---|---|---|---|---|---|---|---|
| η | 0 | 2.1180 | 1.7908 | 1.6160 | 1.5062 | 1.4304 | 1.3747 | 1.3321 | 1.2519 |
| C1 | C2 | C3 | C4 | |
|---|---|---|---|---|
| (,) | ((9,),(1,1)) | ((8,),(1,1)) | ((6,),(1,1)) | ((7,),(1,1)) |
| (,) | ((3,),(4,)) | ((3,),(5,)) | ((2,),(4,)) | ((3,),(4,)) |
| (,) | ((1,1),(9,)) | ((1,1),(8,)) | ((1,1),(6,)) | ((1,1),(7,)) |
| (0.071,0.051) | (0.071,0.055) | (0.091,0.064) | (0.084,0.057) | (0.076,0.055) | |
| (0.258,0.214) | (0.295,0.218) | (0.336,0.259) | (0.276,0.189) | (0.287,0.222) | |
| (0.671,0.735) | (0.633,0.727) | (0.573,0.677) | (0.640,0.754) | (0.637,0.723) | |
| 0.394 | 0.860 | 0.298 | 0.683 | - | |
| 0.041 | 0.050 | 0.048 | 0.050 | - |
| Criteria | Description |
|---|---|
| Basic quality | Age, physical condition, psychological health status and credit standing. |
| Capacity | The benefits created for the organization, optimization of industry output and promotion of the industrial and social development. |
| Contributions | The benefits created for the organization, optimization of industry output and promotion of the industrial and social development. |
| Development potential | Innovations and innovation ability, enterprise, ability to solve difficulties and resist setback. |
| Internationalization | Global perspective and cross-cultural adaptability. |
| C1 | C2 | C3 | C4 | C5 | Weighted | |
|---|---|---|---|---|---|---|
| (0.4722,0.0557) | (0.4963,0.0704) | (0.5274,0.0725) | (0.5954,0.0704) | (0.4963,0.0593) | (0.5164,0.0699) | |
| (0.5274,0.0781) | (0.4906,0.0887) | (0.4041,0.0784) | (0.5730,0.0648) | (0.4861,0.0595) | (0.4977,0.0765) | |
| (0.4121,0.0409) | (0.4079,0.0789) | (0.4121,0.0550) | (0.4068,0.5274) | (0.5274,0.0601) | (0.4280,0.0624) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Zhang, Z.; You, X.; Chen, T. Evaluation and Classification of Overseas Talents in China Based on the BWM for Intuitionistic Relations. Symmetry 2016, 8, 137. https://doi.org/10.3390/sym8110137
Yang Q, Zhang Z, You X, Chen T. Evaluation and Classification of Overseas Talents in China Based on the BWM for Intuitionistic Relations. Symmetry. 2016; 8(11):137. https://doi.org/10.3390/sym8110137
Chicago/Turabian StyleYang, Qing, Zaisheng Zhang, Xinshang You, and Tong Chen. 2016. "Evaluation and Classification of Overseas Talents in China Based on the BWM for Intuitionistic Relations" Symmetry 8, no. 11: 137. https://doi.org/10.3390/sym8110137
APA StyleYang, Q., Zhang, Z., You, X., & Chen, T. (2016). Evaluation and Classification of Overseas Talents in China Based on the BWM for Intuitionistic Relations. Symmetry, 8(11), 137. https://doi.org/10.3390/sym8110137





