Affine Geometry, Visual Sensation, and Preference for Symmetry of Things in a Thing
Abstract
:1. Introduction
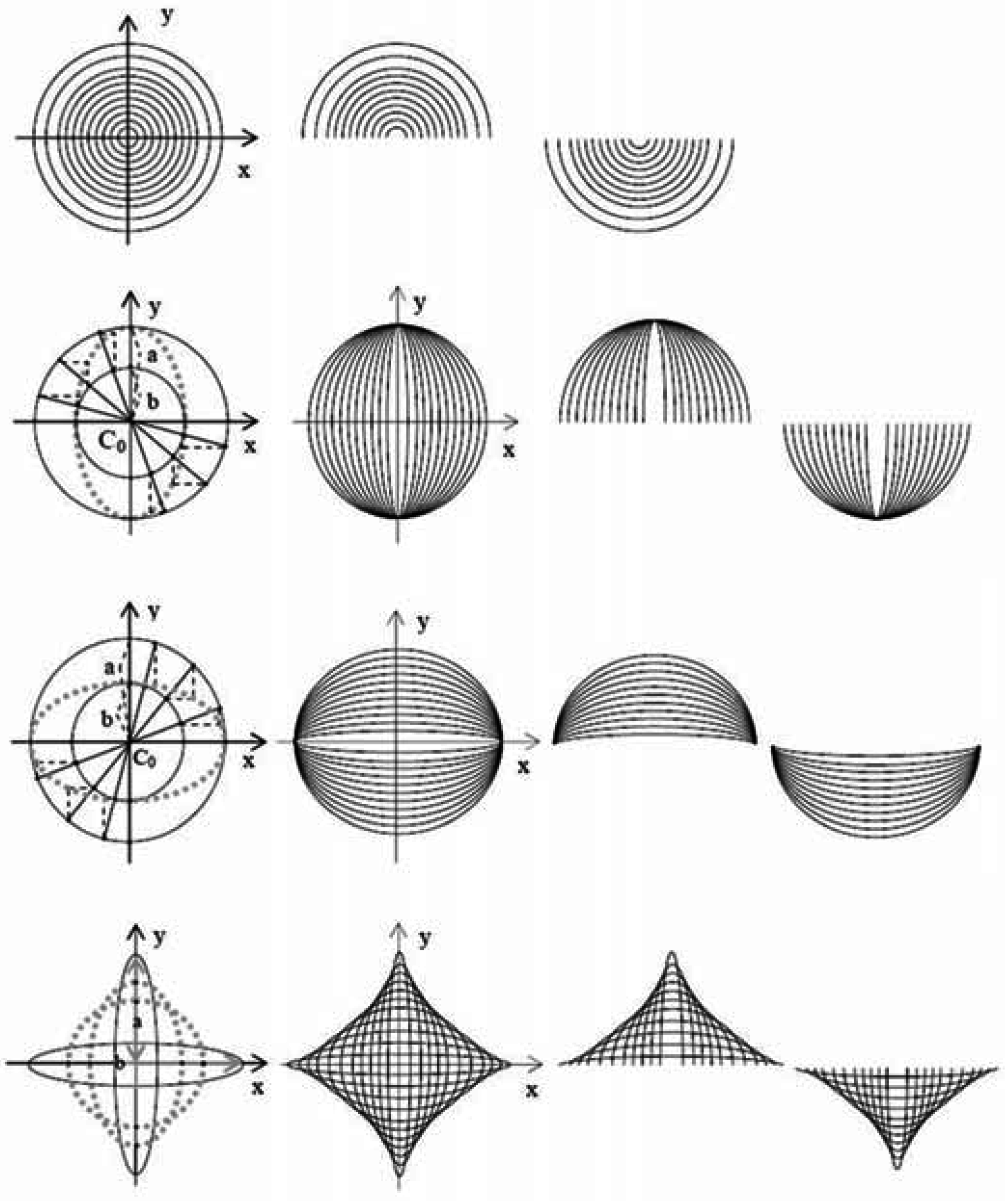
1.1. Affine Geometry and Visual Sensation
1.2. Reflection and Rotational Shape Symmetry
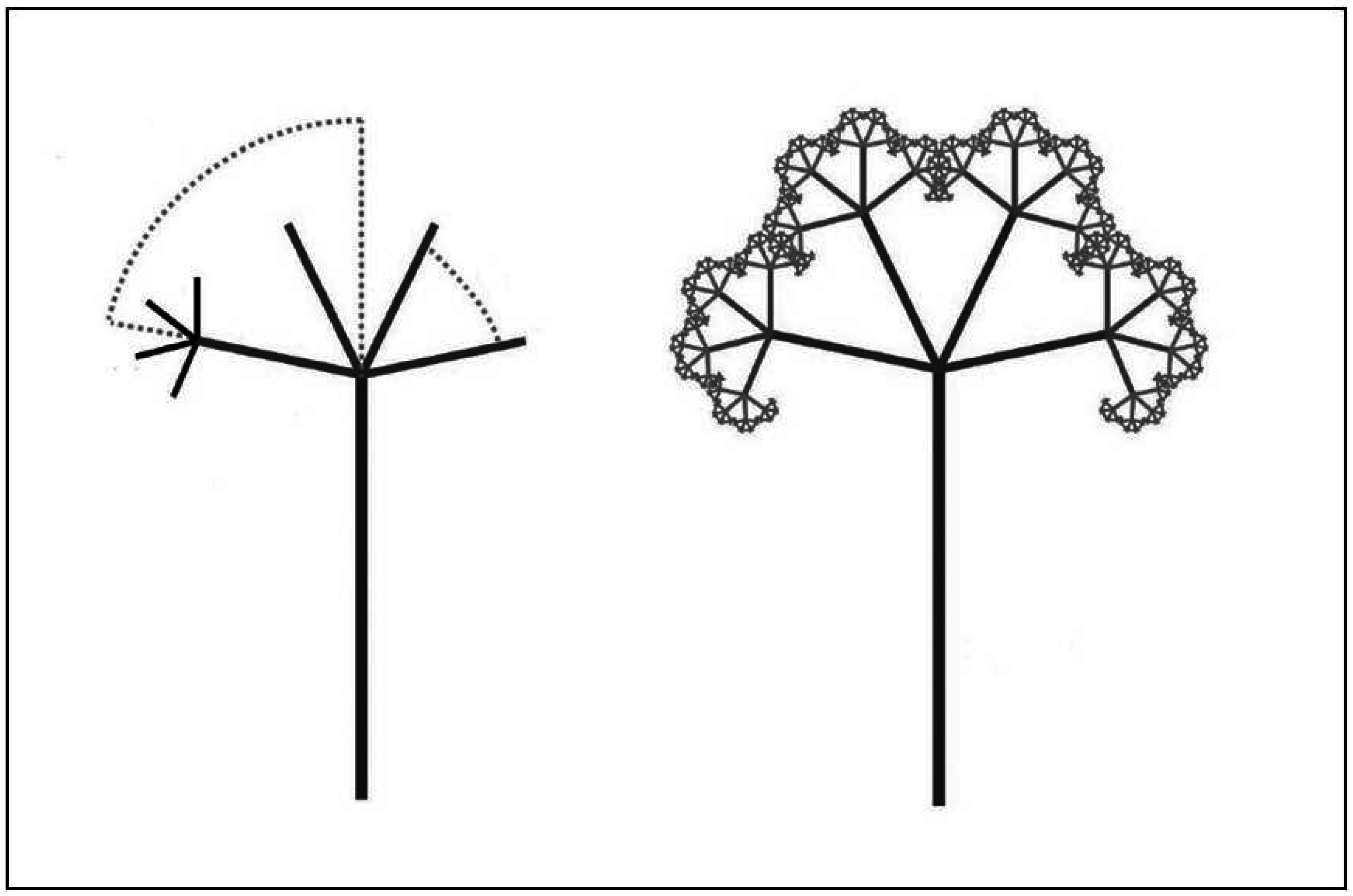
1.3. Nature-Inspired Design and the Symmetry of “Things in a Thing”
2. Materials and Methods
2.1. Subjects
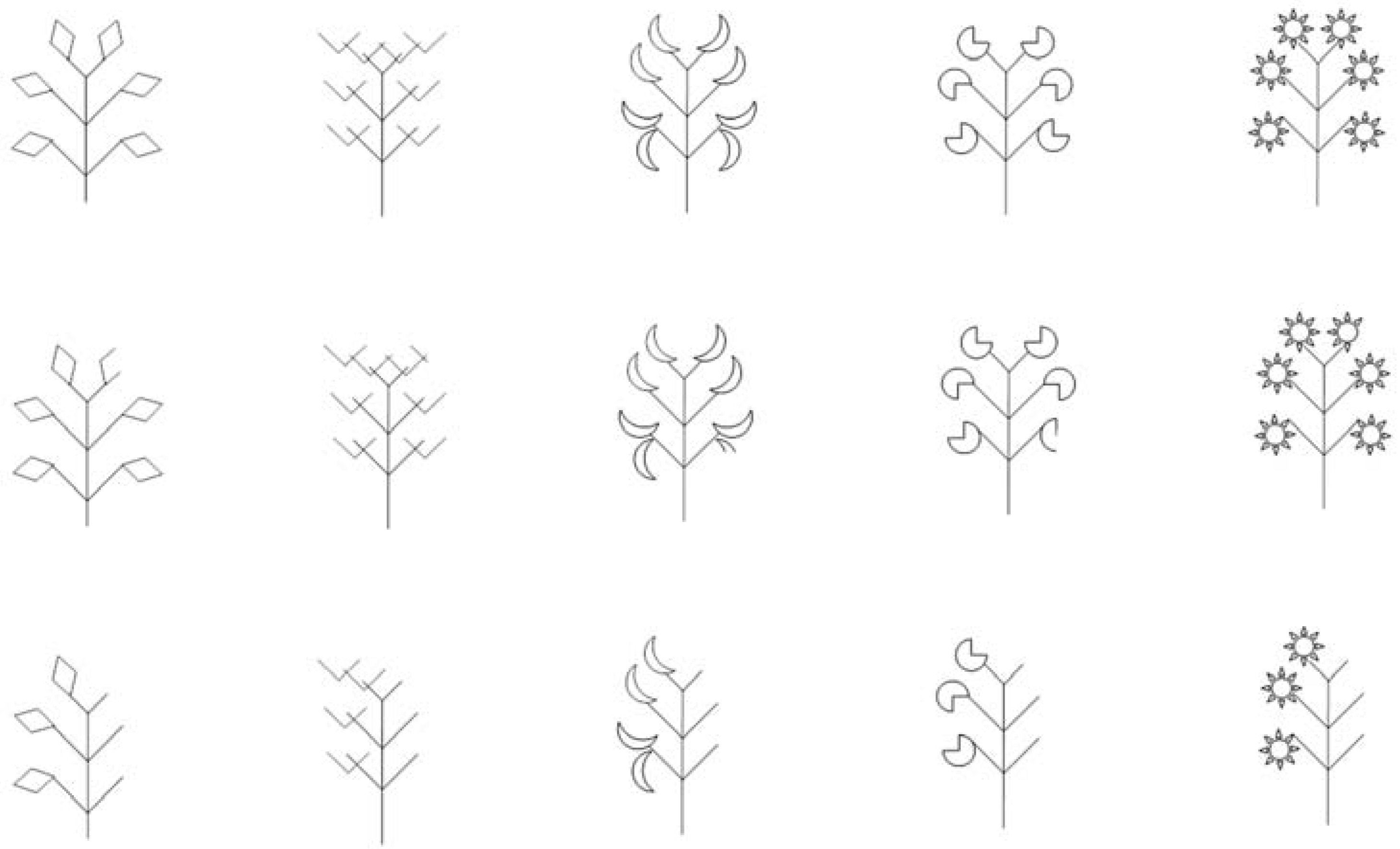
2.2. Stimuli
2.3. Task Instructions
2.4. Procedure
3. Results
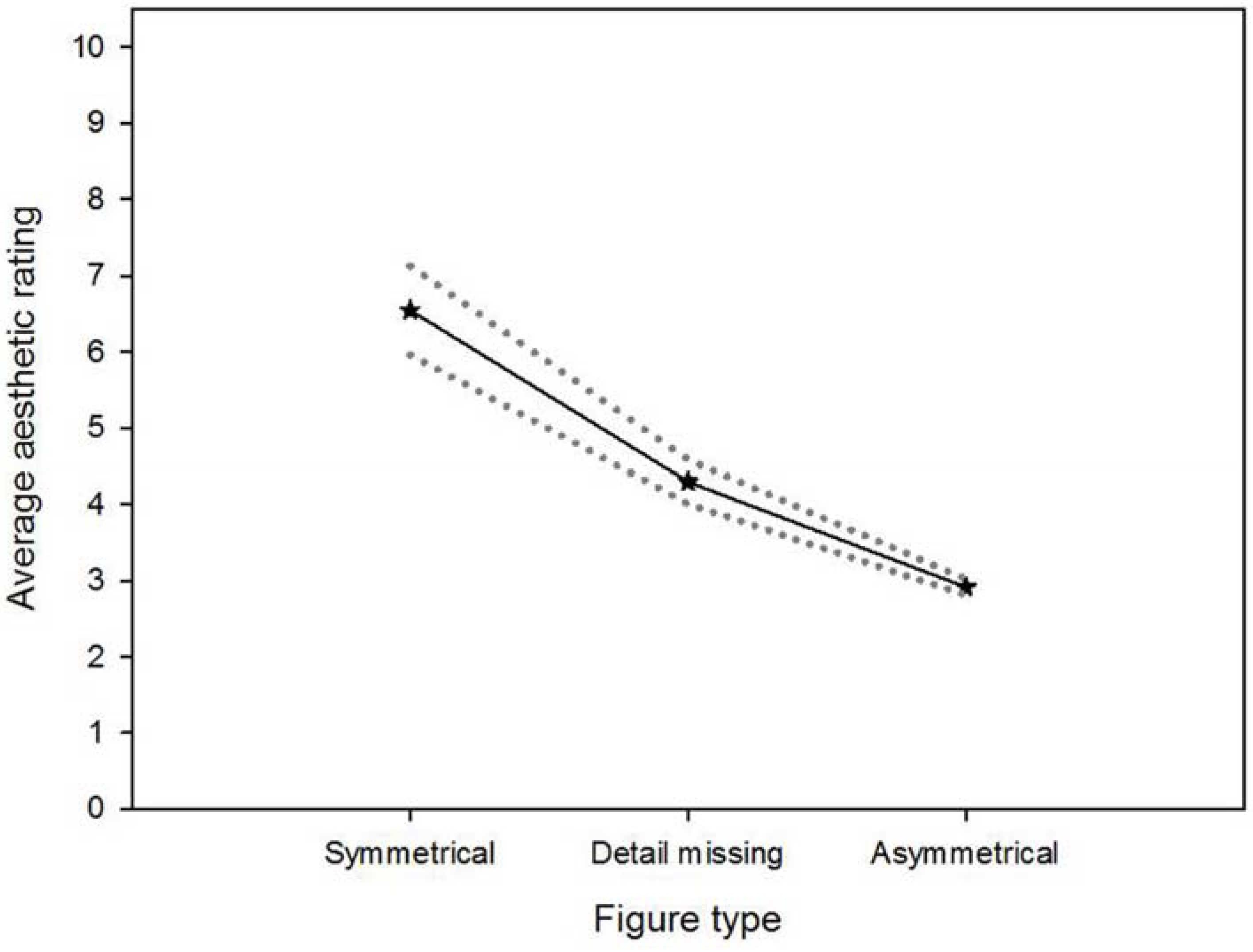
3.1. Aesthetic Ratings
3.2. Preference Judgments
4. Discussion
5. Conclusions
Conflicts of Interest
References
- Amir, O.; Biederman, I.; Hayworth, K.J. Sensitivity to non-accidental properties across various shape dimensions. Vis. Res. 2012, 62, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Amir, O.; Biederman, I.; Herald, S.B.; Shah, M.P.; Mintz, T.H. Greater sensitivity to non-accidental than metric shape properties in preschool children. Vis. Res. 2014, 97, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Biederman, I. Recognition-by-components: A theory of human image understanding. Psychol. Rev. 1987, 94, 115–117. [Google Scholar] [CrossRef] [PubMed]
- Wilson, H.R.; Wilkinson, F. Symmetry perception: A novel approach for biological shapes. Vis. Res. 2002, 42, 589–597. [Google Scholar] [CrossRef]
- Pizlo, Z.; Sawada, T.; Li, Y.; Kropatsch, W.G.; Steinman, R.M. New approach to the perception of 3D shape based on veridicality, complexity, symmetry and volume: A mini-review. Vis. Res. 2010, 50, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Pizlo, Z.; Steinman, R.M. A computational model that recovers the 3D shape of an object from a single 2D retinal representation. Vis. Res. 2009, 49, 979–991. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Sawada, T.; Shi, Y.; Steinman, R.M.; Pizlo, Z. Symmetry is the sine qua non of shape. In Shape Perception in Human and Computer Vision; Dickinson, S., Pizlo, Z., Eds.; Springer: London, UK, 2013; pp. 21–40. [Google Scholar]
- Sabatelli, H.; Lawandow, A.; Kopra, A.R. Asymmetry, symmetry and beauty. Symmetry 2010, 2, 1591–1624. [Google Scholar] [CrossRef]
- Stevens, K.A. The visual interpretation of surface contours. Artif. Intell. 1981, 17, 47–73. [Google Scholar] [CrossRef]
- Stevens, K.A. The information content of texture gradients. Biol. Cybern. 1981, 42, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Foley, J.M.; Ribeiro-Filho, N.P.; Da Silva, J.A. Visual perception of extent and the geometry of visual space. Vis. Res. 2004, 44, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Dresp, B.; Silvestri, C.; Motro, R. Which geometric model for the perceived curvature of 2-D shape contours? Spat. Vis. 2007, 20, 219–264. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B. Why the brain knows more than we do: Non-conscious representations and their role in the construction of conscious experience. Brain Sci. 2012, 2, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B. Generic properties of curvature sensing by vision and touch. Comput. Math. Methods Med. 2013, 2013, 634168. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B. 2D geometry predicts perceived visual curvature in context-free viewing. Comput. Intell. Neurosci. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Strother, L.; Killebrew, K.W.; Caplovitz, G.P. The lemon illusion: Seeing curvature where there is none. Front. Hum. Neurosci. 2015, 9, 95. [Google Scholar] [CrossRef] [PubMed]
- Groves, J.T. The physical chemistry of membrane curvature. Nat. Chem. Biol. 2009, 5, 783–784. [Google Scholar] [CrossRef] [PubMed]
- Hatzakis, N.S.; Bhatia, V.K.; Larsen, J.; Madsen, K.L.; Bolinger, P.Y.; Kunding, A.H.; Castillo, J.; Gether, U.; Hedegård, P.; Stamou, D. How curved membranes recruit amphipathic helices and protein anchoring motifs. Nat. Chem. Biol. 2009, 5, 835–841. [Google Scholar] [CrossRef] [PubMed]
- Gerbino, W.; Zhang, L. Visual orientation and symmetry detection under affine transformations. Bull. Psychon. Soc. 1991, 29, 480. [Google Scholar]
- Whitaker, D.; McGraw, P.W. Geometric representation of the mechanisms underlying human curvature detection. Vis. Res. 1998, 38, 3843–3848. [Google Scholar] [CrossRef]
- Bahnsen, P. Eine Untersuchung über Symmetrie und Asymmetrie bei visuellen Wahrnehmungen. Z. Psychol. 1928, 108, 129–154. [Google Scholar]
- Braitenberg, V. Reading the structure of brains. Network 1990, 1, 1–11. [Google Scholar] [CrossRef]
- Beck, D.M.; Pinsk, M.A.; Kastner, S. Symmetry perception in humans and macaques. Trends Cogn. Sci. 2005, 9, 405–406. [Google Scholar] [CrossRef] [PubMed]
- Tjan, B.S.; Liu, Z. Symmetry impedes symmetry discrimination. J. Vis. 2005, 5, 88–900. [Google Scholar] [CrossRef] [PubMed]
- Barlow, H.B.; Reeves, B.C. The versatility and absolute efficiency of detecting mirror symmetry in random dot displays. Vis. Res. 1979, 19, 783–793. [Google Scholar] [CrossRef]
- Wagemans, J.; Van Gool, L.; D’Ydewalle, G. Detection of symmetry in tachistoscopically presented dot patterns: Effects of multiple axes and skewing. Percept. Psychophys. 1991, 50, 413–427. [Google Scholar] [CrossRef] [PubMed]
- Barrett, B.T.; Whitaker, D.; McGraw, P.V.; Herbert, A.M. Discriminating mirror symmetry in foveal and extra-foveal vision. Vis. Res. 1999, 39, 3737–3744. [Google Scholar] [CrossRef]
- Thornhill, R.; Gangestad, S.W. Facial attractiveness. Trends Cognit. Sci. 1999, 3, 452–460. [Google Scholar] [CrossRef]
- Anderson, J.R.; Kuwahata, H.; Kuroshima, F.; Leighty, K.A.; Fujita, K. Are monkeys aesthetists? Rensch (1957) revisited. J. Exp. Psychol. 2005, 31, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Machilsen, B.; Pauwels, M.; Wagemans, J. The role of vertical mirror symmetry in visual shape perception. J. Vis. 2009, 9. [Google Scholar] [CrossRef] [PubMed]
- Silvestri, C.; Motro, R.; Maurin, B.; Dresp-Langley, B. Visual spatial learning of complex object morphologies through the interaction with virtual and real-world data. Des. Stud. 2010, 31, 363–381. [Google Scholar] [CrossRef]
- Levin, S.M. Biotensegrity: The tensegrity truss as a model for spine mechanics. J. Mech. Med. Biol. 2002, 3–4, 375–388. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; Freeman & Co.: San Francisco, CA, USA, 1982. [Google Scholar]
- Lehrer, M.; Horridge, G.A.; Zhang, S.W.; Gadagkar, R. Shape vision in bees: Innate preference for flower-like patterns. Philos. Trans. R. Soc. Lond. B 1995, 347, 123–137. [Google Scholar] [CrossRef]
- Giurfa, M.; Eichmann, B.; Menzl, R. Symmetry perception in an insect. Nature 1996, 382, 458–461. [Google Scholar] [CrossRef] [PubMed]
- Eisenman, R. Complexity–simplicity: I. Preference for symmetry and rejection of complexity. Psychon. Sci. 1967, 8, 169–170. [Google Scholar] [CrossRef]
- Berlyne, D.E. Aesthetics and Psychobiology; Appleton: New York, NY, USA, 1971. [Google Scholar]
- Jacobsen, T.; Hofel, L. Aesthetics judgments of novel graphic patterns: Analyses of individual judgments. Percept. Motor Skills 2002, 95, 755–766. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, T.; Hofel, L. Descriptive and evaluative judgment processes: Behavioral and electrophysiological indices of processing symmetry and aesthetics. Cognit. Affect. Behav. Neurosci. 2003, 3, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, T.; Schubotz, R.I.; Hofel, L.; van Cramon, D.Y. Brain correlates of aesthetic judgment of beauty. NeuroImage 2006, 29, 276–285. [Google Scholar] [CrossRef] [PubMed]
- Tinio, P.P.L.; Leder, H. Just how stable are stable aesthetic features? Symmetry, complexity, and the jaws of massive familiarization. Acta Psychol. 2009, 130, 241–150. [Google Scholar] [CrossRef] [PubMed]
- Deregowski, J.B. Symmetry, Gestalt and information theory. Q. J. Exp. Psychol. 1971, 23, 381–385. [Google Scholar] [CrossRef] [PubMed]
- Deregowski, J.B. The role of symmetry in pattern reproduction by Zambian children. J. Cross-Cult. Psychol. 1972, 3, 303–307. [Google Scholar] [CrossRef]
- Kayaert, G.; Wagemans, J. Delayed shape matching benefits from simplicity and symmetry. Vis. Res. 2009, 49, 708–717. [Google Scholar] [CrossRef] [PubMed]
- Spehar, B.; Clifford, C.W.G.; Newell, B.; Taylor, R.P. Universal aesthetics of fractals. Comput. Graph. 2003, 27, 813–820. [Google Scholar] [CrossRef]
- Hagerhall, C.M.; Purcell, T.; Taylor, R. Fractal dimension of landscape silhouette outlines as a predictor of landscape preference. J. Environ. Psychol. 2004, 24, 247–255. [Google Scholar] [CrossRef]
- Forsythe, A.; Nadal, M.; Sheehy, N.; Cela-Conde, C.J.; Sawey, M. Predicting beauty: Fractal dimension and visual complexity in art. Br. J. Psychol. 2011, 102, 49–70. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B. Principles of perceptual grouping: implications for image-guided surgery. Front. Psychol. 2015, 6, 1565. [Google Scholar] [CrossRef] [PubMed]
- Dresp, B. On illusory contours and their functional significance. Curr. Psychol. Cognit. 1997, 16, 489–518. [Google Scholar]
- Samuel, F.; Kerzel, D. Judging whether it is aesthetic: Does equilibrium compensate for lack of symmetry? I-Perception 2013, 4, 57–77. [Google Scholar] [CrossRef] [PubMed]
- Belke, B.; Leder, H.; Carbon, C.C. When challenging art gets liked: Evidences for a dual preference formation process for fluent and non-fluent portraits. PLoS ONE 2015, 10, e0131796. [Google Scholar]
- Eisenman, R.; Rappaport, J. Complexity preference and semantic differential ratings of complexity-simplicity and symmetry-asymmetry. Psychon. Sci. 1967, 7, 147–148. [Google Scholar] [CrossRef]
- Eisenman, R.; Gellens, H.K. Preference for complexity—Simplicity and symmetry-asymmetry. Percept. Motor Skills 1968, 26, 888–890. [Google Scholar] [CrossRef] [PubMed]
- Cook, R.; Furnham, A. Aesthetic preferences for architectural styles vary as a function of personality. Imagin. Cogn. Personal. 2012, 32, 103–114. [Google Scholar] [CrossRef]
- Carbon, C.C. The cycle of preference: Long-term dynamics of aesthetic appreciation. Acta Psychol. 2010, 134, 233–244. [Google Scholar] [CrossRef] [PubMed]
- Carbon, C.C. Cognitive mechanisms for explaining dynamics of aesthetic appreciation. I-Perception 2011, 2, 708–719. [Google Scholar] [CrossRef] [PubMed]
- Grammer, K.; Thornhill, R. Human (Homo sapiens) facial attractiveness and sexual selection: The role of symmetry and averageness. J. Comp. Psychol. 1994, 108, 233–242. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B.; Grossberg, S. Neural computation of surface border ownership and relative surface depth from ambiguous contrast inputs. Front. Psychol. 2016, 7, 1102. [Google Scholar] [CrossRef] [PubMed]


| One Way Repeated Measures Analysis of Variance AESTHETIC RATINGS | |||
|---|---|---|---|
| Treatment | N | M | SEM |
| Symmetrical | 30 | 6.347 | 0.222 |
| Detail missing | 30 | 4.487 | 0.258 |
| Asymmetrical | 30 | 3.053 | 0.308 |
| Source of Variation | DF | F | p |
| Between Subjects | 29 | - | - |
| Between Treatments | 2 | 64.323 | <0.001 |
| Residual | 58 | - | - |
| Total | 89 | - | - |
| Comparison | dM | t | p |
| Symmetrical vs. Asymmetrical | 3.293 | 11.311 | <0.001 |
| Symmetrical vs. Detail missing | 1.860 | 6.388 | <0.001 |
| Detail missing vs. Asymmetrical | 1.433 | 4.923 | <0.001 |
| One Way Repeated Measures Analysis of Variance PREFERENCES | |||
|---|---|---|---|
| Treatment | N | M | SEM |
| Symmetrical | 30 | 8.942 | 0.163 |
| Detail missing | 30 | 4.542 | 0.094 |
| Asymmetrical | 30 | 1.517 | 0.145 |
| Source of Variation | DF | F | p |
| Between Subjects | 29 | - | - |
| Between Treatments | 2 | 195.399 | <0.001 |
| Residual | 58 | - | - |
| Total | 89 | - | - |
| Comparison | dM | t | p |
| Symmetrical vs. Asymmetrical | 7.425 | 31.299 | <0.001 |
| Symmetrical vs. Detail missing | 4.400 | 18.547 | <0.001 |
| Detail missing vs. Asymmetrical | 3.025 | 12.751 | <0.001 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dresp-Langley, B. Affine Geometry, Visual Sensation, and Preference for Symmetry of Things in a Thing. Symmetry 2016, 8, 127. https://doi.org/10.3390/sym8110127
Dresp-Langley B. Affine Geometry, Visual Sensation, and Preference for Symmetry of Things in a Thing. Symmetry. 2016; 8(11):127. https://doi.org/10.3390/sym8110127
Chicago/Turabian StyleDresp-Langley, Birgitta. 2016. "Affine Geometry, Visual Sensation, and Preference for Symmetry of Things in a Thing" Symmetry 8, no. 11: 127. https://doi.org/10.3390/sym8110127
APA StyleDresp-Langley, B. (2016). Affine Geometry, Visual Sensation, and Preference for Symmetry of Things in a Thing. Symmetry, 8(11), 127. https://doi.org/10.3390/sym8110127





