1. Introduction
Introduced in 1861 [
1], a Weingarten surface in the Euclidean three-dimensional space
is a surface
M, whose mean curvature
H and Gaussian curvature
K satisfy a non-trivial relation
. Such a surface was introduced by Weingarten. The class of Weingarten surfaces is remarkably large, and it consists of intriguing surfaces in the Euclidean space: the constant mean curvature surfaces, the constant Gaussian curvature surfaces and all rotational surfaces.
As a special case of Weingarten surfaces, we consider that the Weingarten relation Φ is linear in its variables. That is, Φ satisfies the following relation
for
a,
b, and
c are not all zero real numbers. Such a surface with the Equation (
1) is said to be a linear Weingarten surface (briefly, LW-surface). Especially, in the case for
or
in (1), LW-surfaces are Weingarten surfaces either with a constant Gaussian curvature or with a constant mean curvature, respectively. The classification of Weingarten surfaces and linear Weingarten surfaces in the general case is almost completely open today. Several geometers are studying Weingarten surfaces and linear Weingarten surfaces in the ambient spaces, and many interesting results can be found in [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14] etc.
2. Preliminaries
The three-dimensional isotropic space
was introduced by Strubecker in the 1940s, and it is based on the following group
of affine transformations
in
,
where
. Such affine transformations are called isotropic congruence transformations or isotropic motions of
(cf. [
15]). We see that isotropic motions appear as Euclidean motions (a translation and a rotation) in the projection onto the
-plane; the result of this projection
is called "top view". Hence, an isotropic motion is composed of a Euclidean motion in the
-plane and an affine shear transformation in the
z-direction.
On the other hand, the isotropic distance of two points—
and
—is defined as the Euclidean distance of the top views, i.e.,
In fact, two points with the same top views have the isotropic distance of zero, called "parallel points". The isotropic metric (2) degenerates along z-parallel lines, called "isotropic lines". Isotropic angles between straight lines are measured as Euclidean angles in the top view. There are two types of planes in : isotropic planes are planes parallel to the z-direction, and otherwise they are non-isotropic planes.
Let
and
be vectors in
. The isotropic inner product of
and
is defined by
We call a vector of the form in an "isotropic vector", and a "non-isotropic vector" otherwise.
Consider a
-surface
M,
, in
parameterized by
A surface M immersed in is called admissible if it has no isotropic tangent planes. We restrict our framework to admissible regular surfaces.
For such a surface, the coefficients
of its first fundamental form are given by
where
and
On the other hand, the unit normal vector of
M is always the isotropic vector
since it is perpendicular to all tangent vectors to
M. The coefficients
of the second fundamental form of
M are calculated with respect to the normal vector of
M and they are given by
The isotropic Gaussian curvature
K and the isotropic mean curvature
H are defined by
The surface
M is said to be isotropic flat (resp. isotropic minimal ) if
K (resp.
H) vanishes (cf. [
16]).
An isotropic three-dimensional space, which is one of the Cayley-Klein spaces defined from the projective three-dimensional spaces, is obtained from the Euclidean space by substituting the usual Euclidean distance with the isotropic distance. The work of surfaces with special properties in an isotropic three-dimensional space has important applications in several applied sciences, e.g., computer science, image processing, architectural design and microeconomics, see [
15].
In this paper, we study helicoidal surfaces in an isotropic three-dimensional space. The surfaces are invariant by an isotropic motion and a translation. The main purpose of this paper is to construct helicoidal surfaces in an isotropic three-dimensional space satisfying the linear Weingarten relation (1).
3. Main Results
In this section, we completely construct linear Weingarten helicoidal surfaces in an isotropic three-dimensional space
in terms of the Gaussian curvature and the mean curvature of the surface. To define helicoidal surfaces in an isotropic space
, we consider a curve
γ lying in the isotropic
-plane or
-plane without loss of generality. Then, the profile curve
γ is parameterized as
where
f and
g are smooth functions. Together with the Euclidean rotations in the isotropic space
, given by the normal form (in affine coordinates)
and a translation, a helicoidal surface
M in
can be parameterized by
or
where
. Then, the helicoidal surfaces given by (5) and (6) are locally isometric. Our study is concentrated on the helicoidal surface given by (5).
Suppose that a profile curve
is a unit speed curve. Then we can take
. Thus, a helicoidal surface in
is parameterized by
where
and
. In this case, the components of the first fundamental form of
M are given by
and the components of the second fundamental form of
M are
Since
M is a non-degenerate surface,
. From now on,
means the partial derivative with respect to the parameter
u unless mentioned. Thus, the Gaussian curvature
K and the mean curvature
H of
M are given by
and
Let
M be a linear Weingarten helicoidal surface in an isotropic three-dimensional space satisfying the condition
where
. It is well-known that surfaces with a constant Gaussian curvature
and a constant mean curvature
are trivial solutions of linear Weingarten surfaces. On the other hand, Aydin [
17] classified all helicoidal surfaces in an isotropic three-dimensional space with a constant Gaussian curvature and a constant mean curvature.
To obtain non-trivial solutions of linear Weingarten surfaces, we consider
Now, we discuss a helicoidal surface satisfying (9). Put
Then (7) and (8) can be rewritten as the form
respectively.
Suppose that
M is a non-trivial linear Weingarten surface. Then from (11) and (12), Equation (
9) implies
After solving the ordinary differential equation, we obtain
for some constant
c. Thus, we have
By combining (10) and (13), one yields
In (14), there are two functions for g. Without loss of generality, we take the sign + in the above expression (the reasoning is analogous with the choice−).
On the other hand, we can calculate the integral term in (14) with the help of the result in (see [
17], page 7), it follows that
Consequently, we have proven the following result.
Theorem 1. Let M be a helicoidal surface in an isotropic three-dimensional space parameterized by If M is a non-trivial linear Weingarten surface satisfying with , then the function g is given by (15).
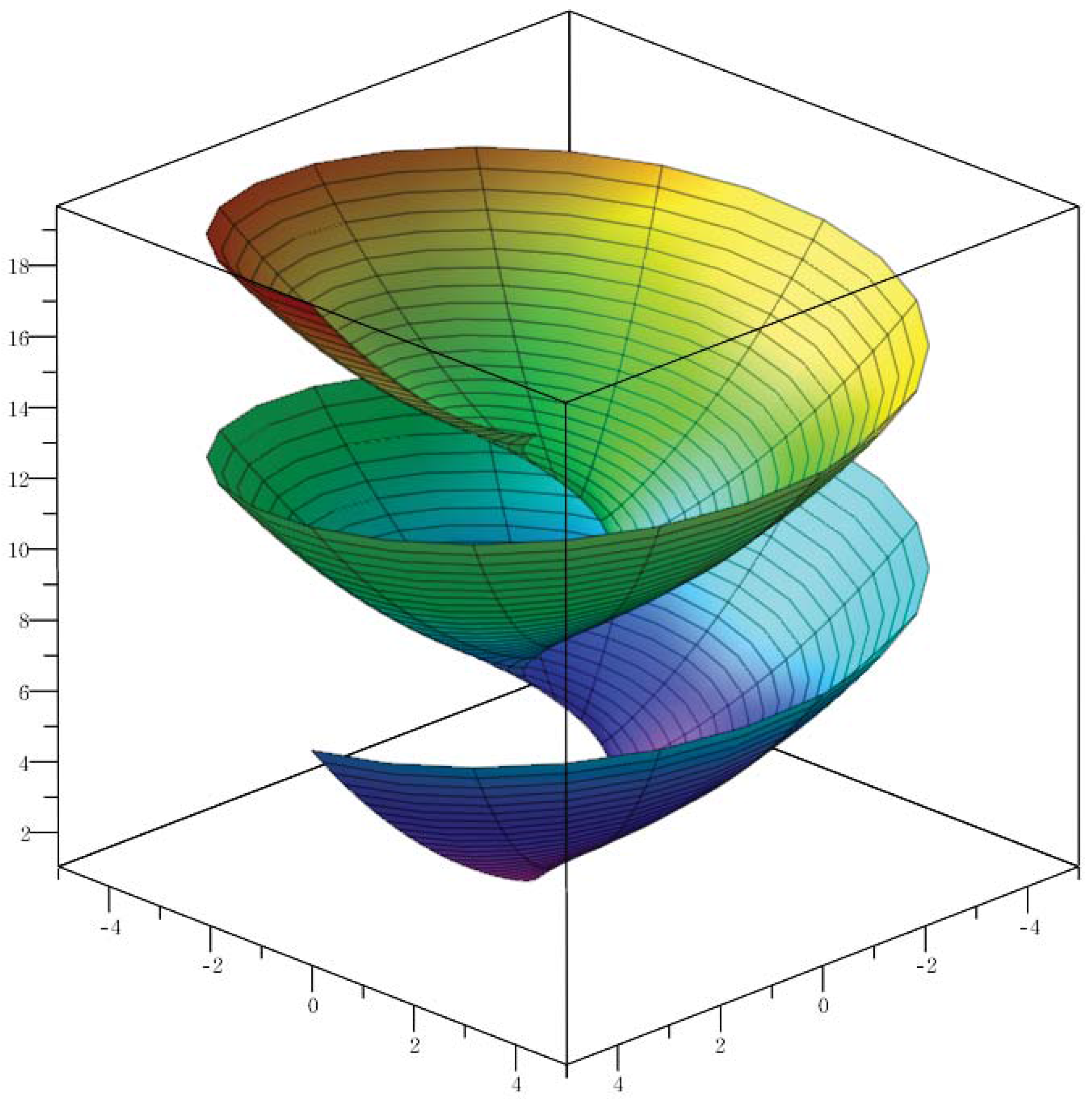
Remark 1. If in (9) (i.e., K is constant.), Theorem 1 is the same as Theorem 3.1 in [17]. Remark 2. For and in (15), we have the LW helicoidal surface (see Figure 1). In the special case that M is a rotational surface (i.e., ) in an isotropic three-dimensional space, we have the same result with Theorem 3.2 in Örenmiş’s work as follows:
Corollary 1. [18] Let M be a rotational surface in an isotropic three-dimensional space parameterized by If M is a non-trivial linear Weingarten surface satisfying with , then the function g is given by Remark 3. For in Corollary 2, we have the LW rotational surface (see Figure 2).