Abstract
Evolution and geometry generate complexity in similar ways. Evolution drives natural selection while geometry may capture the logic of this selection and express it visually, in terms of specific generic properties representing some kind of advantage. Geometry is ideally suited for expressing the logic of evolutionary selection for symmetry, which is found in the shape curves of vein systems and other natural objects such as leaves, cell membranes, or tunnel systems built by ants. The topology and geometry of symmetry is controlled by numerical parameters, which act in analogy with a biological organism’s DNA. The introductory part of this paper reviews findings from experiments illustrating the critical role of two-dimensional (2D) design parameters, affine geometry and shape symmetry for visual or tactile shape sensation and perception-based decision making in populations of experts and non-experts. It will be shown that 2D fractal symmetry, referred to herein as the “symmetry of things in a thing”, results from principles very similar to those of affine projection. Results from experiments on aesthetic and visual preference judgments in response to 2D fractal trees with varying degrees of asymmetry are presented. In a first experiment (psychophysical scaling procedure), non-expert observers had to rate (on a scale from 0 to 10) the perceived beauty of a random series of 2D fractal trees with varying degrees of fractal symmetry. In a second experiment (two-alternative forced choice procedure), they had to express their preference for one of two shapes from the series. The shape pairs were presented successively in random order. Results show that the smallest possible fractal deviation from “symmetry of things in a thing” significantly reduces the perceived attractiveness of such shapes. The potential of future studies where different levels of complexity of fractal patterns are weighed against different degrees of symmetry is pointed out in the conclusion.
1. Introduction
Brain evolution has produced highly specialized processes which enable us to effectively exploit the geometry of visual perceptual space. Some data suggest that the human brain is equipped with an in-built sense of geometry [1,2] which provides a key to recognizing specific object properties, associations between two-dimensional projections, and their correlated three-dimensional structures in the real world [3,4,5,6]. These associations favour structural regularities and, very often, symmetry [6,7], while asymmetry plays a critical role in processes of perceptual discrimination, as discussed recently regarding music and sounds [8]. In the domain of visual objects, symmetry plays an important role in conceptual processes for structural design, and is abundantly exploited by engineers and architects. The following paragraphs will expand on the importance of affine geometry, the symmetry of curves, which may be perceived as single things or as multiples of one and the same thing in a complex shape or object [9,10], and visual sensation. Thereafter, two-dimensional fractal trees based on geometrical principles which produce symmetry of things in a thing will be discussed and made use of psychophysically. The symmetrical structure of these fractal trees results, like 2D curve symmetry, from principles of affine projection, as will become clear in light of further discussions here below.
The use of symmetrical curves dates back to the dawn of building shelter and vernacular architecture, which relies, given the nature of the materials and construction techniques used, almost entirely on symmetry (Figure 1, left). In the Middle Ages, descriptive geometry was used for the planning and execution of building projects for which symmetric curves were the reference model, as in the design of arched hallways and corridors (Figure 1, middle). In the last century, the Spanish designer and architect Antoni Gaudi used the same kind of geometry for the design of the Sagrada Familia in Barcelona (Figure 1, right) and many of his other fabulous structures, which can be appreciated by taking a walk through the Park Guëll, or by visiting the Guëll museum in Barcelona. In Antoni Gaudi’s three-dimensional design of arches, for churches or natural environments, there is a clear distinction between physical (objective) and subjective (perceived) symmetry. Physical symmetry takes into account the principles of gravity. As a consequence, a resulting real-world structure may not necessarily be perceived as perfectly symmetrical (cf. Figure 1, image on right).

Figure 1.
The importance of curve symmetry for human endeavour dates back to the dawn of building shelter and to vernacular architecture (left). Similar geometry is currently used in contemporary free-form architecture (middle), which has been much inspired by the Spanish architect Gaudi, who largely exploited symmetry for the design of the hall and archways of the Sagrada Familia in Barcelona (right).
Antoni Gaudi’s structures were inspired by nature, which abounds with curved shapes and features, and our perception uses these features as cues to shape or object recognition, and for image interpretation [9,10,11,12,13,14,15,16]. In biology, curvature guides physical, chemical, and biological processes, such as protein folding, membrane binding, and other biophysical transformations [17]. The representation and cognition of curvature ranges from the biochemical level of living organisms capable of sensing this property in their near or distant physical environments [18] to perceptual properties extracted from physical stimuli by the human brain, the ultimate product of evolution. In terms of a mathematical property of the physical world, curve symmetry is directly linked to affine geometry [19].
1.1. Affine Geometry and Visual Sensation
In affine geometry, curves derived from circles and ellipses share certain properties, the circle being a particular case of the ellipse. Projective geometry permits generating symmetric curves from ellipses by affinity with concentric circles (Figure 2). Their perception is grounded in biology in the sense that most natural objects can be represented in 2D as symmetrically curved shapes with Euclidean properties of ellipses. Studies comparing between visually perceived curvature by experts in geometry (architects and design engineers) and non-experts [12] by using symmetric curves derived from concentric circles by affine projection have shown that their perceived magnitude is determined by a single geometric parameter, the curves’ aspect ratio. The perceptual responses to such curves are independent of both expertise and sensory modality, given that tactile sensing by sighted blindfolded and congenitally blind observers produces the same results [14]. The symmetry of the curves, however, is a critical factor to these geometry-based perceptual responses [15]. The aspect ratio relates the height (sagitta) to the width of a curve, and in symmetric curves of variable size but constant aspect ratio directly taken from concentric circles (no projection by affinity), perceived curvature is also constant, in both vision and touch. This observation is directly linked to the phenomenon of scale-invariance in visual curvature discrimination [20] and the detection and recognition of shapes in general.
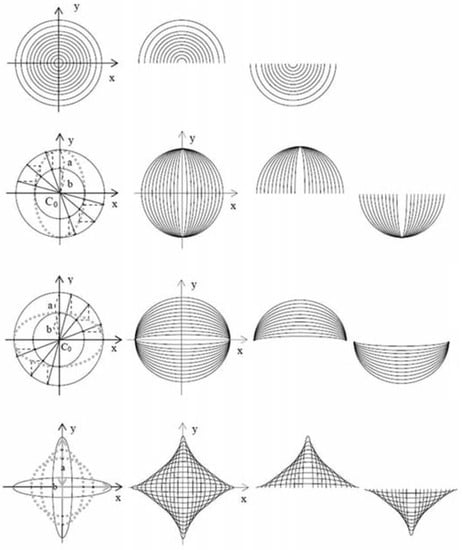
Figure 2.
Projective geometry permits generating symmetric curves from ellipses by affinity with concentric circles. Each such curve may be perceived as a single thing or as a multiple of one and the same thing in a complex shape or object, as shown here. This perception is grounded in biology in the sense that most natural objects can be represented as images of symmetrically curved shapes with the Euclidean properties of ellipses. Symmetric curves yield visual and tactile sensations of curvature which increase exponentially with the aspect ratio of the curves.
1.2. Reflection and Rotational Shape Symmetry
The role of reflection symmetry in visual perception was pointed out by Gestalt psychologists at the beginning of the 20th century [21] as a major factor in shape perception. It refers to specific transformations by transition of points in Euclidean space resulting in mirrored representations. Axial symmetry e.g., which results from point-by-point mirroring across an axis (f (x, y, z) = f (−x, y, z), is an important factor in visual recognition [22,23,24]. Reflection or mirror symmetry is detected quickly [25,26] in foveal and in peripheral vision [27]. Vertical mirror symmetry facilitates face recognition by human [28] and non-human primates [29], and is used by the human visual system as a second-order cue to perceptual grouping [30].
Rotational symmetry of shape plays an important role in architecture and design. The design of complex modern spatial structures is a domain of contemporary relevance. Visual-spatial experiments on expert architects as well as novices have shown that perceiving the rotational symmetry of partial shapes, which constitute the simplest possible tensegrity (tensile integrity) structure, is an important part of our understanding how they are put together. Only once this symmetry is perceived by the expert or novice, will he/she be able to draw the structure from memory into axonometric or topological reference frames provided to that effect [31]. Tensegrity structures have inspired current biological models [32], from the level of single cells to that of the whole human body. They possess what Mandelbrot [33] called “fractal consistency across spatial scales”, or “fractal iterations”, like those seen in large trees that appear to be composed of many smaller trees of the same structure.
1.3. Nature-Inspired Design and the Symmetry of “Things in a Thing”
Fractal geometry is also inspired by nature and its many symmetric visual structures like those found in cells, trees, butterflies and flowers. The term “fractal” was first introduced by Mandelbrot [33] based on the meaning “broken” or “fractured” (fractus). A fractal may be defined as a complex whole (object or pattern) that has the same structural characteristics as its constituent parts. The structural symmetry that results from fractal iterations may be described as the “symmetry of things in a thing”. The radial symmetry of a sunflower is a choice example of fractal symmetry as it exists in nature. Behavioural studies have shown that various animal species are naturally attracted to two-dimensional representations of objects exhibiting flower-like radial symmetry [34,35]. In complex 3D fractal trees, single fractals (“things”) have a symmetrical counterpart within the whole structure (“the thing”), which may possess radial symmetry, reflection symmetry and manifold rotational symmetries, like many objects in nature (plants, snowflakes, etc.) are bound by both reflection and rotational symmetry, and exhibit multiples of one and the same shape (things) repeated in all directions.
Nature-inspired design occupies an important place in contemporary graphic art, and symmetry has been identified as a major defining feature of visual beauty, compositional order, and harmony. Symmetry directly determines aesthetic preferences and the subjectively perceived beauty of two-dimensional visual images and patterns [36,37,38,39,40,41], and symmetrical visual patterns are also more easily remembered and recognized [42,43,44] compared with asymmetrical ones. Sabatelli et al. [8] suggested that natural and artistic creative processes rely on common, possibly fractal transformations. Fractal transformations may describe iterative transitions from simplicity and order (symmetry) to complexity and chaos (asymmetry). Again, fractal trees seem to be a pertinent example here, where simple 2D mirror trees (Figure 3) with reflection and/or radial symmetry open an almost infinite number of possibilities for adding complexity through further transformations leading to complex projections of 3D structures with multiple rotational symmetries (not shown here).
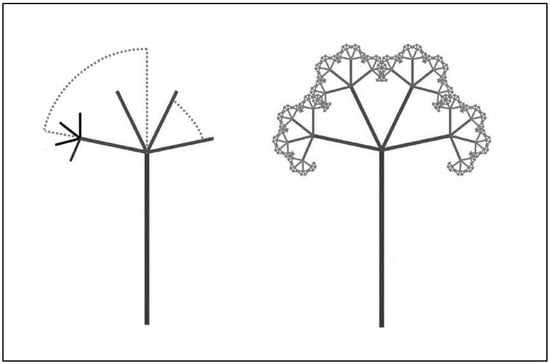
Figure 3.
Fractal geometry and affine geometry share principles of projection in Euclidean space, as illustrated in this example here. Fractal trees, inspired by nature, may be defined as complex wholes where every part repeats itself across multiple fractal iterations, producing “symmetry of things in a thing”. In the 2D fractal mirror-tree shown here, concentric circles and affine projection are the mathematical basis for describing structural regularities with vertical reflection (mirror) symmetry, which has been identified as a major determinant of the visual attractiveness of image configurations.
Whether nature-inspired fractal design appeals to our senses in the same way as the real objects found in nature was studied by [45], who found that human observers produce highly consistent aesthetic preference judgments across fractal images produced by nature, algorithm, or by the human hand. Hagerhall, Purcell, and Taylor [46] found that fractal characteristics of landscape silhouette outlines reliably predict landscape preferences. Fractal characteristics provide a consistent measure of complexity, and were shown to account for judgments of perceived beauty in visual art [47]. Here, we make the prediction that the “symmetry of things in a thing” in 2D fractal objects plays a decisive role in our perception of their aesthetic content and thereby influences visual preference judgments. Given the multiple levels of complexity of fractal objects, trying to address this question requires starting with simple examples. For this pilot study here, we created a series of basic fractal mirror trees based on geometric transformations as shown in Figure 2 and Figure 3. In two psychophysical experiments, one using an aesthetic rating procedure, the other a preference judgment design, we tested whether the subjective attractiveness of such trees is affected by different degrees of violation of symmetry, from an almost imperceptible lack of mirror detail to massive asymmetry.
2. Materials and Methods
The experiments were conducted in accordance with the Declaration of Helsinki (1964) and with the full approval of the corresponding author’s institutional (CNRS) ethics committee. Informed written consent was obtained from each of the participants. Experimental sessions were organized following conditions of randomized, trial-by-trial free image viewing using Python for Windows 7 and a computer with a keyboard and a high resolution monitor. 15 mirror tree images were generated using a comprehensive vector graphics environment (Adobe Illustrator CC) and computer shape library.
2.1. Subjects
30 observers, ranging in age between 25 and 70 and unaware of the hypotheses of the study, participated in the experiments. All subjects had normal or corrected-to-normal visual acuity.
2.2. Stimuli
The stimuli for the two experiments were generated on the basis of 15 images of fractal trees drawn in a vector graphics environment (Adobe illustrator CC) using simple principles of 2D geometry, as shown here above. Five of these images (Figure 4, top row) were mirror trees with vertical reflection symmetry and perfect symmetry of things in a thing. Five of them (Figure 4, middle row) were imperfect mirror trees in the sense that their vertical reflection symmetry excluded one of the elementary parts, which was not mirrored on the right side of the tree. In the asymmetrical images (Figure 4, bottom row), elementary shapes “growing” on the branches of the left side of the trees were not mirrored on the right side. The luminance contrast between figures and backgrounds was constant in the 15 images (same RGB (200, 200, 200) for all figures, same RGB (20, 20, 20) for all backgrounds). The approximate angular height of a fractal tree was 2.25° (vertical mid-axis), the angular width 1.64° (horizontal mid-axis). A trial-loop algorithm written in Python for Windows 7 selected the images or image pairs in random order, and recorded the individual key board responses from the experimental trials.

Figure 4.
Fifteen images of fractal mirror trees were designed using some of the principles of transformation shown in Figure 2 and Figure 3. The first five trees (top) possess perfect “symmetry of things in a thing” across the vertical axis. In the next set of five (middle), the smallest of fractal details is missing on the right. The remaining five trees (bottom) are asymmetrical. It is noted that in these tree structures here, only the symmetrical ones (top) appear perceptually complete.
2.3. Task Instructions
In the aesthetic rating experiment, subjects were instructed to type a number on the keyboard rating the beauty of each of the fifteen individual images on a subjective psychophysical scale from 0 (zero) for “very ugly” to ten (10) for “very beautiful”. In the preference judgment experiment, subjects were instructed to indicate whether they spontaneously preferred the left (hit “1”) or the right (hit “2”) of an image pair. Hitting the response key initiated the next image pair. Half of the subjects started with the rating experiment, the other half with the preference judgment experiment.
2.4. Procedure
Subjects were seated at a distance of about 90 cm from the screen and looked at the center. The images were displayed centrally and presented in random order. In the aesthetic rating experiment, each of the 15 images was presented once to each of the 30 subjects. In the preference judgment experiment, each image from a group of five was paired with its counterpart from the two other groups, and spatial position in a pair (left/right) was counterbalanced (Figure 5). This produced 30 image pairs with 20 presentations for each figure type (10 times on the left, and 10 times on the right). The image pairs were displayed in random order and each pair was displayed twice in an individual session, yielding 60 preference judgments from each of the 30 subjects.

Figure 5.
30 image pairs with 20 presentations for figures of a given type (10 times on the left, and 10 times on the right). The image pairs were displayed in random order, and each pair was displayed twice in an individual session, yielding 60 preference judgments from each of the 30 subjects.
The intervals between stimulus presentations were under the control of the observer, who initiated the next image presentation by striking a given response key (“1” for “left”, “2” for “right”) on the computer keyboard. The individual keyboard responses were coded and automatically written into text files. These were then imported into SYSTAT 11 software for processing and statistical analysis.
3. Results
The raw data were analyzed using Systat/Sigmaplot 11 (Systat Software Inc., 2010, San Jose, CA, USA). One-way analysis of variance (ANOVA) for repeated measures was performed to assess the statistical significance of differences in means across subjects and figure types: ‘symmetrical’, ‘detail missing’ and ‘asymmetrical’. In the data from the preference judgment experiment with figure pairs, a first check of the means showed no effect of secondary variables such as the spatial position (left vs. right) of figures of a type in a pair (Mleft = 4.92 vs. Mright = 5.07), or the order (first vs. second) in which a judgment was formed in response to a figure pair (Mfirst = 5.02 vs. Msecond = 4.95).
3.1. Aesthetic Ratings
The results of the ANOVA on average aesthetic ratings for each individual as a function of the three figure types are given in Table 1. The table summarizes, for each figure type, the sample size (N), the mean (M), the standard error (SEM), and the F value and its probability limits (p). Effect sizes in terms of differences between the means (dM), and the corresponding t values and probability limits for each paired comparison are given. From the results in Table 1 we conclude that symmetrical figures received a significantly higher average aesthetic rating compared with figures where a small detail was missing, which received a significantly higher average aesthetic rating than the asymmetrical figures. A graphic representation of these effects is shown below in Figure 6.

Table 1.
Results from the one-way repeated measures ANOVA on aesthetic ratings for each of the three figure types: Number of observations (N) per figure type, means (M) and standard errors (SEM), and the F value with probability limits (p) are given. Effect sizes, t values and the corresponding probability limits are given at the bottom.
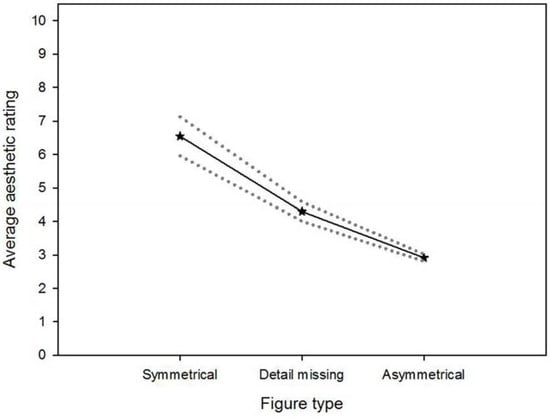
Figure 6.
Average aesthetic ratings on a scale between zero and ten are shown as a function of the figure type.
3.2. Preference Judgments
The SYSTAT results of the ANOVA on average preference judgments of each individual as a function of the three figure types are summarized in Table 2. The table shows, for each figure type, the sample size (N), the mean (M), the standard error (SEM), and the F value and probability limits (p). Effect sizes in terms of differences between the means (dM), and the corresponding t values and probability limits for each paired comparison are given.

Table 2.
Results from the one-way ANOVA for repeated measures of preference judgments for each of the three figure types.
From the results in Table 2 we conclude that symmetrical figures were significantly more often preferred than figures with a detail missing, which were significantly more often preferred than asymmetrical figures. These observations are fully consistent with the effects on aesthetic ratings shown in Figure 6.
4. Discussion
As illustrated by examples from the introduction here above, shape sensation and perception can be related to affine design geometry [15,19,21,22,48,49]. The topology and geometry of fractal objects is controlled in similar ways, as shown in the fractal mirror trees used as stimuli here. The findings show that the smallest “fractal” deviation from perfect “symmetry of things in a thing” in basic mirror trees (any computer shape library can generate them) with vertical reflection symmetry when no fractals are removed, significantly diminishes subjectively perceived beauty and visual preference. These results confirm previous observations from aesthetic perception studies using different two-dimensional configurations [36,37,38,39,40,41]. Perfectly symmetrical trees also produced the strongest consensual results, for both subjective aesthetic ratings and visual preferences, while the ones with a small detail missing and the asymmetrical trees produced more disparate data, indicating higher uncertainty (i.e., less confidence) in the subjects’ perceptual responses.
In the experiments here, subjects could look at the figures or pairs for as long as they wanted to make a perceptual decision and no instruction to respond as swiftly as possible were given, as is often the case in reaction time studies. Reaction times were not measured here. It is to be noted that aesthetic ratings and preference judgments may be driven by low-level heuristics or by higher order cognitive processes [50,51]. Measuring reaction times in future studies will be useful to shed light on how one or the other type of processing may have influenced response strategies. Whenever a figure was symmetrical here, it was also perceptually complete; whenever it was not, it was perceptually incomplete. Using simple response heuristics based on this kind of local detail analysis instead of forming an overall global aesthetic appreciation, for example, would certainly yield faster responses. A way of disentangling perceptual completeness and symmetry in the stimuli is to include a group of perceptually incomplete but symmetrical figures, like fractal trees with a local detail missing on both sides.
In nature, it is difficult to find complete things which do not have at least one axis of mirror or reflection symmetry. On the other hand, things which are incomplete and at the same time symmetrical are very hard to find. Our aesthetic preferences are well-primed for symmetrical objects [41], yet results from earlier studies [52] suggest that things may not be that simple when complexity and symmetry are weighed against each other, and when socio-cultural factors are brought into the equation. Personality and creativity [30,53,54] have been identified as two such variables. Highly creative individuals may have a stronger tendency to prefer asymmetrical objects, especially when these exhibit high levels of complexity, as in the case of fractal objects with multiple rotational symmetries, for example.
Recent work has highlighted that our aesthetic appreciation is essentially dynamic [55,56], and involves reflexive processes which drive cultural evolution and changes in the Zeitgeist, or what the French call l’esprit du temps. The human mind has the ability to master perceptual input which challenges current preferences (otherwise, creative fashion designers would go out of business). By way of cognitive processes these preferences may be overruled and replaced by new ones. Recent studies [51] have identified double mechanisms of preference formation. One is reflected by an immediate and basically conservative perceptual response to what is familiar [57], or deemed the current aesthetic norm, the other by a slowly strengthening disposition to adopt what is new, unusual, or challenging. As pointed out earlier [8], symmetry stands for order, asymmetry for disorder. Their dual subjective appreciation is likely to influence preferences.
Fractal objects offer new perspectives for research on complementary aspects of symmetry and asymmetry in processes of increasing complexity, including processes of visual perception. Fractals are different from other geometric figures because of the way in which they scale across multiple iterations, yielding increasingly complex repetitive structures which are symmetrical by nature. Fractal symmetry is also referred to as “expanding symmetry” or “evolving symmetry,” especially if replication is exactly the same at every scale, as in a detailed pattern that repeats itself across multiple fractal iterations. For the visual scientist, this opens many perspectives as it permits the finely controlled manipulation of each and every shape detail in a given configuration and thereby allows creating visual stimuli where variations in complexity and symmetry can be effectively weighed against each other in further studies.
5. Conclusions
The visual attractiveness of 2D fractal design shapes greatly depends on the “symmetry of things in a thing” in configurations with simple geometry, as shown in this pilot study here on the example of a few very basic fractal mirror-trees. In simple displays, which are often surprisingly well suited for probing the most complex perceptual mechanisms [58], the smallest fractal deviation from a perfect “symmetry of things in a thing” is shown here to have significantly negative effects on subjectively perceived beauty and preference judgments. These findings are to encourage further studies with more sophisticated fractal design objects, and an increasingly large number of fractal iterations, producing more and more complex 2D mirror designs, and shapes with increasing levels of rotational symmetry in 3D. Such design objects are ideally suited for a numerically controlled manipulation of the “symmetry of things in a thing”, and can be tailored for investigating complex interactions between symmetry and complexity in their effects on visual sensation and aesthetic perception.
Conflicts of Interest
The author declares no conflict of interest.
References
- Amir, O.; Biederman, I.; Hayworth, K.J. Sensitivity to non-accidental properties across various shape dimensions. Vis. Res. 2012, 62, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Amir, O.; Biederman, I.; Herald, S.B.; Shah, M.P.; Mintz, T.H. Greater sensitivity to non-accidental than metric shape properties in preschool children. Vis. Res. 2014, 97, 83–88. [Google Scholar] [CrossRef] [PubMed]
- Biederman, I. Recognition-by-components: A theory of human image understanding. Psychol. Rev. 1987, 94, 115–117. [Google Scholar] [CrossRef] [PubMed]
- Wilson, H.R.; Wilkinson, F. Symmetry perception: A novel approach for biological shapes. Vis. Res. 2002, 42, 589–597. [Google Scholar] [CrossRef]
- Pizlo, Z.; Sawada, T.; Li, Y.; Kropatsch, W.G.; Steinman, R.M. New approach to the perception of 3D shape based on veridicality, complexity, symmetry and volume: A mini-review. Vis. Res. 2010, 50, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Pizlo, Z.; Steinman, R.M. A computational model that recovers the 3D shape of an object from a single 2D retinal representation. Vis. Res. 2009, 49, 979–991. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Sawada, T.; Shi, Y.; Steinman, R.M.; Pizlo, Z. Symmetry is the sine qua non of shape. In Shape Perception in Human and Computer Vision; Dickinson, S., Pizlo, Z., Eds.; Springer: London, UK, 2013; pp. 21–40. [Google Scholar]
- Sabatelli, H.; Lawandow, A.; Kopra, A.R. Asymmetry, symmetry and beauty. Symmetry 2010, 2, 1591–1624. [Google Scholar] [CrossRef]
- Stevens, K.A. The visual interpretation of surface contours. Artif. Intell. 1981, 17, 47–73. [Google Scholar] [CrossRef]
- Stevens, K.A. The information content of texture gradients. Biol. Cybern. 1981, 42, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Foley, J.M.; Ribeiro-Filho, N.P.; Da Silva, J.A. Visual perception of extent and the geometry of visual space. Vis. Res. 2004, 44, 147–156. [Google Scholar] [CrossRef] [PubMed]
- Dresp, B.; Silvestri, C.; Motro, R. Which geometric model for the perceived curvature of 2-D shape contours? Spat. Vis. 2007, 20, 219–264. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B. Why the brain knows more than we do: Non-conscious representations and their role in the construction of conscious experience. Brain Sci. 2012, 2, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B. Generic properties of curvature sensing by vision and touch. Comput. Math. Methods Med. 2013, 2013, 634168. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B. 2D geometry predicts perceived visual curvature in context-free viewing. Comput. Intell. Neurosci. 2015, 9. [Google Scholar] [CrossRef] [PubMed]
- Strother, L.; Killebrew, K.W.; Caplovitz, G.P. The lemon illusion: Seeing curvature where there is none. Front. Hum. Neurosci. 2015, 9, 95. [Google Scholar] [CrossRef] [PubMed]
- Groves, J.T. The physical chemistry of membrane curvature. Nat. Chem. Biol. 2009, 5, 783–784. [Google Scholar] [CrossRef] [PubMed]
- Hatzakis, N.S.; Bhatia, V.K.; Larsen, J.; Madsen, K.L.; Bolinger, P.Y.; Kunding, A.H.; Castillo, J.; Gether, U.; Hedegård, P.; Stamou, D. How curved membranes recruit amphipathic helices and protein anchoring motifs. Nat. Chem. Biol. 2009, 5, 835–841. [Google Scholar] [CrossRef] [PubMed]
- Gerbino, W.; Zhang, L. Visual orientation and symmetry detection under affine transformations. Bull. Psychon. Soc. 1991, 29, 480. [Google Scholar]
- Whitaker, D.; McGraw, P.W. Geometric representation of the mechanisms underlying human curvature detection. Vis. Res. 1998, 38, 3843–3848. [Google Scholar] [CrossRef]
- Bahnsen, P. Eine Untersuchung über Symmetrie und Asymmetrie bei visuellen Wahrnehmungen. Z. Psychol. 1928, 108, 129–154. [Google Scholar]
- Braitenberg, V. Reading the structure of brains. Network 1990, 1, 1–11. [Google Scholar] [CrossRef]
- Beck, D.M.; Pinsk, M.A.; Kastner, S. Symmetry perception in humans and macaques. Trends Cogn. Sci. 2005, 9, 405–406. [Google Scholar] [CrossRef] [PubMed]
- Tjan, B.S.; Liu, Z. Symmetry impedes symmetry discrimination. J. Vis. 2005, 5, 88–900. [Google Scholar] [CrossRef] [PubMed]
- Barlow, H.B.; Reeves, B.C. The versatility and absolute efficiency of detecting mirror symmetry in random dot displays. Vis. Res. 1979, 19, 783–793. [Google Scholar] [CrossRef]
- Wagemans, J.; Van Gool, L.; D’Ydewalle, G. Detection of symmetry in tachistoscopically presented dot patterns: Effects of multiple axes and skewing. Percept. Psychophys. 1991, 50, 413–427. [Google Scholar] [CrossRef] [PubMed]
- Barrett, B.T.; Whitaker, D.; McGraw, P.V.; Herbert, A.M. Discriminating mirror symmetry in foveal and extra-foveal vision. Vis. Res. 1999, 39, 3737–3744. [Google Scholar] [CrossRef]
- Thornhill, R.; Gangestad, S.W. Facial attractiveness. Trends Cognit. Sci. 1999, 3, 452–460. [Google Scholar] [CrossRef]
- Anderson, J.R.; Kuwahata, H.; Kuroshima, F.; Leighty, K.A.; Fujita, K. Are monkeys aesthetists? Rensch (1957) revisited. J. Exp. Psychol. 2005, 31, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Machilsen, B.; Pauwels, M.; Wagemans, J. The role of vertical mirror symmetry in visual shape perception. J. Vis. 2009, 9. [Google Scholar] [CrossRef] [PubMed]
- Silvestri, C.; Motro, R.; Maurin, B.; Dresp-Langley, B. Visual spatial learning of complex object morphologies through the interaction with virtual and real-world data. Des. Stud. 2010, 31, 363–381. [Google Scholar] [CrossRef]
- Levin, S.M. Biotensegrity: The tensegrity truss as a model for spine mechanics. J. Mech. Med. Biol. 2002, 3–4, 375–388. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; Freeman & Co.: San Francisco, CA, USA, 1982. [Google Scholar]
- Lehrer, M.; Horridge, G.A.; Zhang, S.W.; Gadagkar, R. Shape vision in bees: Innate preference for flower-like patterns. Philos. Trans. R. Soc. Lond. B 1995, 347, 123–137. [Google Scholar] [CrossRef]
- Giurfa, M.; Eichmann, B.; Menzl, R. Symmetry perception in an insect. Nature 1996, 382, 458–461. [Google Scholar] [CrossRef] [PubMed]
- Eisenman, R. Complexity–simplicity: I. Preference for symmetry and rejection of complexity. Psychon. Sci. 1967, 8, 169–170. [Google Scholar] [CrossRef]
- Berlyne, D.E. Aesthetics and Psychobiology; Appleton: New York, NY, USA, 1971. [Google Scholar]
- Jacobsen, T.; Hofel, L. Aesthetics judgments of novel graphic patterns: Analyses of individual judgments. Percept. Motor Skills 2002, 95, 755–766. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, T.; Hofel, L. Descriptive and evaluative judgment processes: Behavioral and electrophysiological indices of processing symmetry and aesthetics. Cognit. Affect. Behav. Neurosci. 2003, 3, 289–299. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, T.; Schubotz, R.I.; Hofel, L.; van Cramon, D.Y. Brain correlates of aesthetic judgment of beauty. NeuroImage 2006, 29, 276–285. [Google Scholar] [CrossRef] [PubMed]
- Tinio, P.P.L.; Leder, H. Just how stable are stable aesthetic features? Symmetry, complexity, and the jaws of massive familiarization. Acta Psychol. 2009, 130, 241–150. [Google Scholar] [CrossRef] [PubMed]
- Deregowski, J.B. Symmetry, Gestalt and information theory. Q. J. Exp. Psychol. 1971, 23, 381–385. [Google Scholar] [CrossRef] [PubMed]
- Deregowski, J.B. The role of symmetry in pattern reproduction by Zambian children. J. Cross-Cult. Psychol. 1972, 3, 303–307. [Google Scholar] [CrossRef]
- Kayaert, G.; Wagemans, J. Delayed shape matching benefits from simplicity and symmetry. Vis. Res. 2009, 49, 708–717. [Google Scholar] [CrossRef] [PubMed]
- Spehar, B.; Clifford, C.W.G.; Newell, B.; Taylor, R.P. Universal aesthetics of fractals. Comput. Graph. 2003, 27, 813–820. [Google Scholar] [CrossRef]
- Hagerhall, C.M.; Purcell, T.; Taylor, R. Fractal dimension of landscape silhouette outlines as a predictor of landscape preference. J. Environ. Psychol. 2004, 24, 247–255. [Google Scholar] [CrossRef]
- Forsythe, A.; Nadal, M.; Sheehy, N.; Cela-Conde, C.J.; Sawey, M. Predicting beauty: Fractal dimension and visual complexity in art. Br. J. Psychol. 2011, 102, 49–70. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B. Principles of perceptual grouping: implications for image-guided surgery. Front. Psychol. 2015, 6, 1565. [Google Scholar] [CrossRef] [PubMed]
- Dresp, B. On illusory contours and their functional significance. Curr. Psychol. Cognit. 1997, 16, 489–518. [Google Scholar]
- Samuel, F.; Kerzel, D. Judging whether it is aesthetic: Does equilibrium compensate for lack of symmetry? I-Perception 2013, 4, 57–77. [Google Scholar] [CrossRef] [PubMed]
- Belke, B.; Leder, H.; Carbon, C.C. When challenging art gets liked: Evidences for a dual preference formation process for fluent and non-fluent portraits. PLoS ONE 2015, 10, e0131796. [Google Scholar]
- Eisenman, R.; Rappaport, J. Complexity preference and semantic differential ratings of complexity-simplicity and symmetry-asymmetry. Psychon. Sci. 1967, 7, 147–148. [Google Scholar] [CrossRef]
- Eisenman, R.; Gellens, H.K. Preference for complexity—Simplicity and symmetry-asymmetry. Percept. Motor Skills 1968, 26, 888–890. [Google Scholar] [CrossRef] [PubMed]
- Cook, R.; Furnham, A. Aesthetic preferences for architectural styles vary as a function of personality. Imagin. Cogn. Personal. 2012, 32, 103–114. [Google Scholar] [CrossRef]
- Carbon, C.C. The cycle of preference: Long-term dynamics of aesthetic appreciation. Acta Psychol. 2010, 134, 233–244. [Google Scholar] [CrossRef] [PubMed]
- Carbon, C.C. Cognitive mechanisms for explaining dynamics of aesthetic appreciation. I-Perception 2011, 2, 708–719. [Google Scholar] [CrossRef] [PubMed]
- Grammer, K.; Thornhill, R. Human (Homo sapiens) facial attractiveness and sexual selection: The role of symmetry and averageness. J. Comp. Psychol. 1994, 108, 233–242. [Google Scholar] [CrossRef] [PubMed]
- Dresp-Langley, B.; Grossberg, S. Neural computation of surface border ownership and relative surface depth from ambiguous contrast inputs. Front. Psychol. 2016, 7, 1102. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).