Improvement in Scoliosis Top View: Evaluation of Vertebrae Localization in Scoliotic Spine-Spine Axial Presentation
Abstract
:1. Introduction
2. Objectives
3. Materials and Methods
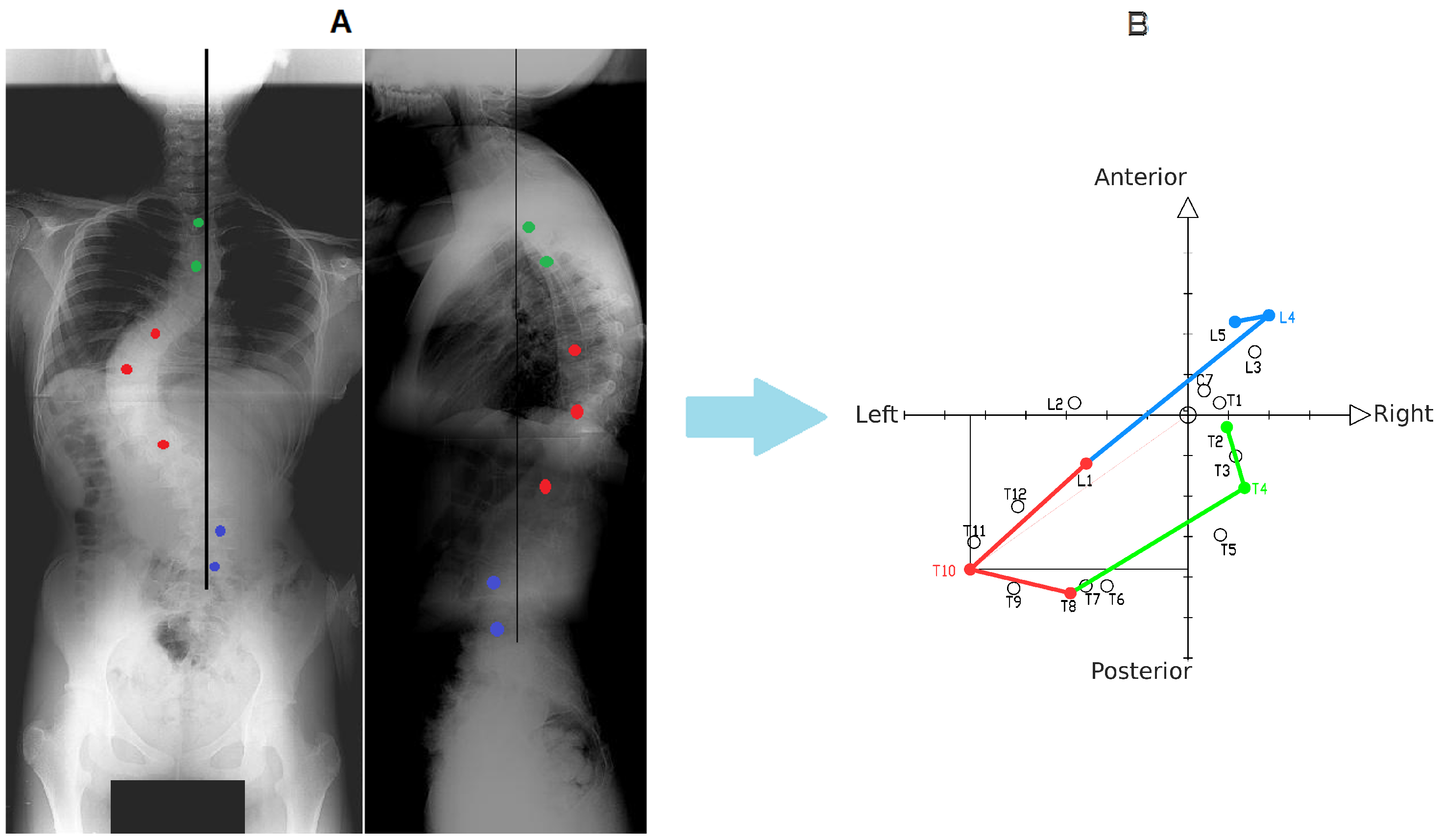
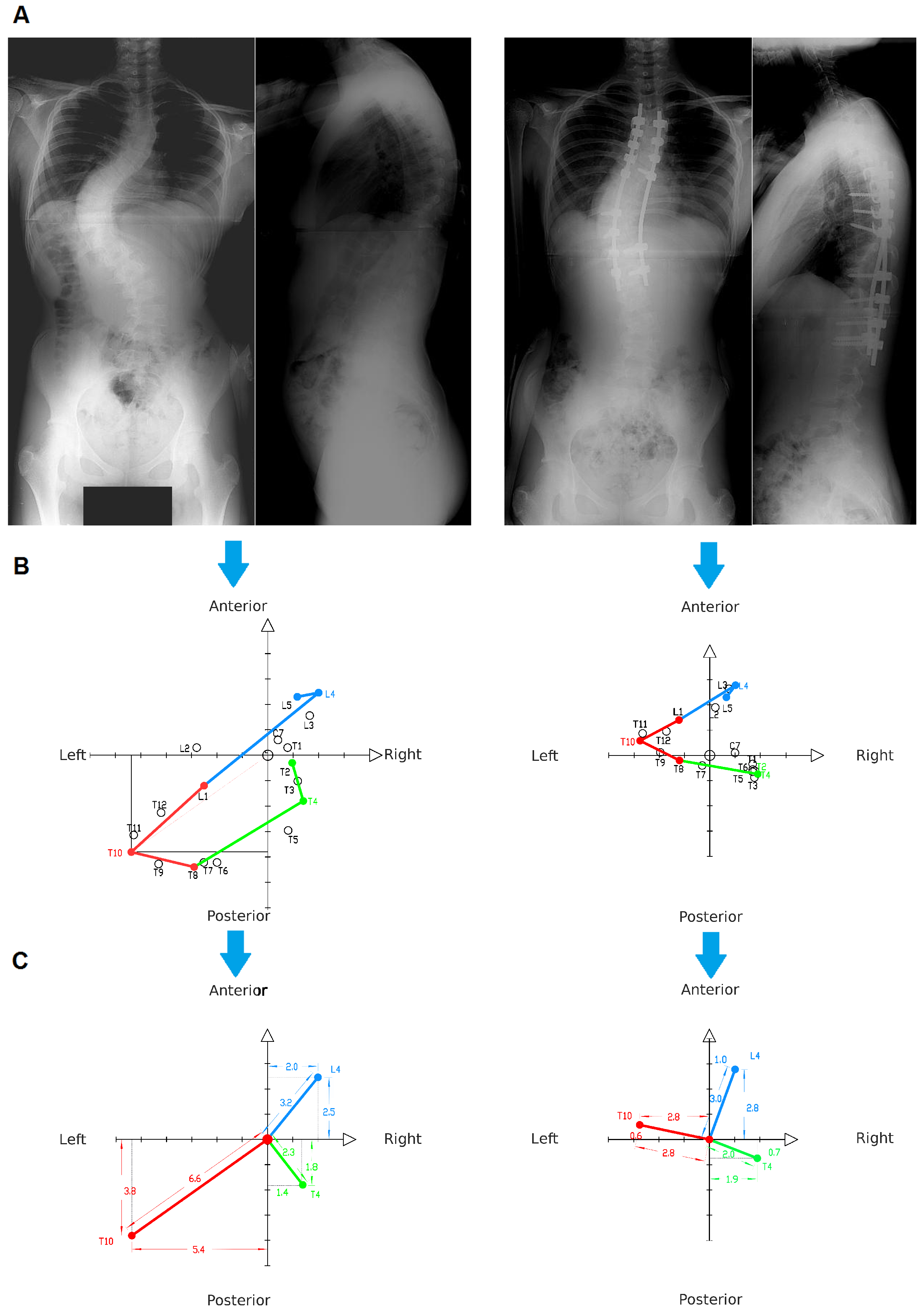
3.1. Procedure for Obtaining Spine Axial Presentation
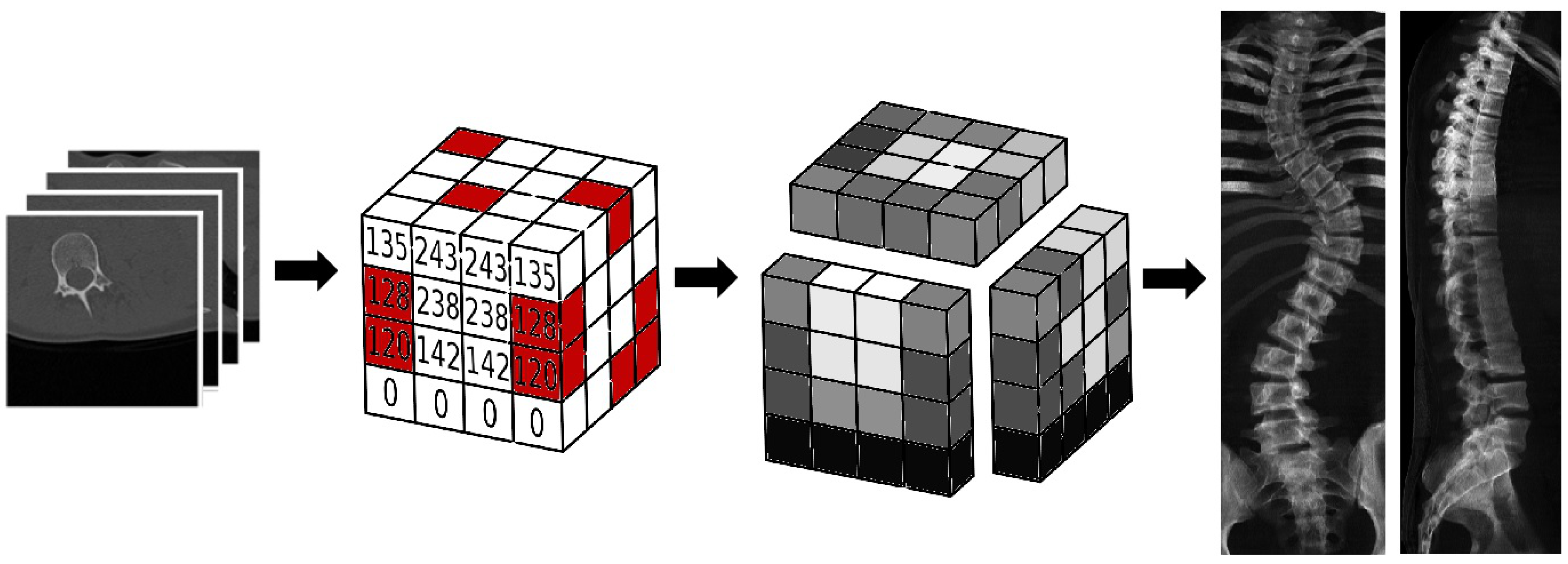
3.2. Procedure for Obtaining Digital Reconstructed Radiograph
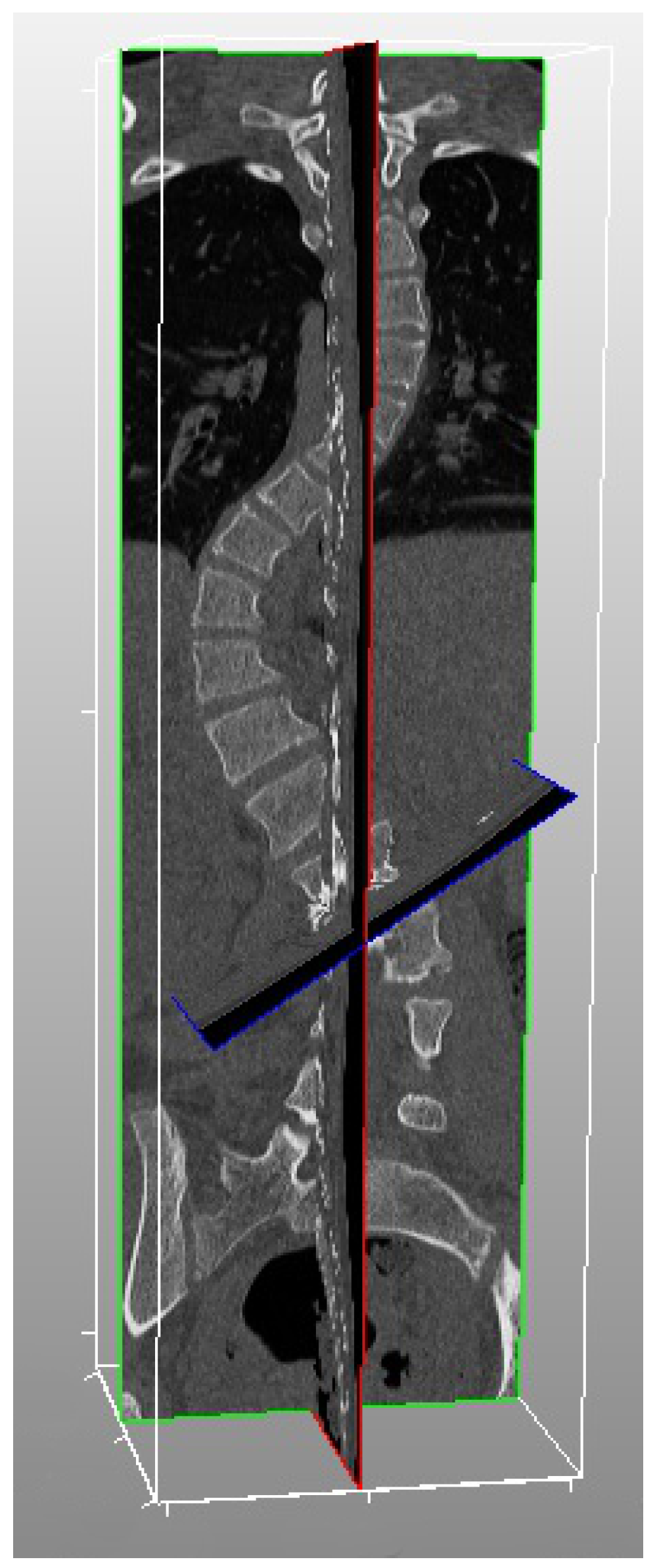
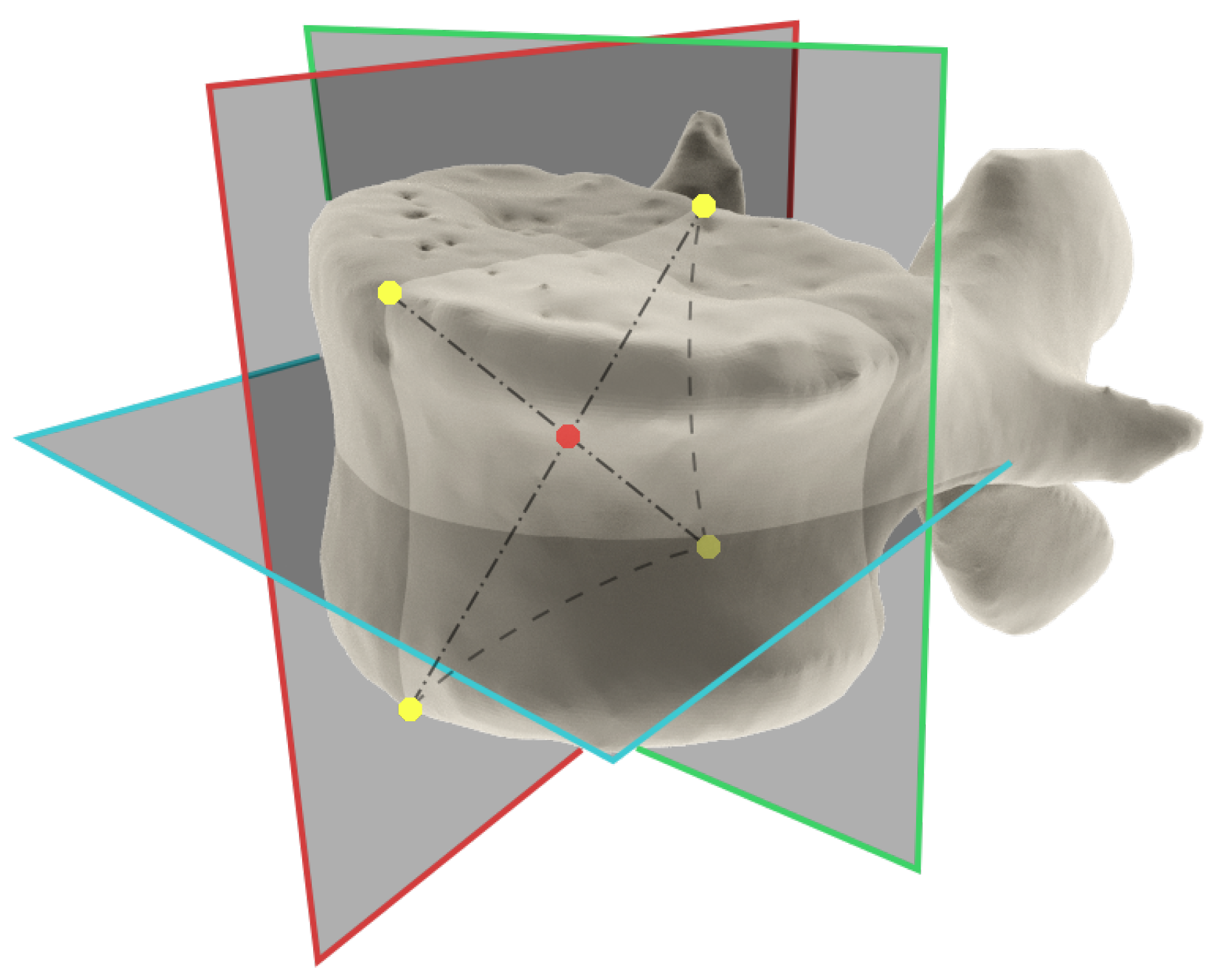
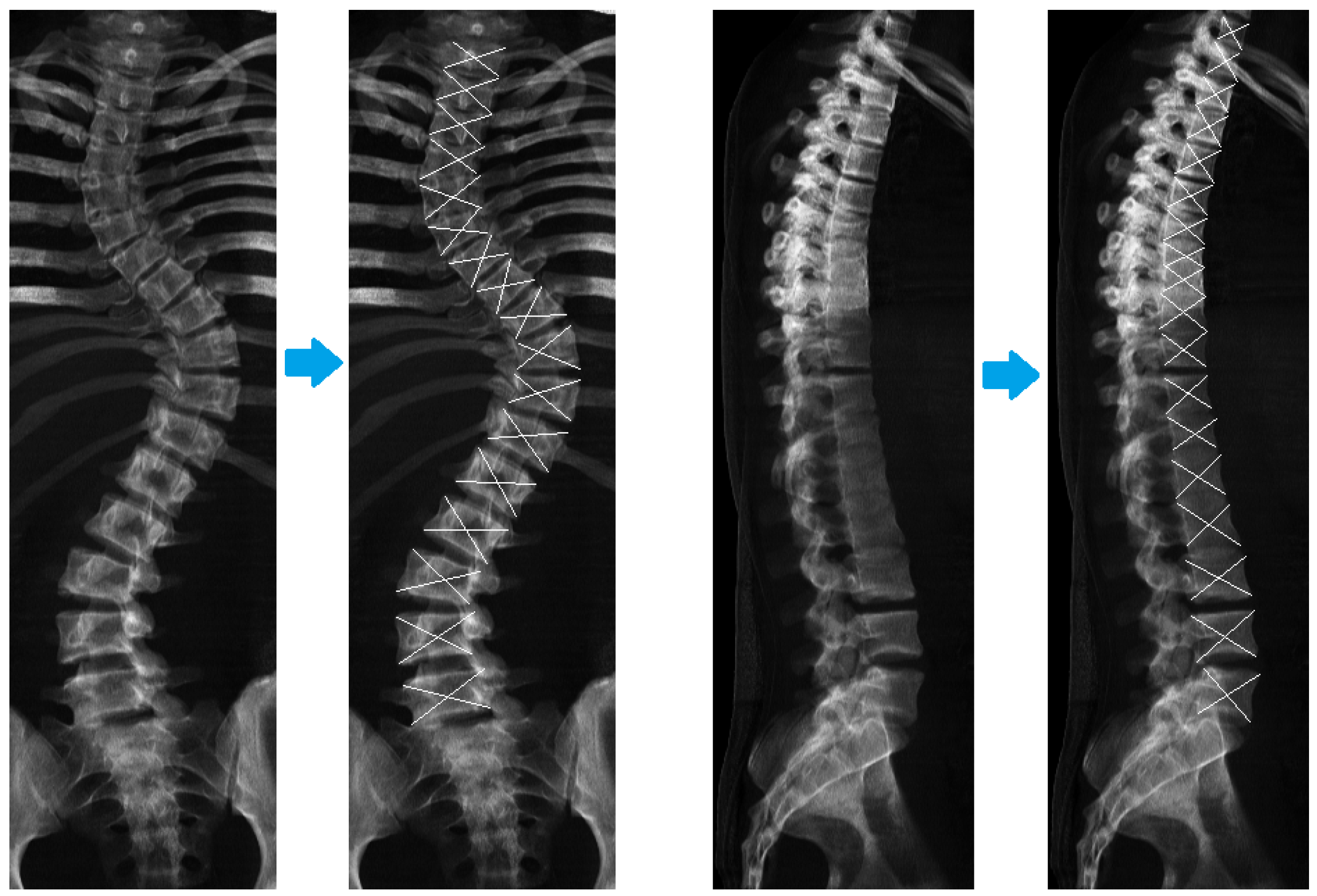
3.3. Procedure for Obtaining Location of the Vertebral Body Central Point from CT Scans
3.4. Procedure for Obtaining Vertebral Body Central Point from DRR
3.5. Comparison of the Central Vertebral Bodies Points Coordinates Obtained from CT Scans Versus the Points from DRRs
3.6. Calculation of Sample Size
4. Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CT | Computed Tomography |
| DRR | Digitally Reconstructed Radiograph |
| SRS | Scoliosis Research Society |
| EOS | biplane Low-dose X-ray Imaging System |
| EAE-planes | End-apical-end Planes |
| SAP | Spine Axial Presentation |
| SVA | Sagittal Vertical Axis |
| CVSL | Central Vertical Sacral Line |
| PNG | Portable Network Graphic |
| DICOM | Digital Imaging and Communications in Medicine |
| ITK | The Insight Segmentation and Registration Toolkit |
| VTK | The Visualization Toolkit |
| AP | Antero-posterior |
| LAT | Lateral |
References
- Hattori, T.; Sakaura, H.; Iwasaki, M.; Nagamoto, Y.; Yoshikawa, H.; Sugamoto, K. In vivo three-dimensional segmental analysis of adolescent idiopathic scoliosis. Eur. Spine J. 2011, 20, 1745–1750. [Google Scholar] [CrossRef] [PubMed]
- Stokes, I.A. Three-dimensional terminology of spinal deformity: A report rresented to the scoliosis research society by the scoliosis research society working group on 3-D terminology of spinal deformity. Spine 1994, 19, 236–248. [Google Scholar] [CrossRef] [PubMed]
- Kotwicki, T.; Negrini, S.; Grivas, T.B.; Rigo, M.; Maruyama, T.; Durmala, J.; Zaina, F. Methodology of evaluation of morphology of the spine and the trunk in idiopathic scoliosis and other spinal deformities-6th SOSORT consensus paper. Scoli. Spinal Disord. 2009, 4, 1. [Google Scholar]
- Kotwicki, T. Evaluation of scoliosis today: Examination, X-rays and beyond. Disabil. Rehabil. 2008, 30, 742–751. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Kim, H.S.; Moon, E.S.; Yoon, C.S.; Chung, T.S.; Song, H.T.; Suh, J.S.; Lee, Y.H.; Kim, S. Scoliosis imaging: What radiologists should know. Radiographics 2010, 30, 1823–1842. [Google Scholar] [CrossRef] [PubMed]
- Ilharreborde, B.; Ferrero, E.; Alison, M.; Mazda, K. EOS microdose protocol for the radiological follow-up of adolescent idiopathic scoliosis. Eur. Spine J. 2016, 25, 526–531. [Google Scholar] [CrossRef] [PubMed]
- Morvan, G.; Mathieu, P.; Vuillemin, V.; Guerini, H.; Bossard, P.; Zeitoun, F.; Wybier, M. Standardized way for imaging of the sagittal spinal balance. Eur. Spine J. 2011, 20, 602–608. [Google Scholar] [CrossRef] [PubMed]
- McKenna, C.; Wade, R.; Faria, R.; Yang, H.; Stirk, L.; Gummerson, N.; Sculpher, M.; Woolacott, N. EOS 2D/3D X-ray imaging system: A systematic review and economic evaluation. Health Technol. Assess. 2012, 16, 1–188. [Google Scholar] [CrossRef] [PubMed]
- De Smet, A.A.; Tarlton, M.A.; Cook, L.T.; Berridge, A.S.; Asher, M.A. The top view for analysis of scoliosis progression. Radiology 1983, 147, 369–372. [Google Scholar] [CrossRef] [PubMed]
- Sangole, A.P.; Aubin, C.E.; Labelle, H.; Stokes, I.A.; Lenke, L.G.; Jackson, R.; Newton, P. Three-dimensional classification of thoracic scoliotic curves. Spine 2009, 34, 91–99. [Google Scholar] [CrossRef] [PubMed]
- Labelle, H.; Aubin, C.E.; Jackson, R.; Lenke, L.; Newton, P.; Parent, S. Seeing the spine in 3D: How will it change what we do? J. Pediatr. Orthop. 2011, 31, S37–S45. [Google Scholar] [CrossRef] [PubMed]
- Donzelli, S.; Poma, S.; Balzarini, L.; Borboni, A.; Respizzi, S.; Villafane, J.H.; Zaina, F.; Negrini, S. State of the art of current 3-D scoliosis classifications: A systematic review from a clinical perspective. J. Neuroeng. Rehabil. 2015, 12, 1. [Google Scholar] [CrossRef] [PubMed]
- Poncet, P.; Dansereau, J.; Labelle, H. Geometric torsion in idiopathic scoliosis: Three-dimensional analysis and proposal for a new classification. Spine 2001, 26, 2235–2243. [Google Scholar] [CrossRef] [PubMed]
- Kohashi, Y.; Oga, M.; Sugioka, Y. A new method using top views of the spine to predict the progression of curves in idiopathic scoliosis during growth. Spine 1996, 21, 212–217. [Google Scholar] [CrossRef] [PubMed]
- Negrini, S.; Atanasio, S.; Fusco, C.; Zaina, F.; Negrini, A. 3-DEMO Classification of Scoliosis: A Useful Understanding of the 3rd Dimension of the Deformity. Stud. Health Technol. Inform. 2008, 135, 139. [Google Scholar] [PubMed]
| No. | Gender M/F | Age | Lenke Type | Primary Curve | Superior Curve | Inferior Curve | No. of Vertebrae Analyzes |
|---|---|---|---|---|---|---|---|
| 1 | F | 15 | 1C - | 79 | 60 | 55 | 18 |
| 2 | F | 14 | 1B N | 88 | 71 | 53 | 17 |
| 3 | F | 7 | 1A N | 77 | 36 | 44 | 16 |
| 4 | M | 9 | 1A - | 71 | 36 | 42 | 17 |
| 5 | F | 17 | 1B - | 88 | 42 | 54 | 17 |
| Average | - | 12.4 | - | 76.8 | 52.8 | 49.6 | 17 |
| Total | - | - | - | - | - | - | 85 |
| Intraobserver Reproducibility | Interobserver Reliability | |||||
|---|---|---|---|---|---|---|
| CT Coordinates | ICC | Mean Difference (mm) | Standard Error of Mean Difference for One Measurement | ICC | Mean Difference (mm) | Standard Error of Mean Difference for One Measurement |
| x | 0.9985 | 0.06 | 0.16 | 0.9815 | 0.32 | 0.58 |
| y | 0.9960 | 0.45 | 0.21 | 0.9960 | 0.54 | 0.2 |
| z | 0.9974 | 2.99 | 0.78 | 0.9975 | 2.87 | 0.77 |
| Intraobserver Reproducibility | Interobserver Reliability | |||||
|---|---|---|---|---|---|---|
| DRR Coordinates | ICC | Mean Difference (mm) | Standard Error of Mean Difference for One Measurement | ICC | Mean Difference (mm) | Standard Error of Mean Difference for One Measurement |
| x | 0.9970 | 0.19 | 1.02 | 0.9004 | 1.3 | 1.32 |
| y | 0.9960 | 0.31 | 0.21 | 0.9946 | 0.19 | 0.24 |
| z | 0.9963 | 0.22 | 0.13 | 0.9969 | 1.05 | 1.28 |
| Intraobserver Reproducibility | Interobserver Reliability | |||||
|---|---|---|---|---|---|---|
| DRR ‘z’ Coordinate | ICC | Mean Difference (mm) | Standard Error of Mean Difference for One Measurement | ICC | Mean Difference (mm) | Standard Error of Mean Difference for One Measurement |
| Z AP | 0.9959 | 0.22 | 0.13 | 0.9940 | 1.05 | 1.28 |
| Z LAT | 0.9967 | 5.41 | 1.66 | 0.9997 | 0.31 | 0.29 |
| Z AP vs LAT | 0.9963 | 4.36 | 1.02 | 0.9969 | 4.24 | 0.28 |
| Intraobserver Reproducibility | Interobserver Reliability | |||||
|---|---|---|---|---|---|---|
| CT / DRR Coordinates | ICC | Mean Difference (mm) | Standard Error of Mean Difference for One Measurement | ICC | Mean Difference (mm) | Standard Error of Mean Difference for One Measurement |
| x | 0.9911 | 1.02 | 0.19 | 0.9877 | 0.26 | 0.46 |
| y | 0.9973 | 0.15 | 0.13 | 0.9882 | 0.24 | 0.14 |
| z | 0.9998 | 0.09 | 0.26 | 0.9998 | 0.29 | 0.25 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Główka, P.; Gaweł, D.; Kasprzak, B.; Nowak, M.; Kotwicki, T. Improvement in Scoliosis Top View: Evaluation of Vertebrae Localization in Scoliotic Spine-Spine Axial Presentation. Symmetry 2016, 8, 125. https://doi.org/10.3390/sym8110125
Główka P, Gaweł D, Kasprzak B, Nowak M, Kotwicki T. Improvement in Scoliosis Top View: Evaluation of Vertebrae Localization in Scoliotic Spine-Spine Axial Presentation. Symmetry. 2016; 8(11):125. https://doi.org/10.3390/sym8110125
Chicago/Turabian StyleGłówka, Paweł, Dominik Gaweł, Bartosz Kasprzak, Michał Nowak, and Tomasz Kotwicki. 2016. "Improvement in Scoliosis Top View: Evaluation of Vertebrae Localization in Scoliotic Spine-Spine Axial Presentation" Symmetry 8, no. 11: 125. https://doi.org/10.3390/sym8110125
APA StyleGłówka, P., Gaweł, D., Kasprzak, B., Nowak, M., & Kotwicki, T. (2016). Improvement in Scoliosis Top View: Evaluation of Vertebrae Localization in Scoliotic Spine-Spine Axial Presentation. Symmetry, 8(11), 125. https://doi.org/10.3390/sym8110125





