Uncertain Quality Function Deployment Using a Hybrid Group Decision Making Model
Abstract
:1. Introduction
2. Literature Review
3. Preliminaries
3.1. Hesitant Fuzzy Linguistic Term Sets
3.2. Interval 2-Tuple Linguistic Model
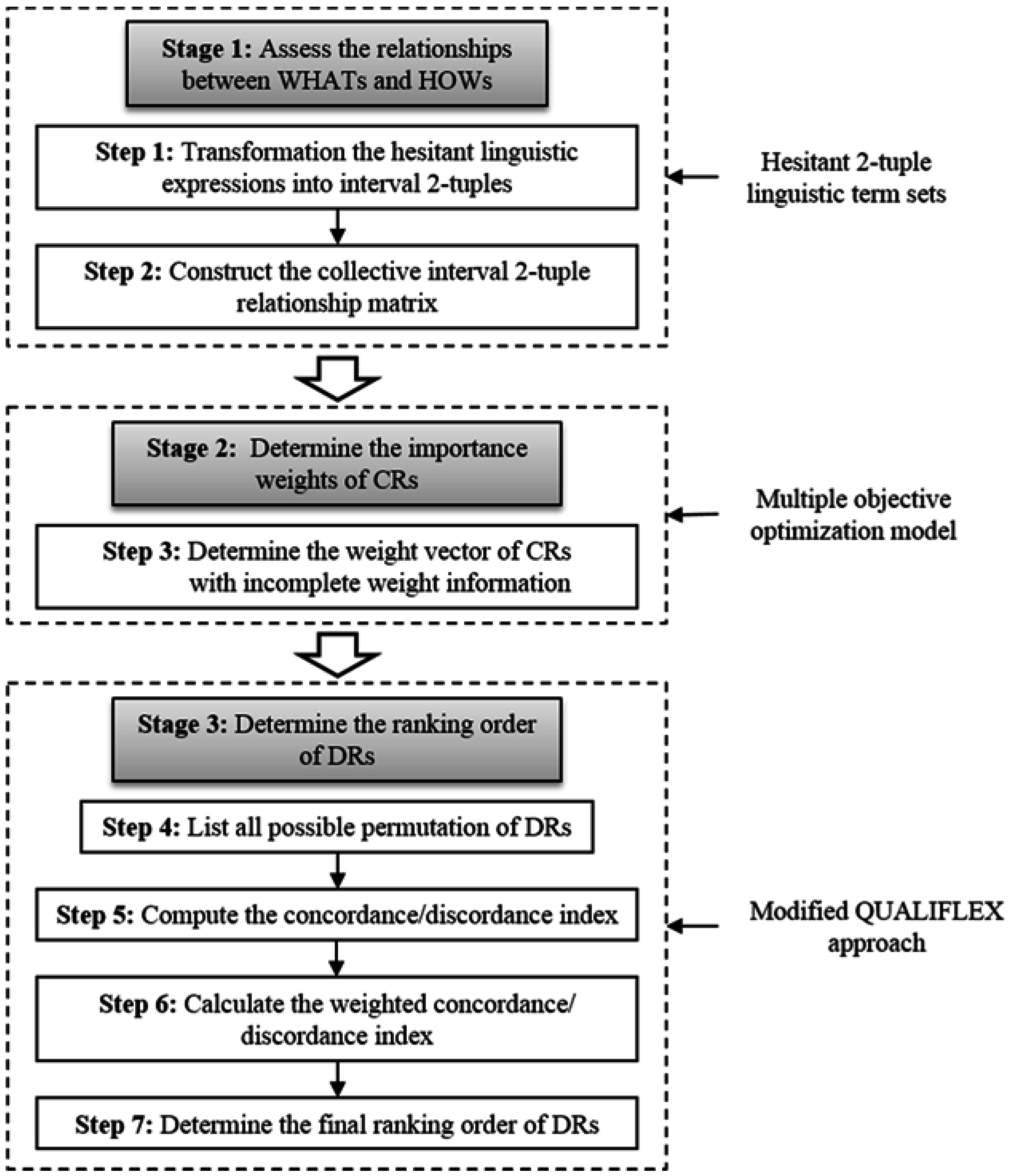
4. QFD Using Hesitant 2-Tuples and QUALIFLEX Method
4.1. Assess the Relationships between WHATs and HOWs
4.2. Determine the Importance Weights of CRs
- A weak ranking: ;
- A strict ranking: ;
- A ranking of differences: ;
- A ranking with multiples: ;
- An interval form: .
4.3. Determine the Ranking Order of DRs
5. Illustrative Example
5.1. Implementation
- P1 = (DR1, DR2, DR3, DR4), P2 = (DR1, DR2, DR4, DR3), P3 = (DR1, DR3, DR2, DR4),
- P4 = (DR1, DR3, DR4, DR2), P5 = (DR1, DR4, DR2, DR3), P6 = (DR1, DR4, DR3, DR2),
- P7 = (DR2, DR1, DR3, DR4), P8 = (DR2, DR1, DR4, DR3), P9 = (DR2, DR3, DR1, DR4),
- P10 = (DR2, DR3, DR4, DR1), P11 = (DR2, DR4, DR1, DR3), P12 = (DR2, DR4, DR3, DR1),
- P13 = (DR3, DR1, DR2, DR4), P14 = (DR3, DR1, DR4, DR2), P15 = (DR3, DR2, DR1, DR4),
- P16 = (DR3, DR2, DR4, DR1), P17 = (DR3, DR4, DR1, DR2), P18 = (DR3, DR4, DR2, DR1),
- P19 = (DR4, DR1, DR2, DR3), P20 = (DR4, DR1, DR3, DR2), P21 = (DR4, DR2, DR1, DR3),
- P22 = (DR4, DR2, DR3, DR1), P23 = (DR4, DR3, DR1, DR2), P24 = (DR4, DR3, DR2, DR1).
5.2. Comparisons and Discussions
- Different types of uncertainties in the implementation of QFD, such as imprecision, uncertainty and hesitation, can be well modeled via the hesitant 2-tuple linguistic term sets. The QFD team members can use more flexible and richer expressions to express their subjective judgments.
- By using the ITOWA operator, the proposed method can relieve the influence of unfair judgments concerning the relationships between CRs and DRs on the QFD analysis results, through assigning very low weights to those “false” or “biased” opinions.
- The proposed approach is able to deal with QFD problems in which the information about CR weights is incompletely known. Under the condition of incomplete weight information, a multiple objective programming model can be established to solve the optimal weights of CRs.
- The proposed methodology can get a more reasonable and credible ranking of DRs by using the modified QUALIFLEX approach, which makes the QFD analysis results certain and facilitates product planning decision-making.
- The proposed model is suitable to solve complicated QFD problems with comprehensive CRs and limited DRs, since the number of CRs has little effect upon the implementation efficiency of the proposed method.
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kwong, C.K.; Bai, H. Determining the importance weights for the customer requirements in QFD using a fuzzy AHP with an extent analysis approach. IIE Trans. 2003, 35, 619–626. [Google Scholar] [CrossRef]
- Akao, Y. Quality Function Deployment: Integrating Customer Requirements into Product Design; Productivity Press: Cambridge, MA, USA, 1990. [Google Scholar]
- Aye Ho, E.S.S.; Lai, Y.J.; Chang, S.I. An integrated group decision-making approach to quality function deployment. IIE Trans. 1999, 31, 553–567. [Google Scholar] [CrossRef]
- Chin, K.S.; Wang, Y.M.; Yang, J.B.; Poon, K.K.G. An evidential reasoning based approach for quality function deployment under uncertainty. Expert Syst. Appl. 2009, 36, 5684–5694. [Google Scholar] [CrossRef]
- Sivasamy, K.; Arumugam, C.; Devadasan, S.R.; Murugesh, R.; Thilak, V.M.M. Advanced models of quality function deployment: A literature review. Qual. Quant. 2016, 50, 1399–1414. [Google Scholar] [CrossRef]
- Kurtulmuşoğlu, F.B.; Pakdil, F.; Atalay, K.D. Quality improvement strategies of highway bus service based on a fuzzy quality function deployment approach. Transp. A Trans. Sci. 2016, 12, 175–202. [Google Scholar] [CrossRef]
- Onar, S.Ç.; Büyüközkan, G.; Öztayşi, B.; Kahraman, C. A new hesitant fuzzy QFD approach: An application to computer workstation selection. Appl. Soft Comput. 2016, 46, 1–16. [Google Scholar] [CrossRef]
- Chan, L.K.; Wu, M.L. A systematic approach to quality function deployment with a full illustrative example. Omega 2005, 33, 119–139. [Google Scholar] [CrossRef]
- Jia, W.; Liu, Z.; Lin, Z.; Qiu, C.; Tan, J. Quantification for the importance degree of engineering characteristics with a multi-level hierarchical structure in QFD. Int. J. Prod. Res. 2016, 54, 1627–1649. [Google Scholar] [CrossRef]
- Zhang, Z.; Chu, X. Fuzzy group decision-making for multi-format and multi-granularity linguistic judgments in quality function deployment. Expert Syst. Appl. 2009, 36, 9150–9158. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martínez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Labella, Á.; Martínez, L. An overview on fuzzy modelling of complex linguistic preferences in decision making. Int. J. Comput. Intell. Syst. 2016, 9 (Suppl. 1), 81–94. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.S.; Wang, H. Heterogeneous multiple criteria group decision making with incomplete weight information: A deviation modeling approach. Inf. Fusion 2015, 25, 49–62. [Google Scholar] [CrossRef]
- Montes, R.; Sanchez, A.M.; Villar, P.; Herrera, F. A web tool to support decision making in the housing market using hesitant fuzzy linguistic term sets. Appl. Soft Comput. 2015, 35, 949–957. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Hesitant fuzzy linguistic VIKOR method and its application in qualitative multiple criteria decision making. IEEE Trans. Fuzzy Syst. 2015, 23, 1343–1355. [Google Scholar] [CrossRef]
- Herrera, F.; Martínez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar]
- Zhang, H. The multiattribute group decision making method based on aggregation operators with interval-valued 2-tuple linguistic information. Math. Comput. Model. 2012, 56, 27–35. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wang, D.D.; Zhang, H.Y.; Chen, X.H. Multi-criteria group decision making method based on interval 2-tuple linguistic information and Choquet integral aggregation operators. Soft Comput. 2015, 19, 389–405. [Google Scholar] [CrossRef]
- Xue, Y.X.; You, J.X.; Zhao, X.; Liu, H.C. An integrated linguistic MCDM approach for robot evaluation and selection with incomplete weight information. Int. J. Prod. Res. 2016, 54, 5452–5467. [Google Scholar] [CrossRef]
- Martínez, L.; Herrera, F. An overview on the 2-tuple linguistic model for computing with words in decision making: Extensions, applications and challenges. Inf. Sci. 2012, 207, 1–18. [Google Scholar] [CrossRef]
- Song, W.; Ming, X.; Han, Y. Prioritising technical attributes in QFD under vague environment: A rough-grey relational analysis approach. Int. J. Prod. Res. 2014, 52, 5528–5545. [Google Scholar] [CrossRef]
- Paelinck, J.H.P. Qualiflex: A flexible multiple-criteria method. Econ. Lett. 1978, 1, 193–197. [Google Scholar] [CrossRef]
- Wang, J.C.; Tsao, C.Y.; Chen, T.Y. A likelihood-based QUALIFLEX method with interval type-2 fuzzy sets for multiple criteria decision analysis. Soft Comput. 2015, 19, 2225–2243. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Z.S. Hesitant fuzzy QUALIFLEX approach with a signed distance-based comparison method for multiple criteria decision analysis. Expert Syst. Appl. 2015, 42, 873–884. [Google Scholar] [CrossRef]
- Chen, T.Y.; Chang, C.H.; Rachel Lu, J.F. The extended QUALIFLEX method for multiple criteria decision analysis based on interval type-2 fuzzy sets and applications to medical decision making. Eur. J. Oper. Res. 2013, 226, 615–625. [Google Scholar] [CrossRef]
- Chen, T.Y. Interval-valued intuitionistic fuzzy QUALIFLEX method with a likelihood-based comparison approach for multiple criteria decision analysis. Inf. Sci. 2014, 261, 149–169. [Google Scholar] [CrossRef]
- Carnevalli, J.A.; Miguel, P.C. Review, analysis and classification of the literature on QFD—Types of research, difficulties and benefits. Int. J. Prod. Econ. 2008, 114, 737–754. [Google Scholar] [CrossRef]
- Chan, L.K.; Wu, M.L. Quality function deployment: A comprehensive review of its concepts and methods. Qual. Eng. 2002, 15, 23–35. [Google Scholar] [CrossRef]
- Armacost, R.L.; Componation, P.J.; Mullens, M.A.; Swart, W.W. An AHP framework for prioritizing customer requirements in QFD: An industrialized housing application. IIE Trans. 1994, 26, 72–79. [Google Scholar] [CrossRef]
- Lam, J.S.L.; Lai, K.H. Developing environmental sustainability by ANP-QFD approach: The case of shipping operations. J. Clean. Prod. 2015, 105, 275–284. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, J.; Chen, Y. Using fuzzy non-linear regression to identify the degree of compensation among customer requirements in QFD. Neurocomputing 2014, 142, 115–124. [Google Scholar] [CrossRef]
- Ji, P.; Jin, J.; Wang, T.; Chen, Y. Quantification and integration of Kano’s model into QFD for optimising product design. Int. J. Prod. Res. 2014, 52, 6335–6348. [Google Scholar] [CrossRef]
- Yan, H.B.; Ma, T. A group decision-making approach to uncertain quality function deployment based on fuzzy preference relation and fuzzy majority. Eur. J. Oper. Res. 2015, 241, 815–829. [Google Scholar] [CrossRef]
- Luo, X.G.; Kwong, C.K.; Tang, J.F.; Sun, F.Q. QFD-based product planning with consumer choice analysis. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 454–461. [Google Scholar] [CrossRef]
- Zhong, S.; Zhou, J.; Chen, Y. Determination of target values of engineering characteristics in QFD using a fuzzy chance-constrained modelling approach. Neurocomputing 2014, 142, 125–135. [Google Scholar] [CrossRef]
- Hosseini Motlagh, S.; Behzadian, M.; Ignatius, J.; Goh, M.; Sepehri, M.; Hua, T. Fuzzy PROMETHEE GDSS for technical requirements ranking in HOQ. Int. J. Adv. Manuf. Technol. 2015, 76, 1993–2002. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Rodríguez, R.; Martínez, L.; Torra, V.; Xu, Z.; Herrera, F. Hesitant fuzzy sets: State of the art and future directions. Int. J. Intell. Syst. 2014, 29, 495–524. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Bedregal, B.; Bustince, H.; Dong, Y.C.; Farhadinia, B.; Kahraman, C.; Martínez, L.; Torra, V.; Xu, Y.J.; Xu, Z.S.; et al. A position and perspective analysis of hesitant fuzzy sets on information fusion in decision making. Towards high quality progress. Inf. Fusion 2016, 29, 89–97. [Google Scholar] [CrossRef]
- Liu, H.; Rodríguez, R.M. A fuzzy envelope for hesitant fuzzy linguistic term set and its application to multicriteria decision making. Inf. Sci. 2014, 258, 220–238. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L. An analysis of symbolic linguistic computing models in decision making. Int. J. Gen. Syst. 2013, 42, 121–136. [Google Scholar] [CrossRef]
- Liu, H.C.; Lin, Q.L.; Wu, J. Dependent interval 2-tuple linguistic aggregation operators and their application to multiple attribute group decision making. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2014, 22, 717–735. [Google Scholar] [CrossRef]
- Liu, H.C.; You, J.X.; You, X.Y. Evaluating the risk of healthcare failure modes using interval 2-tuple hybrid weighted distance measure. Comput. Ind. Eng. 2014, 78, 249–258. [Google Scholar] [CrossRef]
- Wu, J.; Liang, C.; Huang, Y. An argument-dependent approach to determining OWA operator weights based on the rule of maximum entropy. Int. J. Intell. Syst. 2007, 22, 209–221. [Google Scholar] [CrossRef]
- Ureña, R.; Chiclana, F.; Morente-Molinera, J.A.; Herrera-Viedma, E. Managing incomplete preference relations in decision making: a review and future trends. Inf. Sci. 2015, 302, 14–32. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Z.; Yu, X. Group decision making based on incomplete intuitionistic multiplicative preference relations. Inf. Sci. 2015, 295, 33–52. [Google Scholar] [CrossRef]
- Xue, Y.X.; You, J.X.; Lai, X.D.; Liu, H.C. An interval-valued intuitionistic fuzzy MABAC approach for material selection with incomplete weight information. Appl. Soft Comput. 2016, 38, 703–713. [Google Scholar] [CrossRef]
- Qi, X.; Liang, C.; Zhang, J. Generalized cross-entropy based group decision making with unknown expert and attribute weights under interval-valued intuitionistic fuzzy environment. Comput. Ind. Eng. 2015, 79, 52–64. [Google Scholar] [CrossRef]
- Deng, J.L. Introduction to gray system theory. J. Grey Syst. 1989, 1, 1–24. [Google Scholar]
- Liu, H.C.; You, J.X.; Li, P.; Su, Q. Failure mode and effect analysis under uncertainty: An integrated multiple criteria decision making approach. IEEE Trans. Reliab. 2016, 65, 1380–1392. [Google Scholar] [CrossRef]
- Dat, L.Q.; Phuong, T.T.; Kao, H.P.; Chou, S.Y.; Nghia, P.V. A new integrated fuzzy QFD approach for market segments evaluation and selection. Appl. Math. Model. 2015, 39, 3653–3665. [Google Scholar] [CrossRef]
- Xu, Z.S. A method based on linguistic aggregation operators for group decision making with linguistic preference relations. Inf. Sci. 2004, 166, 19–30. [Google Scholar] [CrossRef]
- Estrella, F.J.; Espinilla, M.; Martínez, L. Fuzzy linguistic olive oil sensory evaluation model based on unbalanced linguistic scales. J. Mult. Valued Log. Soft Comput. 2014, 22, 1–21. [Google Scholar]
- Morente-Molinera, J.A.; Pérez, I.J.; Ureña, M.R.; Herrera-Viedma, E. On multi-granular fuzzy linguistic modeling in group decision making problems: A systematic review and future trends. Knowl. Based Syst. 2015, 74, 49–60. [Google Scholar] [CrossRef]
- Dong, Y.; Wu, Y.; Zhang, H.; Zhang, G. Multi-granular unbalanced linguistic distribution assessments with interval symbolic proportions. Knowl. Based Syst. 2015, 82, 139–151. [Google Scholar] [CrossRef]
| WHATs (CRs) | Team Members | HOWs (DRs) | |||
|---|---|---|---|---|---|
| DR1 | DR2 | DR3 | DR4 | ||
| CR1 | TM1 | Greater than MH | ML | Between L and M | M |
| TM2 | H | M | M | At least ML | |
| TM3 | Between H and VH | M | ML | M | |
| TM4 | H | MH | Less than M | M | |
| TM5 | H | At most MH | M | Between ML and MH | |
| CR2 | TM1 | At least H | Greater than MH | Between MH and VH | H |
| TM2 | VH | H | H | Greater than H | |
| TM3 | Greater than H | VH | VH | Between MH and VH | |
| TM4 | H | At least H | Greater than MH | H | |
| TM5 | Between MH and VH | H | H | At least H | |
| CR3 | TM1 | Greater than M | H | At least H | Between MH and VH |
| TM2 | MH | Between MH and VH | VH | H | |
| TM3 | H | H | Greater than H | H | |
| TM4 | At least H | VH | VH | At most H | |
| TM5 | VH | Greater than MH | VH | VH | |
| CR4 | TM1 | Less than H | M | Greater than MH | MH |
| TM2 | H | Between ML and MH | H | H | |
| TM3 | MH | M | H | Less than H | |
| TM4 | M | At most MH | MH | At most MH | |
| TM5 | At most H | Less than MH | Between MH and VH | M | |
| CR5 | TM1 | Between MH and VH | MH | At most H | Between L and ML |
| TM2 | H | H | MH | ML | |
| TM3 | H | Less than H | H | L | |
| TM4 | At least MH | M | M | At most M | |
| TM5 | H | MH | Between MH and VH | ML | |
| WHATs | HOWs | |||
|---|---|---|---|---|
| DR1 | DR2 | DR3 | DR4 | |
| CR1 | [(s5, 0), (s6, 0)] | [(s2, 0), (s2, 0)] | [(s1, 0), (s3, 0)] | [(s3, 0), (s3, 0)] |
| CR2 | [(s5, 0), (s6, 0)] | [(s5, 0), (s6, 0)] | [(s4, 0), (s6, 0)] | [(s5, 0), (s5, 0)] |
| CR3 | [(s4, 0), (s6, 0)] | [(s5, 0), (s5, 0)] | [(s5, 0), (s6, 0)] | [(s4, 0), (s6, 0)] |
| CR4 | [(s0, 0), (s4, 0)] | [(s3, 0), (s3, 0)] | [(s5, 0), (s6, 0)] | [(s4, 0), (s4, 0)] |
| CR5 | [(s4, 0), (s6, 0)] | [(s4, 0), (s4, 0)] | [(s0, 0), (s5, 0)] | [(s1, 0), (s2, 0)] |
| WHATs | HOWs | |||
|---|---|---|---|---|
| DR1 | DR2 | DR3 | DR4 | |
| CR1 | ∆[0.833, 0.884] | ∆[0.884, 0.448] | ∆[0.448, 0.543] | ∆[0.543, 0.322] |
| CR2 | ∆[0.876, 0.994] | ∆[0.994, 0.839] | ∆[0.839, 0.949] | ∆[0.949, 0.833] |
| CR3 | ∆[0.791, 0.935] | ∆[0.935, 0.833] | ∆[0.833, 0.949] | ∆[0.949, 0.994] |
| CR4 | ∆[0.426, 0.709] | ∆[0.709, 0.29] | ∆[0.290, 0.551] | ∆[0.551, 0.782] |
| CR5 | ∆[0.782, 0.884] | ∆[0.884, 0.614] | ∆[0.614, 0.667] | ∆[0.667, 0.614] |
| P1 | CR1 | CR2 | CR3 | CR4 | CR5 |
|---|---|---|---|---|---|
| 0.131 | 0.059 | −0.030 | 0.069 | 0.147 | |
| 0.250 | 0.063 | −0.165 | −0.141 | 0.103 | |
| 0.119 | 0.063 | 0.034 | 0.008 | 0.250 | |
| 0.119 | 0.004 | −0.135 | −0.210 | −0.044 | |
| −0.012 | 0.004 | 0.065 | −0.061 | 0.103 | |
| −0.130 | 0.000 | 0.200 | 0.149 | 0.147 |
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | P11 | P12 |
| 0.0708 | 0.0708 | 0.0250 | 0.0250 | 0.0908 | 0.0908 | −0.0708 | −0.0708 | −0.0458 | −0.0458 | 0.0200 | 0.0200 |
| 0.0250 | 0.0908 | 0.0708 | 0.0908 | 0.0708 | 0.0250 | −0.0458 | 0.0200 | −0.0708 | 0.0200 | −0.0708 | −0.0458 |
| 0.0908 | 0.0250 | 0.0908 | 0.0708 | 0.0250 | 0.0708 | 0.0200 | −0.0458 | 0.0200 | −0.0708 | −0.0458 | −0.0708 |
| −0.0458 | 0.0200 | 0.0458 | 0.0659 | −0.0200 | −0.0659 | 0.0250 | 0.0908 | −0.0250 | 0.0659 | −0.0908 | −0.0659 |
| 0.0200 | −0.0458 | 0.0659 | 0.0458 | −0.0659 | −0.0200 | 0.0908 | 0.0250 | 0.0659 | −0.0250 | −0.0659 | −0.0908 |
| 0.0659 | −0.0659 | 0.0200 | −0.0200 | −0.0458 | 0.0458 | 0.0659 | −0.0659 | 0.0908 | −0.0908 | 0.0250 | −0.0250 |
| 0.0708 | 0.0708 | 0.0250 | 0.0250 | 0.0908 | 0.0908 | −0.0708 | −0.0708 | −0.0458 | −0.0458 | 0.0200 | 0.0200 |
| 0.0250 | 0.0908 | 0.0708 | 0.0908 | 0.0708 | 0.0250 | −0.0458 | 0.0200 | −0.0708 | 0.0200 | −0.0708 | −0.0458 |
| P13 | P14 | P15 | P16 | P17 | P18 | P19 | P20 | P21 | P22 | P23 | P24 |
| −0.0250 | −0.0250 | 0.0458 | 0.0458 | 0.0659 | 0.0659 | −0.0908 | −0.0908 | −0.0200 | −0.0200 | −0.0659 | −0.0659 |
| 0.0458 | 0.0659 | −0.0250 | 0.0659 | −0.0250 | 0.0458 | −0.0200 | −0.0659 | −0.0908 | −0.0659 | −0.0908 | −0.0200 |
| 0.0659 | 0.0458 | 0.0659 | −0.0250 | 0.0458 | −0.0250 | −0.0659 | −0.0200 | −0.0659 | −0.0908 | −0.0200 | −0.0908 |
| 0.0708 | 0.0908 | −0.0708 | 0.0200 | −0.0908 | −0.0200 | 0.0708 | 0.0250 | −0.0708 | −0.0458 | −0.0250 | 0.0458 |
| 0.0908 | 0.0708 | 0.0200 | −0.0708 | −0.0200 | −0.0908 | 0.0250 | 0.0708 | −0.0458 | −0.0708 | 0.0458 | −0.0250 |
| 0.0200 | −0.0200 | 0.0908 | −0.0908 | 0.0708 | −0.0708 | −0.0458 | 0.0458 | 0.0250 | −0.0250 | 0.0708 | −0.0708 |
| −0.0250 | −0.0250 | 0.0458 | 0.0458 | 0.0659 | 0.0659 | −0.0908 | −0.0908 | −0.0200 | −0.0200 | −0.0659 | −0.0659 |
| 0.0458 | 0.0659 | −0.0250 | 0.0659 | −0.0250 | 0.0458 | −0.0200 | −0.0659 | −0.0908 | −0.0659 | −0.0908 | −0.0200 |
| HOWs | QFD | Fuzzy QFD | Linguistic QFD | Proposed Approach | |||
|---|---|---|---|---|---|---|---|
| Wj | Ranking | Ranking | Ranking | ||||
| DR1 | 7.221 | 1 | (0.267, 0.475, 0.724) | 1 | s5.06 | 1 | 1 |
| DR2 | 6.303 | 3 | (0.231, 0.415, 0.659) | 3 | s4.32 | 3 | 3 |
| DR3 | 7.035 | 2 | (0.253, 0.448, 0.689) | 2 | s4.60 | 2 | 2 |
| DR4 | 5.919 | 4 | (0.217, 0.400, 0.641) | 4 | s4.05 | 4 | 4 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.-L.; You, J.-X.; Liu, H.-C. Uncertain Quality Function Deployment Using a Hybrid Group Decision Making Model. Symmetry 2016, 8, 119. https://doi.org/10.3390/sym8110119
Wang Z-L, You J-X, Liu H-C. Uncertain Quality Function Deployment Using a Hybrid Group Decision Making Model. Symmetry. 2016; 8(11):119. https://doi.org/10.3390/sym8110119
Chicago/Turabian StyleWang, Ze-Ling, Jian-Xin You, and Hu-Chen Liu. 2016. "Uncertain Quality Function Deployment Using a Hybrid Group Decision Making Model" Symmetry 8, no. 11: 119. https://doi.org/10.3390/sym8110119
APA StyleWang, Z.-L., You, J.-X., & Liu, H.-C. (2016). Uncertain Quality Function Deployment Using a Hybrid Group Decision Making Model. Symmetry, 8(11), 119. https://doi.org/10.3390/sym8110119






