A POCS Algorithm Based on Text Features for the Reconstruction of Document Images at Super-Resolution

Abstract

In order to address the problem of the uncertainty of existing noise models and of the complexity and changeability of the edges and textures of low-resolution document images, this paper presents a projection onto convex sets (POCS) algorithm based on text features. The current method preserves the edge details and smooths the noise in text images by adding text features as constraints to original POCS algorithms and converting the fixed threshold to an adaptive one. In this paper, the optimized scale invariant feature transform (SIFT) algorithm was used for the registration of continuous frames, and finally the image was reconstructed under the improved POCS theoretical framework. Experimental results showed that the algorithm can significantly smooth the noise and eliminate noise caused by the shadows of the lines. The lines of the reconstructed text are smoother and the stroke contours of the reconstructed text are clearer, and this largely eliminates the text edge vibration to enhance the resolution of the document image text.

1. Introduction

In the early 1980s, Tsai and Huang were the first to use the Fourier-transform method for satellite image reconstruction [1]. Since then, super-resolution image reconstruction has been a hot topic in the field of image processing.

Recently, the use of super-resolution techniques has also drawn many researchers’ attention. Domestic and foreign scholars have performed a great deal of research on image super-resolution reconstruction. For instance, Chen et al. used the iterative gradient algorithm combined with the bilateral total variation algorithm to estimate motion for the subpixel level of target images based on the Taylor expansion, and they achieved good results [2]. Kato et al. estimated the relative displacement of the observed image using subpixel block matching and reconstructed super-resolution images based on sparse representation [3]. Panda et al. used the iterative adaptive regularization method and genetic algorithm for image super-resolution [4]. However, these algorithms are not specific to document images, they do not take the characteristics of the document image into account, and the performance of the application on document images is poor. Scholars have also put forward some super-resolution algorithms for document images. For example, Fan et al. found that regions with highly similar characters can self-register and reconstruct themselves using local consistency [5]. Kumar et al., on the basis of sparse representation, pointed out that, although the shapes of the characters were not consistent, their edges and stroke curves were similar [6]. Finally, they found the ideal high-resolution (HR) image block by training the dictionary. Abed et al. proposed a total variation regularization method based on the directions of the text strokes, and it has achieved good results [7]. However, the algorithms mentioned above have several disadvantages. They are highly complex, require a single noise model, and cannot fully reconstruct the text edge information. For document images, the high-frequency details of the edges of the image are very important, and restoring the edge details is a preferred factor in document image reconstruction. The projection onto convex sets (POCS) algorithm is very inclusive of prior information, and it can restore the details of the text boundaries to a considerable extent, but it requires a large amount of computation and the solution is not unique. Consequently, a POCS algorithm is here proposed for super-resolution of text document images based on text features—which improves the original POCS algorithm over the degraded model and threshold—and optimizes the scale invariant feature transform (SIFT) algorithm at the registration stage to enhance the effect of document image reconstruction and ensure its efficiency.

2. Methodology

2.1. Classical Image Super-Resolution Reconstruction Algorithm

2.1.1. Establishment of Degraded Model

The HR image degradation process usually serves as the observation model, and the relationship between HR and low-resolution (LR) is established through the reduced quality model. Finally, the HR equation is generated. The image degradation model is as follows:

$$g_k=D_k{B}_k{W}_{k}f+n_k,k=1,2,3\dots L$$

(1)

Among these, $D_k$ is the geometric distortion matrix, $B_k$ is the fuzzy matrix, $W_k$ is the down-sampling matrix, $k$ is the number of sequence image frames, and the range is from 1 to L. $f$ and $g_k$ refer to the collected HR original image and LR observation sequence after reducing mass. $n_k$ is the additive Gauss noise.

Let $H_k=D_k{B}_k{W}_k$; Formula (1) can be written as follows:

$$g_k=H_{k}f+n_k$$

(2)

As shown in Formula (2), the image reconstruction process involves estimating the process of reverse $f$ by regression model. In this paper, the process is divided into two steps: image registration and then super-resolution reconstruction using POCS algorithm.

2.1.2. Image Registration Based on SIFT Algorithm

Image registration involves estimating the location of each pixel using the tiny differences in information between different image sequences, thus providing the registration parameters.

The document image is distinguished from the words and the background, and the texture features, which must be extracted during the feature extraction stage, are very visible. However, image rotation, translation, and scaling deformation can affect text considerably, especially small text. It is therefore necessary to find an algorithm suitable for image deformation in the registration. The SIFT algorithm proposed by Lowe in 1999 can reduce the influence of deformation in the registration of the document image and extract more accurate features [8]. Accordingly, this paper uses the SIFT algorithm for image registration.

Steps in the implementation of the SIFT algorithm:

• Construct a scale space
• Detect extreme points in the scale space
• Locate the extreme points accurately
• Determine the main direction of key points
• Find the descriptors of key points

Step 5 involves taking the key-point-centered 16 × 16 pixel neighborhood and then dividing it into 4 × 4 image sub-blocks. Each pixel defines vector information in 8 directions. Then we generate 4 × 4 × 8 = 128-dimensional feature vectors. After generating the SIFT feature vectors of two images, the Euclidean distance of the feature vectors of key points is used to assess the similarity of the key points in the two images.

2.1.3. Image Reconstruction Based on the POCS Algorithm

As shown above, the image degradation model can be expressed as follows:

$$g_k=H_{k}f+n_k$$

(3)

Let $(m_1,m_2)$ be the arbitrary point of LR image, and the corresponding point in HR image is $(n_1,n_2)$. $g(m_1,m_2,l)$ is a pixel of the LR image of coordinates m₁, m₂, and frame l. $f(n_1,n_2)$ is a pixel of the HR image. $n(m_1,m_2,l)$ is the noise carried by the frame $l$ of LR image, which is generally considered additive noise. The corresponding point of $(m_1,m_2)$ in reference frame is $(m_1^{\prime },m_2^{\prime })$. $H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)$ is the point spread function of the observation image at point $(m_1^{\prime },m_2^{\prime })$. Formula (3) can be expressed as follows:

$$g(m_1,m_2,l)={\displaystyle \sum _{n_1,n_2}H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)f(n_1,n_2)+n(m_1,m_2,l)}$$

(4)

According to the data consistency constraint requirements, HR images and any LR image should maintain the same pixel value at the corresponding points under ideal conditions. That is, each observed LR image sequence $g(m_1,m_2,l)$ can be represented by a convex set C [9], such as Formula (5):

$${\mathrm{C}}_{(m_1,m_2,l)}=\left\{f(n_1,n_2,k):|r^{(f)}(m_1,m_2,l)|\le {\delta }_0(m_1,m_2,l)\right\}$$

(5)

Among (5), ${\mathrm{C}}_{(m_1,m_2,l)}$ is the collection of pixels in the LR image, $f(n_1,n_2,k)$ is the current frame HR image estimate, ${\delta }_0(m_1,m_2,l)$ is the threshold, which is determined by noise standard deviation and credibility boundary. $r^{(f)}(m_1,m_2,l)$ is the residual of any point in a convex set.

$$r^{(f)}(m_1,m_2,l)=g(m_1,m_2,l)-{\displaystyle \sum _{n_1,n_2}f(n_1,n_2,k)}\cdot H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)$$

(6)

Among (6), k is the frame number of the HR image. The operator that the pixel $f(n_1,n_2,k)$ mapped to convex set, with $P_{m_1,m_2,l}\left[f(n_1,n_2,k)\right]$.

The basic idea of POCS is to iterate the initial estimation ${\stackrel{\wedge }{f}}^{(0)}(n_1,n_2,k)$ of high-resolution images with POCS operator P and finally produce the high-resolution image [10]. Interpolation is usually used to perform the initial estimation ${\stackrel{\wedge }{f}}^{(0)}(n_1,n_2,k)$ of high-resolution images, and the constraint set of observation sequences is used to correct the ${\stackrel{\wedge }{f}}^{(0)}(n_1,n_2,k)$, until the iteration conditions are met. Assuming that there are t iterations, the basic expression used to reconstruct the high-resolution image $f$ with the POCS algorithm is as follows:

$${\stackrel{\wedge }{f}}^{(t+1)}(n_1,n_2,k)=P_m{P}_{m-1}\cdots P_1{\stackrel{\wedge }{f}}^{(t)}(n_1,n_2,k)$$

(7)

2.2. A POCS Algorithm Based on Text Feature

2.2.1. Features of Document Images

Common document images are based on black and white images. Black represents text and white is background. The gray curve of image is distinguished from text and background and its envelope is a bimodal curve. The bimodal characteristics of document image are shown in Figure 1.

As shown above, the abscissa represents gray value, the ordinate represents the number of corresponding pixels, and ${\mu }_0$ and ${\mu }_1$ represent the positions of the two peaks of the curve. In the ideal gray image, there should be only two gray values, ${\mu }_0$ and ${\mu }_1$. If ${\mu }_0=0$, this indicates that the pixel value of black text area is 0; ${\mu }_1=255$ means that the pixel value of the white area is 255. However, the image no longer shows the two value image in the actual document because of the noise. This should be done to reduce the number of pixels between ${\mu }_0$ and ${\mu }_1$ infinitely close to zero because they may include noise pixels that can blur the image. Bimodal envelope of document image can be expressed as follows:

$$V_{el}(H^{\prime })={(H^{\prime }-{\mu }_0)}^2\cdot {(H^{\prime }-{\mu }_1)}^2$$

(8)

Among (8), $V_{el}(H^{\prime })$ is the number of corresponding pixels and $H^{\prime }$ is the gray value. The closer the number of pixels near the bimodal comes to ${\mu }_0$ or ${\mu }_1$, the closer the envelope comes to the ideal situation, and the better the quality of the document image.

2.2.2. Text Features Based on the POCS Algorithm

This section describes the optimization of the traditional POCS algorithm from the following two aspects.

In POCS steps, building the convex set of low-resolution images is a key step in the introduction of high-frequency information. For document images, because its details are mostly words, the edges are more difficult to discern. The original algorithm is not ideal, especially not for some of the grayer document images. As a consequence, features of the document image were added to the original POCS algorithm in this paper as a priori constraint. These features were then used to repeatedly correct estimation until the results converged.

The original algorithm installs the initial threshold on the basis of noise $n(m_1,m_2,l)$ characteristics in the degradation model. However, in real life, it is difficult to determine the noise characteristics, so a fixed threshold can cause the algorithm to lack flexibility.

In this paper, the fixed threshold was changed to an adaptive threshold, which improved the inclusivity of the algorithm and the quality of the reconstructed image.

• Formula (8) is added to the constraint conditions as an a priori function. The initial estimation is repeatedly revised based on it until the results meet the reconstruction conditions.
• In the original POCS algorithm, the image reduction formula is as follows:

  $$g(m_1,m_2,l)={\displaystyle \sum _{n_1,n_2}\stackrel{\wedge }{H}(n_1,n_2;m_1^{\prime },m_2^{\prime },l)f(n_1,n_2)+n(m_1,m_2,l)}$$

  (9)

There are uncertainty factors in the estimation of the point spread function (PSF) $H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)$ of the image that collected in reality at point $(m_1^{\prime },m_2^{\prime })$. In this paper, the error was taken into account. Set $H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)$ was considered an accurate estimation, $\Delta H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)$ was considered an error estimation, so the actual estimation $\stackrel{\wedge }{H}(n_1,n_2;m_1^{\prime },m_2^{\prime },l)$ was as follows:

$$\stackrel{\wedge }{H}(n_1,n_2;m_1^{\prime },m_2^{\prime },l)=H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)+\Delta H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)$$

(10)

Formula (9) can be written as follows:

$$\begin{array}{cc}\hfill g(m_1,m_2,l)& ={\displaystyle \sum _{n_1,n_2}f(n_1,n_2)\stackrel{\wedge }{H}(n_1,n_2;m_1^{\prime },m_2^{\prime },l)+n(m_1,m_2,l)}\hfill \\ & ={\displaystyle \sum _{n_1,n_2}f(n_1,n_2)[(H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)+\Delta H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)]+n(m_1,m_2,l)}\hfill \\ & ={\displaystyle \sum _{n_1,n_2}f(n_1,n_2)(H+\Delta H)(n_1,n_2;m_1^{\prime },m_2^{\prime },l)+n(m_1,m_2,l)}\hfill \end{array}$$

(11)

This can be deformed into the following:

$$\begin{array}{l}g(m_1,m_2,l)-{\displaystyle \sum _{n_1,n_2}f(n_1,n_2)H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)}\\ ={\displaystyle \sum _{n_1,n_2}f(n_1,n_2)}\Delta H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)+n(m_1,m_2,l)\end{array}$$

(12)

The left side of the formula is the residual $r^{(f)}(m_1,m_2,l)$. At this time, the residual value is determined using the original noise $n(m_1,m_2,l)$ and the added uncertainty factors $f(n_1,n_2)\Delta H(n_1,n_2;m_1^{\prime },m_2^{\prime },l)$. The threshold value is then determined using the mixed noise, which contains added error factors.

After introducing the mixed noise, the new residual was calculated automatically while correcting the projection. Then, the standard variance is counted as the modified threshold. The threshold does not need to be set in advance at the start of the algorithm. It can be given automatically based on the new residual during revision of the LR image.

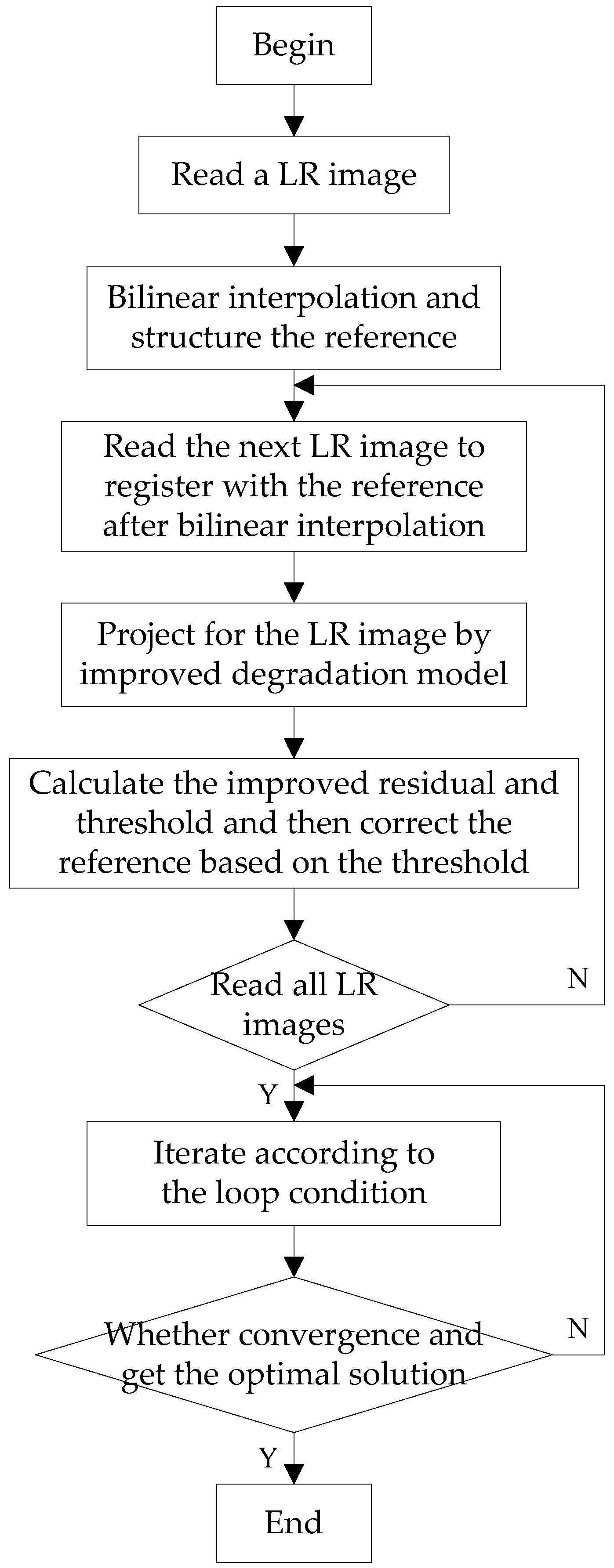
2.2.3. Algorithm Implementation

When reconstructing the super-resolution (SR) image in this paper, an LR image of the observed sequences must first be set as a reference frame and interpolated, and a motion estimation must be made between the LR image and the reference frame to produce the image offset. Then, a low-resolution image is projected using the improved degradation model, and the modified residual and the modified threshold value are then calculated. The reference frame is then corrected based on the threshold. Finally, the current high-resolution estimation was iteratively modified according to the prior constraint condition of the document image until the acceptable reconstruction results were achieved. The specific flow chart is shown in Figure 2:

As shown in Figure 2, we can see that the implementation of the POCS algorithm can be divided into five steps:

• Read an LR image and make a bilinear interpolation of it. The interpolation multiplier is a multiple of the desired improved resolution, then this interpolated image was selected as a reference frame. Let the initial estimate be $f_0$ and the threshold value be ${\delta }_0$.
• Read the remaining LR frames to register with the reference frame after bilinear interpolation, and estimate the motion between each frame and the reference frame to produce the registration mapping parameters.
• Define the convex set C of the sequences and calculate the residual r values to correct the reference frame.
• According to the data consistency constraint, the operator P was calculated, and the relationship between r and ${\delta }_0$ was assessed to correct $f$.
• The cycle end condition was set to $\frac{\Vert f^{(t+1)}-f^{(t)}\Vert }{f^{(t)}}\le \epsilon$. If the conditions are met, then $\stackrel{\wedge }{f^{(t)}}=f^{(t)}$, and the loop ends. Otherwise, let $t=t+1$, and return to the step 3 until $f^{(t+1)}$ meets the convergence conditions. Then $\stackrel{\wedge }{f^{(t)}}$ is the eligible solution of the algorithm.

3. Analysis of Experimental Results

In this paper, under the support of a 64 bit Windows 8 operating system and a 2nd generation Intel Core i5-3210M processor, 2.50 GHz CPU, 4 GB RAM, 500 GB HDD, MATLAB R2013b software is used to perform the experiment. In the experiment, there are three sets of LR sequences, one generated by simulation and the others taken with a camera. The reconstruction of image sequences is evaluated using the peak signal to noise ratio (PSNR), the real images using the mean opinion score (MOS), the execution times, and the memory occupations.

3.1. Registration with the Optimized SIFT Operator

Here, text features were added to the document image during the preprocessing stage of registration to improve the matching accuracy, and the feature descriptors were reduced to the fifth step of the original algorithm SIFT, reducing the dimensions from 128 to 48 to improve the matching speed. The results of registration and analysis are as follows.

Figure 3 is the reference image. Figure 4 is the image to be registered. Figure 5 shows the matching results of the original SIFT algorithm, and Figure 6 is the result of the improved SIFT algorithm.

The results in

Table 1. Analysis of the results.

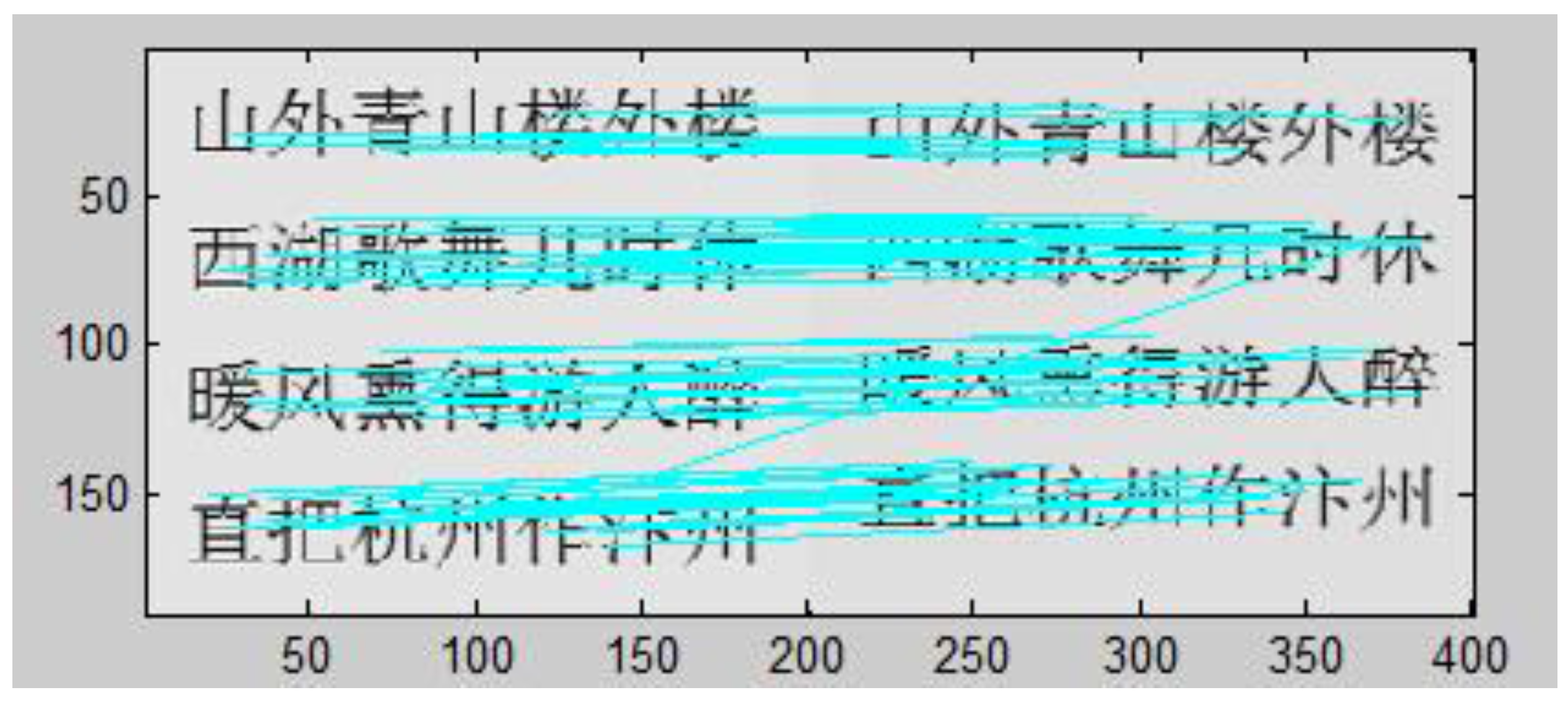
Algorithm Types	Characteristic Points		Matching Points	Matching Points	Time Spent on Matching (s)	The Correct Matching Rate (%)
	n1	n2
Original algorithm	220	227	184	7	1.795	96
Improved algorithm	220	227	180	1	1.763	99

show that there were fewer matched and mismatched points associated with the improved algorithm, which indicates that the algorithm can quickly produce the best registration parameters with high precision. At the same time, the memory space is released due to the reductions in dimensions.

3.2. Reconstructed Results and Analysis

3.2.1. The Reconstructed Result of an LR Image Which Is Generated by Simulation

The original HR image is an image of calligraphy copybook 490 × 391 in size, shown in Figure 7a. The LR image sequences are obtained by down-sampling, panning, blurring, and adding noise to the original HR image, shown in Figure 7b. In these images, down-sampling was performed with a rank sampling of 1/2, and the length of the panning involved selecting parameters randomly between [0, 1]. The size of the blur function window was 3 × 3, and the type of noise added was Gauss noise, of which the standard deviation was 1.

The reconstruction of the original POCS is shown in Figure 7d, and the edges of the words appear ghost in Figure 7d. We compared the performance of the proposed algorithm with the approach in [11], the method in [12], and the improved POCS in this paper. The results are presented in Figure 7e–g, respectively. By comparison, the original POCS algorithm adds high-frequency image details and at the same time introduces a lot of noise. The text edges of the reconstructed document image can gain fuzzy ghosts caused by this noise due to the fixed threshold, which is set by the original algorithm to mix in more noise, so the image quality is affected. There are also some noticeable ringing artifacts in the reconstruction image showed in Figure 7e. The result in Figure 7f shows that the approach in [12] can retain lots of details, but the reconstruction was still unsatisfactory. It can be seen from the Figure 7g that the overall sharpness of the image has been recovered and a significant amount of details has also been restored. Comparison reveals that our approach is superior, as it is able to recover more visual clarity from the LR images, particularly near the textual region.

3.2.2. Reconstruction of Ancient Books and Ancient Inscriptions Taken by Camera

First, the experiment uses a set of LR image sequences of ancient books, four document images with low quality where the words on the images are difficult to identify; the size of the images is 476 × 356, as shown in Figure 8a. Each image shown in Figure 8a was produced using bilinear interpolation, and an interpolated image was selected to register with other LR images one-by-one to produce the reference frame using the improved SIFT algorithm, as shown in Figure 8b. The result of the reconstruction using the original POCS is shown in Figure 8c. As shown in Figure 8c, the area surrounding the document text in the reconstructed image has an obvious procrastination phenomenon, which can be attributed to the incorporation of noise into the reconstruction process. Next, the methods in [11,12] were performed to obtain HR images. It is observed that the obtained results were unsatisfactory as shown in the Figure 8d,e. The reconstructed HR image using the improved POCS method is given in Figure 8f. The Figure 8f demonstrates that the improved POCS algorithm can rebuild the text clearly and the results are visibly improved. This is because our proposed method utilizes the improved SIFT, hence resulting in better registration. The effectiveness of the registration in turn leads to the satisfactory image quality.

A set of LR image sequences of three ancient inscriptions was used here. The images are 449 × 729 in size, as shown in Figure 9a. Because the words were inscribed many years ago, many are illegible in these inscriptions and the defect of the image quality is obvious. Figure 9b shows the reference image. As shown in Figure 9c, the reconstructed image of the inscription as processed using the original algorithm has apparent noise and a ringing effect in edge of the text. The result of implementing the method described in [11] is shown in Figure 9d. The super-resolution method which is proposed in [12] resulted in Figure 9e. Figure 9f shows the implementation of the improved method described in this paper. Comparing Figure 9f to Figure 9c–e, we notice not only has our method removed the outliers more efficiently than other methods, but it has also resulted in sharper edges without any ringing effects.

3.2.3. Reconstruction Quality Evaluation

In the experiment, there were three sets of low-resolution sequences, the first group was generated by simulation and the others were taken with a camera. To ensure fairness in comparison, the simulation environments are given as follows: Windows 8, MATLAB R2013b, 2.50 GHz CPU, and 4 GB RAM. We used the peak signal to noise ratio (PSNR) and the mean opinion score (MOS) to compare the performance of image sequences of each of these methods. The value of MOS ranges from [0, 5], in which larger value of MOS indicates better image quality and smaller ones indicate poorer quality. The various visual feelings generated by 10 observers for the same image are referenced here. Then a reasonable evaluation score was determined using to the clarity of the image and whether there is any blurring or noise. The MOS value, which is the final result of the assessment, was then calculated. Also, we provide an analysis on the computational complexity of the methods using the execution times and the memory occupations.

(a) Evaluation of the first group

As shown in

Table 2. Quantitative comparison of the performance of the copybook experiments.

Algorithm Types	PSNR/dB	MOS	The Execution Time/s	The Memory Occupation/KB
Original POCS	23.29	3.302	7.319	2464.00
the method in [11]	23.57	3.534	7.434	2934.00
the method in [12]	24.31	3.708	7.327	2585.00
Improved POCS	24.68	4.149	7.323	2324.00

, the PSNR and MOS values of the improved POCS are higher than the previous three algorithms, which show the reconstruction of this improved algorithm to be more similar to the original HR image. The evaluation results show that the improved approach gains a better performance both on reconstruction quality and computational time.

(b) Evaluation of the second group

In order to illustrate the experimental performance of the ancient books using the improved POCS approach,

Table 3. Quantitative comparison of the performance of the ancient books experiments.

Algorithm Types	PSNR/dB	MOS	The Execution Time/s	The Memory Occupation/KB
Original POCS	36.97	3.452	10.371	3173.00
the method in [11]	37.34	3.598	11.453	3528.00
the method in [12]	38.16	3.974	11.185	3259.00
Improved POCS	38.23	4.079	10.548	3194.00

shows the quantitative comparison of the four methods. It is clear that the resulting image (Figure 8f) has a better quality than other reconstruction methods.

Table 4. Quantitative comparison of the performance of the ancient inscriptions experiments.

Algorithm Types	PSNR/dB	MOS	The Execution Time/s	The Memory Occupation/KB
Original POCS	37.98	3.548	11.079	3279.00
the method in [11]	38.03	3.746	11.855	3371.00
the method in [12]	38.74	4.032	11.273	3284.00
Improved POCS	38.82	4.214	11.143	3281.00

shows that the improved POCS method has highest values of PSNR and MOS. The execution time and memory occupation are a little higher than other algorithms, but this is acceptable with respect to its image quality. This means that the algorithm in this paper reduces noise more effectively than other algorithms, and the edges of the reconstructed image are much smoother. These objective performance measures illustrate the improved POCS method has the best visual quality and further reconfirm our subjective evaluation of the reconstructed image.

4. Conclusions

An improved super-resolution algorithm for document images based on the optimization of the classical SIFT algorithm and traditional POCS algorithm is proposed in this paper. By enhancing the contrast and reducing the dimensions, the improved SIFT algorithm improved the efficiency in the registration section. The text feature information was added as a prior condition to correct the estimated value, and an uncertain factor was added to the degenerate formula to calculate residue to produce the threshold automatically in the POCS model.

The improved super-resolution scheme provides better results on a wide class of document images. The results of the simulation showed that the method can be used to suppress a great deal of noise pollution, and properly preserve the edge details with good reconstruction effects. As a result, its recognition rate is higher and the operation time is shorter than in the original algorithm.

There are still many factors that the algorithm does not cover. They provide direction for future work. First, this algorithm is applicable to the document image under simple background. If the background is a mixture image of text and natural scenery, the reconstruction will be of poorer quality. It may be possible to combine some image segmentation technology in future works to render the reconstruction more specific. Second, in the reconstruction phase, all of the initial extracted images are grayscale ones, and this article does not involve color images. The next work will include experiments addressing the reconstruction of color document images to render the algorithm more efficient and more widely applicable.