Social Content Recommendation Based on Spatial-Temporal Aware Diffusion Modeling in Social Networks

Abstract

User interactions in online social networks (OSNs) enable the spread of information and enhance the information dissemination process, but at the same time they exacerbate the information overload problem. In this paper, we propose a social content recommendation method based on spatial-temporal aware controlled information diffusion modeling in OSNs. Users interact more frequently when they are close to each other geographically, have similar behaviors, and fall into similar demographic categories. Considering these facts, we propose multicriteria-based social ties relationship and temporal-aware probabilistic information diffusion modeling for controlled information spread maximization in OSNs. The proposed social ties relationship modeling takes into account user spatial information, content trust, opinion similarity, and demographics. We suggest a ranking algorithm that considers the user ties strength with friends and friends-of-friends to rank users in OSNs and select highly influential injection nodes. These nodes are able to improve social content recommendations, minimize information diffusion time, and maximize information spread. Furthermore, the proposed temporal-aware probabilistic diffusion process categorizes the nodes and diffuses the recommended content to only those users who are highly influential and can enhance information dissemination. The experimental results show the effectiveness of the proposed scheme.

1. Introduction

Recommender systems are web-based applications, tools, techniques, and programs that are used to provide suggestions for items and products of interest; they do this by analyzing user interactions and consumed content histories [1,2]. Social content recommendations use social networks and user interactions to model recommendation processes. At present, online social networks (OSNs) are increasing in importance and have become a fundamental medium to diffuse information to a large number of people. The surge of social networking sites (SNSs) has enabled user interactions from anywhere and has opened a new era of social interaction, collaboration, preference collection, and tagging for personalization. Information exchange is the keystone of a structured society, and OSNs play important roles in propagating information and enabling users to receive information of interest across many areas, including interest-based community detection [3], political influence [4,5], and economic networks [5,6,7]. SNSs such as Facebook, Twitter, and LinkedIn enable users to share opinions and status updates (newsfeeds) effortlessly with masses of people on any topic. A recent Facebook study [8] showed that the average separation between users was 4.7 hops. Increasing friends, followers, and acquaintances provides constant information updates, which increases the information overload problem. Koroleva et al. regarded constant information updates as a double-edged sword [9]. On the one hand, the increasing number of users helped to maximize the contagion process to spread information to a large number of OSN users. On the other hand, a user receives hundreds or even thousands of newsfeeds, and most of them are non-newsworthy. User frustration increases when receiving the same newsfeed with non-newsworthy updates at the top of their SNSs walls. Figure 1 shows a newsfeed with updates at different times on a Facebook wall. Figure 1a shows the updated newsfeed after 2 h, and Figure 1b is the same newsfeed with updates after 8 h on the top of the wall. However, there is not much newsworthy information. As a user’s network of friends expands, their continuous newsfeed updates increase the probability that a user will miss important newsfeeds. This paper proposes a selective diffusion based recommendation technique that incorporates spatial-temporal information and user specific information to identify whether or not to recommend specific information to a user.

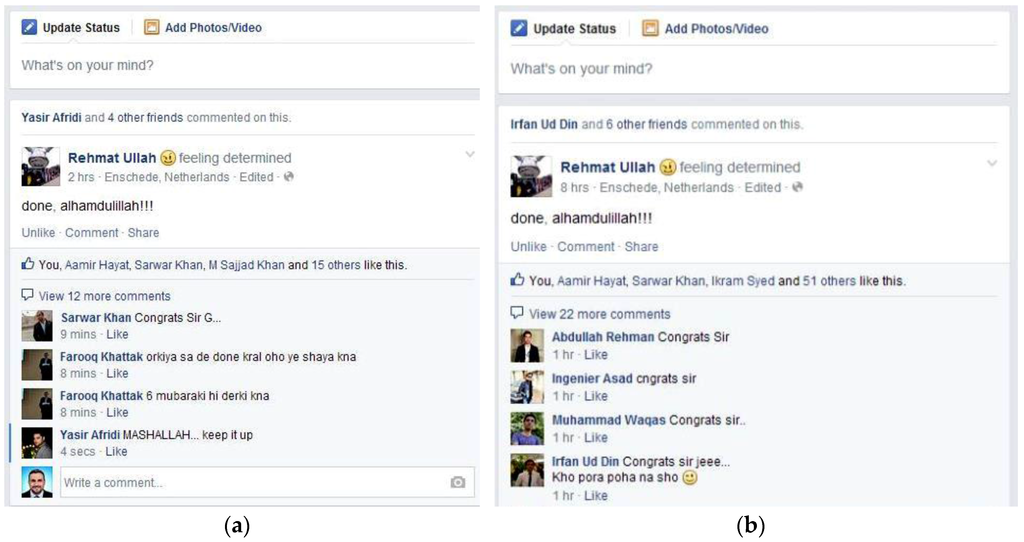
Figure 1. The same newsfeed with updates at the top of a Facebook wall at different times: (a) status of newsfeed after 2 h; and (b) same newsfeed after 8 h with some non-newsworthy updates.

A social network (SN) is modeled as a graph of people (nodes) connected by friendship or mutual interests (links/edges). OSNs not only provide a meeting point and facilitate the building of social relations among a large number of people, they also play important roles in spreading information, news, ideas, and innovations. The link between nodes may be directed or undirected and provides a “word-of-mouth” communication channel [10,11]. The Oxford dictionary [12] defines diffusion as the spreading of something more widely. Connected nodes spread information in OSNs, and a network with high connectivity maximizes the information spread. In 1969, Milgram [13] requested 240 people to write a letter to a stockbroker in Boston. The participants did not know the stockbroker or his address. Nevertheless, 60 letters reached the target destination. It took an average of 6.2 hops for this to happen, creating the six-degrees-of-separation adage. Cheng [14] analyzed 5.2 billion Twitter friendships and discovered five degrees of separation within the Twitter network. These studies only provided a degree of separation for the diffusion of information. They did not determine which pieces of information diffused more frequently, or how and through which path they diffused. Typically, it is unnecessary to diffuse messages to an entire network. Groups such as service providers, politicians, security analysts, and crime prevention services are keenly interested in identifying people in society that are effective at spreading information. This knowledge helps these groups to maximize their own information dissemination.

Influence is the capacity to have an effect on the character, development, or behavior of someone or something, or the effect itself [12]. Social influence is a phenomenon in which an individual impels his connection to behave in a similar way [15]. The flow of information in OSNs is only possible if individuals can influence one another. Teo [16] analyzed demographic and motivation variables associated with Internet usage activities and showed that individuals with similar demographics and behaviors tended to engage in similar activities. Social influence involves a three steps process: (i) a set of nodes that can exert influence; (ii) the method of contagion of the influence; and (iii) the set of nodes that can adapt the influence. In social influence maximization, a small set of nodes is considered that can maximize information diffusion. However, selecting these in a large network is an NP-hard problem [5]. In this work, we model the social ties relationship considering multicriteria information. There are four categories of information—user spatial information, user interactions and activity history for social trust, user opinions on similar items, and user demographics. We rank the nodes considering friends and friends-of-friends to select the most influential nodes for diffusion.

The ubiquity of smart devices, communication technologies, and online social media enables people to be connected all the time, and this in turn makes it possible for information to be diffused at anytime from anywhere. Spatial and temporal circumstances no longer constrain information diffusion. Individuals receive information in a continuous stream over time, merging small pieces of information at different spatial locations and then conveying them to the masses over OSNs. Several mathematical models have been proposed to model the distribution of information in OSNs, but none of them is comprehensive [17]. The heterogeneity of user interactions and mobility concerning links, the dynamic structure of OSNs, and the merging of information over time and space have opened a new era of research on information diffusion and user behaviors in OSNs. This article explores how a piece of information diffuses temporally and provides a mathematical model to control the diffusion process in OSNs.

The rest of the paper is organized as follows. Section 2 explains the related work and background knowledge regarding social networks and information diffusion. Section 3 introduces the proposed scheme, which incorporates a spatial-temporal approach with selective diffusion-based social content recommendations. In Section 4, our approaches are compared to various state-of-the-art ranking and diffusion techniques using simulation results. Finally, the conclusion is presented in Section 5.

2. Background and Related Literature Review

The scope of this paper is closely related to SNS dynamics, social influence, and information diffusion. This section presents the background and related work regarding OSN structures, user interactions and information flows, user influence on direct friends and other users, and information diffusion processes in OSNs.

Web-based SNSs have become a popular socialization-based medium that enables users to provide opinions about various products and items. In sociology, Georg Simmel [18] helped pioneer structural theories such as triad dynamics. Mereno [19] depicted “sociograms” for interpersonal relationships, preferences, and choices within groups. The concept of social networks was first coined by Barnes [20] in his article Class and Committees in a Norwegian Island Parish. In web-based SNSs, individuals: (i) make a public or semi-public profile within a bounded system; (ii) maintain a list of users with whom they want to share a connection; and (iii) view and traverse the shared content by direct connections or by others in the system [21]. OSNs are represented by a graph $G\left(V,E\right)$, where $V$ is the set of nodes and $E$ is the set of edges showing a relationship among members of $V$ [22]. Mostly, the large-scale OSNs are scale-free graph means that their degree distribution follows the power law [23]. The main feature of the scale-free network is that they have higher degree node called hub. Haythornthwaite [24] stated that SNs were initially introduced to connect families and friends.

User interest in the SNSs has opened a new wave of SNS development in the last decade. The first recognizable SNS was SixDegrees.com, which was launched in 1997. This was followed by LiveJournal, AsianAvenue, and BlackPlanet in 1999; LunarStorm and MinGente in 2000; Cyworld and Ryze in 2001; Fotolog, Friendster and Skyblog in 2002; LinkedIn and Last.FM in 2003; and Flicker and Facebook in 2004 [21]. OSNs have been studied and utilized in many fields. Jaeger et al. [25] and Zappen et al. [26] explored the potential use of SN platforms in E-Government to deliver and improve services. Viral marketing is a marketing technique using word-of-mouth effects to achieve marketing objectives and increase brand awareness. SNSs can play a vital role in viral marketing. A mechanism to select a node in viral marketing based on its motivation to forward online content is proposed in [27]. Richardson and Domingos [28] used a probabilistic approach to model the customer’s network value, and this value showed the expected sales profit gained from some other customers with whom this customer was directly or indirectly connected to in the network. Recommender systems [1,2,29] also collect user opinions and personalize content for them. Lada Adamic and Glance [4] analyzed political blogs prior to the US Presidential election of 2004 and revealed two well-separated clusters. Coleman et al. [30] modeled a network for physicians and found that physicians with more academic citations had their prescriptions of new drugs accepted more frequently than physicians with fewer academic citations.

In OSNs, information disseminates where users influence one another. Social influence determines in particular: (i) who are the most popular and influential users in the OSN; (ii) which user influences whom; (iii) why they are influenced; and (iv) why users are attracted to particular services [31]. A novel social influence model is proposed based on bounded rationality of agents in SNs [32]. Influence is modeled as an influence game, where the players are, influencers and followers. The follower is following the influencers considering the measure of bounded rationality. Higher the rationality of a follower with respect to a seed, higher the probability that the follower will follow the state of the influencer. Influence has a long history of study in social sciences, marketing, communication, and political sciences. Katona et al. [33] found that a user who is connected to many users (user degree) have a higher adoption probability. In addition, the density of connections in a group who already adopted has the strong influence on the adaptation of individuals connected to this group. Influence is node specific, and local links between nodes are more important than global links. In addition, links between two users may be multi-aspect, i.e., they can work in opposite directions between two users depending on the topics [34]. Identifying important nodes is a key problem when determining social influence in an SN analysis. Degree, betweenness, and closeness centrality are measures of determining the criticality and importance of nodes [7,35,36]. Piraveenan et al. [37] introduced a new centrality measure (percolation centrality) to analyze the importance of nodes during percolation in networks. They found that the average of percolation centrality overall possible single contagion source reduces to betweenness centrality. In addition, the percolation centrality reduces to betweenness centrality if all the nodes are infected or partially percolated to some extent. Node centrality ranks nodes based on their central positions in SNs considering either edges, shortest paths, or the nodes passing through a node. Google introduced PageRank algorithm [38,39] to rank a web page. The PageRank algorithm ranked solely based on their location in the Web’s graph structure regardless of the web page content. A Webpage has a higher rank that is linked to important WebPages. Zhu et al. [40] suggested a SpreadRank algorithm based on the random walk theory and the spreading ability of the node. Xiang et al. [41] discussed the understanding of PageRank and the relationship between the PageRank and social influence analysis. They developed a linear influence model by introducing the prior knowledge which generalizes the authority computation of PageRank. In this work, Luarn et al. [42] showed that dissemination information frequency was highly affected by the network degree. The social transmission of information and decision-making is highly influenced by the behavior of others [43]. OSN structures and topology affect information diffusion on a large scale [6,44]. In influence diffusion, the node may be either active or inactive. Kempe et al. [45] derived a formula for influence maximization as a discrete optimization problem and suggested two diffusion models—linear threshold (LT) and independent cascade (IC). Suppose $u$ and $v$ are two nodes in an SNS, and $E\left(u,v\right)$ is an edge between these nodes. The LT model [5,40,45,46,47] assigns random weight $w\left(u,v\right)$ from interval $\left[0,1\right]$ to edge $E\left(u,v\right)$ and represents the influence of user $u$ over $v$. The LT model then sums the influence weights of active neighbors $N$ of node $\left({\sum }_{i\in N}{w}_i\right)$ and uses a threshold value to determine whether the node will be switched from inactive to active. The IC model [5,15,40,45] uses a probabilistic approach, and an inactive node is given one chance with a certain probability to activate its inactive neighbors. An extension of IC model is proposed in [48] called independent cascade model with negative opinion (IC-N). They incorporated users’ negativity and stated that negative opinions are more dominant over positive opinion. The IC-N model introduced a quality factor. IC-N first selects a set of nodes and activated them. With certain probability $\left(q\right)$ the seed node becomes positive if he experienced good quality and with $1-q$ becomes negative. Bakshy et al. [49] analyzed 250 million Facebook users and examined the role of information diffusion. The main findings of the analysis were that: (i) an exposed user was more likely to spread information and propagate messages more quickly; and (ii) stronger ties were more influential, but weak ties were of greater help in spreading recent information. Kim et al. [50] introduced a conceptual framework for information diffusion across heterogeneous OSNs and provided a macro-level information diffusion model.

OSN structures and topologies, user positions in an SN, and user interactions play important roles in influence maximization and information diffusion. Kasthurirathna et al. [51] simulated a coordination game on four different classes of complex networks. In the study, they found that in all four types of networks that slightly less connected people first adopt the coordination compared to the highest connected people. However, there are two other important factors with respect to OSNs—the spatial awareness to diffuse information to individuals in the same region who are likely to be more interested in the diffused information, and the temporal awareness to consider the diffused message importance with the passage of time. Temporal- and spatial awareness-based diffusion was studied in [7,52,53,54,55,56], but there is still a great deal of research required in the field of OSNs. Nicosia et al. [53] stated that complex networks were time-varying graphs, and interactions among the users were time varying. In OSNs, most edges are active for a short period. Holme et al. discussed several systems that could benefit from a temporal network infrastructure [54]. Contacts and social networks, telephone networks, and the Internet and mobile networks are all examples where the use of only the network topology does not provide full information. Space (location) is one of the most relevant factors to be considered when attempting to acquire complete information [55]. Spatial information is one of the most important factors for location aware services such as advertisements and entertainment.

The contributions of this paper to the aforementioned literature can be summarized as follows: (i) it proposes social content recommendations based on spatial-temporal aware diffusion in SNs; (ii) it models social ties relationships considering multicriteria such as user spatial information, content trust, opinion similarity and demographics; (iii) it provides a ranking algorithm (SocNodeRank) considering a user’s direct friends and friends-of-friends to select the most influential nodes; (iv) it offers a temporal aware probabilistic diffusion model to maximize information diffusion and minimize contagion time; and (vii) the proposed scheme scales well with a large number of nodes and links, minimizes the contagion time needed to diffuse a message, and controls recommendations based on social diffusion.

3. Social Content Recommendations Based on Spatial-Temporal Aware Diffusion in Social Networks

This section presents the proposed spatial-temporal aware selective flooding-based information diffusion in OSNs. Focus is placed on algorithms that are able to model the multicriteria-based social ties relationships between users, rank nodes to find the most influential individuals from whom the users can accept information, and provide temporal aware probabilistic diffusion-based content recommendations. In OSNs, spatial and temporal information are two important factors along with network topology and user interactions when attempting to understand information dissemination in SNs. We model multicriteria-based social ties relationships between users considering each user’s spatial information, their interactions with respect to content sharing, the extent to which friends share the same content with other users in the SNS, opinions on various items and products, and user demographics. We rank the nodes using the proposed SocNodeRank ranking algorithm to select the Top $K$ nodes as seeds to maximize the information distribution in the SNs. The diffusion process is modeled as a temporal aware probabilistic diffusion model that maximizes the information distribution (i.e., recommendations).

3.1. Multicriteria-Based Social Ties Relationship (Influence) Modeling

The SNS graph will be either directed or undirected. In an undirected network, edges do not have direction and the relationship from either of the nodes remains the same (symmetric). In reality, the heterogeneous nature of user interactions causes OSNs to be directed networks in nature, and the two neighboring users have different levels of influence (asymmetric) on one another. Figure 2 gives a pictorial representation of the proposed social ties relationship modeling considering two direct neighbor users, $\mathrm{u}$ and $\mathrm{v}$.

Figure 2. Pictorial overview of multicriteria-based social ties relationship (influence) modeling.

An SNS provides the location of a user, and we use each user’s position (GPS coordinates) to determine spatial similarity. Equation (1) finds the spatial similarity of two users using the cosine similarity normalized by the geo-distance between the users.

$$spSim\left(u,v\right)=\frac{1}{\left[1+\frac{dist\left(u,v\right)}{1000}\right]}\left(\frac{C_u.C_v}{\left|\left|C_u\right|\right|\left|\left|C_v\right|\right|}\right)$$

(1)

where $dist\left(u,v\right)$ is the geo-distance between the users and can be found by Equation (2) using the Haversine formula [57,58].

$$\{\begin{array}{c}a=si{n}^2\left(\frac{\Delta \varnothing }{2}\right)+cos\left({\varnothing }_{C_u}\right)cos\left({\varnothing }_{C_v}\right)si{n}^2\left(\frac{\Delta \phi }{2}\right);where\Delta \varnothing =\left|{\varnothing }_{C_u}-{\varnothing }_{C_v}\right|,\Delta \phi =\left|{\phi }_{C_u}-{\phi }_{C_v}\right|\\ c=2\mathit{arctan}\left(\frac{\sqrt{a}}{\sqrt{1-a}}\right)\\ dist\left(u,v\right)=R\times c;\mathrm{where}R\mathrm{is}\mathrm{the}\mathrm{radius}\mathrm{of}\mathrm{the}\mathrm{Earth}\end{array}$$

(2)

where $C_u$ and $C_v$ are the GPS coordinates of users $u$ and $v$, respectively. Each GPS point has latitude $(\varnothing )$ and longitude $\left(\phi \right)$ coordinates. ${\varnothing }_{C_u}$ and ${\phi }_{C_u}$ are the latitude and longitude of user $u$ GPS coordinate ($C_u$), and ${\varnothing }_{C_v}$ and ${\phi }_{C_v}$ are the latitude and longitude of user $v$ GPS coordinate ($C_v$). $R$ is the radius of earth, 6371 km.

In OSNs, social relationships vary based on the acceptance and adoption of content by other users. Users like to recommend and share message with people who easily accept that information and share it with other users. In this paper, we consider that users only accept and adopt content from individuals who shared that content with other users. Figure 3 shows the overview of content acceptance by a user, and that content being shared to the walls of other users. Figure 3a shows content being shared by user $u$ to user $v$, and $v$ shares part of that content to his directly neighboring users. Content acceptance (contentTrust) between users $u$ and $v$ in Figure 4a will be $contentTrust\left(u,v\right)=\frac{1}{3}\left(\frac{\left(2+0+1\right)}{3}\right)=\frac{1}{3}$. In Figure 3b, it will be $contentTrust\left(u,v\right)=\frac{1}{3}\left(\frac{3+3+3}{3}\right)=1$. Mathematically, the $contentTrust$ between any two users such as $u$ and $v$ can be found by Equation (3).

$$contentTrust\left(u,v\right)=\frac{1}{\left|CSet\right|}\frac{{\sum }_{c\in CSet}\left|n_{v,c}\right|}{\left|N_v\right|}$$

(3)

where $\left|CSet\right|$ is the set of content user $u$ shared to user $v$, $\left|N_v\right|$ is the number of neighbors of user $v$ and $\left|n_{v,c}\right|$ are the users from $N_v$ diffused by content $c$.

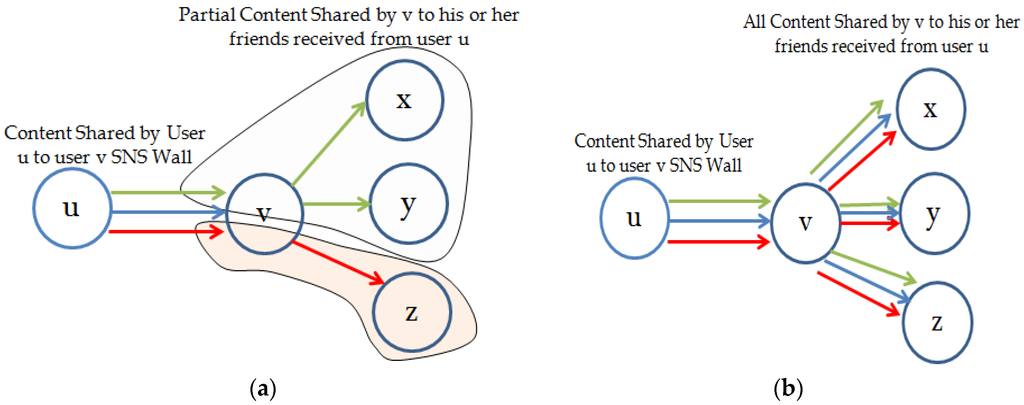
Figure 3. Content sharing by friends and friends-of-friends in an SNS: (a) content sharing by user u to v and v share partial content to his friends; and (b) content sharing by user u to w and w share all content to his friends.

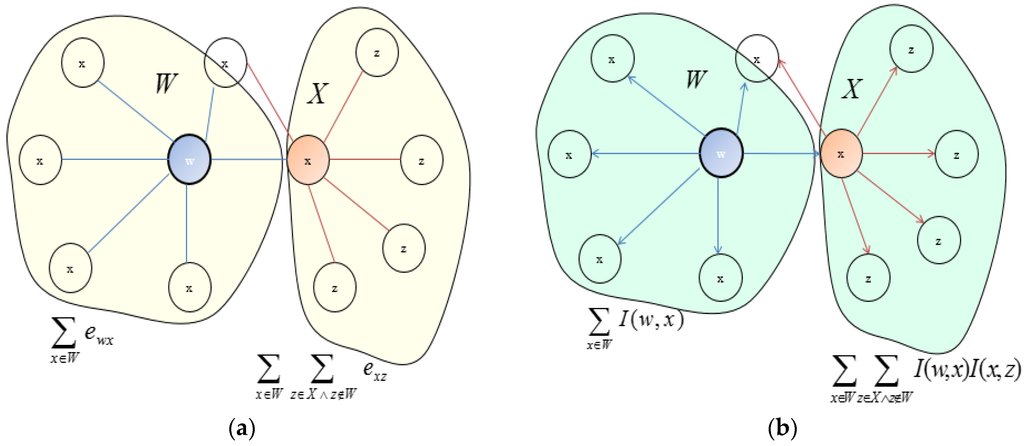
Figure 4. Overview of proposed social node rank (SocNodeRank): (a) SocNodeRank in an undirected network; and (b) SocNodeRank in the directed network.

In OSNs, users easily adopt content from users who experienced content in the past. Recommender systems mostly recommend user content to active users with similar content histories. In this paper, we consider experienced content similarity as a factor to find the influence between users. The content similarity between users $u$ and $v$ can be found by Equation (4)

$$opinionSim\left(u,v\right)=1-\frac{{\sum }_{i\in (CSe{t}_u\cap CSe{t}_v)}\left|R_{u,i}-R_{v,i}\right|}{R_{max}|CSe{t}_u\cap CSe{t}_v|}$$

(4)

where $CSe{t}_u$ and $CSe{t}_v$ are the sets of content experienced by users $u$ and $v$, respectively; $R_{max}$ is the maximum rating; and $i$ is the content experienced by both users $u$ and $v$.

Users with similar demographic characteristics in OSNs are most likely to connect with each other. In reality, most businesses and service providers treat service consumers unequally, and they segment consumers based on demographics such as age, gender, and income for various smart services. This paper considers age, gender, and occupation to find similarities between users using the cosine similarity technique in Equation (5).

$$demoSim\left(u,v\right)=\frac{{\sum }_{i=1}^D{u}_i{v}_i}{\sqrt{{\sum }_{i=1}^D{u}_i^2}\sqrt{{\sum }_{i=1}^D{v}_i^2}}$$

(5)

where $i$ are the demographic attributes of users $u$ and $v$, and $D$ is the total of the demographics attributes. The influence, $I\left(u,v\right)$, of user $u$ on $v$, is depicted in Figure 3, and it can be calculated using Equation (6).

$$I\left(u,v\right)=\alpha spSim\left(u,v\right)+\beta contentTrust\left(u,v\right)+\gamma opinionSim\left(u,v\right)+\omega demoSim\left(u,v\right)$$

(6)

where $\alpha ,\beta ,\gamma ,\mathrm{and}\omega$ are the real numbers from interval $\left[0,1\right]$ such that $\alpha +\beta +\gamma +\omega =1$. We adjust the coefficients by considering the contributions and importance of the criteria in Equation (6).

3.2. Ranking Algorithm for the Selection of the Most Influential Nodes to Initialize the Diffusion Process in an OSN

In this subsection, we introduce the proposed social node ranking algorithm, which is called SocNodeRank, to select the most influential nodes to initialize the information dissemination process. The proposed algorithm considers the user’s direct friends and friends-of-friends to compute the node rank. Numerous ranking algorithms have been proposed, including degree centrality, betweenness centrality and closeness centrality [59,60]. Degree centrality considers the number of edges; a user will be more central if he is more connected. Degree centrality ignores network structure information and instead only considers the ties to direct neighbors. Closeness centrality measures how close a node is to other nodes in the network. The betweenness of a node refers to the number of node pairs passing through a node with the minimum number of edges. Closeness and betweenness consider the network structure, but they lack efficiency in large scale networks.

The SocNodeRank algorithm considers user directed friends and friends-of-friends to determine a ranking value. A network can be directed or undirected, but this paper focuses on directed graph-based social networks. However, we also provide a mechanism to rank the nodes in an undirected network. SocNodeRank considers the direct friends and friends-of-friends. However, if a node is common between the user and his friends, then it will be considered only once, as depicted in Figure 4. Equation (7) finds the rank of the node in an undirected SNS graph.

$$SocNodeRan{k}_{undirected}\left(w\right)={\displaystyle \sum }_{x\in W}{e}_{wx}+{\displaystyle \sum }_{x\in W}{\displaystyle \sum }_{z\in X\cap z\notin W}{e}_{xz}$$

(7)

where $W$ is a neighbor set of $w$, $x$ is one of the neighbors of $w$, and $X$ is a neighbor set of $x$. $e$ is the edge between two users, which is $1$ if present and $0$ otherwise. Figure 4 shows the SocNodeRank algorithm, and Figure 4a is the ranking mechanism of an undirected graph (SNS).

A social relationship between friends is asymmetric in directed networks. In Section 3.1, we introduced the influence modeling and the multicriteria factors that affect influence. We consider the weighted out degree (outgoing edge) to rank nodes in directed networks. The rank of the node in the directed SNS is given by Equation (8), where $I\left(w,x\right)$ is the influence of user $w$ on user $x$.

$$SocNodeRan{k}_{directed}\left(w\right)={\displaystyle \sum }_{x\in W}I\left(w,x\right)+{\displaystyle \sum }_{x\in W}{\displaystyle \sum }_{z\in X\cap z\notin W}I\left(w,x\right)I\left(x,z\right)$$

(8)

We consider the direct influence of the user on his friends and the propagation of influence to his friends-of-friends. Figure 4b depicts the ranking mechanism of the proposed scheme in the directed graph. The proposed scheme needs less time to rank the nodes in an SNS because it considers only 2-hops neighbors of user compared to most ranking algorithms such as betweenness, closeness and PageRank except the degree centrality. The proposed algorithm also captures the properties of the betweenness centrality- and degree centrality-based schemes.

3.3. Temporal Aware Probabilistic Diffusion-Based Social Content Recommendations in OSNs

The growth of SNSs and user interactions helps disseminate information. However, the density of users creates an information overload problem. In this subsection, we introduce the probabilistic diffusion model to model the social content recommendation process. This model operates in a controlled manner that considers the recommended message temporal information, network topology, and user multicriteria influence. In SNSs, users can receive the same diffused messages from many users or with minor information updates, which does not happen with biological diffusion. We place diffusing messages into two categories—one in which the user accepts the message and the other in which the user does not accept the message. We model the influence between users based on multicriteria, and then we rank the nodes and select the most influential (initial spreader) K-nodes to initialize the diffusion process. We extend the concept of the continuous-time Markov chain model in [40] and the social influence diffusion model presented in [61] to control the diffusion process and overcome the information overload problem.

In the diffusion process, a node can be inactive or active. At time $t=1$, $K$ influential nodes are selected to start the diffusion process. At $t=2$, neighbors of the diffusing nodes only become active when the incoming influence from the diffusing node is greater than the outgoing influence and the recommendation (diffusion acceptance threshold). Suppose $u$ is the diffusing node and $v$ might be the accepting (diffusion adopting) node. The activation state of $v$ at $t=2$ is given by Equation (9).

$${P_{Diff}}_{t=2}\left(v\right)=\{\begin{array}{l}I\left(u,v\right);\mathrm{where}I\left(u,v\right)\ge I\left(v,u\right)\mathrm{and}I\left(u,v\right)\ge RA{T}_1\\ 0;\mathrm{otherwise}\end{array}$$

(9)

where ${P_{Diff}}_{t=2}\left(v\right)$ determines whether node $v$ at time $t=2$ will be diffused or not. $RA{T}_1$ is the acceptance threshold of diffusion (recommendation) from direct friends. In this paper, we consider two different thresholds—$RA{T}_1$ is the threshold of the content recommendation acceptance from the direct friends at $t=2$, and $RA{T}_2$ is the threshold for friends-of-friends and so on for $t>2$.

At $t=1$ in Figure 5a, the highest value of $K$ (influential nodes) is selected using the mechanism of Section 3.2, and for simplicity, $K=1$ is considered to explain the procedure. At $t=2$ of Figure 5b, the neighboring nodes $\left\{2,4,6,7,8\right\}$ of $\left\{1\right\}$ are selected for diffusion, but according to Equation (9), only nodes $\left\{2,6,8\right\}$ are diffused because node $\left\{1\right\}$ has a higher influence on them and the diffusion acceptance threshold $RA{T}_1=0.4$. The active node continues to diffuse if the outgoing influence is greater than the incoming influence. The diffusing node accepts only the diffused message if the diffusion contagion probability is greater than the diffusion acceptance threshold. Suppose the threshold of diffusion acceptance is $RA{T}_2\ge 0.5$ for $t>2$ in Figure 5c. Nodes $\left\{3\right\}$ and $\left\{5\right\}$ are diffused because $\left(0.8\times 0.74\right)\ge RA{T}_2$ and $\left(0.65\times 0.8\right)\ge RA{T}_2$, while node $\left\{9\right\}$ is not diffused because $\left(0.55\times 0.35+0.8\times 0.2\right)<RA{T}_2$. Similarly, at $t=4$ in Figure 5d, node $\left\{7\right\}$ is diffused because $\left(0.8\times 0.74\times 0.85\right)\ge RA{T}_2$. Mathematically, the nodes activation probability for ($t+1)\ge 3$ can be given by Equation (10).

$${P_{Diff}}_{t+1}\left(w;V\right)=\{\begin{array}{l}{\displaystyle \sum _{v=1}^V}I\left(v,w\right){P_{Diff}}_t\left(v|V\right);I\left(v,w\right)\ge I\left(w,v\right)\mathrm{and}{P_{Diff}}_{t+1}\left(w;V\right)\ge RA{T}_2\\ 0;\mathrm{otherwise}\end{array}$$

(10)

where $V$ is the set of neighboring nodes of node $w$ that can diffuse $u$ at time $t$ where $\left(t+1\right)\ge 3$. The equation shows that users accept recommendations when a large number of higher similarity friends and friends-of-friends recommend the content.

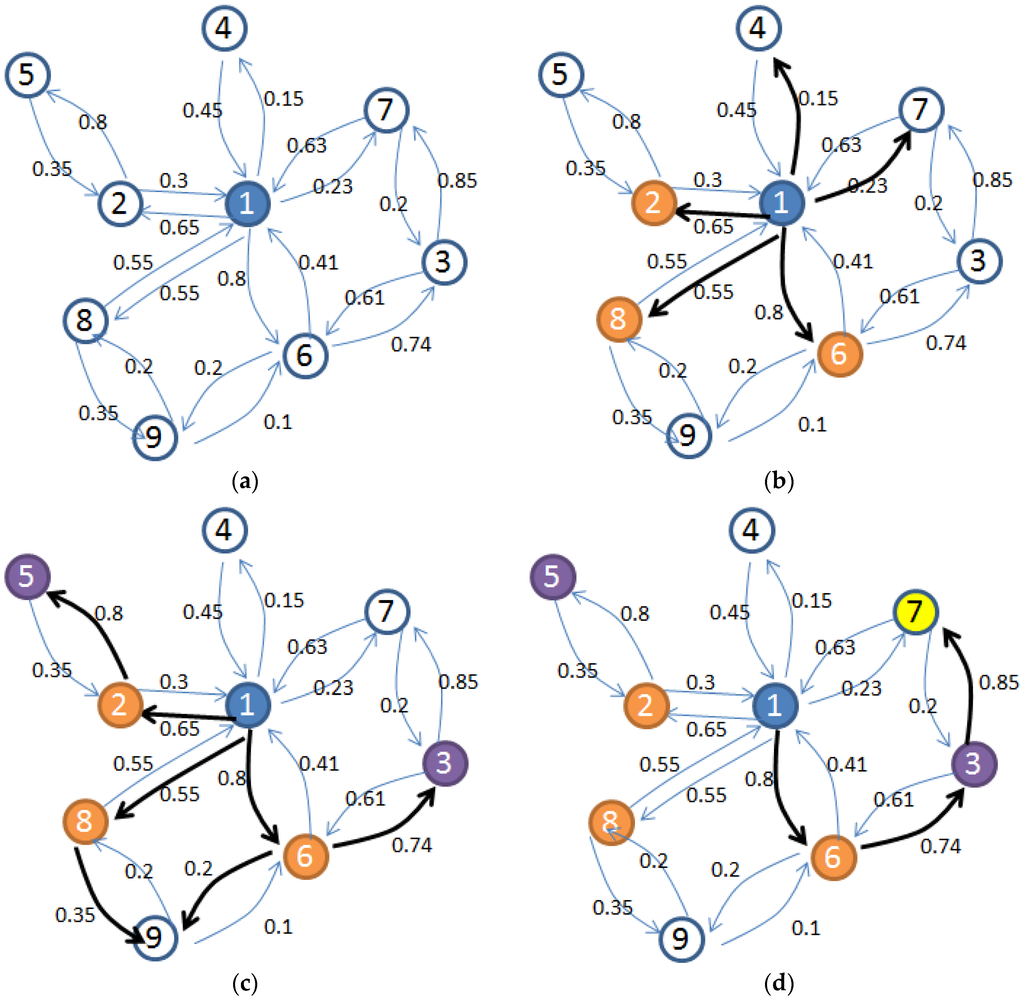
Figure 5. Overview of the proposed temporal aware probabilistic information diffusion process: (a) diffusion process start (t = 1); (b) diffused node at (t = 2); (c) diffusion status at (t = 3); and (d) Information Diffusion at (t = 4).

4. Simulation Results and Discussion

In this section, different real-world publicly available datasets used for this paper are introduced, and a comparison of the proposed schemes with various previous rankings and diffusion algorithms is provided.

4.1. Experimental Results for Social Ties Relationship (Influence) Factors

To the best of our knowledge, there is no single dataset network that contains all of the required attributes to determine influence among users and evaluate the proposed influence modeling scheme. To build a single compilation of network data, we extract user spatial information from [62], Advotago user social trust data from [63], and demographics and user ratings from MovieLens [64]. Table 1 shows the attributes of the dataset used for the evaluation of influence scheme. Finally, the dataset used for the multicriteria relationship modeling has an average degree of $3.345$ and network diameter of $9$.

Table 1. Description of dataset for multicriteria-based influence modeling.

Dataset Attributes	Description/Values of Attributes
Number of users	133
Number of edges	450
Trust value between users	{0.6, 0.8, 1.0}
User demographics	Sex, Age
Minimum times same content evaluated by friends	10

In order to evaluate the different influential factors, Table 2 shows the $\mathrm{Top}-10$ most influential nodes in the multicriteria dataset of Table 1. Extensive simulations are carried out to determine the optimal values of $\alpha$, $\beta$, $\gamma$, and $\omega$ to calculate the actual influence between users using the multicriteria. The nodes are ranked using weighted out-degree for each attribute separately and also for combined using the various coefficient criteria in Equation (6). Selecting the coefficient values, the precision is used to compare the node rankings by individual attribute-based influence with node rankings by multicriteria-based influence. Figure 6 shows the precision comparison of the single attribute and the multicriteria influence-based ranked nodes. The coefficients {$\alpha =0.20,\beta =0.45,\gamma =0.20,\omega =0.15$} are selected because they extract most of the influential nodes of each single attribute.

Table 2. Top-10 influential nodes in the multicriteria influential dataset using weighted out degree.

Spatial Similarity	Content Trust	Opinion Similarity	Demographics Similarity	$\left\{\begin{array}{c}\mathit{\alpha }=\mathbf{0.2},\mathit{\beta }=\mathbf{0.45},\\ \mathit{\gamma }=\mathbf{0.2},\mathit{\omega }=\mathbf{0.15}\end{array}\right\}$	$\left\{\begin{array}{c}\mathit{\alpha }=\mathbf{0.4},\mathit{\beta }=\mathbf{0.4},\\ \mathit{\gamma }=\mathbf{0.1},\mathit{\omega }=\mathbf{0.1}\end{array}\right\}$
70	70	70	70	70	70
29	113	50	109	58	58
58	114	71	58	114	64
27	58	114	85	113	27
64	64	6	114	64	114
102	71	4	61	27	113
78	27	48	32	71	29
32	32	102	55	29	71
4	127	89	1	109	32
99	1	113	127	32	4

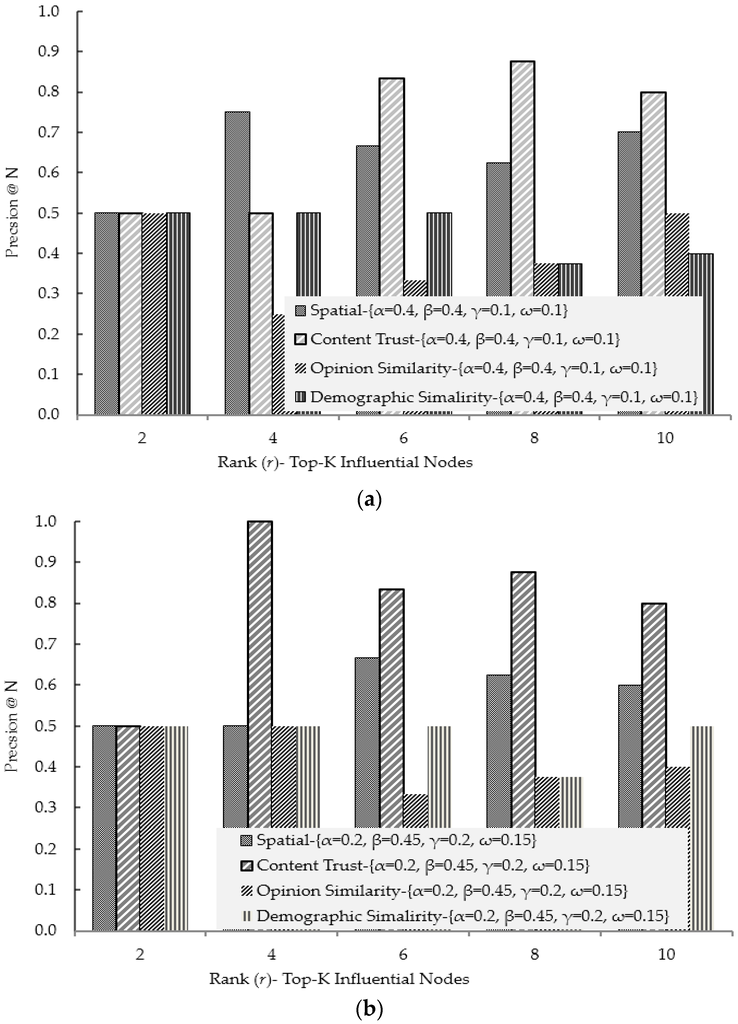
Figure 6. Precision comparison for the selection of multicriteria influence coefficients: (a) precision comparison of the individual attribute based influential node selection with multicriteria consider coefficients $\left\{\alpha =0.4,\beta =0.4,\gamma =0.1,\omega =0.1\right\}$; and (b) precision comparison of the individual attribute based influential node selection with multicriteria consider coefficients $\left\{\alpha =0.2,\beta =0.45,\gamma =0.2,\omega =0.15\right\}$.

4.2. Results of Proposed Social Node Ranking Algorithm (Selection of Highest Influential Nodes)

The results of the proposed SocNodeRank are compared with three state-of-art ranking algorithms—weighted out-degree centrality, closeness centrality, and betweenness centrality. We used the directed weighted networks publicly available datasets for results comparison. The details of the datasets are as follows.

Zachary’s Karate Network [65]: The small-sized karate network is used as a directed network, but the edge weight (1) is the same between users. The dataset consists of 34 members and 78 friend relationships. The karate club was started at an American university in the late 1970s.

Coauthorships in Network Science [66]: This is a weighted directed coauthors network with 1589 nodes and 2742 edges.

Political Blogs of US Elections [4]: This is a directed network of hyperlinks between 2004 US election weblogs. The dataset consists of 1490 nodes and 19,025 edges.

Coappearance network of characters [67]: The co appearance network of characters in the novel Les Miserables is a weighted network with 77 nodes and 254 edges.

To compare the proposed SocNodeRank with other schemes, the ranking similarity metric from [68] is employed. The ranking similarity F(r) of two schemes at rank $r$ can be given by Equation (11).

$$F\left(r\right)=\frac{\left|L\left(r\right)\cap L^{\prime }\left(r\right)\right|}{\left|r\right|}$$

(11)

where $L\left(r\right)$ and $L\prime \left(r\right)$ are the two sets of nodes of two different ranking schemes at rank $r$.

Figure 7 shows the simulation and comparison results of ranking similarity $F\left(r\right)$ for the above specified networks at various $r$ ranking. The figure clearly depicts that the proposed algorithm has higher ranking similarity with the weighted out degree and betweenness. We used Gephi [69] as open source software for most of the ranking algorithm simulation. In the simulation setting for PageRank, we considered (probability = 0.5, Epsilon = 0.1 and use edge weights) and for Eignvector centrality directed and 100 number of iterations. The experimental results show that as the network becomes denser in term of nodes and especially edges (interactions), the proposed SocNodeRank differs from the other schemes. The ranking similarities in Figure 7a (the karate network) and Figure 7b (the coappearance of characters in Les Miserables) are quite alike, whereas the network size increases in Figure 7c (coauthors in Network Science) and Figure 7d (the political blogs of the 2004 US election). SocNodeRank extracts some important potential nodes that can maximize the information diffusion. In addition, it extracts nodes that for the most part have the highest values of betweenness for the 1-edge neighbor friends.

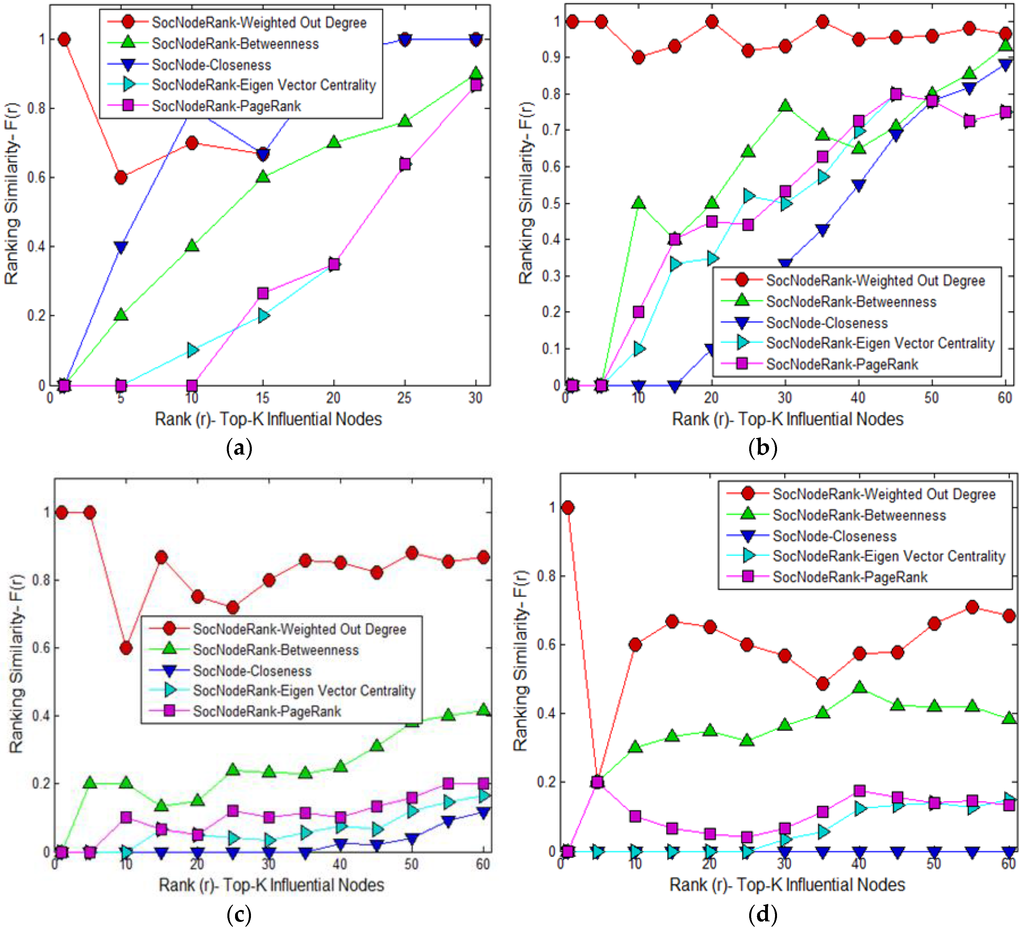
Figure 7. Ranking similarity of the proposed SocNodeRank with weighted out degree, betweenness, and closeness: (a) Zachary’s Karate Network; (b) coappearance network of characters in the novel Les Miserables; (c) coauthorships in Network Science; and (d) political blogs.

Table 3 and Table 4 show the $\mathrm{Top}-10$ highly influential nodes from the coauthorships in Network Science and the 2004 US election political blogs, respectively. In the $\mathrm{Top}-10$ rankings of the coauthorships network, SocNodeRank extracts nodes such as $\left\{1087,132,133\right\}$, which is not extracted by other schemes. Crucially, these nodes for the most part have the highest degree of betweenness and edge centrality for the direct neighbors. Similarly, in the $\mathrm{Top}-10$ rankings of the 2004 US election political blogs, it extracts nodes $\left\{1047,980,1384,615\right\}$. Node $\left\{980\right\}$ has a high level of betweenness nodes $\left\{1051,1041,1101,1479\right\}$ in the direct friends. Therefore, the proposed SocNodeRank scheme captures the properties of edge centrality and betweenness simultaneously, but it takes less time to rank the nodes as compared to the betweenness-only scheme because it considers only the direct friends and friends-of-friends.

Table 3. Top-10 ranked influential nodes (Nodes IDs) in the directed network of coauthorships in network science.

Rank	Weighted Out Degree	Closeness	Betweenness	PageRank	Eign Vector Centrality	Propose SocNodeRank
1	517	1027	78	33	645	517
2	151	492	150	78	1429	54
3	97	866	301	30	1430	516
4	516	867	516	46	1431	151
5	309	986	281	62	1432	34
6	34	450	46	216	1433	132
7	54	1182	151	294	33	1087
8	744	640	307	150	1434	133
9	377	1026	216	34	30	744
10	655	499	71	69	1435	309

Table 4. Top-10 ranked influential nodes (Nodes IDs) in the political blogs of 2004 US election.

Rank	Weighted Out Degree	Closeness	Betweenness	PageRank	Eign Vector Centrality	Propose SocNodeRank
1	855	1490	855	155	55	855
2	454	1405	55	963	155	1047
3	512	1397	1051	855	641	1000
4	387	1247	155	55	729	980
5	880	230	454	641	1051	524
6	363	216	387	1051	642	880
7	1101	1340	1479	1153	756	387
8	1000	1279	1101	1245	535	1384
9	524	926	1041	729	323	615
10	144	833	729	798	1245	1101

4.3. Results of the Temporal Aware Probabilistic Diffusion-Based Social Content Recommendations in OSNs

In this subsection, the simulation results are introduced for users influenced with the diffusion time and number of Top-K (rank-r) initially diffused nodes for the multicriteria dataset introduced in Section 4.1. The proposed SocNodeRank algorithm is used to select highly influential users that can increase the diffusion process. Figure 8 shows the number of influenced users over the simulation (diffusion) time, and it shows that the diffusion rate is higher at the start, but slows as time progresses. The suggested temporal aware probabilistic diffusion model controls the diffusion process and diffuses only those nodes with high levels of similarity. It is able to diffuse the information further. The recommendation acceptance thresholds ($RA{T}_1$ and $RA{T}_2$) have a greater impact on the nodes activation process. If the threshold values are higher, then most of the nodes are excluded from diffusion.

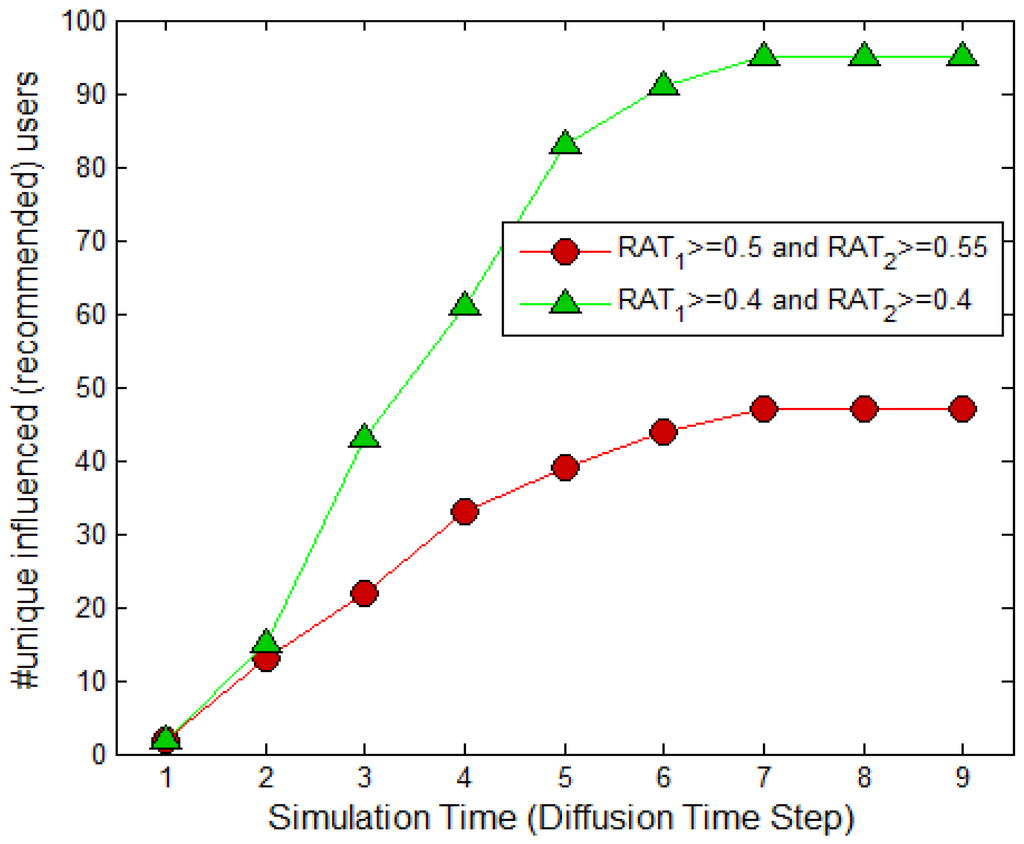
Figure 8. Effect of diffusion time on number of influenced (recommendation accepted) users.

Figure 9 shows the effects of the $\mathrm{Top}-\mathrm{K}$ influential users and the $RA{T}_1$ on the number of influenced (recommended) users. The $\mathrm{Top}-\mathrm{K}$ influential users help to diffuse and increase the number of diffused nodes. However, after a certain value of $\mathrm{K}$, the influence of the $\mathrm{Top}-\mathrm{K}$ users decreases, and it does not improve the diffusion process.

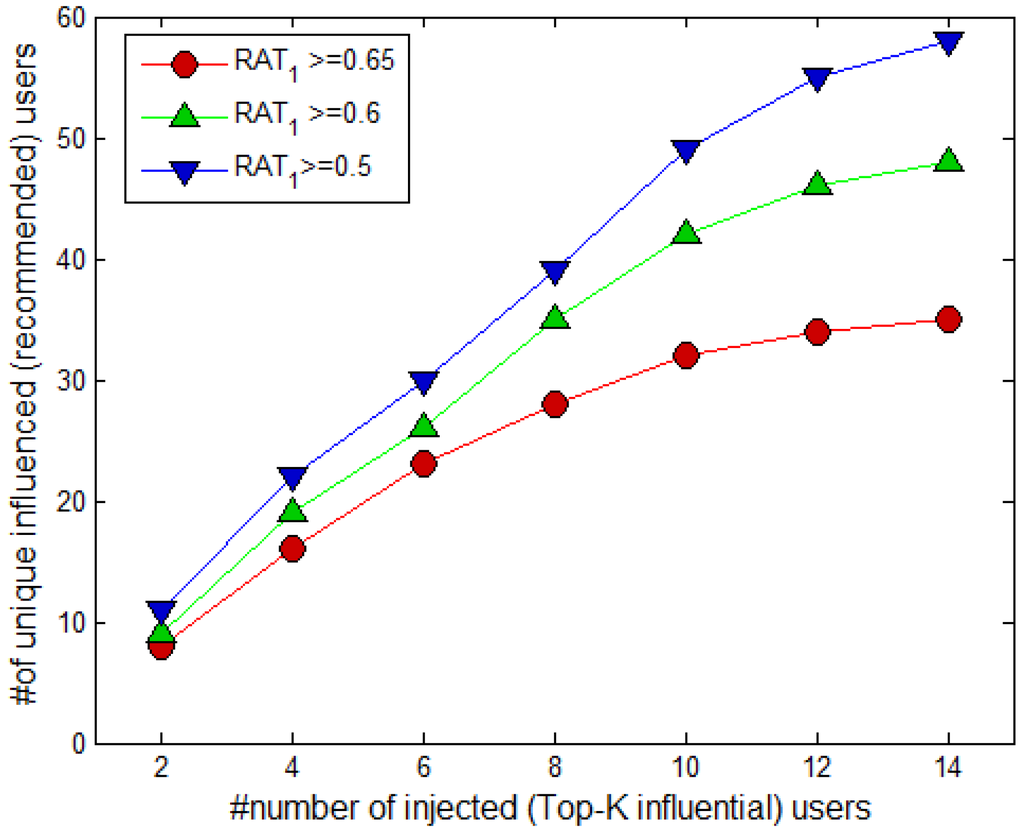
Figure 9. Effect on #number of influenced users by various Top-K influential users and $RA{T}_1$.

5. Conclusions

In this paper, we have presented a method of providing social content recommendations using multicriteria-based relationship modeling between social ties and temporal aware probabilistic diffusion model. We modeled the relationship between social ties to identify users with higher levels of relationship similarity based on multicriteria incorporating user spatial information, content trust, opinion similarity, and demographics. We assigned different weights to each attribute of the multicriteria. We suggested a ranking algorithm for selection of the Top-K most influential nodes considering the influence of friends and friends-of-friends to maximize the information spread. The proposed ranking algorithm has higher ranking similarity with the weight out degree and betweenness. However, it needs less processing time to rank the nodes because it only considers the two hops neighbors of a user compared to betweenness which considers the entire network. Furthermore, the suggested temporal-aware probabilistic diffusion process categorized the nodes based on whether or not they were able to recommend and diffuse content. This enabled the process to overcome the information overload problem. We used different publically available datasets to verify the effectiveness of the proposed social content recommendation scheme. We introduced different thresholds in the proposed probabilistic diffusion model, so the inactive node will be activated if it has highest influential diffused nodes and the higher number of diffused nodes. The proposed scheme scaled well with a large number of nodes and links, and it controlled the diffusion process to recommend content to users with high levels of relationship similarity to overcome the information overload problem.