A Search Complexity Improvement of Vector Quantization to Immittance Spectral Frequency Coefficients in AMR-WB Speech Codec

Abstract

An adaptive multi-rate wideband (AMR-WB) code is a speech codec developed on the basis of an algebraic code-excited linear-prediction (ACELP) coding technique, and has a double advantage of low bit rates and high speech quality. This coding technique is widely used in modern mobile communication systems for a high speech quality in handheld devices. However, a major disadvantage is that a vector quantization (VQ) of immittance spectral frequency (ISF) coefficients occupies a significant computational load in the AMR-WB encoder. Hence, this paper presents a triangular inequality elimination (TIE) algorithm combined with a dynamic mechanism and an intersection mechanism, abbreviated as the DI-TIE algorithm, to remarkably improve the complexity of ISF coefficient quantization in the AMR-WB speech codec. Both mechanisms are designed in a way that recursively enhances the performance of the TIE algorithm. At the end of this work, this proposal is experimentally validated as a superior search algorithm relative to a conventional TIE, a multiple TIE (MTIE), and an equal-average equal-variance equal-norm nearest neighbor search (EEENNS) approach. With a full search algorithm as a benchmark for search load comparison, this work provides a search load reduction above 77%, a figure far beyond 36% in the TIE, 49% in the MTIE, and 68% in the EEENNS approach.

1. Introduction

As explicitly stated in the Abstract, the algebraic code-excited linear-prediction (ACELP)-based speech coding technique [1,2,3,4,5,6] has the double advantage of low bit rate and high speech quality. Accordingly, it is most widely used in speech communication systems, and adopted in many speech codec standards, such as G.723.1, G.729 [1] in International Telecommunication Union (ITU), adaptive multi-rate narrowband (AMR-NB) [2] and wideband (AMR-WB) [3], and in the codec for enhanced voice services (EVS) [4,5] in the 3rd Generation Partnership Project (3GPP). Among such standards, the AMR-WB speech codec with a 16 kHz sampling rate is applied to modern mobile communication systems as a way to improve the speech quality in handheld devices, e.g., smartphones. The AMR-WB codec [3,6,7,8] is a multi-mode speech codec with nine wideband speech coding modes with bitrates of 23.85, 23.05, 19.85, 18.25, 15.85, 14.25, 12.65, 8.85 and 6.6 kbps. The ACELP-based coding technique is developed as an excellent speech coding technique, but a price paid is a high computational complexity required in the AMR-WB codec. Using the AMR-WB speech codec, the speech quality of a smartphone can be improved but at the cost of high power consumption on a smartphone battery.

A vector quantization (VQ) of immittance spectral frequency (ISF) coefficients [9,10,11,12,13] occupies the second largest part of the total computation load required in the AMR-WB encoder. The VQ structure in AMR-WB adopts a combination of split VQ (SVQ) and multi-stage VQ (MSVQ) techniques, referred to as split-multistage VQ (S-MSVQ), to quantize the 16-order ISF coefficients. Conventionally, VQ conducts a full search to ensure that a codeword is best matched with an arbitrary input vector, but the full search requires an enormous computational load. Thus, a continuous effort has been made to simplify the search complexity of an encoding process in a great volume of published studies [14,15,16,17,18,19,20,21,22,23,24,25]. These approaches are further classified into three types in terms of the way the complexity is simplified, including the tree-structured VQ (TSVQ) techniques [14,15,16], the TIE-based approaches [18,19,20] and the equal-average equal-variance equal-norm nearest neighbor search (EEENNS) based algorithms [21,22,23,24,25].

A TIE algorithm was proposed in [18] as a solution to a VQ-based image coding problem in the aspect of computational load reduction. Improved versions of TIE approaches are presented in [19,20] to downsize a search space, giving rise to further reduction in computational load. However, there exists a high correlation between ISF coefficients of neighboring frames in AMR-WB, that is, ISF coefficients evolve smoothly over successive frames. This feature benefits TIE-based VQ encoding, according to which a remarkable computational load reduction is demonstrated, while a moving average (MA) filter is required to smooth the data in advance of VQ encoding of ISF coefficients. As a consequence of data smoothing, the high correlation feature is gone, resulting in a poor performance in computational load reduction. On the other hand, an EEENNS algorithm was derived from equal-average nearest neighbor search (ENNS) and equal-average equal-variance nearest neighbor search (EENNS) approaches. The EEENNS algorithm, as opposed to TIE-based approaches, uses three significant features of a vector, i.e., mean value, variance, and norm, as a three-level elimination criterion to reject impossible codewords.

In view of this, a TIE algorithm equipped with a dynamic and an intersection mechanism, DI-TIE for short, is presented as an efficient way to quantize the ISF coefficients in AMR-WB. Both mechanisms are designed in a way that recursively enhances the performance of the TIE algorithm. On the other hand, a major motivation behind this paper is to meet the energy saving requirement on handheld devices for an extended operation time period.

This paper is outlined as follows. The ISF coefficient quantization in AMR-WB is described in Section 2. Section 3 presents the DI-TIE search algorithm for ISF quantization. Experimental results are demonstrated and discussed in Section 4. This work is summarized at the end of this paper.

2. ISF Coefficient Quantization in AMR-WB

In AMR-WB, a linear prediction analysis is made as follows. As the first step, a speech frame of 20 ms is applied to evaluate linear predictive coefficients (LPC), which are then converted into ISF coefficients. Subsequently, quantized ISF coefficients are obtained following a vector quantization process, which is detailed below.

2.1. Linear Prediction Analysis

In a linear prediction, a Levinson-Durbin algorithm is used to compute the 16th order LPC, a_i, of a linear prediction filter, defined as

$$\frac{1}{A(z)}=\frac{1}{1+{\displaystyle \sum _{i=1}^{16}{a}_i{z}^{-i}}}.$$

(1)

Subsequently, the LPC parameters are converted into the immittance spectral pair (ISP) coefficients for the purposes of parametric quantization and interpolation. The ISP coefficients are defined as the roots of the following two polynomials

$$F_1^{\prime }(z)=A(z)+z^{-16}A(z^{-1}),$$

(2)

$$F_2^{\prime }(z)=A(z)-z^{-16}A(z^{-1}).$$

(3)

$F_1^{\prime }(z)$ and $F_2^{\prime }(z)$ are symmetric and antisymmetric polynomials, respectively. It can be proven that all the roots of such two polynomials lie and alternate successively on a unit circle in the z-domain. Also, $F_2^{\prime }(z)$ has two roots at z = 1 (ω = 0) and z = −1 (ω = π). Such two roots are eliminated by introducing the following polynomials, with eight and seven conjugate roots respectively on the unit circle, expressed as

$$F_1(z)=F_1^{\prime }(z)=(1+a[16]){\displaystyle \prod _{i=0,2,\dots ,14}(1-2q_i{z}^{-1}+z^{-2})},$$

(4)

$$F_2(z)=\frac{F_2^{\prime }(z)}{(1-z^{-2})}=(1-a[16]){\displaystyle \prod _{i=1,3,\dots ,13}(1-2q_i{z}^{-1}+z^{-2})},$$

(5)

where the coefficients q_i are referred to as the ISPs in the cosine domain and a [16] is the last predictor coefficient. A Chebyshev polynomial is used to solve (4) and (5). Finally, derived from the ISP coefficients, 16th order ISF coefficients ω_i can be obtained by taking the transformation ω_i = arccos(q_i).

2.2. Quantization of ISF Coefficients

Before a quantization process, a mean-removed and a first order MA filtering are performed on the ISF coefficients to obtain a residual ISF vector, that is,

$$r(n)=z(n)-p(n),$$

(6)

where z(n) and p(n) respectively denote the mean-removed ISF vector and the predicted ISF vector at frame n by a first order MA prediction, defined as

$$p(n)=\frac{1}{3}\widehat{r}(n-1),$$

(7)

where $\widehat{r}(n-1)$ is the quantized residual vector at the previous frame.

Subsequently, S-MSVQ is performed on r(n). As presented in

Table 1. Structure of split-multistage vector quantization (S-MSVQ) in adaptive multi-rate wideband (AMR-WB) in the 8.85–23.85 kbit/s coding modes.

Structure of S-MSVQ
Stage 1	CB1:			CB2:
	r1 (1–9 order of r)			r2 (10–16 order of r)
	(8 bits)			(8 bits)
Stage 2	CB11:	CB12:	CB13:	CB21:	CB22:
	r(2)1,1–3	r(2)1,4–6	r(2)1,7–9	r(2)2,1–3	r(2)2,4–7
	(6 bits)	(7 bits)	(7 bits)	(5 bits)	(5 bits)

and

Table 2. Structure of S-MSVQ in AMR-WB in the 6.60 kbit/s coding mode.

Structure of S-MSVQ
Stage 1	CB1:		CB2:
	r1 (1–9 order of r)		r2 (10–16 order of r)
	(8 bits)		(8 bits)
Stage 2	CB11:	CB12:	CB21:
	r(2)1,1–5	r(2)1,6–9	r(2)2,1–7
	(7 bits)	(7 bits)	(6 bits)

, S-MSVQ is categorized into two types in terms of the bit rate of the coding modes. In stage 1, r(n) is split into two subvectors, namely, a 9-dimensional subvector r₁(n) associated with codebook CB1 and a 7-dimensional subvector r₂(n) associated with codebook CB2, for VQ encoding. As a preliminary step of stage 2, the quantization error vectors are split into three subvectors for the 6.60 kbps mode or five for the modes with bitrates between 8.85 and 23.85 kbps, symbolized as $r_i^{(2)}=r_i-{\widehat{r}}_i,i=1,2$, respectively. For instance, r⁽²⁾_1,1–3 in Table 1 represents the subvector split from the 1st to the 3rd components of r₁, and then VQ encoding is performed thereon over codebook CB11 in stage 2. Likewise, r⁽²⁾_2,4–7 stands for the subvector split from the 4th to the 7th components of r₂, after which VQ encoding is performed over codebook CB22 in stage 2. Finally, a squared error ISF distortion measure, that is, Euclidean distance, is used in all the quantization processes.

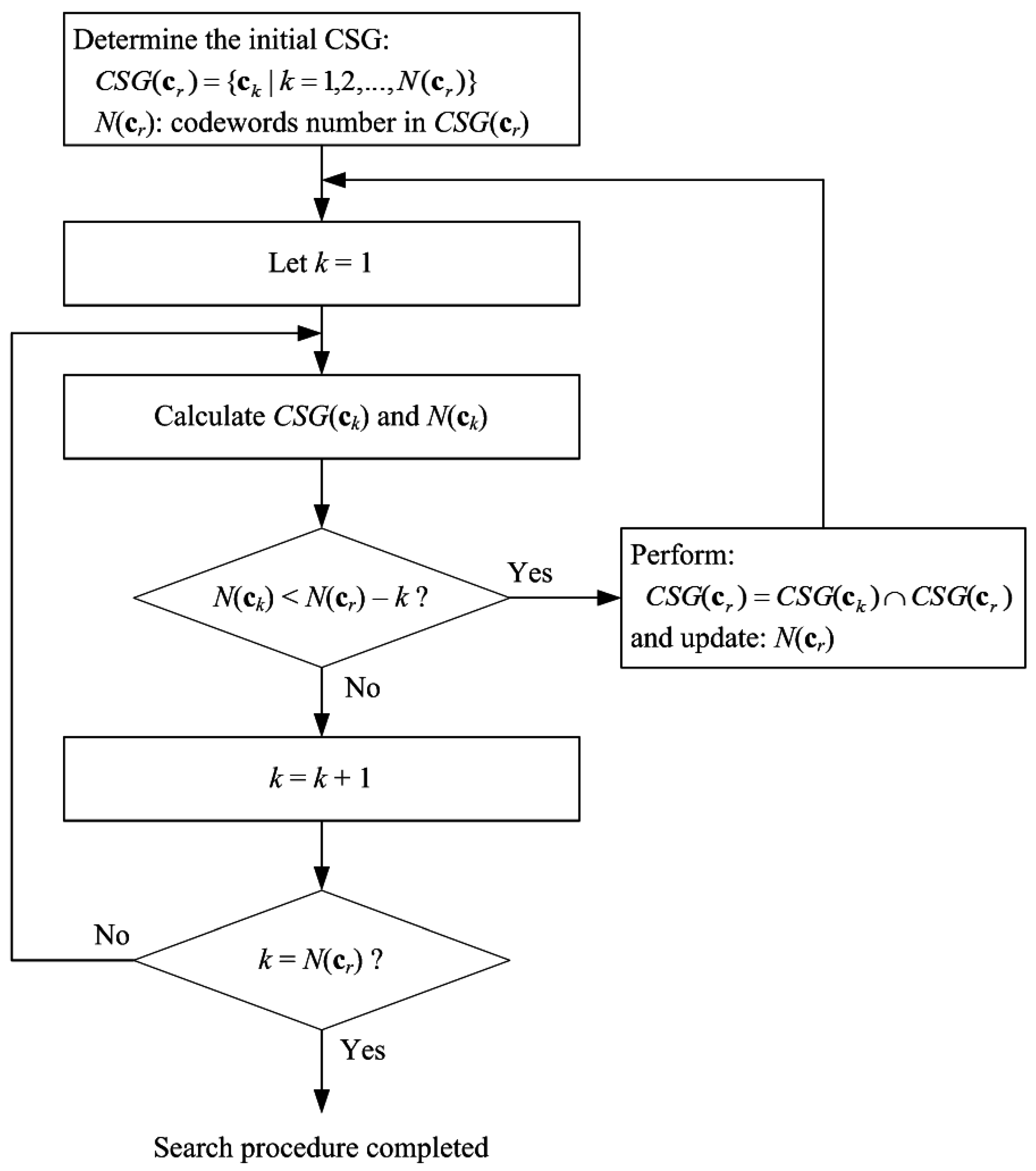
3. DI-TIE Search Algorithm for ISF Quantization

DI-TIE is presented as a two-stage search algorithm, i.e., a dynamic mechanism as the first stage and an intersection mechanism as the second. For the sake of discussion, a TIE algorithm is firstly stated as follows. As presented in [18], a codeword captured from the preceding frame is treated as a reference codeword c_r in the current frame. Subsequently, the Euclidean distance between an input vector x and c_r, symbolized as d(c_r, x), is evaluated. A set, composed of all the codewords c_i satisfying the condition $d(c_r,c_i)<2d(c_r,x)$, is referred to as a candidate search group (CSG), denoted by CSG(c_r) and formulated as

$$\mathrm{TIE}:CSG(c_r)=\left\{c_i\right|d(c_r,c_i)<2d(c_r,x)\},1\le i\le CNum,$$

(8)

where CNum represents the total number of codewords. CSG(c_r) is the search space over which a current codebook search is performed. In addition, a lookup table listing all the codewords sorted by the Euclidean distance is prebuilt for the TIE search algorithm.

The dynamic mechanism refers to a mechanism exclusively developed to downsize a search space dynamically. With N(c_r) representing the number of candidate codewords contained in CSG(c_r), the aim is to find a way to reduce the value of N(c_r). For this sake, each candidate codeword in CSG(c_r), c_k, 1 ≤ k ≤ N(c_r), is treated in turn as a reference codeword. For instance, c_k at k = 1, represented as $c_k{|}_{k=1}$, is initially appointed a reference codeword, according to which CSG(c_k) and N(c_k) are found directly in the lookup table, and merely one time evaluation of d(c_k, x) is required each time CSG(c_k) is determined. Thus, if the updated CSG(c_k) satisfies the condition N(c_k) < N(c_r) – k, the search space can be downsized, and then move forward to stage 2. Otherwise, the above-stated mechanism is repeatedly performed on the rest of c_k until the end.

In stage 2, intersection of the sets CSG(c_r) and CSG(c_k) is performed, in an attempt to locate the optimal codeword that lies in each CSG, and in an effort to downsize the search space for search performance improvement. CSG(c_r) is updated as

$$CSG(c_r)=CSG(c_k)\cap CSG(c_r).$$

(9)

The N(c_r) and the reference codeword are updated until a search task is done. The DI-TIE search algorithm is illustrated as a flowchart in Figure 1, and is described below.

Algorithm 1: Search procedure of DI-TIE

Step 1. Build a TIE lookup table. Step 2. Compute the Euclidean distance d(cr, x), and then determine the initial search space according to (8), that is, $$CSG(c_r)=\left\{c_k\right|k=1,2,\mathrm{...},N(c_r)\}$$ (10) where ck and N(cr) denote the codewords and the number thereof in CSG(cr), respectively. Step 3. Starting at k = 1, assign ck as a new reference codeword, compute d(ck, x), and then determine CSG(ck) and N(ck). Step 4. if (N(ck) < N(cr) − k), then perform the set intersection operation in (9), update N(cr), let k = 1, and repeat Step 3. Otherwise, let k = k + 1, and then repeat Step 3 and Step 4, until k = N(cr).

4. Experimental Results

A performance comparison is made among the presented DI-TIE, a typical TIE [18], a multiple TIE (MTIE) [20] and an EEENNS. Since TIE-based and EEENNS VQ codebook searches are conducted, a 100% search accuracy is obtained by such four algorithms as compared with a full search approach. For this sake, performance is compared in terms of search complexity. The test objects are those selected out of a Chinese language speech database, containing 1694 syllables out of 50 sentences for a duration over 445 s and 22,244 frames.

Table 3. Average number of searches versus search algorithms in the 8.85–23.85 kbit/s modes.

Method		Full Search	TIE	MTIE	EEENNS	DI-TIE
Stage 1	CB1	256	118.08	83.55	60.44	46.83
	CB2	256	158.79	110.16	61.73	41.34
Stage 2	CB11	64	48.41	38.98	14.09	13.22
	CB12	128	96.14	80.91	22.75	14.18
	CB13	128	92.19	76.62	20.58	13.24
	CB21	32	26.79	23.77	11.04	8.97
	CB22	32	29.19	27.57	17.35	12.72

gives a comparison on the average number of searches for coding modes with bitrates between 8.85 and 23.85 kbps, while

Table 4. Complexity reduction representation of Table 3.

Method		Full Search (Benchmark)	TIE	MTIE	EEENNS	DI-TIE
Stage 1	CB1	0	53.87%	67.36%	76.39%	81.71%
	CB2	0	37.97%	56.97%	75.89%	83.85%
Stage 2	CB11	0	24.36%	39.10%	77.99%	79.34%
	CB12	0	24.89%	36.79%	82.23%	88.93%
	CB13	0	27.97%	40.14%	83.93%	89.65%
	CB21	0	16.28%	25.72%	65.50%	71.95%
	CB22	0	8.77%	13.85%	45.79%	60.26%

lists a comparison on the percentage complexity reduction with the search load required in a full search algorithm as a benchmark. An observation in Table 3 and Table 4 reveals two findings. Firstly, DI-TIE is found to provide a remarkable search complexity reduction, relative to its counterparts. Secondly, the percentage complexity reduction is found to have a strong dependence on the codebooks over which a codeword search is carried out, particularly in the case of TIE, and it must be noted that DI-TIE is found to outperform EEENNS.

Taking the codebook CB22 as an instance, the complexity reduction is well maintained at 60.26% in the case of DI-TIE, while plunges to 13.85% and 8.77% in the cases of MTIE and TIE, respectively. This might be due to the reason that CB22 contains a great number of similar codewords, that is, they are very close to each other. Thus, it is respectively required to search a great number of codewords over the search space in MTIE and TIE. In contrast, the search space in DI-TIE is efficiently downsized in such a way that a high search performance can be maintained over codebooks.

Furthermore,

Table 5. Average number of searches versus search algorithms in the 6.60 kbit/s mode.

Method		Full Search	TIE	MTIE	EEENNS	DI-TIE
Stage 1	CB1	256	120.97	85.01	61.43	48.38
	CB2	256	160.93	111.34	62.42	42.27
Stage 2	CB11	128	112.86	104.86	55.99	37.70
	CB12	128	102.88	92.63	36.41	19.80
	CB21	64	62.83	62.76	53.14	40.14

gives a comparison on the average number of searches for the 6.60 kbps mode, and

Table 6. Complexity reduction representation of Table 5.

Method		Full Search (Benchmark)	TIE	MTIE	EEENNS	DI-TIE
Stage 1	CB1	0	52.74%	66.79%	76.01%	81.10%
	CB2	0	37.14%	56.51%	75.62%	83.49%
Stage 2	CB11	0	11.83%	18.08%	56.26%	70.54%
	CB12	0	19.62%	27.64%	71.55%	84.53%
	CB21	0	1.83%	1.93%	16.96%	37.28%

gives a complexity reduction comparison with the full search as a benchmark. The performance superiority of DI-TIE is demonstrated again over EEENNS, MTIE and TIE, particularly in the CB21 case, a finding in agreement with Table 3 and Table 4.

Table 7. Overall performance comparison among various methods.

Method	Percentage Complexity Reduction (%)
	8.85–23.85 kbit/s Modes	6.60 kbit/s Mode
Full search	Benchmark	Benchmark
TIE	41.64	36.26
MTIE	56.55	49.46
EEENNS	76.31	68.62
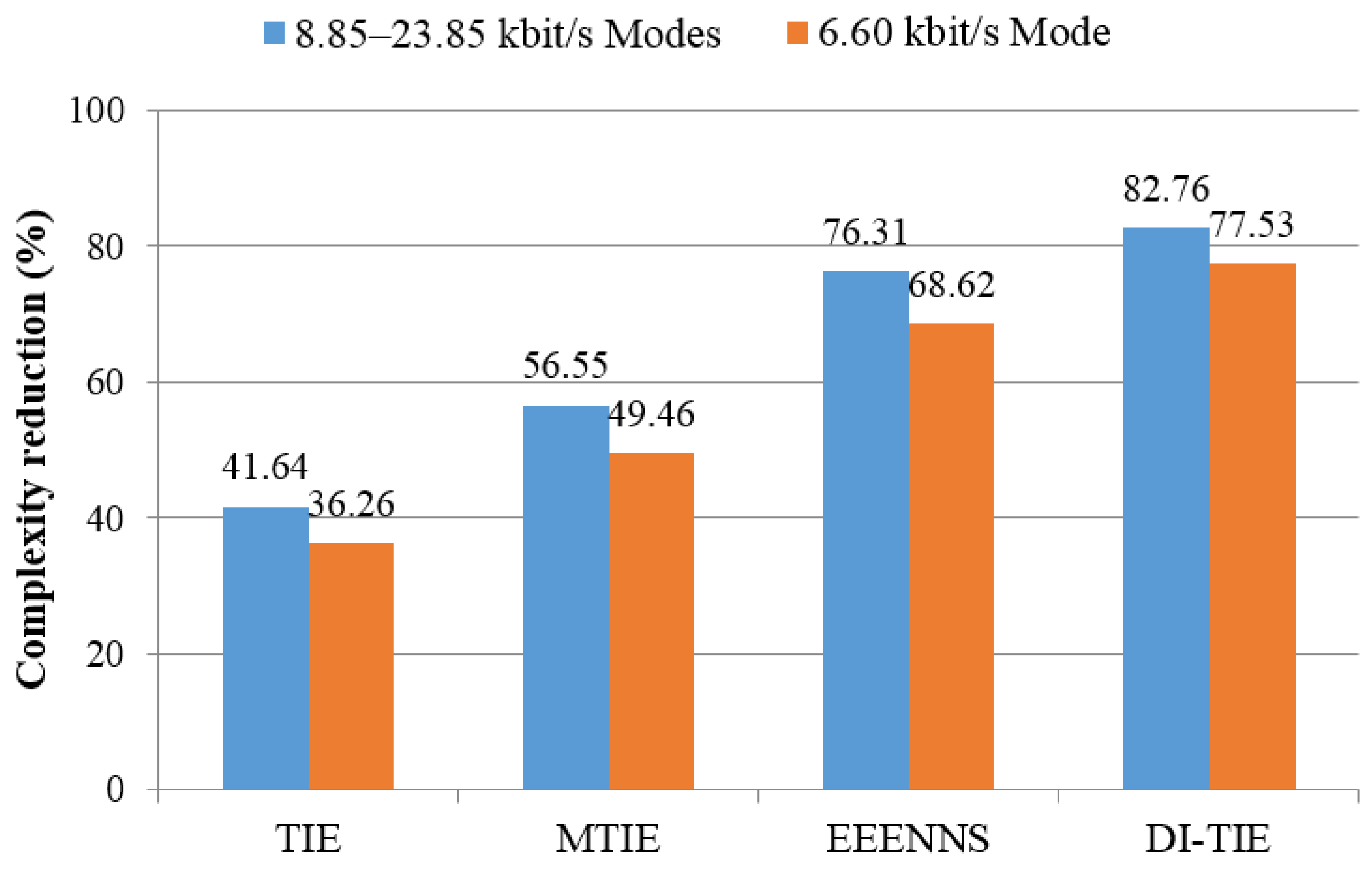
DI-TIE	82.76	77.53

gives an overall performance comparison with the full search as a benchmark, and is presented as well as a bar graph in Figure 2. The overall performance refers to the total search load, defined as the sum of the average number of searches multiplied by the vector dimension in each codebook. As clearly indicated in Figure 2, this proposal is experimentally validated as a superior candidate relative to the EEENNS and the TIE-based counterparts.

5. Conclusions and Future Work

This paper presents a DI-TIE algorithm for ISF vector quantization in the AMR-WB speech codec. As a result, the search complexity is as expected reduced to a great extent, but without a deterioration in the speech coding quality. This complexity reduction superiority is seen when it is applied to a codeword search over five codebooks in the 6.6 kbps mode, and over seven codebooks in the remaining eight modes. In terms of overall complexity reduction, this presented DI-TIE algorithm is validated again by experimental means as superior to TIE, MTIE and EEENNS search approaches.

Furthermore, this improved AMR-WB speech codec can be adopted to improve the VoIP performance on a smartphone. As a consequence, the energy efficiency requirement is achieved for an extended operation time period due to computational load reduction.

As scheduled, the presented search algorithm will be employed to handle VQ codebook search tasks required in speech, audio and video codecs for the purpose of further computational load reduction in the very near future. This move is expected to achieve a tremendous improvement in real-time audio/video compression and transmission in embedded systems.