Cosmological Probes for Supersymmetry
Abstract
: The multi-parameter character of supersymmetric dark-matter models implies the combination of their experimental studies with astrophysical and cosmological probes. The physics of the early Universe provides nontrivial effects of non-equilibrium particles and primordial cosmological structures. Primordial black holes (PBHs) are a profound signature of such structures that may arise as a cosmological consequence of supersymmetric (SUSY) models. SUSY-based mechanisms of baryosynthesis can lead to the possibility of antimatter domains in a baryon asymmetric Universe. In the context of cosmoparticle physics, which studies the fundamental relationship of the micro- and macro-worlds, the development of SUSY illustrates the main principles of this approach, as the physical basis of the modern cosmology provides cross-disciplinary tests in physical and astronomical studies.1. Introduction
The multi-parameter space of supersymmetric (SUSY) models inevitably implies a combination of direct and indirect studies, in which cosmological probes play an important role. Such probes provide supplementary tools to specify the expected properties of SUSY particles, both for their efficient search at accelerators and for their ability to explain cosmological dark matter. In the latter case, the existence of new conservation laws in SUSY models, such as R-parity, leads to the stability of the lightest particle that possesses the corresponding conserved property. Created in the early Universe, such particles should survive to the present day and play the role of dark-matter candidates. This is the simplest and most widely known cosmological impact of supersymmetry.
However, the fundamental basis of supersymmetric models contains a much wider field of cosmological consequences. This basis can naturally include physical mechanisms for inflation and baryosynthesis and could become the physical grounds for modern inflationary cosmology with baryosynthesis and dark matter. Such mechanisms imply physics of the very early Universe, which can hardly be probed by direct experimental means, hence the necessity to extend the set of theoretical tools to study these phenomena. Moreover, the absence of positive results in the experimental search for SUSY particles at accelerators can move their mass scale to values so high, that only indirect methods of study would be appropriate.
Here, following the general framework of discussion of cosmological effects [1,2], we consider some nontrivial features of such effects in their possible application to supersymmetric models, paying special attention to predictions of nonequilibrium particles and primordial nonlinear structures, in which primordial black holes (PBH), the effects of PBH evaporation and even antimatter domains in the baryon asymmetrical Universe can provide nontrivial probes for supersymmetry in astronomical observations and space experiments.
After a brief review of the cosmological traces of particle models and of their possible relationship with SUSY (Section 2), we turn to PBHs that can play the role of a unique theoretical tool in studies of physics of the very early Universe. We consider some mechanisms of PBH formation (Section 3) and possible effects of SUSY particles in PBH evaporation (Section 4). Metastable SUSY particles or evaporating PBHs are the source of nonequilibrium particles after Big Bang nucleosynthesis that can influence the primordial chemical composition or provide a non-thermal production of dark matter particles (Section 5). A succession of phase transitions in the inflationary Universe can result in primordial nonlinear structures (Section 6). A profound signature of a nonhomogeneous SUSY-based mechanism for baryosynthesis is the appearance of antimatter domains in a baryon asymmetric Universe (Section 7). We conclude that the development of supersymmetric models perfectly illustrates the might of the basic principles of cosmoparticle physics [3–8], which studies the physical basis of the modern cosmology and combines probes from cosmology, astrophysics and experimental physics in a systematic way (Section 8).
2. Cosmological Traces of Particle Models
Let us start following [1,2] (see also [9–13]) with a general discussion of a variety of cosmological consequences of particle models and of their possible implementation in the SUSY case.
If R-parity is conserved, the lightest supersymmetric particle (LSP) should be stable. If these particles were created at the early stages of cosmological evolution, they should survive in the Universe until the present time. Therefore, the simplest cosmological effect of supersymmetric models is a gas of new stable massive particles, originated from the early Universe.
For particles with mass m, at high temperature (throughout the paper, we use the units ħ = c = k = 1, if it is not specified otherwise). T > m, the equilibrium condition, n · σv · t > 1, is valid, if their annihilation cross-section σ > 1/(mmpl) is sufficiently large to establish equilibrium. At T < m, such particles go out of equilibrium, and their relative concentration freezes out. Weakly-interacting species decouple from the plasma and the radiation at T > m, when n · σv · t ~ 1, i.e., at . This is the main idea of the calculation of primordial abundances for WIMP-like dark matter candidates, such as the neutralino (see, e.g., [5,8] for details).
The maximal temperature that is reached in an inflationary Universe is the reheating temperature, Tr, after inflation. Therefore, very weakly-interacting particles with annihilation cross-section σ < 1/(Trmpl), as well as very heavy particles with mass m ≫ Tr cannot be in thermal equilibrium, and the detailed mechanism of their production should be considered to calculate their primordial abundances. This is the case for the gravitino, which has a semigravitational interaction cross-section.
By definition, primordial stable particles survive to the present day and should be present in the modern Universe. The net effect of their existence is given by their contribution to the total cosmological density. If they dominate at the matter-dominated stage, they play the role of cosmological dark matter that formed the large-scale structure of the Universe. To be a dark matter candidate, stable particles should decouple from the plasma and the radiation before the beginning of the matter-dominated (MD) stage. This can be satisfied for a very wide range of cross-sections of particle interaction with matter, from superweak to strong. The miracle of weakly interacting massive particles (such as neutralinos) is that their annihilation cross-section provides the frozen out concentration that explains the observed dark matter density. For the cross-sections typical of weak interaction, a direct search for primordial dark-matter particles in underground experiments is possible (see [14–17] and the references therein).
Dark-matter particles can annihilate in the Galaxy, contributing by their annihilation products to the flux of cosmic rays and gamma radiation. It was first found in [18] that such an effect of dark matter annihilation can provide a sensitive tool in indirect studies of dark matter by the measurements of cosmic positron and gamma background fluxes.
There may be several types of new stable particles. Then, multi-component dark matter scenarios are realized. It is interesting that such a multi-component scenario can naturally arise in the heterotic-string phenomenology, which can embed both LSP and other possible types of stable particles or objects.
The mechanism of compactification and symmetry breaking leads to the prediction of homotopically-stable objects [19] and shadow matter [20], giving a wide variety of new types of dark matter candidates.
The embedding of the symmetry of the standard model and supersymmetry within the heterotic string phenomenology can be also accompanied by the prediction of a fourth generation of quarks and leptons [21] with a stable massive fourth neutrino [22] and possibly a stable quark.
Indeed, the comparison between the rank of the unifying group E6 (r = 6) and the rank of the standard model (r = 4) implies the existence of new conserved charges and new (possibly strict) gauge symmetries. A new strict gauge U(1) symmetry (similar to the U(1) symmetry of electrodynamics) is possible, if it is ascribed to the fermions of the fourth generation. This hypothesis explains, in particular, the difference between the three known types of neutrinos and the neutrinos of the fourth generation. The latter possesses a new gauge charge and, being a Dirac particle, cannot have a small Majorana mass due to the see-saw mechanism. If the fourth neutrino is the lightest particle of the fourth quark-lepton family, the strict conservation of the new charge makes it absolutely stable. Following this hypothesis [21], the quarks and the leptons of the fourth generation are the source of a new long-range interaction (y-electromagnetism), similar to the electromagnetic interaction of ordinary charged particles.
New particles with an electric charge and/or a strong interaction can form anomalous atoms and be contained in the ordinary matter as anomalous isotopes. For example, if the lightest quark of the fourth generation is stable, it can form stable charged hadrons, serving as nuclei of anomalous atoms of, e.g., anomalous hydrogen and helium [23–28]. The experimental upper limits on the concentration of anomalous isotopes and especially of anomalous hydrogen severely constrains the possibility of new stable charged particles and practically rules out such particles with charges +1 or −1. However, particles with charge −2 can exist, avoid these constraints and be hidden in O-helium atoms: their neutral atom-like bound states with primordial helium nuclei. The O-helium hypothesis can explain some puzzles of dark matter searches, challenging experimental searches for stable doubly-charged particles at the LHC [1,29]. The −2 charge component of O-helium can originate from stable anti-U quarks of a fourth generation, which can form a -like (ŪŪŪ) state bound by chromoelectric forces [27].
Therefore, together with SUSY candidates, some other types of dark matter candidates—massive stable fourth generation neutrinos, as well as nuclear-interacting O-helium dark atoms, made of stable (anti-)U quarks of the fourth generation—are possible in the heterotic string phenomenology, the framework of which favors a multicomponent analysis of dark-matter effects.
In the multi-component dark matter scenario, a detailed study of the distribution of particles in space, of their condensation in galaxies, of their capture by stars, Sun and Earth, as well as of the effects of their interaction with matter and of their annihilation, provides a sensitive probe for the existence of even subdominant components. In particular, though stable, neutrinos of the fourth generation with masses about 50 GeV are predicted to be the subdominant form of dark matter, contributing less than 0.1% to the total dark matter density [18,22,30–36]; this possibility can be ruled out by direct experimental searches for WIMPs (see [14–17] and the references therein) and by studies of the effects of the annihilation of fourth generation neutrinos and antineutrinos in the Galaxy in the galactic gamma-background. Fourth generation neutrino annihilation inside the Earth should also lead to a flux of underground monochromatic neutrinos of known types, which can be excluded by the analysis of the existing data from underground neutrino detectors.
Primordial unstable particles with a lifetime shorter than the age of the Universe, τ < tU, cannot survive to the present day. However, if their lifetime is sufficiently large to satisfy the condition τ ≫ (mpl/m) · (1/m), their existence in the early Universe can lead to direct or indirect traces. The cosmological flux of decay products contributing to the cosmic- and gamma-ray backgrounds represents the direct trace of unstable particles. If the decay products do not survive to the present time, their interaction with matter and radiation can cause indirect effects in the light element abundance or in the fluctuations of thermal radiation.
If the particle lifetime is much shorter than 1 s, multi-step indirect traces are possible, provided that particles dominate in the Universe before their decay. During the dust-like stage of their dominance, black hole formation takes place, and the spectrum of such primordial black holes traces the particle properties (mass, frozen concentration, lifetime) [37]. Particle decay in the end of the dust-like stage influences the baryon asymmetry of the Universe. In any case, logical chains within a given cosmic phenomenology link the predicted properties of even unstable new particles to the effects accessible in astronomical observations. Such effects may be important for the analysis of the observational data.
The parameters of new stable and metastable particles are also determined by the pattern of symmetry breaking. This pattern is reflected in a succession of phase transitions in the early Universe. First order phase transitions proceed through bubble nucleation, which can result in black hole formation [38] (see e.g., [39,40] for a review and references). Phase transitions of the second order can lead to the formation of topological defects, such as walls, strings or monopoles. The observational data put severe constraints on magnetic monopoles [41,42] and cosmic wall production [43], as well as on the parameters of cosmic strings [44,45]. The structure of the cosmological defects can be changed in successive phase transitions. More complicated forms, such as walls surrounded by strings, can appear. Such structures can be unstable, but their existence can leave a trace in the nonhomogeneous distribution of dark matter and give rise to large-scale structures of nonhomogeneous dark matter, such as archioles [46–48]. Primordial black holes, whose hypothetical existence was first formulated by Zeldovich and Novikov [49], represent a profound signature of such structures.
3. The Reflection of High-Energy Physics in the PBH Spectrum
Primordial black holes (PBHs) are a very sensitive cosmological probe of physics phenomena occurring in the early Universe. They could be formed by many different mechanisms (see, e.g., [1,2] for a review and references).
After formation, PBHs should remain in the Universe and, if they survive to the present day, they should represent a specific form of dark matter (see e.g., [50]). PBH evaporation by Hawking radiation [51] makes them a source of products of evaporation, which contain any type of particles that can exist in our space-time, both known and unknown. For a wide range of parameters, the predicted effect of PBHs contradicts the data and puts restrictions on the mechanisms of PBH formation and on the underlying physics of the very early Universe. On the other hand, for some fixed values of their parameters, PBHs or their evaporation can provide a nontrivial solution to some astrophysical problems.
Here, we outline, following [1,2,50], the relationship of new physics with the mechanisms of PBH formation and the possible reflection of its parameters in the PBH spectrum.
3.1. PBHs from Superheavy Metastable Particles
The formation of a black hole is highly improbable in a homogeneous expanding Universe, since it implies metric fluctuations of order one. For Gaussian metric fluctuations with a dispersion 〈δ2〉 ≪ 1, the probability of such fluctuations is determined by the exponentially small tail of the high-amplitude part of the distribution. This probability can even be more suppressed in the case of non-Gaussian fluctuations [2].
If the Universe has an equation of state p = γϵ, with the numerical factor γ being in the range 0 ≤ γ ≤ 1, the probability to form a black hole from fluctuations within the cosmological horizon is given by [52]:
This provides an exponential sensitivity of the PBH spectrum to the softening of the equation of state in the early Universe (γ → 0) or to the increase of the ultraviolet part of the spectrum of density fluctuations (〈δ2〉 → 1). These phenomena can appear as cosmological consequences of particle theory.
It was first noticed in [53] that the dominance of superheavy metastable particles with lifetime τ ≪ 1 s in the Universe before their decay at t ≤ τ can result in the formation of PBHs, remaining in the Universe after the particles have decayed and keeping some information on the particle properties in their spectrum.
After reheating, at T < T0 = rm, particles with mass m and relative abundance r = n/nr (where n is the frozen-out concentration of particles and nr is the concentration of relativistic species) must dominate in the Universe before their decay. Dominance of these nonrelativistic particles at t > t0, where , corresponds to a dust-like stage with an equation of state p = 0, for which the particle density fluctuations grow as:
The formation of these systems can result in black-hole formation either immediately after the system decouples from the expansion or as a result of the evolution of initially-formed nonrelativistic gravitationally-bound systems [54,55].
If the density fluctuation is especially homogeneous and isotropic, it directly collapses to PBH as soon as the amplitude of fluctuation grows to one and the system decouples from the expansion. The probability for direct PBH formation in the collapse of such homogeneous and isotropic configurations gives a minimal estimate of PBH formation at the dust-like stage.
The mechanism [2,53] is effective for the formation of PBHs with masses in the interval:
The minimal mass corresponds to the mass within the cosmological horizon at time t ~ t0, when particles start to dominate in the Universe, and it is equal to [2,53]:
The maximal mass is indirectly determined by the condition:
The direct mechanism of PBH formation can also be effective during a pre-reheating dust-like post-inflation stage of inflaton field oscillations [56].
3.2. Spikes from Phase Transitions during an Inflationary Stage
A scale-dependent spectrum of fluctuations, in which the amplitude of small-scale fluctuations is enhanced, can be another factor increasing the probability of PBH formation. The simplest functional form of such a spectrum is represented by a blue spectrum with a power law dispersion:
In a chaotic inflation scenario, the interaction of a Higgs field ϕ with the inflaton η can give rise to phase transitions during the inflationary stage, if this interaction induces a positive mass term . When in the course of slow rolling, the amplitude of the inflaton decreases below a certain critical value ηc = mϕ/ν, the mass term in the Higgs potential:
If a phase transition takes place at e-folding N before the end of inflation, the spike re-enters the horizon at the radiation dominance (RD) stage and forms black holes of mass:
If the spike re-enters the horizon during the matter dominance (MD) stage, it should form black holes of mass:
3.3. PBHs from First-Order Phase Transitions in the Early Universe
First-order phase transitions go through bubble nucleation. The simplest way to describe first order phase transitions with bubble creation in the early Universe is based on a scalar field theory with two non-degenerate vacuum states. Being stable at the classical level, the false vacuum state decays due to quantum effects, leading to a nucleation of bubbles of a true vacuum and their subsequent expansion [2]. The potential energy of the false vacuum is converted into the kinetic energy of the bubble walls, thus making them highly relativistic in a short time. The bubble expands till it collides with another one. As was shown in [39], a black hole may be created in a collision of two bubbles.
Just after the collision, the mutual penetration of the walls up to a distance comparable with their width is accompanied by a significant increase in potential energy [2]. Then, the walls reflect each other and accelerate backwards. The space between them gets filled by the field in the false vacuum state, converting the kinetic energy of the wall back to the energy of the false vacuum state and slowing down the velocity of the walls. Meanwhile, the outer area of the false vacuum is absorbed by the outer wall, which expands and accelerates outwards. There is an instant when the central region of the false vacuum is causally separated from the walls [59]. If this false vacuum bag shrinks in its oscillations within its gravitational radius, a black hole is formed. The mass of this PBH is given by (see [39]):
If inflation ends with a first-order phase transition, collisions between bubbles of Hubble size in the percolation regime lead to copious PBH formation with masses:
4. Gravitino Production by PBH Evaporation
Presently, there is no observational evidence proving the existence of PBHs. However, even the absence of PBHs provides a very sensitive theoretical tool to study the physics of the early Universe. PBHs represent a nonrelativistic form of matter, and their density decreases with the scale factor a as a−3 ∝ T 3, while the total density is ∝ a−4 ∝ T4 in the period of radiation dominance (RD). As it must be formed within the horizon, a PBH of mass M can be formed only after:
If they are formed during the RD stage, the smaller are the masses of PBHs, the larger their relative contribution to the total density during the modern MD stage. Therefore, even the modest constraint on the density of PBHs of mass M:
The possibility of PBH evaporation, revealed by Hawking [51], strongly influences the effects of PBHs. In the strong gravitational field near the gravitational radius rg of the PBH, the quantum effect of the creation of particles with momentum p ~ 1/rg is possible. Due to this effect, the PBH becomes a black-body source of particles with temperature (in units ħ = c = k = 1):
The evaporation time scale can be written in the following form:
The relationship between β(M) and α(M) has a more complicated form if PBHs are formed during early dust-like stages [5,37,61,62] or if such stages take place after the PBH formation [5,62]. The relative contribution of PBHs to the total density does not grow during the dust-like stage, and the relationship between β(M) and α(M) is model-dependent. A minimal model-independent factor α(M)/β(M) follows from the enhancement taking place only during the RD stage between the first second of expansion and the end of the RD stage at teq, since radiation dominance in this period is supported by the light element abundances and by the spectrum of the Cosmic Microwave Background (CMB) [5,8,37,61,62].
The effects of PBH evaporation make astrophysical data much more sensitive to the existence of PBHs. Constraining the abundance of primordial black holes can lead to invaluable information on cosmological processes, particularly as they are probably the only viable probe of the power spectrum at very small scales, which remain far from the CMB and from the large-scale structures’ (LSS) sensitivity ranges. To date, only PBHs with initial masses between ~109 g and ~1016 g have led to stringent limits (see, e.g., [37,63–66]) from the consideration of the entropy per baryon, the deuterium destruction, the 4He destruction and the cosmic rays currently emitted by the Hawking process [51]. The existence of light PBHs should lead to important observable constraints, either through the direct effects of the evaporated particles (for initial masses between 1014 g and 1016 g) or through the indirect effects of their interaction with matter and radiation in the early Universe (for PBH masses between 109 g and 1014 g).
Several constraints on the density of PBHs have been derived in different mass ranges assuming the evaporation to standard model particles only: for 109 g < M < 1013 g, the entropy per baryon at nucleosynthesis was used [67] to obtain β < (109 g/M); for 109 g < M < 1011 g, the production of pairs at nucleosynthesis was used [68] to obtain β < 3 × 10−17(109 g/M)1/2; for 1010 g < M < 1011 g, deuterium destruction was used [69] to obtain β < 3 × 10−22(M/1010 g)1/2; for 1011 g < M < 1013 g, spallation of 4He was used [62,70] to obtain β < 3×10−21(M/109 g)5/2; for M ≈ 5×1014 g, the gamma and cosmic rays were used [71,72] to obtain β < 10−28. Slightly more stringent limits were obtained in [73], leading to β < 10−20 for masses between 109 g and 1010 g and in [74], leading to β < 10−28 for M = 5 × 1011 g. Gamma rays and antiprotons were also recently re-analyzed in [75,76], improving a little on the previous estimates. Such constraints, related to phenomena occurring after nucleosynthesis, apply only for black holes with initial masses above ~109 g. Below this value, the only limit for a long time was the very weak entropy constraint (related to the photon-to-baryon ratio).
However, since the evaporation products are created by the gravitational field, any quantum with a mass lower than the black hole temperature should be emitted, independently of the strength of its interaction. This could provide a copious production of superweakly interacting particles that cannot be in equilibrium with the hot plasma of the very early Universe. This makes evaporating PBHs a unique source of all of the species that can exist in the Universe.
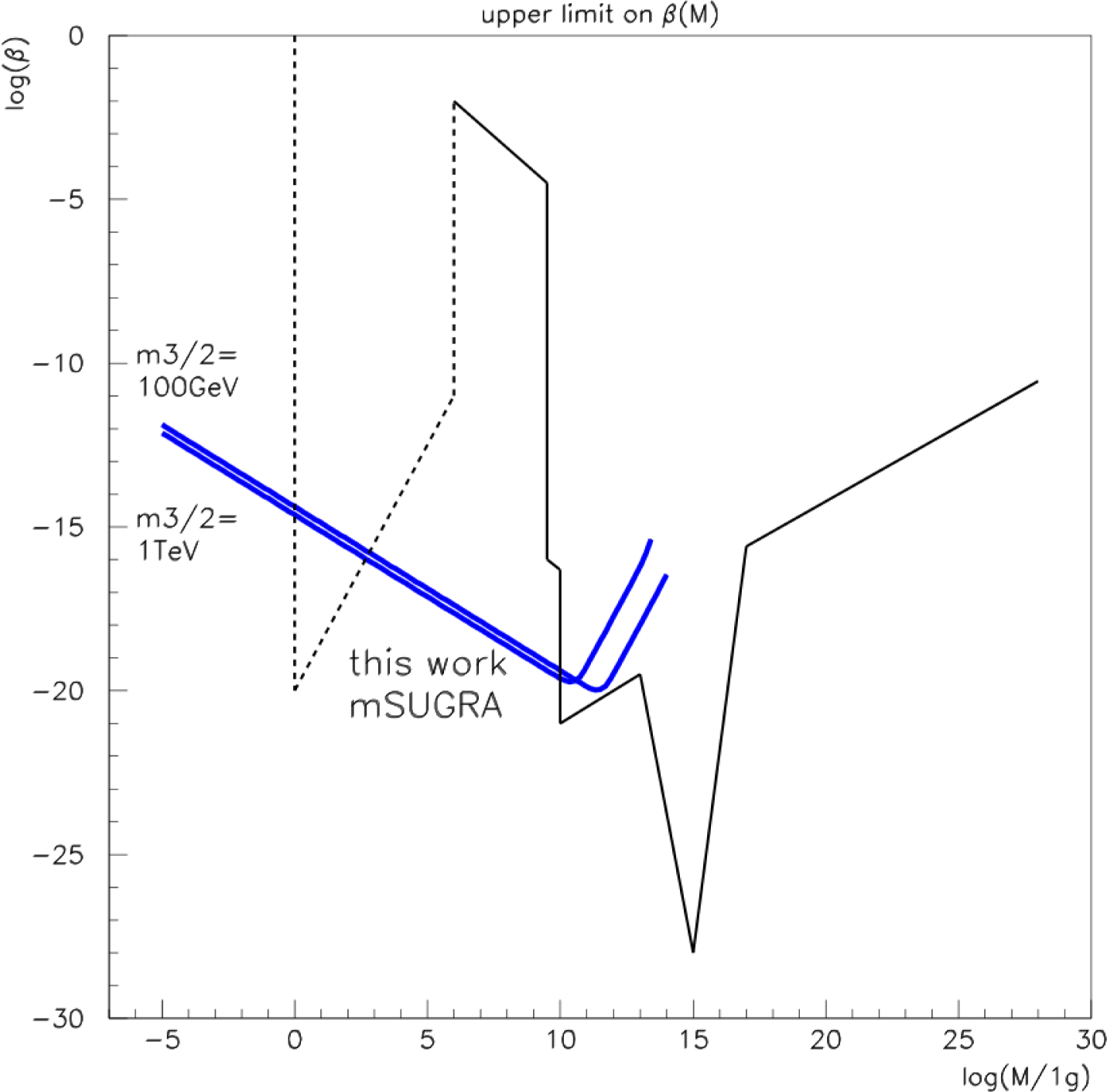
To derive a limit in the initial mass range mpl < M < 1011 g, gravitinos emitted by black holes (the limits on the abundance of PBHs from gravitino production were first calculated in [77]) were considered in [78]. Gravitinos are expected to be present in all local supersymmetric models, which are regarded as the more natural extensions of the standard model of high energy physics (see, e.g., [79] for an introductory review).
Following [5,8,62,80] and [77,81] (but in a different framework and using more stringent constraints), limits on the mass fraction of black holes at the time of their formation (β ≡ ρPBH/ρtot) were derived in [78] using the production of gravitinos during the evaporation process. Depending on whether gravitinos are expected to be stable or metastable, limits are obtained using the requirement that they do not overclose the Universe or that the formation of light nuclei by the interactions of 4He nuclei with a nonequilibrium flux of D, T, 3He and 4He does not contradict the observations. This approach is more constraining than the usual study of photo-dissociation induced by photon-photino pairs emitted by decaying gravitinos. This opened a new window for the upper limits on β below 109 g.
5. Nonequilibrium Particles
Superweakly-interacting gravitinos could not be in thermal equilibrium, and thus, the mechanisms of their production give rise to the appearance of nonequilibrium particles during the radiation-dominated stage. Metastable particles, decaying via hadronic or electromagnetic channels after Big Bang nucleosynthesis, result in fluxes of photons and electron-positron pairs with energies much larger than the thermal energies in this period. Nucleon-antinucleon pairs from such decays represent a profound example of the creation of species that cannot be in equilibrium in the considered period. The interaction of primordial nuclei with nonequilibrium particles from electromagnetic and hadronic cascades leads to recoil nuclei and nuclear fragments with energies above the Coulomb barrier and makes successive nuclear reactions possible.
In the framework of minimal supergravity (mSUGRA), the gravitino mass is, by construction, expected to lie around the electroweak scale, i.e., in the 100-GeV range. In this case, the gravitino is metastable and decays after nucleosynthesis, leading to important modifications of the nucleosynthesis paradigm. Instead of using the usual photon-photino decay channel, the study of [78] relied on the more sensitive gluon-gluino channel. Based on [82–86], the antiprotons produced by the fragmentation of gluons emitted by decaying gravitinos were considered as a source of nonequilibrium light nuclei resulting from collisions of those antiprotons on equilibrium nuclei. Then, 6Li, 7Li and 7Be nuclei production by the interactions of the nonequilibrium nuclear flux with 4He nuclei in equilibrium was taken into account and compared with data (this approach is supported by several recent analyses [87,88], which lead to similar results). The resulting Monte Carlo estimates [85] lead to the following constraint on the concentration of gravitinos: , where m3/2 is the gravitino mass in GeV. This constraint has been successfully used to derive an upper limit on the reheating temperature [85]: TR < 3.8 × 106 GeV. The consequences of this limit on cosmic-rays emitted by PBHs was considered, e.g., in [89]. In the approach of [78], this stringent constraint on the gravitino abundance was related to the density of PBHs through direct gravitino emission. The usual Hawking formula [51] was used for the number of particles of type i emitted per unit of time t and per unit of energy Q. Introducing the temperature defined by Equation (20)T = hc3/(16π2kGM) ≈ (1013g)/M GeV, taking the relativistic approximation for Γs and integrating over time and energy, the total number of quanta of type i can be estimated as:
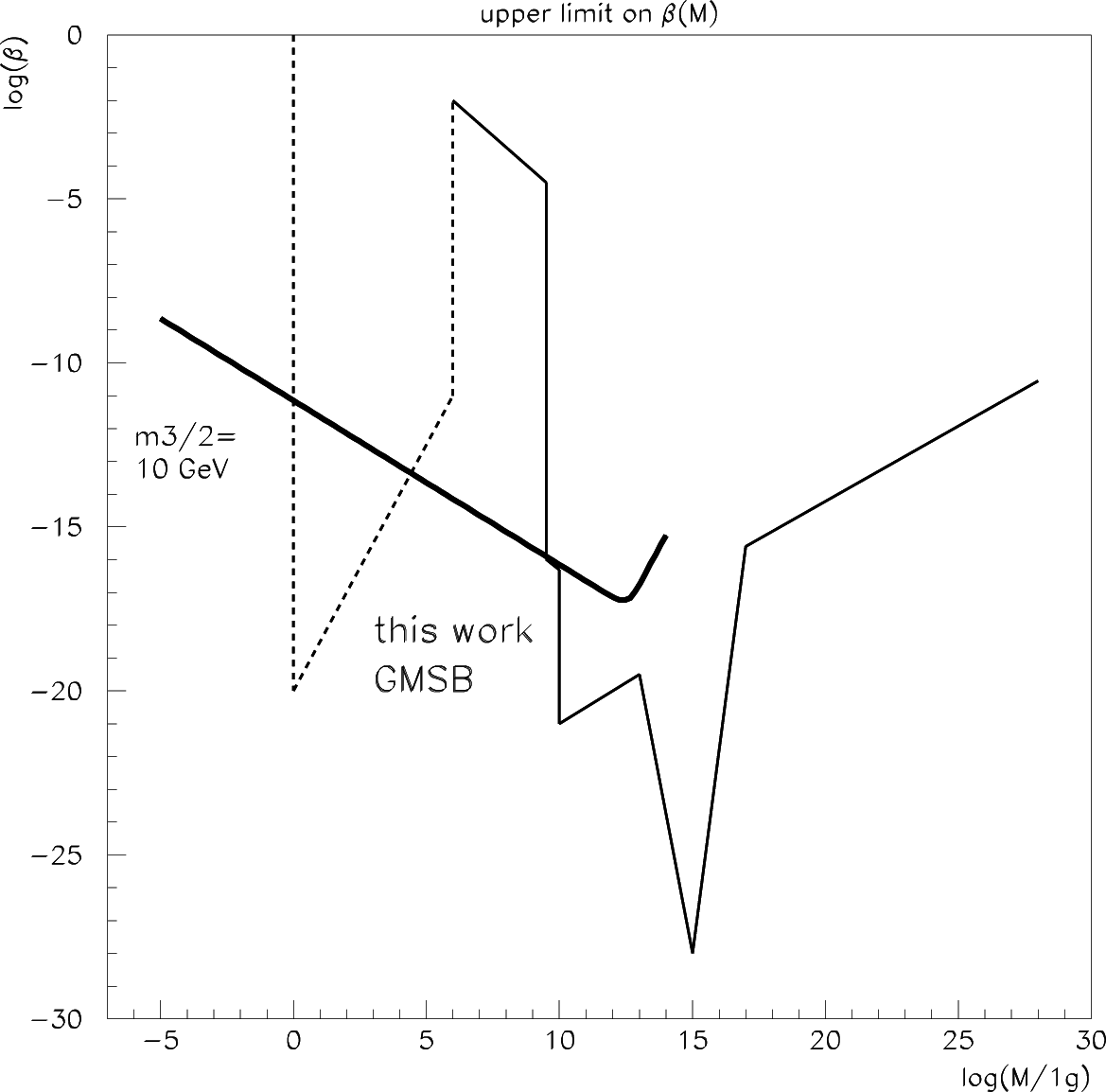
It is also possible to consider limits arising in gauge-mediated SUSY-breaking (GMSB) models [90]. Those alternative scenarios, incorporating a natural suppression of the rate of flavor-changing neutral currents due to the low energy scale, predict the gravitino to be the lightest supersymmetric particle (LSP). The LSP is stable if R-parity is conserved. In this case, a limit was obtained [78] by requiring Ω3/2,0 < ΩM,0, i.e., by requiring that the current gravitino density does not exceed the matter density. It can easily be derived from the previous method, by taking into account the dilution of gravitinos in the period of PBH evaporation and the conservation of gravitinos to keep a specific entropy ratio, that [78]:
6. Massive Primordial Black Holes from the Collapse of Closed Walls
A wide class of particle models possesses a symmetry breaking pattern, which can be effectively described by pseudo-Nambu–Goldstone (PNG) fields and which corresponds to the formation of an unstable topological defect structure in the early Universe (see [40] for a review and references). The Nambu–Goldstone nature of such an effective description reflects the spontaneous breaking of a global U(1) symmetry, resulting in a continuous degeneracy of vacua. The explicit symmetry breaking at a smaller energy scale changes this continuous degeneracy to a discrete vacuum degeneracy. The characteristics of the formed structures is different for phase transitions taking place during post-inflationary or inflationary stages.
6.1. Structures from a Succession of U(1) Phase Transitions
At high temperatures, such a symmetry breaking pattern implies a succession of second order phase transitions. In the first transition, continuous degeneracy of vacua leads, at scales exceeding the correlation length, to the formation of topological defects in the form of a string network; in the second phase transition, continuous transitions in space between degenerate vacua form surfaces: domain walls surrounded by strings. This last structure is unstable, but as was shown in the example of the invisible axion [46–48], it is reflected in the large-scale inhomogeneity of the distribution of energy density of coherent PNG (axion) field oscillations. This energy density is proportional to the initial value of the phase, which acquires the dynamical meaning of the amplitude of the axion field, when the axion mass is switched on in the result of the second phase transition.
The value of the phase changes by 2π around the string. This strong nonhomogeneity of phase leads to a corresponding nonhomogeneity of the energy density of coherent PNG (axion) field oscillations. The usual argument (see, e.g., [94] and the references therein) is essential only on scales corresponding to the mean distance between strings. This distance is small, being of the order of the scale of the cosmological horizon in the period during which PNG field oscillations start. However, since the nonhomogeneity of the phase follows the pattern of the axion string network, this argument misses large-scale correlations in the distribution of the energy density of oscillations.
Indeed, a numerical analysis of string networks (see the review in [95]) indicates that large string loops are strongly suppressed and that a fraction of about 80% of string length, corresponding to long loops, remains virtually the same at all large scales. This property is the other side of the well-known scale-invariant character of string networks. Therefore, the correlations in the energy density should persist on large scales, as was shown in [46–48].
The large-scale correlations in topological defects and their imprints in primordial inhomogeneities constitute an indirect effect of inflation, if phase transitions take place after the reheating of the Universe. Inflation provides in this case identical conditions for the phase transitions, which take place in causally-disconnected regions.
If phase transitions take place during the inflationary stage, new forms of primordial large-scale correlations appear. The value of the phase after the first phase transition is inflated over the region corresponding to the period of inflation, while during inflation, fluctuations of this phase change its initial value within regions of smaller size. Owing to such fluctuations, for a fixed value of θ60 in the period of inflation with e-folding N = 60 corresponding to the part of the Universe within the modern cosmological horizon, strong deviations from this value appear at smaller scales, corresponding to later periods of inflation with N < 60. If θ60 < π, the fluctuations can move the value of θN to θN > π in some regions of the Universe. After reheating as a result of the second phase transition, these regions, which correspond to a vacuum with θvac = 2π, are surrounded by the bulk of the volume with vacuum θvac = 0. As a result, massive walls are formed at the border between the two vacua. Since regions with θvac = 2π are confined, the domain walls are closed. As they fully enter the horizon, closed walls can collapse into black holes.
This mechanism can lead to the formation of primordial black holes of arbitrarily large mass (up to the mass of AGNs [96]; see for the latest review [97]). Such black holes appear in the form of primordial black hole clusters, exhibiting a fractal distribution in space [40,98,99]. They can shed new light on the problem of galaxy formation [40,100].
6.2. Formation of Closed Walls in an Inflationary Universe
To describe a mechanism for the appearance of massive walls of a size essentially greater than the horizon at the end of inflation, let us consider a complex scalar field with the potential [40,96,98,99]:
At the same time, the well-established behavior of quantum field fluctuations on the de Sitter background [102] implies that the wavelength of a vacuum fluctuation of every scalar field grows exponentially, having a fixed amplitude. Namely, when the wavelength of a particular fluctuation, in the inflating Universe, becomes greater than H−1, the average amplitude of this fluctuation freezes out at some non-zero value because of the large friction term in the equation of motion of the scalar field, whereas its wavelength grows exponentially. Such a frozen fluctuation is equivalent to the appearance of a classical field that does not vanish after averaging over macroscopic space intervals. Because the vacuum must contain fluctuations at every wavelength, inflation leads to the creation of more and more new regions containing a classical field of specific amplitude with a scale greater than H−1. In the case of an effectively massless Nambu–Goldstone field considered here, the averaged amplitude of the phase fluctuations generated during each e-fold (time interval H−1) is given by:
Let us assume that the part of the Universe observed inside the contemporary horizon Mpc was inflating, over NU ≃ 60 e-folds, from a single causally-connected domain of size H−1, for which the average value of the phase is θ0. When inflation begins in this region, after one e-fold, the volume of the Universe increases by a factor e3. The typical wavelength of the fluctuation δθ generated during every e-fold is equal to H−1. Thus, the whole domain H−1, containing θ0, after the first e-fold effectively becomes divided into e3 separate, causally-disconnected domains of size H−1. Each domain corresponds to an almost homogeneous phase value θ0 ± δθ. Thereby, more and more domains appear with time, in which the phase differs significantly from the initial value θ0. A crucial point is the appearance of domains with a phase θ > π. Appearing only after a certain period of time during which the Universe exhibited exponential expansion, these domains turn out to be surrounded by a space with phase θ < π. The coexistence of domains with phases θ < π and θ > πλφ > leads, in the following, to the formation of a large-scale structure of topological defects.
The potential Equation (25) possesses a U(1) symmetry, which is spontaneously broken at least after some period of inflation. Note that the phase fluctuations during the first e-folds may, generally speaking, transform into fluctuations of the cosmic microwave radiation, and this will lead to restrictions on the scaling parameter f. This difficulty can be avoided by taking into account the interaction of the field φ with the inflaton field (i.e., by making parameter f a variable [40]). This spontaneous breakdown is holding through the condition of smallness of the radial mass, . At the same time, the condition:
As soon as the angular mass mθ is of the order of the Hubble rate, the phase starts oscillating about the potential minimum, with different initial values being in various space domains. Moreover, in the domains with the initial phase π < θ < 2π, the oscillations proceed around the potential minimum at θmin = 2π, whereas the phase in the surrounding space tends to a minimum at the point θmin = 0. At the end of the decaying phase oscillations, the system contains domains characterized by the phase θmin = 2π surrounded by space with θmin = 0. Apparently, if we move in any direction from the inside to the outside of the domain, we will unavoidably pass through a point where θ = π, because the phase varies continuously. This implies that a closed surface characterized by the phase θwall = π must exist. The size of this surface depends on the moment of the domain formation in the inflation period, while the shape of the surface may be arbitrary. The key point for the subsequent considerations is that the surface is closed. After reheating of the Universe, the evolution of domains with the phase θ > π proceeds on the background of the Friedman expansion and is described by the relativistic equation of state. When the temperature falls down to T∗ ~ Λ, an equilibrium state between the “vacuum” phase θvac = 2π inside the domain and the θvac = 0 phase outside of it is established. Since the equation of motion corresponding to potential Equation (26) admits a kink-like solution (see [95] and the references therein), which interpolates between two adjacent vacua θvac = 0 and θvac = 2π, a closed wall corresponding to the transition region at θ = π is formed. The surface energy density of a wall of width ~ 1/m ~ f/Λ2 is of the order (the existence of such domain walls in the theory of the invisible axion was first pointed out in [103]) of ~fΛ2.
Note that if the coherent phase oscillations do not decay for a long time, their energy density can play the role of CDM. This is the case, for example, in the cosmology of the invisible axion (see [94] and the references therein).
It is clear that immediately after the end of inflation, the size of domains that contain a phase θvac > 2π exceeds by far the horizon size. This situation is replicated in the size distribution of vacuum walls, which appear at the temperature T∗ ~ Λ, whence the angular mass mθ starts to build up. Those walls, which are larger than the cosmological horizon, still follow the general FLRW expansion until the moment when they get causally connected as a whole; this happens as soon as the size of a wall becomes equal to the horizon size Rh. Evidently, internal stresses developed in the wall after crossing the horizon initiate processes tending to minimize the wall surface. This implies that the wall tends, first, to acquire a spherical shape and, second, to contract toward its center. For simplicity, we will consider below the motion of closed spherical walls (the motion of closed vacuum walls has been derived analytically in [104,105]).
The wall energy is proportional to its area at the instant of crossing the horizon. At the moment of maximum contraction, this energy is almost completely converted into kinetic energy [106]. Should the wall at the same moment be localized within the gravitational radius, a PBH is formed.
A detailed study of black hole (BH) formation was made in [96]. The results of these calculations are sensitive to the parameter Λ and to the initial phase θU. As the Λ value decreases to ~1 GeV, still greater PBHs appear with masses of up to ~1040 g. A change in the initial phase leads to sharp variations in the total number of black holes. As was shown above, each domain generates a family of subdomains in its close vicinity. The total mass of such a cluster is only 1.5 to 2-times that of the largest initial black hole in this space region. Thus, the calculations confirm the possibility of formation of clusters of massive PBHs (~100 M⊙ and above) in the earliest stages of the evolution of the Universe at a temperature of ~1 to 10 GeV. These clusters represent stable energy density fluctuations around which baryonic matter (and cold dark matter) may concentrate in the subsequent stages, followed by the evolution into galaxies.
It should be noted that additional energy density is supplied by closed walls of small sizes. Indeed, because of the smallness of their gravitational radius, they do not collapse into BHs. After several oscillations, such walls disappear, leaving coherent fluctuations of the PNG field. These fluctuations contribute to a local energy density excess, thus facilitating the formation of galaxies.
The mass range of formed PBHs is constrained by the fundamental parameters of the model f and Λ. The maximal BH mass is determined by the condition that the wall does not dominate locally before it enters the cosmological horizon. Otherwise, local wall dominance leads to a superluminal a ∝ t2 expansion for the corresponding region, separating it from the other parts of the Universe. This condition corresponds to the mass [40]:
The minimal mass follows from the condition that the gravitational radius of BH exceeds the width of the wall and is equal to [40,98]:
Closed wall collapse leads to a primordial gravitational wave spectrum, peaked at [2]:
At f ~ 1014 GeV, this primordial gravitational wave background can reach ΩGW ≈ 10−9. For the physically-reasonable values of:
Another profound signature of the considered scenario consists of gravitational wave signals from the merging of PBHs in the PBH cluster. These effects can provide tests of the considered approach in the eLISA experiment.
7. Antimatter in a Baryon-Asymmetric Universe?
Primordial strong inhomogeneities can also appear in the baryon charge distribution. The appearance of antibaryon domains in the baryon asymmetrical Universe, reflecting the inhomogeneity of baryosynthesis, is a profound signature of such a strong inhomogeneity [107]. In the model of spontaneous baryosynthesis (see [108] for a review), the possibility of the existence of antimatter domains, surviving to the present day in an inflationary Universe with inhomogeneous baryosynthesis, was considered in [109].
The mechanism of spontaneous baryogenesis [110] implies the existence of a complex scalar field carrying the baryonic charge. The U(1) symmetry, which corresponds to the baryon charge, is spontaneously and explicitly broken. The explicit breakdown of the U(1) symmetry is caused by the phase-dependent term:
The possible baryon- and lepton-number violating interaction of the field χ with matter fields can have the following structure [108]:
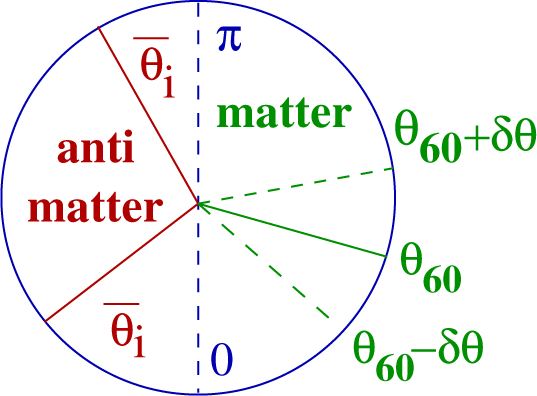
In the early Universe, at a time when the friction term, induced by the Hubble constant, becomes comparable to the angular mass , the phase θ starts to oscillate around the minima of the potential and decays into matter fields according to Equation (36). The coupling Equation (36) gives rise to the following [108]: as the phase starts to roll down in the clockwise direction (Figure 3), it preferentially creates an excess of baryons over antibaryons, while the opposite is true as it starts to roll down in the opposite direction.
The fate of such antimatter regions depends on their size. If their physical size is larger than the critical size Lc = 8 h2 kpc [109], they survive annihilation with surrounding matter. The evolution of sufficiently dense antimatter domains can lead to the formation of antimatter globular clusters [111]. The existence of such a cluster in the halo of our Galaxy should lead to the pollution of the galactic halo by antiprotons. Their annihilation can reproduce [112] the observed galactic gamma background in the range of tens to hundreds of MeV. The prediction of an antihelium component in cosmic rays [113], accessible to searches for cosmic ray antinuclei in the AMS02 experiment, as well as of antimatter meteorites [114] provides a direct experimental test for this hypothesis. The possibility of the formation of dense antistars within an extension of the Affleck–Dine scenario of baryogenesis and the strategies for their search were recently considered in [115].
Therefore, primordial strong inhomogeneities in the distribution of total, dark matter and baryon density in the Universe are a new important phenomenon in cosmological models based on physics beyond the standard model.
8. Supersymmetry in the Context of Cosmoparticle Physics
Observational cosmology offers strong evidence favoring the existence of new physics and suggests experimental approaches to their investigation. Cosmoparticle physics [3–5,8], studying the physical, astrophysical and cosmological impact of new laws of Nature, explores new forms of matter and their physical properties. The development of SUSY models follows the main principles of cosmoparticle physics and offers a great challenge for theoretical and experimental research. Physics of dark matter in all its aspects plays important role in this process.
The necessity to extend the standard model by supersymmetry has serious theoretical reasons: aesthetically, because it helps to achieve full unification for the standard model; practically, because it removes its internal tensions. Supersymmetry can also provide a complete physical basis for cosmology. It can pretend to explain inflation, baryosynthesis and nonbaryonic dark matter. The white spots in the representations of supersymmetric models correspond to new unknown particles. The extension of the symmetry of the gauge group introduces new gauge fields, mediating new interactions. Global symmetry breaking results in the existence of Goldstone boson fields.
In particle physics, direct experimental probes for the predictions of particle theory are the most attractive. The predicted supersymmetric partners of known particles are accessible to experimental search at accelerators if their masses are within a few TeV range. However, the predictions related to a higher energy scale need non-accelerator or indirect means for their test.
Cosmoparticle physics offers complementary tools via indirect and non-accelerator direct searches for new physics and its possible properties. In experimental cosmoarcheology, data can be obtained that link the new physics with astrophysical observations (see [117]). In experimental cosmoparticle physics, the parameters, fixed from the consistency of cosmological models and observations, define the level at which the new types of particle processes should be searched for (see [118]). These basic principles of cosmoparticle physics have been widely implemented in the development of supersymmetric models.
The theory of everything should provide a complete physical basis for cosmology and naturally involve supersymmetry. The problem is that string theory [119] is now in the form of “theoretical theory”, for which many doubt that experimental probes exist. Cosmoparticle physics can remove these doubts.
For a long time, scenarios with primordial black holes belonged dominantly to cosmological “fantasies”, as they provided restrictions on physics of the very early Universe from the contradiction of their predictions with observational data. Even this negative type of information makes PBHs an important theoretical tool. Being formed in the very early Universe as an initially nonrelativistic form of matter, PBHs should have increased their contribution to the total density during the RD stage of expansion, while the effect of PBH evaporation should have strongly increased the sensitivity of astrophysical data to their presence. Indeed, astrophysical constraints on hypothetical sources of cosmic or gamma rays, on light element abundances and on the spectrum of the CMB can be linked to restrictions on superheavy particles in the early Universe and on first- and second-order phase transitions, thus making astrophysical data a sensitive probe of particle symmetry structure and of the pattern of its breaking at superhigh energy scales.
The gravitational mechanism of particle creation in PBH evaporation makes evaporating PBHs a unique source of any species of particles that can exist in our space-time. At least theoretically, PBHs can be treated as the source of such particles, which are strongly suppressed in any other astrophysical mechanism of particle production, either due to a very large mass of these species or owing to their superweak interaction with ordinary matter.
By construction, astrophysical constraints exclude effects predicted to be larger than observed. At the edge, such constraints convert into an alternative mechanism for the observed phenomenon. At some fixed values of parameters, the PBH spectrum can play a positive role and shed new light on old astrophysical problems.
Common sense dictates that PBHs should have small sub-stellar mass. The formation of PBHs within the cosmological horizon, which was very small in the very early Universe, seems to argue for this viewpoint. However, phase transitions during the inflationary stage can provide spikes in the spectrum of fluctuations at any scale or lead to the formation of closed massive domain walls of any size.
In the latter case, the existence of primordial clouds of massive black holes around an intermediate-mass or supermassive black hole is possible. Such clouds have a fractal spatial distribution. This approach suggests a radically new scenario for galaxy formation. Traditionally, the Big Bang model assumes a homogeneous distribution of matter at all scales, whereas the appearance of observed inhomogeneities is related to the growth of small initial density perturbations. However, the analysis of the cosmological consequences of the particle theory indicates the possible existence of strongly inhomogeneous primordial structures in the distribution of both dark matter and baryons. These primordial structures represent a new factor in galaxy formation theory. Topological defects, such as the cosmological walls and filaments, primordial black holes, archioles in the models of axionic CDM and inhomogeneous baryosynthesis (leading to the formation of antimatter domains in a baryon-asymmetric Universe [5,8,40,107,109–114,120–125]), are an incomplete list of possible primary inhomogeneities inferred from the existing elementary particle models.
We can conclude that, within the modern cosmological paradigm, from the very beginning to the present time, the evolution of the Universe was governed by physical laws that we still do not fully know. These laws must come from a fundamental particle symmetry beyond the standard model, and they imply the use of methods of cosmoparticle physics for their study. Cosmoparticle physics originates from the well-established relation between the microscopic and the macroscopic descriptions in theoretical physics. This is reminiscent of the links between statistical physics and thermodynamics or between electrodynamics and the theory of the electron. At the end of the 20th Century, a new instance of this kind of relationship was realized. It came both from the cosmological necessity to go beyond the world of known elementary particles to settle the physical grounds for inflationary cosmology with baryosynthesis and dark matter and from the necessity for particle theory to use cosmological tests as an important and, in many cases, unique way to probe its predictions. The development of supersymmetric models perfectly reflects this direction of fundamental knowledge.
Acknowledgments
I express my gratitude to David Cline for the kind invitation to contribute to this Special issue and to all my co-authors of the original papers, on which the present review is based. I am grateful to Jean-Rene Cudell for reading the manuscript and the valuable comments and to Kevin Benattar for technical help. The work on initial cosmological conditions was supported by the Ministry of Education and Science of Russian Federation, Project 3.472.2014/K, and the work on the forms of dark matter was supported by Grant RFBR 14-22-03048.
Conflicts of Interest
The author declares no conflict of interest.
References
- Khlopov, M.Y. Fundamental Particle Structure in the Cosmological Dark Matter. Int. J. Mod. Phys. A 2013, 28. [Google Scholar] [CrossRef]
- Khlopov, M.Y. Primordial Black Holes. Res. Astron. Astrophys 2010, 10, 495–528. [Google Scholar]
- Sakharov, A.D. Cosmoparticle physics—A multidisciplinary science. Vestn. AN SSSR 1989, 4, 39–40. [Google Scholar]
- Khlopov, M.Y. Fundamental cross-disciplinary studies of microworld and Universe. Vestn. Russ. Acad. Sci 2001, 71, 1133–1137. [Google Scholar]
- Khlopov, M.Y. Cosmoparticle Physics; World Scientific: New York, NY, USA, 1999. [Google Scholar]
- Khlopov, M.Y. Beyond the standard model in particle physics and cosmology: Convergence or divergence? In Neutrinos and Explosive Events in the Universe; Springer: Berlin, Germany, 2005; pp. 73–82. [Google Scholar]
- Khlopov, M.Y. Cosmoparticle physics: Cross-Disciplinary study of physics beyond the standard model. Bled Workshops Phys 2006, 7, 51–62. [Google Scholar]
- Khlopov, M.Y. Fundamentals of Cosmoparticle Physics; CISP-Springer: Cambridge, UK, 2012. [Google Scholar]
- Bertone, G. Particle Dark Matter: Observations, Models and Searches; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Frenk, C.S.; White, S.D.M. Dark matter and cosmic structure. Ann. Phys 2012, 524, 507–534. [Google Scholar]
- Gelmini, G.B. Search for Dark Matter. Int. J. Mod. Phys. A 2008, 23, 4273–4288. [Google Scholar]
- Aprile, E.; Profumo, S. Focus on dark matter and particle physics. New J. Phys 2009, 11. [Google Scholar] [CrossRef]
- Feng, J.L.; Dark, Matter. Candidates from Particle Physics and Methods of Detection. Ann. Rev. Astron. Astrophys 2010, 48, 495–545. [Google Scholar]
- Bernabei, R.; Belli, P.; d’Angelo, S.; di Marco, A.; Montecchia, F.; Cappella, F.; d’Angelo, A.; Incicchitti, A.; Caracciolo, V.; Castellano, S.; et al. Dark Matter investigation by DAMA at Gran Sasso. Int. J. Mod. Phys. A 2013, 28. [Google Scholar] [CrossRef]
- Agnese, R.; Ahmed, Z.; Anderson, A.J.; Arrenberg, S.; Balakishiyeva, D.; Basu Thakur, R.; Bauer, D.A.; Borgland, A.; Brandt, D.; Brink, P.L.; et al. Silicon detector results from the first five-tower run of CDMS II. Phys. Rev. D 2013, 88. [Google Scholar] [CrossRef]
- Aprile, E.; Alfonsi, M.; Arisaka, K.; Arneodo, F.; Balan, C.; Baudis, L.; Bauermeister, B.; Behrens, A.; Beltrame, P.; Bokeloh, K.; et al. Dark Matter Results from 225 Live Days of XENON100 Data. Phys. Rev. Lett 2012, 109. [Google Scholar] [CrossRef]
- Akerib, D.S.; Araujo, H.M.; Bai, X.; Bailey, A.J.; Balajthy, J.; Bedikian, S.; Bernard, E.; Bernstein, A.; Bolozdynya, A.; Bradley, A.; et al. First results from the LUX dark matter experiment at the Sanford Underground Research Facility. Phys. Rev. Lett 2014, 112. [Google Scholar] [CrossRef]
- Zeldovich, Ya.B.; Klypin, A.A.; Khlopov, M.Yu.; Chechetkin, V.M. Astrophysical bounds on the mass of heavy stable neutral leptons. Sov. J. Nucl. Phys 1980, 31, 664–669. [Google Scholar]
- Kogan, Ia.I.; Khlopov, M.Y. Homotopically stable particles in superstring theory. Sov. J. Nucl. Phys 1987, 64, 193–194. [Google Scholar]
- Kogan, Ia.I.; Khlopov, M.Y. Cosmological consequences of the E(8) × E(8)′ superstring models. Sov. J. Nucl. Phys 1986, 44, 873–874. [Google Scholar]
- Khlopov, M.Yu.; Shibaev, K.I. New physics from superstring phenomenology. Gravit. Cosmol. Suppl 2002, 8, 45–52. [Google Scholar]
- Golubkov, Y.A.; Fargion, D.; Khlopov, M.Y.; Konoplich, R.V.; Mignani, R. Possible effects of the existence of the fourth generation neutrino. JETP Lett 1999, 69, 434–440. [Google Scholar]
- Belotsky, K.M.; Khlopov, M.Y. Cosmoparticle physics of the 4th generation neutrino. Gravit. Cosmol 2001, 7, 189–192. [Google Scholar]
- Belotsky, K.M.; Fargion, D.; Khlopov, M.Y.; Konoplich, R.V.; Ryskin, M.G.; Shibaev, K.I. Heavy hadrons of 4th family hidden in our Universe and close to detection? Gravit. Cosmol. Suppl 2005, 11, 3–15. [Google Scholar]
- Fargion, D.; Khlopov, M.Y. Tera-Leptons Shadows over Sinister Universe. Gravit. Cosmol 2013, 19, 219–231. [Google Scholar]
- Fargion, D.; Khlopov, M.Y.; Stephan, C.A. Cold dark matter by heavy double charged leptons? Class. Quantum Gravity 2006, 23, 7305–7354. [Google Scholar]
- Khlopov, M.Y. Composite dark matter from 4th generation. JETP Lett 2006, 83, 1–4. [Google Scholar]
- Belotsky, K.M.; Khlopov, M.Y.; Shibaev, K.I. Composite Dark Matter and its Charged Constituents. Gravit. Cosmol 2006, 12, 1–7. [Google Scholar]
- Khlopov, M.Y. Physics of Dark Matter in the Light of Dark Atoms. Mod. Phys. Lett. A 2011, 26, 2823–2839. [Google Scholar]
- Fargion, D.; Khlopov, M.Y.; Konoplich, R.V.; Mignani, R. Bounds on very heavy relic neutrinos by their annihilation in the Galactic halo. Phys. Rev. D 1995, 52, 1828–1836. [Google Scholar]
- Fargion, D.; Konoplich, R.V.; Grossi, M.; Khlopov, M.Y. Galactic Gamma Halo by Heavy Neutrino annihilations? Astropart. Phys 2000, 12, 307–314. [Google Scholar]
- Belotsky, K.M.; Khlopov, M.Y. Astrophysical Signature of the 4th Neutrino. Gravit. Cosmol. Suppl 2002, 8, 112–117. [Google Scholar]
- Belotsky, K.M.; Fargion, D.; Khlopov, M.Yu.; Konoplich, R.V. May Heavy neutrinos solve underground and cosmic ray puzzles? Phys. At. Nucl 2008, 71, 147–161. [Google Scholar]
- Belotsky, K.M.; Khlopov, M.Y.; Shibaev, K.I. Monochromatic neutrinos from massive fourth generation neutrino annihilation in the Sun and in the Earth. Part. Nucl. Lett 2001, 108, 5–17. [Google Scholar]
- Belotsky, K.M.; Khlopov, M.Y.; Shibaev, K.I. Monochromatic neutrinos from the annihilation of fourth-generation massive stable neutrino in the Sun and in the Earth. Phys. At. Nucl 2002, 65, 382–391. [Google Scholar]
- Belotsky, K.M.; Damour, T.; Khlopov, M.Y. Implications of a solar-system population of massive 4th generation neutrinos for underground searches of monochromatic neutrino-annihilation signals. Phys. Lett. 2002, B529, 10–18. [Google Scholar]
- Polnarev, A.G.; Khlopov, M.Yu. Cosmology, Primordial Black Holes, And Supermassive Particles. Sov. Phys. Uspekhi 1985, 28, 213–232. [Google Scholar]
- Hawking, S.W.; Moss, I.G.; Stewart, J.M. Bubble Collisions in the Very Early Universe. Phys. Rev. D 1982, 26, 2681–2693. [Google Scholar]
- Konoplich, R.V.; Rubin, S.G.; Sakharov, A.S.; Khlopov, M.Y. Formation of black holes in the first order phase transitions as cosmological test of mechanisms of symmetry breaking. Phys. At. Nucl 1999, 62, 1593–1600. [Google Scholar]
- Khlopov, M.Y.; Rubin, S.G. Cosmological Pattern of Microphysics in Inflationary Universe; Kluwer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Zeldovich, Y.B.; Khlopov, M.Y. On the concentration of relic magnetic monopoles in the Universe. Phys. Lett. 1978, B79, 239–242. [Google Scholar]
- Preskill, J.P. Cosmological Production of Superheavy Magnetic Monopoles. Phys. Rev. Lett 1979, 43, 1365–1374. [Google Scholar]
- Zeldovich, Y.B.; Kobzarev, I.Y.; Okun, L.B. Cosmological Consequences of the Spontaneous Breakdown of Discrete Symmetry. Sov. Phys. JETP 1975, 40, 1–5. [Google Scholar]
- Zeldovich, Y.B. Cosmological fluctuations produced near a singularity. Mon. Not. R. Astron. Soc 1980, 192, 663–667. [Google Scholar]
- Vilenkin, A. Cosmological density fluctuations produced by vacuum strings. Phys. Rev. Lett 1981, 46, 1169–1172. [Google Scholar]
- Khlopov, M.Y.; Sakharov, A.S. The nonhomogeneity problem for the primordial axion field. Phys. At. Nucl 1994, 57, 485–487. [Google Scholar]
- Khlopov, M.Y.; Sakharov, A.S.; Sokoloff, D.D. Large scale modulation of the distribution of coherent oscillations of a primordial axion field in the Universe. Phys. At. Nucl 1996, 59, 1005–1010. [Google Scholar]
- Khlopov, M.Y.; Sakharov, A.S.; Sokoloff, D.D. The nonlinear modulation of the density distribution in standard axionic CDM and its cosmological impact. Nucl. Phys. Proc. Suppl 1999, 72, 105–109. [Google Scholar]
- Zeldovich, Y.B.; Novikov, I.D. The Hypothesis of Cores Retarded during Expansion and the Hot Cosmological Model. Sov. Astron 1967, 10, 602–609. [Google Scholar]
- Belotsky, K.M.; Dmitriev, A.D.; Esipova, E.A.; Gani, V.A.; Grobov, A.V.; Khlopov, M.Y.; Kirillov, A.A.; Rubin, S.G.; Svadkovsky, I.V. Signatures of primordial black hole dark matter. Mod. Phys. Lett. A 2014, 29. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle Creation by Black Holes. Commun. Math. Phys 1975, 43, 199–220. [Google Scholar]
- Carr, B.J. The primordial black hole mass spectrum. Astrophys. J 1975, 201, 1–19. [Google Scholar]
- Khlopov, M.Yu.; Polnarev, A.G. Primordial Black Holes as a Cosmological Test Of Grand Unification. Phys. Lett. 1980, B97, 383–387. [Google Scholar]
- Kalashnikov, O.K.; Khlopov, M.Y. On the possibility of checking the cosmology of asymptotically free SU(5) theory. Phys. Lett. 1983, B127, 407–422. [Google Scholar]
- Kadnikov, A.F.; Maslyankin, V.I.; Khlopov, M.Y. Modelling of evolution of quasi-stellar systems, formed by particles and antiparticles in early Universe. Astrophysics 1990, 31, 523–531. [Google Scholar]
- Khlopov, M.Yu.; Malomed, B.A.; Zel’dovich, Y.B. Gravitational instability of scalar fields and formation of primordial black holes. Mon. Not. R. Astron. Soc 1985, 215, 575–589. [Google Scholar]
- Kofman, L.A.; Linde, A.D. Generation of Density Perturbations in the Inflationary Cosmology. Nucl. Phys. B 1987, 282, 555–626. [Google Scholar]
- Sakharov, A.S.; Khlopov, M.Y. Cosmological signatures of family symmetry breaking in multicomponent inflation models. Phys. At. Nucl 1993, 56, 412–417. [Google Scholar]
- Dymnikova, I.; Khlopov, M.Y.; Koziel, L.; Rubin, S.G. Quasilumps from first-order phase transitions. Gravit. Cosmol 2000, 6, 311–318. [Google Scholar]
- Novikov, I.D.; Polnarev, A.G.; Starobinski, A.A.; Zeldovich, Ya.B. Primordial black holes. Astron. Astrophys 1979, 80, 104–109. [Google Scholar]
- Polnarev, A.G.; Khlopov, M.Yu. Dustlike Stages in the Early Universe and Constraints on the Primordial Black-Hole Spectrum. Sov. Astron 1982, 26, 391–395. [Google Scholar]
- Chechetkin, V.M.; Khlopov, M.Y.; Sapozhnikov, M.G. Anti-Proton Interactions with Light Elements as a Test of Gut Cosmology. Riv. Nuovo Cimento 1982, 5, 1–79. [Google Scholar]
- Carr, B.J.; Gilbert, J.H.; Lidsey, J.E. Black hole relics and inflation: Limits on blue perturbation spectra. Phys. Rev. D 1994, 50, 4853–4867. [Google Scholar]
- Carr, B.J.; MacGibbon, J.H. Cosmic rays from primordial black holes and constraints on the early universe. Phys. Rep 1998, 307, 141–154. [Google Scholar]
- Liddle, A.R.; Green, A.M. Cosmological constraints from primordial black holes. Phys. Rep 1998, 307, 125–131. [Google Scholar]
- Cline, D.B. Primordial black holes and short gamma-ray bursts. Phys. Rep 1998, 307, 173–180. [Google Scholar]
- Miyama, S.; Sato, K. The Upper Bound of the Number Density of Primordial Black Holes From the Big Bang Nucleosynthesis. Prog. Theor. Phys 1978, 59, 1012–1018. [Google Scholar]
- Zeldovich, Y.B.; Starobinski, A.A.; Khlopov, M.Y.; Chechetkin, V.M. Primordial black holes and the problem of deuterium. Sov. Astron. Lett 1977, 3, 110–112. [Google Scholar]
- Lindley, D. Primordial black holes and the deuterium abundance. Mon. Not. R. Astron. Soc 1980, 193, 593–601. [Google Scholar]
- Vainer, B.V.; Dryzhakova, D.V.; Nasselskii, P.D. Primordial black holes and cosmological nucleosynthesis. Sov. Astron. Lett 1978, 4, 185–187. [Google Scholar]
- MacGibbon, J.H.; Carr, B.J. Cosmic rays from primordial black holes. Astrophys. J 1991, 371, 447–469. [Google Scholar]
- Barrau, A.; Blais, D.; Boudoul, G.; Polarski, D. Galactic cosmic rays from pbhs and primordial spectra with a scale. Phys. Lett. B 2003, 551, 218–225. [Google Scholar]
- Kohri, K.; Yokoyama, J. Primordial black holes and primordial nucleosynthesis. 1. Effects of hadron injection from low mass holes. Phys. Rev. D 2000, 61. [Google Scholar] [CrossRef]
- Barrau, A.; Boudoul, G.; Derome, L. An improved gamma-ray limit on the density of pbhs. 28th ICRC Conference, Tsukuba, Japan, 31 July–7 August 2003; pp. 1697–1699.
- Barrau, A.; Boudoul, G.; Donato, F.; Maurin, D.; Salati, P.; Taillet, R. Antiprotons from primordial black holes. Astron. Astrophys 2002, 388, 676–687. [Google Scholar]
- Custodio, P.S.; Horvath, J.E. Bounds on the cosmological abundance of primordial black holes from diffuse sky brightness: Single mass spectra. Phys. Rev. D 2002, 65. [Google Scholar] [CrossRef]
- Lemoine, M. Moduli constraints on primordial black holes. Phys. Lett. B 2000, 481, 333–338. [Google Scholar]
- Khlopov, M.Y.; Barrau, A.; Grain, J. Gravitino production by Primordial Black Hole evaporation and constraints on the inhomogeneity of the early Universe. Class. Quantum Gravity 2006, 23, 1875–1882. [Google Scholar]
- Olive, K.A. Introduction to supersymmetry: Astrophysical and phenomenological constraints. In The Primordial Universe; Binetruy, P., Schaffer, R., Silk, J., David, F., Eds.; Springer-Verlag: Berlin, Germany, 2001; pp. 221–293. [Google Scholar]
- Khlopov, M.Y.; Chechetkin, V.M. Antiprotons in the Universe as a cosmological test of Grand Unification. Sov. J. Part. Nucl 1987, 18, 267–288. [Google Scholar]
- Green, A.M. Supersymmetry and primordial black hole abundance constraints. Phys. Rev. D 1998, 60. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Linde, A.D. Is it easy to save gravitino? Phys. Lett. 1984, B138, 265–268. [Google Scholar]
- Balestra, F.; Piragino, G.; Pontecorvo, D.B.; Sapozhnikov, M.G.; Falomkin, I.V.; Khlopov, M.Y. Low-Energy Anti-p He-4 Annihilation and Problems of the Modern Cosmology, Gut and Susy Models. Sov. J. Nucl. Phys 1984, 39, 626–631. [Google Scholar]
- Levitan, Y.L.; Sobol, I.M.; Khlopov, M.Y.; Chechetkin, V.M. Production of light elements in cascades from energetic antiprotons in early Universe and problems of nuclear cosmoarcheology. Sov. J. Nucl. Phys 1988, 47, 109–115. [Google Scholar]
- Khlopov, M.Y.; Levitan, Y.L.; Sedelnikov, E.V.; Sobol, I.M. Nonequilibrium cosmological nucleosynthesis of light elements: Calculations by Monte Carlo method. Phys. At. Nucl 1994, 57, 1393–1397. [Google Scholar]
- Sedel’nikov, E.V.; Filippov, S.S.; Khlopov, M.Y. Kinetic theory of nonequilibrium cosmological nucleosynthesis. Phys. At. Nucl 1995, 58, 235–242. [Google Scholar]
- Jedamzik, K. Did something decay, evaporate, or annihilate during Big Bang nucleosynthesis? Phys. Rev. D 2004, 70. [Google Scholar] [CrossRef]
- Kawasaki, M.; Kohri, K.; Moroi, T. Hadronic decay of late—Decaying particles and Big-Bang Nucleosynthesis. Phys. Lett. 2005, B625, 7–12. [Google Scholar]
- Barrau, A.; Ponthieu, N. Could the next generation of cosmology experiments exclude supergravity? Phys. Rev. D 2004, 69. [Google Scholar] [CrossRef]
- Kolda, C.F. Gauge mediated supersymmetry breaking: Introduction, review and update. Nucl. Phys. Proc. Suppl 1998, 62, 266–275. [Google Scholar]
- Ade, P. A.R.; Aghanim, N.; Arnaud, M.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck 2015 Results. XIII. Cosmological Parameters. Available online: http://arxiv.org/abs/1502.01589 accessed on 6 February 2015.
- Jedamzik, K.; Lemoine, M.; Moultaka, G. Gravitino dark matter in gauge mediated supersymmetry breaking. Phys. Rev. 2006, D73. [Google Scholar] [CrossRef]
- Lemoine, M.; Moultaka, G.; Jedamzik, K. Natural gravitino dark matter in SO(10) gauge mediated supersymmetry breaking. Phys. Lett. 2007, B645, 222–227. [Google Scholar]
- Kim, J.E. Light Pseudoscalars, Particle Physics and Cosmology. Phys. Rep 1987, 150, 1–177. [Google Scholar]
- Vilenkin, A.; Shellard, E.P.S. Cosmic Strings and Other Topological Defects; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Rubin, S.G.; Sakharov, A.S.; Khlopov, M.Yu. Formation of primordial galactic nuclei at phase transitions in the early Universe. JETP 2001, 92, 921–929. [Google Scholar]
- Dokuchaev, V.; Eroshenko, Y.; Rubin, S. Early formation of galaxies initiated by clusters of primordial black holes. Astron. Rep 2008, 52, 779–789. [Google Scholar]
- Rubin, S.G.; Khlopov, M.Y.; Sakharov, A.S. Primordial nonlinear structures and massive black holes from early Universe. Gravit. Cosmol. Suppl 2000, 6, 51–58. [Google Scholar]
- Khlopov, M.Y.; Rubin, S.G.; Sakharov, A.S. Primordial Structure of Massive Black Hole Clusters. Astropart. Phys 2005, 23, 265–277. [Google Scholar]
- Dokuchaev, V.; Eroshenko, Y.; Rubin, S. Quasars formation around clusters of primordial black holes. Gravit. Cosmol 2005, 11, 99–104. [Google Scholar]
- Adams, F.C.; Bond, J.R.; Freese, K.; Frieman, J.A.; Olinto, A.V. Natural inflation: Particle physics models, power law spectra for large scale structure, and constraints from COBE. Phys. Rev. D 1993, 47, 426–455. [Google Scholar]
- Starobinsky, A. A new type of isotropic cosmological models without singularity. Phys. Lett. 1980, 91B, 99–102. [Google Scholar]
- Sikivie, P. Domain Walls, and the Early Universe. Phys. Rev. Lett 1982, 48, 1156–1159. [Google Scholar]
- Berezin, V.A.; Kuzmin, V.A.; Tkachev, I.I. Thin Wall Vacuum Domains Evolution. Phys. Lett. 1983, 120B, 91–96. [Google Scholar]
- Ipser, J.; Sikivie, P. Gravitationally repulsive domain wall. Phys. Rev. D 1984, 30, 712–719. [Google Scholar]
- Rubin, S.G. Expansion of true vacuum bubbles at the end of inflation. Gravit. Cosmol 1999, 5, 127–134. [Google Scholar]
- Chechetkin, V.M.; Khlopov, M.Yu.; Sapozhnikov, M.G.; Zeldovich, Ya.B. Astrophysical aspects of antiproton interaction with He (Antimatter in the Universe). Phys. Lett. B 1982, 118, 329–332. [Google Scholar]
- Dolgov, A.D. Matter and antimatter in the universe. Nucl. Phys. Proc. Suppl 2002, 113, 40–49. [Google Scholar]
- Khlopov, M.Yu.; Rubin, S.G.; Sakharov, A.S. Possible origin of antimatter regions in the baryon dominated universe. Phys. Rev. D 2000, 62. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Freese, K.; Rangarajan, R.; Srednicki, M. Baryogenesis during reheating in natural inflation and comments on spontaneous baryogenesis. Phys. Rev. D 1997, 56, 6155–6165. [Google Scholar]
- Khlopov, M.Y. An antimatter globular cluster in our galaxy: A probe for the origin of matter. Gravit. Cosmol 1998, 4, 69–72. [Google Scholar]
- Golubkov, Y.A.; Khlopov, M.Y. Anti-Protons annihilation in the galaxy as a source of diffuse gamma background. Phys. At. Nucl 2001, 64, 1821–1829. [Google Scholar]
- Belotsky, K.M.; Golubkov, Y.A.; Khlopov, M.Y.; Konoplich, R.V.; Sakharov, A.S. Anti-Helium flux as a signature for antimatter globular clusters in our galaxy. Phys. At. Nucl 2000, 63, 233–239. [Google Scholar]
- Fargion, D.; Khlopov, M.Y. Antimatter bounds by anti-asteroids annihilations on planets and sun. Astropart. Phys 2003, 19, 441–446. [Google Scholar]
- Blinnikov, S.I.; Dolgov, A.D.; Postnov, K.A. Antimatter and antistars in the universe and in the Galaxy. ArXiv E-Prints, 2014. arXiv:1409.5736 Available online: http://arxiv.org/abs/1409.5736 accessed 27 May 2015. [Google Scholar]
- Khlopov, M.Y. Primordial nonlinear structures and massive black holes from early Universe. J. Phys. Conf. Ser 2007, 66. [Google Scholar] [CrossRef]
- Khlopov, M.Y. Cosmoarcheology. Direct and indirect astrophysical effects of hypothetical particles and fields. In Cosmion-94; Editions Frontieres: Paris, France, 1996; pp. 67–76. [Google Scholar]
- Belotsky, K.M.; Khlopov, M.Y.; Sakharov, A.S.; Shklyaev, A.A.; Sudarikov, A.L. Experimental cosmoparticle physics: Experimental probes for dark matter physics at particle accelerators. Gravit. Cosmol. Suppl 1998, 4, 70–78. [Google Scholar]
- Green, M.; Schwarz, J.; Witten, E. Superstring Theory; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Cohen, A.G.; Kaplan, D.B. Thermodynamic Generation of the Baryon Asymmetry. Phys. Lett. 1987, B199, 251–258. [Google Scholar]
- Stecker, F.W.; Puget, J.-L. Galaxy formation from annihilation-generated turbulence in the baryon symmetric big bang cosmology. Astrophys. J 1972, 178, 57–72. [Google Scholar]
- Steigman, G.A. Observational tests of antimatter cosmologies. Annu. Rev. Astron. Astrophys 1976, 14, 339–372. [Google Scholar]
- Cohen, A.G.; de Rujula, A.; Glashow, S.L. A Matter—Antimatter universe? Astrophys. J 1998, 495, 539–549. [Google Scholar]
- Kinney, W.H.; Kolb, E.W.; Turner, M.S. Ribbons on the CBR sky: A Powerful test of a baryon symmetric universe. Phys. Rev. Lett 1997, 79, 2620–2623. [Google Scholar]
- Khlopov, M.Y.; Konoplich, R.V.; Mignani, R.; Rubin, S.G.; Sakharov, A. Evolution and observational signature of diffused antiworld. Astropart. Phys 2000, 12, 367–372. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khlopov, M. Cosmological Probes for Supersymmetry. Symmetry 2015, 7, 815-842. https://doi.org/10.3390/sym7020815
Khlopov M. Cosmological Probes for Supersymmetry. Symmetry. 2015; 7(2):815-842. https://doi.org/10.3390/sym7020815
Chicago/Turabian StyleKhlopov, Maxim. 2015. "Cosmological Probes for Supersymmetry" Symmetry 7, no. 2: 815-842. https://doi.org/10.3390/sym7020815
APA StyleKhlopov, M. (2015). Cosmological Probes for Supersymmetry. Symmetry, 7(2), 815-842. https://doi.org/10.3390/sym7020815





