Abstract
We propose an entropic argument as partial explanation of the observed scarcity of twinned structures in crystalline samples of synthetic organic polymeric materials. Polymeric molecules possess a much larger number of conformational degrees of freedom than low molecular weight substances. The preferred conformations of polymer chains in the bulk of a single crystal are often incompatible with the conformations imposed by the symmetry of a growth twin, both at the composition surfaces and in the twin axis. We calculate the differences in conformational entropy between chains in single crystals and chains in twinned crystals, and find that the reduction in chain conformational entropy in the twin is sufficient to make the single crystal the stable thermodynamic phase. The formation of cyclic twins in molecular dynamics simulations of chains of hard spheres must thus be attributed to kinetic factors. In more realistic polymers this entropic contribution to the free energy can be canceled or dominated by nonbonded and torsional energetics.1. Introduction
Twins are regular aggregates consisting of individual crystals of the same species joined together in definite and specific mutual orientations. A common source of twinning is the simultaneous formation of individual crystals in the course of a liquid-to-solid phase change. In this type of twinning (growth twinning), several individuals are nucleated at a common location and continue to grow independently while maintaining the original geometric relations to each other.
Whereas twinning in crystals of low molecular weight substances, both organic and inorganic, is comparatively frequent (see [1–8] and references therein), twinning in polymers is rather an exceptional phenomenon: the first widely accepted observation of twinning in polymer crystals [7] was reported as late as 1963 (in the following, the term “polymer” refers primarily to synthetic macromolecules made up of one or a few repeat units, lacking the very specific monomeric succession and interactions found in biological macromolecules such as proteins; coordination and purely inorganic polymers are also excluded from the present work).
Undoubtedly, this scarcity is in part due to the difficulty of obtaining high-quality, well developed, and clearly differentiated polymer crystals, twinned or not. However, based on published data [9,10], the ratio of the number of reported cases of twinning in polymers [11–14] to the total number of documented polymer crystals is far smaller than the corresponding ratio for low molecular weight substances. Twins are somewhat exceptional occurrences in simple polymers, i.e., polymers consisting of relatively simple repeat units. Twinning in crystals of proteins is more frequently observed [15].
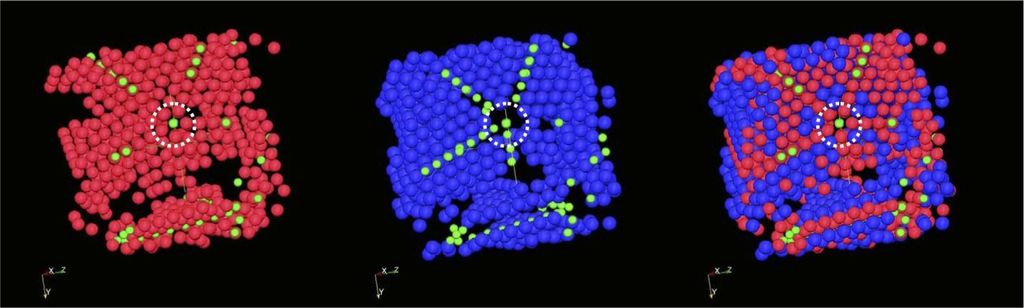
In addition to the experimental evidence, computer studies of the crystallization of assemblies of single (monomeric) hard spheres have shown that twinned morphologies form very easily during crystallization of monomeric (single) hard spheres [16], almost regardless of the details of the simulation methods and protocols. Figure 1 shows an example of a well-developed cyclic twin, formed by five tetrahedral sectors around a common twin axis, marked by the circle in dashed white line.
On the other hand, systems of freely-jointed chains of strictly tangent hard spheres have also been found to crystallize, although only in simulations with advanced Monte Carlo (MC) methods, and at much higher computational cost [18,19]. The only, but by no means minor, structural difference between chain packings and monomeric analogs is the connectivity between individual spheres: in the simplest chain model, individual hard spheres (monomers) are strictly tangent and are arranged in linear strings.
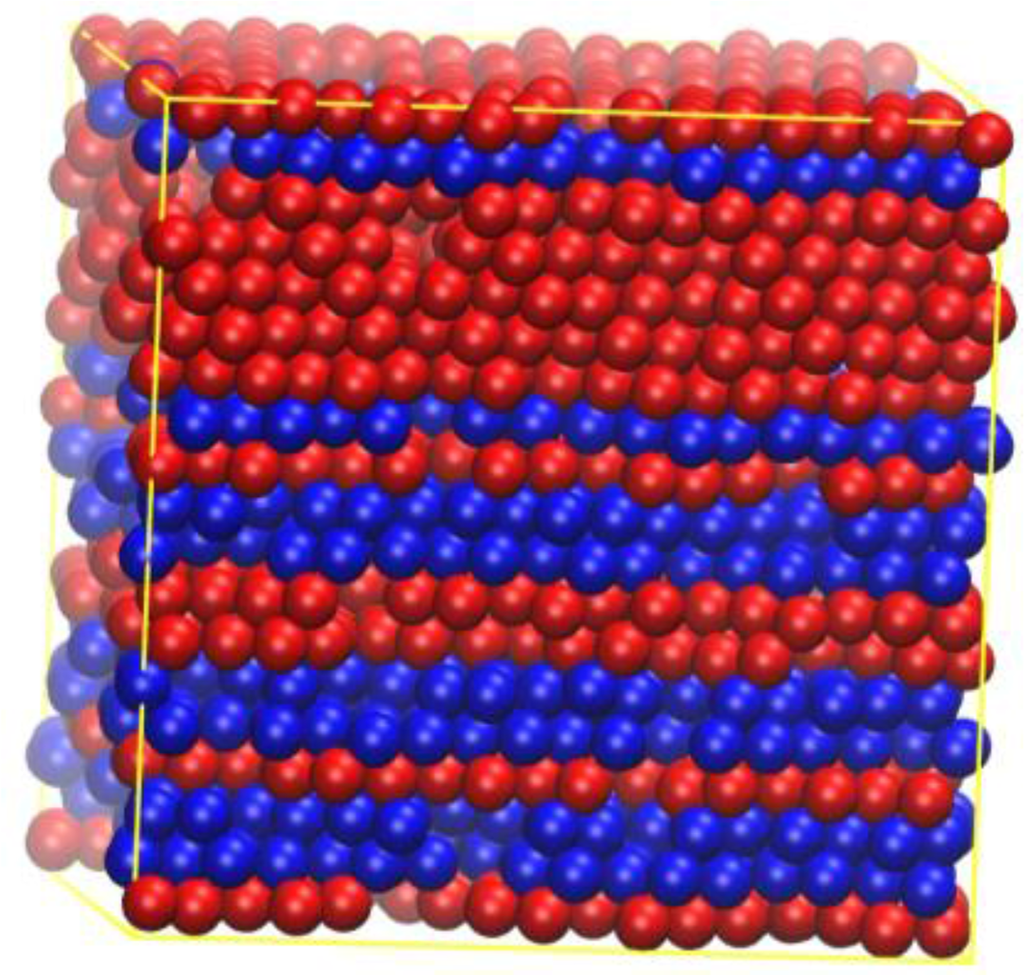
Quite surprisingly, these freely-jointed chains of tangent hard spheres crystallize in layered structures of mixed hcp (hexagonal closed packed) and fcc (face centered cubic) character (Figure 2, to be described in more detail below), but twinned structures have not been observed to date.
2. Enthalpic versus Entropic Effects on Polymer Twinning
It is likely that this conspicuous dearth of polymeric twins both in experiments and in increasingly refined simulations has several causes. It is however not unreasonable to suspect that some characteristics intrinsic to polymeric substances may be the main cause for the marked comparative lack of polymeric twins.
Since phase stability, in the thermodynamic sense, is controlled by differences in Helmholtz free energy between competitive phases, an investigation of the causes of the scarcity of twins in polymers will in general involve enthalpic and entropic contributions. Given the rarity of twinning in polymeric systems, quite independently of the chemical nature of the polymer, it is natural to take as a first working hypothesis that that bonded (torsional and bending), and non-bonded (inter- and intramolecular) interactions play a subordinate role. Since these interactions are primarily of enthalpic origin, the observation of twinning (or its absence) in systems in which enthalpy effects are negligible would help decide whether enthalpy, entropy, or both are the primary cause for twin suppression.
Hard-sphere systems of either monomers or chains are ideally suited to this end, since their interactions are, by definition, entirely controlled by entropic effects. In both cases, the statistical mechanical ensembles are composed of all configurations in which there is no overlap between spheres.
These so-called “athermal” physical models are well suited to computer simulations. Systems of individual hard spheres have been used since the very origins of computer simulations of condensed matter. Crystallization of individual hard spheres is observed readily with moderate computational effort and with virtually all simulation techniques [16]. In such simulations, growth twins appear conspicuously with a pentagonal arrangement of sectors (Figure 1).
Dense systems of strictly tangent hard sphere chains are harder to simulate, especially through molecular dynamics (MD) methods, and at the very high densities required for crystalline phases to form. This difficulty is caused by chain entanglements, which slow system dynamics down into practical unobservability. For the time being, it is only through the use of advanced Monte Carlo (MC) techniques that crystallization of freely-jointed chains of tangent hard spheres can be achieved [18,19]. In these simulations, only layered structures of varying degrees of perfection were obtained (Figure 2).
Interestingly, relaxing the condition of strict tangency along the polymer chain (i.e., rendering the bonds between spheres less “hard”) makes it much easier for the chains to crystallize. It also promotes the formation of growth twins, which appear copiously in simulations, and which are virtually indistinguishable from those formed by single spheres (Figure 1 above and Figure 4 of [21] are virtually indistinguishable, although the former is a single-sphere system and the latter a chain system).
These observations strongly suggest that there is a very specific, non-enthalpic mechanism related to connectivity that makes twinning highly improbable in polymeric systems of strictly tangent hard spheres. Since only entropy can be responsible for the appearance or suppression of twins in athermal systems, the search for the mechanism of twin suppression can be narrowed down a great deal. In addition, the gross morphological features of closed-packed assemblies of spherical particles must be primarily dictated by geometric (i.e., packing) considerations.
Finally, the observation that chains of soft spheres form twins just as readily as systems of single spheres, also suggests that translational contributions to the entropy make polymer systems behave like monomeric ones, at least with respect to the formation of twins.
For these reasons we have focused our work on dense systems of chains of strictly tangent hard spheres, in which entropy differences between twinned and untwinned phases can only be of conformational origin.
It is also important to emphasize that the strictly tangent, hard-sphere chain model is a drastic simplification of real polymers, in which energetic interactions (intra-, intermolecular, bending and torsional) may play a dominant role. The results and conclusions described below cannot directly be applied to polymers in which the energetic contributions (from bonded, and non-bonded interactions)to the free energy of the crystal dominate entropic ones.
3. Morphology of Twins in Systems of Monoatomic Hard Spheres
The cyclic twinned structures that appear in event-driven MD simulations of crystallization of monoatomic hard spheres [16] consist of partially or fully developed cyclic sector twins with a pseudo-fivefold rotation axis, resembling those in [1,22,23]. In our structures, between three and five such sectors can be resolved. Each of the sectors consists of a random stacking of compactly packed layers of spheres, thus resulting in stack faulted twin sectors of randomly alternating hcp and fcc character (known as rhcp) (Figure 1).
The rhcp structure, i.e., the random alternation between hcp and fcc layers in the twin sectors, is favored by the very small differences in Helmholtz free energy (entropy in our athermal system) between hcp and fcc stackings of hard spheres [24,25] and to the small free energy (entropy) penalty associated with the existence of twin boundaries [26]. Due to the inherent variability in the initial amorphous configurations, and to the small free energy differences between competing morphologies, a rich variety of more or less perfect twinned configurations is observed (the necessity of using cubic periodic boundary conditions in the simulation also has an effect on twin perfection through non-commensurability of simulation cell and crystal lattice).
In the morphologies typically encountered in event-driven MD, a quantitative analysis of the twin elements [27] confirms that morphologies such as that in Figure 1 are indeed multiple, cyclic twins with twin rotation 70.7° ± 0.4° (one standard deviation in the mean), in very good agreement with the expected tetrahedral value of 70.53°. A rational lattice row [110] is found to coincide for both adjacent sectors, and twinning axes and planes are identified in all cases as [110] and (111) respectively.
In most cases, three or four twin sectors are well developed. Less frequently, a fifth sector develops beyond a vestigial stage. A full description of the twinned structures can be found elsewhere [27,28]. In the most completely developed twinned structures, all coherent primary twins were Σ = 3 boundaries. Nevertheless, these cyclic twins are imperfect due to faulting of the stacks in each twin. In some cases the structure of defective twins can be identified as a partial dislocation with stacking sequence […ABC·ABABAB·CBA…] with Burgers vector , but in many others the defective twin is too irregular for a simple description. This type of morphologies can be consistently interpreted as fragments of the simplest cyclic, multiply twinned structure (the pentagonal dipyramid or decahedron) of varying degrees of perfection. Regarding the composition surfaces, the reflection relation between pairs of adjacent twins also determines a layer succession of the type […ABC–ran–AB]C[BA–ran–ABC…], where each pair of brackets belongs to one of two adjacent twins, the C layer is the composition surface common to both sectors, and the underlined part shows the obligatory hcp character of the spheres lying on the composition surface.
Figure 1 is an example of a well-developed cyclic twin, with the view vector set parallel to the twin axis. Clipping planes have been used to remove all spheres lying between the twin and the observer. As mandated by the pseudo fivefold symmetry, spheres along the axis have a fivefold symmetric environment. The structure along the axis can also be viewed as a linear array of parallel stacked pentagons, or a pile of pentagonal bipyramids, as in [1,23,29] closely related to the Bagley structure [30].
4. Calculation of Entropic Loss Caused by Twinning
The proposed entropic mechanism for the absence of twinned structures in crystals of strictly tangent hard sphere chains must be supported by quantitative calculations of entropy differences between twinned and untwinned structures. These calculations must be carried out to the greatest possible accuracy, because order-disorder and polymorphic transitions in hard sphere systems are known [24,25] to sensitively depend on small entropy differences between the phases involved.
In systems of hard sphere chains an exact calculation of the entropic loss associated with the formation of pentagonal cyclic twinned structures is analytically unfeasible. Its numerical evaluation using standard procedures such as the Einstein crystal method [31,32] is also a major computational challenge, chiefly due to the difficulty of finding a kinetically accessible path between the untwinned and twinned states along which to carry out thermodynamic integration.
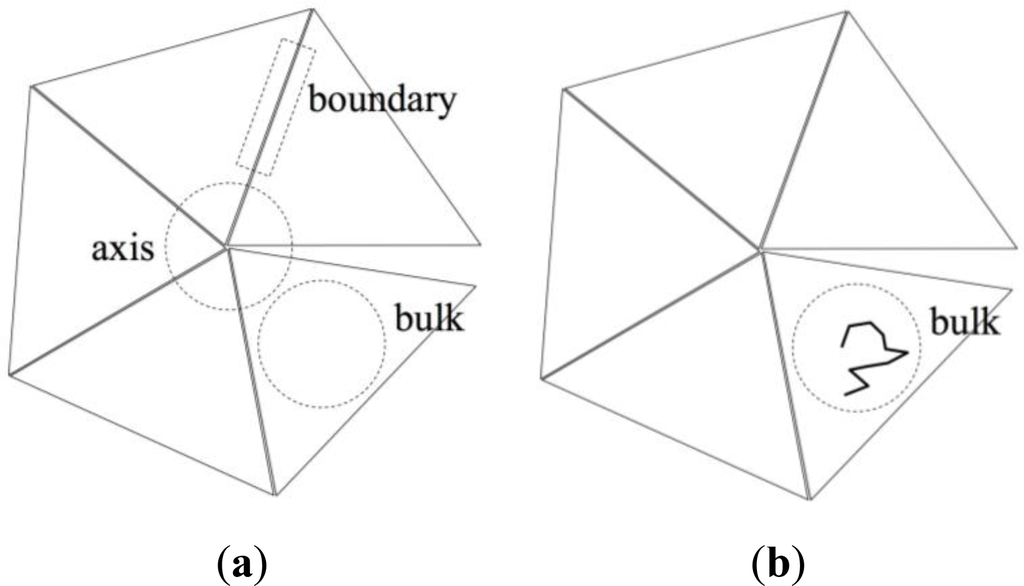
However, the geometrically simple structure of the ideal pentagonal twin shown in Figure 3 suggests an alternative, approximate method based on a decomposition of the entropy change ΔS in contributions stemming from:

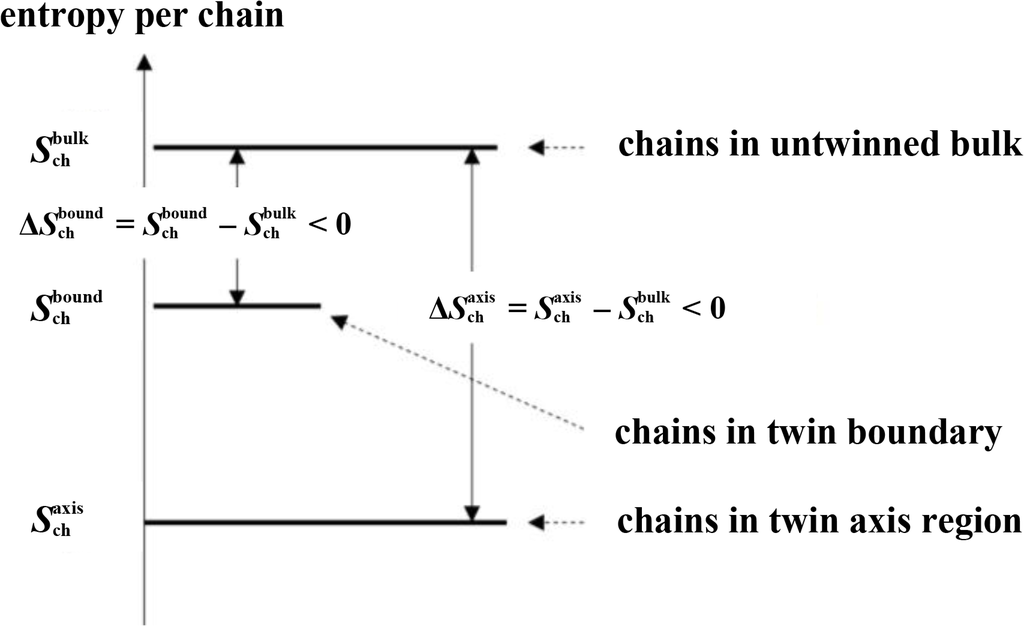
Chains that are entirely contained in one of the twin sectors (“bulk” in Figure 4b), having no monomers in the twin axis region nor in the twin boundary region. These chains are referred to as “bulk chains”.
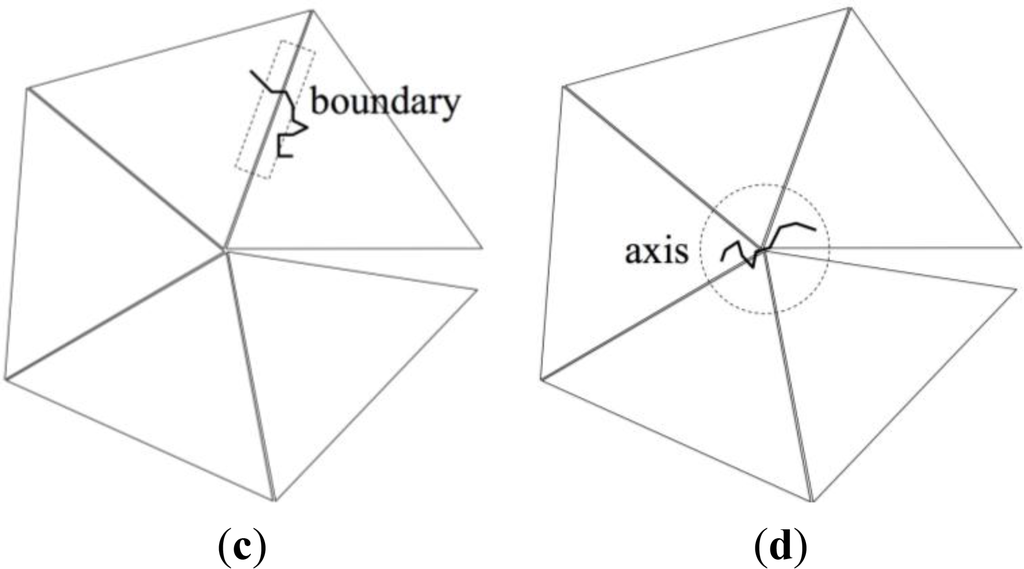
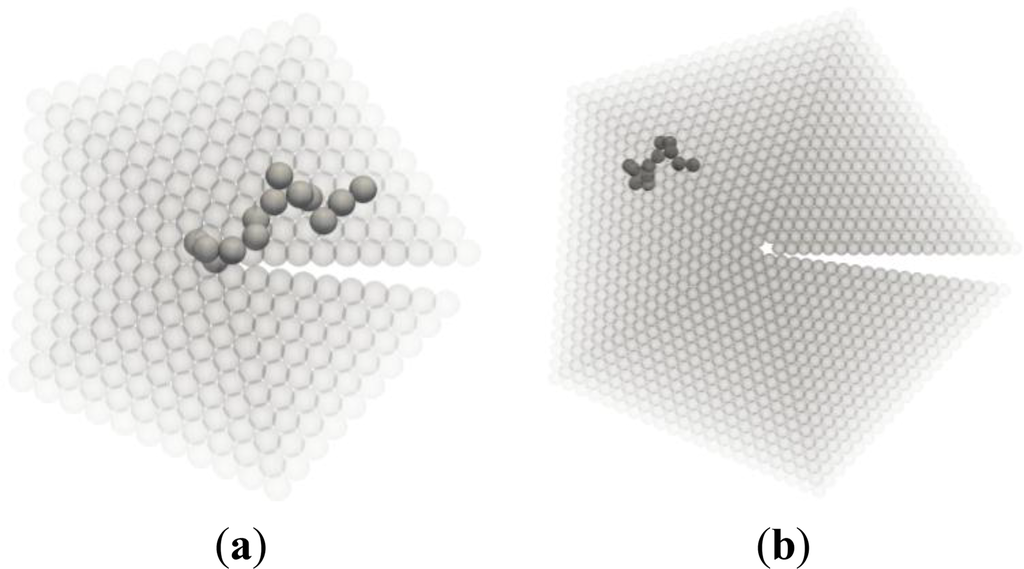
Chains that contain at least one monomer in the twin boundary region (“boundary” in Figure 4c). These chains are referred to as “boundary chains”.
Chains that contain at least one monomer in the twin axis region (“axis” in Figure 4d). These chains are referred to as “axis chains”.
Since each of the sectors in the ideal cyclic twin is made up of fcc layers with perfect stacking, individual conformations of bulk chains of a given length N can be generated easily by performing discrete random walks of unit length between contiguous monomers in an ideal fcc crystal large enough to contain the largest possible (fully extended) chain conformation.
A similar procedure can be applied to the generation of axis and boundary chains by performing similar random walks in the cyclic twin and selecting those that contain at least one monomer in the axis (axis chains) or in the boundary region (boundary chains), respectively. This is the basis of the calculation of entropic differences by exhaustive ensemble enumeration described below.
However, due to the very fast growth of ensemble size with chain length, the method of exhaustive ensemble enumeration works for rather short chains only. In order to reach the truly polymeric regime, i.e., N → ∞, we have resorted to the Rotational Isomeric State (RIS) model [33], which is described in Section 4.2.
In the following, all lengths are measured in monomer (hard sphere) diameters. Entropy is always expressed in terms of multiples of the Boltzmann constant kB.
4.1. Calculation of Entropic Loss by Exhaustive Enumeration
As mentioned above, an exact calculation of the entropy difference between chain ensembles in the bulk, boundary, and axis regions presents formidable problems for all but the shortest chains. However, an exact calculation of these entropy differences is still possible by exhaustive enumeration of the chain ensemble if the chain length is not too large.
Since the coordinates of all sites, which can be occupied by chain monomers, and the neighborhood relationships are known for and remain fixed in the ideal pentagonal twin (Figure 3), the construction of chain ensembles is reduced to a purely combinatorial problem: starting from each individual site, a first chain of the desired length N is generated as a self-avoiding, discrete random walk on the pre-defined lattice. This lattice is:
an fcc lattice for chains in the bulk,
two fcc lattices separated by a (111) composition plane (the twin Σ = 3 boundary) for boundary chains, or
five fcc lattices arranged as a cyclic twin for axis chains.
In all cases, the linear size of the individual lattices is chosen so as to be able to accommodate the maximum possible end-to-end length of the random walk of length N, which, measured in units of the monomer diameter, is N − 1.
After the first chain has been generated, successive chains are generated starting from all possible sites within a cutoff radius equal to twice the radius of gyration of the chain, until every single site has been occupied by a chain, i.e., the chain ensemble of Nch discrete random walks of length N completely fills the cutoff volume. The number of possible ensemble configurations that fulfill the previous constraints grows very fast with the total number of monomers (product of chain length N and number of chains Nch). Clearly, an analytic evaluation of the number of configurations is out of the question. Two typical conformations of axis and boundary chains are shown in Figure 5.
As an efficient alternative to the analytic calculation, we have used the numerical combinatorial approach of Tutte’s [34], which is based on Pólya’s enumeration theorem [35,36]. The algorithm starts by mapping the geometrical neighborhood relations between sites (i.e., which sites are tangent to a given one) onto a connectivity grid. Individual chains are realized as (random) graphs on this connectivity grid. Pólya’s enumeration theorem is then applied to exhaustively enumerate all possible configurations of the Nch chains of length N under the constraints that (a) chain monomers reside on the sites of the fcc lattice and (b) no sites remain unoccupied (no frustration). The computational effort of this procedure scales roughly as O((NchN)3Nch logN) and could be applied to chains of a maximum length N = 9 before computational effort became sm prohibitive.
The number of configurations Ω generated in this manner for the bulk, boundary, and axis ensembles, i.e., the size of the statistical mechanical ensemble of chain conformations, is the partition function of the ensemble of chains on the fcc lattice, since all of them have the same Boltzmann weight. It is the exact analog of the partition function Z obtained by means of the RIS theory (see below), and is also a direct measure of the absolute entropy of the ensemble.
Entropy was computed by S = kBlnΩ directly from the enumerated ensembles for all three types of chain ensembles (bulk, boundary, and axis). Entropy per chain was obtained as the quotient . It is important to note that the present chain enumeration task, although computationally expensive, is simpler than similar problems encountered in granular materials because chain monomers are forced to occupy predetermined sites on one or more fcc lattices. Entropy determination in granular materials [37] involves additional questions such as isostaticity and mechanical stability which are absent in our system.
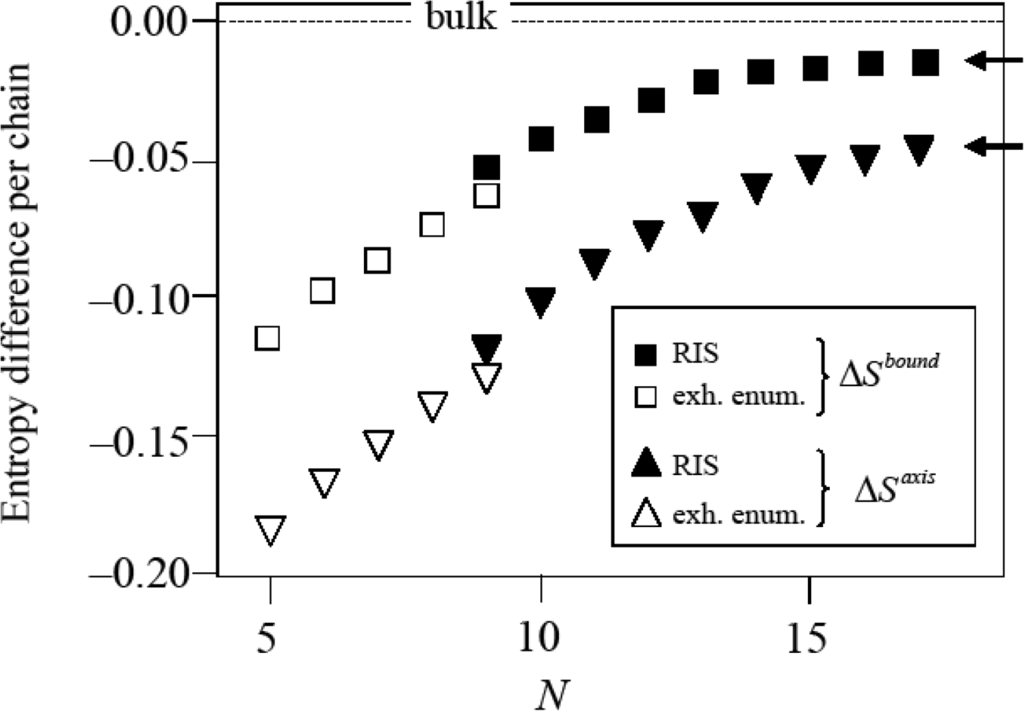
In all entropy values reported below chains in the bulk fcc crystal are taken as the reference state defining the entropy zero point (Figure 6). The results of these calculations, which build the basis of the phase stability calculation of Section 5 are presented in Figure 7. The empty symbols are the entropy differences per chain ΔSbound = Sbound − Sbulk < 0 and ΔSaxis = Saxis − Sbulk < 0 for chains of lengths in the range N = 5…9. In this range, chain entropy difference between boundary/axis chains and bulk chains grows monotonically with chain size for these short chains. The trend changes as the polymeric limit is approached. The implications of these two observations are discussed below.
For longer chains, an exhaustive enumeration of the ensemble, and hence a determination of absolute entropy, was computationally unfeasible. However, since it is the entropy difference between phases that determines their thermodynamic stability, we resorted to an alternative method that allows the accurate and efficient calculation of entropy differences by means of the Rotational Isomeric State (RIS) theory, which is not computationally limited by the length of the chain N.
4.2. Calculation of Entropic Loss Using Rotational Isomeric State (RIS) Theory
The rotational isomeric state (RIS) theory is based on the generator matrix method of Kramers and Wannier [38,39] and was first applied to polymers by Volkenstein (see [40] and refs. therein). Although its original formulation was relatively cumbersome for complex macromolecules, it was incrementally improved and streamlined by several authors [33,41]. Its current formulation is largely due to Flory [42], many of whose collaborators have used it extensively. RIS calculations can now be performed for branched, star, and cyclic chains of virtually any composition and structure.
In very simplified terms, setting up an RIS formalism for a polymer chain without side groups, as in our case, consists of the following steps:
Identify all skeletal bonds in the main chain around which a rotation is possible.
Determine the most probable angles each of these bonds and its adjoining bonds can simultaneously assume. Each of these torsion angle values is identified with a rotational isomer, i.e., a discrete state of the individual torsional degree of freedom. A particular set of rotational states, endowed with appropriate statistical weights, is taken as a discretized representation of the conformational ensemble.
Partition intramolecular interactions into those that depend on a single torsion angle (first order), and those that involve two successive torsion angles (second order).
Compute appropriate statistical weights, usually in the form of Boltzmann factors, to the populations of each particular local conformation.
Assemble statistical weight matrices, U, one for each skeletal bond. The statistical weight matrices have size νi−1 × νi, where νi is the number of rotational states of the i-th bond. For chains made up of identical bonds, all Ui matrices are of the same ν × ν size. For chains consisting of two or more types of bonds along the main chain, different Ui matrices are required. If these different bonds also have different numbers of rotational states, the Ui matrices must have conformable sizes as well.
Once the statistical weight matrices are available, the RIS approach allows for very efficient computation of the conformational partition function. For simple linear macromolecules, like those of our model hard sphere chains, consisting of N − 1 skeletal bonds, the partition function is given by:
For our present purpose, it is, however, the partition function Z itself that is of interest, as the most direct route to entropy differences. Although it is well known that the absolute magnitude of lnZ, computed with RIS, is dependent on technical features of the particular RIS implementation, and should not be used to compute absolute entropies, relative magnitudes, such as entropy differences between states, or temperature dependences , which are based on the ratio of partition functions, can be very accurately computed by the RIS scheme [42]. Since our goal is the estimation of entropy differences between chain ensembles in twinned and in un-twinned structures, using the RIS method is perfectly acceptable.
The price to pay for the simplicity in the calculation of Z is the need to develop the detailed RIS scheme. Setting up a detailed and quantitatively predictive RIS model for a polymer chain involves considerable effort, but once it is done, the power of the RIS method allows computation of the partition function via a simple product of statistical weight matrices with negligible computational cost.
Before describing the details of the RIS model for our hard-sphere chains, a word on its applicability to freely jointed chains is in order. At the heart of the RIS model lies the assumption that the chain has rotational freedom but has fixed bond angles. The latter assumption seems to be in contradiction with the freely jointed nature of our hard-sphere chains, in which the bond angle is free to vary except for the geometrical constraints imposed by monomer overlaps. Our use of the RIS relies on the representation of the freely jointed chains by RIS chains with fixed bond angles and a discrete set of rotational isomeric states that accurately reproduce the known bond angle fbond (θ) and bond torsion ftors (φ) distributions, both of which have been accurately measured [18,19,43,44]. The bending angle distribution in the crystal fbond (θ) (Figure 1 in Ref. [43]) shows two sharply defined maxima that correspond to the most probable arrangement of two consecutive bonds along a chain at 60° and 120°.
Similarly, the distribution of torsion angles ftors (φ) (Figure 2 in Ref. [43]), as defined by three successive bonds, is characterized by five sharp maxima at φ = 0°, ±70.5°, ±109.5° and three broader maxima at θ = ±54.7° and 180°. The peaks in the bond angle and torsion angle distributions stem from the most probable three-sphere (bond angle) and four-sphere (bond torsion) arrangements. These most probable arrangements have been positively correlated [43] with simple configurations of three or four consecutive spheres obtained by placing them on the vertices of one or two tetrahedra that share an edge or a face [22,23].
The existence of two peaks in the distribution of bond angles naturally leads to the choice of a RIS model with two distinct constitutional repeat units A and B, [ran-poly(AB)], where A stands for the θ = 60° bending angle, and B for the θ = 120° bending angle. Similarly, the maxima in the torsion angle distribution suggest a seven-state RIS scheme for each of the two constitutional repeat units A, B.
The statistical nature of the succession of bending angles in our freely jointed chains is achieved by randomly alternating the A and B repeat units with a statistical selection criterion that assigns probabilities of 0.46 and 0.54 to the A and B states. These statistical weights are obtained as the integrals of the bond angle distribution curve in the intervals θ ∈ [60°, 90°) for state A, and θ ∈ [90°, 180°) for state B. To further account for the random nature of the succession of A and B bond angles [ran-poly(AB)], the entropy difference calculations were performed for a large number (5 × 104) of different realizations of the A, B succession.
For each of these bond angles a set of first and second order contributions to the Ui matrices were calculated so as to accurately reproduce the observed torsion angle distribution ftors (φ); more specifically, the statistical weights for each of the two states were determined in order to reproduce the conditional angle distributions ftors (φ|θ = 60°) when the repeat unit was of type A, and ftors (φ|θ = 120°)when the repeat unit was of type B.
For both types of repeat units, it was found that a 7-state RIS scheme could accurately reproduce the known torsion angle distribution and the chain end-to-end vector distribution. The seven rotational isomeric states were named t, t*+, t*−, g*+, g*−, g+, g− according to a commonly used scheme [33], and their torsional angles were assigned the following numerical values t = 180°, t*+ = 125°, t*− = −125°, g*+ = 105°, g*− = −105°, g+ = 60°, and g− = −60°. The statistical weight matrices were, both for A and B repeat units, and also for chains in the twinned and bulk regions, of the form:
Finally, since our goal is the calculation of entropy differences between twinned and untwinned crystal structures, a set of RIS parameters was determined for chains in the bulk, a second one for boundary chains, and a third set for axis chains. Numerical values of the RIS states and parameters for each type of residue and each region are given in Tables 1 and 3. In these tables, the label “twinned” applies to RIS parameters valid for ensembles of boundary chains or ensembles of axis chains in the cyclic pentatwin axis region; the label “untwinned” applies to bulk chains in the untwinned crystal.
The statistical weights in these tables do not take the form of Boltzmann factors usually found in the RIS scheme for thermal systems, but have a fixed value ξj, as corresponds to an athermal ensemble.
Once the RIS parameters have been determined, entropy differences per chain between chain ensembles in twinned and untwinned regions are given by:
In Figure 7, the agreement of the results obtained by the two methods described above is very satisfactory. Although the two methods cannot be more dissimilar (one is exact, based on the complete enumeration of the members of the ensemble, and yields absolute entropies, the other involves a discretization of the torsional degree of freedom and yields only entropy differences) there is only a small discontinuity in the computed entropy differences when switching between the exact (for N ≤ 9) and the approximate (for N ≥ 9) methods. The exhaustive enumeration procedure and the RIS theory agree to within 17% for boundary chains and to within 12% for axis chains. The discrepancy is due to the approximate nature of the RIS scheme which replaces the continuum of torsional angles by a discrete set.



5. Chain Entropy Loss and Calculation of Phase Stability
Figure 7 constitutes the basis of the calculation of phase stability. From the trends observed in this figure it is clear that chains in the boundary or in the axis regions have systematically lower entropies than those in the bulk for all chain lengths. The entropy difference per chain between chains in twinned and untwinned regions is largest for the shortest chains and decreases (in absolute value) with increasing chain length.
The initial (up to N ≃ 12) linear growth of ΔS with chain length flattens to an asymptotic approach to constant values. For sufficiently long chains the differences , approach non-zero values (marked by arrows in the figure). This is consistent with the expected [45] asymptotic behavior in the infinite chain limit: for a given, fixed type of chain molecule, the contribution of each additional monomer to the chain entropy (the incremental, partial monomer molar entropy ) tends to a constant as N → ∞. In other words, for sufficiently long chains, increasing chain length by an extra monomer increases chain entropy by a constant amount, since, on average, the added monomer is insensitive to the small-scale details of the chain. Its contribution to the entropy comes from its interaction with a conformationally smoothed environment.
On the other hand, for small N, the addition of a new monomer is very sensitive to the small-scale details of the chain. This is so because short chains in the bulk, in the boundary, and in the axis are conformationally very different, since most of the monomers lie either in the bulk, or in the boundary or in the axis. For example, short chains in the axis region must adopt conformations with torsional angles that conform to the pentagonal symmetry of the axis. This pentagonal symmetry is very unlikely in chains in the bulk or in a sector boundary.
However, as the chain length increases, a larger part of a boundary or axis chain wanders away from these regions and into the bulk. This part of the chain increasingly resembles chains in the bulk. Adding a new monomer to such a chain is not very different from adding a monomer to a chain that is entirely located in the bulk.
Figure 8 is a qualitative depiction of this phenomenon: the portions of boundary and axis chains, marked by arrows, contained in these regions (drawn as a dashed line rectangle and circle respectively) are conformationally quite different from the rest of the chain, which lies outside these anomalous regions. The entropic loss for the chains located in the boundary and in the axis stems primarily from the anomalous conformations that part of the chain must adopt in order to fit in the boundary or axis regions. In particular, the portions of the chains residing in the twin axis are forced to adopt very “unnatural” conformations due to the nearly perfect pentagonal symmetry about the twin axis. These are conformations of very low probability for bulk chains. The number of possible chain conformations that are compatible with the pentacyclic symmetry of the axis region is considerably lower than for chains in the bulk. A similar situation applies to chains in the boundary, although the reduction in the number of conformations is much less drastic than in the axis region.
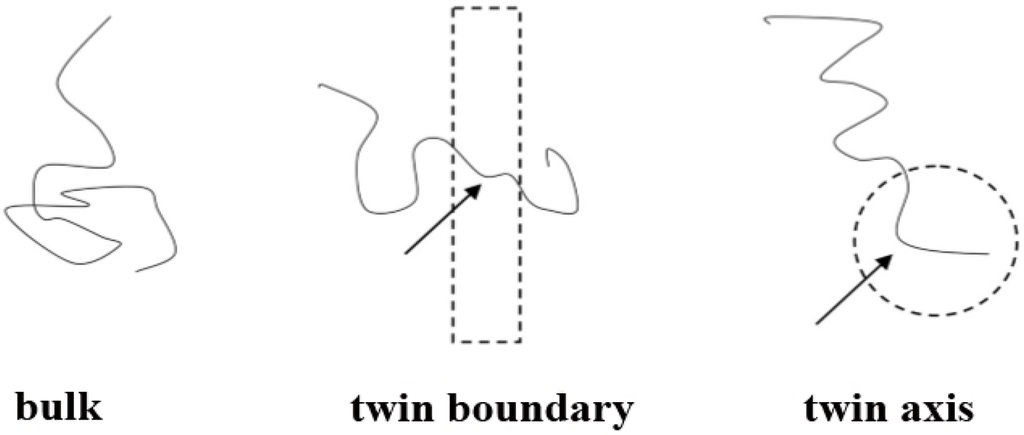
As the chain length increases, the local entropy loss due to parts of the chains residing in the boundary or in the axis regions is progressively diluted by the increasingly greater number of monomers lying outside the boundary or axis regions. As a consequence, the asymptotic behavior of the entropy for the three types of chains should therefore be of the form [46]:
This is a direct consequence of the fact that for N → ∞, on average, most of the chain resides in the bulk of the twin sector. Addition of an extra monomer takes place in the bulk with overwhelming probability. From the data in Figure 7 one obtains: nbound(abound − abulk) → −0.0162kB as N → ∞ (upper arrow in Figure 7) and similarly for a chain in the axis region naxis(aaxis − abulk) → −0.0437kB as N → ∞ (lower arrow in Figure 7).
The values of the average number of monomers of a chain in the boundary region, nbound, and of the average number of monomers of a chain in the axis region, naxis, were directly obtained from an analysis of the ensembles of the chains generated in the exhaustive enumeration algorithm: nbound = 8.1 ±0.2 and naxis = 5.9 ± 0.2 (one standard deviation in the mean). From these values of nbound and naxis and using:
It is immediate to obtain the numerical values of the differences: abound − abulk = −0.002kB, aaxis − abulk = −0.074kB.
In addition, the value of abulk can be computed from the RIS scheme, which is especially accurate for long chains, as :
The terms abound − abulk and aaxis − abulk have a clear physical interpretation: abound − abulk is the entropy difference per monomer between chain monomers located in the boundary region and monomers in the bulk; aaxis − abulk is the entropy difference per monomer between monomers located in the axis region and monomers in the bulk. Note that although these differences have constant, nonzero values, the entropy differences per chain vanish in the infinite chain limit, as they should, since both the twin boundary and the twin axis are localized surface (2D) and line (1D) defects and most of the chain lies outside these defects for N → ∞.
It is interesting to compare the numerical values of abound − abulk and aaxis − abulk with the entropy differences between the fcc (Sfcc) and hcp (Shcp) crystals of hard spheres [24,25]. Current estimates of the tiny difference Shcp − Sfcc vary between −0.0009kB and −0.0023kB per hard sphere, thus making the fcc crystal the more stable of the two forms. Our value abound − abulk = −0.002kB for the difference between chain monomers in the boundary and in the bulk regions is comparable with Shcp − Sfcc for individual hard spheres. This agreement suggests that the loss of entropy (per monomer) due to a chain spanning the boundary between twin sectors is of the same order of magnitude as the entropy difference (per hard sphere) between the fcc and the hcp crystals of single hard spheres. This is consistent with the fact that the (111) sector twin boundary (composition surface) can be viewed as an hcp defect between two fcc crystals. This entropic penalty at a twin boundary does not introduce a significant global entropic penalty in the system. Or at least not much greater than the entropy difference between fcc and hcp crystals of single hard spheres.
On the other hand, the value aaxis − abulk = −0.074kB, is about 35 times larger, indicating that the entropic penalty is a great deal larger for monomers residing in the axis region than in the boundary. The nature of this entropic loss in chain systems is very different from that of entropy differences between fcc and hcp crystals of monoatomic hard spheres. In chain systems it is due to the drastic reduction in the number of chain conformations compatible with the fivefold symmetry of the axis. In single sphere systems it is mainly positional entropy associated with spatial fluctuations of individual spheres.
Armed with the measured values of abound − abulk and aaxis − abulk, the calculation of the total entropy difference between a perfect, untwinned fcc crystal of chains, and an ideal pentacyclic twin is straightforward, based on the additivity of the entropy. For a given size of the twin (to be defined below), its total entropy is the sum of the contributions from its bulk, boundary, and axis regions. In addition, its total entropy difference (loss) with respect to the perfect fcc crystal of chains is the analogous sum of contributions to the entropy differences:
The two terms in Equation 8 can be evaluated from the known monomer entropy differences, and the volumes of the bulk, boundary and axis regions, which follow from the tetrahedral shape of each of the twin sectors. We have taken Nedge − 1 as characteristic, linear size of each tetrahedral sector. Each of the five sectors thus contains a total of monomers and a volume of cubic monomer diameters. The number of monomers on the boundary plane (111) is ; its area is and the volume of the boundary region is where the last factor comes froms assigning a thickness of twice the persistence length lK.
Similarly, the cylindrical axis region has a length of Nedge − 1 and a volume of where a value of has been assigned to the radius of the cylindrical axis region.
Persistence lengths and were computed from the exact RIS expression (see Equation (46), Chapter IV of [42]):
For a given chain length N, a system characterized by the linear size Nedge − 1 of one tetrahedral sector, contains a total of monomers, split in Nch = Nedge/N chains of length N. The total entropy difference for the system ΔStotal, as given by Equation 8, is presented in Figure 9 as a function of twin volume Vtwin and of Nedge for three different chain lengths N = 20, 100 and 500. Convergence to the polymeric N → ∞ limit is clearly fulfilled.
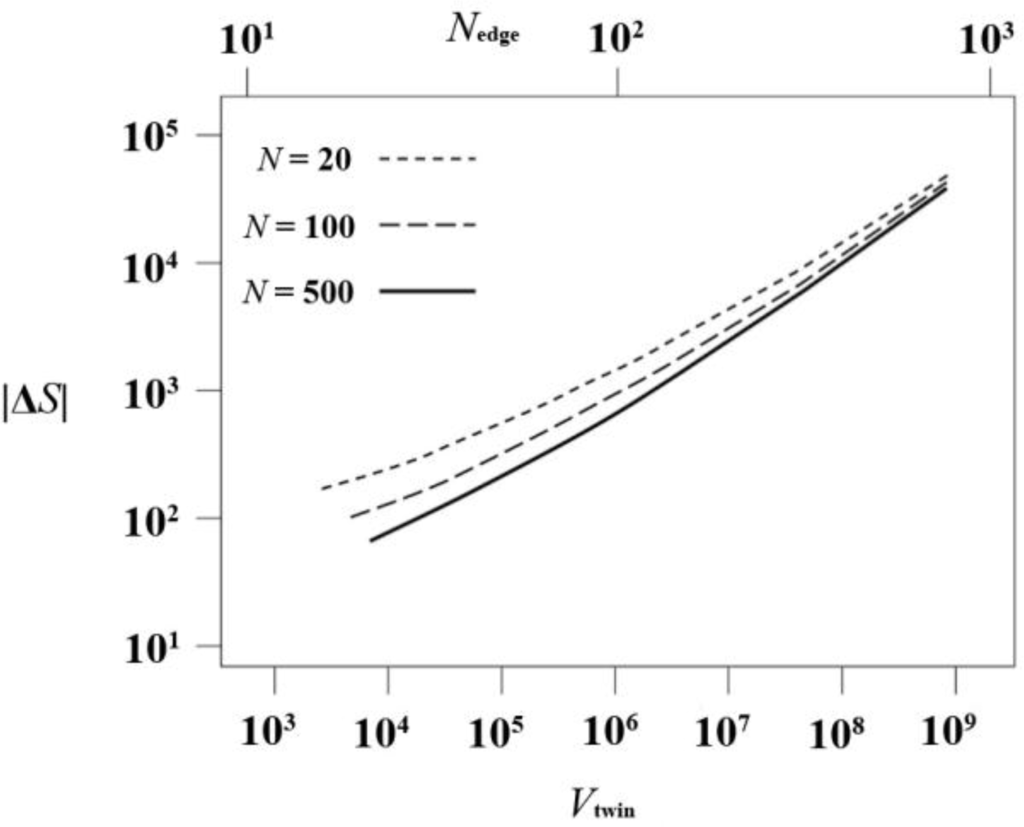
In Figure 10 we present the entropy loss per unit volume (in absolute value; ΔS is negative) of the cyclic twin. As expected, the entropy difference per unit volume approaches zero in the thermodynamic (V → ∞) limit because the axis and the sector composition surfaces are of lower dimensionality, i.e., they can be considered line and surface defects respectively. However, in judging the emergence of a twinned versus an utwinned phase it is not the entropy difference per unit volume that decides the question, but the difference in entropy between the untwinned and the twinned crystal.
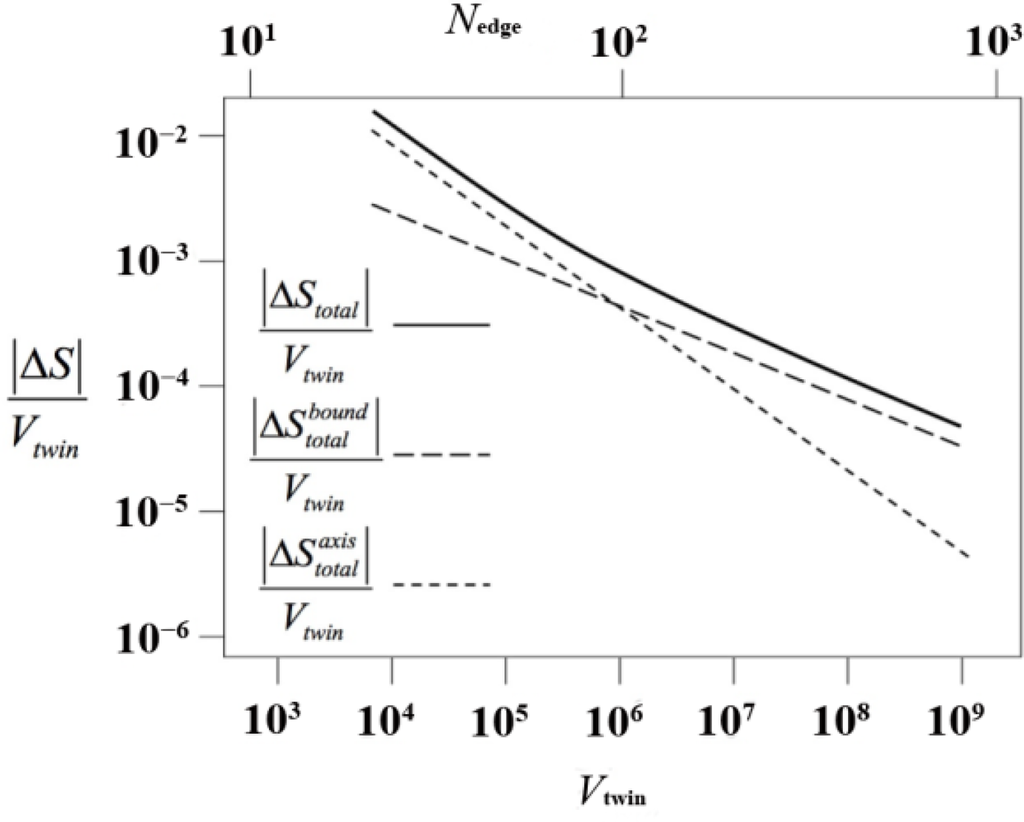
This entropy difference is presented in Figure 11 (again as |ΔS|), split in its contributions from the axis and from the boundary regions. For all sizes of the twin (either measured as its volume or as its characteristic linear dimension), ΔS < 0 and the twinned structure is entropically far less favorable. Up to a crossover size of Nedge ≃ 85, axis chains make the main contribution to the entropic loss. Above that value, boundary chains have a larger share. Thus, the formation of twinned structures in our model polymer system is very strongly suppressed by the entropic loss associated with chains in the axis. These chains must adopt conformations of low probability in order to fit in the pentagonally symmetric environment of the axis. In terms of ensembles, and for chains of a given length, the ensemble of axis chains is much smaller than the ensemble of bulk chains.
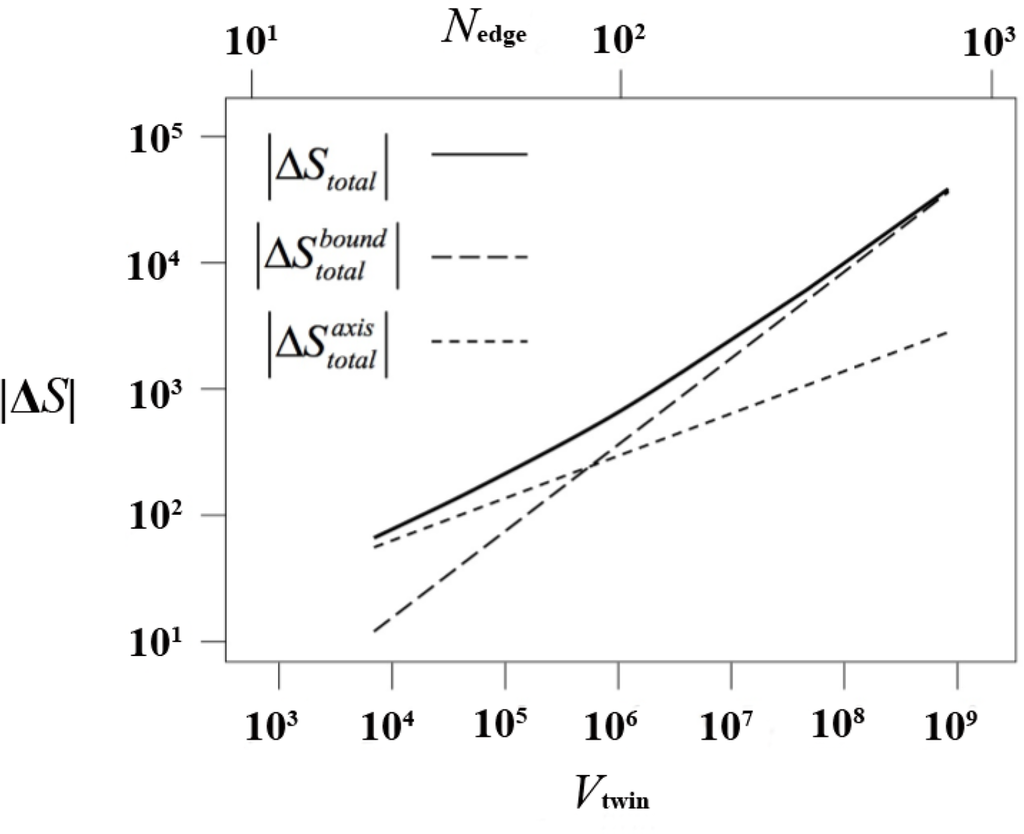
This entropic loss mechanism is of sufficient strength to explain the absence of twinned structures in our simulated chain crystals. Furthermore, the MC scheme used in the simulation of crystallization is not limited by arrested kinetic factors which could have been invoked as an alternative explanation if an MD method had been used.
The contribution of the twin boundaries to the entropy loss is much less for twins up the Nedge ≃ 85 crossover. The conformational entropy loss due to chains spanning the sector composition surface is not much larger (per monomer) than the entropy difference per sphere in fcc and hcp crystals of single spheres. As a consequence, crystal structures having polysynthetic (lamellar) morphologies are far less unfavorable entropically. The fact that they appear readily both in experiments and simulations [47] indicates that, in addition, they are kinetically accessible by simulation.
Regarding the crossover value, a value of Nedge ≃ 85 corresponds to a twin containing approx. 3 × 105 monomers, which must be accompanied by a comparable number of monomers in the surrounding undercooled bulk liquid. The atomistic simulation of crystallization in such a huge system is well beyond the reach of current computational capabilities. However, more importantly, a twin of that size is unlikely ever to be formed in a simulation, since chain axis entropy loss will not allow cyclic twins to develop beyond the seed stage. Should a small cyclic twin precursor be formed, it would quite rapidly be replaced in the course of the MC simulation by higher entropy alternatives such as the layered rchp crystal or, although somewhat less likely, a polysynthetic twin.
The role played by symmetry in the present context is quite a different one from that in a monatomic pentatwin. In the untwinned structure, the distribution of chain configurations is highly symmetric: it is isotropic, in the sense that the distribution of any (1st-order tensorial) conformational measure like the end-to-end vector, is independent of orientation. In the twin, this high symmetry is destroyed by the presence of twin boundaries (which reduce the symmetry from the limit class ∞∞m down to ∞/mm) and by the presence of the twin axis (which further reduces the symmetry of the distribution functions to a single 5̄ axis). The reduction in symmetry is what ultimately causes the loss in entropy.
6. Conclusions
A calculation of entropy by means of exhaustive enumeration and by the rotational isomeric scheme supports the hypothesis that chain conformational entropy loss is the primary underlying mechanism for the thermodynamic stability of the single crystal vs. the twinned crystal in simple polymers. In particular, the highly unlikely conformations that chains in the axis of the twin must adopt to fit in this environment seem to be the main source of entropy loss.
Twinned structures observed in MD simulations are therefore a consequence of kinetic trapping of the algorithm, which is unable to surmount the free energy barrier that separates the single and the twinned crystals.
Conformational entropy losses associated with chains that span sector boundaries are considerably lower and not likely to suppress twinning except for very large crystal sizes.
Although our calculations show that the twinned crystal is thermodynamically unstable, they do not shed any light on whether the hcp or the fcc crystal (as for single hard spheres) is the stable phase for crystals of chains of strictly tangent hard spheres.
All previous conclusions do not apply to crystal of complex biological polymers such as proteins, in which very specific interactions and monomeric sequence overwhelm the entropic effect discussed here. Besides, twinning in protein crystals is not related to the twinning of polymers, because a large fraction of the volume of the protein crystal is filled with small molecules (primarily water with ions and some small molecules).
Acknowledgments
N.Ch.K. acknowledges support through projects “Ramon y Cajal” (RYC-2009-05413), “I3” and “MAT2010-15482” of the Spanish Ministry of Economy and Competitiveness (MINECO). K.F. acknowledges support through projects “Ramon y Cajal” (RYC-2010/06804) and “MAT2011-24834” of MINECO. M.L. gratefully acknowledges support from the Xàbia Physics School. Authors thankfully acknowledge the computer resources, technical expertise and assistance provided by the Centro de Computacion y Visualizacion de Madrid (CeSViMa).
Author Contributions
N.Ch.K. performed extensive Monte Carlo simulations on hard sphere chains; determined morphologies of ordered phases; critically revised first version of manuscript; helped with revisions suggested by reviewers. K.F. performed event-driven molecular dynamics simulations on monomeric hard spheres; formulated and employed the crystallographic-based analysis of the computer-generated structures; critically revised first version of manuscript; helped with revisions suggested by reviewers. M.L. implemented RIS and exhaustive enumeration methods; performed calculation of entropy differences; wrote first version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Friedel, G. Leçons de Cristallographie; Berger-Levrault: Paris, France, 1926; Reprinted by Blanchard: Paris, France, 1964. [Google Scholar]
- Giacovazzo, C.; Monaco, H.L.; Artioli, G.; Viterbo, D.; Ferraris, G.; Gilli, G.; Zanotti, G.; Gatti, M. Fundamentals of Crystallography; International Union of Crystallography: Oxford, UK, 2005. [Google Scholar]
- Cahn, R.W. Twinned crystals. Adv. Phys 1954, 3, 363–445. [Google Scholar]
- Parsons, S. Introduction to twinning. Acta Cryst D 2003, 59, 1995–2003. [Google Scholar]
- Armstrong, R.W.; Zerilli, F.J. Deformation twinning: From atomic modeling to shock wave loading. In Advances in Twinning; Ankem, S., Pande, C.S., Eds.; The Minerals, Metals & Materials Society: Warrendale, PA, USA, 1997; pp. 67–81. [Google Scholar]
- Le Page, Y.; Donnay, J.D.H.; Donnay, G. Crystal-setting ambiguities, their relation to crystal orientation an twinning by merohedry. Acta Cryst. A 1984, 40, 679–690. [Google Scholar]
- Carazzolo, G.; Leghissa, S.; Mammi, M. Polyoxymethylene from trioxane by solid state polimerization: A case of twinning in a synthetic polymer. Makrom. Chem 1963, 60, 171–190. [Google Scholar]
- Kitaigorodskii, A.L. Mixed Crystals; Springer Verlag: Berlin, Germany, 1984. [Google Scholar]
- Dorset, D.L. Crystallography of the Polymethylene Chain; Oxford University Press: Oxford, UK, 2005. [Google Scholar]
- Mandelkern, L. Crystallization of Polymers; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Miyaji, H.; Toda, A. Crystal Growth of Polymers. Solid Status Phys 1989, 24, 723–728. [Google Scholar]
- Toda, A.; Kiho, H. Crystal-Growth of Polyethylene from Dilute Solution-Growth Kinetics of (110) Twins and Diffusion-Limited Growth of Single Crystals. J. Polym. Sci. B Polym. Phys 1989, 27, 53–61. [Google Scholar]
- Toda, A. Nucleation-controlled growth in polyethylene single-crystals. J. Polym. Sci. B Polym. Phys 1989, 27, 1721–1729. [Google Scholar]
- Vancso, G.J.; Nisman, R.; Snétivy, D.; Schönherr, H.; Smith, P.; Ng, C.; Yang, H. Morphological studies of ordered, solid polymers by scanning force microscopy. Colloids Surf 1994, 87, 263–275. [Google Scholar]
- Yeates, T.O.; Fam, B.C. Protein crystals and their evil twins. Structure 1999, 7, R25–R29. [Google Scholar]
- O’Malley, B.; Snook, I.K. Crystal Nucleation in the Hard Sphere System. Phys. Rev. Lett 2003, 90. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The characteristic crystallographic element norm: A descriptor of local structure in atomistic and particulate systems. J. Chem. Phys 2009, 130. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Entropy-Driven Crystallization in Dense Systems of Athermal Chain Molecules. Phys. Rev. Lett 2009, 103. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Abrams, C.F.; Laso, M. Modeling of crystal nucleation and growth in athermal polymers: Self-assembly of layered nano-morphologies. Soft Matter 2010, 6, 2160–2173. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph 1996, 14, 33–38. [Google Scholar]
- Ni, R.; Dijkstra, M. Effect of bond length fluctuations on crystal nucleation of hard bead chains. Soft Matter 2013, 9, 365–369. [Google Scholar]
- Anikeenko, A.V.; Medvedev, N.N. Homogeneous crystallization of the Lennard-Jones liquid. Structural analysis based on Delaunay simplices method. J. Struct. Chem 2006, 47, 267–276. [Google Scholar]
- Anikeenko, A.V.; Medvedev, N.N.; Bezrukov, A.; Stoyan, D. Observation of fivefold symmetry structures in computer models of dense packing of hard spheres. J. Non-Cryst. Solids 2007, 353, 3545–3549. [Google Scholar]
- Woodcock, L.V. Entropy difference between the face-centred cubic and hexagonal close-packed crystal structures. Nature 1997, 385, 141–143. [Google Scholar]
- Bolhuis, P.G.; Frenkel, D.; Mau, S.-C.; Huse, D.A. Entropy difference between crystal phases. Nature 1997, 388, 235–236. [Google Scholar]
- Barnard, A.S. A thermodynamic model for the shape and stability of twinned nanostructures. J. Phys. Chem. B 2006, 110, 24498–24504. [Google Scholar]
- Karayiannis, N.C.; Malshe, R.; Kroger, M.; de Pablo, J.J.; Laso, M. Evolution of fivefold local symmetry during crystal nucleation and growth in dense hard-sphere packings. Soft Matter 2012, 8, 844–858. [Google Scholar]
- Karayiannis, N.C.; Malshe, R.; de Pablo, J.J.; Laso, M. Fivefold symmetry as an inhibitor to hard-sphere crystallization. Phys. Rev. E 2011, 83. [Google Scholar] [CrossRef]
- Ino, S.; Ogawa, S. Multiply twinned particles at earlier stages of gold film formation on alkali halide crystals. J. Phys. Soc. Jpn 1967, 22, 1365–1374. [Google Scholar]
- Bagley, B.G. 5-fold Pseudosymmetry. Nature 1970, 225, 1040–1041. [Google Scholar]
- Frenkel, D.; Ladd, A.J.C. New Monte Carlo method to compute the free energy of arbitrary solids. Application to the fcc and hcp phases of hard spheres. J. Chem. Phys 1984, 81, 3188–3193. [Google Scholar]
- De Miguel, E.; Marguta, R.G.; del Río, E.M. System-size dependence of the free energy of crystalline solids. J. Chem. Phys 2007, 127. [Google Scholar] [CrossRef]
- Rehahn, M.; Mattice, W.L.; Suter, U.W. Rotational Isomeric State models in Macromolecular Systems; Advances in Polymer Science; Springer: Berlin, Germany, 1997. [Google Scholar]
- Tutte, W.T. An algorithm for determining whether a given binary matroid is graphic. Proc. Am. Math. Soc 1960, 11, 905–917. [Google Scholar]
- Pólya, G. Kombinatorische Anzahlbestimmungen für Gruppen, Graphen und chemische Verbindungen. Acta Math 1937, 68, 145–254. (In German). [Google Scholar]
- Harary, F. Graph Theory; Addison Wesley: Reading, MA, USA, 1969. [Google Scholar]
- Hoy, R.S.; Harwayne-Gidansky, J.; O’Hern, C.S. Structure of finite sphere packings via exact enumeration: Implications for colloidal crystal nucleation. Phys. Rev. E 2012, 85. [Google Scholar] [CrossRef]
- Kramers, H.A.; Wannier, G.H.S. Statistics of the two-dimensional ferromagnet Part I. Phys. Rev 1941, 60, 252–262. [Google Scholar]
- Kramers, H.A.; Wannier, G.H.S. Statistics of the two-dimensional ferromagnet Part II. Phys. Rev 1941, 60, 263–276. [Google Scholar]
- Leonard, W.J., Jr.; Jernigan, R.L.; Flory, P.J. Dipole moments in relation to configuration of n-alkane chains bearing alpha, omega dipolar substituents. J. Chem. Phys 1965, 43, 2256–2261. [Google Scholar]
- Lifson, S.J. Neighbor interactions and internal rotations in polymer molecules. III. Statistics of independent rotations and their application to the polyethylene molecule. J. Chem. Phys 1959, 30, 964–967. [Google Scholar]
- Flory, P.J. Statistical Mechanics of Chain Molecules; Wiley-Interscience: New York, NY, USA, 1969. [Google Scholar]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. The structure of random packings of freely jointed chains of tangent hard spheres. J. Chem. Phys 2009, 130. [Google Scholar] [CrossRef]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Contact network in nearly jammed disordered packings of hard-sphere chains. Phys. Rev. E 2009, 80. [Google Scholar] [CrossRef]
- Kumar, S.K. The chain-length dependence of the chemical potentials of macromolecular systems at zero density. J. Chem. Phys 1992, 96, 1490–1497. [Google Scholar]
- De Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Cornell, NY, USA, 1979. [Google Scholar]
- Karayiannis, N.C.; Foteinopoulou, K.; Laso, M. Spontaneous crystallization in athermal polymer packings. Int. J. Mol. Sci 2013, 14, 332–358. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).