Symmetry-Adapted Fourier Series for the Wallpaper Groups

Abstract

Two-dimensional (2D) functions with wallpaper group symmetry can be written as Fourier series displaying both translational and point-group symmetry. We elaborate the symmetry-adapted Fourier series for each of the 17 wallpaper groups. The symmetry manifests itself through constraints on and relations between the Fourier coefficients. Visualising the equivalencies of Fourier coefficients by means of discrete 2D maps reveals how direct-space symmetry is transformed into coefficient-space symmetry. Explicit expressions are given for the Fourier series and Fourier coefficient maps of both real and complex functions, readily applicable to the description of the properties of 2D materials like graphene or boron-nitride.

1. Introduction

The central concept for describing the structure of crystalline solids is that of the unit cell, the periodic repetition of which results in a spatially extended crystal exhibiting particular symmetries. For both three- and two-dimensional (3D and 2D) crystals, the enumeration of possible unit cell symmetries was first carried out by E.S. Fedorov at the end of the nineteenth century [1,2,3]. Deriving the possible (3D or 2D) unit cell symmetries requires combining a crystal’s possible point group symmetry operations (rotations, rotation-inversions or reflections leaving one point of the crystal lattice invariant) with translations. It is well known that for three dimensions, this results in 230 so-called “space groups”. For two dimensions, only 17 planar groups, the so-called “wallpaper groups”, are possible. All information on space/wallpaper groups is nowadays collected in the many-volume International Tables for Crystallography [4,5,6,7,8].

The information compiled in the “International Tables” [4,5,6,7,8] is particularly useful for interpreting diffraction experiments: X-ray, neutron, and electron diffraction are the de facto methods for crystal structure determination and provide access not only to a crystal’s space group but also to the contents of its unit cell. In particular, the notion of extinctions (systematic absences of certain types of reflections due to specific symmetries present in the structure) is often fundamental for correctly determining a crystal’s space group.

The crystallinity—in other words, translational periodicity—of a solid is the essential starting-point in solid-state physics. For example, the quantum theory of electrical conductivity, involving Bloch waves, completely relies on the repetition of a unit cell for the concepts of reciprocal space and band structures to be valid (see e.g., [9]). Surprisingly, while the translational periodicity of a solid is used extensively in theory, considerations concerning the unit cell’s symmetry are far less frequently encountered.

Translational symmetry naturally leads to a Fourier series. Submitting a Fourier series to additional symmetry constraints then results in relations between Fourier coefficients, or even in the vanishing of certain terms of the Fourier series. In this paper, we revisit the symmetry-adapted Fourier series for the planar wallpaper groups, and focus on the symmetry pattern formed by equivalent Fourier coefficients in 2D discrete coefficient space. Apart from the explicit expressions for the symmetry-adapted Fourier series and the symmetry relations between Fourier coefficients, we provide visualisations showing how direct-space symmetry is transformed into coefficient-space symmetry.

In the first sections of the paper (Section 2, Section 3 and Section 4) we provide a pedestrian approach to the problem, work out some examples in detail, and make the link with the information contained in the “International Tables” [4,5,6,7,8] used by crystallographers. The bulk of the paper is formed by the 17 tables with detailed information on the Fourier series and Fourier coefficients for each of the wallpaper groups (Section 5). In Section 6, we discuss some points in more detail and summarise our results.

While the paper is hoped to have pedagogical merits, we also strive for completeness and applicability: The information derived is relevant for present-day materials science. For example, graphene [10], a 2D honeycomb network of carbon atoms, is at present one of the most extensively investigated materials. Its equilibrium properties (e.g., electronic density) are expected to display the 2D symmetry of its underlying atomic structure (wallpaper group $p6mm$, see below).

2. Two-Dimensional Translational Symmetry

We consider a scalar function $f(\overrightarrow{r})\equiv f(x,y)$ depending on the spatial coordinates $\overrightarrow{r}=x{\overrightarrow{e}}_x+y{\overrightarrow{e}}_y\equiv (x,y)$ of 2D coordinate space; ${\overrightarrow{e}}_x\equiv (1,0)$ and ${\overrightarrow{e}}_y\equiv (0,1)$ are the basis vectors of the underlying Cartesian axes system. It is well known that if f is periodic along two linearly independent vectors ${\overrightarrow{a}}_1$ and ${\overrightarrow{a}}_2$, it can be written as a Fourier series

$$\begin{array}{c}\hfill f(\overrightarrow{r})=\sum _{k_1=-\infty }^{+\infty }\sum _{k_2=-\infty }^{+\infty }{c}_{\overrightarrow{k}(k_1,k_2)}{e}^{i\overrightarrow{k}(k_1,k_2)·\overrightarrow{r}}\end{array}$$

(1)

with

$$\begin{array}{c}\hfill \overrightarrow{k}(k_1,k_2)=k_1{\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2\end{array}$$

(2)

where ${\overrightarrow{b}}_1$ and ${\overrightarrow{b}}_2$ are obtained from ${\overrightarrow{a}}_1=a_{1x}{\overrightarrow{e}}_x+a_{1y}{\overrightarrow{e}}_y$ and ${\overrightarrow{a}}_2=a_{2x}{\overrightarrow{e}}_x+a_{2y}{\overrightarrow{e}}_y$ via

$$\begin{array}{cc}\hfill {\overrightarrow{b}}_1& =\frac{2\pi }{s}\left[({\overrightarrow{a}}_2·{\overrightarrow{a}}_2){\overrightarrow{a}}_1-({\overrightarrow{a}}_1·{\overrightarrow{a}}_2){\overrightarrow{a}}_2\right]\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\overrightarrow{b}}_2& =\frac{2\pi }{s}\left[({\overrightarrow{a}}_1·{\overrightarrow{a}}_1){\overrightarrow{a}}_2-({\overrightarrow{a}}_1·{\overrightarrow{a}}_2){\overrightarrow{a}}_1\right]\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill s& =({\overrightarrow{a}}_1·{\overrightarrow{a}}_1)({\overrightarrow{a}}_2·{\overrightarrow{a}}_2)-{({\overrightarrow{a}}_1·{\overrightarrow{a}}_2)}^2\hfill \end{array}$$

(5)

The Fourier coefficients $c_{\overrightarrow{k}}$ are obtained by integration,

$$\begin{array}{c}\hfill c_{\overrightarrow{k}}=\frac{1}{\Sigma }{\int }_{\Sigma }f(\overrightarrow{r})e^{-i\overrightarrow{k}·\overrightarrow{r}}d\overrightarrow{r}\end{array}$$

(6)

where we have introduced the shorthand notation $\overrightarrow{k}\equiv \overrightarrow{k}(k_1,k_2)$; $\Sigma$ is the area spanned by the vectors ${\overrightarrow{a}}_1$ and ${\overrightarrow{a}}_2$ (most generally, ${\overrightarrow{a}}_1$ and ${\overrightarrow{a}}_2$ define a parallelogram).

In the context of the planar wallpaper groups, ${\overrightarrow{a}}_1$ and ${\overrightarrow{a}}_2$ are of course the (primitive) basis vectors of a Bravais lattice and ${\overrightarrow{b}}_1$ and ${\overrightarrow{b}}_2$ the associated reciprocal basis vectors, satisfying the property

$$\begin{array}{c}\hfill {\overrightarrow{a}}_l·{\overrightarrow{b}}_m=2\pi {\delta }_{lm}\end{array}$$

(7)

For planar space groups, there are only 5 Bravais lattices. Their primitive basis vectors and reciprocal basis vectors are summarized in

Table 1. Basis vectors $({\overrightarrow{a}}_1,{\overrightarrow{a}}_2)$ and reciprocal basis vectors $({\overrightarrow{b}}_2,{\overrightarrow{b}}_2)$ of the 5 planar Bravais lattices. For the non-centered lattices, ${\overrightarrow{a}}_1$ can always be chosen parallel to ${\overrightarrow{e}}_x$ without loss of generality. For the hexagonal lattice, the angle between the basis vectors is taken to be ${60}^{\circ }$ rather than ${120}^{\circ }$.

oblique	${\overrightarrow{a}}_1=a(1,0)$	${\overrightarrow{b}}_1=\frac{2\pi }{a}(1,-\frac{a_{2x}}{a_{2y}})$
	${\overrightarrow{a}}_2=(a_{2x},a_{2y})$	${\overrightarrow{b}}_2=\frac{2\pi }{a_{2y}}(0,1)$
rectangular	${\overrightarrow{a}}_1=a(1,0)$	${\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)$
	${\overrightarrow{a}}_2=b(0,1)$	${\overrightarrow{b}}_2=\frac{2\pi }{b}(0,1)$
centered rectangular	${\overrightarrow{a}}_1=(\frac{a}{2},-\frac{b}{2})$	${\overrightarrow{b}}_1=2\pi (\frac{1}{a},\frac{1}{b})$
	${\overrightarrow{a}}_2=(\frac{a}{2},\frac{b}{2})$	${\overrightarrow{b}}_2=2\pi (\frac{1}{a},-\frac{1}{b})$
square	${\overrightarrow{a}}_1=a(1,0)$	${\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)$
	${\overrightarrow{a}}_2=a(0,1)$	${\overrightarrow{b}}_2=\frac{2\pi }{a}(0,1)$
hexagonal	${\overrightarrow{a}}_1=a(1,0)$	${\overrightarrow{b}}_1=\frac{2\pi }{a}(1,-\frac{1}{\sqrt{3}})$
	${\overrightarrow{a}}_2=a(\frac{1}{2},\frac{\sqrt{3}}{2})$	${\overrightarrow{b}}_2=\frac{2\pi }{a}(0,\frac{2}{\sqrt{3}})$

.

It is easy to show that for f to be real, the condition

$$\begin{array}{c}\hfill c_{\overrightarrow{k}}^{*}=c_{-\overrightarrow{k}}\end{array}$$

(8)

needs to be fulfilled.

3. Full Wallpaper Group Symmetry

In addition to translational symmetry, each wallpaper group (except the $p1$ group) displays additional symmetry: invariance under rotations, reflections and/or glide reflections. Note that the latter are neither point group nor translational group elements. (The planar crystallographic point groups are 1, 2, m, $2mm$, 4, $4mm$, 3, $3m$, 6 and $6mm$ [4].) The purpose of the present paper is to derive restrictions on the Fourier coefficients $c_{\overrightarrow{k}}$ for each of the 16 non-$p1$ wallpaper groups. Indeed, a specific symmetry requirement (i.e., invariance of f under a certain symmetry operation) must be reflected in Fourier expansion Equation (1), which is only possible by having certain relations between its Fourier coefficients [similar to the reality criterion—Equation (8)].

3.1. Rotations

A rotation over $\varphi$ about the origin (or about the “virtual” z-axis) moves a point with coordinates $\overrightarrow{r}=(x,y)$ to the point ${\overrightarrow{r}}^{\prime }$ with coordinates

$$\begin{array}{c}\hfill {\overrightarrow{r}}^{\prime }=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=M_{\varphi }\overrightarrow{r}=\left(\begin{array}{cc}cos\varphi & -sin\varphi \\ sin\varphi & cos\varphi \end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\end{array}$$

(9)

Rotating the function rather than the coordinates results in the transformed function $f^{\prime }$, given by

$$\begin{array}{c}\hfill f^{\prime }(\overrightarrow{r})=f(M_{\varphi }^{-1}\overrightarrow{r})\end{array}$$

(10)

For f to be invariant by the rotation, one must have $f=f^{\prime }$, so that

$$\begin{array}{c}\hfill \sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{k}·\overrightarrow{r}}=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{k}·(M_{\varphi }^{-1}\overrightarrow{r})}\end{array}$$

(11)

By rewriting the scalar product $\overrightarrow{k}·(M_{\varphi }^{-1}\overrightarrow{r})$ as

$$\begin{array}{c}\hfill \overrightarrow{k}·(M_{\varphi }^{-1}\overrightarrow{r})=\overrightarrow{K}·\overrightarrow{r}\end{array}$$

(12)

and establishing the relationship between $\overrightarrow{K}=K_1{\overrightarrow{b}}_1+K_2{\overrightarrow{b}}_2$ and $\overrightarrow{k}=k_1{\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2$ one obtains the symmetry rule for the $c_{\overrightarrow{k}}$ coefficients associated with a rotation over $\varphi$.

As an example, let us consider $\varphi =\frac{2\pi }{6}$—6-fold rotational symmetry. The matrix $M_{\varphi }$ reads

$$\begin{array}{c}\hfill M_{\varphi =\frac{2\pi }{6}}=\left(\begin{array}{cc}\frac{1}{2}& -\frac{\sqrt{3}}{2}\\ \frac{\sqrt{3}}{2}& \frac{1}{2}\end{array}\right)\end{array}$$

(13)

and the scalar product $\overrightarrow{k}·(M_{\varphi }^{-1}\overrightarrow{r})$ is obtained as

$$\begin{array}{c}\hfill \overrightarrow{k}·(M_{\varphi }^{-1}\overrightarrow{r})=\frac{1}{2}\left[k_x(x+\sqrt{3}y)+k_y(-\sqrt{3}x+y)\right]\end{array}$$

(14)

where $\overrightarrow{k}=k_x{\overrightarrow{e}}_x+k_y{\overrightarrow{e}}_y$. For a hexagonal lattice—implied by the presence of 6-fold rotational symmetry—we have (see Table 1) $k_x=\frac{2\pi }{a}{k}_1$ and $k_y=\frac{2\pi }{a}(-\frac{1}{\sqrt{3}}{k}_1+\frac{2}{\sqrt{3}}{k}_2)$, so that

$$\begin{array}{c}\hfill \overrightarrow{k}·(M_{\varphi }^{-1}\overrightarrow{r})=\frac{2\pi }{a}(k_1-k_2)x+\frac{2\pi }{\sqrt{3}a}(k_1+k_2)y\end{array}$$

(15)

On the other hand, we have for $\overrightarrow{K}=K_x{\overrightarrow{e}}_x+K_y{\overrightarrow{e}}_y$ that

$$\begin{array}{c}\hfill \overrightarrow{K}·\overrightarrow{r}=K_{x}x+K_{y}y=\frac{2\pi }{a}{K}_{1}x+\frac{2\pi }{\sqrt{3}a}(-K_1+2K_2)y\end{array}$$

(16)

Equating $\overrightarrow{k}·(M_{\varphi }^{-1}\overrightarrow{r})$ and $\overrightarrow{K}·\overrightarrow{r}$ for arbitrary $\overrightarrow{r}$ then leads to the system of equations

$$\begin{array}{cc}\hfill K_1& =k_1-k_2\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill -K_1+2K_2& =k_1+k_2\hfill \end{array}$$

(18)

from which the dependence $\overrightarrow{K}(\overrightarrow{k})$ follows:

$$\begin{array}{cc}\hfill K_1& =k_1-k_2\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill K_2& =k_1\hfill \end{array}$$

(20)

Recalling Equation (11), we have

$$\begin{array}{c}\hfill f(\overrightarrow{r})=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{K}(\overrightarrow{k})·\overrightarrow{r}}\end{array}$$

(21)

and since the range of both double summation indices $\overrightarrow{k}$ and $\overrightarrow{K}$ is the same (${\mathbb{Z}}^2$), we can write

$$\begin{array}{cc}\hfill f(\overrightarrow{r})& =\sum _{\overrightarrow{K}}{c}_{\overrightarrow{K}}^{\prime }{e}^{i\overrightarrow{K}·\overrightarrow{r}}\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill c_{\overrightarrow{K}}^{\prime }& =c_{\overrightarrow{k}(\overrightarrow{K})}\hfill \end{array}$$

(23)

with $\overrightarrow{k}(\overrightarrow{K})$ given by the inverse relations of Equations (19) and (20):

$$\begin{array}{cc}\hfill k_1& =K_2\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill k_2& =K_2-K_1\hfill \end{array}$$

(25)

We can change the notation for the double summation index from $\overrightarrow{K}$ to $\overrightarrow{k}$ in Equation (22) so that

$$\begin{array}{c}\hfill f(\overrightarrow{r})=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{k}·\overrightarrow{r}}=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}^{\prime }{e}^{i\overrightarrow{k}·\overrightarrow{r}}\end{array}$$

(26)

Since Fourier coefficients are uniquely defined, we arrive at the following property for the coefficients $c_{\overrightarrow{k}}$:

$$\begin{array}{c}\hfill c_{\overrightarrow{k}}^{\prime }=c_{\overrightarrow{k}}\end{array}$$

(27)

Explicitly:

$$\begin{array}{c}\hfill c_{k_2,-k_1+k_2}=c_{k_1,k_2}\end{array}$$

(28)

If we perform a second rotation over $\frac{2\pi }{6}$, the function f remains invariant. Therefore, we can repeat relation Equation (28) and put

$$\begin{array}{c}\hfill c_{-k_1+k_2,-k_1}=c_{k_2,-k_1+k_2}\end{array}$$

(29)

Continuing to repeat relation Equation (28) leads to the following sequence of equalities:

$$\begin{array}{c}\hfill c_{k_1,k_2}=c_{k_2,-k_1+k_2}=c_{-k_1+k_2,-k_1}=c_{-k_1,-k_2}=c_{-k_2,k_1-k_2}=c_{k_1-k_2,k_1}[p6]\end{array}$$

(30)

It turns out that after six repetitions we are back at $c_{\overrightarrow{k}}$, which corresponds to the observation that repeating rotation $M_{\varphi =\frac{2\pi }{6}}$ 6 times is equivalent to the identity operation. Any index pair $\overrightarrow{k}=(k_1,k_2)\in {\mathbb{Z}}^2$ (excluding $(k_1,k_2)=(0,0)$) belongs to a set $S_{\overrightarrow{k}}$ of 6 equivalent indices that cyclically transform into one another via relation Equation (30).

As a result, a hexagonal Bravais lattice with a 6-fold rotation axis at its center—i.e., the $p6$ wallpaper group—implies that the scalar function $f(\overrightarrow{r})$ can be written as

$$\begin{array}{cc}\hfill f(\overrightarrow{r})& =c_{0,0}+\sum _{(k_1,k_2)\in D_6}{c}_{k_1,k_2}[e^{i\left[k_1{\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[k_2{\overrightarrow{b}}_1+(-k_1+k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(-k_1+k_2){\overrightarrow{b}}_1-k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}\hfill \\ \hfill & +e^{i\left[-k_1{\overrightarrow{b}}_1-k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[-k_2{\overrightarrow{b}}_1+(k_1-k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(k_1-k_2){\overrightarrow{b}}_1+k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}]\hfill \end{array}$$

(31)

where $D_6$ is a domain of $(k_1,k_2)\ne (0,0)$ integer pairs that contains exactly one of the 6 equivalent $(k_1,k_2)$ pairs of each of the sets of double indices $S_{\overrightarrow{k}}$ defined via Equation (30).

In Figure 1(a) we show the equivalence of $(k_1,k_2)$ points in the range $(-5\le k_1\le 5,-5\le k_2\le 5)$ (forming a domain D). The 6 points of each set $S_{k_1,k_2}$ are represented by squares with a same color and number. One can nicely see how the 6-fold rotational symmetry in $(x,y)$ coordinate space is mapped onto a “distorted” hexagonal symmetry in $(k_1,k_2)$ index space. Figure 1(b) shows a possible choice of $D_6$ for the numbered points in Figure 1(a); the grey points all have an equivalent representative in the triangle of colored points. The latter can be thought of as a kind of “asymmetric unit” for Fourier coefficients. It is also reminiscent of the so-called “irreducible (wedge of the) Brillouin zone (IBZ)”, a.k.a. “representation domain”, which contains only one vector of each star of $\overrightarrow{k}$ in the Brillouin zone (see e.g., [5], Chapter 1.5 and [7], Chapter 2.2.7). Indeed, from knowledge of the values of the Fourier coefficients with indices in the minimal domain $D_6$, the values of the Fourier coefficients with indices from all coefficient space can be generated by using the symmetry property for Fourier coefficients, Equation (30).

Fourier series Equation (32) can be elaborated into a more explicit form. The domain $D_6$ shown in Figure 1(b) contains the points in the range $(0<k_1,0\le k_2<k_1)$. Combining exponentials with opposite arguments and using the explicit expressions for ${\overrightarrow{b}}_1$ and ${\overrightarrow{b}}_2$ for the hexagonal lattice (see Table 1), we obtain

$$\begin{array}{cc}\hfill f(\overrightarrow{r})& =c_{0,0}+2\sum _{k_1>0}\sum _{\begin{array}{c}{k}_2\\ 0\le k_2<k_1\end{array}}{c}_{k_1,k_2}[cos\frac{2\pi \left[\sqrt{3}{k}_{1}x+(-k_1+2k_2)y\right]}{\sqrt{3}a}\hfill \\ \hfill & +cos\frac{2\pi \left[\sqrt{3}{k}_{2}x+(-2k_1+k_2)y\right]}{\sqrt{3}a}+cos\frac{2\pi \left[\sqrt{3}(k_1-k_2)x+(k_1+k_2)y\right]}{\sqrt{3}a}]\hfill \end{array}$$

(32)

Interestingly, for the $p6$ wallpaper group, we see from Equation (30) that

$$\begin{array}{c}\hfill c_{-\overrightarrow{k}}=c_{\overrightarrow{k}}\end{array}$$

(33)

from which it follows that the Fourier coefficients of a real $p6$ function must be real [see Equation (8)]. This is consistent with the explicit Fourier series [Equation (33)], where any imaginary contribution can only come from imaginary components of the Fourier coefficients $c_{k_1,k_2}$.

The power of establishing relation Equation (30) and the therefrom derived Fourier series Equations (32) and (33) is the reduction of the number of Fourier coefficients. The non-constant part $f(\overrightarrow{r})-c_{0,0}$ can be characterised by 6 times less coefficients than for a “brute-force” approach without using the analytic result. In Figure 2 we show contours of an exemplary (real) function $f(\overrightarrow{r})$ with hexagonal translation symmetry and 6-fold rotational symmetry with only two non-zero independent Fourier coefficients ($c_{1,0}=-\frac{1}{2}$ and $c_{3,1}=\frac{1}{4}$). The hexagonal translation and the 6-fold rotational symmetry are correctly observed.

3.2. Reflection Axes

A reflection about the ${\overrightarrow{a}}_1$ axis (which can always be chosen parallel to the x-axis without loss of generality, see Table 1) is achieved by the coordinate transformation

$$\begin{array}{c}\hfill {\overrightarrow{r}}^{\prime }=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=R_{{\overrightarrow{a}}_1}\overrightarrow{r}=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\end{array}$$

(34)

Proceeding as for rotations, we put

$$\begin{array}{c}\hfill f^{\prime }(\overrightarrow{r})=f(R_{{\overrightarrow{a}}_1}^{-1}\overrightarrow{r})=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{k}·(R_{{\overrightarrow{a}}_1}^{-1}\overrightarrow{r})}=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{K}(\overrightarrow{k})·\overrightarrow{r}}=f(\overrightarrow{r})=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{k}·\overrightarrow{r}}\end{array}$$

(35)

This leads to the following system of Equations:

$$\begin{array}{cc}\hfill k_1{b}_{1x}+k_2{b}_{2x}& =K_1{b}_{1x}+K_2{b}_{2x}\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill -k_1{b}_{1y}-k_2{b}_{2y}& =K_1{b}_{1y}+K_2{b}_{2y}\hfill \end{array}$$

(37)

Continuing with the case of a hexagonal Bravais lattice, we obtain

$$\begin{array}{cc}\hfill k_1& =K_1\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill k_2& =K_1-K_2\hfill \end{array}$$

(39)

and the property

$$\begin{array}{c}\hfill c_{k_1,k_2}=c_{k_1,k_1-k_2}\end{array}$$

(40)

Repeating the reflection results in the identity operation; this is consistent with property Equation (40) displaying a cycle of 2. Combining this symmetry operation with the 6-fold rotational symmetry of the preceding subsection results in the $p6mm$ wallpaper group. The resulting restrictions on the Fourier coefficients are obtained by applying relation Equation (30) to both $c_{k_1,k_2}$ and $c_{k_1,k_1-k_2}$, which leads to

$$\begin{array}{cc}\hfill c_{k_1,k_2}& =c_{k_2,-k_1+k_2}=c_{-k_1+k_2,-k_1}=c_{-k_1,-k_2}=c_{-k_2,k_1-k_2}=c_{k_1-k_2,k_1}\hfill \\ \hfill & =c_{k_1,k_1-k_2}=c_{k_1-k_2,-k_2}=c_{-k_2,-k_1}=c_{-k_1,-k_1+k_2}=c_{-k_1+k_2,k_2}=c_{k_2,k_1}[p6mm]\hfill \end{array}$$

(41)

At first sight, we can then write a “reduced” Fourier series for $f(\overrightarrow{r})-c_{0,0}$ as in Equation (32) with the indices running over a domain $D_{12}$ which now covers one-twelfth of the original $(k_1,k_2)$ space (excluding $(0,0)$). However, for some combinations of $k_1$ and $k_2$, relation Equation (42) reduces to a 6-cycle. This can be seen in Figure 3(a) where we show the equivalence of $(k_1,k_2)$ points—according to relation Equation (42)—in a domain D. The points with $k_2=0$ for example all belong to sets of only 6 rather than 12 equivalent points. The domain containing representative $(k_1,k_2$) points, shown in Figure 3(b), can be divided into a subdomain $D_6$ where points display a 6-cycle [Figure 3(c)] and a subdomain $D_{12}$ where points display a 12-cycle [Figure 3(d)]. The resulting Fourier series therefore needs to be formulated as

$$\begin{array}{cc}\hfill f(\overrightarrow{r})& =c_{0,0}+\sum _{(k_1,k_2)\in D_6}{c}_{k_1,k_2}[e^{i\left[k_1{\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[k_2{\overrightarrow{b}}_1+(-k_1+k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(-k_1+k_2){\overrightarrow{b}}_1-k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}\hfill \\ \hfill & +e^{i\left[-k_1{\overrightarrow{b}}_1-k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[-k_2{\overrightarrow{b}}_1+(k_1-k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(k_1-k_2){\overrightarrow{b}}_1+k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}]\hfill \\ \hfill & +\sum _{(k_1,k_2)\in D_{12}}{c}_{k_1,k_2}[e^{i\left[k_1{\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[k_2{\overrightarrow{b}}_1+(-k_1+k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(-k_1+k_2){\overrightarrow{b}}_1-k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}\hfill \\ \hfill & +e^{i\left[-k_1{\overrightarrow{b}}_1-k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[-k_2{\overrightarrow{b}}_1+(k_1-k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(k_1-k_2){\overrightarrow{b}}_1+k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}\hfill \\ \hfill & +e^{i\left[k_1{\overrightarrow{b}}_1+(k_1-k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(k_1-k_2){\overrightarrow{b}}_1-k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[-k_2{\overrightarrow{b}}_1-k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}\hfill \\ \hfill & +e^{i\left[-k_1{\overrightarrow{b}}_1+(-k_1+k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(-k_1+k_2){\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[k_2{\overrightarrow{b}}_1+k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}]\hfill \end{array}$$

(42)

In a way, the coefficients in domain $D_6$ can be considered “doubly degenerate”. Note that technically, the point $(k_1=0,k_2=0)$ has a cycle of 1 (identity operation) and forms a domain $D_1$ by itself.

The criterion for points $(k_1,k_2)$ belonging to domain $D_6$ can be easily obtained by realizing that for $(k_1,k_2)\in D_6$, the cycle of 6 [Equation (30)] must “intersect” the cyle of 2 [Equation (40)]. We are therefore looking for solutions of the following 6 systems of Equations:

$$\begin{array}{c}\left\{\begin{array}{c}{k}_1=k_1\hfill \\ k_1-k_2=k_2\hfill \end{array}\right.\hfill \end{array}$$

(43)

$$\begin{array}{c}\left\{\begin{array}{c}{k}_1=-k_2+k_1\hfill \\ k_1-k_2=k_1\hfill \end{array}\right.\hfill \end{array}$$

(44)

$$\begin{array}{c}\left\{\begin{array}{c}{k}_1=-k_2\hfill \\ k_1-k_2=-k_2+k_1\hfill \end{array}\right.\hfill \end{array}$$

(45)

$$\begin{array}{c}\left\{\begin{array}{c}{k}_1=-k_1\hfill \\ k_1-k_2=-k_2\hfill \end{array}\right.\hfill \end{array}$$

(46)

$$\begin{array}{c}\left\{\begin{array}{c}{k}_1=k_2-k_1\hfill \\ k_1-k_2=-k_1\hfill \end{array}\right.\hfill \end{array}$$

(47)

$$\begin{array}{c}\left\{\begin{array}{c}{k}_1=k_2\hfill \\ k_1-k_2=k_2-k_1\hfill \end{array}\right.\hfill \end{array}$$

(48)

The respective solutions are:

$$\begin{array}{cc}\hfill k_1& =2k_2\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill k_2& =0\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill k_1& =-k_2\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill k_1& =0\hfill \end{array}$$

(52)

$$\begin{array}{cc}\hfill k_2& =2k_1\hfill \end{array}$$

(53)

$$\begin{array}{cc}\hfill k_1& =k_2\hfill \end{array}$$

(54)

These 6 relations correspond to 6 lines of $(k_1,k_2)$ points which are visually discernible in Figure 3(a).

The domain $D_6\cup D_{12}$ shown in Figure 3(b) is defined as the set of points $(k_1,k_2)$ for which $0<k_1$ and $0\le k_2\le \frac{k_1}{2}$. For $D_6$ one has $0<k_1$ and $k_2=0\mathrm{or}{k}_2=\frac{k_1}{2}$; $D_{12}$ is defined by $0<k_1$ and $0<k_2<\frac{k_1}{2}$. The explicit Fourier expansion for a function $f(x,y)$ with $p6mm$ wallpaper group symmetry then reads:

$$\begin{array}{cc}\hfill f(\overrightarrow{r})& =c_{0,0}+2\sum _{k_1>0}{c}_{k_1,0}\left[2cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{1}y}{\sqrt{3}a}+cos\frac{4\pi k_{1}y}{\sqrt{3}a}\right]\hfill \\ \hfill & +2\sum _{\begin{array}{c}{k}_1>0\\ k_1\mathrm{even}\end{array}}{c}_{k_1,\frac{k_1}{2}}\left[2cos\frac{\pi k_{1}x}{a}cos\frac{\pi k_1\sqrt{3}y}{a}+cos\frac{2\pi k_{1}x}{a}\right]\hfill \\ \hfill & +4\sum _{k_1>0}\sum _{\begin{array}{c}{k}_2\\ 0<k_2<\frac{k_1}{2}\end{array}}{c}_{k_1,k_2}[cos\frac{2\pi k_{2}x}{a}cos\frac{2\pi (k_1+k_2)y}{\sqrt{3}a}+cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi (k_1-2k_2)y}{\sqrt{3}a}\hfill \\ \hfill & +cos\frac{2\pi (k_1-k_2)x}{a}cos\frac{2\pi (2k_1-2k_2)y}{\sqrt{3}a}]\hfill \end{array}$$

(55)

This rather complicated expression reflects the high symmetry of the $p6mm$ group. (In fact, $p6mm$ has the highest number of symmetry operations of all wallpaper groups.) Note that from this explicit expression, it follows that for $f(\overrightarrow{r})$ to have no imaginary part, the coefficients $c_{\overrightarrow{k}}$ need to be real—consistent with reality criterion Equation (8).

In Figure 4 we have plotted the contours of a real function with one independent non-zero Fourier coefficient from domain $D_6$ ($c_{2,0}=\frac{1}{4}$) and one non-zero coefficient from domain $D_{12}$ ($c_{2,1}=-1$). The honeycomb symmetry of the $p6mm$ wallpaper group is nicely recovered.

We stress the importance of the foregoing symmetry analysis: A function displaying wallpaper group symmetry can be characterised with only a few independent Fourier coefficients. The $p6mm$ wallpaper group is of particular interest because of the emergence of graphene [10] as a material with remarkable physical properties and promising applications.

3.3. Glide Reflection Axes

The last category of possible symmetry operations consists of glide reflection axes, combining a mirror operation about an axis with a translation parallel to that axis (the translation vector being half a lattice vector). Let us consider the glide reflection ${\mathcal{T}}_{\overrightarrow{t}}$, with $\overrightarrow{t}=\frac{{\overrightarrow{a}}_1}{2}=\frac{a}{2}{\overrightarrow{e}}_x$, transforming the point $(x,y)$ to $(x^{\prime },y^{\prime })$ according to

$$\begin{array}{c}\hfill {\overrightarrow{r}}^{\prime }=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)={\mathcal{T}}_{\overrightarrow{t}}\overrightarrow{r}=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}\frac{a}{2}\\ 0\end{array}\right)\end{array}$$

(56)

Imposing invariance of $f(x,y)$ under the transformation ${\mathcal{T}}_{\overrightarrow{t}}$ implies

$$\begin{array}{c}\hfill f({\mathcal{T}}_{\overrightarrow{t}}^{-1}\overrightarrow{r})=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{k}·({\mathcal{T}}_{\overrightarrow{t}}^{-1}\overrightarrow{r})}=f(\overrightarrow{r})=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{k}·\overrightarrow{r}}\end{array}$$

(57)

Because of the translational component of the symmetry operation ${\mathcal{T}}_{\overrightarrow{t}}$, it is insufficient to propose a Fourier series ${\sum }_{\overrightarrow{k}}{c}_{\overrightarrow{k}}{e}^{i\overrightarrow{K}(\overrightarrow{k})·\overrightarrow{r}}$ for $f({\mathcal{T}}_{\overrightarrow{t}}^{-1}\overrightarrow{r})$, equate the scalar products $\overrightarrow{K}(\overrightarrow{k})·\overrightarrow{r}$ and $\overrightarrow{k}·({\mathcal{T}}_{\overrightarrow{t}}^{-1}\overrightarrow{r})$, and solve $\overrightarrow{K}(\overrightarrow{k})$ as we did for rotational and mirror operations. Instead, we have to introduce a phase factor $h_{\overrightarrow{k}}$,

$$\begin{array}{c}\hfill f({\mathcal{T}}_{\overrightarrow{t}}^{-1}\overrightarrow{r})=\sum _{\overrightarrow{k}}{c}_{\overrightarrow{k}}{h}_{\overrightarrow{k}}{e}^{i\overrightarrow{K}(\overrightarrow{k})·\overrightarrow{r}}\end{array}$$

(58)

and equate $h_{\overrightarrow{k}}{e}^{i\overrightarrow{K}(\overrightarrow{k})·\overrightarrow{r}}$ and $e^{i\overrightarrow{k}·({\mathcal{T}}_{\overrightarrow{t}}^{-1}\overrightarrow{r})}$ for arbitrary $\overrightarrow{r}$. This leads to the following set of Equations:

$$\begin{array}{cc}\hfill e^{i(k_1{b}_{1x}+k_2{b}_{2x})\frac{a}{2}}& =h_{\overrightarrow{k}}\hfill \end{array}$$

(59)

$$\begin{array}{cc}\hfill k_1{b}_{1x}+k_2{b}_{2x}& =K_1{b}_{1x}+K_2{b}_{2x}\hfill \end{array}$$

(60)

$$\begin{array}{cc}\hfill -k_1{b}_{1y}-k_2{b}_{2y}& =K_1{b}_{1y}+K_2{b}_{2y}\hfill \end{array}$$

(61)

As an example, let us take the wallpaper group $pg$, which has a rectangular lattice (reciprocal basis vectors ${\overrightarrow{b}}_1=\frac{2\pi }{a}$ and ${\overrightarrow{b}}_2=\frac{2\pi }{b}$, see Table 1) and only a glide reflection axis ($\overrightarrow{t}=\frac{{\overrightarrow{a}}_1}{2}$) as a non-trivial symmetry operation. Equations (59)–(61) then reduce to

$$\begin{array}{cc}\hfill h_{\overrightarrow{k}}& =e^{i{k}_1\pi }={(-1)}^{k_1}\hfill \end{array}$$

(62)

$$\begin{array}{cc}\hfill k_1& =K_1\hfill \end{array}$$

(63)

$$\begin{array}{cc}\hfill k_2& =-K_2\hfill \end{array}$$

(64)

from which the following condition for the Fourier coefficients $c_{\overrightarrow{k}}$ follows:

$$\begin{array}{c}\hfill c_{k_1,k_2}={(-1)}^{k_1}{c}_{k_1,-k_2}[pg]\end{array}$$

(65)

A function $f(\overrightarrow{r})$ with $pg$ wallpaper group symmetry can therefore be written as

$$\begin{array}{c}f(\overrightarrow{r})=c_{0,0}+\sum _{(k_1,k_2)\in D_1^0}{c}_{k_1,k_2}{e}^{i\left[k_1{\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}\hfill \\ \hfill +\sum _{(k_1,k_2)\in D_2}{c}_{k_1,k_2}\left[e^{i\left[k_1{\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+{(-1)}^{k_1}{e}^{i\left[k_1{\overrightarrow{b}}_1-k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}\right]\end{array}$$

(66)

As before, not all points display a cycle of 2 when repeatedly applying the transformation $\overrightarrow{K}(\overrightarrow{k)}$ given by Equations (63) and (64). Points with $k_2=0$ form a domain $D_1$ with cycle 1; the remaining points ($k_2\ne 0$) can be mapped onto a domain $D_2$ of representative points from which all coefficients $c_{\overrightarrow{k}\notin (D_1^0\cup D_2)}$ can be calculated according to property Equation (65). In Equation (66) we have introduced the notation $D_1^0$ for the domain of points with cycle 1 excluding $(0,0)$: $D_1^0=D_1\backslash \left\{(0,0)\right\}$. From Equation (65) it follows that for points in domain $D_1^0$

$$c_{k_1,0}={(-1)}^{k_1}{c}_{k_1,0}$$

(67)

which implies that $c_{k_1,0}=0$ for $k_1$ odd.

In Figure 5, we visualize the domains D, $D_1^0\cup D_2$, $D_1^0$ and $D_2$ and the equivalence of Fourier coefficients. Equivalence through phase factors 1 and $-1$ is marked by squares and discs, respectively. Necessarily vanishing Fourier coefficients [due to Equation (67)] are marked by the circle-in-square symbol “⌼”. It is again instructive to elaborate the Fourier expansion for $f(x,y)$ into a more explicit form (displaying the rectangular lattice parameters a and b and using the $(k_1,k_2)$ ranges for domains $D_1^0$ and $D_2$). The result reads

$$\begin{array}{cc}\hfill f(x,y)& =c_{0,0}+\sum _{\begin{array}{c}{k}_1\mathrm{even}\\ k_1\ne 0\end{array}}{c}_{k_1,0}[cos\frac{2\pi k_{1}x}{a}+isin\frac{2\pi k_{1}x}{a}]\hfill \\ \hfill & +2\sum _{k_2>0}\{\sum _{k_1\mathrm{even}}{c}_{k_1,k_2}\left[cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}+isin\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}\right]\hfill \\ \hfill & +\sum _{k_1\mathrm{odd}}{c}_{k_1,k_2}\left[-sin\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{2}y}{b}+icos\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{2}y}{b}\right]\}\hfill \end{array}$$

(68)

Combining reality criterion Equation (8) with $pg$ property Equation (65) results in the requirement $c_{k_1,k_2}^{*}={(-1)}^{k_1}{c}_{-k_1,k_2}$; this requirement indeed removes any imaginary part in expression Equation (69). It also establishes relations between coefficients within the domain $D_1^0\cup D_2$. For example, $c_{1,1}^{*}=-c_{-1,1}$, or $c_{0,2}^{*}=c_{0,2}$ from which it follows that $c_{0,2}$ must be real.

In Figure 6 we have plotted a real function with $pg$ symmetry; the only non-vanishing independent Fourier coefficients are $c_{1,1}=\frac{1}{2}$ and $c_{2,1}=1+i$. (The reality criterion then implies that $c_{-1,1}=-\frac{1}{2}$ and $c_{-2,1}=1-i$ are then also non-zero.)

4. Derivation of Fourier Coefficient Relations

The foregoing examples show how to derive relations between the Fourier coefficients of a function $f(\overrightarrow{r})$ with a given wallpaper group symmetry. In particular, we have discussed how to deal with a 6-fold rotation axis, a reflection axis, and a glide reflection axis. In this section, we will elaborate the symmetry properties of all other possible symmetry operations present in the wallpaper groups, and provide a summary. The restrictions on the Fourier coefficients for a specific wallpaper group then follow from combining symmetry properties (for example, the addition of a reflection axis to the group $p6$ converts it into the group $p6mm$). Our goal is to arrive at a table with an entry for each of the 17 wallpaper groups, containing all necessary information, in formulas and in a visualised form, concerning the Fourier expansion and the associated Fourier coefficients for the symmetry group.

4.1. Rotation Axes

Most wallpaper groups have a rotation axis at the origin of the unit cell. The transformation matrix for a 2-fold rotation at the origin reads

$$\begin{array}{c}\hfill M_{\varphi =\frac{2\pi }{2}}=\left(\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right)\end{array}$$

(69)

so that equating $\overrightarrow{k}·(M_{\varphi }^{-1}\overrightarrow{r})=\overrightarrow{K}·\overrightarrow{r}$ leads to

$$\begin{array}{c}\hfill -\overrightarrow{k}·\overrightarrow{r}=\overrightarrow{K}·\overrightarrow{r}\end{array}$$

(70)

from which it follows that

$$\begin{array}{c}\hfill k_1=-K_1\end{array}$$

(71)

$$\begin{array}{c}\hfill k_2=-K_2\end{array}$$

(72)

The Fourier coefficients then obey the following 2-cycle:

$$\begin{array}{c}\hfill c_{k_1,k_2}=c_{-k_1,-k_2}\end{array}$$

(73)

In

Table 2. Fourier coefficient properties for generating symmetry elements of the 16 non-trivial wallpaper groups.

symmetry operation	Bravais lattice	Fourier coefficients	wallpaper groups
⬮	oblique	$c_{k_1,k_2}=c_{-k_1,-k_2}$	$p2$
	rectangular		$p2mm$, $p2mg$, $p2gg$
	centered rectangular		$c2mm$
▲	hexagonal	$c_{k_1,k_2}=c_{-k_1+k_2,-k_1}$	$p3$, $p3m1$, $p31m$
		$\phantom{c_{k_1,k_2}}=c_{-k_2,k_1-k_2}$
◆	square	$c_{k_1,k_2}=c_{-k_2,k_1}$	$p4$, $p4mm$, $p4gm$
		$\phantom{c_{k_1,k_2}}=c_{-k_1,-k_2}=c_{k_2,-k_1}$
⬢	hexagonal	$c_{k_1,k_2}=c_{k_2,-k_1+k_2}$	$p6$, $p6mm$
		$\phantom{c_{k_1,k_2}}=c_{-k_1+k_2,-k_1}=c_{-k_1,-k_2}$
		$\phantom{c_{k_1,k_2}}=c_{-k_2,k_1-k_2}=c_{k_1-k_2,k_1}$
reflection axis #1	rectangular	$c_{k_1,k_2}=c_{k_1,-k_2}$	$pm$, $p2mm$
	square		$p4mm$
	centered rectangular	$c_{k_1,k_2}=c_{k_2,k_1}$	$cm$, $c2mm$
	hexagonal	$c_{k_1,k_2}=c_{k_1,k_1-k_2}$	$p31m$, $p6mm$
glide reflection axis #1	rectangular	$c_{k_1,k_2}={(-1)}^{k_1}{c}_{k_1,-k_2}$	$pg$
reflection axis #2	rectangular	$c_{k_1,k_2}={(-1)}^{k_2}{c}_{k_1,-k_2}$	$p2mg$
glide reflection axis #2	rectangular	$c_{k_1,k_2}={(-1)}^{k_1+k_2}{c}_{k_1,-k_2}$	$p2gg$
	square		$p4gm$
reflection axis #3	hexagonal	$c_{k_1,k_2}=c_{k_2,k_1}$	$p3m1$

we quote this symmetry property (together with the properties of the other symmetry operations). Note that this results does not depend on the lattice type, i.e., the lattice can be oblique, rectangular, centered rectangular, square, or hexagonal. The presence of a 2-fold symmetry axis with a square or hexagonal Bravais lattice implies a higher-order symmetry axis, however (4-fold and 6-fold, respectively). We therefore only quote the oblique, rectangular and centered rectangular lattices in the entry for ⬮ in Table 2.

For a 3-fold rotation, the rotation matrix reads

$$\begin{array}{c}\hfill M_{\varphi =\frac{2\pi }{3}}=\left(\begin{array}{cc}-\frac{1}{2}& -\frac{\sqrt{3}}{2}\\ \frac{\sqrt{3}}{2}& -\frac{1}{2}\end{array}\right)\end{array}$$

(74)

The existence of a 3-fold rotation axis implies a hexagonal lattice. With the hexagonal basis vectors given in Table 1, the equality of the scalar products $\overrightarrow{k}·(M_{\varphi }^{-1}\overrightarrow{r})$ and $\overrightarrow{K}·\overrightarrow{r}$ results in the following conditions:

$$\begin{array}{cc}\hfill k_1& =-K_1+K_2\hfill \end{array}$$

(75)

$$\begin{array}{cc}\hfill k_2& =-K_1\hfill \end{array}$$

(76)

The symmetry property for the Fourier coefficients $c_{\overrightarrow{k}}$ then becomes

$$\begin{array}{c}\hfill c_{k_1,k_2}=c_{-k_1+k_2,-k_1}=c_{-k_2,k_1-k_2}\end{array}$$

(77)

displaying—as it should—a 3-cycle.

The 4-fold rotation matrix reads

$$\begin{array}{c}\hfill M_{\varphi =\frac{2\pi }{4}}=\left(\begin{array}{cc}0& -1\\ 1& 0\end{array}\right)\end{array}$$

(78)

For a square lattice, required for a 4-fold rotation axis, the relation between $\overrightarrow{k}$ and $\overrightarrow{K}$ reads

$$\begin{array}{cc}\hfill k_1& =-K_2\hfill \end{array}$$

(79)

$$\begin{array}{cc}\hfill k_2& =K_1\hfill \end{array}$$

(80)

which results in the following 4-cycle of Fourier coefficients:

$$\begin{array}{c}\hfill c_{k_1,k_2}=c_{-k_2,k_1}=c_{-k_1,-k_2}=c_{k_2,-k_1}\end{array}$$

(81)

Note that the requirement for a 2-fold symmetry axis is also fulfilled [Equation (73)].

The case of a 6-fold rotation axis (hexagonal Bravais lattice) has been treated in the previous section [Equation (30)]. It comprises both the 2-fold and 3-fold rotation axis conditions (and can in fact be constructed from combining these two).

4.2. Reflection Axes

The wallpaper groups are not distinguishable by rotation axes alone, as shown by the example of the $p6$ and $p6mm$ groups in the previous section. Other symmetry operations have to be considered. A first category is that of reflection axes. In the previous section we have treated the case when the x-axis is a reflection axis (which we from now on call reflection axis #1), for a hexagonal lattice. Here we consider the remaining possible lattices.

For a rectangular or a square lattice, Equations (36) and (37) lead to

$$\begin{array}{cc}\hfill k_1& =K_1\hfill \end{array}$$

(82)

$$\begin{array}{cc}\hfill k_2& =-K_2\hfill \end{array}$$

(83)

so that

$$\begin{array}{c}\hfill c_{k_1,-k_2}=c_{k_1,k_2}\end{array}$$

(84)

For a centered rectangular lattice, Equations (36) and (37) result in

$$\begin{array}{cc}\hfill k_1& =K_2\hfill \end{array}$$

(85)

$$\begin{array}{cc}\hfill k_2& =K_1\hfill \end{array}$$

(86)

$$\begin{array}{cc}\hfill c_{k_2,k_1}& =c_{k_1,k_2}\hfill \end{array}$$

(87)

Note that the combination of a rotation axis with a reflection axis can generate additional reflection axes. For example, in the case of the rectangular lattice with a 2-fold rotation axis, the x-axis being a reflection axis implies the y-axis also being a reflection axis. Only one of the two reflection axes is a generating (independent) symmetry element. The choice of which one of the two to include as a generating element is arbitrary, though. In Table 2, only (conveniently but otherwise arbitrarily chosen) generating elements are listed.

A second independent reflection axis (labelled #2) is present in the $p2mg$ group (rectangular Bravais lattice). It is the line parallel to the x-axis and going through the point $\frac{{\overrightarrow{a}}_2}{4}$. The transformation law reads

$$\begin{array}{c}\hfill {\overrightarrow{r}}^{\prime }=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)={\mathcal{T}}_{\overrightarrow{t}}\overrightarrow{r}=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}0\\ \frac{a_2}{2}\end{array}\right)\end{array}$$

(88)

In combination with a rectangular Bravais lattice, the phase factor $h_{\overrightarrow{k}}$ and the relations $\overrightarrow{k}(\overrightarrow{K})$ read

$$\begin{array}{cc}\hfill k_1& =K_1\hfill \end{array}$$

(89)

$$\begin{array}{cc}\hfill k_2& =-K_2\hfill \end{array}$$

(90)

$$\begin{array}{cc}\hfill h_{\overrightarrow{k}}& ={(-1)}^{k_2}\hfill \end{array}$$

(91)

The resulting Fourier symmetry property then reads

$$\begin{array}{c}\hfill {(-1)}^{k_2}{c}_{k_1,-k_2}=c_{k_1,k_2}\end{array}$$

(92)

A third and final generating reflection axis (labelled #3) occurs in the $p3m1$ group (hexagonal Bravais lattice). It is the line coinciding with the vector ${\overrightarrow{a}}_1+{\overrightarrow{a}}_2$. The transformation has the same form as that of a rotation and reads

$$\begin{array}{c}\hfill {\overrightarrow{r}}^{\prime }=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=S\overrightarrow{r}=\left(\begin{array}{cc}\frac{1}{2}& \frac{\sqrt{3}}{2}\\ \frac{\sqrt{3}}{2}& -\frac{1}{2}\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)\end{array}$$

(93)

Equating $\overrightarrow{K}·\overrightarrow{r}$ and $\overrightarrow{k}·(S\overrightarrow{r})$ (no phase factor is required) gives

$$\begin{array}{c}\hfill K_1=k_2\end{array}$$

(94)

$$\begin{array}{c}\hfill K_2=k_1\end{array}$$

(95)

whence the symmetry property

$$\begin{array}{c}\hfill c_{k_2,k_1}=c_{k_1,k_2}\end{array}$$

(96)

4.3. Glide Reflection Axes

In SubSection 3.3 we considered the glide reflection axis encountered in the $pg$ group (glide reflection axis #1 in Table 2). A second, independent, type of glide reflection axis (labelled #2) is found in the groups $p2gg$ and $p4gm$: The line parallel to the x-axis going through the point $\frac{{\overrightarrow{a}}_2}{4}$ is the axis, the shift vector is $\frac{{\overrightarrow{a}}_1}{2}$. The transformation reads

$$\begin{array}{c}\hfill {\overrightarrow{r}}^{\prime }=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)={\mathcal{T}}_{\overrightarrow{t}}\overrightarrow{r}=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}\frac{a_1}{2}\\ \frac{a_2}{2}\end{array}\right)\end{array}$$

(97)

implying (for rectangular and square lattices)

$$\begin{array}{cc}\hfill K_1& =k_1\hfill \end{array}$$

(98)

$$\begin{array}{cc}\hfill K_2& =-k_2\hfill \end{array}$$

(99)

$$\begin{array}{cc}\hfill h_{\overrightarrow{k}}& ={(-1)}^{k_1+k_2}\hfill \end{array}$$

(100)

so that

$$\begin{array}{c}\hfill {(-1)}^{k_1+k_2}{c}_{k_1,-k_2}=c_{k_1,k_2}\end{array}$$

(101)

This completes our analysis of the Fourier symmetry properties resulting from symmetry operations encountered in the wallpaper groups; all results are summarized in Table 2.

4.4. Combining Rotation Axes and (Glide) Reflection Axes

With the help of Table 2, the symmetry properties for the Fourier coefficients $c_{\overrightarrow{k}}$ can be derived for all wallpaper groups. The groups can be divided into two categories based on whether there is a rotation axis at the origin or not. The groups without a rotation axis are $p1$ (the trivial group), $pm$, $cm$ and $pg$; their symmetry properties can be directly read out from Table 2. (For $p1$ there are no restrictions on $c_{\overrightarrow{k}}$.) The groups exhibiting a rotation axis can be further subdivided into groups featuring additional symmetry elements and groups only containing the rotation axis. The latter are $p2$, $p3$, $p4$ and $p6$; their symmetry properties follow immediately from Table 2. The former groups are $p2mm$, $p2mg$, $p2gg$, $c2mm$, $p3m1$, $p31m$, $p4mm$, $p4gm$ and $p6mm$; their Fourier coefficients obey conditions following from combining the rotation-axis property with the condition implied by the second (independent) symmetry element.

In SubSection 3.2 we showed how to combine a 6-fold rotational axis with reflection axis #1 resulting in the $p6mm$ wallpaper group of graphene. To illustrate the procedure once more, we consider the wallpaper group $p3m1$. The presence of a three-fold rotation axis implies $c_{k_1,k_2}=c_{-k_1+k_2,-k_1}=c_{-k_2,k_1-k_2}$, while reflection axis #3 implies $c_{k_1,k_2}=c_{k_2,k_1}$. Combining these two properties results in the identity of 6 Fourier coefficients:

$$\begin{array}{c}\hfill c_{k_1,k_2}=c_{-k_1+k_2,-k_1}=c_{-k_2,k_1-k_2}=c_{k_2,k_1}=c_{k_1-k_2,-k_2}=c_{-k1,-k_1+k_2}.[p3m1]\end{array}$$

(102)

For certain values of $(k_1,k_2)\ne (0,0)$, this property breaks down to the identity of only 3 Fourier coefficients (3-cycle). The remaining $(k_1,k_2)$ combinations exhibit the full 6-cycle given by Equation (102). It is easy to show that the coefficients with a 3-cycle must obey one of the following 3 equations:

$$\begin{array}{cc}\hfill k_1& =k_2\hfill \end{array}$$

(103)

$$\begin{array}{cc}\hfill k_1& =0\hfill \end{array}$$

(104)

$$\begin{array}{cc}\hfill k_2& =0\hfill \end{array}$$

(105)

As before, the presence of cycles allows to take only independent Fourier coefficients from minimal domains (D${}_3$ and D${}_6$, see Figure 7), and to write the general Fourier series for a function $f(x,y)$ with $p3m1$ symmetry as

$$\begin{array}{cc}\hfill f(x,y)& =c_{0,0}+\sum _{(k_1,k_2)\in D_3}{c}_{k_1,k_2}\left[e^{i\left[k_1{\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(-k_1+k_2){\overrightarrow{b}}_1-k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[-k_2{\overrightarrow{b}}_1+(k_1-k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}\right]\hfill \\ \hfill & +\sum _{(k_1,k_2)\in D_6}[e^{i\left[k_1{\overrightarrow{b}}_1+k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(-k_1+k_2){\overrightarrow{b}}_1-k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[-k_2{\overrightarrow{b}}_1+(k_1-k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}\hfill \\ \hfill & +e^{i\left[k_2{\overrightarrow{b}}_1+k_1{\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[-k_1{\overrightarrow{b}}_1+(-k_1+k_2){\overrightarrow{b}}_2\right]·\overrightarrow{r}}+e^{i\left[(k_1-k_2){\overrightarrow{b}}_1-k_2{\overrightarrow{b}}_2\right]·\overrightarrow{r}}]\hfill \end{array}$$

(106)

Realising that domain $D_3$ contains the points for which $k_1>0$ and $k_2=0\mathrm{or}{k}_2=k_1$ (see Figure 7) and that domain $D_6$ consists of the points with $k_1>0$ and $0<k_2<k_1$, we arrive at the following explicit expression for $f(x,y)$:

$$\begin{array}{cc}\hfill f(x,y)& =c_{0,0}+\sum _{k_1>0}\left\{(c_{k_1,0}+c_{k_1,k_1})\right[2cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{1}y}{\sqrt{3}a}+cos\frac{4\pi k_{1}y}{\sqrt{3}a}\hfill \\ & +i(c_{k_1,0}-c_{k_1,k_1})\left(-2cos\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{1}y}{\sqrt{3}a}+sin\frac{4\pi k_{1}y}{\sqrt{3}a}\right)]\hfill \\ & +2\sum _{\begin{array}{c}{k}_2\\ 0<k_1<k_2\end{array}}{c}_{k_1,k_2}[cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi (k_1-2k_2)y}{\sqrt{3}a}+cos\frac{2\pi k_{2}x}{a}cos\frac{2\pi (2k_1-k_2)y}{\sqrt{3}a}\hfill \\ & +cos\frac{2\pi (k_1-k_2)x}{a}cos\frac{2\pi (k_1+k_2)y}{\sqrt{3}a}+i(-cos\frac{2\pi k_{1}x}{a}sin\frac{2\pi (k_1-2k_2)y}{\sqrt{3}a}\hfill \\ & +cos\frac{2\pi k_{2}x}{a}sin\frac{2\pi (2k_1-k_2)y}{\sqrt{3}a}-cos\frac{2\pi (k_1-k_2)x}{a}sin\frac{2\pi (k_1+k_2)y}{\sqrt{3}a}\left)\right]\}\hfill \end{array}$$

(107)

For $f(x,y)$ to be real, we combine the reality criterion [Equation (8)] with $c_{k_1,k_2}=c_{-k_1,-k_1+k_2}$ (see Table 2) and obtain

$$c_{k_1,k_2}^{*}=c_{k_1,k_1-k_2}$$

(108)

Note that this equation connects points in domain $D_3\cup D_6$. Indeed, taking $(k_1,k_2)$ with $k_1>0$ and $0\le k_2\le k_1$ results in $c_{k_1,k_1-k_2}\equiv c_{K_1,K_2}=c_{k_1,k_2}^{*}$, with $(K_1=k_1,K_2=k_1-k_2)\in (D_3\cup D_6)$. The reality criterion for $p3m1$ therefore imposes further restrictions on the domain $D_3\cup D_6$ of independent Fourier coefficients. For example, the coefficient $c_{2,0}$ is equal to the complex conjugate of $c_{2,2}$, and $c_{2,1}$ is equal to its own complex conjugate and hence real. In Figure 8, the function with $c_{2,0}=c_{2,2}^{*}=\frac{1}{4}+i$ and $c_{2,1}=c_{2,1}^{*}=-1$ as only non-vanishing coefficients is shown.

4.5. Centering

When using the non-primitive basis for centered rectangular lattices, i.e., the rectangular basis $({\overrightarrow{a}}_1=a{\overrightarrow{e}}_x,{\overrightarrow{a}}_2=b{\overrightarrow{e}}_y)$, centering should be considered a symmetry operation of the unit cell and has to be accounted for appropriately.

To distinguish from the case where we use the non-primitive basis vectors (see Table 1), we write $\overrightarrow{q}=(q_1,q_2)$ and $\overrightarrow{Q}=(Q_1,Q_2)$ for the Fourier summation indices and $c_{\overrightarrow{q}}$ and $c_{\overrightarrow{Q}}$ for the Fourier coefficients. It is easy to show that the relations between $\overrightarrow{k}$ and $\overrightarrow{q}$ read

$$\begin{array}{cc}\hfill q_1& =k_1+k_2\hfill \end{array}$$

(109)

$$\begin{array}{cc}\hfill q_2& =k_1-k_2\hfill \end{array}$$

(110)

and

$$\begin{array}{cc}\hfill k_1& =\frac{q_1+q_2}{2}\hfill \end{array}$$

(111)

$$\begin{array}{cc}\hfill k_2& =\frac{q_1-q_2}{2}\hfill \end{array}$$

(112)

Clearly, the centering transformation law reads

$$\begin{array}{c}\hfill {\overrightarrow{r}}^{\prime }=\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=C\overrightarrow{r}=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)+\left(\begin{array}{c}\frac{a}{2}\\ \frac{b}{2}\end{array}\right)\end{array}$$

(113)

A phase factor $h_{\overrightarrow{q}}$ is required for matching Fourier series:

$$\begin{array}{c}\hfill \sum _{\overrightarrow{q}}{c}_{\overrightarrow{q}}{e}^{i\overrightarrow{q}·(C^{-1}\overrightarrow{r})}=\sum _{\overrightarrow{q}}{c}_{\overrightarrow{q}}{h}_{\overrightarrow{q}}{e}^{i\overrightarrow{Q}(\overrightarrow{q})·\overrightarrow{r}}\end{array}$$

(114)

The result reads

$$\begin{array}{cc}\hfill q_1& =Q_1\hfill \end{array}$$

(115)

$$\begin{array}{cc}\hfill q_2& =Q_2\hfill \end{array}$$

(116)

$$\begin{array}{cc}\hfill h_{q_1,q_2}& ={(-1)}^{q_1+q_2}\hfill \end{array}$$

(117)

so that the centering symmetry property becomes

$$\begin{array}{c}\hfill {(-1)}^{q_1+q_2}{c}_{q_1,q_2}=c_{q_1,q_2}\end{array}$$

(118)

from which it immediately follows that coefficients with odd $q_1+q_2$ have to vanish.

In

Table 3. Fourier coefficient properties for generating symmetry elements of the centered rectangular wallpaper groups.

symmetry operation	Bravais lattice	Fourier coefficients	wallpaper groups
centering	centered rectangular	$c_{q_1,q_2}={(-1)}^{q_1+q_2}{c}_{q_1,q_2}$	$cm$, $c2mm$
⬮	centered rectangular	$c_{q_1,q_2}=c_{-q_1,-q_2}$	$c2mm$
reflection axis #1	centered rectangular	$c_{q_1,q_2}=c_{q_2,q_1}$	$cm$, $c2mm$

we list the Fourier coefficient properties for generating symmetry elements of the centered rectangular wallpaper groups in the non-primitive description. By combining the appropriate symmetry elements one obtains the Fourier properties for the Fourier coefficients $c_{\overrightarrow{q}}$:

$$\begin{array}{cc}\hfill c_{q_1,q_2}& =c_{q_1,-q_2}={(-1)}^{q_1+q_2}{c}_{q_1,q_2}={(-1)}^{q_1+q_2}{c}_{q_1,-q_2}[cm]\hfill \end{array}$$

(119)

$$\begin{array}{cc}\hfill c_{q_1,q_2}& =c_{-q_1,-q_2}=c_{q_1,-q_2}=c_{-q_1,q_2}={(-1)}^{q_1+q_2}{c}_{q_1,q_2}\hfill \\ & ={(-1)}^{q_1+q_2}{c}_{-q_1,-q_2}={(-1)}^{q_1+q_2}{c}_{q_1,-q_2}={(-1)}^{q_1+q_2}{c}_{-q_1,q_2}[c2mm]\hfill \end{array}$$

(120)

Note that the $cm$ and $c2mm$ wallpaper groups are obtained by centering the $pm$ and $p2mm$ groups, respectively. On the level of Fourier expansions, the $cm$ and $c2mm$ Fourier series are simply obtained by taking the expressions for $pm$ and $c2mm$, respectively, and excluding the terms for which $q_1+q_2$ is odd. The $c2mm$ wallpaper group and its Fourier series can also be generated from centering the $p2gg$ group.

4.6. Structure Factors in Crystallography

The implications of the foregoing mathematical considerations are widely used in crystallography and crystal structure determination. The periodic function one considers is the electronic density $\rho (\overrightarrow{r})$, the Fourier coefficients of which are known as the structure factors $F(\overrightarrow{k})$. The central formula expressing the space group (wallpaper group) symmetry reads [5,11]

$$\begin{array}{c}\hfill F(\overrightarrow{k})=F(P^{-1}\overrightarrow{k})e^{-i\overrightarrow{k}·\overrightarrow{t}}\end{array}$$

(121)

with P and $\overrightarrow{t}$ being the rotation and translation parts of the space group operations $(P|\overrightarrow{t})$, respectively. Elaborating Equation (121) results in symmetry relations for the structure factors and is equivalent to carrying out the procedures described above for the various types of wallpaper group symmetry operations. In Vol. B of the “International Tables” [4,5,6,7,8], the functional forms of the Fourier expansions of the electronic density $\rho (\overrightarrow{r})$ are tabulated in a compact way in structure-factor tables for wallpaper groups (Table A1.4.3.1 in [5]) and space groups (Tables A1.4.3.2–A1.4.3.7 in [5]). Note, however, that in the “International Tables” [4,5,6,7,8] the ${120}^{\circ }$ rather than the ${60}^{\circ }$ convention for hexagonal lattices (see Table 1) is used. In a (single-crystal) diffraction experiment, the symmetry relations between structure factors manifest themselves in the extinction and/or the equal (non-zero) intensity (proportional to $|F(\overrightarrow{k}){|}^2$) of certain Bragg reflections. The Fourier coefficient maps, labeled “D”, shown throughout this paper and in

Table 4. $p1.$

$p1$ oblique	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=(a_{2x},a_{2y})\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,-\frac{a_{2x}}{a_{2y}})\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a_{2y}}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_1^0$	$D_{\min }=D_1^0$
$\begin{array}{c}{c}_{0,1}=c_{0,-1}^{*}=-2+4i\hfill \\ c_{1,0}=c_{-1,0}^{*}=1-\frac{1}{2}i\hfill \end{array}$		$(k_1,k_2)\ne (0,0)$
${\displaystyle c_{k_1,k_2}}$
${\displaystyle f(x,y)=c_{0,0}+\sum _{(k_1,k_2)\ne (0,0)}{c}_{k_1,k_2}[cos\frac{2\pi \left[k_1{a}_{2y}x+(-k_1{a}_{2x}+k_{2}a)y\right]}{a{a}_{2y}}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}+\sum _{(k_1,k_2)\ne (0,0)}{c}_{k_1,k_2}[}+isin\frac{2\pi \left[k_1{a}_{2y}x+(-k_1{a}_{2x}+k_{2}a)y\right]}{a{a}_{2y}}]}$
${\displaystyle [\mathbb{R}]c_{-k_1,-k_2}=c_{k_1,k_2}^{*}}$

,

Table 5. $p2.$

$p2$ oblique	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=(a_{2x},a_{2y})\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,-\frac{a_{2x}}{a_{2y}})\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a_{2y}}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_2$	$D_{\min }=D_2$
$\begin{array}{c}{c}_{0,1}=c_{0,1}^{*}=-\frac{1}{4}\hfill \\ c_{1,1}=c_{1,1}^{*}=1\hfill \end{array}$		$\begin{array}{c}(k_1>0,0)\\ (k_1,k_2>0)\end{array}$
${\displaystyle c_{k_1,k_2}=c_{-k_1,-k_2}}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{k_1>0}{c}_{k_1,0}cos\frac{2\pi k_1(a_{2y}x-a_{2x}y)}{a{a}_{2y}}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+2\sum _{k_1}\sum _{k_2>0}{c}_{k_1,k_2}cos\frac{2\pi \left[k_1{a}_{2y}x+(-k_1{a}_{2x}+k_{2}a)y\right]}{a{a}_{2y}}}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

,

Table 6. $pm.$

$pm$ rectangular	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=b(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{b}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_1^0\cup D_2$	$D_{\min }=D_1^0\cup D_2$
$\begin{array}{c}{c}_{1,0}=c_{-1,0}^{*}=-\frac{1}{4}+\frac{1}{8}i\hfill \\ c_{1,1}=c_{-1,1}^{*}=1-\frac{1}{4}i\hfill \end{array}$		$\begin{array}{c}(k_1\ne 0,0)\\ (k_1,k_2>0)\end{array}$
	$D_1^0$	$D_2$
	$(k_1\ne 0,0)$	$(k_1,k_2>0)$
${\displaystyle c_{k_1,k_2}=c_{k_1,-k_2}}$
${\displaystyle f(x,y)=c_{0,0}+\sum _{k_1\ne 0}{c}_{k_1,0}\left[cos\frac{2\pi k_{1}x}{a}+isin\frac{2\pi k_{1}x}{a}\right]}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+2\sum _{k_1}\sum _{k_2>0}{c}_{k_1,k_2}\left[cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}+isin\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}\right]}$
${\displaystyle [\mathbb{R}]c_{-k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{0,k_2}\in \mathbb{R}}$

,

Table 7. $pg.$

$pg$ rectangular	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=b(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{b}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_1^0\cup D_2$	$D_{\min }=D_1^0\cup D_2$
$\begin{array}{c}{c}_{1,1}=-c_{-1,1}^{*}=\frac{1}{2}\hfill \\ c_{2,1}=c_{-2,1}^{*}=1+i\hfill \end{array}$		$\begin{array}{c}(k_1\mathrm{even}\ne 0,0)\\ (k_1,k_2>0)\end{array}$
	$D_1^0$	$D_2$
	$(k_1\mathrm{even}\ne 0,0)$	$(k_1,k_2>0)$
${\displaystyle c_{k_1,k_2}={(-1)}^{k_1}{c}_{k_1,-k_2}}$		${\displaystyle c_{2n+1,0}=0}$
${\displaystyle f(x,y)=c_{0,0}+\sum _{\begin{array}{c}{k}_1\mathrm{even}\\ k_1\ne 0\end{array}}{c}_{k_1,0}[cos\frac{2\pi k_{1}x}{a}+isin\frac{2\pi k_{1}x}{a}]}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+2\sum _{k_2>0}\{\sum _{k_1\mathrm{even}}{c}_{k_1,k_2}\left[cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}+isin\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}\right]}$
${\displaystyle \phantom{f(x,y)=c_{0,0}+2\sum _{k_2>0}\{}+\sum _{k_1\mathrm{odd}}{c}_{k_1,k_2}\left[-sin\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{2}y}{b}+icos\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{2}y}{b}\right]\}}$
${\displaystyle [\mathbb{R}]c_{-k_1,k_2}={(-1)}^{k_1}{c}_{k_1,k_2}^{*}}$		${\displaystyle c_{0,k_2}\in \mathbb{R}}$

,

Table 8. $cm.$

$cm$ centered rectangular	$\begin{array}{c}{\overrightarrow{a}}_1=(\frac{a}{2},-\frac{b}{2})\hfill \\ {\overrightarrow{a}}_2=(\frac{a}{2},\frac{b}{2})\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=2\pi (\frac{1}{a},\frac{1}{b})\hfill \\ {\overrightarrow{b}}_2=2\pi (\frac{1}{a},-\frac{1}{b})\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_1^0\cup D_2$	$D_{\min }=D_1^0\cup D_2$
$\begin{array}{c}{c}_{0,1}=c_{-1,0}^{*}=-\frac{1}{4}+\frac{1}{8}i\hfill \\ c_{1,1}=c_{-1,-1}^{*}=\frac{1}{8}\hfill \end{array}$		$\begin{array}{c}(k_1\ne 0,k_1)\\ (k_1,k_2<k_1)\end{array}$
	$D_1^0$	$D_2$
	$(k_1\ne 0,k_1)$	$(k_1,k_2<k_1)$
${\displaystyle c_{k_1,k_2}=c_{k_2,k_1}}$
${\displaystyle f(x,y)=c_{0,0}+\sum _{k_1\ne 0}{c}_{k_1,k_1}[cos\frac{4\pi k_{1}x}{a}+isin\frac{4\pi k_{1}x}{a}]}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+2\sum _{k_1}\sum _{\begin{array}{c}{k}_2\\ k_2<k_1\end{array}}{c}_{k_1,k_2}[cos\frac{2\pi (k_1+k_2)x}{a}cos\frac{2\pi (-k_1+k_2)y}{b}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}+2\sum _{k_1}\sum _{\begin{array}{c}{k}_2\\ k_2<k_1\end{array}}{c}_{k_1,k_2}[}+isin\frac{2\pi (k_1+k_2)x}{a}cos\frac{2\pi (-k_1+k_2)y}{b}]}$
${\displaystyle [\mathbb{R}]c_{-k_2,-k_1}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,-k_1}\in \mathbb{R}}$

,

Table 9. $cm$—non-primitive basis.

$cm$ rectangular	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=b(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{b}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_1^0\cup D_2$	$D_{\min }=D_1^0\cup D_2$
$\begin{array}{c}{c}_{1,1}=c_{-1,1}^{*}=-\frac{1}{4}+\frac{1}{8}i\hfill \\ c_{2,0}=c_{-2,0}^{*}=\frac{1}{8}\hfill \end{array}$		$\begin{array}{c}(q_1\mathrm{even},q_2\mathrm{even}\ge 0)\ne (0,0)\\ (q_1\mathrm{odd},q_2\mathrm{odd}>0)\end{array}$
	$D_1^0$	$D_2$
	$(q_1\mathrm{even}\ne 0,0)$	$\begin{array}{c}(q_1\mathrm{even},q_2\mathrm{even}>0)\\ (q_1\mathrm{odd},q_2\mathrm{odd}>0)\end{array}$
${\displaystyle c_{q_1,q_2}=c_{q_1,-q_2}}={(-1)}^{q_1+q_2}{c}_{q_1,q_2}={(-1)}^{q_1+q_2}{c}_{q_1,-q_2}$		$c_{2n,2m+1}=c_{2n+1,2m}=0$
${\displaystyle f(x,y)=c_{0,0}+\sum _{\begin{array}{c}{q}_1\ne 0\\ q_1\mathrm{even}\end{array}}{c}_{q_1,0}\left[cos\frac{2\pi q_{1}x}{a}+isin\frac{2\pi q_{1}x}{a}\right]}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+2\left(\sum _{q_1\mathrm{even}}\sum _{\begin{array}{c}{q}_2>0\\ q_2\mathrm{even}\end{array}}+\sum _{q_1\mathrm{odd}}\sum _{\begin{array}{c}{q}_2>0\\ q_2\mathrm{odd}\end{array}}\right)c_{q_1,q_2}\left[cos\frac{2\pi q_{1}x}{a}cos\frac{2\pi q_{2}y}{b}+isin\frac{2\pi q_{1}x}{a}cos\frac{2\pi q_{2}y}{b}\right]}$
${\displaystyle [\mathbb{R}]c_{-q_1,q_2}=c_{q_1,q_2}^{*}}$		${\displaystyle c_{0,q_2}\in \mathbb{R}}$

,

Table 10. $p2mm.$

$p2mm$ rectangular	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=b(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{b}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_2\cup D_4$	$D_{\min }=D_2\cup D_4$
$\begin{array}{c}{c}_{1,0}=c_{1,0}^{*}=\frac{1}{4}\hfill \\ c_{2,1}=c_{2,1}^{*}=-\frac{1}{2}\hfill \end{array}$		$(k_1\ge 0,k_2\ge 0)\ne (0,0)$
	$D_2$	$D_4$
	$\begin{array}{c}(k1>0,0)\\ (0,k_2>0)\end{array}$	$(k_1>0,k_2>0)$
${\displaystyle c_{k_1,k_2}=c_{-k_1,-k_2}=c_{k_1,-k_2}=c_{-k_1,k_2}}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{k_1>0}{c}_{k_1,0}cos\frac{2\pi k_{1}x}{a}+2\sum _{k_2>0}{c}_{0,k_2}cos\frac{2\pi k_{2}y}{b}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+4\sum _{k_1>0}\sum _{k_2>0}{c}_{k_1,k_2}cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

,

Table 11. $p2mg.$

$p2mg$ rectangular	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=b(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{b}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_2\cup D_4$	$D_{\min }=D_2\cup D_4$
$\begin{array}{c}{c}_{2,0}=c_{2,0}^{*}=\frac{1}{4}\hfill \\ c_{2,1}=c_{2,1}^{*}=-\frac{1}{2}\hfill \end{array}$		$\begin{array}{c}(k_1>0,k_2\ge 0)\\ (0,k_2\mathrm{even}>0)\end{array}$
	$D_2$	$D_4$
	$\begin{array}{c}(k_1>0,0)\\ (0,k_2\mathrm{even}>0)\end{array}$	$(k_1>0,k_2>0)$
${\displaystyle c_{k_1,k_2}=c_{-k_1,-k_2}}={(-1)}^{k_2}{c}_{k_1,-k_2}={(-1)}^{k_2}{c}_{-k_1,k_2}$		${\displaystyle c_{0,2n+1}=0}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{k_1>0}{c}_{k_1,0}cos\frac{2\pi k_{1}x}{a}+2\sum _{\begin{array}{c}{k}_2\mathrm{even}\\ k_2>0\end{array}}{c}_{0,k_2}cos\frac{2\pi k_{2}y}{b}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+4\sum _{k_1>0}\left\{\sum _{\begin{array}{c}{k}_2\mathrm{even}\\ k_2>0\end{array}}{c}_{k_1,k_2}cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}-\sum _{\begin{array}{c}{k}_2\mathrm{odd}\\ k_2>0\end{array}}{c}_{k_1,k_2}sin\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{2}y}{b}\right\}}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

,

Table 12. $p2gg.$

$p2gg$ rectangular	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=b(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{b}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_2\cup D_4$	$D_{\min }=D_2\cup D_4$
$\begin{array}{c}{c}_{1,1}=c_{1,1}^{*}=\frac{1}{2}\hfill \\ c_{1,2}=c_{1,2}^{*}=\frac{1}{4}\hfill \end{array}$		$\begin{array}{c}(k_1\mathrm{even}>0,0)\\ (0,k_2\mathrm{even}>0)\\ (k_1>0,k_2>0)\end{array}$
	$D_2$	$D_4$
	$\begin{array}{c}(k_1\mathrm{even}>0,0)\\ (0,k_2\mathrm{even}>0)\end{array}$	$(k_1>0,k_2>0)$
${\displaystyle c_{k_1,k_2}=c_{-k_1,-k_2}={(-1)}^{k_1+k_2}{c}_{k_1,-k_2}={(-1)}^{k_1+k_2}{c}_{-k_1,k_2}}$		${\displaystyle c_{0,2n+1}=c_{2n+1,0}=0}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{\begin{array}{c}{k}_1\mathrm{even}\\ k_1>0\end{array}}{c}_{k_1,0}cos\frac{2\pi k_{1}x}{a}+2\sum _{\begin{array}{c}{k}_2\mathrm{even}\\ k_2>0\end{array}}{c}_{0,k_2}cos\frac{2\pi k_{2}y}{b}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+4\sum _{\begin{array}{c}{k}_1\mathrm{even}\\ k_1>0\end{array}}\left\{\sum _{\begin{array}{c}{k}_2\mathrm{even}\\ k_2>0\end{array}}{c}_{k_1,k_2}cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}-\sum _{\begin{array}{c}{k}_2\mathrm{odd}\\ k_2>0\end{array}}{c}_{k_1,k_2}sin\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{2}y}{b}\right\}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+4\sum _{\begin{array}{c}{k}_1\mathrm{odd}\\ k_1>0\end{array}}\left\{-\sum _{\begin{array}{c}{k}_2\mathrm{even}\\ k_2>0\end{array}}{c}_{k_1,k_2}sin\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{2}y}{b}+\sum _{\begin{array}{c}{k}_2\mathrm{odd}\\ k_2>0\end{array}}{c}_{k_1,k_2}cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}\right\}}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

,

Table 13. $c2mm.$

$c2mm$ centered rectangular	$\begin{array}{c}{\overrightarrow{a}}_1=(\frac{a}{2},-\frac{b}{2})\hfill \\ {\overrightarrow{a}}_2=(\frac{a}{2},\frac{b}{2})\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=2\pi (\frac{1}{a},\frac{1}{b})\hfill \\ {\overrightarrow{b}}_2=2\pi (\frac{1}{a},-\frac{1}{b})\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_2\cup D_4$	$D_{\min }=D_2\cup D_4$
$\begin{array}{c}{c}_{0,1}=c_{0,1}^{*}=\frac{1}{4}\hfill \\ c_{1,1}=c_{1,1}^{*}=-1\hfill \end{array}$		$(k_1>0,|k_2|\le k_1)$
	$D_2$	$D_4$
	($k_1>0,\pm k_1$)	$(k_1>0,|k_2|<k_1)$
${\displaystyle c_{k_1,k_2}=c_{-k_1,-k_2}=c_{k_2,k_1}=c_{-k_2,-k_1}}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{k_1>0}\{c_{k_1,k_1}cos\frac{4\pi k_{1}x}{a}+c_{k_1,-k_1}cos\frac{4\pi k_{1}y}{b}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+2\sum _{\begin{array}{c}{k}_2\\ |k_2|<k_1\end{array}}{c}_{k_1,k_2}cos\frac{2\pi (k_1+k_2)x}{a}cos\frac{2\pi (k_1-k_2)y}{b}\}}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

,

Table 14. $c2mm$—non-primitive basis.

$c2mm$ rectangular	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=b(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{b}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_2\cup D_4$	$D_{\min }=D_2\cup D_4$
$\begin{array}{c}{c}_{1,1}=c_{1,1}^{*}=\frac{1}{4}\hfill \\ c_{2,0}=c_{2,0}^{*}=1\hfill \end{array}$		$\begin{array}{c}(q_1\mathrm{even}\ge 0,q_2\mathrm{even}\ge 0)\ne (0,0)\\ (q_1\mathrm{odd}>0,q_2\mathrm{odd}>0)\end{array}$
	$D_2$	$D_4$
	$\begin{array}{c}(q_1\mathrm{even}>0,0)\\ (0,q_2\mathrm{even}>0)\end{array}$	$\begin{array}{c}(q_1\mathrm{even}>0,q_2\mathrm{even}>0)\\ (q_1\mathrm{odd}>0,q_2\mathrm{odd}>0)\end{array}$
${\displaystyle c_{q_1,q_2}=c_{-q_1,-q_2}=c_{q_1,-q_2}=c_{-q_1,q_2}={(-1)}^{q_1+q_2}{c}_{q_1,q_2}}$		$c_{2n,2m+1}=c_{2n+1,2m}=0$
${\displaystyle \phantom{c_{q_1,q_2}}={(-1)}^{q_1+q_2}{c}_{-q_1,-q_2}={(-1)}^{q_1+q_2}{c}_{q_1,-q_2}={(-1)}^{q_1+q_2}{c}_{-q_1,q_2}}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{\begin{array}{c}{q}_1>0\\ q_1\mathrm{even}\end{array}}{c}_{q_1,0}cos\frac{2\pi q_{1}x}{a}+2\sum _{\begin{array}{c}{q}_2>0\\ q_2\mathrm{even}\end{array}}{c}_{0,q_2}cos\frac{2\pi q_{2}y}{b}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+4\left(\sum _{\begin{array}{c}{q}_1>0\\ q_1\mathrm{even}\end{array}}\sum _{\begin{array}{c}{q}_2>0\\ q_2\mathrm{even}\end{array}}+\sum _{\begin{array}{c}{q}_1>0\\ q_1\mathrm{odd}\end{array}}\sum _{\begin{array}{c}{q}_2>0\\ q_2\mathrm{odd}\end{array}}\right)c_{k_1,k_2}cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{b}}$
${\displaystyle [\mathbb{R}]c_{q_1,q_2}=c_{q_1,q_2}^{*}}$		${\displaystyle c_{q_1,q_2}\in \mathbb{R}}$

,

Table 15. $p4$.

$p4$ square	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=a(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_4$	$D_{\min }=D_4$
$\begin{array}{c}{c}_{2,0}=c_{2,0}^{*}=-\frac{1}{4}\hfill \\ c_{2,1}=c_{2,1}^{*}=1\hfill \end{array}$		$(k_1>0,k_2\ge 0)$
${\displaystyle c_{k_1,k_2}=c_{-k_2,k_1}=c_{-k_1,-k_2}=c_{k_2,-k_1}}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{k_1>0}\sum _{k_2\ge 0}{c}_{k_1,k_2}\left[cos\frac{2\pi (k_{1}x+k_{2}y)}{a}+cos\frac{2\pi (-k_{2}x+k_{1}y)}{a}\right]}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

,

Table 16. $p4mm.$

$p4mm$ square	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=a(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_4\cup D_8$	$D_{\min }=D_4\cup D_8$
$\begin{array}{c}{c}_{2,0}=c_{2,0}^{*}=\frac{1}{4}\hfill \\ c_{2,1}=c_{2,1}^{*}=-\frac{1}{2}\hfill \end{array}$		$(k_1>0,0\le k_2\le k_1)$
	$D_4$	$D_8$
	$\begin{array}{c}(k_1>0,0)\\ (k_1>0,k_1)\end{array}$	$(k_1>0,0<k_2<k_1)$
${\displaystyle c_{k_1,k_2}=c_{-k_2,k_1}=c_{-k_1,-k_2}=c_{k_2,-k_1}=c_{k_1,-k_2}=c_{k_2,k_1}=c_{-k_1,k_2}=c_{-k_2,-k_1}}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{k_1>0}\{c_{k_1,0}\left[cos\frac{2\pi k_{1}x}{a}+cos\frac{2\pi k_{1}y}{a}\right]+2c_{k_1,k_1}cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{1}y}{a}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}+2\sum _{k_1>0}\{}+2\sum _{\begin{array}{c}{k}_2\\ 0<k_2<k_1\end{array}}{c}_{k_1,k_2}\left[cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{a}+cos\frac{2\pi k_{2}x}{a}cos\frac{2\pi k_{1}y}{a}\right]\}}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

,

Table 17. $p4gm.$

$p4gm$ square	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=a(0,1)\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,0)\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a}(0,1)\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_4\cup D_8$	$D_{\min }=D_4\cup D_8$
$\begin{array}{c}{c}_{1,1}=c_{1,1}^{*}=\frac{1}{2}\hfill \\ c_{1,2}=c_{1,2}^{*}=\frac{1}{4}\hfill \end{array}$		$\begin{array}{c}(k_1\mathrm{even}>0,0)\\ (k_1>0,0<k_2\le k_1)\end{array}$
	$D_4$	$D_8$
	$\begin{array}{c}(k_1\mathrm{even}>0,0)\\ (k_1>0,k_1)\end{array}$	$(k_1>0,0<k_2<k_1)$
${\displaystyle c_{k_1,k_2}=c_{-k_2,k_1}=c_{-k_1,-k_2}=c_{k_2,-k_1}}$		${\displaystyle c_{0,2n+1}=c_{2n+1,0}=0}$
${\displaystyle \phantom{c_{k_1,k_2}}={(-1)}^{k_1+k_2}{c}_{k_1,-k_2}={(-1)}^{k_1+k_2}{c}_{k_2,k_1}}$
${\displaystyle \phantom{c_{k_1,k_2}}={(-1)}^{k_1+k_2}{c}_{-k_1,k_2}={(-1)}^{k_1+k_2}{c}_{-k_2,-k_1}}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{\begin{array}{c}{k}_1\mathrm{even}\\ k_1>0\end{array}}{c}_{k_1,0}\left[cos\frac{2\pi k_{1}x}{a}+cos\frac{2\pi k_{1}y}{a}\right]+4\sum _{k_1>0}{c}_{k_1,k_1}cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{1}y}{a}}$
${\displaystyle \phantom{f(x,y)=}+4\left(\sum _{\begin{array}{c}{k}_1\mathrm{even}\\ k_1>0\end{array}}\sum _{\begin{array}{c}{k}_2\mathrm{even}\\ 0<k_2<k_1\end{array}}+\sum _{\begin{array}{c}{k}_1\mathrm{odd}\\ k_1>0\end{array}}\sum _{\begin{array}{c}{k}_2\mathrm{odd}\\ 0<k_2<k_1\end{array}}\right)c_{k_1,k_2}[cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{2}y}{a}}$
${\displaystyle \phantom{f(x,y)=+4\left(\sum _{\begin{array}{c}{k}_1\mathrm{even}\\ k_1>0\end{array}}\sum _{\begin{array}{c}{k}_2\mathrm{even}\\ 0<k_2<k_1\end{array}}+\sum _{\begin{array}{c}{k}_1\mathrm{odd}\\ k_1>0\end{array}}\sum _{\begin{array}{c}{k}_2\mathrm{odd}\\ 0<k_2<k_1\end{array}}\right)c_{k_1,k_2}[}+cos\frac{2\pi k_{2}x}{a}cos\frac{2\pi k_{1}y}{a}]\}}$
${\displaystyle \phantom{f(x,y)=}+4\left(\sum _{\begin{array}{c}{k}_1\mathrm{even}\\ k_1>0\end{array}}\sum _{\begin{array}{c}{k}_2\mathrm{odd}\\ 0<k_2<k_1\end{array}}+\sum _{\begin{array}{c}{k}_1\mathrm{odd}\\ k_1>0\end{array}}\sum _{\begin{array}{c}{k}_2\mathrm{even}\\ 0<k_2<k_1\end{array}}\right)c_{k_1,k_2}[-sin\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{2}y}{a}}$
${\displaystyle \phantom{f(x,y)=+4\left(\sum _{\begin{array}{c}{k}_1\mathrm{even}\\ k_1>0\end{array}}\sum _{\begin{array}{c}{k}_2\mathrm{odd}\\ 0<k_2<k_1\end{array}}+\sum _{\begin{array}{c}{k}_1\mathrm{odd}\\ k_1>0\end{array}}\sum _{\begin{array}{c}{k}_2\mathrm{even}\\ 0<k_2<k_1\end{array}}\right)c_{k_1,k_2}[}+sin\frac{2\pi k_{2}x}{a}sin\frac{2\pi k_{1}y}{a}]\}}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

,

Table 18. $p3.$

$p3$ hexagonal	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=a(\frac{1}{2},\frac{\sqrt{3}}{2})\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,-\frac{1}{\sqrt{3}})\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a}(0,\frac{2}{\sqrt{3}})\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_3$	$D_{\min }=D_3$
$\begin{array}{c}{c}_{2,0}=c_{2,2}^{*}=-\frac{1}{4}+\frac{1}{8}i\hfill \\ c_{2,1}=c_{1,2}^{*}=1-\frac{1}{8}i\hfill \end{array}$		$(k_1>0,k_2\ge 0)$
${\displaystyle c_{k_1,k_2}=c_{-k_1+k_2,-k_1}=c_{-k_2,k_1-k_2}}$
${\displaystyle f(x,y)=c_{0,0}}$
${\displaystyle \phantom{f(x,y)=}+\sum _{k_1>0}\sum _{k_2\ge 0}{c}_{k_1,k_2}[cos\frac{2\pi \left[\sqrt{3}{k}_{1}x+(-k_1+2k_2)y\right]}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=}+cos\frac{2\pi \left[\sqrt{3}(-k_1+k_2)x-(k_1+k_2)y\right]}{\sqrt{3}a}+cos\frac{2\pi \left[-\sqrt{3}{k}_{2}x+(2k_1-k_2)y\right]}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=}+i(sin\frac{2\pi \left[\sqrt{3}{k}_{1}x+(-k_1+2k_2)y\right]}{\sqrt{3}a}+sin\frac{2\pi \left[\sqrt{3}(-k_1+k_2)x-(k_1+k_2)y\right]}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=}+sin\frac{2\pi \left[-\sqrt{3}{k}_{2}x+(2k_1-k_2)y\right]}{\sqrt{3}a})]}$
${\displaystyle [\mathbb{R}]c_{k_1-k_2,k_1}=c_{k_1,k_2}^{*}}$

,

Table 19. $p3m1.$

$p3m1$ hexagonal	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=a(\frac{1}{2},\frac{\sqrt{3}}{2})\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,-\frac{1}{\sqrt{3}})\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a}(0,\frac{2}{\sqrt{3}})\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_3$	$D_{\min }=D_3\cup D_6$
$\begin{array}{c}{c}_{2,0}=c_{2,2}^{*}=\frac{1}{4}+i\hfill \\ c_{2,1}=c_{2,1}^{*}=-1\hfill \end{array}$		$(k_1>0,0\le k_2\le k_1)$
	$D_3$	$D_6$
	$\begin{array}{c}(k_1>0,0)\\ (k_1>0,k_1)\end{array}$	$(k_1>0,0<k_2<k_1)$
${\displaystyle c_{k_1,k_2}=c_{-k_1+k_2,-k_1}=c_{-k_2,k_1-k_2}=c_{k_2,k_1}=c_{-k_1,-k_1+k_2}=c_{k_1-k_2,-k_2}}$
${\displaystyle f(x,y)=c_{0,0}+\sum _{k_1>0}\{(c_{k_1,0}+c_{k_1,k_1})[2cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{1}y}{\sqrt{3}a}+cos\frac{4\pi k_{1}y}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}+\sum _{k_1>0}\{}+i(c_{k_1,0}-c_{k_1,k_1})\left(-2cos\frac{2\pi k_{1}x}{a}sin\frac{2\pi k_{1}y}{\sqrt{3}a}+sin\frac{4\pi k_{1}y}{\sqrt{3}a}\right)]}$
${\displaystyle \phantom{f(x,y)=}+2\sum _{\begin{array}{c}{k}_2\\ 0<k_1<k_2\end{array}}{c}_{k_1,k_2}[cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi (k_1-2k_2)y}{\sqrt{3}a}+cos\frac{2\pi k_{2}x}{a}cos\frac{2\pi (2k_1-k_2)y}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=+2\sum _{\begin{array}{c}{k}_2\\ 0<k_1<k_2\end{array}}}+cos\frac{2\pi (k_1-k_2)x}{a}cos\frac{2\pi (k_1+k_2)y}{\sqrt{3}a}+i(-cos\frac{2\pi k_{1}x}{a}sin\frac{2\pi (k_1-2k_2)y}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=+2\sum _{\begin{array}{c}{k}_2\\ 0<k_1<k_2\end{array}}}+cos\frac{2\pi k_{2}x}{a}sin\frac{2\pi (2k_1-k_2)y}{\sqrt{3}a}-cos\frac{2\pi (k_1-k_2)x}{a}sin\frac{2\pi (k_1+k_2)y}{\sqrt{3}a})]\}}$
${\displaystyle [\mathbb{R}]c_{k_1,k_1-k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{2k_2,k_2}\in \mathbb{R}}$

,

Table 20. $p31m.$

$p31m$ hexagonal	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=a(\frac{1}{2},\frac{\sqrt{3}}{2})\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,-\frac{1}{\sqrt{3}})\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a}(0,\frac{2}{\sqrt{3}})\hfill \end{array}$
	$D=D_3\cup D_6$	$D_{\min }=D_3\cup D_6$
$\begin{array}{c}{c}_{2,0}=c_{2,0}^{*}=\frac{1}{4}\hfill \\ c_{2,1}=c_{1,2}^{*}=-1-\frac{1}{2}i\hfill \end{array}$		$\begin{array}{c}(k_1>0,0\le k_2\le \frac{k_1}{2})\\ (k_1>0,k_2\ge 2k_1)\end{array}$
	$D_3$	$D_6$
	$\begin{array}{c}(k_1\mathrm{even}>0,\frac{k_1}{2})\\ (k_1\mathrm{even}>0,2k_1)\end{array}$	$\begin{array}{c}(k_1\mathrm{even}>0,0\le k_2<\frac{k_1}{2})\\ (k_1\mathrm{even}>0,k_2>2k_1)\end{array}$
${\displaystyle c_{k_1,k_2}=c_{-k_1+k_2,-k_1}=c_{-k_2,k_1-k_2}=c_{k_1,k_1-k_2}=c_{-k_2,-k_1}=c_{-k_1+k_2,k_2}}$
${\displaystyle f(x,y)=c_{0,0}+\sum _{\begin{array}{c}{k}_1>0\\ k_1\mathrm{even}\end{array}}{c}_{k_1,\frac{k_1}{2}}[2cos\frac{\pi k_{1}x}{a}cos\frac{\pi k_1\sqrt{3}y}{a}+cos\frac{2\pi k_{1}x}{a}+i(-2sin\frac{\pi k_{1}x}{a}cos\frac{\pi k_1\sqrt{3}y}{a}}$
${\displaystyle \phantom{f(x,y)=}+sin\frac{2\pi k_{1}x}{a})]+\sum _{k_1>0}{c}_{k_1,2k_1}[cos\frac{4\pi k_{1}x}{a}+2cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_1\sqrt{3}y)}{a}}$
${\displaystyle \phantom{f(x,y)=}+i\left(2sin\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_1\sqrt{3}y}{a}-sin\frac{4\pi k_{1}x}{a}\right)]}$
${\displaystyle \phantom{f(x,y)=}+2\sum _{k_1>0}\left(\sum _{\begin{array}{c}{k}_2\\ 0\le k_2<\frac{k_1}{2}\end{array}}+\sum _{\begin{array}{c}{k}_2\\ k_2>2k_1\end{array}}\right)c_{k_1,k_2}[cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi (k_1-2k_2)y}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=}+cos\frac{2\pi (k_1-k_2)x}{a}cos\frac{2\pi (k_1+k_2)y}{\sqrt{3}a}+cos\frac{2\pi k_{2}x}{a}cos\frac{2\pi (2k_1-k_2)y}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=}+i(sin\frac{2\pi k_{1}x}{a}cos\frac{2\pi (k_1-2k_2)y}{a}}$
${\displaystyle \phantom{f(x,y)=}-sin\frac{2\pi (k_1-k_2)x}{a}cos\frac{2\pi (k_1+k_2)y}{\sqrt{3}a}-sin\frac{2\pi k_{2}x}{a}cos\frac{2\pi (2k_1-k_2)y}{\sqrt{3}a})]}$
${\displaystyle [\mathbb{R}]c_{k_2,k_1}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,0}\in \mathbb{R}}$

,

Table 21. $p6.$

$p6$ hexagonal	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=a(\frac{1}{2},\frac{\sqrt{3}}{2})\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,-\frac{1}{\sqrt{3}})\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a}(0,\frac{2}{\sqrt{3}})\hfill \end{array}$
	$D=\left\{(0,0)\right\}\cup D_6$	$D_{\min }=D_6$
$\begin{array}{c}{c}_{1,0}=c_{1,0}^{*}=-\frac{1}{2}\hfill \\ c_{3,1}=c_{3,1}^{*}=\frac{1}{4}\hfill \end{array}$		$(k_1>0,0\le k_2<k_1)$
${\displaystyle c_{k_1,k_2}=c_{k_2,-k_1+k_2}=c_{-k_1+k_2,-k_1}=c_{-k_1,-k_2}=c_{-k_2,k_1-k_2}=c_{k_1-k_2,k_1}}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{k_1>0}\sum _{\begin{array}{c}{k}_2\\ 0\le k_2<k_1\end{array}}{c}_{k_1,k_2}[cos\frac{2\pi \left[\sqrt{3}{k}_{1}x+(-k_1+2k_2)y\right]}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}+2\sum _{k_1>0}\sum _{\begin{array}{c}{k}_2\\ 0\le k_2<k_1\end{array}}{c}_{k_1,k_2}[}+cos\frac{2\pi \left[\sqrt{3}{k}_{2}x+(-2k_1+k_2)y\right]}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}+2\sum _{k_1>0}\sum _{\begin{array}{c}{k}_2\\ 0\le k_2<k_1\end{array}}{c}_{k_1,k_2}[}+cos\frac{2\pi \left[\sqrt{3}(k_1-k_2)x+(k_1+k_2)y\right]}{\sqrt{3}a}]}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

and

Table 22. $p6mm.$

$p6mm$ hexagonal	$\begin{array}{c}{\overrightarrow{a}}_1=a(1,0)\hfill \\ {\overrightarrow{a}}_2=a(\frac{1}{2},\frac{\sqrt{3}}{2})\hfill \end{array}$	$\begin{array}{c}{\overrightarrow{b}}_1=\frac{2\pi }{a}(1,-\frac{1}{\sqrt{3}})\hfill \\ {\overrightarrow{b}}_2=\frac{2\pi }{a}(0,\frac{2}{\sqrt{3}})\hfill \end{array}$
	$D=\{(0,0\}\cup D_6\cup D_{12}$	$D_{\min }=D_6\cup D_{12}$
$\begin{array}{c}{c}_{2,0}=c_{2,0}^{*}=\frac{1}{4}\hfill \\ c_{2,1}=c_{2,1}^{*}=-1\hfill \end{array}$		$(k_1>0,0\le k_2\le \frac{k_1}{2})$
	$D_6$	$D_{12}$
	$\begin{array}{c}(k_1>0,0)\\ (k_1\mathrm{even}>0,\frac{k_1}{2})\end{array}$	$(k_1>0,0<k_2<\frac{k_1}{2})$
${\displaystyle c_{k_1,k_2}=c_{k_2,-k_1+k_2}=c_{-k_1+k_2,-k_1}=c_{-k_1,-k_2}=c_{-k_2,k_1-k_2}=c_{k_1-k_2,k_1}}$
${\displaystyle \phantom{c_{k_1,k_2}}=c_{k_1,k_1-k_2}=c_{k_1-k_2,-k_2}=c_{-k_2,-k_1}=c_{-k_1,-k_1+k_2}=c_{-k_1+k_2,k_2}=c_{k_2,k_1}}$
${\displaystyle f(x,y)=c_{0,0}+2\sum _{k_1>0}{c}_{k_1,0}\left[2cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi k_{1}y}{\sqrt{3}a}+cos\frac{4\pi k_{1}y}{\sqrt{3}a}\right]}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+2\sum _{\begin{array}{c}{k}_1>0\\ k_1\mathrm{even}\end{array}}{c}_{k_1,\frac{k_1}{2}}\left[2cos\frac{\pi k_{1}x}{a}cos\frac{\pi k_1\sqrt{3}y}{a}+cos\frac{2\pi k_{1}x}{a}\right]}$
${\displaystyle \phantom{f(x,y)=c_{0,0}}+4\sum _{k_1>0}\sum _{\begin{array}{c}{k}_2\\ 0<k_2<\frac{k_1}{2}\end{array}}{c}_{k_1,k_2}[cos\frac{2\pi k_{1}x}{a}cos\frac{2\pi (k_1-2k_2)y}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}+2\sum _{k_1>0}\sum _{\begin{array}{c}{k}_2\\ 0<k_2<\frac{k_1}{2}\end{array}}{c}_{k_1,k_2}[}+cos\frac{2\pi k_{2}x}{a}cos\frac{2\pi (2k_1-k_2)y}{\sqrt{3}a}}$
${\displaystyle \phantom{f(x,y)=c_{0,0}+2\sum _{k_1>0}\sum _{\begin{array}{c}{k}_2\\ 0<k_2<\frac{k_1}{2}\end{array}}{c}_{k_1,k_2}[}+cos\frac{2\pi (k_1-k_2)x}{a}cos\frac{2\pi (k_1+k_2)y}{\sqrt{3}a}]}$
${\displaystyle [\mathbb{R}]c_{k_1,k_2}=c_{k_1,k_2}^{*}}$		${\displaystyle c_{k_1,k_2}\in \mathbb{R}}$

(see below) are complementary to the information in the “International Tables” [4,5,6,7,8], and can be thought of as elementary diffraction patterns of functions (structures) with wallpaper group symmetry.

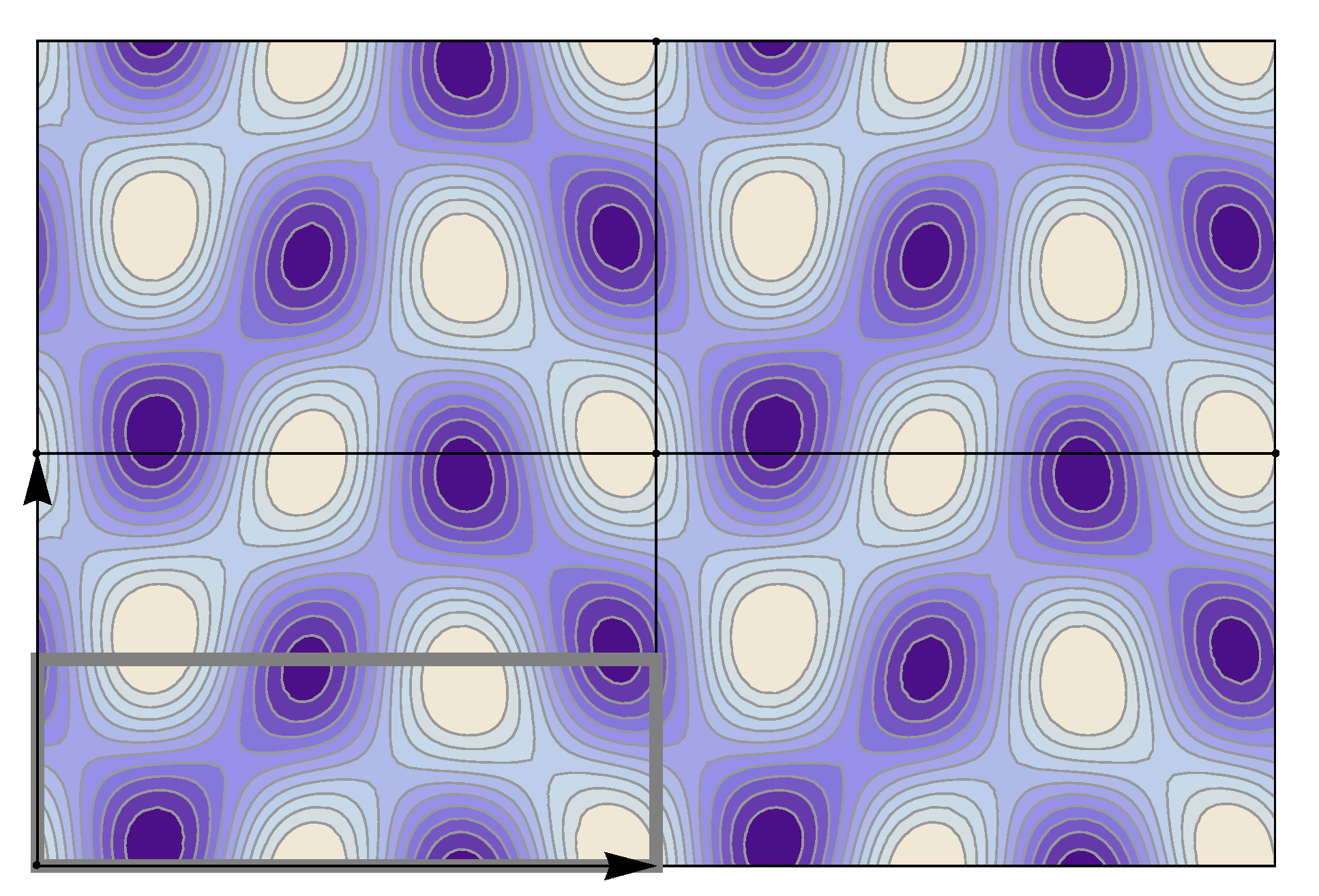
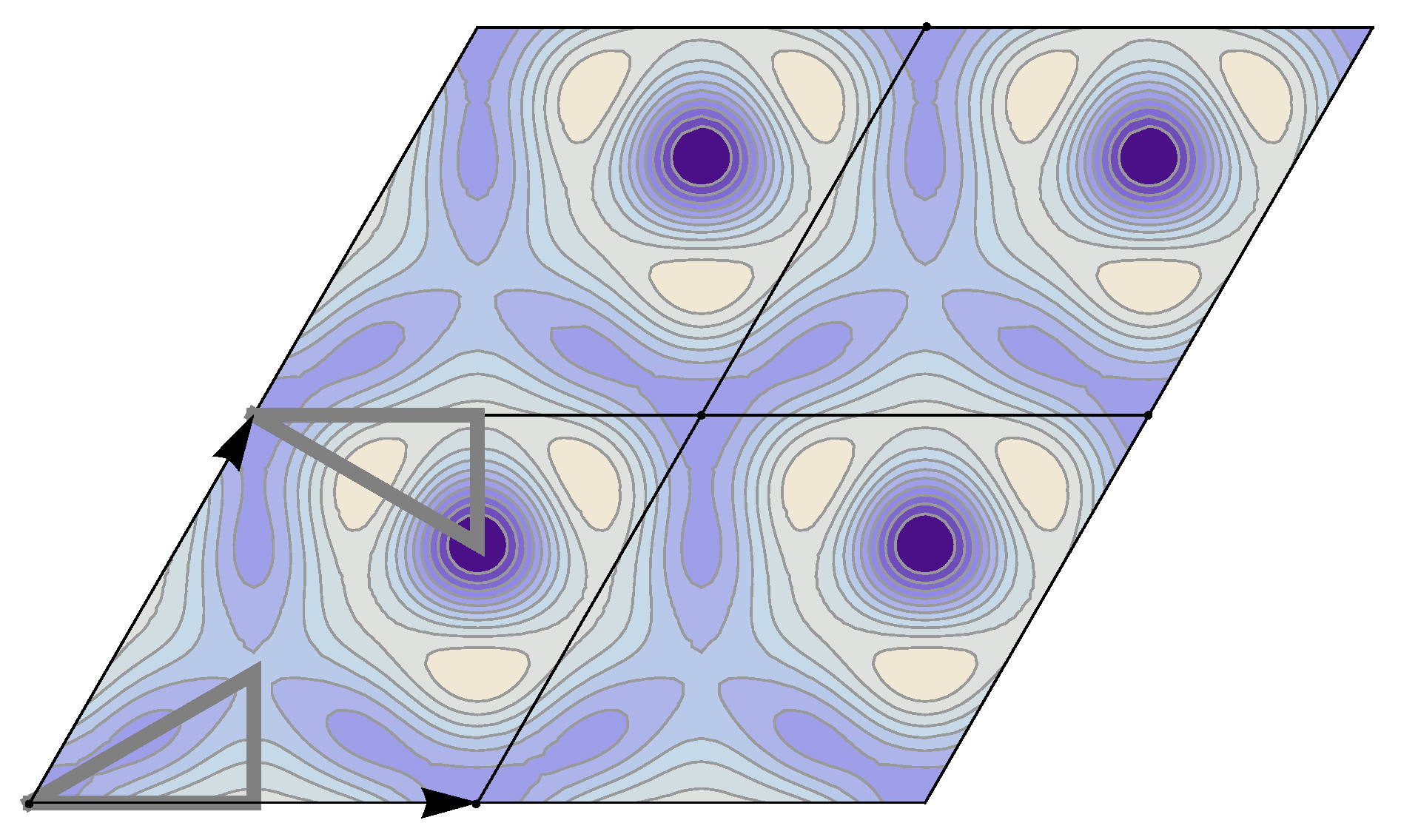
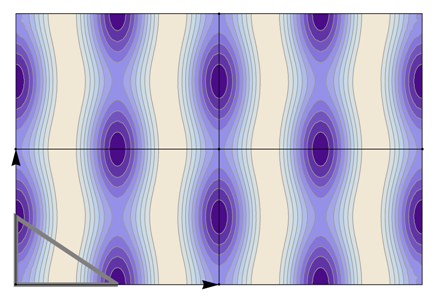
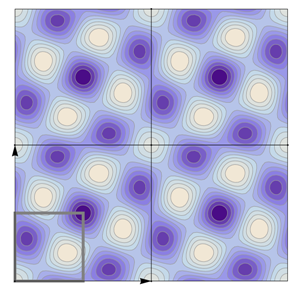
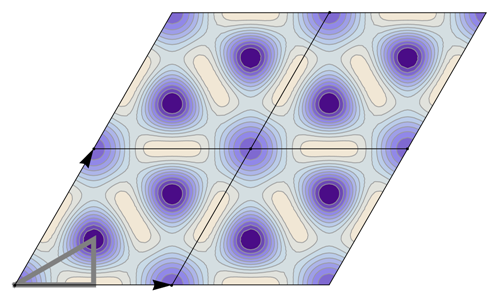
5. Wallpaper Group Tables

In the preceding sections we have shown how wallpaper group symmetry can be used to construct maximally-symmetric 2D Fourier series. The derivations and examples given contain many of the mathematical issues involved. At this point, it should be clear how to proceed for obtaining symmetry properties of Fourier coefficients and the Fourier series itself for a given wallpaper group.

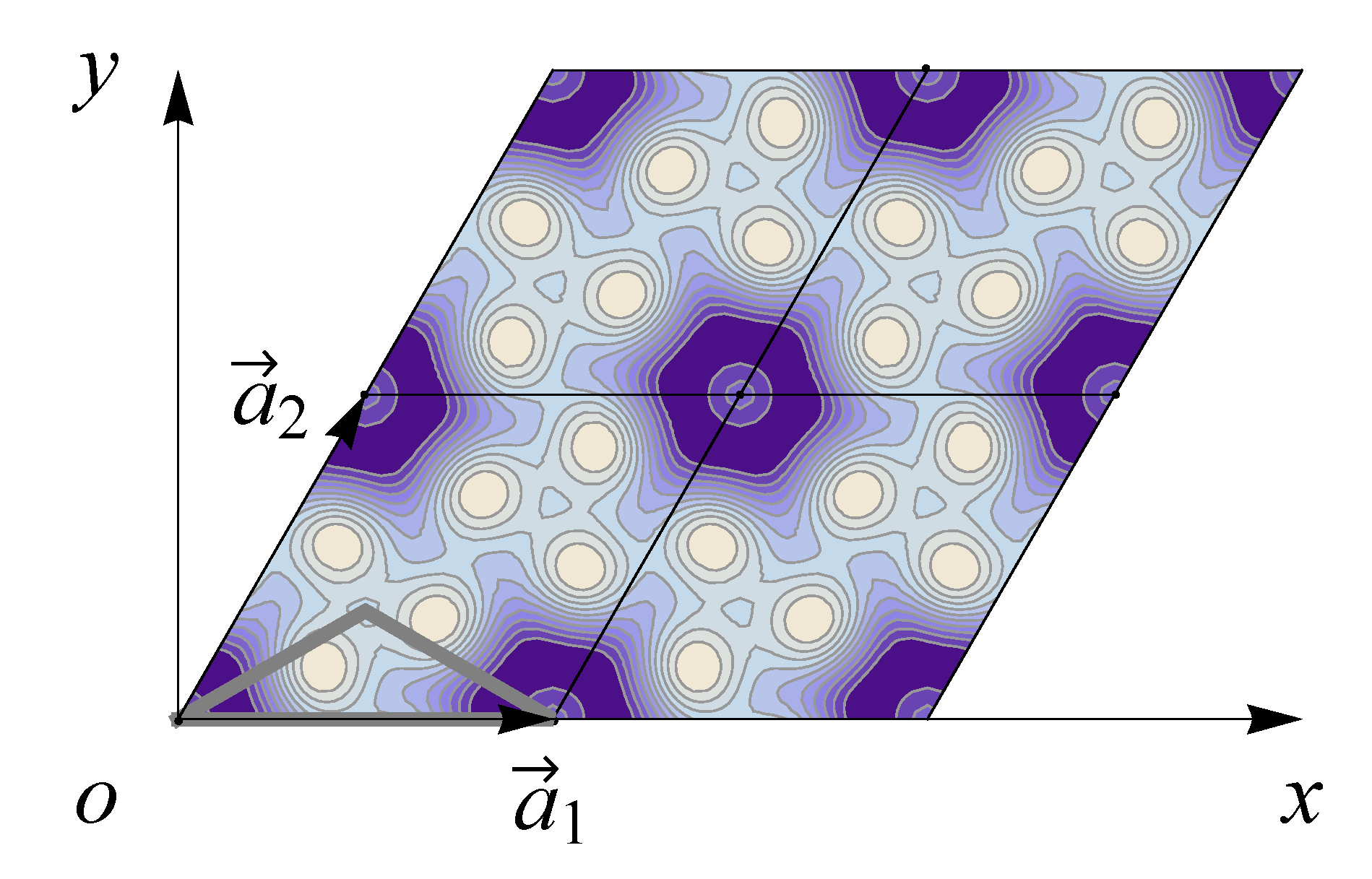
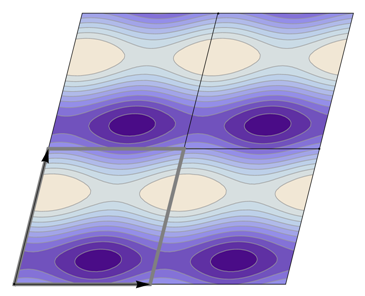
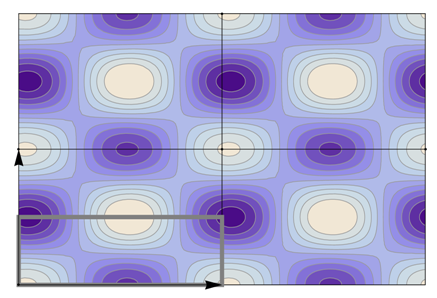
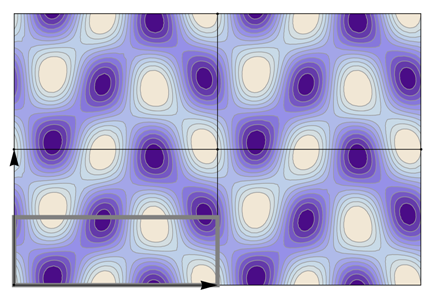
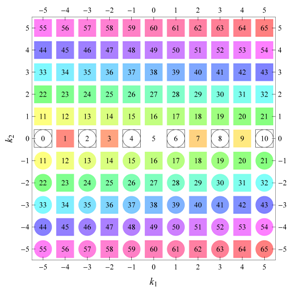
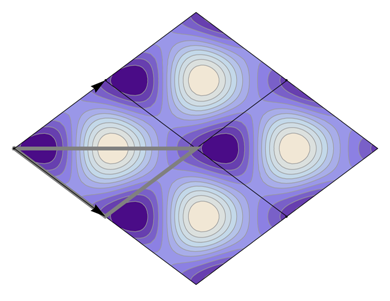
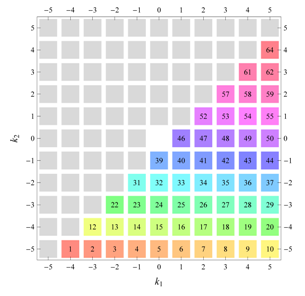
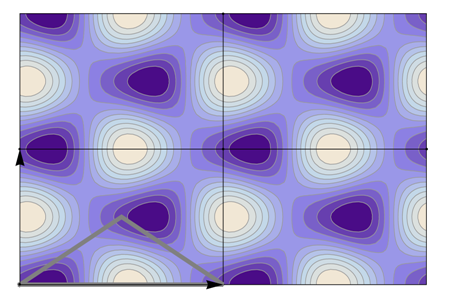
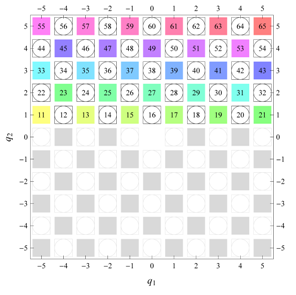
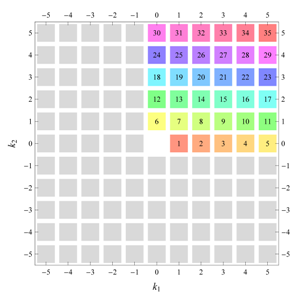
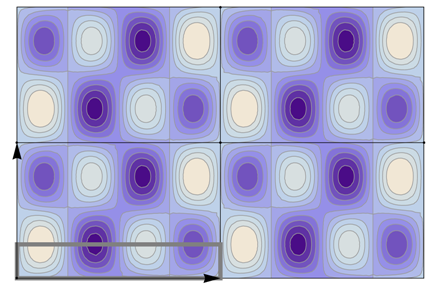
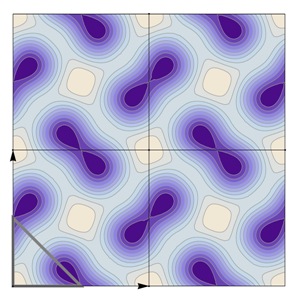
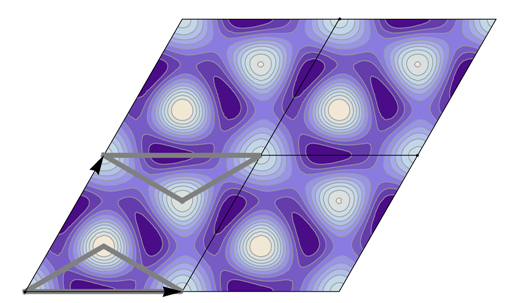
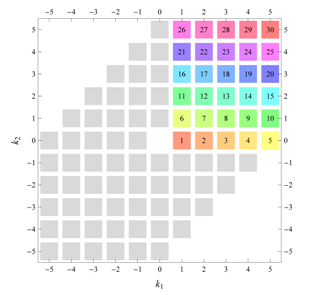
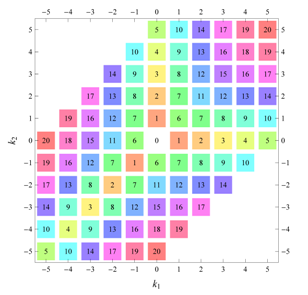
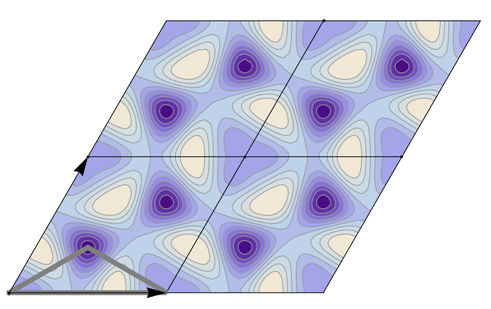
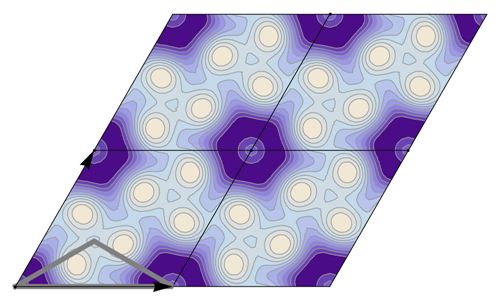
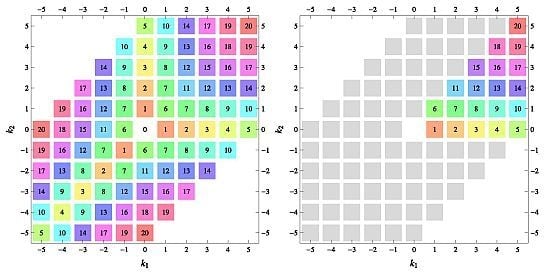
We have made a systematical investigation of all wallpaper groups; in Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21 and Table 22 all relevant wallpaper group information (Fourier coefficients symmetry property, independent Fourier coefficients domains, Fourier series) is summarized visually and analytically. The upper part of each table contains the wallpaper group’s label, the Bravais lattice type, the direct and the reciprocal basis vectors. 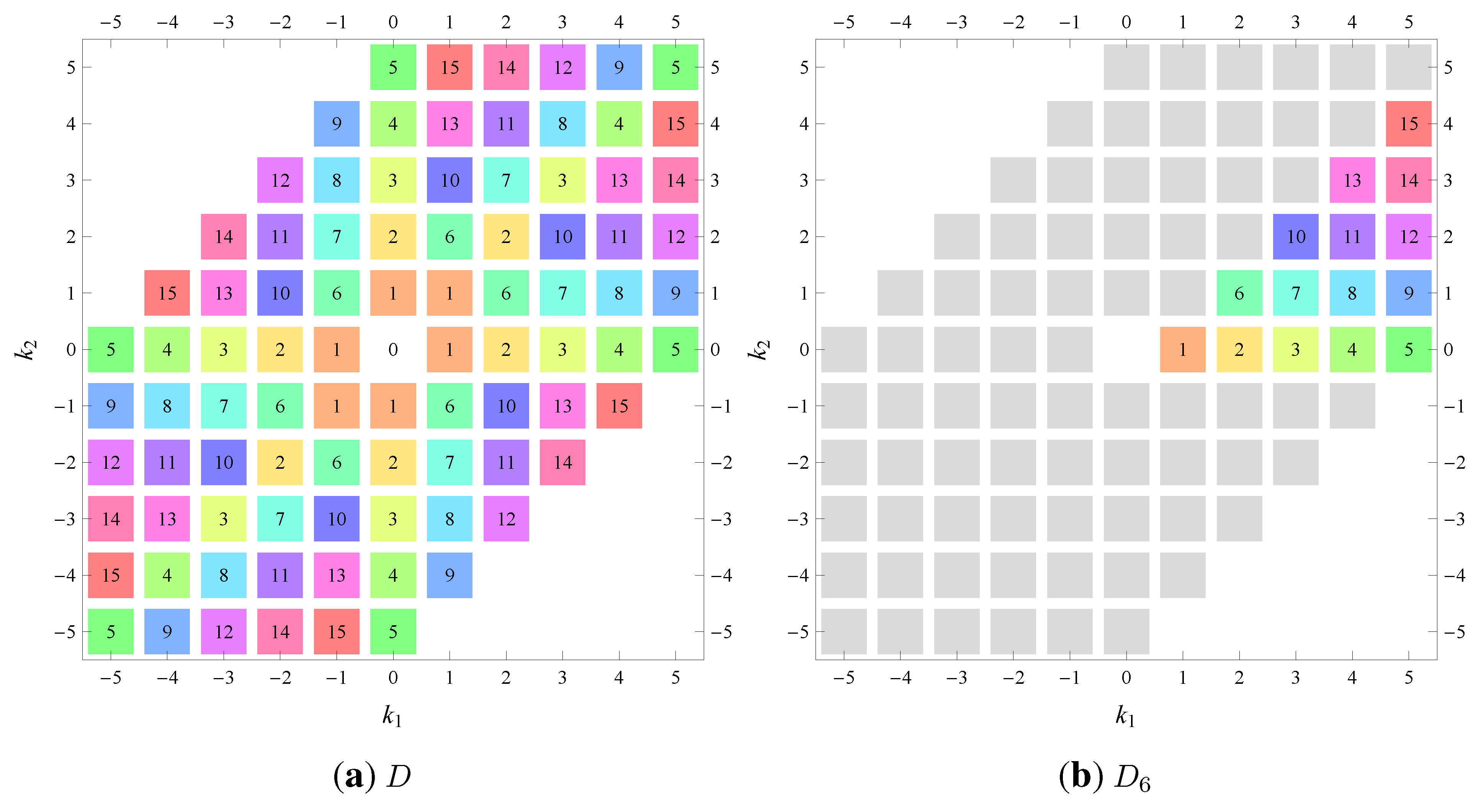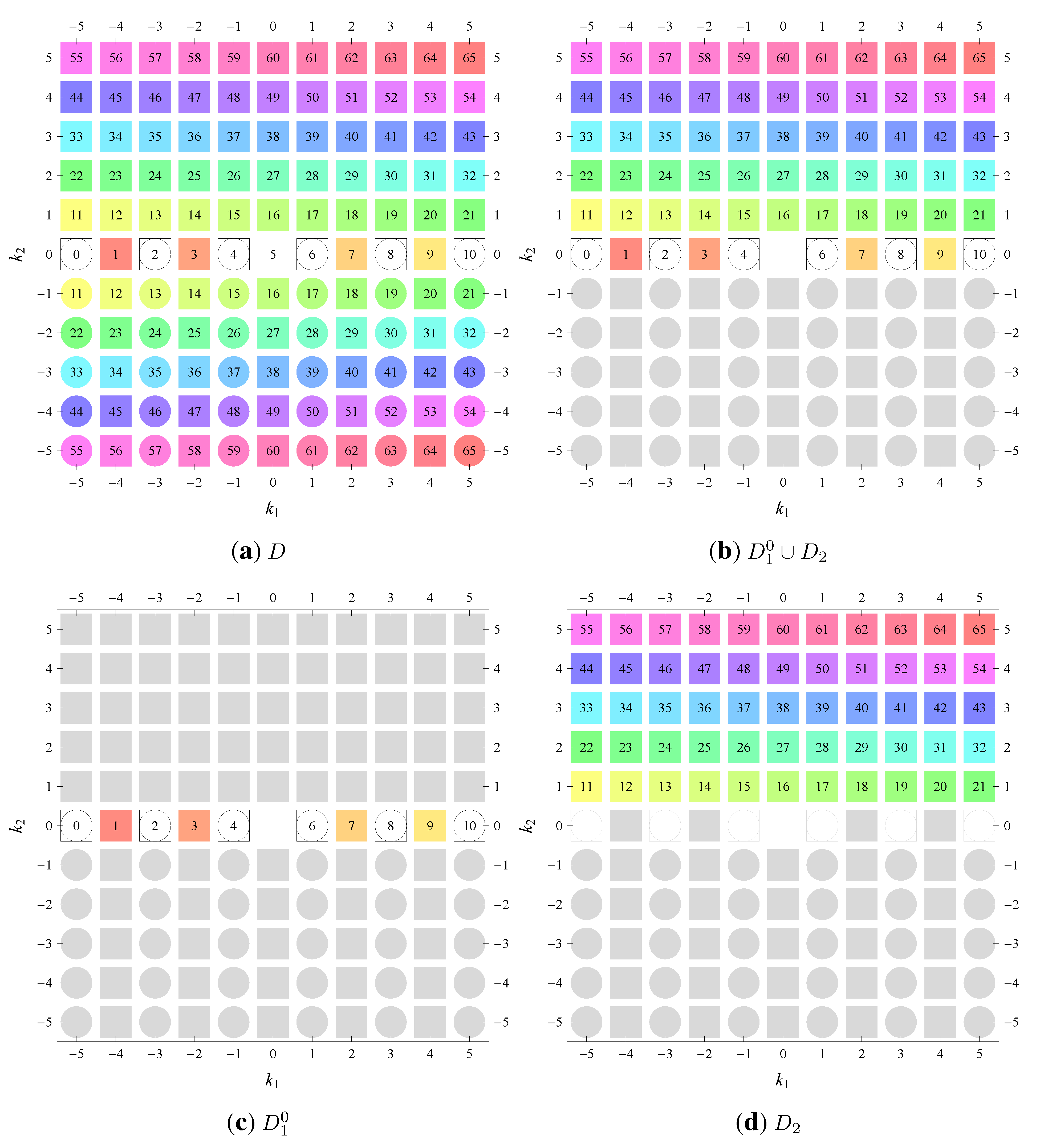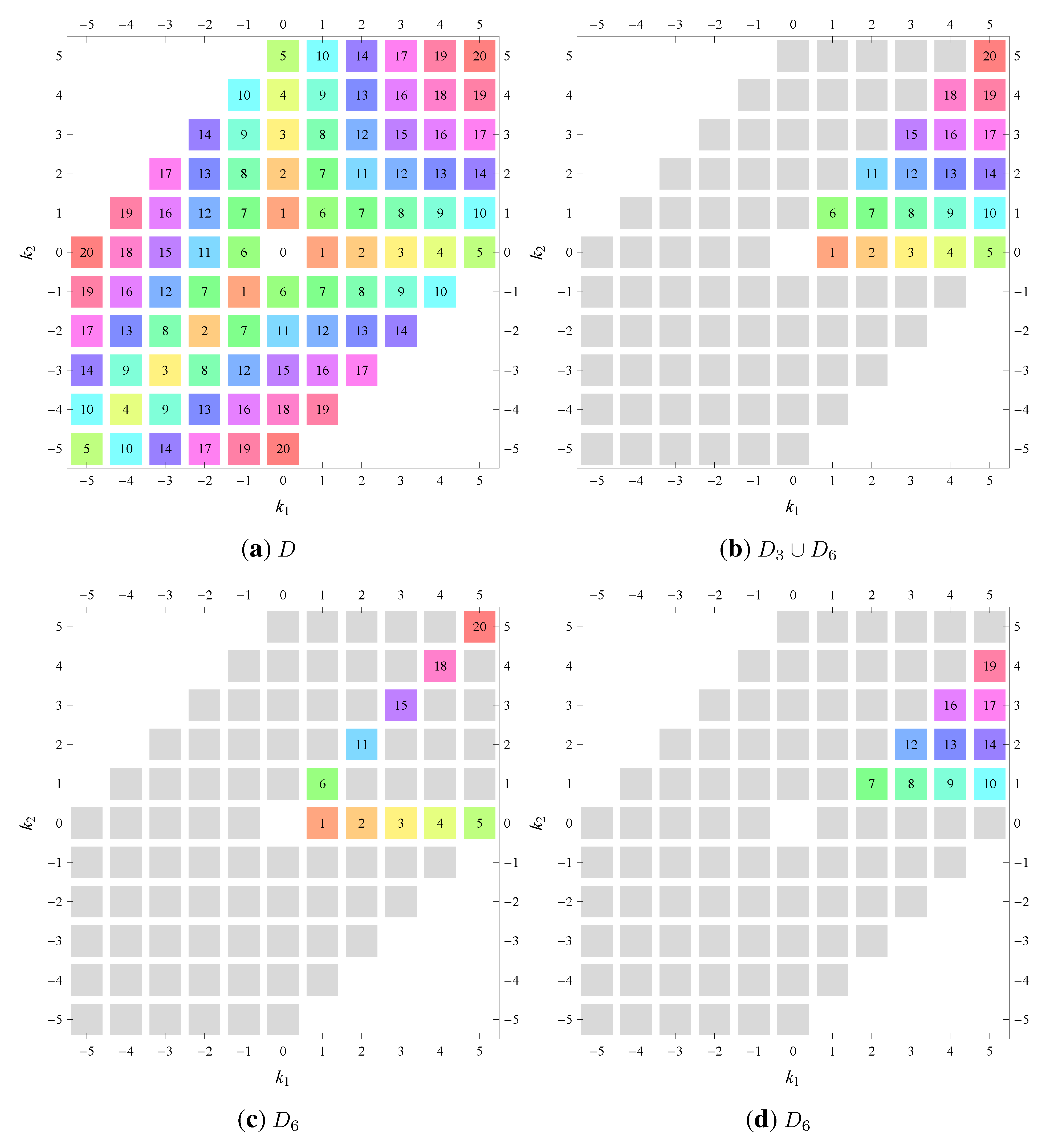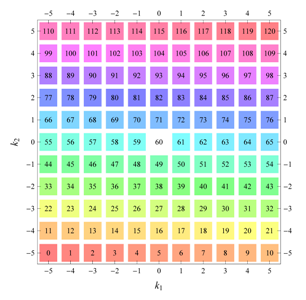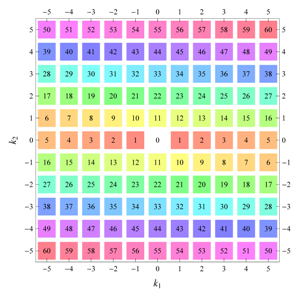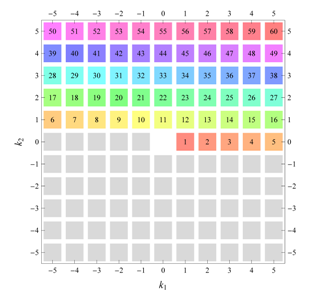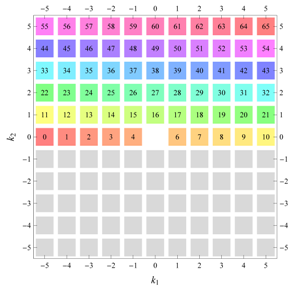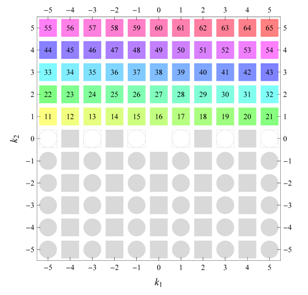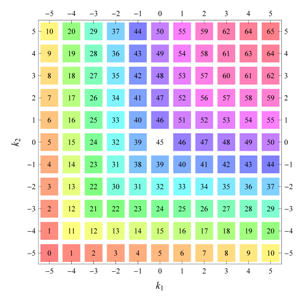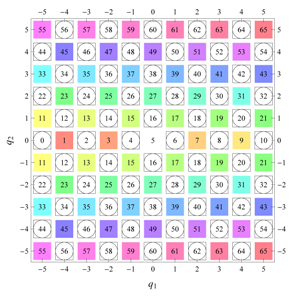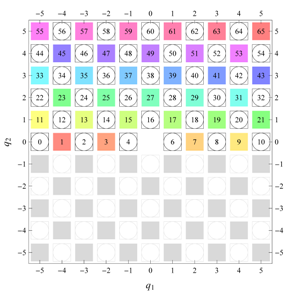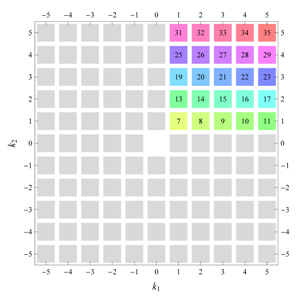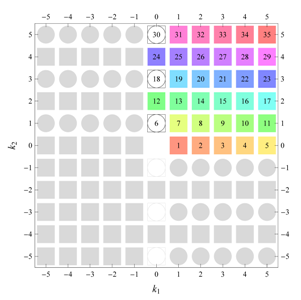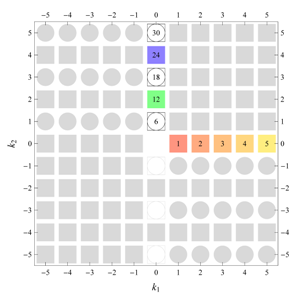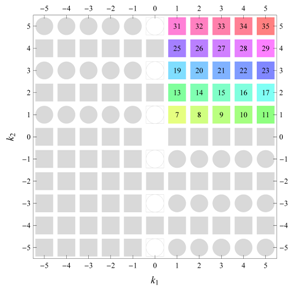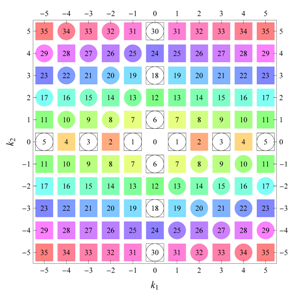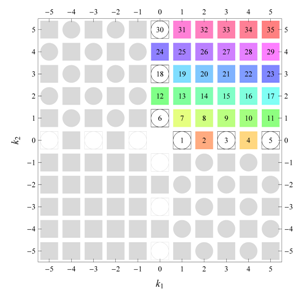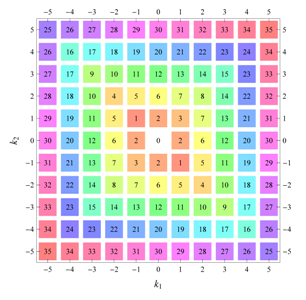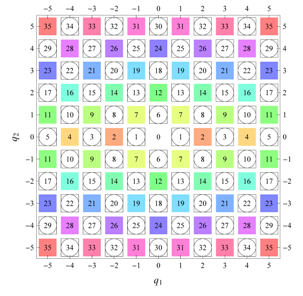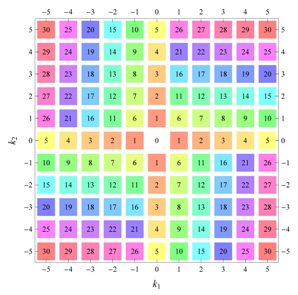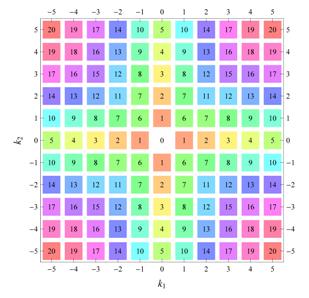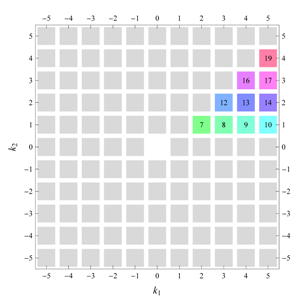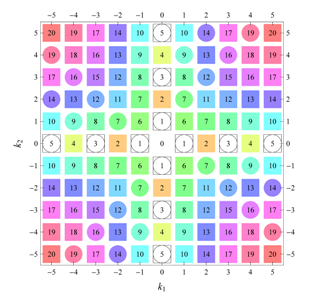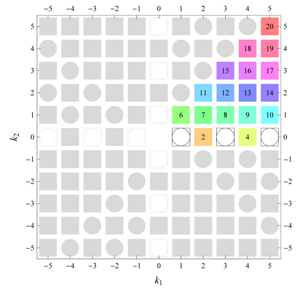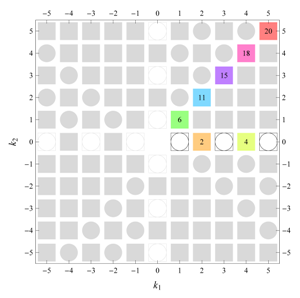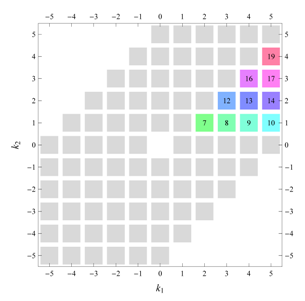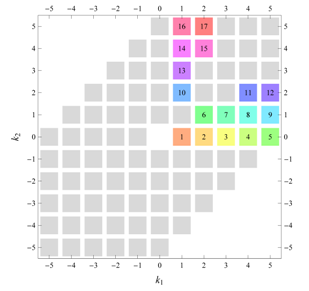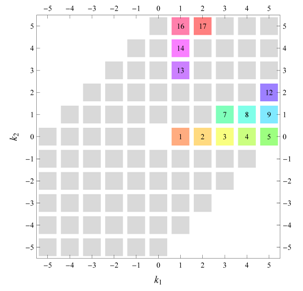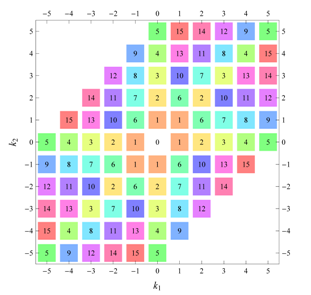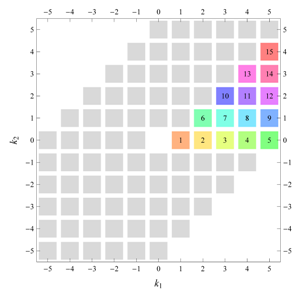Then, an example (a contour plot spanning four unit cells of a real function $f(x,y)$) displaying translational and point group symmetry is shown; the values of the non-vanishing Fourier coefficients used for the example are indicated below the contour plot. Basis vectors and a possible choice for the asymmetric unit are drawn on the figure. Next to the example, the domains showing equivalence of Fourier coefficients are shown. The total domain D shows which coefficients in the range $(-5\le k_1\le 5,-5\le k_2\le 5)$ are equivalent (equal or opposite); $(k_1,k_2)$ coordinates with equivalent Fourier coefficients $c_{k_1,k_2}$ are given a same color and number. When not all equivalent $(k_1,k_2)$ coordinates of a point lie in the range $(-5\le k_1\le 5,-5\le k_2\le 5)$, that point is left blank and unnumbered. 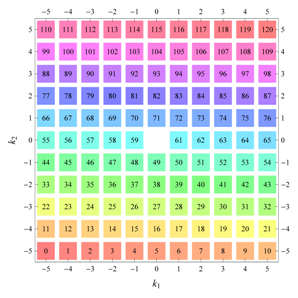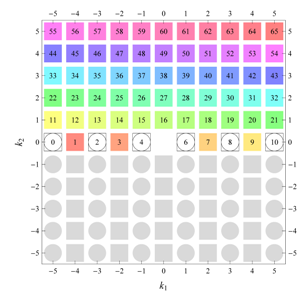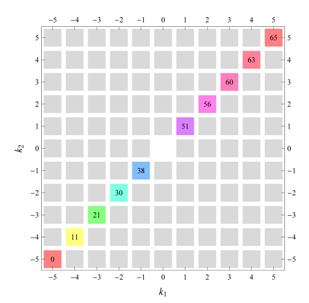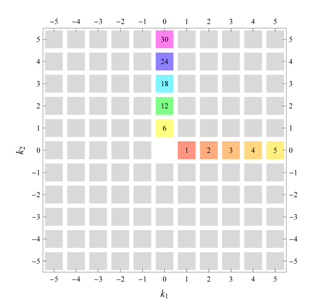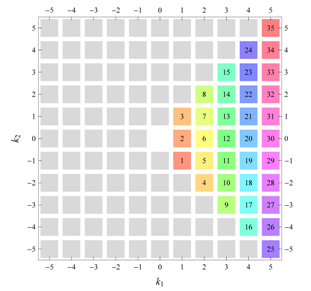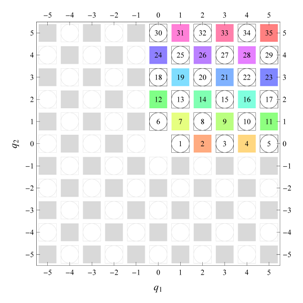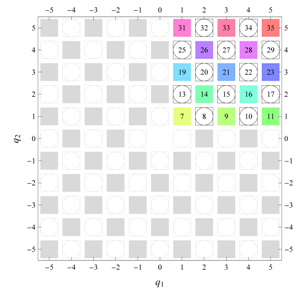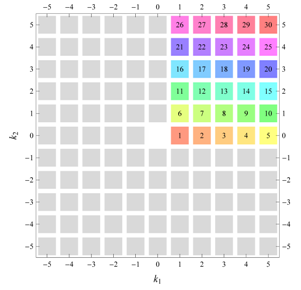(This occurs only for the hexagonal wallpaper groups.) To the right of the total domain D, the subdomain $D_{\min }$ containing exactly one independent representative (colored and numbered) of each set of equivalent points is shown; the remaining points are now shown shaded gray and unnumbered. For $D_{\min }$, an infinite number of possible choices exists; we recall that for a given cycle $S_{\overrightarrow{k}}$ of Fourier coefficient indices $\overrightarrow{k}$ generated by the symmetry property for Fourier coefficients, only one pair of indices $\overrightarrow{k}$ should be contained within $D_{\min }$. For, e.g., $p2$ (Table 5), one could equally well take $(k_1>0,k_2)$, $(0,k_2>0)$ rather than $(k_1>0,0)$, $(k_1,k_2>0)$. Our choices for $D_{\min }$ are simply based on convenience. In the case of subdomains with different cycles, the decomposition is shown below D and $D_{\min }$. The origin $(k_1,k_2)=(0,0)$ is always excluded from the subdomain $D_{\min }$ (but included in the total domain D), which is why the notation $D_1^0$ is used for subdomains with cycle 1 excluding $(0,0)$. Opposite Fourier coefficients are shown by discs and squares of the same color and labeled with a same number in the total domain D. In the case of necessarily vanishing Fourier coefficients, the symbol “⌼” is used. Below the example and the domains, the symmetry property for Fourier coefficients is given. To the right, if applicable, implications of the symmetry rule on the vanishing of Fourier coefficients (“extinction rules”) are given. Next, an explicit, symmetry-adapted, expression for the Fourier series of $f(x,y)$ is given, containing only (apart from the $c_{0,0}$ term) independent coefficients from the subdomain $D_{\min }$. Finally, an elaborated version of the reality criterion is given: The complex conjugate of $c_{k_1,k_2}$ with $(k_1,k_2)\in D_{\min }$ is equated to an expression involving the same or another coefficient in $D_{\min }$. Implications on the reality of coefficients are given to the right, if applicable.

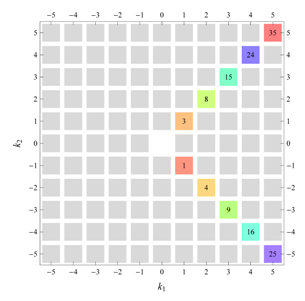
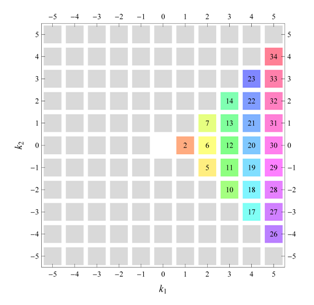
For the centered rectangular wallpaper groups $cm$ and $c2mm$, alternate (non-primitive) versions of the tables are given as well, with Fourier indices labeled $q_1$ and $q_2$ (Table 9 and Table 14).

It is interesting to see how for each group, the real-space (point-group) symmetry is converted into coefficient-space symmetry. Indeed, the distribution of equivalent Fourier coefficients in domain D also displays rotation axes and mirror axes. Particularly intriguing is how the hexagonal groups divide coefficient space into 3-, 6- or 12-cycle domains.

6. Discussion and Conclusions

Having established Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21 and Table 22, it is useful to consider some points in more detail.

A first issue is the reality criterion. Trivially, for all wallpaper groups, for $f(x,y)$ to be real, $c_{0,0}$ must be real. Considering general coefficients $c_{k_1,k_2}\ne c_{0,0}$, it follows from Equation (8) and the $p2$ symmetry property (Table 5) that for wallpaper groups having a 2-fold rotation axis at the origin, all coefficients $c_{k_1,k_2}$ must be real for $f(x,y)$ to be real. Since in two dimensions a 2-fold rotation axis is equivalent to an inversion center, we can speak of centrosymmetric and non-centrosymmetric wallpaper groups. The reality criteria for the non-centrosymmetric groups are summarized in

Table 23. Non-centrosymmetric wallpaper groups and their reality criteria.

Bravais lattice	wallpaper group	reality criterion
		general	special
oblique	$p1$	$c_{k_1,k_2}^{*}=c_{-k_1,-k_2}$
rectangular	$pm$	$c_{k_1,k_2}^{*}=c_{-k_1,k_2}$	$c_{0,k_2}\in \mathbb{R}$
	$pg$	$c_{k_1,k_2}^{*}={(-1)}^{k_1}{c}_{-k_1,k_2}$	$c_{0,k_2}\in \mathbb{R}$
centered rectangular	$cm$	$c_{k_1,k_2}^{*}=c_{-k_2,-k_1}$	$c_{k_1,-k_1}\in \mathbb{R}$
hexagonal	$p3$	$c_{k_1,k_2}^{*}=c_{k_1-k_2,k_1}$
	$p3m1$	$c_{k_1,k_2}^{*}=c_{k_1,k_1-k_2}$	$c_{2k_2,k_2}\in \mathbb{R}$
	$p31m$	$c_{k_1,k_2}^{*}=c_{k_2,k_1}$	$c_{k_1,0}\in \mathbb{R}$

. As indicated already when discussing examples in the preceding sections, for a non-centrosymmetric wallpaper group, the reality criterion imposes further restrictions on the coefficients in the subdomain $D_{\min }$. In general, a coefficient in $D_{\min }$ needs to be equal to the complex conjugate of another coefficient in $D_{\min }$; in some special cases, this results in the reality of Fourier coefficients (see Table 23). It is important to note, however, that the definition in terms of matrices of the inversion operation used throughout the “International Tables” [4,5,6,7,8] is not only that the inversion matrix is the negative of the identity matrix but also that its determinant is negative. In that sense, there can be no inversion in two dimensions, and centrosymmetric and non-centrosymmetric wallpaper groups should rather be referred to as displaying and lacking 2-fold rotational symmetry, respectively.

A second point is the necessary vanishing of certain Fourier coefficients. As demonstrated in Section 2, a glide reflection axis introduces a phase factor in the symmetry property for the Fourier coefficients, which in turn leads to certain Fourier coefficients having to be zero. This occurs for the groups $pg$, $p2mg$, $p2gg$ and $p4gm$ (all containing a “g” in their label). Observed rules for vanishing coefficients are $c_{2n+1,0}=0$ or $c_{0,2n+1}=0$, with $n\in \mathbb{Z}$. These are analogous to the diffraction extinction rules associated with the presence of glide reflection axes [4,5,6,7,8]. The centering operation discussed in SubSection 4.5 also implies Fourier coefficients to be zero ($c_{2n,2m+1}=c_{2n+1,2m}=0$, $n,m\in \mathbb{Z}$)—in analogy with the diffraction extinction rules for centered unit cells [4,5,6,7,8].

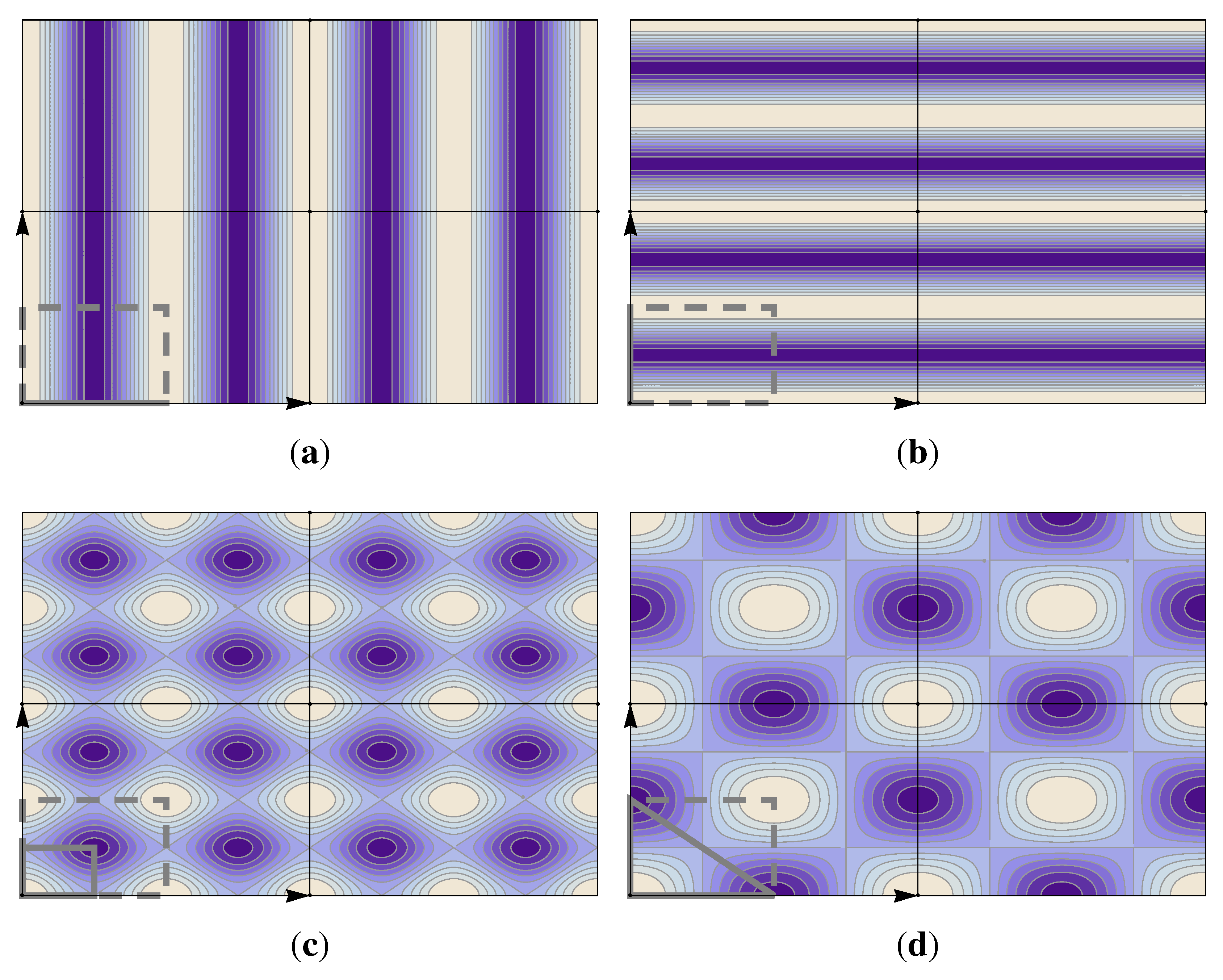
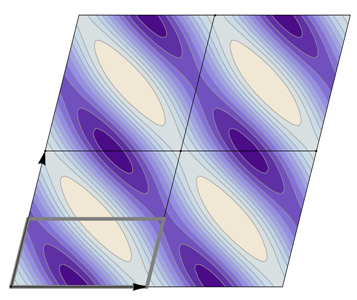
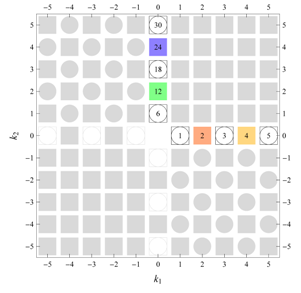
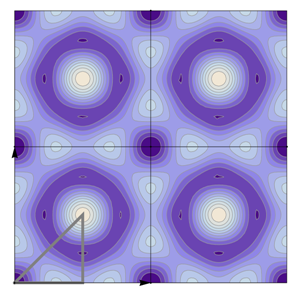
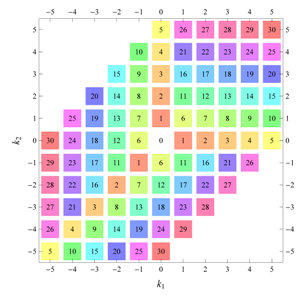
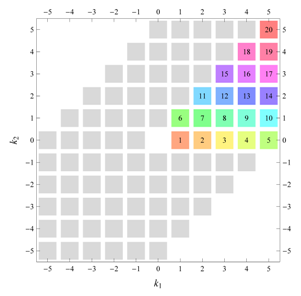
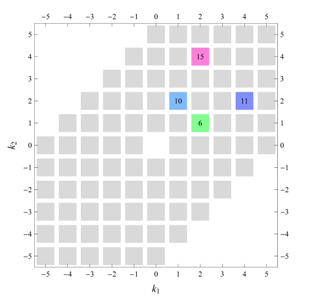
A next issue is that of the notion of a “minimal” Fourier series. To correctly represent a given wallpaper group symmetry, a Fourier series must indeed contain sufficient non-vanishing Fourier coefficients resulting in the correct x- and y-dependence. Let us for example consider the group $p2gg$ (Table 12). Trivially, if we take only the term $c_{0,0}$ we have no $(x,y)$-dependence. If we take only $c_{2,0}$ or $c_{0,2}$ different from zero ($p2gg$ symmetry implies $c_{1,0}=c_{0,1}=c_{-1,0}=c_{0,-1}=0$) we create a function with only x- or y-dependence, respectively. 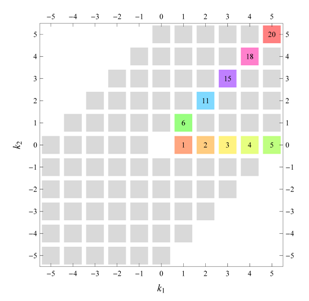This is illustrated in Figure 9(a,b). If we assign, however, simultaneously both to $c_{2,0}$ and $c_{0,2}$ non-zero values, we have a $(x,y)$-dependent function, but its periodicity in both x- and y-direction is half that of the intended lattice, and the symmetry of the reduced unit cell is $p2mm$ [Figure 9(c)]. The series with only $c_{1,1}$ “switched on” results in a function with the right translational symmetry, and does indeed have $p2gg$ symmetry, but its asymmetric unit has half the size of the general $p2gg$ asymmetric unit [Figure 9(d)]: The wallpaper group is actually $c2mm$ (compare Table 12 and Table 14). While independence on x and/or y and periodicity reduction can be relatively easily avoided by inspecting the explicit expression of the Fourier expansion and including necessary (low-$k_1$ and low-$k_2$) Fourier coefficients, the last observation (a $p2gg$ Fourier series displaying $c2mm$ symmetry) involves more subtle considerations. It can be understood by realising that the $p2gg$ group is a subgroup of the $c2mm$ group. A rectangular lattice Fourier series with $c_{1,1}=c_{-1,1}=c_{-1,-1}=c_{1,-1}$ (and all other Fourier coefficients equal to zero) fulfills both the symmetry properties of $p2gg$ and $c2mm$, which can be clearly seen by comparing the domains D of Table 12 and Table 14. Even more, it also complies with the symmetry of the $p2mm$ wallpaper group (Table 10), which is also a subgroup of $c2mm$ (see also SubSection 4.5). The net symmetry will therefore be that of the higher-symmetry group, $c2mm$. 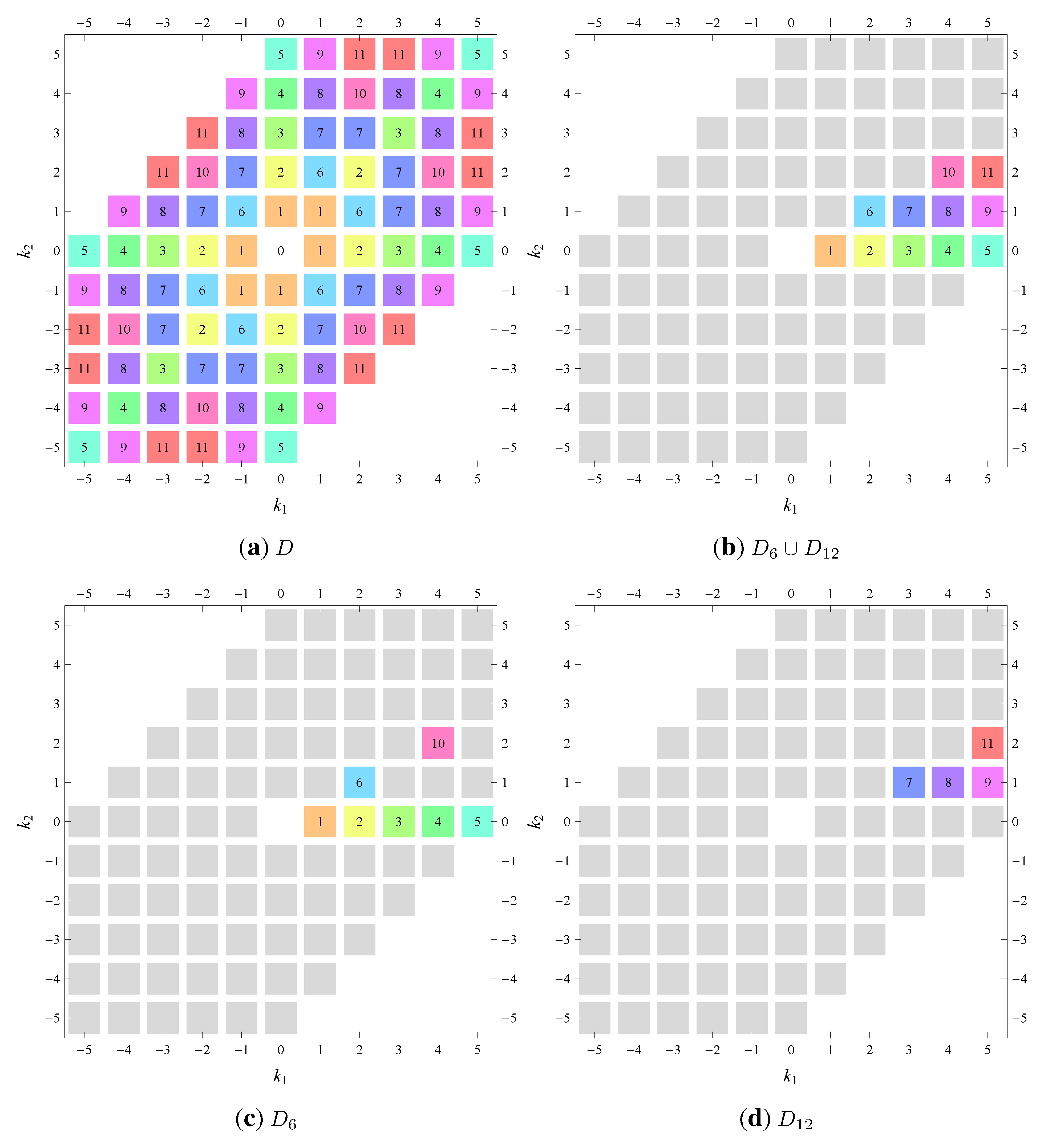To have a Fourier series with true $p2gg$ (or $p2mm$) symmetry, it is necessary to include non-zero coefficients $c_{k_1,k_2}$ with $k_1+k_2$ odd, as in the example in Table 12 where both $c_{1,1}$ and $c_{1,2}$ have been assigned non-zero values. Hence, to avoid apparent higher symmetry, a wallpaper group should be compared with any supergroup of which it is a subgroup; its pattern of non-zero and equivalent Fourier coefficients should distinguish itself from that of the supergroup. As a further illustration, let us consider the wallpaper groups $p6$ and $p6mm$ (Table 21 and Table 22, respectively). The former is a subgroup of the latter. If the expression for the Fourier expansion for a $p6$ function contains only Fourier coefficients that belong to the $D_6$ subdomain of the $p6mm$ group, this will result in a function displaying $p6mm$ symmetry. A true $p6$ function therefore needs to contain at least one non-zero Fourier coefficient from the $p6mm$-$D_{12}$ subdomain. The example functions in the preceding sections and in Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10, Table 11, Table 12, Table 13, Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20, Table 21 and Table 22 have been selected carefully to yield true wallpaper group symmetry with a small number of non-vanishing Fourier coefficients (in every example, only two independent coefficients were assigned non-zero values).

A more formal approach for deriving minimal symmetry-adapted functions for the wallpaper groups involves group theory; each wallpaper group should be decomposed into irreducible representations (IRREPs) [12]. The terms of the Fourier series developed in this work should then be rearranged into linear combinations $g_{\overrightarrow{k}}(x,y)$ that belong to the different IRREPs of the wallpaper group. The linear combinations belonging to the unit representation then display the full wallpaper group symmetry without apparent higher symmetry [13]. The situation is similar to the decomposition of (planar) point groups. For example, the lowest-order function displaying $4mm$ point group symmetry is $G(x,y)=x^4+y^4$ or, in polar coordinates, $G(r,\theta )=r^4(1-2{cos}^2\theta {sin}^2\theta )$. A decomposition of the wallpaper groups into IRREPs is beyond the scope of the present paper.

Finally, a few suggestions on how to use the Fourier series developed in this work. Our motivation came from the need of a continuous and infinitely differentiable function with the symmetry of the graphene lattice—i.e., the $p6mm$ wallpaper group. In the context of solid-state physics, the 2D functions $f(x,y)$ with wallpaper group symmetry that naturally come to mind are (complex) electronic wave functions $\psi (x,y)$ or (real) electronic densities $\rho (x,y)$ of the new family of 2D materials like graphene or boron-nitride. Electronic densities can nowadays be calculated from ab-initio principles; a first application of our calculations could therefore be the fit of an ab-intio obtained electronic density to the symmetry-adapted Fourier series. By limiting the number of fitted coefficients [calculated numerically via Equation (6)], one obtains a handy, analytical expression for $\rho (x,y)$, which can then subsequently be used in further calculations. If necessary, the extension of the density above and below the atomic plane can be taken into account by making the Fourier coefficients z-dependent.

Another situation where symmetry-adapted Fourier series could be used is when fitting X-ray diffraction data to a structural model. Rather than putting atoms in the unit cell and adjusting their positions and the unit cell’s parameters, one could conceive an approach where a limited number of Fourier coefficients of the electronic density $\rho (x,y)$—responsible for the scattering of X-rays—is taken as the adjustable parameter set (together with the unit cell’s dimensions), after which an atomic distribution matching the electronic density $\rho (x,y)$ can be sought.

Note that the results obtained here can also be used for identifying or discriminating wallpaper groups (see e.g., [14]): A numerical calculation of the Fourier coefficients of a given function $f(x,y)$ and testing for Fourier coefficient symmetry properties can indeed help to distinguish the planar symmetry of $f(x,y)$.

Planar wallpaper groups are not only relevant for describing 2D crystals but also useful for analysing surfaces of three-dimensionally periodic crystals, and they can be a tool for studying crystal growth [15].

In summary, it is hoped that the symmetry-adapted Fourier series presented in this paper will turn out to be useful for dealing with periodic functions in two dimensions in various situations.