Lie Symmetry Preservation by Finite Difference Schemes for the Burgers Equation
Abstract
1. Introduction
2. Basics and Problem Formulation
2.1. Background
3. Scheme Parametrization Algorithm
- Start with a numerical scheme:where U represents the stencil of the discrete equation
- From the prolonged action of the r-dimensional symmetry group G on :where are the symmetry parameters, write down the expression of the transformed scheme:where the discrete points are in the transformed stencil
- Then for each symmetry parameters, suppose an algebraic form that depends on constant real coefficients, that is for :The transformed discrete equation has an expression that depends on those real constant coefficients:for .
- For each symmetry parameter, compute the equivariance relation:
- Compute conditions over the constant coefficients from the order of accuracy of the scheme:

4. Numerical Illustration: The Burgers Equation
- Spatial translation:
- Time translation:
- Projection:
- Scale transformation:
- Galilean boost:
4.1. Construction of Invariant Numerical Scheme
4.1.1. Construction of the moving frames
4.1.2. Order of Accuracy
4.2. Numerical Applications
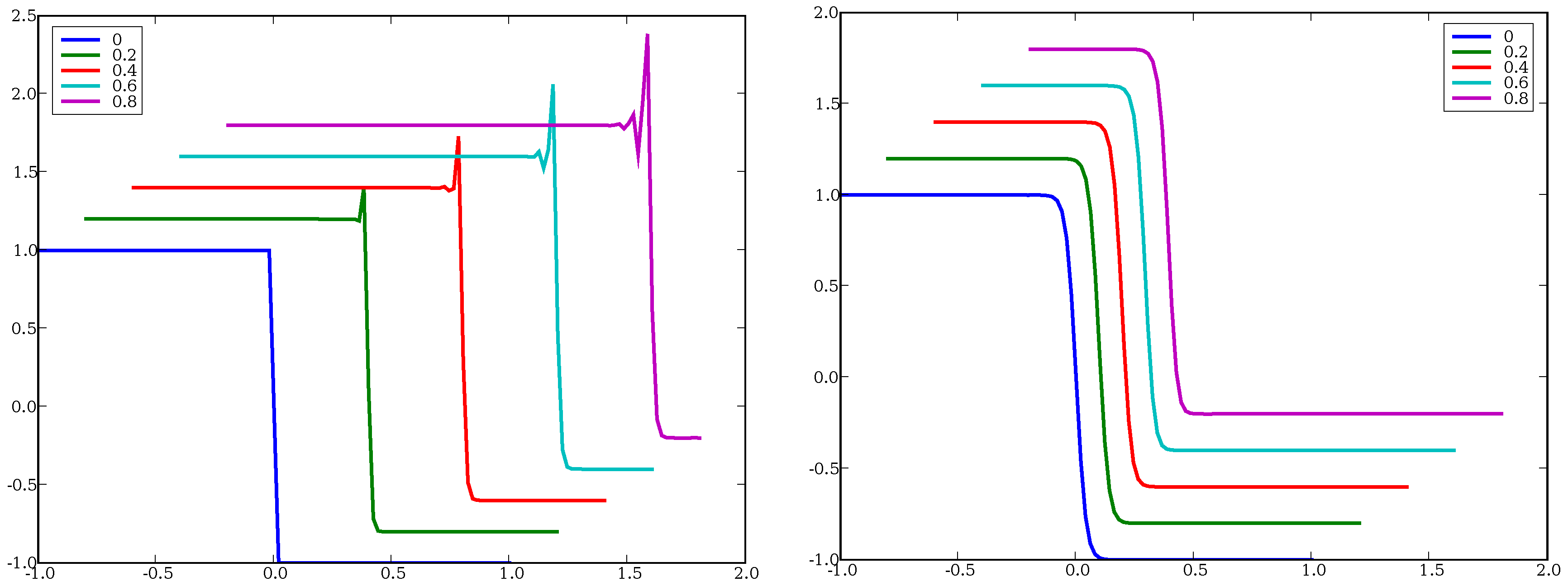
4.2.1. Self-Similar Solutions
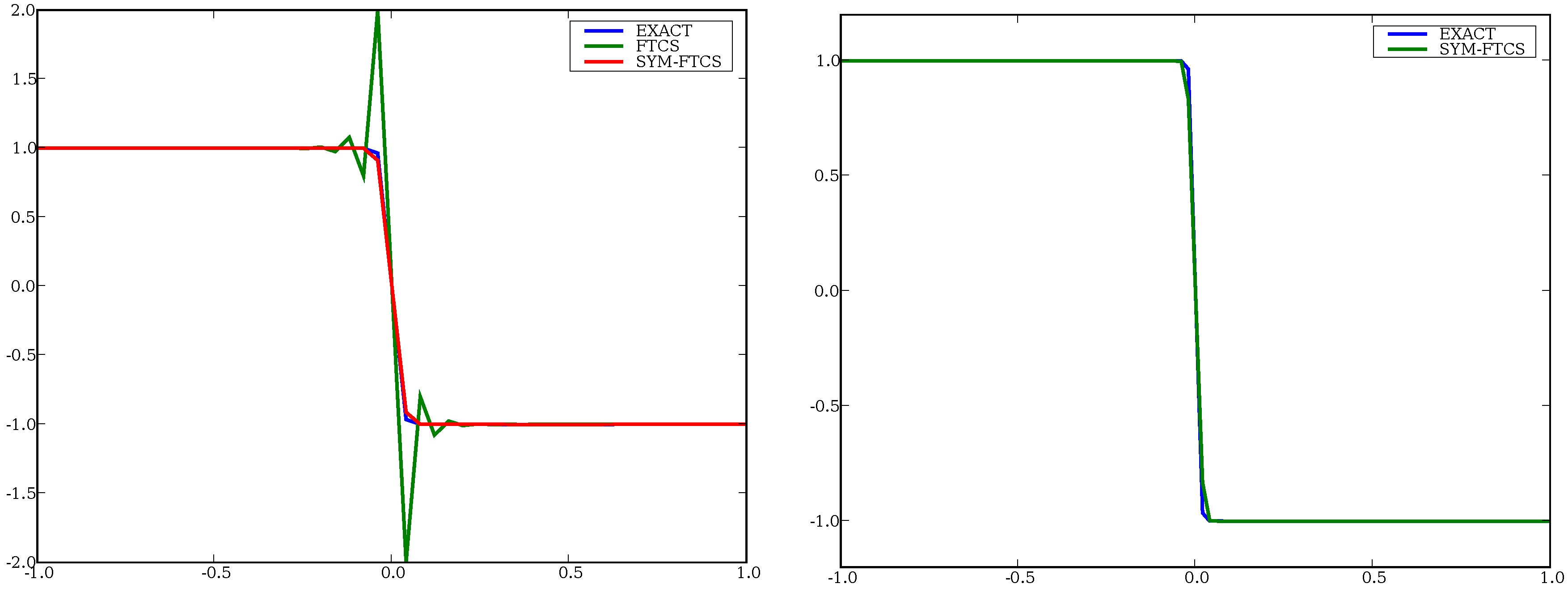
4.2.2. Galilean Invariance
5. Conclusions
References
- Grassi, V.; Leo, R.A.; Soliani, G.; Tempesta, P. Vorticies and invariant surfaces generated bysymmetries for the 3D Navier-Stokes equation. Physica A 2000, 286, 79–108. [Google Scholar] [CrossRef]
- Oberlack, M. A unified approach for symmetries in plane parallel turbulent shear flows. J. Fluid Mech. 2001, 427, 299–328. [Google Scholar] [CrossRef]
- Oberlack, M.; Cabot, W.; Pettersson Reif, B.; Weller, T. Group analysis, direct numerical simulation and modelling of a turbulent channel flow with streamwise rotation. J. Fluid Mech. 2006, 562, 383–403. [Google Scholar] [CrossRef]
- Unal, G. Application of equivalence transformations to inertial subrange of turbulence. Lie Group Appl. 1994, 1, 232–240. [Google Scholar]
- Lindgren, B.; Osterlund, J.M.; Johansson, A.V. Evaluation of scaling laws derived from Lie group symmetry methodsin zero-pressure-gradient turbulent boundary layers. J. Fluid Mech. 2004, 502, 127–152. [Google Scholar] [CrossRef]
- Razafindralandy, D.; Hamdouni, A. Subgrid models preserving the symmetry group of the Navier-Stokes equations. C. R. Acad. Sci. Mec. 2005, 333, 481–486. [Google Scholar] [CrossRef]
- Razafindralandy, D.; Hamdouni, A.; Oberlack, M. Analysis and development of subgrid turbulence models preserving the symmetry properties of the Navier-Stokes equations. Eur. J. Mech. B/Fluids 2006, 26, 531–550. [Google Scholar] [CrossRef]
- Razafindralandy, D.; Hamdouni, A.; Béghein, C. A class of subgrid-scale models preserving the symmetry group of the Navier-Stokes equations. Comm. Nonlinear Sci. Numer. Sim. 2007, 12, 243–253. [Google Scholar] [CrossRef]
- Razafindralandy, D.; Hamdouni, A. Invariant subgrid modelling in large-eddy simulation of heat convection turbulence. Theor. Comput. Fluid Dyn. 2007, 21, 231–244. [Google Scholar] [CrossRef][Green Version]
- Hairer, E.; Nørsett, S.P.; Wanner, G. Solving Ordinary Differential Equations, 2nd ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Calvo, M.P.; Hairer, E. Accurate long-term integration of dynamical systems. J. Appl. Math. 1995, 18, 95–105. [Google Scholar] [CrossRef]
- Sanz-Serna, J.M. Symplectic integrators for Hamiltonian problems: an overview. Acta Numer. 1992, 1, 243–286. [Google Scholar] [CrossRef]
- Marsden, J.E.; Ratiu, T.S. Introduction to Mechanics and Symmetry, 2nd ed.; Springer: New York, NY, USA, 1999. [Google Scholar]
- Moore, E.B.; Reich, S. Multi-symplectic integration methods for Hamiltonian PDEs. Future Gener. Comput. Syst. 2003, 19, 395–402. [Google Scholar] [CrossRef]
- Kozlov, R. Conservation laws of semidiscrete Hamiltonian equations. J. Math. Phys. 2001, 42, 1708–1727. [Google Scholar] [CrossRef][Green Version]
- Quispel, G.R.W.; Dyt, C. Solving ODE’s Numerically while Preserving Symmetries, Hamiltonian Structure, Phase Space Volume or First Integrals. GRW Quispel, C Dyt-Proceedings IMALS 1997, 2, 601–607. [Google Scholar]
- Rodriguez, M.A.; Winternitz, P. Lie symmetries and exact solutions of first-order difference schemes. J. Phys. A Math. Gen. 2004, 37, 6129–6142. [Google Scholar] [CrossRef]
- Dorodnitsyn, V.A.; Kozlov, R.; Winternitz, P. Lie group classification of second-orderordinary difference schemes. J. Math. Phys. 2000, 41, 480–504. [Google Scholar] [CrossRef]
- Rodriguez, M.A.; Winternitz, P. Lie point symmetries of multidimensional difference equations. J. Phys. A Math. Gen. 2004, 37, 6129–6142. [Google Scholar]
- Bourlioux, A.; Cyr-Gagnon, C.; Winternitz, P. Difference schemes with point symmetries and their numerical tests. J. Phys. A Math. Gen. 2006, 39, 6877–6896. [Google Scholar] [CrossRef]
- Dorodnitsyn, V.A. The Group Properties of Difference Equations; Fizmatlit: Moscow, Russia.
- Levi, D.; Winternitz, P. Continuous symmetries of difference equations. J. Phys. A: Math. Gen. 2006, 39, R1–R63. [Google Scholar] [CrossRef]
- Shokin, Y.I. The Method of Differential Approximation; Springer: New York, NY, USA, 1983. [Google Scholar]
- Yanenko, N.N.; Shokin, Y.I. Group classification of difference schemes for a system of one-dimensional equations of gaz dynamics. Amer. Math. Soc. Transl. 1976, 2, 259–265. [Google Scholar]
- Hoarau, E.; David, C.; Sagaut, P.; Le, T.H. Lie group study of finite difference schemes. Discret. Contin. Dyn. Syst. 2007, 495–505. [Google Scholar]
- Bakirova, M.I.; Doronitsyn, V.A.; Kozlov, R.V. Symmetry-preserving differences schemes for some heat transfer equations. J. Phys. A: Math. Gen. 1997, 30, 8139–8155. [Google Scholar] [CrossRef]
- Budd, C.J.; Piggott, M. Geometric integration and its applications. In Handbook of Numerical Analysis, XI; North–Holland: Amsterdam, The Netherlands, 2003; pp. 35–139. [Google Scholar]
- Budd, C.J.; Collins, G.J. Symmetry based numerical methods for partial differential equations. Numer. Anal. 1998, 380, 16–36. [Google Scholar]
- Olver, P.J. Moving frames. J. Symb. Comp. 2003, 3, 501–512. [Google Scholar] [CrossRef]
- Fels, M.; Olver, P.J. Moving coframes I. a practical algorithm. Acta Appl. Math. 1998, 51, 161–213. [Google Scholar] [CrossRef]
- Fels, M.; Olver, P.J. Moving coframes II. regularization and theoretical foundations. Acta Appl. Math. 1999, 55, 127–208. [Google Scholar] [CrossRef]
- Kim, P. Invariantization of Numerical Schemes using Moving Frames. BIT Numer. Math. 2007, 47, 525–546. [Google Scholar] [CrossRef]
- Kim, P. Invariantization of the Crank Nicolson method for Burgers equation. Physica D 2008, 237, 243–254. [Google Scholar] [CrossRef]
- Chhay, M.; Hamdouni, A. A new construction for invariant numerical schemes using moving frames. C. R. Acad. Sci. Mec. 2010, 338, 97–101. [Google Scholar] [CrossRef]
- Kim, P. Invariantization of Numerical Schemes for Differential Equations Using Moving Frames. PhD thesis, School of Mathematics, University of Minnesota, Minneapolis, MN, USA, 2006. [Google Scholar]
- Cicogna, G. A discussion on the different Notions of symmetry of differential equations. In Proceedings of the Institute of Mathematics of NAS of Ukraine; 2004; volume 50, pp. 77–84. [Google Scholar]
- Cartan, E. Exposés de Géométrie. In La Méthode du Repère Mobile, La Théorie des Groupes Continues, et Les Espaces Généralisés; Hermann: Paris, France, 1935. [Google Scholar]
- Olver, P.J. Applications of Lie Groups to Differential Equations, 2nd ed.; Springer-Verlag: New York, NY, USA, 1993. [Google Scholar]


| 0. | 0.2 | 0.4 | 0.6 | 0.8 | 1. | ||
| Error | Classic | 0.00367055 | 0.125886 | 0.214256 | 0.272098 | 0.30876 | 0.327396 |
| Invariant | 0.0153383 | 0.0152615 | 0.0151855 | 0.0151103 | 0.0150359 | 0.0149625 | |
| Error | Classic | 0.00148657 | 0.0677236 | 0.123145 | 0.161583 | 0.182489 | 0.189093 |
| Invariant | 0.00462526 | 0.0046253 | 0.00462535 | 0.0046254 | 0.00462544 | 0.0046255 |
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Chhay, M.; Hamdouni, A. Lie Symmetry Preservation by Finite Difference Schemes for the Burgers Equation. Symmetry 2010, 2, 868-883. https://doi.org/10.3390/sym2020868
Chhay M, Hamdouni A. Lie Symmetry Preservation by Finite Difference Schemes for the Burgers Equation. Symmetry. 2010; 2(2):868-883. https://doi.org/10.3390/sym2020868
Chicago/Turabian StyleChhay, Marx, and Aziz Hamdouni. 2010. "Lie Symmetry Preservation by Finite Difference Schemes for the Burgers Equation" Symmetry 2, no. 2: 868-883. https://doi.org/10.3390/sym2020868
APA StyleChhay, M., & Hamdouni, A. (2010). Lie Symmetry Preservation by Finite Difference Schemes for the Burgers Equation. Symmetry, 2(2), 868-883. https://doi.org/10.3390/sym2020868




