The Role of Stochastic Models in Interpreting the Origins of Biological Chirality
Abstract
:1. Introduction
2. Stochastic Experimental Observations Relevant for Chirality and Autocatalysis
3. Statistical Tests without Chemical Models
4. Model-Based Stochastic Kinetic Approaches
- Traditional demonstration of autocatalysis by experiments using the initial addition of enantiomer-enriched products. Autocatalysis is a possible reason for inherent stochastic nature in macroscopic experiments, but autocatalysis can be tested under circumstances where no stochastic behavior is expected.
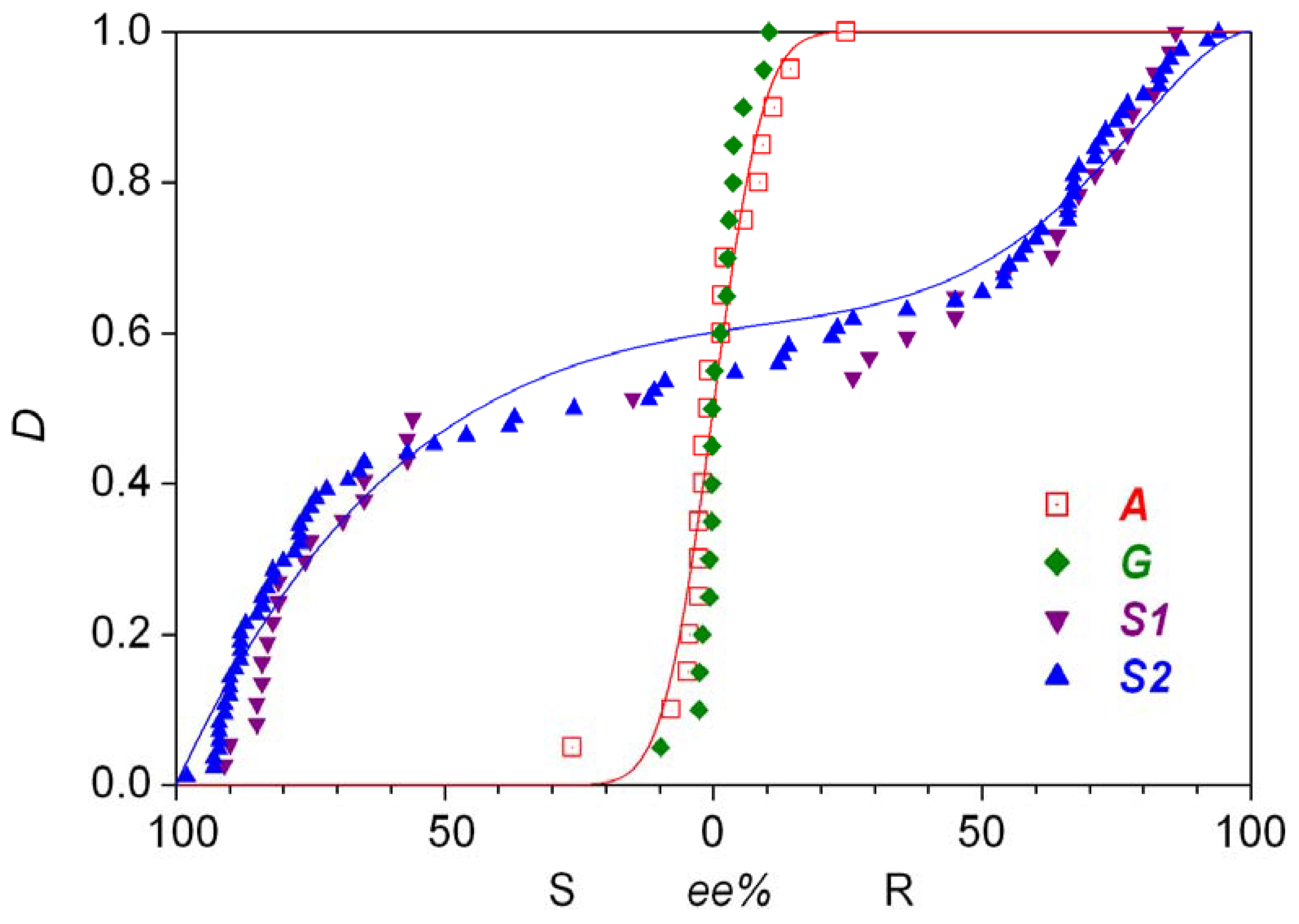
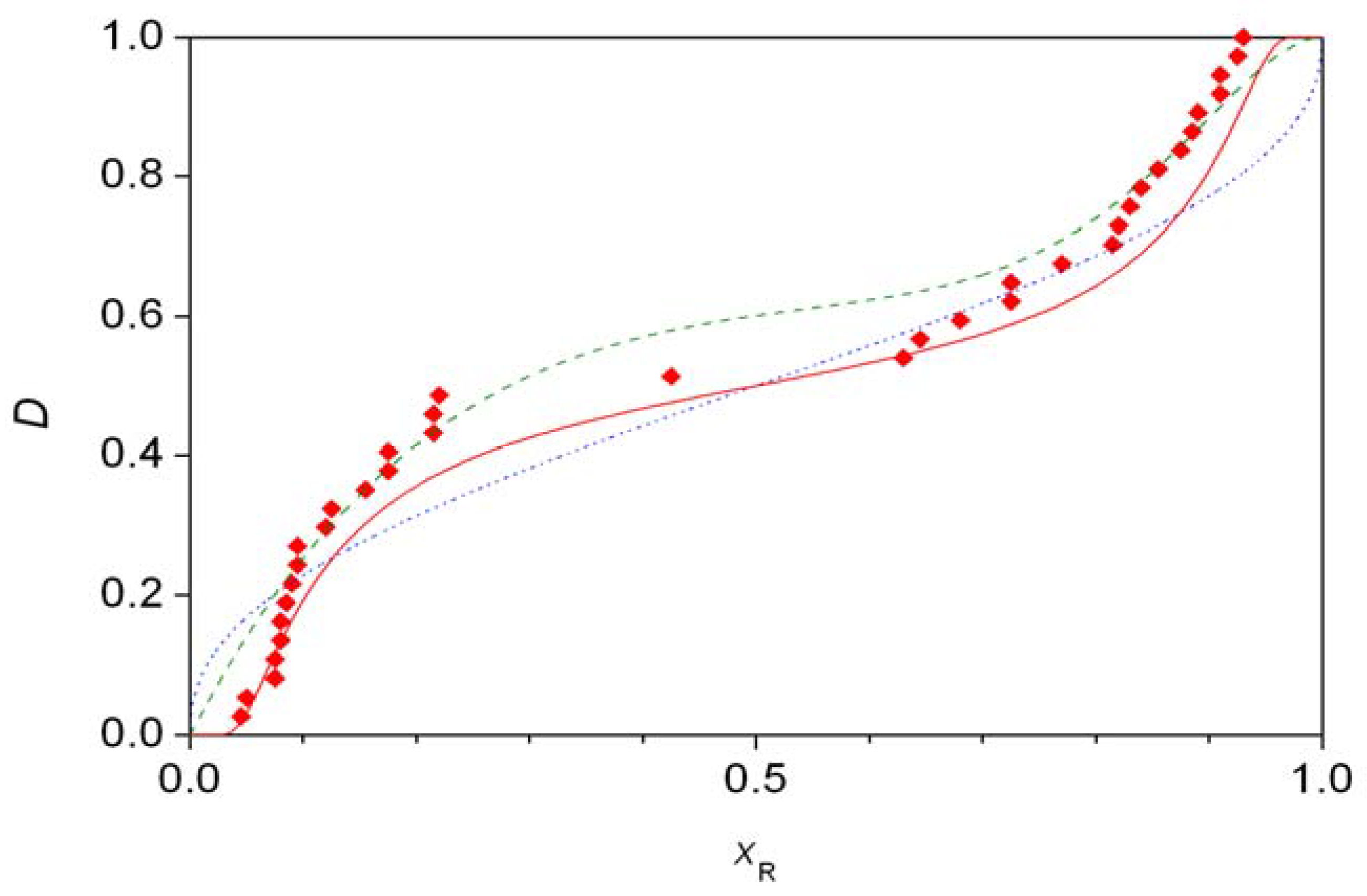
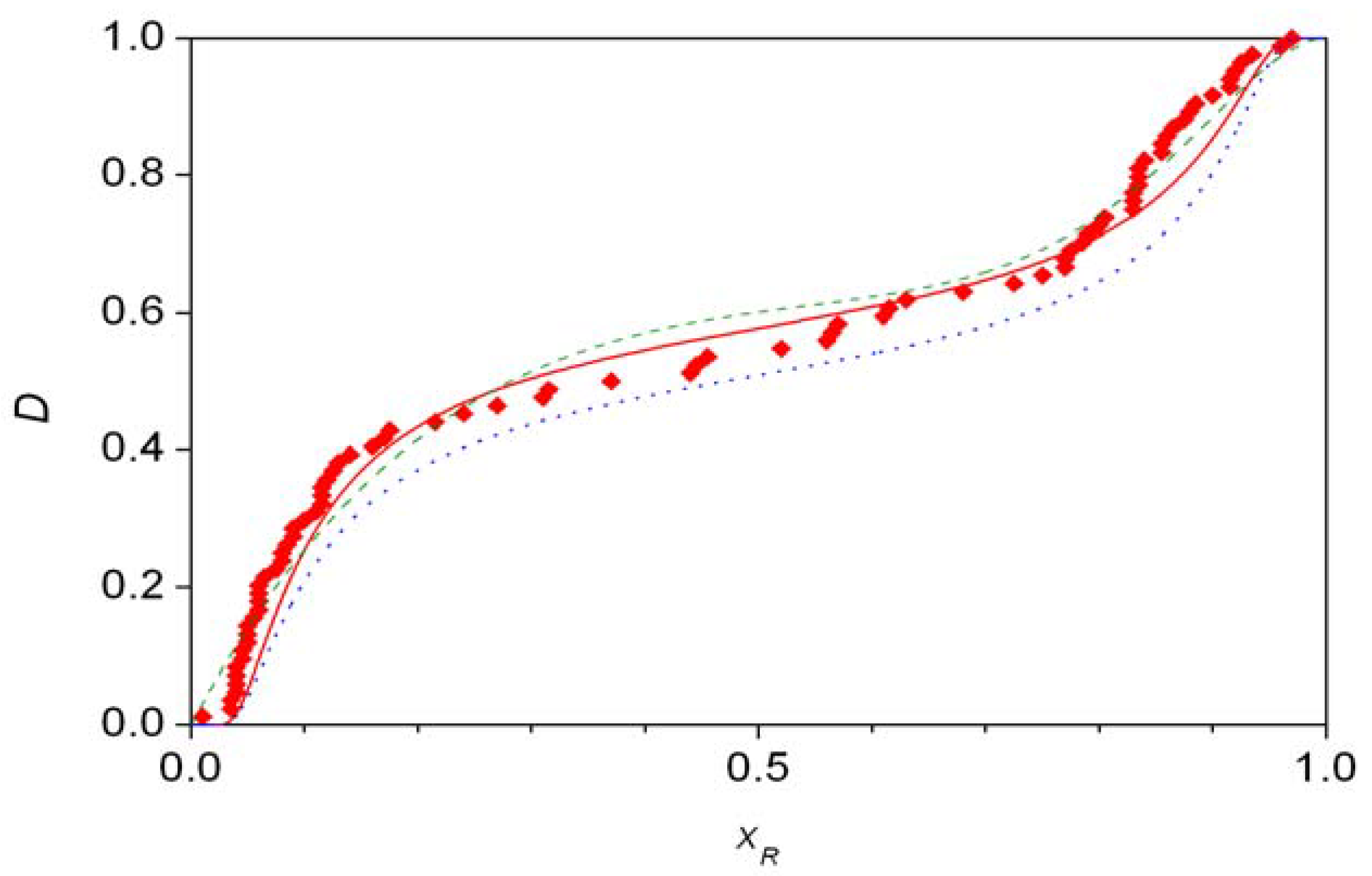
- Analysis of the stochastic distribution of enantiomers through a high number (preferably > 50) of repetitive experiments. In most cases, symmetric distributions are expected and a significantly asymmetric experimental distribution may point to an uncontrolled (most often also unidentified) but significant external influence.
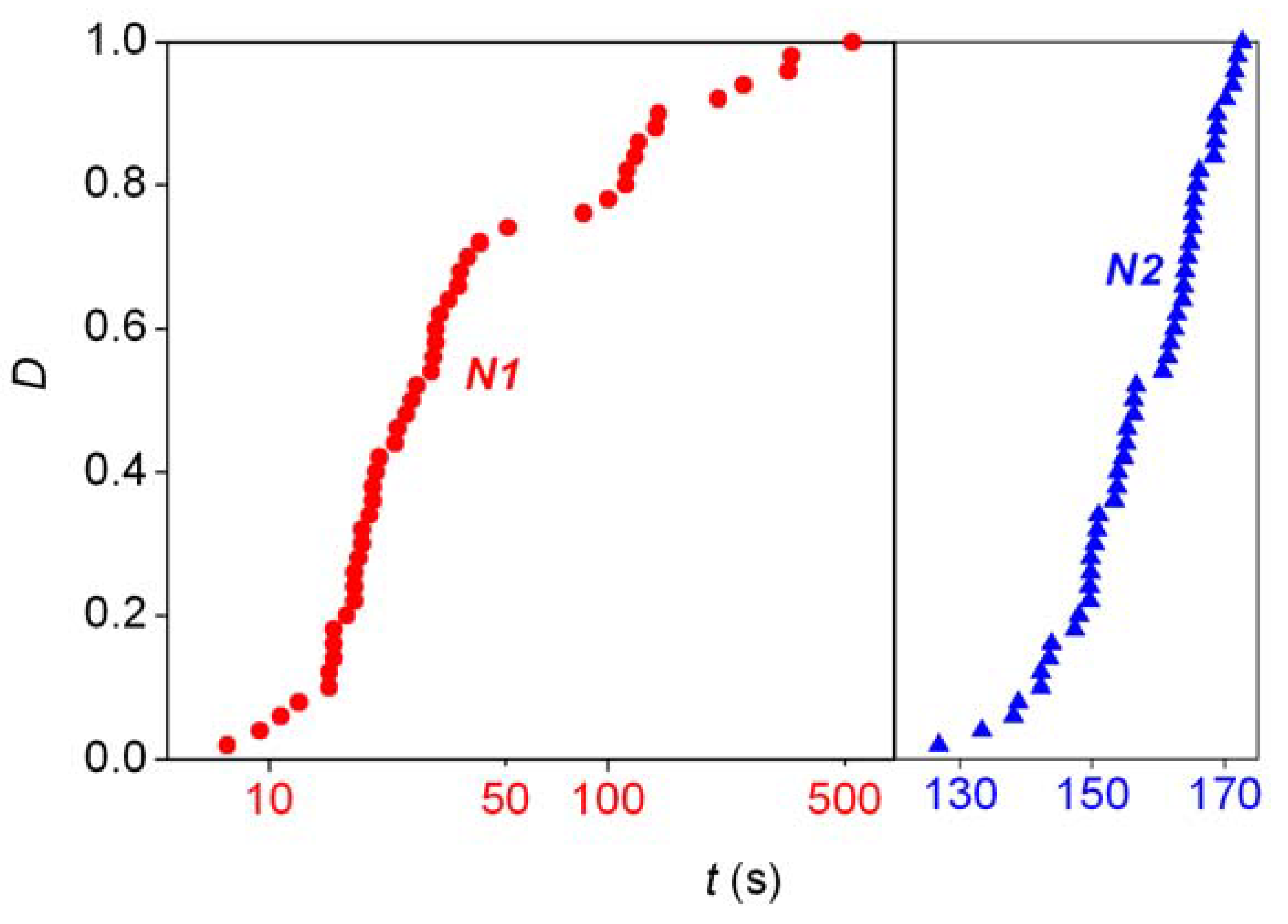
- Detection of random fluctuations in reaction time. If a random enantiomeric distribution is indeed caused by inherent stochastic nature, the time-dependent kinetics should also show random variations.
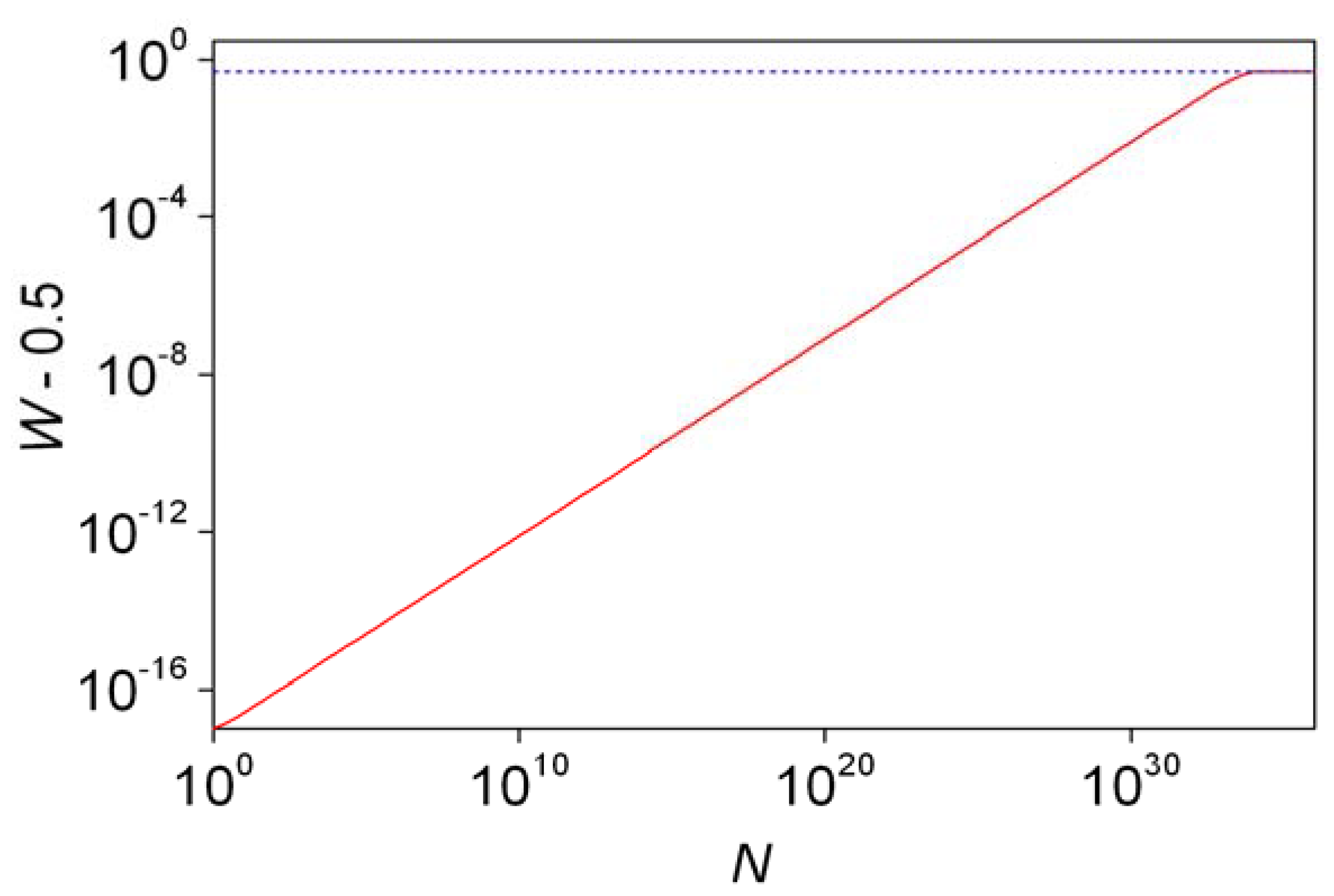
- The final distribution of enantiomeric excess and reaction times should be dependent on the overall volume even if the very same initial concentrations are used. This is a theoretically well known phenomenon that is usually expressed by saying that stochastic kinetics is equivalent to deterministic kinetics at the limit of infinite volume [48].
5. The Continuous Time Discrete State Approach
5.1. General Characterization
5.2. Simple Autocatalytic Schemes
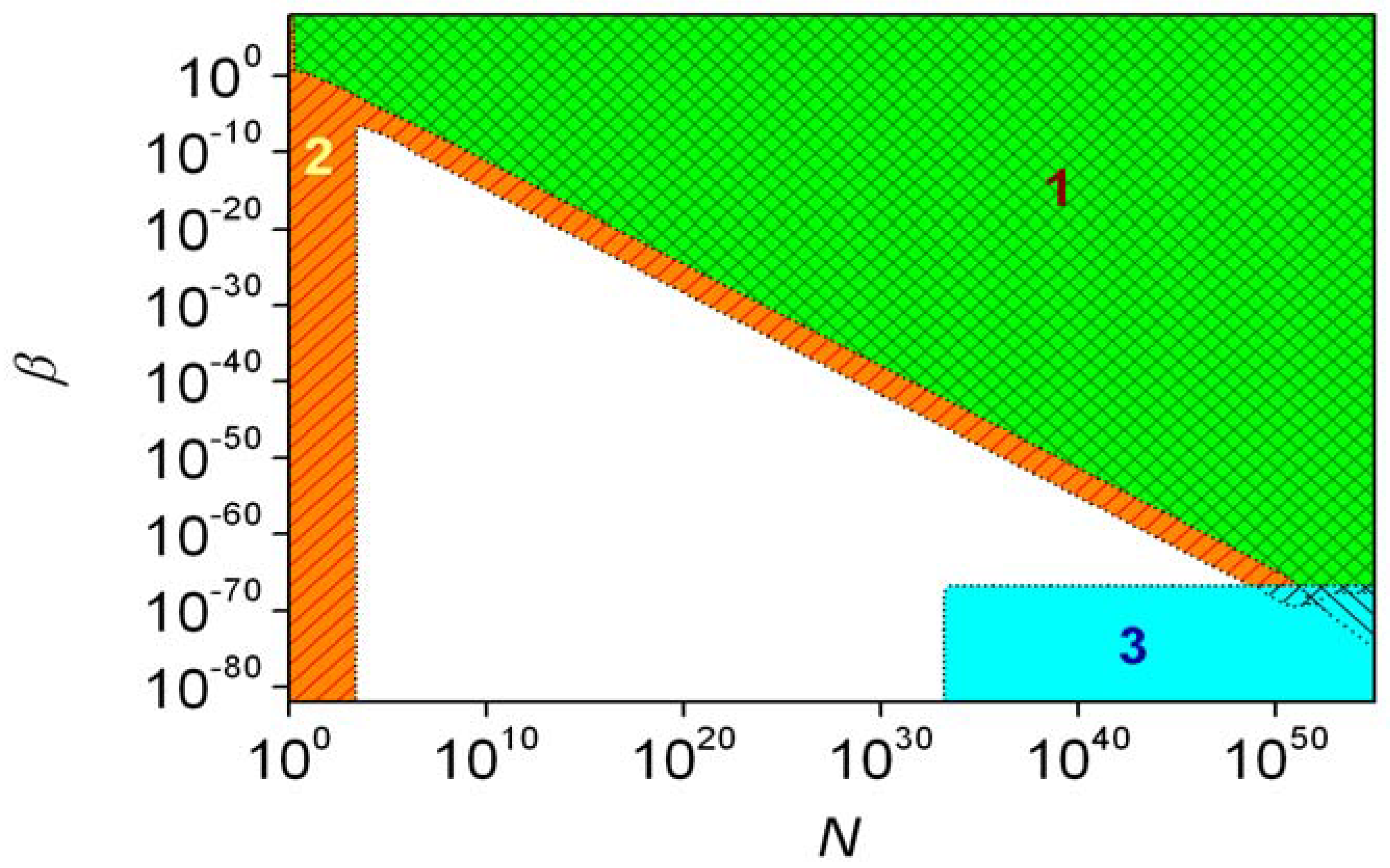
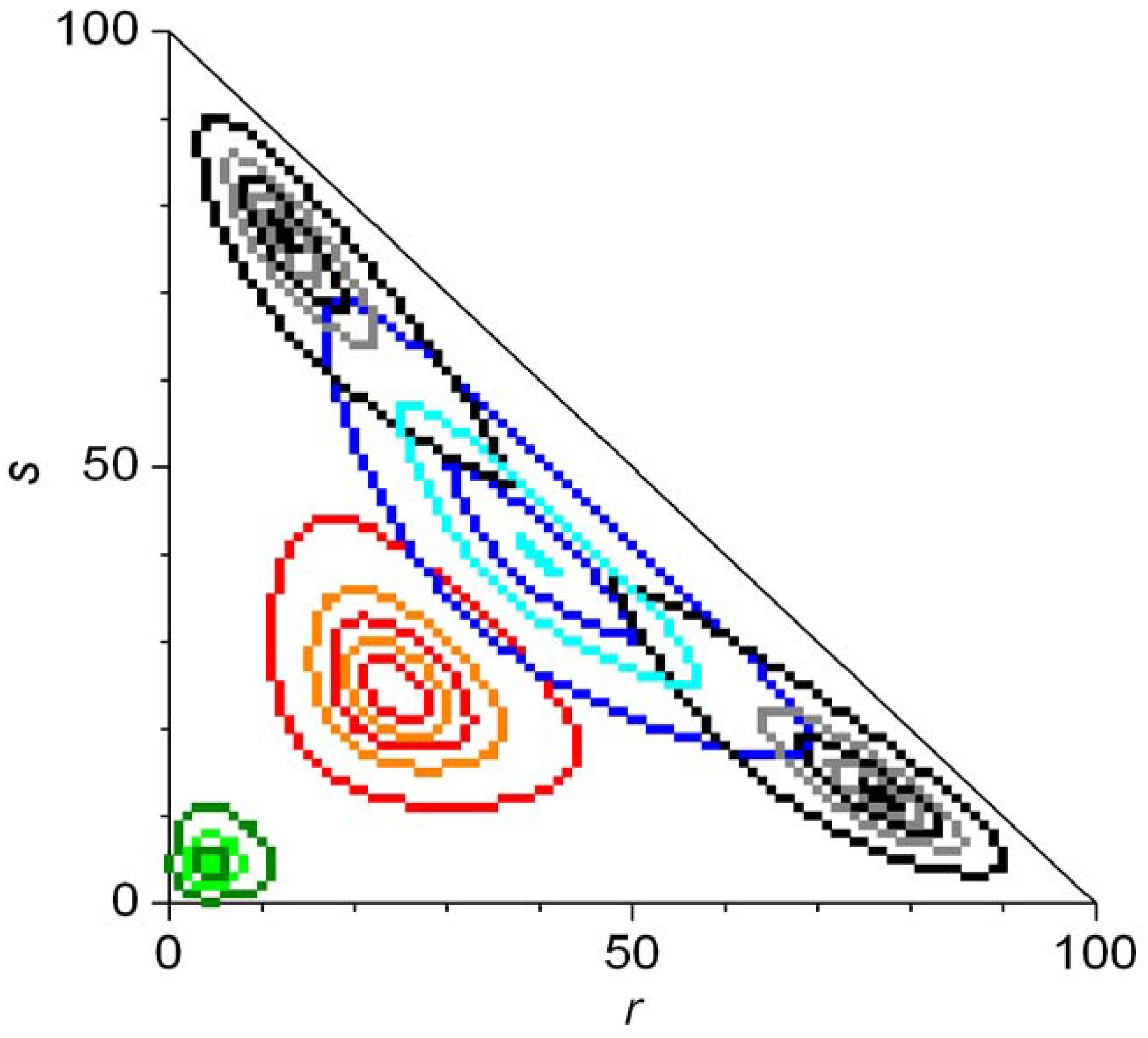
5.3. Schemes with Recycling
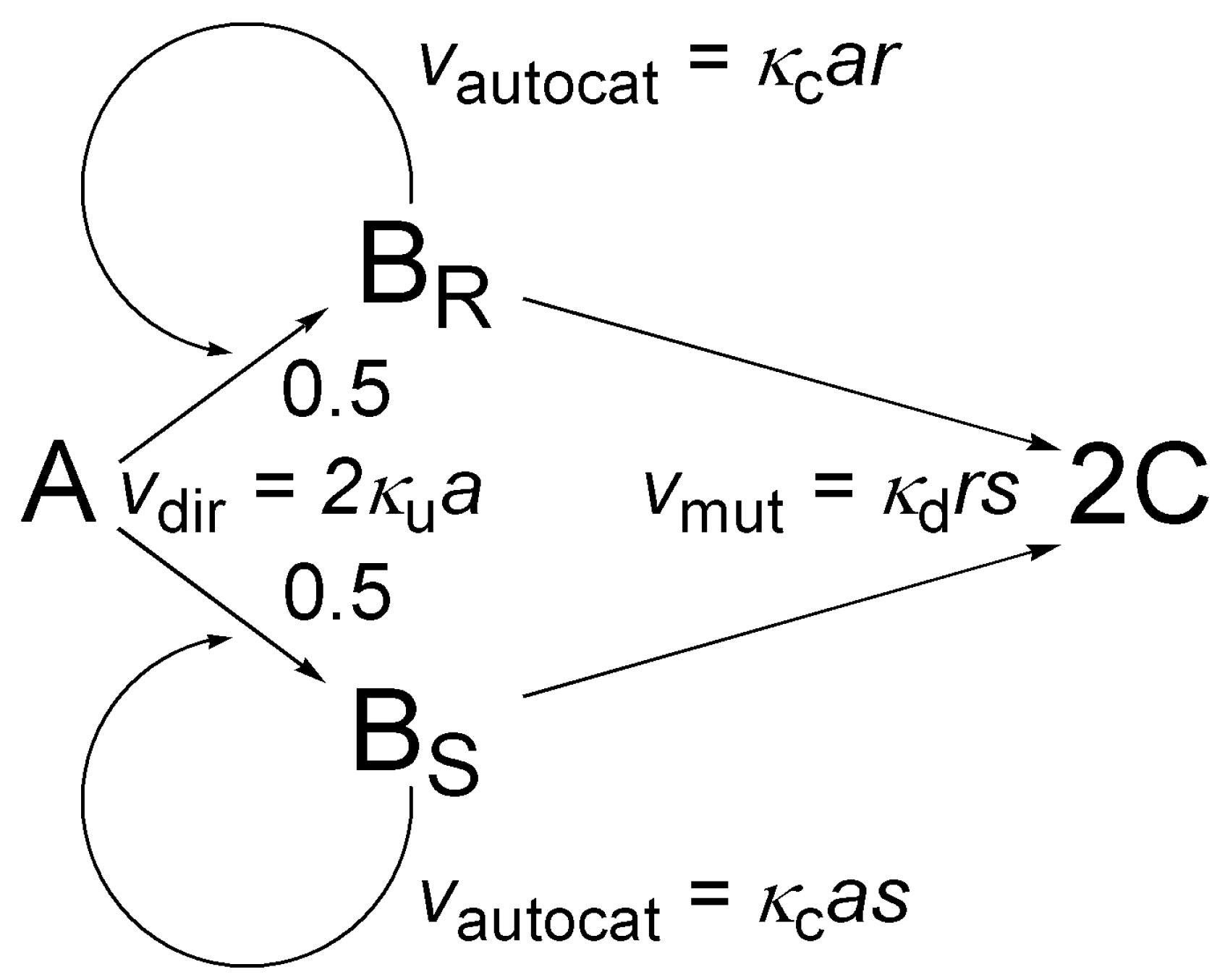
5.4. The Frank Model
6. Conclusions and Outlook
References and Notes
- Kennedy, D.; Norman, C. What is the origin of homochirality in nature? Science 2005, 309, 86–86. [Google Scholar]
- Progress in Biological Chirality; Pályi, G.; Zucchi, C.; Caglioti, L. (Eds.) Elsevier: Oxford, UK, 2004. [Google Scholar]
- Mislow, K. Absolute Asymmetric Synthesis: A Commentary. Collect. Czech. Chem. Commun. 2003, 68, 849–864. [Google Scholar] [CrossRef]
- Available on line: http://mathworld.wolfram.com/ (accessed on March 26, 2010).
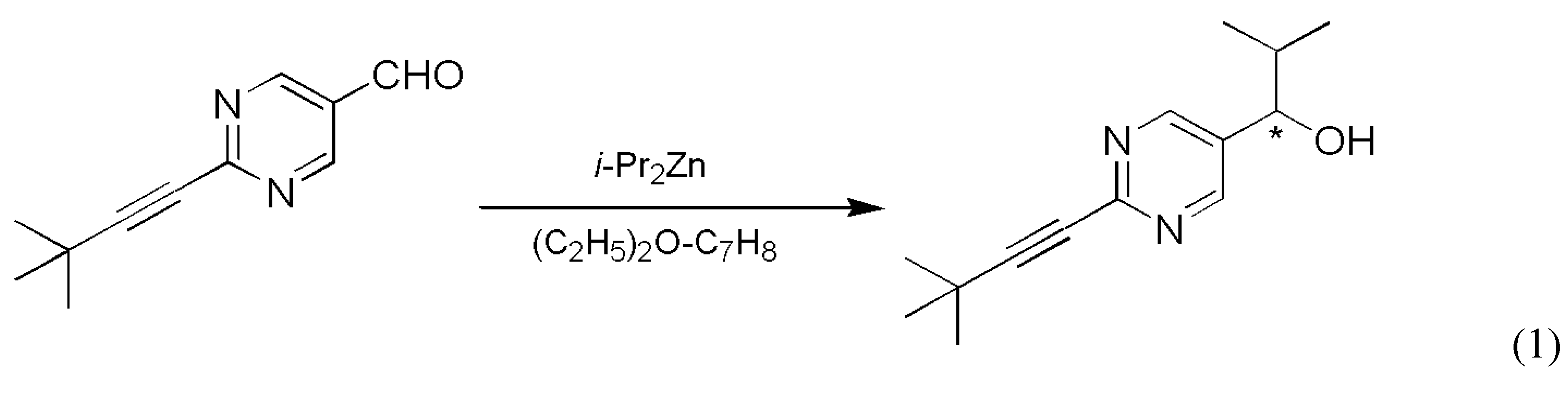
- Soai, K.; Shibata, T.; Morioka, H.; Choji, K. Asymmetric autocatalysis and amplification of enantiomeric excess of a chiral molecule. Nature 1995, 378, 767–768. [Google Scholar] [CrossRef]
- Soai, K.; Shibata, T.; Kowata, Y. Production of Optically Active Pyrimidylalkyl Alcohol by Spontaneous Asymmetric Synthesis (in Japanese). Japan Kokai Tokkyo Koho JP 19979-268179. Application date: 1 February and 18 April, 1996.
- Soai, K.; Sato, I.; Shibata, T.; Komiya, S.; Hayashi, M.; Matsueda, Y.; Imamura, H.; Hayase, T.; Morioka, H.; Tabira, H.; Yamamoto, J.; Kowata, Y. Asymmetric synthesis of pyrimidyl alkanol without adding chiral substances by the addition of diisopropylzinc to pyrimidine-5-carbaldehyde in conjunction with asymmetric autocatalysis. Tetrahedron Asymmetry 2003, 14, 185–188. [Google Scholar] [CrossRef]
- Kawasaki, T.; Suzuki, K.; Shimizu, M.; Ishikawa, K.; Soai, K. Spontaneous absolute asymmetric synthesis in the presence of achiral silica gel in conjunction with asymmetric autocatalysis. Chirality 2006, 18, 479–482. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, T.; Shimizu, M.; Nashiyama, D.; Ito, M.; Ozawa, H.; Soai, K. Asymmetric autocatalysis induced by meteoritic amino acids with hydrogen isotope chirality. Chem. Commun. 2009, 4396–4398. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, T.; Matsamura, Y.; Tsutsumi, T.; Suzuki, K.; Ito, M.; Soai, K. Asymmetric autocatalysis triggered by carbon isotope (13C/12C) chirality. Science 2009, 324, 492–495. [Google Scholar] [CrossRef] [PubMed]
- Soai, K.; Kawasaki, T. Asymmetric autocatalysis: Automultiplication of chiral molecules. Chimica Oggi 2009, 27, 3–7. [Google Scholar]
- Gridnev, I.D.; Serafimov, J.M.; Quiney, H.; Brown, J.M. Reflections on spontaneous asymmetric synthesis by amplifying autocatalysis. Org. Biomol. Chem. 2003, 1, 3811–3819. [Google Scholar] [CrossRef]
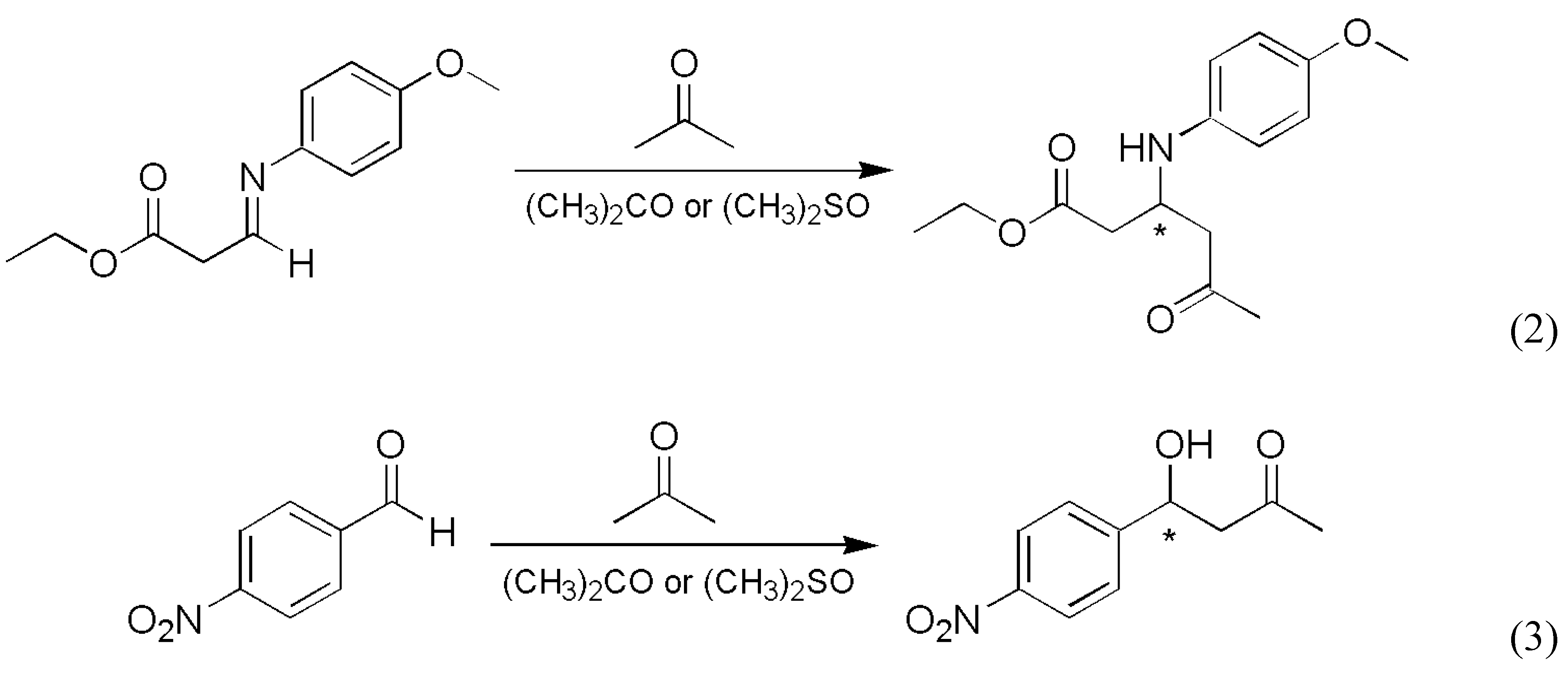
- Singleton, D.A.; Vo, L.K. Enantioselective synthesis without discrete optically active additives. J. Am. Chem. Soc. 2002, 124, 10010–10011. [Google Scholar] [CrossRef]
- Singleton, D.A.; Vo, L.K. A few molezcules can control the enantiomeric outcome. Evidence supporting absolute asymmetric synthesis using the soai asymmetric autocatalysis. Org. Lett. 2003, 5, 4337–4339. [Google Scholar] [CrossRef] [PubMed]
- Mauksch, M.; Tsogoeva, S.B.; Wei, S.; Martynova, I.M. Demonstration of spontaneous chiral symmetry breaking in asymmetric Mannich and Aldol reactions. Chirality 2007, 19, 816–825. [Google Scholar] [CrossRef] [PubMed]
- Asakura, K.; Ikumo, A.; Kurihara, K.; Osanai, S.; Kondepudi, D.K. Random chiral asymmetry generation by chiral autocatalysis in a far-from-equilibrium reaction system. J. Phys. Chem. A 2000, 104, 2689–2694. [Google Scholar] [CrossRef]
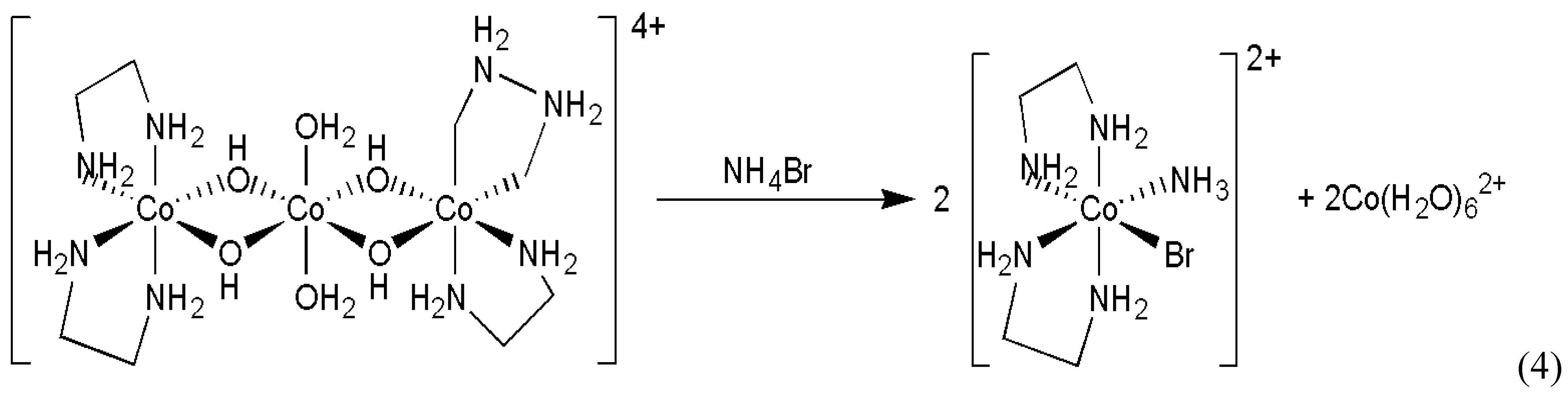
- Asakura, K.; Osanai, S.; Kondepudi, D.K. Mechanism of chiral asymmetry generation by chiral autocatalysis in the preparation of chiral octahedral cobalt complex. Chirality 1998, 10, 343–348. [Google Scholar] [CrossRef]
- Asakura, K.; Inoue, K.; Osanai, S.; Kondepudi, D.K. Formation of the intermediate, aquohydroxobis(ethylenediamine)cobalt(II) complex, in the preparation of cis-bromoamminebis-(ethylenediamine)cobalt(III) bromide by the reaction of bis[bis(ethylenediamine)cobalt(III)-μ-dihydroxo]diaquocobalt(II) sulfate with ammonium bromide in water. J. Coord. Chem. 1998, 46, 159–164. [Google Scholar]
- Asakura, K.; Osanai, S.; Kondepudi, D.K. Conditions for chiral asymmetry generation in the preparation of the chiral octahedral cobalt complex. Chirality 2001, 13, 435–440. [Google Scholar] [CrossRef]
- Nagypál, I.; Epstein, I.R. Fluctuations and stirring rate effects in the chlorite-thiosulfate reaction. J. Phys. Chem. 1986, 90, 6285–6292. [Google Scholar] [CrossRef]
- Nagypál, I.; Epstein, I.R. Stochastic behavior and stirring rate effects in the chlorite-iodide Reaction. J. Chem. Phys. 1988, 89, 6925–6928. [Google Scholar] [CrossRef]
- Lente, G.; Fábián, I.; Bazsa, G. What is and what isn’t a clock reaction? New J. Chem. 2007, 31, 1707. [Google Scholar] [CrossRef]
- Pasteur, L. Research on the relationship between crystalline form, chemical composition, and the sense of rotatory polarization (in French). Ann. Chem. Phys. (3rd Ser.) 1848, 24, 442–459. [Google Scholar]
- Gal, J. The Discovery of Biological Enantioselectivity: Louis Pasteur and the Fermentation of Tartaric Acid, 1857-A Review and Analysis 150 Year Later. Chirality 2008, 20, 5–19. [Google Scholar] [CrossRef] [PubMed]
- Kondepudi, D.K.; Kaufman, R.J.; Singh, N. Chiral symmetry breaking in sodium chlorate crystallization. Science 1990, 250, 975–976. [Google Scholar] [CrossRef] [PubMed]
- Kondepudi, D.K.; Culha, M. Chiral interaction and stochastic kinetics in stirred crystallization of amino acids. Chirality 1998, 10, 238–245. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Asakura, K. Chiral autocatalysis, spontaneous symmetry breaking, and stochastic behavior. Acc. Chem. Res. 2001, 34, 946–954. [Google Scholar] [CrossRef] [PubMed]
- Matsuura, T.; Koshima, H. Introduction to chiral crystallization of achiral organic compounds. Spontaneous generation of chirality. J. Photochem. Photobiol. C Photochem. Rev. 2005, 6, 7–24. [Google Scholar] [CrossRef]
- Viedma, C. Chiral Symmetry Breaking During Crystallization: Complete Chiral Purity Induced by Nonlinear Autocatalysis and Recycling. Phys. Rev. Lett. 2005, 94, 065504:1–065504:4. [Google Scholar] [CrossRef] [PubMed]
- Gridnev, I.D. Chiral symmetry breaking in chiral crystallization and soai autocatalytic reaction. Chem. Lett. 2006, 35, 148–153. [Google Scholar] [CrossRef]
- Pérez-García, L.; David, B.; Amabilino, D.B. Spontaneous Resolution, Whence and Whither: From Enantiomorphic Solids to Chiral Liquid Crystals, Monolayers and Macro- and Supra-Molecular Polymers and Assemblies. Chem. Soc. Rev. 2007, 36, 941–967. [Google Scholar] [CrossRef]
- McBride, J.M.; Tully, J.C. Did life grind to a start? Nature 2008, 452, 161–162. [Google Scholar] [CrossRef]
- Blackmond, D.G.; Klussmann, M. Spoilt for Choice: Assessing Phase Behavior Models for the Evolution of Homochirality. Chem. Commun. 2007, 3990–3996. [Google Scholar] [CrossRef]
- Tamura, R.; Iwama, S.; Takahashi, H. Chiral symmetry breaking phenomenon caused by a phase transition. Symmetry 2010, 2, 112–135. [Google Scholar] [CrossRef]
- Lente, G. Stochastic Kinetic Models of Chiral Autocatalysis: A General Tool for the Quantitative Interpretation of Total Asymmetric Synthesis. J. Phys. Chem. A 2005, 109, 11058–11063. [Google Scholar] [CrossRef] [PubMed]
- Barabás, B.; Caglioti, L.; Micskei, K.; Pályi, G. Data-based stochastic approach to absolute asymmetric synthesis by autocatalysis. Bull. Chem. Soc. Jpn. 2009, 82, 1372–1376. [Google Scholar] [CrossRef]
- Lente, G. Homogeneous Chiral Autocatalysis: A Simple, Purely Stochastic Kinetic Model. J. Phys. Chem. A 2004, 108, 9475–9478. [Google Scholar] [CrossRef]
- Lente, G. The effect of parity violation on kinetic models of enantioselective autocatalysis. Phys. Chem. Chem. Phys. 2007, 9, 6134–6141. [Google Scholar] [CrossRef] [PubMed]
- Barabás, B.; Caglioti, L.; Zucchi, C.; Maioli, M.; Gál, E.; Micskei, K.; Pályi, G. Violation of distribution symmetry in statistical evaluation of absolute enantioselective synthesis. J. Phys. Chem. B 2007, 111, 11506–11510. [Google Scholar] [CrossRef] [PubMed]
- Caglioti, L.; Barabás, B.; Faglioni, F.; Florini, N.; Lazzeretti, P.; Maioli, M.; Micskei, K.; Rábai, G.; Taddei, F.; Zucchi, C.; Pályi, G. On the track of absolute enantioselective catalysis. Chimica Oggi 2008, 26, 30–32. [Google Scholar]
- Barabás, B.; Caglioti, L.; Faglioni, F.; Florini, N.; Lazzaretti, P.; Maioli, M.; Micskei, K.; Rabai, G.; Taddei, F.; Zucchi, C.; Pályi, G. On the traces of absolute enantioselective synthesis. AIP Conf. Proc. 2008, 963B, 1150–1152. [Google Scholar]
- Delbrück, M. Statistical fluctuation in autocatalytic reactions. J. Chem. Phys. 1940, 8, 120. [Google Scholar] [CrossRef]
- Érdi, P.; Tóth, J. Stochastic reaction kinetics = "nonequilibrium thermodynamics" of the state space? React. Kinet. Catal. Lett. 1976, 4, 81–85. [Google Scholar] [CrossRef]
- Érdi, P.; Tóth, J. Mathematical Models of Chemical Reactions; Manchester University Press: Manchester, UK, 1989; pp. 91–161. [Google Scholar]
- de Marcillac, P.; Coron, N.; Dambier, G.; Leblanc, J.; Moalic, J.P. Experimental detection of α-particles from the radioactive decay of natural bismuth. Nature 2003, 422, 876–878. [Google Scholar] [CrossRef] [PubMed]
- Yukalov, V.I. Systems with symmetry breaking and restoration. Symmetry 2010, 2, 40–68. [Google Scholar] [CrossRef]
- Singer, K. Application of the theory of stochastic processes to the study of irreproducible chemical reactions and nucleation processes. J. Roy. Stat. Soc. Ser. B. 1953, 15, 92–106. [Google Scholar] [CrossRef]
- Kurtz, T.G. The relationship between stochastic and deterministic models for chemical reactions. J. Chem. Phys. 1972, 57, 2976–2978. [Google Scholar] [CrossRef]
- Mills, W. Some aspects of stereochemistry. Chem. Ind. (London) 1932, 51, 750–759. [Google Scholar] [CrossRef]
- Siegert, A.J.F. On the approach to statistical equilibrium. Phys. Rev. 1949, 76, 1708–1714. [Google Scholar] [CrossRef]
- Caglioti, L.; Zucchi, C.; Pályi, G. Single-molecule chirality. Chimica Oggi 2005, 23, 38–43. [Google Scholar]
- Weissbuch, I.; Leiserowitz, L.; Lahav, M. Stochastic “Mirror Symmetry Breaking” via Self-Assembly, Reactivity and Amplification of Chirality: Relevance to Abiotic Conditions. Top. Curr. Chem. 2005, 259, 123–165. [Google Scholar]
- Pályi, G.; Micskei, K.; Zékány, L.; Zucchi, C.; Caglioti, L. Racemates and the soai reaction (in Hungarian). Magyar Kém. Lapja 2005, 60, 17–24. [Google Scholar]
- Lente, G. Stochastic analysis of the parity-violating energy differences between enantiomers and its implications for the origin of biological chirality. J. Phys. Chem. A 2006, 110, 12711–12713. [Google Scholar] [CrossRef]
- Caglioti, L.; Hajdu, C.; Holczknecht, O.; Zékány, L.; Zucchi, C.; Micskei, K.; Pályi, G. The concept of racemates and the soai-reaction. Viva Origino 2006, 34, 62–80. [Google Scholar]
- Caglioti, L.; Pályi, G. Chiral chemistry of single molecules. Chimica Oggi 2008, 26, 41–42. [Google Scholar]
- Barabás, B.; Caglioti, L.; Micskei, K.; Zucchi, C.; Pályi, G. Isotope Chirality and Asymmetric Autocatalysis: A Possible Entry to Biological Chirality. Orig. Life Evol. Biosph. 2008, 38, 317–327. [Google Scholar]
- Fuß, W. Does life originate from a single molecule? Chirality 2009, 21, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Fuß, W. Biological homochirality as result from a single event. Coll. Surf. B: Biointerf. 2009, 74, 498–503. [Google Scholar] [CrossRef] [PubMed]
- Quack, M. How important is parity violation for molecular and biomolecular chirality? Angew. Chem. Int. Ed. 2002, 41, 4619–4630. [Google Scholar] [CrossRef] [PubMed]
- Faglioni, F.; Lazzeretti, P.; Pályi, G. Parity violation energy of 5-pyrimidyl alkanol, a chiral autocatalytic molecule. Chem. Phys. Lett. 2007, 435, 346–349. [Google Scholar] [CrossRef]
- Todorović, D.; Gutman, I.; Radulović, M. A stochastic chiral amplification model. Chem. Phys. Lett. 2003, 372, 464–468. [Google Scholar] [CrossRef]
- Frank, F.C. On spontaneous asymmetric synthesis. Biochim. Biophys. Acta 1953, 11, 459–463. [Google Scholar] [CrossRef]
- Cruz, J.M.; Parmananda, P.; Buhse, T. Noise-induced enantioselection in chiral autocatalysis. J. Phys. Chem. A 2008, 112, 1673–1676. [Google Scholar] [CrossRef] [PubMed]
- Rivera Islas, J.; Lavabre, D.; Jean-Michel Grevy, J.M.; Hernández Lamoneda, R.; Rojas Cabrera, H.; Micheau, J.C.; Buhse, T. Mirror-Symmetry Breaking in the Soai Reaction: A Kinetic Understanding. Proc. Natl. Acad. Sci. USA 2005, 101, 5732–5736. [Google Scholar]
- Micskei, K.; Rábai, G.; Gál, E.; Caglioti, L.; Pályi, G. Oscillatory symmetry breaking in the soai reaction. J. Phys. Chem. B 2008, 112, 9196–9200. [Google Scholar] [CrossRef] [PubMed]
- Hochberg, D.; Zorzano, M.P. Reaction-noise induced homochirality. Chem Phys. Lett. 2006, 431, 185–189. [Google Scholar] [CrossRef]
- Hochberg, D.; Zorzano, M.P. Mirror symmetry breaking as a problem in dynamic critical phenomena. Phys. Rev. E 2007, 76, 021109:1–021109:8. [Google Scholar] [CrossRef] [PubMed]
- Hochberg, D. Mirror Symmetry Breaking and Restoration: The Role of Noise and Chiral Bias. Phys. Rev. Lett. 2009, 102, 248101:1–248101:4. [Google Scholar] [CrossRef] [PubMed]
- Hochberg, D. Effective potential and chiral symmetry breaking. Phys. Rev E 2010, 81, 016106:1–016106:13. [Google Scholar] [CrossRef] [PubMed]
- Gleiser, M.; Walker, S.I. An Extended Model for the Evolution of Prebiotic Homochirality: A Bottom-Up Approach to the Origin of Life. Orig. Life Evol. Biosph. 2008, 38, 293–315. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Deterministic limit of stochastic chemical kinetics. J. Phys. Chem. B 2009, 113, 1640–1644. [Google Scholar] [CrossRef] [PubMed]
- Bartholomay, A.F. A stochastic approach to statistical kinetics with application to enzyme kinetics. Biochem. 1962, 1, 223–230. [Google Scholar] [CrossRef]
- Arányi, P.; Tóth, J. A full stochastic description of the Michaelis-Menten reaction for small systems. Acta Biochim. Biophys. Acad. Sci. Hung. 1977, 12, 375–388. [Google Scholar]
- Kou, S.C.; Cherayil, B.J.; Min, W.; English, B.P.; Xie, X.S. Single-molecule michaelis-menten equations. J. Phys. Chem. B 2005, 109, 19068–19081. [Google Scholar] [CrossRef] [PubMed]
- Velonia, K.; Flomenbom, O.; Loos, D.; Masuo, S.; Cotlet, M.; Engelborghs, Y.; Hofkens, J.; Rowan, A.E.; Klafter, J.; Nolte, R.J.M.; de Schryver, F.C. Single-enzyme kinetics of CALB-catalyzed hydrolysis. Angew. Chem. Int. Ed. 2005, 44, 560–564. [Google Scholar] [CrossRef] [PubMed]
- Choi, P.J.; Cai, L.; Frieda, K.; Xie, X.S. A stochastic single-molecule event triggers phenotype switching of a bacterial cell. Science 2008, 322, 442–446. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.; Liu, L. Stochastic Fluctuations and Chiral Symmetry Breaking: Exact Solution of Lente Model. J. Phys. Chem. A 2007, 111, 9570–9572. [Google Scholar] [CrossRef] [PubMed]
- Saito, Y.; Sugimori, T.; Hyuga, H. Stochastic approach to enantiomeric excess amplification and chiral symmetry breaking. J. Phys. Soc. Japan 2007, 76, 044802:1–044802:14. [Google Scholar] [CrossRef]
- Sugimori, T.; Hyuga, H.; Saito, Y. Fluctuation induced homochirality. J. Phys. Soc. Japan 2008, 77, 064606:1–064606:6. [Google Scholar] [CrossRef]
- Blackmond, D.G.; Matar, O.K. Re-examination of reversibility in reaction models for the spontaneous emergence of homochirality. J. Phys. Chem. B 2008, 112, 5098–5104. [Google Scholar] [CrossRef]
- Lente, G. Theromdynamic unfeasibility of recycling in chiral autocatalytic kinetic models. React. Kinet. Catal. Lett. 2008, 95, 13–19. [Google Scholar] [CrossRef]
- Blackmond, D.G. “If Pigs Could Fly” Chemistry: A Tutorial on the Principle of Microscopic Reversibility. Angew. Chem. Int. Ed. 2009, 48, 2648–2654. [Google Scholar] [CrossRef]
- Lente, G. Open system approaches in deterministic models of the emergence of homochirality. Chirality 2010, 22. [Google Scholar] [CrossRef]
- Lente, G.; Ditrói, T. Stochastic kinetic analysis of the frank model. Stochastic approach to flow-through reactors. J. Phys. Chem. A 2009, 113, 7237–7242. [Google Scholar] [CrossRef] [PubMed]
- Ishida, K. Stochastic Approach to nonequilibrium thermodynamics of first-order chemical reactions. II. Open systems. J. Phys. Chem. 1968, 72, 92–96. [Google Scholar] [CrossRef]
- Buhse, T. A tentative kinetic model for chiral amplification in autocatalytic alkylzinc additions. Tetrahedron Asymmetry 2003, 14, 1055–1061. [Google Scholar] [CrossRef]
- Lavabre, D.; Micheau, J.C.; Rivera Islas, J.; Buhse, T. Mirror-symmetry breaking in the Soai reaction: A kinetic understanding. J. Phys. Chem. A 2007, 111, 281–286. [Google Scholar] [CrossRef] [PubMed]
- Schiaffino, L.; Ercolani, G. Unraveling the Mechanism of the Soai Asymmetric Autocatalytic Reaction by First-Principles Calculations: Induction and Amplification of Chirality by Self-assembly of Hexanuclear Complexes. Angew. Chem. Int. Ed. 2008, 47, 6832–6835. [Google Scholar] [CrossRef] [PubMed]
- Crusats, J.; Veintemillas-Verdaguer, S.; Ribó, J.M. Homochirality as a consequence of thermodynamic equilibrium? Chem. Eur. J. 2006, 12, 7576–7581. [Google Scholar] [CrossRef] [PubMed]
- Klussmann, M.; Iwamura, H.; Mathew, S.P.; Wells, D.H., Jr.; Pandya, U.; Armstrong, A.; Blackmond, D.G. Thermodynamic control of asymmetric amplification in amino acid catalysis. Nature 2006, 441, 621–623. [Google Scholar] [CrossRef]



© 2010 by the author; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Lente, G. The Role of Stochastic Models in Interpreting the Origins of Biological Chirality. Symmetry 2010, 2, 767-798. https://doi.org/10.3390/sym2020767
Lente G. The Role of Stochastic Models in Interpreting the Origins of Biological Chirality. Symmetry. 2010; 2(2):767-798. https://doi.org/10.3390/sym2020767
Chicago/Turabian StyleLente, Gábor. 2010. "The Role of Stochastic Models in Interpreting the Origins of Biological Chirality" Symmetry 2, no. 2: 767-798. https://doi.org/10.3390/sym2020767
APA StyleLente, G. (2010). The Role of Stochastic Models in Interpreting the Origins of Biological Chirality. Symmetry, 2(2), 767-798. https://doi.org/10.3390/sym2020767



