Symmetry and Beauty in Plato

Abstract

Plato writes about Beauty in many of his dialogues, particularly in the Symposium, but he has no word equivalent to our "Symmetry", and this concept was not then formalised. Nevertheless, there are indications that some aspects of the concept were understood, if only intuitively. Plato has a very abstract concept of beauty, and when he uses "beauty" to characterise the so-called "Platonic Solids" in the Timaeus, he seems to be emphasising at least their regularity. It can be argued that the way in which he specifies the detailed construction of the solids is remarkably close to a modern description in terms of (point) symmetry. For Plato, something of our symmetry is included in what he means by beauty, and the long mathematical approach to symmetry starts with the Timaeus.

1. Introduction

“Euclid alone has looked on Beauty bare" wrote Edna St. Vincent Millay, twice in one stanza [1]. It is not clear what led her to this idea, and it would be rather difficult to check. It can hardly have been the beauty of Euclid’s Greek, which has a rigid formulaic structure, with the catchphrases lego hoti (I say that....) and hoper edei poiẽsai (QED) echoing through thirteen volumes and two and a quarter millenia. It may be that here as elsewhere Millay is being ironic. There is of course a grandeur to Euclid’s concept of summarising and systematising all known geometry, but there is not much evidence of this being driven by aesthetic considerations. Much of Euclid was derived from earlier work in Plato’s Academy [2], particularly that of Theaetetus and of Eudoxus. Indeed it is possible to see much of the structure of the Elements as a slow build- up to the final constructions of Book 13 in which the ’Platonic Solids" are built up in an extraordinary intellectual tour de force. Nevertheless if anyone has a claim to have first seen true mathematical beauty, it must be either Plato, who also writes particularly beautiful Greek, or his friend Theaetetus. It is almost certain that it is the work of Theaetetus on the regular solids which forms the base on which Plato builds the second half of his dialogue Timaeus, which is discussed below. There is no surviving written record from Theaetetus, though it is likely that books 10 and 13 of Euclid are largely his work [2]. By default the regular solids have been called Platonic; perhaps Theaetetic would be more accurate, but it does have some pronunciation problems.

A historical account such as the one I am attempting here would normally spend some time in setting the wider context of symmetry. However two excellent accounts of the development of symmetry from the earliest history, through the work of Galois, Abel and Lie and on to modern research, have appeared recently. These are "Why beauty is truth: a history of symmetry” by Ian Stewart [3], and "Finding Moonshine" by Marcus du Sautoy [4]. These works have very different approaches; either may be consulted for a more extended view than the one given here. In addition to discussing Plato and Theaetetus, du Sautoy’s book illustrates some very early examples of symmetric objects, some prehistoric, which may have constructed for what we would call ‘aesthetic’ reasons. There is also a very useful short summary in Artmann [5], where the relation to ideas of beauty is also discussed briefly [6]. The next two sections are to some extent expansions of Artmann’s comments.

2. Symmetry, and the use of the word "summetria" by Plato

The relation of symmetry and beauty is not an easy subject to address, and my title, simple though it appears to be, may have implied too much. There is an asymmetry hidden in it, since although Plato has a great deal to say about Beauty, most notably in his discourse Symposium, he has nothing direct to say about Symmetry as we understand this word nowadays. This is hardly surprising, since there was no word at that time which conveys this meaning. Hon and Goldstein have argued [7] that our modern use of the word ’symmetry’ was unknown until Legendre developed the concept in the 18th century. Some translations from classical Greek do indeed use this word, or the associated adjective symmetric, but this is unfortunate, and can be misleading. The Greek noun summetria, and the associated adjective summetros, both of which are used quite frequently by Plato in the Timaeus, (though rarely elsewhere) mean literally ’the same measure’ or ’of the same measure’. The principal uses of the noun are to convey the senses of ’commensurability’ or of ’proportion’ [8]. The adjective has a number of uses, including connections with pitch and rhythm in music, but the principal meaning is ‘commensurable’, having a common measure. A citation for summetros from the principal Classical Greek dictionary by Liddell, Scott and Jones [9] makes the point well:

“in Mathematics, having a common measure; freq. denied of the relation between the diagonal of a square and its side.”

In our terms, the incommensurability here is the irrationality of √2. A more sophisticated version is also cited with this comment, from Plato’s Theaetetus. This shows the main character as a young student who is already working on generalising this incommensurability problem, and classifying all integers according to whether or not they have an integer square root.

Despite the lack of a word, there are aspects of Greek geometry where symmetry is implicit. The facts that the diameter of a circle splits it into two equal halves, and that the basal angles of an isosceles triangle are equal, are assumed to be "obvious", but only because of the symmetry of these examples. Not long after Plato, Pappus of Alexandria produced a proof of the second of these, which used to be called the ‘Pons asinorum’ (Euclid’s Elements, Book 1, Proposition 5). Coxeter [10] points out that this proof from Pappus is equivalent to invoking the symmetry operations of reflection or rotation of the diagram. Thus, even though nobody was in a position to formalise the concept of symmetry, the mathematical importance of it was beginning to emerge in Plato’s time, and there is another example of this implied rotation or reflection operation in one of Plato’s earlier dialogues, the Meno, which is discussed below.

At one point in the Timaeus (87e) [11] Plato may even be referring directly to the reflection symmetry of the normal human body, by taking as an example someone who has "one leg longer than the other". (The translations here and elsewhere for the Timaeus are from Waterfield [12]). This, Plato says, would be ametros, without measure. One translation has “disproportionate”, another gives “dissymmetric” which seems more appropriate here. However it should be noted that the text is ambiguous, and uses an unusual word which could mean that both legs are too long, and hence out of proportion with the rest of the body (the first meaning is the one given in Reference [9]). Whichever is the true meaning, in the context of the following section it is important that Plato has been discussing proportion and beauty, and says that such a deformity, being out of proportion, would be ugly.

3. Beauty in Plato

Many of the dialogues refer to this concept, and only a brief sketch is appropriate here. Before describing the approach of the Symposium, it is worth quoting the Philebus, (51c-d) where, as usual, Plato writes as if Socrates is providing the ideas, though in reality it is probably Plato’s thinking that we get. ’Socrates’ says:

“I do not mean by beauty of form such beauty as that of animals or pictures, which many would suppose to be my meaning; but, says the argument, understand me to mean straight lines and circles, and the plane or solid figures which are formed out of them by turning-lathes and rulers and measures of angles; for these I affirm to be not only relatively beautiful, like other things, but they are eternally and absolutely beautiful, and they have peculiar pleasure, quite unlike the pleasures of scratching.”

Although Socrates is using real man-made objects, which are inevitably imperfect, as his examples, his principle of beauty here refers to the eternal perfect forms which underlie these objects, and the surrounding text from which this is taken confirms this. Notably, all his examples of true, absolute beauty here have high symmetry in the modern sense. The "plane figures" here are probably the regular polygons; it is clear from Euclid that the study of these was important in Greek geometry. The mention of turning on a lathe suggests that Plato/Socrates considers cylindrical symmetry to be particularly beautiful, and this correlates well with the use of spherical symmetry in the Timaeus, described below. According to legend, the entrance to Plato’s Academy was decorated with a slogan usually translated as "Let no-one ignorant of Geometry enter". Similarly, it was said that for Plato, "God is always doing geometry". Although these quotes are probably mythical, they illustrate something very important, that geometry was considered to be one of the highest of studies. Plato’s God, as we will see, constructs the entire universe on geometrical principles, but a geometry which gives highly symmetrical results, which would certainly satisfy the conditions of beauty laid down here by Socrates, since it generates the ’solid figures’ mentioned.

The dialogue Symposium is mainly concerned with Eros, Love. The translation used here is by Griffith [13]. Some real characters of Plato’s time are given speeches which illustrate various aspects, all with a strong sexual context, mostly homosexual, though the one from a doctor takes Eros as a principle underlying all of Nature. The final major speech is given to Socrates, who begins in his usual style, taking apart the arguments of the previous speaker; in particular he attacks the idea that Eros is beautiful. However, in sharp contrast to his usual practice, Socrates presents his arguments as something he learnt from someone else, and, remarkably for the time, from a woman, Diotima. Diotima begins by downgrading Eros, who, she argues, far from being beautiful, is ugly, but seeks beauty. Thereafter the ground shifts subtly from a description of homoerotic love into a discussion of beauty, and describes higher and higher levels of a generalised beauty.

Initially the student of beauty may start from the beauty of the body of a particular lover, but then he should move on to become a "lover of all physical beauty". Following this, he should learn to prefer mental beauty to physical beauty, and thence to "see the beauty of different types of knowledge", and to "gaze upon the limitless ocean of beauty". Even this is not the highest level, but if the student (Socrates) persists, he may

“come to the final end and goal of this education. Then suddenly he will see a beauty of a breathtaking nature, Socrates, the beauty which is the justification of all his efforts so far. It is eternal, neither coming to be nor passing away, neither increasing nor decreasing. Moreover it is not beautiful in part, and ugly in part, nor is it beautiful at one time, and not at another........It exists for all time, by itself and with itself, unique....”

This extraordinary rhapsody, not given in full here (see 210a-212a), makes it very clear that for Plato, Beauty is one of the highest ideals. It does have a connection to simple physical appearance, since " All other forms of beauty derive from it ", but goes far beyond that. It incorporates knowledge in all its forms, including, as we saw in the Philebus, mathematical objects, and comes very close to Plato’s highest ideal, the Form of the Good. Plato’s prose-poem overwhelms the poem of Millay with which this article began, and clearly she should have cited Plato rather than Euclid.

4. The Meno argument

In the dialogue Meno, Plato shows Socrates trying to demonstrate that memory is built-in, from a previous existence, the so-called ’theory of recollection’. Part of his argument is that a simple slave-boy, with little or no mathematical education, can be shown to have an innate understanding of the principles of the advanced science of geometry. With what seems to us a set of rather leading questions, he sets out to demonstrate that the boy has a knowledge of how to generate a square of double the area of a starting square. This is of course, closely related to the question of incommensurability mentioned above, though Socrates does not take the matter so far.

Beginning with the starting square, Socrates goes through a long exercise of getting the boy to count up various numbers of equal squares, ultimately demonstrating that the side length of the doubled square cannot be an integral multiple of that of the starting square. As this goes on the original diagram of one square becomes a matrix of equal squares. Then comes the punch line of the argument. We the readers are meant to understand that Socrates draws in a diagonal across one of these squares.

Socrates: "And does not this line, reaching from corner to corner, bisect each of these spaces?”

The unfortunate slave-boy who is being made to jump through hoops replies "yes" to this question. Apparently this answer is ’obvious’ and needs no proof, but it is only obvious because of the symmetry of the divided square, and Socrates is using the rotation or reflection symmetry of the construction for his demonstration. From here it is only necessary to do this four times in the matrix of squares which has been built up during the earlier part, and a doubled square appears, assembled from four halves, and rotated by 45º from the originals. We will encounter this 4-fold symmetric structure again in the following section. Plato makes no reference to beauty in this section of the Meno, but in the Timaeus, symmetry and beauty are brought together in a way which has already been hinted at in the citation above from the Philebus.

5. The Timaeus

This dialogue, written in his later years, is Plato’s presentation of a ’Theory of Everything’. (Much more detailed expositions than can be given here can be found in [12,14,15]). In the first part Plato shows a divine being, his ’Demiurge’ or ’Craftsman’, taking on a chaotic universe and bringing order into it. This is not a creatio ex nihilo, but a working with what is available. The Demiurge makes the universe according to an ideal pre-existing model, and builds it to be the best possible one; it is to be both beautiful and good. Plato wastes no time on defining what he means by these; probably he expects his readers to be familiar with both the Symposium and the Republic. Two principles are of particular significance for the Demiurge, that order "is in all ways better" than chaos (30a), and that similarity is "incomparably superior to dissimililarity" (33b). All the stuff available to the Demiurge is combined in ratios which are based on the mathematics of music, the harmonic series (35b-c). The combined material is then used to construct the macrocosmos, with a spherical earth at the centre of a spherical universe. His definition of spherical form (33b) has an implication of working on a lathe [16], paralleling the citation from the Philebus in Section 3 above, but he also gives a more abstract definition, “equidistant in all directions from its centre to its extremes.” The very interesting reason which Plato gives for the use of the sphere is that:

“there is no shape more perfect and none more similar to itself.”

(33b)

The rather odd phrase " none more similar to itself" has not attracted much comment in modern studies. Although Plato gives us no more information on this, it seems plausible that he is thinking of a cube, for instance, as being ’similar to itself’, but this is only true when it is rotated through specific angles about particular axes, e.g. 90º for the 4-fold axes, i.e it is regular. I will return to the concept of regularity below, but it is clear that Plato considers that the sphere is the most perfect shape because there is a multiplicity of ways in which it can be made similar to itself. Indeed " none more similar to itself" is remarkably similar to our description of spherical symmetry as possessing an infinite number of rotation axes. It is also interesting that he says here that the sphere “includes all shapes within itself”. Here “all shapes” is probably to be interpreted as meaning the five regular solids, and “includes” refers to the fact that they can all be inscribed within a sphere; there is a specific reference to this point for the tetrahedron later, at (55a).

The spherical universe rotates on two inclined circles, much as in late mediaeval and Renaissance "armillary sphere" models, and with this structure Plato begins to give a description of the complex motions of the sun, moon and planets through the sky. The description is of course very incomplete, but it provided a framework for later Greek astronomers [17].

The second part of the dialogue goes back to the beginning again and describes in more detail the nature of the stuff with which the Demiurge has made the universe. The traditional fire, air, water and earth are used (32c), but whereas earlier thinkers had considered these to be primitive, true ’elements’, Timaeus/Plato is rather scornful of this and insists that he can go to a deeper level (48c).

The ’elements’ are each made up as assemblies of particles having a particular shape, and the shapes are those of the regular solids discovered earlier by Theaetetus. These shapes are, for Plato, kallistos, "most beautiful" (53e and following); by using these, the Demiurge can construct the most beautiful universe possible. The nature of Theaetetus’ discovery has been analysed by Waterhouse [18], who argues that there are a number of important aspects. One is the elegant proof that there are five and only five such bodies. The other really significant discovery is the concept of regularity, that all side lengths, side shapes and angles are equal. This idea had to be discovered by someone, and Waterhouse makes a good case for Theaetetus. Waterhouse does not mention Plato’s phrase ’similar to itself’, but this could serve very well as a definition of regularity, remembering that for Plato/Timaeus, similarity is "incomparably superior to dissimilarity".

Theaetetus is believed to have discovered the icosahedron, and, according to an ancient tradition discussed by Waterhouse, also the octahedron. Many commentators have been sceptical that the octahedron discovery could be so late, particularly Sir Thomas Heath, who comments that the Egyptians, experts on pyramids, could surely have imagined putting two together, and an octahedron "is only a double pyramid with a square base’ [19]. (A somewhat similar comment appears in du Sautoy [20]).

However, this completely misses Waterhouse’s point about regularity. The height of most Egyptian pyramids is less than half the diagonal of the base, and in modern terms, Heath’s imagined Egyptian construction has only D_4h symmetry. Theaetetus’s discovery means that if, and only if, the dimensions of such an object are adjusted correctly, then a previously unrecognised regular figure, one which is ’similar to itself’, the regular octahedron, appears. Bipyramids might well have been constructed or visualised at earlier times, but there would have been nothing special about any of them before the concept of regularity had been recognised.

Given the elegance both of the concept of regularity and of the proof that there are only five, and the discovery of one or possibly two new regular solids, it is not surprising that Plato, with his elevated sense of beauty shown in the Philebus and in the Symposium, should find this set of solids to be supremely beautiful.

He uses the tetrahedron as his unit of fire, the octahedron for air, and the icosahedron for water, and because all of these are defined by the same triangular faces, he can allow interconversions between these elements. The fourth element earth is assigned to the cube, which has square faces and so cannot interconvert with the others. The remaining solid, the dodecahedron, is assigned to the whole universe, as some sort of decoration (55b). The universe has already been described as spherical, so the 12-sided ’decoration’ may be referring to the zodiacal signs [21].

Compelling evidence that Plato is thinking in terms of regularity appears in the way in which he analyses the sub-structure of the units of his ’elements’. He argues that the fundamental units are not the bodies themselves, and not even the faces mentioned above, but particular right triangles, ones which in our language have sides of length (1, 1, √2) and (1, √3, 2), i.e. isosceles with angles of (45º, 45º, 90º) and scalene with angles (30º, 60º, 90º). Using the scalene triangle, he gives very precise specifications of how the equilateral faces of the first three elements are to be constructed (54d-e).

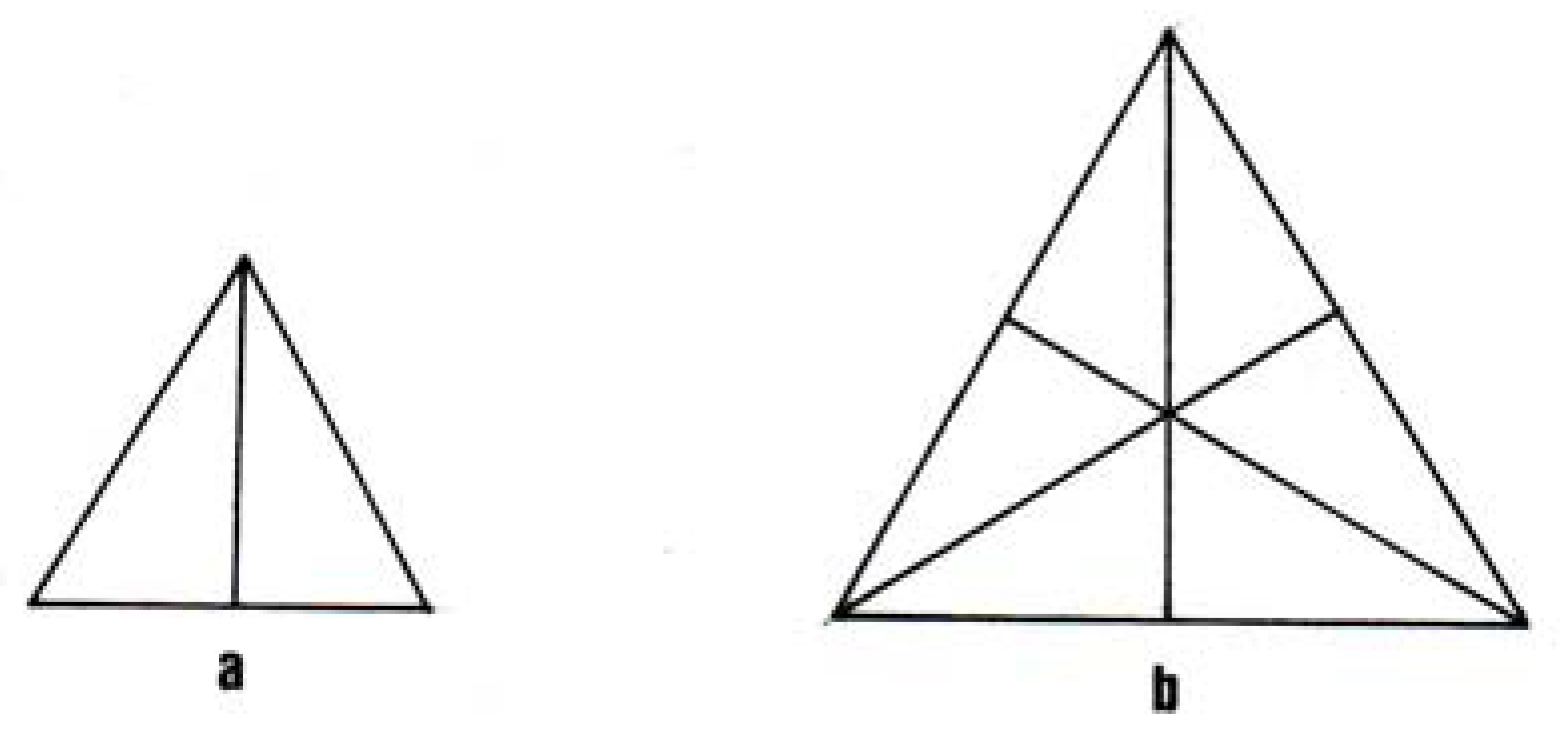
The final result of the specification is shown in Figure 1b. The assembly instructions begin by joining two scalene triangles "at their hypotenuses" (kata diametron), so that these form the long diagonal of a quadrilateral, then this is done three times, generating three such quadrilaterals. Finally the three are joined " so that all the hypotenuses and short sides converge at the centre.”

As we have seen, Plato did not have our language of symmetry, and to what extent he was aware of the underlying concepts is difficult to assess. Nevertheless his description of the construction draws attention, first to the mirror symmetry of the pair, and then to the three-fold axis of the final composite equilateral triangle. By adopting this construction, Plato has preserved the full symmetry of an undivided equilateral triangle. A rather similar comment has been made by Brisson [22] who notes that "On peut cependant penser que, dans le cas du carré et dans celui du triangle équilatéral, Platon veut trouver un centre de symétrie axiale.”

Even if Plato was not conscious of symmetry as we understand it, if we follow Waterhouse [18], the idea of regularity in three dimensions would have been available. Taylor [23] connected regularity with Plato’s kallistos, "most beautiful", as long ago as 1928, and this connection is discussed in some detail by Artmann and Schäfer [21]. Their view that kallistos, when applied to the solids, is principally a description of regularity, is that adopted here.

Having constructed the equilateral triangle, Plato then assembles four of these into a tetrahedron, eight into an octahedron, twenty into an icosahedron. Since he has used composite triangles with the full symmetry of undivided triangles, the bodies he assembles from these have the true symmetries T_d, O_h and I_h of the regular polyhedra [24,25]. In language which might have been easier to explain to Plato, he has preserved the regularity of the bodies by using his composition of the triangles.

That this is no trivial point can be seen from the fact that most modern commentators have been puzzled as to why Plato does not use an apparently simpler composition, that shown in Figure 1a, for his equilateral triangles. Cornford [26] had suggested that Plato’s intention was that many different constructions were to be understood for the equilateral triangle, and that the text gives us only a ’sample’ construction. He proposed that in each case Plato’s ’sample’ construction is for the second member of a series; the first would use only two of the constituent elementary triangles, Figure 1a. The higher members of this series are then generated using a pair of geometrical constructions from Euclid. This proposal received wide acceptance in the literature in English. However, Artmann and Schäfer [21] pointed out that 1a, the first member of Cornford’s series, and also the third, have lost the symmetry of the equilateral triangle. Corrrespondingly, such 1a triangles cannot generate bodies which are truly regular polyhedra. Furthermore, 1a triangles can be assembled into polyhedra with a variety of different orientations, giving a multiplicity of varieties for each individual element. In chemical terms, use of the 1a triangles would generate bodies which have many isomeric forms [25,28]. This is in clear opposition to Plato’s requirement, at 53e, that each of the bodies is "of a single kind" (kath’ hen genos); this requirement of course follows automatically if the triangles have been made up according to his specification (Figure 1b), since the bodies are then regular.

Plato’s construction of the equilateral triangle amounts to a tripling of a smaller triangle [21]; if two of the scalene triangles are connected as in Figure 1a, the area of this equilateral is one third of the 1b triangle. In the same way, Plato constructs his cubes (earth) with squares made up from four of his elemental isosceles right triangles, assembled exactly as in the diagram which Socrates drew for the slave-boy in the Meno to demonstrate the doubling of the square. Since such composite squares have full 4-fold symmetry, the cubes constructed from them are true regular cubes. This of course, would not be so if the squares were made up by the ‘simpler’ method of joining only two triangles along the hypotenuse.

In addition to the emphasis that the bodies are kallistos, most beautiful, Plato also describes the scalene triangles used for constructing three of them in the same way. Artmann and Schäfer [21] have discussed this description for the triangles. They conclude that it can be explained by the specific proportions of the composite triangle in Figure 1b. These follow a geometric proportion argument which Plato has already used at 31c-32a, and this can only be true if 30º, 60º, 90º scalene triangles are used. It is very likely that this is indeed a part of Plato’s reason for calling the triangles kallistos. However, immediately following this description at 54c, Plato states that his reason for this is "too long a story" (logos pleiôn). This cannot be true of the proportion argument, which he has already set out in detail.

The problem of keeping the length of the discourse within reasonable limits also occurs at 40c-d, where the details of the motions of the celestial bodies are said to be so complex that "To describe all this without visible models would be labour spent in vain". A similar comment would apply at least as strongly to any attempt to demonstrate that the regularity of a body made up from Plato’s composite triangles is unchanged from that of the simple regular body of the same form. An appropriate mathematical language for this was not available, and to attempt the explanation of such a point verbally would have been a very long task. However, examination of appropriate models immediately makes it clear that the regularity of a body made up from the composite 1b equilateral triangles is indeed that of the simple body. As an example, a model of an octahedron made in this way is shown in Figure 2.

Using such models, whether physical or imagined, it would have been evident to Plato that bodies constructed in this way are completely regular, kallistos, even though an attempt to explain the argument in writing would have been tedious, a logos pleiôn. A principal reason for labeling the 30º, 60º, 90º triangle as kallistos is then that this triangle, and only this one, allows these symmetric constructions [29].

6. Final remarks

Symmetry runs through much of modern science, and for many of us it has become almost automatic to respond to the mathematical aspect only; we find a new structure and we reach for our character tables. Nevertheless, the history of the subject is intertwined with a human response to beauty, and this has almost certainly helped to drive the subject forward to its present high sophistication. The theme, that the universe has been constructed to be the most beautiful possible, runs throughout the Timaeus. However, Plato’s concept of beauty is a very refined one, and it is clear from the Symposium citation that this is not merely a matter of outside appearance. According to Stewart and Golubitsky [30]:

“There is no evidence that either Plato or Euclid possessed a mathematical formulation of the concept of symmetry; to them the appeal of the regular solids seems to have been primarily aesthetic.”

The first part of this is not particularly surprising, given the lack of an appropriate language. However, if "aesthetic" refers to outward appearances only, Plato might have taken exception to the remark. For him there could be no dichotomy between the mathematical aspects and the beauty of these objects. Aristotle relates a story of a large audience attending a lecture of Plato on "The Good", only to be completely baffled when the entire lecture was on mathematics. For Plato, his kallistos description is a mathematical description. Clearly he did not understand symmetry as we do, but when he speaks of the units of his elements as being "most beautiful", it seems very likely that he means at least something like our regularity. Although there is evidence of earlier construction and use of symmetric objects [2,4], it is with Plato, presenting his own ideas, but also relying heavily on Theaetetus, that we can find the first hints, expressed in the language of beauty, of the mathematical ideas which ultimately lead on to our modern symmetry theory.