Abstract
Fluctuating asymmetry consists of random deviations from perfect symmetry in populations of organisms. It is a measure of developmental noise, which reflects a population’s average state of adaptation and coadaptation. Moreover, it increases under both environmental and genetic stress, though responses are often inconsistent. Researchers base studies of fluctuating asymmetry upon deviations from bilateral, radial, rotational, dihedral, translational, helical, and fractal symmetries. Here, we review old and new methods of measuring fluctuating asymmetry, including measures of dispersion, landmark methods for shape asymmetry, and continuous symmetry measures. We also review the theory, developmental origins, and applications of fluctuating asymmetry, and attempt to explain conflicting results. In the process, we present examples from the literature, and from our own research at “Evolution Canyon” and elsewhere.
1. Introduction
Symmetry is ubiquitous in the living world []. Bilateral, radial, rotational, dihedral, and translational symmetries are present in all major groups of organisms. Even sponges, which are widely regarded as lacking symmetry, have fractal symmetry (i.e., symmetry of scale) []. These symmetries, however, are approximate and only large-sample averages approach the perfectly symmetrical objects of geometricians. The extent to which the average individual departs from perfect symmetry is fluctuating asymmetry [,], a measure of developmental noise and developmental instability [,,]. Fluctuating asymmetry is important to population biologists because it reflects a population’s state of adaptation and coadaptation []. Consequently, it has numerous applications, theoretical and practical, in evolutionary biology, quantitative genetics, environmental biology, conservation biology, anthropology, agriculture, and medicine. Interest in fluctuating asymmetry has already spawned several book-length reviews [,,,]. In this paper, we review the methods, theory, and applications of fluctuating asymmetry.
Because all life forms are more or less symmetrical, one can demonstrate fluctuating asymmetry in all taxa [,]. One can even demonstrate it in extinct life forms [], bacteria [], and viruses []. The ubiquity of symmetry is a major advantage of fluctuating asymmetry over other measures of developmental instability. One could conceivably compare developmental instabilities of vertebrates and viruses, and attempt to decipher the underlying causal stress.
From an initial emphasis on fluctuating bilateral asymmetry [,,,,], research on fluctuating asymmetry now encompasses diverse symmetries (i.e., radial and dihedral symmetry, translational symmetry, etc.), shape asymmetry, and continuous symmetry measures [,,,,]. Nevertheless, most practitioners are unaware of the diversity of approaches to the study of fluctuating asymmetry. Thus, we begin with an overview of symmetry in living organisms.
2. Symmetries
Living organisms display symmetries at every turn []. Vertebrates, for example, are bilaterally symmetrical, and adult echinoderms have dihedral symmetry. The flower of the periwinkle is rotationally symmetrical, and colonial flagellates, such as Volvox, are spherically symmetrical. Filamentous algae, on the other hand, are translationally symmetrical. Gastropods and nucleic acids have helical symmetry. Bacterial and fungal colonies exhibit various forms of symmetry, including fractal symmetry. All of these symmetries are potentially the basis for studies of fluctuating asymmetry.
2.1. Types of Symmetry
Beloussov [] proposed a taxonomy of symmetries, related to one another by a series of invariant transformations. These transformations are rotation, reflection, and translation, as well as all possible combinations of these three operations. Rotation moves an object in a circular motion. Reflection transforms it to its mirror image. Translation slides it to a new location.
A sphere is the most symmetrical object in three dimensions. It has neither dorso-ventral, nor right-left axes. An infinity of rotational and reflective axes pass through the center of a sphere. Oocytes, blastulas, and colonial algae, such as Volvox, have spherical symmetry (Figure 1A). Flattened disk-shaped organisms (e.g., centric diatoms, mushroom caps, and bacterial colonies) are a special case of radial symmetry—circular symmetry (Figure 1B-C). These also have an infinity of rotational and reflective axes, but only in two dimensions.

Figure 1.
Spherical and circular symmetries. A. Volvox (© www.micrographia.com). B. Cap of a mushroom. C. Centric diatom. (© www.micrographia.com).
Rotational symmetry involves rotation around one or more axes of symmetry (Figure 2). If an object also has mirror symmetry, it has dihedral symmetry [], which is a property of regular polygons. Most echinoderms, including adult starfish (Figure 2A), have five-fold dihedral symmetry. Moreover, most flowers and inflorescences have three-fold, four-fold, or five-fold dihedral symmetries (Figure 2B). Some flowers, such as the periwinkle, Vinca major (Apocynaceae: Angiospermae), which resembles a pinwheel, are rotationally symmetrical (Figure 2C). Breaking dihedral symmetry produces a bilaterally symmetrical object having just one reflective axis of symmetry.

Figure 2.
Dihedral and rotational symmetries. A. Starfish (Bill Davin, Department of Biology, Berry College). B. Aster inflorescence. C. Periwinkle flower.
Bilateral, or mirror, symmetry involves reflection across an axis of symmetry (Figure 3). Left and right sides are mirror images of one another. It is the most common form of symmetry in the animal kingdom (Figure 3A), and is the rule in the leaves of plants (Figure 3B) and in the flowers of orchids and legumes, such as Clitoria (Figure 3C). Vertebrates, flatworms, and arthropods are bilaterally symmetrical. Even some sand dollars (Clypeasteroida: Echinodermata) display bilateral symmetry, though it verges on dihedral symmetry (Figure 3D). Breaking bilateral symmetry produces an object having handedness (or chirality). If most individuals in a population have handedness in the same direction, the asymmetry is directional asymmetry. If the population is a mixture of random left- and right-handed individuals, the asymmetry is antisymmetry. The mammalian heart and brain are directionally asymmetric, and the claws of male lobsters and fiddler crabs are antisymmetric.

Figure 3.
Bilateral symmetry. A. Skull of a turtle. B. Leaf of Quercus calliprinos. C. Flower of Clitoria. D. Sand dollar.
Translational symmetry involves translation, a rigid movement (or sliding) of an object in one direction. Filamentous cyanobacteria, such as Nostoc (Figure 4A), have translational symmetry of individual cells, and annelid worms, such as Glycera (Figure 4C), have translational symmetry of metameres (Figure 4). The breaking of translational symmetry in many arthropods produces structurally distinct segments, as in the lobster. The internodes of vascular plants, such as Equisetum (Figure 4B), usually have broken translational symmetry as well.

Figure 4.
Translational symmetry. A. Filament of a cyanobacterium, Nostoc (Ashwani K. Rai, Department of Botany, Banaras Hindu University). B. Internodes of a horsetail, Equisetum arvense (Eric Guinther, public domain). C. Metameres of the polychaete Glycera (NOAA Photo Library).
Helical symmetry involves rotation, along with translation along the axis of rotation. Snails, spirochetes, tobacco mosaic virus particles, and deoxyribonucleic acid molecules have helical symmetry (Figure 5). Breaking of helical symmetry in gastropods produces the oddly shaped terrestrial snail Opisthostoma (Diplommatinidae: Gastropoda).
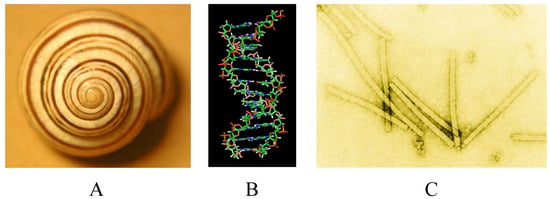
Figure 5.
Helical symmetry. A. The snail Cepaea nemoralis. B. DNA double helix (Richard Wheeler [Zephyris], http://en.wikipedia.org/wiki/DNA). C. Tobacco mosaic virus (Agricultural Research Center, USDA, at http://emu.arsusda.gov/typesof/pages/tmv2.html).
Fractal symmetry is symmetry of scale. Fractals are self-similar. For example, a mathematical fractal, such as the Sierpinski gasket, looks the same at all scales. Fractals in the living world, however, are finite, random fractals. Examples of such fractals include skull sutures and branching corals (Figure 6). Fractals having more than one scaling property are called multifractals. The time series of human heartbeat is a multifractal.

Figure 6.
Fractal symmetry. A. Human skull suture. B. Staghorn coral (Bill Davin, Department of Biology, Berry College).
2.2. Symmetry Groups
An n-dimensional object is mirror (i.e., bilaterally) symmetric if it is invariant under a reflection about a hyperplane of dimension (n − 1) passing through the object’s center of mass. Thus a 2-dimensional object is mirror symmetric if it is invariant under a reflection about a line (the mirror-symmetry axis) (Figure 7b), and a 3-dimensional object is mirror symmetric if it is invariant under a reflection about a plane [,]. A 2-dimensional object has rotational symmetry of order n if it is invariant under rotation of radians about the symmetry center of the object (Figure 7a). A 3-dimensional object has rotational symmetry of order n if it is invariant under rotation of radians about an axis passing through the center of the object. This axis is the rotational symmetry axis. Rotational symmetry of order n is denoted -symmetry. Dihedral symmetry is the symmetry of a 2-dimensional object having both mirror symmetry and -symmetry (such objects have 2n axes of mirror symmetry) (Figure 7c). Dihedral symmetry of order n is denoted -symmetry. Radial symmetry is C∞ -symmetry (see Figure 7d). It differs from rotational and dihedral symmetries because the number of rotational and reflective axes of symmetry is infinite. An object displays translational symmetry if each of its segments is equal to the other segments of the object located at equal translational distances [].

Figure 7.
Example of symmetries: a) rotational symmetry (C8-symmetry), b) mirror symmetry, c) dihedral symmetry (D8-symmetry), d) radial symmetry (C∞-symmetry) (from []).
Symmetry is a major trait of life, partly because it requires less free energy than asymmetric alternatives. Oocytes, for example, are invariably spherical, because a sphere has the smallest surface to volume ratio, and hence the least free energy, of any membrane-enclosed object suspended in a fluid (air or another liquid). A sphere is the most symmetrical of objects, with symmetry order ∞/∞∙m, where ∞/∞ indicates the order of rotational symmetries (i.e., the number of rotations) and m indicates the presence of mirror symmetry. Other kinds of symmetry arise by breaking spherical symmetry. In sea urchins [], a spherical oocyte transforms into a directionally asymmetrical larva. The change involves a gradual reduction in the symmetry order of the entire embryo (∞/∞∙m [oocyte] → ∞∙m [fertilized egg] → 2∙m [2-cell stage] → 4∙m [4-cell stage] → 8∙m [8-cell stage] → ∞∙m [blastula] → 1∙m [early bilaterally symmetrical larva] → 1 [mature directionally asymmetrical larva]).
Symmetry is often adaptive. Bilateral symmetry, for example, usually occurs in actively moving organisms, such as most animals, where efficient locomotion is important [,]. It influences flight efficiency of birds [,] and improves internal circulation []. Radial, dihedral, and rotational symmetries occur in sedentary organisms, such as adult echinoderms, which interact with the environment from all directions []. Translational symmetry occurs in filamentous algae and bacteria, plants, and fungi, which require large surface to volume ratios. Metamerism, a form of translational symmetry, is an easy way to build a multicellular organism from serially repeated parts [,]. Finally, fractal symmetry is an energetically efficient way for an organism to fill space [,,,], as well as an efficient design for conduits to distribute nutrients and gases to all cells of a multicellular organism [].
2.3. Types of Objects
Symmetrical objects may be consistent, partially consistent, or inconsistent. One can apply asymmetry measures to all three categories.
Consistently symmetrical objects have a consistent topology of specific landmarks displaying some form of symmetry. The position of the corresponding landmarks, and the distances among them, may vary (Figure 8A), but their number is maintained. The methods of geometric morphometrics [,] are suitable for quantifying asymmetry of consistent objects. A detailed review is given in Section 3.2. Studies using this approach have been done with Drosophila wings [], mite exoskeletons [], honey bee wings [], and house mouse mandibles [].
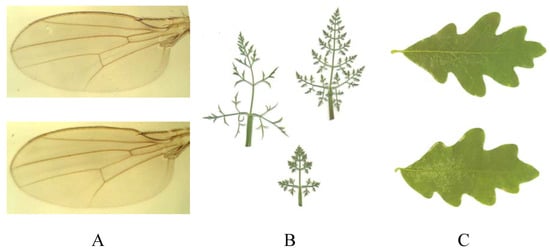
Figure 8.
Three types of objects for quantifying metric asymmetry. A. Structures having consistent topology and number of landmarks (Drosophila melanogaster wings). B. Structures having consistent topology, but varying number of corresponding landmarks among specimens (the secondary veins of Daucus carota leaves). C. Variable structures having no consistent topology, no quantitative consistency, and sometimes no matching points (lobes and sinuses on the leaves of Quercus alba).
Partially consistent objects have consistent topology, but the number of homologous landmarks varies among specimens (Figure 8B). The landmark method is suitable here as well, although characteristics of specific landmarks cannot be quantified. An example of partial consistency would be the wild carrot, Daucus carota (Apiaceae: Angiospermae), where individual leaves differ in the number of secondary veins.
Inconsistent objects have no homologous landmarks, no consistent topology, no quantitative consistency, and sometimes no matching points (Figure 8C). Besides the continuous symmetry measure (CSM) and its applications (detailed review is given in section 3.3), there are no general methods for quantifying asymmetry of inconsistently symmetrical objects. An example would be leaves of the white oak, Quercus alba (Fagaceae: Angiospermae), which often have different numbers of lobes and sinuses on left and right sides.
To quantify asymmetry of inconsistently symmetrical objects, Milner et al. [,] determined anchor points (in contrast to landmarks) on left and right sides of a bilateral structure, and used these as matching points. Since no geometric or structural consistency could be assumed, they introduced the idea of defining matching points, based on biological growth models, for Palestine oak (Quercus calliprinos) [].
3. Measuring Deviations from Perfect Symmetry
Deviations from perfect symmetry may be measured as variances (or related measures of dispersion) of linear dimensions, shape variation involving landmarks, or as continuous symmetry measures. We begin by applying these approaches to bilaterally symmetrical structures.
The first step in measuring the asymmetry of bilaterally symmetrical structures is determining matching points on left and right sides. In perfectly symmetrical objects, these points will be mirror images of one another. Using mathematical notation, these points form an orbit of the given symmetry group. When there are no matching points, artificial points can be created, for example, by choosing points where the margin of an object intersects a line that (1) crosses the axis of symmetry at its mid-point, and (2) is orthogonal to the axis of symmetry [,,]. Other alternatives include sampling along the contour of an object [] or comparing the width of corresponding elements [].
The second step in measuring asymmetry is selecting a function that returns a measure of asymmetry. This measure may be applied to Procrustes, Hausdorff, or Euclidian distances (e.g., width, distance to origin, absolute distance, etc.).
Before proceeding further, one should verify that the asymmetry is fluctuating asymmetry, and not a broken symmetry, such as directional asymmetry or antisymmetry [,]. Ordinarily, fluctuating bilateral asymmetry is symmetrically distributed about a mean of zero. Directionally asymmetric traits will have a mean other than zero, and antisymmetric traits will have either a platykurtic or bimodal distribution about a mean of zero. Directionally asymmetric and antisymmetric traits should be studied separately [,]. In fact, Graham et al. [] and Van Dongen [] have developed methods for either removing the directional component or decomposing a mixture distribution into fluctuating, directional, and antisymmetric components.
Asymmetry measurements are made on individuals, or repeated parts of individuals (leaves, flowers, etc.). Nevertheless, fluctuating asymmetry is largely a population parameter [,]. It has been applied to individuals [], but with only limited success. Finally, studies of fluctuating asymmetry can be based upon single [] or multiple traits [,].
3.1. Measures of Dispersion
The classic measure of fluctuating bilateral asymmetry is the variance (or standard deviation) of the difference between the value of a trait on left and right sides [,]. If di = li – ri, where di is the left-right asymmetry of individual i, li is the value of the trait on the left side, and ri is the value of the same trait on the right side, then a measure of fluctuating asymmetry is Var(di), or its square root (standard deviation). Trait values (l, r) can be either continuous or discrete.
An alternative to the variance is the mean absolute deviation []. This is the expectation E of |xi – μ|, where xi is an individual observation and μ is the population mean. Assuming μ = 0, which is routine in studies of fluctuating asymmetry, the mean absolute value of d is E|di|. It is less sensitive to outliers than the variance [], and |di| lends itself to analysis of variance [,,]. If di is normally distributed, then |di| has a half-normal distribution. One can normalize |di| with a power transform: (|di|+ 0.00005)0.33 []. The value of the mean absolute deviation is approximately 0.8 of the standard deviation [].
Measures of dispersion are easily generalized to other kinds of symmetry as well. For a pentameric starfish, for example, one can measure within-individual variation in arm length as a variance: Var(xi), where xi is the length of arm i. Because all starfish have five arms, this would be a population variance, rather than a sample variance (if all five arms were measured). Used in this way, Var(xi) is analogous to di, and is a measure of individual asymmetry. The mean of Var(xi) (or the standard deviation) would be the actual measure of fluctuating asymmetry for a sample of starfish. In addition to the variance, the mean absolute deviation can be applied to other kinds of symmetry. For the starfish mentioned earlier, individual asymmetry would be E|xi – μ|, where xi is the length of arm i and μ is the mean of all five arms. Similar approaches can be taken with translational symmetry. For reasons discussed previously, we prefer the mean absolute deviation.
On the other hand, traditional measures of dispersion completely ignore the shape of a structure (e.g., rotations, translations, etc.), but refer only to linear distances of morphometric traits or counts of meristic traits. Landmark methods give the appropriate attention to consistent and partially consistent objects, and continuous symmetry measures extend that attention to inconsistent objects.
3.2. Landmark Methods for Shape Asymmetry
Landmark methods for the analysis of bilateral shape asymmetry were developed by Bookstein [] and first used by Auffray et al. [] and Smith et al. []. These approaches have been reviewed by Auffray et al. [].
Bilateral symmetry can be either matching symmetry or object symmetry []. With matching symmetry, a structure is present in two separate copies, located on the left and right sides as mirror images of one another (e.g., Drosophila wings). The symmetry axis does not pass through matching symmetries. With object symmetry, in contrast, the structure itself is symmetric (e.g., human face), and the symmetry axis passes through the object. By using developmentally homologous points (i.e., landmarks), rather than conventional measurements of distance, it is possible to quantify asymmetry in complex structures using matching symmetry [] or object symmetry [].
Klingenberg and McIntyre [] suggest the following procedure for quantifying matching asymmetry via landmarks.
1. Select morphological landmarks and digitize their x and y coordinates (Figure 9). Klingenberg and McIntyre [] used wing vein intersections for their landmarks, but this approach can be applied to many other situations, such as the mouse mandible [] and the ventral face of the mite exoskeleton [].
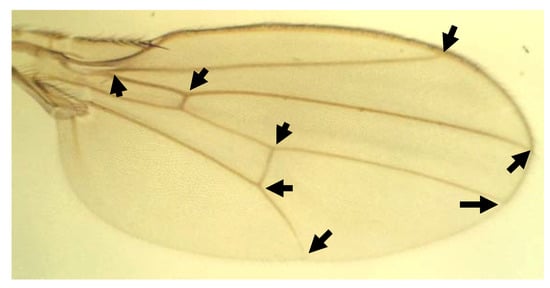
Figure 9.
The right wing of Drosophila melanogaster. The arrowheads point to the landmarks.
2. Reflect the landmarks on one side of the body to their mirror image (left wing in the example) to align corresponding landmarks on both sides (Figure 10).
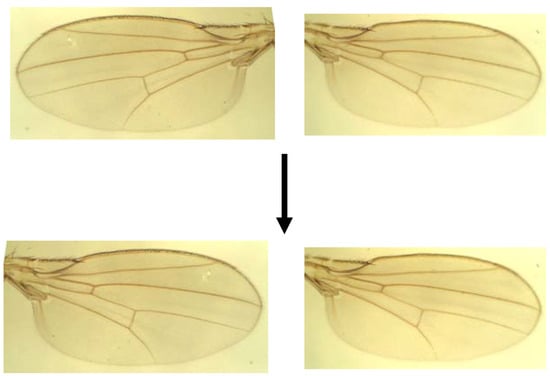
Figure 10.
Left wing reflected to its mirror image.
3. Scale both configurations on left and right sides to have the same unit centroid size (Figure 11). The centroid size is the square root of the sum of the squared distances from the landmarks to the common centroid (i.e., the geometric center).

Figure 11.
Scale both wings to the same unit centroid size.
4. Superimpose the wings (configurations of landmarks) by shifting the left and right centroids to a common set of x and y coordinates [0, 0] (Figure 12).
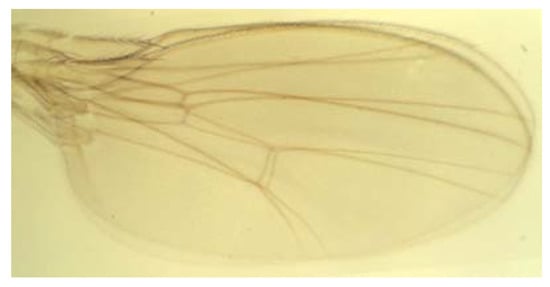
Figure 12.
Superimpose the two wings.
5. Rotate both configurations around their centroids to achieve the optimal fit of corresponding landmarks (Figure 13). This is a least-squares approach. The optimal fit minimizes the sum of the squared deviations between the paired landmarks.

Figure 13.
Rotate the wings to achieve an optimal fit of the landmarks [adapted from ].
6. The difference between homologous landmarks on right and left sides of a specimen is calculated as . The total difference between landmarks within an individual is calculated as , where k = the number of landmarks. Palmer and Strobeck [] pointed out that is conceptually the same as , the most common index of asymmetry for a single trait. Normalization for unit centroid size eliminates size differences in much the same way as normalizing asymmetry by trait size does (e.g., .
Klingenberg and colleagues [] have suggested a measurement for quantifying object symmetry via landmarks. We illustrate their approach with ten landmarks (Figure 14, vertices). The vertical line defines the single axis of symmetry, whereas the remaining eight vertices are in four pairs on right and left sides. The diagram shows the original configuration (solid black line). The procedure consists of three steps:
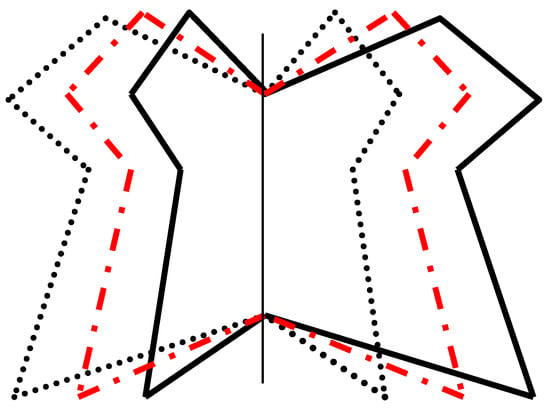
Figure 14.
Asymmetry of eight landmarks. The diagram shows the original configuration (solid black) and its reflected and relabeled copy (dotted black), after least-squares Procrustes superimposition. The Procrustes average (dashed-dotted red) is perfectly symmetrical. (Adapted from []).
1. Generate a reflected copy of each landmark by reversing the side of its x-coordinate. Then the paired landmarks of the reflected copies are re-labeled so that each paired landmark obtains the label of its counterpart (dotted black line).
2. The Procrustes average is then defined (dashed-dotted red line) as the middle of the line passing between the original landmark and the reflected copy of the corresponding landmark. The new shape created by connecting these average landmarks is perfectly symmetrical.
3. The asymmetry of the entire object is then the difference between the original and the mirror configurations, or equivalently, the landmark deviations of the original configuration from the average landmarks.
Landmark methods are suitable for analyzing bilateral asymmetry in either 2- or 3-dimensions. Unfortunately, they are restricted to objects having homologous left and right landmarks. In the next section, we present an overview of the continuous symmetry measure (CSM), defined for all symmetry groups in all dimensions, regardless of whether or not there are homologous landmarks.
3.3. Continuous Symmetry Measures (CSM)
Continuous symmetry measures (CSM) are a flexible alternative to measures of dispersion and landmark methods of shape asymmetry []. Moreover, they are the only suitable approach for inconsistent objects having variable structural elements. Hence, they encompass the landmark methods.
The continuous symmetry measure (CSM) was developed for the computer vision and computer graphics community []. Its novelty for this community is treating symmetry as a continuous feature rather than a binary feature (i.e., whether it exists or not). Developmental instability is a continuous property of organisms. Thus, the amount of asymmetry should provide information about the level of developmental instability. CSM can do this as well. Moreover, because the CSM quantifies asymmetry in all dimensions and for all types of symmetry, it is an efficient tool for analyzing deviations from symmetry in living organisms.
The underlying mathematics of symmetry relies on the concept of symmetry groups, groups of symmetry-preserving operations [,]. We define a symmetric object as a set of points invariant under the actions of any element of a symmetry group (e.g., bilateral, translational, rotational, dihedral, or a mixture of all of these). A point x of an object, and all its transformations under the group members, is called an orbit. This implies that an object is symmetric if one can partition it into orbits invariant under the operations of the symmetry group. For example, an equilateral triangle in 2-dimensions is rotationally symmetric (order 3) and one can partition it into orbits containing three points each. The vertices of the triangle form one such orbit. Consequently, given a point x, every point in its orbit is naturally associated with an element of the symmetry group. For example, in Figure 15d, the orbit of point consists of the points which are associated with (rotations of for i = 0, 1, 2), respectively.
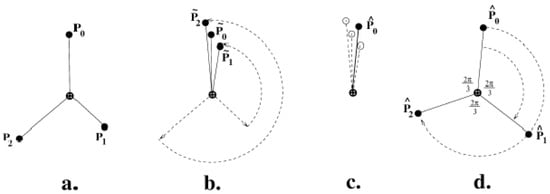
Figure 15.
The folding-unfolding algorithm applied to a single orbit (from []). CSM with respect to rotational symmetry of order 3 is calculated. The points are associated with the rotations , respectively: a) Original 3 points . b) Fold – apply the inverse symmetry element to each point (i.e., rotate by ). Points are obtained. c) Average – points are averaged, obtaining d) Unfold – apply the symmetry elements to average point (i.e., rotate by ), obtaining points ). CSM is calculated: CSM = .
The continuous symmetry measure (CSM) involves the amount of ’effort’ required to transform a given shape (composed of orbits) into a symmetric shape. This ’effort’ is the mean of the squared distances each point must move from its original position to one of perfect symmetry. Note that we assume no a priori symmetric reference shape. Denote by the space of all shapes of a given dimension, where each shape P is represented by a sequence of n points . A metric d is defined on this space as follows:
This metric defines a distance function between any two shapes in . We define the symmetry transform of a shape P as the symmetric shape closest to P in terms of metric d. The continuous symmetry measure (CSM) of a shape P is the distance between P and its symmetry transform:
.
Thus, the CSM explicitly implies invariance to rotation and translation. Normalizing the original shape prior to the transformation also allows the invariance to scale. An additional feature of the CSM is that we obtain the symmetric shape ’closest’ to the given one, enabling visual evaluation (Figure 15d).
Zabrodsky et al. [] developed a geometric algorithm for deriving the symmetry transform of a shape and, accordingly, the CSM value. For a specific symmetry group, the process of evaluating the CSM involves two steps.
1. Partitioning the object into orbits, i.e. determining the points or features of the input that will form each orbit and associating an element of the symmetry group with each point.
2. Evaluating the symmetry transform and CSM value given the orbits. Typically, there are numerous possibilities for partitioning the input points into orbits. We seek the partition providing the minimal distance between the original set and its symmetry transform. The algorithm implementing step 2 is referred to as the folding-unfolding method because of its geometric visualization. Given an orbit of points , with associated symmetry group members , the folding-unfolding method involves the following steps:
1) Fold—apply the inverse symmetry element to each point, i.e., apply to for The folded points are obtained.
2) Average—if the original points were perfectly symmetrical, then (by definition) they would converge onto a single point. In general, however, they do not. Thus, we average the points , obtaining
3) Unfold the average point by applying back the symmetry element . We obtain the unfolded points , where .
4) The first three steps are applied independently to each orbit. The CSM is calculated by averaging the deviation of each orbit from perfect symmetry .
An example of the algorithm is shown in Figure 15, for a single orbit of the C3 symmetry group, namely, the rotational symmetry group of order 3. For a set of orbits, we calculate the CSM independently for every orbit, with the appropriate symmetry operation applied about the center of mass of all points rather than about the origin. This algorithm can be implemented for all symmetry groups in any dimension. Proof and details can be found in [,,]. An example of a hexagon and its CSM value and symmetry transform for various symmetry groups is given in Figure 16.
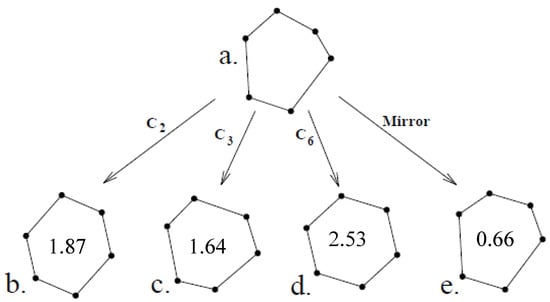
Figure 16.
Hexagon and its CSM value and symmetry transform for various symmetry groups (from []).
3.3.1. CSM in Physics and Chemistry
Symmetry is closely associated with the chemical and physical characteristics of materials, whether natural or man-made []. The study of symmetry is important in chemistry and physics, where the symmetry of a molecule correlates with its chemical and physical properties [,,]. The CSM has been used in the study of structures ranging from single molecules [,,,,], through clusters [], and up to crystals []. Correlations have been shown between CSM values and nuclear-magnetic resonance values [], energy changes accompanying molecular isomerization [], optical rotations [], pressure and temperature structural effects [], as well as enzymatic activity [] and more [].
3.3.2. Measuring Asymmetry in the Absence of Landmarks
Symmetry measures based upon landmarks are limited to single, relatively rigid, elements (e.g., vertebrate bones, arthropod limb segments and wings, and body outlines of fish) []. The CSM can quantify asymmetry when there are no landmarks, no consistent topology, no quantitative consistency, and sometimes no matching points (Figure 8C). Hence, CSM is not limited to rigid elements.
3.3.3. Analysis of Asymmetry Using Anchor Points
One approach to evaluating symmetry of partially consistent and inconsistent objects (see section 2.3) is the use of anchor points. In contrast to landmarks, anchor points are features selected on a specimen-by-specimen basis. They may vary in number, relative location, form, and characteristics among individuals. A classic example is the leaf venation pattern. Typically, the middle and secondary veins of leaves display planar, tree-like (i.e., bifurcating) geometry. The general layout of the veins consists of a central main vein, the symmetry axis from which secondary veins bifurcate on both sides. Individual leaves may vary in the number of secondary veins, their bifurcation points along the main vein, their lengths, and their angles.
To apply anchor points, we first define a bifurcating structure as a set of points interconnected by line segments (see Figure 17A). The approach requires matching pairs of points to be deformed into symmetric pairs. With our bifurcating structure, this pairing of points reduces to a pairing of secondary veins. Figure 17B shows an example where points on paired veins have been matched (point Pk matches point Qk). When a secondary vein is ‘missing’, we insert a new zero-length vein, marked as two endpoints located at the bifurcation point. Figure 17C shows the paired points, where P1 and P2 are the endpoints of the new vein inserted as a match for Q1 and Q2, respectively. One can estimate the optimal pairing of points with a dynamic programming algorithm [,].
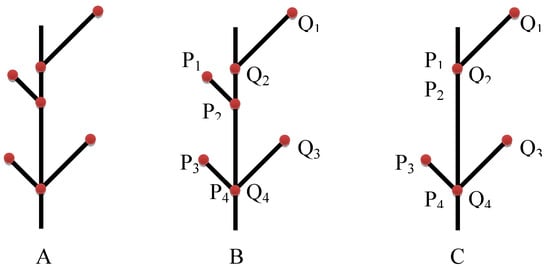
Figure 17.
A bifurcating structure consisting of a main vein and secondary veins branching off the main vein. A. The bifurcating structure is a set of points interconnected by segments. B. Points Pk and Qk on paired veins have been matched. C. A new vein is inserted as points P1 and P2 (matching Q1 and Q2), the endpoints of the new vein. Points P1, P2, and Q2 coincide.
Given a set of paired anchor points, one can use the CSM approach (section 3.3) to evaluate the bilateral symmetry of the structure. Given a paired set of veins (whether two existing veins or an inserted missing vein), the CSM of a pair of veins is computed using the folding-unfolding method [] (see section 3.3). The CSM value of the entire leaf’s venation pattern is the average CSM value of both sets of matching veins (i.e., matching secondary veins). See Figure 18 for an example of the folding-unfolding method used on a matched pair of secondary veins. Note that the symmetric bifurcating structure closest to the original is a byproduct of the CSM method (Figure 18D). The unfolded points form a symmetric configuration ‘closest’ to the original in terms of the average mean squared distance (see Zabrodsky et al. [] for further details and proofs). One can easily see the CSM calculations (and the folding-unfolding method) applied to all the veins simultaneously (independently). The CSM value of the whole structure is the average CSM value of each pair of matching veins.
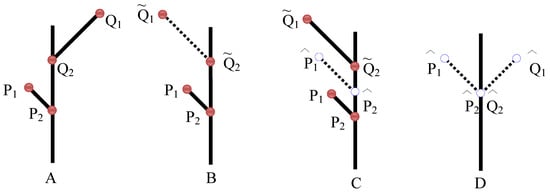
Figure 18.
Computing the CSM using the folding-unfolding method applied to two paired secondary veins, each represented by 2 points. A. Original bifurcating structure with matching points marked. B. Fold – Vein Q is reflected across the symmetry axis, obtaining the folded points and . C. Average – The folded points are averaged with their matching points, obtaining the points and . D. Unfold – The average points are reflected back across the symmetry axis, obtaining the unfolded points and . The CSM value is the average distance squared between the original points and the corresponding unfolded points: .
The CSM approach constrains the bifurcating end-points of the secondary veins to remain positioned along the main vein. The approach allows veins to change length, translate bifurcation points, and add additional veins to the structure. Thus, the deformation applied by the CSM (and the folding-unfolding method) maintains the structure within the bifurcating structure class defined earlier.
The CSM global approach has been extended to more complex bifurcating structures having 3rd and 4th order veins []. These structures are inherently hierarchical, where every sub-structure is itself a bifurcating structure, as can be seen in Figure 19.
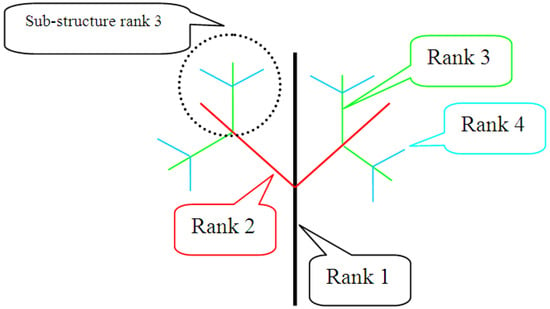
Figure 19.
An example of a bifurcating structure. Sub-structures and ranks are marked.
In bifurcating structures with three or more ranks, a distinction can be made between Global Mirror Symmetry, with the whole structure symmetric with respect to the main vein (the rank-1 vein) (Figure 20a), and Local Mirror Symmetry, with every substructure symmetric with respect to its respective main vein (a high-ranking vein) (Figure 20b). Thus, Frid, Raz, and Hel-Or [] defined Complete Symmetry, which has both Global and Local Symmetry (Figure 20c). They then extended the CSM approach to Complete Symmetry of complex bifurcating structures.
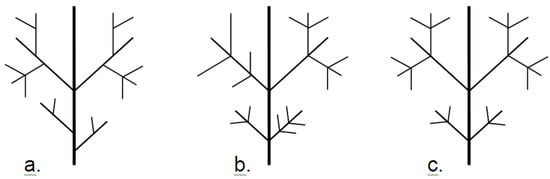
Figure 20.
Symmetry of bifurcating structures. a) Global Symmetry. b) Local Symmetry. c) Complete Symmetry.
To evaluate Complete Symmetry, the algorithm must simultaneously account for both local and global perspectives. The structure is traversed recursively, and the symmetry of the sub-structures is evaluated. These symmetry values are then combined into a single complete symmetry value. The algorithm combines both top-down and bottom-up approaches. The top-down part of the algorithm incorporates local symmetry, and the bottom-up part incorporates global symmetry. Figure 21 shows a flow chart of these two parts of the Complete CSM algorithm applied on a 4-ranked structure (Figure 21.1). The top-down part of the algorithm recursively selects sub-structures (marked in blue) and the bottom-up part of the algorithm imposes local symmetry, recursively up the structure (marked in green), resulting in Global Symmetry. The result of the Complete CSM algorithm is a CSM value as well as a Complete Symmetric structure (closest to the original in terms of CSM), as shown in Figure 22.
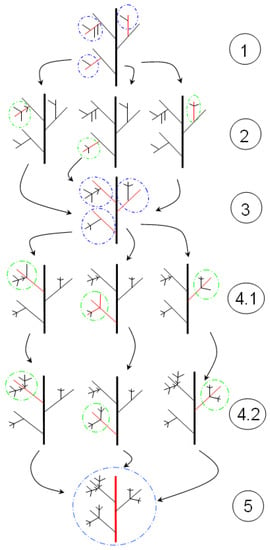
Figure 21.
An example of the Complete CSM algorithm.
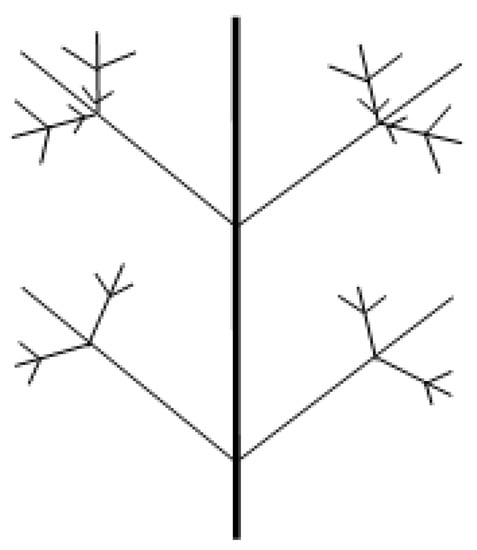
Figure 22.
Resulting symmetric structure after applying the Complete CSM algorithm.
We used the Complete CSM approach on the leaves of fringed rue, Ruta chalepensis (Sapindales: Angiospermae), growing on the opposite slopes of "Evolution Canyon II," in Nahal Kziv, Israel. This is part of the "Evolution Canyon" project (see section 10). Using the Complete CSM, we demonstrated that leaves on the south-facing slope were significantly more asymmetrical, on average, than those on the north-facing slope, and those differences were stronger when using the 3rd and 4th order veins than when using only the 2nd order veins [].
3.3.4. CSM-Developmental Stability Measurement
Fluctuating asymmetry (i.e., symmetrical distribution around a mean of zero) is the most reliable measure of developmental instability. Fortunately, the CSM can absorb the standard statistics of fluctuating asymmetry. As with the landmark method [], the CSM approach incorporates estimates of measurement error, to obtain an unbiased estimate of fluctuating asymmetry. In either approach, the x and y coordinates of the anchor points, or landmarks, contain information about measurement error (the difference in locations between replicate sets of digitized landmarks). The asymmetry is the true difference between the locations of the reflected landmarks on right and left sides; the variance components for both fluctuating asymmetry and measurement error may be estimated by using a modification of the standard mixed-model ANOVA []. In the next section, we present a method for quantifying measurement error based on fuzzy analysis.
The average right-left differences among all of the aligned landmarks yield a single, multivariate estimate of an individual’s deviation from perfect symmetry. A sample of these estimates can then be analyzed using the standard tests for fluctuating asymmetry. Moreover, it is easy to verify that the distribution is indeed fluctuating asymmetry (symmetrical right-left distribution around a mean of zero), and not a broken symmetry (directional asymmetry or antisymmetry).
Unlike bilateral structures, rotationally, dihedrally, or radially symmetrical structures do not have directionality. Thus, one cannot easily verify that asymmetry has been broken (and hence is not fluctuating asymmetry). We suggest adding two statistics (variance and entropy) to the CSM measurement. The CSM procedure already includes folding, finding the average of the folded points, and quantifying the distance from this average. Variance and entropy describe the distribution around the average, and are conceptually similar to the moments of a normal asymmetry distribution.
4. Measurement Error
Measurement error inflates variances, mean absolute deviations, and continuous symmetry measures. It is especially harmful in its effect on asymmetry distributions, generating mixed distributions that can generate spurious associations []. Thus, there is a need for replicate measurements in all studies of fluctuating asymmetry.
To obtain a true estimate of developmental instability, one must estimate measurement error and subtract it from the asymmetry mean square. The most widely used, but not exclusive, technique for performing this is a mixed-model ANOVA introduced by Leamy [], and expanded and advocated by Palmer and Strobeck []. Nested ANOVA may also be used, but the advantage of the mixed-model design is that one can estimate directional asymmetry and measurement error simultaneously. A similar approach is available for landmark methods, and fuzzy analysis can be used for continuous symmetry measures.
4.1. Mixed-Model ANOVA
The ANOVA used most frequently for fluctuating asymmetry is a two-way, mixed-model ANOVA with replication. The main fixed effect is sides (S), which has two levels (left and right). The block effect is individuals (I), which is a random sample of individuals from a population. The sides by individuals interaction (S x I) is a mixed effect. Finally, an error term (m) represents measurement error (replications within sides by individuals). Although individuals are randomly sampled from a population, this is not a randomized block design. Left and right sides cannot be assigned at random; individuals come with left and right sides already determined. The design is thus a nonrandomized observational design that incorporates blocking []. From the standpoint of fluctuating asymmetry, the nice aspect of this design is that one can simultaneously test for directional asymmetry and partition the total phenotypic variance into three random components.
Statisticians debate the expected mean squares and tests of significance in two-way mixed-model ANOVAs (see Samuels [,] and commentary [,,]). The main controversy is over whether σ 2S x I should appear in the expected mean square for individuals. The model used by Palmer and Strobeck [], Samuels’ Model 2, includes σ 2S x I. Her Model 1, however, excludes it. Although Samuels [] favors Model 1, the best model for studies of fluctuating asymmetry is still unclear. According to Samuels, Model 1 is more appropriate for nonrandomized observational designs like those represented by fluctuating asymmetry. Indeed, her example of such a design is density of neurons in right and left hemispheres of the brain. Nevertheless, Model 2 is more appropriate when the goal of a mixed-model ANOVA is estimating components of variance. This is because all of the random terms in Model 2 are uncorrelated [].
Table 1 shows an ANOVA table with expected mean squares for a mixed-model ANOVA. This is like the table given by Palmer and Strobeck []. In particular, we treat the number of sides as a constant, rather than as a variable. As with Palmer and Strobeck [], we use expected mean squares associated with Model 2. The expected mean squares consist of variance components for each effect, and the appropriate coefficients. The effect called sides is the variation between the two sides; it is a measure of directional asymmetry. The effect called individuals is the variation among individual genotypes; the individuals mean square is a measure of total phenotypic variation and it is random. The individual by sides interaction is the failure of the effect of individuals to be the same from side to side; it is a measure of fluctuating asymmetry and antisymmetry. It is a mixed effect. The error term is the measurement error; it is a random effect.

Table 1.
Variance components σ 2 in a mixed-model ANOVA (after []). N is the number of individuals and R is the number of replicate measurements per individual. <σ 2S > is not a true variance component, since sides are fixed. σ 2m is a random component due to measurement error.
The similarity between this design and Kozhara’s [,] partitioning of total phenotypic variance into two components, factorial and stochastic, is evident. Total phenotypic variance (assuming no directional asymmetry) is the mean square for individuals
and the stochastic component (including measurement error) is equal to the interaction mean square
MS I = ½Var(l + r)
MS S x I = ½Var(l − r).
Kozhara’s factorial component is the total phenotypic variance minus the stochastic component (MS I − MS S x I). It is the variation among individuals; the stochastic component is the variation within individuals.
Although many researchers test for a significant interaction (and individuals) effect, it is superfluous to do so. Tests of significance in ANOVA are primarily reserved for fixed effects. A fixed effect is one whose levels the researcher has an interest in comparing (e.g., left and right sides) of the factor. For fixed effects, we compare the means. Thus, it is perfectly legitimate to test the significance of sides, since the null hypothesis is that the mean of the left side equals the mean of the right side (Ho: μ l = μ r). The two means are tested by comparing variances (the mean squares). For random effects, however, one does not (cannot) compare levels. For a random effect, the levels of the effect are a random sample from a large population. It is more meaningful to estimate variance components.
While it is possible to entertain the hypothesis that a particular variance associated with a random effect is not significantly different from zero (say H0: σ 2S x I = 0, under Model 2), it does not make much sense to do so. For metric traits, no two individuals are identical, no two sides in an otherwise symmetrical individual are ever identical, and no two measurements of the same object are ever identical. Variation is pervasive. One can always find a difference, no matter how small. Thus, we know beforehand that the null hypothesis for a random effect is not true; it cannot be true. The only reason one might consider testing the null hypothesis that fluctuating asymmetry is not significantly greater than zero would be during trait selection. Traits having small amounts of asymmetry may not be worth the effort.
Instead of testing the significance of the random effects, researchers should estimate the three estimable variance components (σ 2m, σ 2S x I, σ 2I), and test only for differences between sides. The variance component for individuals (σ 2I) is an estimate of the shape and size variation among individuals. The variance component for the interaction effect (σ 2S x I) is an estimate of the non-directional asymmetry (fluctuating asymmetry and antisymmetry). The variance component for replicates (σ 2m) is an estimate of measurement error. Provided that the sides effect is insignificant, and that there is no obvious antisymmetry, one can interpret σ 2I and σ 2S x I as factorial and stochastic variances. Their sum is the total phenotypic variance, minus measurement error.
If the sides effect is significant (i.e., Ho: μ l ≠ μ r), the variance component estimate for the interaction (i.e., fluctuating asymmetry) may be biased, depending upon how directional asymmetry is manifested []. This is because the ANOVA’s additivity assumption may be violated. Nothing more can be done with the mixed-model ANOVA. Alternate methods of partitioning out directional asymmetry have been proposed by Graham et al. [] and Van Dongen et al. []. The mixed-model ANOVA should be viewed then as the beginning, not the end of an asymmetry analysis.
An additional problem for most studies of fluctuating asymmetry is that the error models for size and asymmetry usually differ from those for measurement error. Size and asymmetry usually fit a multiplicative error model (see section 5.1). But measurement error is usually additive. This creates a problem because the additivity assumption is violated, even if the data are transformed. If measurement error is small, then it is best to use a log transform. If measurement error is large, however, it may be best not to transform the data. Either way is a compromise. A better solution is to take multiple replicate measurements, average them, and then at some later (random) time take several more and average them. This reduces the measurement error so that it does not seriously influence the analysis.
Nevertheless, the mixed-model ANOVA is widely misused []. Our main objection is that many researchers focus exclusively on tests of hypotheses rather than on estimating variance components [,]. In reality, the one important test is for sides. Moreover, some researchers confuse mean squares and variance components. Just because measurement error (σ 2m) is equal to or greater than fluctuating asymmetry (σ 2S x I) does not mean fluctuating asymmetry is insignificant. Finally, it is always best to express measurement error (MSerror or σ 2m ) as a percentage of either the total phenotypic variation (MS I) or the asymmetry variance (σ 2S x I).
4.2. Fuzzy Analysis for Quantifying Measurement Error
The CSM for fuzzy data [] considers input points of imprecise location. Specifically, the locations of the input points are a probability distribution. For example, Figure 23a shows a point configuration whose locations are given by a normal-distribution function. The dots represent the point locations, and the rectangles represent their uncertainty (i.e., measurement error). The widths and lengths of the rectangles are proportional to their standard deviations. The CSM approach for fuzzy data [] provides the most probable symmetric configuration represented by the fuzzy-input points and the probability distribution of the symmetry distance values for those points.
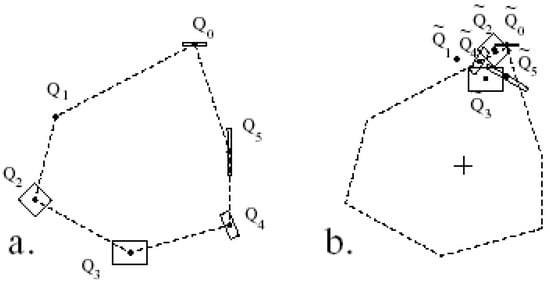
Figure 23.
Folding a set of n measurements: a) A configuration of 6 measurement points: Q0.....Q5. b) Each measurement Qi is rotated by 2π/6 radians about the centroid of the expected point location (marked as +), obtaining measurements Q0.....Q5 (from []).
A variant of the folding method (presented in 3.3 for Cn-symmetry) is used to evaluate the most probable symmetric shape under the maximum likelihood criterion. This variant considers the fuzzy-input points as n measurements, ~, where Pi is the mean and Ai is the covariance of the point-location distribution. The folding-unfolding method is applied to these n measurements. (See Figure 23, which shows the method applied to a rotationally symmetrical object of order n. The approach for mirror symmetry, or any other symmetry, is similar.)
When given m = qn measurements, they are divided into q interlaced sets of n points (each forming an orbit), and the folding method is applied separately to each set of measurements. Derivations and proof can be found in []. The folding-unfolding method results in the most probable symmetric shape, as well as a probability distribution of CSM values for the given set of measurements. Figure 24 displays distributions of the CSM value for various measurements. As expected, the distribution becomes broader as the uncertainties (the variance of the distribution) of the measurements increase.
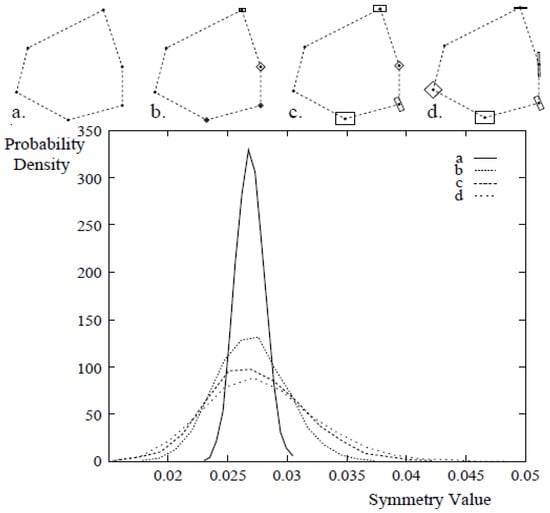
Figure 24.
Probability distribution of CSM values depends on measurement error. a-d) Measurement error of the points increases from left to right. e) Probability density and symmetry values (-symmetry) for configurations a-d (from []).
5. Error Models and Size Scaling
Positive size scaling is a common problem. It occurs when asymmetry increases with size. If left uncorrected, it can easily generate spurious differences among populations. Larger individuals may be mistakenly judged more developmentally unstable than smaller individuals. Positive size scaling arises when growth is active (i.e., old tissue contributes to the production of new tissue), and errors are multiplicative []. Negative size scaling is also a potential problem, especially if measurement error is significant. It can generate spurious differences as well.
5.1. Error Models and Probability Distributions
Multiplicative errors are ubiquitous, whenever tissue at time t – 1 actively participates in the production of tissue at time t []. The tissue generating the structure is growing continuously. If the size of a structure Xt at time t is a random proportion of its size Xt-1 at a previous time t – 1, such that Xt = Xt-1 + εt Xt-1, then Xt is asymptotically lognormally distributed [,]. Thus, multiplicative error generates a lognormal distribution (but see []). Examples of such active growth include leaves, petals and stems of plants, and bones and soft tissues of animals (Figure 25A).
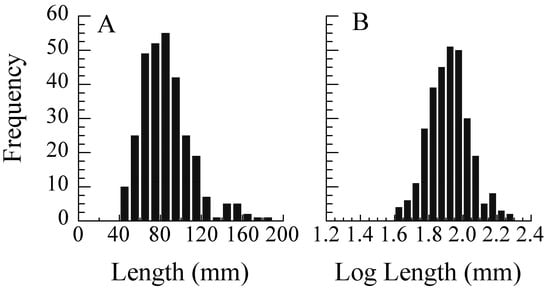
Figure 25.
Frequency distributions of lobe lengths of 300 fig leaves, Ficus carica (from []). A. Lognormal distribution of lobe length. B. Normal distribution of the same data after logarithmic transformation.
Additive error occurs whenever tissue at time t – 1 does not actively participate in the production of tissue at time t. The tissue generating the inert structure does not grow. If the size of a structure Xt at time t is independent of its size Xt-1 at a previous time t – 1, such that Xt = Xt-1 + εt, then Xt is asymptotically normally distributed. Additive error generates a normal distribution. Examples of such inert growth include nails, scales, bristles, feathers, teeth, and exoskeletons. Measurement error is additive as well.
Errors, however, are rarely just multiplicative or just additive. Researchers usually deal with mixed error models and mixture distributions. A mixture of lognormal and normal distributions is most commonly encountered and has appeared in every study of leaf asymmetry we have undertaken [,,].
5.2. Transformations for Size Scaling
The most commonly used transformation for positive size scaling is essentially a coefficient of variation (Table 2). Either (l – r)/((l + r)/2) or (l – r)/(l + r) are commonly employed []. Logarithmic transforms (Figure 25B), however, have better statistical properties if trait values fit a lognormal distribution. We suggest log l – log r [] (Figure 26), which is identical to Palmer and Strobeck’s [] log(l/r). To evaluate the success of a log transform, |log l – log r| should be regressed on (log l + log r).

Table 2.
Common transformations for fluctuating asymmetry studies.
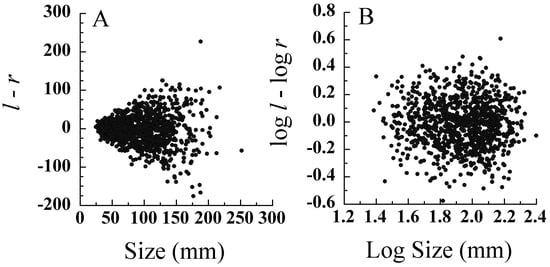
Figure 26.
Size-scaling of asymmetry (from []). l and r are lognormally distributed and correlated. A. Size-scaling of asymmetry l – r plotted against size (l + r)/2. B. Lack of size-scaling of asymmetry log l – log r plotted against size (log l + log r)/2.
A logarithmic transform of l and r may also remedy some leptokurtic asymmetry distributions [], because the difference between two lognormal distributions is leptokurtic, and the difference between two normal distributions is normal. Consequently, a transformation changing a lognormal distribution of (l + r) into a normal distribution, will likely change a leptokurtic distribution of (l – r) into a normal distribution of (log l – log r).
Problems can arise when log (or other) transformations are applied uncritically to correct size scaling (Figure 27A-B). It often occurs that a positive slope of |l – r| regressed on (l + r) is replaced by a negative slope when |log l – log r| is regressed on (log l + log r). This is usually, in our experience, caused by a mixture of lognormal and normal distributions. When the normally distributed part of the mixture is measurement error, one may simply average the replicates and use the averages. Measurement error decreases by σ2 – ((σ2/n)/ σ2)100 with each replicate averaged.
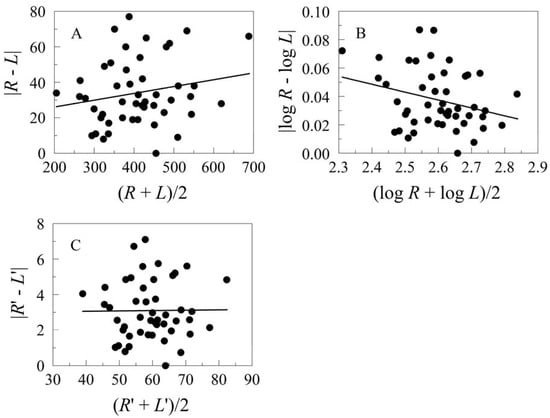
Figure 27.
Positive and negative size scaling of leaf asymmetry in Olea europaea from the “African” slope of “Evolution Canyon” I. A. Untransformed data showing positive size scaling. B. Log transformation generates negative size scaling. C. Power transformation (λ = 0.6) removes all size scaling. R’ and L’ are transformed variates.
Power transforms (Table 2) are useful when one cannot eliminate the additive error in a mixture distribution (Figure 27C). This might occur when there are not enough (or no) replicate measurements to work with, or when other sources of additive error are present.
One should not apply these transformations to methods that adjust landmarks to a unit centroid size. Doing so will amount to transforming the data twice. Moreover, mixture distributions are a likely problem with landmark methods, just as they are with conventional methods. If negative size scaling is a problem, we suggest averaging replicate x, y coordinates before proceeding with a landmark analysis.
5.3. Recommended Approaches
Sample sizes in studies of fluctuating asymmetry should be as large as practical. Moreover, replicate measurements are essential, for the reasons discussed previously. If necessary, two or three replicates are not too much. Before deciding how many replicates to measure, it is worthwhile estimating how much of the observed asymmetry variance is measurement error. Finally, combining more than one trait in a composite index of fluctuating asymmetry helps to maximize the power to reject the null hypothesis.
Composite indices of fluctuating asymmetry, combining data from more than one independent trait, are considerably more powerful than indices based on single traits []. According to Leung et al. [], the simplest composite index involves computing a standardized, summed asymmetry value for each individual, and using Levene’s test to compare composite asymmetries of different groups. The asymmetry values are standardized to insure equal weight for different traits. Leung and colleagues standardize |di| by the average of that trait for the population. An alternative for highly leptokurtic data is to total the ranks of the asymmetry values.
The choice of traits to study is often dictated by convenience. Nevertheless, some traits may have greater inherent variation than others. In plants, for example, leaves seem to be more variable than flowers []. This has been attributed to the functional importance of flower symmetry in attracting pollinators. In animals, functionally important traits, such as those involved in locomotion, are less variable than functionally unimportant traits, such as foramina []. In general, functionally unimportant traits, including sexually-selected ornaments, may be more sensitive to stress than functionally important traits [].
In addition to morphometric characters, meristic (i.e., countable) characters are useful. In fact, they are often more variable and less canalized than morphometric characters []. Nevertheless, they have a built-in bias caused by thresholds in the continuous morphogen distribution underlying the discrete trait. Young [] has developed an unbiased maximum likelihood metric for meristic traits, and established a general method to remove bias caused by counting errors.
Fluctuating asymmetry must be distinguished from directional asymmetry and antisymmetry [,]. These two broken symmetries are, nevertheless, interesting [,], and may increase under stress. They should, however, be treated separately from fluctuating asymmetry. Occasionally, an asymmetry distribution may be partitioned into fluctuating, directional, and antisymmetric components [,].
In addition to reporting the first and second moments of di (location and variance), one should also report the third and fourth moments of the distribution (i.e., skew and kurtosis). Moreover, for the sake of future meta-analyses, one should report both signed and unsigned asymmetries. For a full discussion of sampling and statistical considerations, see Palmer and Strobeck [].
Finally, researchers will want to compare fluctuating asymmetries among populations. This is most often accomplished using analysis of variance. Levene’s test, a one-way ANOVA on |l – r|, is often recommended []. If the assumptions of the analysis of variance are violated, nonparametric approaches are also an option. In addition to these frequentist approaches, Bayesian approaches are also available [].
6. Developmental Homeostasis, Canalization, and Developmental Stability
The stability of development is one of its most general characteristics []. Consider the remarkable similarity of identical (monozygotic) twins, or the symmetrical wings of a butterfly. To explain this stability, Waddington [] proposed the concept of developmental homeostasis (or homeorhesis), the stabilized flow of a developmental trajectory. Schmalhausen [] arrived independently at the same concept, which he called autoregulation. Moreover, today’s systems biologists use the term robustness in more or less the same way [].
Developmental homeostasis has two independent components: canalization and stability [,,]. Canalization is the stability of development under different environmental and genetic conditions. Developmental stability, on the other hand, is the stability of development under constant environmental and genetic conditions.
Canalization is assessed either by raising individuals having the same genotype in different environments (environmental canalization) or by raising individuals having different genotypes in the same environment (genetic canalization). The converse of environmental canalization is developmental plasticity []. To demonstrate environmental canalization, Waddington [] raised Bar mutants of Drosophila melanogaster at two different temperatures. At 18°C, flies had more than 150 facets in both eyes, but at 25°C they had fewer than 60. By selecting for increased canalization, he was able to reduce the difference to fewer than six facets in some lines. Consequently, canalization is heritable.
Stability is the ability of a system to correct minor fluctuations. Doing so requires feedback and the ability to detect fluctuations (or perturbations). Development is stable if a developmental trajectory returns to its original course after having been perturbed. But stability is not the whole story. Homeostasis also involves buffering (i.e., resilience). Buffering refers to the ability of a system to minimize, or soften, perturbations. It is analogous to C. S. Holling’s [, p. 17] concept of resilience, which he defined as “the ability to absorb changes of state variables, driving variables, and parameters, and still persist.”
To understand developmental instability, one must distinguish fluctuations and perturbations. Fluctuations are intrinsic deviations spontaneously generated by the system []. Perturbations, on the other hand, are local changes communicated from the environment []. Perturbations can obviously generate fluctuations, but the two concepts are nevertheless independent. Small perturbations, for example, can generate large fluctuations, and large perturbations can generate small fluctuations. Fluctuations are intrinsic; perturbations are extrinsic.
Developmental stability, then, involves stability, resilience, fluctuation, and perturbation. To use an analogy, consider an automobile and driver trying to maintain a stable trajectory on a highway. Feedback between driver and steering system represents the stability of the system, the integrity of the shocks and tires represents its resilience, the roughness of the road and the velocity and direction of the wind are perturbations, and the vehicle’s random variation around its trajectory represents fluctuation. Stability, resilience, and perturbation influence the roughness of the ride, which is analogous to developmental noise. If we assume perturbations are small and constant, or nearly so, then we can estimate the stability and resilience of the system by examining its fluctuations.
One can estimate developmental instability, the converse of developmental stability, by raising genetically identical individuals in a common environment. Because genotype and environment are controlled, the residual variation (except for measurement error) must be random developmental variation (developmental noise). A second way of measuring developmental instability is to examine random variation between right and left sides of traits that are, on average, bilaterally symmetrical. Both sides of a symmetrical structure are genetically identical. Moreover, they have had a similar history of gene activity. Finally, they have experienced the same environment. This is fluctuating asymmetry.
7. Random Developmental Variation
Fluctuating asymmetry measures stochastic variation and deterministic variation indistinguishable from stochastic variation []. As mentioned previously, both developmental stability (including resilience) and perturbation influence the stochastic variation one observes. The influence of perturbation, however, is usually small, so the observed variation is largely developmental instability. (We discuss the distinctions between stress and perturbation later in this paper.)
7.1. Nature, Nurture, and Noise
Fluctuating asymmetry is a stochastic component of phenotypic variation []. When one partitions total phenotypic variation (σ2p) into genetic (σ2g) and environmental (σ2e) components, fluctuating asymmetry is part of the environmental component []. But the stochastic component is often as large as, or larger than, the genetic and true environmental components. Consequently, several authors have argued that it should stand on an equal footing [,,,]. Kozhara [,], as mentioned previously, decomposes σ2p into factorial (σ2f) and stochastic (σ2s) components. The factorial component is the variation among individuals, and the stochastic component is the variation within individuals. For symmetrical traits, σ2p = ½Var(l + r), and σ2f = ½Var(l + r) − ½Var(l − r). The factorial component combines genetic and environmental variation.
Developmental noise arises at multiple levels: molecular, cellular, tissue, and organ-levels. At the molecular level, for example, gene expression is inherently noisy [,,]. Elowitz et al. [] showed that random variation in the expression of identical promoters in Escherichia coli influences numbers of cyan and yellow fluorescent proteins in each bacterial cell. This variation at the molecular level generates visible color variation at the cellular level. Random variation may also arise at the cellular level. Random cell-cell interactions, for example, may contribute to variation within a three-dimensional matrix []. Moreover, cell migration has a random component partly under genetic control []. At the tissue level, the induction of one tissue by a neighboring tissue contains stochastic elements. During embryonic development in vertebrates, for example, diffusible signals induce ectodermal cells overlying the notochord to develop into the neural plate. Diffusion is a stochastic process: the net transport of matter from a region of higher concentration to one of lower concentration by random molecular motion []. In Drosophila, random variation in morphogen gradients is minimized by a network of extracellular proteins [].
7.2. Deterministic Chaos
In addition to noise, deterministic chaos contributes to some of the stochastic variation. It resembles noise, and has its origins in nonlinear feedback [,]. Moreover, delays in feedback loops may interact with noise to generate oscillations in gene expression []. In our view, much of the variation regarded as stochastic may include deterministic components.
7.3. Population and Individual Fluctuating Asymmetry
Population estimates of fluctuating asymmetry are usually far more useful and reliable than individual estimates. For bilateral fluctuating asymmetry, only one degree of freedom is associated with the estimate of individual asymmetry. In contrast, population estimates have n – 1 degrees of freedom, where n is the sample size. One simply cannot say much about the developmental instability of a single individual from a single measurement.
This admonition against individual fluctuating asymmetry applies only to non-modular organisms. One can reliably estimate individual fluctuating asymmetry (and consequently developmental instability) in modular organisms having many repeated parts. Plants, for example, have tens to hundreds of leaves, flowers, and branches. Cowart and Graham [] sampled 60 leaves from each of five fig plants, Ficus carica L. (Moraceae: Angiospermae), and concluded there were significant differences in leaf asymmetry among the five individuals; the smallest of the five plants had the most symmetrical leaves. Other studies have sampled up to 10 flowers to estimate individual developmental instability [].
Individual fluctuating asymmetry has been applied, with much controversy, to studies of sexual selection and individual fitness. In this review, we mostly refer to population estimates of fluctuating asymmetry.
8. Origins of Developmental Homeostasis
The most fundamental adaptation is the harmonious physiological and developmental functioning of an organism [,]. Consequently, both physiological and developmental homeostasis should be important components of fitness []. Physiological homeostasis, for example, maintains an organism’s internal environment, permitting it to function under a range of external conditions. Developmental homeostasis produces consistent phenotypes for a particular genotype and environment.
8.1. Adaptation, Coadaptation, and Heterozygosity
The genetic basis of fitness and, by association, developmental stability, has been controversial for nearly 60 years []. The roles of heterozygosity and genomic coadaptation have been especially contentious. Dobzhansky [, p. 301], in an influential paper, attributed the higher fitness of inversion heterozygotes in Drosophila pseudoobscura to polygenic complexes that “have become mutually adjusted, or coadapted, by natural selection in the course of the evolutionary process.” Because the inversions hinder crossing over, they maintain high levels of heterozygosity. Nevertheless, Dobzhansky’s [] emphasis was clearly on coadapted gene complexes rather than allelic heterozygosity per se. In contrast, Lerner [, p. 6], in his classic Genetic Homeostasis, suggested that coadapted heterozygosity was important: “ontogenetic self-regulation (developmental homeostasis) is based on the greater ability of the heterozygote to stay within the norms of canalized development.” His emphasis was clearly on the greater fitness of allelic heterozygotes (overdominance). In the ensuing years, the overdominance hypothesis has fallen into disfavor [,] (but see []). Nevertheless, there are several good examples of fitness overdominance [,,]. Invariably, they involve genes for respiratory enzymes and cellular energy homeostasis, such as phosphoglucomutase and isocitrate dehydrogenase in rainbow trout [] and adenylate kinase, phosphoglucomutase, octopine dehydrogenase, and glutamate-oxaloacetate transaminase in the deep-sea scallop Placopecten [].
Parsons [, p. 592] has argued that energetic efficiency is “a measure of fitness in a stressed world.” Thus, the best examples of fitness overdominance are those involving energy efficiency []. Nevertheless, the actual mechanism whereby such allelic variation is adaptive remains elusive. Heterozygotes can produce n + 1 versions of the same enzyme, where n is the number of protein subunits. They can produce two different versions of the same monomeric enzyme, three different versions of the same dimeric enzyme, and five different versions of the same tetrameric enzyme. As we suggest later in this review, the superiority of heterozygotes may be related to the distributed robustness of metabolic networks (i.e., their topology). Because these enzymes are involved in the synthesis of ATP and NADPH, they are linked to every reaction in the cell requiring energy. Thus, even a small advantage may be multiplied across the metabolome by the number of links.
Overdominance, however, is only one advantage of heterozygosity. Heterogeneous habitats can maintain multiple allelic systems [], especially in the presence of stress, across Israel [,,,,] and across the globe []. Consequently, the hypothesis that heterozygosity modulates fitness has been demonstrated locally, regionally, and globally.
In contrast to heterozygosity, genomic coadaptation has received much more attention from those studying fluctuating asymmetry [,,,]. Genomic coadaptation refers to the coadapted, harmonious interactions among gene loci. Selection at one locus influences selection at other loci, in a system of mutual interaction. Inbreeding and hybridization disturb these interactions, and both have been associated with increased developmental instability [,].
Hybrid zones, though, are especially enlightening. Under the overdominance hypothesis, both fitness and developmental stability should be greater in hybrid zones between species and subspecies, because hybrids have greater heterozygosity. Under the coadaptation hypothesis, however, fitness and developmental stability should be reduced, because the genomes of hybrids have been disturbed. Most natural hybrid zones support the coadaptation hypothesis []. For example, in the blind mole rat, Spalax, selection against hybrids in narrow hybrid zones may rise to 90% []. Several hybrid zones, however, including those between subspecies of Mus musculus, Artemisia tridentata, Hyla spp., Sceloporus grammaticus, and Lepomis macrochirus, have hybrids more developmentally stable than their parental subspecies []. The situation in big sagebrush, A. tridentata, is interesting because the hybrids have higher fitness and stability, but only in the center of a narrow hybrid zone [,]. They have lower fitness and stability elsewhere.
Directional selection should also increase fluctuating asymmetry [] by disrupting coadapted genomes, but there is virtually no evidence it does so, at least in Drosophila [,].
An additional consequence of the relationship between genetic variation (heterozygosity and homozygosity) and fluctuating asymmetry is that small island populations [] and populations on the edge of a species range [] should have greater asymmetry. There are several good examples of both in the literature [,,].
The genetic architecture of fluctuating asymmetry is still largely unknown []. In general, narrow-sense heritabilities (h2) for fluctuating asymmetry are small, but not zero [,]. Nevertheless, estimates of heritability require large sample sizes, and most are not large enough to distinguish between heritabilities h2 of 0.1 and 0.5 [,]. In contrast, epistatic interactions account for much of the genetic variation in fluctuating asymmetry within laboratory populations of Mus musculus [,].
The search for specific genes modulating phenotypic variation, and influencing developmental stability, has focused on those coding for molecular chaperones, such as Hsp90. Some studies find that its role, and that of Hsp83, is minimal [,,], while others find a significant role [].
Other research supports the hypothesis that environmental canalization and developmental stability share underlying regulatory mechanisms, but environmental and genetic canalization do not []. Moreover, fluctuating asymmetry and phenodeviants in Drosophila bipectinata share a common buffering system []. Understanding the underlying basis of developmental instability is critically important to the future development of the field []. There is still much work to do.
8.2. Distributed Robustness
The robustness of living organisms arises from redundancy and distributed robustness [,]. Redundancy involves duplicate parts: genes, cells, etc. If there are two or more identical copies of a particular gene, inactivating one of them will have minimal impact on fitness. Distributed robustness, in contrast, involves the complexity of genetic and metabolic networks. If a link in a network is broken, it may often be bypassed. Wagner and colleagues [,] believe distributed robustness is more important than redundancy.
If distributed robustness is the main contributor to developmental stability, then the topology of genomic and metabolic networks should be critically important. These networks are termed small-world networks [,,], and they are robust to perturbation [,]. But a metabolic pathway’s Achilles’ heel is the highly connected nodes in the network. Error tolerance comes at a price []. Knock out a highly connected node and the system fails.
Networks consist of nodes and links []. In a metabolic network, the nodes are chemical intermediates (substrates), and the links are enzymatically mediated reactions (enzymes). A highly connected node is a hub. In a small-world network, the connectivity P(k) of nodes follows a power-law, P(k) ≈ k-γ, distribution. Most nodes have few links, but a few hubs may have hundreds or thousands of links. The hubs connect the less connected nodes to the system. These systems are typically scale-free [] and hierachical [].
In yeast, Saccharomyces cerevisiae, hubs buffer phenotypic variation. Working with 4,718 strains of haploid single-gene knockouts, Levy and Siegal [] estimated the overall phenotypic variance resulting from single deleted genes. They called this the phenotypic potential, which is equivalent to the variation among clone mates in a common environment, an alternate estimator of developmental instability. Most deletions have almost no effect on phenotypic variation because they are not hubs.
What are the implications of distributed robustness and the network topologies for fluctuating asymmetry? At first glance, one might expect negative power-law (i.e., Pareto) distributions of fluctuating asymmetry because that is how the links are distributed. (This is not the distribution of d = l – r, but the distribution of Var(d) or E|xi – μ| among different populations or genotypes.) If the response to a specific, local perturbation to a node or link is proportional to the connectedness of the node, then fluctuating asymmetry should also be distributed as a negative power-law. Clearly, this does not occur, because a small amount of noise is necessary for normal development and gene regulation [,]. We have never seen a continuous trait that did not have some asymmetry. Thus, one would expect a skewed distribution with fat tails. The Double Pareto lognormal distribution is such a distribution; it is a mixture of lognormal and Pareto distributions. Babbitt and colleagues [,,] have fit the double Pareto lognormal distribution to asymmetry data (though the data appear to contain artifactual antisymmetries). Nevertheless, the distribution may still be useful in testing the hypothesis that distributed robustness mediates developmental instability.
Under our model, most perturbations should have little effect on organism-wide developmental instability, unless they perturb a hub. These perturbations are probably responsible for most of the minor developmental noise. Stress, on the other hand, lessens energy efficiency, consequently involving several important hubs (metabolic intermediates). For example, stress-related decreases in ATP or NADH production should influence thousands of linked metabolic reactions. This hypothesis has important implications for fluctuating asymmetry as an indicator of stress: organisms should be far more robust to perturbations than scientists have imagined, but the effects of stress are more likely to manifest themselves at hubs, not nodes.
8.3. Environmental Stress
Stress and perturbation are distinct concepts. Whereas perturbation is energy or mass communicated from the environment, stress is anything (physical, chemical, genetic, psychological, etc.) dissipating energy away from growth and production [,,,,]. By doing so, stress usually limits productivity []. Nutrient loading, however, can increase productivity, but qualifies as a stress if it simultaneously causes a decrease in the efficiency of energy metabolism []. Stress also interferes with stability and resilience of development, though we have a poor understanding of the mechanisms.
According to Escós et al. [, p. 331], “defining stress exclusively in terms of production decline may be misleading.” They define stress as “any environmental factor that causes a reduction in the efficient use of energy, causing a reduction in developmental homeostasis, and finally reducing long-term, total inclusive fitness.”
Stress might lessen developmental stability by dissipating energy away from feedback loops, either by changing gene-expression patterns [] or by changing the flux through metabolic pathways []. Expression of heat-shock (stress) proteins, for example, has negative effects on growth and development []. Stress might also change the topology of genetic and metabolic networks. Salt-tolerant varieties of rice maintain the expression of homeostatic genes involved in energy supply, transcription, cell transport, cell wall synthesis, and DNA synthesis in the face of salt stress; salt-sensitive varieties down-regulate these same genes prior to death [].
9. Applications
Fluctuating asymmetry has numerous applications. Most notably, it is an (albeit controversial) index of environmental and genetic stress. Furthermore, developmental instability, which it measures, may be correlated with individual fitness, and is widely viewed as an index of adaptation and coadaptation. Recently, a few scientists have used fluctuating asymmetry to study developmental integration, under the assumption that parts sharing asymmetries must share a common developmental basis. Finally, we explore several applications beyond the usual fluctuating bilateral asymmetry, such as fluctuating translational asymmetry. Throughout this section, we present “Evolution Canyon,” at Mount Carmel, Israel, and other “Evolution Canyons” as important model systems for fluctuating asymmetry.
9.1. Stress
Fluctuating asymmetry is an indicator of environmental (Table 3) and genetic (Table 4) stress. Nevertheless, it is not without its detractors and skeptics. Presumed stressors often have no effect on asymmetry, even while decreasing growth and increasing mortality []. Moreover, fluctuating asymmetry can be a poor indicator of both stress and individual fitness []. Such findings, however, do not invalidate fluctuating asymmetry as an indicator of stress. Here, we discuss both sides of the controversy and argue that fluctuating asymmetry is indeed a valuable indicator, if it is put in perspective.

Table 3.
Natural environmental stress and fluctuating asymmetry: a small sampling of studies and stressors. All studies are of fluctuating bilateral asymmetry.

Table 4.
Genetic stress and fluctuating asymmetry: a small sampling of studies and stressors.
To begin with, fluctuating asymmetry seems a less sensitive indicator of stress than specific physiological and morphological modifications. These modifications will have evolved to minimize even minor stress. Consequently, they should be exquisitely sensitive to it, providing the stress is a normal part of the organism’s evolutionary history. Nevertheless, this is also an advantage for fluctuating asymmetry, because adaptive modifications contribute to the resiliency of development. They buffer stress. According to West-Eberhard [, p. 507], “an environmental condition that was originally stressful or extreme, and disadvantageous to the organism, eventually, if recurrent, may become part of normal development and would no longer be regarded as a ‘stress’.” Fluctuating asymmetry, on the other hand, is never (or rarely) adaptive, and it does not contribute to the resiliency of development.
Some small amount of random variation, however, is necessary for normal development. Some developmental decisions at the cellular level are best left to chance []. Moreover, when Mather [] selected for decreased asymmetry of sternopleural bristles in Drosophila melanogaster, the result was a dramatic decline in fitness, which is contrary to the common notion that zero asymmetry is optimal. When selection was relaxed, fitness returned to normal. Elena and Sanjuán [] discuss similar trade-offs between robustness and fitness in viruses.
Decreased growth is often a more sensitive indicator of stress than is fluctuating asymmetry [,]. This is unsurprising because a decline in growth is simultaneously a direct indicator of stress (i.e., stress may dissipate energy away from growth []) and a likely adaptive modification maintaining lifetime fitness.
Stressed individuals not shunting energy away from growth may have lower lifetime fitness [,,]. In plants, for example, the cost of reproduction often increases with size in a habitat-dependent way []. In other words, there should be an optimum size for reproduction, and it should vary with habitat. The optimum size is usually smaller under stressful conditions. Consequently, it is difficult to say with certainty whether smaller size indicates stress, or is simply a way of avoiding stress.
Excessive nutrients, beyond the adaptive norm, are an exception to the generalization that small size indicates stress. Excess nutrients can simultaneously increase both growth and asymmetry [,,,], and growth and mortality []. Saline solutions, on the other hand, can stop plant growth completely, with no increase in fluctuating asymmetry [,,].
There may also be a trade off between rapid growth and developmental stability. In some studies, faster growth is associated with greater asymmetry (but see Pélabon et al. []). Martel et al. [], for example, stimulated faster leaf growth in the birch Betula pubescens by breaking apical dominance. Those treated leaves reached the same size as the control leaves, but did so in a shorter time. They also had more asymmetrical leaves. Wells et al. [] found that Brazilian boys with the fastest early growth were more asymmetrical at age nine, even though both groups attained the same average size. Wells and colleagues attributed the effect to greater compensatory growth in small newborns.
Leaf size of 12 plant species at “Evolution Canyon,” Israel (see section 10.2 and section 10.3), demonstrates how phenotypic modifications are more sensitive to stress than fluctuating asymmetry [,]. The main stresses for plants at “Evolution Canyon” are water availability and evapotranspiration on the south-facing “African” slope and light availability on the north-facing “European” slope. To minimize water loss on the south-facing slope, all 12 species there have smaller leaves. Moreover, larger leaves on the north-facing slope maximize light interception, and consequently photosynthesis. Besides leaf size, plants on the opposing slopes differ in leaf thickness []. In contrast to these phenotypic modifications, our preliminary results suggest less dramatic differences in leaf asymmetry between the 12 populations on the two slopes [].
The leaf size example at “Evolution Canyon” begs the question: was stress still present after the modification? It was obviously present before the modification, and undoubtedly triggered the modification, but was it present for the development of each leaf? Adaptive modifications are not easily reversed [], so they can indicate only that stress occurred sometime during the development of the leaf.
In a similar study, Escós et al. [] examined fluctuating asymmetry of Anthyllis cytisoides (Fabaceae: Angiospermae), on north- and south-facing slopes of Rambla Honda Valley, near Tabernas, Spain. Unlike “Evolution Canyon,” which is Mediterranean and mesic, this microsite is arid (218 mm rainfall per year), with most rain falling in the winter. Plants on the north-facing slope had larger leaves, longer shoots, allocated more resources to reproduction, and had greater fractal dimension (a measure of how much the plant fills space). The plants maintained developmental stability at the expense of productivity. The less productive plants on the more arid south-facing slope, however, had lower fluctuating asymmetry than those on the north-facing slope during an extreme drought. The authors attributed the difference to the burden of extra biomass in the plants on the north-facing slope. As additional evidence, grazed plants on both slopes had a lower water deficit, better survival, and increased developmental stability, presumably because grazing removed the burden of extra biomass.
Besides aridity, other environmental stresses have been associated with higher fluctuating asymmetry (Table 3). For example, dental asymmetry of the Middle East blind mole rat, Spalax ehrenbergi (Spalacidae: Mammalia), in Israel is unrelated to aridity. Asymmetry, however, increases with altitude, minimum January temperature, and the amount of indurated (i.e., compacted) soil [].
Fluctuating asymmetry is also an indicator of genetic stresses, such as inbreeding and outbreeding []. As with environmental stress, many unresolved questions remain. Several meta-analyses, for example, have failed to find significant associations between heterozygosity and developmental instability [].
Hochwender and Fritz [], though, designed an especially elegant experiment comparing the effects of genetic and environmental stress on two species of willow (Salix sericea, S. eriocephala, and their F1 and F2 hybrids (Salicaceae: Angiospermae)). Although they sampled only one leaf from each plant, they sampled leaves from 2359 plants. Genetic stress was more important than environmental stress. F2 hybrids had the greatest leaf asymmetry, but water stress, pathogen attack, and competition had no effect on leaf asymmetry. Fluctuating asymmetry also decreased with plant size.
Fluctuating asymmetry increases when adaptive modifications fail to buffer stress. Therefore, even if fluctuating asymmetry is less sensitive than adaptive modification, it indicates more severe stress, and it indicates when stress has exceeded an organism’s homeostatic abilities. In particular, it indicates when stress has influenced developmental stability.
9.2. Fitness
Evolutionary biologists sometimes use fluctuating asymmetry as an indicator of individual fitness, but they have done so with varying degrees of success [,]. The promise of an easily measured component of fitness has not borne out. The initial optimism has been replaced with skepticism, and the belief that fluctuating asymmetry is a weak measure of developmental instability, and consequently a poor measure of individual fitness [,,,]. The main problem is that with only two sides to a bilaterally symmetrical trait, only one degree of freedom is available to estimate a variance and a sample size n = 2 to estimate a mean absolute deviation. Given such small samples, the estimate of the underlying developmental instability is apt to be imprecise [,,]. Estimates of the repeatability () of fluctuating asymmetry (i.e., proportion of the asymmetry variance due to developmental instability) average a low 0.08 [].
The difference between left and right sides, the individual asymmetry, is actually an estimate of variation, too. In fact, the unsigned asymmetry, |d| = |l – r|, is exactly twice the mean absolute deviation of a sample (l, r) of size n = 2. The mean absolute deviation is the mean of |xi – μ|, where the xis are the individual observations on left and right sides and μ is the mean. Consequently, the mean deviation is Σ|xi – μ|/n, and with n = 2, it may be reduced to |xl – xr|/2.
Of course, this criticism is irrelevant if one is working with a modular organism having multiple symmetrical parts (e.g., leaves, flowers, and branches of plants), because one can sample more than one repeated part. In fact, only the number of repeated parts limits the sample size. Consequently, one can estimate developmental instability of a single individual (or clone mate) with much greater precision.
Unfortunately, few studies have taken advantage of the potentially larger samples available with plants. Andalo et al. [], for example, sampled three leaves and flowers from each plant, and Pélabon et al. [] and Handy et al. [] sampled one leaf from each plant. Unsurprisingly, these studies found no relationship between fluctuating asymmetry and individual fitness. Samples of modular parts from individuals should be at least 30-40, as they are in comparisons of fluctuating asymmetry at the population level.
To our knowledge, only one study in the literature [] has attempted to establish a link between fluctuating asymmetry (a composite of three measurements on each leaf) and overall fitness (itself a composite of juvenile survival, numbers of seeds, and their germination rate) in a long-term (4-year) study. Leaves of big sagebrush Artemisia tridentata (Asteraceae: Angiospermae) were measured in a common-garden experiment involving three gardens, two subspecies, and three categories of hybrids. The common gardens were in the actual hybrid zone. Five leaves were sampled from each plant. In general, plants not native to a garden had lower fitness and higher leaf asymmetry. Fluctuating asymmetry was negatively correlated with fitness (r = −0.495, P < 0.005).
Further work is essential if fluctuating asymmetry is to be a trustworthy indicator of individual fitness []. In particular, we need to sample more traits on non-modular organisms, and we need larger sample sizes of repeated parts on modular organisms. We also need to eliminate, or reduce, measurement error by making replicate measurements, and we need to take size scaling and mixed-error distributions into account. Far too many studies use only one or two traits, use inadequate sample sizes, apply scaling uncritically, and disregard replicate measurements and mixed-error distributions.
9.3. Developmental Integration
Fluctuating asymmetry is a useful tool for evolutionary developmental biology because it reveals direct interactions among modular parts of organisms [,,,,,,,,]. In particular, covariation of fluctuating asymmetries among traits is evidence they share developmental pathways []. Klingenberg and Zaklan [], for example, studied morphological integration between developmental compartments of the Drosophila wing. Earlier studies had suggested that anterior and posterior compartments of the wing were distinct developmental modules; but landmarks spanning the entire wing show evidence of persistent covariation. The Drosophila wing is, therefore, a single developmental unit.
9.4. Diverse Fluctuating Asymmetries
Although most applications have dealt with fluctuating bilateral asymmetry, there are numerous examples of other kinds of asymmetry in the literature. We summarize some notable examples.
9.4.1. Fluctuating Rotational, Dihedral, and Radial Asymmetries
A 2-dimensional object has rotational symmetry of order n if it is invariant when rotated radians about the symmetry center of the object. This axis is the axis of rotational symmetry. Dihedral symmetry is the symmetry of a 2-dimensional object having both mirror symmetry and rotational symmetry. Radial symmetry is rotational symmetry with an infinite number of rotations.
Despite their potential application, no published models for fluctuating rotational, dihedral, and radial asymmetry take into account two- and three-dimensional geometry and shape [,]. Nevertheless, Raz, Lefel, Hel-Or, Graham, and Nevo [] are working on a novel model for quantifying fluctuating radial asymmetry. They are now applying it to bacterial and fungal colonies growing on plate culture.
As demonstrated earlier (see 3.1), measures of dispersion are easily generalized to many kinds of fluctuating asymmetry. Var(xi), for example, is analogous to |l – r|, and is a measure of individual dihedral and rotational asymmetry. The mean of Var(xi) (or the standard deviation) is the actual measure of fluctuating asymmetry for a sample. Unfortunately, this method completely ignores shape and rotation. Therefore, it is usually a poor measure of fluctuating rotational, dihedral, and radial asymmetries. Occasionally, as in the lengths of ray flowers in the inflorescence of a sunflower, it may be the best approach.
A few studies have looked at fluctuating asymmetry of flowers displaying dihedral symmetry. Møller and Eriksson [], for example, measured flower asymmetry as either the difference between two randomly chosen petals, or the difference between the longest and the shortest petals. The deviations from dihedral symmetry were reduced to one-dimensional measurements of length and the problem was approached in terms of bilateral asymmetry (i.e., only two measurements were made on each flower or inflorescence, and the statistics of bilateral fluctuating asymmetry were applied).
9.4.2. Fluctuating Translational Asymmetry
Translational symmetry occurs in the internode lengths of plants and algae [] and in the bristle counts of metameres (segments) in arthropods []. When this symmetry has not been broken, the analysis is straightforward; the within-individual variance is a measure of individual asymmetry. The mean of the within-individual variances is then an estimate of fluctuating translational asymmetry at the population level. Tracy et al. [], for example, studied within-plant variation in internode length of the aquatic macrophyte Elodea canadensis (Hydrocharitaceae: Angiospermae) in polluted and unpolluted streams in Michigan, USA. Internode lengths of Elodea in the Clinton River, polluted with heavy metals, PCBs, grease, and pesticides, were more variable than those of plants in an unpolluted tributary. In contrast to Elodea, Ceratophyllum demersum (Ceratophyllaceae: Angiospermae) showed no significant differences in translational fluctuating asymmetry of internode lengths between these sites. Unlike Elodea, which is rooted in the sediments, Ceratophyllum is an unrooted macrophyte. Most of the pollutants were sequestered in the sediments.
To use this approach, though, one must first verify that the trait value (i.e., internode length in Elodea) is unrelated to its order. We recommend regressing the trait value on its order and examining the residuals before accepting the null hypothesis. If trait value changes with order, then translational symmetry has been broken. This is analogous to handedness of bilateral traits, and specialized methods are required to estimate fluctuating translational asymmetry.
More often than not, translational symmetry is broken. In arthropods, segment (metamere) length and width, as well as numbers of bristles, show consistent variation from anterior to posterior ends. By modeling this relationship, one can estimate individual asymmetry as a lack of fit to the model. Astaurov [], for example, studied variation in bristle count in the millipede Geophilus ferrugineus (Geophilidae: Myriapoda). For the first 15 segments, beginning at the anterior end, the number of bristles on each side averaged about 19. Between segments 15 and 30, the number of bristles declined to about 16, and remained unchanged to segment 46. In segment 47, the number of bristles decreased to 13 on each side. In general, the number of bristles declined from anterior to posterior ends of Geophilus. This variation was strictly deterministic, but the number of bristles varied in a random fashion, both within segments and between neighboring segments. This corresponds to fluctuating bilateral and translational asymmetry. Astaurov [] used deviations from a moving average as a measure of random translational variation. Paxman [] used a similar approach with variation in leaf length of Nicotiana rustica (Solanaceae: Angiospermae). In contrast to Astaurov’s [] moving average, Paxman used the standard error of the estimate Sy∙x of leaf length on leaf order as a measure of developmental instability. The standard error of the estimate, however, varies with the mean of the dependent variable. Zar [] prefers Sy∙x/ as a measure of variation around the regression.
All of these approaches assume a simple linear or nonlinear relationship between the trait and the segment (or internode) order. A more complex model, such as a higher-order polynomial, can always be made to fit the data more and more closely. Some judgement is necessary, and the residuals should be examined before Sy∙x/ is used to estimate fluctuating translational asymmetry. Sy∙x/ is estimated on a per individual basis, and the mean of Sy∙x/ across the sample is the estimate of fluctuating translational asymmetry.
In plants, internode lengths and widths show consistent variation from older to newer internodes. This relationship is a consequence of allometry and inhibition []. Alados et al. [] studied fluctuating translational asymmetry in Anthyllis cytisoides L. (Fabaceae: Angiospermae). The relation between internode length and internode order fits the general equation L = kNae-bN, where L is internode length, N is internode order starting from the base of the shoot, e is the base of natural logarithms, and k, a, and b are fitted constants []. The kNa reflects the allometric relationship between internode length and node order, and e-bN reflects apical inhibition. Stress presumably decreases the accuracy of the curve fitting. The standard error of the estimate (S y∙x/), the statistical noise in the allometric relation, is a measure of individual asymmetry.
Under controlled laboratory conditions involving a known stressor (cadmium), fluctuating translational asymmetry has proven a more reliable indicator of stress than fluctuating bilateral asymmetry, and more sensitive than either growth or reproduction []. It was used to assess environmental stress associated with water pollution [,,], soil cadmium [], and soil salinity [,].
9.4.3. Fluctuating Helical Asymmetry
Certain snails have a spiral shell approximating an equiangular spiral. Graham et al. [] studied deviations from a perfect equiangular spiral in three populations of the terrestrial snail Cepaea nemoralis (Helicidae: Gastropoda) in the Ukraine.
The equation for an equiangular spiral is
where r is the radius from apex to curve, a is a constant, e is the base of natural logarithms, θ is the angle made with a reference line passing through the apex, and Φ is the constant angle at which the radius vector cuts the curve. Graham et al. [] regressed loge r on loge a + θ cot Φ for each individual snail and used the standard error of the estimate, divided by the mean of the dependent variable, (Sy∙x/) as an estimate of individual asymmetry. Populations exposed to ammonia emissions and pesticides showed higher levels of asymmetry. Individuals in the population having the greatest helical asymmetry also showed erosion of their periostracum, which was not evident in the other two populations.
r = aeθ cot Φ,
9.4.4. Fractal Dimension
Fractals are objects invariant with respect to scaling [,]. They represent a form of symmetry, appearing the same at both high and low magnification. The fractal dimension (D) of an object is a measure of its complexity. While lines, planes, and solids have discrete dimensions (1, 2, and 3, respectively), fractals have fractional dimensions. A skull suture or a time series has a dimension between one and two (1 < D < 2). Clouds and bushes have dimensions between two and three (2 < D < 3). Indeed, fractal is short for fractional dimension. A skull suture having D = 1.7 fills more of a plane than one having D = 1.2. A bush having D = 2.8 fills more space than one having D = 2.3.
Graham et al. [] first suggested that fractals might be useful in studies of developmental instability, though it was unclear at the time how the fractal dimension of an object might respond to stress. Theory suggested it might decrease under stress, under the assumption that stress dissipates energy away from the development of space-filling fractals []. Work on the fractal dynamics of human heartbeat had also suggested that nonlinear complexity declined with aging and disease []. Nevertheless, we found fractal dimension usually decreasing under stress, though it could increase as well [,].
Fractal dimension decreases under stress in the roots of nitrogen-starved corn [], in the pulmonary arteries of hypertensive individuals [], in the crown of shrubs exposed to grazing [,,], in the saggital sutures of inbred Damas gazelles [], in the branching complexity of virally infected pepper [], in the behavioral time series of Spanish ibex parasitized with scabies [,], in time series associated with heart disease and Huntington’s disease [] (but see []), and in the vasculature of pituitary tumors []. Shandorff [], however, found no difference in the fractal dimension of skull sutures in Harbor Seals before and after the advent of pollution in the Baltic Sea, but the left-right fractal asymmetry of these sutures was greater during the period of greatest pollution. The fractal dimension of skull sutures in Harbor Seals was only slightly larger than 1.0, so they were never complex to begin with. Indeed, if they were not significantly greater than 1.0, one would have difficulty calling them fractal sutures.
Examples of fractal dimension increasing under stress are more difficult to find. The rockweed Fucus sp. (Fucaceae: Phaeophyceae) shows greater fractal dimension at polluted sites in Puget Sound, near Seattle, Washington []. The increased fractal dimension is associated with increased irregularity of rockweed’s surface.
Clearly, changes in the fractal dimension of a trait have more in common with phenotypic modifications (i.e., decrease in growth rate) than they do with developmental instability. Because the fractal dimension of an object is usually estimated as the slope of a regression line, Graham et al. [] also suggested the standard error of the estimate (S y∙x/) be used as an index of developmental instability. There are, however, many methodological problems associated with such estimates []. For example, if techniques devised to estimate monofractals are blindly applied to multifractals, then D will be biased and S y∙x/ will be inflated, because multifractals are more complex than monofractals [,]. More research is needed.
9.5. Fluctuating Asymmetry and Developmental Instability of Diverse Taxonomic Groups
9.5.1. Viruses
There have been few studies of developmental instability (and environmental robustness) in viruses. Moreover, many of the studies of genetic robustness address canalization, not stability. Nevertheless, some studies have examined within-genotype variation. Commoner [] and colleagues, including Symington et al. [], examined variation in length of the Tobacco Mosaic Virus, a helical RNA virus. The rods vary greatly in length, from 50-600 mμ. The modal length is 300 mμ. Rods longer than 300 mμ arise by polymerization during preparation, but most of the rods measuring less than 300 mμ are due to natural biosynthetic variation, not in vivo breakage during preparation for electron microscopy []. The short rods probably represent aborted forms of the virus [], and they make up much of the population. Assuming all of these rods are genetically identical (they came from the same purified strain), this work suggests biosynthesis of Tobacco Mosaic Virus is inherently unstable.
According to Elena and Sanjuán [], viral thermostability is a form of environmental robustness, and hence a measure of developmental stability. It is also an essential characteristic of vaccines [].
RNA viruses are also less robust to mutation than comparable DNA viruses or RNA products in bacteria and eukaryotes []. This is largely a consequence of their compact genome, high mutation rate, and large population size []. Nevertheless, such hypersensitive RNA viruses often induce, and then take advantage of, their host’s molecular chaperones. Moreover, co-infection by different genotypes introduces an element of distributional robustness. Therefore, while mutational robustness is low for individuals, it may be large for populations within a host.
Bacteriophage plaques could be a useful model system for the study of developmental stability. Phenotypic variation among plaques of a single haplotype, and fluctuating radial asymmetry of individual plaques, could be used to study response to environmental or genetic stresses. Nevertheless, we are unaware of studies examining plaque variation and asymmetry in bacteriophage.
9.5.2. Archaea and Eubacteria
To our knowledge, there is only one study of developmental instability of eubacteria [], and none of Archaea, in the literature. For the most part, measuring asymmetry of individual bacteria is impractical. Nevertheless, random variation in gene expression within a genetically homogeneous population is developmental instability [].
Costas and Lopez-Rodas [] found copper sulphate and DCMU-herbicide both increasing asymmetry between sister cells in the cyanobacterium Microcystis aeruginosa. The sister cells are analogous to bilateral symmetry, though there is no way to specify right and left.
Despite the difficulty of measuring asymmetry of individual bacteria, bacterial colonies are large enough for asymmetry estimates. Moreover, microbiologists often see bacterial colonies as multicellular organisms [], albeit simple ones. Many bacteria produce disk-like colonies on agar medium, and the shape of these colonies may change under stress [].
Many bacterial colonies produce branching fractal patterns, a product of cell-cell interactions []. The fractal dimension of these colonies can change under stress. According to Ben-Jacob [], colonies of Paenibacillus dendritiformis, a lubricating bacterium, can shift from compact, to tip-splitting, to bushy fractal, to dihedral branches as peptone concentration is lowered in its medium.
In studies of colony asymmetry, one needs to distinguish asymmetric sectors caused by mutation from those caused by random variation []. Because cell numbers are enormous, mutations early in the development of a colony can generate significant variation at the level of the colony itself.
By using continuous symmetry measures, one can estimate fluctuating radial asymmetry of bacterial colonies even in the absence of landmarks. We are preparing a study of colony asymmetry of soil bacteria and their phages from north- and south-facing slopes of “Evolution Canyon,” Israel.
9.5.3. Fungi
As with bacteria, fluctuating asymmetry studies of fungal species are rare. Levy and Siegel’s [] study of Saccharomyces cerevisiae, however, is an excellent example of work with unicellular fungi. They found 300 gene products that, when absent in single-gene knockouts, caused an increase in morphological variation among cells. The 300 gene products included proteins influencing or mediating chromosome organization and DNA integrity, RNA elongation, protein modification, cell cycle, and response to stress. These proteins were also among the most highly connected hubs in Saccharomyces’ metabolic network.
Fungi are excellent subjects for studies of fluctuating asymmetry. The fruiting bodies of several fungal groups, including the basidiomycota and ascomycota, often exhibit radial symmetry. Moreover, clones usually produce several fruiting bodies, so one can compare clones. Finally, the prevalence of haploidy in fungi suggests genetic and environmental robustness may be low. Haploid fungi should, theoretically, have greater developmental instability than diploid organisms, such as plants and animals.
Fungal colonies on agar medium are also amenable to studies of fluctuating radial asymmetry. We have begun a study of colony asymmetry in the soil fungus Aspergillus niger (Trichocomaceae: Ascomycota) from “Evolution Canyon.” The conidia of populations on the south-facing slope have greater melanin content than do those on the north-facing slope []. This is presumably an adaptation to UV-stress on the exposed south-facing slope.
9.5.4. Plants
Plants are excellent subjects for studies of fluctuating asymmetry [,]. Their modular design is a distinct advantage, allowing researchers to estimate individual fluctuating asymmetry. One disadvantage of plants is that they are immobile, which means environmental stress may vary among a plant’s different parts []. Cowart and Graham [], for example, found outer leaves in the crown of Ficus carica more asymmetrical than inner leaves. If leaf location is included as a source of variation, however, one can account for it statistically.
Studies of fluctuating asymmetry in plants have addressed leaf asymmetry of angiosperms [], needle asymmetry of conifers [], flower asymmetry [], dichotomous branching [,], fractal branching [,,], and fractal time series [,].
Plants also lend themselves to experimental manipulation [].
9.5.5. Animals
Most studies of fluctuating asymmetry have been done with animals (see references mentioned throughout this review), including arthropods (insects, millipedes, arachnids), molluscs, and vertebrates (fish, reptiles, birds, and mammals). Nevertheless, there have been, to our knowledge, no comparative studies of different taxonomic groups, and no studies of the parazoa or radiata.
9.6. Fossil Material
There have been few studies of fluctuating asymmetry among fossil populations []. There are serious limitations, of course; specimens are compressed, deformed, and fragmented during fossilization. Nevertheless, some meristic traits, such as the number of facets in left and right eyes of trilobites, or the arrangement of foramina in vertebrate skulls, might permit reliable evaluation of asymmetry. In addition, one can study objects resistant to deformation, such as teeth. Unfortunately, it is difficult to assign teeth to individuals if the skull is fragmented.
Despite these challenges, the study of fluctuating asymmetry in fossil populations is the only way of testing some important evolutionary questions. Palmer [], for example, suggested that comparisons of fluctuating asymmetry among prehistoric populations, or between prehistoric and extant populations, might be the only means of inferring genetic and environmental stress in the fossil record. Moreover, fluctuating asymmetry might reveal changes in morphological integration over evolutionary time []. To date, however, few studies of this sort have been published.
Van Valen [] conducted the earliest study of fluctuating asymmetry on fossil material: dental asymmetry of the Pliocene horse Griphippus gratus (Equidae: Mammalia). The difficulties of working with Griphippus are typical. Of 400 specimens, only 36 had complete upper jaws with teeth on both sides. Van Valen reported the existence of random variation, but made no attempt to compare populations.
Smith [] studied asymmetry in nine genera of early Paleozoic (lower Cambrian through Silurian) trilobites (Trilobita: Arthropoda). The idea that the Cambrian Explosion was due, in part, to lax developmental constraints suggested that fluctuating asymmetry might decline through the Paleozoic. Smith, however, found no evidence of a decline in fluctuating asymmetry of five bilateral traits measured on the cranidium (part of the head shield) over the nearly 100 million years.
Palmqvist et al. [] attributed bilateral asymmetry and dental anomalies in a single complete skull of the large lower-Pleistocene canid Canis (Xenocyon) falconeri to possible isolation and small population size. Of 66 skeletal remains of this species, all but this one skull were fragmented and scattered; most teeth could not be assigned to particular individuals.
9.7. Molecular Robustness
Both genetic and environmental robustness can be studied at the molecular level, and these studies address basic questions regarding the evolution of robustness. Szöllősi and Derényi [], for example, examined the robustness of miRNA precursors to thermal fluctuations. They concluded that the genetic robustness of miRNA sequences is a byproduct of selection for environmental robustness (but see []). See also the section 9.5.1, on viruses.
9.8. Specific Disciplines
Here we present a brief sampling of the literature on fluctuating asymmetry in different disciplines. For many of these disciplines, this is a small fraction of the literature.
9.8.1. Ecotoxicology
Fluctuating asymmetry has been widely used as an indicator of anthropogenic stress, including air and water pollution, elevated carbon dioxide, pesticides, and heavy metals (Table 5). A comparison of Table 5 with the small sample of studies in Table 3 and Table 4 reveals proportionately more anthropogenic stressors showing positive results. Novel stressors, such as pesticides, are more likely to interfere with development simply because populations have not had time to adapt (but see []). But elevated carbon dioxide, a greenhouse gas, actually decreased the amount of leaf asymmetry in two oaks []. Nevertheless, unnatural toxins tend, in general, to increase fluctuating asymmetry.

Table 5.
Anthropogenic stress and fluctuating asymmetry; a small sampling of studies and stressors.
9.8.2. Conservation Biology
Threatened and endangered species often suffer from inbreeding and outbreeding depression. Inbreeding occurs because populations of rare species are small. Outbreeding occurs when rare species hybridize with more abundant related species. Both inbreeding and outbreeding depression sometimes increase fluctuating asymmetry [].
In addition to inbreeding and outbreeding, anthropogenic stress, such as deforestation, habitat fragmentation, and urbanization, can increase fluctuating asymmetry of endangered species. Moreover, anthropogenic stress can exacerbate the effects of inbreeding depression. The Taita Thrush, Turdus helleri (Turdidae: Aves), for example, is a critically endangered species suffering from both inbreeding and forest fragmentation. Inbreeding has a greater effect on fluctuating asymmetry in more fragmented habitats than in less fragmented ones [,].
One may combine data on fluctuating asymmetry with GIS data and map areas of disturbance. Teixeira et al. [], for example, combined data on fluctuating asymmetry of Didelphis albiventris, a marsupial (Didelphinae: Mammalia), with GIS data on environmental composition. Though the sample sizes in this study were small, opossums in the least impacted natural environment had statistically lower levels of asymmetry.
9.8.3. Anthropology and Evolutionary Psychology
Anthropologists and evolutionary psychologists are doing some of the most interesting research involving fluctuating asymmetry. The literature, especially in anthropology, is large. We point out some of the highlights here. See Perzigian [] for a review of the older literature on dental asymmetry in human populations.
Studies of human cranial asymmetry have produced surprising results. Modern humans, for example, have greater cranial asymmetry than Medievals from Cedynia and Grózdek in Poland [,]. Modern humans also have greater dental asymmetry than the great apes (Pan, Gorilla, Pongo) []. In contrast, Medieval Nubians (Sudanese Nubia) from the early Christian period display greater cranial asymmetry than those from the later Christian period []. Independent evidence suggests individuals from the early period were also less healthy.
Research on fluctuating asymmetry of fossil hominids is limited by the number of intact skeletons and the availability of complete left and right dental archs []. Even with limited sample sizes, Homo habilis, H. neaderthalensis, and H. sapiens (Hominidae: Mammalia) all seem to have greater dental asymmetry than the great apes []. Moreover, the small sample of H. habilis seems to have lower fluctuating dental asymmetry than either Australopithecus africanus or Australopithecus (Paranthropus) robustus [,]. Larger samples will be necessary to distinguish between species of Australopithecus, Paranthropus, and the extinct species of Homo. As more material becomes available, researchers may be able to infer environmental and genetic stresses in our evolutionary past.
There has been much work on fluctuating asymmetry and sexual selection in humans. Women, for example, rate the dancing of symmetrical men more highly than that of asymmetrical men [].
Finally, there are applications in psychology. Fluctuating asymmetry, for example, is associated with male, but not female, sexual orientation []. Moreover, it is positively associated with schizophrenia [,], human reactive aggression [], and attention-deficit hyperactivity disorder [,], but is unrelated to psychosis [].
9.8.4. Medicine and Public Health
Other than the association between fractal dimension and disease states, which we reviewed in section 9.4.5, there have been few applications of fluctuating asymmetry to medicine and public health, despite Thornhill and Møller’s [] “wake-up call” to the health professions. If fluctuating asymmetry is truly a marker of “good health,” as they argue, then it should be a useful tool. We agree, but feel it will be more useful as an indicator of community (i.e., population) health, than as an indicator of individual health.
As a recent example of a public-health application, high school students (especially males) from a slum in Ankara, Turkey had greater facial asymmetry than those from an upper-class neighborhood []. Moreover, the students from the slum were 9 kg lighter and 7 cm shorter than those from the upper-class neighborhood [].
Van Dongen et al. [] studied fluctuating asymmetry of human fetuses with severe developmental disorders. Surprisingly, skeletal asymmetry was significantly greater than that of controls for only four of 17 developmental disorders. The disorders having elevated fluctuating asymmetry were those associated with left–right patterning, limb defects, and problems of bronchopulmonary and urogenital systems. Moreover, even for these four kinds of disorders, levels of fluctuating asymmetry were smaller than expected.
For a review of the literature on symmetry and physical health, see [].
9.8.5. Agriculture and Aquaculture
Fluctuating asymmetry is also a potentially useful indicator of animal [] and plant [,] health and welfare. Almeida et al. [], for example, found higher fluctuating asymmetry in ornamental goldfish than in their wild relatives. Moreover, mortality of commercial oysters is related to shell asymmetry []. In contrast, stress does not increase fluctuating asymmetry of domestic chickens [].
10. Fluctuating Asymmetry: Problems and Solutions
10.1. Inconsistencies among Studies of Fluctuating Asymmetry
The results of fluctuating asymmetry studies are inconsistent. In some studies, for example, fluctuating asymmetry increases under environmental and genetic stress [,]. Conversely, fluctuating asymmetry does not increase under stress in other studies [,]. Indeed, Leung and Forbes [, p. 403] have stated that fluctuating asymmetry "may be a poor general predictor of either stress or fitness." Complex environments, adaptation to stress, and inadequate methodology may contribute to this inconsistency, at least in part. Here we examine some likely reasons for these inconsistencies, as well as partial solutions.
Various biotic and abiotic stressors impinge on individuals in natural populations. The biotic stressors include competition, predation, herbivory, parasitism, and disease. The abiotic stressors include high and low temperature, insufficient light, and inadequate water and nutrients. Together, they present a complex spatio-temporal pattern. One can control these variables in a lab or field experiment [,], but studying fluctuating asymmetry of natural populations is problematic. At the outset, we usually have little information about the kinds and amounts of stress. Indeed, we usually take the opposite approach and try to infer stress through fluctuating asymmetry.
Extreme environments are stressful (or not) only when they interact with organisms, or more precisely, when they interact with the different parts of organisms. Some parts, such as the wings of a fruitfly, may respond to stress, and others, such as its sternopleural bristles, may not [,]. Fluctuating asymmetry of one trait rarely correlates with fluctuating asymmetry of other traits []. This is especially true when one is looking at fluctuating asymmetry of several traits in a single individual [,].
While individual-wide fluctuating asymmetry is rare, population-wide asymmetry is common. If one trait is more asymmetric in one population, other traits are likely more asymmetric as well. To estimate population-wide asymmetry, researchers sometimes use Kendall’s Coefficient of Concordance.
Responses to stress are trait-specific, and may remain undetected unless the appropriate traits are measured []. Consequently, particular environmental conditions will affect only some developmental pathways leading to specific responses []. In addition, individuals and populations may be well adapted to an environment appearing stressful to us, or may be able to avoid stress through behavioral modifications [].
Measuring and comparing fluctuating asymmetry is not as easy and straightforward as it seems. The signal is small, and the chance of producing spurious results is high. If one is careless, one may miss a real signal (false negative) or find a false signal (false positive). Measurement error, size scaling, and the statistical distribution should be handled carefully (see [], and section 5 in this review).
10.2. The “Evolution Canyon” Microsites
Controlling abiotic and biotic stressors in a controlled experiment may provide a partial solution to the inconsistency problem. One cannot, however, control these stressors in natural situations, though their number can be reduced. By using standardized sampling and measurement, as well as by collecting data from many species in a variety of taxa, we may be better able to evaluate developmental instability.
Divergent microsites provide an opportunity for reducing the number of environmental factors in studies of natural populations. We found this in the “Evolution Canyon” microsites (Figure 28), where south-facing "African" slopes abut north-facing "European" slopes. The “African” slopes, which are xeric and tropical, are (on average) 200 m from the “European” slopes, which are mesic and temperate.

Figure 28.
The four “Evolution Canyons” in Israel (EC I – EC IV). Note the interslope divergence in vegetation, even in EC III in the Negev Desert [].
The two slopes of the “Evolution Canyon” microsites provide a wonderful opportunity for studying developmental instability in a partly controlled natural experiment. The rocks, soils, and topography are similar on the opposing slopes. Microclimate alone is the major abiotic difference. The “African” slope is more stressful for many terrestrial organisms [,,,,,,], hence we know, in part, the amount of stress on each slope, especially since microclimate on the opposite slopes is known [].
One consequence of the contrasting stressors is that terrestrial and aquatic communities respond differently to microclimate on the two slopes. There are more terrestrial species on the “African” slope, and more aquatic species on the “European” slope. Moreover, phenotypic and genetic variation differs between the two slopes. For example, nine of 14 model organisms (bacteria to vertebrates) have significantly greater genetic polymorphism on the more stressful “African” slope. Moreover, some species have greater rates of mutation, gene conversion, recombination, and DNA repair, as well as larger genome sizes and more small sequence repeats (SSRs), single nucleotide polymorphisms (SNPs), retrotransposons, transposons, candidate gene diversity, and genome-wide gene expression and regulation on the more stressful “African” slope (reviews in [,,,,]. Remarkably, incipient sympatric speciation is occurring across all taxa, from bacteria to mammals, on the two slopes.
10.3. Ongoing Research on Fluctuating Asymmetry at the “Evolution Canyon” Microsites
The interdisciplinary study of fluctuating asymmetry at the “Evolution Canyon” microsites includes the development and use of novel, trait-specific measures of fluctuating asymmetry, as well as the use of conventional indices. Some of the novel methods include measures of leaf asymmetry involving secondary [,] and higher order [] veins. We have used these approaches on leaves of Quercus calliprinos and Salvia fruticosa at “Evolution Canyon I,” as well as Ruta chalepensis at “Evolution Canyon II.” All of these studies have shown higher fluctuating asymmetry on the dry “African” slope. We are currently conducting a study of leaf asymmetry of 12 plant species at “Evolution Canyon” I [].
Previously, Auslander et al. [] studied the developmental instability of Pistacia lentiscus on the opposite slopes of two “Evolution Canyons” in Israel (e.g., Nahal Keziv and Nahal Oren) and an additional canyon, Nahal Mearot. The average leaves at the three canyons were 20% larger on the “European” slope than on the “African” slope. In addition, leaf asymmetry (standardized by leaf size) was similar on “African” and “European” slopes of Nahal Mearot and Nahal Keziv, whereas it was two times higher on the “African” slope of Nahal Oren (i.e., “Evolution Canyon” I). In contrast, we found no difference in leaf asymmetry of P. lentiscus at Nahal Oren, probably because the power transformation we used compensated for overcorrection almost certainly present in the Auslander study. Prior to the power transformation, our data also indicated greater asymmetry on the “African” slope [].
One study of fluctuating asymmetry in an animal species has been completed at “Evolution Canyon” (though more are in progress). Derzhavets et al. [] found greater fluctuating asymmetry of wing dimensions in Drosophila melanogaster on the “African” slope. Unlike the Auslander [] study, five replicate measurements were averaged prior to the analysis, to minimize measurement error. Overcorrection was not a problem here. Low humidity on the “African” slope is a likely stressor for D. melanogaster [].
In addition to this completed work, the group at the Institute of Evolution at the University of Haifa, as well as their collaborators elsewhere, is currently developing an image-processing-based CSM for fluctuating radial asymmetry, and is already using it with seven fungal species from the opposite slopes of “Evolution Canyon” I. Moreover, the group is developing a new CSM for 3-dimensional branches of plants. Finally, a study of the fluctuating asymmetry of beetles is in our immediate plans. Future studies will address fluctuating asymmetry of bacteria, additional arthropods, and mammals, to see if different taxa across life share a similar drought stress on the “African” slope and light stress on the “European” slope.
11. Conclusions
Fluctuating asymmetry is a useful indicator of stress, not because it is more sensitive to stress than phenotypic modification, but because it reveals the average individual’s robustness and stability in the face of stress. In this respect, it is the only indicator that addresses developmental homeostasis. Consequently, if fluctuating asymmetry remains unchanged in the face of a stressor that has influenced growth and reproduction (e.g., clutch size), it may simply mean that developmental homeostasis was not disturbed. Moreover, if one accepts the definition of stress advocated by Escós et al. [] and Walter Cannon [], then one might infer that, despite changes in growth and reproduction, the population was unstressed. In future work, researchers might compare indices of developmental and physiological homeostasis.
Fluctuating asymmetry may occasionally correlate with individual fitness. Nevertheless, we do not advocate using it as an index of individual fitness. Scientists should measure relative reproductive success, not symmetry. Nevertheless, it may be worthwhile to understand when and how fluctuating asymmetry correlates with individual fitness. The best opportunity for doing so is with organisms having repeated modular elements, such as plants.
Regardless of whether it is used as either an indicator of stress or a correlate of fitness, fluctuating asymmetry must be used with more care than has been typical in the literature. Sample sizes should be large, and replicate measurements are essential. Moreover, researchers must address mixed error distributions and size-scaling. Failure to do so can easily generate spurious associations.
Future work should focus on resolving the current controversies regarding developmental instability, stress, and fitness. These issues are too important to ignore, and the recent genomic revolution provides unlimited opportunity to dissect the genetic architecture of developmental instability. We also suggest that ecologically divergent microsites, such as “Evolution Canyon,” might serve as natural laboratories for the study of developmental instability across all of life. Consequently, we have initiated studies of fluctuating asymmetry in several species of plants, fungi, bacteria, and animals on both slopes of “Evolution Canyon,” sharing drought stress on the “African” slope and light stress on the “European” slope. We also plan to compare and contrast these taxa in at least two “Evolution Canyons,” one in the mountains of Carmel and the other in Uppper Galilee (EC I and EC II).
Acknowledgements
We thank Larry Leamy, Inma Alados, Peter Parsons, Kevin Floate, and an anonymous reviewer for their comments on a preliminary draft of the manuscript. We also thank Tomas Pavlíček and Avigdor Beiles, who are continuous collaborators, and we benefited from discussions with Larry Leamy, Stefan Van Dongen, Peter Parsons, Barış Özener, and Gregory Babbitt. Catherine Chamberlin-Graham helped with the literature search, photography, and proofread the draft. Bill Davin and Ashwani K. Rai provided additional photographs. JHG was supported by a sabbatical and endowed chair from Berry College. We also thank the Ancell-Teicher Research Foundation for Genetics and Molecular Evolution for financial support.
References
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Abraham, E.R. The fractal branching of an arborescent sponge. Mar. Biol. 2001, 138, 503–510. [Google Scholar] [CrossRef]
- Astaurov, B.L. Analyse der erblichen Störungsfälle der bilateralen Symmetrie. Z. Indukt. Abstamm. Ver. 1930, 55, 183–262. [Google Scholar] [CrossRef]
- Ludwig, W. Das Rechts-Links Problem im Tierreich und beim Menschen; Springer: Berlin, Germany, 1932. [Google Scholar]
- Mather, K. Genetical control of stability in development. Heredity 1953, 7, 297–336. [Google Scholar] [CrossRef]
- Van Valen, L. A study of fluctuating asymmetry. Evolution 1962, 16, 125–142. [Google Scholar] [CrossRef]
- Soulé, M. Phenetics of natural populations. II. Asymmetry and evolution in a lizard. Am. Nat. 1967, 101, 141–160. [Google Scholar] [CrossRef]
- Jones, J.S. An asymmetrical view of fitness. Nature 1987, 325, 298–299. [Google Scholar] [CrossRef]
- Zakharov, V.M.; Graham, J.H. (Eds.) Developmental Stability in Natural Populations; Finnish Zoological Publishing Board: Helsinki, Finland, 1992. [Google Scholar]
- Markow, T.A. (Ed.) Developmental Instability: Its Origins and Evolutionary Implications; Kluwer: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Møller, A.P.; Swaddle, J.P. Asymmetry, Developmental Stability, and Evolution; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
- Polak, M. (Ed.) Developmental Instability: Causes and Consequences; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Zakharov, V.M. Future prospects for population phenogenetics. Sov. Sci. Rev. F, Physiol. Gen. Biol. Rev. 1989, 4, 1–79. [Google Scholar]
- Zakharov, V.M. Population phenogenetics: analysis of developmental stability in natural populations. Acta Zool. Fenn. 1992, 191, 7–30. [Google Scholar]
- Babcock, L.E. Asymmetry in the fossil record. Eur. Rev. 2005, 13, 135–143. [Google Scholar] [CrossRef]
- Costas, E.; Lopez-Rodas, V. Copper sulphate and DCMU-herbicide treatments increase asymmetry between sister cells in the toxic cyanobacteria Microcystis aeruginosa: implications for detecting environmental stress. Water Res. 2006, 40, 2447–2451. [Google Scholar] [CrossRef] [PubMed]
- Steven, A.C.; Trus, B.L.; Booy, F.P.; Cheng, N.; Zlotnick, A.; Caston, J.R.; Conway, J.F. The making and breaking of symmetry in virus capsid assembly: glimpses of capsid biology from cryoelectron microscopy. FASEB J. 1997, 11, 733–742. [Google Scholar] [CrossRef] [PubMed]
- Danforth, C.H. Resemblance and difference in twins. J. Hered. 1919, 10, 399–409. [Google Scholar] [CrossRef]
- Sumner, F.B.; Huestis, R.R. Bilateral asymmetry and its relation to certain problems of genetics. Genetics 1921, 6, 445–485. [Google Scholar] [PubMed]
- Graham, J.H.; Freeman, D.C.; Emlen, J.M. Developmental stability: a sensitive indicator of populations under stress. In Environmental Toxicology and Risk Assessment; ASTM STP 1179; Landis, W.G., Hughes, J., Lewis, M.A., Eds.; American Society for Testing and Materials: Philadelphia, PA, USA, 1993; pp. 136–158. [Google Scholar]
- Klingenberg, C.P.; McIntyre, G.S. Geometric morphometrics of developmental instability: analyzing patterns of fluctuating asymmetry with procrustes methods. Evolution 1998, 52, 1363–1375. [Google Scholar] [CrossRef] [PubMed]
- Freeman, D.C.; Graham, J.H.; Emlen, J.M.; Tracy, M.; Hough, R.A.; Alados, C.L.; Escós, J. Plant developmental instability: new measures, applications, and regulation. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 367–386. [Google Scholar]
- Milner, D.; Hel-Or, H.; Keren, D.; Raz, S.; Nevo, E. Analyzing symmetry in biological systems. Proc. IEEE Int. Conf. Image Proc. 2005, 1, 361–364. [Google Scholar]
- Milner, D.; Raz, S.; Hel-Or, H.; Keren, D.; Nevo, E. A new measure of symmetry and its application to classification of bifurcating structures. Pattern Recogn. 2007, 40, 2237–2250. [Google Scholar] [CrossRef]
- Beloussov, L.V. The Dynamic Architecture of a Developing Organism; Kluwer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Symmetry as a continuous feature. IEEE T. Pattern Anal. 1995, 17, 1154–1166. [Google Scholar] [CrossRef]
- Beklemishev, V.N. Principles of Comparative Anatomy of Invertebrates; University of Chicago Press: Chicago, IL, USA, 1964. [Google Scholar]
- Grabowsky, G.L. Symmetry, locomotion, and the evolution of an anterior end: a lesson from sea urchins. Evolution 1994, 48, 1130–1146. [Google Scholar] [CrossRef]
- Thomas, A.L.R. The aerodynamic costs of asymmetry in the wings and tail of birds: asymmetric birds can’t fly round tight corners. Proc. R. Soc. Lond. B 1993, 254, 181–189. [Google Scholar]
- Brown, C.R.; Brown, M.B. Intense natural selection on body size and wing and tail asymmetry in Cliff Swallows during severe weather. Evolution 1998, 52, 1461–1475. [Google Scholar] [CrossRef]
- Finnerty, J.R. Did internal transport, rather than directed locomotion, favor the evolution of bilateral symmetry in animals? BioEssays 2005, 27, 1174–1180. [Google Scholar] [CrossRef] [PubMed]
- Davis, G.K.; Patel, N.H. The origin and evolution of segmentation. Trends Biochem. Sci. 1999, 24, M68–M72. [Google Scholar] [CrossRef]
- Couso, J.P. Segmentation, metamerism and the Cambrian explosion. Int. J. Dev. Biol. 2009, 53, 1305–1316. [Google Scholar] [CrossRef] [PubMed]
- Weibel, E.R. Fractal geometry: a design principle for living organisms. Am. J. Physiol. Lung Cell. Mol. Physiol. 1991, 261, L361–L369. [Google Scholar] [CrossRef] [PubMed]
- Enquist, B.J. Universal scaling in tree and vascular plant allometry: toward a general quantitative theory linking plant form and function from cells to ecosystems. Tree Physiol. 2002, 22, 1045–1064. [Google Scholar] [CrossRef] [PubMed]
- Farnsworth, K.D.; Niklas, K.J. Theories of optimization, form and function in branching architecture in plants. Funct. Ecol. 1995, 9, 355–363. [Google Scholar] [CrossRef]
- West, G.B.; Brown, J.H.; Enquist, B.J. The origin of universal scaling laws in biology. In Scaling in Biology; Brown, J.H., West, G.B., Eds.; Oxford University Press: New York, NY, USA, 2000. [Google Scholar]
- Banavar, J.R.; Maritan, A.; Rinaldo, A. Size and form in efficient transportation networks. Nature 1999, 399, 130–132. [Google Scholar] [CrossRef] [PubMed]
- Klingenberg, C.P.; Barluenga, M.; Meyer, A. Shape analysis of symmetric structures: quantifying variation among individuals and asymmetry. Evolution 2002, 56, 1909–1920. [Google Scholar] [CrossRef] [PubMed]
- Radwan, J.; Watson, P.J.; Farslow, J.; Thornhill, R. Procrustean analysis of fluctuating asymmetry in the bulb mite Rhizoglyphus robini Claparede (Astigmata: Acaridae). Biol. J. Linn. Soc. 2003, 80, 499–505. [Google Scholar] [CrossRef]
- Smith, D.R.; Crespi, B.J.; Bookstein, F.L. Fluctuating asymmetry in the honey bee, Apis mellifera: effects of ploidy and hybridization. J. Evol. Biol. 1997, 10, 551–574. [Google Scholar] [CrossRef]
- Auffray, J.-C.; Alibert, P.; Renaud, S.; Orth, A.; Bonhomme, F. Fluctuating asymmetry in Mus musculus subspecific hybridization: traditional and Procrustes comparative approach. In Advances in Morphometrics; Marcus, L.F., Corti, M., Loy, A., Naylor, G.J.P., Slice, D.E., Eds.; Plenum Press: New York, NY, USA, 1996; pp. 275–283. [Google Scholar]
- Møller, A.P.; Van Dongen, S. Ontogony of asymmetry and compensational growth in Elm Ulmus glabra leaves under different environmental conditions. Int. J. Plant. Sci. 2003, 164, 519–526. [Google Scholar] [CrossRef]
- Nagamitsu, T.; Kawahara, T.; Hotta, M. Phenotypic variation and leaf fluctuating asymmetry in isolated populations of an endangered dwarf birch Betula ovalifolia in Hokkaido, Japan. Plant Spec. Biol. 2004, 19, 13–21. [Google Scholar] [CrossRef]
- Kozlov, M.V.; Wilsey, B.J.; Koricheva, J.; Haukioja, E. Fluctuating asymmetry of birch leaves increases under pollution impact. J. Appl. Ecol. 1996, 33, 1489–1495. [Google Scholar] [CrossRef]
- Meissner, W.; Zolkos, K. What to divide leaves into ten parts for? The proposition of shape indices of leaf blade. Dendrobiology 2008, 60, 29–33. [Google Scholar]
- Sinclair, C.; Hoffmann, A.A. Monitoring salt stress in grapevines: are measures of plant trait variability useful? J. Appl. Ecol. 2003, 40, 928–937. [Google Scholar] [CrossRef]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry: measurement, analysis, patterns. Annu. Rev. Ecol. Syst. 1986, 17, 391–421. [Google Scholar] [CrossRef]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry analyses revisited. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 279–319. [Google Scholar]
- Graham, J.H.; Freeman, D.C.; Emlen, J.M. Antisymmetry, directional asymmetry, and dynamic morphogenesis. Genetica 1993, 89, 121–137. [Google Scholar] [CrossRef]
- Graham, J.H.; Emlen, J.M.; Freeman, D.C. Nonlinear dynamics and developmental instability. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 35–50. [Google Scholar]
- Graham, J.H.; Emlen, J.M.; Freeman, D.C.; Leamy, L.J.; Kieser, J. Directional asymmetry and the measurement of developmental instability. Biol. J. Linn. Soc. 1998, 64, 1–16. [Google Scholar] [CrossRef]
- Van Dongen, S.; Lens, L.; Molenberghs, G. Mixture analysis of asymmetry: modelling directional asymmetry, antisymmetry and heterogeneity in fluctuating asymmetry. Ecol. Lett. 1999, 2, 387–396. [Google Scholar]
- Swaddle, J.P.; Witter, M.S.; Cuthill, I.C. The analysis of fluctuating asymmetry. Anim. Behav. 1994, 48, 986–989. [Google Scholar] [CrossRef]
- Palmer, A.R. Fluctuating asymmetry analyses: a primer. In Developmental Instability: Its Origins and Evolutionary Implications; Markow, T.A., Ed.; Kluwer: Dordrecht, The Netherlands, 1994; pp. 335–364. [Google Scholar]
- Glasser, G.J. Variance formulas for the mean difference and coefficient of concentration. J. Am. Stat. Assoc. 1962, 57, 648–654. [Google Scholar] [CrossRef]
- Gorard, S. Revisiting a 90-year-old debate: the advantages of the mean deviation. Brit. J. Educ. Stud. 2005, 53, 417–430. [Google Scholar] [CrossRef]
- Levene, H. Robust tests for equality of variances. In Contributions to Probability and Statistics; Olkin, I., Ed.; Stanford University Press: Stanford, CA, USA, 1960; pp. 278–292. [Google Scholar]
- Palmer, A.R.; Strobeck, C. Fluctuating asymmetry as a measure of developmental stability: implications of non-normal distributions and power of statistical tests. Acta Zool. Fenn. 1992, 191, 57–72. [Google Scholar]
- Goldstein, D.G.; Taleb, N.N. We don’t quite know what we are talking about when we talk about volatility. J. Portfolio Manage. 2007, 33, 84–86. [Google Scholar] [CrossRef]
- Bookstein, F.L. Morphometric Tools for Landmark Data; Cambridge University Press: New York, NY, USA, 1991. [Google Scholar]
- Auffray, J.–C.; Debat, V.; Alibert, P. Shape asymmetry and developmental stability. In On Growth and Form: Spatio-temporal Pattern Formation in Biology; Chaplain, M.A.J., Singh, G.D., McLachlan, J.C., Eds.; John Wiley & Sons: London, UK, 1999; pp. 309–324. [Google Scholar]
- Mardia, K.V.; Bookstein, F.L.; Moreton, I.J. Statistical assessment of bilateral symmetry of shapes. Biometrika 2000, 87, 285–300. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Leamy, L.J. Quantitative genetics of geometric shape in the mouse mandible. Evolution 2001, 55, 2342–2352. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures. J. Am. Chem. Soc. 1992, 114, 7843–7851. [Google Scholar] [CrossRef]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry for shapes. In Aspects of Visual Form Processing; Arcelli, C., Cordella, L., Sanniti di Baja, G., Eds.; World Scientific Publ.: Singapore, 1994; pp. 594–613. [Google Scholar]
- Rowland, H.A. The Physical Papers of Henry Augustus Rowland. Johns Hopkins Press: Baltimore, MD, USA, 1902; http://www.archive.org/details/physicalpapersof00rowlrich accessed on 18 March 2010.
- Zabrodsky, H.; Peleg, S.; Avnir, D. Continuous symmetry measures 2: Symmetry groups and the tetrahedron. J. Am. Chem. Soc. 1993, 115, 8278–8289. [Google Scholar] [CrossRef]
- Avnir, D.; Katzenelson, O.; Keinan, S.; Pinsky, M.; Pinto, Y.; Salomon, Y.; Hel-Or, H. The measurement of symmetry and chirality: conceptual aspects. In Concepts in Chemistry; Rouvray, D.H., Ed.; Research Studies Press: Somerset, UK, 1997; pp. 283–324. [Google Scholar]
- Zabrodsky, H.; Avnir, D. Continuous symmetry measures. 4. Chirality. J. Am. Chem. Soc. 1995, 117, 462–473. [Google Scholar] [CrossRef]
- Kanis, D.R.; Wong, J.S.; Marks, T.J.; Ratner, M.A.; Zabrodsky, H.; Keinan, S.; Avnir, D. Continuous symmetry analysis of hyperpolarizabilities. Characterization of second-order non-linear optical response of distorted benzene. J. Phys. Chem. 1995, 99, 11061–11066. [Google Scholar] [CrossRef]
- Alvarez, S.; Alemany, P.; Casanova, D.; Cirera, J.; Llunell, M.; Avnir, D. Shape maps and polyhedral interconversion paths in transition metal chemistry. Coordin. Chem. Rev. 2005, 249, 1693–1708. [Google Scholar] [CrossRef]
- Pinsky, M.; Avnir, D. Continuous symmetry measures. 5. The classical polyhedra. Inorg. Chem. 1998, 37, 5575–5582. [Google Scholar] [CrossRef] [PubMed]
- Katzenelson, O.; Hel-Or, H.; Avnir, D. Chirality of large supramolecular structures. Chem. Eur. J. 1996, 2, 174–181. [Google Scholar] [CrossRef]
- Yogev-Einot, D.; Avnir, D. The temperature-dependent optical activity of quartz: from Le Châtelier to chirality measures. Tetrahedron-Asymmetr. 2006, 17, 2723–2725. [Google Scholar] [CrossRef]
- Steinberg, A.; Karni, M.; Avnir, D. Continuous symmetry analysis of NMR chemical shielding anisotropy. Chem. Eur. J. 2006, 12, 8534–8538. [Google Scholar] [CrossRef] [PubMed]
- Pinto, Y.; Fowler, P.W.; Mitchell, D.; Avnir, D. Continuous chirality analysis of model stone—Wales rearrangements in fullerenes. J. Phys. Chem. 1998, 102, 5776–5784. [Google Scholar] [CrossRef]
- Yogev-Einot, D.; Avnir, D. Pressure and temperature effects on the degree of symmetry and chirality of the molecular building blocks of low quartz. Acta Crystallogr. 2004, B60, 163–173. [Google Scholar] [CrossRef] [PubMed]
- Keinan, S.; Avnir, D. Quantitative symmetry in structure-activity correlations: the near C2 symmetry of inhibitor/hiv-protease complexes. J. Am. Chem. Soc. 2000, 122, 4378–4384. [Google Scholar] [CrossRef]
- Keinan, S.; Avnir, D. Continuous symmetry analysis of tetrahedral/planar distortions. Copper chlorides and other AB4 species. Inorg. Chem. 2001, 40, 318–323. [Google Scholar] [CrossRef] [PubMed]
- Frid, A.; Raz, S.; Hel-Or, H. Complete symmetry of multilevel bifurcating structures: merging global and local symmetry. Pattern Recogn. to be submitted for publication.
- Graham, J.H.; Shimizu, K.; Emlen, J.M.; Freeman, D.C.; Merkel, J. Growth models and the expected distribution of fluctuating asymmetry. Biol. J. Linn. Soc. 2003, 80, 57–65. [Google Scholar] [CrossRef]
- Leamy, L. Morphometric studies in inbred and hybrid house mice. V. Directional and fluctuating asymmetry. Am. Nat. 1984, 123, 579–593. [Google Scholar] [CrossRef]
- Samuels, M.L.; Casella, G.; McCabe, G.P. Interpreting blocks and random factors. J. Am. Stat. Assoc. 1991, 86, 798–808. [Google Scholar] [CrossRef]
- Samuels, M.L.; Casella, G.; McCabe, G.P. Interpreting blocks and random factors: rejoinder. J. Am. Stat. Assoc. 1991, 86, 818–821. [Google Scholar] [CrossRef]
- Harville, D.A. Interpreting blocks and random factors: comment. J. Am. Stat. Assoc. 1991, 86, 812–815. [Google Scholar] [CrossRef]
- Hocking, R.R. Interpreting blocks and random factors: comment. J. Am. Stat. Assoc. 1991, 86, 811. [Google Scholar] [CrossRef]
- Speed, T.P. Interpreting blocks and random factors: comment. J. Am. Stat. Assoc. 1991, 86, 808–811. [Google Scholar] [CrossRef]
- Kozhara, A.V. On the ratio of components of phenotypic variances of bilateral characters in populations of some fishes. Genetika 1989, 25, 1508–1513. (in Russian). [Google Scholar]
- Kozhara, A.V. Phenotypic variance of bilateral characters as an indicator of genetic and environmental conditions in bream Abramis brama (L.) (Pisces, Cyprinidae) population. J. Appl. Ichthyol. 1994, 10, 167–181. [Google Scholar] [CrossRef]
- Bennington, C.C.; Thayne, W.V. Use and misuse of mixed model analysis of variance in ecological studies. Ecology 1994, 75, 717–722. [Google Scholar] [CrossRef]
- Kempthorne, O. Fixed and mixed models in the analysis of variance. Biometrics 1975, 31, 473–486. [Google Scholar] [CrossRef]
- Yoccoz, N.G. Use, overuse, and misuse of significance tests in evolutionary biology and ecology. Bull. Ecol. Soc. Am. 1991, 72, 106–111. [Google Scholar]
- Zabrodsky, H.; Peleg, S.; Avnir, D. Symmetry of fuzzy data. Proc. CVPR IEEE 1994, 1, 499–504. [Google Scholar]
- Mosimann, J.E.; Campbell, G. Applications in biology: simple growth models. In Lognormal Distributions: Theory and Applications; Crow, E.L., Shimizu, K., Eds.; Marcel Dekker: New York, NY, USA, 1988; pp. 287–302. [Google Scholar]
- Aitchison, J.; Brown, J.A.C. The Lognormal Distribution; Cambridge University Press: Cambridge, UK, 1963. [Google Scholar]
- Crow, E.L.; Shimizu, K. (Eds.) Lognormal Distributions: Theory and Applications; Marcel Dekker: New York, NY, USA, 1988. [Google Scholar]
- Van Dongen, S.; Møller, A.P. On the distribution of developmental errors: comparing the normal, gamma, and log-normal distribution. Biol. J. Linn. Soc. 2007, 92, 197–210. [Google Scholar] [CrossRef]
- Cowart, N.M.; Graham, J.H. Within- and among-individual variation in fluctuating asymmetry of leaves in the fig (Ficus carica L.). Int. J. Plant Sci. 1999, 160, 116–121. [Google Scholar] [CrossRef]
- Freeman, D.C.; Brown, M.L.; Dobson, M.; Jordan, Y.; Kizy, A.; Micallef, C.; Hancock, L.C.; Graham, J.H.; Emlen, J.M. Developmental instability: measures of resistance and resilience using pumpkin (Cucurbita pepo). Biol. J. Linn. Soc. 2003, 78, 27–41. [Google Scholar] [CrossRef]
- Raz, S.; Graham, J.H.; Hel-Or, H.; Nevo, E. Developmental instability of vascular plants in contrasting microclimates at “Evolution Canyon.”. To be submitted for publication.
- Leung, B.; Forbes, M.R.; Houle, D. Fluctuating asymmetry as a bioindicator of stress: comparing efficacy of analyses involving multiple traits. Am. Nat. 2000, 155, 101–115. [Google Scholar] [CrossRef] [PubMed]
- Sherry, R.A.; Lord, E.M. Developmental stability in flowers of Clarkia tembloriensis (Onagraceae). J. Evol. Biol. 1996, 9, 911–930. [Google Scholar] [CrossRef]
- Karvonen, E.; Merilä, J.; Rintamäki, P.T.; Van Dongen, S. Geography of fluctuating asymmetry in the greenfinch, Carduelis chloris. Oikos 2003, 100, 507–516. [Google Scholar] [CrossRef]
- Van Dongen, S. Fluctuating asymmetry and developmental instability in evolutionary biology: past, present and future. J. Evol. Biol. 2006, 19, 1727–1743. [Google Scholar] [CrossRef]
- Lajus, D.L. Variation patterns of bilateral characters: variation among characters and among populations in the White Sea herring, Clupea pallasi marisalbi (Berg) (Clupeidae, Teleosti). Biol. J. Linn. Soc. 2001, 74, 237–253. [Google Scholar]
- Young, J.R. Removing bias for fluctuating asymmetry in meristic characters. J. Agr. Biol. Envir. St. 2007, 12, 485–497. [Google Scholar] [CrossRef]
- Van Dongen, S.; Lens, L. Modelling developmental instability as the joint action of noise and stability: a Bayesian approach. BMC Evolutionary Biology 2002, 2, 11. Accessed at http://www.biomedcentral.com/1471-2148/2/11. [CrossRef]
- Hamdoun, A.; Epel, D. Embryo stability and vulnerability in an always changing world. Proc. Natl. Acad. Sci. USA 2007, 104, 1745–1750. [Google Scholar] [CrossRef] [PubMed]
- Waddington, C.H. The Strategy of the Genes; George Allen Unwin: London, UK, 1957. [Google Scholar]
- Schmalhausen, I.I. Factors of Evolution; Blakiston Company: Philadelphia, PA, USA, 1949. [Google Scholar]
- De Visser, J.A.G.M.; Hermisson, J.; Wagner, G.P.; Meyers, L.A.; Bagheri-Chaichian, H.; Blanchard, J.L.; Chao, L.; Cheverud, J.M.; Elena, S.F.; Fontana, W.; Gibson, G.; Hansen, T.F.; Krakauer, D.; Lewontin, R.C.; Ofria, C.; Rice, S.H.; Von Dassow, G.; Wagner, A.; Whitlock, M.C. Perspective: evolution and detection of genetic robustness. Evolution 2003, 57, 1959–1972. [Google Scholar] [CrossRef] [PubMed]
- Nijhout, H.F.; Davidowitz, G. Developmental perspectives on phenotypic variation, canalization, and fluctuating asymmetry. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 3–13. [Google Scholar]
- Waddington, C.H. Experiments on canalizing selection. Genet. Res. 1960, 1, 140–150. [Google Scholar] [CrossRef]
- Holling, C.S. Resilience and stability of ecological systems. Annu. Rev. Ecol. Syst. 1973, 4, 1–23. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Exploring Complexity: An Introduction; Freeman: New York, NY, USA, 1989. [Google Scholar]
- Lajus, D.L.; Graham, J.H.; Kozhara, A.V. Developmental instabilty and the stochastic component of total phenotypic variance. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 343–363. [Google Scholar]
- Falconer, D.S.; MacKay, T.F.C. Introduction to Quantitative Genetics, 4th ed; Longman: Essex, UK, 1996. [Google Scholar]
- Gärtner, K. A third component causing random variability beside environment and genotype. A reason for the limited success of a 30 year long effort to standardize laboratory animals? Lab Animal 1990, 24, 71–77. [Google Scholar] [CrossRef]
- Pinker, S. The Blank Slate: The Modern Denial of Human Nature; Penguin Putnam: New York, NY, USA, 2002. [Google Scholar]
- Lajus, D.L.; Alekseev, V.R. Phenotypic variation and developmental instability of life-history traits: a theory and a case study on within-population variation of resting eggs formation in Daphnia. J. Limnol. 2004, 63, 37–44. [Google Scholar] [CrossRef]
- McAdams, H.H.; Arkin, A. Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. USA 1997, 94, 814–819. [Google Scholar] [CrossRef]
- McAdams, H.H.; Arkin, A. It’s a noisy business: genetic regulation at the nanomolar scale. Trends Genet. 1999, 15, 65–69. [Google Scholar] [CrossRef]
- Raser, J.M.; O’Shea, E.K. Noise in gene expression: origins, consequences, and control. Science 2005, 309, 2010–2013. [Google Scholar] [CrossRef] [PubMed]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef] [PubMed]
- Cukierman, E.; Pankov, R.; Yamada, K.M. Cell interactions with three-dimensional matrices. Curr. Opin. Cell Biol. 2002, 14, 633–639. [Google Scholar] [CrossRef]
- Pankov, R.; Endo, Y.; Even-Ram, S.; Araki, M.; Clark, K.; Cukierman, E.; Matsumoto, K.; Yamada, K.M. A Rac switch regulates random versus directionally persistent cell migration. J. Cell Biol. 2005, 170, 793–802. [Google Scholar] [CrossRef] [PubMed]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: New York, NY, USA, 1980. [Google Scholar]
- Eldar, A.; Dorfman, R.; Weiss, D.; Ashe, H.; Shilo, B.-Z.; Barkai, N. Robustness of the BMP morphogen gradient in Drosophila embryonic patterning. Nature 2002, 419, 304–308. [Google Scholar] [CrossRef] [PubMed]
- Kan, K.-J.; Ploeger, A.; Raijmakers, M.E.J.; Dolan, C.V.; van der Maas, H.L.J. Nonlinear epigenetic variance: review and simulations. Developmental Sci. 2010, 13, 11–27. [Google Scholar] [CrossRef]
- Bratsun, D.; Volfson, D.; Tsimring, L.S.; Hasty, J. Delay-induced stochastic oscillations in gene regulation. Proc. Natl. Acad. Sci. USA 2005, 102, 14593–14598. [Google Scholar] [CrossRef] [PubMed]
- Helsen, P.; Van Dongen, S. The normal distribution as appropriate model of developmental instability in Opuntia cacti flowers. J. Evol. Biol. 2009, 22, 1346–1353. [Google Scholar] [CrossRef]
- Cannon, W.B. The Wisdom of the Body; Norton: New York, NY, USA, 1932. [Google Scholar]
- Lerner, I.M. Genetic Homeostasis; Oliver & Boyd: Edinburgh, UK, 1954. [Google Scholar]
- Calow, P. Homeostasis and fitness. Am. Nat. 1982, 120, 416–419. [Google Scholar] [CrossRef]
- Woolf, C.M.; Markow, T.A. Genetic models of developmental homeostasis: historical perspectives. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 99–115. [Google Scholar]
- Dobzhansky, Th. Genetics of natural populations. XIX. Origin of heterosis through natural selection in populations of Drosophila pseudoobscura. Genetics 1950, 35, 288–302. [Google Scholar] [PubMed]
- Dobzhansky, Th.; Levene, H. Genetics of natural populations. XXIV. Developmental homeostasis in natural populations of Drosophila pseudoobscura. Genetics 1955, 40, 797–808. [Google Scholar] [PubMed]
- Clarke, G.M. The genetic basis of developmental stability. I. Relationships between stability, heterozygosity and genomic coadaptation. Genetica 1993, 89, 15–23. [Google Scholar] [CrossRef]
- Clarke, G.M. Developmental stability-fitness relationships in animals: some theoretical considerations. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 187–195. [Google Scholar]
- Zachos, F.E.; Hartl, G.B.; Suchentrunk, F. Fluctuating asymmetry and genetic variability in the roe deer (Capreolus capreolus): a test of the developmental stability hypothesis in mammals using neutral molecular markers. Heredity 2007, 98, 392–400. [Google Scholar] [CrossRef] [PubMed]
- Pogson, G.H.; Zouros, E. Allozyme and RFLP heterozygosities as correlates of growth rate in the scallop Placopecten magellanicus: a test of the associative overdominance hypothesis. Genetics 1994, 137, 221–231. [Google Scholar] [PubMed]
- Thelen, G.C.; Allendorf, F.W. Heterozygosity-fitness correlations in rainbow trout: effects of allozyme loci or associative overdominance? Evolution 2001, 55, 1180–1187. [Google Scholar] [CrossRef] [PubMed]
- Myrand, B.; Tremblay, R.; Sévigny, J.-M. Selection against blue mussels (Mytilus edulis L.) homozygotes under various stressful conditions. J. Hered. 2002, 93, 238–248. [Google Scholar] [CrossRef] [PubMed]
- Parsons, P.A. Environments and evolution: interactions between stress, resource inadequacy and energetic efficiency. Biol. Rev. 2005, 80, 589–610. [Google Scholar] [CrossRef]
- Koehn, R.K.; Bayne, B.L. Towards a physiological and genetical understanding of the energetics of the stress response. Biol. J. Linn. Soc. 1989, 37, 157–171. [Google Scholar] [CrossRef]
- Levene, H. Genetic equilibrium when more than one ecological niche is available. Am. Nat. 1953, 87, 331–333. [Google Scholar] [CrossRef]
- Nevo, E. Genetic variation in natural populations: patterns and theory. Theor. Pop. Biol. 1978, 13, 121–177. [Google Scholar] [CrossRef]
- Nevo, E. Genetic diversity in nature: patterns and theory. Evol. Biol. 1988, 23, 217–247. [Google Scholar]
- Nevo, E. Molecular evolution and ecological stress at global, regional, and local scales: the Israeli perspective. J. Exp. Zool. 1998, 282, 95–119. [Google Scholar] [CrossRef]
- Nevo, E. Evolution in action across life at “Evolution Canyons”, Israel. Trends Evol. Biol. 2009, 1, e3. [Google Scholar] [CrossRef]
- Nevo, E.; Beiles, A. Genetic parallelism of protein polymorphism in nature: ecological test of the neutral theory of molecular evolution. Biol. J. Linn. Soc. 1988, 35, 229–245. [Google Scholar] [CrossRef]
- Nevo, E.; Beiles, A.; Ben-Shlomo, R. The evolutionary significance of genetic diversity: ecological, demographic and life history correlates. In Lecture Notes in Biomathematics, Vol. 53, Evolutionary Dynamics of Genetic Diversity; Mani, G.S., Ed.; Springer-Verlag: Berlin, Germany, 1984; pp. 13–213. [Google Scholar]
- Graham, J.H.; Felley, J.D. Genomic coadaptation and developmental stability within introgressed populations of Enneacanthus gloriosus and E. obesus (Pisces: Centrarchidae). Evolution 1985, 39, 104–114. [Google Scholar] [PubMed]
- Leary, R.F.; Allendorf, F.W.; Knudsen, K.L. Developmental instability and high meristic counts in interspecific hybrids of salmonid fishes. Evolution 1985, 39, 1318–1326. [Google Scholar] [CrossRef]
- Graham, J.H. Genomic coadaptation and developmental stability in hybrid zones. Acta Zool. Fenn. 1992, 191, 121–131. [Google Scholar]
- Alibert, P.; Auffray, J.-C. Genomic coadaptation, outbreeding depression, and developmental instability. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 116–134. [Google Scholar]
- Leamy, L.J.; Klingenberg, C.P. The genetics and evolution of fluctuating asymmetry. Annu. Rev. Ecol. Evol. Syst. 2005, 36, 1–21. [Google Scholar] [CrossRef]
- Nevo, E. Speciation in action and adaptation in subterranean mole rats: patterns and theory. Boll. Zool. 1985, 52, 65–95. [Google Scholar] [CrossRef]
- Wang, H.; McArthur, E.D.; Sanderson, S.C.; Graham, J.H.; Freeman, D.C. Narrow hybrid zone between two subspecies of big sagebrush (Artemisia tridentata: Asteraceae). IV. Reciprocal transplant experiments. Evolution 1997, 51, 95–102. [Google Scholar]
- Tracy, M.; Freeman, D.C.; Duda, J.J.; Miglia, K.J.; Graham, J.H.; Hough, A. Developmental instability: an appropriate indicator of plant fitness components. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 196–212. [Google Scholar]
- Pélabon, C.; Hansen, T.F.; Carlson, M.L.; Armbruster, W.S. Patterns of asymmetry in the twining vine Dalechampia scandens (Euphorbiaceae): ontogenetic and hierarchical perspectives. New Phytol. 2006, 170, 65–74. [Google Scholar]
- Vishalakshi, C.; Singh, B.N. Effect of directional selection for body size on fluctuating asymmetry in certain morphological traits in Drosophila ananassae. J. Biosci. 2009, 34, 275–285. [Google Scholar] [CrossRef] [PubMed]
- Soulé, M. The epistasis cycle: a theory of marginal populations. Annu. Rev. Syst. Ecol. 1973, 4, 165–187. [Google Scholar] [CrossRef]
- Kat, P.W. The relationship between heterozygosity for enzyme loci and developmental homeostasis in peripheral populations of aquatic bivalves (Unionidae). Am. Nat. 1982, 119, 824–832. [Google Scholar] [CrossRef]
- White, T.A.; Searle, J.B. Mandible asymmetry and genetic diversity in island populations of the common shrew, Sorex araneus. J. Evol. Biol. 2008, 21, 636–641. [Google Scholar] [CrossRef] [PubMed]
- Johnson, W.; Gangestad, S.W.; Segal, N.L.; Bouchard, T.J., Jr. Heritability of fluctuating asymmetry in a human twin sample: the effect of trait aggregation. Am. J. Hum. Biol. 2008, 20, 651–658. [Google Scholar] [CrossRef] [PubMed]
- Fuller, R.C.; Houle, D. Inheritance of developmental instability. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: Oxford, UK, 2003; pp. 157–186. [Google Scholar]
- Van Dongen, S. What do we know about the heritability of developmental instability? Answers from a Bayesian model. Evolution 2007, 61, 1033–1042. [Google Scholar] [CrossRef]
- Leamy, L.J.; Routman, E.J.; Cheverud, J.M. An epistatic genetic basis for fluctuating asymmetry of mandible size in mice. Evolution 2002, 56, 642–653. [Google Scholar] [CrossRef] [PubMed]
- Milton, C.C.; Huynh, B.; Batterham, P.; Rutherford, S.L.; Hoffmann, A.A. Quantitative trait symmetry independent of Hsp90 buffering: distinct modes of genetic canalization and developmental stability. Proc. Natl. Acad. Sci. USA 2003, 100, 13396–13401. [Google Scholar] [CrossRef] [PubMed]
- Milton, C.C.; Batterham, P.; McKenzie, J.A.; Hoffmann, A.A. Effect of E(sev) and Su(Raf) Hsp83 mutants and trans-heterozygotes on bristle trait means and variation in Drosophila melanogaster. Genetics 2005, 171, 119–130. [Google Scholar] [CrossRef]
- Debat, V.; Milton, C.C.; Rutherford, S.; Klingenberg, C.P.; Hoffmann, A.A. Hsp90 and the quantitative variation of wing shape in Drosophila melanogaster. Evolution 2006, 60, 2529–2538. [Google Scholar] [CrossRef] [PubMed]
- Sangster, T.A.; Salathia, N.; Undurraga, S.; Milo, R.; Schellenberg, K.; Lindquist, S.; Queitsch, C. HSP90 affects the expression of genetic variation and developmental stability in quantitative traits. Proc. Natl. Acad. Sci. USA 2008, 105, 2963–2968. [Google Scholar] [CrossRef]
- Santos, M.; Iriarte, P.F.; Céspedes, W. Genetics and geometry of canalization and developmental stability in Drosophila subobscura. BMC Evol. Biol. 2005, 5, 7. [Google Scholar] [CrossRef] [PubMed]
- Polak, M.; Taylor, P.W. A primary role of developmental instability in sexual selection. Proc. R. Soc. Lond. B 2007, 274, 3133–3140. [Google Scholar] [CrossRef] [PubMed]
- Félix, M.-A.; Wagner, A. Robustness and evolution: concepts, insights, and challenges from a developmental model system. Heredity 2008, 100, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Wagner, A. Distributed robustness versus redundancy as causes of mutational robustness. Bioessays 2005, 27, 176–188. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.-L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvai, Z.N.; Barabási, A.-L. The large-scale organization of metabolic networks. Nature 2000, 407, 651–654. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.; Mason, S.P.; Barabási, A.-L.; Oltvai, Z.N. Lethality and centrality in protein networks. Nature 2001, 411, 41–42. [Google Scholar] [CrossRef]
- Barkai, N.; Leibler, S. Robustness in simple biochemical networks. Nature 1997, 387, 913–917. [Google Scholar] [CrossRef]
- Bhalla, U.S.; Iyengar, R. Emergent properties of networks of biological signaling pathways. Science 1999, 283, 381–387. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Jeong, H.; Barabási, A.-L. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J.; Barabási, A.-L.; Watts, D.J. The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Ravasz, E.; Somera, A.L.; Mongru, D.A.; Oltvai, Z.N.; Barabási, A.-L. Hierarchical organization of modularity in metabolic networks. Science 2002, 297, 1551–1555. [Google Scholar] [CrossRef] [PubMed]
- Levy, S.F.; Siegal, M.L. Network hubs buffer environmental variation in Saccharomyces cerevisiae. PLoS Biol. 2008, 6, e264. [Google Scholar] [CrossRef] [PubMed]
- Babbitt, G.A. Inbreeding reduces power-law scaling in the distribution of fluctuating asymmetry: an explanation of the basis of developmental instability. Heredity 2006, 97, 258–268. [Google Scholar] [CrossRef] [PubMed]
- Babbitt, G.A. How accurate is the phenotype? – An analysis of developmental noise in a cotton aphid clone. BMC Dev. Biol. 2008, 8, 19. [Google Scholar] [CrossRef]
- Babbitt, G.A.; Kiltie, R.; Bolker, B. Are fluctuating asymmetry studies adequately sampled? Implications of a new model for size distribution. Am. Nat. 2006, 167, 230–245. [Google Scholar] [CrossRef]
- Alekseeva, T.A.; Zinichev, V.V.; Zotin, A.I. Energy criteria of reliability and stability of development. Acta Zool. Fenn. 1992, 191, 159–165. [Google Scholar]
- Hoffmann, A.A.; Parsons, P.A. Evolutionary Genetics and Environmental Stress; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Parsons, P.A. Fluctuating asymmetry: an epigenetic measure of stress. Biol. Rev. 1990, 65, 131–145. [Google Scholar] [CrossRef]
- Parsons, P.A. Fluctuating asymmetry: a biological monitor of environmental and genomic stress. Heredity 1992, 68, 361–364. [Google Scholar] [CrossRef]
- Grime, J.P. Plant Strategies and Vegetation Processes; John Wiley & Sons: Chichester, UK, 1979. [Google Scholar]
- Escós, J.M.; Alados, C.L.; Pugnaire, F.I.; Puigdefábregas, J.; Emlen, J.M. Stress resistance strategy in arid land shrub: interaction between developmental instability and fractal dimension. J. Arid Environ. 2000, 45, 325–336. [Google Scholar] [CrossRef]
- Morgan, M.B.; Edge, S.E.; Snell, T.W. Profiling differential gene expression of corals along a transect of waters adjacent to the Bermuda municipal dump. Mar. Pollut. Bull. 2005, 51, 524–533. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, J.G.; Kristensen, T.N.; Loeschcke, V. The evolutionary and ecological role of heat shock proteins. Ecol. Lett. 2003, 6, 1025–1037. [Google Scholar] [CrossRef]
- Kawasaki, S.; Borchert, C.; Deyholos, M.; Wang, H.; Brazille, S.; Kawai, K.; Galbraith, D.; Bohnert, H.J. Gene expression profiles during the initial phase of salt stress in rice. Plant Cell 2001, 13, 889–905. [Google Scholar] [CrossRef] [PubMed]
- Bjorksten, T.; David, P.; Pomiankowski, A.; Fowler, K. Fluctuating asymmetry of sexual and nonsexual traits in stalk-eyed flies: a poor indicator of developmental stress and genetic quality. J. Evol. Biol. 2000, 13, 89–97. [Google Scholar] [CrossRef]
- Cárcamo, H.A.; Floate, K.D.; Lee, B.L.; Beres, B.L.; Clarke, F.R. Developmental instability in a stem-mining sawfly: can fluctuating asymmetry detect plant host stress in a model system? Oecologia 2008, 156, 505–513. [Google Scholar] [CrossRef]
- West-Eberhard, M.J. Developmental Plasticity and Evolution; Oxford University Press: New York, NY, USA, 2003. [Google Scholar]
- Losick, R.; Desplan, C. Stochasticity and cell fate. Science 2008, 320, 65–68. [Google Scholar] [CrossRef]
- Elena, S.F.; Sanjuán, R. Virus evolution: insights from an experimental approach. Annu. Rev. Ecol. Evol. Syst. 2007, 38, 27–52. [Google Scholar] [CrossRef]
- Black-Samuelsson, S.; Andersson, S. The effect of nutrient stress on developmental instability in leaves of Acer platanoides (Aceraceae) and Betula pendula (Betulaceae). Am. J. Bot. 2003, 90, 1107–1112. [Google Scholar] [CrossRef]
- Fair, J.M.; Breshears, D.D. Drought stress and fluctuating asymmetry in Quercus undulata leaves: confounding effects of absolute and relative amounts of stress? J. Arid Environ. 2005, 62, 235–249. [Google Scholar] [CrossRef]
- Zhu, J.-K. Salt and drought stress signal transduction in plants. Annu. Rev. Plant Biol. 2002, 53, 247–273. [Google Scholar] [CrossRef] [PubMed]
- Williams, G.C. Natural selection, the costs of reproduction and a refinement of Lack’s principle. Am. Nat. 1966, 100, 687–690. [Google Scholar] [CrossRef]
- Stearns, S.C. The Evolution of Life Histories; Oxford University Press: New York, NY, USA, 1992. [Google Scholar]
- Charnov, E.L. The optimal balance between growth rate and survival in mammals. Evol. Ecol. Res. 2004, 6, 307–313. [Google Scholar] [CrossRef]
- Obeso, J.R. Tansley Review No. 139. The costs of reproduction in plants. New Phytol. 2002, 155, 321–348. [Google Scholar] [CrossRef]
- Freeman, D.C.; Graham, J.H.; Emlen, J.M. Developmental stability in plants: symmetries, stress and epigenesis. Genetica 1993, 89, 97–119. [Google Scholar] [CrossRef]
- Lappalainen, J.H.; Martel, J.; Lempa, K.; Wilsey, B.; Ossipov, V. Effects of resource availability on carbon allocation and developmental instability in cloned birch seedings. Int. J. Plant Sci. 2000, 161, 119–125. [Google Scholar] [CrossRef] [PubMed]
- Milligan, J.R.; Krebs, R.A.; Mal, T.K. Separating developmental and environmental effects on fluctuating asymmetry in Lythrum salicaria and Penthorum sedoides. Int. J. Plant Sci. 2008, 169, 625–630. [Google Scholar] [CrossRef]
- Lovelock, C.E.; Ball, M.C.; Martin, K.C.; Feller, I.C. Nutrient enrichment increases mortality of mangroves. PLoS One 2009, 4, e5600. [Google Scholar] [CrossRef] [PubMed]
- Anne, P.; Mawri, F.; Gladstone, S.; Freeman, D.C. Is fluctuating asymmetry a reliable biomonitor of stress? A test using life history parameters in soybean. Int. J. Plant Sci. 1998, 159, 559–565. [Google Scholar] [CrossRef]
- Pélabon, C.; Hansen, T.F.; Carter, A.J.R.; Houle, D. Response of fluctuating and directional asymmetry to selection on wing shape in Drosophila melanogaster. J. Evol. Biol. 2006, 19, 764–776. [Google Scholar] [CrossRef]
- Martel, J.; Lempa, K.; Haukioja, E. Effects of stress and rapid growth on fluctuating asymmetry and insect damage in birch leaves. Oikos 1999, 8, 208–216. [Google Scholar] [CrossRef]
- Wells, J.C.; Hallal, P.C.; Manning, J.T.; Victora, C.G. A trade-off between early growth rate and fluctuating asymmetry in Brazilian boys. Ann. Hum. Biol. 2006, 33, 112–124. [Google Scholar] [CrossRef] [PubMed]
- Nevo, E.; Bolshakova, M.A.; Martyn, G.I.; Musatenko, L.I.; Sytnik, K.M.; Pavlíček, T.; Beharav, A. Drought and light anatomical adaptive leaf strategies in three woody species caused by microclimatic selection at “Evolution Canyon”, Israel. Isr. J. Plant Sci. 2000, 48, 33–46. [Google Scholar]
- Auffray, J.-C.; Renaud, S.; Alibert, P.; Nevo, E. Developmental stability and adaptive radiation in Spalax ehrenbergi superspecies in the Near East. J. Evol. Biol. 1999, 12, 207–221. [Google Scholar] [CrossRef]
- Hódar, J.A. Leaf fluctuating asymmetry of Holm oak in response to drought under contrasting climatic conditions. J. Arid Environ. 2002, 52, 233–243. [Google Scholar] [CrossRef]
- Souza, G.M.; Viana, J.O.F.; Oliveira, R.F. Asymmetrical leaves induced by water deficit show asymmetric photosynthesis in common bean. Braz. J. Plant Physiol. 2005, 17, 223–227. [Google Scholar] [CrossRef]
- Hochwender, C.G.; Fritz, R.S. Fluctuating asymmetry in a Salix hybrid system: the importance of genetic versus environmental causes. Evolution 1999, 53, 408–416. [Google Scholar] [CrossRef] [PubMed]
- Midgley, G.F.; Wand, S.J.E.; Musil, C.F. Repeated exposure to enhanced UV-B radiation in successive generations increases developmental instability (leaf fluctuating asymmetry) in a desert annual. Plant Cell Environ. 1998, 21, 437–442. [Google Scholar] [CrossRef]
- Breuker, C.J.; Brakefield, P.M. Heat shock in the developmentally sensitive period of butterfly eyespots fails to increase fluctuating asymmetry. Evol. Dev. 2003, 5, 231–239. [Google Scholar] [CrossRef]
- Hosken, D.J.; Blanckenhorn, W.U.; Ward, P.I. Developmental stability in yellow dung flies (Scathophaga stercoraria): fluctuating asymmetry, heterozygosity and environmental stress. J. Evol. Biol. 2000, 13, 919–926. [Google Scholar] [CrossRef]
- Hagen, S.B.; Ims, R.A.; Yoccoz, N.G.; Sørlibråten, O. Fluctuating asymmetry as an indicator of elevation stress and distribution limits in mountain birch (Betula pubescens). Plant Ecol. 2008, 195, 157–163. [Google Scholar] [CrossRef]
- Swaddle, J.P.; Witter, M.S. Food, feathers and fluctuating asymmetry. Proc. R. Soc. Lond. B 1994, 255, 147–152. [Google Scholar]
- Campero, M.; De Block, M.; Ollevier, F.; Stoks, R. Metamorphosis offsets the link between larval stress, adult asymmetry and individual quality. Funct. Ecol. 2008, 22, 271–277. [Google Scholar] [CrossRef]
- Hopton, M.E.; Cameron, G.N.; Cramer, M.J.; Polak, M.; Uetz, G.W. Live animal radiography to measure developmental instability in populations of small mammals after a natural disaster. Ecol. Indic. 2009, 9, 883–891. [Google Scholar] [CrossRef]
- Pertoldi, C.; Kristensen, T.N.; Andersen, D.H.; Loeschcke, V. Developmental instability as an estimator of genetic stress. Heredity 2006, 96, 122–127. [Google Scholar] [CrossRef] [PubMed]
- Vøllestad, L.A.; Hindar, K.; Møller, A.P. Meta-analysis of fluctuating asymmetry in relation to heterozygosity. Heredity 1999, 83, 206–218. [Google Scholar] [CrossRef]
- Pélabon, C.; Carlson, M.L.; Hansen, T.F.; Armbruster, W.S. Effects of crossing distance on offspring fitness and developmental stability in Dalechampia scandens (Euphorbiaceae). Am. J. Bot. 2005, 92, 842–851. [Google Scholar] [CrossRef]
- Handy, S.M.; McBreen, K.; Cruzan, M.B. Patterns of fitness and fluctuating asymmetry across a broad hybrid zone. Int. J. Plant Sci. 2004, 165, 973–981. [Google Scholar] [CrossRef]
- Kark, S.; Safriel, U.N.; Tabarroni, C.; Randi, E. Relationship between heterozygosity and asymmetry: a test across the distribution range. Heredity 2001, 86, 119–127. [Google Scholar] [CrossRef][Green Version]
- Woodruff, R. (Bowling Green State University, Bowling Green, OH). Personal communication, 2009.
- Stige, L.C.; Slagsvold, T.; Vøllestad, L.A. Individual fluctuating asymmetry in Pied Flycatchers (Ficedula hypoleuca) persists across moults, but is not heritable and not related to fitness. Evol. Ecol. Res. 2005, 7, 381–406. [Google Scholar][Green Version]
- Bartoš, L.; Bahbouh, R.; Vach, M. Repeatability of size and fluctuating asymmetry of antler characteristics in red deer (Cervus elaphus) during ontogeny. Biol. J. Linn. Soc. 2007, 91, 215–226. [Google Scholar] [CrossRef]
- Mateos, C.; Alarcos, S.; Carranza, J.; Sánchez-Prieto, C.B.; Valencia, J. Fluctuating asymmetry of red deer antlers negatively relates to individual condition and proximity to prime age. Anim. Behav. 2008, 75, 1629–1640. [Google Scholar] [CrossRef]
- Whitlock, M.C. The heritability of fluctuating asymmetry and the genetic control of developmental stability. Proc. R. Soc. Lond. B 1996, 263, 849–853. [Google Scholar]
- Whitlock, M.C. The repeatability of fluctuating asymmetry: a revision and extension. Proc. R. Soc. Lond. B 1998, 265, 1429–1431. [Google Scholar] [CrossRef]
- Van Dongen, S. How repeatable is the estimation of developmental stability by fluctuating asymmetry? Proc. R. Soc. Lond. B 1998, 265, 1423–1427. [Google Scholar] [CrossRef]
- Gangestad, W.; Thornhill, R. Fluctuating asymmetry, developmental instability, and fitness: toward model-based interpretation. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 62–80. [Google Scholar]
- Andalo, C.; Bazin, A.; Shykoff, J.A. Is there a genetic basis for fluctuating asymmetry in the plant Lotus corniculatus grown in different environmental conditions? Int. J. Plant Sci. 2000, 161, 213–220. [Google Scholar] [CrossRef] [PubMed]
- Lens, L.; Van Dongen, S.; Kark, S.; Matthysen, E. Fluctuating asymmetry as an indicator of fitness: can we bridge the gap between studies? Biol. Rev. 2002, 77, 27–38. [Google Scholar] [CrossRef] [PubMed]
- Leamy, L. Morphological integration of fluctuating asymmetry in the mouse mandible. Genetica 1993, 89, 139–153. [Google Scholar] [CrossRef]
- Klingenberg, C.P.; Zaklan, S.D. Morphological integration between developmental compartments in the Drosophila wing. Evolution 2000, 54, 1273–1285. [Google Scholar] [CrossRef]
- Hallgrímsson, B.; Willmore, K.; Hall, B.K. Canalization, developmental stability, and morphological integration in primate limbs. Yearb. Phys. Anthropol. 2002, 45, 131–158. [Google Scholar] [CrossRef]
- Klingenberg, C.P. Developmental instability as a research tool: using patterns of fluctuating asymmetry to infer the developmental origins of morphological integration. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 427–442. [Google Scholar]
- Klingenberg, C.P. Developmental constraints, modules and evolvability. In Variation; Hallgrímsson, B., Hall, B.K., Eds.; Academic Press: San Diego, CA, USA, 2005; pp. 219–247. [Google Scholar]
- Klingenberg, C.P. Morphological integration and developmental modularity. Annu. Rev. Ecol. Evol. Syst. 2008, 39, 115–132. [Google Scholar] [CrossRef]
- Klingenberg, C.P. Morphometric integration and modularity in configurations of landmarks: tools for evaluating a priori hypotheses. Evol. Dev. 2009, 11, 405–421. [Google Scholar] [CrossRef] [PubMed]
- Badyaev, A.V.; Foresman, K.R.; Young, R.L. Evolution of morphological integration: developmental accommodation of stress-induced variation. Am. Nat. 2005, 166, 382–395. [Google Scholar] [PubMed]
- Webster, M.; Zelditch, M.L. Integration and regulation of developmental systems in trilobites. In Advances in Trilobite Research, Rábano, I., Gozalo, R., García-Bellido, D., Eds.; Instituto Geológico y Minero de España: Madrid, Spain, 2008; pp. 427–433. [Google Scholar]
- Møller, A.P.; Eriksson, M. Patterns of fluctuating asymmetry in flowers: implications for sexual selection in plants. J. Evol. Biol. 1994, 7, 97–113. [Google Scholar] [CrossRef]
- Raz, S.; Gishkan, I.; Lefel, Y.; Hel-Or, H.; Graham, J.H.; Nevo, E. Analyzing fluctuating radial asymmetry. To be submitted for publication.
- Tracy, M.; Freeman, D.C.; Emlen, J.M.; Graham, J.H.; Hough, R.A. Developmental instability as a biomonitor of environmental stress: an illustration using plants and macroalgae. In Biomonitors and Biomarkers as Indicators of Environmental Change; Butterworth, F.M., Corkum, L.D., Guzmán-Rincón, J., Eds.; Plenum Press: New York, NY, USA, 1995; pp. 313–337. [Google Scholar]
- Paxman, G.J. Differentiation and stability in the development of Nicotiana rustica. Ann. Bot.-London 1956, 20, 331–347. [Google Scholar] [CrossRef]
- Zar, J.H. Biostatistical Analysis; Prentice-Hall: Englewood Cliffs, NJ, USA, 1984. [Google Scholar]
- Escós, J.; Alados, C.L.; Emlen, J.M. Impact of grazing on plant fractal architecture and fitness of a Mediterranean shrub Anthyllis cytisoides L. Funct. Ecol. 1997, 11, 66–78. [Google Scholar] [CrossRef]
- Alados, C.L.; Navarro, T.; Escós, J.; Cabezudo, B.; Emlen, J.M. Translational and fluctuating asymmetry as tools to detect stress in stress-adapted and nonadapted plants. Int. J. Plant Sci. 2001, 162, 607–616. [Google Scholar] [CrossRef]
- Emlen, J.M.; Freeman, D.C.; Graham, J.H. The adaptive basis of developmental instability: a hypothesis and its implications. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 51–61. [Google Scholar]
- Tan-Kristano, A.; Hoffmann, A.; Woods, R.; Batterham, P.; Cobbett, C.; Sinclair, C. Translational asymmetry as a sensitive indicator of cadmium stress in plants: a laboratory test with wild-type and mutant Arabidopsis thaliana. New Phytol. 2003, 159, 471–477. [Google Scholar] [CrossRef]
- Ambo-Rappe, R.; Lajus, D.L.; Schreider, M.J. Translational fluctuating asymmetry and leaf dimension in seagrass, Zostera capricorni Aschers in a gradient of heavy metals. Environ. Bioindic. 2007, 2, 99–116. [Google Scholar] [CrossRef]
- Ambo-Rappe, R.; Lajus, D.L.; Schreider, M.J. Increased heavy metal and nutrient contamination does not increase fluctuating asymmetry in the seagrass Halophila ovalis. Ecol. Indic. 2008, 8, 100–103. [Google Scholar] [CrossRef]
- Sinclair, C.; Hoffmann, A.A. Developmental stability as a potential tool in the early detection of salinity stress in wheat. Int. J. Plant Sci. 2003, 164, 325–331. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Fractals: Form, Chance, and Dimension; W. H. Freeman: San Francisco, CA, USA, 1977. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman: New York, NY, USA, 1982. [Google Scholar]
- Emlen, J.M.; Freeman, D.C.; Graham, J.H. Nonlinear growth dynamics and the origin of fluctuating asymmetry. Genetica 1993, 89, 77–96. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.N.; Hausdorff, J.M.; Ivanov, P.C.; Peng, C.-K.; Stanley, H.E. Fractal dynamics in physiology: alterations with disease and aging. Proc. Natl. Acad. Sci. USA 2002, 99, 2466–2472. [Google Scholar] [CrossRef] [PubMed]
- Eghball, B.; Settimi, J.R.; Maranville, J.W. Fractal analysis for morphological description of corn roots under nitrogen stress. Agron. J. 1993, 85, 287–289. [Google Scholar] [CrossRef]
- Boxt, L.M.; Katz, J.; Liebovitch, L.S.; Jones, R.; Esser, P.D.; Reid, L. Fractal analysis of pulmonary arteries: the fractal dimension is lower in pulmonary hypertension. J. Thorac. Imag. 1994, 9, 8–13. [Google Scholar] [CrossRef]
- Alados, C.L.; Emlen, J.M.; Wachocki, B.; Freeman, D.C. Instability of development and fractal architecture in dryland plants as an index of grazing pressure. J. Arid Environ. 1998, 38, 63–76. [Google Scholar] [CrossRef]
- Alados, C.L.; Escós, J.; Emlen, J.M. Fluctuating asymmetry and fractal dimension of the sagittal suture as indicators of inbreeding depression in dama and dorcas gazelles. Can. J. Zool. 1995, 73, 1967–1974. [Google Scholar] [CrossRef]
- Escós, J.; Alados, C.L.; Emlen, J.M. Fractal structures and fractal functions as disease indicators. Oikos 1995, 74, 310–314. [Google Scholar] [CrossRef]
- Alados, C.L.; Escós, J.M.; Emlen, J.M. Fractal structure of sequential behaviour patterns: an indicator of stress. Anim. Behav. 1996, 51, 437–443. [Google Scholar] [CrossRef]
- Tan, C.O.; Cohen, M.A.; Eckberg, D.L.; Taylor, J.A. Fractal properties of human heart period variability: physiological and methodological implications. J. Physiol. 2009, 587, 3929–3941. [Google Scholar] [CrossRef]
- Di Ieva, A.; Grizzi, F.; Ceva-Grimaldi, G.; Russo, C.; Gaetani, P.; Aimar, E.; Levi, D.; Pisano, P.; Tancioni, F.; Nicola, G.; Tschabitscher, M.; Dioguardi, N.; Baena, R.R. Fractal dimension as a quantitator of the microvasculature of normal and adenomatous pituitary tissue. J. Anat. 2007, 211, 673–680. [Google Scholar] [CrossRef] [PubMed]
- Schandorff, S. Developmental stability and skull lesions in the harbour seal (Phoca vitulina) in the 19th and 20th Centuries. Ann. Zool. Fenn. 1997, 34, 151–166. [Google Scholar]
- Górski, A.Z.; Skrzat, J. Error estimation of the fractal dimension measurements of cranial sutures. J. Anat. 2006, 208, 353–359. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. Intermittent turbulence in self-similar cascades: divergence of high moments and dimension of the carrier. J. Fluid. Mech. 1974, 62, 331–358. [Google Scholar] [CrossRef]
- Commoner, B.; Shearer, G.B.; Yamada, M. Linear biosynthesis of tobacco mosaic virus: changes in rod length during the course of infection. Proc. Natl. Acad. Sci. USA 1962, 48, 1788–1795. [Google Scholar] [CrossRef] [PubMed]
- Symington, J.; Commoner, B.; Yamada, M. Linear biosynthesis of tobacco mosaic virus: evidence that short virus rods are natural products of TMV biosynthesis. Proc. Natl. Acad. Sci USA 1962, 48, 1675–1683. [Google Scholar] [CrossRef] [PubMed]
- Galazka, A.; Milstien, J.; Zaffran, M. Thermostability of Vaccines; World Health Organization, Global Programme for Vaccines and Immunization: Geneva, Switzerland, 1998. [Google Scholar]
- Elena, S.F.; Carrasco, P.; Daròs, J.-A.; Sanjuán, R. Mechanisms of genetic robustness in RNA viruses. EMBO Rep. 2006, 7, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Shapiro, J.A. Thinking about bacterial populations as multicellular organisms. Annu. Rev. Microbiol. 1998, 52, 81–104. [Google Scholar] [CrossRef]
- Ben-Jacob, E. Bacterial self-organization: co-enhancement of complexification and adaptability in a dynamic environment. Phil. Trans. R. Soc. Lond. A 2003, 361, 1283–1312. [Google Scholar] [CrossRef]
- Matsuyama, T.; Matsushita, M. Fractal morphogenesis by a bacterial cell population. Crit. Rev. Microbiol. 1993, 19, 117–135. [Google Scholar] [CrossRef]
- Singaravelan, N.; Grishkan, I.; Beharav, A.; Wakamatsu, K.; Ito, S.; Nevo, E. Adaptive melanin response of the soil fungus Aspergillus niger to UV radiation stress at ‘‘Evolution Canyon’’, Mount Carmel, Israel. PLoS One 2008, 3, e2993. [Google Scholar] [CrossRef] [PubMed]
- Bagchi, S.K.; Sharma, V.P.; Gupta, P.K. Developmental instability in leaves of Tectona grandis. Silvae Genet. 1989, 38, 1–6. [Google Scholar]
- Sakai, K.; Shimamoto, Y. Developmental instability in leaves and flowers of Nicotiana tabacum. Genetics 1965, 51, 801–813. [Google Scholar] [PubMed]
- Kozlov, M.V.; Niemelä, P. Difference in needle length—a new and objective indicator of pollution impact on scots pine (Pinus sylvestris). Water Air Soil Poll. 1999, 116, 365–370. [Google Scholar] [CrossRef]
- Palmer, R.A. Inferring relative levels of genetic variability in fossils: the link between heterozygosity and fluctuating asymmetry. Paleobiology 1986, 12, 1–5. [Google Scholar] [CrossRef]
- Smith, L.H. Asymmetry of early Paleozoic trilobites. Lethaia 1998, 31, 99–112. [Google Scholar] [CrossRef]
- Palmqvist, P.; Arribas, A.; Martinez-Navarro, B. Ecomorphological study of large canids from the lower Pleistocene of southeastern Spain. Lethaia 1999, 32, 75–88. [Google Scholar] [CrossRef]
- Szöllősi, G.J.; Derényi, I. Congruent evolution of genetic and environmental robustness in microRNA. Mol. Biol. Evol. 2009, 26, 867–874. [Google Scholar] [CrossRef] [PubMed]
- Borenstein, E.; Ruppin, E. Direct evolution of genetic robustness in microRNA. Proc. Natl. Acad. Sci. USA 2006, 103, 6593–6598. [Google Scholar] [CrossRef] [PubMed]
- McKenzie, J.A.; Clarke, G.M. Diazinon resistance, fluctuating asymmetry and fitness in the Australian Sheep Blowfly, Lucilia cuprina. Genetics 1988, 140, 213–220. [Google Scholar]
- Cornelissen, T.; Stiling, P.; Drake, B. Elevated CO2 decreases leaf fluctuating asymmetry and herbivory by leaf miners on two oak species. Global Change Biol. 2003, 10, 27–36. [Google Scholar] [CrossRef]
- Graham, J.H.; Roe, K.; West, T.B. Effects of lead and benzene on developmental stability of Drosophila melanogaster. Ecotoxicology 1993, 2, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Polak, M.; Kroeger, D.E.; Cartwright, I.L.; Ponce deLeon, C. Genotype-specific responses of fluctuating asymmetry and of preadult survival to the effects of lead and temperature stress in Drosophila melanogaster. Environ. Pollut. 2004, 127, 145–155. [Google Scholar] [CrossRef]
- Pankakoski, E.; Koivisto, I.; Hyvärinen, H. Reduced developmental stability as an indicator of heavy metal pollution in the common shrew Sorex araneus. Acta Zool. Fenn. 1992, 191, 137–144. [Google Scholar]
- Estes, E.C.; Katholi, C.R.; Angus, R.A. Elevated fluctuating asymmetry in eastern mosquitofish (Gambusia holbrooki) from a river receiving paper mill effluent. Environ. Toxicol. Chem. 2006, 25, 1026–1033. [Google Scholar] [CrossRef] [PubMed]
- Hao, Z.; Xiangrong, W. Leaf developmental stability of Platanus acerifolia under urban environmental stress and its implication as an environmental indicator. Front. Biol. China 2006, 4, 411–417. [Google Scholar]
- Kozlov, M.V.; Niemelä, P.; Mälkönen, E. Effects of compensatory fertilization on pollution-induced stress in scots pine. Water Air Soil Poll. 2002, 134, 307–318. [Google Scholar] [CrossRef]
- Söderman, F.; Van Dongen, S.; Pakkasmaa, S.; Merilä, J. Environmental stress increases skeletal fluctuating asymmetry in the moor frog Rana arvalis. Oecologia 2007, 151, 593–604. [Google Scholar] [CrossRef]
- Allen, D.; Leamy, L.J. Effects of 2,3,4,8-tetrachloro-p-dioxin on directional and fluctuating asymmetry of mandible characters in mice. Ecotoxicology 2001, 10, 167–176. [Google Scholar] [CrossRef]
- Keller, J.M.; Allen, D.E.; Davis, C.R.; Leamy, L.J. 2,3,7,8-Tetrachlorodibenzo-p-dioxin affects fluctuating asymmetry of molar shape in mice, and an epistatic interaction of two genes for molar size. Heredity 2007, 98, 259–267. [Google Scholar] [CrossRef]
- Graham, J.H.; Fletcher, D.; Tigue, J.; McDonald, M. Growth and developmental stability of Drosophila melanogaster in low frequency magnetic fields. Bioelectromagnetics 2000, 21, 465–472. [Google Scholar] [CrossRef]
- Freeman, D.C.; Brown, M.; Duda, J.J.; Graham, J.H.; Emlen, J.H.; Krzysik, A.J.; Balbach, H.E.; Kovacic, D.A.; Zak, J.C. Photosynthesis and fluctuating asymmetry as indicators of plant response to soil disturbance in the fall-line sandhills of Georgia: a case study using Rhus copallinum and Ipomoea pandurata. Int. J. Plant Sci. 2004, 165, 805–816. [Google Scholar] [CrossRef]
- Freeman, D.C.; Brown, M.L.; Duda, J.J.; Graham, J.H.; Emlen, J.M.; Krzysik, A.J.; Balbach, H.; Kovacic, D.A.; Zak, J.C. Leaf fluctuating asymmetry, soil disturbance and plant stress: a multiple year comparison using two herbs, Ipomoea pandurata and Cnidoscolus stimulosus. Ecol. Indic. 2005, 5, 85–95. [Google Scholar] [CrossRef]
- Leary, R.F.; Allendorf, F.W. Fluctuating asymmetry as an indicator of stress: implications for conservation biology. Trends Ecol. Evol. 1989, 4, 214–217. [Google Scholar] [CrossRef]
- Lens, L.; Van Dongen, S.; Galbusera, P.; Schenck, T.; Matthysen, E.; Van de Casteele, T. Developmental instability and inbreeding in natural bird populations exposed to different levels of habitat disturbance. J. Evol. Biol. 2000, 13, 889–896. [Google Scholar] [CrossRef]
- Lens, L.; Van Dongen, S.; Matthysen, E. Fluctuating asymmetry as an early warning system in the critically endangered Taita Thrush. Conserv. Biol. 2002, 16, 479–487. [Google Scholar] [CrossRef]
- Teixeira, C.P.; Hirsch, A.; Perini, H.; Young, R.J. Marsupials from space: fluctuating asymmetry, geographical information systems and animal conservation. Proc. Biol. Sci. B 2006, 273, 1007–1012. [Google Scholar] [CrossRef]
- Perzigian, A.J. Fluctuating dental asymmetry: variation among skeletal populations. Am. J. Phys. Anthropol. 1977, 47, 81–88. [Google Scholar] [CrossRef]
- Teul, I.; Czerwiński, F.; Gawlikowska, A.; Konstanty-Kurkiewicz, V.; Sławiński, G. Asymmetry of the ovale and spinous foramina in mediaeval and contemporary skulls in radiological examinations. Folia Morphol. 2002, 61, 147–152. [Google Scholar]
- Gawlikowska, A.; Szczurowski, J.; Czerwiński, F.; Miklaszewska, D.; Adamiec, E.; Dzieciolowska, E. The fluctuating asymmetry of mediaeval and modern human skulls. Homo 2007, 58, 159–172. [Google Scholar] [CrossRef]
- Frederick, M.J.; Gallup, G.G., Jr. Fluctuating dental asymmetry in great apes, fossil hominins, and modern humans: implications for changing stressors during human evolution. Acta Psychologica Sinica 2007, 39, 489–494. [Google Scholar]
- DeLeon, V.B. Fluctuating asymmetry and stress in a Medieval Nubian population. Am. J. Phys. Anthropol. 2007, 132, 520–534. [Google Scholar] [CrossRef] [PubMed]
- Kegley, A.D.T.; Hemingway, J. Assessing fluctuating odontometric asymmetry among fossil hominin taxa through alternative measures of central tendency: effect of outliers and directional components on reported results. Homo 2007, 58, 33–52. [Google Scholar] [CrossRef] [PubMed]
- Kegley, A.D.T.; Hemingway, J. Surveying stress and developmental stability in Homo habilis via fluctuating odontometric asymmetry: assessing generic patterns and australopithecine differentiation. In Voyages in Science: Essays by South African Anatomists in Honour of Phillip V. Tobias’ 80th Birthday; Štrkalj, G., Pather, N., Kramer, B., Eds.; Content Solutions: Pretoria, South Africa, 2005; pp. 35–49. [Google Scholar]
- Brown, W.M.; Cronk, L.; Grochow, K.; Jacobson, A.; Liu, C.K.; Popović, Z.; Trivers, R. Dance reveals symmetry especially in young men. Nature 2005, 438, 1148–1150. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.S.; Hoffmann, H.L.; Mustanski, B.S. Fluctuating asymmetry and sexual orientation in men and women. Arch. Sex. Behav. 2008, 37, 150–157. [Google Scholar] [CrossRef] [PubMed]
- Markow, T.A.; Wandler, K. Fluctuating dermatoglyphic asymmetry and the genetics of liability to schizophrenia. Psychiat. Res. 1986, 19, 323–328. [Google Scholar] [CrossRef]
- Mellor, C.S. Dermatoglyphic evidence of fluctuating asymmetry in schizophrenia. Brit. J. Psychiat. 1992, 160, 467–472. [Google Scholar] [CrossRef]
- Benderlioglu, Z.; Sciulli, P.W.; Nelson, R.J. Fluctuating asymmetry predicts human reactive aggression. Am. J. Hum. Biol. 2004, 16, 458–469. [Google Scholar] [CrossRef]
- Burton, C.; Stevenson, J.C.; Williams, D.C.; Everson, P.M.; Mahoney, E.R.; Trimble, J.E. Attention-deficit hyperactivity disorder (AD/HD) and fluctuating asymmetry (FA) in a college sample: an exploratory study. Am. J. Hum. Biol. 2003, 15, 601–619. [Google Scholar] [CrossRef]
- Stevenson, J.C.; Everson, P.M.; Williams, D.C.; Hipskind, G.; Mahoney, E.R.; Mehler, M.; Cawley, M.; Chamberlin, W.; Watts, L. Attention-deficit hyperactivity disorder and fluctuating asymmetry in another college sample. Am. J. Hum. Biol. 2006, 18, 402–414. [Google Scholar] [CrossRef]
- Saha, S.; Loesch, D.; Chant, D.; Welham, J.; El-Saadi, O.; Fañanás, L.; Mowry, B.; McGrath, J. Directional and fluctuating asymmetry in finger and a-b ridge counts in psychosis: a case-control study. BMC Psychiatry 2003, 3, 3. [Google Scholar] [CrossRef]
- Thornhill, R.; Møller, A.P. Developmental stability, disease and medicine. Biol. Rev. 1997, 72, 497–548. [Google Scholar] [CrossRef] [PubMed]
- Özener, B.; Fink, B. Facial symmetry in young girls and boys from a slum and a control area of Ankara, Turkey. Evol. Hum. Behav. submitted for publication.
- Özener, B.; Duyar, İ.; Atamtürk, D. Body composition of young laborers: the results of a bioelectrical impedance analysis. Collegium Antropol. 2007, 31, 949–954. [Google Scholar]
- Van Dongen, S.; Wijnaendts, L.C.D.; Ten Broek, C.M.A.; Galis, F. Flutuating asymmetry does not consistently reflect severe developmental disorders in human fetuses. Evolution 2009, 63, 1832–1844. [Google Scholar] [CrossRef] [PubMed]
- Weeden, J.; Sabini, J. Physical attractiveness and health in Western societies: a review. Psychol. Bull. 2005, 131, 635–653. [Google Scholar] [CrossRef] [PubMed]
- Knierim, U.; Van Dongen, S.; Forkman, B.; Tuyttens, F.A.M.; Špinka, M.; Campo, J.L.; Weissengruber, G.E. Fluctuating asymmetry as an animal welfare indicator—a review of methodology and validity. Physiol. Behav. 2007, 92, 398–421. [Google Scholar] [CrossRef] [PubMed]
- Almeida, D.; Almodóvar, A.; Nicola, G.G.; Elvira, B. Fluctuating asymmetry, abnormalities and parasitism as indicators of environmental stress in cultured stocks of goldfish and carp. Aquaculture 2008, 279, 120–125. [Google Scholar] [CrossRef]
- Fréchette, M.; Goulletquer, P.; Daigle, G. Fluctuating asymmetry and mortality in cultured oysters (Crassostrea gigas) in Marennes-Oléron basin. Aquat. Living Resour. 2003, 16, 339–346. [Google Scholar] [CrossRef]
- Van Poucke, E.; Van Nuffel, A.; Van Dongen, S.; Sonck, B.; Lens, L.; Tuyttens, F.A.M. Experimental stress does not increase fluctuating asymmetry of broiler chickens at slaughter age. Poult. Sci. 2007, 86, 2110–2116. [Google Scholar] [CrossRef]
- Hoffmann, A.A.; Woods, R.E. Associating stress with developmental stability: problems and patterns. In Developmental Instability: Causes and Consequences; Polak, M., Ed.; Oxford University Press: New York, NY, USA, 2003; pp. 387–401. [Google Scholar]
- Leung, B.; Forbes, M.R. Fluctuating asymmetry in relation to stress and fitness: effects of trait type as revealed by meta-analysis. Ecoscience 1996, 3, 400–413. [Google Scholar] [CrossRef]
- Indrasamy, H.; Woods, R.E.; McKenzie, J.A.; Batterham, P. Fluctuating asymmetry for specific bristle characters in Notch mutants of Drosophila melanogaster. Genetica. 2000, 109, 151–159. [Google Scholar] [CrossRef] [PubMed]
- Nevo, E. Asian, African and European biota meet at “Evolution Canyon” Israel: local tests of global biodiversity and genetic diversity patterns. Proc. Roy. Soc. Lond. B 1995, 262, 149–155. [Google Scholar]
- Nevo, E. Evolution in action across phylogeny caused by microclimatic stresses at “Evolution Canyon”. Theor. Pop. Biol. 1997, 52, 231–243. [Google Scholar] [CrossRef] [PubMed]
- Nevo, E. Evolution of genome-phenome diversity under environmental stress. Proc. Natl. Acad. Sci. USA 2001, 98, 6233–6240. [Google Scholar] [CrossRef] [PubMed]
- Nevo, E. "Evolution Canyon": a microcosm of life’s evolution focusing on adaptation and speciation. Isr. J. Ecol. Evol. 2006, 52, 485–506. [Google Scholar] [CrossRef]
- Nevo, E.; Raz, S.; Beiles, A. Biodiversity of reptiles at "Evolution Canyon", Lower Nahal Oren, Mount Carmel, Israel. Isr. J. Zool. 1996, 42, 395–402. [Google Scholar]
- Raz, S.; Retzkin, S.; Pavlíček, T.; Hoffman, A.; Kimchi, H.; Zehavi, D.; Beiles, A.; Nevo, E. Scorpion biodiversity and interslope divergence at “Evolution Canyon”, Lower Nahal Oren microsite, Mt. Carmel, Israel. PLoS ONE 2009, 4, e5214. [Google Scholar] [CrossRef] [PubMed]
- Pavlíček, T.; Sharon, D.; Kravchenko, V.; Saaroni, H.; Nevo, E. Microclimatic interslope differences underlying biodiversity contrasts in “Evolution Canyon”, Mt. Carmel, Israel. Isr. J. Earth Sci. 2003, 52, 1–9. [Google Scholar] [CrossRef]
- Auslander, M.; Nevo, E.; Inbar, M. The effects of slope orientation on plant growth, developmental instability and susceptibility to herbivores. J. Arid Environ. 2003, 55, 405–416. [Google Scholar] [CrossRef]
- Derzhavets, E.; Korol, A.; Nevo, E. Differences in fluctuating asymmetry in Drosophila melanogaster caused by microclimatic contrasts. Dros. Inf. Serv. 1997, 80, 73–75. [Google Scholar]
- Kennington, W.J.; Killeen, J.R.; Goldstein, D.B.; Partridge, L. Rapid laboratory evolution of adult wing area in Drosophila melanogaster in response to humidity. Evolution 2003, 57, 932–936. [Google Scholar] [CrossRef] [PubMed]
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).