A Probabilistic Framework for Forecasting Cryptographic Security Under Quantum and Classical Threats

Abstract

This paper presents a probabilistic, multi-layered framework designed to forecast the longevity and security of cryptographic systems under the dual pressures of classical and quantum computational threats. The model integrates thermodynamic decay analogies, stochastic transitions via Hidden Markov Models, and an adapted financial option pricing method to quantify cryptographic degradation, strategic risk, and transition readiness. This framework can guide standardization roadmaps, cipher retirement, or quantum-migration planning, guiding proactive, instead of reactive, crypto agility. Furthermore, it provides a quantitative methodology to complement the current opinions expressed in surveys, as well as a qualitative approach to cryptographic security risk projections.

1. Introduction

The transition toward quantum-resilient cryptographic standards (e.g., NIST’s ML-KEM, ML-DSA, and SLH-DSA standards) requires predictive tools [1,2,3] that not only model technical degradation but also capture probabilistic events, such as the discovery of new quantum algorithms or hardware breakthroughs [4,5,6,7,8,9,10]. We introduce a composite framework that unifies multiple analytical domains to forecast cryptographic security trajectories. Traditional assessments often treat cryptographic security as static or binary (e.g., “secure” vs. “broken”), lacking structures to capture evolving threats and decision-relevant metrics under uncertainty [9,10].

Our contributions are threefold: (i) we model time-dependent security erosion using a calibrated decay process, (ii) we infer probabilistic regime shifts using a Hidden Markov formulation, and (iii) we translate these technical trajectories into migration-timing incentives via an option-style valuation model [11]. This end-to-end pipeline is intended to support risk-based decision-making for algorithm retirement and post-quantum migration under uncertain threat arrival timelines, and is designed to be multipurpose across stakeholders (e.g., security engineering, risk governance, and standards planning) through task-specific parameterization. This quantitative probabilistic framework compliments current survey-based qualitative approaches to risk forecasts [12].

The remainder of the paper is organized as follows: Section 2 reviews related work and presents their contributions. Section 3 introduces the component models (decay, HMM state inference, and option-style valuation). Section 5 describes how these components are coupled into an end-to-end workflow, and Section 6 provides illustrative simulations and a migration demonstration.

2. Related Work and Comparative Analysis

The need to anticipate cryptographic degradation has led to modeling approaches spanning standard guidance, security-state inference, and decision analysis. However, most existing frameworks address isolated aspects of the problem and do not provide an integrated, end-to-end forecasting and decision pipeline. Table 1 summarizes how representative prior approaches compare against the proposed framework.

NIST lifecycle models and migration guidance. NIST’s post-quantum cryptography program and transition guidance define phased lifecycles (approval, usage, deprecation) and emphasize inventories and staged migration, but do not provide an organization-specific quantitative forecasting model for degradation and retirement timing [4,5,7,8,9].

Stochastic state models. Hidden Markov Models and related probabilistic methods are widely used to infer latent regimes from observations in security and other domains [13]. In cybersecurity specifically, regime-switching/state-based models have been used to represent evolving risk conditions and to classify security states under changing signals, providing motivation for the latent-state design used in Stage II [14,15]. These approaches support stochastic transitions, but are not typically coupled to continuous security-strength decay trajectories and decision valuation for migration timing.

Decision valuation and real options. Real-option methods value flexibility under uncertainty and have been applied broadly in technology strategy and investment timing [11,16,17,18]. In this work, Stage III adapts this decision-analytic perspective to cryptographic migration, informed in part by practitioner approaches to IP valuation (Pecen, personal communication, 4 September 2025).

Attack trees and risk scoring. Attack trees and risk frameworks such as FAIR help structure adversarial pathways and quantify impact and likelihood, but they are not designed for longitudinal security-strength decay coupled to migration valuation [19].

Adaptive cryptography. Adaptive cryptographic mechanisms can switch primitives in response to context or threat conditions [20], but these approaches are typically reactive and do not provide forward-looking forecasts of threshold-crossing timelines under uncertain quantum and classical threat evolution.

Table 1. Comparison of prior models and frameworks against the proposed integrated approach.

Model/Framework	Time	Stochastic	Valuation	Quantum	Simulatable	Lifecycle
NIST Lifecycle/PQC Guidance [4,5]	No	No	No	Partial	No	Yes
Attack Trees (Schneier) [19]	No	Yes (implicit)	No	No	No	Yes
FAIR Risk Model [21]	No	Yes	No	No	No	Yes
Bayesian/Markov Security Models [13]	Yes	Yes	No	No	Partial	No
Trigeorgis (Real Options) [16]	Yes	No	Yes	No	Yes	Yes
Pecen (Practitioner IP valuation; personal communication) [22]	Yes	No	Yes	No	Yes	Yes
This Work (Proposed)	Yes	Yes	Yes	Yes	Yes	Yes

Table 1. Comparison of prior models and frameworks against the proposed integrated approach.

Model/Framework	Time	Stochastic	Valuation	Quantum	Simulatable	Lifecycle
NIST Lifecycle/PQC Guidance [4,5]	No	No	No	Partial	No	Yes
Attack Trees (Schneier) [19]	No	Yes (implicit)	No	No	No	Yes
FAIR Risk Model [21]	No	Yes	No	No	No	Yes
Bayesian/Markov Security Models [13]	Yes	Yes	No	No	Partial	No
Trigeorgis (Real Options) [16]	Yes	No	Yes	No	Yes	Yes
Pecen (Practitioner IP valuation; personal communication) [22]	Yes	No	Yes	No	Yes	Yes
This Work (Proposed)	Yes	Yes	Yes	Yes	Yes	Yes

Research Status and Open Issues

Recent post-quantum migration guidance (e.g., NIST PQC and transition reports) emphasizes inventories, staged deployment, and risk-based prioritization, but generally does not provide an organization-specific quantitative forecast for when legacy primitives should be retired under uncertain threat arrival timelines [4,5,6,7,8,9]. In parallel, security-strength guidance provides static mappings between key sizes and target strengths [10], yet does not model how those targets evolve as classical and quantum capabilities progress. A further gap is that decision frameworks used in governance (e.g., the NIST CSF) motivate continuous monitoring but do not specify a mathematical pipeline that converts evolving technical signals into timing decisions and migration incentives [9,21]. These gaps motivate an integrated approach combining (i) time-dependent security erosion, (ii) probabilistic regime inference, and (iii) decision valuation for migration timing. Operationally, such forecasts are only proactively actionable if systems can transition algorithms and keys within bounded lead times (crypto agility) [23].

3. Model Components

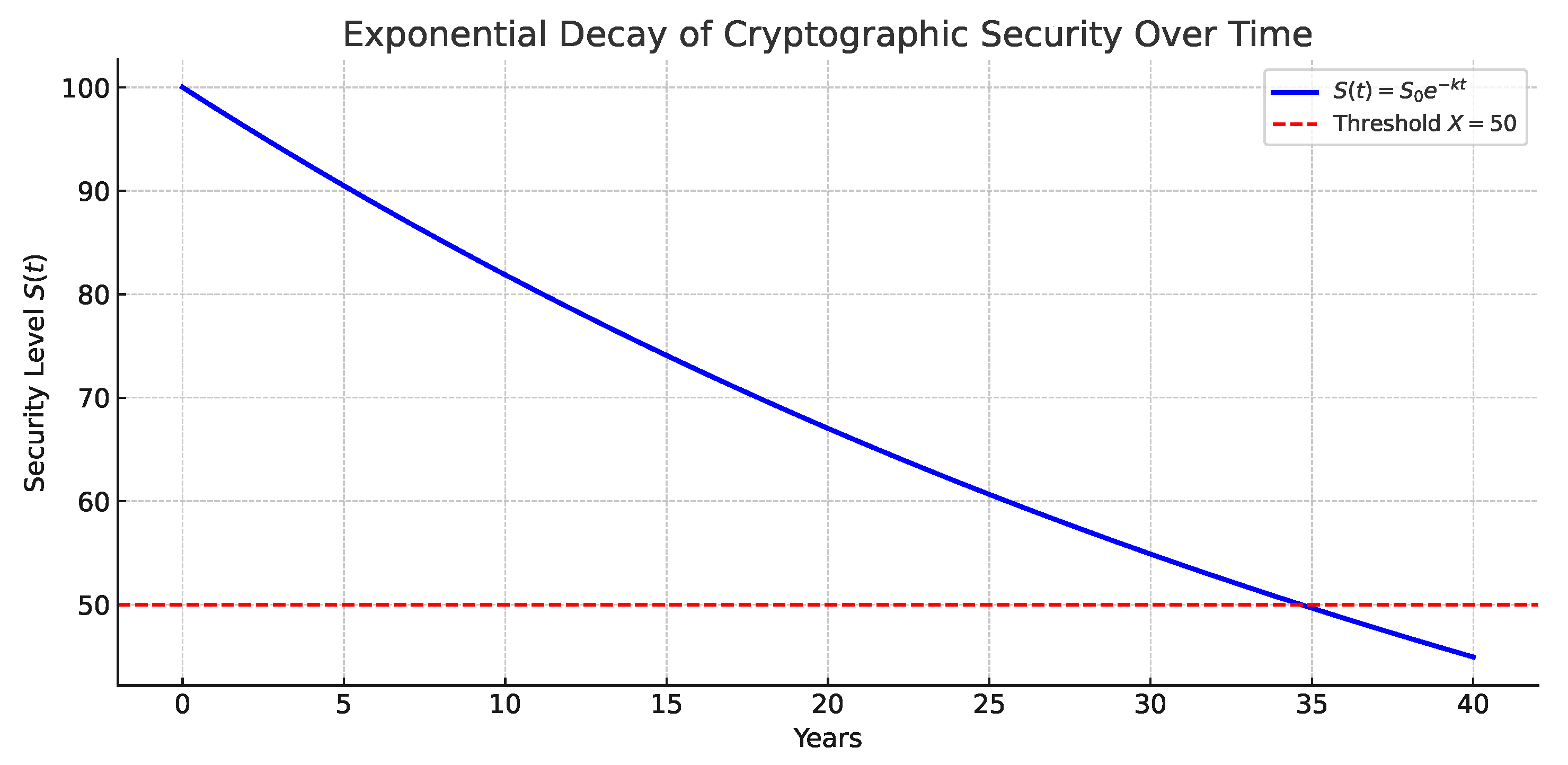
3.1. Exponential Security Decay Model

We adopt a first-order exponential decay model, commonly used in thermodynamics, information theory [24], and reliability engineering, to represent the gradual erosion of cryptographic strength over time. The model assumes that the rate of decline in effective security $S\left(t\right)$ is proportional to its current value:

$${\displaystyle \frac{dS}{dt}}=-kS\left(t\right),$$

(1)

where $k>0$ is a decay constant representing the rate at which entropy or resistance to attack deteriorates under ambient conditions (e.g., hardware improvements, algorithmic refinements).

Solving the differential equation yields the general solution:

$$S\left(t\right)=S_0{e}^{-kt},$$

(2)

where $S_0$ is the initial security strength at $t=0$. It is the change in $S_0$ that is of interest, so its absolute magnitude is irrelevant, and can be chosen to ease interpretation of the change. $S_0$ can be understood as today’s dimensionless reference point (a baseline), and may be set to 1 or 100 purely for convenience, e.g., choosing $S_0=100$ makes subsequent values interpretable as a direct percent-of-baseline. For example, if $S_0$ is set to 100, then future values of S easily reveal percentage change. In contrast, confidence in the absolute value of k is critical to model projections and must in general be determined by experts (See Section 5.1 for an example). In practice, k uncertainty implications can be understood through, for example, sensitivity analysis or deeper Markov modeling. This form captures the asymptotic weakening of ciphers over time and can be empirically calibrated using historical cryptanalytic data.

In practice, k is estimated from time-stamped evidence of security-strength erosion, using public cryptanalytic records, standardization transitions, and measured attack-cost trends. Let $S_c\left(t\right)$ denote an effective security proxy for primitive c (e.g., “bits of work” inferred from the best-known attacks and implementation-scale records at time t). Given observations $\left\{(t_i,S_c\left(t_i\right))\right\}$, a first-order estimate follows from log-linear regression [25,26]

$$ln{S}_c\left(t_i\right)=ln{S}_{0,c}-k_c{t}_i+{ϵ}_i,$$

(3)

or by finite differences:

$${\widehat{k}}_c\left(t_i\right)={\displaystyle \frac{1}{t_{i+1}-t_i}}ln\left({\displaystyle \frac{S_c\left(t_i\right)}{S_c\left(t_{i+1}\right)}}\right).$$

(4)

Historical cryptanalytic progress can therefore be used for calibration by constructing within-family progress curves (e.g., factoring and discrete-log records for public-key schemes; published cryptanalysis margins for symmetric schemes), while treating major discontinuities (e.g., credible new attacks or paradigm shifts) as regime changes handled in Stage II rather than forcing a single constant k.

3.2. Discrete-State Security Transition Modeling via Hidden Markov Processes

We represent the cryptographic system as a discrete-time, discrete-state stochastic process whose latent security condition evolves over time. Due to the partially observable nature of cryptographic robustness (e.g., undisclosed attacks or unknown algorithmic advancements), a Hidden Markov Model (HMM) is well-suited to characterize the transition dynamics between different security states.

Let the set of hidden states be defined as:

$$\mathcal{S}=\{S_1:\mathrm{Highly}\mathrm{Secure},S_2:\mathrm{Moderately}\mathrm{Secure},S_3:\mathrm{At}\mathrm{Risk}\}.$$

The model assumes that at each time step t, the system is in some hidden state $s_t\in \mathcal{S}$, and transitions are governed by the Markov property:

$$P(s_{t+1}\mid s_t,s_{t-1},\dots ,s_0)=P(s_{t+1}\mid s_t),$$

(5)

This yields a transition probability matrix T:

$$T=\left[\begin{array}{ccc}P(S_1\to S_1)& P(S_1\to S_2)& P(S_1\to S_3)\\ P(S_2\to S_1)& P(S_2\to S_2)& P(S_2\to S_3)\\ P(S_3\to S_1)& P(S_3\to S_2)& P(S_3\to S_3)\end{array}\right],$$

Each element $T_{ij}=P(s_{t+1}=S_j\mid s_t=S_i)$ reflects the likelihood of moving from one cryptographic state to another between discrete time steps. These probabilities can be empirically estimated or scenario-driven (e.g., conditioned on a timeline to quantum supremacy, adversarial investment, or regulatory lag).

Observed indicators (e.g., security-strength estimates, deprecation notices, cryptanalytic reports, or structured threat-modeling artifacts such as attack trees [21]) are treated as emissions that probabilistically depend on the latent state.

Real-world signals may be uncertain (e.g., unverified attack claims, partial disclosures, or conflicting reports). We attach a credibility weight $q_t\in [0,1]$ to each observation $y_t$ and use a mixture emission model:

$$P(y_t\mid s_t)=q_{t}f(y_t;{\theta }_{s_t})+(1-q_t)g\left(y_t\right),$$

(6)

where $f(·)$ is the state-conditional emission model (e.g., Gaussian over security-strength estimates) and $g(·)$ is an outlier/heavy-tail component capturing rumor/noise. This prevents a single low-confidence observation from dominating posteriors, while allowing confirmed observations (high $q_t$) to rapidly update the inferred risk regime [13].

This formulation supports both gradual regime changes and abrupt shocks (e.g., a new cryptanalytic result) while remaining tractable; see ref. [13].

3.3. Real Options Approach to Cryptographic Security Valuation (After Pecen)

An option is a financial contract that gives its holder the right to buy or sell an underlying asset at a fixed price within a specified time period. A call option gives the holder the right to buy an underlying asset at a certain price, while a put option gives the holder the right to sell an underlying asset at a certain price. Options are considered a “wasting asset”, as their value goes to zero upon expiry. The value of an option is based on the value of the underlying asset along with the exercise price of the option, market volatility and time to expiry. Inspired by Pecen’s application of real options theory to intellectual property valuation (M. Pecen, personal communication, 4 September 2025), we model the residual value of a cryptographic system under uncertainty using a discrete-time binomial framework. This approach treats cryptographic security as a real asset whose future utility can fluctuate due to advances in classical or quantum computational power, breakthroughs in cryptanalysis, or shifts in industry standards.

We begin with the classical Black–Scholes-style representation as a conceptual basis [27]. While Black–Scholes provides useful intuition, its assumptions (e.g., continuous trading, log-normal returns, and efficient and liquid public markets) do not hold for cryptographic systems. Moreover, Black–Scholes can overestimate option values in regimes analogous to far out-of-the-money cases when applied to non-traded real assets. Hence, we use the Black–Scholes framework only for conceptual grounding and adopt a discrete binomial lattice for practical evaluation.

For reference, the Black–Scholes European call value is

$$V=SN\left(d_1\right)-X{e}^{-rt}N\left(d_2\right),$$

(7)

where, following standard notation [27],

$$d_1={\displaystyle \frac{ln(S/X)+\left(r+\frac{1}{2}{\sigma }^2\right)t}{\sigma \sqrt{t}}},d_2=d_1-\sigma \sqrt{t}.$$

(8)

In the classical interpretation, $d_1$ and $d_2$ are standardized distances that map the underlying-to-threshold ratio into the normal CDF terms $N\left(d_1\right)$ and $N\left(d_2\right)$ used in Equation (7).

Here, V is the option-like value, S is the current effective security (treated as the underlying), X is the minimum acceptable security threshold (strike), r is an effective discount/decay rate, $\sigma$ is a volatility parameter, t is the time horizon, and $N(·)$ is the standard normal cumulative distribution function.

However, since cryptographic systems are not traded in efficient markets and changes occur in discrete technological phases, we refine this approach using a binomial tree model. Let u and d be the up and down factors per period, and p the risk-neutral probability of an upward move. Over n periods, the security value evolves across a lattice, and the expected option-like value of the cipher is computed by backward induction.

Let

1.

$u=e^{\sigma \sqrt{\Delta t}}$ and $d=e^{-\sigma \sqrt{\Delta t}}$ be multiplicative security shift factors;

2.

$\sigma$ be the volatility of cryptographic risk (e.g., measured from historical compromise timelines);

3.

$p={\displaystyle \frac{e^{\mathsf{r}\Delta t}-d}{u-d}}$ be the risk-neutral transition probability.

Interpretation of the “risk-neutral” probability in a security context. Cryptographic assets are not traded and adversary behavior is not market-driven. Here, “risk-neutral” is used as a decision-analytic normalization (a computational device for discounted expectation on the lattice), not as a claim of market efficiency. In an operational variant, p may be replaced with a threat-driven probability inferred from Stage II (e.g., derived from ${\pi }^{(c,a)}\left(t\right)$ and the transition matrix T), while risk appetite is represented through r (or via an explicit loss/utility mapping). This preserves the lattice mechanics while grounding probabilities in inferred adversarial regimes rather than financial-market assumptions.

At each node, the expected value is

$$V_{i,j}=e^{-r\mathsf{\Delta }t}[p·V_{i+1,j+1}+(1-p)·V_{i+1,j}]$$

(9)

with the terminal condition:

$$V_{n,j}=max(S_{n,j}-X,0)$$

(10)

This binomial valuation scheme allows for dynamic decision-making (e.g., retire, reinforce, or transition a cipher) based on real-time threat evolution and security valuation thresholds [17,18]. Furthermore, the binomial tree approach can easily adapt to differing levels of volatility over time, and can be further extended to even a trinomial, or higher-level, model to evaluate multiple related assets.

4. Notation and Definitions

For interdisciplinary readability across cryptography, statistics, and finance,

Table 2. Notation used in the modeling framework.

Symbol	Description
$S\left(t\right),S_0,k$	Effective security trajectory, initial level, and decay constant.
$s_t,T_{ij}$	Latent HMM state at time t and transition probabilities.
$X^{\left(a\right)}$	Asset-dependent minimum acceptable security threshold (“strike”).
${\pi }_s^{(c,a)}\left(t\right)$	Posterior probability of latent state s for cipher–asset pair $(c,a)$.
$V^{(c,a)}\left(t\right)$	Option-style value used to compare retain/migrate decisions over time.
$r,\sigma$	Effective discount rate and volatility parameter in the lattice model.
$u,d,p,n$	Binomial up/down factors, risk-neutral probability, and number of steps.

provides a compact reference for symbols used throughout the pipeline.

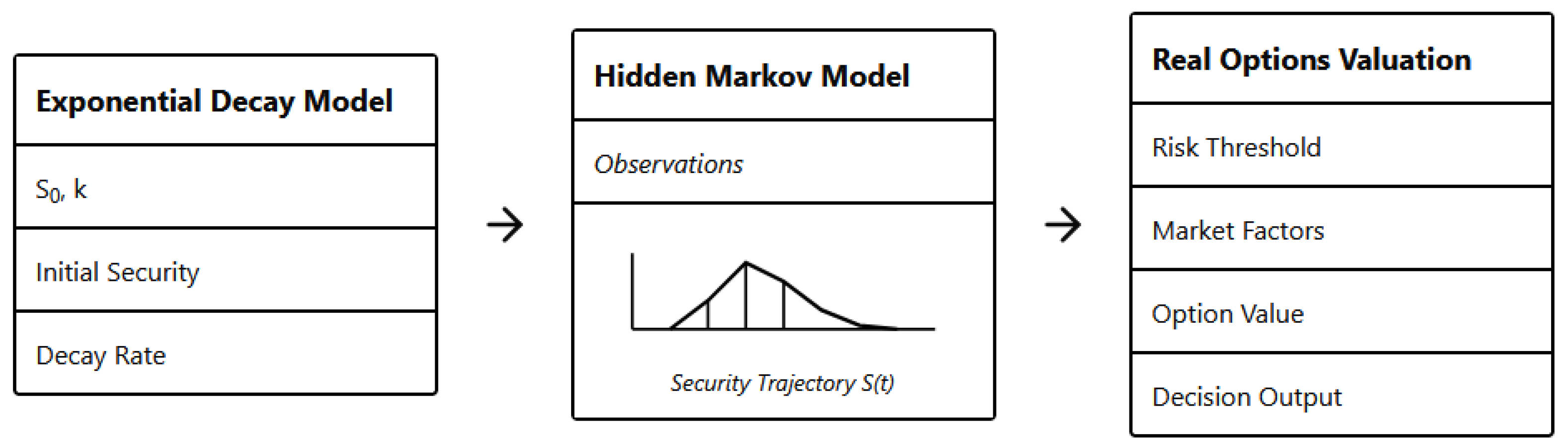
5. Model Integration Architecture

The proposed framework is composed of three interdependent sub-models, each capturing a distinct dimension of cryptographic lifecycle degradation. The integration of these models enables both continuous monitoring and forward-looking valuation under uncertainty. In practical use, they are executed as a pipeline: Stage I produces time-dependent security trajectories, Stage II consumes these trajectories to infer probabilistic risk states, and Stage III maps both quantities into migration-timing and valuation outputs.

5.1. Stage I: Continuous Security Degradation (Exponential Decay)

The security level $S\left(t\right)$ is computed as a time-dependent decay function:

$$S\left(t\right)=S_0{e}^{-kt}$$

(11)

where k is a cipher-specific decay rate calibrated to historical cryptanalytic progress and published security-strength guidance (e.g., key management and security-strength mappings), Moore’s law [28] (or Neven’s Law [29] in quantum), and empirical measurements of implementation erosion (e.g., side-channel leakage growth).

Separate stochastic factors beyond Shor. Beyond Shor-capable quantum computers, the erosion rate can be modeled as a multi-factor process rather than a single monolithic constant. For example [30,31],

$$k\left(t\right)=k_{\mathrm{class}}\left(t\right)+k_{\mathrm{qc}\text{-}\mathrm{shor}}\left(t\right)+k_{\mathrm{qc}\text{-}\mathrm{grover}}\left(t\right)+k_{\mathrm{hw}\text{-}\mathrm{accel}}\left(t\right)+\dots ,$$

(12)

where $k_{\mathrm{qc}\text{-}\mathrm{grover}}\left(t\right)$ captures sub-quadratic quantum speedups relevant to symmetric primitives, and $k_{\mathrm{hw}\text{-}\mathrm{accel}}\left(t\right)$ captures classical hardware acceleration (e.g., GPU/ASIC, software–hardware co-design). Each factor can be scenario-driven or treated as a stochastic process, enabling the framework to represent both quantum and classical acceleration effects as distinct contributors to effective security erosion.

In an operational setting, this stage is instantiated per cipher and per asset class. For each cipher–asset pair $(c,a)$ in an organization’s portfolio, the model produces a trajectory

$$S^{(c,a)}\left(t\right)=S_0^{(c,a)}{e}^{-k^{(c,a)}t},$$

(13)

sampled at discrete time points $t=0,\Delta t,2\Delta t,\dots ,T$.

Output: The output of Stage I is therefore a matrix of trajectories $\left\{S^{(c,a)}\left(t\right)\right\}$ that summarize the expected erosion of security for each cipher and asset over time. This matrix is treated as an observable emission signal and passed as input to the HMM in Stage II.

5.2. Stage II: Probabilistic State Transition (Hidden Markov Model)

The time-evolving values $S^{(c,a)}\left(t\right)$ are used as observable inputs (emission signals) to infer the latent security state $s_t\in \{S_1,S_2,S_3\}$ using a Hidden Markov Model. For each cipher–asset pair, we construct an observation sequence

$$Y_t^{(c,a)}=S^{(c,a)}\left(t\right),t=0,\Delta t,2\Delta t,\dots ,T,$$

(14)

which captures how its effective security evolves under the assumed classical and quantum threat models.

To connect continuous security levels to discrete risk regimes, we define a risk-tolerance matrix R whose entries $R_{a,s}$ encode, for each asset class a and latent state $s\in \{S_1,S_2,S_3\}$, the minimum acceptable security level (e.g., “bits of security”). Ranges of $S^{(c,a)}\left(t\right)$ are mapped to provisional labels such as hlHighly Secure, Moderately Secure, or At Risk using R, providing symbol sequences that initialize or constrain HMM training.

Standard HMM algorithms (e.g., Baum–Welch for parameter estimation and Viterbi decoding for state inference) are then applied to the sequences $\left\{Y_t^{(c,a)}\right\}$, yielding both the most likely state $s_t^{(c,a)}$ and posterior state probabilities

$${\pi }_s^{(c,a)}\left(t\right)=P(s_t=s\mid Y_{0:t}^{(c,a)})$$

(15)

For each cipher–asset pair and time. These probabilities capture, for example, when a classical algorithm is likely to move from Moderately Secure to At Risk under a given quantum-computing scenario.

Output: The numerical outputs of Stage II are trajectories of inferred states and state probabilities, together with an estimated transition matrix T, which together describe how quickly different ciphers are expected to enter unacceptable risk regimes. These quantities parameterize the valuation model in Stage III.

5.3. Stage III: Security Option Valuation (Binomial Model)

Both $S^{(c,a)}\left(t\right)$ and the current inferred state information from Stage II feed into a real-option framework to quantify the residual security value and migration incentives. For each cipher–asset pair, we construct a binomial lattice whose parameters are directly derived from earlier stages:

1.

The latest continuous security level $S^{(c,a)}\left(t\right)$ represents the underlying value of cryptographic strength in the lattice.

2.

The policy-defined minimum acceptable security threshold $X^{\left(a\right)}$ (the “strike”) is taken from the risk-tolerance matrix R for asset class a.

3.

The volatility ${\sigma }^{(c,a)}$ and effective discount rate $r^{(c,a)}$ are modulated by the HMM output, for example, by increasing ${\sigma }^{(c,a)}$ as the probability ${\pi }_{S_3}^{(c,a)}\left(t\right)$ of being in the At Risk state grows, or by raising $r^{(c,a)}$ when adversarial activity is believed to be accelerating.

Quantitative Derivation of $\sigma$ from Posterior HMM Outputs

To avoid arbitrary scaling, we derive a time-varying volatility ${\sigma }^{(c,a)}\left(t\right)$ directly from the posterior distribution ${\pi }_s^{(c,a)}\left(t\right)=P(s_t=s\mid Y_{0:t}^{(c,a)})$ produced by Stage II. One convenient posterior-uncertainty index is the Gini impurity:

$$U^{(c,a)}\left(t\right)=1-\sum _{s\in \{S_1,S_2,S_3\}}{\left({\pi }_s^{(c,a)}\left(t\right)\right)}^2,$$

(16)

which is near 0 when the inferred state is unambiguous and increases as evidence becomes mixed or conflicting. We then map this to volatility using calibrated bounds:

$${\sigma }^{(c,a)}\left(t\right)={\sigma }_{min}^{(c,a)}+\left({\sigma }_{max}^{(c,a)}-{\sigma }_{min}^{(c,a)}\right)U^{(c,a)}\left(t\right),$$

(17)

where ${\sigma }_{min}^{(c,a)}$ and ${\sigma }_{max}^{(c,a)}$ can be estimated from historical variability in security-strength reassessments or attack-cost revisions for similar primitives and deployment contexts. An equivalent estimator uses the rolling variance of posterior drift (e.g., $\mathrm{Var}(\Delta {\pi }_{S_3})$), so that volatility increases precisely when probability mass rapidly shifts toward the At Risk regime [32].

The binomial option valuation then proceeds using backward induction, yielding an option-style value $V^{(c,a)}\left(t\right)$ for maintaining or migrating each cipher–asset pair. Comparing $V^{(c,a)}\left(t\right)$ across time and across candidate post-quantum algorithms (e.g., replacing RSA-2048 with Kyber-768 or Dilithium-3) provides a quantitative basis for determining the time window during which proactive migration is economically and operationally justified.

Operational normalization of option-like values. While $V^{(c,a)}\left(t\right)$ is computed in the same units as the chosen underlying proxy S, it can be mapped to operational decision units by linking security margin to expected loss. For an asset class a with impact $I^{\left(a\right)}$ (e.g., cost, mission impact), define a compromise-probability map such as

$$P_{\mathrm{comp}}\left(t\right)={\displaystyle \frac{1}{1+exp\left(\beta (S^{(c,a)}\left(t\right)-X^{\left(a\right)})\right)}},$$

(18)

and expected loss

$$\mathrm{EL}\left(t\right)=I^{\left(a\right)}{P}_{\mathrm{comp}}\left(t\right).$$

(19)

Option outputs can then be reported as avoided expected loss (or avoided tail risk) over the planning horizon, enabling direct operational trade-offs against migration cost [33].

Output: Stage III outputs a time-indexed option value and, by identifying when $V^{(c,a)}\left(t\right)$ falls below a policy-defined threshold, an implied “latest safe migration date” for each cipher–asset pair (see Figure 1).

5.4. Functional Coupling Summary

Stage I produces security trajectories $\left\{S^{(c,a)}\left(t\right)\right\}$ and calibrated decay parameters; Stage II maps these observations into latent-state probabilities and transition dynamics; and Stage III converts both continuous security and inferred risk into option-style values and migration windows. This modular structure allows any component to be refined independently as better data, threat intelligence, or standards guidance becomes available.

Cryptographic assets may share common mathematical failure modes (e.g., RSA and ECDSA under Shor-capable quantum computing). To capture correlation, Stage II can be generalized from independent HMMs to coupled/factorial models by introducing a shared latent factor $z_t$ (e.g., “quantum-capable regime” or “new lattice reduction breakthrough”) that influences all primitives:

$$P(\left\{s_{t+1}^{\left(i\right)}\right\}\mid \left\{s_t^{\left(i\right)}\right\},z_t)=\prod _{i}P(s_{t+1}^{\left(i\right)}\mid s_t^{\left(i\right)},z_t).$$

(20)

This models common-mode shocks and correlated transitions without requiring each primitive to be inferred in isolation [34].

5.5. Practical Implementation Workflow

To move from conceptual modeling to an implementable tool, we outline a workflow that links the three stages of the framework to concrete data inputs and computational steps. The goal is that a standards body or system operator can start from an inventory of deployed ciphers and derive migration recommendations without modifying the underlying mathematics.

1.

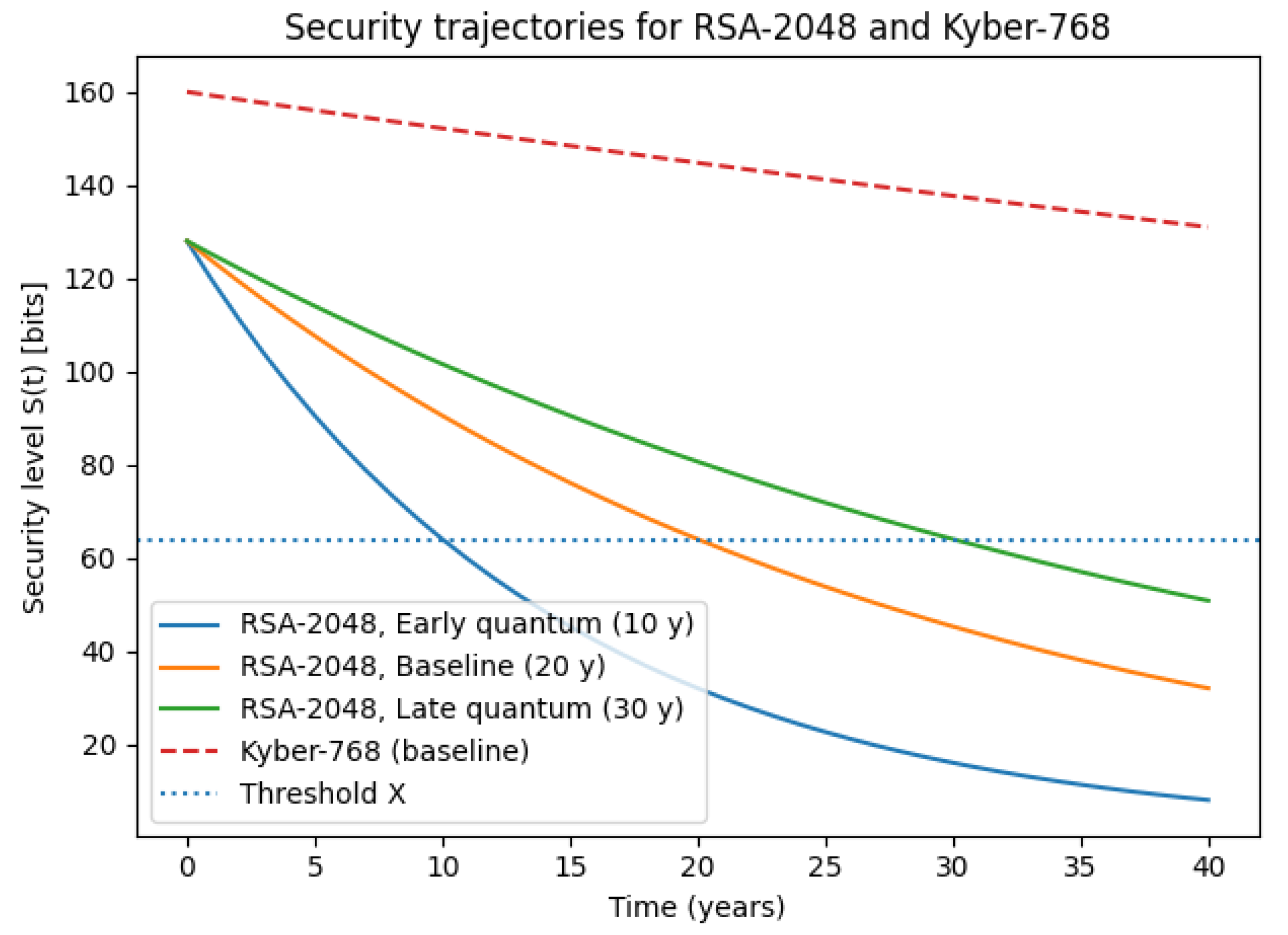
Portfolio and parameter initialization. The practitioner first compiles a portfolio of cryptographic mechanisms $\mathcal{C}=\{c_1,\dots ,c_m\}$ used across asset classes (e.g., RSA-2048 for TLS key exchange, AES-256-GCM for bulk encryption, and post-quantum candidates such as Kyber-768 or Dilithium-3). For each cipher–asset pair $(c,a)$, the initial security level $S_0^{(c,a)}$ is expressed in “bits of (classical and quantum) security,” together with performance and deployment metadata (latency constraints, key-size limits, presence of hardware accelerators) [20]. Scenario-specific decay constants $k^{(c,a)}$ are then specified for classical-only, quantum-enabled, and aggressive-quantum threat models.

2.

Running Stage I and constructing observation sequences (output of Stage I → Stage II). Stage I is evaluated over a discrete horizon to obtain trajectories $S^{(c,a)}\left(t\right)=S_0^{(c,a)}{e}^{-k^{(c,a)}t}$ for all $(c,a)$. These trajectories are sampled at yearly or quarterly resolution to form observation sequences $Y_t^{(c,a)}=S^{(c,a)}\left(t\right)$. At this point, the artifact produced by Stage I is a matrix of security levels over time whose rows are cipher–asset pairs and columns are time steps; this matrix becomes the emission data for the HMM.

3.

Risk-tolerance matrix and HMM calibration (Stage II implementation). The organization specifies a risk-tolerance matrix R with rows indexed by asset class and columns by latent state $\{S_1,S_2,S_3\}$. Entry $R_{a,S_2}$, for example, encodes the minimum acceptable security level for asset class a to be considered Moderately Secure. Each element of $Y_t^{(c,a)}$ is mapped to a provisional state label using R, producing symbol sequences that are fed into a Hidden Markov Model. Using standard libraries, the practitioner estimates the transition matrix T and obtains posterior state probabilities ${\pi }_s^{(c,a)}\left(t\right)$, which summarize when each cipher–asset pair is likely to become At Risk under the specified quantum scenarios.

4.

Mapping to option parameters and valuation (Stage III implementation). For each cipher–asset pair, Stage III takes as input the latest security level $S^{(c,a)}\left(t\right)$ from Stage I and the risk metrics from Stage II. The current underlying in the binomial lattice is set to $S=S^{(c,a)}\left(t\right)$; the strike $X^{\left(a\right)}$ is taken from the risk-tolerance matrix as the minimum acceptable security for asset class a; and the volatility ${\sigma }^{(c,a)}$ is calibrated from the variability of ${\pi }_{S_3}^{(c,a)}\left(t\right)$ over the planning horizon. Migration costs—including the expected performance overhead of PQC candidates (e.g., increased ciphertext size or handshake latency) and re-engineering effort—are folded into the effective discount rate $r^{(c,a)}$. Running the binomial option model then yields an option value $V^{(c,a)}\left(t\right)$ for migrating from a legacy cipher to a selected PQC algorithm.

5.

Decision outputs and iteration. The final artifacts of the implementation are (i) a ranked list of cipher–asset pairs by their option values $V^{(c,a)}\left(t\right)$, (ii) recommended migration windows and “latest safe migration dates” for each pair, and (iii) sensitivity analyses under different quantum-threat scenarios. In practice, the workflow is executed periodically as new cryptanalytic results, hardware benchmarks, or PQC performance measurements become available, updating $k^{(c,a)}$, R, T, and the resulting migration roadmap without changing the core structure of the framework.

6. Simulation Results

This section provides an illustrative simulation using synthetic parameters to demonstrate how the framework’s outputs (security trajectories, inferred risk states, and option-style values) are generated end-to-end.

6.1. Exponential Security Decay

Given initial conditions $S_0=100$ and $k=0.02$/year, the security level over time follows

$$S\left(t\right)=100e^{-0.02t}$$

(21)

As discussed in Section 3, $S_0$ is chosen to ease interpretation of results, in this case to easily reveal percentage change in S. The selection of k, a best-estimate parameter, requires expert understanding of the past, present, and expected future. For example, if computational speed, which is affected by transistor speed, algorithm efficiency, parallelism, software–hardware co-design, quantum computing, etc., was the only factor affecting effective security S, then Moore’s Law today would suggest a doubling in speed every 48–66 months [35], or $k=0.17$ yr⁻¹ to $0.13$ yr⁻¹, respectively. However, algorithmic breakthroughs can also shift effective attack feasibility beyond pure hardware scaling; for example, a recent preprint proposes the Jesse–Victor–Gharabaghi (JVG) quantum factorization approach, replacing QFT with a QNTT circuit and reporting reduced resource growth relative to Shor’s algorithm (e.g., reductions in CX-gate growth and circuit depth in simulation, and reduced runtime growth and X-gate counts on hardware) [36]. However, in addition to understanding processes affecting increases in computational speed, consideration by the expert must also involve factors that decrease k such as advancements in algorithms, hardware, and implementation. For example, over time the number of bits in RSA encryption has steadily increased. Given that the focus of this paper is the presentation of a framework for forecasting cryptographic security, and not an expert evaluation of a specific future scenario, k was chosen as $0.02$ yr⁻¹ for illustrative purposes only with the only constraint applied that k be less than that needed to compensate solely for Moore’s Law’s empirical trend.

At $t=40$ years, we compute

$$S\left(40\right)\approx 44.93$$

(22)

The decay curve is shown in Figure 2.

6.2. Hidden Markov Transitions

States are defined by thresholding $S\left(t\right)$:

1.

$S\left(t\right)\ge 70$: Highly Secure;

2.

$50\le S\left(t\right)<70$: Moderately Secure;

3.

$S\left(t\right)<50$: At Risk.

From these transitions, the estimated transition matrix T is

$$T=\left[\begin{array}{ccc}0.944& 0.056& 0.000\\ 0.000& 0.941& 0.059\\ 0.000& 0.000& 1.000\end{array}\right]$$

(23)

This matrix reflects the observed transitions during the decay horizon and serves as an example of how Stage I trajectories can be converted into Stage II transition probabilities.

6.3. Binomial Option Valuation

With parameters:

1.

$r=0.01$ (discount rate);

2.

$\sigma =0.15$ (volatility);

3.

$X=50$ (minimum security threshold);

4.

$T=10$ years;

5.

$n=10$ (binomial steps).

We treat the current security level $S\left(0\right)=100$ as the underlying asset and interpret crossing the threshold $X=50$ as entering an unacceptable risk regime. Applying the binomial option valuation yields an option value of

$$V\left(0\right)\approx 55.36$$

(24)

indicating that, under this synthetic scenario, the cipher retains value above the operational threshold but with limited margin—consistent with a situation in which migration planning should begin.

Sensitivity to the Policy Threshold X and the Latest Safe Migration Date

For the decay model alone, the threshold-crossing time $t^{*}$ satisfies $S_0{e}^{-k{t}^{*}}=X$, hence

$$t^{*}={\displaystyle \frac{1}{k}}ln\left({\displaystyle \frac{S_0}{X}}\right),{\displaystyle \frac{\partial t^{*}}{\partial X}}=-{\displaystyle \frac{1}{kX}}.$$

(25)

This shows that even small changes in the policy-defined threshold X can materially shift the implied “latest safe migration date,” especially when k is small or when $S\left(t\right)$ is near X. In practice, we therefore report a sensitivity band over $(X,k,\sigma )$ rather than a single point estimate.

6.4. Demonstration: Migration from RSA-2048 to Kyber-768

To illustrate how the three stages of the framework can support post-quantum migration planning, we consider a simplified demonstration in which an Internet-facing service currently uses RSA-2048 for TLS key exchange and evaluates Kyber-768 (standardized as ML-KEM-768) as a post-quantum candidate [1]. The asset under consideration is a latency-sensitive API, and we express security levels in bits of effective security against combined classical and quantum attackers.

6.4.1. Security Decay Under Quantum-Arrival Scenarios

We set the initial security levels to $S_0^{\mathrm{RSA}}=128$ bits and $S_0^{\mathrm{Kyber}}=160$ bits. The policy threshold for acceptable security is fixed at $X=64$ bits. For RSA-2048, we consider three quantum-arrival scenarios in which the algorithm first crosses the threshold X after $t_q\in \{10,20,30\}$ years, representing early, baseline, and late availability of large-scale quantum computers capable of running Shor’s algorithm [30].

Using the exponential model of Section 3, the corresponding decay constants are obtained by solving

$$S_0^{\mathrm{RSA}}{e}^{-k_{\mathrm{RSA}}^{\left(q\right)}{t}_q}=X\Rightarrow k_{\mathrm{RSA}}^{\left(q\right)}={\displaystyle \frac{1}{t_q}}ln\left({\displaystyle \frac{S_0^{\mathrm{RSA}}}{X}}\right),$$

(26)

which yields $k_{\mathrm{RSA}}^{\left(10\right)}\approx 0.0693$, $k_{\mathrm{RSA}}^{\left(20\right)}\approx 0.0347$, and $k_{\mathrm{RSA}}^{\left(30\right)}\approx 0.0231$. For Kyber-768, we assume a much slower decay, $k_{\mathrm{Kyber}}=0.005$, capturing incremental algorithmic progress rather than a single catastrophic breakthrough.

For each cipher and scenario, the Stage I trajectories are

$$S^{\mathrm{RSA},\left(q\right)}\left(t\right)=S_0^{\mathrm{RSA}}{e}^{-k_{\mathrm{RSA}}^{\left(q\right)}t},S^{\mathrm{Kyber}}\left(t\right)=S_0^{\mathrm{Kyber}}{e}^{-k_{\mathrm{Kyber}}t},$$

(27)

evaluated on a 40-year horizon with yearly time steps. Figure 3 shows that, while RSA-2048 crosses the threshold X between 10 and 30 years depending on the scenario, Kyber-768 remains comfortably above X throughout the horizon.

6.4.2. State Transitions for the Baseline Scenario

For the baseline scenario ($t_q=20$ years), we discretize $S^{\mathrm{RSA}}\left(t\right)$ into the three latent states of Section 3 using the risk-tolerance matrix R for an exposed online service:

$$\begin{array}{cc}\hfill S_1\left(\mathrm{Highly}\mathrm{Secure}\right)& :S\left(t\right)\ge 100,\hfill \\ \hfill S_2\left(\mathrm{Moderately}\mathrm{Secure}\right)& :70\le S\left(t\right)<100,\hfill \\ \hfill S_3\left(\mathrm{At}\mathrm{Risk}\right)& :S\left(t\right)<70.\hfill \end{array}$$

Applying these thresholds to the yearly samples of $S^{\mathrm{RSA}}\left(t\right)$ produces a state sequence that starts in $S_1$, spends several years in $S_2$, and eventually enters $S_3$.

From this sequence, we estimate the empirical transition matrix for RSA-2048 in the baseline scenario as

$$T_{\mathrm{baseline}}^{\mathrm{RSA}}=\left[\begin{array}{ccc}0.875& 0.125& 0.000\\ 0.000& 0.900& 0.100\\ 0.000& 0.000& 1.000\end{array}\right],$$

(28)

indicating that once the At Risk state is reached, it is absorbing, and that the probability of remaining in Highly Secure or Moderately Secure states declines over time. Under the same thresholds, the Kyber-768 trajectory remains in $S_1$ for the full horizon, yielding a degenerate transition matrix with $T_{11}^{\mathrm{Kyber}}=1$.

6.4.3. Option-Style Valuation of Migration Incentives (Stage III)

To capture the economic incentive to migrate, we apply the binomial option model described in Section 3 separately to RSA-2048 and Kyber-768 in the baseline scenario. For RSA-2048, we set $S=S_0^{\mathrm{RSA}}=128$, strike $X=64$, horizon $T=10$ years, volatility ${\sigma }_{\mathrm{RSA}}=0.15$, discount rate $r=0.01$, and $n=10$ time steps. For Kyber-768, we take $S=S_0^{\mathrm{Kyber}}=160$, $X=80$, ${\sigma }_{\mathrm{Kyber}}=0.12$, and the same T, r, and n.

Using backward induction on the corresponding binomial trees, we obtain option-style values:

$$\begin{array}{cc}\hfill V^{\mathrm{RSA}}\left(0\right)& \approx 70.86,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill V^{\mathrm{Kyber}}\left(0\right)& \approx 87.84.\hfill \end{array}$$

(30)

The higher option value for Kyber-768 reflects both its larger initial security margin and its slower decay under the assumed quantum-threat model. Taken together with the transition matrix above, this demonstration shows how the framework can prioritize migration from RSA-2048 to Kyber-768: the Stage I trajectories identify when RSA-2048 will fall below policy thresholds under various quantum-arrival scenarios, Stage II quantifies the probability of entering the At Risk state, and Stage III converts these technical assessments into a comparative valuation that favors early adoption of the post-quantum cipher.

7. Limitations and Future Work

This model currently operates under several simplifying assumptions:

1.

The decay rate k is constant over time, though it may vary in real-world conditions.

2.

Hidden Markov transitions are based solely on $S\left(t\right)$ thresholds and do not yet incorporate noisy emissions or adversarial signals.

3.

The option pricing model assumes a fixed time horizon and deterministic policy threshold X.

4.

The framework forecasts when security may cross policy thresholds, but does not yet explicitly model crypto-agility constraints (e.g., migration lead time and deployment feasibility) [23].

Future work will explore the following:

1.

Calibration using real-world cryptanalytic event timelines (e.g., factoring breakthroughs, side-channel disclosures) and operational response timelines (e.g., disclosure-to-patch delays for high-impact vulnerabilities), which directly affect practical exposure windows [37].

2.

Monte Carlo uncertainty propagation through the full pipeline. Rather than a single deterministic run, we sample uncertain parameters (e.g., $k^{(c,a)}$, HMM parameters $(T,\theta )$, and valuation parameters $(\sigma ,r)$) from fitted/posterior distributions and execute Stage I → Stage II → Stage III per sample. Aggregating results yields confidence intervals for $V^{(c,a)}\left(t\right)$ and for the “latest safe migration date”, and supports stress-testing against rare-but-plausible cryptanalytic shocks.

3.

Incorporating migration lead time and deployment feasibility into Stage III so that recommended migration windows reflect operational constraints [23].

4.

Integration with standard post-quantum algorithm migration plans and cryptographic lifecycle guidelines.

To our knowledge, no existing framework integrates time-dependent security decay, probabilistic transitions, and financial valuation for cryptographic lifecycle forecasting. This model bridges a key gap between theoretical cryptography and actionable cybersecurity risk management.

8. Conclusions

This framework, blending continuous degradation, probabilistic transitions, and financial risk models, offers a predictive approach for cryptographic lifecycle management. It is extensible, data-calibrated, and designed for the evolving landscape of classical and quantum threats.

Operationally, the framework produces decision-facing artifacts that can be used in practice: (i) posterior probabilities over latent regimes (Highly Secure, Moderately Secure, At Risk) that summarize uncertainty and regime shifts, (ii) a quantitatively derived volatility signal from Stage II that can be propagated into Stage III rather than heuristically scaled, and (iii) an option-like value $V^{(c,a)}\left(t\right)$ that supports portfolio prioritization by comparing migration timing incentives across cipher–asset pairs. In this way, the pipeline links evolving cryptanalytic and implementation evidence to a policy-defined threshold $X^{\left(a\right)}$, yielding not only a point estimate but a sensitivity-aware “latest safe migration date” that can be updated as new evidence arrives. While the binomial lattice uses standard discounted-expectation mechanics, it is interpreted here as a decision-analytic tool rather than a market-efficiency claim; in operational deployments, lattice probabilities can be replaced with threat-driven transition likelihoods inferred from the HMM. Beyond cipher retirement, the same forecasting-and-valuation pipeline can be applied to key-rotation policy selection (where X encodes minimum residual strength at rotation), digital signature lifecycles (certificate validity periods and algorithm sunsets), and post-quantum hybrid deployments where latent states capture “hybrid safety” versus “single-point-of-failure” regimes. This positions the approach as a reusable lifecycle decision framework that supports proactive crypto agility under uncertainty.