A New Hybrid Weibull–Exponentiated Rayleigh Distribution: Theory, Asymmetry Properties, and Applications

Abstract

The choice of probability distribution is strongly data-dependent, as observed in several studies. Given the central role of statistical distribution in predictive analytics, researchers have continued to develop new models that accurately capture underlying data behaviours. This study proposes the Hybrid Weibull–Exponentiated Rayleigh distribution developed by compounding the Weibull and Exponentiated Rayleigh distributions via the T-X transformation framework. The new three-parameter distribution is formulated to provide a flexible modelling framework capable of handling data exhibiting non-monotone failure rates. The properties of the proposed distribution, such as the cumulative distribution function, probability density function, survival function, hazard function, linear representation, moments, and entropy, are studied. We estimate the parameters of the distribution using the Maximum Likelihood Estimation technique. Furthermore, the impact of the proposed distribution parameters on the distribution’s shape is studied, particularly its symmetry properties. The shape of the distribution varies with its parameter values, thereby enabling it to model diverse data patterns. This flexibility makes it especially useful for describing the presence or absence of symmetry in real-world failure processes. Simulation studies are conducted to assess the behaviour of the estimators under different parameter settings. The proposed distribution is applied to real-world data to demonstrate its performance. Comparative analysis is performed against other well-established models. The results indicate that the proposed distribution outperforms other models in terms of goodness-of-fit, demonstrating its potential as a superior alternative for modelling lifetime data and reliability analysis based on Akaike Information Criterion and Bayesian Information Criterion.

1. Introduction

Statistical modelling is a tool employed across several scientific and engineering disciplines to elucidate mathematical relationships in real-world data. The development of new statistical distributions plays a central role in enhancing this process, particularly in cases where existing models do not have an efficient capability to meet this goal. In order to construct an efficient distribution that is flexible and has high capability to deal with real-world data, the T-X family framework is employed. The T-X framework, presented by [1], provides a general method for generating new probability distributions by applying a transformation function (T) to a baseline distribution, together with an auxiliary random variable (X). The addition of extra shape parameters enhances the model’s capability, adaptability, and flexibility in capturing real-world phenomena. These extra features strengthen modelling in reliability analysis, survival analysis studies, and lifetime data analysis, where data exhibit skewness, heavy tails, or multimodal behaviours; the conditions under which standard normal models show inadequacy.

One of the commonly studied distributions is the Weibull distribution. It is a widely used model in lifetime data analysis that has undergone various modifications to improve its flexibility. Notably, extensions such as the flexible Weibull [2] and exponentiated Weibull [3], have been proposed to accommodate non-monotonic hazard functions. Other modifications proposed include the Alpha logarithmic transform Weibull (ALTW) distribution [4], the beta-Weibull distribution by [5], the Kumaraswamy Weibull Distribution [6], and the beta modified Weibull distribution by [7]. Furthermore, the additive modified Weibull distribution proposed by [8], ref. [9] presented a five-parameter distribution from the family of Marshall Olkin distributions called Marshall Olkin Weibull-Burr XII and the Topp-Leone modified Weibull Model introduced by [10], and application of the Weibull Half-Laplace [11].

Similarly, modifications to the Rayleigh distribution, such as the exponentiated Weibull Rayleigh distribution due to [12], parameter estimation of Weibull Rayleigh [13], Weibull inverse Rayleigh [14], beta generalized Inverse Rayleigh distribution presented by [15], the exponentiated Rayleigh [16], have aimed at enhancing its ability to model skewed and heavy-tailed data. The extensive modifications of the Weibull and Rayleigh distributions have demonstrated the need for more flexible statistical models capable of capturing diverse hazard-rate behaviours and accommodating heavy-tailed data. Previous studies have introduced many extensions of classical distributions, such as exponentiated forms and inverse-type modifications, primarily to improve model fit to real data. Even with these developments, many lifetime distributions still struggle when the data show non-monotonic hazard rates, a pattern that often appears but is not easy to capture. This limitation suggests the need for models that are more flexible and can borrow strengths across different families without inheriting their weaknesses.

In this work, we propose the Hybrid Weibull–Exponentiated Rayleigh Distribution (HWERD) as an attempt to bridge that gap. In developing the HWERD, we used the T-X framework, taking the exponentiated Rayleigh distribution as the starting point and then applying a Weibull-type transformation. This combination combines properties of both distributions, providing the new model with additional flexibility when analyzing lifetime or reliability data. We note that the original formulation with four parameters ($\alpha ,\beta ,\omega ,\varphi$) is non-identifiable because the parameters $\beta$ and $\varphi$ appear only through their product $\lambda =\varphi \beta$. Therefore, we present a three-parameter model ($\alpha ,\lambda ,\omega$) that is identifiable and retains the flexibility of the original formulation. As the results show, it can offer improved parameter estimation and a better overall fit compared to several existing alternatives.

Another area to explore is how the model behaves symmetrically. In reliability and survival analysis, the data is rarely perfectly symmetric. Often, failure times are skewed. There may be failures or a long tail of late failures. The shape parameters of the HWERD give an idea of skewness. When we examine how the shape parameters control the asymmetry, we can see the symmetry of the process that generates the data. This line of inquiry fits well within the broader scope of studying symmetry in mathematical models.

The remainder of the article is organized as follows. The methodology framework is presented in Section 2, Section 3 includes the simulation studies, real dataset application, results, and discussion, Section 4 presents the conclusions and future work direction.

2. Materials and Methods

2.1. Formulation of HWERD

The T-X framework provides a general method for creating new distribution families by applying a transformation to a baseline cumulative distribution function (CDF). For the HWERD, we start with the CDF of the exponentiated Rayleigh distribution and apply the Weibull transformation.

Let the CDF of the exponentiated Rayleigh distribution be

$$F_R(x;\omega ,\varphi )={\left(1-e^{-\omega x^2}\right)}^{\varphi },$$

(1)

where $\omega >0$ and $\varphi >0$ are shape parameters.

The CDF of the Weibull distribution is as follows:

$$F_W(x;\alpha ,\beta )=1-e^{-\alpha x^{\beta }},$$

(2)

where $\alpha >0$ and $\beta >0$ are shape parameters.

The T-X framework with Weibull transformer applied to $F_R\left(x\right)$ yields the following:

$$F\left(x\right)=F_W\left(F_R\left(x\right)\right)=1-e^{-\alpha {\left[F_R\left(x\right)\right]}^{\beta }}.$$

However, this construction leads to a defective distribution because ${lim}_{x\to \infty }F\left(x\right)=1-e^{-\alpha }<1$. To obtain a proper distribution, we need to apply the Weibull transformation to the survival function of the exponentiated Rayleigh distribution, yielding the Weibull-G family:

$$F\left(x\right)=F_W(1-F_R\left(x\right))=1-e^{-\alpha {[1-F_R\left(x\right)]}^{\beta }}.$$

Substituting $F_R\left(x\right)$ from Equation (1) yields the following:

$$F\left(x\right)=1-e^{-\alpha {\left[1-{\left(1-e^{-\omega x^2}\right)}^{\varphi }\right]}^{\beta }}.$$

(3)

We observe that the parameters $\varphi$ and $\beta$ appear only through their positions in the nested structure. To ensure identifiability and reduce the number of parameters while maintaining flexibility, we propose the following reparameterization.

Proposed 3-Parameter Model: Let $\lambda =\varphi \beta$ and reparameterize to obtain the following:

$$F\left(x\right)=1-e^{-\alpha \left[1-{\left(1-e^{-\omega x^2}\right)}^{\lambda }\right]},$$

(4)

where $\alpha >0$, $\lambda >0$, and $\omega >0$.

This corrected formulation ensures that ${lim}_{x\to \infty }F\left(x\right)=1$, making it a proper probability distribution.

To obtain the probability density function (PDF), we differentiate $F\left(x\right)$ with respect to x:

$$f\left(x\right)={\displaystyle \frac{d}{dx}}F\left(x\right)={\displaystyle \frac{d}{dx}}\left[1-e^{-\alpha {(1-e^{-\omega x^2})}^{\gamma }}\right].$$

(5)

Applying the chain rule,

$$\begin{array}{cc}\hfill f\left(x\right)& =e^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}·{\displaystyle \frac{d}{dx}}\left[\alpha {(1-e^{-\omega x^2})}^{\lambda }\right]\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & =\alpha \lambda e^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}{(1-e^{-\omega x^2})}^{\lambda -1}·{\displaystyle \frac{d}{dx}}\left(1-e^{-\omega x^2}\right)\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & =\alpha \lambda e^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}{(1-e^{-\omega x^2})}^{\lambda -1}·\left(2\omega x{e}^{-\omega x^2}\right).\hfill \end{array}$$

(8)

Thus, the PDF of the three-parameter HWERD is as follows:

$$f(x;\alpha ,\lambda ,\omega )=2\alpha \lambda \omega x{e}^{-\omega x^2}{e}^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}{(1-e^{-\omega x^2})}^{\lambda -1}.$$

(9)

The support of the distribution is $x>0$, and it can be verified that

$${\int }_0^{\infty }f\left(x\right)dx=1.$$

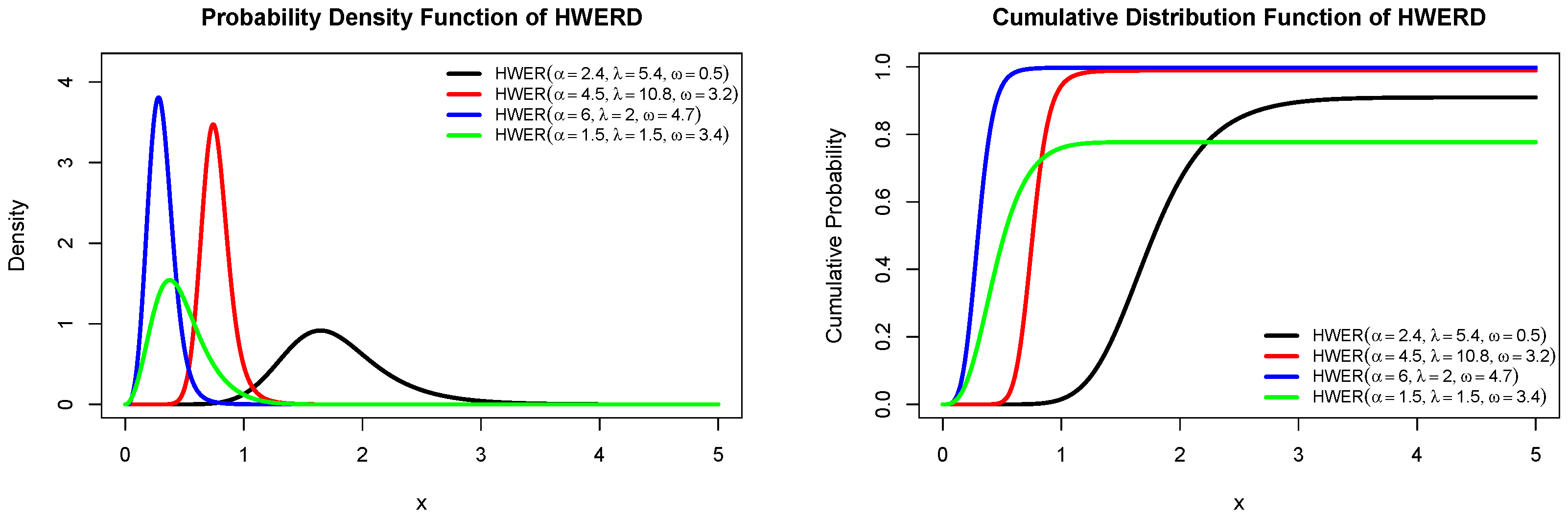
The HWERD PDF plot in Figure 1 shows how variations in the combination of parameters affected the shape and the spread of the density function. The PDF curves are predominantly unimodal and right-skewed, which shows that higher values of $\alpha$ and $\lambda$ move the HWERD peak near smaller X values, indicating short lifetimes or a higher rate of event occurrence. However, there are more dispersed event times at small values of $\omega$ that yield flatter, broader curves, suggesting longer-tailed distributions.

The CDF plot shows the corresponding cumulative probabilities for the parameter sets. As expected from a valid cumulative distribution, the curves increase monotonically from 0 to 1. Curves associated with larger values of $\alpha$ and $\lambda$ rise more sharply, signifying a higher likelihood of events occurring early and a faster accumulation of probability.

Furthermore, by setting parameters to different values, Figure 1 displays the capability of the HWERD to capture a range of lifetime behaviours. The ability of HWERD to model data with different survival or failure features is illustrated by its ability to yield strongly spiked and more spread-out shapes. For example, quick failures resonate with higher values of $\alpha$ and $\lambda$, while prolonged survival times are associated with smaller parameter values. Due to this versatility, the HWERD is a strong choice for applications related to lifetime, including survival modelling and reliability studies, where hazard trends can vary substantially across datasets.

2.2. Statistical Properties of HWERD

It is very important to examine the distributional properties of the proposed model to understand its behaviour and uniqueness. The properties include the moments, order statistics, entropy, and reliability functions. This examination gives clear insight to the flexibility of the model.

2.2.1. Survival and Hazard Functions

Reliability analysis helps determine whether a system or component performs well over time without failure. Interpreting the usefulness of the proposed distribution in lifetime or survival studies will be easier by understanding its reliability behaviour. The survival and hazard rate functions of model HWERD are presented in this section.

The survival function is given by the following:

$$S\left(x\right)=1-F\left(x\right)=e^{-\alpha {\left(1-e^{-\omega x^2}\right)}^{\lambda }}.$$

(10)

The derivation of the HWERD hazard function is as follows:

$$h\left(x\right)={\displaystyle \frac{f\left(x\right)}{S\left(x\right)}}.$$

$$h\left(x\right)={\displaystyle \frac{2\alpha \lambda \omega x{e}^{-\omega x^2}{e}^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}{(1-e^{-\omega x^2})}^{\lambda -1}}{e^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}}}.$$

(11)

Taking out the like terms, the hazard function simplifies to the following:

$$h\left(x\right)=2\alpha \lambda \omega x{e}^{-\omega x^2}{(1-e^{-\omega x^2})}^{\lambda -1}.$$

(12)

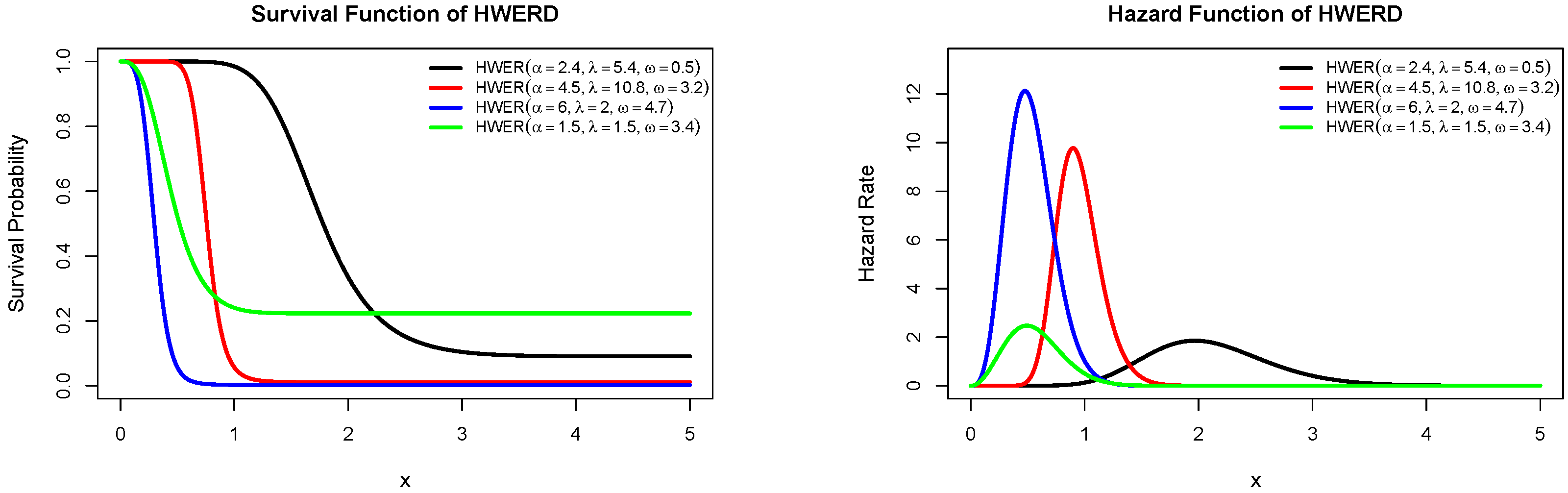
Figure 2’s HWERD survival and hazard plots provide important information about the reliability characteristics that are regulated by its parameter. The probability of survival decreased steadily, as evidenced by the decline in the survival curves. Higher parameter values accelerate this by showing faster rates of deterioration, whereas lower parameter values indicate longer survival. The hazard plot exhibits a unimodal failure rate with non-monotonic behavior, characterized by an initial increase followed by a decrease. It indicates that the HWERD captures early failures, the wear-out period, and a constant operational phase. From these plots, HWERD exhibits the flexibility and sustainability of modelling different lifetime behaviors in reliability and survival studies.

2.2.2. Linear Representation

For a clearer mathematical structure, it is helpful to express the distribution in a linear form. The linear representation of the model is presented in this section.

Proposition 1.

If a random variable X follows an HWER distribution, then its PDF can be expressed as a linear combination of modified Inverse Rayleigh (or Exponentiated Rayleigh) densities.

$$f\left(x\right)=2\alpha \lambda \omega \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right)x{e}^{-\omega (1+j)x^2}.$$

(13)

Proof. 

Given the PDF of HWERD from Equation (9):

$$f\left(x\right)=2\alpha \lambda \omega x{e}^{-\omega x^2}{e}^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}{(1-e^{-\omega x^2})}^{\lambda -1}.$$

(14)

Expanding the exponential term using the Taylor series:

$$e^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}=\sum _{k=0}^{\infty }{(-1)}^k{\displaystyle \frac{{\alpha }^k{(1-e^{-\omega x^2})}^{\lambda k}}{k!}}.$$

(15)

Substituting Equation (9) into Equation (13):

$$f\left(x\right)=2\alpha \lambda \omega x{e}^{-\omega x^2}\sum _{k=0}^{\infty }{(-1)}^k{\displaystyle \frac{{\alpha }^k{(1-e^{-\omega x^2})}^{\lambda k+\lambda -1}}{k!}}.$$

(16)

We can rearrange the terms:

$$f\left(x\right)=\sum _{k=0}^{\infty }{(-1)}^k{\displaystyle \frac{{\alpha }^{k+1}\lambda }{k!}}·2\omega x{e}^{-\omega x^2}{(1-e^{-\omega x^2})}^{\lambda k+\lambda -1}.$$

(17)

Now, expand ${(1-e^{-\omega x^2})}^{\lambda k+\lambda -1}$ using the binomial theorem:

$${(1-e^{-\omega x^2})}^{\lambda k+\lambda -1}=\sum _{j=0}^{\infty }{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right)e^{-\omega j{x}^2}.$$

(18)

Substituting Equation (17) into Equation (18):

$$f\left(x\right)=\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^{k+1}\lambda }{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right)·2\omega x{e}^{-\omega x^2}{e}^{-\omega j{x}^2}.$$

(19)

Combine the exponential terms:

$$e^{-\omega x^2}{e}^{-\omega j{x}^2}=e^{-\omega (1+j)x^2}.$$

(20)

Therefore, the final linear representation of HWERD is as follows:

$$f\left(x\right)=2\alpha \lambda \omega \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right)x{e}^{-\omega (1+j)x^2}.$$

(21)

□

2.2.3. Quantile Function of HWERD

In this section, the quantile function of the proposed HWERD is presented. It is majorly useful in describing percentiles and generating random samples from the distribution.

Proposition 2.

If X is a random variable that follows the HWER$(x,\alpha ,\lambda ,\omega )$ distribution, then the quantile function $Q_X\left(q\right)$ for $0\le q\le 1$ is given by the following:

$$Q_X\left(q\right)=\sqrt{{\displaystyle \frac{-1}{\omega }}log\left\{1-{\left[-{\displaystyle \frac{log(1-q)}{\alpha }}\right]}^{{\displaystyle \frac{1}{\lambda }}}\right\}.}$$

(22)

Proof. 

From Equation (4), we have the following:

$$F\left(x\right)=1-e^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}.$$

Setting $F\left(x\right)=q$, we get the following:

$$1-e^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}=q.$$

(23)

Taking the natural logarithm on both sides:

$$log\left[e^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}\right]=log(1-q)$$

(24)

$$-\alpha {(1-e^{-\omega x^2})}^{\lambda }=log(1-q)$$

(25)

Thus, the quantile function is as follows:

$$X_q=\sqrt{{\displaystyle \frac{-1}{\omega }}log\left\{1-{\left[-{\displaystyle \frac{log(1-q)}{\alpha }}\right]}^{{\displaystyle \frac{1}{\lambda }}}\right\}}.$$

(26)

□

2.2.4. Moments, Skewness, and Kurtosis

Moments are essential for describing the shape, center, and spread of a probability distribution. The $r^{th}$ raw moment is defined as follows:

$${\mu }_r^{\prime }=E\left(X^r\right)={\int }_0^{\infty }{x}^{r}f\left(x\right)dx.$$

(27)

Proposition 3.

Given a random variable X that follows a HWER distribution with parameters α, λ, and ω, the $r^{th}$ moment of the HWERD is given by the following:

$${\mu }_r^{\prime }=E\left(X^r\right)=2\alpha \lambda \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right){\displaystyle \frac{\mathsf{\Gamma }\left(\frac{r+2}{2}\right)}{{\left[\omega (1+j)\right]}^{\frac{r+2}{2}}}}.$$

(28)

Proof. 

Using the linear representation of HWERD from Equation (21):

$$f\left(x\right)=2\alpha \lambda \omega \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right)x{e}^{-\omega (1+j)x^2}.$$

(29)

Substituting into the moment definition:

$$\begin{array}{cc}\hfill {\mu }_r^{\prime }& ={\int }_0^{\infty }{x}^r\left[2\alpha \lambda \omega \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right)x{e}^{-\omega (1+j)x^2}\right]dx\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & =2\alpha \lambda \omega \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right){\int }_0^{\infty }{x}^{r+1}{e}^{-\omega (1+j)x^2}dx.\hfill \end{array}$$

(31)

Now, evaluate the integral using the Gamma function. Let $u=\omega (1+j)x^2$, then $du=2\omega (1+j)xdx$ and $x=\sqrt{u/\left[\omega \right(1+j\left)\right]}$. Thus:

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{x}^{r+1}{e}^{-\omega (1+j)x^2}dx& ={\int }_0^{\infty }{\left({\displaystyle \frac{u}{\omega (1+j)}}\right)}^{{\displaystyle \frac{r+1}{2}}}{e}^{-u}·{\displaystyle \frac{du}{2\omega (1+j)\sqrt{u/\left[\omega \right(1+j\left)\right]}}}\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{1}{2{\left[\omega (1+j)\right]}^{\frac{r}{2}+1}}}{\int }_0^{\infty }{u}^{{\displaystyle \frac{r}{2}}}{e}^{-u}du\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & ={\displaystyle \frac{\lambda \left(\frac{r}{2}+1\right)}{2{\left[\omega (1+j)\right]}^{\frac{r}{2}+1}}}.\hfill \end{array}$$

(34)

Substituting back gives the following:

$${\mu }_r^{\prime }=\alpha \lambda \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right){\displaystyle \frac{\lambda \left(\frac{r}{2}+1\right)}{{\left[\omega (1+j)\right]}^{\frac{r}{2}+1}}}.$$

(35)

This can be written more compactly as follows:

$${\mu }_r^{\prime }=\alpha \lambda \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{\psi }_{k,j}{\displaystyle \frac{\lambda \left(\frac{r}{2}+1\right)}{{\left[\omega (1+j)\right]}^{\frac{r}{2}+1}}},$$

(36)

where

$${\psi }_{k,j}={(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right).$$

(37)

□

First and Second Moments: From the general formula, we obtain specific moments:

• First Moment (Mean): Setting $r=1$:

  $${\mu }_1^{\prime }=E\left(X\right)=\alpha \lambda \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right){\displaystyle \frac{\sqrt{\pi }}{{\omega }^{3/2}{(1+j)}^{3/2}}}.$$

  (38)

  since $\lambda (3/2)=\sqrt{\pi }/2$.
• Second Moment: Setting $r=2$:

  $${\mu }_2^{\prime }=E\left(X^2\right)=\alpha \lambda \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{\psi }_{k,j}{\displaystyle \frac{\lambda \left(2\right)}{{\left[\omega (1+j)\right]}^2}}=\alpha \lambda \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{\psi }_{k,j}{\displaystyle \frac{1}{{\left[\omega (1+j)\right]}^2}},$$

  (39)

  $${\mu }_2^{\prime }=E\left(X^2\right)=\alpha \lambda \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j}{\displaystyle \frac{{\alpha }^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right){\displaystyle \frac{1}{\omega (1+j)}}.$$

  since $\lambda \left(2\right)=1$.

Variance: The variance is obtained from $\mathrm{Var}\left(X\right)={\mu }_2^{\prime }-{\left({\mu }_1^{\prime }\right)}^2$.

Skewness and Kurtosis: To assess whether the data are symmetric, the skewness measure is used. A value near zero points to a roughly symmetric bell shape. The further it gets from zero, the more asymmetric or skewed the distribution becomes. Since our model allows this value to vary, it enables us to directly test and model the level of symmetry in a dataset. Because the distribution does not have simple closed-form expressions for skewness and kurtosis via moments, we use quantile-based measures [17,18] skewness and kurtosis as stated below. Alternatively, moment-based measures can be computed numerically using the moment formulas above.

$$S={\displaystyle \frac{Q\left(\frac{3}{4}\right)-2Q\left(\frac{1}{2}\right)+Q\left(\frac{1}{4}\right)}{Q\left(\frac{3}{4}\right)-Q\left(\frac{1}{4}\right)}}.$$

Quantile function of HWERD:

$$Q(q;\alpha ,\lambda ,\omega )=\sqrt{-{\displaystyle \frac{1}{\omega }}log\left\{1-{\left[-{\displaystyle \frac{log(1-q)}{\alpha }}\right]}^{{\displaystyle \frac{1}{\lambda }}}\right\}}.$$

$$\mathrm{Skewness}={\displaystyle \frac{\sqrt{-\frac{1}{\omega }log\left\{1-{\left[-\frac{log\left(\frac{1}{4}\right)}{\alpha }\right]}^{\frac{1}{\lambda }}\right\}}-2\sqrt{-\frac{1}{\omega }log\left\{1-{\left[-\frac{log\left(\frac{1}{2}\right)}{\alpha }\right]}^{\frac{1}{\lambda }}\right\}}+\sqrt{-\frac{1}{\omega }log\left\{1-{\left[-\frac{log\left(\frac{3}{4}\right)}{\alpha }\right]}^{\frac{1}{\lambda }}\right\}}}{\sqrt{-\frac{1}{\omega }log\left\{1-{\left[-\frac{log\left(\frac{1}{4}\right)}{\alpha }\right]}^{\frac{1}{\lambda }}\right\}}-\sqrt{-\frac{1}{\omega }log\left\{1-{\left[-\frac{log\left(\frac{1}{2}\right)}{\alpha }\right]}^{\frac{1}{\lambda }}\right\}}.}}$$

$$K={\displaystyle \frac{Q\left(\frac{7}{8}\right)-Q\left(\frac{5}{8}\right)+Q\left(\frac{3}{8}\right)-Q\left(\frac{1}{8}\right)}{Q\left(\frac{3}{4}\right)-Q\left(\frac{1}{4}\right)}}.$$

2.2.5. Order Statistics of HWERD

To study the behaviour of the smallest and largest observations in a sample, order statistics are essential. The order statistics for the proposed model, HWERD, are presented in this part.

Proposition 4.

Let $X_1,X_2,\dots ,X_n$ be a random sample from the HWERD. Let $X_{\left(1\right)},X_{\left(2\right)},\dots ,X_{\left(n\right)}$ be the corresponding order statistics. Then the PDF of the s-th order statistic for the HWERD $(\alpha ,\lambda ,\omega )$ is given by the following:

$$\begin{array}{cc}\hfill f_{(s:n)}\left(x\right)& ={\displaystyle \frac{n!}{(s-1)!(n-s)!}}\sum _{m=0}^{\infty }\sum _{t=0}^{n-s}\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j+m+t}{\displaystyle \frac{{\alpha }^{k+1}{(1+m)}^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{s+t-1}{m}}\right)\hfill \\ \hfill & \times \left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right)2\lambda \omega x{e}^{-\omega (1+j)x^2}.\hfill \end{array}$$

(40)

Proof. 

The PDF of the s-th order statistic is given by the following:

$$f_{(s:n)}\left(x\right)={\displaystyle \frac{n!}{(s-1)!(n-s)!}}f\left(x\right){\left[F\left(x\right)\right]}^{s-1}{[1-F\left(x\right)]}^{n-s},1\le s\le n,$$

(41)

where $f\left(x\right)$ and $F\left(x\right)$ are the PDF and CDF of HWERD, respectively.

Using the binomial series expansion of ${[1-F\left(x\right)]}^{n-s}$, we obtain the following:

$${[1-F\left(x\right)]}^{n-s}=\sum _{t=0}^{n-s}{(-1)}^t\left({\displaystyle \genfrac{}{}{0pt}{}{n-s}{t}}\right){\left[F\left(x\right)\right]}^t.$$

(42)

Substituting Equation (41) into Equation (40):

$$f_{(s:n)}\left(x\right)={\displaystyle \frac{n!}{(s-1)!(n-s)!}}\sum _{t=0}^{n-s}{(-1)}^t\left({\displaystyle \genfrac{}{}{0pt}{}{n-s}{t}}\right)f\left(x\right){\left[F\left(x\right)\right]}^{s+t-1}.$$

(43)

Now, expand ${\left[F\left(x\right)\right]}^{s+t-1}$ using the binomial theorem:

$${\left[F\left(x\right)\right]}^{s+t-1}={\left[1-e^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}\right]}^{s+t-1}=\sum _{m=0}^{s+t-1}{(-1)}^m\left({\displaystyle \genfrac{}{}{0pt}{}{s+t-1}{m}}\right)e^{-\alpha m{(1-e^{-\omega x^2})}^{\lambda }}.$$

(44)

From the HWERD PDF in Equation (9):

$$f\left(x\right)=2\alpha \lambda \omega x{e}^{-\omega x^2}{(1-e^{-\omega x^2})}^{\lambda -1}{e}^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}.$$

(45)

Substituting Eqsuations (41) and (42) into Equation (40):

$$\begin{array}{cc}\hfill f_{(s:n)}\left(x\right)& ={\displaystyle \frac{n!}{(s-1)!(n-s)!}}\sum _{t=0}^{n-s}\sum _{m=0}^{s+t-1}{(-1)}^{m+t}\left({\displaystyle \genfrac{}{}{0pt}{}{n-s}{t}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{s+t-1}{m}}\right)\hfill \\ \hfill & \times 2\alpha \lambda \omega x{e}^{-\omega x^2}{(1-e^{-\omega x^2})}^{\lambda -1}{e}^{-\alpha (1+m){(1-e^{-\omega x^2})}^{\lambda }}.\hfill \end{array}$$

(46)

Now, expand the exponential term using the Taylor series:

$$e^{-\alpha (1+m){(1-e^{-\omega x^2})}^{\lambda }}=\sum _{k=0}^{\infty }{(-1)}^k{\displaystyle \frac{{\left[\alpha (1+m)\right]}^k{(1-e^{-\omega x^2})}^{\lambda k}}{k!}}.$$

(47)

Substituting Equation (44) into Equation (43):

$$\begin{array}{cc}\hfill f_{(s:n)}\left(x\right)& ={\displaystyle \frac{n!}{(s-1)!(n-s)!}}\sum _{t=0}^{n-s}\sum _{m=0}^{s+t-1}\sum _{k=0}^{\infty }{(-1)}^{k+m+t}\left({\displaystyle \genfrac{}{}{0pt}{}{n-s}{t}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{s+t-1}{m}}\right){\displaystyle \frac{{\left[\alpha (1+m)\right]}^k}{k!}}\hfill \\ \hfill & \times 2\alpha \lambda \omega x{e}^{-\omega x^2}{(1-e^{-\omega x^2})}^{\lambda k+\lambda -1}.\hfill \end{array}$$

(48)

Now, expand ${(1-e^{-\omega x^2})}^{\lambda k+\lambda -1}$ using the binomial theorem:

$${(1-e^{-\omega x^2})}^{\lambda k+\lambda -1}=\sum _{j=0}^{\lambda k+\lambda -1}{(-1)}^j\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right)e^{-\omega j{x}^2}.$$

(49)

Substituting Equation (46) into Equation (45):

$$\begin{array}{cc}\hfill f_{(s:n)}\left(x\right)& ={\displaystyle \frac{n!}{(s-1)!(n-s)!}}\sum _{t=0}^{n-s}\sum _{m=0}^{s+t-1}\sum _{k=0}^{\infty }\sum _{j=0}^{\lambda k+\lambda -1}{(-1)}^{k+j+m+t}\left({\displaystyle \genfrac{}{}{0pt}{}{n-s}{t}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{s+t-1}{m}}\right)\hfill \\ \hfill & \times \left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right){\displaystyle \frac{{\left[\alpha (1+m)\right]}^k}{k!}}2\alpha \lambda \omega x{e}^{-\omega x^2}{e}^{-\omega j{x}^2}.\hfill \end{array}$$

(50)

Combine the exponential terms:

$$e^{-\omega x^2}{e}^{-\omega j{x}^2}=e^{-\omega (1+j)x^2}.$$

(51)

Therefore, the PDF of the s-th order statistic is as follows:

$$\begin{array}{cc}\hfill f_{(s:n)}\left(x\right)& ={\displaystyle \frac{n!}{(s-1)!(n-s)!}}\sum _{t=0}^{n-s}\sum _{m=0}^{s+t-1}\sum _{k=0}^{\infty }\sum _{j=0}^{\lambda k+\lambda -1}{(-1)}^{k+j+m+t}\hfill \\ \hfill & \times \left({\displaystyle \genfrac{}{}{0pt}{}{n-s}{t}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{s+t-1}{m}}\right)\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{j}}\right){\displaystyle \frac{{\alpha }^{k+1}{(1+m)}^k}{k!}}2\lambda \omega x{e}^{-\omega (1+j)x^2}.\hfill \end{array}$$

(52)

For simplicity and to match the infinite series representation from Proposition 1, we can extend the upper limits to infinity, which gives the final form:

$$\begin{array}{cc}\hfill f_{(s:n)}\left(x\right)& ={\displaystyle \frac{n!}{(s-1)!(n-s)!}}\sum _{m=0}^{\infty }\sum _{t=0}^{\infty }\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{(-1)}^{k+j+m+t}{\displaystyle \frac{{\alpha }^{k+1}{(1+m)}^k}{k!}}\left({\displaystyle \genfrac{}{}{0pt}{}{s+t-1}{m}}\right)\hfill \\ \hfill & \times \left({\displaystyle \genfrac{}{}{0pt}{}{\lambda k+\lambda -1}{d}}\right)2\lambda \omega x{e}^{-\omega (1+j)x^2}.\hfill \end{array}$$

(53)

□

2.2.6. Shannon Entropy

The Shannon entropy quantifies the degree of uncertainty or randomness in a probability distribution. For a continuous random variable X with PDF $f\left(x\right)$, the Shannon entropy is defined as follows:

$$H\left(X\right)=-\mathbb{E}[logf\left(X\right)]=-{\int }_0^{\infty }f\left(x\right)logf\left(x\right)dx.$$

(54)

For the HWERD, substituting the PDF from Equation (7) gives the following:

$$\begin{array}{cc}\hfill H\left(X\right)& =-{\int }_0^{\infty }\left[log\left(2\alpha \lambda \omega x\right)-\omega x^2-\alpha {\left(1-e^{-\omega x^2}\right)}^{\lambda }\right.\hfill \\ \hfill & \left.+(\lambda -1)log\left(1-e^{-\omega x^2}\right)\right]f\left(x\right)dx.\hfill \end{array}$$

(55)

This expression does not simplify to a closed form in terms of elementary functions. However, it can be expressed in series form using the linear representation. For practical applications, we recommend computing the Shannon entropy numerically.

2.3. Model Identifiability and Reparameterization

A statistical model is said to be identifiable if distinct parameter values produce distinct probability distributions. Identifiability is a fundamental requirement for meaningful statistical inference, as it ensures that model parameters can be uniquely recovered from the observed data.

Let $\mathit{\theta }=(\alpha ,\lambda ,\omega )$ denote the parameter vector of the Hybrid Weibull–Exponentiated Rayleigh Distribution (HWERD). The model is identifiable if

$$f(x;{\mathit{\theta }}_1)=f(x;{\mathit{\theta }}_2)\mathrm{for}\mathrm{all}x>0⟹{\mathit{\theta }}_1={\mathit{\theta }}_2.$$

(56)

Consider two parameter vectors ${\mathit{\theta }}_1=({\alpha }_1,{\lambda }_1,{\omega }_1)$ and ${\mathit{\theta }}_2=({\alpha }_2,{\lambda }_2,{\omega }_2)$. From the probability density function of the HWERD,

$$\begin{array}{cc}\hfill f(x;\alpha ,\lambda ,\omega )& =2\alpha \lambda \omega x{e}^{-\omega x^2}{e}^{-\alpha {(1-e^{-\omega x^2})}^{\lambda }}{(1-e^{-\omega x^2})}^{\lambda -1},\hfill \end{array}$$

(57)

equality of densities for all $x>0$ implies equality of their logarithms. By examining the limiting behavior of the density as $x\to 0^{+}$ and $x\to \infty$, the exponential decay term $e^{-\omega x^2}$ uniquely determines $\omega$, yielding ${\omega }_1={\omega }_2$. Substituting this result back into the density and comparing the remaining terms implies ${\lambda }_1={\lambda }_2$, and consequently ${\alpha }_1={\alpha }_2$. Hence, the HWERD is identifiable.

An alternative argument follows from the quantile function of the HWERD. If two parameter vectors yield the same quantile function for all $q\in (0,1)$, then the corresponding distributions must coincide. Since the quantile function is injective in $(\alpha ,\lambda ,\omega )$, this further establishes identifiability.

Practical estimation indicates a high reliance between the parameters $\alpha$ and $\lambda$ even though the HWERD is identifiable in its original form. To address this problem and enhance numerical stability, a reparameterization is proposed by defining

$${\lambda }^{*}=\alpha \lambda .$$

(58)

Under this transformation, the parameter vector becomes ${\mathit{\theta }}^{*}=(\alpha ,\lambda ,\omega )$, with ${\lambda }^{*}=\lambda /\alpha$.

In addition to lowering parameter correlation and increasing the stability of maximum likelihood estimation, this reparameterization maintains identifiability. Therefore, the reparameterized form of the HWERD is used in all the following inference, simulation investigations, and applications in this study.

The identifiability of HWERD guarantees valid statistical inference based on these parameters and well-defined parameter estimation. The consistency of maximum likelihood estimators depends on this feature.

2.4. Parameter Estimation

The method used to estimate the HWERD parameters is maximum likelihood estimation (MLE). Let $x_1,x_2,\dots ,x_n$ be a random sample of size n drawn from the HWERD distribution $(\alpha ,\lambda ,\omega )$. The probability density function is given by the following:

$$f\left(x\right)=2\alpha \lambda \omega x{e}^{-\omega x^2}{\left(1-e^{-\omega x^2}\right)}^{\lambda -1}exp\left(-\alpha {\left(1-e^{-\omega x^2}\right)}^{\lambda }\right).$$

The likelihood function is as follows:

$$L(\alpha ,\lambda ,\omega ;x)={\left(2\alpha \lambda \omega \right)}^n\prod _{i=1}^n{x}_i\prod _{i=1}^n{e}^{-\alpha {(1-e^{-\omega x_i^2})}^{\lambda }}\prod _{i=1}^n{\left(1-e^{-\omega x_i^2}\right)}^{\lambda -1}.$$

(59)

Taking the natural logarithm of the likelihood function, we get the log-likelihood:

$$\begin{array}{cc}\hfill \ell (\alpha ,\lambda ,\omega )& =nln\left(2\right)+nln\left(\alpha \right)+nln\left(\lambda \right)+nln\left(\omega \right)\hfill \\ \hfill & +\sum _{i=1}^{n}ln\left(x_i\right)-\omega \sum _{i=1}^n{x}_i^2-\sum _{i=1}^n\alpha {\left(1-e^{-\omega x_i^2}\right)}^{\lambda }\hfill \\ \hfill & +(\lambda -1)\sum _{i=1}^{n}ln\left(1-e^{-\omega x_i^2}\right).\hfill \end{array}$$

(60)

To obtain the maximum likelihood estimates of the parameter vector $\widehat{\mathit{\theta }}=(\widehat{\alpha },\widehat{\lambda },\widehat{\omega })$, we differentiate Equation (60) with respect to each parameter and set it to zero. The numerical approach used to maximize the log-likelihood function is the Newton–Raphson method or another optimization algorithm.

The asymptotic distribution of the maximum likelihood estimator $\widehat{\mathit{\theta }}=(\widehat{\alpha },\widehat{\lambda },\widehat{\omega })$ is given by

$$\sqrt{n}(\widehat{\mathit{\theta }}-\mathit{\theta })\sim {\mathcal{N}}_3(0,{\mathbf{\Sigma }}^{-1}),$$

where ${\mathbf{\Sigma }}^{-1}$ is the inverse of the expected Fisher information matrix.

2.4.1. Initial Values and Optimization

To ensure reliable convergence of the maximum likelihood estimators, the following strategies were adopted:

• Method-of-moments estimates were used to obtain suitable initial values.
• Multiple starting points were employed to reduce the risk of convergence to local optima.
• Log-transformations were applied to parameters to enforce positivity constraints.
• Robust numerical optimization algorithms with parameter bounds were utilized.

2.4.2. Model Validation Checks

To confirm the proposed model’s numerical stability and mathematical validity, the following validation procedures were implemented:

• Verification that the cumulative distribution function approaches unity as $x\to \infty$.
• Numerical confirmation that the probability density function integrates to one.
• Comparison of simulated sample moments with their theoretical counterparts.
• Assessment of quantile–quantile plots to evaluate parameter recovery.

3. Results

The performance of the HWERD is studied for robustness and superiority through simulations and real-data applications. Using relevant tables and figures to provide a more thorough explanation, this section examines the conclusions drawn from statistical analysis, simulation results, and real-world dataset applications.

3.1. Simulation Study

The simulation was done using the quantile function of the HWER distribution. Parameter estimations were obtained using the maximum likelihood estimator. The procedures for the simulation study to estimate HWERD parameters are described below:

• The sample sizes are fixed as $n=50,100,200,500,$ and 1000.
• Random variable X from the quantile function is used to generate the dataset.
• Setting the parameter to different values.
• The process is repeated 1000 times.
• The above procedure is repeated using maximum likelihood estimators.
• Bias: the estimated bias of the parameter estimator, computed as follows:

  $$\widehat{\mathrm{Bias}}\left(\widehat{\theta }\right)=\overline{\widehat{\theta }}-\theta ={\displaystyle \frac{1}{1000}}\sum _{i=1}^{1000}{\widehat{\theta }}_i-\theta ,$$

  where $\overline{\widehat{\theta }}$ is the average of 1000 estimates, and $\theta$ is the true parameter value.
• Root Mean Square Error (RMSE): the estimated root mean square error, measuring the accuracy of the parameter estimates:

  $$\widehat{\mathrm{RMSE}}\left(\widehat{\theta }\right)=\sqrt{{\displaystyle \frac{1}{1000}}\sum _{i=1}^{1000}{({\widehat{\theta }}_i-\theta )}^2}.$$
• Mean, standard deviation, skewness, and kurtosis of the estimated parameters are also obtained.

The parameter estimates and their standard errors for different sample sizes are shown in

Table 1. Parameter estimates with standard errors (SEs) for the HWERD model.

Sample	True Parameters			Estimates (SE)
Size	$\mathit{\alpha }$	$\mathit{\lambda }$	$\mathit{\omega }$	$\widehat{\mathit{\alpha }}$	$\widehat{\mathit{\lambda }}$	$\widehat{\mathit{\omega }}$
Parameter set 1: $\alpha =1.1$, $\lambda =0.9$, $\omega =0.55$
50	1.1	0.9	0.55	1.056 (0.100)	0.904 (0.102)	0.540 (0.053)
100	1.1	0.9	0.55	1.047 (0.087)	0.920 (0.071)	0.545 (0.040)
200	1.1	0.9	0.55	1.059 (0.085)	0.914 (0.054)	0.546 (0.027)
500	1.1	0.9	0.55	1.100 (0.063)	0.898 (0.047)	0.549 (0.016)
1000	1.1	0.9	0.55	1.118 (0.052)	0.890 (0.042)	0.550 (0.013)
Parameter set 2: $\alpha =1$, $\lambda =1$, $\omega =0.5$
50	1.0	1.0	0.50	1.005 (0.045)	0.977 (0.085)	0.491 (0.048)
100	1.0	1.0	0.50	1.007 (0.037)	0.987 (0.062)	0.496 (0.036)
200	1.0	1.0	0.50	1.002 (0.022)	0.990 (0.044)	0.496 (0.025)
500	1.0	1.0	0.50	1.002 (0.017)	0.997 (0.026)	0.499 (0.015)
1000	1.0	1.0	0.50	1.002 (0.013)	0.998 (0.020)	0.500 (0.011)
Parameter set 3: $\alpha =1.1$, $\lambda =0.5$, $\omega =0.25$
50	1.1	0.5	0.25	0.967 (0.116)	0.524 (0.052)	0.246 (0.025)
100	1.1	0.5	0.25	0.979 (0.120)	0.527 (0.043)	0.249 (0.018)
200	1.1	0.5	0.25	0.994 (0.130)	0.523 (0.038)	0.248 (0.012)
500	1.1	0.5	0.25	1.032 (0.169)	0.516 (0.043)	0.250 (0.008)
1000	1.1	0.5	0.25	1.052 (0.169)	0.512 (0.043)	0.250 (0.006)
Parameter set 4: $\alpha =0.9$, $\lambda =0.8$, $\omega =0.4$
50	0.9	0.8	0.4	0.963 (0.063)	0.762 (0.083)	0.393 (0.041)
100	0.9	0.8	0.4	0.970 (0.064)	0.765 (0.064)	0.397 (0.029)
200	0.9	0.8	0.4	0.981 (0.069)	0.764 (0.049)	0.398 (0.021)
500	0.9	0.8	0.4	0.981 (0.062)	0.769 (0.034)	0.400 (0.012)
1000	0.9	0.8	0.4	0.997 (0.053)	0.760 (0.026)	0.400 (0.008)

. The results support the effectiveness and stability of the estimators, demonstrating improved accuracy, depicting the accuracy of the estimation as the sample size increases. Standard errors decrease as the sample size increases, indicating greater stability of the estimators for larger samples. The results suggest that the estimators behave well, with their accuracy and precision improving steadily as the sample size increases. Consequently, based on the findings of this simulation study, we affirm that the maximum likelihood estimation method is suitable for estimating the parameters of the HWERD model. The results show that MLE provides stable and consistent estimates across sample sizes.

Further insight into the HWERD’s shape characteristics comes from skewness and kurtosis measurements.

Table 2. Mean, standard deviation, median, skewness, and kurtosis for different parameter values of HWERD $(x,\alpha ,\lambda ,\omega )$.

Sample Size	True $\mathit{\alpha }$	True $\mathit{\lambda }$	True $\mathit{\omega }$	Mean	SD	Median	Skewness	Kurtosis
50	2	1	1.2	2.131	0.446	2.079	−0.052	2.443
100	2	1	1.2	2.124	0.497	1.882	0.157	2.096
200	2	1	1.2	2.069	0.420	1.930	0.714	2.483
500	2	1	1.2	1.915	0.215	1.907	1.658	6.473
1000	2	1	1.2	1.874	0.128	1.879	0.407	2.162
50	1	1	0.5	1.005	0.041	0.996	0.831	4.142
100	1	1	0.5	1.004	0.030	0.999	0.627	4.155
200	1	1	0.5	1.003	0.022	1.000	0.437	3.897
500	1	1	0.5	1.002	0.014	1.000	0.416	3.950
1000	1	1	0.5	1.001	0.009	1.000	0.605	4.095
50	1.1	0.5	0.25	0.966	0.111	0.979	−0.166	2.486
100	1.1	0.5	0.25	0.978	0.116	1.001	−0.263	2.471
200	1.1	0.5	0.25	0.988	0.132	1.015	−0.147	2.438
500	1.1	0.5	0.25	1.018	0.162	1.036	0.239	3.285
1000	1.1	0.5	0.25	1.050	0.177	1.043	0.402	3.685
50	0.9	0.8	0.4	0.959	0.053	0.960	0.020	3.668
100	0.9	0.8	0.4	0.974	0.063	0.970	0.388	3.723
200	0.9	0.8	0.4	0.981	0.064	0.975	0.471	4.086
500	0.9	0.8	0.4	0.981	0.047	0.980	0.494	5.170
1000	0.9	0.8	0.4	0.989	0.038	0.996	−0.082	4.036

reports the mean, median, skewness, kurtosis, and standard deviation for several parameter combinations and sample sizes. The results show that kurtosis varies with sample size: In some cases, it takes negative values, implying lighter tails compared with the normal distribution, while in others it becomes quite high, suggesting the presence of heavy tails. This pattern highlights the HWERD’s flexibility in modeling distributions with different tail behaviors.

At larger sample sizes, the standard deviation remains relatively stable, which reinforces the reliability of HWERD for estimating parameters with minimal fluctuation. The observed variations in skewness and kurtosis across parameter settings further illustrate the distribution’s adaptability to different data patterns, making it particularly useful for analyzing complex or heterogeneous datasets.

Table 3. Estimated bias and RMSE for HWERD parameters based on 1000 replications.

Sample Size	True $\mathit{\alpha }$	True $\mathit{\lambda }$	True $\mathit{\omega }$	Bias $\mathit{\alpha }$	Bias $\mathit{\lambda }$	Bias $\mathit{\omega }$	RMSE $\mathit{\alpha }$	RMSE $\mathit{\lambda }$	RMSE $\mathit{\omega }$
Parameter set 1: $(\alpha =1.1,\lambda =0.9,\omega =0.55)$
50	1.1	0.9	0.55	−0.0444	0.0038	−0.0101	0.1095	0.1017	0.0542
100	1.1	0.9	0.55	−0.0531	0.0202	−0.0049	0.1016	0.0739	0.0399
200	1.1	0.9	0.55	−0.0410	0.0136	−0.0042	0.0946	0.0554	0.0275
500	1.1	0.9	0.55	0.0001	−0.0019	−0.0010	0.0626	0.0468	0.0163
1000	1.1	0.9	0.55	0.0176	−0.0103	−0.0002	0.0552	0.0434	0.0125
Parameter set 2: $(\alpha =1,\lambda =1,\omega =0.5)$
50	1.0	1.0	0.50	0.0051	−0.0234	−0.0092	0.0454	0.0885	0.0493
100	1.0	1.0	0.50	0.0069	−0.0125	−0.0045	0.0375	0.0631	0.0362
200	1.0	1.0	0.50	0.0019	−0.0096	−0.0038	0.0217	0.0448	0.0250
500	1.0	1.0	0.50	0.0018	−0.0030	−0.0009	0.0168	0.0266	0.0148
1000	1.0	1.0	0.50	0.0015	−0.0016	−0.0002	0.0130	0.0197	0.0114
Parameter set 3: $(\alpha =1.1,\lambda =0.5,\omega =0.25)$
50	1.1	0.5	0.25	−0.1331	0.0242	−0.0038	0.1764	0.0569	0.0250
100	1.1	0.5	0.25	−0.1207	0.0271	−0.0013	0.1702	0.0505	0.0179
200	1.1	0.5	0.25	−0.1063	0.0230	−0.0016	0.1676	0.0444	0.0125
500	1.1	0.5	0.25	−0.0680	0.0164	−0.0003	0.1817	0.0461	0.0081
1000	1.1	0.5	0.25	−0.0478	0.0118	−0.0001	0.1758	0.0450	0.0058
Parameter set 4: $(\alpha =0.9,\lambda =0.8,\omega =0.4)$
50	0.9	0.8	0.40	0.0626	−0.0385	−0.0070	0.0905	0.0917	0.0410
100	0.9	0.8	0.40	0.0703	−0.0352	−0.0035	0.0952	0.0733	0.0292
200	0.9	0.8	0.40	0.0798	−0.0363	−0.0019	0.1054	0.0609	0.0207
500	0.9	0.8	0.40	0.0808	−0.0313	0.0003	0.1017	0.0461	0.0122
1000	0.9	0.8	0.40	0.0970	−0.0399	−0.0004	0.1105	0.0477	0.0083

presents the estimated bias and RMSE values for different sample sizes and true parameter values. As the sample size increases, both bias and RMSE consistently decline for parameter sets 1 to 3, once again confirming the robustness and accuracy of the proposed estimation method. This is consistent where estimators become more accurate and stable when sample sizes are higher. When the true value of $\alpha$ is 1.1 for parameter set 1, the RMSE decreases from 0.1095 at a sample size of 50 to 0.0.0552 at a sample size of 1000. This is also evident for other parameters. In general, from the results, there is an indication that the estimators performed well as the sample size increased, demonstrating the robustness of the estimation techniques.

3.2. Application of HWERD to Real Datasets

The HWER distribution is fitted to real datasets that include data on remission duration for bladder cancer patients and the breaking stress of carbon fibers. The results of HWERD’s performance in relation to existing distributions are presented in

Table 4. Average estimate of the MLEs, standard error, AIC, BIC, and HQIC of the bladder cancer data.

Model	Parameter	Estimate	Std. Error	AIC	BIC	HQIC
HWERD	$\alpha$	0.5740	0.0447	832.261	840.820	835.737
	$\lambda$	6.4802	1.7000
	$\omega$	0.0004	0.0003
EWED	$\alpha$	1.7721	0.0001	1005.656	1017.064	1010.291
	$\beta$	0.3858	0.0257
	$\lambda$	0.6694	0.0257
	$\pi$	1.8205	0.3356
EWRD	$ϵ$	4.1454	0.2199	849.221	860.629	853.856
	$\alpha$	0.8651	0.8953
	$\lambda$	0.6509	0.0230
	$\pi$	0.0001	0.0544
WED	$ϵ$	1.2096	0.0899	845.667	854.247	849.153
	$\alpha$	0.0132	0.0038
	$\lambda$	5.7326	1.3853
EED	$ϵ$	1.1554	0.1400	850.401	856.121	852.725
	$\lambda$	0.1117	0.0127

and

Table 5. Average estimates and standard errors of the MLEs, AIC, BIC, and HQIC of the breaking stress of carbon fibers of length 50.

Model	Parameter	Estimate	SE	AIC	BIC	HQIC
HWERD	$\alpha$	15.3307	9.7523	288.5790	296.3945	291.7420
	$\lambda$	1.5589	0.2301
	$\omega$	0.0225	0.0127
EWRD	$\alpha$	15.4451	3.5731	290.5778	300.9985	294.7953
	$\beta$	1.2483	1.4150
	$\delta$	1.2483	0.4275
	$\gamma$	0.2240	1.5124
EWED	$\alpha$	6.0211	5.9201	302.2090	312.6297	306.4265
	$\beta$	2.2860	0.2519
	$\delta$	4.1706	2.1453
	$\gamma$	1.4419	0.4610
WED	$\alpha$	3.3907	0.2464	305.2584	313.1037	308.4344
	$\beta$	0.0095	0.0030
	$\gamma$	3.0806	0.4289
EED	$\alpha$	7.7882	1.4962	296.3646	301.5749	298.4733
	$\lambda$	1.0132	1.0132

. All models were estimated using the MLE method. The performance of the model was evaluated on the basis of the commonly used model selection criteria, that is, AIC, BIC, and HQIC. These evaluate how well the model fits its complexity, penalizing the number of parameters to avoid overfitting.

3.2.1. Dataset 1

HWERD was applied to the bladder cancer remission time data for 128 patients, initially reported in [19]. The description of the data is monthly remission times until recurrence after treatment, and has been widely utilized in the lifetime distribution. The data is presented in

Table A1. Bladder cancer remission duration dataset (128 patients) [19].

0.08	2.09	3.48	4.87	6.94	8.66	13.11	23.63
0.20	2.23	3.52	4.98	6.97	9.02	13.29	0.40
2.26	3.57	5.06	7.09	9.22	13.80	25.74	0.50
2.46	3.64	5.09	7.26	9.47	14.24	25.82	0.51
2.54	3.70	5.17	7.28	9.74	14.76	26.31	0.81
2.62	3.82	5.32	7.32	10.06	14.77	32.15	2.64
3.88	5.32	7.39	10.34	14.83	34.26	0.90	2.69
4.18	5.34	7.59	10.66	15.96	36.66	1.05	2.69
4.23	5.41	7.62	10.75	16.62	43.01	1.19	2.75
4.26	5.41	7.63	17.12	46.12	1.26	2.83	4.33
5.49	7.66	11.25	17.14	79.05	1.35	2.87	5.62
7.87	11.64	17.36	1.40	3.02	4.34	5.71	7.93
1.46	18.10	11.79	4.40	5.85	8.26	11.98	19.13
1.76	3.25	4.50	6.25	8.37	12.02	2.02	13.31
4.51	6.54	8.53	12.03	20.28	2.02	3.36	12.07
6.76	21.73	2.07	3.36	6.93	8.65	12.63	22.69

. Among the studies that have analyzed the dataset are [20,21,22]. The HWERD model was compared with other well-known distributions, which include Weibull exponential, exponentiated Weibull exponential, exponentiated exponential, and exponentiated Weibull Rayleigh.

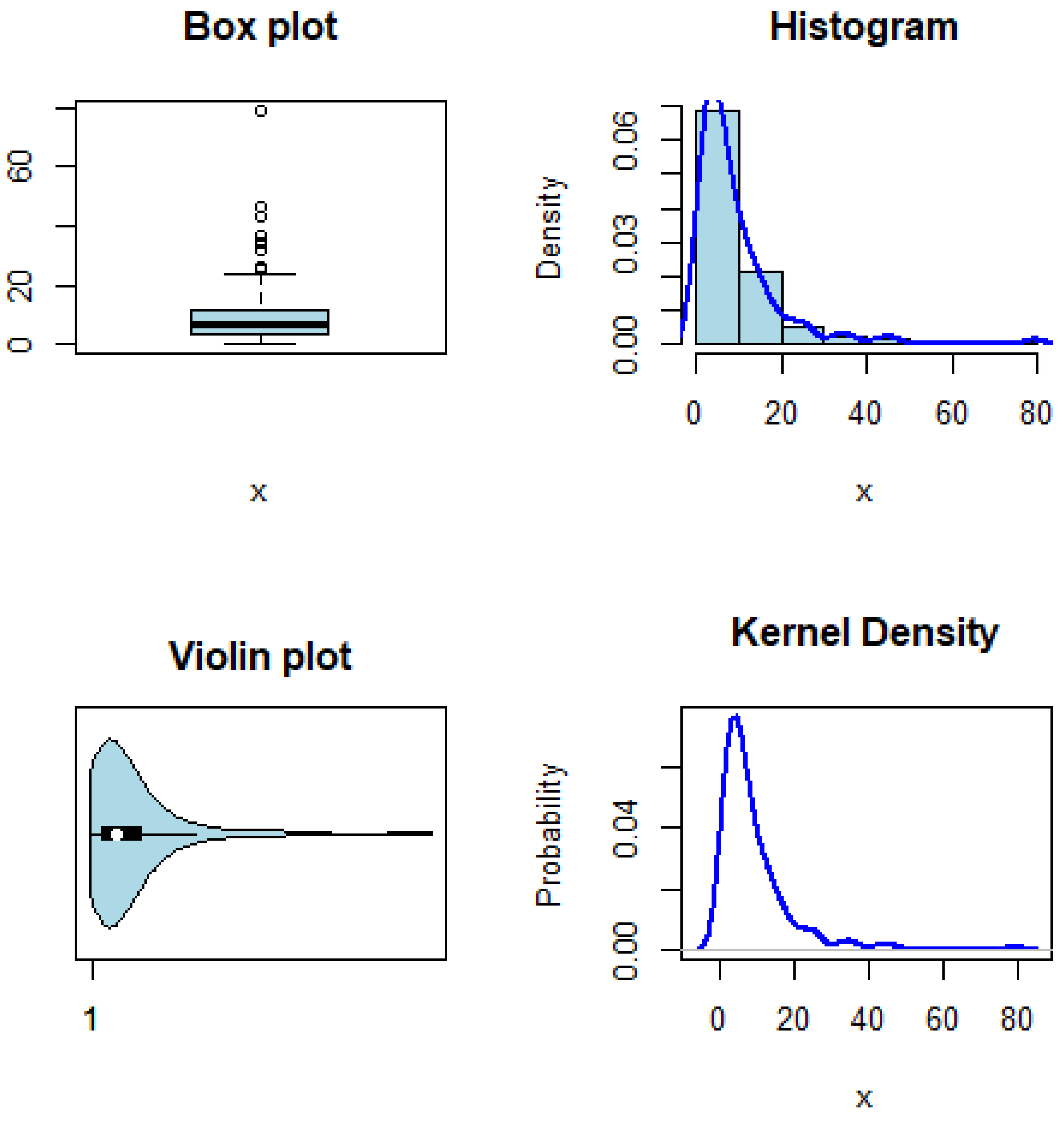
Figure 3 presents exploratory plots of the remission time data. The boxplot and violin plot reveal a right-skewed distribution with the majority of remission times clustered at shorter durations. These illustrations demonstrate how well HWERD models long-tailed distributions, making it a strong, viable choice for survival analysis in medical research.

Table 4 presents the results, which indicate that HWERD outperforms other considered distributions such as Exponentiated Weibull Exponential distribution (EWED), Exponentiated Weibull Rayleigh distribution (EWRD), Weibull Exponential distribution (WED), and Exponentiated Exponential distribution (EED). For bladder cancer remission data, the HWERD distribution has the lowest AIC value of 832.261 and the lowest BIC value of 840.821, thus providing a better fit than that provided by any other considered model for this medical survival data set.

The HWERD provides the best fit according to all information criteria. It is notable that the estimate for the shape parameter $\omega$ is very close to zero ($\widehat{\omega }=0.00037$) with a relatively small standard error. This indicates the ability of the model to adjust towards simpler nested forms when appropriate, without compromising its overall flexibility when needed. Nevertheless, the full HWERD formulation achieved the optimal balance between fit and complexity for this data.

3.2.2. Dataset 2

The second dataset presented in

Table A2. The breaking stress of carbon fibers dataset [23].

0.39	0.81	0.85	0.98	1.08	1.12	1.17	1.18
1.22	1.25	1.36	1.41	1.47	1.57	1.57	1.59
1.59	1.61	1.61	1.69	1.69	1.71	1.73	1.80
1.84	1.84	1.87	1.89	1.92	2.00	2.03	2.03
2.05	2.12	2.17	2.17	2.17	2.35	2.38	2.41
2.43	2.48	2.48	2.50	2.53	2.55	2.55	2.56
2.59	2.67	2.73	2.74	2.76	2.77	2.79	2.81
2.81	2.82	2.83	2.85	2.87	2.88	2.93	2.95
2.96	2.97	2.97	3.09	3.11	3.11	3.15	3.15
3.19	3.19	3.22	3.22	3.27	3.28	3.31	3.31
3.33	3.39	3.39	3.51	3.56	3.60	3.65	3.68
3.68	3.68	3.70	3.75	4.20	4.38	4.42	4.70
4.90	4.91	5.08	5.56

consists of the breaking stress of carbon fibers, measured across 50 fiber lengths which was firstly reported by [23]. The dataset has been analyzed in various studies such as reliability and lifetime [24,25,26]. To use the dataset, an experiment with 1000 simulation runs was conducted, and the HWERD was assessed against other existing models, including Weibull exponential, exponentiated Weibull exponential, exponentiated exponential, and exponentiated Weibull Rayleigh distributions.

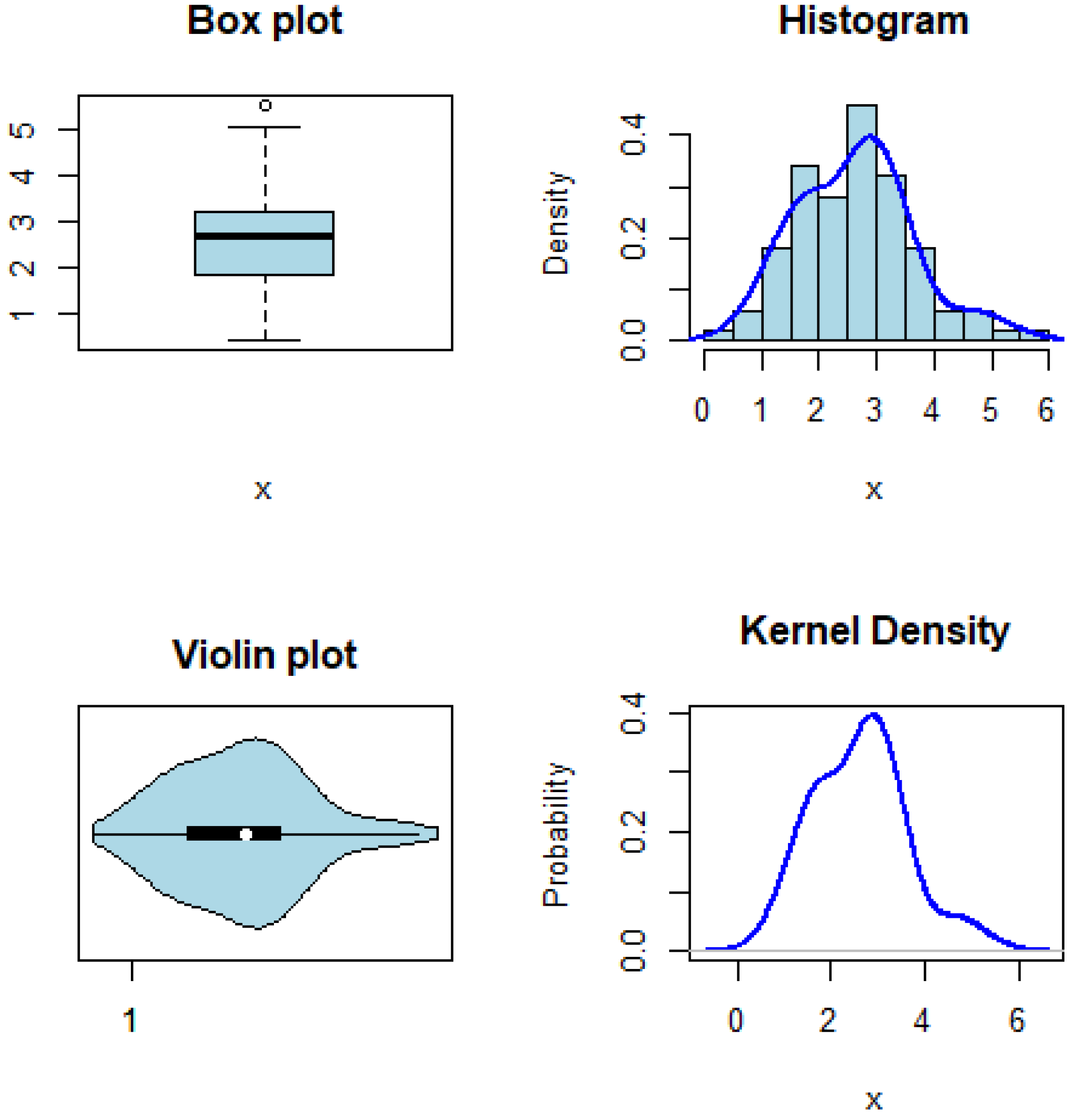
The distribution of the break-stress values is shown in Figure 4, where HWERD effectively represents the variation in the failure rates of the material.

The results of the model comparison for the break Stress of Carbon fiber data are displayed in Table 5. HWERD achieves the lowest values in all criteria, indicating that it offers the optimal balance between fit and model complexity. Among all fitted models, HWERD yielded the smallest AIC (288.57), indicating the best overall fit of the data, given model complexity and fit. The BIC and HQIC values of HWERD (296.40 and 291.74, respectively) were also the lowest among all models to further confirm its better performance.

4. Conclusions

This paper proposes a new lifetime distribution, the Hybrid Weibull–Exponentiated Rayleigh Distribution (HWERD). The model is obtained by combining the Weibull and Exponentiated Rayleigh distributions via the T-X framework, yielding a flexible form that can accommodate a range of failure-rate behaviours. It is particularly useful in cases where the hazard function is non-monotonic, a feature often encountered in data from engineering systems, medical survival studies, and environmental processes. To ensure identifiability, we presented a three-parameter reparameterization $(\alpha ,\lambda ,\omega )$ where $\lambda =\varphi \omega$ captures the combined shape effect.

The HWERD successfully combines the strengths of the Weibull and Exponentiated Rayleigh distributions, enabling it to exhibit a wide range of hazard functions, including non-monotonic forms, and handle data with large tails. In this study, we examine several properties of the model, including its survival and hazard functions, moments (including skewness and kurtosis), and a linear representation. We also estimated the model parameters using maximum likelihood estimation. A comprehensive simulation study across diverse parameter values showed that the MLE estimators are consistent and stable, with accuracy and precision improving as sample size increases.

Finally, the HWERD was applied to two real-world datasets: bladder cancer remission times and the breaking stress of carbon fibers. In both applications, the HWERD provided a noticeably better fit than the existing models, as reflected by lower AIC, BIC, and other goodness-of-fit measures. The findings suggest that HWERD is well-suited to describe complex data patterns, particularly those exhibiting skewness, high kurtosis, or heavy tails. In general, the HWERD distribution is a strong and versatile model for lifetime and reliability data. Its mathematical tractability, strong estimation performance, and superior goodness-of-fit indicate potential future applications.

Overall, the HWERD provides a practical three-parameter model with a clear and interpretable structure for examining symmetry in data. Its parameters offer direct and intuitive control over the distributional shape, including skewness, making the model particularly useful in applications where understanding asymmetry in failure times or material strength is important.

Future research will investigate robust estimation techniques for HWERD parameters in order to compare with MLE and their applications in other domains. Further theoretical work will characterize the parameter identifiability in detail and develop diagnostic tools to guide applied researchers when parameters are near non-identifiable boundaries. Furthermore, future study will explore an exponentiated extension of the hybrid Weibull–Exponentiated Rayleigh distribution and assess its ability to improve model fit.