Parametric Analysis of Reinforced Concrete Hollow Piers Based on an Axial–Flexure–Shear Model Under Cyclic Loading and Earthquake Conditions
Abstract
1. Introduction
2. Description of the Modeling Approach
2.1. Axial–Flexure–Shear-Interaction-Membrane-Beam-Truss-Element Model (AFSI-MBTEM)
2.2. Numerical Implementation of the AFSI-MBTEM
2.3. Experimental Validation of the AFSI-MBTEM
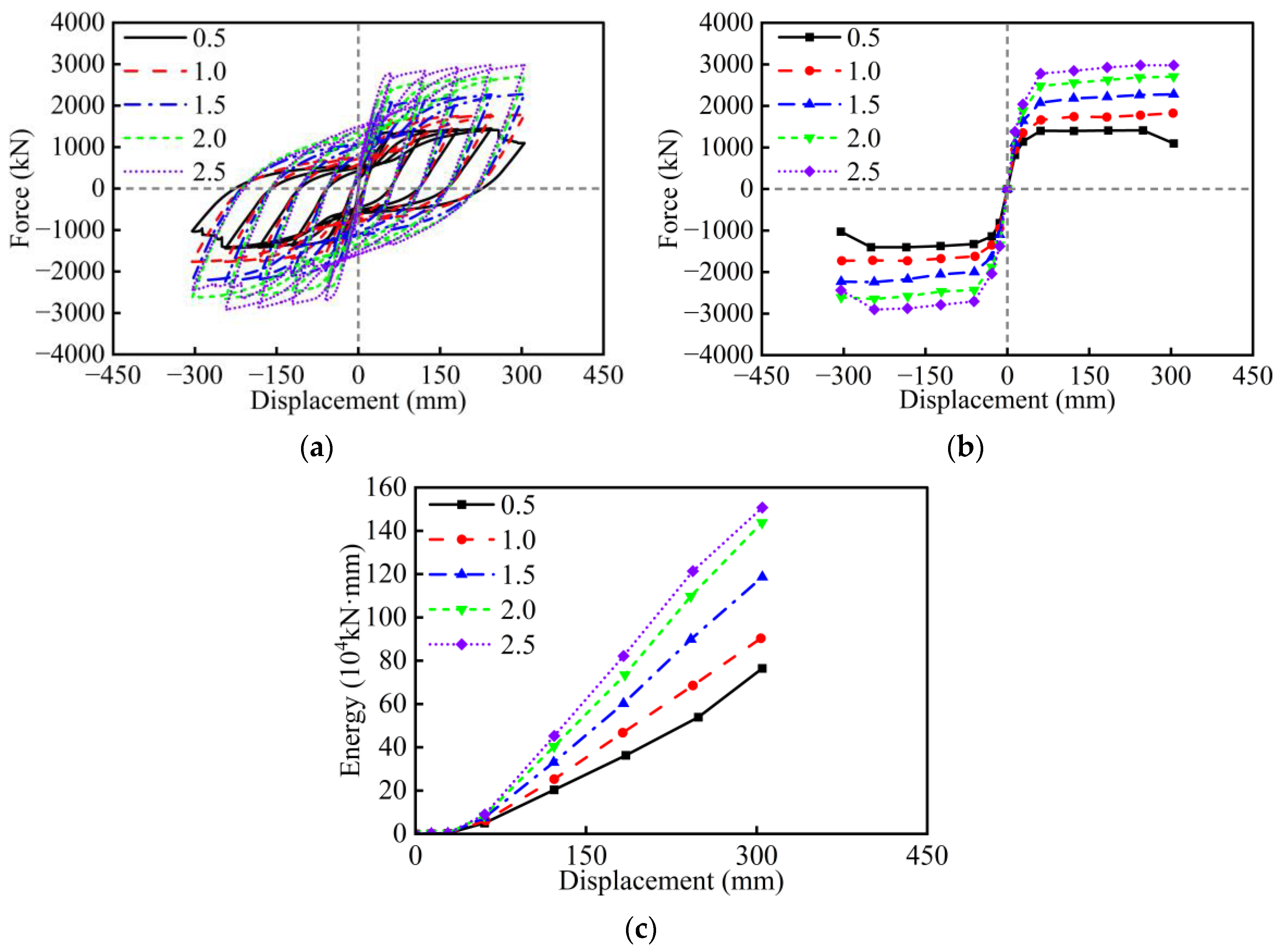
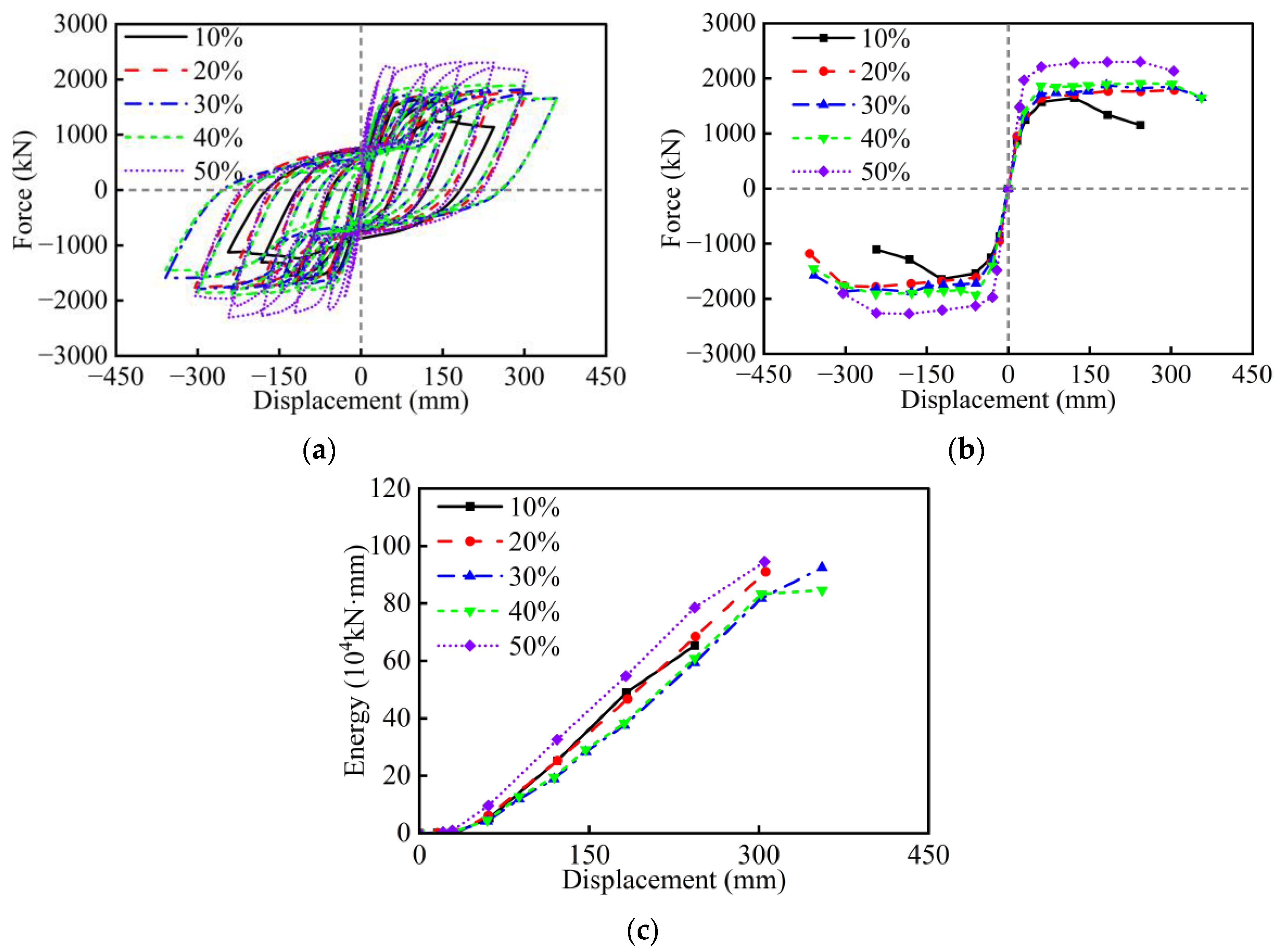
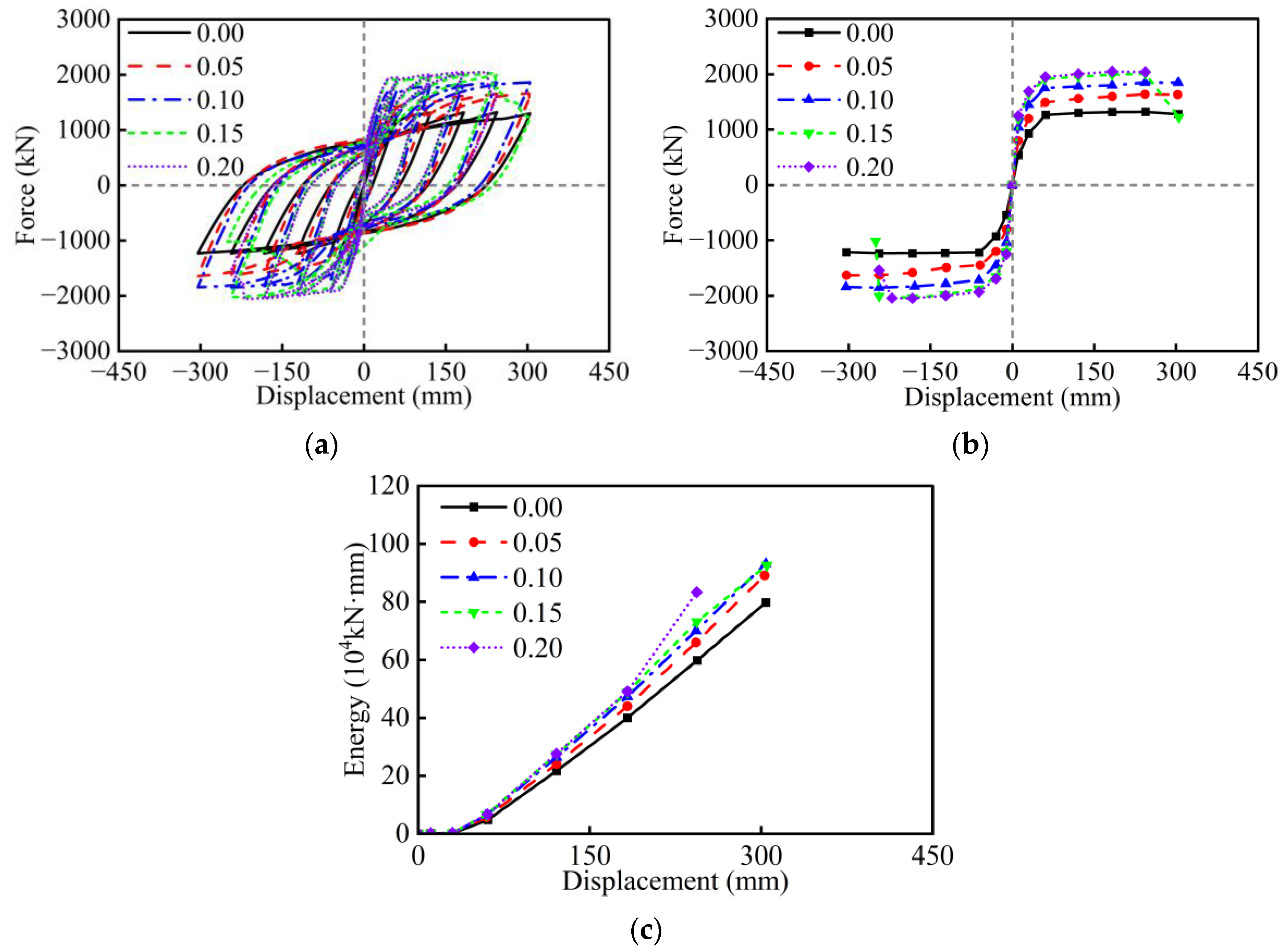
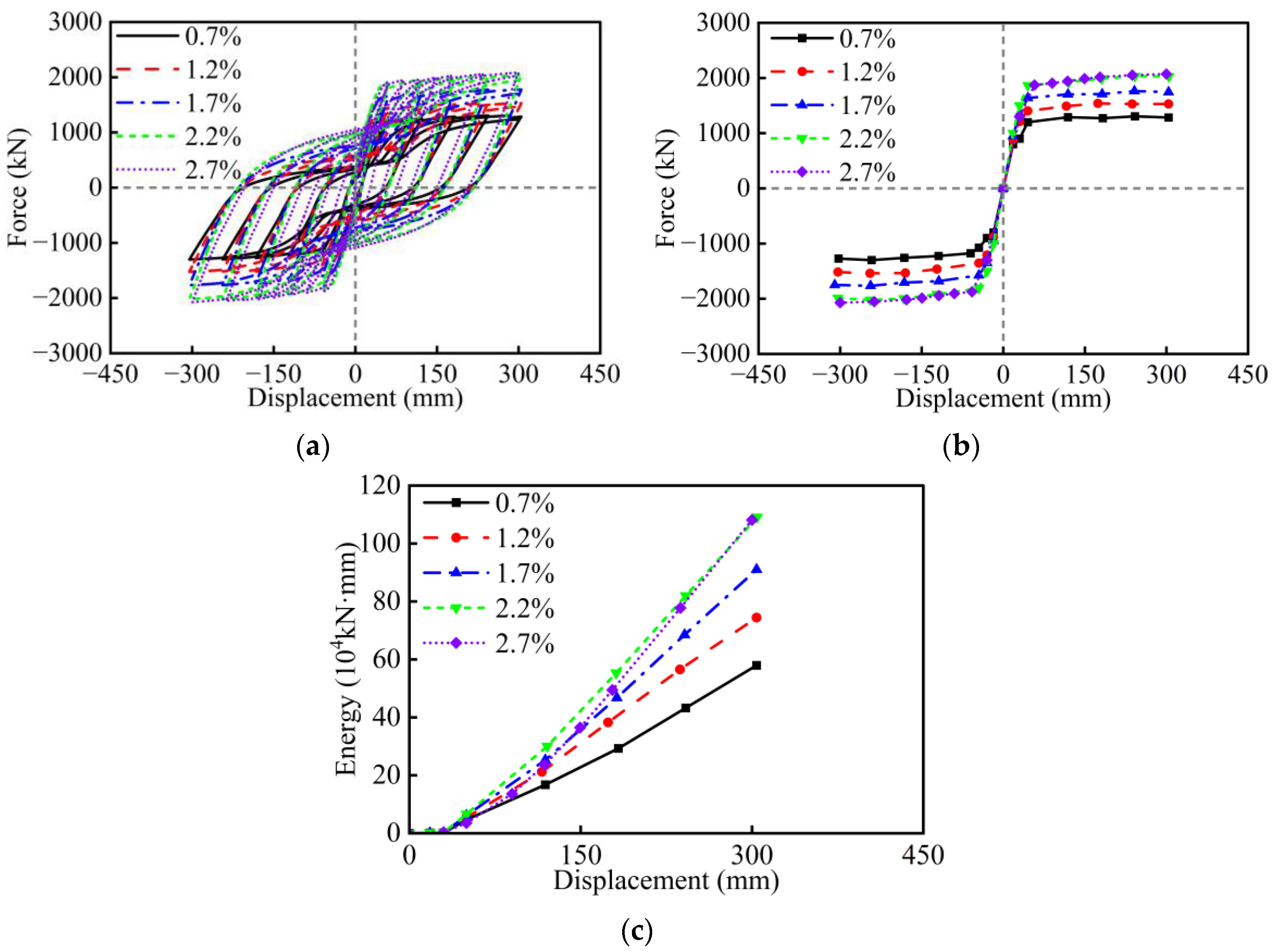
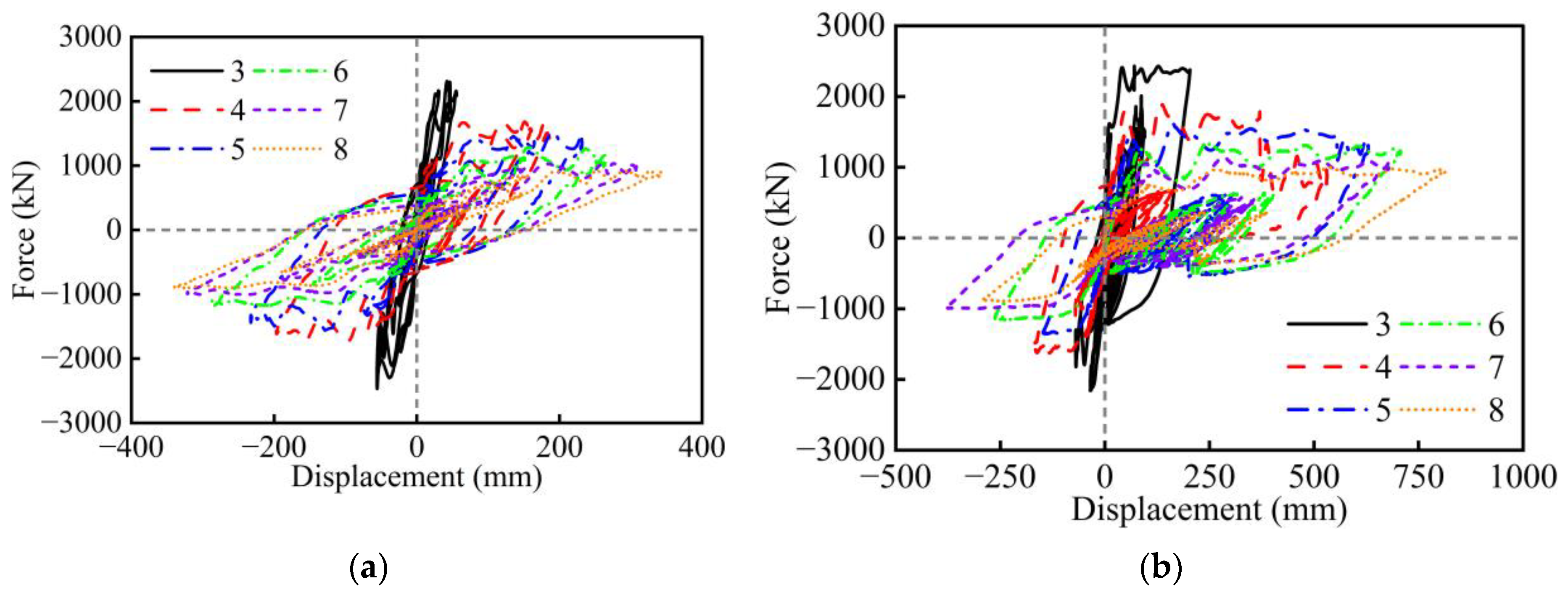
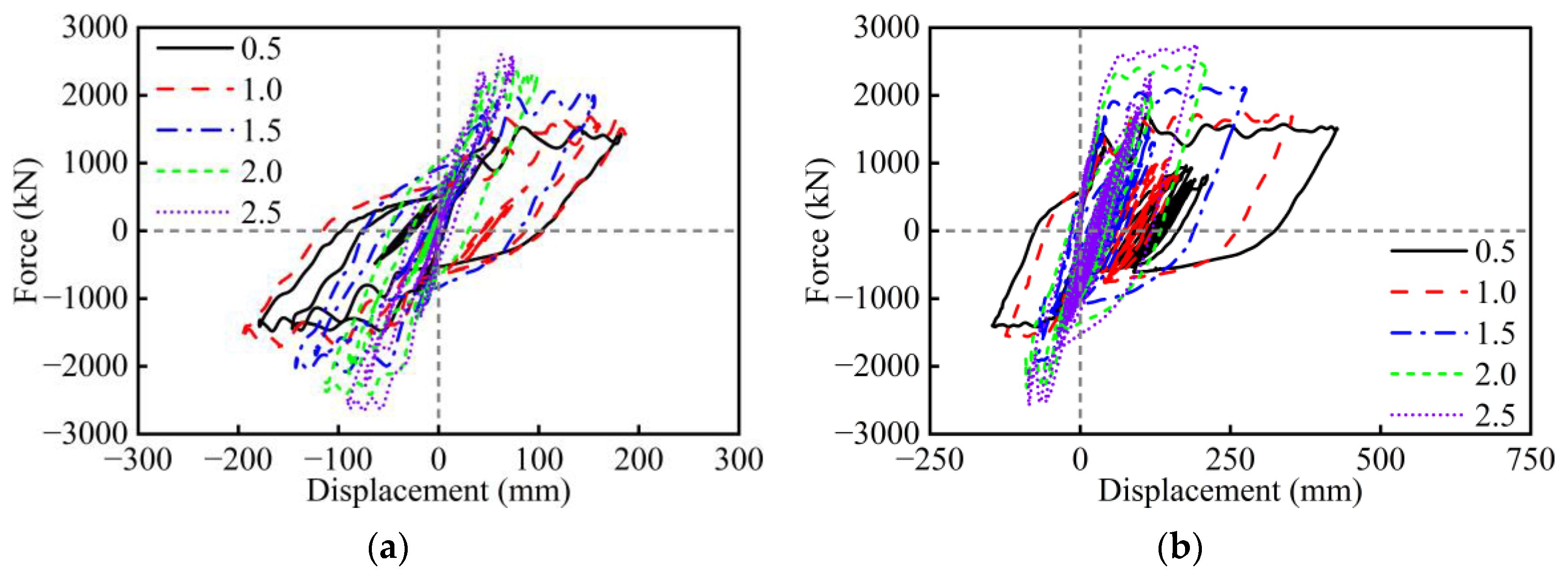
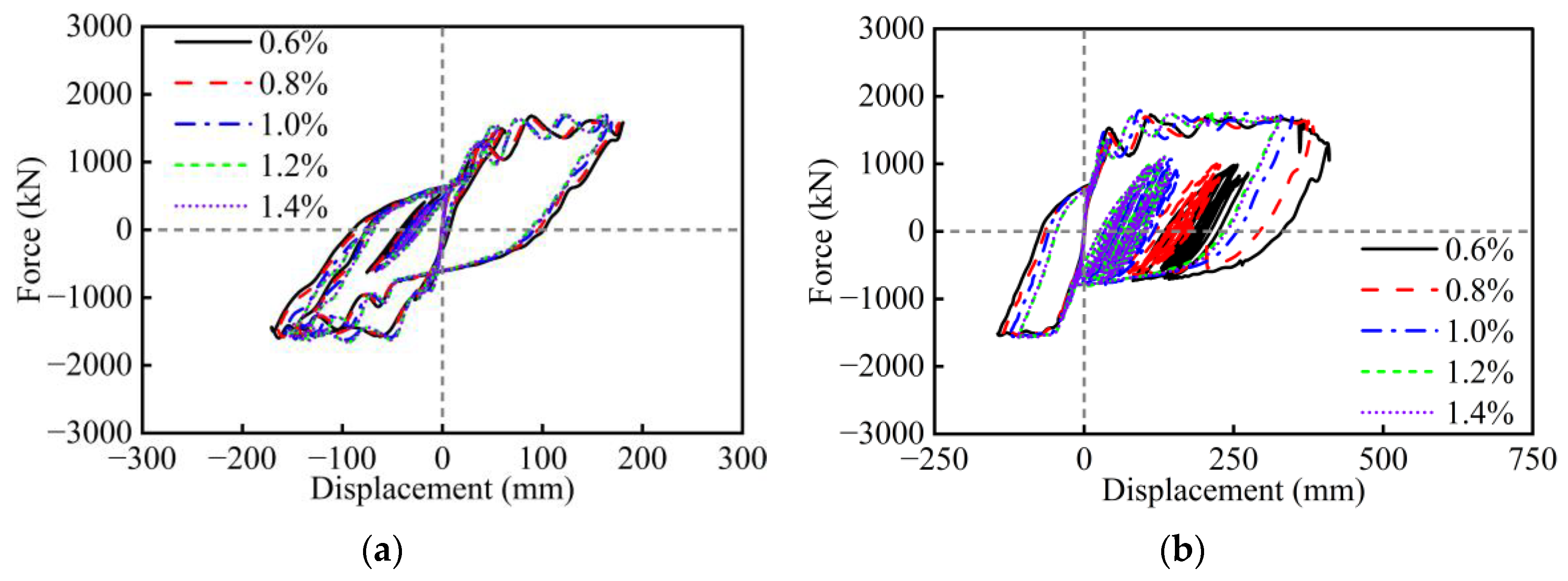
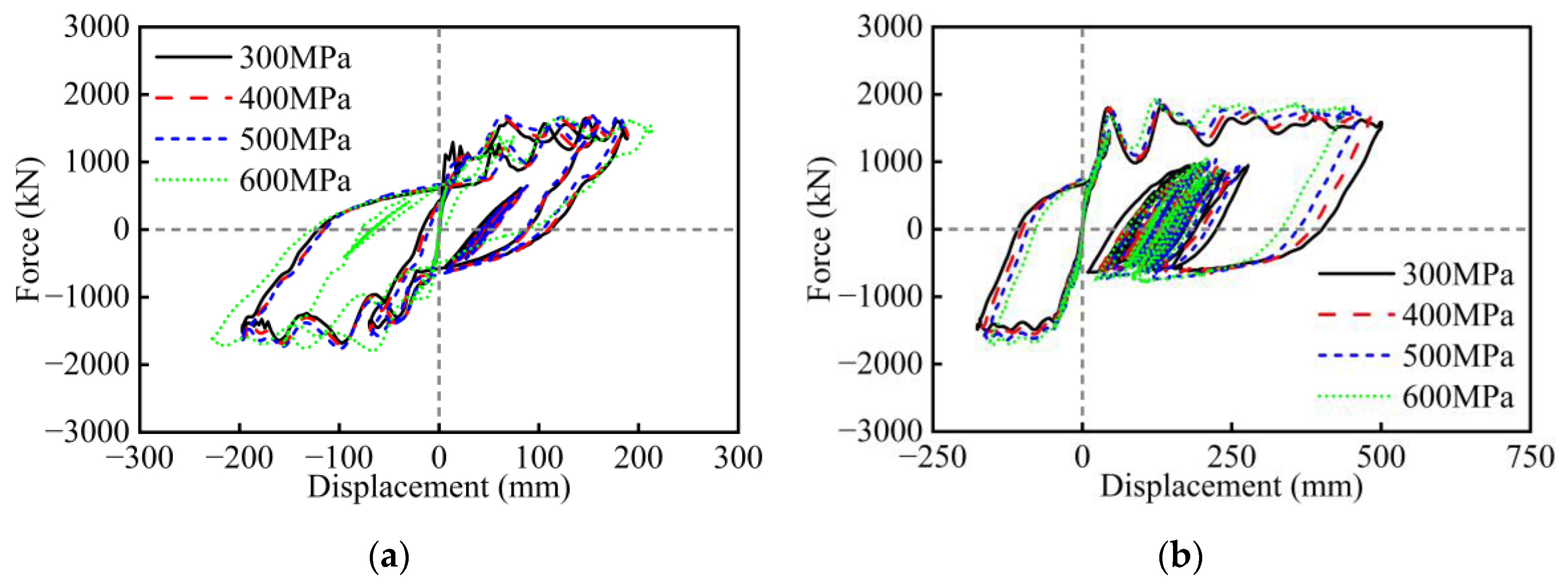
3. Parametric Analysis Under Cyclic Loading
4. Parametric Analysis Under Earthquakes
5. Parametric Analysis Under Different PGAs
6. Conclusions
- The AFSI-MBTEM successfully reproduces the symmetric experimental hysteretic results of three full-scale RC rectangular hollow piers with flexure and shear failure modes. It predicts the initial stiffness, yield plateau, peak strength, and most hysteretic characteristics, including strength degradation, stiffness degradation, pinching effect, plastic displacement, and energy dissipation with excellent accuracy, convergence, and efficiency, demonstrating its capability for reliable nonlinear seismic analysis of hollow piers.
- Under cyclic loading, the aspect ratio, width-to-depth ratio, wall thickness ratio, axial load ratio, and longitudinal rebar ratio have a significant influence on the seismic performance of RC hollow piers. However, the effects of stirrup ratio, concrete strength, and longitudinal rebar strength are relatively minor. Specifically, excessively small values of the width-to-depth ratio and wall thickness ratio, as well as an excessively large axial load ratio, will lead to sudden drops in the lateral strength of RC hollow piers. The amount of longitudinal rebar and stirrup, as well as the strength of materials, should take into account the seismic performance, cost, and construction.
- Under earthquakes, the seismic responses of RC hollow piers exhibit a similar trend to those observed under cyclic loading, though asymmetric hysteretic responses are observed due to the asymmetric main velocity pulses of near-field earthquakes. However, the influence of stirrup ratio, concrete strength, and longitudinal rebar strength becomes clear under strong earthquakes, especially in terms of residual deformation.
- Compared with other relevant studies, the influence trend of the design parameters on the seismic behavior of RC hollow piers under cyclic loading and earthquakes maintains consistency with experimental results. Moreover, reasonable ranges of the design parameters suggested in this study for RC hollow piers are as follows: aspect ratio of 4–6, width-to-depth ratio of 1.0–2.0, wall thickness ratio of 20–40%, axial load ratio of 0.05–0.10, longitudinal rebar ratio of 1.2–2.2%, stirrup ratio of 0.8–1.2%, concrete strength of C40, and longitudinal rebar strength of 400 MPa and 500 MPa.
- Under different PGA conditions, the aspect ratio, width-to-depth ratio, wall thickness ratio, and longitudinal rebar ratio have a significant influence on the displacement responses of RC hollow piers. However, axial load ratio, stirrup ratio, concrete strength, and longitudinal rebar strength have minor effects under different PGAs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Parghi, A.; Alam, M.S. Seismic collapse assessment of non-seismically designed circular RC bridge piers retrofitted with FRP composites. Compos. Struct. 2017, 160, 901–916. [Google Scholar] [CrossRef]
- Qi, Q.; Shao, C.; Cui, H.; Huang, H.; Wei, W.; Wang, C.; Zhuang, W. Shaking table tests and numerical studies on the seismic behaviors of FPB in railway continuous beam bridges. Eng. Struct. 2023, 290, 116318. [Google Scholar] [CrossRef]
- Zhang, Y.-y.; Harries, K.A.; Yuan, W.-c. Experimental and numerical investigation of the seismic performance of hollow rectangular bridge piers constructed with and without steel fiber reinforced concrete. Eng. Struct. 2013, 48, 255–265. [Google Scholar] [CrossRef]
- Tong, T.; Yuan, S.; Zhuo, W.; He, Z.; Liu, Z. Seismic retrofitting of rectangular bridge piers using ultra-high performance fiber reinforced concrete jackets. Compos. Struct. 2019, 228, 111367. [Google Scholar] [CrossRef]
- Billah, A.M.; Alam, M.S.; Bhuiyan, M.R. Fragility analysis of retrofitted multicolumn bridge bent subjected to near-fault and far-field ground motion. J. Bridg. Eng. 2013, 18, 992–1004. [Google Scholar] [CrossRef]
- Qi, Q.; Shao, C.; Wei, W.; Xiao, Z.; He, J. Seismic performance of railway rounded rectangular hollow tall piers using the shaking table test. Eng. Struct. 2020, 220, 110968. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, D.; Wang, T.; Wu, S.; Guo, X. Investigation on seismic behavior of bridge piers with thin-walled rectangular hollow section using quasi-static cyclic tests. Eng. Struct. 2019, 200, 109708. [Google Scholar] [CrossRef]
- Shao, C.; Qi, Q.; Wang, M.; Xiao, Z.; Wei, W.; Hu, C.; Xiao, L. Experimental study on the seismic performance of round-ended hollow piers. Eng. Struct. 2019, 195, 309–323. [Google Scholar] [CrossRef]
- Li, Z.-X.; Du, C.-y.; Liang, X.; Zhao, B. Flexural behavior of circular hollow RC piers with reduced amounts of inner hoops. Int. J. Concr. Struct. Mater. 2020, 14, 9. [Google Scholar] [CrossRef]
- Liang, X.; Du, C.; Zhao, B.; Li, Z. Seismic performance of circular hollow concrete columns. Struct. Concr. 2021, 22, 3140–3155. [Google Scholar] [CrossRef]
- Nie, L.; Jiang, L.; Zhou, W.; Wu, X.; Lai, Z.; Feng, Y. Seismic performance of railway rocking hollow tall piers under near-fault ground motions. Soil Dyn. Earthq. Eng. 2023, 166, 107774. [Google Scholar] [CrossRef]
- Xu, X.; Wen, X.; Han, Z.; Chen, G.; Li, C.; Zheng, W.; Zhnag, S.; Ren, Z.; Xu, C.; Tan, X. Lushan M S7. 0 earthquake: A blind reserve-fault event. Chi. Sci. Bull. 2013, 58, 3437–3443. [Google Scholar] [CrossRef]
- Parsons, T.; Ji, C.; Kirby, E. Stress changes from the 2008 Wenchuan earthquake and increased hazard in the Sichuan basin. Nature 2008, 454, 509–510. [Google Scholar] [CrossRef] [PubMed]
- Ni, S.; Wang, W.; Li, L. The April 14th, 2010 Yushu earthquake, a devastating earthquake with foreshocks. Sci. China Earth Sci. 2010, 53, 791. [Google Scholar] [CrossRef]
- Mander, J.; Priestley, M.; Park, R. Behaviour of ductile hollow reinforced concrete columns. Bull. N. Z. Soc. Earthq. Eng. 1983, 16, 273–290. [Google Scholar] [CrossRef]
- Yeh, Y.-K.; Mo, Y.; Yang, C. Full-scale tests on rectangular hollow bridge piers. Mater. Struct. 2002, 35, 117–125. [Google Scholar] [CrossRef]
- Yeh, Y.-K.; Mo, Y.; Yang, C. Seismic performance of rectangular hollow bridge columns. J. Struct. Eng. 2002, 128, 60–68. [Google Scholar] [CrossRef]
- Mo, Y.; Nien, I. Seismic performance of hollow high-strength concrete bridge columns. J. Bridg. Eng. 2002, 7, 338–349. [Google Scholar] [CrossRef]
- Pinto, A.; Molina, J.; Tsionis, G. Cyclic tests on large-scale models of existing bridge piers with rectangular hollow cross-section. Earthq. Eng. Struct. Dyn. 2003, 32, 1995–2012. [Google Scholar] [CrossRef]
- Calvi, G.M.; Pavese, A.; Rasulo, A.; Bolognini, D. Experimental and numerical studies on the seismic response of RC hollow bridge piers. Bull. Earthq. Eng. 2005, 3, 267–297. [Google Scholar] [CrossRef]
- Cassese, P.; Ricci, P.; Verderame, G.M. Experimental study on the seismic performance of existing reinforced concrete bridge piers with hollow rectangular section. Eng. Struct. 2017, 144, 88–106. [Google Scholar] [CrossRef]
- Han, Q.; Du, X.; Zhou, Y.; Lee, G.C. Experimental study of hollow rectangular bridge column performance under vertical and cyclically bilateral loads. Earthq. Eng. Eng. Vibr. 2013, 12, 433–445. [Google Scholar] [CrossRef]
- Zahn, F.; Park, R.; Priestley, M. Flexural strength and ductility of circular hollow reinforced concrete columns without confinement on inside face. Struct. J. 1990, 87, 156–166. [Google Scholar]
- Yeh, Y.-K.; Mo, Y.; Yang, C. Seismic performance of hollow circular bridge piers. Struct. J. 2001, 98, 862–871. [Google Scholar]
- Cassese, P.; De Risi, M.T.; Verderame, G.M. Seismic assessment of existing hollow circular reinforced concrete bridge piers. J. Earthq. Eng. 2020, 24, 1566–1601. [Google Scholar] [CrossRef]
- Zhou, J.; Li, J.; Shen, Y. Quasi-static testing of railway rounded rectangular hollow tall piers having semi-hinged column-base details. Eng. Struct. 2022, 250, 113403. [Google Scholar] [CrossRef]
- Chen, X.; Li, C. Seismic assessment of tall pier bridges with double-column bents retrofitted with buckling restrained braces subjected to near-fault motions. Eng. Struct. 2021, 226, 111390. [Google Scholar] [CrossRef]
- Lu, W.; Peng, W.-Q.; Zhu, L.; Gao, C.; Tang, Y.-D.; Zhou, Y.-W.; Su, W.; Zeng, B. Experimental and numerical study of static behavior of precast segmental hollow bridge piers. Materials 2022, 15, 6991. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Z.; Zhang, Y.; Pan, W.; Wang, J.; Shi, J. Seismic performance of the PVA fiber reinforced concrete prefabricated hollow circular piers with socket and slot connection. Buildings 2022, 12, 1339. [Google Scholar] [CrossRef]
- Cassese, P.; De Risi, M.T.; Verderame, G.M. A modelling approach for existing shear-critical RC bridge piers with hollow rectangular cross section under lateral loads. Bull. Earthq. Eng. 2019, 17, 237–270. [Google Scholar] [CrossRef]
- Yu, J.; Li, J.; Guo, W.; Fan, C.; Zeng, C.; Chen, X. Seismic evaluation method on shear strength models for round-end hollow piers of high-speed railway bridges. Structures 2023, 50, 23–38. [Google Scholar] [CrossRef]
- Qi, Q.; Shao, C.; Yang, H.; Cui, H.; Chen, Z.; Gong, W. Axial-flexure-shear model for seismic analysis of RC thin-walled hollow piers. Soil Dyn. Earthq. Eng. 2025, 195, 109375. [Google Scholar] [CrossRef]
- Qi, Q.; Jiang, L.; Shao, C.; Yang, H.; Shao, J.; Zhou, Y.; Cui, H. Hysteretic behavior modeling of RC walls considering axial-flexure-shear interaction. J. Build. Eng. 2025, 111, 113628. [Google Scholar] [CrossRef]
- Mo, Y.; Zhong, J.; Hsu, T.T. Seismic simulation of RC wall-type structures. Eng. Struct. 2008, 30, 3167–3175. [Google Scholar] [CrossRef]
- Polimeru, V.K.; Laskar, A. CSMM based seismic fragility analysis of shear dominant RC hollow rectangular bridge piers. Bull. Earthq. Eng. 2021, 19, 5051–5085. [Google Scholar] [CrossRef]
- Feng, D.-C.; Wu, G.; Sun, Z.-Y.; Xu, J.-G. A flexure-shear Timoshenko fiber beam element based on softened damage-plasticity model. Eng. Struct. 2017, 140, 483–497. [Google Scholar] [CrossRef]
- Berto, L.; Saetta, A.; Scotta, R.; Talledo, D. A coupled damage model for RC structures: Proposal for a frost deterioration model and enhancement of mixed tension domain. Constr. Build. Mater. 2014, 65, 310–320. [Google Scholar] [CrossRef]
- Lu, X.; Xie, L.; Guan, H.; Huang, Y.; Lu, X. A shear wall element for nonlinear seismic analysis of super-tall buildings using OpenSees. Finite Elem. Anal. Des. 2015, 98, 14–25. [Google Scholar] [CrossRef]
- Kolozvari, K.; Orakcal, K.; Wallace, J.W. New opensees models for simulating nonlinear flexural and coupled shear-flexural behavior of RC walls and columns. Comput. Struct. 2018, 196, 246–262. [Google Scholar] [CrossRef]
- Lu, Y.; Panagiotou, M.; Koutromanos, I. Three-dimensional beam-truss model for reinforced concrete walls and slabs–part 1: Modeling approach, validation, and parametric study for individual reinforced concrete walls. Earthq. Eng. Struct. Dyn. 2016, 45, 1495–1513. [Google Scholar] [CrossRef]
- Ceresa, P.; Petrini, L.; Pinho, R.; Sousa, R. A fibre flexure–shear model for seismic analysis of RC-framed structures. Earthq. Eng. Struct. Dyn. 2009, 38, 565–586. [Google Scholar] [CrossRef]



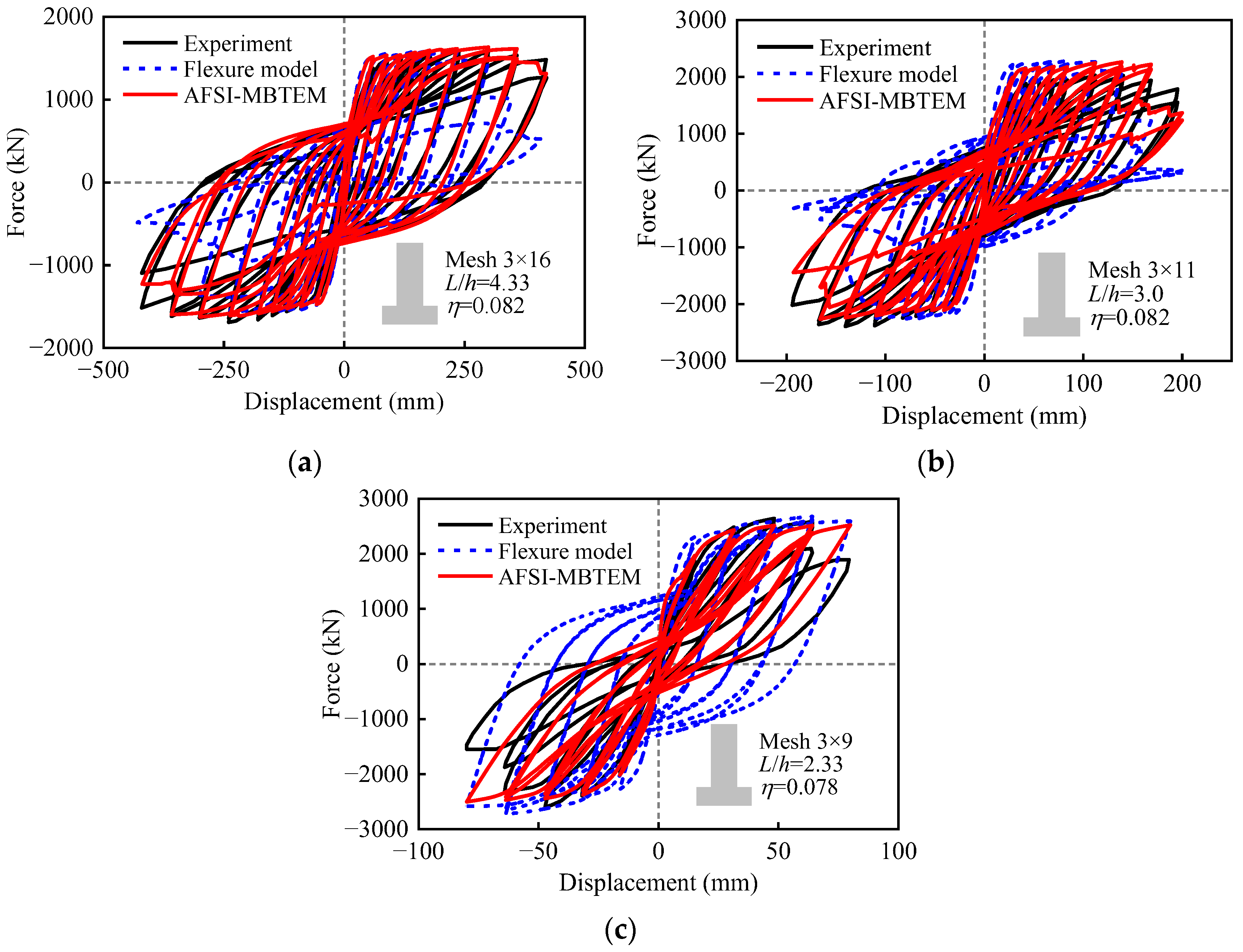











| No. | Specimen | Failure Mode | Height | Depth | L/h | fc | Longitudinal Rebar | Stirrup | η | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| L (mm) | h (mm) | (MPa) | Layout | ρ1 (%) | fyl (MPa) | s (mm) | ρw (%) | fyw (MPa) | |||||
| 1 | PS1 | F | 6500 | 1500 | 4.33 | 34.0 | 64ϕ22 | 1.72 | 460 | 80 | 1.10 | 343 | 0.082 |
| 2 | PI1 | F | 4500 | 1500 | 3.0 | 34.0 | 64ϕ22 | 1.72 | 460 | 120 | 0.43 | 510 | 0.082 |
| 3 | PI2 | S | 3500 | 1500 | 2.22 | 34.0 | 64ϕ22 | 1.72 | 418 | 200 | 0.26 | 420 | 0.078 |
| Design Parameter | Value | Note |
|---|---|---|
| Aspect ratio | 3, 4, 5, 6, 7, 8 | Geometry |
| Width-to-depth ratio | 0.5, 1.0, 1.5, 2.0, 2.5 | |
| Wall thickness ratio (%) | 10, 20, 30, 40, 50 | |
| Axial load ratio | 0, 0.05, 0.1, 0.15, 0.2 | Gravity |
| Longitudinal rebar ratio (%) | 0.7, 1.2, 1.7, 2.2, 2.7 | Reinforcement |
| Stirrup ratio (%) | 0.6, 0.8, 1.0, 1.2, 1.4 | |
| Concrete strength (MPa) | C30, C40, C50, C60 | Strength |
| Longitudinal rebar strength (Mpa) | 300, 400, 500, 600 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Z.; Qi, Q.; Duan, L.; Yang, H.; Shao, C.; Li, J.; Cui, H. Parametric Analysis of Reinforced Concrete Hollow Piers Based on an Axial–Flexure–Shear Model Under Cyclic Loading and Earthquake Conditions. Symmetry 2025, 17, 1553. https://doi.org/10.3390/sym17091553
Pan Z, Qi Q, Duan L, Yang H, Shao C, Li J, Cui H. Parametric Analysis of Reinforced Concrete Hollow Piers Based on an Axial–Flexure–Shear Model Under Cyclic Loading and Earthquake Conditions. Symmetry. 2025; 17(9):1553. https://doi.org/10.3390/sym17091553
Chicago/Turabian StylePan, Ziang, Qiming Qi, Linxi Duan, Huaping Yang, Changjiang Shao, Jingru Li, and Haomeng Cui. 2025. "Parametric Analysis of Reinforced Concrete Hollow Piers Based on an Axial–Flexure–Shear Model Under Cyclic Loading and Earthquake Conditions" Symmetry 17, no. 9: 1553. https://doi.org/10.3390/sym17091553
APA StylePan, Z., Qi, Q., Duan, L., Yang, H., Shao, C., Li, J., & Cui, H. (2025). Parametric Analysis of Reinforced Concrete Hollow Piers Based on an Axial–Flexure–Shear Model Under Cyclic Loading and Earthquake Conditions. Symmetry, 17(9), 1553. https://doi.org/10.3390/sym17091553





